こんにちは！この記事をかいているKenだよ。登山で日焼けしたね。
三角柱の体積の求め方には公式があるんだ。
三角形の底辺の長さをa、底辺からの高さをb、立体の高さがhっていう三角柱を想像してみて。
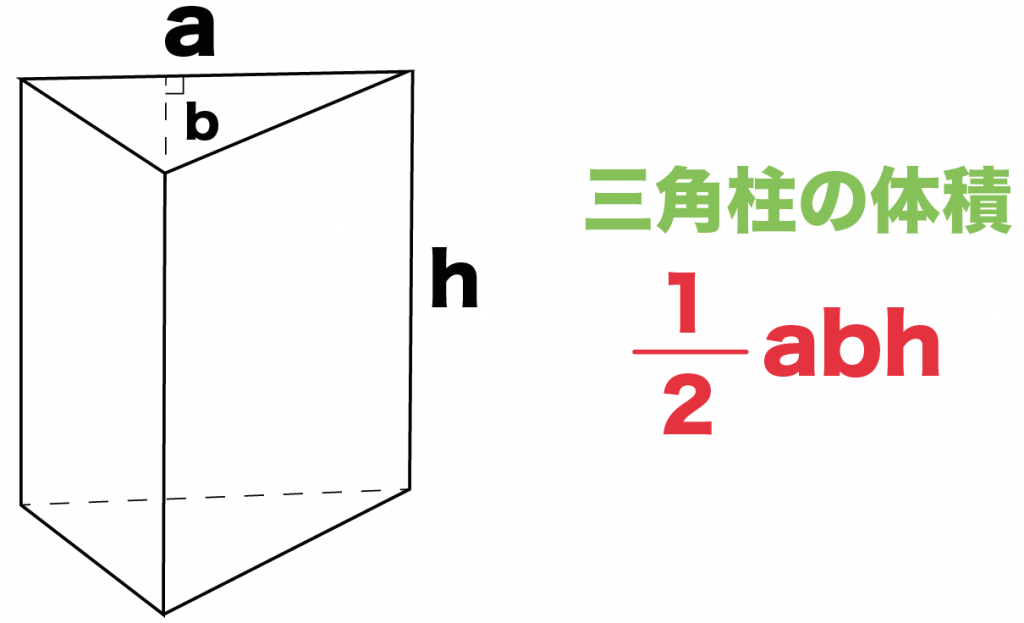
このとき、
三角柱の体積は、
1/2 abh
で求めることができるんだ。
つまり、
1/2 ×（底面の底辺）×（底辺からの高さ）×（三角柱の高さ）
ってことになるね。
この公式では何も特別なことをやってるわけじゃない。
ただ、
底面積×高さ
という「角柱の体積の公式」を使っているだけなんだ。
今日はこの公式をわかりやすく解説していくよ。
よかったら参考にしてみてね！
三角柱の体積は2ステップで計算できちゃうんだ。
つぎの例題をときながら求め方を確認していこう。
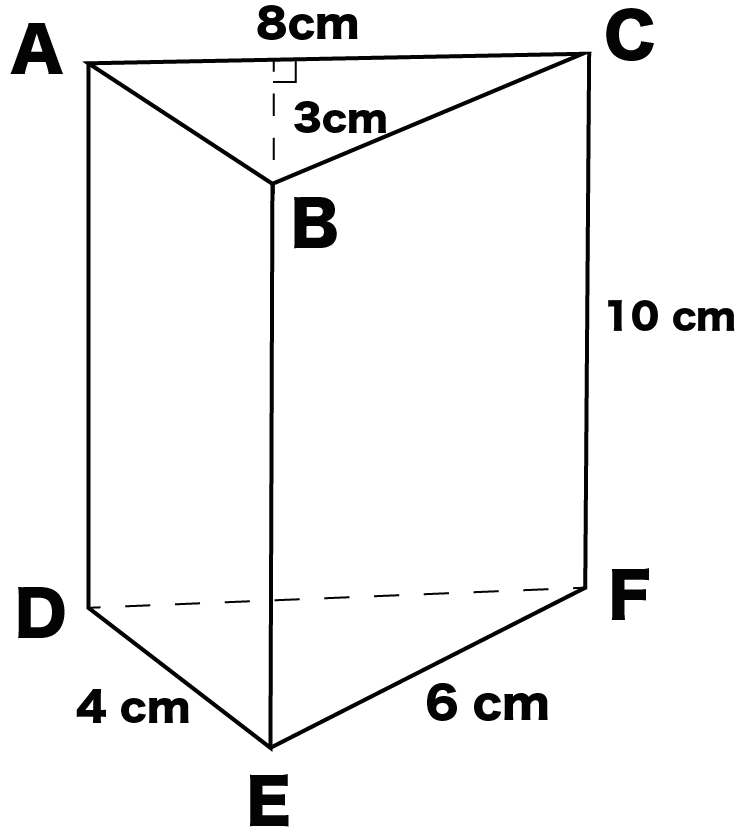
まずは三角柱の底面積を求めてみよう。
三角柱の底面は「三角形」であるはずだから、
底辺 × 高さ× 1/2
で面積をゲットできるよね？？
例題でいうと、
底辺の長さが「8 cm」、高さが「3 cm」だから、
8×3 × 1/2
= 12 [cm^2]
になるね！
さっき計算した「底面積」に「三角柱の高さ」をかけてみよう！
なぜなら、
底面積×高さ
を計算すると立体の体積を求めることができるからね。
例題でいうと、
Step1で計算した底面積は10[cm^2]、三角柱の高さは10[cm]だから、
三角柱ABCDEFの体積は、
12×10
= 120[cm^3]
になるんだ。
これで三角柱の体積を求めることができたね！
三角柱の体積の求め方はどうだった？？
三角柱の体積の求め方はとってもシンプル。
「底面積×高さ」という計算をしてやるだけだよ。
ゆっくりと慎重に計算すれば大丈夫だから、どんどん三角柱の体積を計算していこう。
そんじゃねー
Ken
こんにちは、この記事をかいているKenだよ。ティッシュは便利だね。
直方体の表面積の求め方にも公式があるよ。
タテの長さをa、ヨコの長さをb、高さをcとすると、
2(ab+bc+ac)
で直方体の表面積が計算できちゃうんだ。
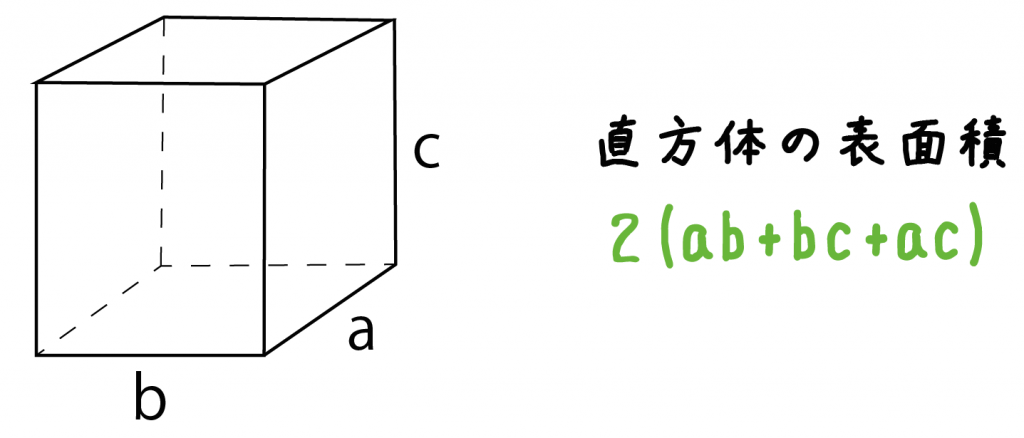
つまり、
「タテ」と「ヨコ」と「高さ」をそれぞれかけたものを足して、それを2倍すればいいってこと！
どう？？ むちゃくちゃ便利じゃない？？
だがしかし。
直方体の表面積の公式をテストで忘れちゃうこともある。
今日はそんなときに備えて、
公式に頼らない「直方体の表面積の求め方」を3つのステップで解説していくよ。
テスト前に確認してみてね。
つぎの例題ときながらみていこう。
例題
タテ 4cm、ヨコ 3cm、高さ5cmの直方体の表面積を計算してみな！
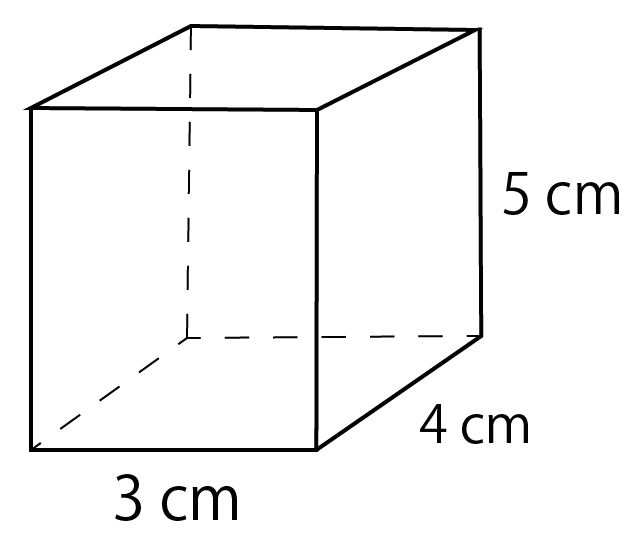
直方体の表面積は3つの長方形でなりたっているんだ。
まずはそいつらの面積を計算してくよ。
えっ。なぜ3種類なのかって？？
それは、直方体の展開図をかいてみるとわかるんだ。
展開図をよーくみてみると、
(1)、(2)、(3)の3種類の長方形しかないことがわかる。
まずはこいつらの面積を計算してあげよう。
長方形の面積の求め方は「タテ×ヨコ」だから、
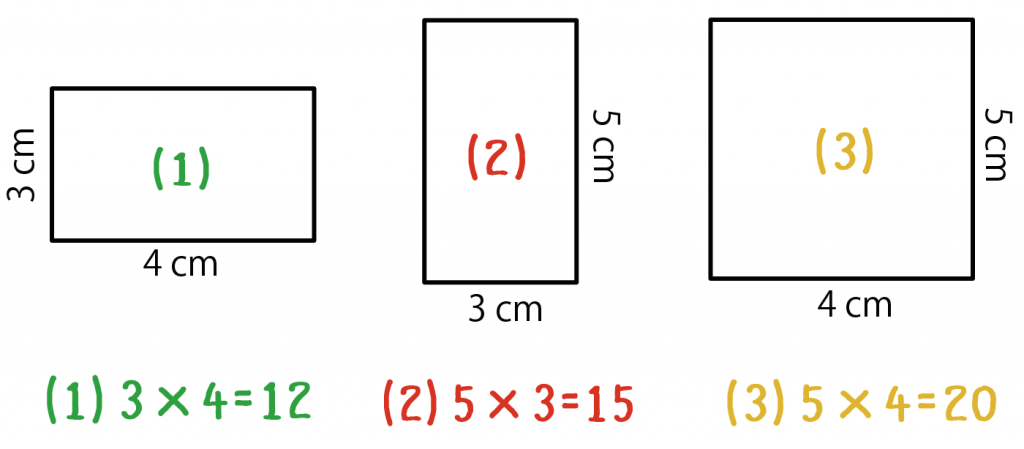
になるね！
3つの長方形の面積を足し合わせてみよう！
12 + 15 + 20
= 47
って感じで！
最後は3つの長方形の合計を2倍するよ。
なぜ2倍するのか？？
それは、
直方体の展開図には3種類の長方形が2つずつあるから
なんだ。
例題でいうと、3つの長方形の面積の合計は「47平方センチメートル」だったね？？
こいつを2倍してやると、
94平方センチメートル
になる。
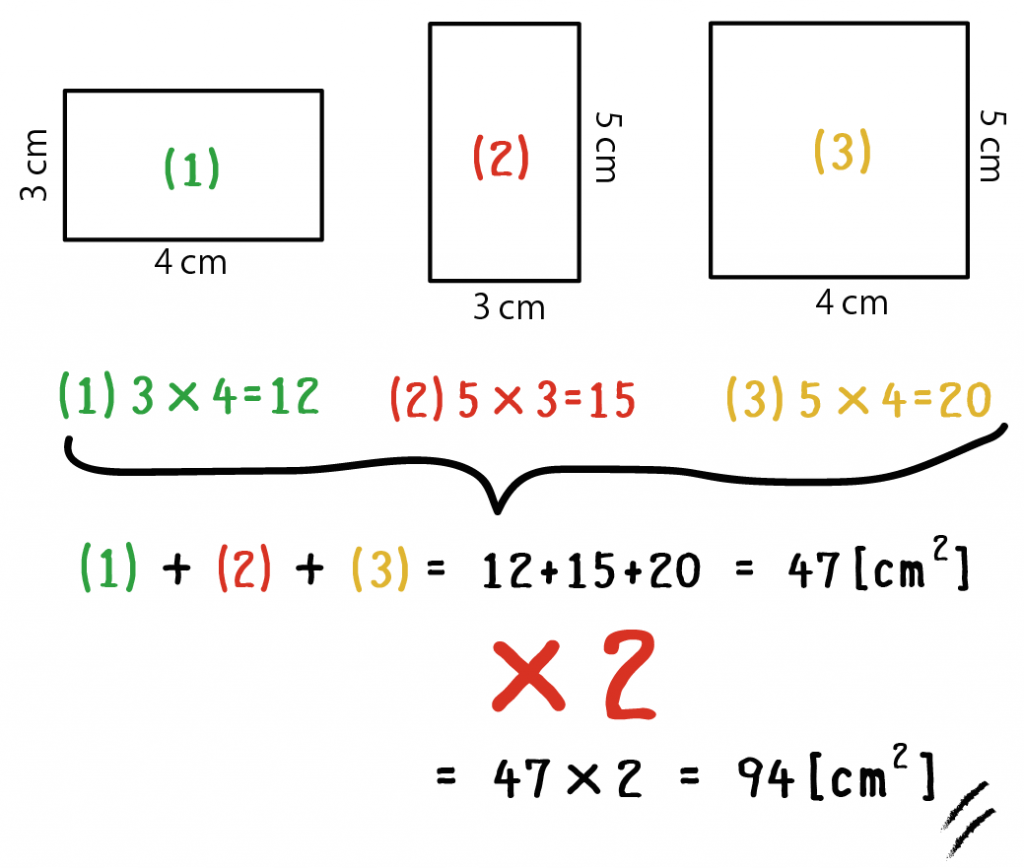
これで直方体の表面積を計算できたね！おめでとう。
直方体の表面積の公式はどうだった？？
3種類の長方形の面積を足して、それを2倍するだけ！
直方体の表面積の問題がでたらバンバン解いていこう。
そんじゃねー
Ken
こんにちは、この記事をかいているKenだよ。犬の散歩が趣味だね。
円錐の体積の求め方の公式は、
底面積×高さ×1/3
だったよね。
もう少し詳しくかいてあげると、
半径×半径×円周率×円錐の高さ×1/3
になるんだ。
これなら3秒で円錐の体積を計算できちゃいそうだね。
ただ、そのスピード感について来れないときもあるだろうから、今日は、円錐の体積の求め方をチョーゆっくり公式をつかってといてみるよ。
「円錐の体積の求め方がどうしてもわからん！」
ってなったときに参考にしてみてね！
円錐の体積の求め方はつぎの3ステップをで計算できちゃうよ。
つぎの例題をときながらみていこう！
半径3cm、高さ10cmの円錐の体積を計算して。
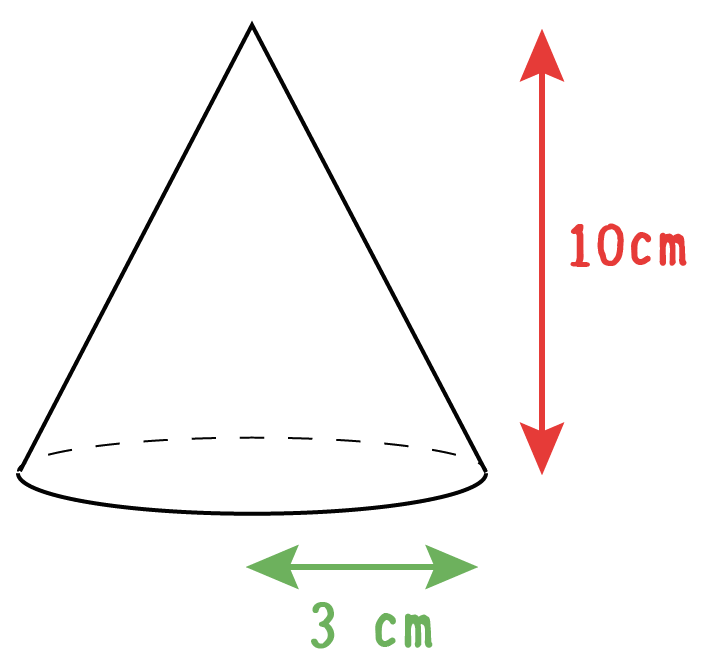
まずは円錐の底面積を計算してみよう。
円錐の底面は「円」になっているね。
ってことは、円の面積の公式をつかって、ちゃちゃっと面積をだしてやればいいんだ。
円の面積の求め方は、
半径×半径×円周率
で求められるよね？？
だから例題の円錐の底面積は、
3×3×π= 9π
となるんだ。
つぎは「円錐の高さ」を底面積にかけてみよう。
例題の円錐の高さは10cmなので、
9π×10= 90π
になるっ！
いよいよ最後のステップ。
Step2で求めた「底面積×高さ」の値に「1/3」をかけてみよう。
例題でいうと、「底面積×高さ」は「90π」だったから、
最終的な円錐の体積は、
90π×1/3=30π
になる！
おめでとう。これで円錐の体積を計算できるようになったね。
えっ。なんで「1/3」をかける必要があるのだって？！？
その理由は高校数学で勉強する「積分」を使えば説明できるんだけど、完全に中学数学の範囲をこえているんだ。
とりあえず、中学数学では、
錐体（先がとんがってるやつ）の体積を求めるときは「1/3」をかける
ということを覚えておこう。
だから、三角錐の体積を求めるときも「1/3」をかけるんだ。
円錐の体積の求め方はどうだったかな？？
底面積×高さ×1/3
という公式は意外とシンプルだったよね。
最後に1/3をかけることさえ忘れなければ、ぜったいにテストでも間違えないはず。
分数がややこしかったら、「÷3」をするって覚えてもいいね。
この公式をつかってじゃんじゃん円錐の体積を計算していこう！
円錐の体積の求め方をマスターしたら、次は「円錐の表面積の求め方」を勉強してみよう。
そんじゃねー
Ken
こんにちは、この記事をかいているKenだよ。梨ジュースはウマいね。
円錐の表面積の求め方の公式って知ってる？？
円錐の半径をr、母線の長さをLとすると、円錐の表面積はつぎのように計算できちゃうんだ。
πr（L＋r）
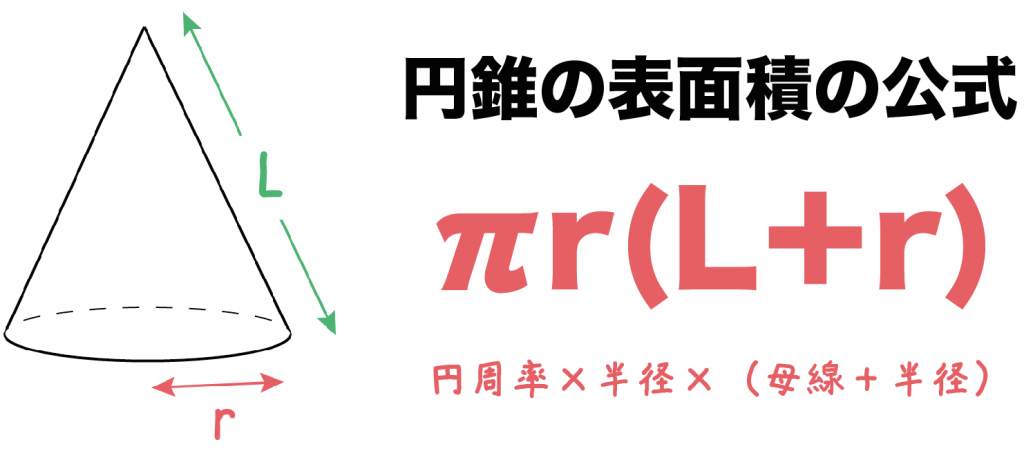
つまり、
（円周率）×（半径）×（母線＋半径）
ってことだね。
見ての通り、ちょー便利な計算公式なんだけど、
忘れたらヤバい
っていうリスクがあるんだ。
だから、公式に頼らない円錐の表面積の求め方をおぼえておくと便利だよ。
円錐の表面積は3ステップで計算できちゃう。
つぎの例題をときながらみてみよう。
半径3cm、母線の長さが10cmの円錐の表面積を10秒以内に計算して。
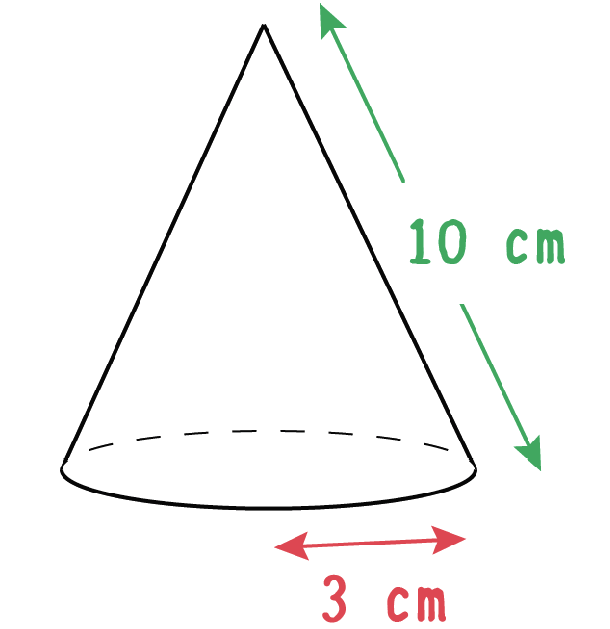
まずは底面の「円周の長さ」を計算しちゃおう。
円周の長さの求め方って、
直径×円周率
だったよね？？
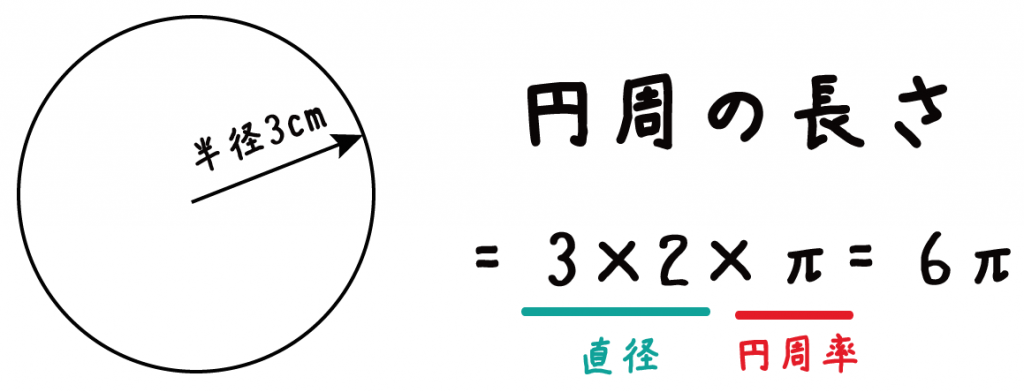
例題でいうと、半径が3cmの円が底面になっているから、
3×2×π = 6π
が円周の長さになるね。
円錐の「側面の中心角」をもとめてあげよう。
Step1で計算した
「底面の円周長さ」
と
「側面の扇形の弧の長さ」
が等しい
っていうことを方程式にしてあげると求められるんだ。
例題でいうと、
10×2×π×α/360 = 6π
っていう方程式になるね。
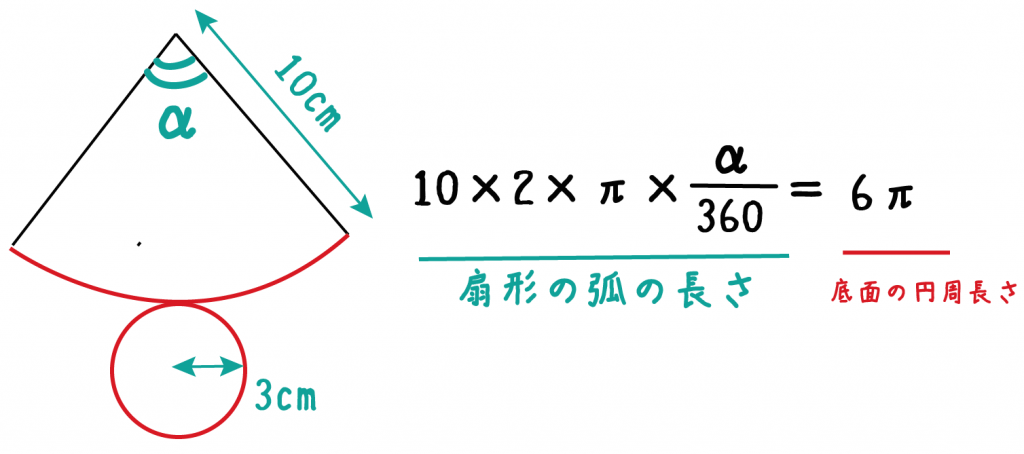この方程式をαについて解いてあげると、
α = 108°
という中心角がゲットできるね。
円錐の展開図って、
「側面」と「底面」の2つから成り立ってるよね↓↓
だから、円錐の表面積を計算するときは、
側面積＋底面積
をもとめてやればいいんだ。
例題でいうと、
10×10×π×108/360＋3×3×π
= 39π
になるよ！
この合計値が円錐の表面積ってことになるよ！
おめでとう！！
「円錐の表面積」は公式なら一発で計算できちゃう。
だけれども、
テストで忘れたらチョーヤバい。
だから、公式に頼らない求め方を知っておくと心強いよ。
ってことで、もう一度最後に復習しておこう。
（円周率）×（半径）×（母線＋半径）
円錐の表面積をマスターしたら次は円錐の体積を求めてみよう！
そんじゃねー
Ken
こんにちは、この記事をかいているKenだよ。アップルティーにはまってるね。
円柱の体積の求め方はむちゃくちゃ簡単。
底面積×高さ
っていう公式をつかえば、一発で体積を求めることができるんだ。
そんで、
底面積は、
半径×半径×円周率
だから、円周の体積はつぎの計算式で求められるよ。
半径×半径×円周率×高さ
この公式をつかって円柱の体積を求めていこう！
次の2つのステップで「円柱の体積」を求めることができるんだ。
つぎの例題をみていこう。
底面の半径が5[cm]、高さが10[cm]の円柱の体積を3秒ぐらいでもとめてね！
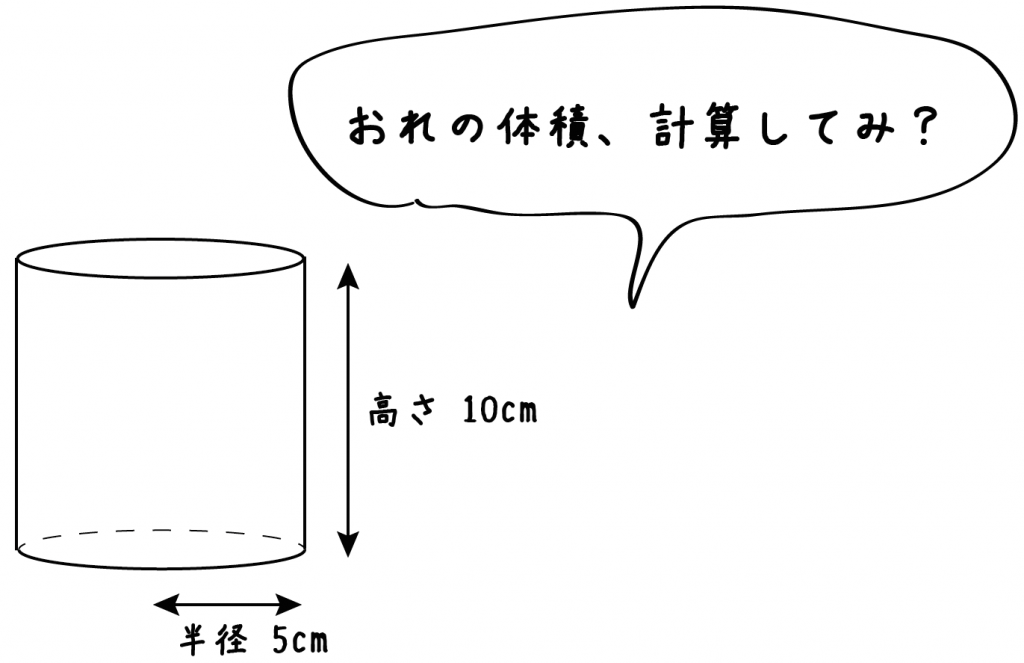
円柱の底面積を計算しちゃおう！
円柱の底面はもちろん「円」。
円の面積の求め方って「半径×半径×円周率」だったよね？？
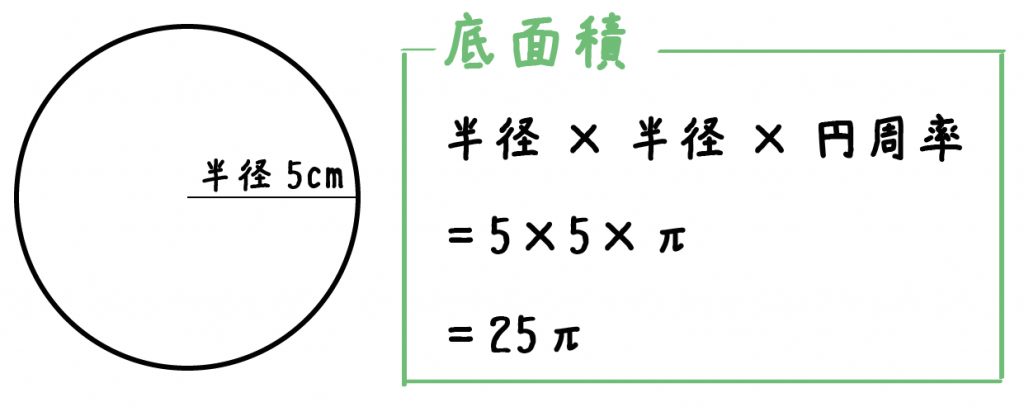
だから、例題の円柱の底面積は、
5×5×π = 25π [cm² ]
になる！！
さっき計算した円柱の「底面積」と「高さ」をかけてみよう！
それが円柱の体積になるはずだ。
例題をみてみよう。
円柱の底面積は25π[cm² ]だったよね？？
あとはコイツを「円柱の高さ」にかけてやればいいんだ。
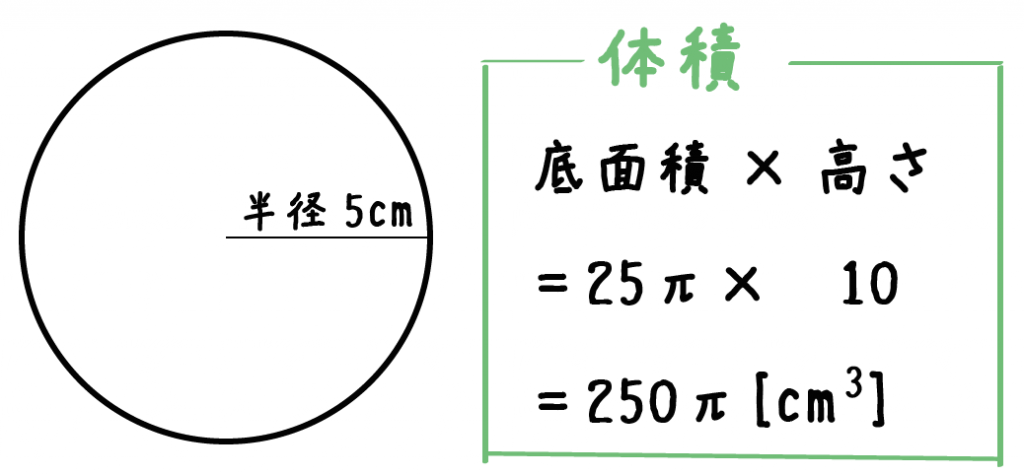
円柱の高さは10[cm]だから、
25π×10 = 250π [cm³]
になる！
これで円柱の体積の求め方はおわりだよー！！
円柱の体積の求め方はどうだったかな？？
半径×半径×円周率×高さ
で円柱の体積は計算できたね。
円柱の体積を計算できるようになったらついでに円柱の表面積の求め方にもチャレンジしてみよう！
そんじゃねー！
Ken
こんにちは、この記事をかいているKenだよ。やっぱ土日はすばらしいね。
円柱の表面積を3秒ぐらいで計算したい。
そんなときは、
円柱の表面積の求め方の公式をつかってしまえば2秒ぐらいで計算できちゃうんだ。
下の図のように、円柱底面の半径をr、高さをhとすると、
2πr(h+r)
で求めることができるよ。
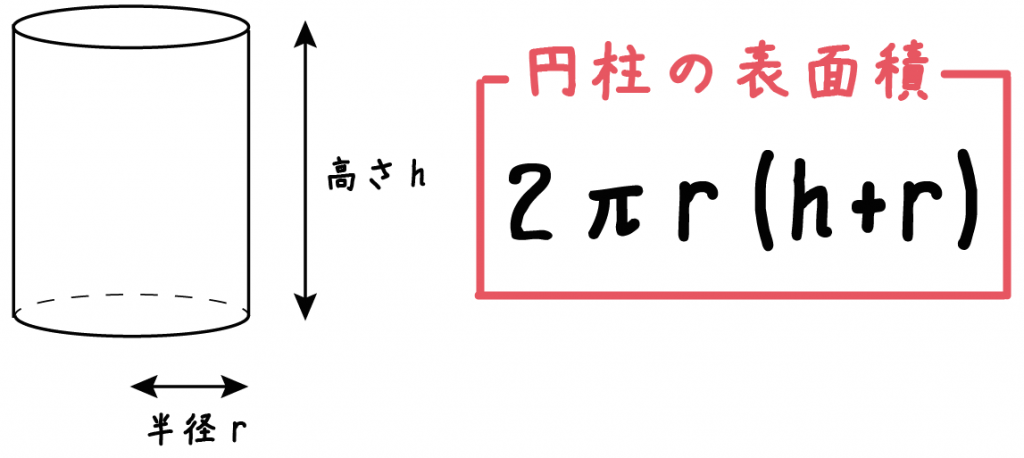
つまり、
2×円周率×半径×（高さ+半径）
ってわけだね。
公式はむちゃくちゃ便利だけど、テストで忘れちゃうかもしれないよね？？
そういうときのために今日は、
円柱の表面積の求め方を3ステップで解説していくよ。
例題をときながら円柱の表面積の求め方を勉強していこう。
例題
半径3cm、高さ10cmの円柱の表面積を求めなさい。
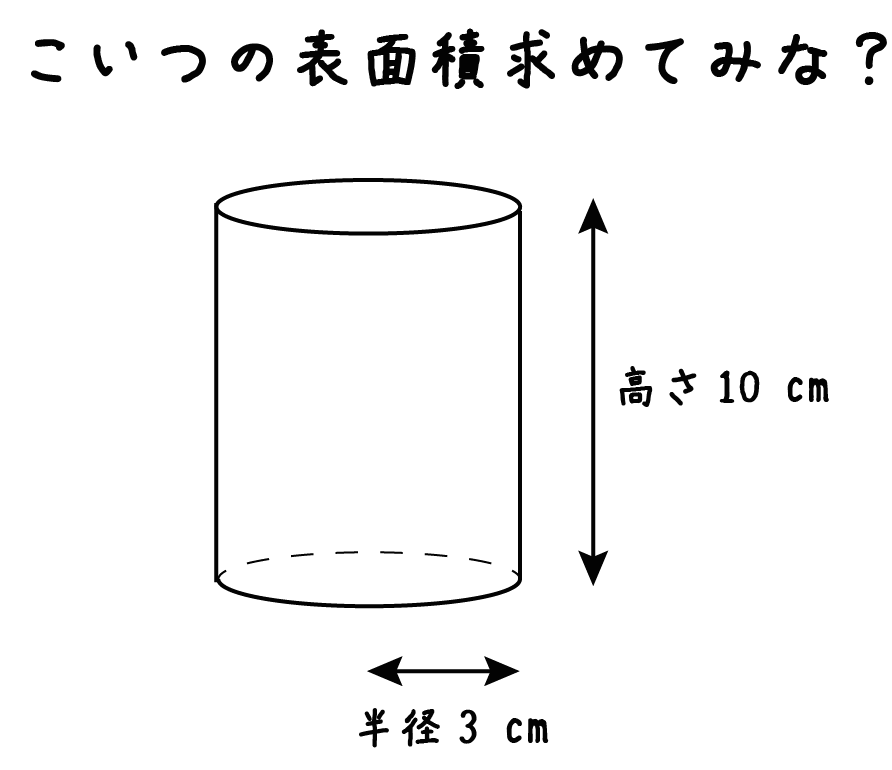
つぎの3ステップで求めることができるんだ。
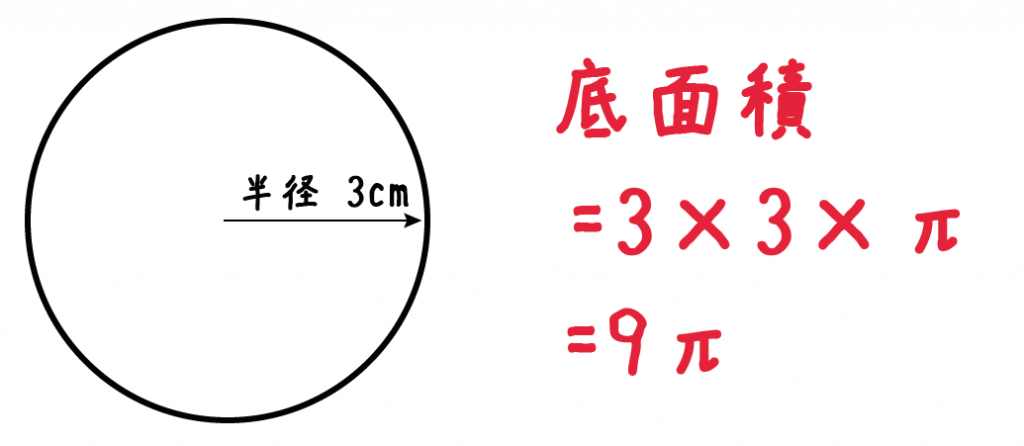
円柱の底面積をもとめてみよう。
円柱の底面は「円」。
よって、底面積の求め方は、
半径×半径×円周率
になるよね！？？
ってことで、例題の円柱の表面積は、
3×3×π = 9π
になるね！
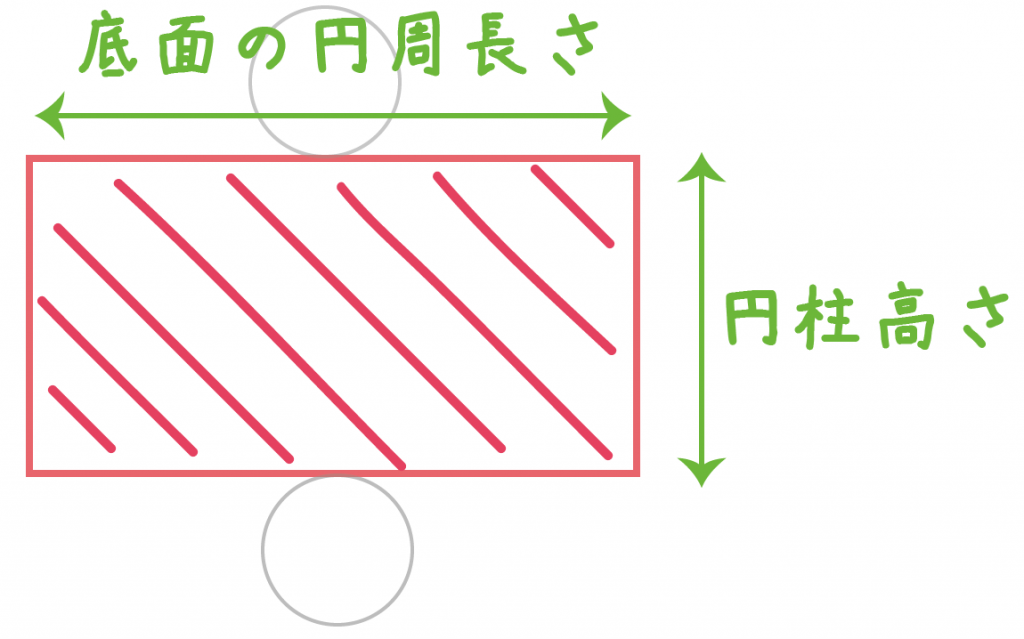
つぎは円柱の側面積を計算しちゃおう！
円柱の側面積は、
（底面の円周長さ）×（円柱高さ）
で求められるだったよね？？
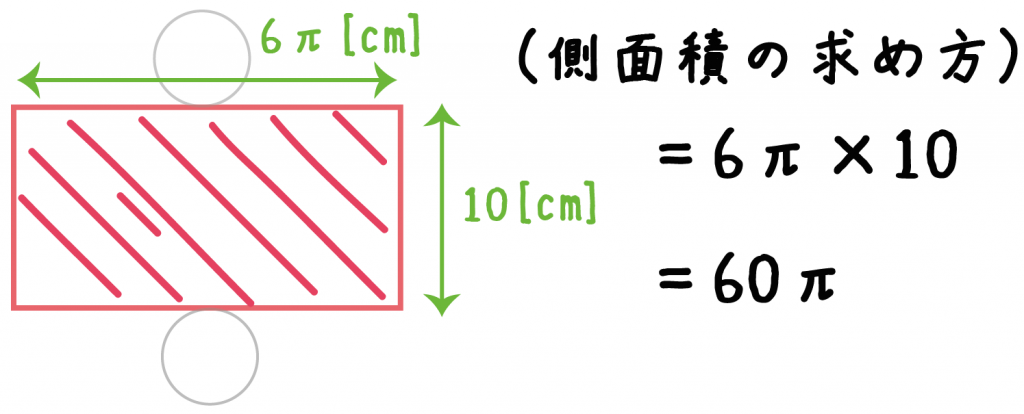
底面の円周長さは6πになるよね。ってことは、例題の円柱の側面積は、
6π×10= 60π
になる。
円柱の展開図をイメージしてみると、
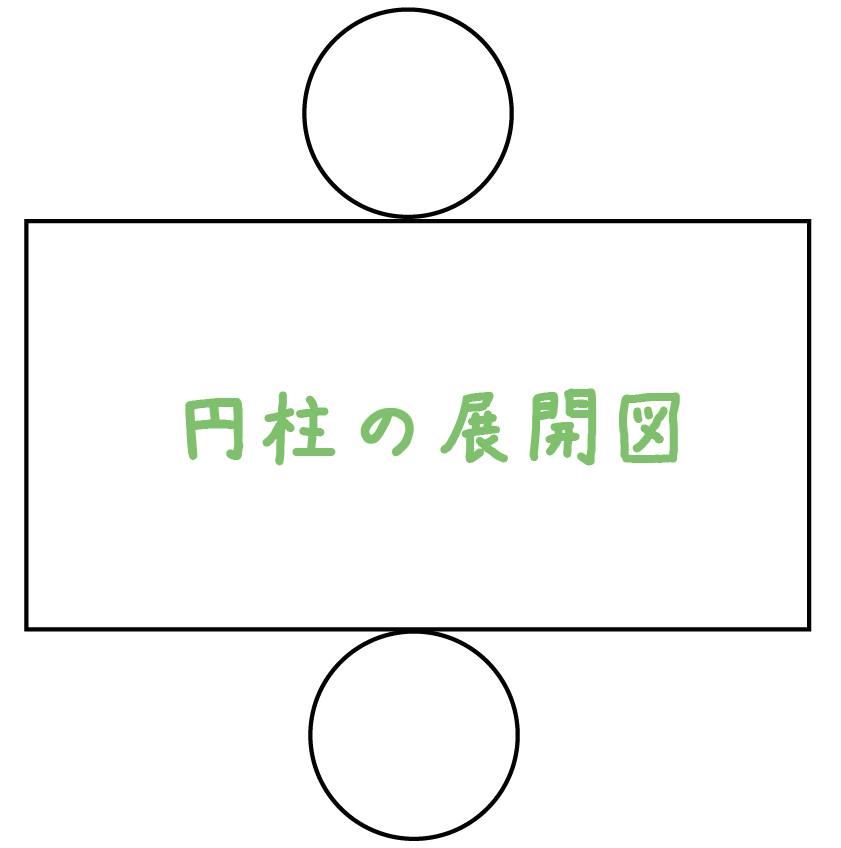
「底面が2つ」＋「側面が1つ」
になっていることがわかるよね？？ だから、円柱の表面積は、
（底面積）×2 + 側面積
で求められるってこと！
さっそく、例題の表面積を求めてみよう。
底面が2つ、側面が1つだから、
9π×2 + 60π
= 78π
になるね！
おめでとう！円柱の表面積の問題を瞬殺できるようになったね！！
円柱の表面積は公式を使えば2秒で計算できる。
だけれども、公式に頼らなくたって、5分ぐらいで計算できちゃうよね。
ってことで、公式に頼らない求め方もおぼえておこう！
そんじゃねー
Ken
こんにちは、この記事を書いているKenだよ。朝シャンは神だね。
空間図形で「投影図」っていうのを勉強していくよ。
ただ、投影図なんて聞いたことないし、似たような「平面図」とか「立面図」なんてものまである。
ややこしすぎるよね？？。;;
そこで今日は、
投影図・立面図・平面図の意味
をわかりやすく解説していくね。よかったら参考にしてみて。
投影図・立面図・平面図っていう数学用語を解説していこう！
さて。
むかーしむかし、2枚の平面PとQが垂直に交わっていたんだ。直線XYを境にね。
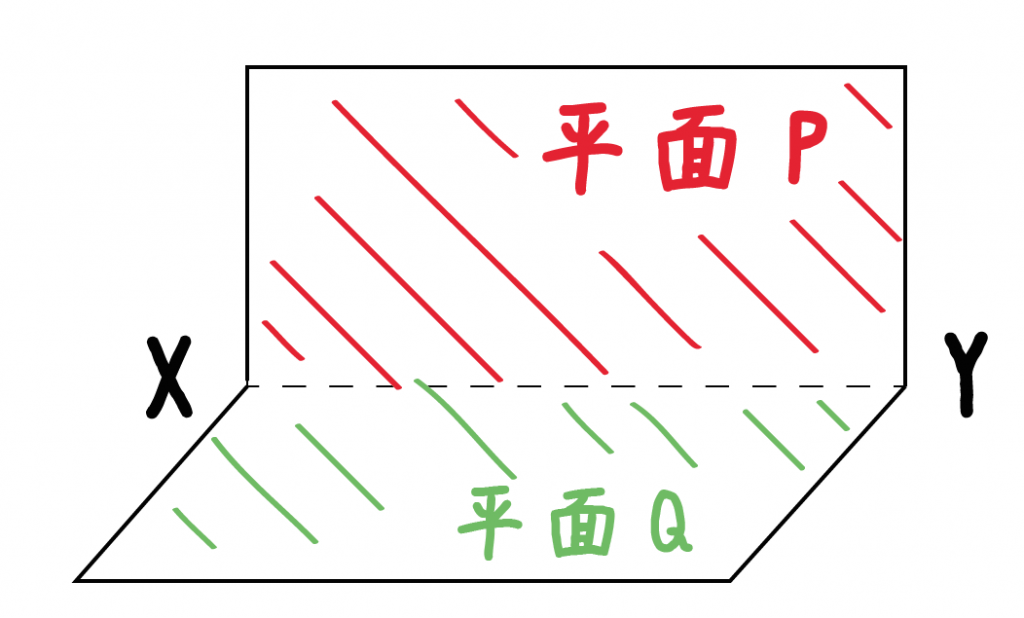
ちょっとわかりづらいときは、そこらへんで売っているブックスタンドを思い浮かべてくれ。
そんで、
この平面図PとQのあいだに「ある立体」が浮かんでいるんだ。平面PにもQにもギリギリ触れないぐらいの高さでね。
エスパー系の超能力をつかっていると考えてもらってもいい。
たとえば三角柱が浮かんでいるとしよう。ギリギリ平面PにもQにも触れない高さで宙に浮いているんだ。
このとき、三角柱を正面からみた図を「立面図」といい、
立面図
真上から立体をみた図を「平面図」というんだ。
平面図
この三角柱の場合、「立面図」と「平面図」をかくと次のようになるよ。
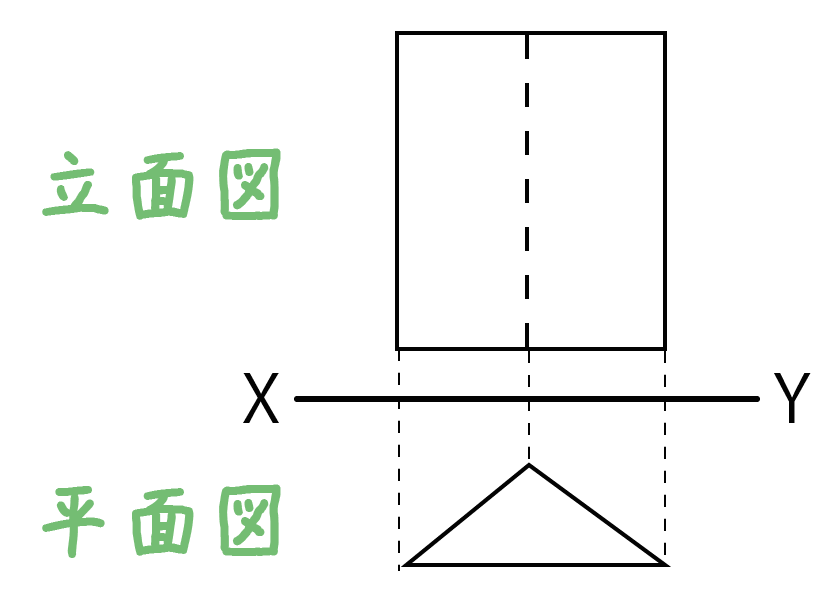
直線XYの上に「立面図」、下に「平面図」をかけばいいってことだね。
それで、
「立面図」と「平面図」を2つセットで「投影図」って呼んでいるんだ。
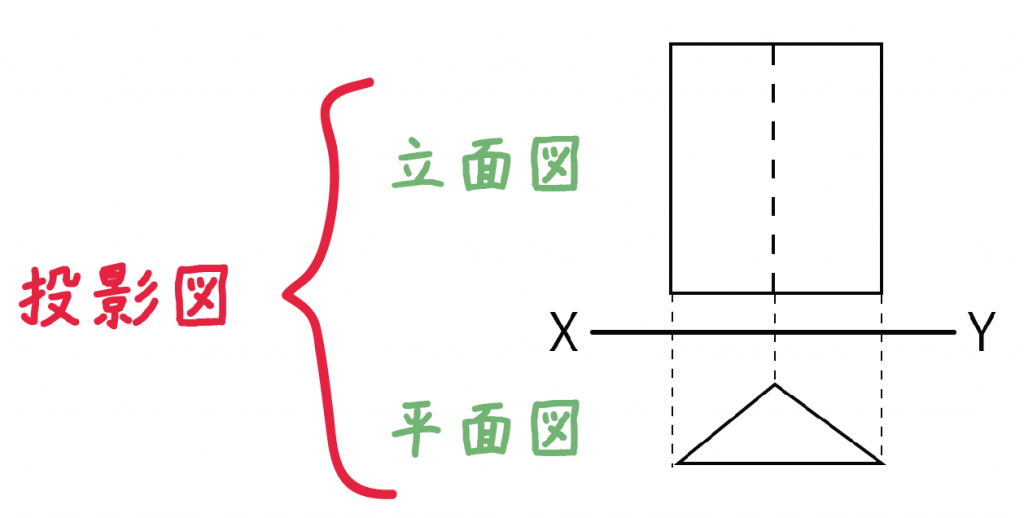
「ムサシ」と「コジロウ」を2人あわせたら「ロケット団」になるの同じさ。
立体を正面から見るとどうのか？？
また、真上からだったらどうなのか？？っていうことをイメージして、投影図をかいてみてね。
「立面図・平面図・投影図」の意味をここまで説明してきた。
ここでキミが思っていることって、たぶん、
立面図・平面図（投影図）は何のためにあるのか？？
ということじゃない？。
だって、投影図なんてなくても生きていけるし、見ていて楽しいものでもないからね。
じつは、立面図・平面図（投影図）って「ある立体の説明書」みたいなものなんだ。「投影図」っていう説明書があれば、
会ったことがない立体を想像できるんだ。
投影図は世界共通語みたいなものかもしれない。
これがあれば、中国人やアメリカン人にだって「自分がみている立体がどんな形をしているのか？？」を伝えられるんだ。
ね？？ちょっと便利でしょ。
ここまでみてきた投影図の意味はどうだったかな？？
中学数学では、
の2つを勉強していくよ。
「立面図・平面図（投影図）の書き方」を知っていて、なおかつ、投影図から立体を読み取ればいいということだね。
イメージ力を膨らませながらガンガン投影図について勉強していこう。
そんじゃねー
Ken
こんにちは、この記事をかいているKenだよ。肌の手入れは大事だね。
母線の意味ってなんだっけ？？
母線はキミの母ちゃんとはまったく別の話。立体図形の勉強ででてくる1つの数学用語なんだ。
今日はテストで狙われやすい、
円錐の母線の長さの求め方を3つ紹介するね。よかったら参考にしてみてね。
~もくじ~
まず「母線の意味」をおさらいしてみよう。
母線とは、
動くと、立体がかける線分のこと
だ。たとえば、むかーしむかし、線分ABというヤツがいたとしよう。
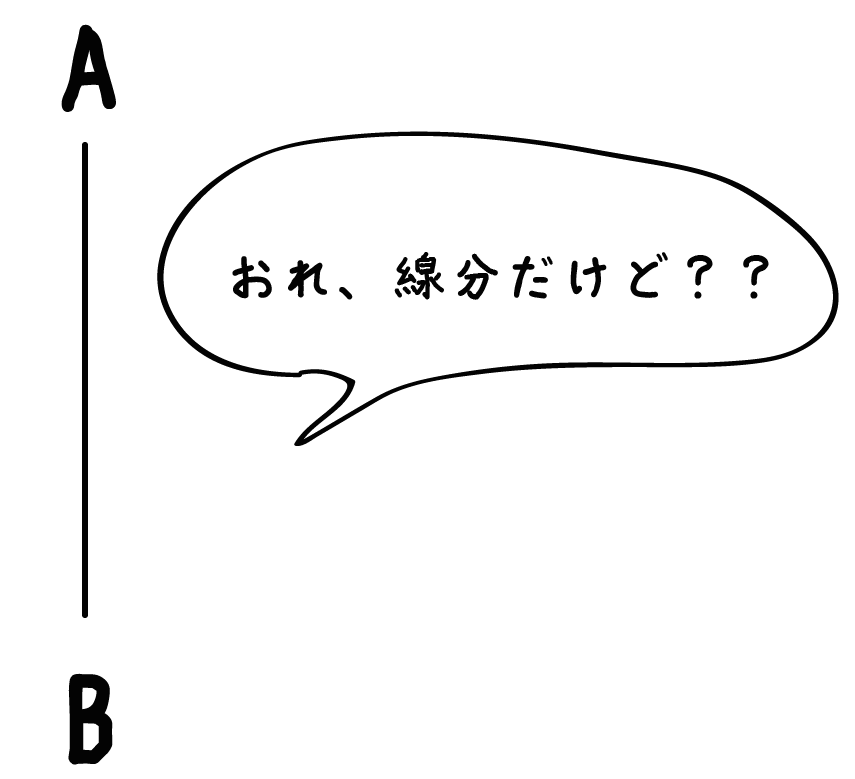
こいつを放っておいたらただの線分でしかないよね。だけど、コイツを円周上に回転させて移動させると、
円柱ができちゃうんだ！！
線分ABは円柱を産んだわけだ。つまり、円柱の母ちゃんになった線分とも呼べるね。
だから、こいつは母線とよばれているよ。
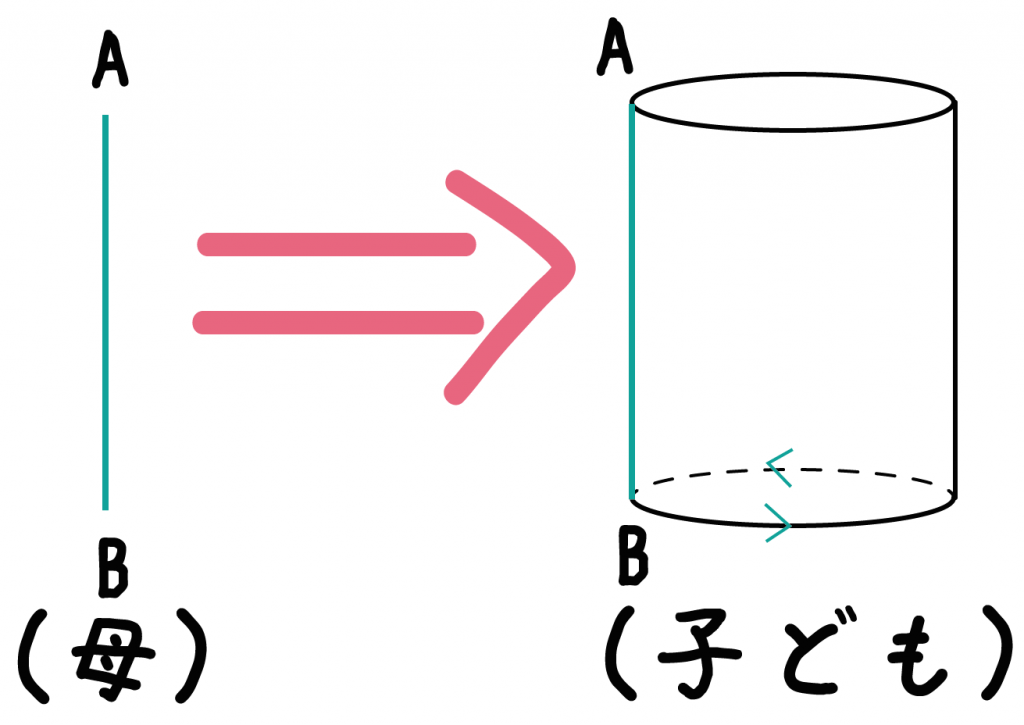
円錐の場合、線分ABのAを固定して、Bを円に沿って移動させればいいんだ。
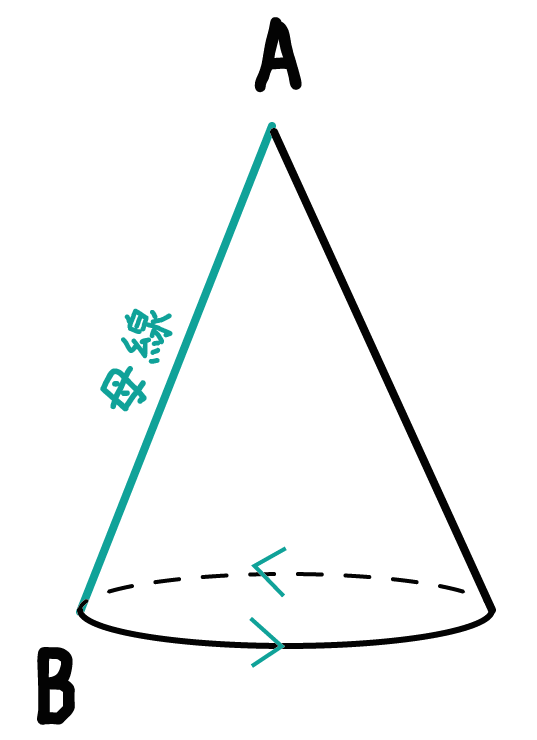
だから、円錐の母線はつぎの線分ABになるってことだね。
そんで、
「円錐の母線の長さ」を求める問題はだいたい2つのパターンにわかれるよ。
せっかくだから、2つの「母線の求め方」をみていこう。
「円錐の半径」と「側面の中心角」がわかっているときの「母線の求め方」をみていこう。
つぎの例題をときながら解説していくよ。
半径が5cm、側面の中心角が150°の円錐の母線の長さを求めてくれ！
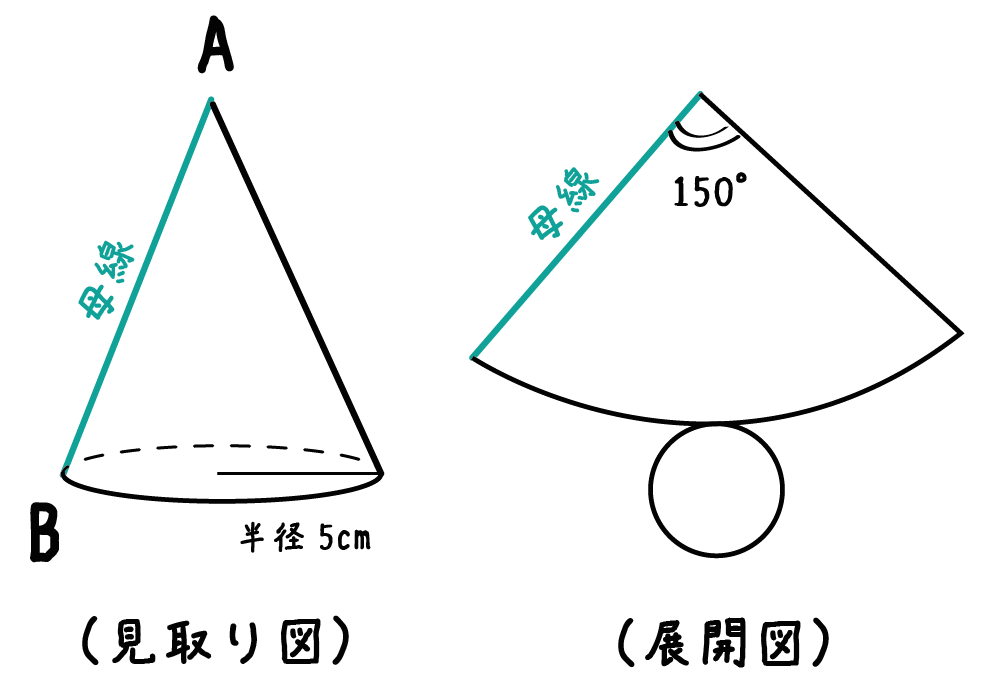
つぎの2ステップでとけちゃうんだ！
底面の「円周の長さ」を計算しちゃおう。
円周の長さの求め方は「直径×円周率」だったよね？？
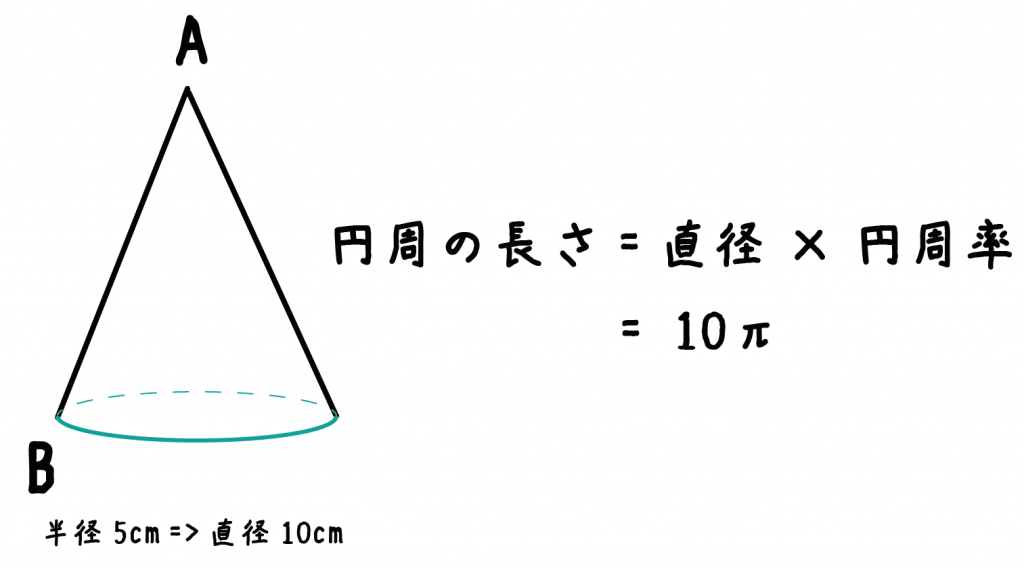
だから、例題では10π[cm]になるね！
つぎは「母線の長さ」をxとして方程式をたててみよう。
ここで思い出してほしいのは「扇形の中心角の求め方」。
母線をx[cm]としてやると、
2πx × 150/360 = 10π
っていう方程式がたてられるんだ。
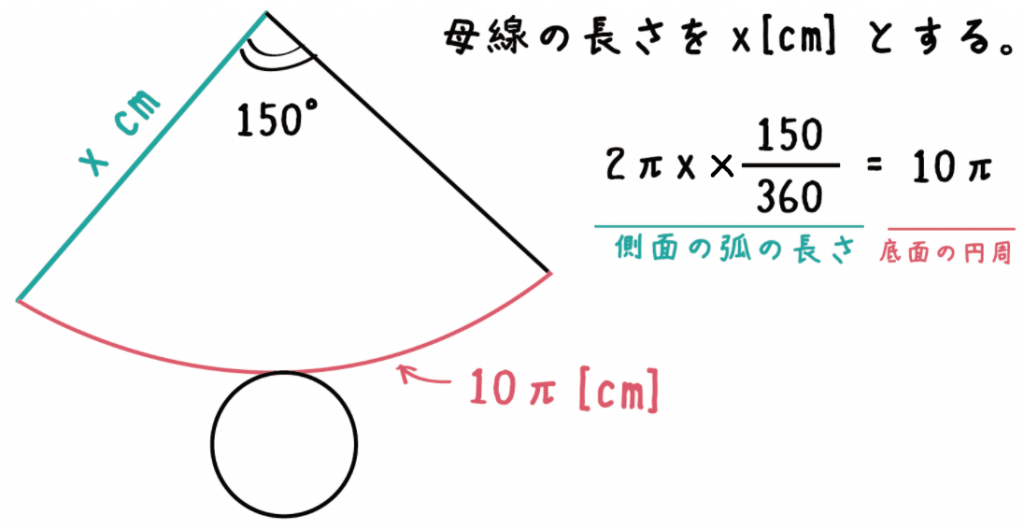
なぜなら、「側面の弧の長さ」は「底面の円周の長さ」に等しいからね。
こいつを解いてやると、
x = 12[cm]
って答えがゲットできるね！やった。
つぎは、円錐の「半径」と「高さ」がわかっている問題をみていこう。
たとえば、つぎの例題のような感じ。
半径が5[cm]、高さが10[cm]の円錐の母線の長さを求めてね
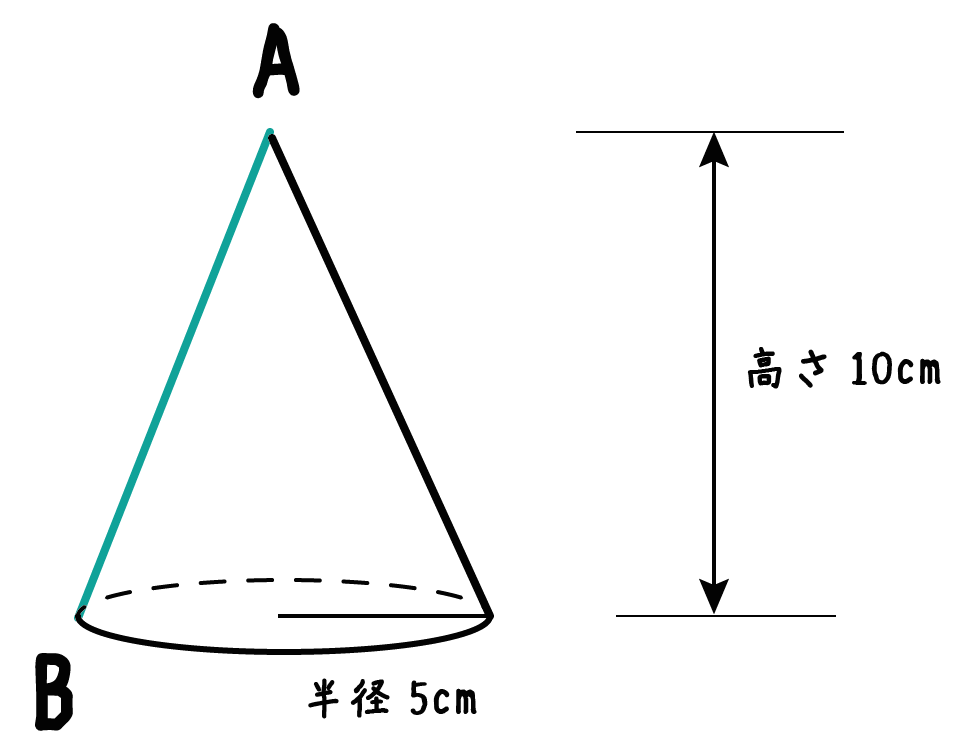
ここでは、中3数学で勉強する「三平方の定理」をガンガン使っていくよ。これは中1数学の範囲ではないよ。
つぎの3ステップで母線の長さを求めることができるんだ！
円錐をそこらへんの日本刀で真っ二つに切ってみよう。
頂点で二等分されるように切ってみてね。
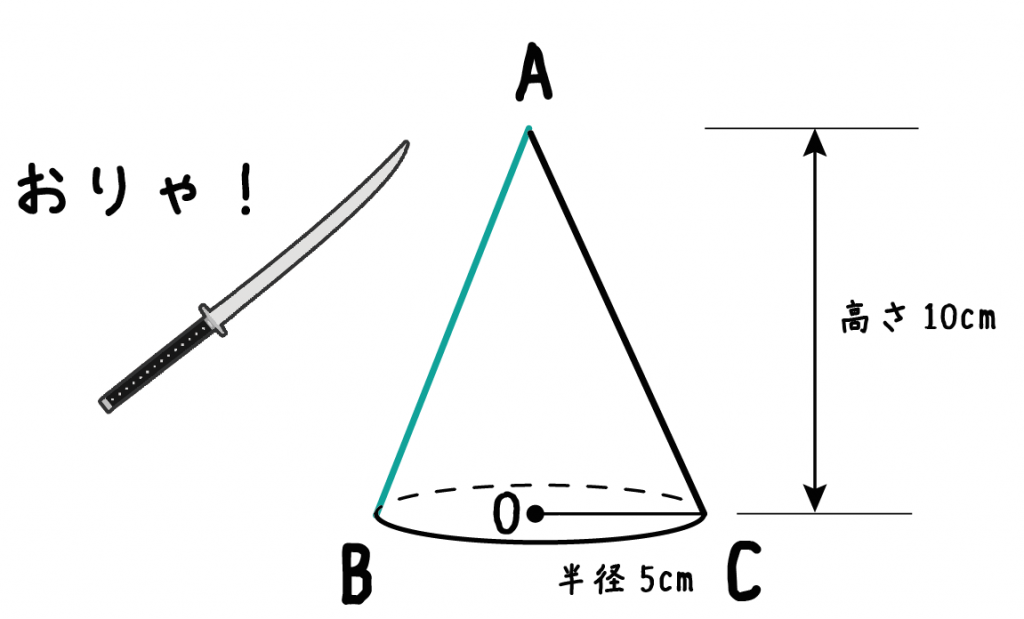
つぎに円錐を切ったあとの断面図に注目してみよう。円錐を頂点で2つに切ってやると、断面は三角形になるはず！
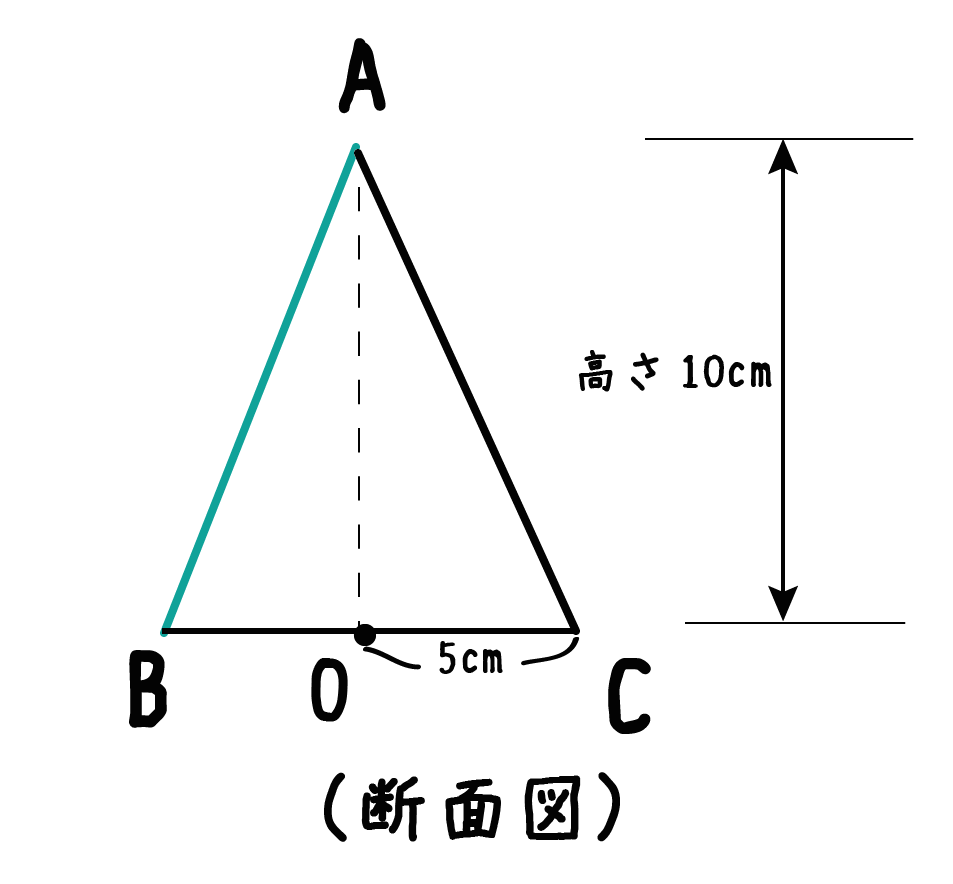
例でいうと、三角形ABCが断面になっているでしょ？？ これでいいんだ！
つぎに、「母線」、「底面の半径」、「円錐の高さ」をふくむ直角三角形をさがそう。例でいうと、
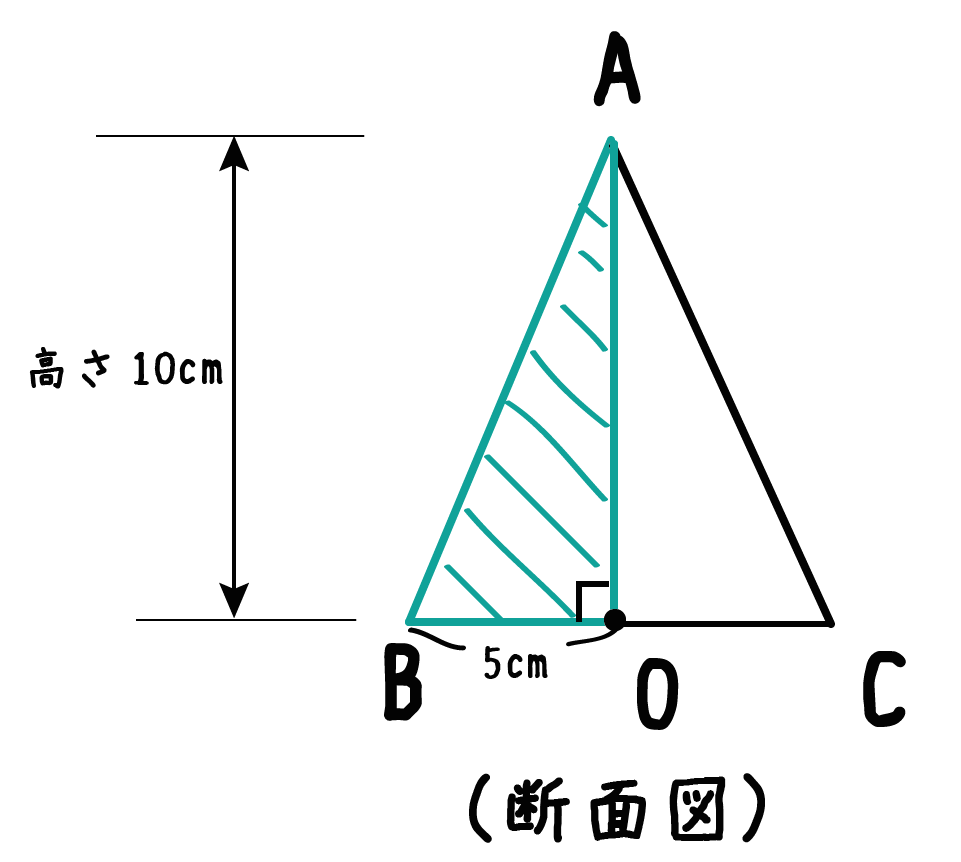
三角形ABOだね。斜辺以外の辺の長さはわかっているよね？？（半径5cm、高さ10cmより）
あとは「三平方の定理」をつかって斜辺の長さを計算してやればいいんだ。
例題で言うと、
母線ABの長さは5√5になるね。
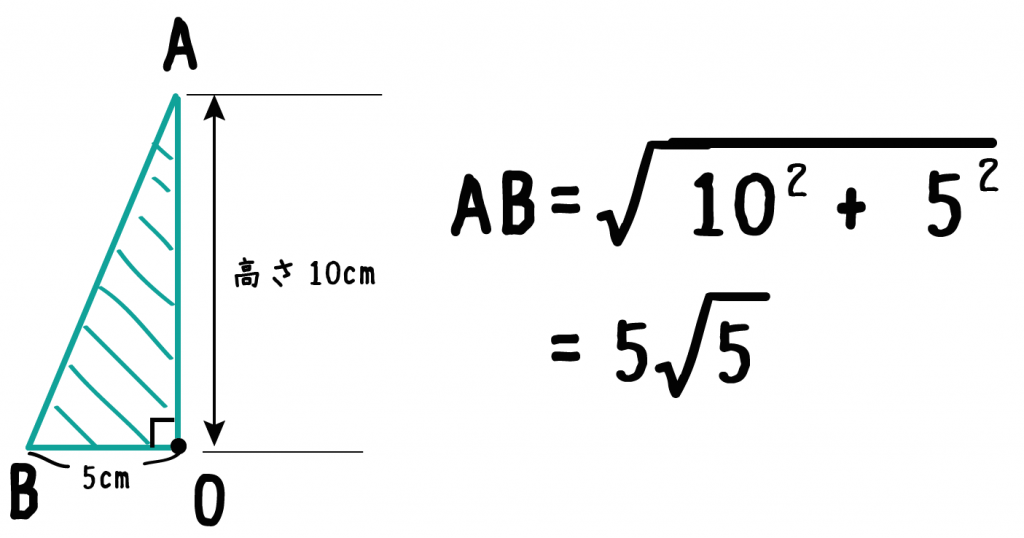
つまり、母線をふくむ直角三角形をさがして、三平方の定理をつかって計算すればいいってことだね！
おめでとう、これで母線の長さを求められたね。
この2つのパターン以外にも、
とかとか色々ある。正直、ちょっと混乱しちゃうよね？？
だけれども、どいつもこいつも結局、さっきの2つの求め方にいきつくんだ。
複雑な問題がだされたら、まずはその問題がどっちのタイプなのか考えてみよう！
どっちかわかったら、紹介した求め方でゆっくり解いてみてね。
そんじゃねー
Ken
こんにちは、この記事をかいているKenだよ。できれば鼻をかみたくないね。
空間図形で「回転体」っていうモンスターを勉強するよね。
「回転体」とは教科書によると、
1つの平面図形を、その平面上の直線lのまわりに1回転させてできる立体
のことってかいてある。
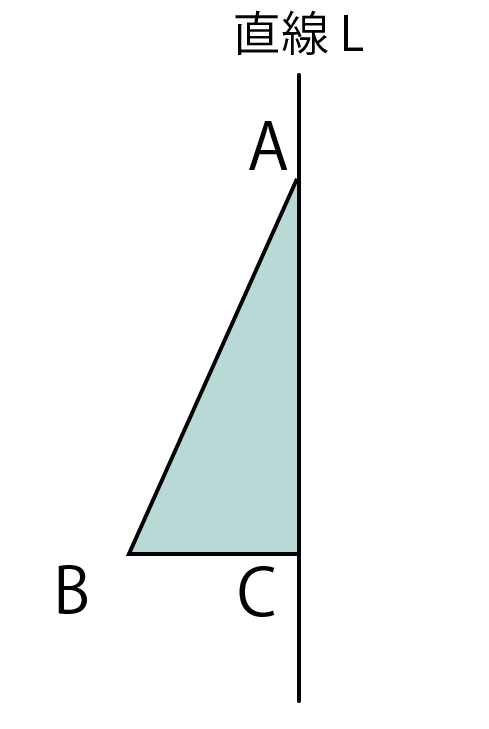
たとえば、直角三角形ABCを直線Lのまわりに1回転させて立体を作図してみると、
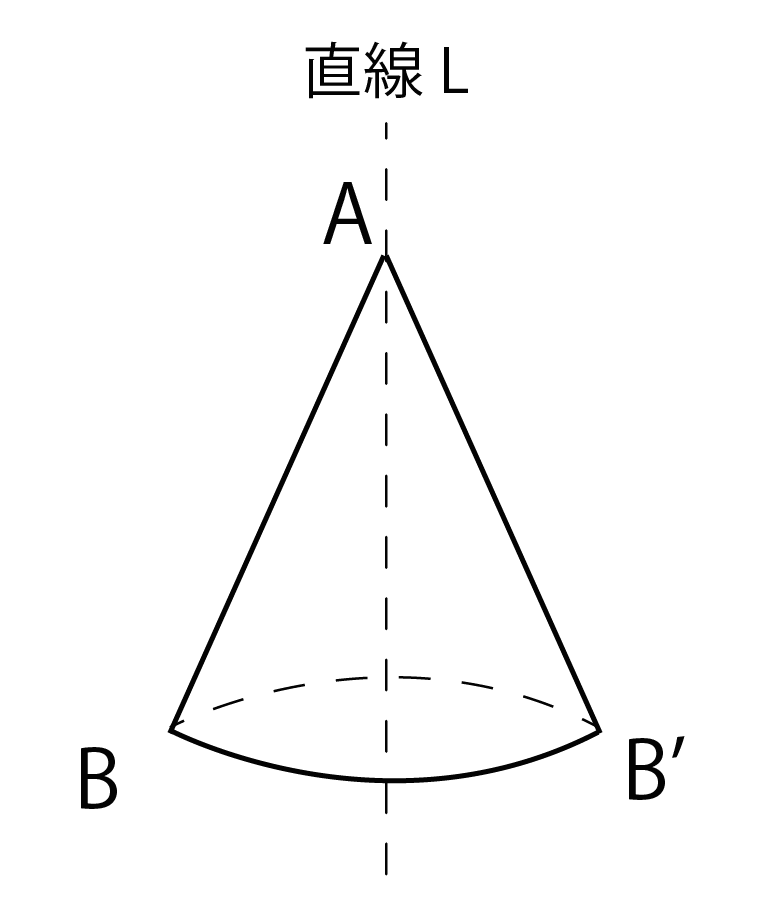
三角錐ABB’っていう立体ができちゃうんだ。
このとき、回転によってできた立体（この場合、三角錐ABB’）を「回転体」、直線Lを「回転の軸」って呼んでるわけだね。
それじゃあ、どうやって、回転体の見取り図をかくんだろう？？ これができたら、回転体の体積を簡単に求められるよね。
そこで今日は、
回転体の見取り図の書き方
をわかりやすく解説していくよ。たった4ステップで作図できちゃうんだ。困ったときに参考にしてみてね。
見取り図の書き方を解説しながら、つぎの例題をといていくよ。
つぎの長方形ABCDを直線Lを回転の軸として、1回転してできる回転体の見取り図をかきなさい。
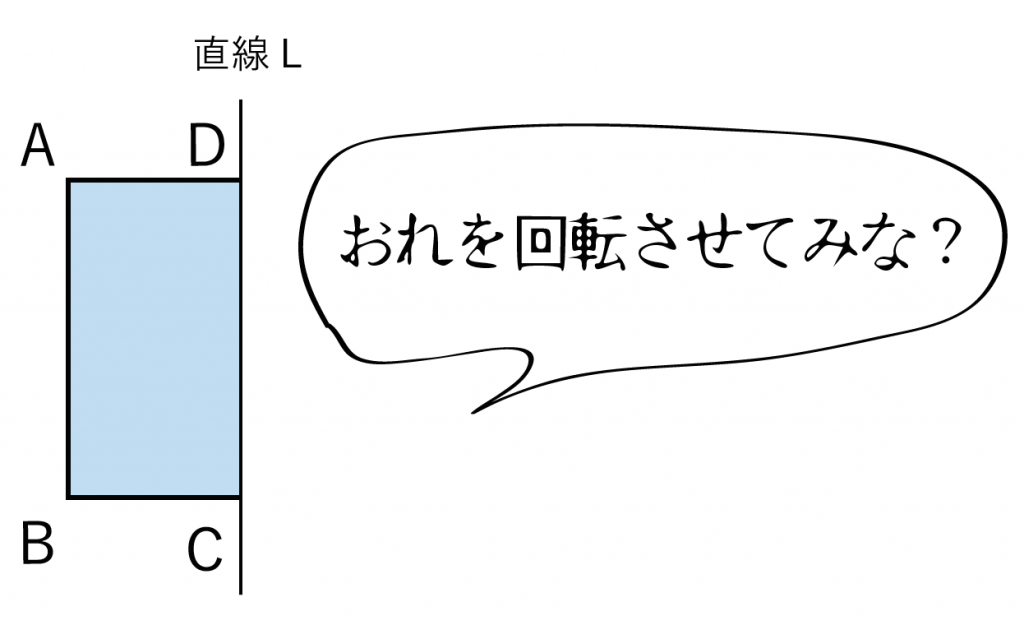
さっそく書き方をみてみよう！！
まずは与えられた平面図形を「回転の軸」で対称移動させた図形をかいてみよう。いわゆる線対称というやつだ。
対称移動をちょっと忘れていたら対称移動の書き方の記事をみてみてね。
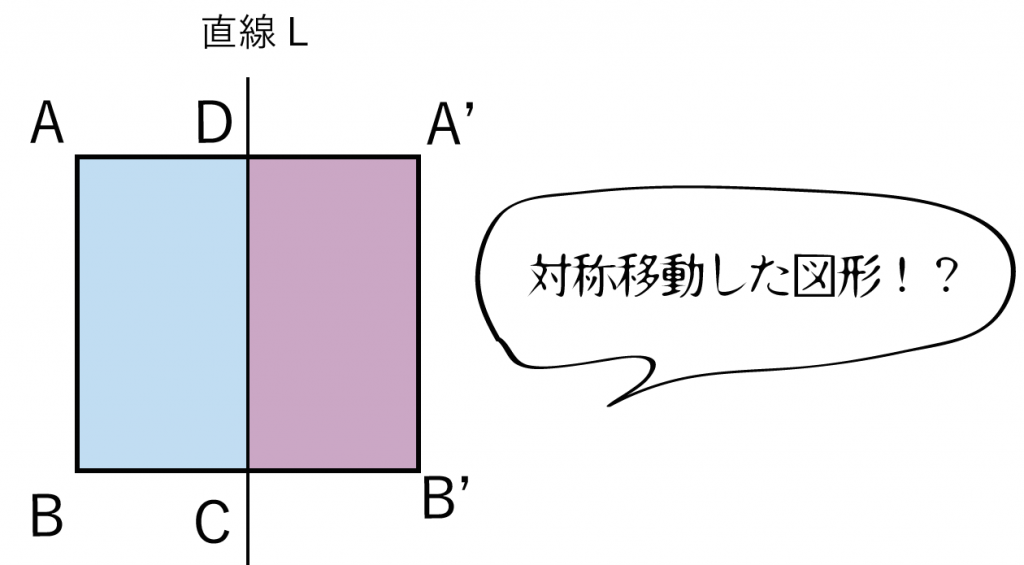
例題でいえば、
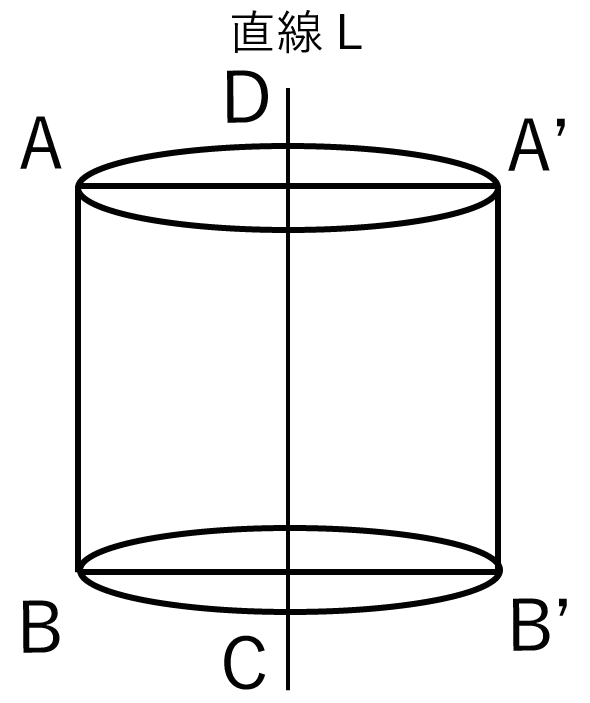
長方形ABCDを直線Lで対称移動させた図形は「長方形DA’B’C」になるね。ちょっとパープルの色をしているやつさ。
どう？？ 回転の軸で対称移動できた？？
つぎに、「回転の軸」にのっかっていない頂点に注目してみよう。対称移動させた「対応する頂点」を細長い円（楕円）でむすぶんだ。
ちょっとわかりづらいから例題をみてみよう。
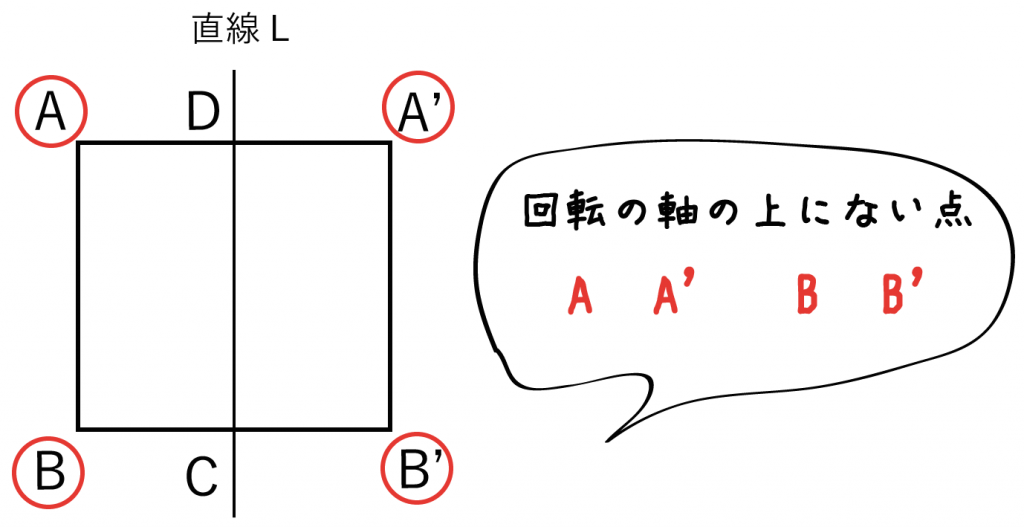
「回転の軸」上にない頂点は、
の4点だね。そのうち、対称移動させた図形同士の対応する頂点はつぎの2組。
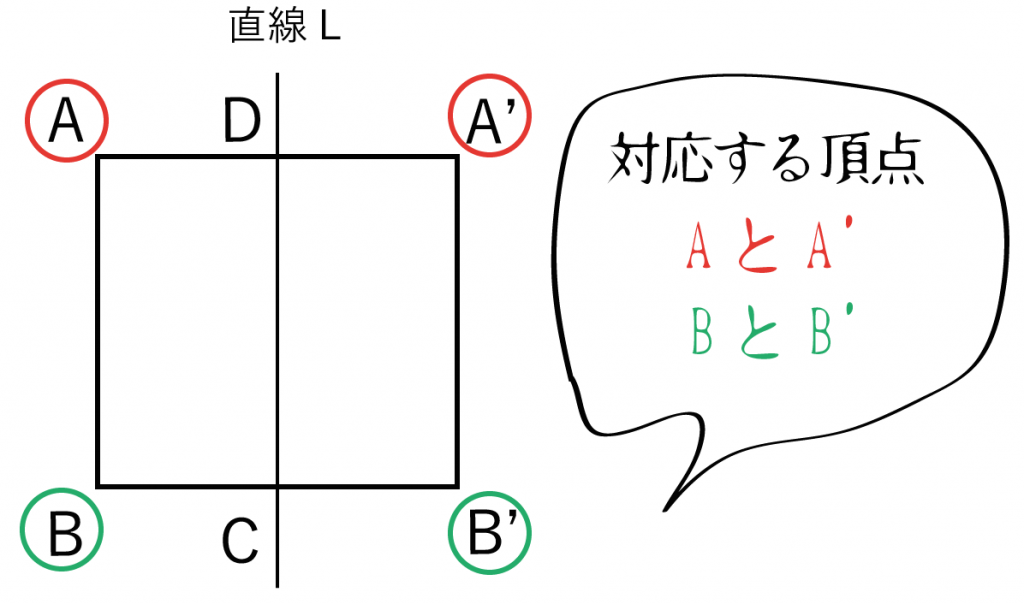
そして、この対応する頂点同士を「細ながーい円」でむすんであげるんだ。
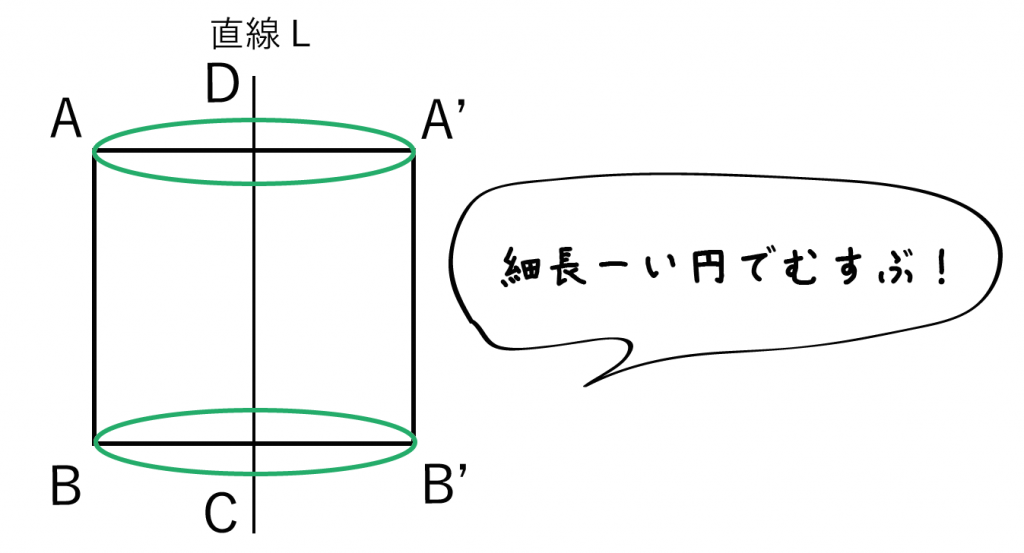
対応する頂点同士を円の両端にしてね。
上図のようにぴったりと細長い円をうめこんでやろう！
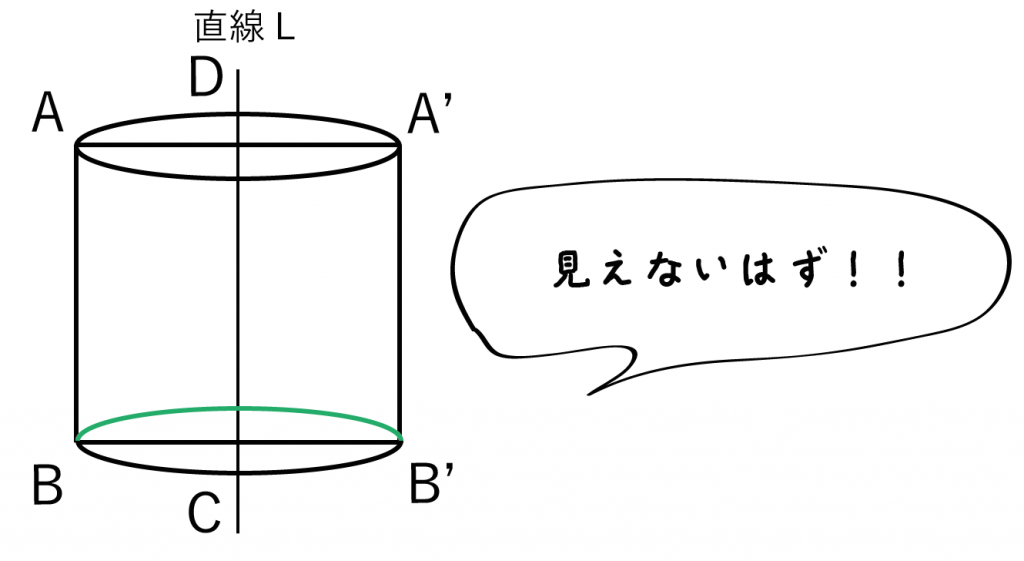
立体の見取り図では、立体の中の線は「点線」になってるんだ。
だから、ここでも見えないはずの線を「点線」にしてあげよう！
例題では、細長い円を埋め込んだだけだと、こうなっているね↓↓
だけれども、円BB’の上の弧（緑のやつ）は外からみたら見えないはずの線。
だからこいつを点線にしてあげよう↓↓
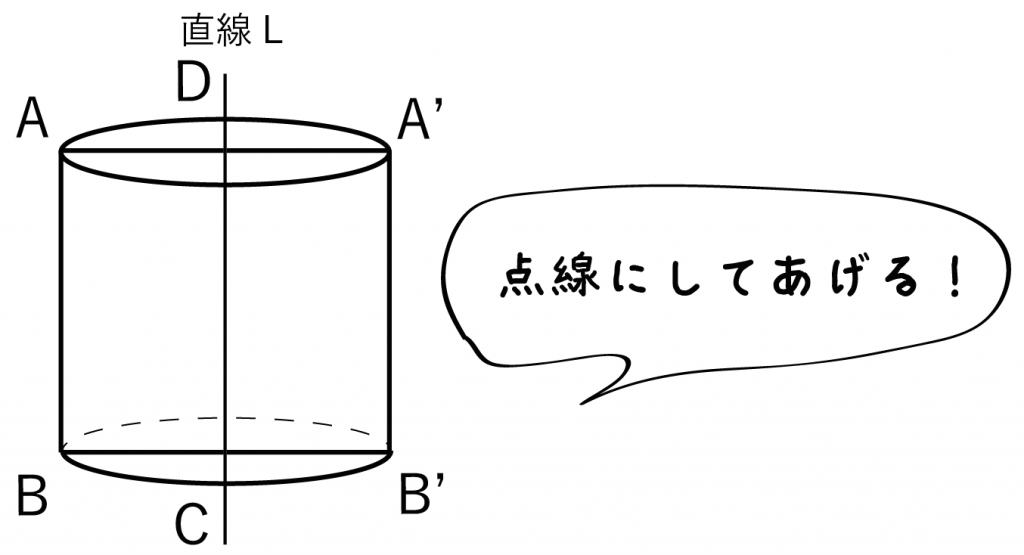
いよいよ最後のステップ。
あとは回転体の半径の線を削除すればいいだけ！
例題でいうと、
の2つだね。
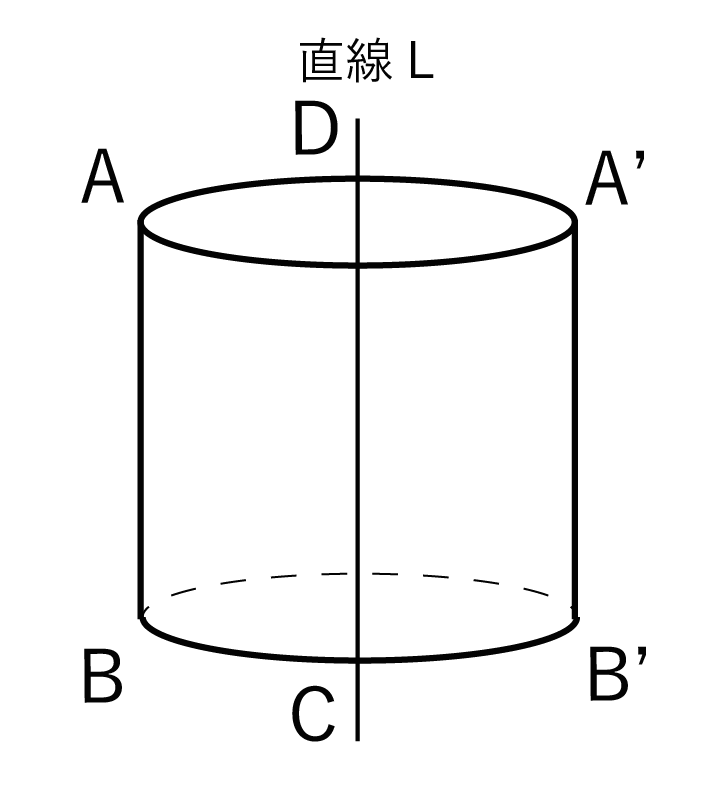
どう？？ きれいな円柱ができたでしょ！？
おめでとう。回転体の見取り図が無事にかけたね。
回転体の見取り図はかけるようになったかな？？
次回は「回転体の体積」の記事をかいていくよ。
よかったら参考にしてみてね。
そんじゃねー
Ken
こんにちは、この記事をかいているKenだよ。カレーは1日4回までだね。
「直方体の展開図の書き方」って何通りあるんだろう？？
って考えたことあるかな。
じつは「54通り」もあるんだ。
多すぎておぼえられないよね？？！
ただ、テストでいい点をとるためには書き方をすべておぼえなくていいんだ。
どれか1つ知っていればどうにかなるよー！
今日は、おぼえやすい「直方体の展開図の書き方」を解説していくよ。
その名も、
ハンマー型の展開図
だ。
「ハンマー型」の展開図の書き方はどんなものなのか？？
いかにも攻撃力が高そうでしょ？。
その実態にせまっていこう。
つぎの例題といっしょに解説していくよ。
例題
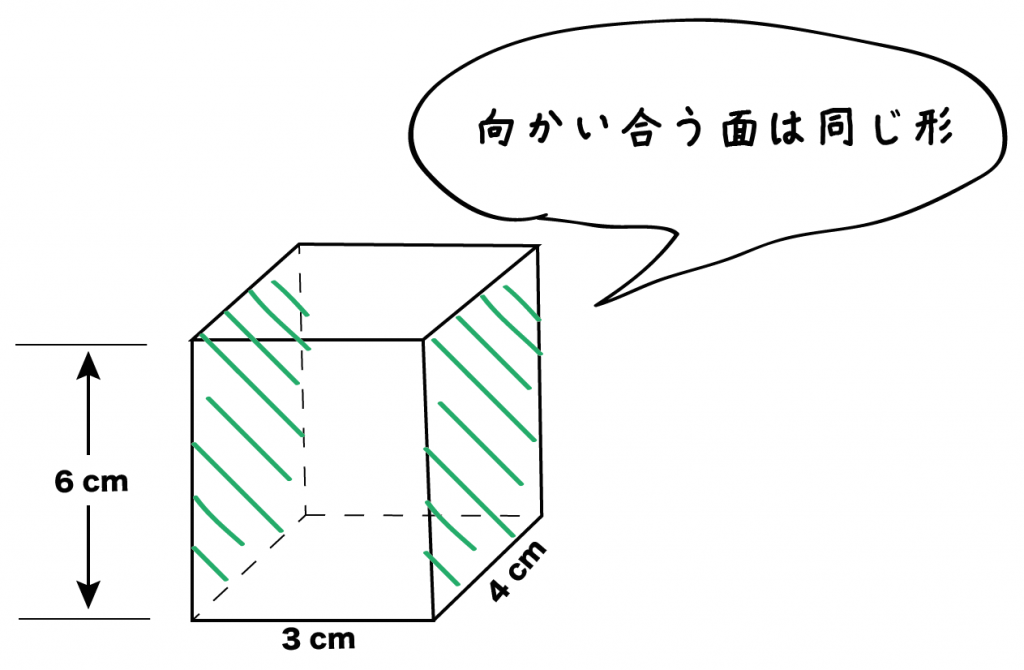
つぎの直方体（3 × 4 × 6）の展開図を作図しなさい。
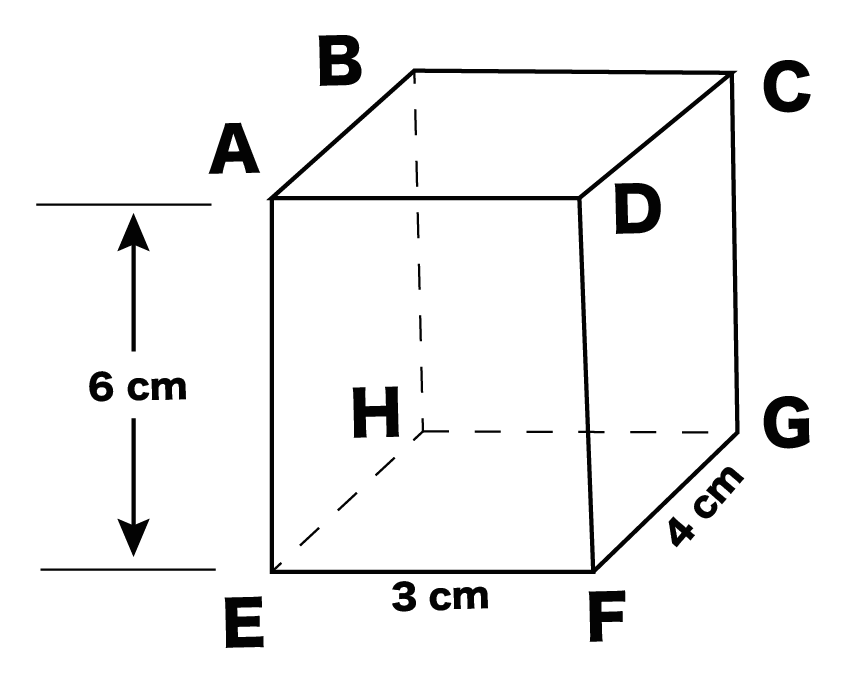
展開図を5ステップでかけちゃうんだ！
直方体の「側面」に注目してみよう。
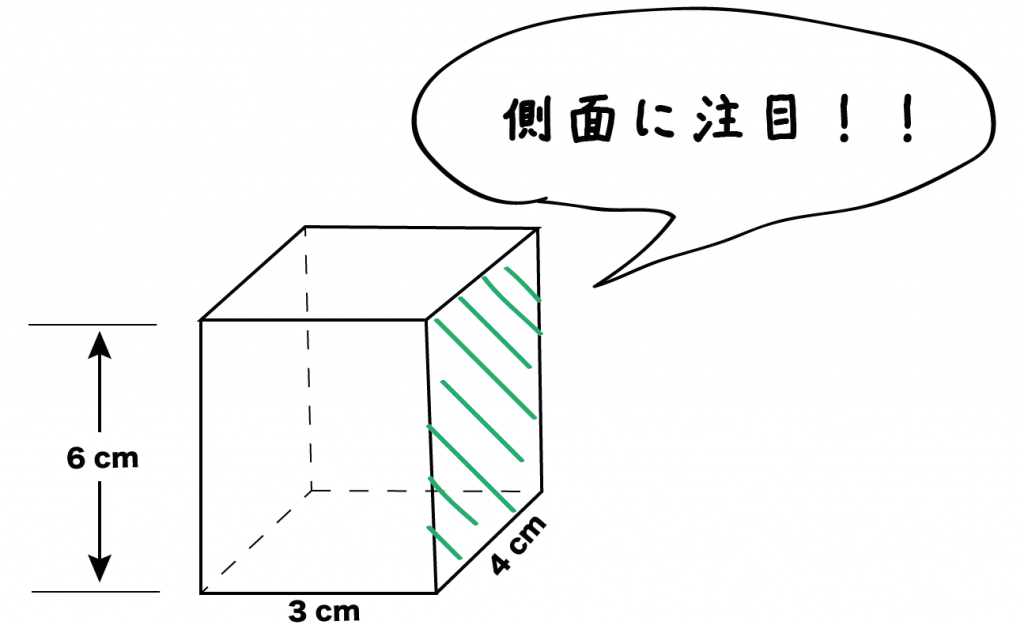
直方体の側面はぜんぶで4つあるね。そのうちの1つをテキトーに選んじゃおう。
側面は「長方形」だから、三角定規があればさらっとかけるはず。
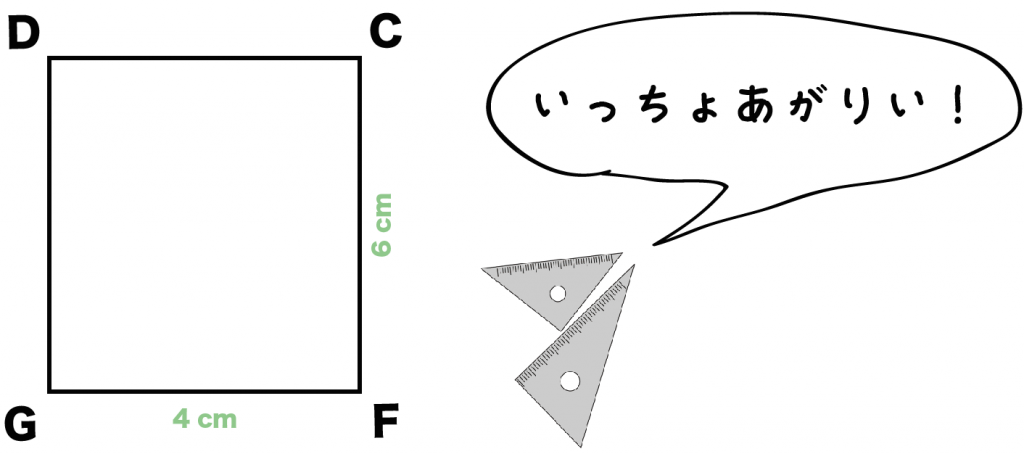
例題では、たて6cm・よこ4cmの「長方形BCFG」をえらんでみたよ。
側面はたった2種類しかないんだ。だって、向かい合う面同士は同じ形だからね。
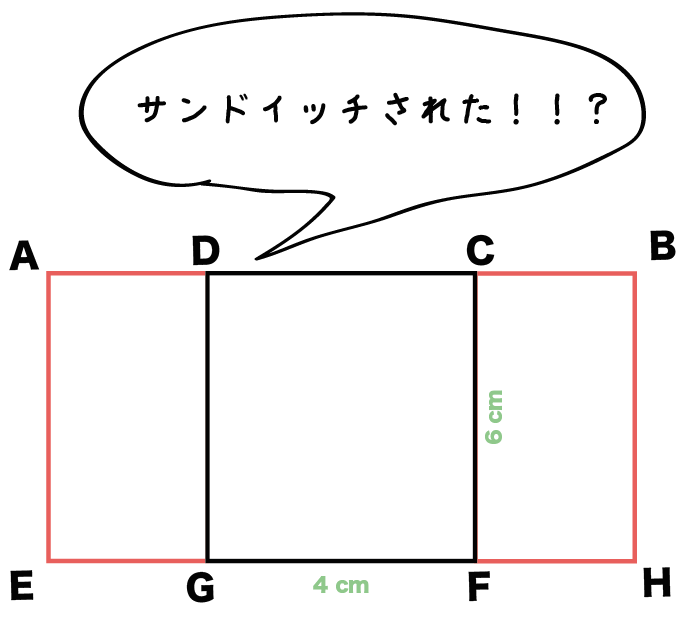
このステップでは、「さっきかいた長方形」を「別の側面たち」でサンドイッチするんだ。
例題でいうと、
「長方形ADGE」と「長方形CBHF」で、
「長方形DCFG」を挟んであげるんだ。
対応する辺同士はいっしょにしてね。
この例でいうと、辺DGと辺CFだよー
サンドイッチされた黙っちゃいないのが長方形。
サンドイッチされた長方形でハサミ返してみよう！ ハサム長方形は右のやつでも左のやつでも構わないよ。
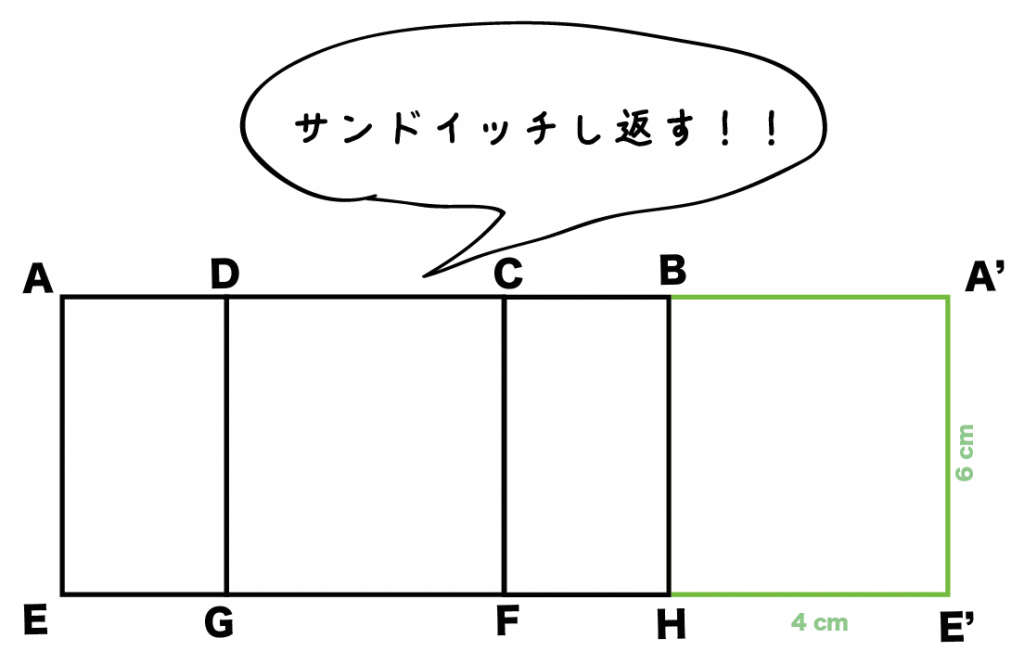
例題でいうと、
長方形CBHFを長方形BA’E’Hではさんであげたよ。対応する辺BHでうまく合体させてみよう。
側面の展開図はこれでおしまい。
つぎは直方体の底面を2つ付けるだけ！
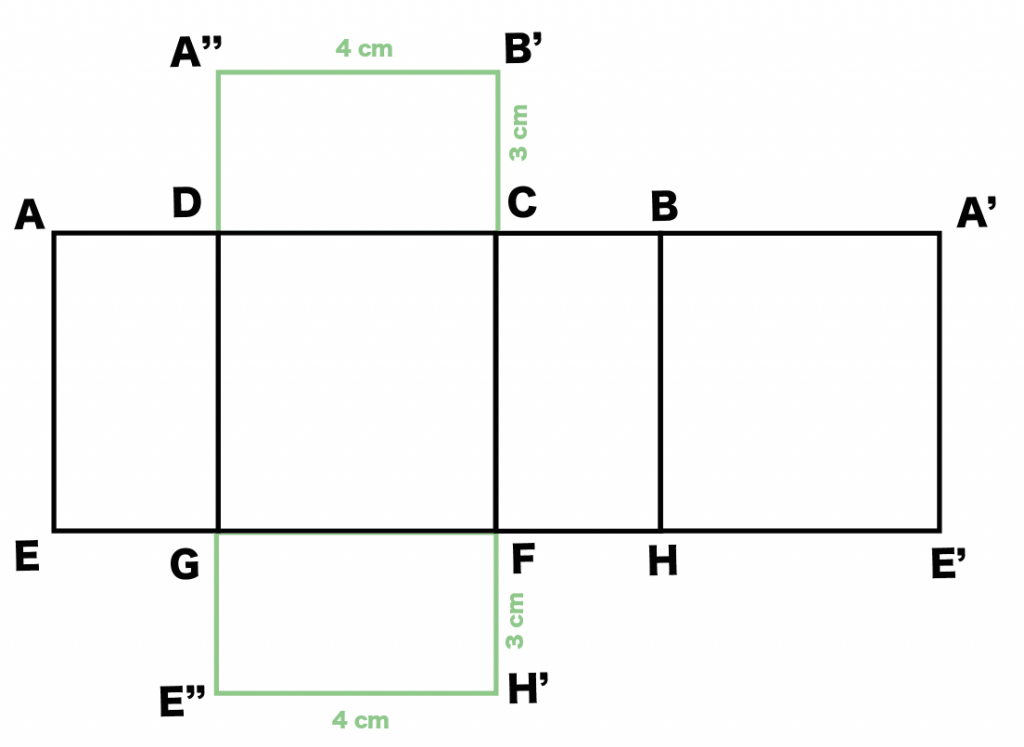
例題では、「長方形DCFG」に底面の「長方形ABCD」と「長方形EFGH」を連結させてみたよ。
いよいよ最後のステップだね。
あとは展開図の折り目を「点線」にするだけ。
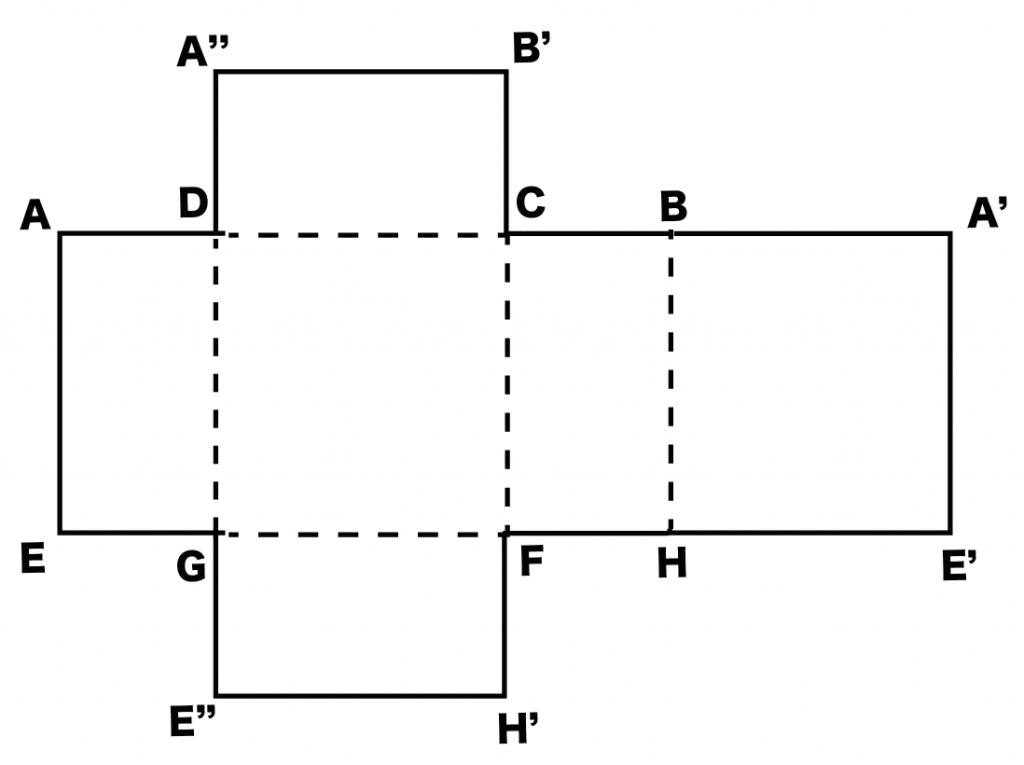
例題でいうと、
という5つの辺だね。こいつらを点線にしてやればいいんだ。折り目は「面の辺が2つ以上かさなったところ」だね。
これで直方体の展開図も完成！おめでとう！！
えっ。なんでこれが「ハンマー型」の展開図なのかって！？
た、たしかに。
いや、
いやいや。
よーくみてると、ハンマーにそっくりじゃないか。
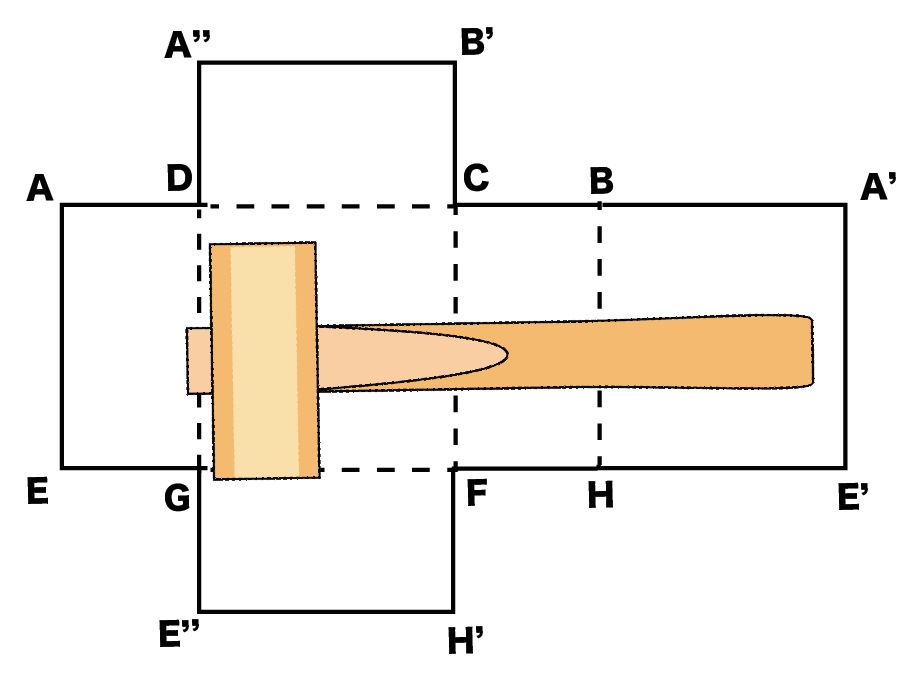
とくに指定がなかったら、このハンマー型の書き方でガンガン攻めていこう！！
そんじゃねー
Ken
こんにちは、この記事をかいているKenだよ。犬のしつけに失敗したね。
立体の展開図の書き方をたくさんみてきた。
もう空間図形の展開図なんて飽きた！ おれは平面がいい！！
なんて思うかもしれないね。 だけど、今日はもう一つ新しい「立体の展開図」を勉強していこう。
それは、
三角錐の展開図の書き方
だ。
まるで、とんがりコーンのような三角錐。
展開図の書き方は次の2種類あるんだ。
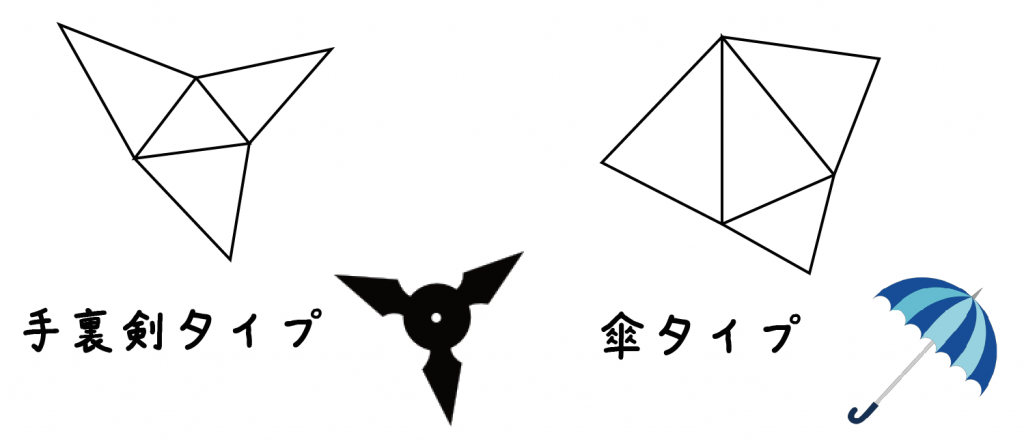
今日はせっかくだから、2つの作図法をマスターしちゃおう。
つぎの例題をときながらみていくよ。
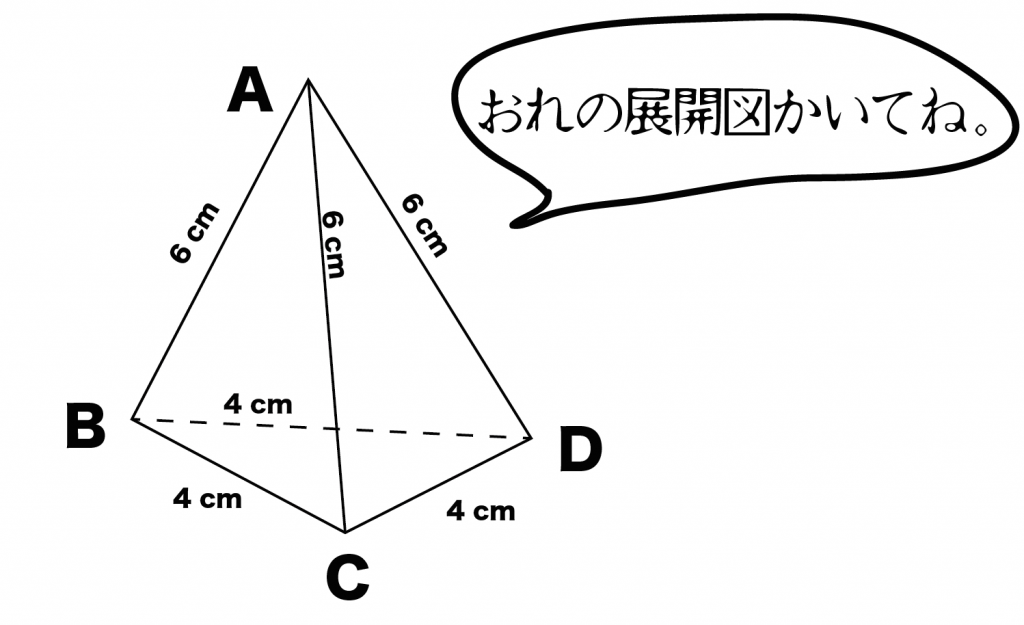
例題
つぎの三角錐ABCDの展開図をかきなさい。そったら100点あげるよ。
まずは1つ目の「手裏剣タイプ」の書き方をみていこう。
この書き方では、つぎの4ステップで作図できちゃうんだ。
底面の三角形をかいてみよう。気合で。
例題でいうと、三角形BCDだね。
コンパスや定規やをつかってみてね。
「ステップ1でかいた底面」に側面をつけたしてやろう！
各辺に対応するように側面をかいてあげるんだ。タケノコが生えるみたいにニョキニョキっとね。
例題でいうと、
でつなげちゃおう！
最後に、展開図の折り目を「点線」にしてあげよう。展開図でいう「折り目」は展開図のうちがわの線のこと。
例題でいうと、
の内側の3辺がそれにあたるね。
これで三角錐の展開図は終了！ やっぱ手裏剣に似てるっしょ？？。
手裏剣タイプをマスターしたね？？ そのつぎはなんと、傘。
そう、
よくダイソーとかに売っている傘のことだよ。
傘タイプの書き方はつぎの4ステップなんだ。
三角錐の側面を1つかいてあげよう。
側面は3つあるけど、もう、ほんっとどれもでもいい。好きな奴をピックアップしてみよう。
例題では、側面の三角形ABCをえらんでみたよ。
さっきかいた三角形の側面に、のこり2つの側面をつなげてあげよう。
対応する辺同士で合体させてやればいいんだ。
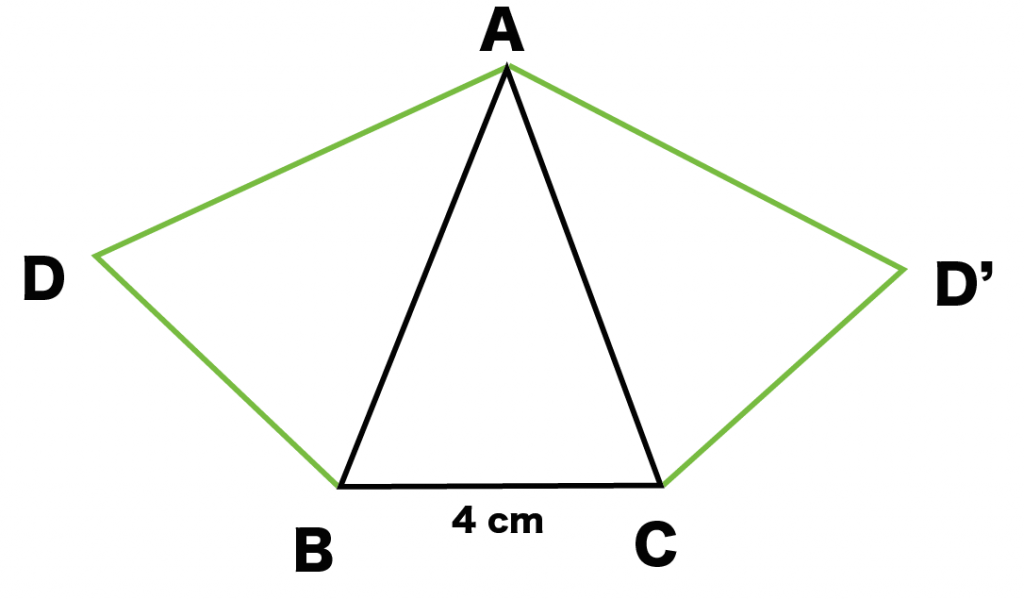
例題では、
三角形ABDを辺ABで合体させ、三角形ACDを辺ACでくっつけてみたよ。
センスみたいな形になればとりあえずオッケー！
底面の三角形もつなげてしまおう！
もちろん、対応する辺で合体させてね。
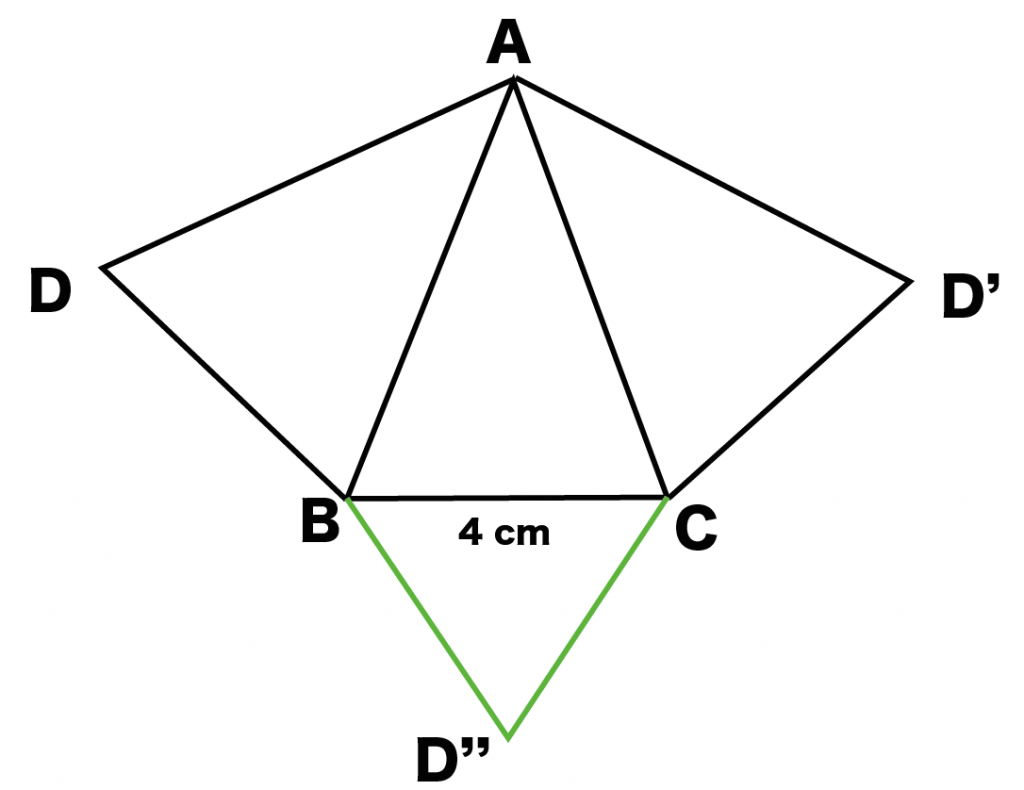
例題では、辺BCで底面の三角形BCDをくっつけているね。
コンパスと定規をつかって渾身の三角形をかいてくれ！
展開図の折り目を「点線」にするよ。
展開図の折り目って、
展開図の内側の線のことだったね？？
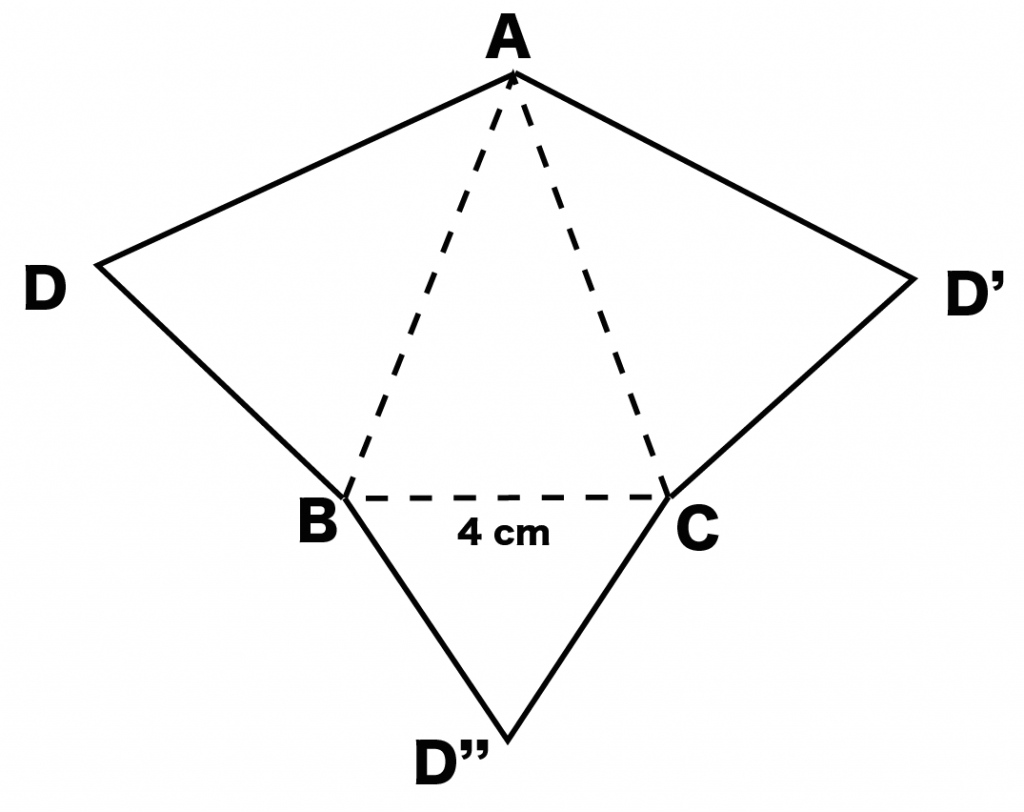
例題でいうと、三角形ABCの辺がすべて折り目になっているよ。だって、展開図のなかにあるからね。だから、
をすべて点線にしてあげよう。
これで三角錐の展開図のできあがりだね。傘にそっくりじゃない？？。
おめでとう！！
三角錐の展開図の書き方って意外とシンプルだったでしょ？？
書き方うんぬんよりも、三角形をいかに正確に作図できるか？？っていうスキルを持っていることが大切かもしれないね。
三角形の書き方はこっちの記事を参考にしてみて。
この2つの方法でじゃんじゃん三角錐を展開していこう！！
そんじゃねー
Ken
こんにちは、この記事をかいているKenだよ。フリスビーで遊びたいね。
「三角柱の展開図」ってヤッカイだよね？？
展開しろっていわれても、なかなかイメージしずらいし、三角柱をみているとケーキみたいで腹がへってくる。
三角柱の展開図を瞬殺したい
って誰もが思っているはずだ。
そこで今日は、
三角柱の展開図の書き方・作図方法を2つだけ解説していくね。
困ったときに参考にしてみて。
~もくじ~
三角柱の展開図の書き方が42通りある、らしい。
だけれども、だいたい次の2つの書き方に分類することができるんだ。
それは、
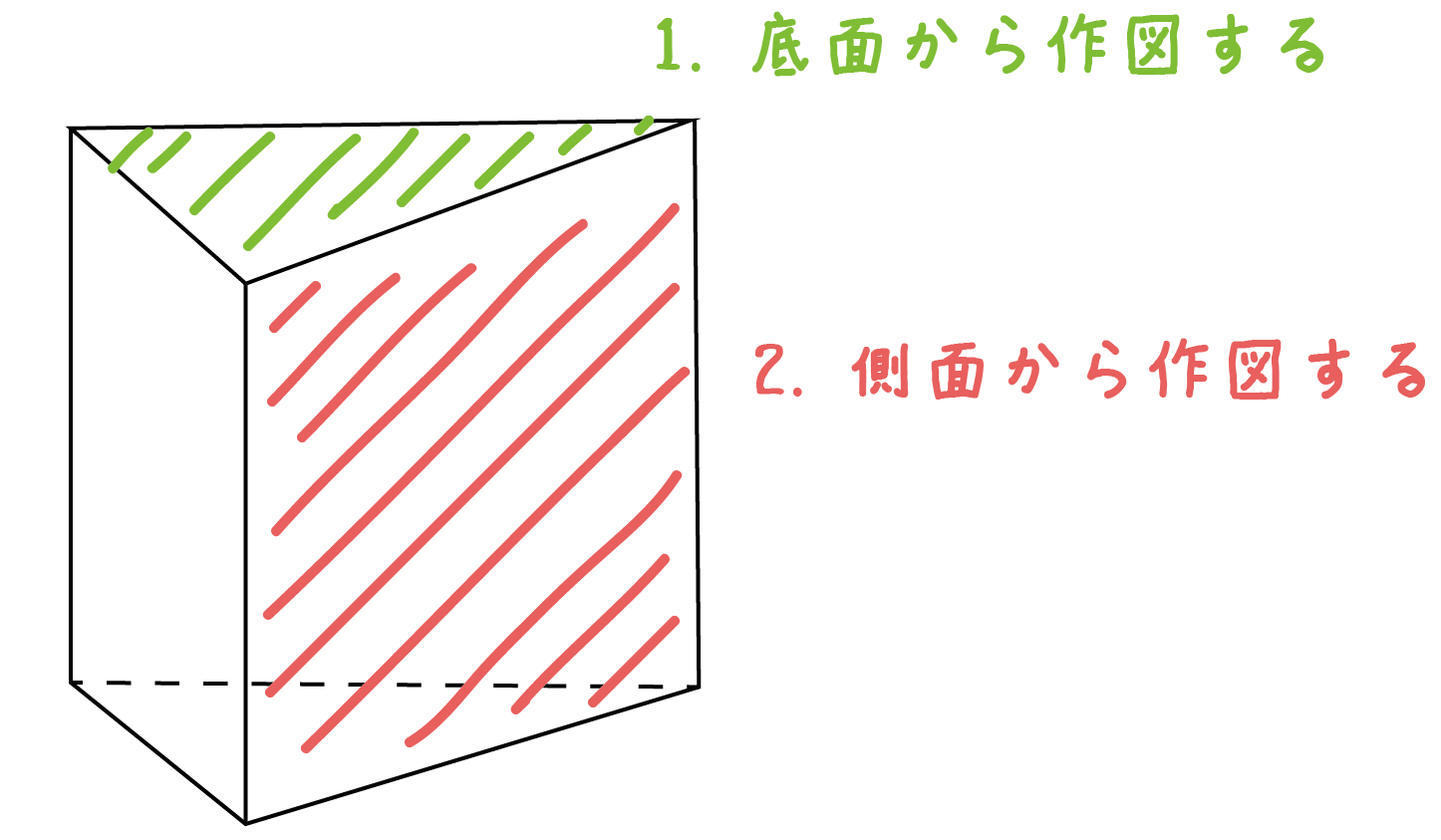
上の図でいえば、「赤い側面」から展開図をかいてもいいし、「緑の底面」から作図してもいいってことなのさ。
つぎの例題の「三角柱の展開図」をかいていくよ！
例題
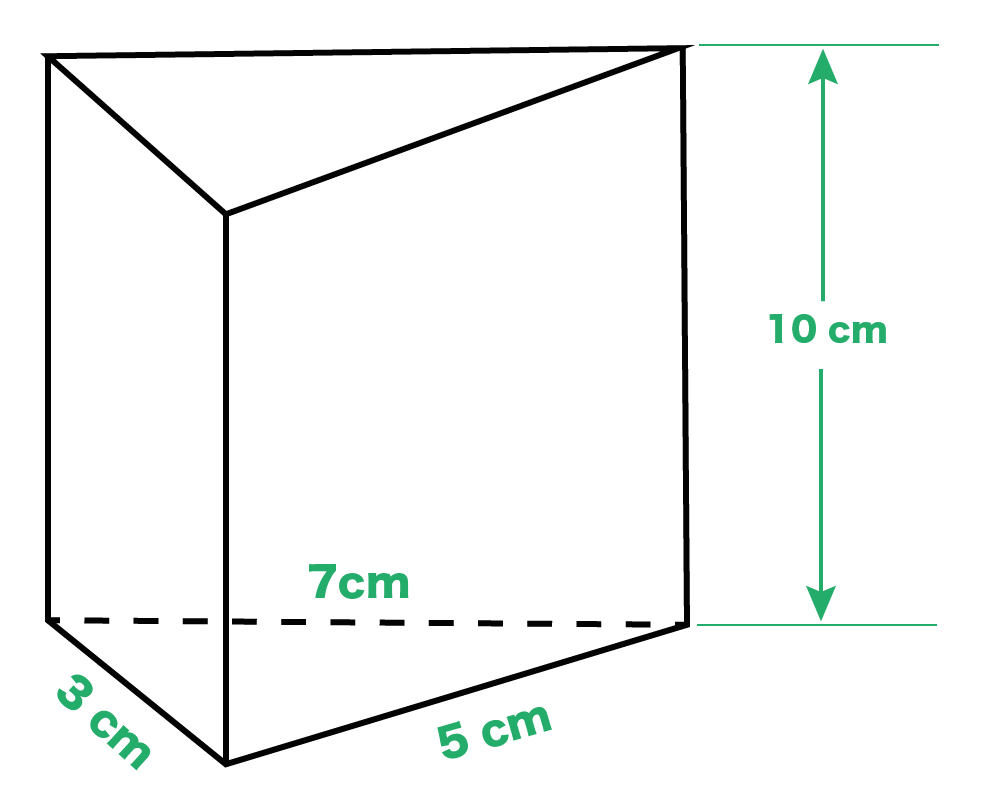
つぎの三角柱の展開図を作図してね。
底面の三角形の辺の長さ（3, 5, 7cm）、三角柱の高さ10 cm
もっとも人気のある、
側面から作図する書き方
をみていこう。
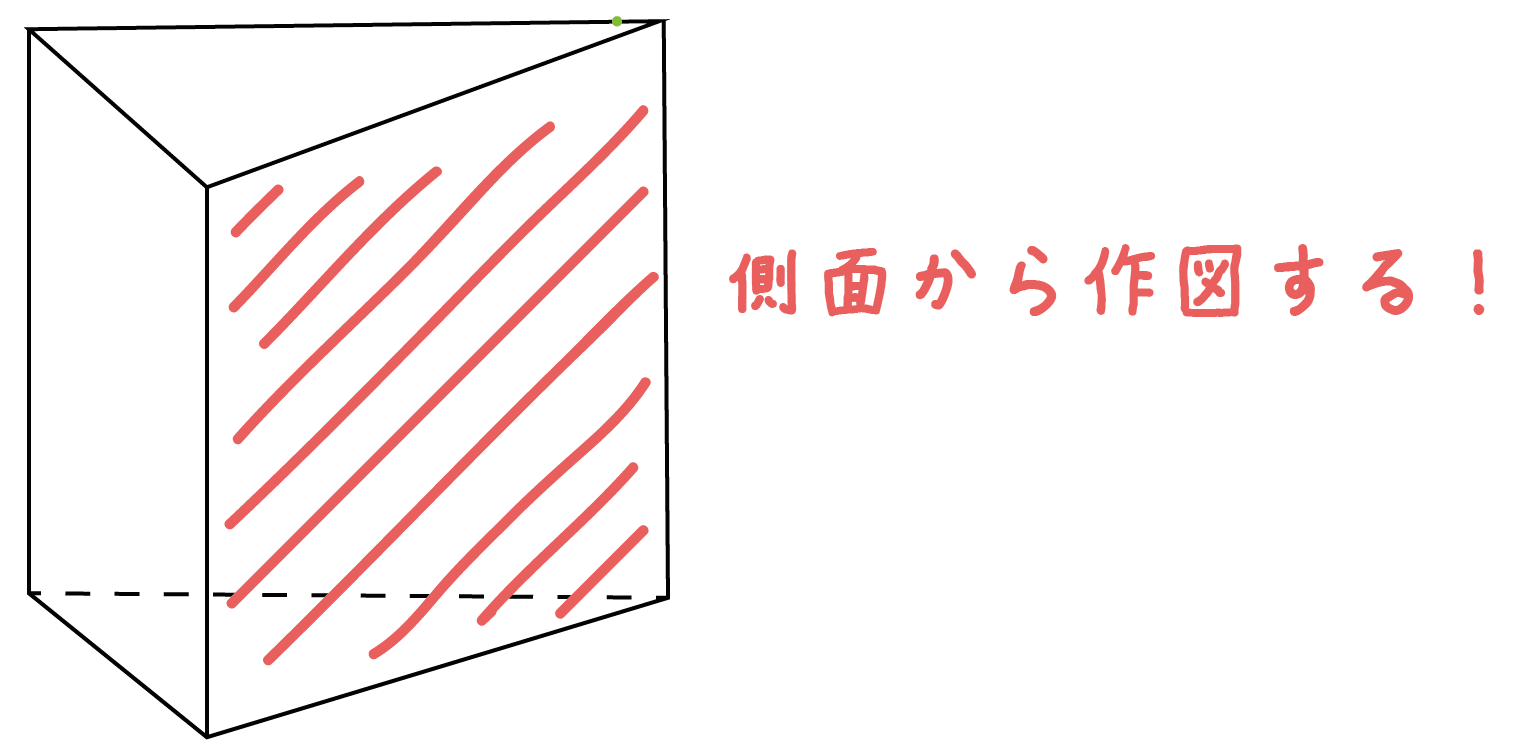
この書き方では、3つのステップで展開図を作図できちゃうんだ。
三角柱の側面は3つあるよね。
そのうち、1つの側面をかいてあげよう。
ようは、長方形を1つだけ作図するってこと。これなら楽勝さ。
三角柱の頂点に適当に名前をつけてみよう。
A, B, C, D, E, Fといった感じで。
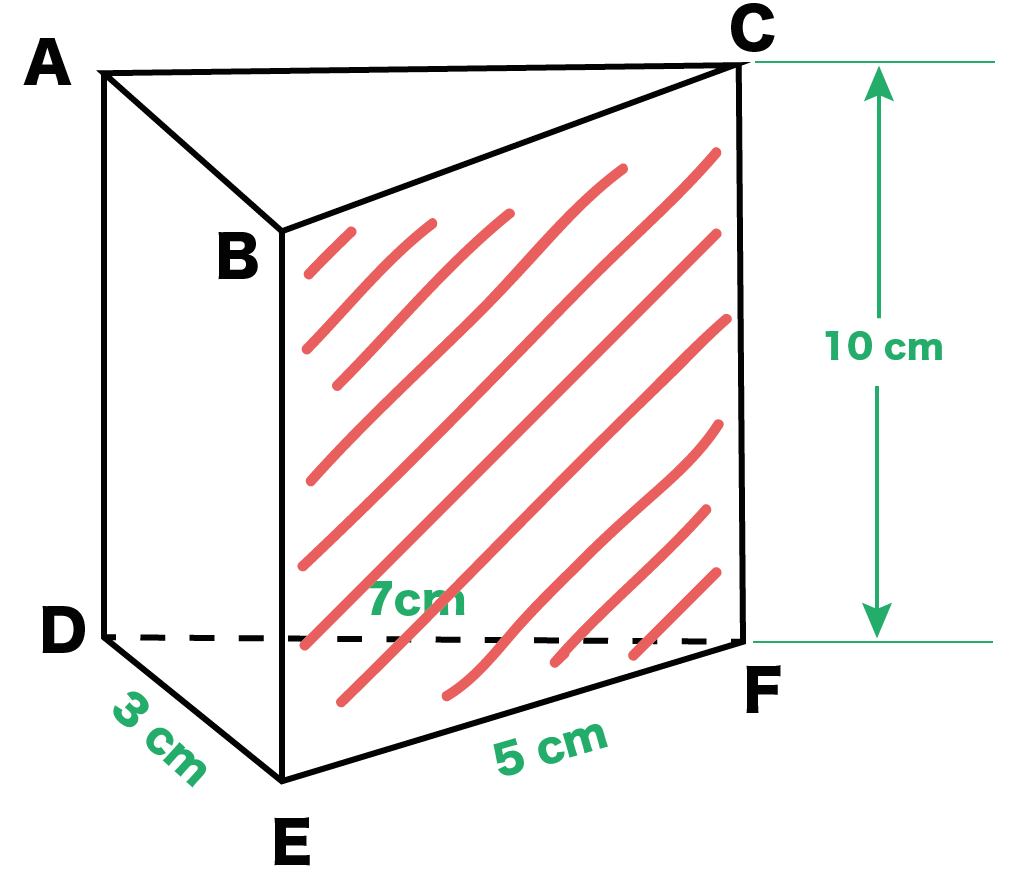
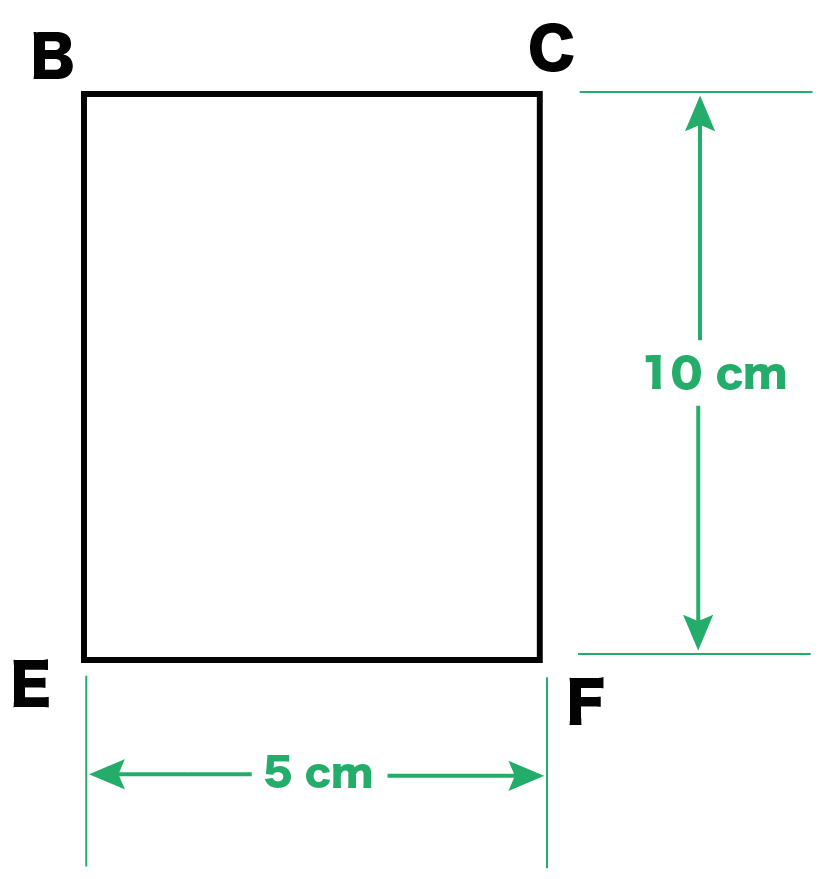
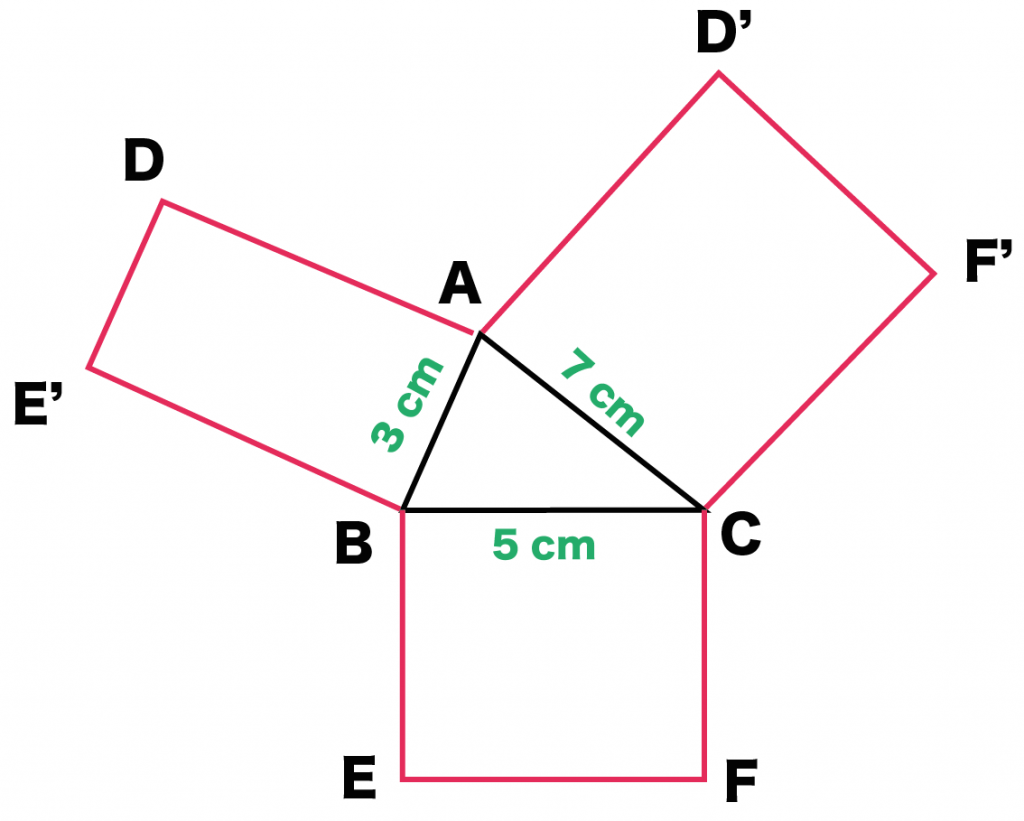
そんで、側面の1つである「長方形BCFE」をかいてみてね。
長方形を気合でかくと、こんな感じになるはずだ↓↓
「もう2つの側面」を連結してあげよう！！
例題でいうと、
「長方形ABDE」と「長方形ACFD」だね。
こいつらをさっきの「長方形BCFE」と合体させてやるんだ。
合体の方法は、
「対応する同じ辺」をつなげてやるだけ！ すると、こうなる↓↓
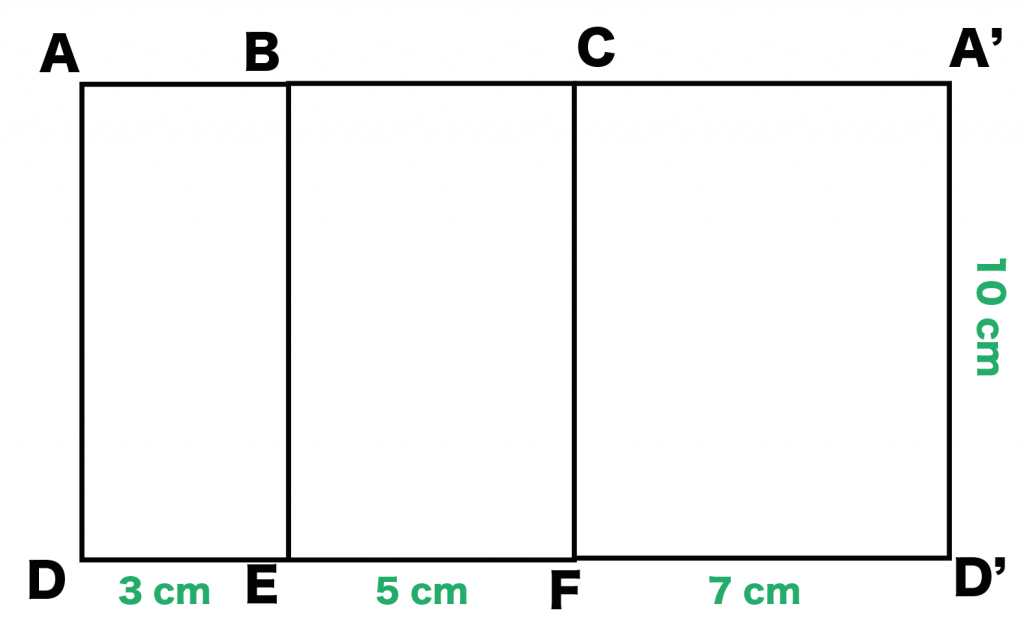
ただ、同じ頂点が2つでてきちゃうよね。
この例でいうと、AとDだ。
そういうときは、2つめの頂点に「’ （ダッシュ）」をつけてあげて目印をつけてやろう。こいつは2つめの点だぞ！ってね。
もし、3つめの同じ頂点ができそうだったら「”（ダッシュ）」を2つつけてみてー！
最後に残ったのは底面だね。
あとはコイツらを展開図につけるだけでいいんだ。
「ステップ1でかいた長方形」と「2つの三角形」を対応する辺で合体させてみよう！
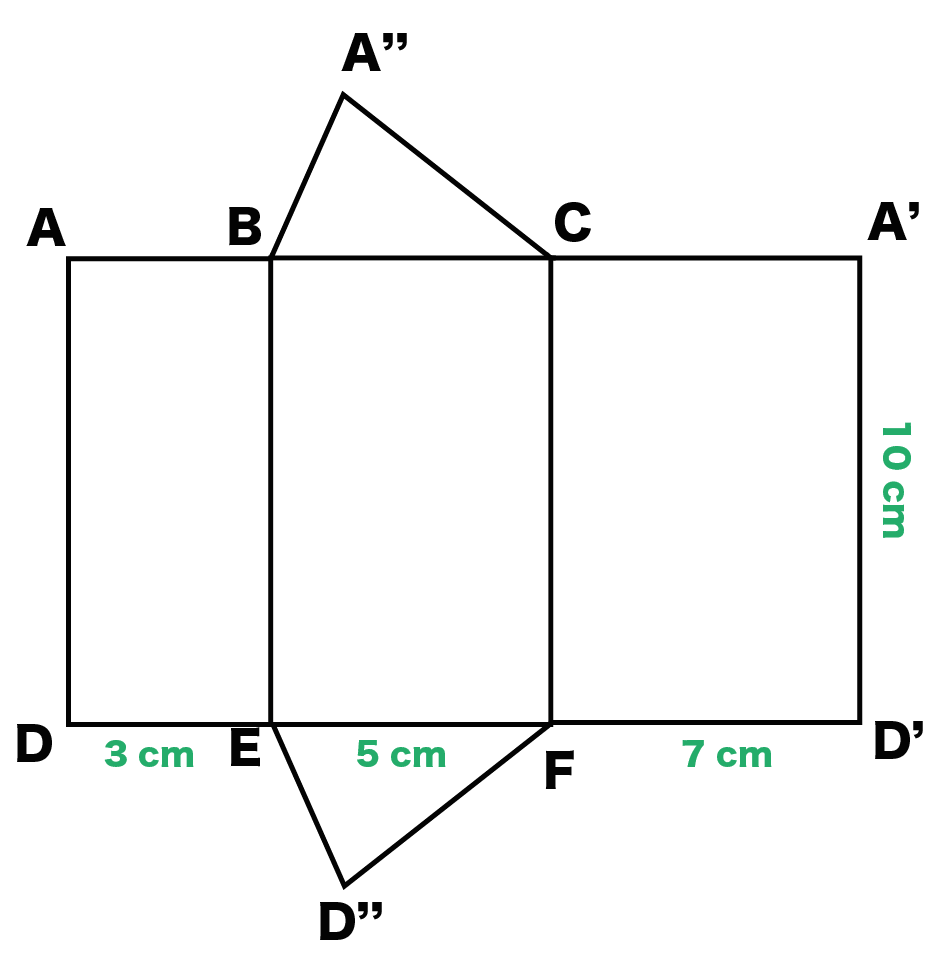
例題でいうと、
「三角形ABC」と「三角形DEF」を「長方形BCEF」と連結させるってことだね。
これで三角柱の展開図は終了だ！おめでとう！
つづいては、底面から作図する方法だ。
お腹いっぱいになってきたけど、もうちょっと頑張ってみよう。
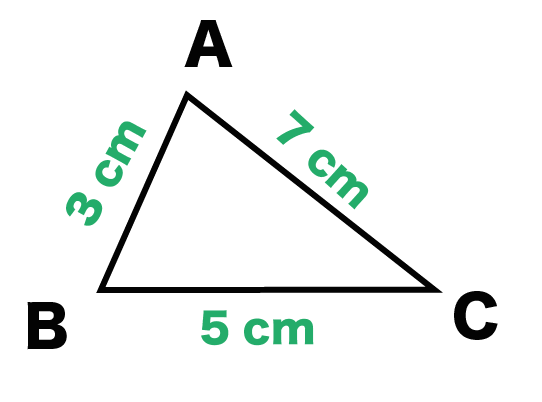
上でも下でもどっちもいい。
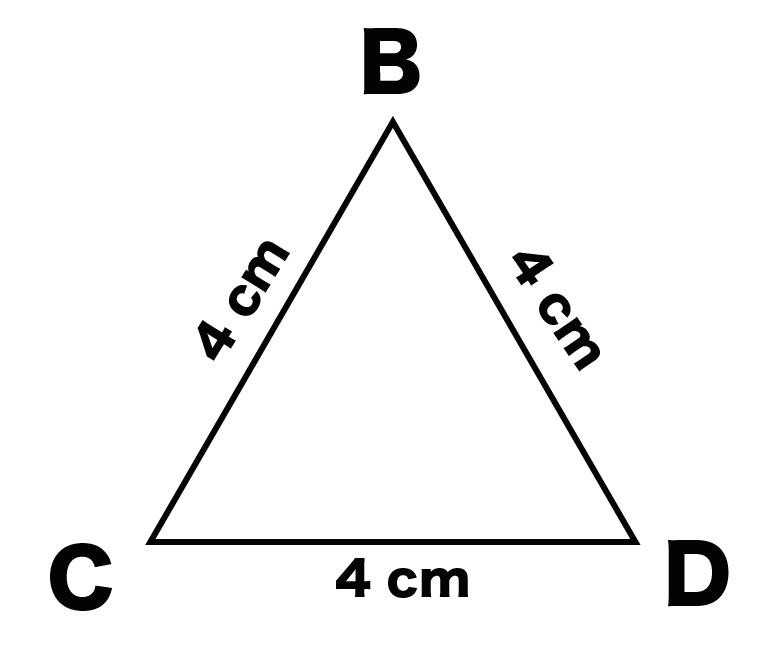
三角柱の底面の「三角形」をかいてみよう。
例題でいうと、
三角形ABCをかくって感じ↓↓
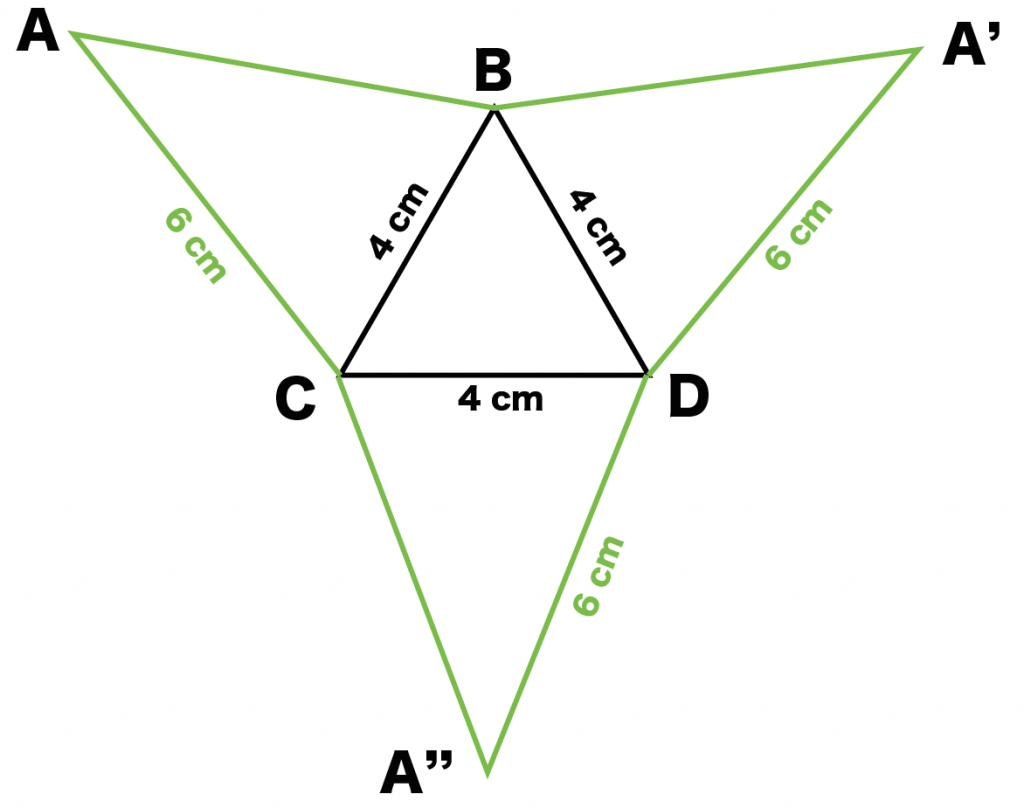
3つの長方形（側面）を合体させてみよう！
方法はいたって簡単。
対応する辺同士を連結させてやるだけさ。
例題だと、こんな感じになるよ↓↓
長方形を定規で3つかいてあげよう！！
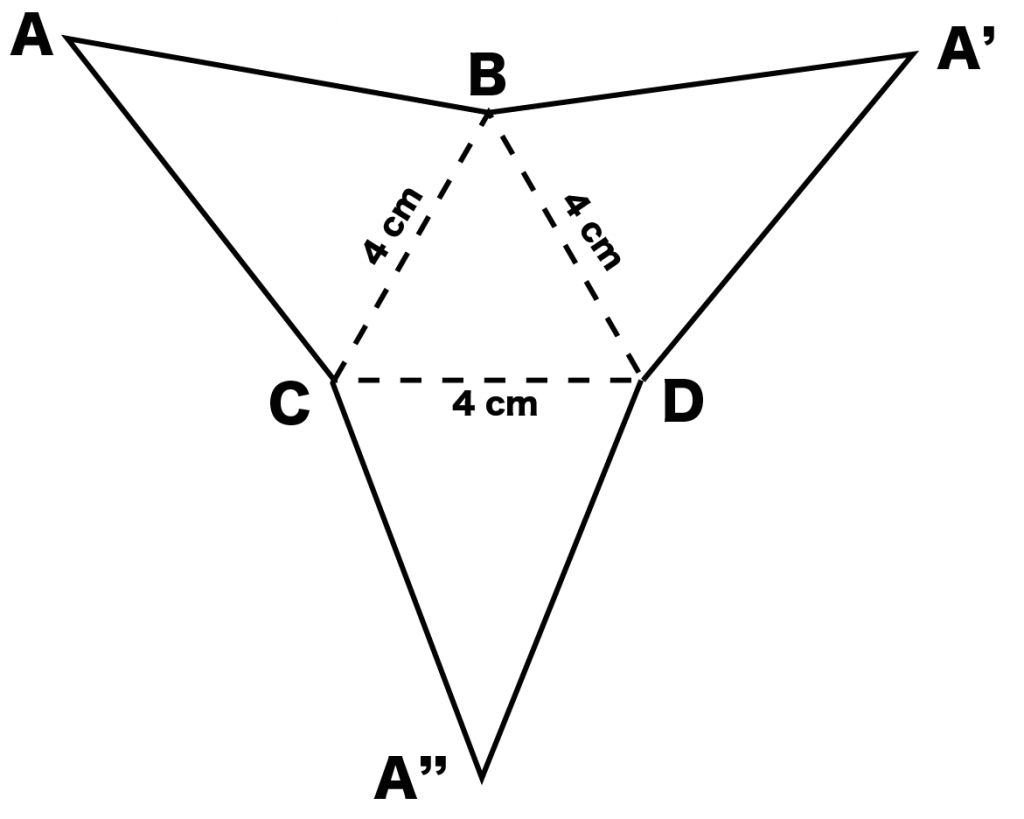
残されたのはあと1つ。もう一方の底面だけさ。
あとはコイツを長方形のうえにのせてあげよう！ 対応する辺同士をくっつけるればいいんだ。
例題でいうと、
「三角形DE”F’」を「長方形ACF’D」のうえにちょこんとのせているね。
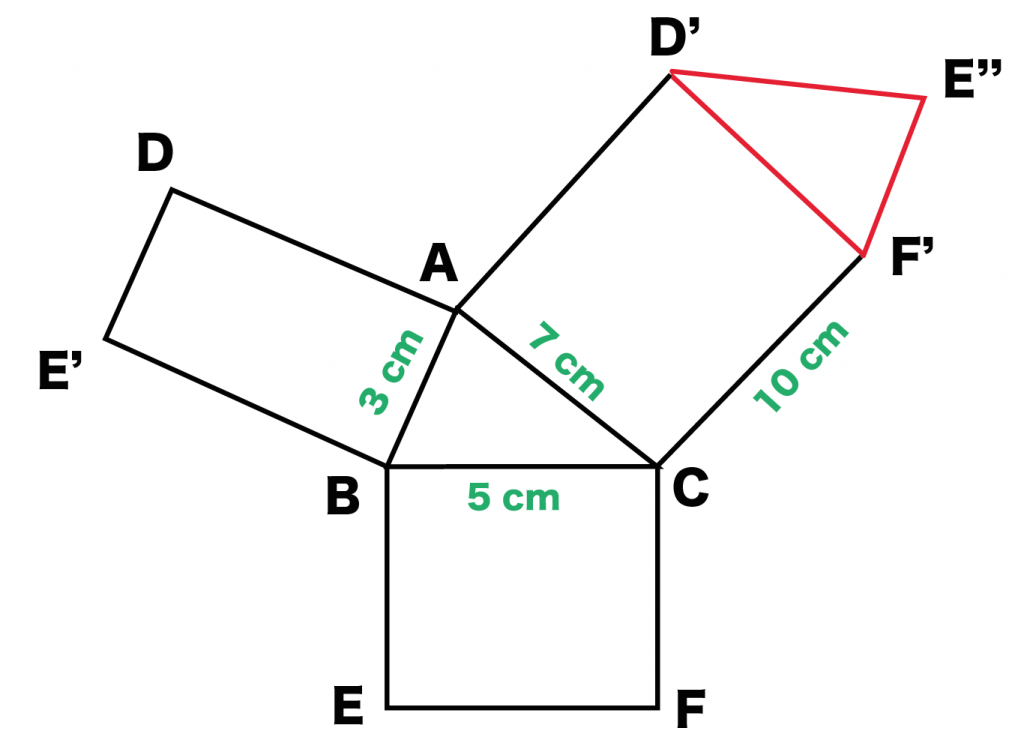
対応する辺は「DF」。一緒にくっつけることを忘れずに。
底面からでも展開図をかけたね！おめでとう！！
三角柱の展開図の作図はどうだった？？
テストででても慌てずにゆっくりと作図してみてね。
そんじゃねー
Ken
