やあやあ、Dr.リードだよ。
3年生の数学もいよいよ大詰め。
今日は、高校入試でよく出てくる、
正四角錐の高さを求める問題
を解説していくぞ。
正四角錐って、底面が正方形で、先っちょが尖ってる立体のことだったね。

ちょうど、エジプトのピラミッドが正四角錐だな。
正四角錐の高さを求めるためには、中3で勉強した三平方の定理も使っていくぞ。
正四角錐の高さの求め方はつぎの4ステップだ。
つぎの例題をいっしょに解いていこう。
練習問題
つぎの正四角錐の立体の高さを求めなさい。
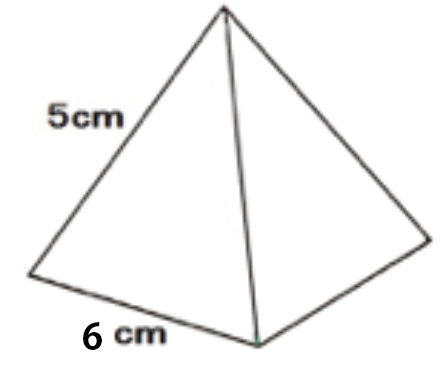
まずは、補助線をガンガン入れる。直角にも印をつけるといい。
正四角錐の中の直角三角形を見つけやすくするためだ。
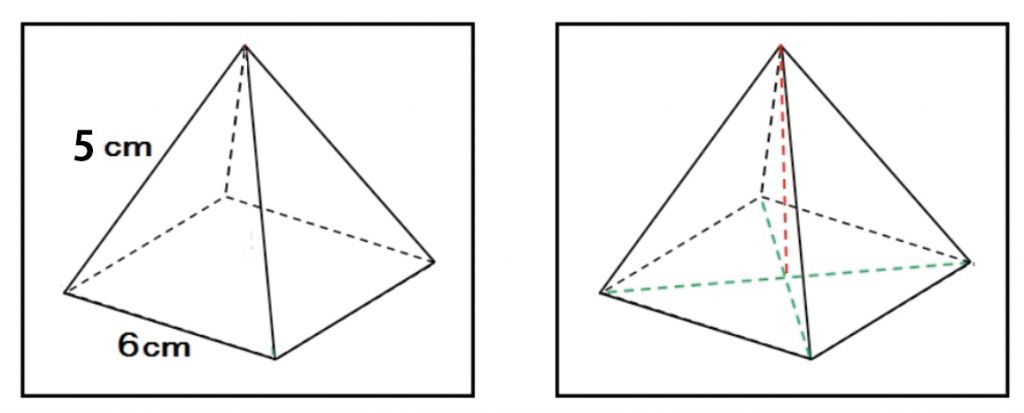
つぎは、正四角錐の底面に注目してみよう。
底面の正方形の対角線の長さを計算していくんだ。
底面は1辺が6cmの正方形だったな?
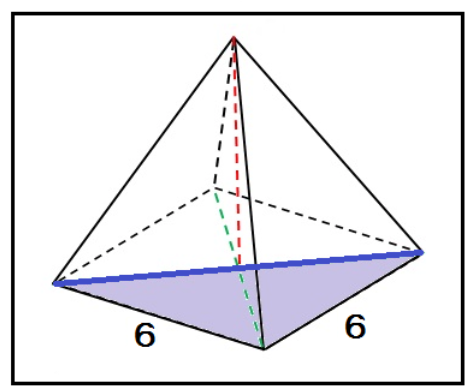
この正方形の半分の直角三角形で三平方の定理を使ってやると、
6² + 6² = x²
x = √72 = 6√2
になるぞ。
ってことは、正四角錐の底面の対角線の半分の長さは、
6√2÷2 = 3√2
だ。
つぎは、正四角錐の頂点からの垂線に注目。
垂線をふくむ直角三角形を探して、三平方の定理を使えばいいんだ。
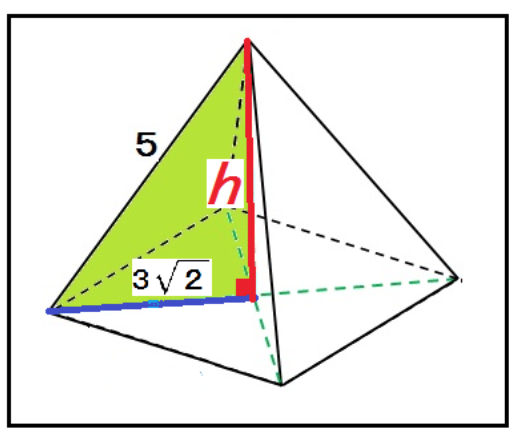
さっき見つけた正四角錐の頂点からの高さを求めてみよう。
使うのは、もちろん、
三平方の定理!
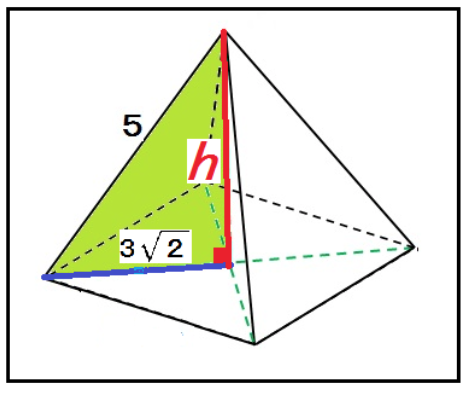
正四角錐の頂点からの高さをhとしてやると、
5² = (3√2)² + h²
h = √7
になるね。
つまり、この正四角錐の高さは√7 cmってわけ!
正四角錐の高さの求め方はどうだったかな?
つぎの4ステップで計算できちゃったな。
入試問題によく出てくるから復習しておこう。
正四角錐の高さが計算できたら次は円錐の高さに挑戦してみよう。
じゃあな
Dr.リード
こんにちは!この記事をかいてるKenだよ。そろそろ進撃したいね。
半球の表面積の公式は簡単。
半径をrとすると、
3πr^2
で計算できちゃうんだ。
つまり、
半径×半径×円周率×3
ってわけだね。
たとえば、半径が6cmの半球があったすると、こいつの表面積は、
半径×半径×円周率×3
= 6 × 6 × π × 3
= 108π [cm^2]
になるんだ。
どう??
半径と円周率かけるだけさ!
半球の表面積の求め方はわかった。
だけど、
なんで球の表面積の半分じゃないの??
って思うよね。
半球の体積は「球の体積の半分」だったのに・・・ってね。
じつは球の表面積は、
っていう2つの面積で成り立っているんだ。
モンブランケーキでいえば、
って感じ。
こいつらの面積を別々に求めて、最後にたしてるんだ。
試しに、半径6cmの半球の表面積を計算してみよう!!
まずは、球の表面積の半分をだそう。
モンブランでいうと、クリームがついている部分だね。
4πrの二乗
だったよね??
ってことはその半分は、
2πrの二乗
になるはず!
だから、半径が6cmの半球のクリーム部は、
半径×半径×円周率×2
= 6×6×π×2
= 72π [cm^2]
になるんだ。
つぎは半球の断面積だ。
つまり、底面の面積をたせばいいよ。
モンブランでいうと「タルト」にあたるね。
半球の断面積は円。
円の面積の公式は、
半径×半径×円周率
だったよね??
だから、例の半径6cmの半球の断面積でいうと、
半径×半径×円周率
= 6×6×π
= 36π [cm^2]
になるね。
あとは、
の2つをたすだけ。
例の半径6cmの半球の表面積は、
(球の表面積の半分)+(断面積)
= 72π + 36π
= 108π [cm^2]
になるんだ。
おめでとう!
これで半球の表面積も計算できちゃうね。
半球の表面積はトリッキー。
球の表面積の半分じゃないんだ。
球の表面積の半分に、底面積をたすからね。
半球の体積の求め方とはひと味ちがうから注意しよう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。シャツほしいね。
半球の体積を求め方には公式があるよ。
半径rの半球の体積は、
(3分の2π) × (rの3乗)
になるんだ。
つまり、
半径×半径×半径×円周率×2÷3
ってわけだ。
えっ。
覚えられないだって??!
じつはこの公式。
球の体積のちょうど半分なんだ!
球の体積の公式は、
(3分の4)×(円周率)×(半径)×(半径)×(半径)
だったよね??
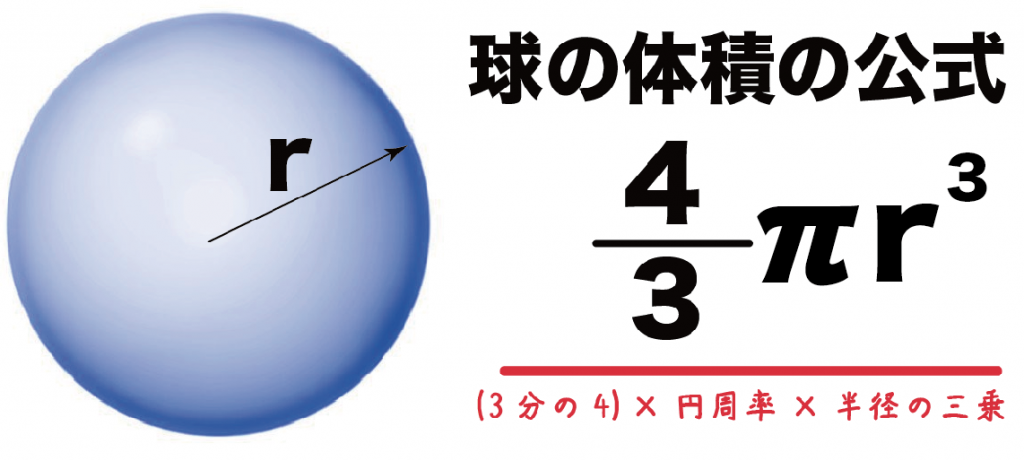
それを半分にしたのが「半球の体積の公式」になる。
なぜなら、
半球は球をスパッと半分にきったものだからね。
体積は球の半分になるってわけ。
たとえば、半径6cmの半球Aがあったとしよう。
こいつの体積は公式をつかうと、
(半球Aの体積)
=(半径)×(半径)×(半径)×(円周率)× 2 ÷ 3
= 6 × 6 × 6 × π × 2 ÷ 3
= 144π [cm^3]
になるんだ。
どう??半球の体積を求められたかな??
半球の体積なんてぜんぜん使わなくね??
って思ってない?。
ぶっちゃけ、半球をみくびってるよね。
その気持ちわかるw
ただ、半球の体積の求め方は、
立体の応用問題で役に立つんだ。
たとえば、つぎのような問題だね↓↓
この問題は3ステップでとけちゃうよ。
まずソフトクリームを、
「アイス」と「コーン」に分解してみよう。
つまり、上の「半球」と下の「円錐」にわけるってことさ。
これが第1ステップ!!
「半球」と「円錐」の体積をべつべつに計算してみよう!
体積の求め方の公式はそれぞれ、
だったよね??
まず半球の体積は、
6×6×6×π×2÷3
= 144π [cm^3]
になる。
半径×半径×円周率×高さ÷3
だったよね??
こいつで下のコーンの体積を計算してやると、
半径×半径×円周率×高さ÷3
= 6×6×π×12÷3
= 144π [cm^3]
になるはずだ。
これが第2ステップ!!
最後に、
の体積をたしてみよう。
例題での体積はそれぞれ、
だったよね?
こいつらをたしてやると、
ソフトクリームの体積
= (半球の体積)+(円錐の体積)
= 144π + 144π
= 288π [cm^3]
になるね。
おめでとう!
これで応用問題もクリアだね。
半球の体積の公式はマイナー。
だけど、覚えておいて損はない。
ソフトクリームみたいな立体の体積もわかっちゃうし。
半球の体積は「球の体積の半分」っておぼえておこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。バターチキン最高。
円錐にひもをかける問題ってあるよね???
たとえば、つぎのような問題だ。
例題
母線の長さ PA = 6 cm、底面の半径OAの長さ = 1 cmの円錐Pがある。この円錐に赤いひもが最短距離になるようにかけたとき、この「ひも」の長さを求めてください。
なんで円錐にひも???
って思うかもしれないね。
正直、とくのがつらい。
だけど、
円錐にかけたひもの最短距離を求める問題
ってよくでてくるんだ。
今日はこのタイプの問題の、
円錐にかけたひもの最短距離を求める問題の解き方
を3ステップで解説してみたよ。
よかったら参考にしてみてね。
3ステップでとけちゃうよ。
例題をといていこう。
例題
母線の長さ PA = 6 cm、底面の半径OAの長さ = 1 cmの円錐Pがある。この円錐に赤いひもが最短距離になるようにかけたとき、この「ひも」の長さを求めてください。
円錐の展開図をかいてみよう。
とりあえず、円錐の展開図っぽいやつをかこう。
中心角は気にしなくていいよ。
これが第1ステップさ。
つぎは側面の「扇形の中心角」をだしてみよう。
出し方は簡単。
中心角をxとして方程式をたてればいいんだ。
側面の扇形の弧の長さ
と
底面の円周の長さ
が等しい
っていう式をつくればOK。
例題をみてみよう。
中心角をxとしたから、
になるね。
だから方程式は、
(扇形の弧の長さ)=(底面の円周長さ)
2×6 ×π× X ÷ 360 = 2× 1 × π
になる。
これをといてやると、
中心角X = 60°
になるはずだ。
つぎは展開図に「ひも」をかいてみよう。
例題でいうと、赤いひもは、
AからスタートしてAにもどってきているよね??
しかも、その長さが最短距離。
ってことは、展開図でいうと、
A
と
組み立てたらAに重なるA’
を直線でむすんでやればいいんだ。
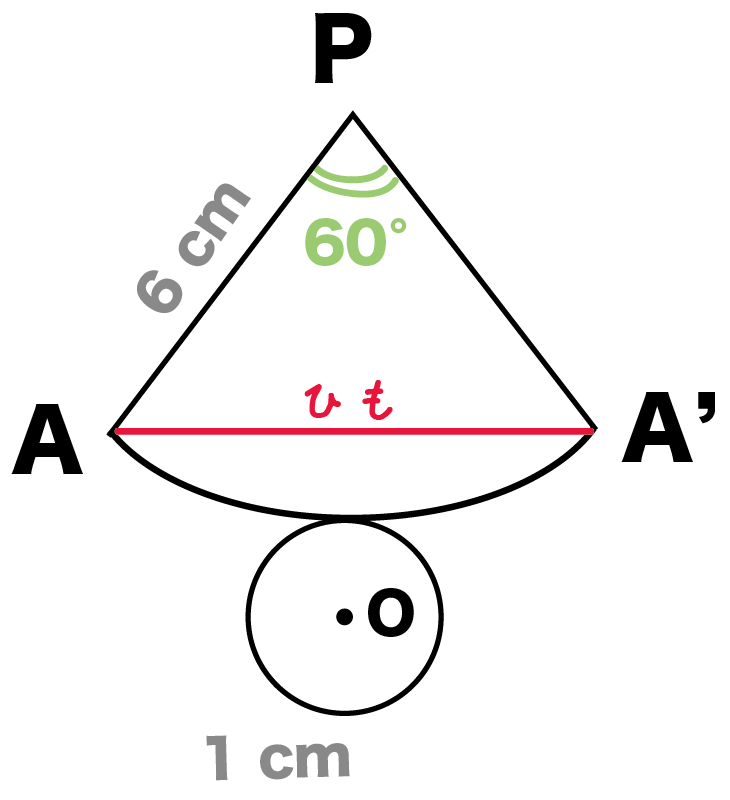
最後は直角三角形の比をつかおう。
「ひも」と「母線」でできた三角形に注目してくれ。
例題でいうと、△PAA’だね。
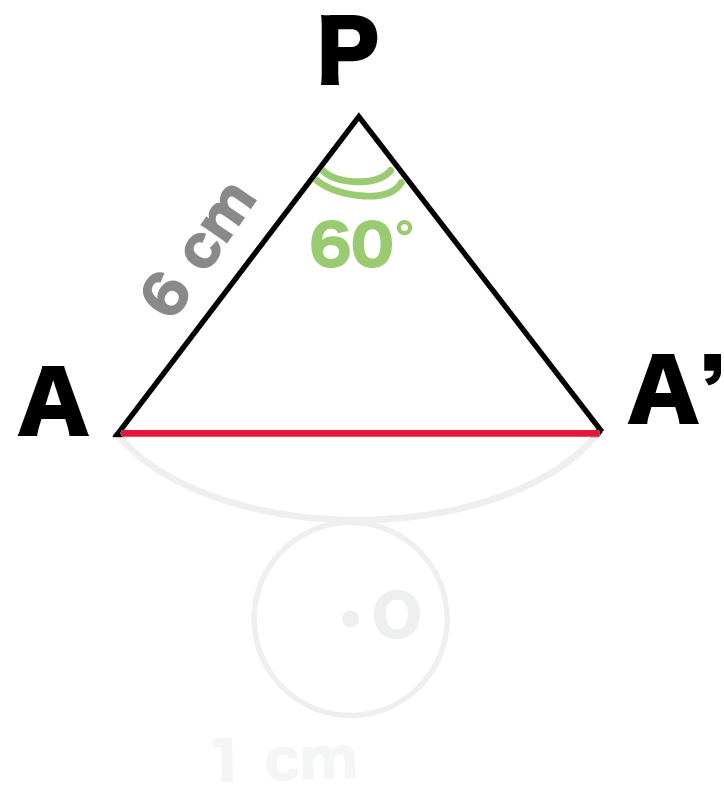
こいつは、
の二等辺三角形。
頂角の二等分線は底辺を垂直に二等分する
というやつを使ってみよう。
PからAA’に二等分線をひく。
交点をHとすると、
になるね。
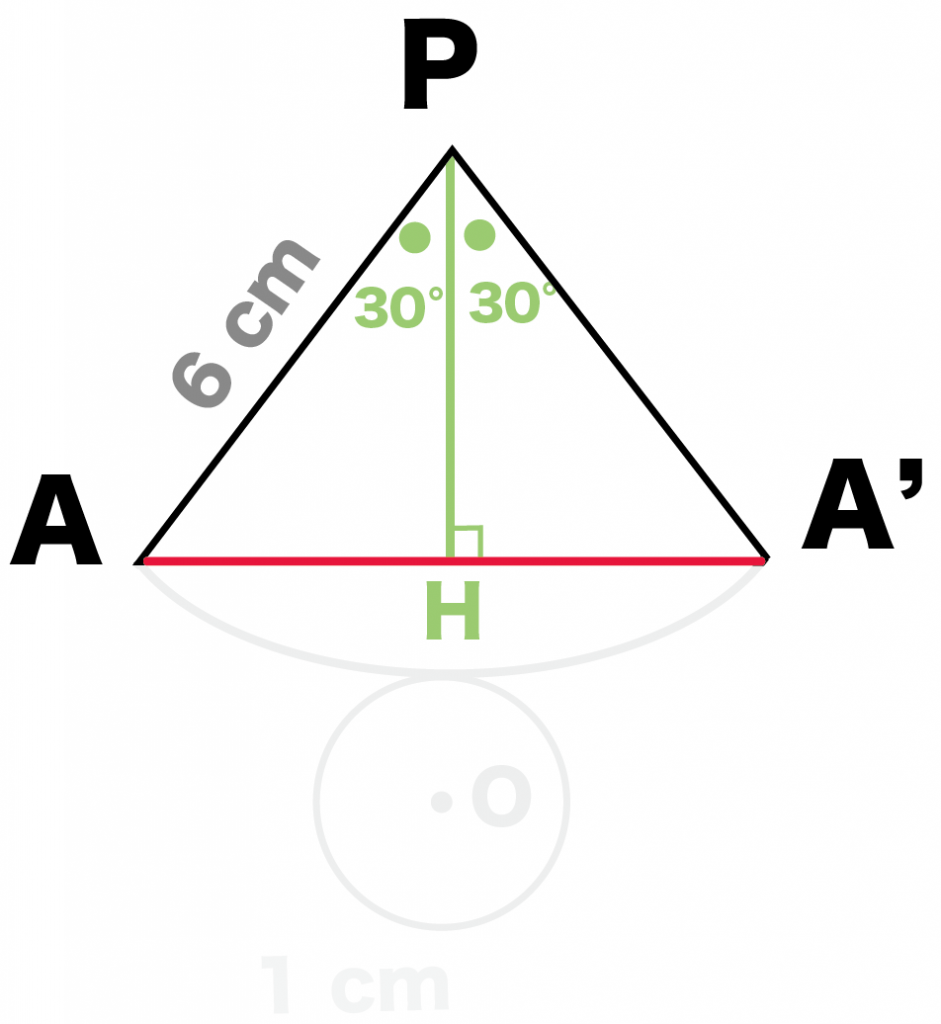
んで、
△APHは頂角30°の直角三角形だから、
1 : 2: √3
の辺の比になっているはず。
よって、
AP: AH = 2: 1
AH = 3 cm
になる。
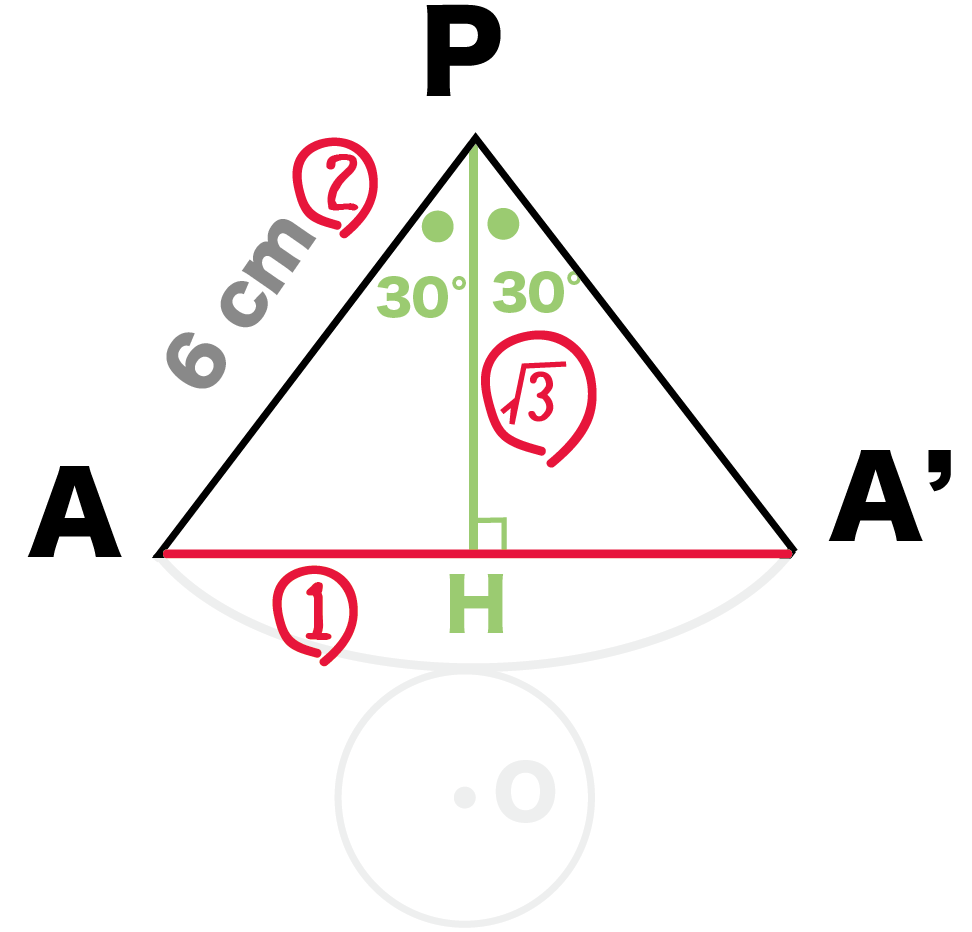
PHはAA’の垂直二等分線になっているはず。
よって、
ひもの長さAA’
= 2 × AH = 6 cm
になるね。
おめでとう!
これで、ひもでも糸でもなんでもこいだね!
最短距離の問題って、
の知識が必要になってくる。
ってことはつまり、
1~3年生の知識をフル活用しないと解けない。
だから入試問題にでやすいのかもね。
テスト前によーく復習しておこう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。トマトはヘルシーだね。
円錐の高さを求める問題
ってたまにでるね??
こいつは中1数学でならった
と、
中3でマスターする「三平方の定理」でといていくんだ。
かなりくせ者だね。
今日はコイツを攻略するために、
円錐の高さの求め方がわかる3ステップ
を解説していくよ。
よかったら参考にしてみて。
3ステップで求められるよ。
例題をといてみよう!
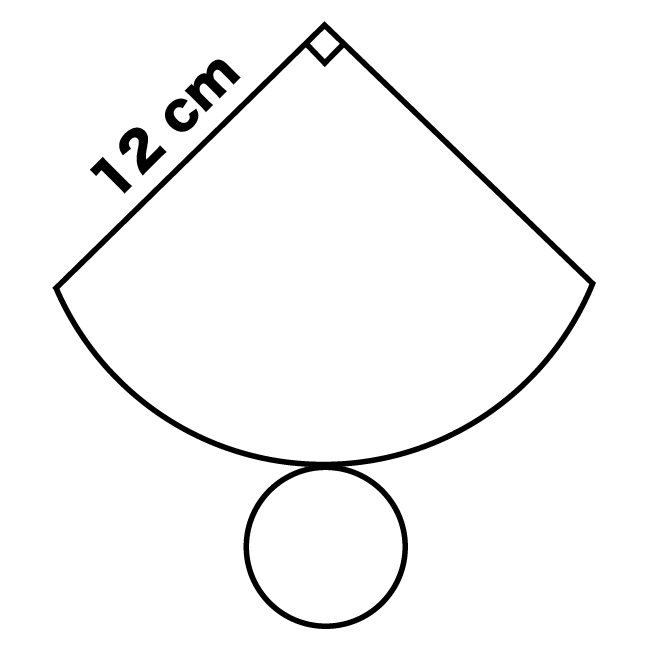
例題
下の図は円錐の展開図です。円錐の側面が、半径12cm、中心角90°のとき、円錐の高さを求めなさい。
まずは円錐の側面の、
弧の長さ
を計算しよう。
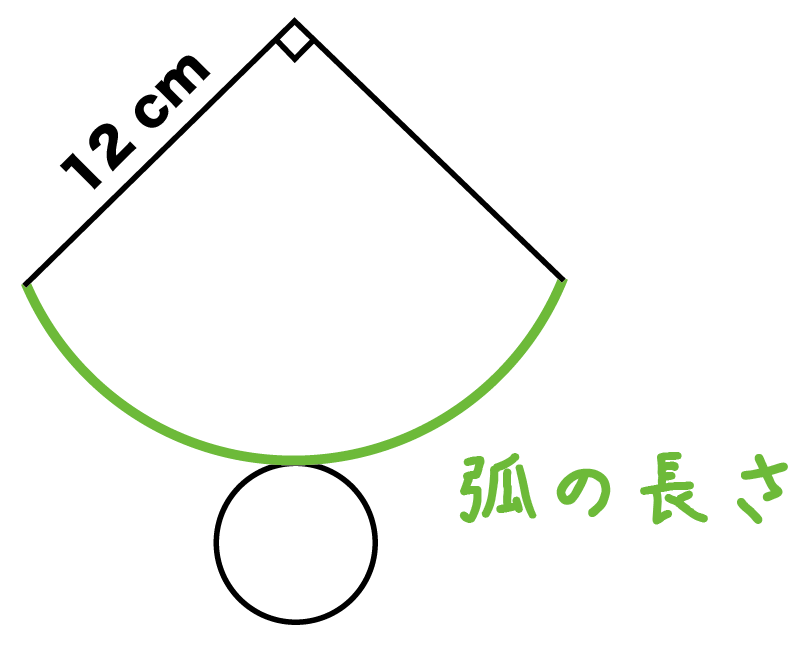
えっ。
弧の長さの出し方がわからないって??
円錐の側面は「おうぎ形」だったね。
だから、
をつかえばいいんだ。
扇形の弧の長さは、
直径×円周率×中心角÷360
で計算できたね。
例題の扇形は、
だ。
公式をつかってみると、
(扇形の弧の長さ)
= (直径)×(円周率)×(中心角)÷ 360
= 24 × π × 90 ÷ 360
= 6π
になる。
これが第1ステップ!!
つぎは円錐の底面に注目。
半径を計算するんだ。
半径の長さをrとして方程式をたてるよ。
円錐の展開図をくみたてると、
「底面の円」
と
「側面の弧」
がかさなるでしょ??
だから、
(底面の円周の長さ)= (側面の扇形の弧の長さ)
っていう方程式がつくれるんだ。
(底面の円周の長さ)= (側面の扇形の弧の長さ)
(直径×円周率)= (直径×円周率×中心角÷360°)
2 × r × π = 2 × 12 × π × 90° ÷ 360°
r = 3 [cm]
になるね!
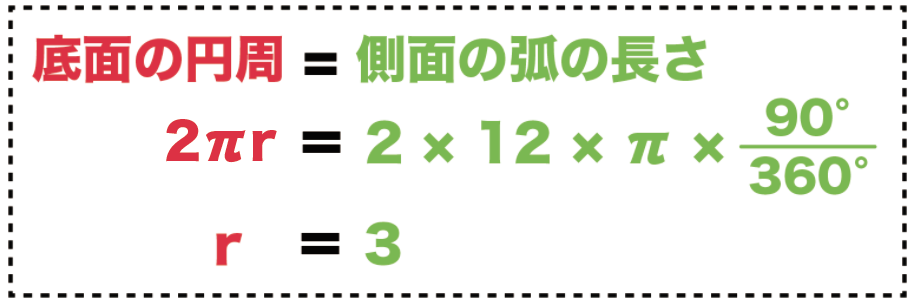
底面の半径は「3 cm」ってことさ。
第2ステップ終了!
最後は三平方の定理をつかうよ。
円錐をナイフできってやると、
直角三角形がでてくるでしょ??
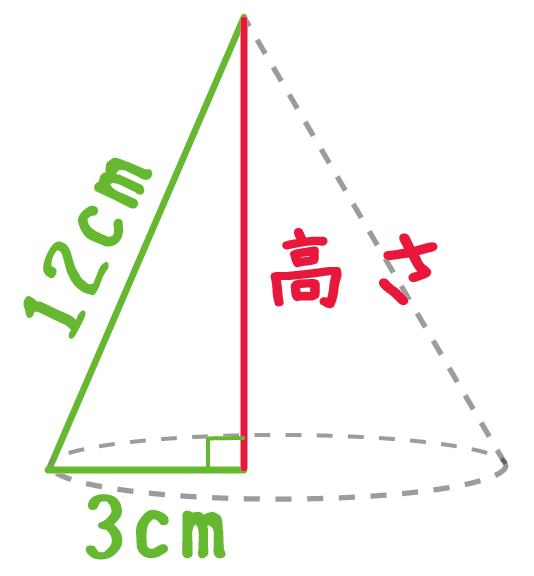
三平方の定理をつかうと、
(円錐の高さ)
= √(斜辺の二乗)- (その他の1辺の二乗)
= √ (12)² – 3²
= √135
になるね。
おめでとう。
円錐の高さもゲットだね!
円錐の高さを求めるのはむずそう。
だけど、基本をおさえれば大丈夫。
の3ステップで、
じゃんじゃん求めていこう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。アップルティーはいつ飲んでもうまいね。
中学数学ででてくる球の公式って次の2つあったよね??
※球の半径をrとした場合

この2つの公式を覚えていないとテストで問題をとけないし、
クラスの人気ものにはなれない。
しかも、がんばって2つとも暗記したとしても・・・・
球の体積と表面積の公式がごっちゃまぜになっちまうかもしれないんだ。
たとえば、
4πrの二乗って数式は覚えてるんだけど・・
これって・・・体積・表面積のどっちだっけ??
みたいな感じでね。

今日はそんな緊急事態を避けるため、
球の体積と表面積の公式を見分けるポイント
を2つ紹介するよ。
テスト本番で公式を忘れるのが怖いっていうときに参考にしてみて。
球の体積と表面積の公式をごっちゃまぜにしないためポイントはつぎの2つさ。
1つ目のポイントは、
rが何乗されているか??
ということを確認する方法だ。
つまり、rの乗数をチラ見するってわけ!
rが何乗されているかによって、
次のように「体積」と「表面積」の公式を見分けることができるよ。

つまり、
4/3πrの三乗という公式は「rが三乗されている」から「球の体積の公式」ってこと!
また、
4πrの二乗は「rが二乗されている」から「球の表面積の公式」になるってことだね。

二次元の表面積を計算するときは「rを2回かける」、
三次元の立体の体積を計算するときは「rを3回かける」、
って感じでrをかける回数をおぼえておこう!
球の体積と表面積の公式がごちゃまぜになったときは、
rが何乗されているのか??
ということを必ず確認してみてね。
2つめのポイントは、
1/3をかけているかどうか
だ。
もし、1/3が混じっている公式ならそいつは「球の体積の公式」ってことになるよ。

とくに理由はないんだけど、
1/3をかけるのは「錐体(先がとんがっている立体)」の体積の公式と同じでしょ??
たとえば、四角錐の体積の求め方とかね。
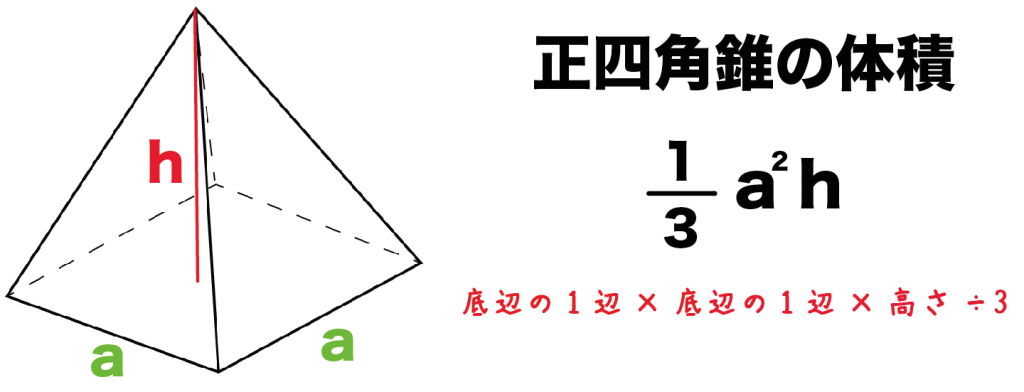
だから、錐体の体積の求め方と同じように「1/3」をかけている計算式は「球の体積の公式」だよ
っておぼえておこう!!
これなら表面積の公式とごっちゃにならないはず。
上の2つのポイントを覚えておけば、
球の体積と表面積の公式をごちゃまぜにする
というミスはないはずだ!
本番前にはもう一度公式を確認してみてねー!
そんじゃねー
Ken
なぜ球の体積の公式がつかえるか気になったらみてみて↓
こんにちは!この記事をかいているKenだよ。豚肉を今日もいためたね。
球の表面積の求め方には公式があるんだ。
球の半径をrとすると、その表面積は、
4πr^2
になるよ。

つまり、
4 × 円周率 × 半径 × 半径
ってわけだね。
たとえば、半径30cm のサッカーボールがあったとしよう。
このボールの皮の面積、つまり表面積は、

4 × π × 30 × 30
= 3600π [cm^2]
になるんだ。公式にいれて計算するだけでいいんだ。
チョー便利な公式じゃない?。
ただ、球の表面積には、
チョー覚えにくい
っていう欠点もある。
4をかけてπをかけて半径を2回かけるなんて覚えるのはむずかしすぎる!ってなるよね。
だって、4とかどっから出てきたのかよくわからないし。
そこで今日は、
球の表面積の求め方の公式を1発でおぼえる方法
をひそかに伝授しよう。公式をおぼえたいときに参考にしてみてね。
球の表面積の求め方の公式である、
4×π×半径の二乗
を一発で暗記してできちゃう語呂を紹介しよう。
このイメージさえ掴んじまえば、テストでも公式を忘れないはず!
球の表面積の公式を暗記するための語呂は、
9匹のヒョウの捕獲に失敗したあるじ
だ。
銃を持っているけど、弾切れでヒョウを捕獲できない「あるじ」を思い浮かべてみて!
えっ。なんでこれが球の表面積の公式になるのかって?!?
じつは、
になっているんだ。
つまり、
9匹(球)のヒョウ(表面積)の捕獲に失敗(4π)したあるじ(rの二乗)
っていう感じで球の表面積の公式が覚えられるってわけ!!
どう?球の表面積をおぼえるなんて簡単でしょ??。
球の表面積の公式はおぼえられた??
9匹(球)のヒョウ(表面積)の捕獲に失敗(4π)したあるじ(rの二乗)
という語呂さえおぼえておけば大丈夫。
表面積と体積の公式をごっちゃまぜにすることなんてないはずだよ。
がんばって暗記してみてね。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。ビニール傘を買っちゃったね。
球の体積の求め方には公式があるんだ。
球の半径をrとすると、体積の求め方は、
$$\frac{4}{3}πr^3$$
になるよ。
つまり、
3分の4 × 円周率 × 半径 × 半径 × 半径
ってことだね。
この公式でどんなボールの体積も計算できちゃうんだ。
たとえば、半径30 [cm]のサッカーボールがあったとしよう。

こいつの体積は「4/3 × π × 半径の三乗」という公式をつかってやると、
$$\frac{4}{3} × π × 30 × 30 × 30= 36000π [cm³]$$
になるね。
これってサッカーボールの中にどれぐらい空気が入っているか?ってことなんだ。
ちょっとすごくない。?
ただ、この公式にも一つだけ欠点がある。
それは、
むちゃくちゃ暗記がむずかしい
ってことさ。
3分の4なんてどっから来た数字かわからないし、半径を何回かけたらいいのかわからない。
これじゃあ球の体積の問題をだされたらやばすぎる・・・・
そこで、今日は、
中学生でもおぼえられる「球の体積の求め方」を解説していくよ。
球の体積の公式を忘れちゃったときに参考にしてみて。
「球の体積の公式」を暗記する方法を伝授しよう。
3分の4 × 円周率 × 半径の三乗
という公式はつぎの語呂を使えばおぼえられちゃうよ。
さんしろう、おいしいパイを持ってある日参上

えっ。
あ、大事だからもう一度繰り返すよ。
さんしろう、おいしいパイを持ってある日参上
なぜこの語呂で「球の体積の公式」おぼえられるのか。
それは、
さんし(3分の4)ろう、美味しいパイ(π)を持ってある(r)日参上(三乗)
になるからさ。
つまり、
という感じで、それぞれの言葉が対応してるってわけ。
だから、
さんしろう、美味しいパイを持ってある日参上

という語呂を覚えてしまえば「球の体積の求め方」の公式も一生忘れないってことさ。
おめでとう!!
中学数学では「球の体積の公式」が使える理由がわからない。
完全に理解するためには「積分」という知識を使わなきゃいけないんだ。
だからこそ、中学生の間は、
さんしろう、美味しいパイを持ってある日参上

という語呂で「球の体積の公式(3分の4 × 円周率 × 半径の三乗)」をおぼえてしまおう。
テスト前にがんばって暗記してみてね。
そんじゃねー
Ken
なぜ球の公式がつかえるのか気になったらみてみて↓
こんにちは!この記事をかいているKenだよ。ライチティーうまいね。
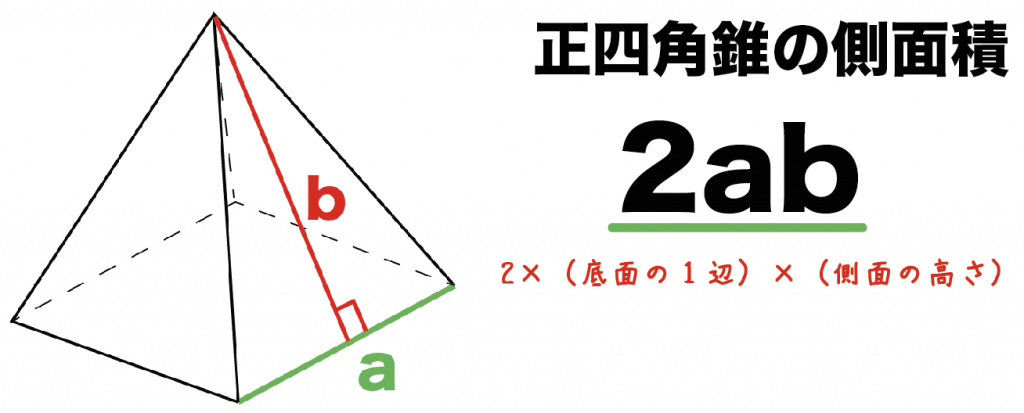
正四角錐の側面積の求め方にも公式があるんだ。
底面の1辺の長さをa、側面の三角形の高さをbとすると、
2ab
で側面積を求めることができるよ。
つまり、
「正方形の1辺」×「側面の三角形の高さ」× 2
を計算すればいいってことだね。
今日はこの公式を使えるようにするために例題をといていこう!
つぎの例題をみてくれ↓↓
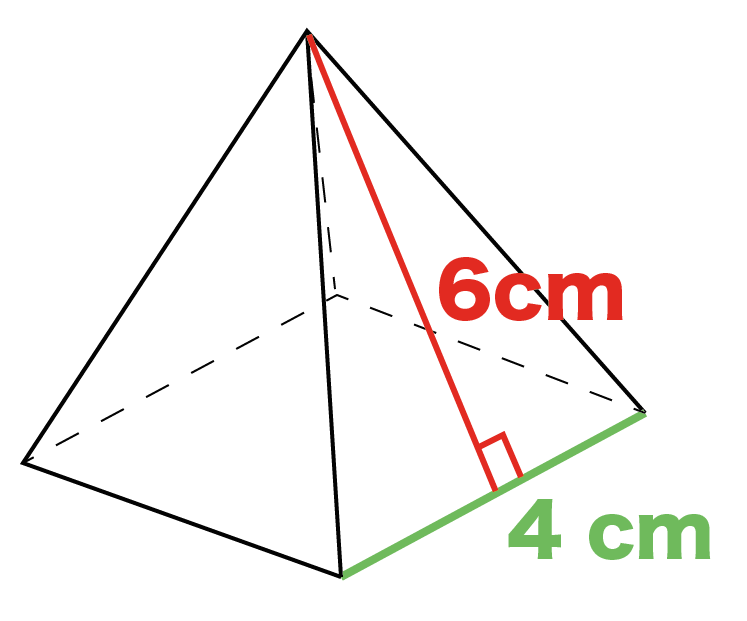
例題
底面の正方形の長さが「4cm」、側面の三角形の高さを「6 cm」の正四角錐の側面積を求めなさい。
この手の問題は2ステップでとけちゃうよ。
1つの側面の面積を計算してみよう。
正四角錐の側面は「三角形」だから、
底面×高さ×1/2
で求めることができるね。

例題の側面の三角形の底辺は「4 cm」、高さは「6 cm」 だったはず。
こいつの面積を公式通りに計算してやると、
4×6×1/2
= 12 [cm^2]
になるね!
ステップ1で求めた「1つの側面積」を4倍するよ!
えっ。なんで4倍なのかって??
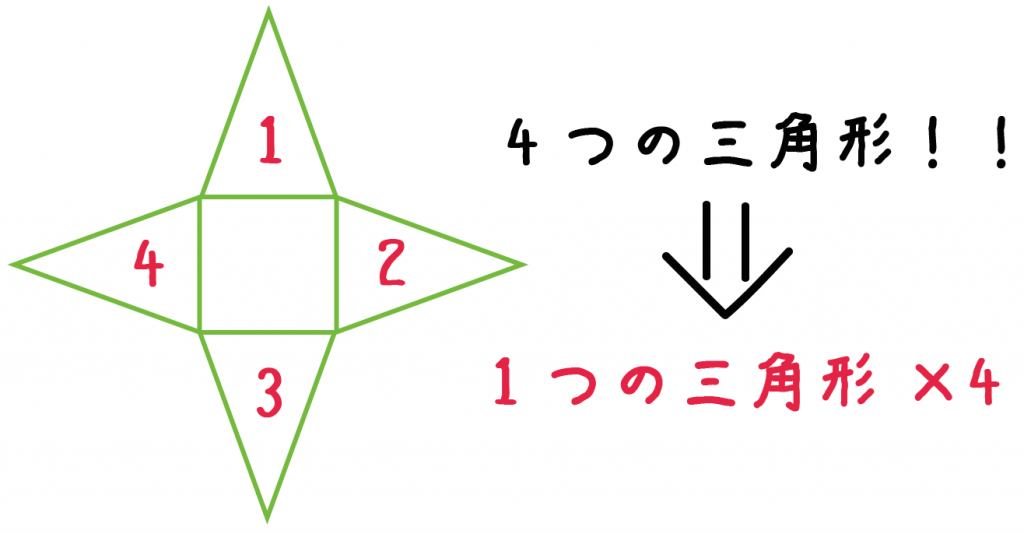
それは正四角錐の展開図をみるとわかるよ。
展開図をかいてみると、
同じ三角形が4つあることに気づくでしょ??
ってことは、1つの側面の面積を4倍してやれば正四角錐の側面積になるわけ!
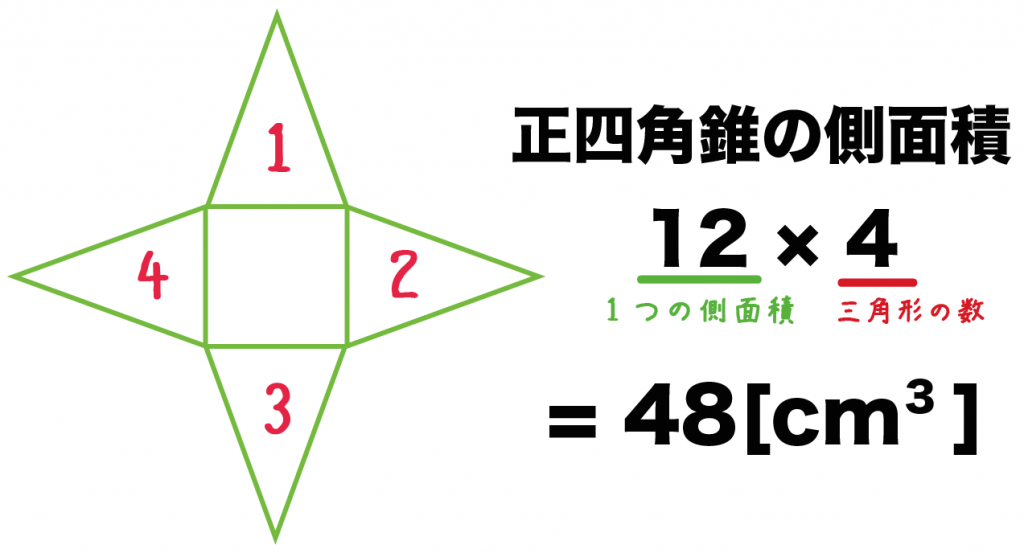
例題の1つの側面積は「12 cm^2」だったよね??
ってことは、こいつを4倍した値が正四角錐の側面積ってことだ。
12×4
= 48[m^3]
になるね。
おめでとう!これで正四角錐の側面積を計算できちゃったね!。
正四角錐の側面積の求め方はどうだった??
公式をつかったら一瞬で計算できちゃう。
だって、
「底面の1辺」と「側面の三角形の高さ」をかけて2倍すればいいんだからね。
公式を使わなくても、正四角錐の展開図をイメージできれば答えらるよ!
テストではミスをしないように気をつけてね。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。コーヒーは無糖に限るね。
直方体の体積の求め方には公式があるんだ。
直方体のタテの長さをa、ヨコの長さをb、高さをcとしよう。
このとき直方体の体積は、
abc
で計算できちゃうんだ。
つまり、
タテ×ヨコ×高さ
ってことだね。
今日は公式をマスターするために、例題を一緒にといてみよう!
つぎの例題をといてくよ↓↓
例題
ヨコの長さ3cm、タテの長さ6cm、高さを8cmの直方体の体積を求めなさい!
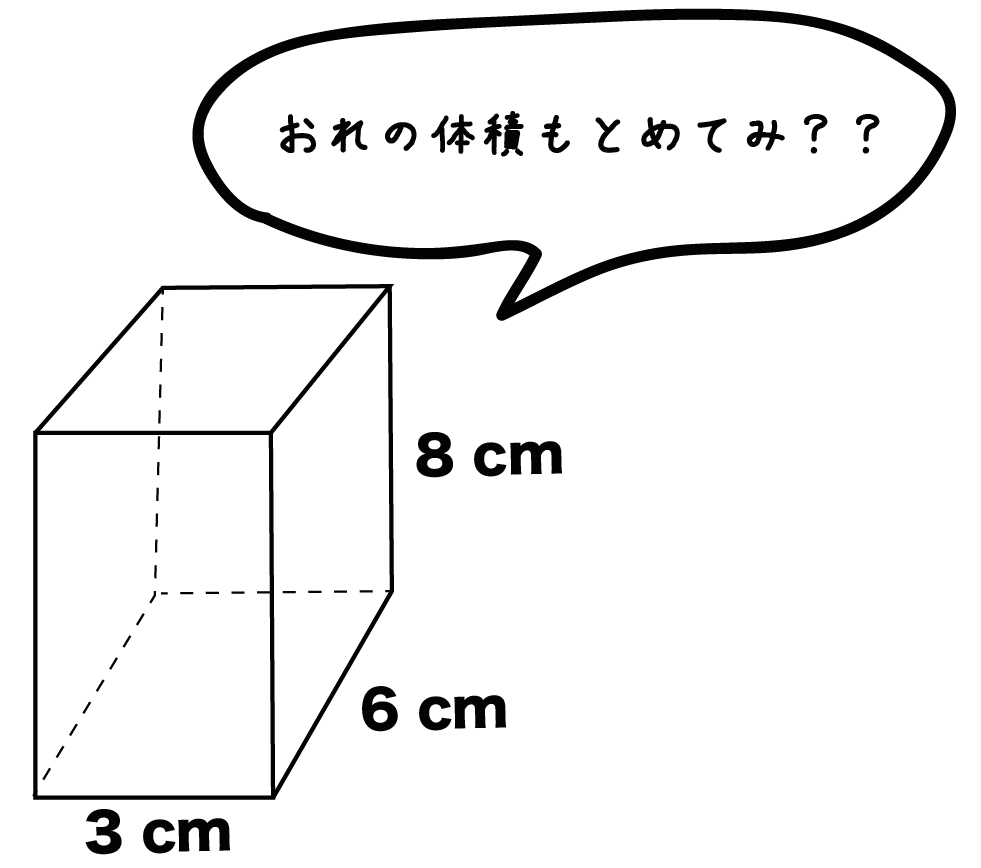
まずは直方体の「ヨコ」と「タテ」の長さをかけてみよう。
「ヨコ」と「タテ」をかけると直方体の底面積が計算できちゃうんだ。

例題でいうと、
タテの長さは「6cm」、ヨコの長さは「3cm」だったね。
こいつらを掛け合わせてやると、
6×3
= 18
になる。
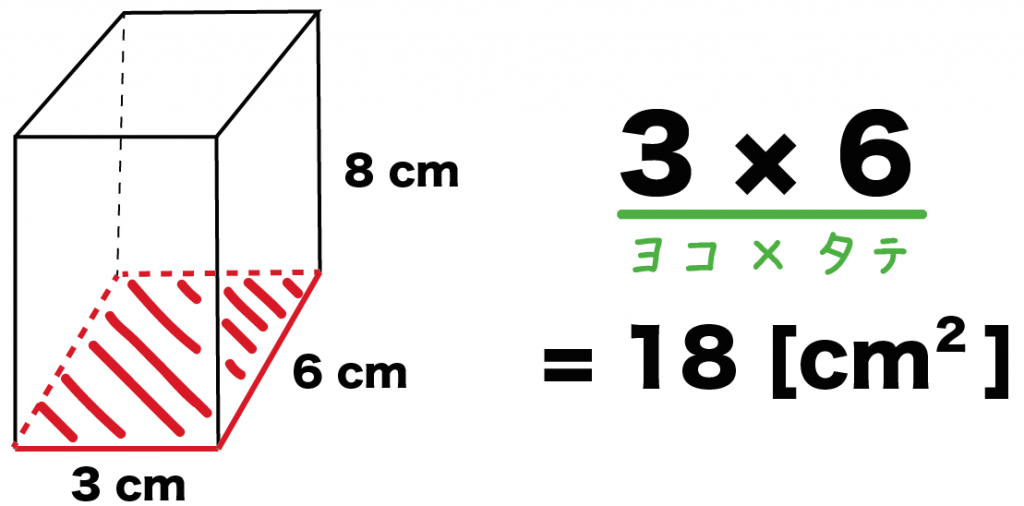
これで直方体の底面積を求めることができたってことさ!
最後に直方体の「高さ」をかけてあげよう。
さっきは直方体の底面積を計算していたよね。これに高さをかけると、直方体の体積になるんだ。

例題の直方体の高さは「8 cm」だったよね??
こいつを「タテ×ヨコ」にかけてやると、
3×6×8
= 144[cm^3]
になるよ。
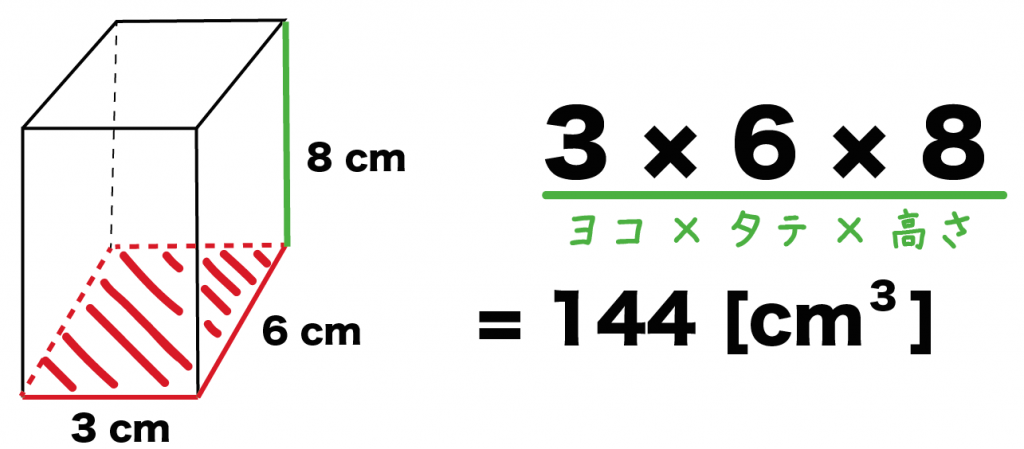
これで直方体の体積を計算できたね。
おめでとう。
直方体の体積の求め方はどうだったかな??
「タテ×ヨコ×高さ」
っていうシンプルな計算だけでいいんだ。
テスト前に復習してみてね。
そんじゃねー
Ken
こんにちは、この記事をかいているKenだよ。鉛筆削りが好きだね。
四角柱の体積の求め方の公式って知ってる??
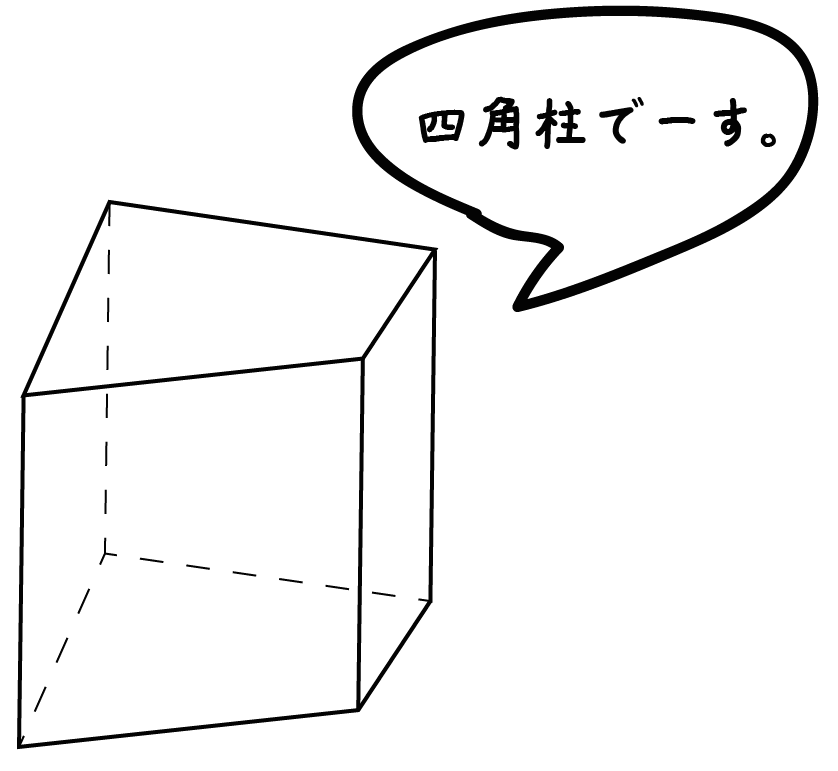
四角柱の底面積をS、高さをhとしてあげると、
四角柱の体積は、
Sh
で計算できちゃうんだ。
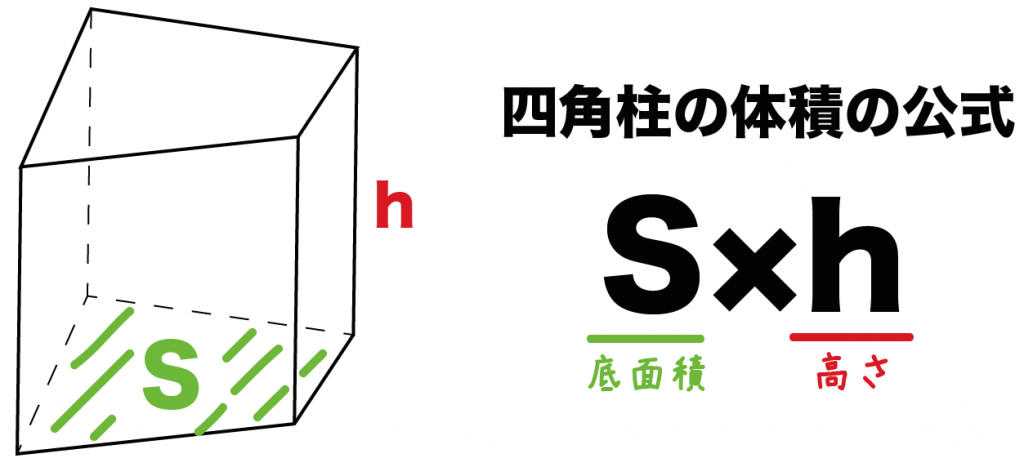
つまり、
底面積×高さ
っていう掛け算だね。なんだかいけそうな気がするっしょ??。
今日はこの公式をつかって実際に例題をといてみよう!
つぎの例題をときながらみていこう。
例題
つぎの四角柱の体積を求めてね。
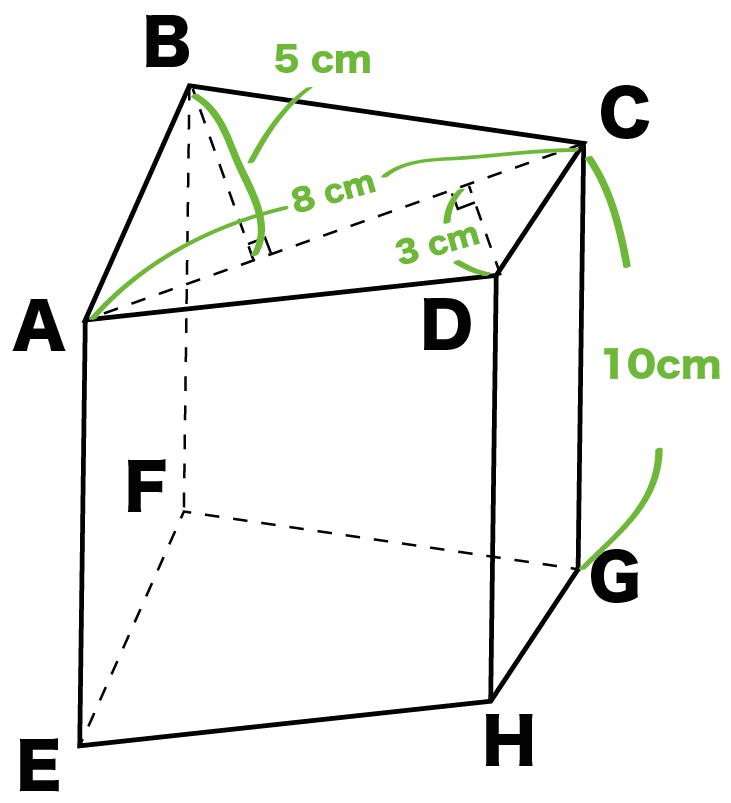
まずは四角柱の底面積を求めよう。
四角柱の底面は「四角形」。公式とかをつかって計算してみてね。
例題の四角柱の底面はちょっと普通じゃない四角形だね。
台形でもないし、ひし形でもないし、もちろん正方形でもない。
こういう四角形は、
2つの三角形の面積を求めて足し合わせる
という作戦で計算してみよう!
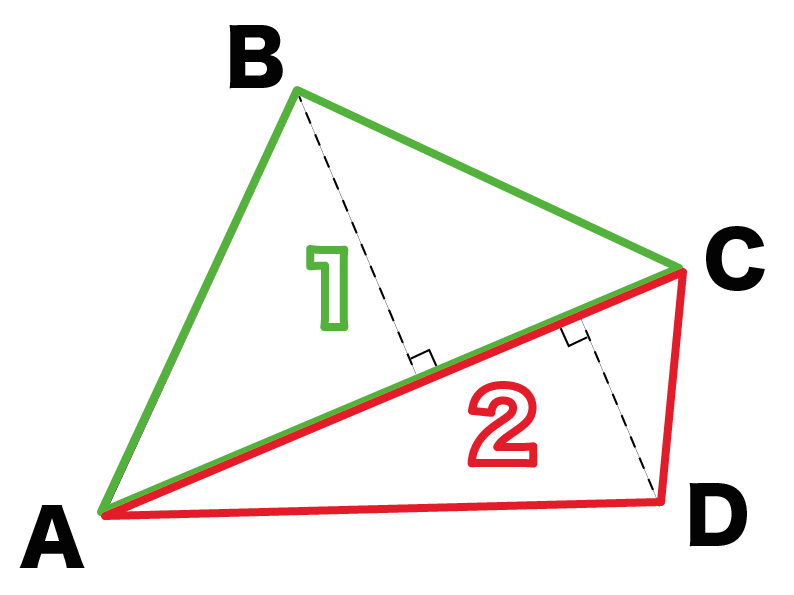
例の底面は緑の「三角形 (1)」、赤の「三角形 (2)」に分割することができるね。
緑と赤の三角形の面積はそれぞれ、
だから、
この四角柱の底面積はその合計の32[cm^2]になるね。
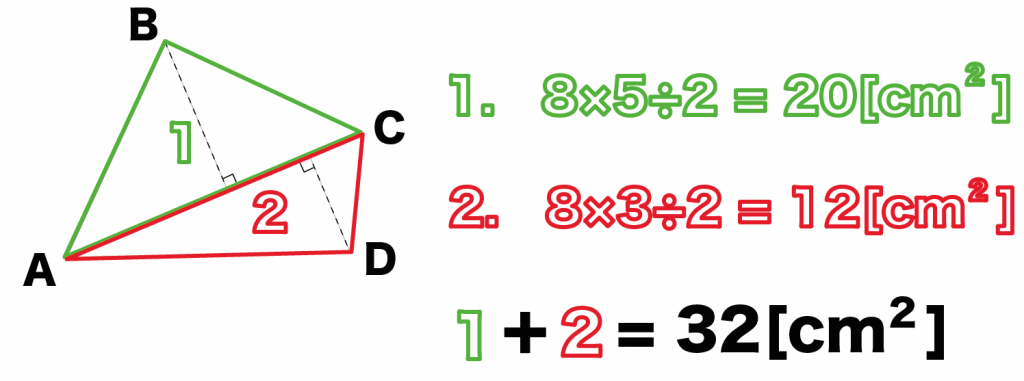
さっき計算した「底面積」に「高さ」をかけてあげちゃおう。
そうすれば四角柱の体積が求まるはずだ。
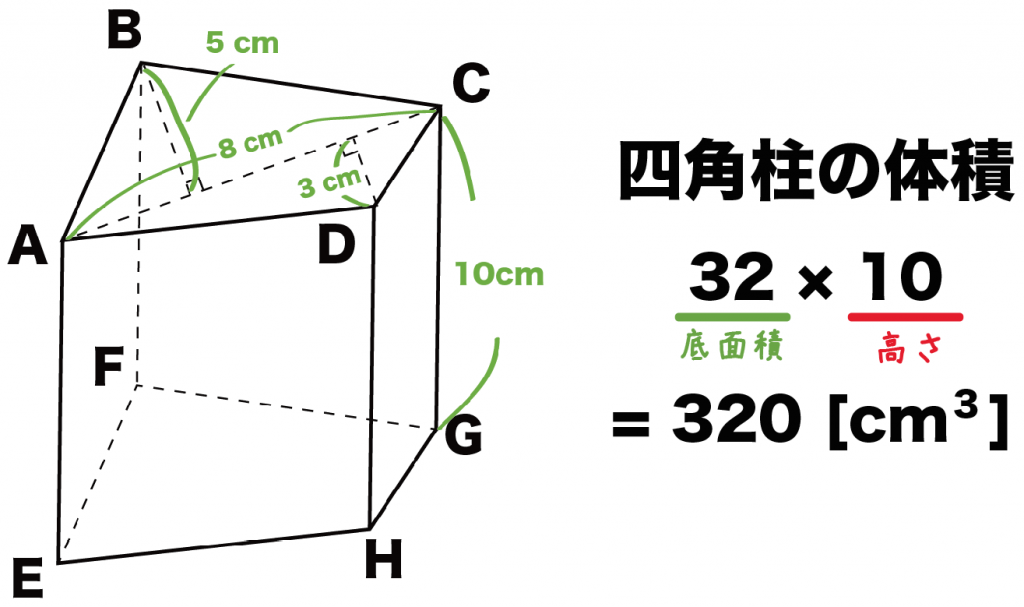
例題の四角柱の高さは10[cm]。
これを底面積である32[cm^2]にかけてやると、
32×10
= 320[cm^3]
になるね。
おめでとう!これで四角柱の体積を計算できたね。
四角柱の体積の求め方はどうだった??
底面の四角形の面積を計算して、それに高さをかけるだけだね。
テストに四角柱の体積がでてきたらバシバシといていこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。青い空が好きだね。
正四角錐の体積の求め方には公式があるんだ。
正四角錐って底面が正方形で、先がとんがっている立体のことだったよね。
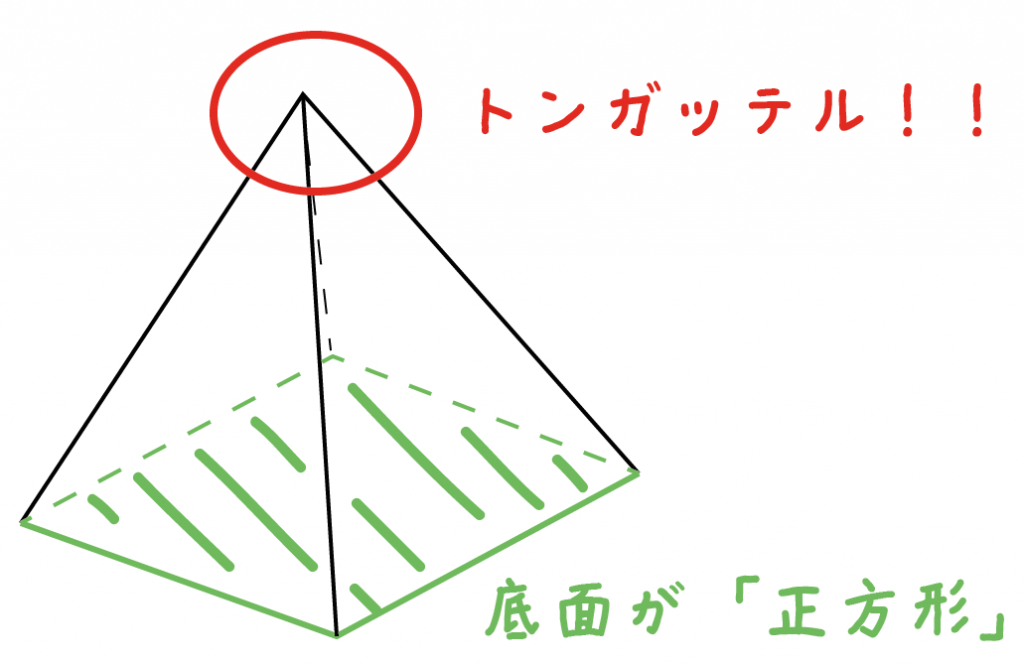
底面の1辺の長さをa、高さをhとすると、体積はつぎのようにあらわせるよ。
1/3 a²h
つまり、
(底辺の1辺)×(底辺の1辺)×(正四角錐の高さ)÷3
ってことだね。
今日は、この計算公式をどうやって使うのか??
ということをわかりやすく解説していくよ。
正四角錐の体積は3つのステップで計算できちゃうんだ。
例題をときながらみていこう!
底辺の1辺の長さが6 [cm]、高さが8 [cm]の正四角錐の体積を求めてください。
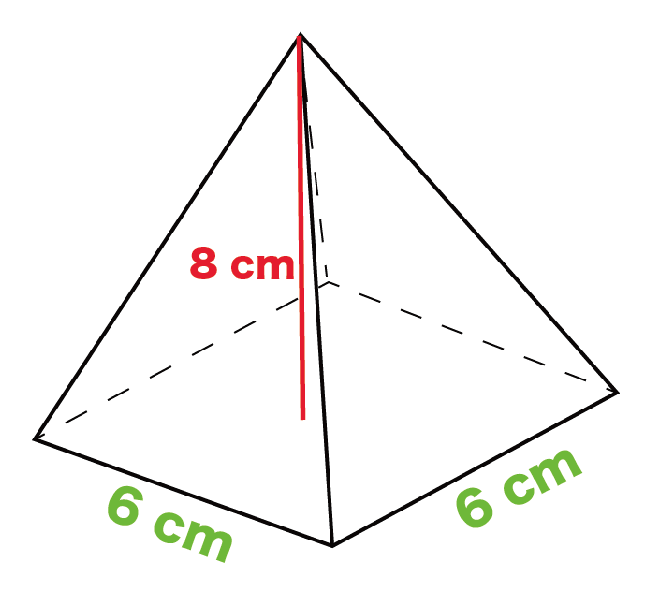
まずは正四角錐の底面積を求めてみよう。
正四角錐の底面は「正方形」だよね?? 正方形の面積を「1辺×1辺」という公式をつかって計算してくれ。

例題でいうと、
底面の正方形の1辺は6[cm]だよね。だから、底面積は、
6×6 = 36[cm²]
になる。
さっき計算した底面積に「高さ」をかけてみよう!
例題の正四角錐の高さは8 [cm]だから、
36×8
= 288[cm³]
になるね。
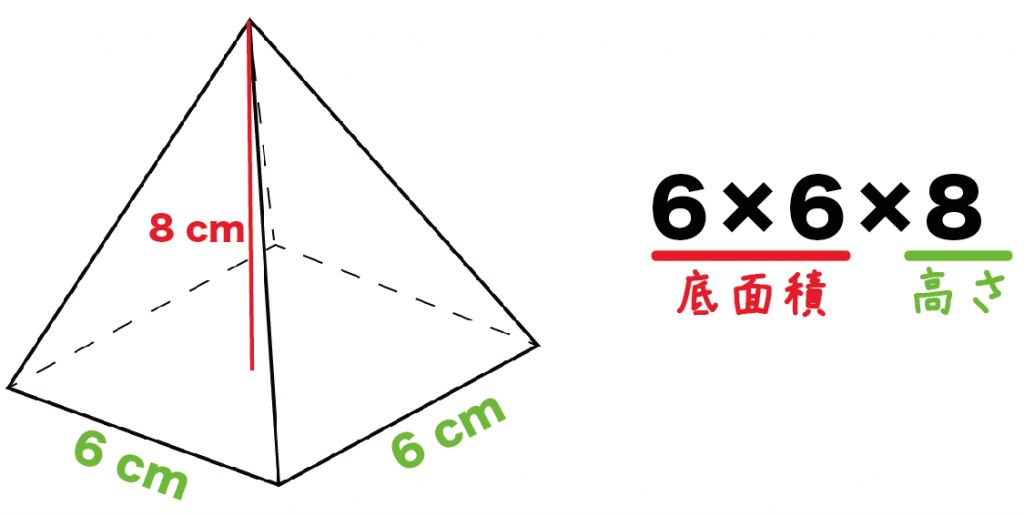
計算ミスに気をつけてね。
底面積に高さもかけたし・・・
と安心してはダメ。
先がとんがっているタイプの「錐体」では、体積を求めるときに必ず「1/3」をかけなきゃいけないんだ。
えっ。なぜ1/3をかけるのかって??
それは円錐の体積の求め方でも触れたけど、
高校数学でならう「積分」を使わないと説明できないんだ。
だから、中学数学ではとりあえず、
先がとんがっている立体の体積の計算は「底面積×高さ×1/3」になる
って覚えておけば問題ないよ。
だから例題の正四角錐の体積は、
6×6×8×1/3
= 96[cm³]
になるんだ。
おめでとう!これで正四角錐の体積を計算できたね。
正四角錐の体積の公式はどうだった??
底面積×高さ×1/3
という計算をゆっくりしてみてね。テスト前に復習しておくと心強いかも!
そんじゃねー
Ken