bが偶数のときに大活躍！判別式 4分のD の公式の使い方

クマシロ

よう、消しゴムの妖精のくましろだ。

前回、判別式の使い方を勉強してきたよな。

tomo

2024.05.18

3分でわかる！判別式の公式の使い方〜なぜ「D」を使うのか〜

https://text.tomo.school/discriminant

 よう、消しゴムの妖精のくましろだ。 高校数学の二次方程式では、判別式（はんべつしき）というツールを使っていくぞ。 こいつを使えば、二次方程式の実数の解（実数解）の個数がわかるんだ。 判別式の公式の使い方とある二次方程式 「$a{x}^2+bx+c=0$」があったとしよう。そいつの判別式の公式は次の通りさ。判別式は英語の大文字「D」で表すぞ。 $$D=b^2-4ac$$ そんでな、$D$の値を次の3パターンにわけるんだ。  $D$が0より大きい（$D>0$） $D$が0（$D=0$） $D$が0より小さい（$D &lt...

判別式は次の公式だったことを思い出してくれ。

$$D=b^2-4ac$$

こいつはベーシックなノーマルタイプ。

どんな二次方程式にも使える判別式なんだ。

だがな、世の中には便利なものがあって、

$\frac{D}{4}$

という判別式も存在しているんだ。

これは二次方程式程「$a{x}^2+bx+c=0$」の「$b$」が「偶数」の時に使える特殊な公式さ。

$b=2b^{\prime }$とすると、

$$\frac{D}{4}=b^{\prime 2}-ac$$

で表せるんだ。

もし、二次方程式の$b$が偶数だったら、その$b$を半分にしたやつ（$b^{\prime }$）を2乗。

そこから$a$と$c$をかけたものを引けばいい、ってことだな。

判別式 4分のD の公式の使い方

例えば、次の二次方程式があったとする。

$$3x^2+6x+7=0$$

ありがたいことに、偶然、$b$は偶数の$6$だよな。

だから、4分のDの判別式を使うと計算が楽になる。早速使ってみよう。

この場合、$a\mathrm{と}{b}^{\prime }\mathrm{と}c$は次のようになるな。

• $a=3$
• $b^{\prime }=3$
• $c=7$

$\frac{D}{4}$という判別式は、次のように計算できる。

$\frac{D}{4}=b^{\prime 2}-ac$

$=3^2-3\times 7$

$=9-21$

$=-12$

$\frac{D}{4}$は0より小せえ！

だから、この二次方程式は実数解を持たない、ってわけな。

別に、$\frac{D}{4}$じゃなくて$D$でもいいんだが、$ac$の前の係数 4がなくなって計算がちっと楽になるってことよ。

なぜ判別式の4分のDが使えるのか？

でも、なんで$b$が偶数の時の判別式$\frac{D}{4}$が便利なんだろうな？

その理由は、中学数学で勉強してきた「解の公式の偶数バージョン」を思い出せばわかるぞ。

tomo

2016.08.26

3分でわかる！bが偶数のときの解の公式の使い方

https://text.tomo.school/quadratic-formula-even

解の公式のbが偶数だといいことある？？こんにちは。けんいちだよ。 二次方程式では、便利な「解の公式」を勉強したね。2次方程式「ax² + bx + c = 0」において、  解のxが、x = {-b±√(b² -4ac)}÷2aになる公式だったね。   じつはこの解の公式。なんと、bが偶数のときは解の公式が使いやすくなるんだ。 b'をxの係数（b）を半分にしたやつとすると、x = {-b' ± √(b'²-ac)}/aで計算できちゃうのよ。 たとえば、xの係数が偶数の二次方程式、x² - 6x +1 = 0があったとしよう。この...

$b$が偶数の時は、次のような解の公式を使えるんだったな。

$$x=\frac{-b^{\prime }\pm \sqrt{b^{\prime 2}-ac}}{a}$$

この式の右上に注目だ。

そう、ルートの中身が

$$b^{\prime 2}-ac$$

で、こいつはまさしく正真正銘のさっき出てきた$\frac{D}{4}$ではあるまいか。

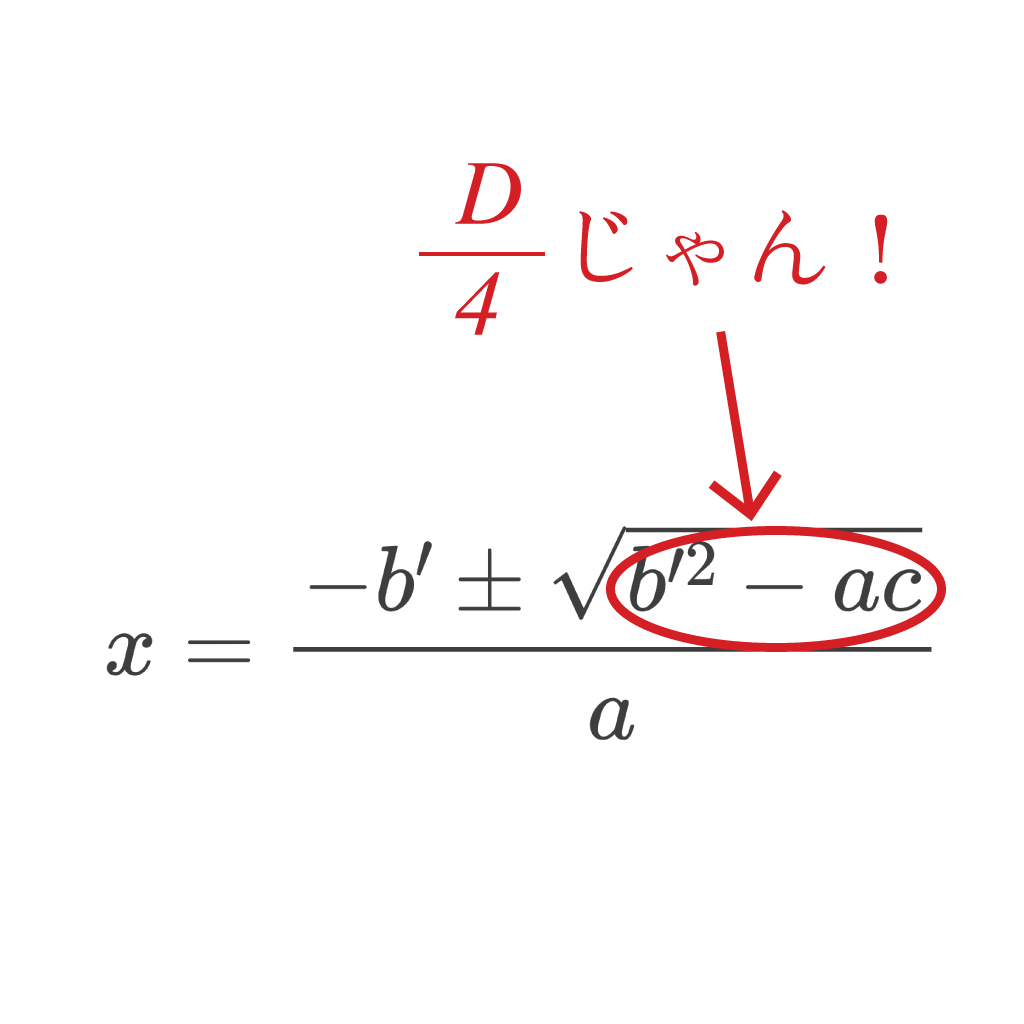
つまり、この右上のプラスマイナスルートの中身の「$b^{\prime 2}-ac$」が正の数だったら、プラスマイナスの符号がついてるから、2つの実数解が誕生する。

一方、プラスマイナスルートの中身が$0$ならば、厄介なルート部分が消えて解は1つになる。

ルートの中身がマイナスになるなら「実数解じゃない解」しか得られないことになる。

こんな感じで、4分のDでも同じように、bが偶数の場合は実数解の個数を判別できる、ってわけよ。

そしてこの「$b^{\prime 2}-ac$」というやつは、$D$を4分の1にしたものになってるな。

$b^{\prime }=\frac{b}{2}$を「$b^{\prime 2}-ac$」に代入してみるぞ。

すると、次の式になる。

$b^{\prime 2}-ac$

$=(\frac{b}{2}{)}^2-ac$

$=\frac{b^2}{4}-ac$

$=\frac{b^2-4ac}{4}$

この「$b^{\prime 2}-ac$」の正体は「Dを4分の1したやつ」だったんだな。

こんな感じで、中学数学で勉強してきた解の公式偶数バージョンを思い出せば、判別式の$\frac{D}{4}$のその生まれの理由もわかるはずだ。

判別式の4分のDは覚える必要ある？

ここまで判別式4分のDの使い方を紹介してきた。

どうだ？

覚える気になったか？？

覚える公式が1つ増えた・・・・なんて思っていないか。

確かにな、でも安心しろ。

この判別式$\frac{D}{4}$を覚えるのはマストではない。

「あれば便利で使えるもの」と思っておこう。

あったら便利だけど、なくても生きていける。

例えるなら、雨の日に活躍する長靴だな。

雨の日に長靴を履けば、靴の内部が濡れなくてハッピー。

でも、その一方で長靴がなくても大丈夫だよな。

普通の靴でも雨の中歩行して生きていけるだろ？　それと同じだ。

判別式の4分のDがしっくり来たな？

クマシロ

次は判別式を使って重解を求める問題に挑戦しよう

それじゃあなぁ！