3分でわかる!判別式の公式の使い方〜なぜ「D」を使うのか〜

高校数学の二次方程式では、
判別式(はんべつしき)
というツールを使っていくぞ。
こいつを使えば、
二次方程式の実数の解(実数解)の個数がわかるんだ。
判別式の公式の使い方
とある二次方程式 「$ax^2+bx+c = 0$」があったとしよう。
そいつの判別式の公式は次の通りさ。判別式は英語の大文字「D」で表すぞ。
$$D=b^2-4ac$$
そんでな、$D$の値を次の3パターンにわけるんだ。
- $D$が0より大きい($D > 0$)
- $D$が0($D = 0$)
- $D$が0より小さい($D < 0$)
Dがどのパターンに当てはまるかによって、実数解の個数が次の表のようにわかるんだな。
| $D$のパターン | 実数解の個数 |
|---|---|
| $D > 0$ | 2 |
| $D = 0$ | 1(重解) |
| $D < 0$ | なし |
いまいちしっくりきていないお前のために、次の2次方程式で判別式を使ってみようか。
$$2x^2+3x-5 = 0$$
この二次方程式では、
- $a = 2$
- $b = 3$
- $c=-5$
だよな?
ってことで、こいつらを判別式の公式「$D=b^2-4ac$」に代入だ。
$D=b^2-4ac$
$D=3^2-4×2×(-5)$
$D=9+40$
$D=49$
うん、$D$は楽勝で0より大きくなるな!
ってことで、さっきの判別式の表と照らし合わせてみよう。
| $D$のパターン | 実数解の個数 |
|---|---|
| $D > 0$ | 2 |
| $D = 0$ | 1(重解) |
| $D < 0$ | なし |
つまり、$D > 0$のパターン。
よって、この二次方程式の実数解は
2つ
だ!
なぜ判別式が使えるのか?
ここまでで判別式の使い方、わかってきたな。
それじゃあなぜ、判別式が使えるんだろうか??
なぜ「$b^2-4ac$」で二次方程式の実数の解の個数がわかっちまうのか、ちょっと気になるはずだ。
その答えは、中学数学で勉強してきた「解の公式」にあるぞ。
解の公式は、
$$x = \frac{-b±\sqrt{b² – 4ac}}{2a}$$
っつう、呪文みたいな公式だったな。
この解の公式の右上の「$±\sqrt{b² – 4ac}$」に注目してくれ。
もしかして、プラスマイナスルートの中身が、判別式の公式$D$じゃないかよ!?
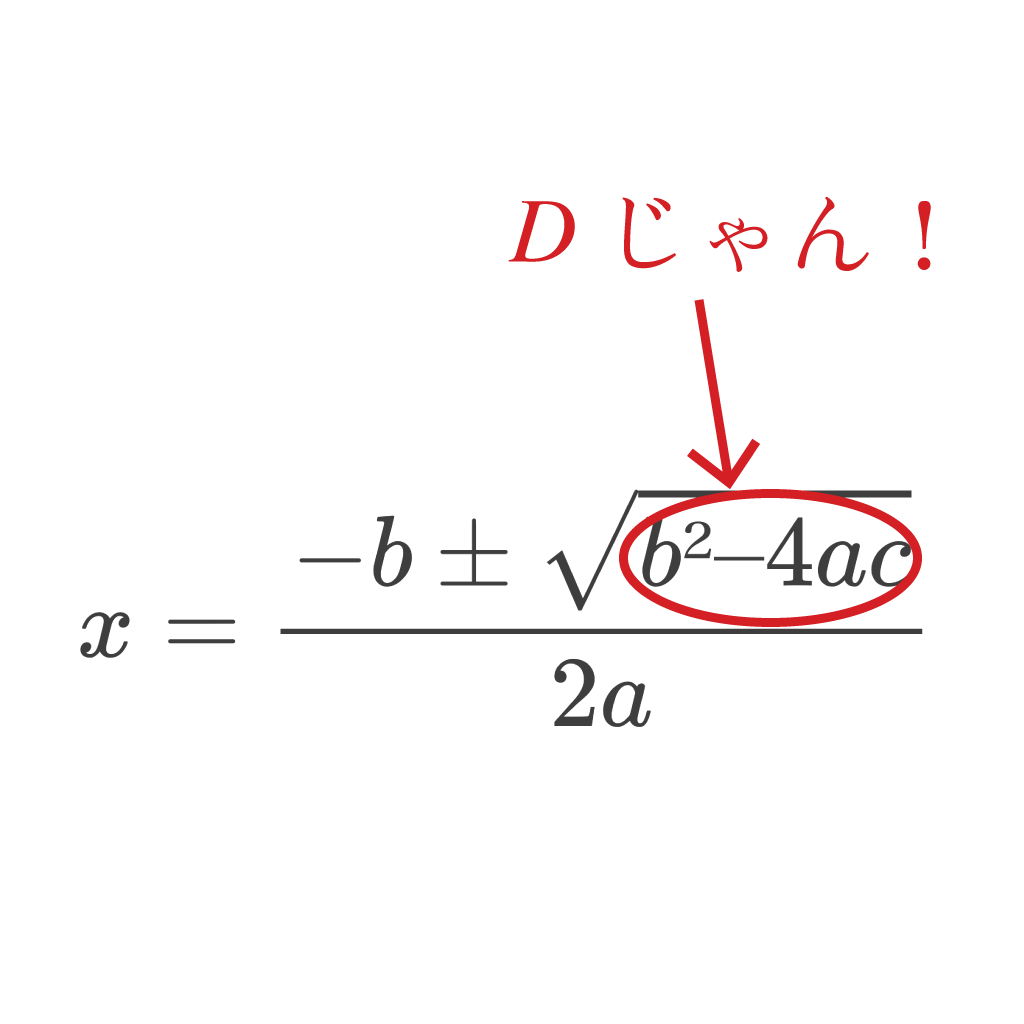
このルートの中身($b² – 4ac$)が0より大きいなら、$±$の符号がついているから、
- プラス
- マイナス
で2つの解が存在するはずだ。
一方、ルートの中身が0だったら、どうなる??
そう、そもそもルートの部分は存在しない!
だから、二次方程式の解はルート部分を除いた
$$x = -\frac{b}{2a}$$
になるよな。$±$の符号を考えなくていいから、もちろん解は1つさ。
で、ルートの中身()のが0より小さかったら・・・・・・
そう、実数ではない解になっちまうな。
なぜなら、ルートの中身が0より小さいなんて実数ではありえねえからな。2乗してマイナスになる数なんて想像できない・・・だろ?
ってことで、$D$が0より小さいときは、実数解の個数は「ゼロ」ってことになる。
とまあ、高校数学では「判別式」というかっこいい言葉を使っているが、やっていることはシンプルだ。
中学数学で勉強してきた「解の公式」を思い出せばそのカラクリに気づくだろう。
なぜ判別式は「$D$」なのか?
よし、判別式の公式もわかったし、使い方もわかった。
しかも、なぜ判別式を使えるのか、もわかってきた。
でもさ、最後にまだまだしっくりこないのが
$D$
じゃないか?
なぜ、判別式が「$D$」なのか。
別に、「$F$」でも「$G$」でも「$Z$」でもいいはずだ。
明らかに、日本語の「判別式」とは関係がなさそうだよな。
その推察は正しいぞ。
じつは、この判別式の「$D$」は英語で判別式にあたる
Discriminant
から来ているんだ。
ドラえもんの$D$でもないし、ダイビングの$D$でもなかったんだな、残念だけど。
えっ、「Discriminant」が覚えられないだって?
そういう時はな、高校英語で勉強する、
discriminate
という動詞を思い出してくれ。
こいつは
識別する
という意味があったよな。
だからこの「discriminate」があーしてこうなって派生して、判別式の「Discriminant」に進化した、と思っておけばいいさ。
これで、なぜ判別式が「$D$」を使うのかまでしっくりきたはずだ。

それじゃあなぁ!


