【高校数学 I 】二次関数の対称移動の公式(基本編)
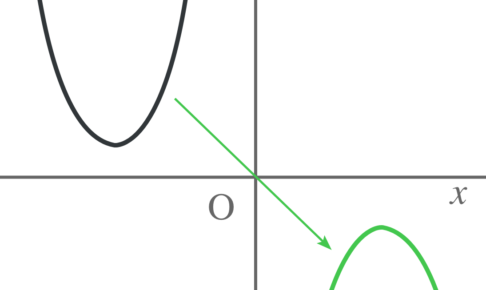
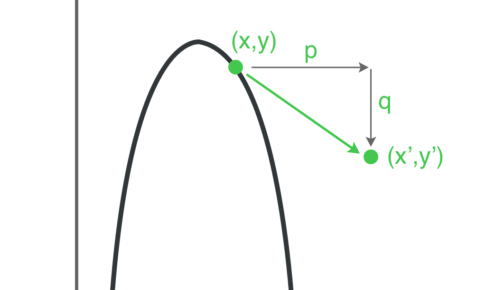
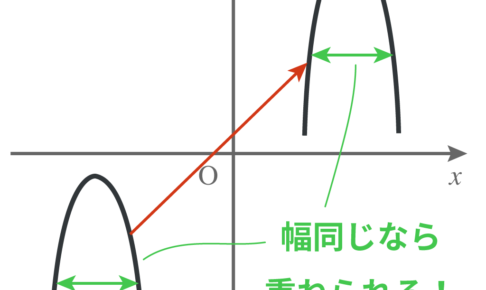
高校数学では二次関数を平行移動してきたな。 だが、しかし。 高校数学は二次関数を平行移動するだけじゃおさまらねぇ。 なんと、 二次関数を対称移動させてくんだ。 対称移動とは復習す…
 数学 I
数学 I
高校数学では二次関数を平行移動してきたな。 だが、しかし。 高校数学は二次関数を平行移動するだけじゃおさまらねぇ。 なんと、 二次関数を対称移動させてくんだ。 対称移動とは復習す…
 数学 I
数学 I
関数のグラフの点を全て同じ方向に移動させること を 平行移動 っていうんだ。 で、高校数学では二次関数をガンガン平行移動させていくぞ。 ありがたいことにな、二次関数のグラフの平行…
 数学 I
数学 I
中学数学では「2点を通る一次関数の求め方」、勉強してきたよな。 なんと、高校ではな、こいつをステップアップさせて、 3点を通る二次関数の放物線の求め方 を勉強していくぞ。 例えば次のような問題…
 数学 I
数学 I
二次関数$y=ax^2+bx +c$ってさ、 いろんな形してるよな。 こんなんだって、 あんなのだってあるだろうし。 じつは、この二次関数のグラフの形は、 $a$の大きさによって変化するんだ。…
 数学 I
数学 I
前回、平方完成で二次関数の軸と頂点を求めるやり方、勉強してきた。 でもさ、毎回平方完成してしないとなんて、大変不便だよな。 そんなことを思っちゃったお前に朗報だ。 じつはな、二次…
 数学 I
数学 I
前回、二次関数の軸と頂点の基本の求め方を勉強してきたよな。 これでこの基本形、 $$y=a(x-p)^2 + q$$ になっている二次関数の軸と頂点なら容易にゲットできるようにな…
 数学 I
数学 I
高校生では中学数学と同じように二次関数を勉強していくぞ。 二次関数とは復習すると、 $x$の次数が「2」の関数 だったよな。 中学数学では $$y=ax^2$$ っ…
 数学 I
数学 I
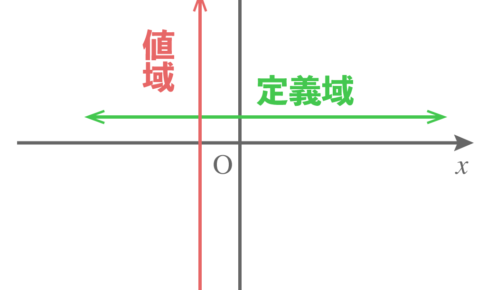
高校数学の二次関数では多くのニューワードが出現するぜ。 この前勉強した「象限」に加えて、今回は 定義域 値域 が新登場。 しかも、この2つはごっちゃにしやすく間違えやすいときてるんだ。 ってこ…
 数学 I
数学 I
高校数学でも関数を勉強していくんだが、1つ、新しい言葉が登場するぞ。 それは、 象限(しょうげん) だ。 ズバリ、 座標平面の場所の名前のこと さ。 人間の身体にも「頭」とか「首…
 数学 I
数学 I
判別式って便利だよな。 なんせ、二次方程式の係数を代入するだけで、実数解の個数がわかっちまうんだからよ。 でもな、それだけで終わらないのが判別式だ。 なんと、逆に、 二次方程式の…
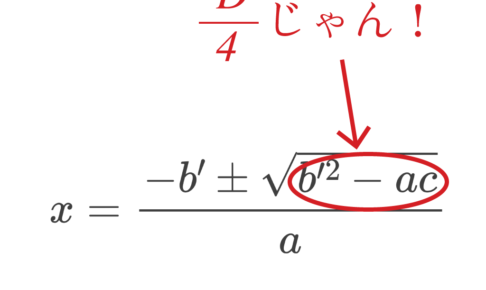 数学 I
数学 I
前回、判別式の使い方を勉強してきたよな。 判別式は次の公式だったことを思い出してくれ。 $$D=b^2-4ac$$ こいつはベーシックなノーマルタイプ。 どんな二次…
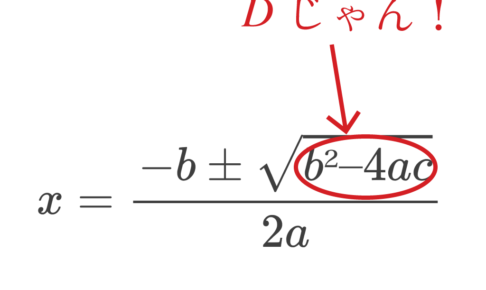 数学 I
数学 I
高校数学の二次方程式では、 判別式(はんべつしき) というツールを使っていくぞ。 こいつを使えば、 二次方程式の実数の解(実数解)の個数がわかるんだ。 判別式の公式…
 数学 I
数学 I
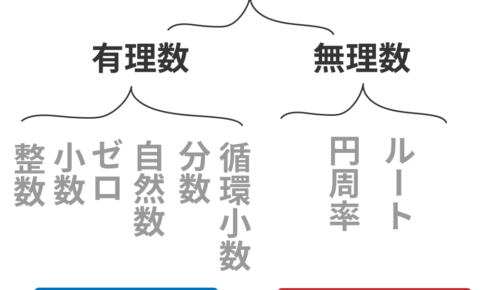
高校数学で二次方程式を勉強していると、3秒に1回ぐらい目にするのが 実数(じっすう) という言葉だ。 一体この「実数」とはどんな数なのか?? 今日はその実数の意味をわかりやすく解説していくぞ。…