こんにちは!この記事を書いているKenだよ。コーヒー、ドリップしたね。
中1理科の光の世界の単元で一番の山場。
それは、凸レンズの作図問題だよね。
作図問題と聞くと難しそうに聞こえるけど、これまで勉強してきた2つの基本である、
を押さえておけば解けるはずなんだ。
今日は、その凸レンズの作図問題の中でも、
実像
を作図する問題を一緒に解いていこう。
レンズに映って見えるものや、レンズを通してスクリーンに映しだせるものを「像(ぞう)」と呼んでたね?
この像の中でも「実像」は、
物体から飛び出た光が凸レンズの逆側で1点に集まってできる像のこと
を言うんだ。
しかも、上下左右が逆向きの像。
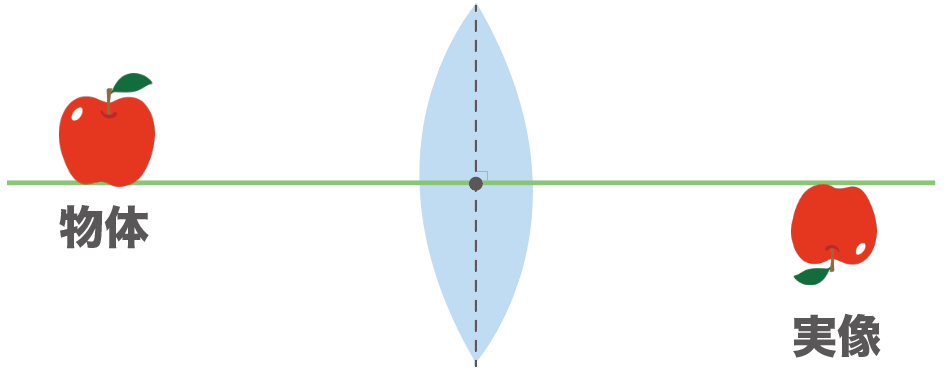
たとえば、りんごの実像を映し出してみたとすると、こんな感じでへたが下向きになって映し出されるはず。
これが実像。
でもでも、凸レンズに24時間365日どこでも実像がうつるわけじゃない。
じつは、
凸レンズの焦点よりも外側にうつす物体を置いた時だけ
なんだ。
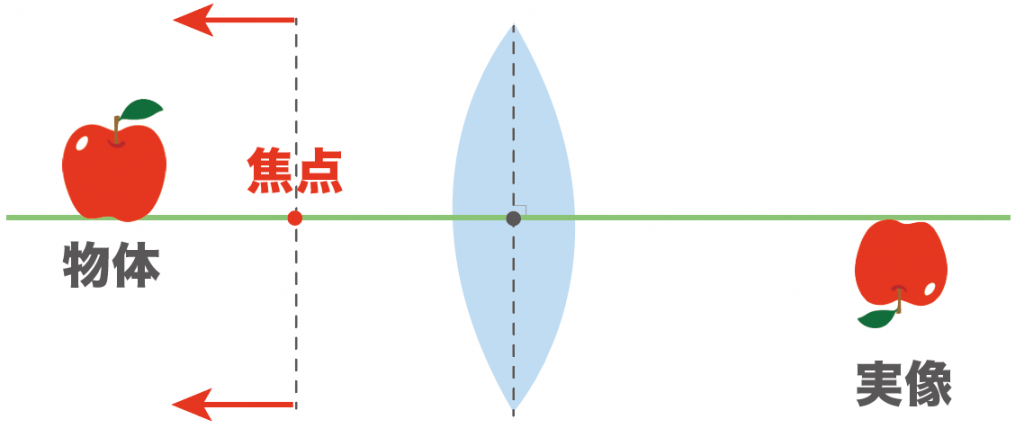
焦点の上に置いたり、
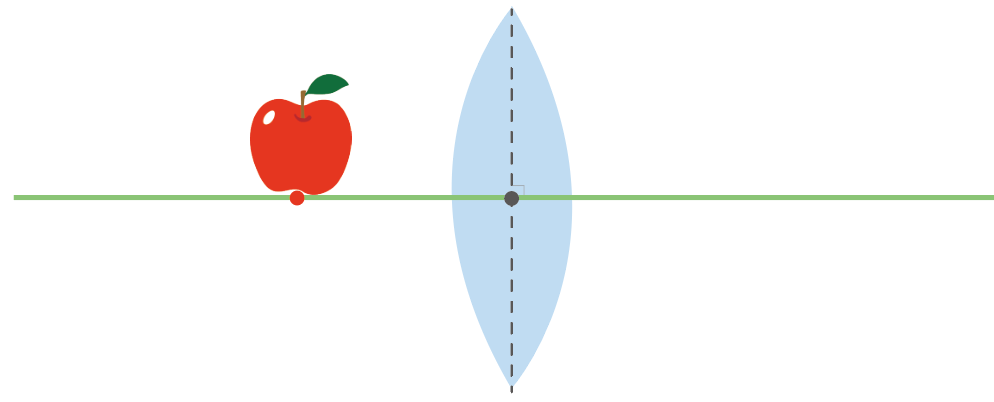
焦点よりレンズに近い位置に物体を置いても、実像はできないってわけさ。
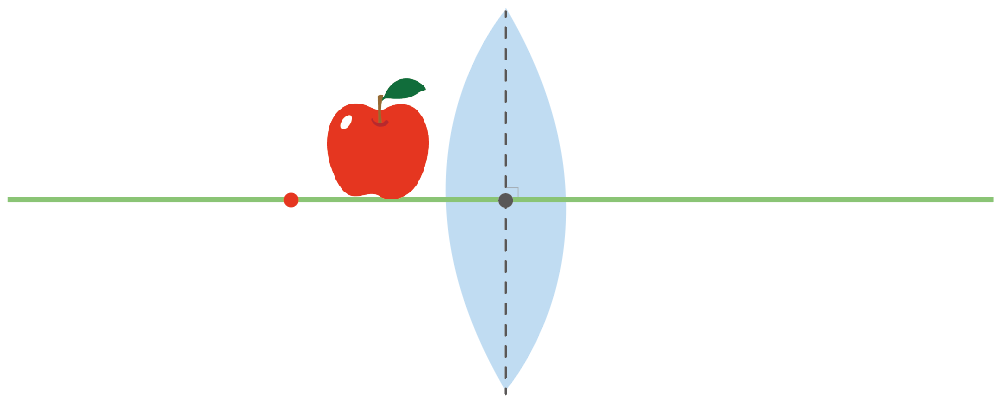
それじゃあ凸レンズにできる実像を作図する問題を解いていこう。
凸レンズの焦点の外側に、こんな感じで矢印の物体が置かれている時、この凸レンズによってできる実像を作図しなさい
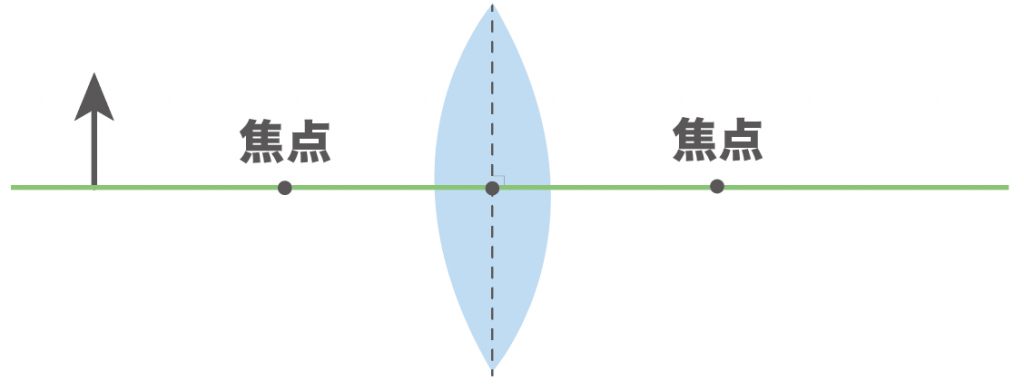
このタイプの作図問題は次の3つのステップを踏めば大丈夫。
凸レンズの中心を通る光を書いてみよう。
物体の頭から出た光のうち、凸レンズの中心を通る光だけかくんだ。
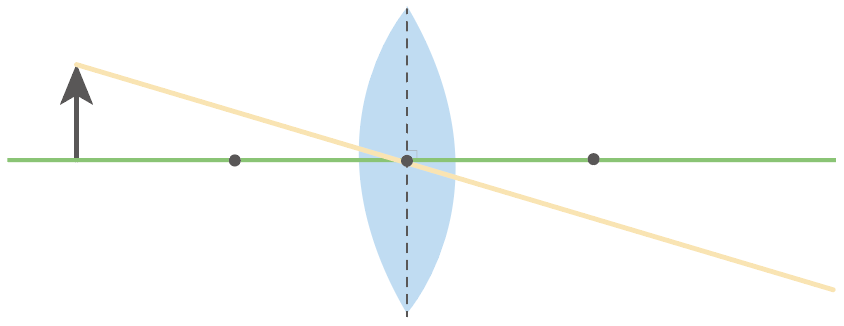
凸レンズの光の進み方で勉強したように、凸レンズの中心を通る光はそのまままっすぐ進むんだったね??
まっすぐな光の道筋の線を引ければオッケー。
続いて、凸レンズの軸に平行な光をかいてみよう。
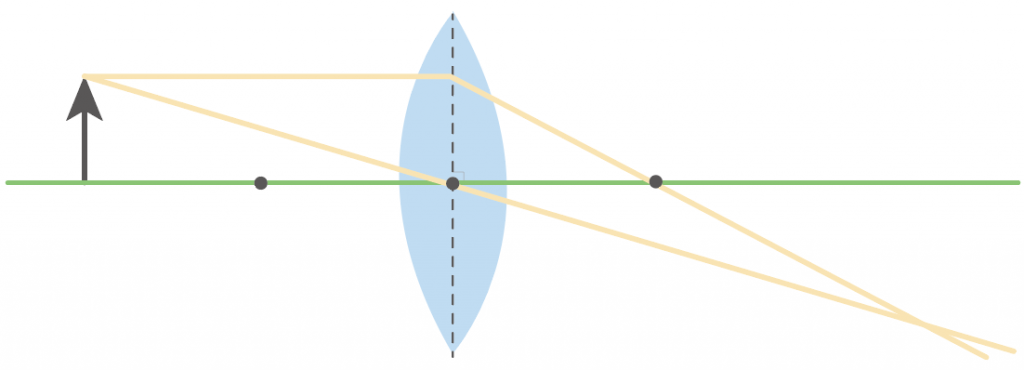
このタイプの光は、
凸レンズにあたると焦点を通過するんだったね?
最後に、凸レンズの焦点を通った光の道筋をかこう。
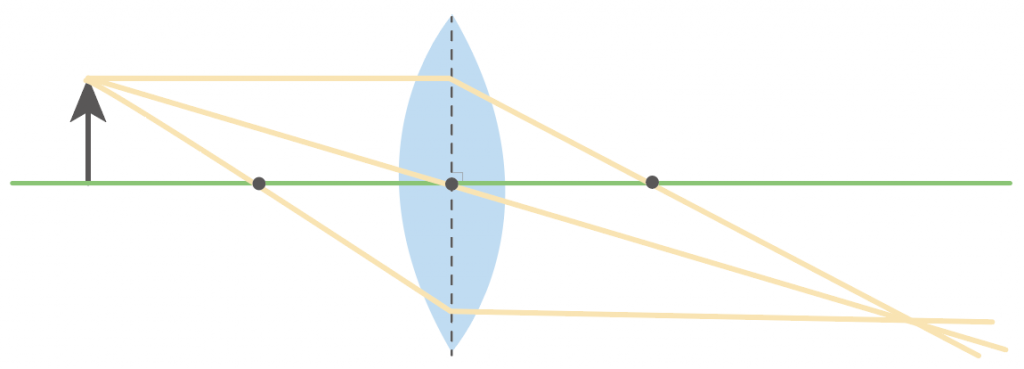
凸レンズを通過した後に、レンズの軸に平行しなきゃいけないから作図が難しい。
Step2までに引いた2つの光の道筋の交点を目指すとかきやすくなるよ。
ここまで3つの光を作図してきたけど、たぶん、うまく作図できると3つが一点で交わってるんじゃないかな。
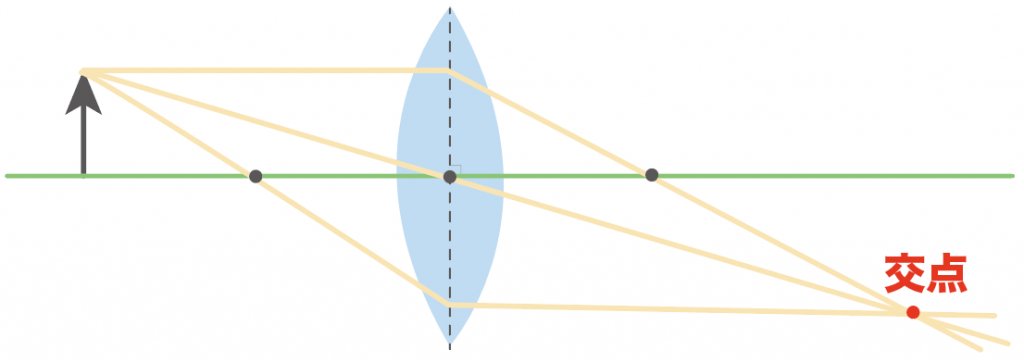
そのとき、交わっている交点には、光がスタートした地点のパーツを書いてあげよう。
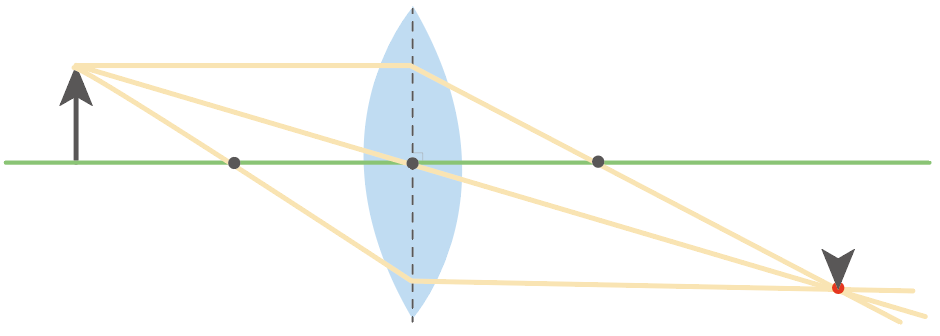
今回は、矢印の物体の頭から光を発射したから、矢印の頭のてっぺんがこの光の道筋の交点にくるはず。
そしたら、そのほかのパーツの残りも描いてあげよう。実像だから上下左右逆さまになってるね。
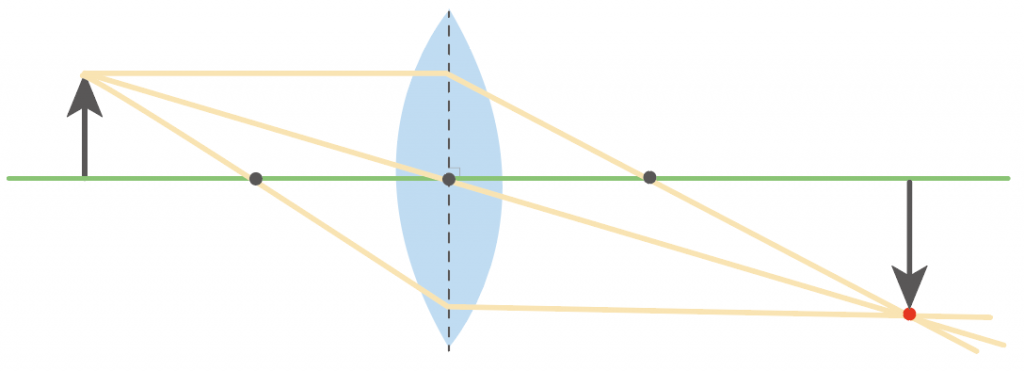
あとは凸レンズの実像について知っておくと便利なことを2つばかり紹介するよ。
焦点距離のちょうど2倍の地点に物体をセッティングしてやると、凸レンズでできる実像は、本物の物体の大きさと同じになるよ。
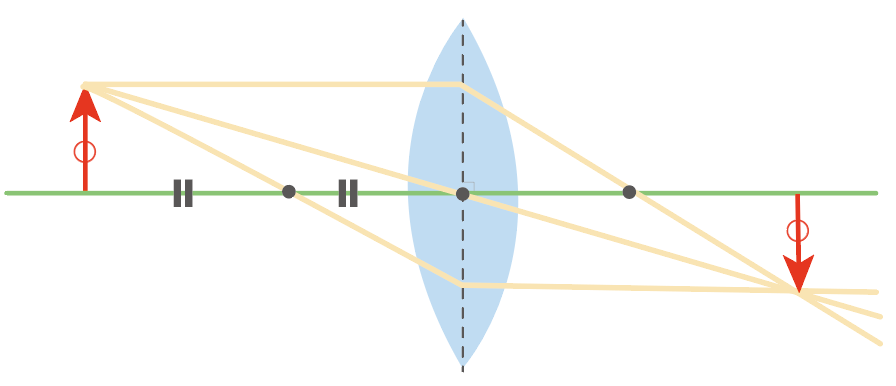
あくまでも大きさだけだから、向きは左右上下逆になってるのは変わらないけどね。
もし、物体の位置を焦点距離からもっと遠ざかるようにセッティングすると、
実像がもっと小さくなるんだ。
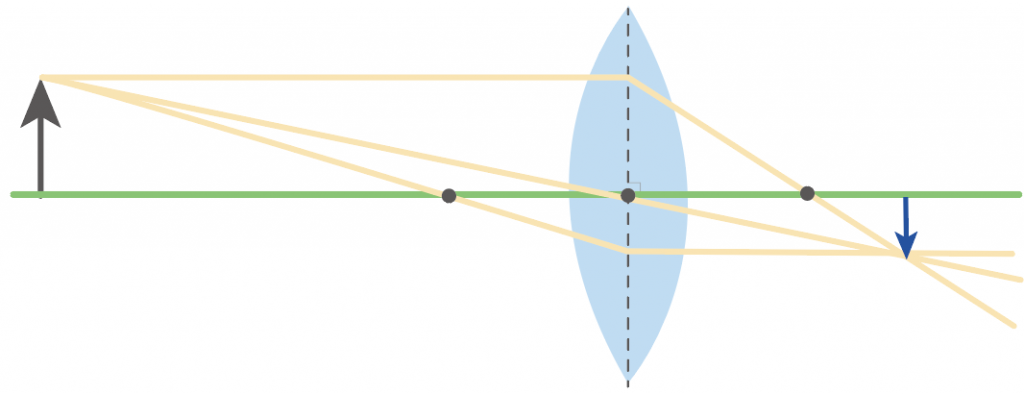
逆に、焦点の位置に物体を近づけると実像は大きくなるけどね。
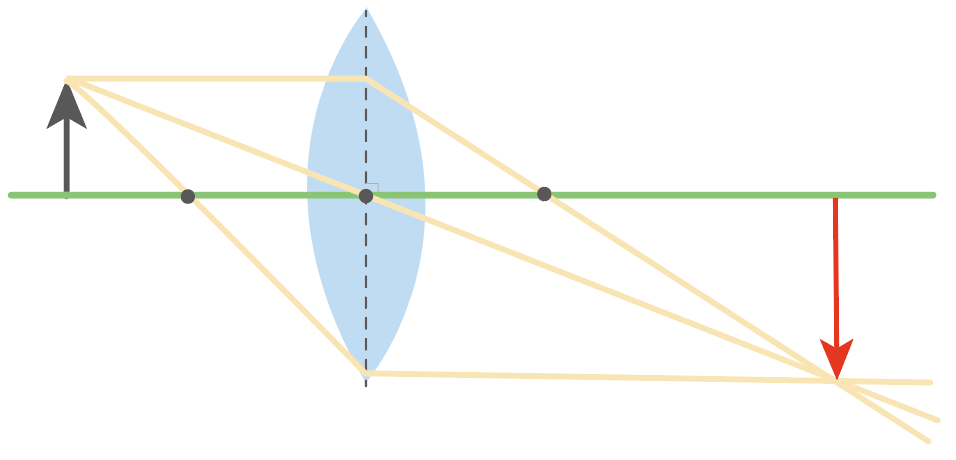
ただ、焦点の位置ぴったりに物体をセッティングすると、何も見えなくなることに注意してね。
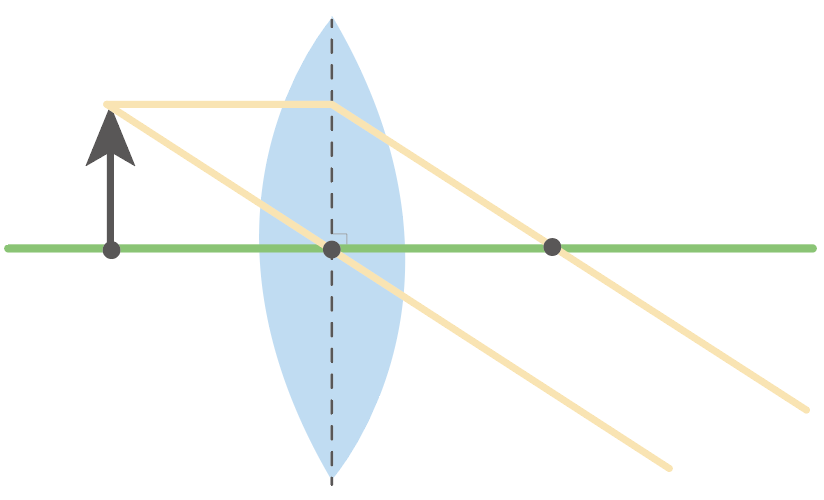
以上が、凸レンズにできる実像を作図する問題の解き方だよ。
さえ押さえて、落ち着いてテストに臨めば解けるはず。
実像の作図問題をマスターしたら次は虚像の作図にチャレンジしてみよう!
そんじゃねー
Ken
こんにちは!この記事を書いているKenだよ。はちみつ、ゆずだね。
中1理科の光の世界の単元では、
凸レンズの作図問題
がよく出題されるよね。
その作図問題を制覇するために知っておきたいことの1つとして、
凸レンズの光の進み方があるよ。
つまり、
凸レンズを通った光の道筋がどう変化するのか??
っていうルールのことね。
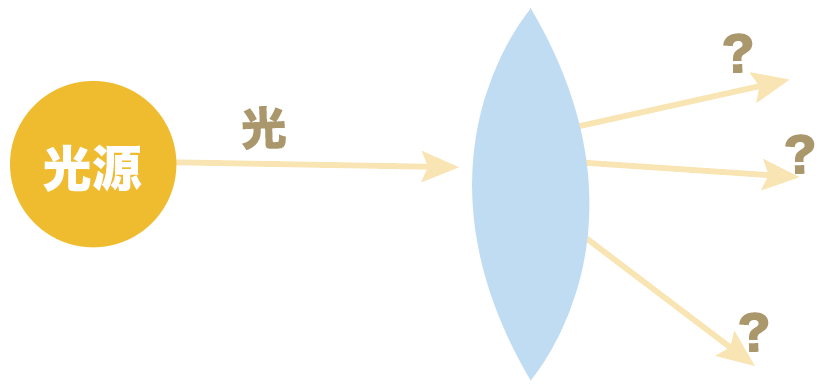
今日はこいつの基本をみっちり押さえていこう!
凸レンズに光が当たったとき、どう道筋を変えるんだろうね??
まず、1つ目のルール。
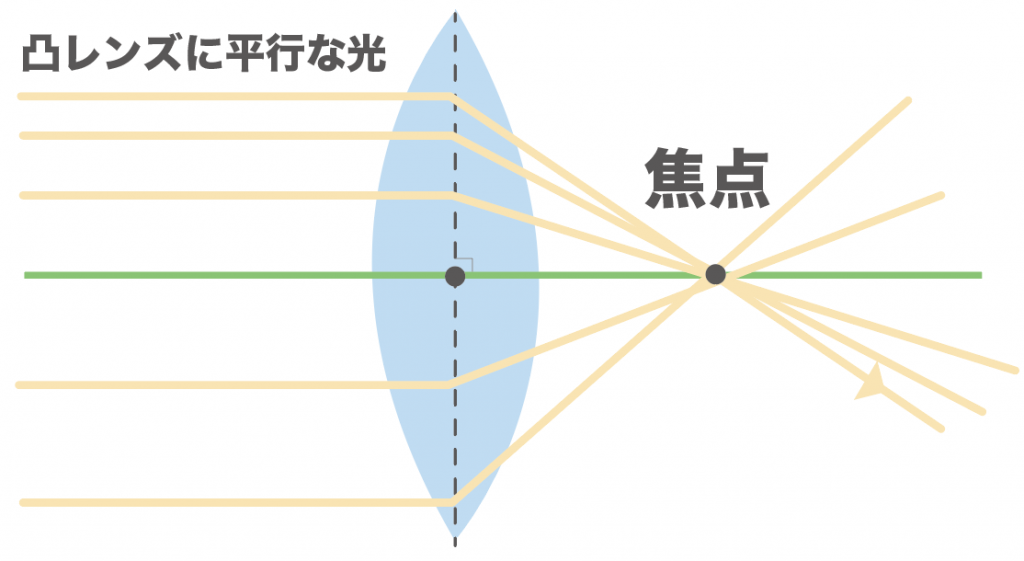
凸レンズの軸に平行な光の道筋は焦点を通るんだ。
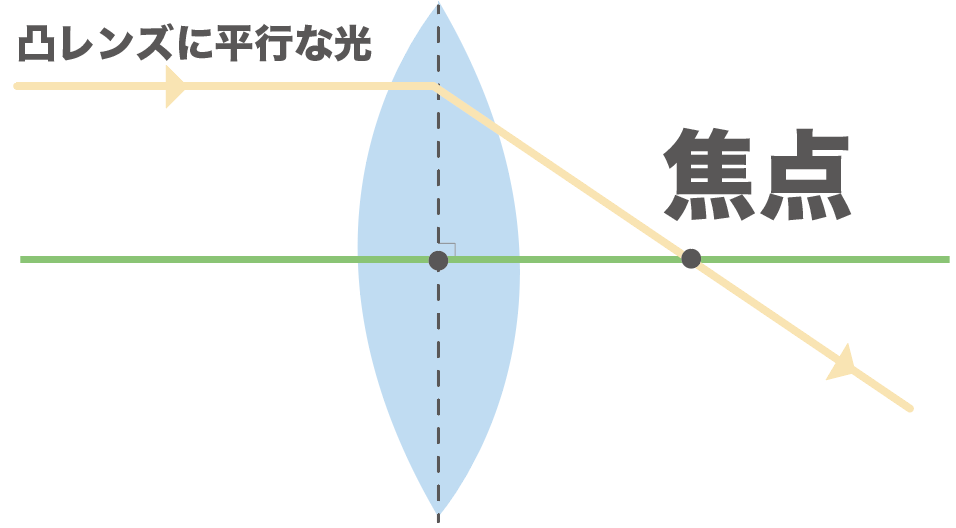
「凸レンズの軸」は凸レンズの中心を通る、凸レンズの中心線に垂直な直線のことだったよね??
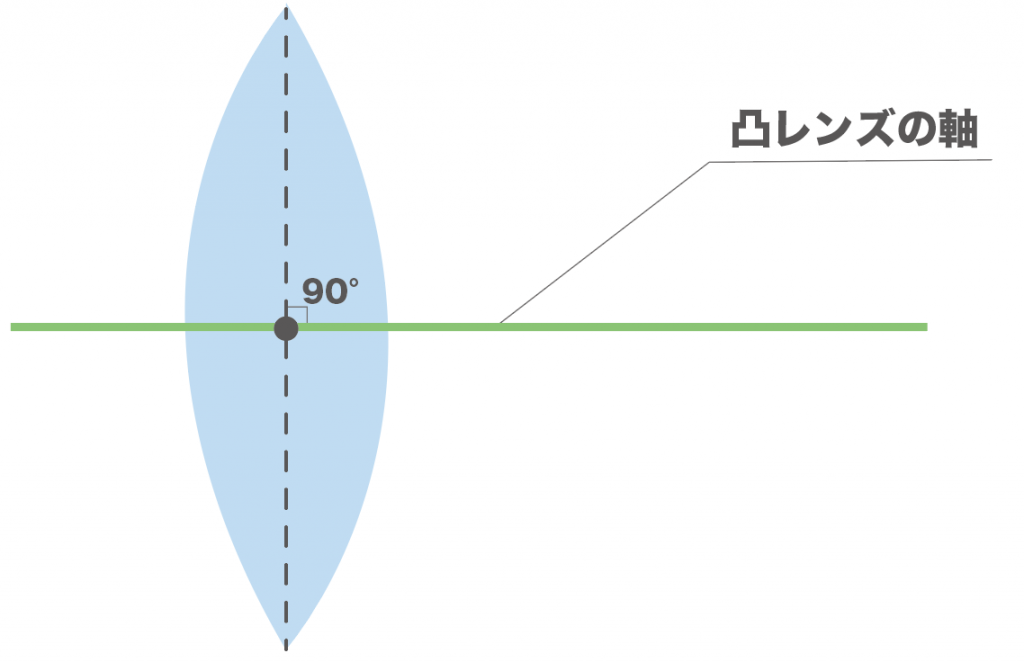
こいつに平行な直線をどこから凸レンズに当てても、必ず逆側の焦点を通るようになっているんだよ。
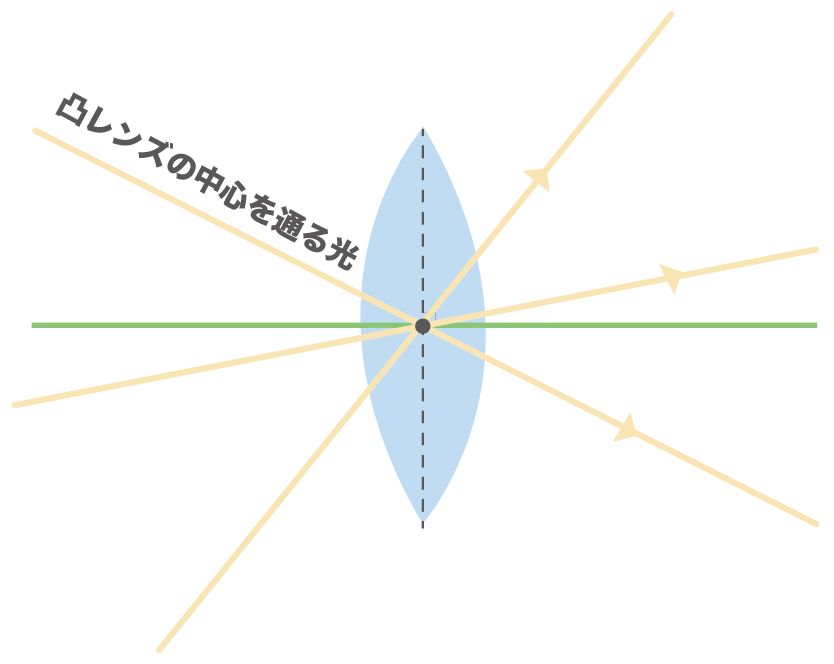
次は凸レンズの中心を通る光のルールね。
光の進み方のルールはシンプルで、
凸レンズの中心を通る光はそのまま直進するんだ。
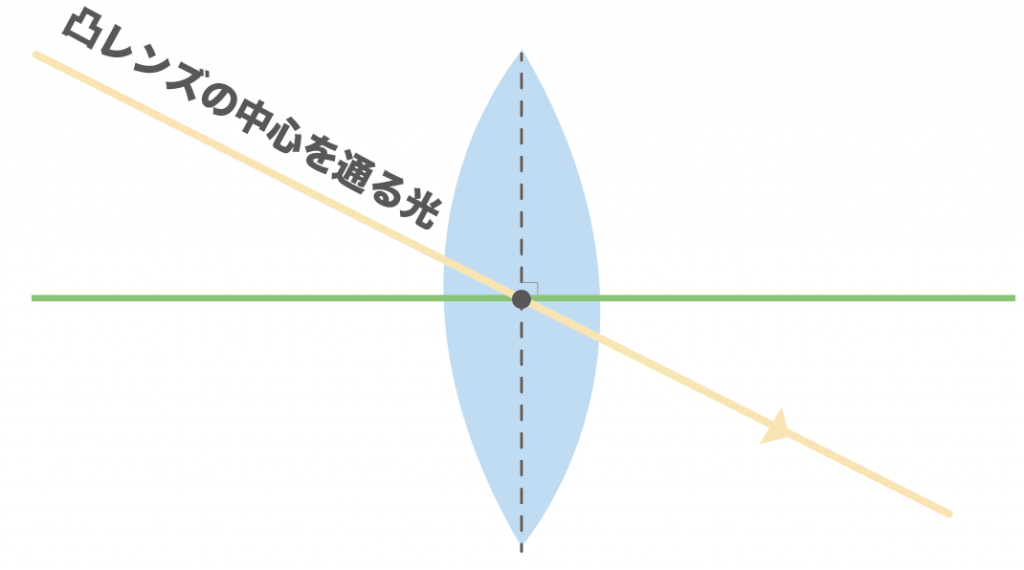
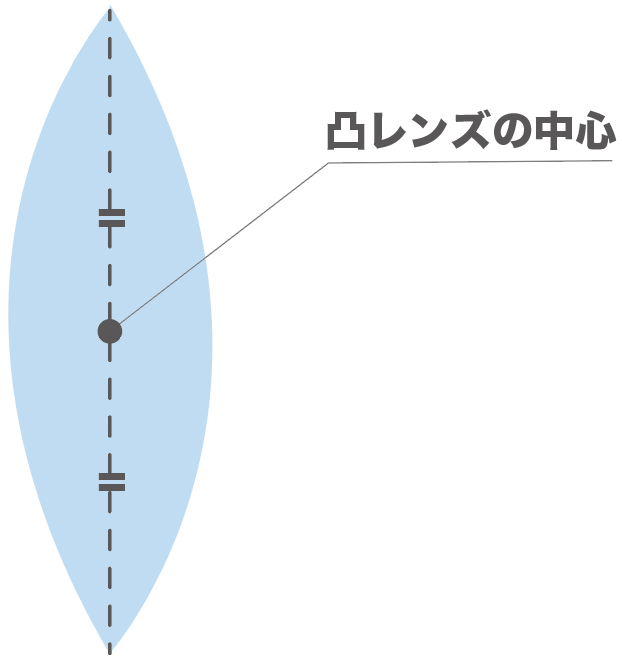
「凸レンズの中心」って、
凸レンズの中心線の中点のこと
だったよね??
この凸レンズの中心を通る光なら、どこから、どの角度から当ててもまっすぐと進んでいくんだ。
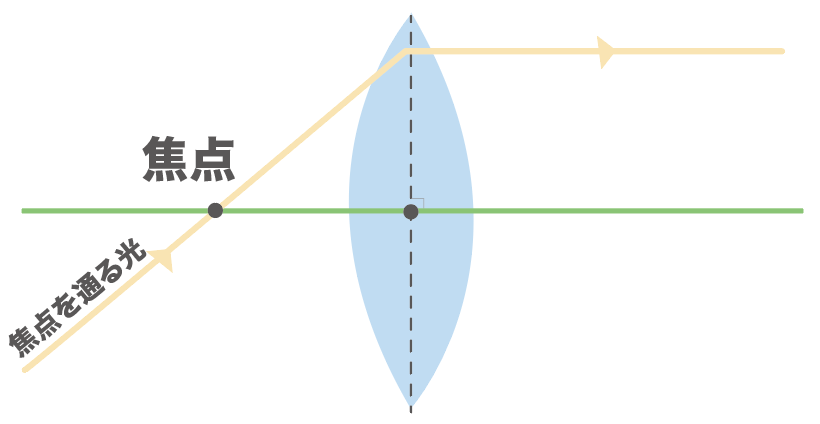
これはルール1の逆だね。
凸レンズの焦点を通った光が凸レンズを通過すると、凸レンズの軸に平行に進むんだ。
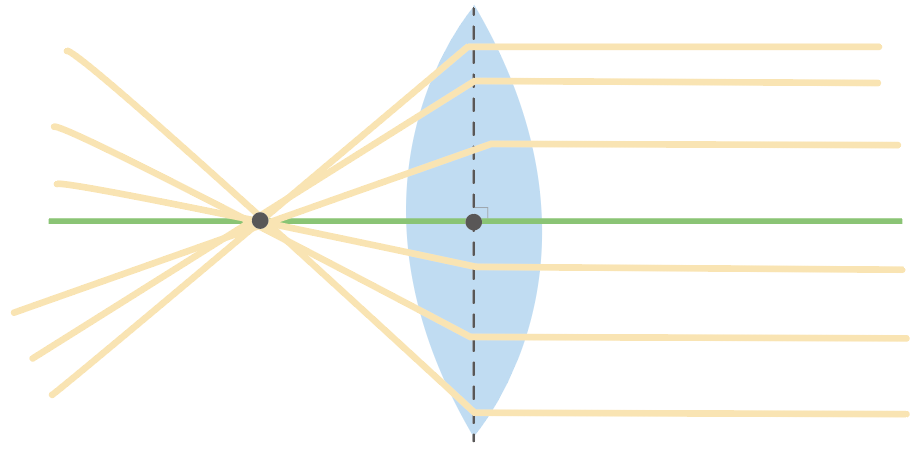
これまでのルールと一緒で、どこからどの角度から凸レンズに光を当てようが関係ない。
焦点を通ってしまえば凸レンズの軸に平行に進むようになってるんだ。
以上が、凸レンズの光の進み方のルールだったね。
という3つを押さえておけば大丈夫。
この基本を押さえて凸レンズの作図問題を倒していこう!
もし、凸レンズの専門用語がわからなすぎて理解できない!
っていうときは、「凸レンズの基本名称」で復習してみてね。
そんじゃねー
Ken
こんにちは!この記事を書いてるKenだよ。アルフォート最高。
中学理科の光の世界の単元では、
凸レンズに入った光がどう進むのか??
ってことをなぜか深く勉強していくよ。
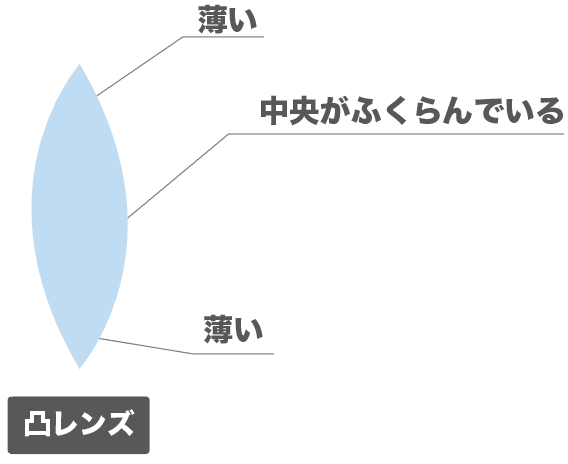
凸レンズとは、虫眼鏡にも使われているレンズのことで、

中央が膨らんでいて、周辺に向かうほど薄くなるレンズのこと
だったね。
んで、中学理科では、この凸レンズの光の進み方の作図とか、実像とか虚像とか、いっぱい厄介なことを勉強していくんだ。残念ながら。
ただ、これらの勉強って、
凸レンズの性質や名称の基本さえ押さえておけばかなり簡単。
名前を覚えてしまえば凸レンズの基本ルールが言ってることがわかるようになるからね。
ってことで、今日は今後、凸レンズを勉強していくにあたって苦戦しないように、凸レンズの基本の名称をマスターしていこう。
凸レンズについていっぱい専門用語が出現してくるけど、だいたい次の5つの名称を押さえておけば問題ないかな。
まずは「凸レンズの中心線」ってやつだ。
これは凸レンズが薄くなっている端っこと端っこを結んだ線のことね。
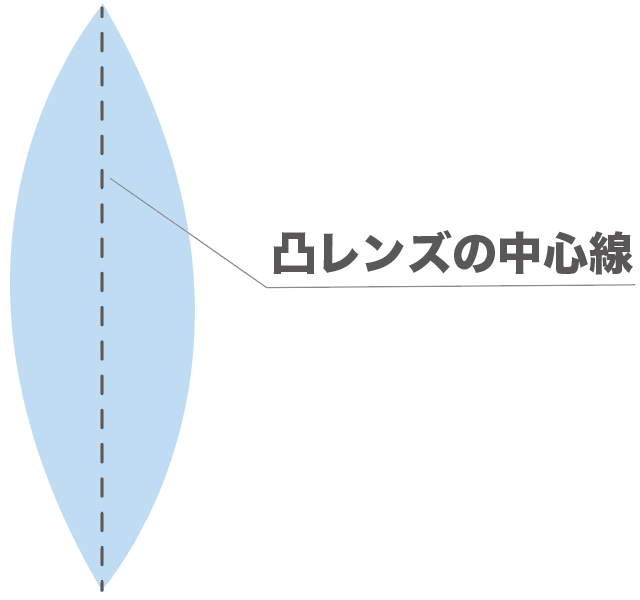
大抵、凸レンズは線対称になっているから、この中心線で凸レンズを折りたためば重なることになる。
これが凸レンズの中心線。
続いては、凸レンズの中心だ。
これは、
凸レンズの中心線の中点のこと
だ。

端っこから端っこまでの距離が等しい点のことだね。
凸レンズの中心は中心線上にあるんだ。
たとえば、凸レンズの端っこをA、Bとして、レンズの中心をOとしてやると、
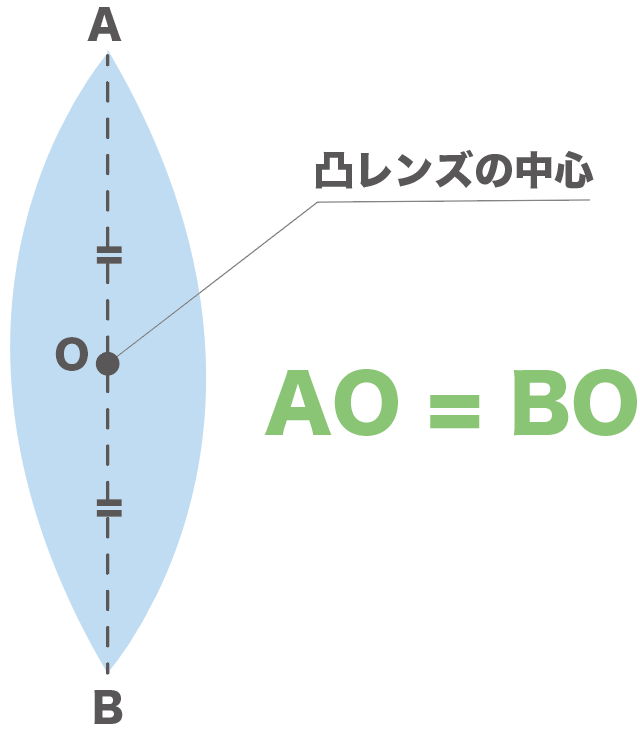
AO = BO
になるわけだ。
凸レンズの中心線に垂直で、なおかつ、凸レンズの中心を通る直線のことを、
凸レンズの軸
って呼んでるよ。

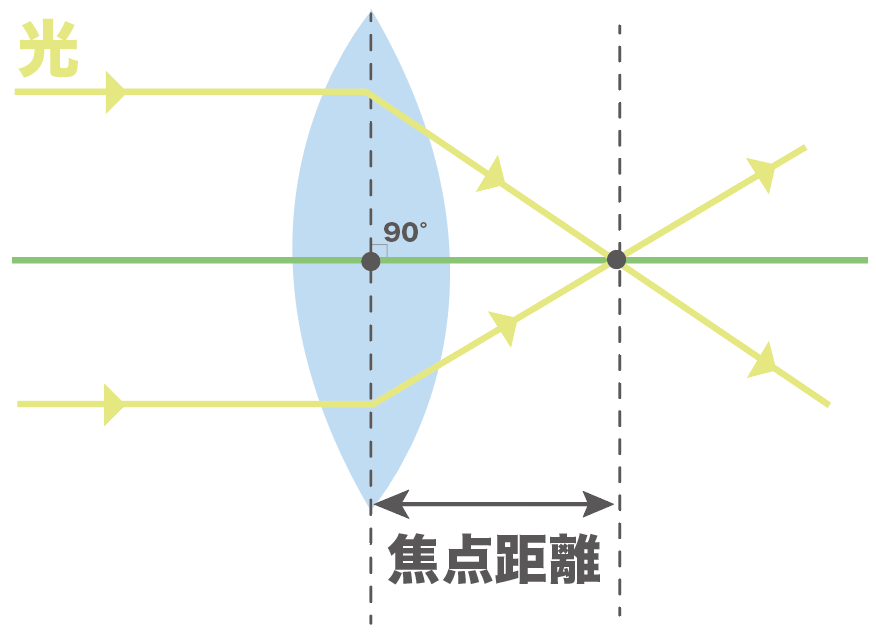
凸レンズに凸レンズの軸に平行な光を当ててやったとする。
このとき、じつは、
光が屈折して1点に集まるようになってるんだ。
この凸レンズの軸に平行な光たちが集まる点のことを「焦点(しょうてん)」って呼んでるよ。
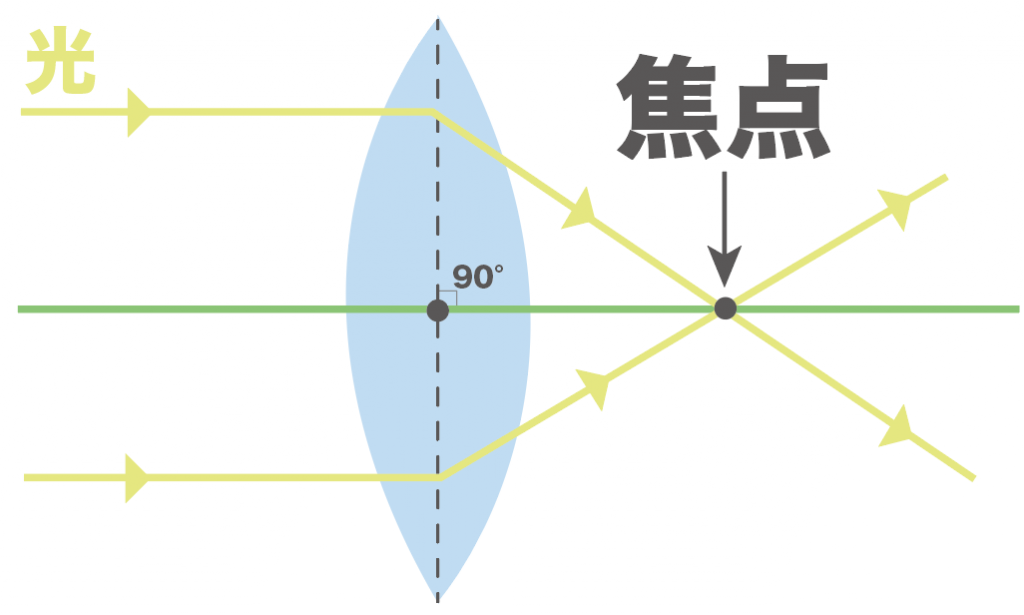
んで、凸レンズの中心から焦点までの距離のことを、
焦点距離
って呼んでるんだ。
なるほどね〜〜
以上が凸レンズの基本の名称たちだね。
最後に復習しておこう。
凸レンズの薄い端っこと端っこを結ぶ線を「凸レンズの中心線」、

凸レンズの中心線の中点を「凸レンズの中心」、

さらに、凸レンズの中心線に垂直で、かつ、凸レンズの中心を通る直線を「凸レンズの軸」というんだったね。

凸レンズの軸に平行な光を当てた時、光が集まる点を焦点、凸レンズの中心から焦点までの距離を「焦点距離」と覚えておこう。

そんじゃねー
Ken
こんにちは!この記事を書いてるKenだよ。鳩、目があったね。
中学1年例の光の世界の単元では、いくつか重要な事柄を勉強してきたね。
今日はもう一つ重要な光の現象を紹介するよ。
その名も、
全反射(ぜんはんしゃ)
というやつだ。
ってことで、全反射をわかりやすく復習していこう。
まずは全反射が起こるシチュエーションから。
全反射が起こるのは、水やガラスなどの透明な物体から、空気中へ光が通るときなんだ。
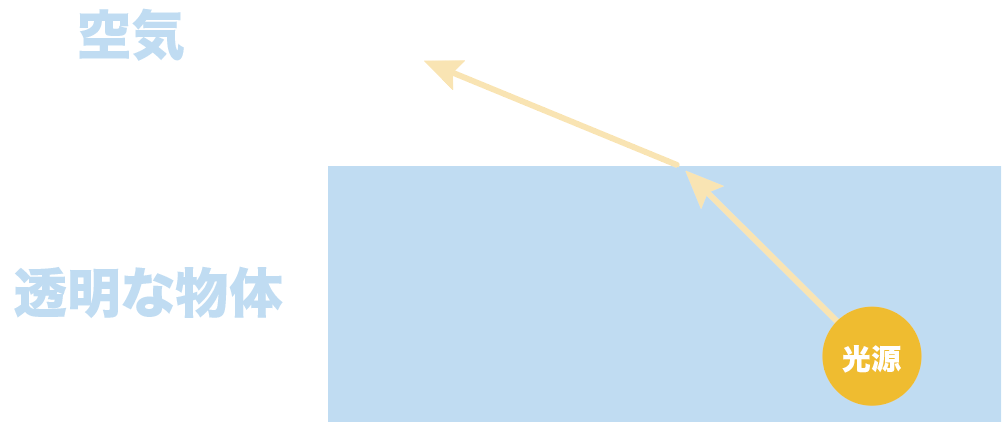
その逆の、空気から透明な物体へ光が入ってくるときは全反射は起きないと覚えておいてね。
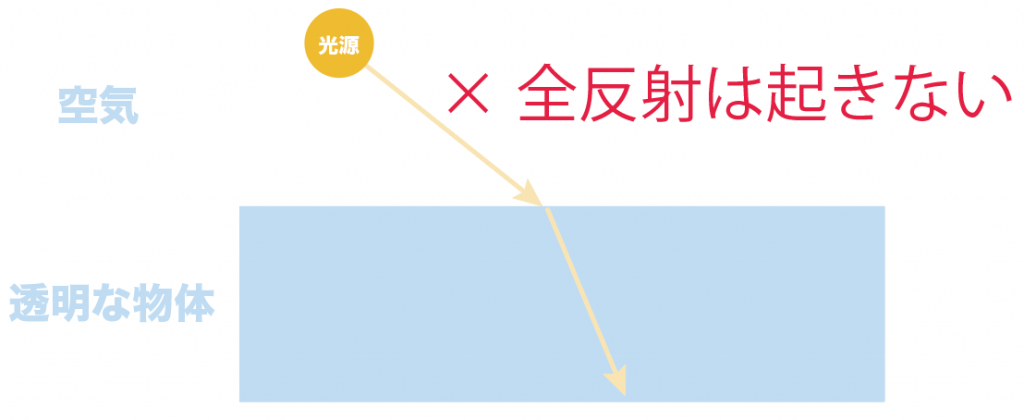
んで、このシチュエーションのとき、何が起こるのかを見てみよう。
全反射とはズバリ、
入射角を大きくしていくと、光が屈折しないで反射してしまう現象のことだ。

透明な物体から空気中に光が飛び出さず、また透明な物体の方向へ跳ね返されてしまうわけ。
ここで、光の屈折の法則を思い出して欲しい。
光の屈折の法則によると、
透明な物体から空気へ光が通るとき、屈折角は入射角よりも大きい
って習ったよね??
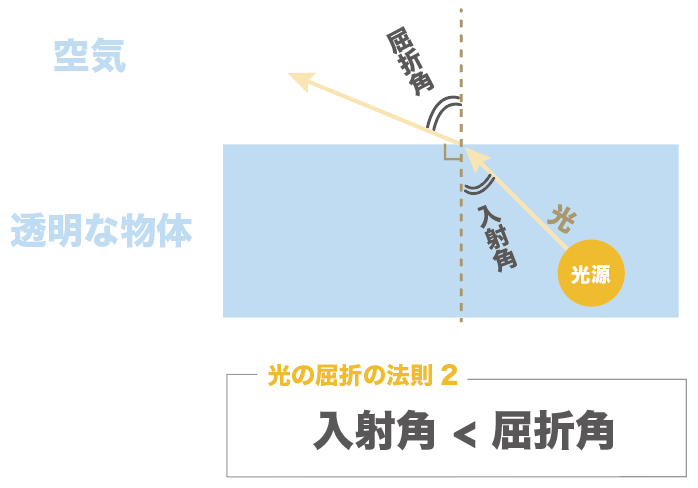
だから、入射角をどんどん大きくして、
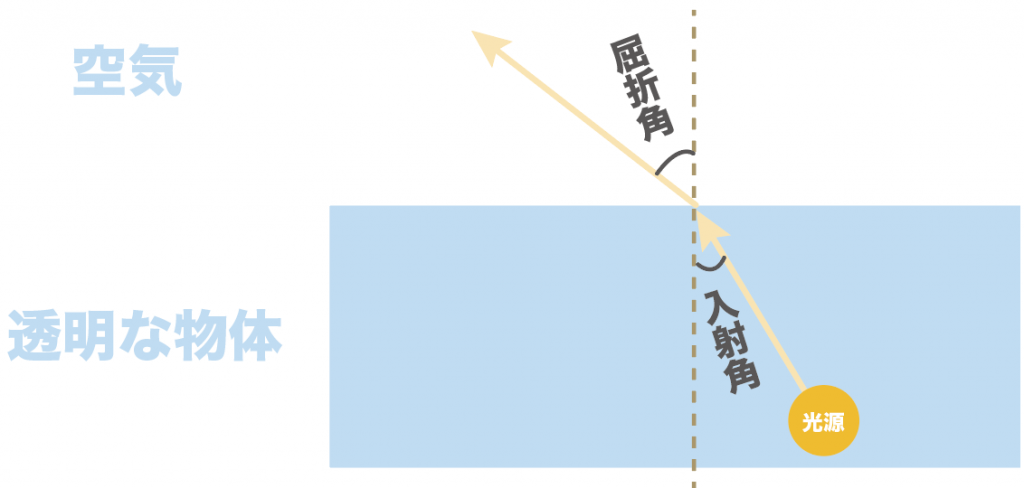
徐々に90度に近づいてくると、
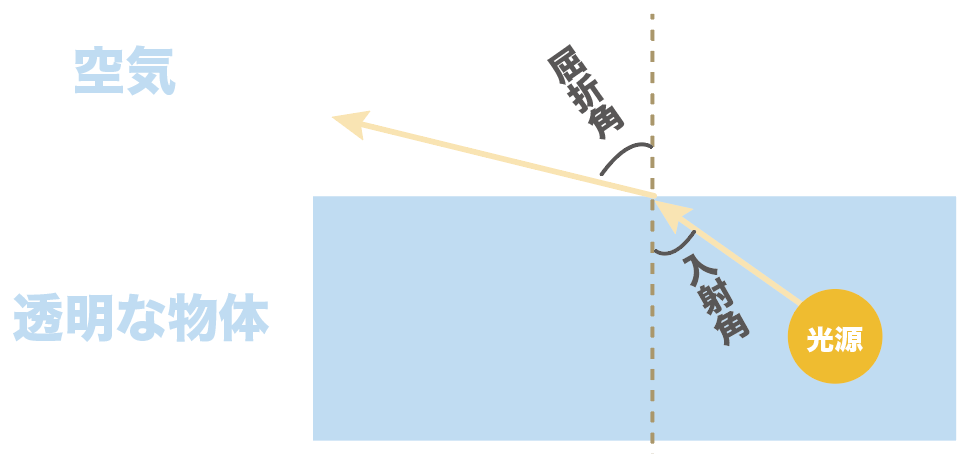
入射角よりも屈折角の方が先に90度に達してしまうんだ。
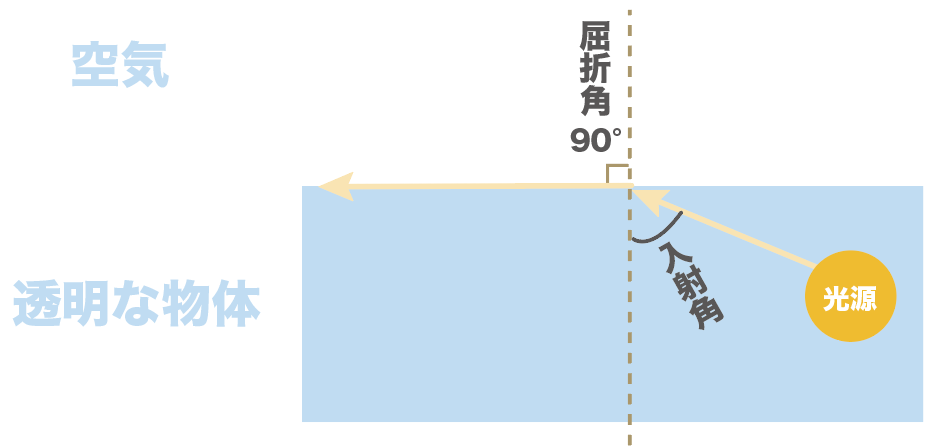
屈折角が90度ってことは、透明な物体と空気の境界面と平行に光が進んでいくことになるよね??
それよりも入射角を大きくして屈折角が90度より大きくなると、光は境界面を飛び越えて空気へ行けなくなっちゃう。
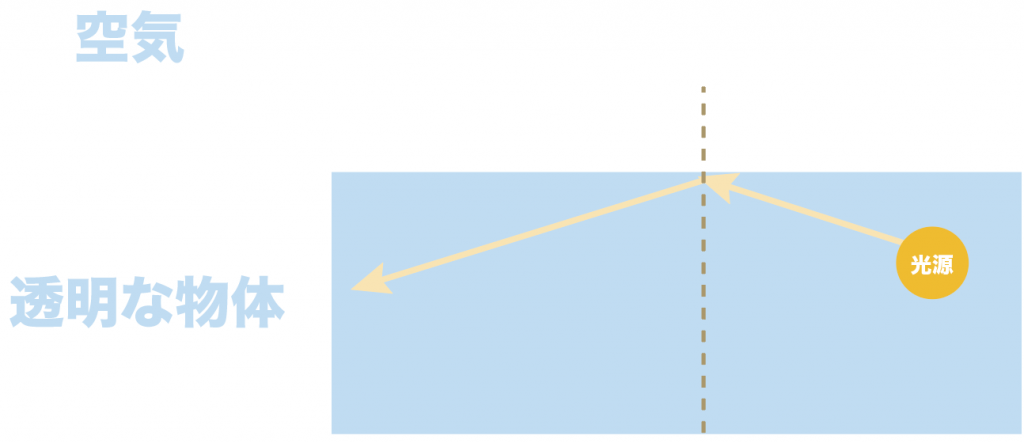
これが全反射だ。
一度全反射になると、光の道筋には「光の反射の法則」が適用される。
どういうことかっていうと、
入射角と反射角が等しい
ってことさ。
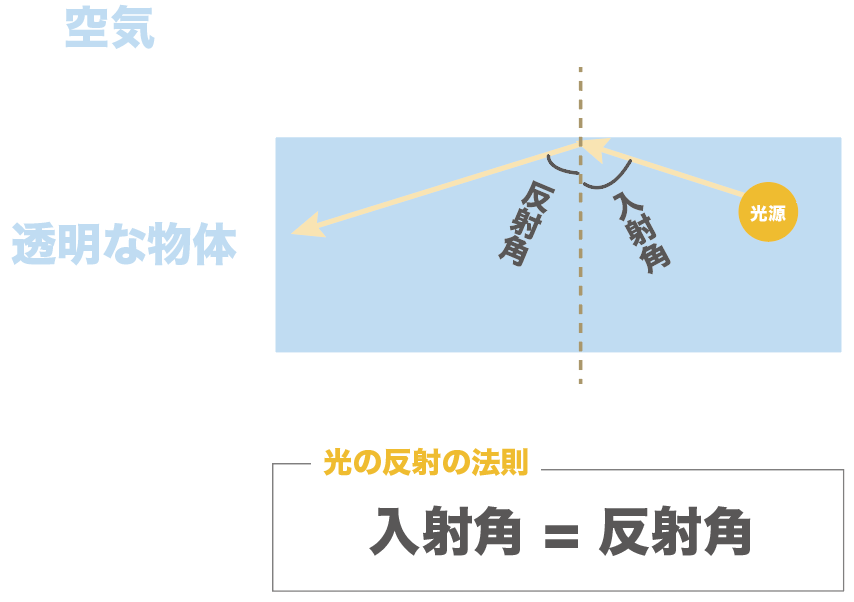
もはや屈折してないから屈折角じゃなくて名前が反射角になってる点に注意してね。
以上で全反射の概要終わり!
テストにも出やすいからよーく復習しておこう!
そんじゃねー
Ken
こんにちは!この記事を書いているKenだよ。麦茶、冷えてるね。
中1理科では「光の屈折」という光の性質を勉強してきた。
光の屈折の法則とは簡単にいうと、
光がある透明な物体を通過すると、光の道筋が曲がる
というものだったね。
>>詳しくは「光の屈折」を参照
この光の屈折の効果を確認できる実験として、よく、
コップにコインを入れて、水を注ぐと浮かび上がって見える
というものが実施されるね。
どういう実験か具体的に見ていこう。
まず、何も入ってないからのコップがあるとしよう。
こいつにコインをチャリーンと入れる。
この状態だと、コップのふちに隠れて外からはコインが見えないはず。
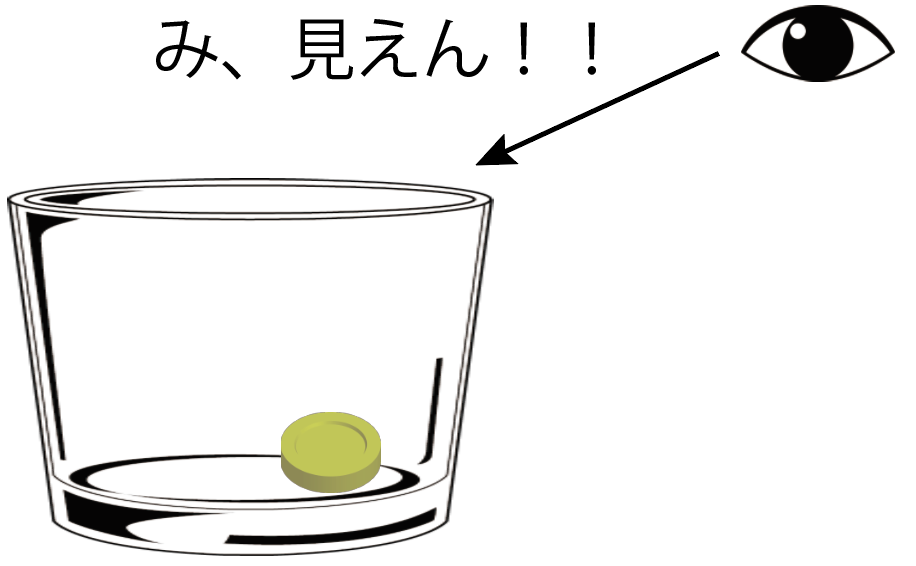
ここで、コップに水をドボドボ注いでみよう。
すると、どうだろう??
さっきまで見えなかったコインが浮き出て見えるようになってるじゃないか!
実際にリアルの世界でも実験してみても、やっぱり浮かび上がって見える。
こ、これはどういうことなんだ?!
それじゃあ、なんで水を入れた途端にコインが浮かび上がって見えるんだろうね??
じつはその理由は、
光の屈折の法則
にあるんだ。
水を入れないと、このコインからの光が目に届かない。
光が目に届かないと、目がコインが見えたっていう指令を脳に送らないから、結果的にいくら踏ん張っても見えないまま。
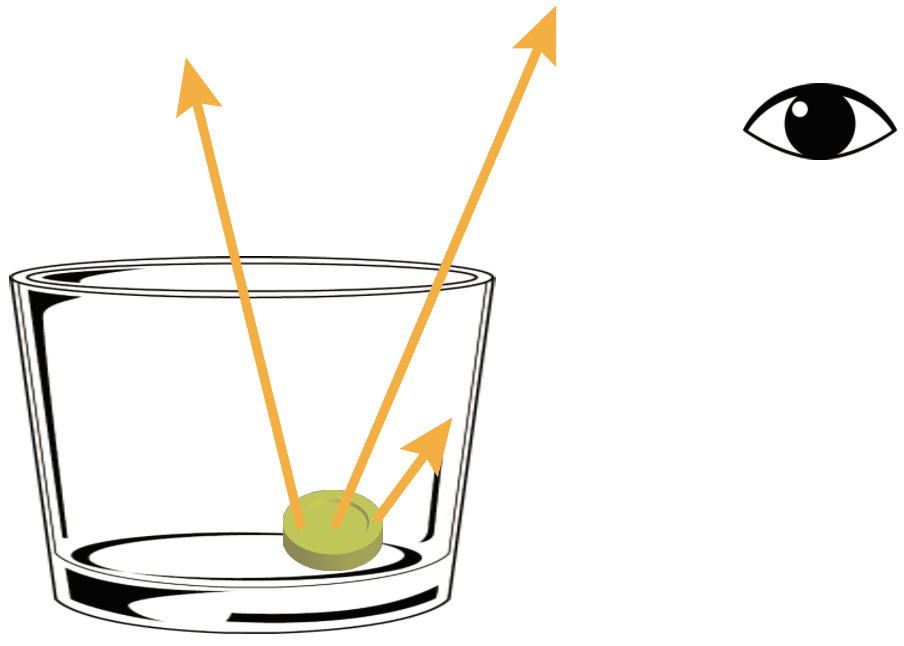
水を入れると、コインからの反射した光が屈折して、無事に目に届くようになるんだ。
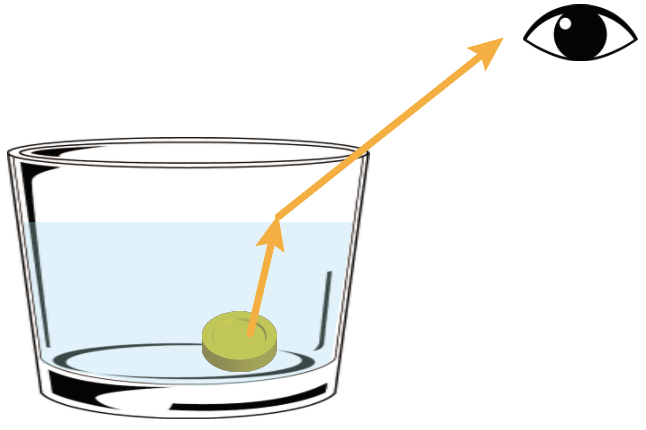
だから、コインは実際の位置ではなくて、目からすると、屈折した光の延長上に見えることになるってわけ。
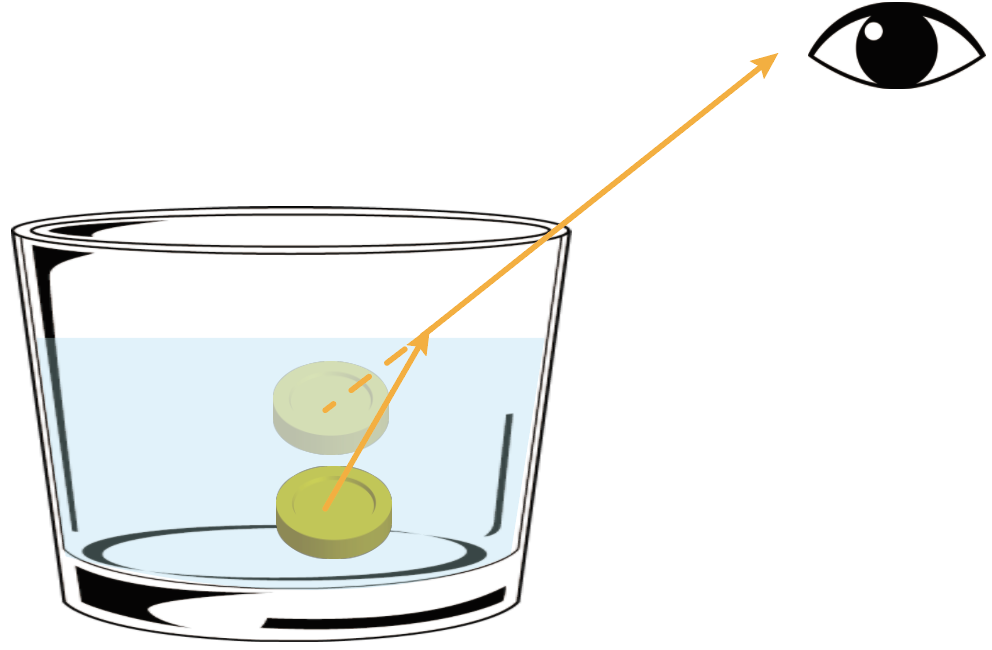
光の屈折の法則さまさまだ。
じつは、このコインが浮かび上がる実験はテストでも狙われやすいんだよ。
たとえば、次のような作図問題がよく出題されるかな。
水が入ったコップにコインを入れると浮かび上がって見えた。
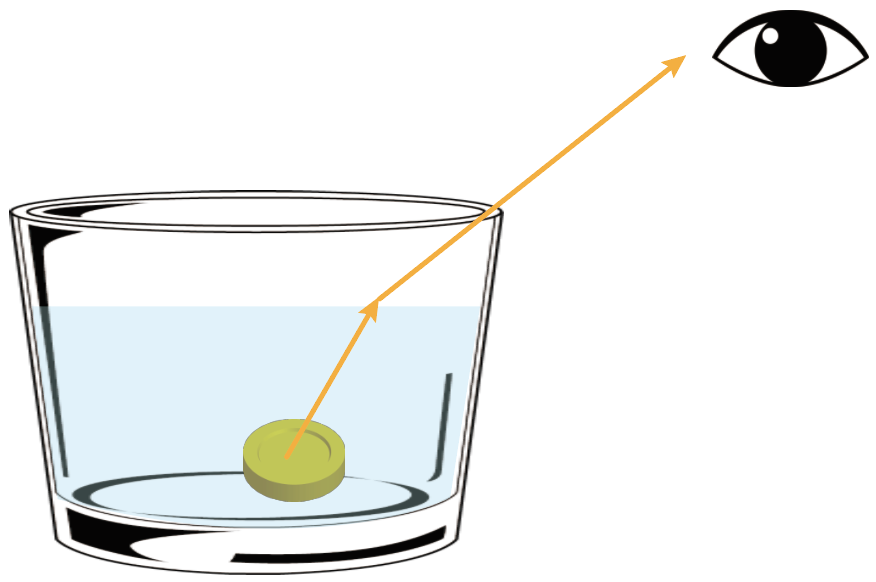
コインの中央からの光が図のように屈折して目に入る時、コインが浮かび上がって見える位置を作図してください。
という問題。
こういう問題では、屈折した光の道筋を逆方向にまっすぐ延長させればいいんだ。
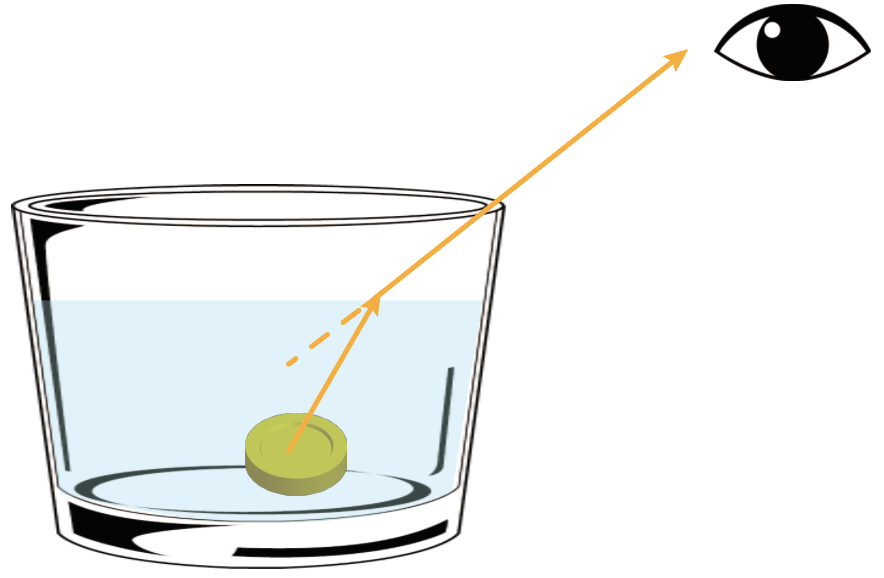
まっすぐ延長線をかくために定規を使ってやろう。
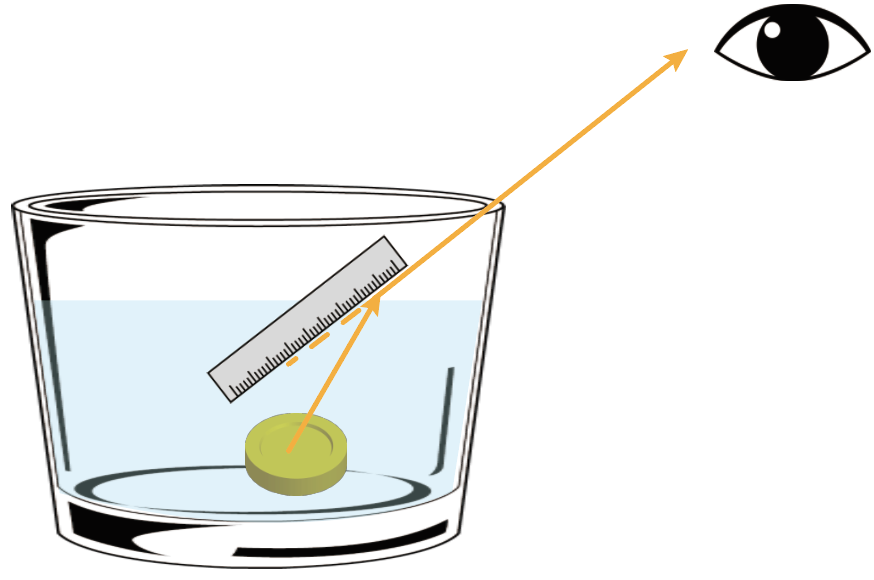
その延長線上にコインが見えているはずだから、だいたい元のコインの位置の真上にコインを作図してやればオッケー。

この手の問題はよくテストに出るから復習しておこう!
そんじゃねー
Ken
こんにちは!この記事を書いているKenだよ。のど飴、100個ぐらい欲しいね。
中学1年生の理科では、
光の屈折の法則
を勉強していくよ。
この法則とはズバリ、
光が空気中から透明な物体に入るとき、入射角の方が屈折角より大きくなる。
逆に、透明な物体から空気中に光が入ってくるとき、屈折角の方が入射角より大きくなる。
というやつだったね。
えっ。
「屈折角」とか「入射角」とか意味がわからないだって!?
今日はそんな光の屈折の法則を完璧に忘れちゃったときのために、一からわかりやすく覚え方まで解説してみたよ。
よかったら参考にしてみて。
まずは、光の屈折の法則で出てくるキーワード、
の2つの意味を確認していこう。
これらの2つの言葉はすべて、
空気中から透明な物体へ光をあててみたり、
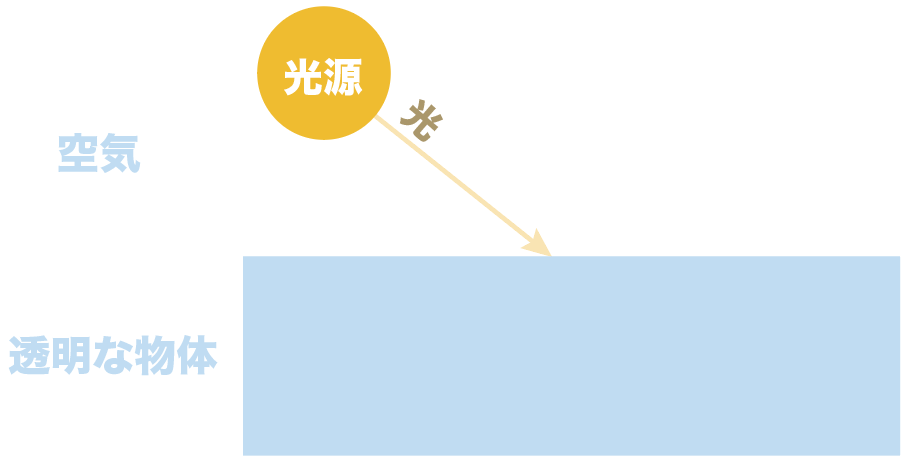
逆に、透明な物体から空気中へ光を当ててみたり、

っていうシチュエーションで使う言葉だよ。
あんまりイメージ湧かないかもしれないけど、この状況で出現する用語だと認識しておいてね。
入射角とは、
入ってくる光の道筋と境界面に垂直な線との角度のこと
なんだ。
ここでいう「境界面」とは、
の境目のことね。

入射角っていう言葉は「光の反射の法則」でも出てきたから馴染みあるかもね。
たとえば、空気から透明な物体(半円レンズ)に光を入れたときは、この角度が入射角になるよ。
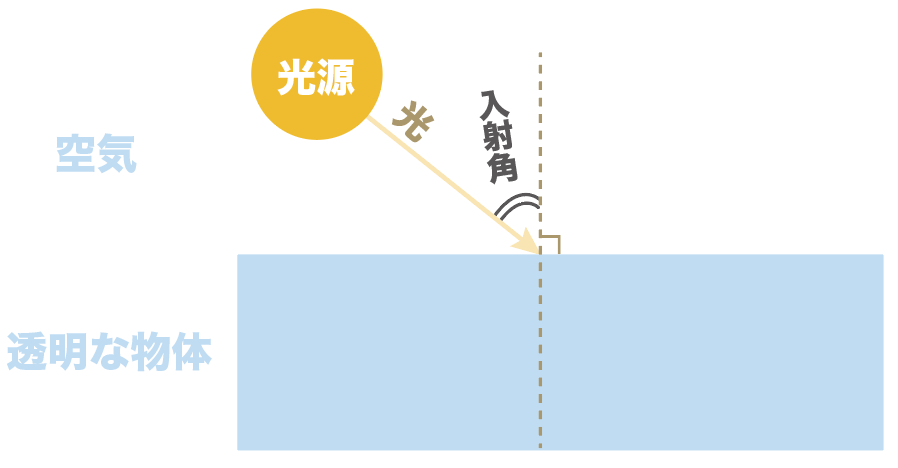
逆に、透明な物体から空気に光を入れた場合はこっちが入射角だけどね。
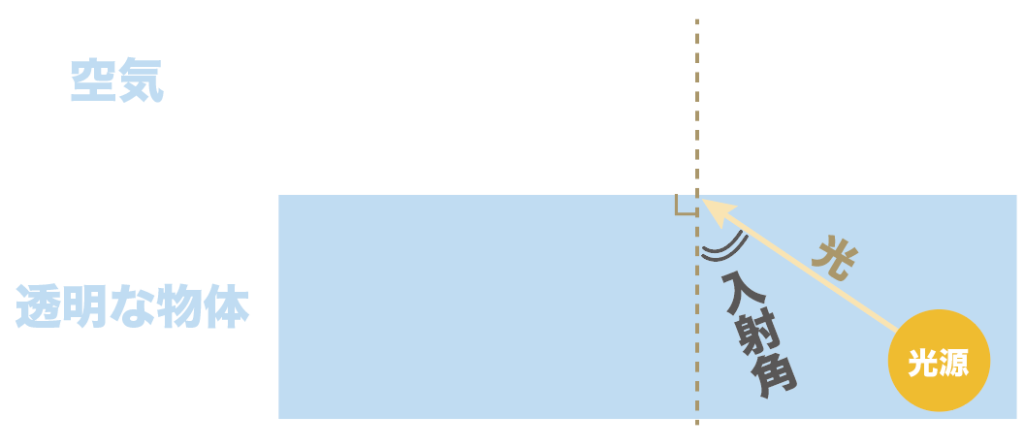
屈折角とは、
出ていくときの光の道筋と境界面に垂直な線との角度のこと
なんだ。
出ていくときの道筋はまっすぐじゃなくて屈折(曲がる)から、屈折角と呼ばれているんだ。
たとえば、空気から透明な物体(半円レンズ)に光を入れたときは、ここが屈折角。
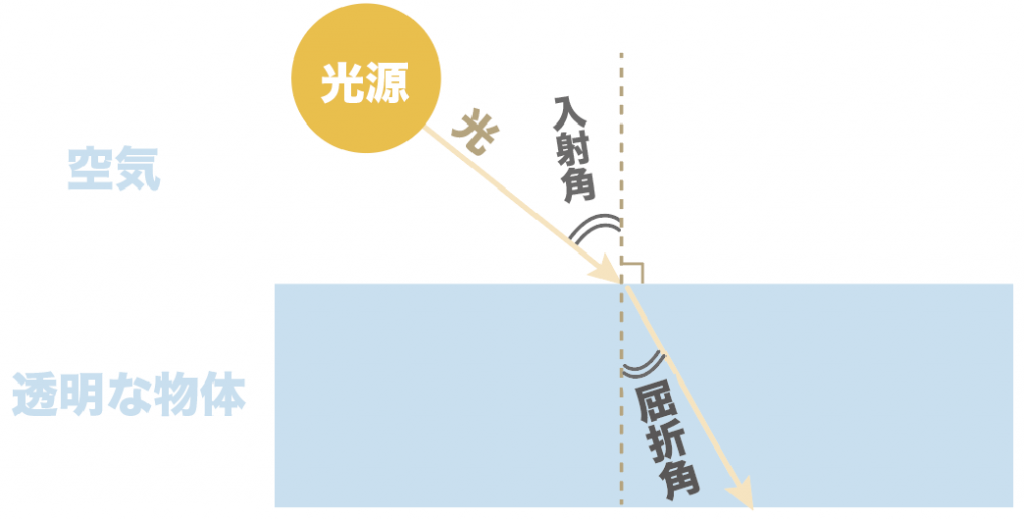
逆に、透明な物体から空気に光を入れたときは、ここが屈折角になるのね。
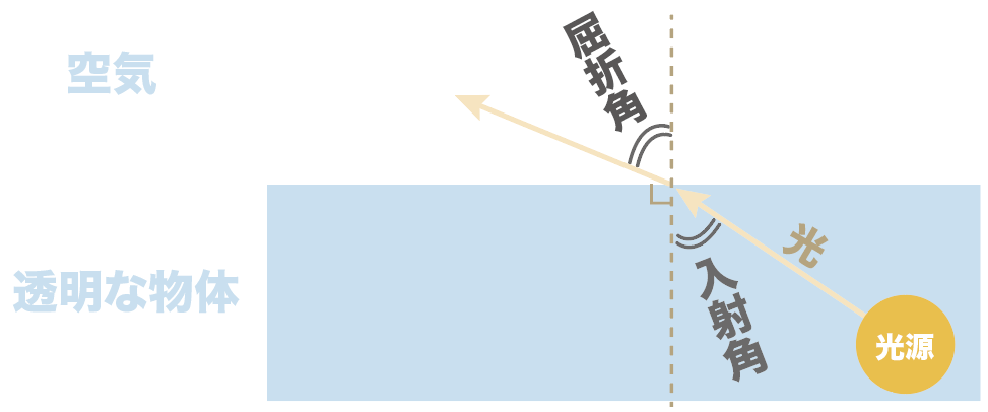
さて、入射角と屈折角の意味がわかったから、光の屈折の法則に戻ってみようか。
光の屈折の法則とは、
光が空気中から透明な物体に入るとき、入射角の方が屈折角より大きくなる。
逆に、透明な物体から空気中に光が入ってくるとき、屈折角の方が入射角より大きくなる。
だったね。
つまり、光の入り方が、
っていう2つのパターンのときの、入射角と屈折角の関係を表した法則なんだ。
それぞれのパターンについてみていこう。
まず、空気中から透明な物体に光が入るときのパターンね。
このとき、光の屈折の法則によると、
入射角の方が屈折角より大きくなるんだ。
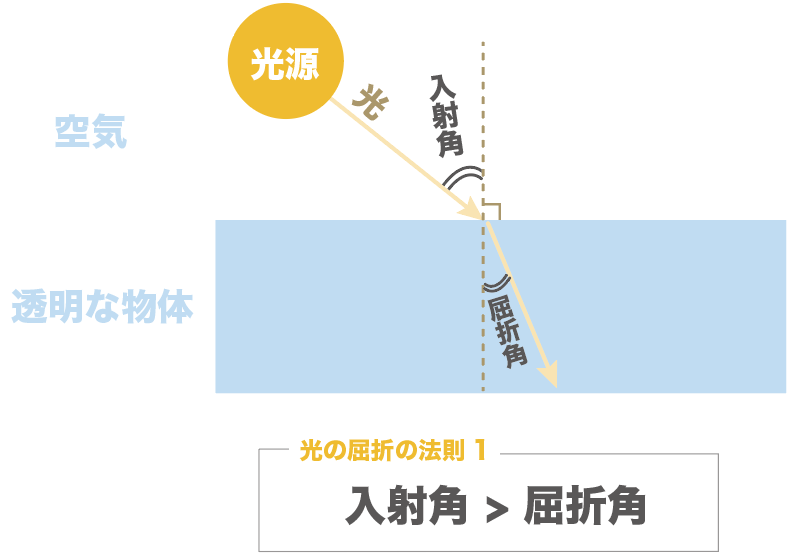
不等号で表すとこうなるよ↓↓
入射角>屈折角
今度は、逆に、
透明な物体から空気中に光が入ってくるパターンね。
この場合は、
屈折角の方が入射角より大きくなるんだ。

不等号であらわすと、
入射角 < 屈折角
つまり、どういうこと言ってるのかというと、
空気中から透明な物体に入れたり、その逆のことをすると、
入れた光はまっすぐ進むんじゃなくて境界面で曲がって光の道筋が変化するよ
ってことを言ってるわけね。
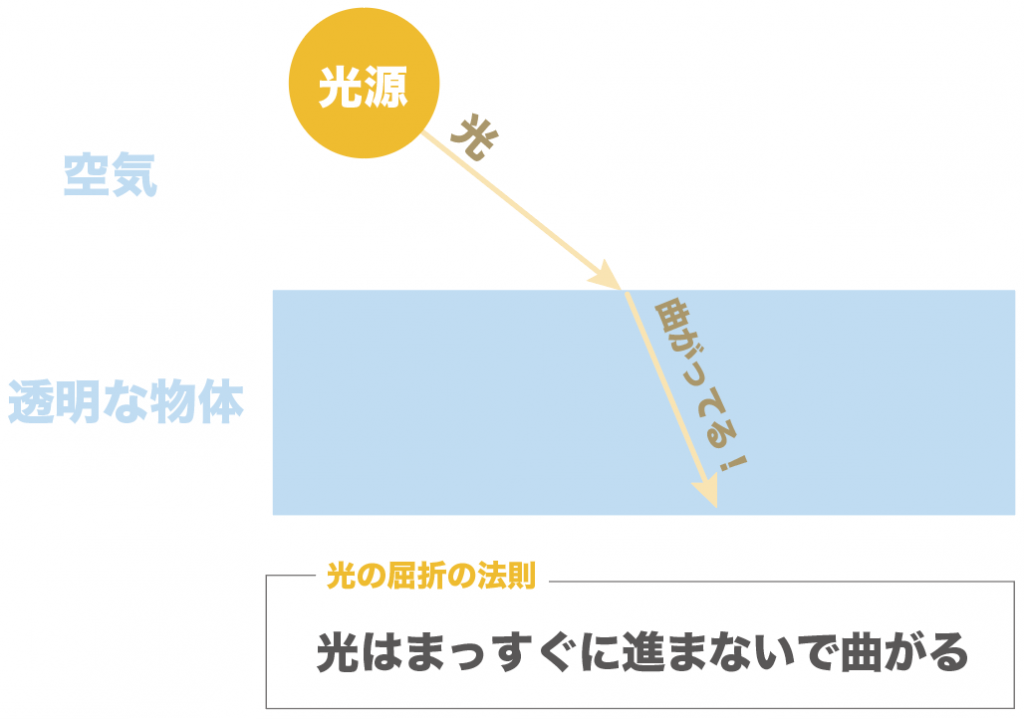
だいたい光の屈折の法則はわかって来た。
だけどさ、
この光の屈折の法則って覚えづらくない??
どっちのパターンの時に、入射角が大きくなるとか屈折角が小さくなるとか、もうね、勘弁して欲しいよ。
そんなときは次の光の屈折の法則の覚え方を使ってみて。
ヤクザの事務所に乗り込む親父をイメージしてくれ。
覚え方はズバリ、
入り口では屈しなかった親父も、帰りは屈してしまった
だ。
ここでは、ヤクザの事務所を「透明な物体」、事務所の外側を「空気」としているよ。
さすがに頑固でマッチョな親父も組織的なヤクザには勝てなかったみたいね。
行き(空気中から透明な物体へ)は、屈しなく、入射角の方が大きかったんだけど、
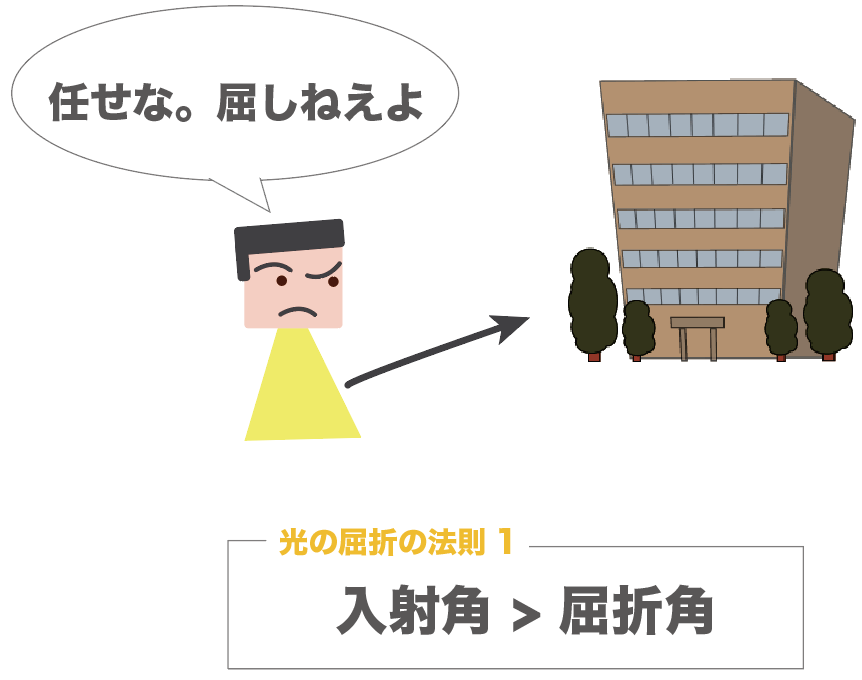
帰り(透明な物体から空気中へ)は、屈してしまい、屈折角の方が大きくなってしまったんだ。
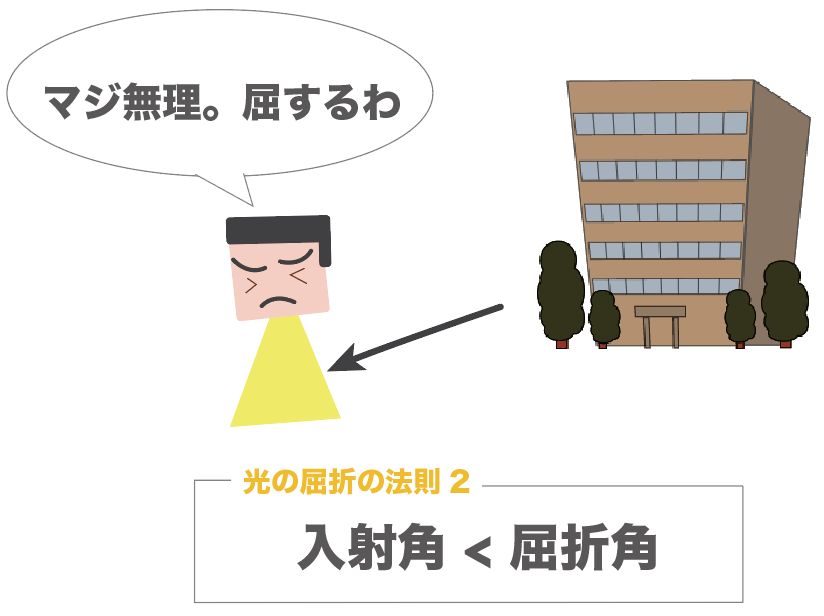
光の屈折の法則では、
の大小だけを語っている法則だから、2つのパターンにおいてどっちの角度の方が大きくなるってことを覚えておけばいいね。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。ローヤルゼリー注入したね。
中学理科で光の勉強をしていると、
乱反射(らんはんしゃ)
という言葉を勉強していくよね??
乱反射とは、
表面がデコボコしている物体に光を当てたときに、いろんな方向に反射すること
をいうんだ。
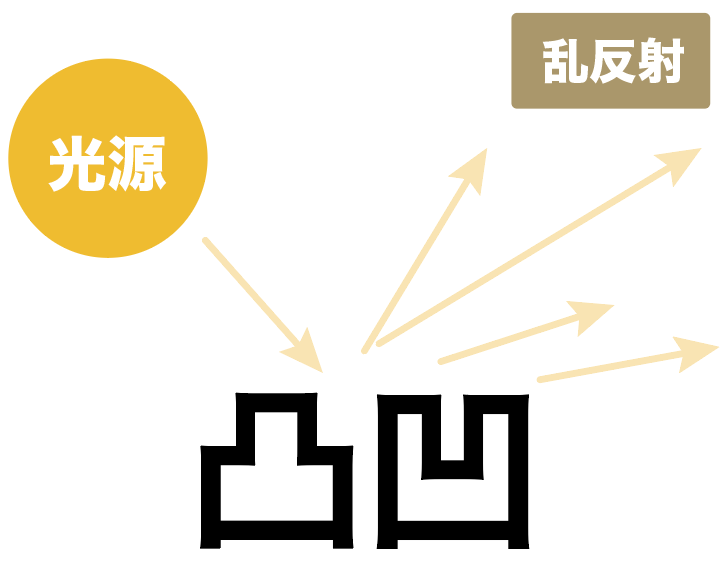
たとえば、ちょっとデコボコしているフランスパンに光を当てているシチュエーションを想像してくれ。

光源が一つしかないとき、このパンを見たかったらどこに移動する??
光の反射の法則を勉強したやつは、
「入射角と反射角が等しくなる位置に移動すれば見える!」
って答えるかもしれないね。
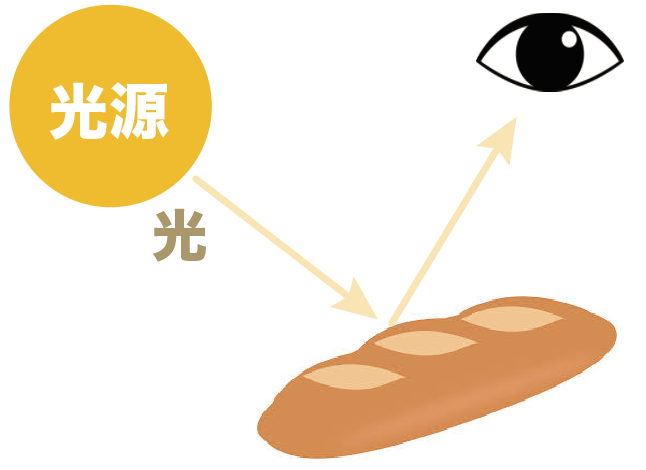
いや、確かに入射角と反射角が等しくなる位置に移動しても見えるんだけど、それだけじゃああない。
フランスパンの表面はデコボコしてるから、光をあてると乱反射が起きる。
つまり、一つの方向からの光源しかなくても、いろんな方向に光が進んでいくんだ。
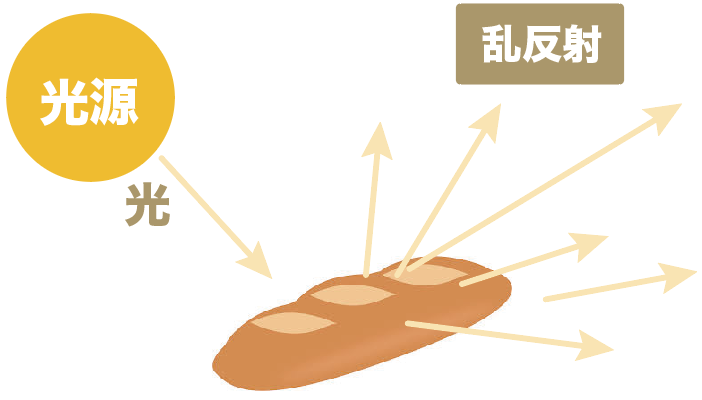
だから、ぶっちゃけ、フラスパンの近くにある程度いればどの方向からも見えるはずだ。
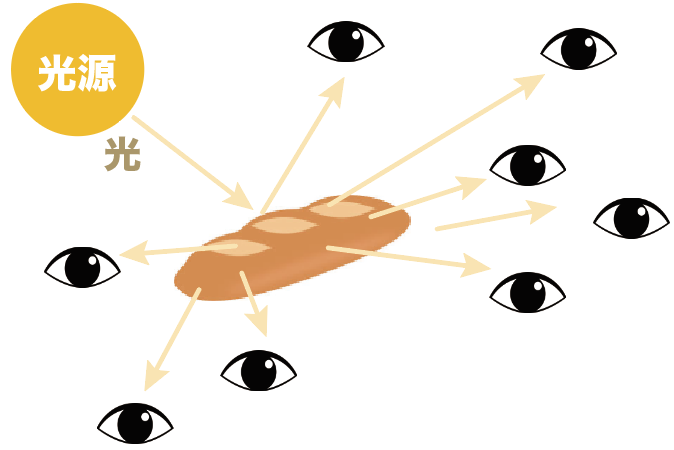
って感じで、光源からの光をデコボコの表面がいろんな方向に反射してしまう乱反射。
一見、「光の反射の法則」を無視しているように思うけど、じつは、
ちゃんと光の反射の法則に従っているんだ。
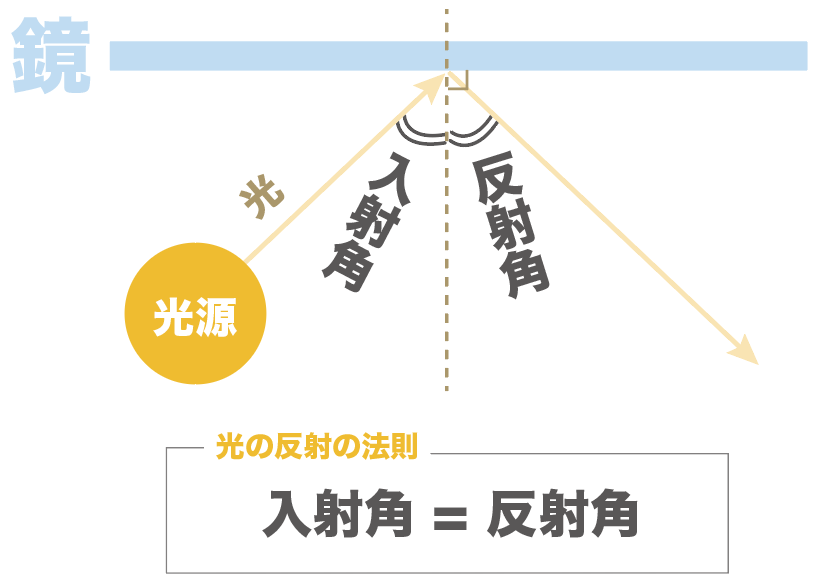
光の反射の法則は、
入射角と反射角が等しい
だったね。
さっきのフランスパンを見てみよう。
フランスパンの表面を虫眼鏡で拡大してやると、こんな感じでびっくりするぐらいデコボコ。
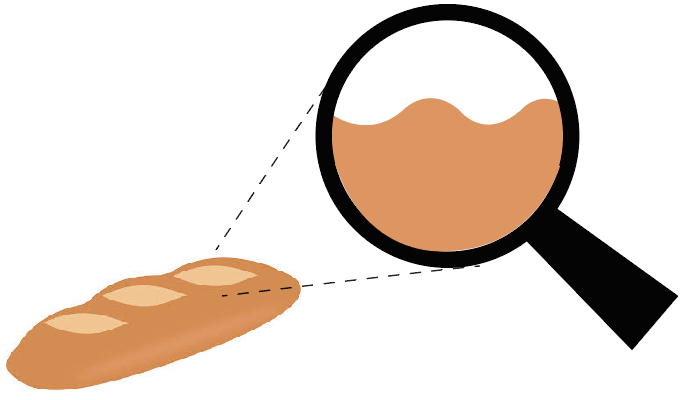
光源からフランスパンに光を当てたときは、こんな感じで、ひとつひとつの光の道筋が「光の反射の法則」に従ってしっかりと反射しているんだ。
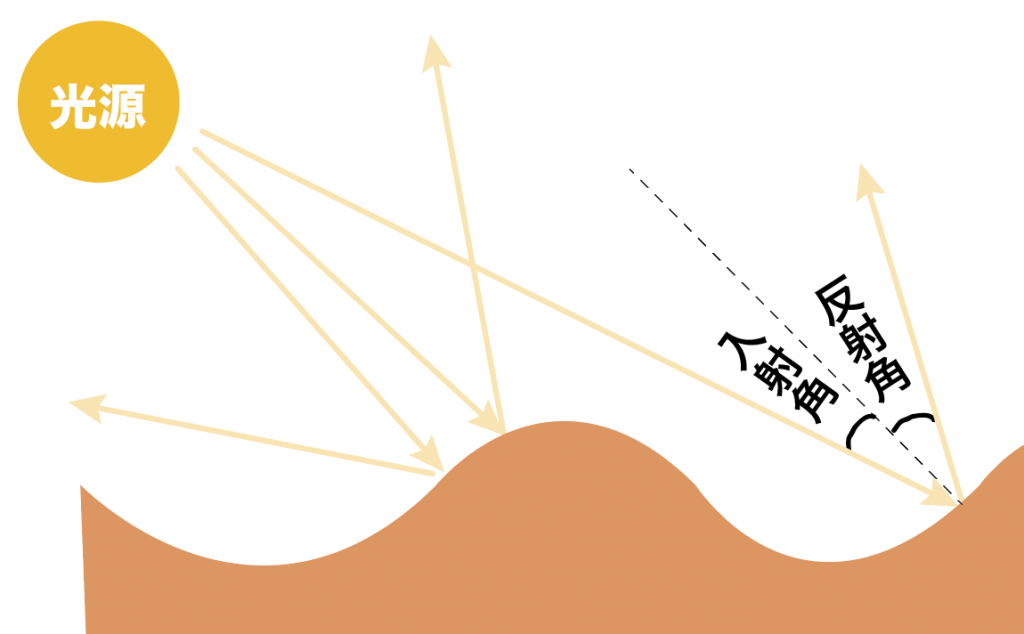
だから、表面がデコボコしている物体に光をあてると乱反射しているのね。
ちょっとしっくりこなかった時は「光の反射の法則」から復習してみよう。
そんじゃねー
Ken
こんにちは!この記事を書いているKenだよ。ペッパー、最高。
中学理科では、
光の反射の法則
というものを勉強していくよ。
光の反射の法則とはズバリ、
鏡に光を当てたとき、入射角と反射角が等しくなる
っていう法則なんだ。
ふむふむ・・・なるほどね・・・
えっ。
「入射角」と「反射角」って初めて耳にした言葉だって!?
そうだね、じゃあ今日は光の反射の法則を理解するために、入射角と反射角の復習から始めよう。
光の反射の法則の基礎となる、
を解説していくよ。
この2つのキーワードは、両方とも、
鏡に光を当てたときにできる角度のこと
なんだ。
光源から光を発射しているシチュエーションを想像してくれ。
まず入射角からね。
入射角とは、
鏡に光を当てたときに、「入ってくる光の道筋」と「鏡に垂直な線」がつくる角度のこと
なんだ。
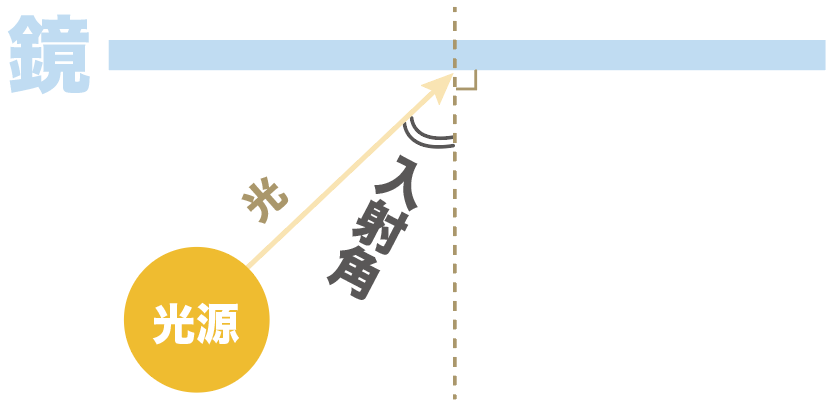
光線がある物体に当たることを「入射」っていうから、入射(光源から鏡へ当たるとき)するときの、鏡に対する角度を「入射角」と呼んでいるんだ。
一方、反射角とは、
「反射した光の道筋」と「鏡に対して垂直な直線」との角度のことをいうんだ。
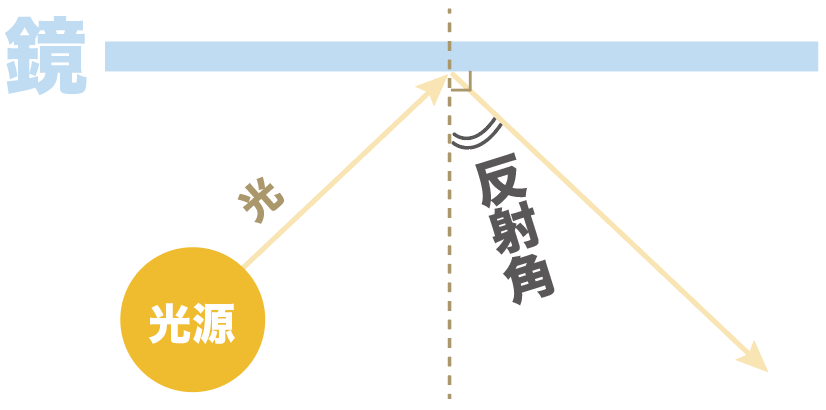
どう?入射角と反射角の違いもしっくり来たかな。
光の鏡に対する角度っていうのは同じなんだけど、入ってくる光との角度のなのか、反射する光との角度なのかが異なるんだ。
ここまでで、
の2つの意味はだいたいわかったね。
で、一番最初に紹介した光の反射の法則とは、
鏡に光を当てたとき、入射角と反射角が等しくなる
っていうやつだったね?
そう、文字通り、鏡に光を当てたとき、
入射角=反射角
になるんだよ。

たとえば、鏡に光を当てたとき、入射角が36度だったとしよう。
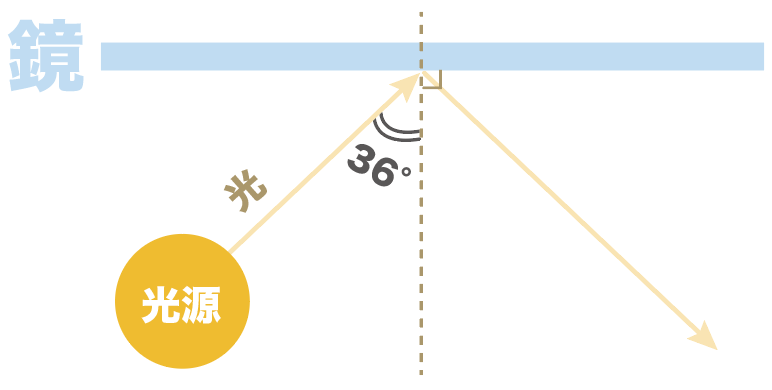
このとき、光の反射の法則より、反射角も36度になるんだ。
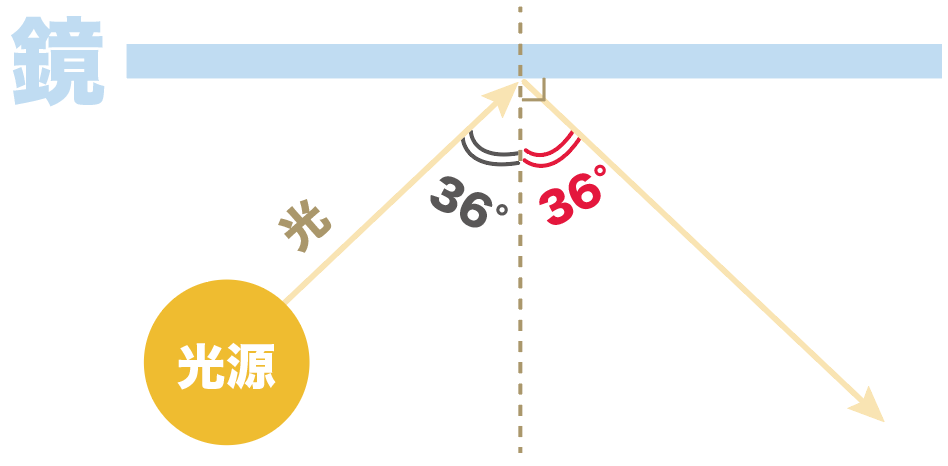
なるほどね。
これで光の反射の法則は終わり!
次は光の屈折の法則を勉強してみよう。
そんじゃねー
Ken
こんにちは!この記事を書いているKenだよ。水、有料だね。
中1理科では「身のまわりの現象」という単元で、
光の進み方
を勉強していくよね。
ここでは文字通り、光がどんな感じで進んでいくのかを勉強していくんだけど、この単元を理解する基礎となるのが、
っていう3つのキーワードなんだ。
こいつらさえ押さえておけば、テストで慌てることはない。逆に知っていると武者震いしてくるはずだ。
そこで今日は、光源・光の反射・光の直進をわかりやすく解説していくよ。
よかったら参考にしてみて。
まず基礎中の基礎。
光源とは、
自分から光を発している物体のこと
だよ。

たとえば、身近な例でいうと、太陽とか、蛍光灯とか、スマホとかパソコンかな。

もちろん、世界には光源じゃないものだってあるよ。
光源じゃないのは、たとえば、紙でできた教科書とか、人間とか、牛丼とか、牛とか、草とか、かな。

光源じゃない物体は光を発してないんだ。
続いて、光の反射だ。
光の反射とは、
光が物体の表面に当たってはね返えること
をいうんだ。
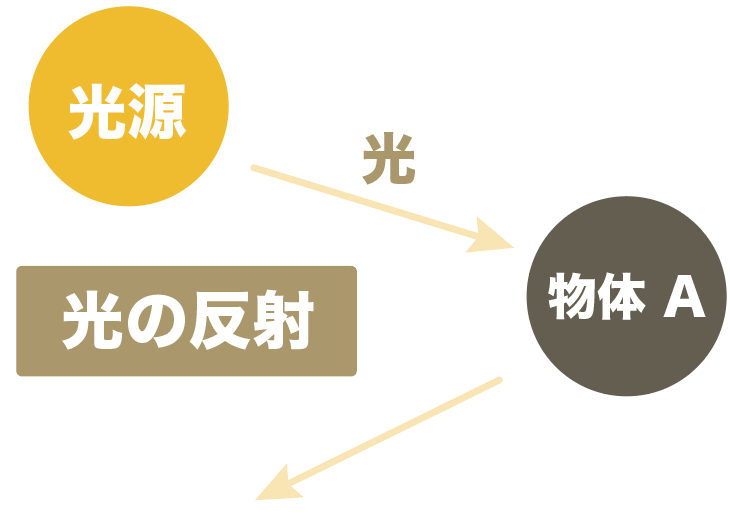
さっき紹介した光源じゃないものたちを、ぼくら人間の目で見ることができるのは、
光源から発せられた光が、物体の表面に反射して、目に届くからなんだね。
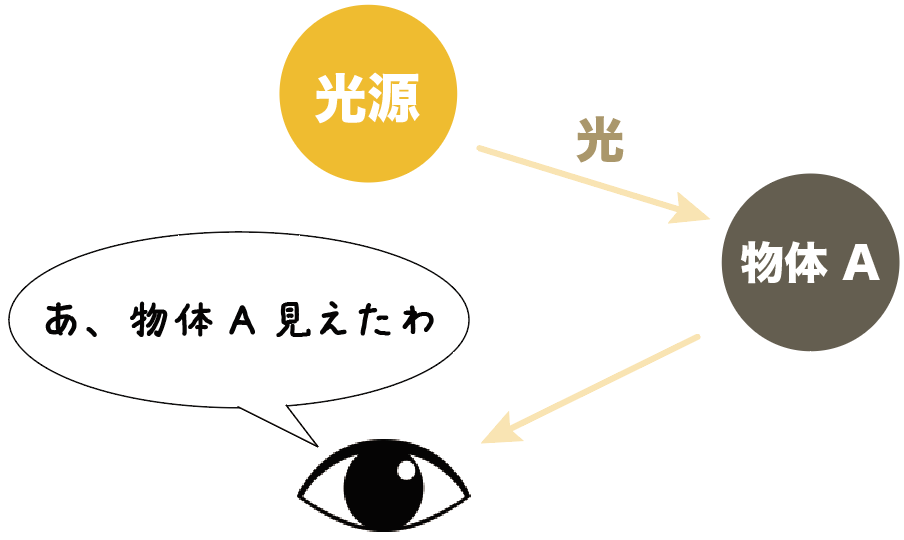
光源の物体は光の反射を利用しなくても目に見えるということだ。
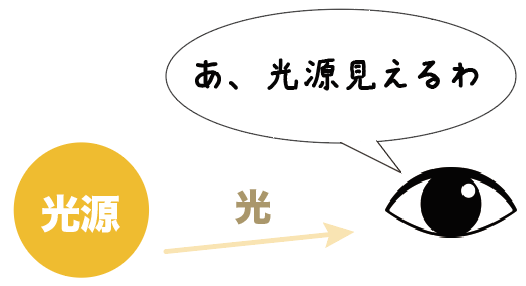
お次は「光の直進」だ。
光の直進とは、
光源から発射された光がまっすぐに進むこと
をいうんだ。

光源から出た光は、こんな風にクネクネしないし、

一筆書きの絵を描いたりしない。

まっすぐ進むんだ。

以上が、
の3つのキーワードだよ。
最後に復習しておこう。
光源とは、自ら光を発している物体で、

光の反射とは、物体に光が当たってはね返えること。

光の直進とは、光が光源から出たらまっすぐ進むことだったね。

どれもこれも中学の光の勉強で基礎となる用語たちだからしっかり押さえておこう。
そんじゃねー
Ken
こんにちは!この記事を書いているKenだよ。ジンジャー、注入したね。
中1理科の身のまわりの物質では、
蒸留(じょうりゅう)
という言葉を勉強していくよね??
中学理科の授業で「蒸留」はテストにでやすいだけじゃなくて、蒸留の実験も行われたりするから、蒸留とは何かを理解しておくに越したことはないんだ。
そこで今日は、中学理科で勉強する蒸留とはなにかをわかりやすく解説していくよ。
よかったら参考にしてみて。
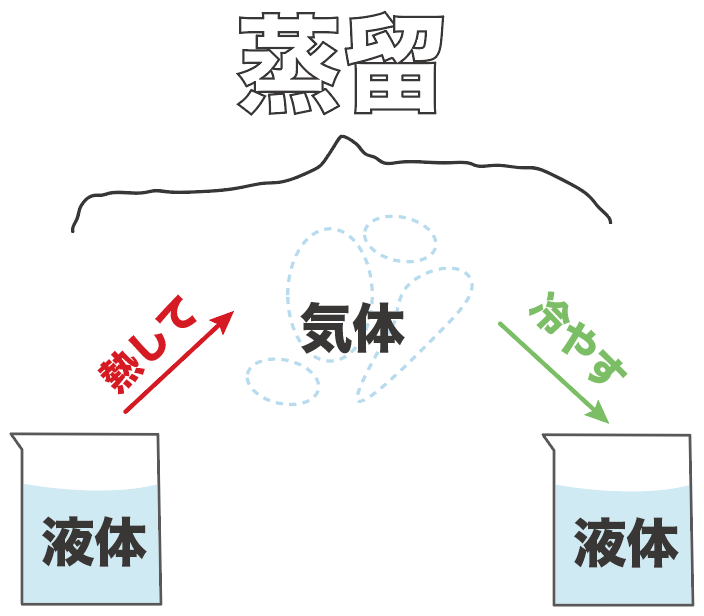
ズバリ、蒸留とは、
ある「液体」の物質を「気体」にして「液体」にもう一回戻して取り出すこと
なんだ。
たとえば、25℃の水を蒸留で取り出すシチュエーションを想像してみてくれ。
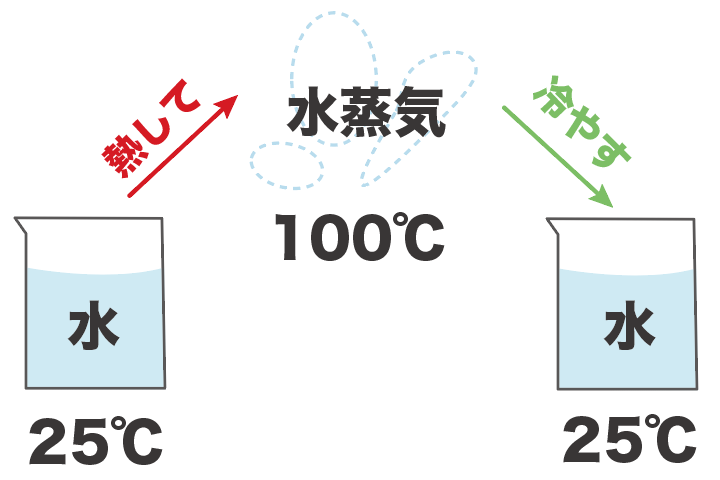
まず、水を熱して、100度まで持っていく。
すると、水が水蒸気になるから、この水蒸気を取りこぼさないように確保。
この水蒸気をもう一回冷やすことで、水に戻して、水自体をゲットするわけだ。
これが蒸留ね。
ただ、蒸留の真価が問われるのは、
色々混ざっている液体から、ある特定の液体を取り出したいとき
だ。
たとえば、
の4つの物質が混じっている液体があったとしよう。
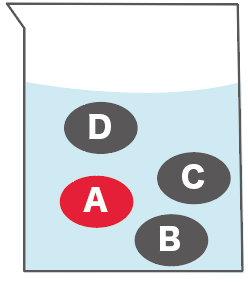
この液体からきれいさっぱりAだけ取り出したいときがあるよね。そんな時は蒸留を使って取り出すと便利。
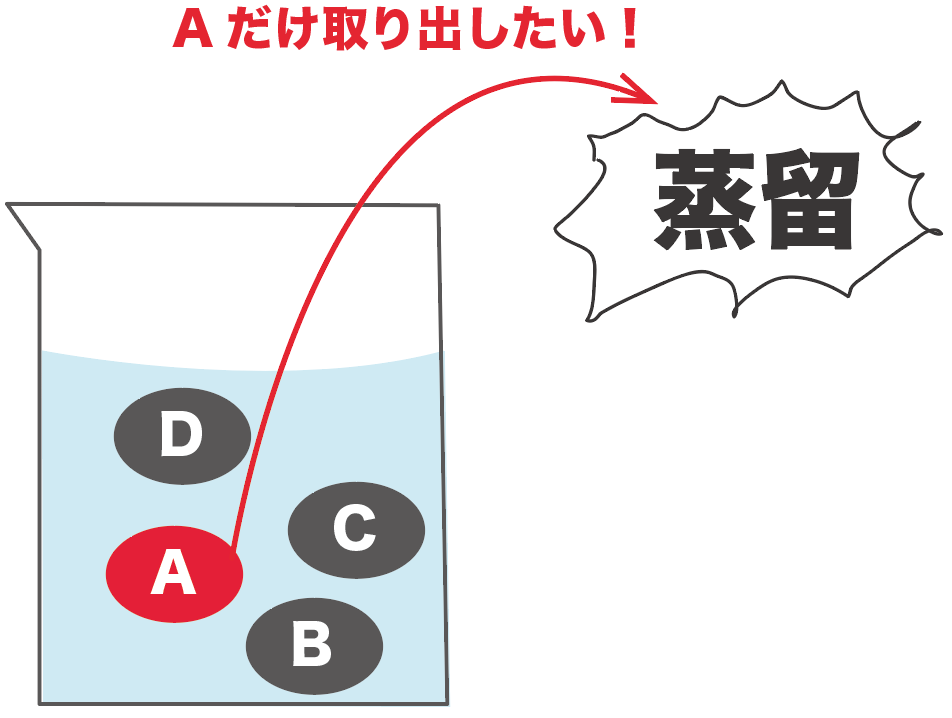
蒸留は物質の種類によって沸点が異なることを利用していくよ。
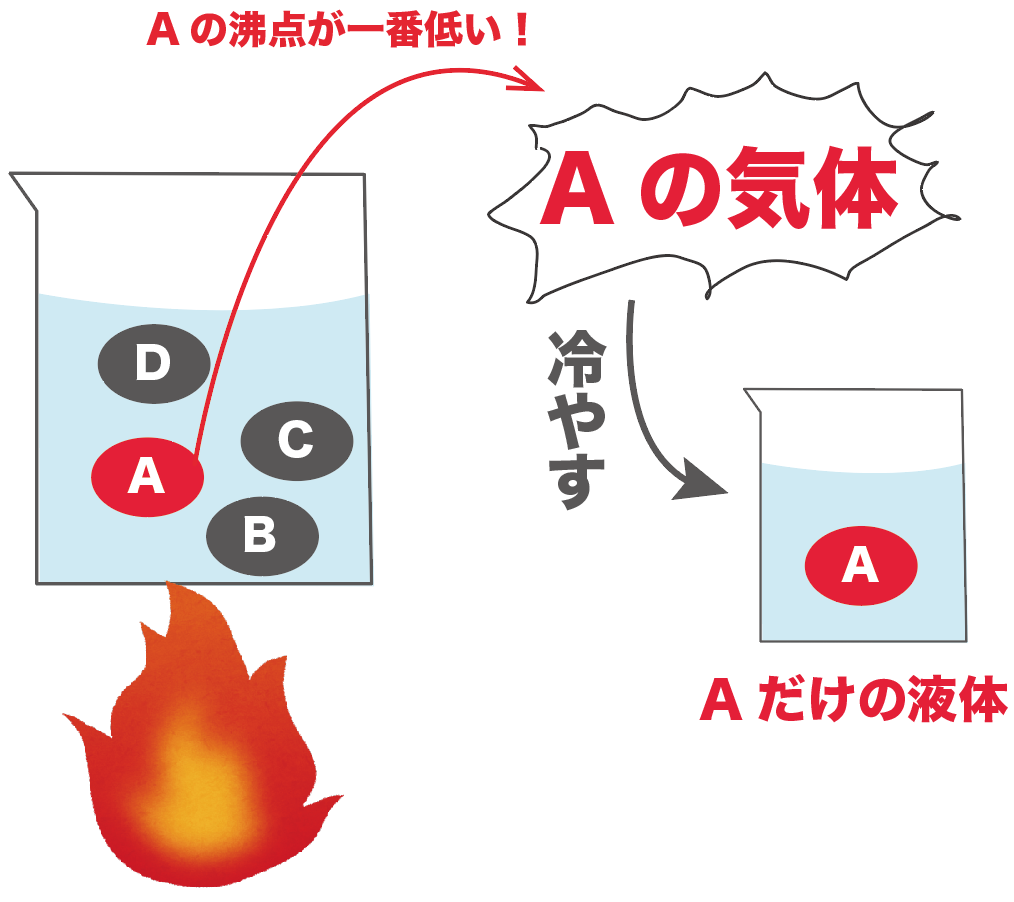
とりえあず、いろいろ混じっている液体を熱してみる。
すると、沸点が低い物質は、他の物質よりも先に気体になるよね??
ってことは、その時点で気体になっているのはこの沸点の低い物質だけだ。
この気体を冷やして液体にしてみると、純度100%の液体が取り出せるわけね。
たとえば、水とエタノールが混じった液体があるとしよう。
こいつを熱してあげると、どうなる??
エタノールの方が水よりも沸点が低いから、まずはエタノールの方が気体になっていくんだ。
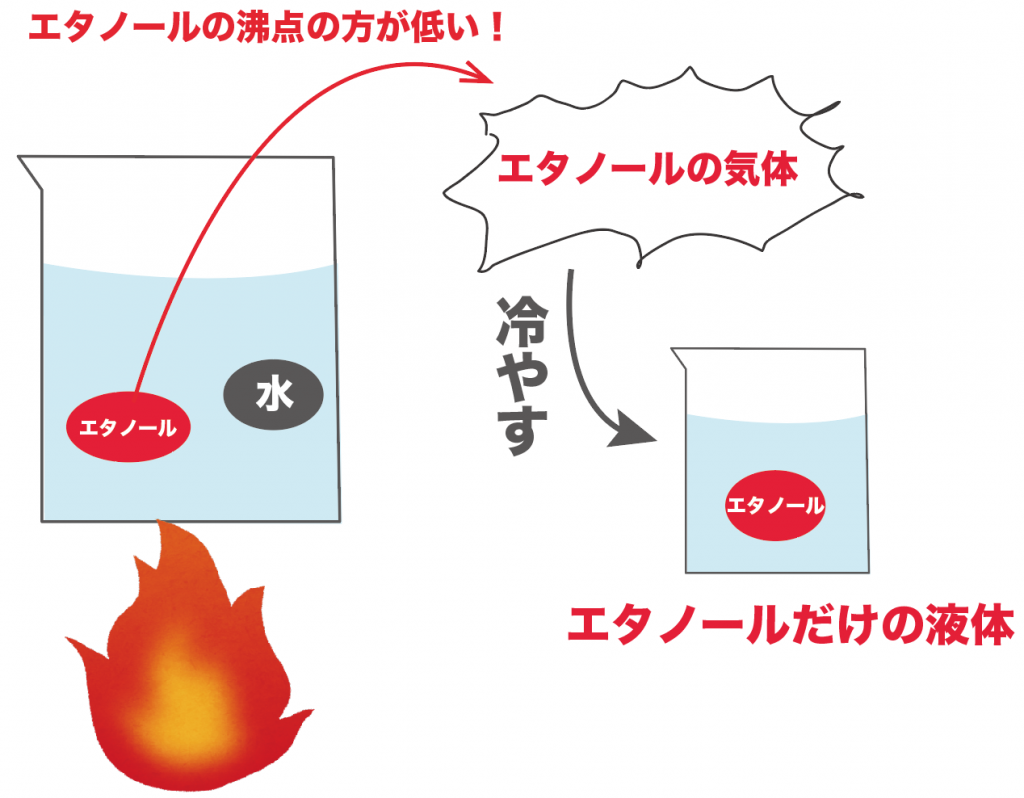
この出てきた気体を冷やすと、水が混ざっていないエタノールを100%の純度で取り出せるわけだ。
以上が蒸留だったね。
最後に復習しておこう。
蒸留とは、
ある液体の物質を熱して気体にして、冷やして液体に戻して取り出す方法だ。

なぜ蒸留を行うかというと、
沸点の異なる物質が混ざった混合物から、特定の物質を取り出すためなんだ。

蒸留はテストにでやすいからよーく復習しておこう。
そんじゃねー
Ken
こんにちは!この記事を書いているKenだよ。チキンスープの匂いがするね。
中学1年生の理科では、
っていう2つのちょっと紛らわしい理科の用語を勉強していくよ。
「沸点」と「融点」はともに、
ある物質が状態変化する温度のことなんだ。
今日はテストでもごっちゃ混ぜにして間違えないように、沸点と融点の違いをわかりやすく解説してみたよ。
よかったら参考にしてみてね。
それじゃあ早速、沸点と融点の違いをみていこう。
沸点とはズバリ、
液体が気体に変化するときの温度のこと
だよ。
たとえば、25℃の液体の水を熱し続けて、100℃にしたとき、水が水蒸気に変化し始めたとしよう。
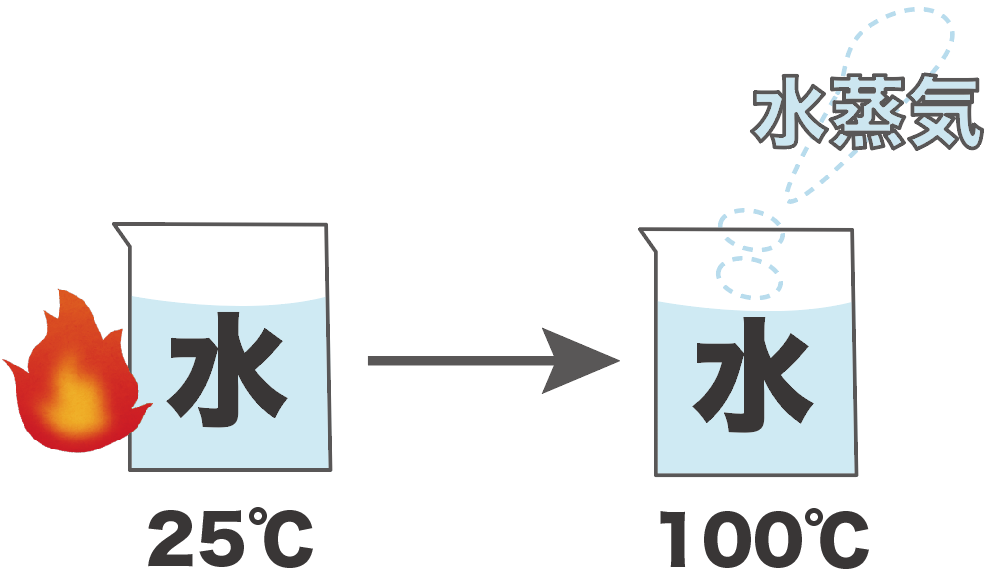
このとき、この水の沸点は100度だ。
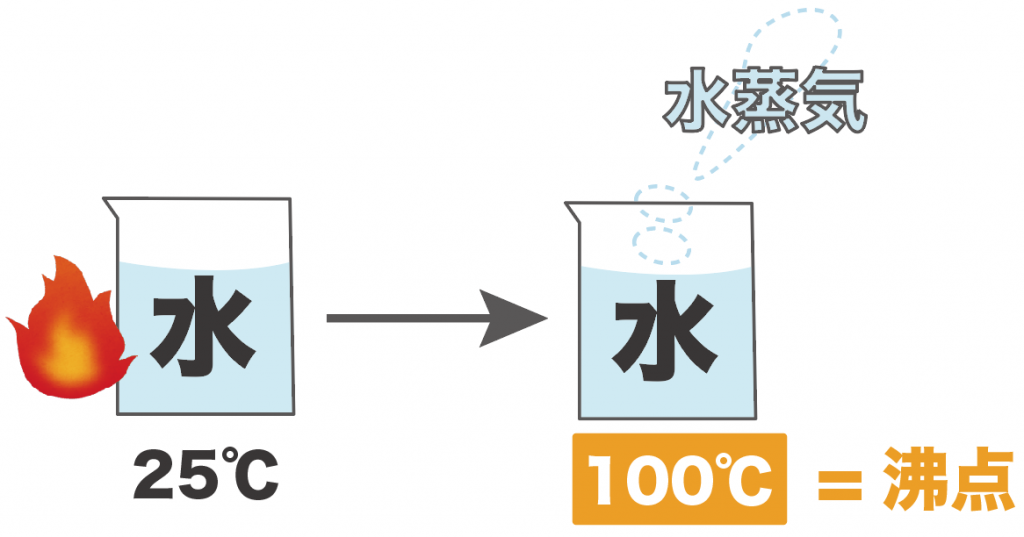
なぜなら、液体の水が100度で水蒸気という気体に変化したからね。
縦軸を温度、横軸を熱した時間のグラフをかいてあげると、次の温度が沸点になるはずだ。
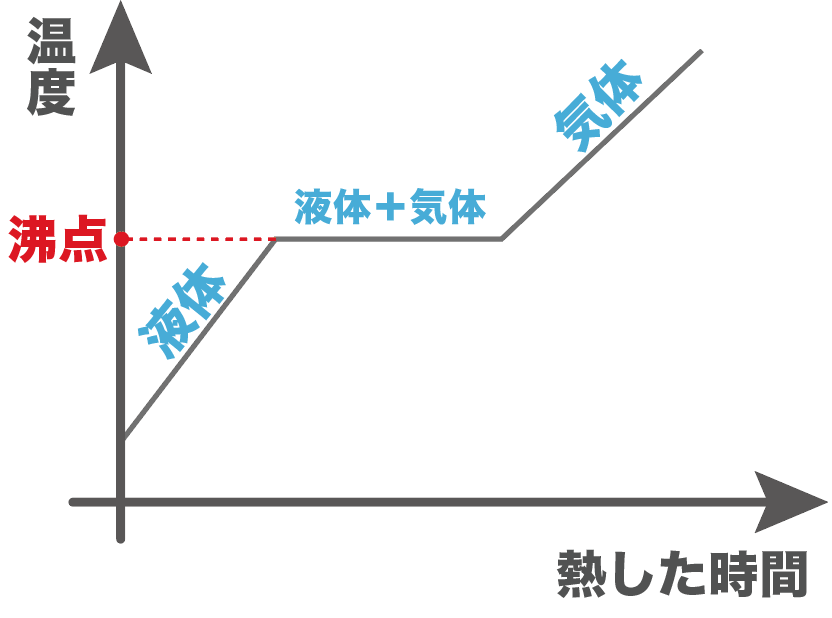
続いて、融点。
融点とは、
固体が溶けて液体に変化するときの温度のこと
だ。沸点は液体から気体への変化する温度だったけど、今度は固体から液体ってわけ。
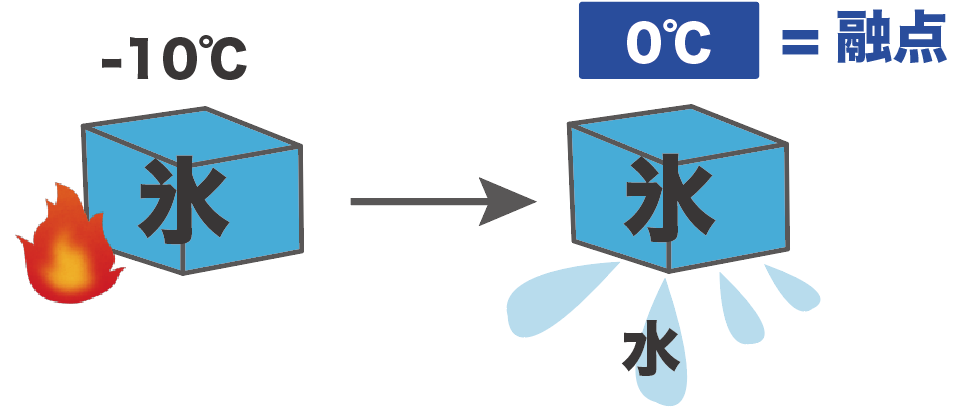
たとえば、-10℃の固体の氷をあっためていたら、0℃で溶け出して水に変化し始めたとしよう。
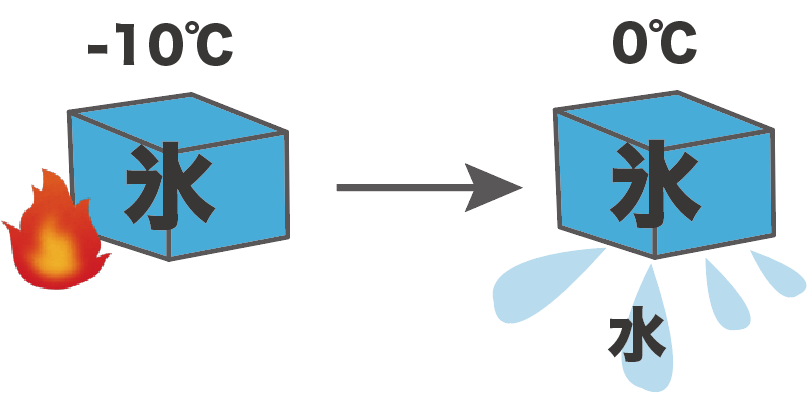
このとき、水の融点は0度。
なぜなら、氷(固体)が水(液体)に変化した温度だからね。
温度と熱した時間のグラフをかくと、次の温度が融点ってことになるね。
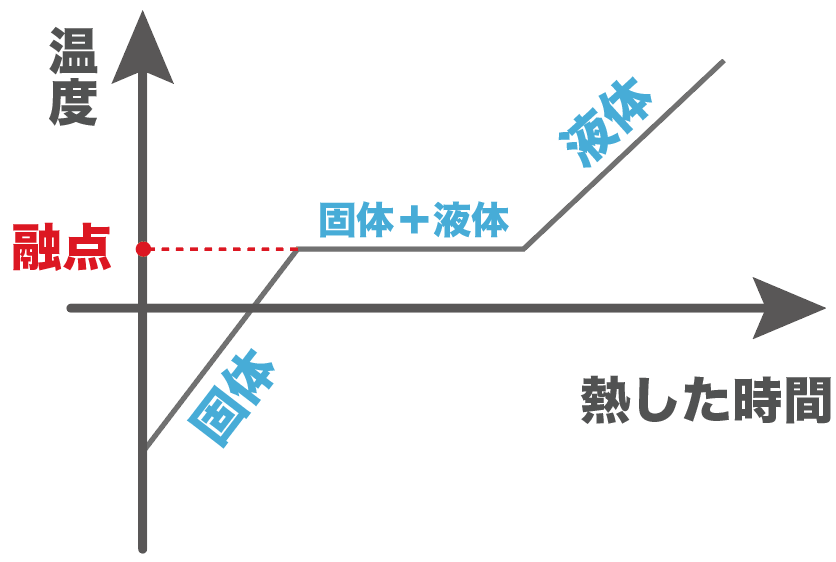
ここまでが沸点と融点の基礎だったね。
あと、1つ知っておいた方がいいのが、
沸点と融点は物質によって異なる
ってことだ。
物質の量は関係なく、純粋に何が状態変化するのかで決まってくるんだ。
たとえば、下の表は、各物質の沸点と融点を記載している表だよ。
| 物質名 | 融点 [℃] | 沸点 [℃] |
|---|---|---|
| 鉄 | 1535 | 2750 |
| 金 | 1064 | 2807 |
| 水 | 0 | 100 |
| エタノール | -115 | 78 |
| 窒素 | -210 | -196 |
物質によってここまで沸点と融点が違うとはね・・・!
鉄や金の沸点は半端ないぜ。
以上が沸点と融点の違いだったよ。
もう一度復習すると、沸点と融点は両方とも「物質の状態が変化する温度」のことなんだけど、
沸点と融点では、状態変化のフェーズが違うんだ。
沸点とは「液体」が「気体」になるときの温度で、

融点とは、固体が液体になるときの温度だ。

2つの用語は紛らわしいから、テスト前によーく復習して間違えないようにしよう。
そんじゃねー
Ken
こんにちは!この記事を書いているKenだよ。セコム、入ってるね。
中学1年生の理科では、状態変化を習ったよね。
状態変化とは復習すると、
物質が固体、液体、気体の3つの状態に変化すること
だったね。
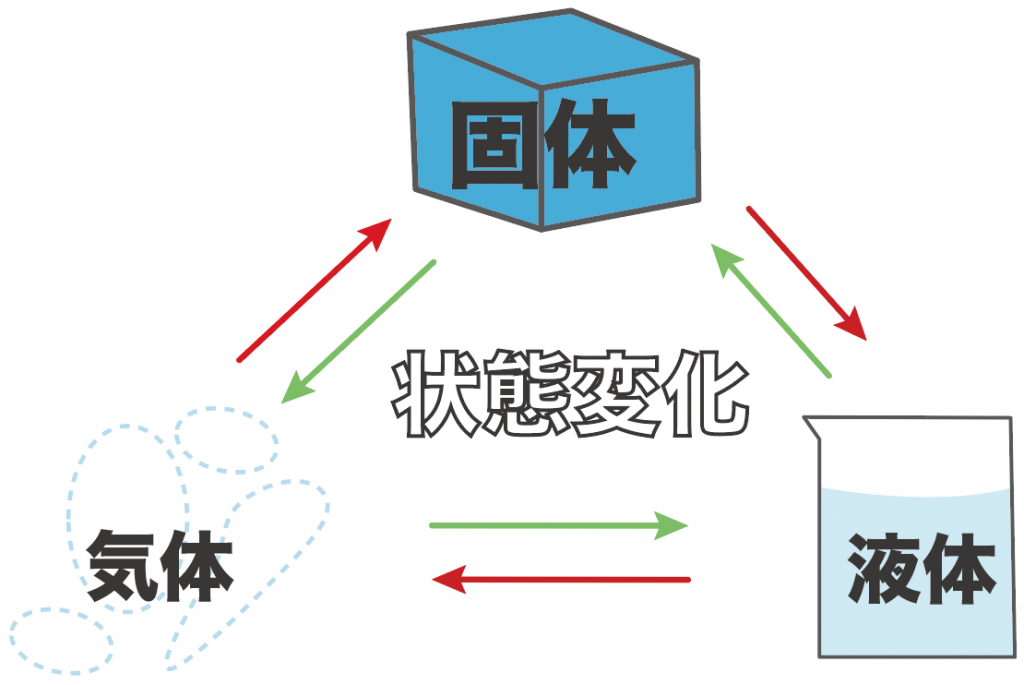
水の状態変化の場合は、それぞれ、
| 状態 | 名前 |
|---|---|
| 固体 | 氷 |
| 液体 | 水 |
| 気体 | 水蒸気 |
になるってことね。
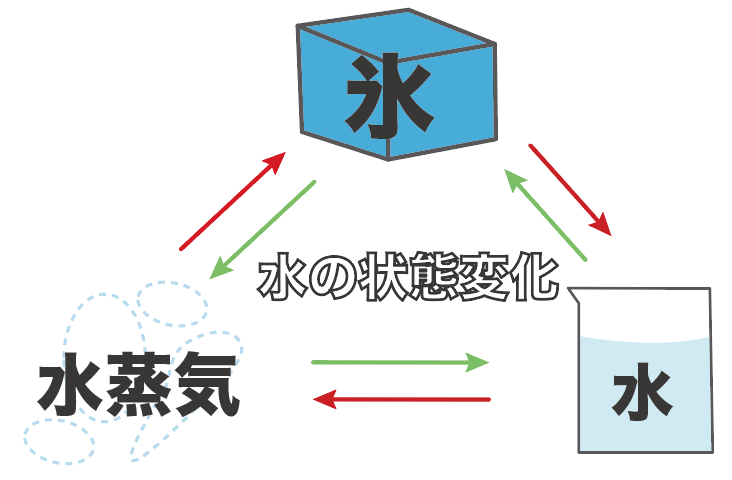
氷とか水とか水蒸気は日頃から目にしているから身近だよね。
一見、水の状態変化は他の物質の状態変化と変わらなく見えるんだけど、たった1つのポイントでとんでもなく異なっているんだ。
それは、
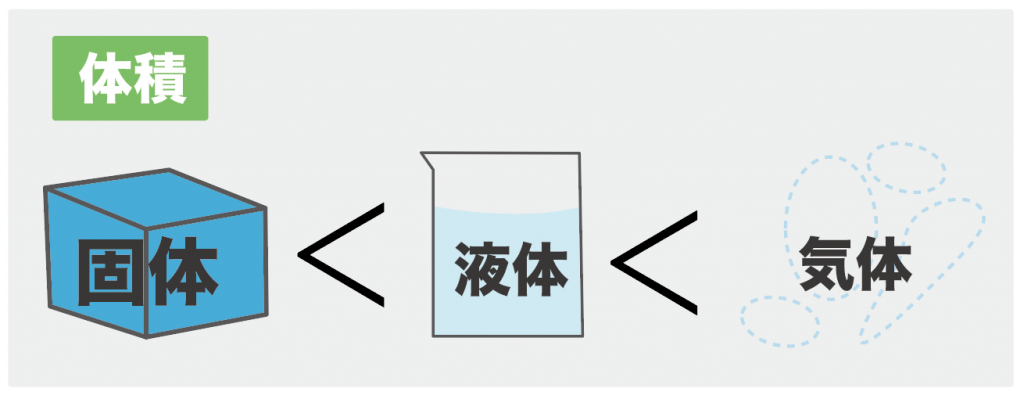
状態変化したときの体積の変化だ!
水の状態変化ではなんと、
「体積の変化」が他の物質の状態変化とは異なるんだよ。
具体的にいうと、
液体(水)から固体(氷)になるとき、体積が増えるんだ。
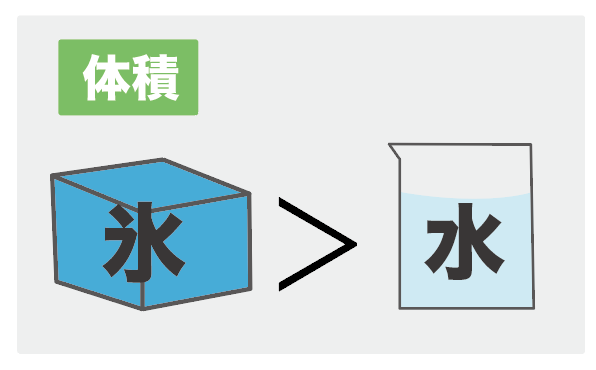
状態変化で勉強したように、他の物質では、液体から固体に変化すると、体積が小さくなることで知られているね。
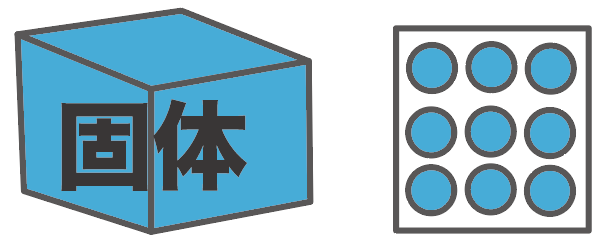
粒子モデルで考えるとわかりやすいんだけど、熱が少ない固体の状態だと、粒子の動きが小さくなってしまうから、物質の体積が小さくなるはずなんだ。
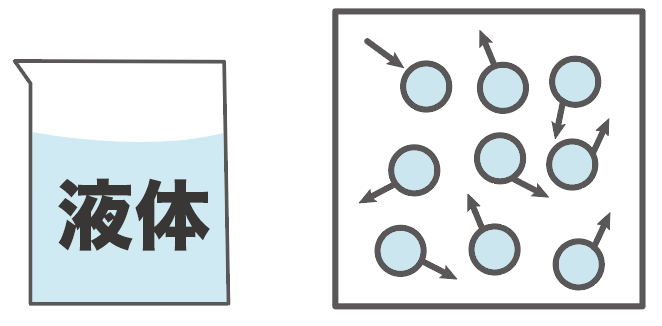
だがしかし、水の状態変化は一味違う。
液体から固体に変化すると、体積が増えてしまうんだ!!
水にはこの性質があるから、ペットボトルに水を満タンに入れて凍らせて固体にするとまあ大変。
水の時よりも体積が増えているから、ペットボトルがパンパンに膨らんでしまうはずなんだ。
じゃあ、なんで水の状態変化では固体の体積の方が液体よりも大きいんだろうね??
中学1年生の理科の範囲だと難しすぎるんだけど、簡単にいうと、
水を構成している粒子(分子)の構造によるからなんだ。
水の粒子は液体の時に、それぞれの隙間が小さくなるよに動くんだ。
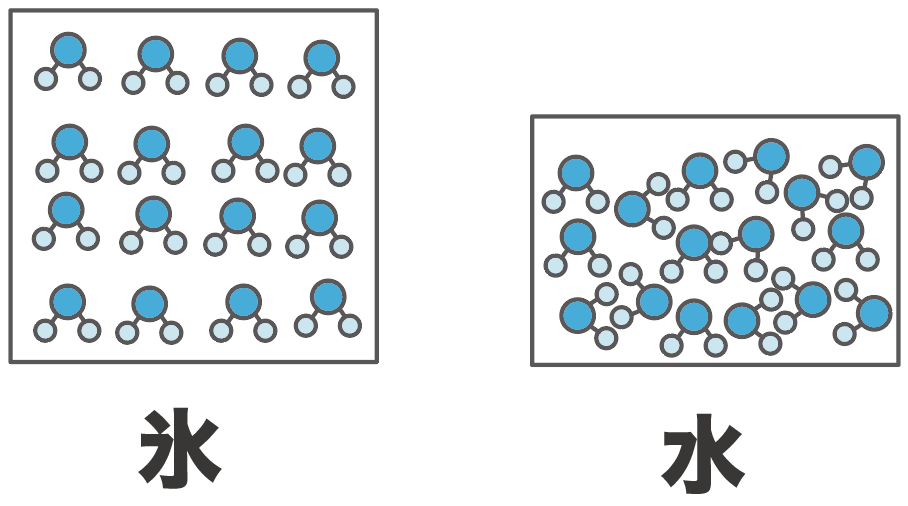
だから、水の場合は粒子の動きは活発になっているけど、粒子同士の隙間が少なくなって、体積が小さくなるんだ。
一方、氷の場合はどうだろう。
粒子たちの動きは活発じゃないんだけど、水の分子が止まって並ぶと隙間が空いているところがいっぱいあるように並んじゃう。結果的に水の時よりも体積が増えてしまうんだ。
っていう感じで、水の状態変化で気をつける点はただ一つ。
固体の方が液体よりも体積が大きいってこと。

つまり、密度でいうと、固体の氷の方が小さくなるってことね。
他の物質の状態変化とこの点で異なるから気をつけてようぜ!
そんじゃねー
Ken