こんにちは!この記事をかいているKenだよ。鮭は焼くとうまいね。
数学の先生から、
1から100までの素数を覚えなさい
って言われた??
えっ。
ふつうにむちゃむちゃ。
だって、1から100までの素数は「25」個もあんだぜ??
いくらなんでも無理な注文だよ。
しかも数字なんて覚えにくい。
電話番号でギリギリ。
1から100までの素数なんて覚えられねえ。。。
まじ助けて欲しい・・・・・
・・・・・・・・・・・・・
そんなときに役に立つのが「語呂合わせ」というアイテム。
25個の素数をたのしみながら覚えられるんだ。
今日はマイ勉オリジナルの、
1から100までの素数の覚え方がわかる語呂合わせ
を紹介するよ。
よかったら参考にしてみて。
語呂がストーリーになってるよ。
読みながら「1から100までの素数」がおぼえらるはず。
さっそくよんでみよう!
兄さんと午後にセブンイレブンにいってみた。。
2, 3 5, 7, 11
意味もなく、ブラブラしてみたけど、誰もいないじゃん。
13, 17
暇すぎるから、塾で勉強しようかと思ったぐらいだよ。
19
そしたらさ!
兄さんがおれの肉まん食べちゃったんだよ。
23, 29
もうケンカだよ、ケンカ。
しかも、
肉まんだけじゃない。
サーティーワンアイスまでみな食べちゃったんだよ。
31, 37

もう、信じられる???
よい子のふりして立ち読みしてる場合じゃなかった!
41, 43
しかも兄さん、
しなっとしたゴミ袋おれにわたしてさ、
47, 53
「ご苦労さん」
59
っていったんだ。
ふざけんな!
おれに肉まんとアイス買ってよ!!泣
無意味にむなしいだけじゃん!
61, 67

財布もってないんだよ。
71
これじゃあ、
牛丼の並み盛りも食えねえよ。
73
もう、
泣くしかないぜ。
79
もうわかった。
いいよ、兄さん。
くれぐれも、
ヤーさん・ヤクザの急な絡みに気をつけてね。
83, 89, 97
・・・・・・・・・・・
と以上が語呂合わせだ。
最後はミステリアスな展開になったね。
ストーリーをおさらいして、
1から100までの素数をおぼえてみよう!
1から100までの素数??
そんなの語呂で一発さ。
25個もあるけど大丈夫。
どうしようもない兄弟ケンカの物語を思い浮かべればいいんだ。
がんばって暗記してみよう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。腸の調子がいいね。
中3数学では、
素数(そすう)
を勉強していくよ。
いままで、
整数とか、自然数とか、約数とか、公倍数とか、最小公倍数とか・・・・
いろいろな数をならってきたね。
だけど・・・・
素数なんて一度も聞いたことがない!
って驚いてると思うんだ。
だから今日は、
「素数とは何か」をわかりやすく解説してみたよ。
よかったら参考にしてみて。
〜もくじ〜
素数をWikipediaでしらべてみると、
正の約数が 1 と自分自身のみである自然数で、1 でない数のこと
ってかいてあるね。
ちょっとよくわからない!? うん、ちょっとむずい。
もっと簡単にいってやると、
「1」と「自分」でしか割り切れない自然数のこと
だよ。
えっ。
まだピンときてないだって!??
そうだね。
素数の具体例をみていこう!
いきなりだけど、数字の「5」をイメージしてほしい。
そうそう。
よくある数字の5だよ。
じつは「5」は素数なんだ。
なぜなら、
1
と
5(自分)
でしか割り切れないからね。
あっ、自然数の割り算に限定したときね。;
2で割っても余り1になっちゃう。
3で割っても余りが2になっちゃう。
4でも無理ゲーだね。
「5」を割り切れる自然数は、
「1」と「5(自分)」しかない。
うん、ないない。
だから、
「5」は「素数」といえるんだ!
つぎはそのお隣の、
6
をみてみよう。
「6」という自然数は、
素数じゃない
んだ。
なぜなら、
1と自分(6)以外の自然数でも割り切れちゃうからね。
2でも割り切れちゃうし、
3でも割り切れる。

よゆーで、
「1と自分以外の自然数」でわりきれちゃうじゃん。
だから、「6」は素数ではないんだ。
どう??納得したかな??
雰囲気的に、
1は素数なのかも・・・・
って思っちゃうかもしれない。
だって、「1」と「自分(1)」で割り切れちゃってるし。
だけど、覚えておいてほしいのは、
「1」は素数でもなんでもない
ってこと。

これだけはおさえておこう。
なんだろうな、そういうものだと思っちゃおう。
星は夜空に輝くものだとか、
熊はほ乳類だとか、
週刊少年ジャンプは面白いだとか・・・
みたいな感じでそういうものだと思おう。
えっ。
納得しないだって?!
どっからどう見ても1が素数にみれるって??
うーん、そうだな。
こう覚えてみたら??
素数とは、
「1」と「自分」でしか割り切れない自然数で、
「1」と「自分」はいっしょになっちゃいけない
ってね。
こう覚えておけば、1が素数じゃない気がしてくる。
なぜなら、
1にとっての「自分」は「1」だからね。
とにかく。
「1」は素数じゃない
っておぼえておこう!!
素数とは何かをここまで解説してきたね。
どう??納得したかな??
数学を勉強していて、
あれ・・・素数ってなんだろう・・・??
って思ったらちょっとストップ。
基本を復習してみよう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。チーズとバターは紙一重だね。
中3数学を勉強してると、
因数(いんすう)
ってでてくるね??
小学校の算数じゃきいたことない。
友だちと因数について話すチャンスもない。
うん、むずかしそうだし、よくわからない。。
そこで今日は、中3数学でスタートダッシュをきるためにも、
因数とはなにか??
を解説してみたよ。
よかったら参考にしてみて。
因数とはずばり、
ある数・文字式を、あえてかけ算であらわしたときに、
かけられている数・文字式のこと
だよ。
えっ。ぜんぜん意味がわからないだって?!?
そうだね。
因数の具体例をみていこう!
文字と数にわけて考えてみたよ。
まずは「数」の因数の例だね。
そうだなあ、たとえば、
21
っていう自然数をイメージしてみて。
あえて。
あえて、かけ算の形になおしてみると、
7×3
にできるよね???
だって、「さんしちにじゅういち」だからさ。
ある数をかけ算になおしたとき、
かけられているものを「因数」というんだったね??
ってことは、21の因数は、
だ。
どう??
ちょっと因数に近づけたかな???
つぎは「文字式」の因数の例だね。
例として、
a² – a
をイメージしてみて。
この文字式もあえて、
あえて、かけ算になおしてみるんだ。
aで()でくくってやると、
a × (a – 1)
っていうかけ算になるよね。
かけ算になおしたときに、かけられているやつが「因数」。
よって、a² – aの因数は、
の2つになるんだ。
どう??
文字式の場合もしっくりきた??
因数とはなんだろう??
そう感じたらまず、
数や文字式を「かけ算」になおしてみよう!
そうすれば因数がでてくるはずだ。
がんばって探してみてね。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。シロップに要注意だね。
中学数学でならう公式は3つある。
ぶっちゃけ公式覚えてれば大丈夫。
もうね、楽勝。
公式通りに計算すればいいからね。
だけどさ、
乗法公式はなんでつかえるんだろう??
ぶっちゃけ怪しいんだよね。
知らないおじさんについていくみたいでさ。
そんな疑問を解消するために今日は、
乗法公式(式の展開の公式)はなぜつかえるのか??
を解説していくよ。
よかったら参考にしてみてね。
式の展開の公式を証明するために使うのはただ1つ。
それは、
さ。
えっ。分配法則なんて忘れただって??
そうだね。
分配法則とはずばり、
()の外側の数字や文字を()内の項に順番にかけて展開すること
だよ。
たとえば、
(a+b)(c+d)
っていう計算式があったとしよう。
分配法則つかえば一瞬で展開できるんだ。
まず、「a」をうしろにある()内の項にそれぞれかける。
そして、たす。
(a+b)(c+d)
= ac + ad
つぎは「b」をうしろの()内の項にかけて、たしてやるんだ。
つまり、
「b」を「c」と「d」にかけてたせばいいのさ。
よって、
(a+b)(c+d)
= ac + ad +bc + bd
になるね。
この分配法則が使えればOK。
乗法公式も証明できちゃうよ。
さっそく一つ目の、
(x+a)(x+b)
を証明してみよう。
分配法則で展開してやればいい。
まず、「x」をうしろの()の2つの中にかける。
(x+a)(x+b)
= x^2 + bx
つぎは、「a」をうしろの2つの項にかけてたしてやる。
すると、
(x+a)(x+b)
=x^2 + bx +ax +ab
になるね。
あとは同類項「bx」、「ax」をまとめるだけさ。
(x+a)(x+b)
= x^2 + bx +ax +ab
= x^2 +(a+b)x + ab
すると、乗法公式のできあがり!
いっちょ上がりさ。
つぎは平方の公式の証明だね。
こいつも分配法則で証明できちゃう。
まず、(a+b)^2をかけ算になおしてみよう。
すると、
(a+b)^2
= (a+b)(a+b)
になるね。
これをさっきみたいに分配法則で展開してみよう。
まず、いちばん左の「a」を後ろの「a」と「b」にかける。
そして、たす。
(a+b)^2
= (a+b)(a+b)
= a^2 + ab
つぎは、「b」を後ろの「a」と「b」にかける。
そして、たす。
(a+b)^2
= (a+b)(a+b)
= a^2 + ab + ab + b^2
あとは同類項をまとめるだけ。
すると、
(a+b)^2
= (a+b)(a+b)
= a^2 + ab + ab + b^2
= a^2 + 2ab + b^2
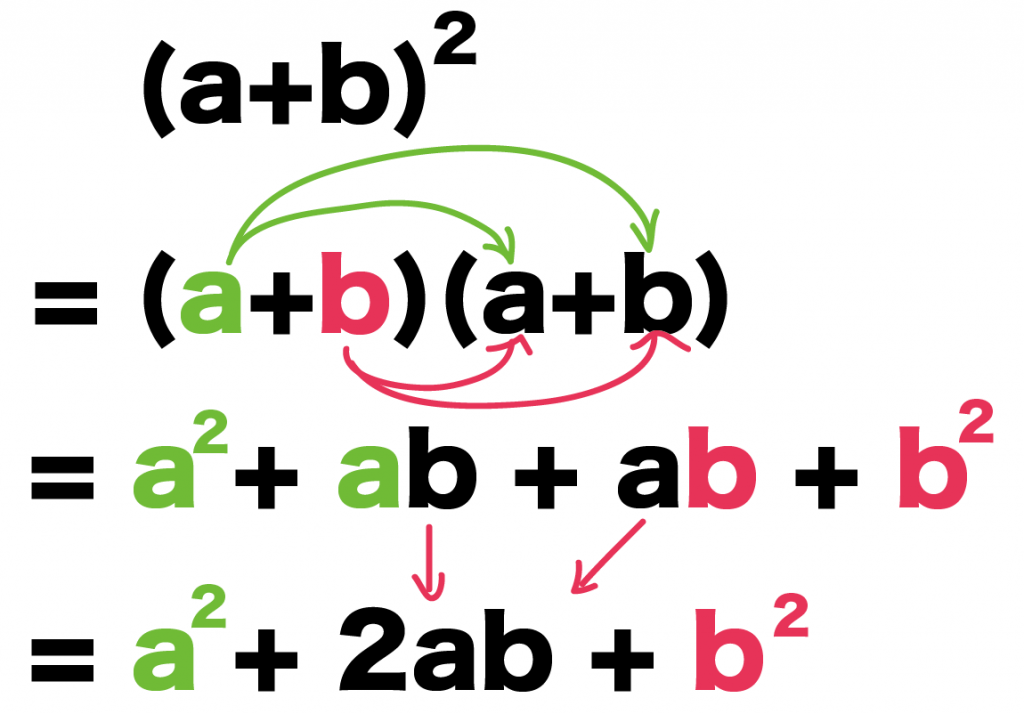
あら。
平方の公式のできあがり!
いよいよ「和と差の積」の公式の証明だ。
こいつも分配法則で一発。
まず、いちばん左のaを右の()内の項にかける。
そして、たす。
(a +b) (a-b)
= a^2 – ab
2つめの「b」を後ろの()にかけてやると、
(a +b) (a-b)
= a^2 – ab +ab -b^2
になるね。
あとは同類項をまとめてやろう。
の2つだね。
こいつらをたして消してやると、
ほら!
乗法の公式の「和と差の積」のできがあがり。
乗法公式を覚えることは大切。
だけど、
テストで忘れたら危機。危機におちいる。
だからこそ、
なぜ乗法公式がつかえるのか??
ってとこまでおさえておこう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。おしぼりはアツいほうがいいね。
中学3年生で最初にならうのは、
式の展開のやり方
だ。
一度マスターすればもう大丈夫。
どんな展開の問題もとけちゃう。
テスト前に身につけておきたいワザだね。
そこで今日は、
式の展開の問題の解き方
を3ステップで解説していくよ。
よかったら参考にしてみて。
さっそく解き方を紹介していこう。
つぎの3ステップでとけちゃうよ。
いっしょに例題をといていこう。
例題
次の式を展開しなさい。
(x+1)(x+3) -3 (2x +6)
はじめに、
乗法公式がつかえるかどうか
を確認しよう!
公式がつかえる??
じゃあガンガン使おうぜ。
例題をみてみると、
(x+1)(x+3)
で公式がつかえそうだね。
公式で展開してやると、
(x+1)(x+3)
= x^2 + 4x + 3
になるはず。
まず公式つかえるか確認。
いけそうなら公式をつかう。
これが第1ステップさ!
つぎは分配法則で展開してやろう。
()をはずす
ってこと。
ゆっくり計算してみよう。
例題でいうと、後ろの、
-3(2x + 6)
で分配法則がつかえそうだね。
()をはずしてやると、
-3(2x + 6)
= -3×(2x) -3 × 6
= -6x -18
になるね!
これが第2ステップ!!
最後に同類項をまとめてみよう。
同類項って、
文字と次数がおなじ項のこと
だったね。
たとえば、
とか。
文字はおなじで、
かけられている数が同じなら「同類項」というんだ。
例題では、
が同類項だ。
なぜなら、文字と次数が一致しているからね。
数字は数字同士が同類項になるよ。
同類項はまとめることができる。
係数同士をたしてやると、
になるはず。
おめでとう!!これで式の展開が完了したよ。
式の展開の解き方はカンタン。
の3ステップでいいんだ。
乗法公式おぼえるのが大変だけど、
問題をときまくっておぼえていこう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。牛乳を小分けで買ったね。
中学3年生になると、
乗法の公式
をおぼえなきゃいけない。
いや、べつに覚えなくても大丈夫。
根性でとける。
ぶっちゃけね。
だけど、公式をおぼえてると便利。
とくスピードがむちゃ速くなるんだ。
公式つかえば3秒。
使わなかったら5分。
それなら公式つかいたいよね??
今日は便利な乗法公式をおぼえるために、
中学数学の乗法公式の3つの覚え方
を紹介するよ。
よかったら参考にしてみて。
公式はつぎの3つだよ。

覚え方を紹介していこう!
まず1つめの、
(x+a)(x+b) = x^2 +(a+b)x + ab
の覚え方だね。
この公式は、
指で文字を隠しておぼえられるよ。
覚え方は、
右・左・エックス・左
だ。
なんか格ゲーのコマンドみたいだね。
さっそく紹介しよう。
まず()の右を指でかくす。
xが2つみえるでしょ??
だからxを2回かけてやればいいんだ。
つぎは()の左をかくしてみよう。
指を左にずらしてやるんだ。
そしたら、
a + b
がでてくるでしょ??
これをさっきの式にたしてみよう。
つぎはスペシャルコマンドの「x」をつける。
このボタンをおさないと必殺ワザは決まらない。
最後にもう1度左を隠してみよう。
そしたら今度は、
aとb
がみえるでしょ??
こいつらをかけて、最後にたしてやる。
すると、
(x+a)(x+b) = x^2 +(a+b)x + ab
のできあがりさ。
これで(x+a)(x+b)の展開公式もマスターしたね。
この乗法公式なら1瞬でとけちゃう。
たとえば、
(x + 1) (x +2)っていう計算式があったとしよう。
公式で計算すれば瞬殺さ。
公式にあてはめてみると、
だね。
すると、
(x+1)(x+2)
= x^2 + (1+2) x + (1×2)
= x^2 + 3x + 2
になるね。
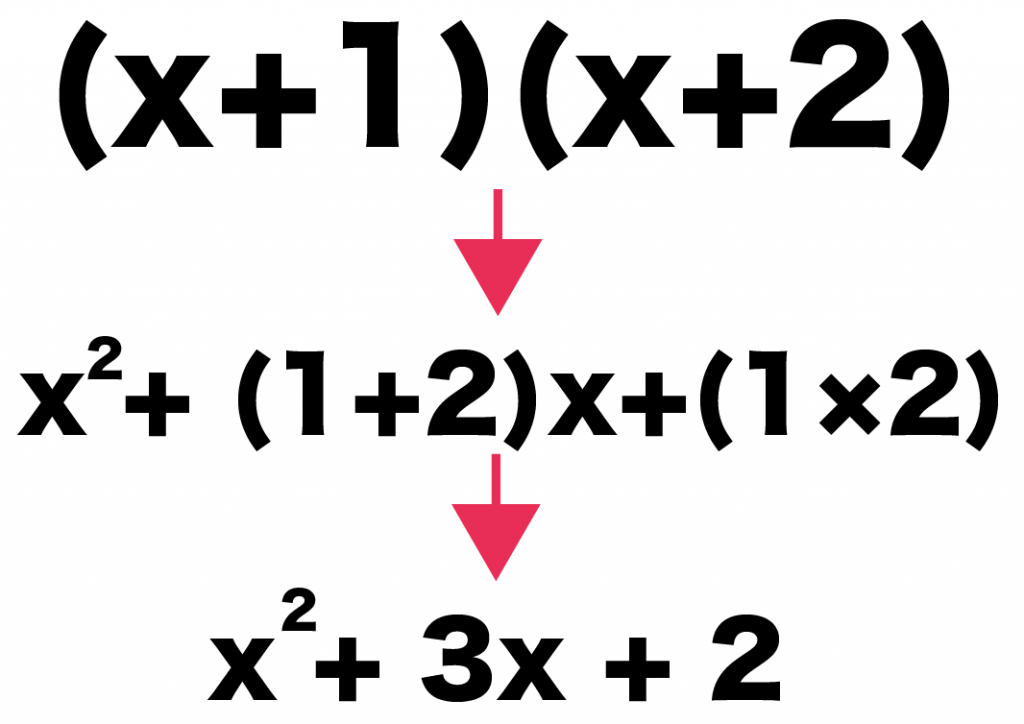
むちゃくちゃ楽だぜ!
つぎは「平方の公式」の覚え方さ。
この展開公式は、
(a + b)^2 = a^2 + 2ab + b^2
だったね。
この展開公式の覚え方はずばり、
ニミッツ、a、b、ab!!
だ。
魔女の呪文みたい。
まず「2」を「3つ」かいてみよう。
呪文のなかの「ニミッツ(2が3つ)」にあたるよ。
つぎは「a」と「b」を前後の「2」の前においてあげよう。
そして最後に、
「ab」を真ん中の「2」の後ろにおいてね。
こいつらを「+」でむすんであげれば・・・・
ほら!
式の展開の公式の、
(a+b)^2 = a^2 + 2ab + b^2
のできあがり!
いっとくけど、この公式はむちゃ便利。
たとえば、
(2a+3)^2
っていう問題があったとしよう。
平方の公式を使えば一発さ。
(2a+3)^2
= (2a)^2 + (2 × 2a × 3) + 3^2
= 4a^2 + 12a + 9
になるね!
ガンガンつかっていこう!!
最後に「和と差の積の公式」をおぼえていこう。
(a+b)(a-b) = a^2 -b^2
だったね。
覚え方はずばり、
Aチーム2点、Bチーム2点でひきわけ!!
だ。
バスケのレフリーを思い浮かべてほしい。
白熱しすぎてAとBチームが引き分けてしまった場面。
よくあるよね。
えっ。ぜんぜん公式がおぼえられないだって?!?
ちょっと落ち着いてほしい。
この語呂はこうやってつかうんだ。
まず、公式の中に「a」が何個あるか数えるんだ。
「aの数」がAチームの得点になるよ。
がんばってさがしてみると、
aは2つある。
よって、Aチームは2点ってことさ。
2回「a」をかけてあげよう。
おつぎはbの番さ。
式のbの数をかぞえてみると、
2つあるね。
ってことはBチームも2点だってこと。
Bも2回かけてあげよう。
これで両チームの得点はでそろったね。
よって、
この試合はひきわけ!
だから最後に、
マイナス(ひきわけ)
をあいだにいれてあげるんだ!
この公式を実際につかってみよう。
たとえば、
(x+3)(x-3)
っていう展開の式があったとする。
公式つかえば、
(x+3)(x-3)
= x^2 – 3^2
= x^2 – 9
になるね!
乗法公式はおぼえられそうかな??
ぶっちゃけると、
数学の公式をおぼえるためには語呂とかよりも、
その公式を使いまくるのがいちばんなんだ。
使って、
使って、
使いまくる。
問題をときまくって公式をみにつけていこう!
そんじゃねー
Ken
こんにちは!この記事をかいてるKenだよ。風呂リフォームしたいね。
中3数学ではじめにならうのは、
式の展開
という単元だね。
うきうき気分で新学期をむかえた。
だけど、
式の展開っていったいなんだろう??
って思わない??
日常生活ではゼッタイに使わない単語だし。
おまえ昨日、式の展開みたー?
なんて言わないよね。
今日は新学期からつまずかないために、
式の展開とはなにか??
を解説していくよ。
よかったら参考にしてみて。
式の展開とはなんだろう??
教科書をみてみると、
積の形で書かれた式を計算して、和の形で表すこと
ってかいてあるね。
もっと簡単にいうと、
「かけ算の式」を計算して「足し算の式」にする
ってことさ。
たとえば、
A×B
っていうかけ算の式があったとしよう。
こいつを計算して、
足し算の形にしてやるんだ。
このことを、
「A×B」を展開する
っていうよ。
えっ。
イマイチわからないだって??
たしかに。
これじゃあピンとこないよね。。
式の展開の具体例をみてみようか。
たとえば、
(2a+5b)(3a-b)
っていう「かけ算の式」を展開してみよう。
これを分配法則で計算してやると、
(2a+5b)(3a-b)
= {2a×3a +2a × (-b) +5b × 3a + 5b×(-b)}
= 6a^2 -2ab +15ab -5b^2
= 6a^2 +13ab -5b^2
になるね。
この計算のことを、
(2a+5b)(3a-b)を展開する
っていうんだ。
どう??ピンときたかな??
式の展開はシンプル。
「かけ算の式」を計算して「たし算の式」にすること
を展開というんだ。
式の展開のやり方をいっしょに勉強していこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。バターチキン最高。
円錐にひもをかける問題ってあるよね???
たとえば、つぎのような問題だ。
例題
母線の長さ PA = 6 cm、底面の半径OAの長さ = 1 cmの円錐Pがある。この円錐に赤いひもが最短距離になるようにかけたとき、この「ひも」の長さを求めてください。
なんで円錐にひも???
って思うかもしれないね。
正直、とくのがつらい。
だけど、
円錐にかけたひもの最短距離を求める問題
ってよくでてくるんだ。
今日はこのタイプの問題の、
円錐にかけたひもの最短距離を求める問題の解き方
を3ステップで解説してみたよ。
よかったら参考にしてみてね。
3ステップでとけちゃうよ。
例題をといていこう。
例題
母線の長さ PA = 6 cm、底面の半径OAの長さ = 1 cmの円錐Pがある。この円錐に赤いひもが最短距離になるようにかけたとき、この「ひも」の長さを求めてください。
円錐の展開図をかいてみよう。
とりあえず、円錐の展開図っぽいやつをかこう。
中心角は気にしなくていいよ。
これが第1ステップさ。
つぎは側面の「扇形の中心角」をだしてみよう。
出し方は簡単。
中心角をxとして方程式をたてればいいんだ。
側面の扇形の弧の長さ
と
底面の円周の長さ
が等しい
っていう式をつくればOK。
例題をみてみよう。
中心角をxとしたから、
になるね。
だから方程式は、
(扇形の弧の長さ)=(底面の円周長さ)
2×6 ×π× X ÷ 360 = 2× 1 × π
になる。
これをといてやると、
中心角X = 60°
になるはずだ。
つぎは展開図に「ひも」をかいてみよう。
例題でいうと、赤いひもは、
AからスタートしてAにもどってきているよね??
しかも、その長さが最短距離。
ってことは、展開図でいうと、
A
と
組み立てたらAに重なるA’
を直線でむすんでやればいいんだ。
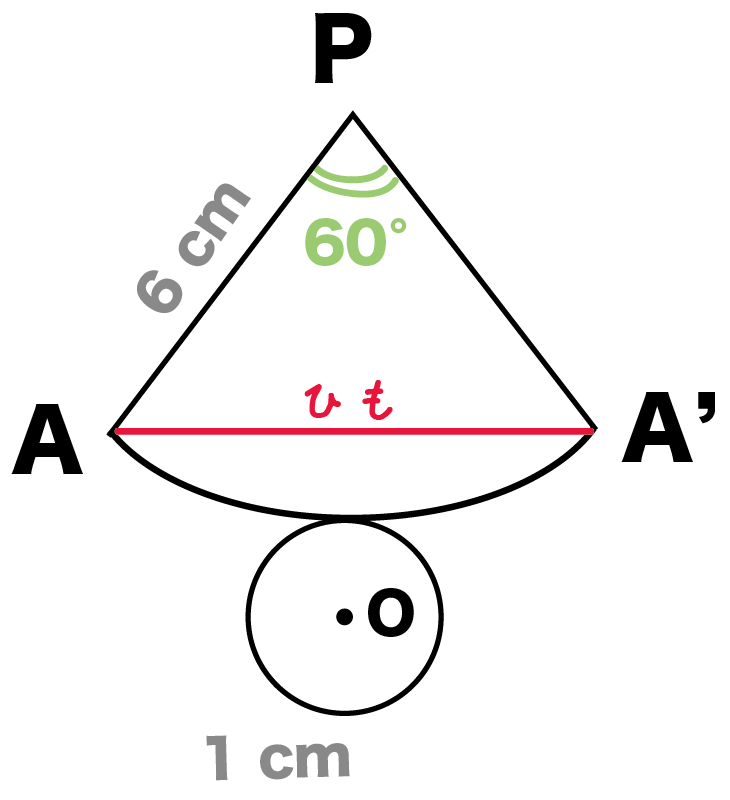
最後は直角三角形の比をつかおう。
「ひも」と「母線」でできた三角形に注目してくれ。
例題でいうと、△PAA’だね。
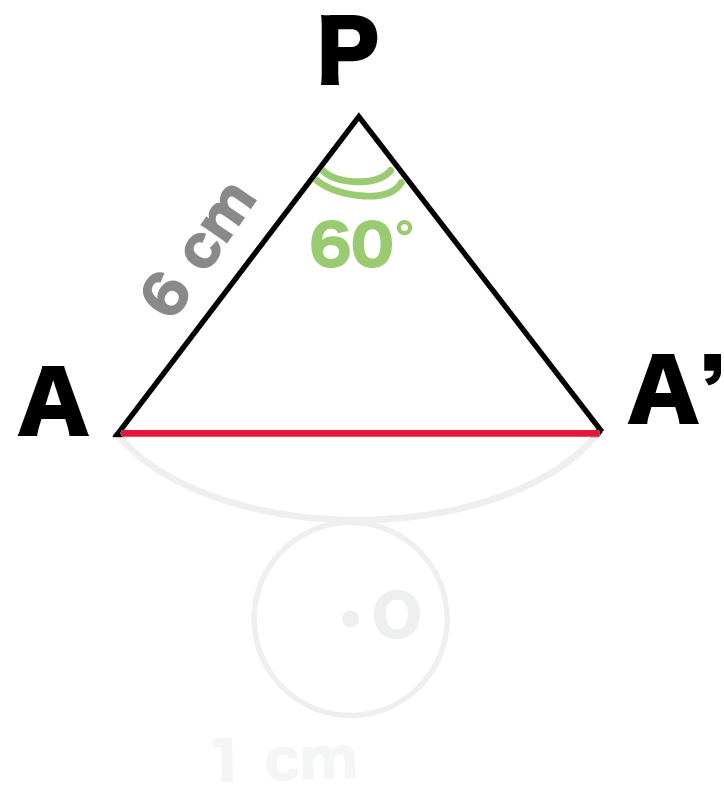
こいつは、
の二等辺三角形。
頂角の二等分線は底辺を垂直に二等分する
というやつを使ってみよう。
PからAA’に二等分線をひく。
交点をHとすると、
になるね。
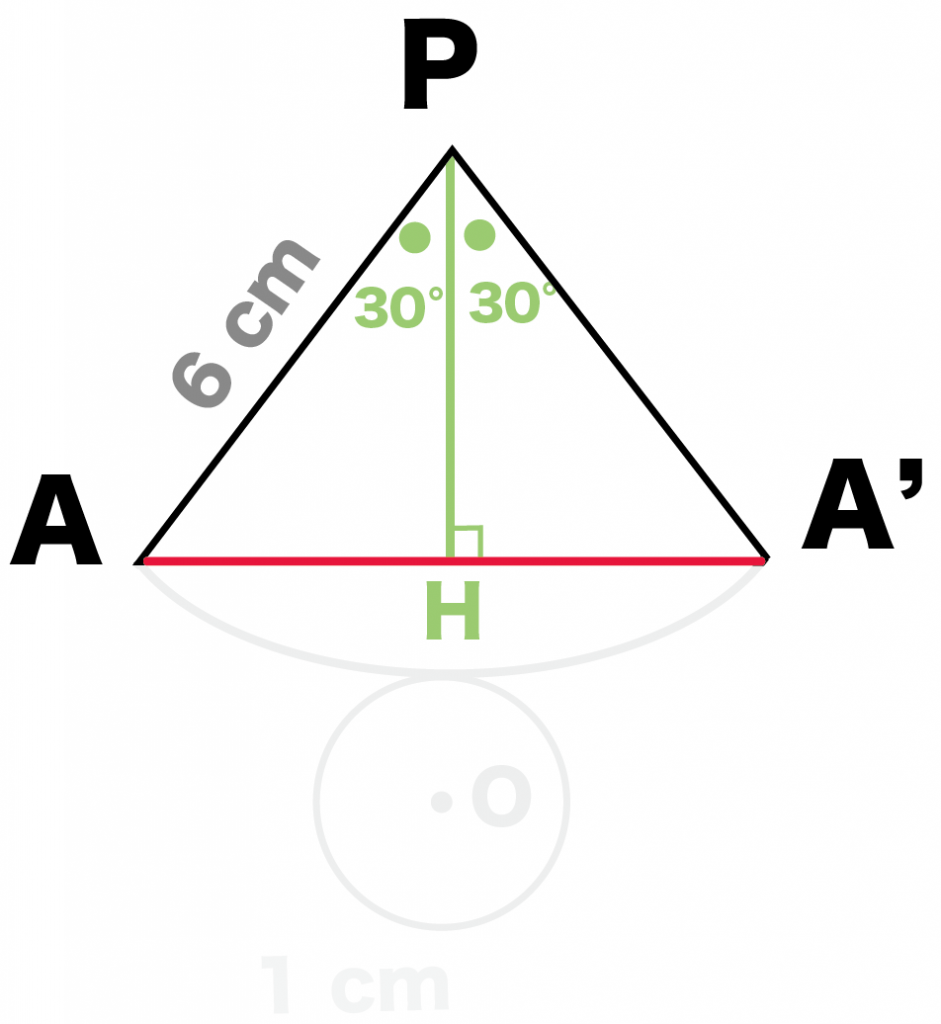
んで、
△APHは頂角30°の直角三角形だから、
1 : 2: √3
の辺の比になっているはず。
よって、
AP: AH = 2: 1
AH = 3 cm
になる。
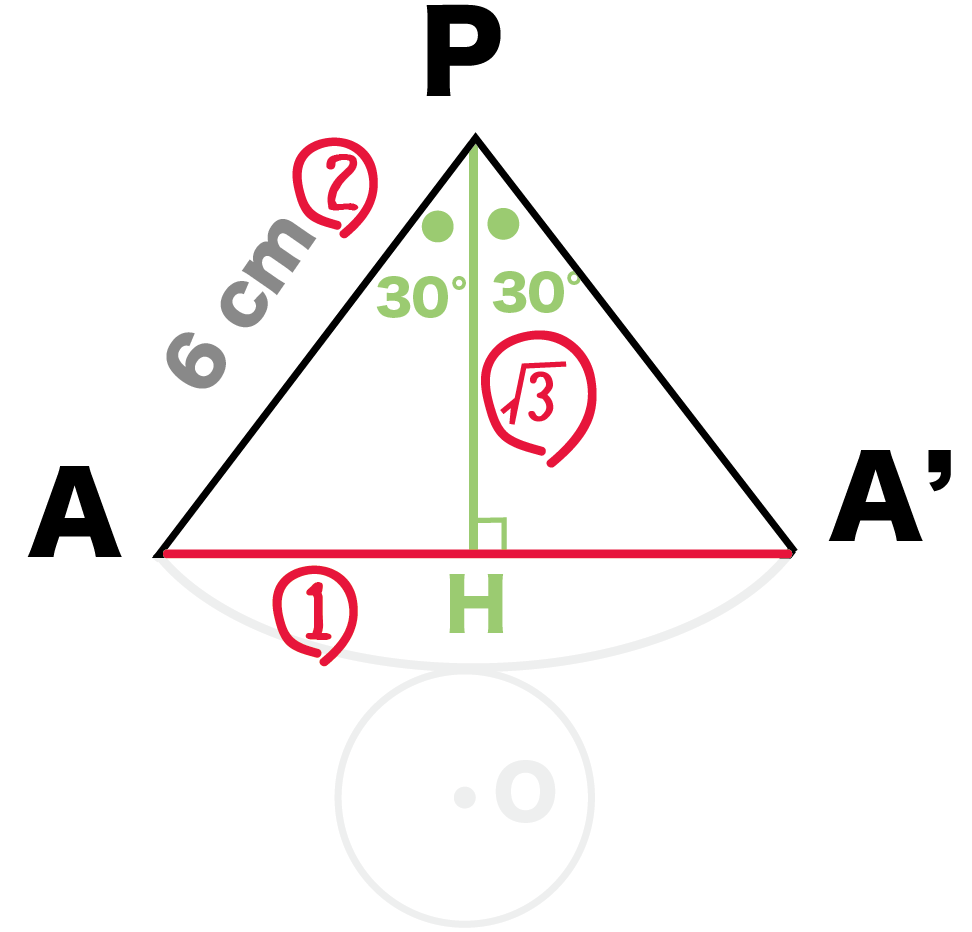
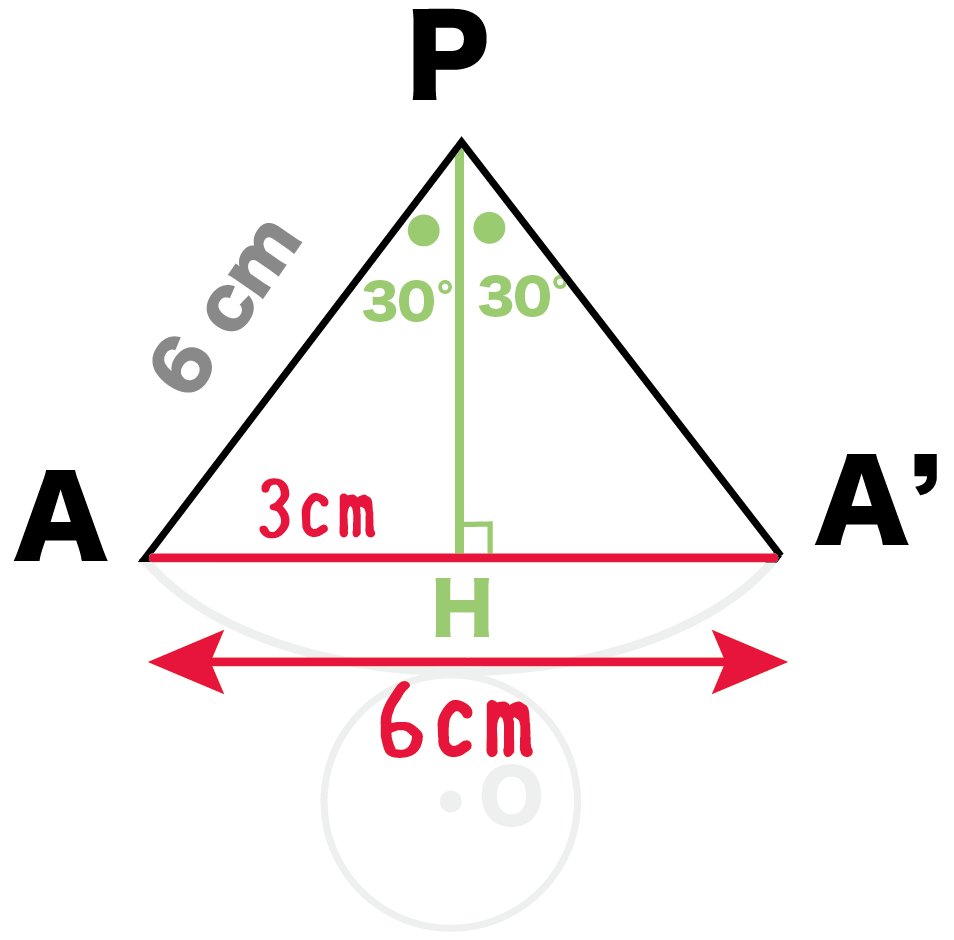
PHはAA’の垂直二等分線になっているはず。
よって、
ひもの長さAA’
= 2 × AH = 6 cm
になるね。
おめでとう!
これで、ひもでも糸でもなんでもこいだね!
最短距離の問題って、
の知識が必要になってくる。
ってことはつまり、
1~3年生の知識をフル活用しないと解けない。
だから入試問題にでやすいのかもね。
テスト前によーく復習しておこう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。トマトはヘルシーだね。
円錐の高さを求める問題
ってたまにでるね??
こいつは中1数学でならった
と、
中3でマスターする「三平方の定理」でといていくんだ。
かなりくせ者だね。
今日はコイツを攻略するために、
円錐の高さの求め方がわかる3ステップ
を解説していくよ。
よかったら参考にしてみて。
3ステップで求められるよ。
例題をといてみよう!
例題
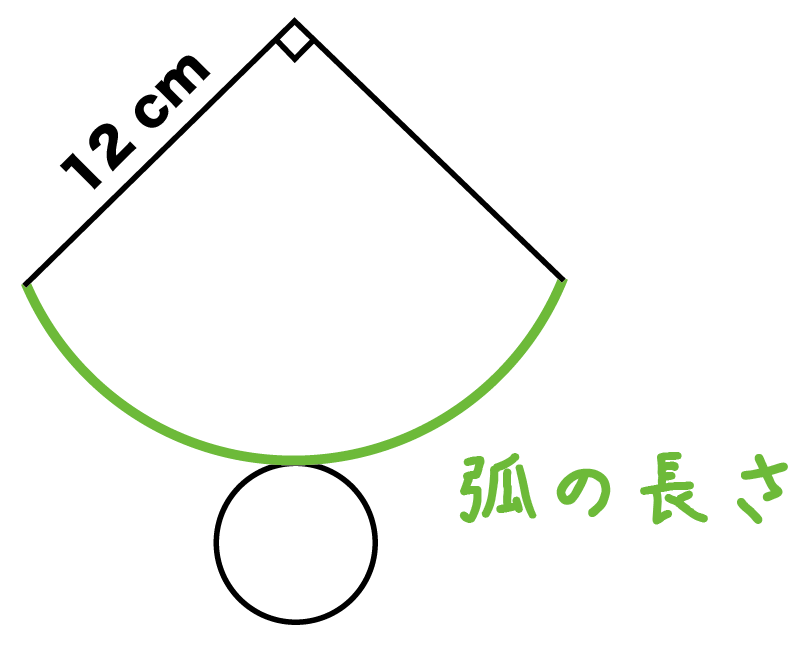
下の図は円錐の展開図です。円錐の側面が、半径12cm、中心角90°のとき、円錐の高さを求めなさい。
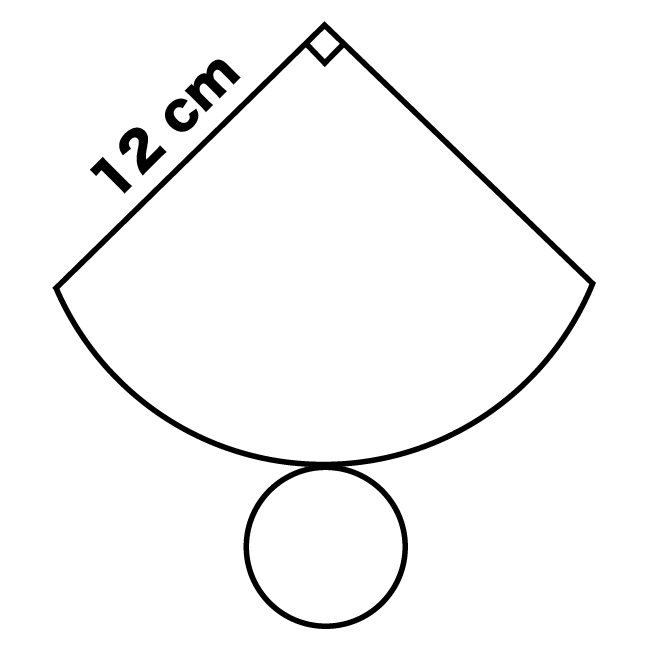
まずは円錐の側面の、
弧の長さ
を計算しよう。
えっ。
弧の長さの出し方がわからないって??
円錐の側面は「おうぎ形」だったね。
だから、
をつかえばいいんだ。
扇形の弧の長さは、
直径×円周率×中心角÷360
で計算できたね。
例題の扇形は、
だ。
公式をつかってみると、
(扇形の弧の長さ)
= (直径)×(円周率)×(中心角)÷ 360
= 24 × π × 90 ÷ 360
= 6π
になる。
これが第1ステップ!!
つぎは円錐の底面に注目。
半径を計算するんだ。
半径の長さをrとして方程式をたてるよ。
円錐の展開図をくみたてると、
「底面の円」
と
「側面の弧」
がかさなるでしょ??
だから、
(底面の円周の長さ)= (側面の扇形の弧の長さ)
っていう方程式がつくれるんだ。
(底面の円周の長さ)= (側面の扇形の弧の長さ)
(直径×円周率)= (直径×円周率×中心角÷360°)
2 × r × π = 2 × 12 × π × 90° ÷ 360°
r = 3 [cm]
になるね!
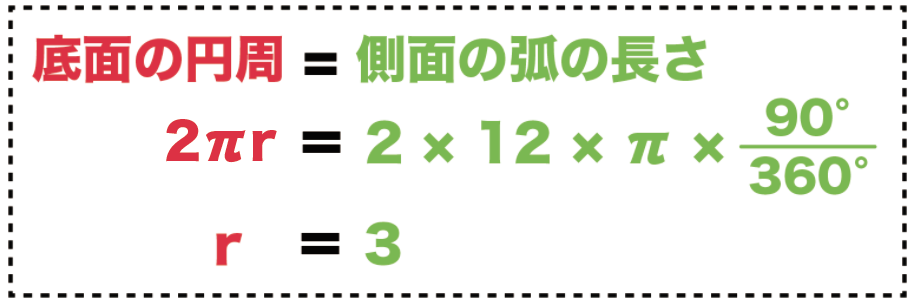
底面の半径は「3 cm」ってことさ。
第2ステップ終了!
最後は三平方の定理をつかうよ。
円錐をナイフできってやると、
直角三角形がでてくるでしょ??
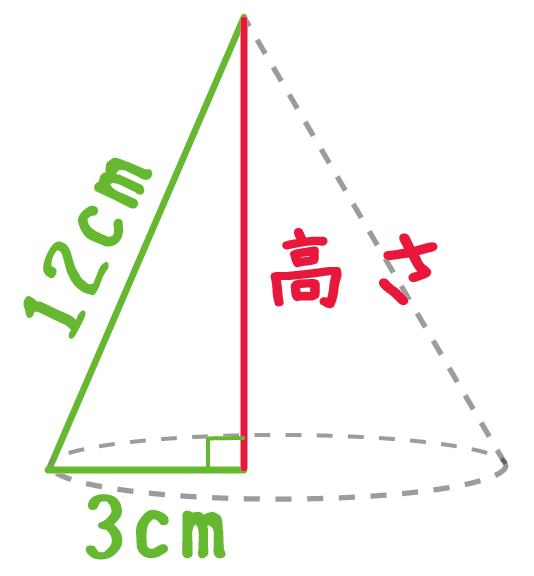
三平方の定理をつかうと、
(円錐の高さ)
= √(斜辺の二乗)- (その他の1辺の二乗)
= √ (12)² – 3²
= √135
になるね。
おめでとう。
円錐の高さもゲットだね!
円錐の高さを求めるのはむずそう。
だけど、基本をおさえれば大丈夫。
の3ステップで、
じゃんじゃん求めていこう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。卵は便利だね。
正方形の対角線の求め方には公式があるよ。
正方形の1辺をaとすると、対角線は、
√2 a
で計算できちゃうんだ。
つまり、
(正方形の対角線)= √2 × (正方形の1辺)
ってわけだ。
たとえば、1辺が4cmの正方形ABCDがあったとしよう。
こいつの対角線BDの長さは、
√2 × (正方形の1辺)
= 4√2 [cm]
になるんだ。
正方形の1辺に「√2 」をかけるだけ!簡単だね。
でもさ、
なんで公式がつかえるんだろう??
便利すぎてこわいね。
そこで今日は、
正方形の対角線の長さの求め方を3ステップで解説していくよ。
よかったら参考にしてみてね。
例として、
正方形ABCDの対角線を求めていこう!
正方形に対角線をひいてみよう。
正方形ABCDでいうと、
対角線BDをすーーーーーっとひいてみて。
これが第1ステップだ。
つぎは、正方形の中から直角三角形をみつけよう。
虫眼鏡もルーペもいらない。
裸眼でも大丈夫。
正方形に対角線をひいたら、
直角三角形が2つできあがっているはずだ。
正方形ABCDでいうと、
の2つだね。
直角三角形がみつかれば第2ステップ終了さ。
あとは、三平方の定理をつかうだけ!
直角三角形の斜辺を計算するんだ。
正方形ABCDでいうと、
直角三角形ABDをえらんでみたよ。
この直角三角形で三平方の定理をつかって、
斜辺BDを計算しよう。
BD = √(AD^2 + AB ^2 )
= √(4^2 + 4^2)
= 4√2 [cm]
になるね!
おめでとう!
これで正方形の対角線の求め方をマスターしたね!
正方形の対角線の公式は、
「正方形の1辺」に「√2」をかけるだけ。
むちゃシンプルだね。
だからこそ、なぜ公式がつかえるのか??
を知っておこう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。スパゲッティゆでまくったね。
ひし形の対角線の問題ってたまにでるよね??
たとえばつぎのようなやつ↓↓
例題
1辺の長さが10のひし形ABCDがある。2本の対角線のうち、一方は他方より4 cm長いとすると、対角線は何cmになりますか?? ※対角線の交点をMとする
この問題はぱっと見、むずかしい。
だけど、
うまーく問題をといてあげれば、
3ステップで答えをだせちゃうんだ。
今日は、
ひし形の対角線の求め方の3つのステップ
をわかりやすく解説してみたよ。
よかったら参考にしてみて。
さっそく解説していくよ。
例題をといていこう!
例題
1辺の長さが10のひし形ABCDがある。2本の対角線のうち、BDはACより4 cm長いとすると、対角線ACは何cmになりますか?? ※対角線の交点をMとする
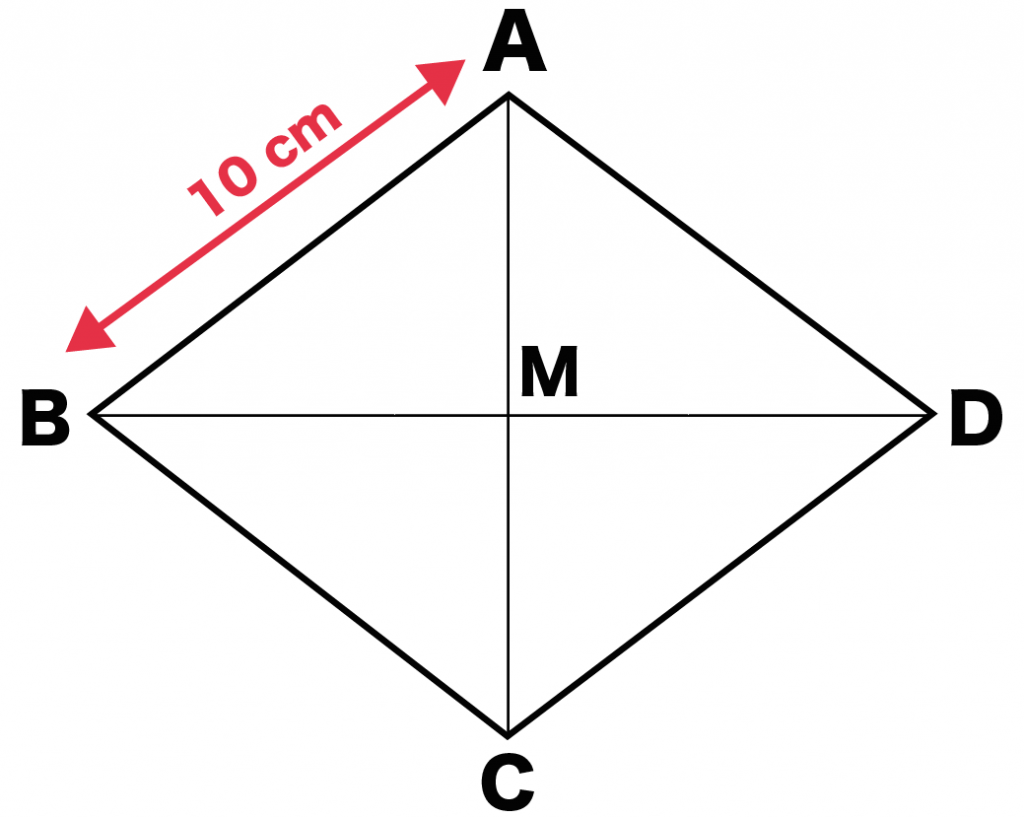
まず、対角線の長さを「x」とおこう。
例題では対角線ACをx cmとおいたよ。
対角線BDはACよりも4cm長いはずだから、
x + 4
になるね。
これが第1ステップ!!
つぎは、
ひし形の対角線の「半分」を求めよう!
ひし形の定義で、
ひし形は平行四辺形である
ってならったよね??
ってことは、ひし形でも平行四辺形の性質の、
対角線は中点で交わる
ってやつが使えるんだ。
ひし形ABCDでいうと、対角線ACとBDは中点Mでまじわっているはず。
ってことは、
MはACの中点だね。
計算してやると、
AM = 1/2 x
になる。
おなじように、
MがBDの中点でもあるから、
BM = (x+4)/2
になるね。
これが第2ステップ!!
最後は、三平方の定理で方程式をつくろう。
対角線をひいてできた、
「小さな三角形」に注目するんだ。
ひし形ABCDでいうと、
三角形ABMだね。
垂直に交わる
があったね。
つまり、三角形ABMは角AMB= 90°の直角三角形なんだ。
こいつで三平方の定理をつかってやると、
10^2 = (1/2x)^2 + {(x+4)/2}^2
っていうxについての方程式ができるはずだ!
こいつを分数をふくむ方程式の解き方でといてやると、
x = 12
になるね。
つまり、
対角線ACは12[cm]ってことになる。
おめでとう!
ひし形の対角線の長さを求められたね!
ひし形の対角線の求め方はちょっと複雑。
でも基本をおさえてしまえば、
っていう3つで対角線をもとめられるね。
どんどん問題になれていこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。ミッションインポッシブルだね。
長方形の対角線の求め方、しってる??
じつは公式があるんだ。
長方形のヨコの長さをa、タテの長さをbとすると、
√(a^2 + b^2)
で計算できちゃうんだよ。
つまり、
√( タテ×タテ + ヨコ×ヨコ)
になるわけさ。
たとえば、ヨコの長さが4cm、
タテの長さが3cmの長方形がいたとする。
対角線の長さは、
√(4^2 + 3^2)
= √25
= 5 [cm]
になるんだ。
むちゃくちゃ便利な公式だね!
だがしかし、
なぜ公式で対角線の長さが計算できちゃうんだろう???
って疑問に思うよね。
その理由はずばり、
直角三角形で三平方の定理をつかっているから
なんだ。
長方形で対角線をひいたら、
2つの三角形にわかれるでしょ??
そのうちの1つの直角三角形をえらぼう。
そいつで、
三平方の定理をつかって対角線の長さを求めるんだ!
対角線をひいて三平方の定理をつかうだけなんて簡単でしょ!?
長方形の対角線の長さは、
三平方の定理で1発さ。
長方形から直角三角形をみつけていこう!
そんじゃねー
Ken