こんにちは!この記事をかいてるKenだよ。植物は癒しだね。
正の約数の個数を求めたい。
そんなとき・・あるよね。。
小さい数の約数なら簡単。
たとえば、
みたいなかんじで、がんばれば約数の個数はわかっちゃう。
だけどね。
むちゃでかい自然数の正の約数の個数を求めたいとき。
こいつはそう簡単にうまくいかない。
たとえば、360の約数の個数を求める問題。
1, 2, 3, ,,,4, ,5, ,,,, 6,,,,,,12,,,,,
って数えてたら日がくれちゃうね。気合だけじゃのりきれない。
そこで今日は、どんなに大きな数でも使える、
約数の個数の求め方の公式
を紹介するよ。
よかったら参考にしてみて。
正の約数の求め方には公式があるよ。
約数の個数を求めたい自然数をNとしよう。
んで、
N = a^p × b^q × c^r
って素因数分解できたとする。
すると、正の約数の個数は、
(p+1)(q+1)(r+1)
になるんだ。
つまり、
(素因数の指数+1)をかけあわせるだけでいいんだ。
たとえば、自然数20の約数の個数を求めてみよう。
こいつを素因数分解すると、
20 = 2^2 × 5
になるね。
正の約数の個数は、(指数+1)をかけあわせればいいから、
(2+1)×(1+1)
= 6
になるってわけ。
今日はこの公式になれるため、20よりもう少し大きい、
360
の約数の個数をもとめてみよう!
つぎの3ステップで約数の個数を求めることができるよ。
自然数を素因数分解してみよう。
360を素因数分解してやると、
・・っおっと。
1がでてきたのでここでストップだね。
わった素数をあつめて因数にすると、
360 = 2^3 × 3^2 × 5
になるね!
つぎは、素因数の指数をかぞえよう。
自然数の360は、
360 = 2^3 × 3^2 × 5
になったね。
素因数の指数に注目してやると、
になってるね。
最後は、
指数に1をたしたもの
を掛け合わせてみよう。
360の素因数の指数はそれぞれ、
だったよね??
だから、360の正の約数の個数は、
(2の約数の個数+1) × (3の約数の個数) × (5の約数の個数)
= (3+1) × (2+1) × (1+1)
= 24
になる。
つまり、360の正の約数の個数は「24」になるってわけ!
でもさ、ちょっとあやしくない??
約数の個数の求め方が、こんなに簡単だなんて・・・
じつは、
「 約数の個数」=「それぞれの素因数をかけるパターン数」
なんだ。
たとえば、さっきの自然数Nが、
N = a^p × b^q × c^r
に素因数分解できるとしよう。
このとき、素因数aの掛け方の方法は、
の (p+1)通りあるはず。
おなじように、他の素因数も考えてやると、
になるはずだ。
1つの素因数あたりの指数のパターンは、
ある。
だから、自然数Nの約数の個数は、
(p+1)×(q+1)×(r+1)
になるんだ。
どう??しっくりきたかな??
約数の個数??
そんなの簡単さ。
素因数分解して、指数に1をたして、かけあわせればいいんだ。
じゃんじゃん素因数分解していこう!
そんじゃねー
Ken
こんにちは!この記事をかいてるKenだよ。クロアチアに住みたいね。
たすき掛けの因数分解はむちゃ便利。
因数分解の公式が使えないときとか、
共通因数をくくりだせないときとかね。
ほんとうに重宝するぜ。
だがしかし、さ。
なぜ、たすき掛けで因数分解できちゃうんだろう??
やり方が複雑すぎる。
ぶっちゃけ、怪しいんだよね。
信用できない。
そこで今日は、
なぜたすき掛けの因数分解が使えるのか??
をわかりやすく解説してみたよ。
よかったら参考にしてみて。
さっそく、たすき掛けの因数分解を証明してみよう。
ax^2 + bx + c
を例として因数分解してみよう!
まずは、たすき掛け因数分解したい式を、
うまーく因数分解できちゃったことにしよう。
とりあえずね。
さっきの例でいうと、
ax^2 + bx + c
を、
(Ax + B)(Cx + D)
に因数分解できちゃったことにすればいいんだ。
でも、これは「とりあえず」だよ。
さっき据え置きした、
(Ax + B)(Cx + D)
を展開しちゃおう。分配法則ですーっと()をはずせばいいんだ。
こいつを展開してやると、
(Ax + B)(Cx + D)
= ACx^2 + ACx + BCx + BD
= ACx^2 + (AD+BC)x + BD
になるね!
つぎは、
をくらべてみよう。
さっきの例でいうと、
の2つだね。
こいつらは「かりの姿」と「オリジナル」の式。
まるまる同じ式のはずだ。
だから、
は一致するはずなんだよ。ゼッタイ。
っていうことは、
になるはずだね。
あとは、仮に置いた文字の正体をあばくだけ。
になるようなA・B・C・Dの組み合わせをみつければいいんだ。
で、でも、どうやって??
って思うよね。
そこで、だ。
たすき掛けマシーンの登場だね。
まっすぐな線をかいて、
xの二乗の係数、定数項、xの係数の順番にならべてやる。
ax^2 + bx + c
でいうと、
a、c、b
の順番だね。
「かけたらaになる2つの組み合わせ」をaの上に、
「かけたらcになる組み合わせ」をcの上におこう。
今回は、
だったから、
こんなかんじになりそうだ。
ただ、今回はもう1つ条件がある。
そう。
b = AD+BC
だったね。
こいつをみたすためには、
4つの数字をたすき掛けのかけ算をして、それぞれたしたらbになるか??
ってことをたしかめればいいよね。
つまり、
AD + BC = b
になってればいいわけだ。
これならうまく、
をみたすA・B・C・Dを求められるね!
たすき掛けの因数分解では、
をイメージして、たすき掛けをしたらxの係数になればいいんだ。
どう??すっきりしたかな??
たすき掛けのやり方は複雑。
正直わからないし謎だ。
だけど、因数分解できちゃうと仮定すれば大丈夫。
腐らずたすきをかけていこう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。紅茶は午後にかぎるね。
因数分解にはいろいろな問題があるよね。
ときどき、ぜんぜん解けなくて泣きたくなるときも、ある。
よくあるのが、
因数分解の公式が使えない
とか、
共通因数でくくれない
って問題だと思うんだ。
そんなときに助けてくれるのが、
たすき掛けの因数分解
だ。
たすき(襷)といえば、
駅伝とか、
宴会の余興をイメージしちゃうかもね。
だけど、因数分解にもじつは、
たすき掛けという解き方があるんだ。
今日は、この解き方を5ステップで解説していくよ。
よかったら参考にしてみてね。
さっきもいったけど、
たすき掛けはつぎのときに役立つよ。
たとえば、つぎの例題みたいにね。
つぎの式を因数分解しなさい。
3x² + 5x -2

なぜなら、
公式は使えなさそうだし、
共通の因数もぜんぜんみつからないからね。
まさに、たすき掛けの因数分解にはもってこいの問題だ。
今日はこの例題をいっしょにといてみよう!
まずは、まっすぐな線をかいてみて。
定規は使わなくて大丈夫。
フリーハンドでいいから、すーっと直線をかいてみてね。
これが第1ステップ!
つぎは、直線の下に係数をならべよう。
かりに、
ax² + bx +c
を因数分解するなら、
a、c、b
の順番に係数をならべてあげるんだ。
つまり、
ってかんじで左から順番にね。
例題の、
3x² + 5x -2
でもおなじさ。
直線の下に、左から、
の順番に係数をかけばいいんだ。
真ん中のxの係数がトリッキーな動きをするから、
順番を間違えないようにね。
つぎは、かけ算のパターンを考えてみよう。
左2つの係数の、
になる組み合わせをみつければいいんだ。
たとえば、
ax² + bx +c
だったら、
をさがせばいいんだよ。
例題でいうと、
の組み合わせだね。
かけて3になるのは、
の2つかな。
かけて-2になるのは、
の2パターンだね。
これで第2ステップ終了!
さっきの数字の組み合わせの中から、
たすき掛けの計算にはまるもの
をえらぼう!
えっ。たすき掛けの計算とか知らないって??
たすき掛けの計算とはずばり、
斜めの数字同士をかけたやつらをたすと、右下の数になる
ってやつなんだ。
たとえば、
ax² + bx +c
だったら、
になるような、○・◎・△・▲の組み合わせをみつければいいんだ。
言葉では説明しずらいから例題をみてみよう。
これは力技だ。
当てはまりそうな数をいれて、たすき掛けを試してみよう。
かけたら3になる組み合わせとして、
の2つをぶちこんでみる。
つぎはかけたら-2になる組み合わせだ。
のペアーなんてどうだろう??
この4つの数字でたすき掛けしてみると、
になる。こいつらをたすと、
-6 + 1 = -5
になるね。
こ、こいつはxの係数の5じゃない!
この組み合わせじゃダメだ!!
じゃあさ、
-2と1の符号を入れ替えたらどうよ??
-1 と2って感じでさ。
そうすると・・・
になるね。
で、たしてみると、
6 -1 = 5
っておおお!
たすき掛け成立しちゃってんじゃん??
これだ!この組み合わせだ!!
・・・・・・・・
・・・・・・・・
っていうかんじで、
因数を変更してみたり、
符号を変えたりするんだ。
たすき掛けの因数分解になるまでねばってみよう。
たすき掛けもいよいよ終盤。
たすきがけの組み合わせがわかったら、
因数分解っぽい形にしてみよう。
たすき掛けで書き出した数字のうち、
いちばん左のやつがxの係数、
真ん中のやつが定数(数字だけの項)になるんだ。
ax² + bx +c
の例だったら、
(○x+△)(◎x+▲)
になるんだ。
例題では、
の組み合わせだったね??
よって、
xの係数は、
で、定数の項は、
になるんだ。
つまり、
3x² + 5x -2
= (x+2)(3x-1)
になるってわけさ。
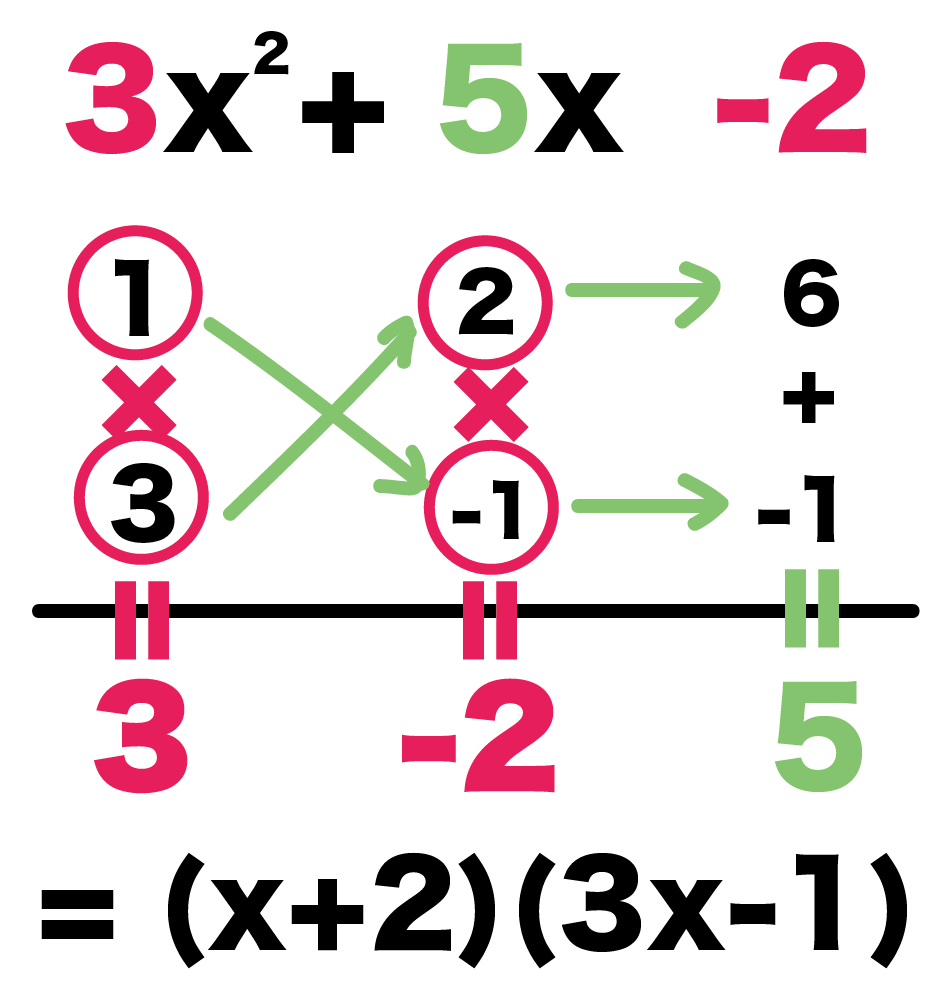
おめでとう!
これでたすき掛けもマスターだね。
たすき掛けの因数分解はぶっちゃけむずい。
説明するのも苦しかったよ。うん。
だけど、解き方をおぼえちゃえばもうね、無敵。
必殺ワザをおぼえるものだと思って、
たすき掛けをマスターしちゃおう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。爪は大事だね。
因数分解の応用問題の1つに、
置き換え問題
ってやつがいる。
世界には数えきれないほど因数分解の問題があるから、
ぜんぜんピンときてないかもね。
置き換え問題はつぎのようなやつだよ↓↓
こんなかんじで、
式のなかに「おなじ文字式」がちらほらしている問題。
えっ、この問題でいうと、
(2x+3)
がちらほらしてるじゃん??
このタイプの解き方は一択。
チラホラしている文字式を「別の文字」で置き換えればいいんだ。
むちゃ解きやすくなる。
だから、
置き換えタイプの因数分解
とよんでるよ。
今日はこいつの解き方を5ステップで解説していくね。
置き換え問題は4ステップでとけちゃうよ。
それじゃあ、さっきの例題をといていこう。
例題
つぎの式を因数分解しなさい。
(2x + 3)² – 4(2x+3) + 4
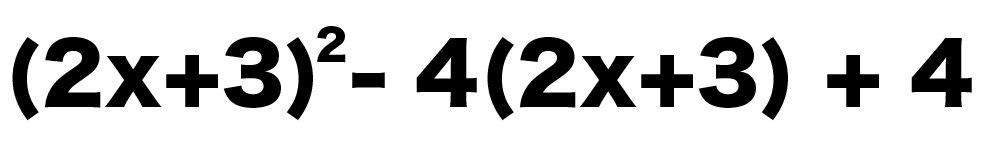
まず、式の中にふくまれている、
2回以上登場する文字式
をみつけてみよう!
これが探せないと始まらないね。
例題をみてみると、あきらかに、
2x+3
が何回もでてきてるよね??
まあ、、2回だけどねw
こいつみたいに、怪しい文字式をみつけてみよう!
つぎは、2回以上でてきた文字式を「A」とおこう。
そう、
アルファベットのAだ。
他の文字と区別するために大文字にしてね。
すると、例題ではこんな感じで置き換えられるよ↓↓
A² – 4A + 4
これが第2ステップ。
つぎはふつーに因数分解してみよう。
置き換えた式を因数分解の解き方で計算すればいいのさ。
例題の式は、
A² – 4A + 4
に生まれ変わったよね??
こいつを公式で因数分解してやろう。
因数分解したい文字式の項を数えてみると、
「3つ」あるね。
3つの項を因数分解する公式は、
(x+a)(x+b) = x² +(a+b) +ab
だったよね??
これはパズル型の公式。
かけて右に、たして真ん中になる数の組み合わせを考えればいいんだ。
例題の、
A² – 4A + 4
でいうと、
になる組み合わせを考えればいいんだ。
まず、かけて「4」になる組み合わせは、
の4通りだ。
このうち、たしたら「-4」になるのは2番目の、
だね。
こいつらを公式のaとbに代入してやると、
A² – 4A + 4
= (A-2)(A-2)
= (A-2)²
になるね。
最後はAに文字式を代入しなおそう。
つまり、
Aをもとの文字式にもどすってことだね。
例題では、
A = 2x + 3
っておいてたよね??
こいつをさっき因数分解した、
(A-2)²
に代入してみよう。
さっそく代入してみると、
(A-2)²
= (2x +3 -2)²
= (2x +1)²
になるね!
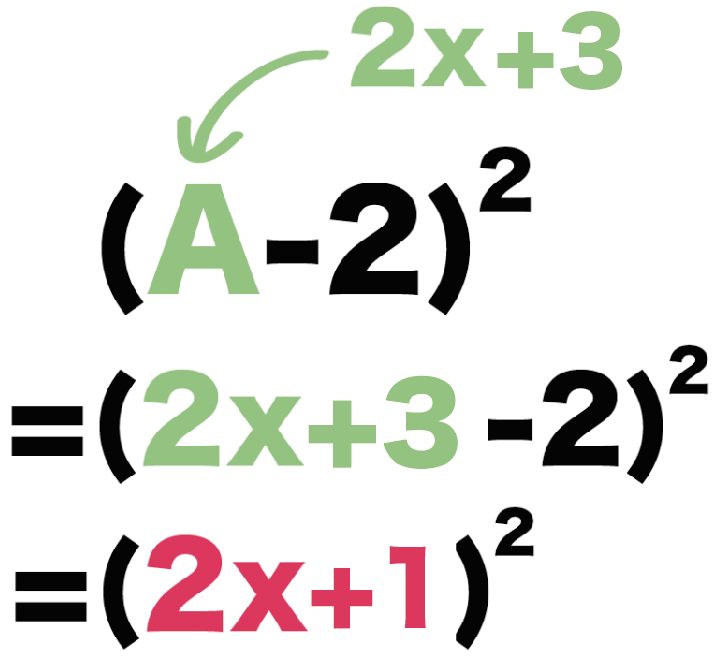
おめでとう!
これで置き換えの因数分解もマスターだ。
因数分解の置き換えの問題??
びびることはない。
おなじ文字式をいったんAとおいて、因数分解する。
最後にAをもとにもどせばいいんだ。
ガンガン置き換えていこう!
そんじゃねー
Ken
因数分解の攻略記事
こんにちは!この記事をかいているKenだよ。コーヒーはSに限るね。
因数分解とは何か??ってとこまで勉強してきたね。
だけど、解き方・やり方はピンときてないと思うんだ。
そこで今日は、
中学数学でならう因数分解の解き方・やり方を簡単に解説してみたよ。
よかったら参考にしてみて。
因数分解のやり方は3ステップさ。
っていわれてもわからんよね??
今日はいっしょに例題をといてみよう。
つぎの多項式を因数分解してください。
5a³ x² + 25a³x -30a³
まず共通因数をくくりだすよ。
各項にかかっている同じ因数をくくりだせばいいんだ
⇒くわしい共通因数のくくり方はこちら
例題での共通因数は「5a³」だね。
なぜなら、
すべての項に「5a³」がふくまれているからさ。
共通因数をとりだして()でくくってやると、
5a³ (x² + 5x -6)
になるね!
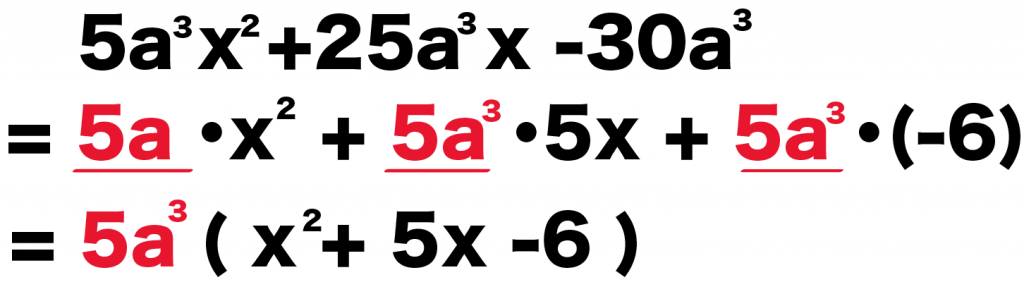
つぎは因数分解の公式をえらぼう!
中学数学でならう因数分解の公式には、
があったよね??
因数分解する「項の数」で公式をえらぶんだ。
ってかんじ。
例題で因数分解したいのは()の中の、
x² + 5x -6
だ。
こいつの項の数は「3」。
だから、パズル型の公式をえらんでみよう!
公式で因数分解してみよう。
例題では共通因数をだしたあとの、
x² + 5x -6
をパズル型で因数分解するよ。
パズル型では、数・文字のペアーを探すんだったね。
この場合だと、
になるペアーをさがせばいいよ。
まず、かけ算が-6になるパターンを思い浮かべてみると、
の4パターンある。
そのうち、たしたら5になる組み合わせは、
「-1」と「6」
の1パターンしかないね。
だから、x² + 5x -6 を因数分解すると、
(x-1) (x+6)
になるはずだ。
んで、
くくりだした共通因数をくっつけると、
5a³ (x-1) (x+6)
になる。
おめでとう!
これで因数分解の解き方もマスターだね!
因数分解の解き方はシンプル。
共通因数をくくりだしてすっきりさせる。
そったら、公式をつかえばいいんだ。
問題をといて慣れていこう!
公式を使った因数分解ができるようになったら、次は置き換えの因数分解の問題にチャレンジしてみよう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。豆乳にはハチミツだね。
因数分解の基本ワザに、
共通因数でくくる
があるよ。
これは基本中の基本。
柔道でいうと背負い投げ。
空手でいうとかわら割りかもしれない。
今日はそんな因数分解の基本の、
共通因数のくくり方を4ステップで解説してみたよ。
よかったら参考にしてみて。
=もくじ=
共通因数とは、
2つ以上の項に含まれるおなじ因数のこと
なんだ。
たとえば、
6 + 8
っていう多項式があったとしよう。
この、
の項に注目してほしい。
こいつらの共通因数は「2」だ。
なぜなら、2つの自然数を素因数分解してみると、
になってて、共通する因数は「2」だからね。
どう??
しっくりきたかな??
共通因数のくくり方は4ステップでいけちゃうよ。
例として、
9a²b³ – 21b²
から共通因数をとりだしてみよう!
まず、各項をかるく因数分解してみよう。
係数は素因数分解して、
文字は指数をばらせばいいんだ。

例題でもかるーく因数分解してみると、
になるね。
これが第1ステップ。
つぎは、因数から共通のものをみつけよう。
例題では、
3×b×b
が共通因数っぽいね!
だって、2つの項に共通してふくまれてるし。
もれなく数や文字をカウントしよう!
共通因数を項からとり出してみよう。
ただ取り出すだけじゃない。
ついでに()でくくらなきゃいけないね。
共通因数「3×b×b」をとり出して()でくくると、
3×b×b ( 3×a×a×b – 7)
になるね。
最後はかけ算を元にもどすだけ。
例題でかけ算をなくしてやると、
3×b×b ( 3×a×a×b – 7)
= 3b²(3a² b-7)
になるはずだ。
おめでとう!
無事に共通因数でくくれたね。
共通因数のくくり方はどうだったかな??
項をかるーく因数分解して、共通の因数をみつければいいんだ。
くくりだして問題になれていこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。シチリアに行きたいね。
素因数分解の問題はたーくさんあるよ。
ほとんどの問題はただ素因数分解するだけ。
でもたまーに、
素因数分解の応用問題がでてくるよ。
たとえば、つぎのようなやつね↓↓
今日はこの応用問題を3ステップで解説していくよ。
よかったら参考にしてみてね。
例題をいっしょにといてみよう。
3ステップでとけちゃうよ。
まず素因数分解してみよう。
素因数分解のやり方で分解すればいいんだ。
例題では、60を素因数分解してみよう。
素因数分解の解き方の鉄則は、
小さい素数から順番にわっていく
だったよね??
だから、いちばん小さい素数の2から割りはじめよう。
割り算の答えが「1」になるまで素数で割り続けてみてね。
すると、
になるはず。
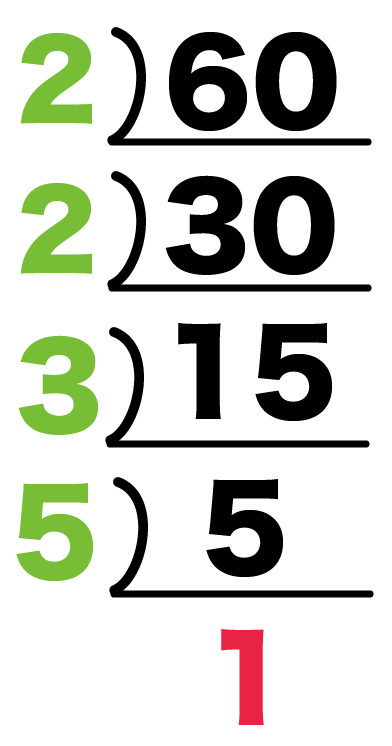
あとはわった素数をあつめて「×」で結んでみて。
すると、
60 = 2^2 × 3 × 5
になるね!
つぎは、素因数のなかから、
指数が奇数になってるやつ
をさがそう。
60の素因数のうち、
の指数は奇数だね。
これが第2ステップ!
最後は、
指数が奇数の素因数を1つずつかけてみよう!
それが答えになるよ。
なぜなら、すべての素因数の指数を偶数にすれば、
「○○の二乗」になるからね。
例題をみてみよう。
60を素因数分解すると、
60 = 2^2 × 3 × 5
になったよね??
指数が奇数になってるのは、
の素因数。
よって、ぜんぶの指数を偶数にするためには、
「60」に「3」と「5」をかければいいね。
そうすると、
2^2 × 3^2 × 5^2
になる。
こいつを2乗でくくってやると、
(2×3×5)^2
になるね!
つまり、
60に自然数15をかけてやると、900になって、
そいつは30の二乗になってるんだ。
今回の例題では、
できるだけ小さい数をかける
って条件があったね。だから、
3×5、つまり、15が答えになるよ。
応用問題の解き方はわかったね。
っていう3ステップさ。
慎重にといてみよう!
そんじゃねー
Ken
こんにちは!この記事をかいてるKenだよ。列がうまれたね。
中学数学でならう因数分解の公式は3つあるよ。
また公式おぼえるのかよ。。。。。
って感じだよね。ただ、安心してほしい。
じつはこれ、
展開の公式(乗法公式)を逆にしただけなんだ。
べつに新しいことを学んでるわけじゃない。
見方を逆にしただけさ。
だけど、乗法公式の逆っていわれてもピンとこないし、
因数分解に特化した公式の覚え方を知りたいよね。
そこで今日は、
因数分解の公式の覚え方
をわかりやすく解説してみたよ。
公式をおぼえたいときに参考にしてみて。
中学数学でならう因数分解の公式はシンプル。
おおきくわけると2種類しかないんだ。教科書では3つぐらいあるってならうけどね。
それは、
の2つさ。
因数分解したい文字式の項が何個あるのか??
ってことによって使い分けるんだ。
さっきの公式でいうと、
a² – b² = (a+b)(a-b)
が2つの項専用の因数分解の公式。
ほかの2つの、
が3つの項を因数分解するときにつかう公式なんだ。
2種類なら公式を覚えれそうだね!
それぞれ順番にみていこう!
2つの項を因数分解できる公式は1つしかないよ。
a² – b² = (a+b)(a-b)
この因数分解の公式はなんというか、
分解型の公式
だね。
なぜなら、2乗になっている数字をバラバラにしてあげて、+と-でくっつけるだけだからね。
2つ重なっているものを1つずつに分解してまとめてあげる。
だから、ぼくは分解型ってよんでるんだ。
とりあえず、焼き肉をイメージしてほしい。
同じ肉が重なっちゃっていて、うまく焼けてないお肉たちをね。
こいつらをおいしく調理するために、いっかいバラバラにしてやる。
んで、わけたお肉には違うたれ(符号)をつけてやるんだ。
ぜんぶおなじ味じゃ飽きちゃうでしょ??
焼き肉のたれをかけるやつと、ポン酢かけるやつにわけてみるって感じ。
こんな感じで、
2つの項を因数分解する公式は、
っていう2ステップで因数分解できちゃうのさ。
たとえば、
9x² – 4y²
を因数分解してみよう。
これをまずは、
a² – b²
の形になおしてやろう。
だから、
9x² – 4y²
= (3x)² – (2y)²
になるね。
つまり、重なっているお肉は「3x」と「2y」なわけだ。
お肉をバラバラにして、違うソース(符号)でむすんでやると、
9x² – 4y²
= (3x)² – (2y)²
= (3x +2y) (3x -2y)
になるよ。
この公式を使うときは、
「○○の2乗」になるように分解してみよう!
因数分解の公式で「3つの項」を因数分解できるのは、
の2つだね。
だけど、実際は最後の、
x² + (a+b)x + ab = (x+a)(x+b)
さえ覚えてれば大丈夫。
3つめの公式の「b」に「a」を代入すると2つめの公式になるからね。
2つ目の「a² + 2ab + b²」は覚えなくても痛くもない。ちょっとカユいけどね。
ぼくは個人的に、この因数分解の公式を、
パズル型の公式
とよんでいるよ。なぜなら、
かけたら右、たしたら真ん中になる2つの数・文字を推理するからね。
まるで、クロスワードパズルみたいでしょ?
たとえば、
○² + △○ + □
っていう式があったとしよう。
このとき、
になる2つの数字・文字の組み合わせを考えればいいんだ。
まずは、「かけたら□になる組み合わせ」を考えてみよう。
もし、a・bっていう2つの文字が、
になるとしたら、
○² + △○ + □ = (x+a)(x+b)
になるんだ。
つまり、3つの項を因数分解する公式では、
2つの数字・文字の組み合わせを推理すればいいんだ。
たとえば、
x² + 6x + 8
をイメージしてみて。
3つの項でできているから、
x² + (a+b)x + ab = (x+a)(x+b)
のパズル型の公式をつかうよ。
になる組み合わせを推理していこう。
まず、「かけたら8になる数」を考えてみる。
かけたら8になる数の組み合わせは、
の4通りだね。
この4通りの組み合わせのうち、たしたら6になるのは、
のペアーだ。
これが因数分解の公式のaとbにあたるってことさ。
だから、公式で因数分解してやると、
x² + 6x + 8 = (x+2)(x+4)
になるね。
おめでとう!
項が2つ3つでもどーんとこいだね!!
因数分解の公式はたくさんあるように思えるけど、
実際わけてみると2種類。
しかないんだ。
自分が因数分解したい文字式の項は何個あるのか??
をチェックしてみよう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。塩は大事だね。
ってことは習ったね。
だけどさ、
実際、素因数分解ってどうやるんだろう??
やり方なんてぜんぜんイメージできないよね。
だって、素因数分解したことないんだもん。
そこで今日は、
素因数分解のやり方を5ステップで解説してみたよ。
よかったら参考にしてみて。
素因数分解のやり方はずばり、
素数でわりまくって、割れた素数を集めて因数にする
方法だ。
だから、素因数分解で大切なのは、
素数で割りまくる根性
と、
素数かどうか見分ける力
なんだ。
この2つさえあれば素因数分解なんて楽勝さ。
素因数分解は5ステップでできちゃうよ。
例として、自然数の360を素因数分解してみよう!
まず、素因数分解したい自然数をかいてみよう。
鉛筆でもシャープペンでもいいからかいてみて。
例題でいうと、
360
だね。
うまくかけたらつぎにいこう。
つぎは素因数分解するための準備。
自然数の周りに線をかいてみて。
これは素数で割りまくるための道具なんだ。
この線の横に、自然数を割る素数、
自然数の下にその割り算の答えをかいていくんだ。
もし、「割り算の答え」が素数でわれるようだったら、
こんな感じで下に続けていって、素数でわりまくるんだ。
例題でもおんなじさ。
360の下にこのきんとんうんのような線をちょこっとかいてあげよう。
これが第2ステップ!!
いよいよ素因数分解の山場。
素数でわりまくる
っていうステップだ。
ここでのコツは、
小さい素数から割りまくる
ってこと。
つまり、素数でいちばん小さい「2」から割りまくるのさ。
2で割り切れなくなったら3、
3で割り切れなくなったら5、
・・・・
というように徐々に素数を大きくしていこう。
割り算の答えが1になるまで続けてみてね。
例題の「360」もまずは素数2でわりまくってみよう。
すると、
っていう感じで3回われたね!
45は残念ながら2で割り切れないから3にバトンタッチだ。
おなじように、3で割りまくってみると、
っていう感じで2回われたね。
お次は素数の5の出番。
おなじように割り算の答えをわってみると、
・・・
おや!
1がでてきたね!
割り算の答えが1になったからストップ。
割ってきた素数を集めるフェーズだ。
左の素数をかきあつめて「×」でむすんでみよう。
たとえば、自然数が素数1から素数nまでわれちゃったとしよう。
このとき、割れちゃった素数を「×」でむすんでやると、
素数1×素数2×素数3×・・・×素数n
になるね。
これを360の素因数分解でもやってみよう。
割った素数はぜんぶで、
の6つだね??
こいつらを「×」でむすんでやると、
360 = 2×2×2×3×3×5
になるね。
最後は指数でシンプルにしよう。
同じ素数を指数でまとめればいいのさ。
360の素因数分解でいうと、
が指数でまとめられそうだね。
指数でコンパクトにしてやると、
360 = 2^3 × 3^2 × 5
になるはずだ。
おめでとう!
これで素因数分解のやり方もマスターだね。
素因数分解は基本的に、
素数で自然数をわりまくって、
あつめて、
かけ算にしてやるだけ。
あとは指数でととのえればよし。
素因数分解はいろいろな計算に使えて便利。
やり方・解き方はおぼえておこうね。
えっ、もっと高速に素因数分解したい??
そんな君のために、素因数分解電卓アプリ「Soin」をつくったよ。
よかったら試してみて。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。強風にあおられたね。
世界にはたくさん因数分解がある。
地球は広い。ほんとに。
その因数分解の1つに、
素因数分解(そいんすうぶんかい)
ってものがある。

名前からしてちょっと怪しい。
ぶっちゃけ遠ざけたい。
だけど、テストにでてくるくせ者なんだ。
そこで今日はこの「素因数分解」と仲良くするためにも、
素因数分解とはなにか??
を解説してみたよ。
よかったら参考にしてみて。
ずばりいってしまおう。
素因数分解とは、
「自然数」を「素数」の「かけ算」になおすこと
だよ。
もっと因数分解的にいってやると、
自然数を素数の因数に分解すること
なんだ。
素数の因数のことを略して「素因数」ってよんでるよ。

えっ。
ごちゃごちゃしてるって!??
うーん、そうだね。
たとえば、35という自然数をイメージしてみて。
こいつを素因数分解、つまり、
素数のかけ算になおしてやると、
35 = 5 × 7
になる。
だって、「しちごさんじゅうご」だもん。
「5」も「7」も素数だから素因数分解になるんだ。
このとき、
「5」と「7」を「35」の「素因数」ってよんでるよ。
なぜなら、素数の因数だからね。
せっかくだから、
素因数分解じゃない例を紹介していくよ。
どれか1つにあてはまるようなら、
そいつはもう、素因数分解でもなんでもない。
ただの因数分解ってことさ。
因数分解する数字が「自然数」じゃない
っていうケースだ。
スタート地点から間違っているね。
たとえば、
-35
を「- 5 × 7」に因数分解したとしよう。
いっけん素因数分解っぽいけど、こいつは素因数分解じゃない。
なぜなら、
因数分解したもとの「-35」が自然数じゃないからね。
素因数分解かたしかめるときは、かならず、
もとの数が自然数かどうか
をチェックしてみよう。
つぎは、因数が素数じゃないケースだ。
これはヒューマンエラーというか、ただのミスだね。
たとえば、もし、35を「1×35」って因数分解しちゃっとしよう。
この因数分解は素因数分解なんかじゃない。
なぜなら、
は素数じゃないからね。
因数分解はできてるんだけど、素数のかけ算に分解できてないんだ。
だから、ただの因数分解になっちゃってる。
素因数分解したあとにはかならず、
因数が「素数」になっているかどうか
を確認してみよう!
素因数分解とは因数分解の一種。
自然数を素数の因数に分解することを「素因数分解」っていうんだ。
テストによくでてくるから、
素因数分解のやり方もおさえておこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。魚は2匹までだね。
中3数学では、
因数分解
をならうよ。
じつはこれ、けっこう重要な単元なんだ。
因数分解の問題がよくでることはもちろん、
二次方程式をとくためにも必要だからね。
もう、ぶっちゃけ、
因数分解を制するものは中3数学を制する
といっても過言じゃない。
そこで今日は手始めとして、
因数分解とはなにものなのか??
を解説していくよ。
よかったら参考にしてみて。
因数分解とはずばり、
「数」や「文字式」をあえて「かけ算」になおすこと
だ。
このとき、
かけられている数字・文字式を「因数」っていうんだ。
えっ??
ぜんぜんピンとこないって??
それじゃあ因数分解の例をみていこう!
自然数の「35」をイメージしてみて。
因数分解とは、
あえて「かけ算」になおすこと
だったよね??
「ごしちさんじゅうご」だから、35を因数分解すると、
5× 7
になる。
こんな感じで、
「35」を「5×7」になおすことを「因数分解」っていうんだ。

かけられている数を「因数」といったね??
だから35の因数は、
の2つになるのさ。
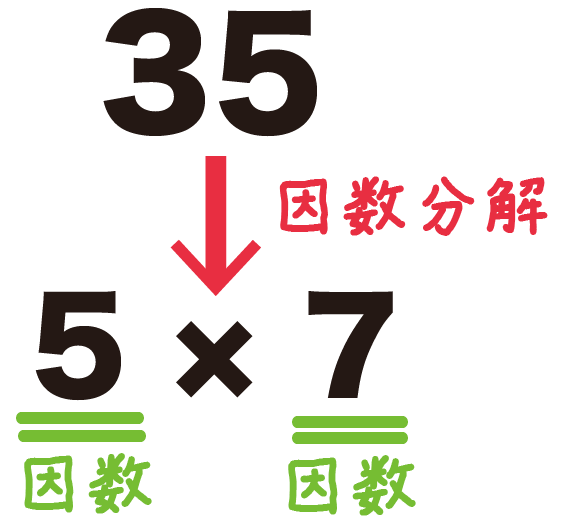
これが数字の因数分解の例だよ。
つぎは文字式の因数分解だ。
とりあえず、
a^2 -a
をイメージしてみて。

こいつをかけ算になおしてやろう。
aで()でくくってやると、
a^2 -a
= a×(a-1)
になるよね。
「a^2 -a 」を「a × (a-1)」になおすことを「因数分解」っていうんだ。
そして、
「かけられているやつら」は「因数」だったよね??
だから因数は、
の2つになるよ。
どう??
納得したかな??
ここまで因数分解とは、
数や文字式をあえて「かけ算」になおすこと
っていってきたね。
だけど、これじゃあよくわからない。
もっと簡単な覚え方ないかな??
じつはもっとシンプルな方法があるんだ。
それは、
因数分解とは「展開の逆」
という覚え方。

展開とは、
かけ算を足し算の形になおすこと
だったよね。
()をはずしたり、展開の公式で計算したりしたやつだよ。
ずばり、
因数分解とは「展開とは逆のこと」をするんだ。
たとえば、「a^2 -a 」と「a(a-1)」の関係をみてみよう。
「a^2 -a 」を因数分解すると「a(a-1)」になったね??
今度は逆に、
「a(a-1)」を分配法則で展開すると、
a(a-1)
= a^2 -a
になるね。
あら。
因数分解する前の「a^2 -a 」に戻っちゃったね。
これからわかるのは、
因数分解すると展開前の式になるし、
展開すると因数分解前の式にもどる
ってことさ。
つまり、
因数分解とは「展開の逆」をしているんだね。
因数分解とは、
展開の逆。
これがいちばん覚えやすいかも。
因数分解する前によーく復習しておこう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。中華は鉄板だね。
素数は何かってなんとなくわかった。
だけど、
どうやって素数を求めればいいんだろう??
正直、求め方がわからない。
勘?? 運?? 電卓??・・・
じつは素数の求め方の1つに、
エラトステネスのふるい(篩)
っていう方法があるんだ。
ちょっと正直、ひびきがうさんくさいね。
だけど、使い方をおぼえるとチョー便利だから、
「エラストテネスのふるい」を5ステップでつかってみよう。
これをマスターすれば大丈夫。
素数を1発で求められるよ!
5ステップで素数を求めていくよ。
例として、
を求めてみよう!
求めたい範囲の自然数をかいてみよう。
今回でいうと、
1から100までの素数を求めたい
んだったね??
だから、1から100までの自然数をかけばいいのさ。
えっ。
自然数のかきかたがわからんって??
そうだね。
1行あたりに10個の自然数をかいてみて。
ちょうどこんな感じ↓↓
手が疲れるかもしないけど、ここが一番きついとこ。
歯をくしいばって自然数をかいてみよう。
最初のほうの素数に○をつけよう。
えっ。
どこまでの素数に○つければいいのかって??
じつは、
2乗しても範囲をこえない素数
まで○でかこえばいいんだ。
1から100までの自然数にふくまれる素数だったら、
範囲でいちばん大きいのは100でしょ??
2乗しても100をこえない最大の素数は「7」だね。
なぜなら、つぎの素数の「11」は2乗すると「121」になるからね。
100をこえちゃう。
だから、7までの素数の、
の4つを○でかこうんだ。
これが第2ステップ!
左上の「1」を斜線でけそう。
赤でも緑でも構わない。
とにかく、消してやろう。
1は素数じゃないから消すんだ。
今度は○がついてる素数の倍数をけすよ。
なぜなら、
「素数の倍数」は素数じゃないからね。
「1」と「自分」以外でも割れちゃうようになるもん。
例題でいうと、まず「2」の倍数をけしてやる。
偶数をぜーんぶ消すんだ。
おつぎは3の倍数。
斜めにしゅーっと線をひいてあげよう。
つぎは5の倍数。
5の倍数は、
の2通りになるはず。
だから「5」と「10」の下の数字たちはみーんな消されちゃう。
最後に7の倍数。
100以下で7の倍数になっている、
をけしてやろう!
最後まで生き残った自然数を○でかこってみて。
○がついたぜーんぶの自然数が、
素数
だ。
どう? 案外簡単でしょ??
エラストテネスの篩はちょー便利。
簡単でわかりやすい。
ただ、ちょっと残念なのが、
最初に自然数をたくさんかくところだ。
もし、1から1000までの素数を求めなきゃいけなかったら、
1000個の自然数をかかなきゃいけない。ゼッタイに手が震えるね。
でも、最初さえ乗り切れればあとは楽になる。
エラストテネスのふるいでガンガン素数を求めていこう!
そんじゃねー
Ken