こんにちは!この記事をかいているKenだよ。髪は軽いほうがいいね。
正方形の定義っておぼえてる??
教科書によると正方形の定義とは、
4つの辺がすべて等しく、4つの角がすべて等しい四角形
ってかいてあるね。
つまり、
ぜーんぶの「辺」と「角」が等しい四角形
ってことなんだ。
だから、
正方形の1つの角度は90°になる。
だって、四角形の内角の和は360°だからね。
んで、1つの辺が4cmだとすると、
ぜーんぶの辺の長さも4cmってことになる。
わかりやすい四角形だね!
ただ、
4つの「辺だけ」がすべて等しくても正方形じゃない。
そいつは「ひし形」だよ。
また、4つの「角だけ」すべて等しくたってダメだ。
そいつは長方形になっちゃう。
4つの「角」と「辺」がすべて等しくなっている四角形が
正方形だってことをおぼえておこう。
最後にひとつだけおぼえておこう。
それは、
正方形が「平行四辺形」でもあり「ひし形」でもあり、「長方形」である
ということだ。
えっ。ぜんぜんよくわからないだって??!
そうだね、順番に説明していこう。
じつは、
正方形は平行四辺形の1種なんだ。
なぜなら、
正方形の定義が平行四辺形になる条件をみたしているからね。
4つの辺・角がすべて等しい四角形
が正方形だったよね??
ってことは、
向かい合う2の辺が等しい、
向かい合う角が等しい
ともいえるね?
だから、
正方形は平行四辺形でもあるんだ。
正方形はひし形でもあるよ。
その理由は、
ひし形の定義をみたしているからなんだ。
ひし形の定義は、
4つの辺がすべて等しい四角形
だったよね??
正方形の辺もすべて等しいから、
ひし形の定義をみたしていることになる。
よって、
正方形はひし形であるわけさ。
長方形の定義をみたしているから
正方形が長方形である
といえるんだ。
長方形の定義は、
4つの角がすべて等しい四角形
だったよね??
ってことは、正方形の定義はそれをみたしているんだ。
だから、正方形は長方形といえるわけさ。
正方形は平行四辺形でもあり、
長方形でもあり、
ひし形でもある、
といってきたね。
長方形・ひし形も平行四辺形だから、
この状態を図にあらわすとこうなる↓↓
つまり、
正方形は平行四辺形でありつつ、
「長方形」と「ひし形」の特徴も同時にあわせもつ、
ハイブリッドな四角形ってことさ。
ぶっちゃけ、
正方形は「CCレモン」と立ち位置がにているね。
清涼飲料水というグループの中に、
のいずれも入ってるはずだ。
CCレモンは、
サイダー(炭酸)とレモン水(レモンっぽさ)の特徴をもっているよね??
清涼飲料水でありつつ、
2種類の飲み物のいいところどりしてるってわけさ。
この立ち位置は正方形とにている。
だって、
正方形は平行四辺形でありつつ、
ひし形と長方形の性質もあわせもっているんだからね。
正方形はCCレモンと似ている
ってことをおぼえておこう!
正方形の定義は、
4つの辺がすべて等しく、4つの角がすべて四角形
だったね。
この定義は「ひし形」と「長方形」の定義もふくんでいる
ってことをおさえておこう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。
中2数学を勉強していると、
逆(ぎゃく)
っていう言葉がでてくるね。
日常生活で「逆」ってことばはよく使う。
マリオカートをプレイすると、
おまえ、「逆」走してね??
とかよく言うでしょ?
その「逆」だよ。
今日はその、
「逆」が数学ではどういう意味があるのか??
をわかりやすく解説していくよ。
よかったら参考にしてみてね。
数学の「逆」とはずばり、
「あることがら」の「仮定」と「結論」を入れ替えたもの
さ。
たとえば、つぎのことがらがあったとしよう。
AならばBである
ってやつね。
こいつの逆をつくってみよう。
仮定がA、結論がBだね。
こいつらを入れ替えてやると、
BならばAである
ってなる。
たとえば、
馬ならば動物である
っていう「ことがら」があっとしよう。
このとき、
だね。
だから、逆をつくるために、
仮定と結論をいれかえてやると、
動物ならば馬である
ってなるね。
逆をつくるのは簡単だね。
だって、
「仮定」と「結論」を入れ替えるだけだから。
ただ、数学で逆をつくるときに知っておいてほしいのは、
あることが正しくても、その逆は正しいとは限らない
ということさ。
つまり、正しいことがらの逆をつくってみたけど、
逆をつくってみたら正しくなくなっちゃった・・・
ってことがあるってこと。
たとえば、さっきの馬の例をみてみよう。
馬ならば動物である
っていうことがらはどうだろう??
こいつはただしそうだね。
だって、馬は動物だから。
だけれども、その逆をみてほしい。
動物ならば馬である
って正しくないよね??
だって、動物は馬だけじゃないから。
ライオンだって、
ねずみだって、
牛だっている。

したがって、
馬ならば動物である
の逆は正しくないんだ。
最後に、数学の逆の例を2つみてみよう。
平行線の性質は逆にしても正しいよ。
平行線の性質って、
2つの直線が平行ならば、同位角は等しい
だったね。
たとえば、
lとmが平行だったら、同位角のaとbが等しいってやつさ↓↓
じつは、この「平行線の性質」ということがらは、
逆も正しいといえるんだ。
つまり、
同位角が等しいならば、2つの直線が平行である
っていえるんだ。
たとえば、さっきの例でいうと、
同位角のaとbが等しかったら、直線lとmが平行になっている
ってことがいえるんだ。
合同な図形の性質は逆にしたら正しくなくなっちゃう。
合同な2つの図形には、
対応する角の大きさが等しい
っていう性質があったよね?
2つの図形が合同ならば対応する角が等しい
ってことが成り立っていたわけだ。
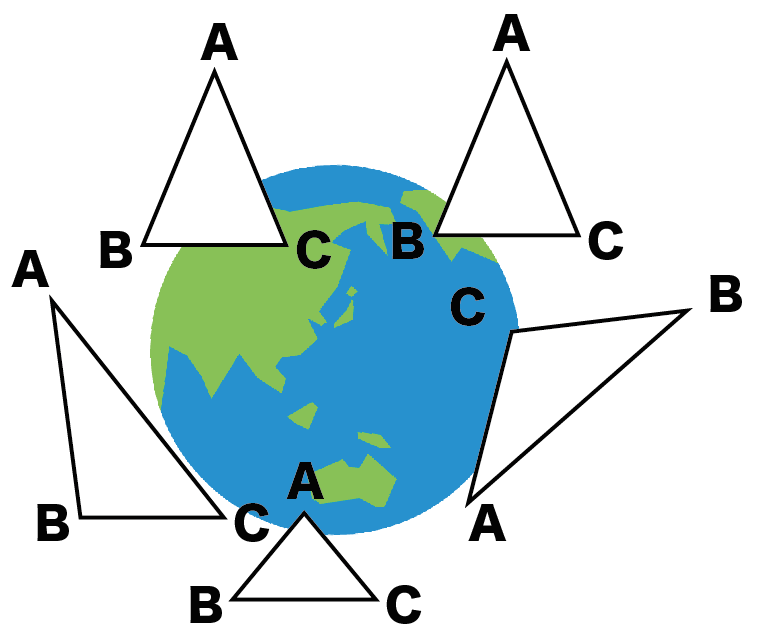
たとえば、△ABC ≡ △DEFだったら、
ってことがいえるわけだね。
でも、ところがどっこい。
逆にしたら正しくなくなっちゃうんだ。
逆にすると、
対応する角が等しいならば2つの図形が合同である
になるでしょ??
これはまちがっているね。
なぜなら、
ぜんぶの対応する角が等しくても合同じゃない場合があるからだ。
たとえば、下のような△ABCと△DEFみたいな感じでね。
こいつらは、
なんだけど、
合同じゃないよね。
大きさ違いすぎて重ならないね。ゆえに、合同なんかじゃない。
これが逆が正しくない例だよ。
逆の作り方は簡単。
だけれども、
逆が正しくないことがけっこうある。
っていうか、そのほうが多いね。
逆が正しいか?
正しくないか?
に注意して問題をといてみてね。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。コーン、最高。
図形の証明問題
ってむずかしいよね。
図形の面積を計算する問題とは
ちょっと違うタイプ。
苦手な中学生も多いはずだ。

今日はそんな苦手をなくすために、
【中2数学】図形の証明問題を攻略できる6つのコツ
っていう記事をかいてみたよ。
証明問題のせいで数学が嫌いになりそう、
ってときに参考にしてみてね。
つぎの例題をときながら解説するよ。
数学の証明問題でいちばん最初にやることは、
仮定と結論をみつけてやることさ。
仮定とは、カンタンにいってしまえば、
問題文であたえられている条件
で、
結論とは、
仮定をつかえば正しいといえること
さ。
たとえば、さっきの例題でいうと、
っていうのが仮定だよ。
だって問題文中に、
AB = DC、AB // DCの△ABCと△CDAがあったとします。
ってかいてあるからね。
この問題にかぎっての正しい
って言ってくれてるてることなんだ。
これが仮定だ。
それじゃあ、「結論」をさがしてみよう。
結論は問題文でいうところの、
○○を証明しなさい。
の○○にあたるところさ。
つまり、
問題で証明してほしいことが「結論」なのさ。
この例題でいうと、
角ABC = 角CDA
が結論だね。
「仮定」を図に書きこんでみよう!
これをすると、
っていうメリットがあるよ。
あと、わからなかったときでも、
テスト用紙にがんばった形跡が残って、
先生に「がんばったアピール」ができるね。
たとえば、さっきの例題で、
が仮定だったよね??
こいつを図に書き込んでやると、
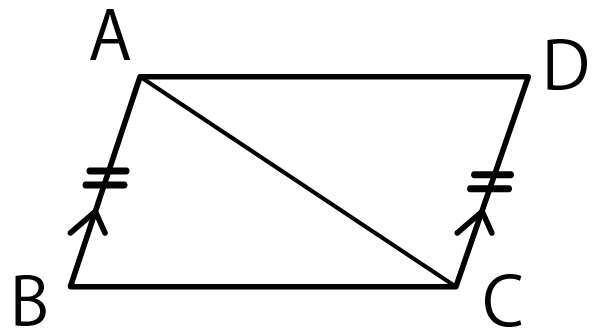
こうなる。
※図形の記号を復習してみて。
ただ、「結論」をいっしょに書き込まないでね。
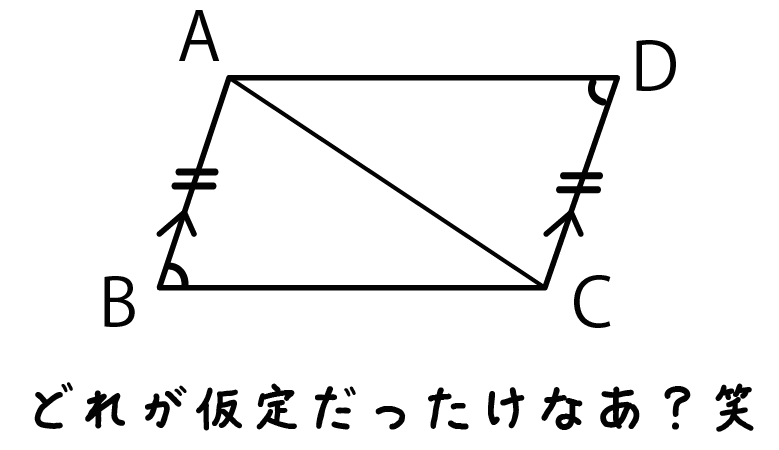
「仮定」と「結論」をごちゃまぜにすると混乱するからさ。。
結論も書き込みたいってときは、
色違いのペンでかきこんであげよう。
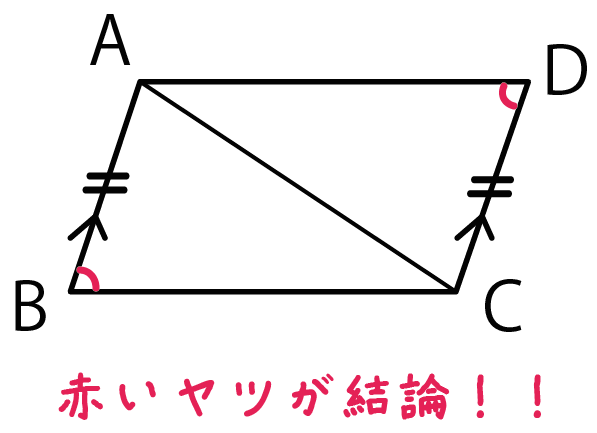
赤ペンとかでね。
仮定と結論を整理し終わったら、
結論までの道のりをイメージしよう。
証明問題の特徴は、
ゴールが事前にあたえられているってこと。
つまり、逆にいってしまえば、
ゴールがみえているから、そこへの行き方を考えるだけ
ってことになる。
いわば、ゴールがみえている迷路みたいなもんさ。

チーズがあるのはわかってるから、
あとは道順を考えるだけでいいんだ。
たとえば、例題の結論である、
角ABC = 角CDA
をゲットする道順を考えてみよう。
うーん、
えっと、
そうだなあ。。。
あっ!
△ABCと△CDAが合同である
ってことをいえればゴールできそうじゃね??
だって、
合同な図形の「対応する角はそれぞれ等しい」
ってことを使えば、
角ABC = 角CDA
がいえそうだからね。
結論までをイメージするためには、
「根拠となることがら」を覚えている必要があるんだ。
多ければ多いほどいいね。
たとえば、さっきの例題でも、
を暗記していないとゴールまでイメージできなかった。
「合同な図形の性質」以外にもたとえば、
・・・・・・・・
などなど、図形の性質や合同条件をおぼえていればいるほど、
証明問題はときやすくなる。
辛いけど、これが事実だ。
最初はおぼえられなくても大丈夫。
徐々に問題をときながらみにつけていこう!
アルファベットといえば、
A, B, C, D , E, F, G……
という順番だね。思わず歌いだすやつもいるかもしれない。
ただ、証明問題においては、
アルファベット順に英文字を並べるのはNG
なんだ。
たとえば、例題で、
赤と緑の2つの三角形について証明していくよ
っていいたいとしよう。
このとき、なにも考えずにアルファベット順に、
△ABCと△ACDにおいて
とか書いちゃダメだ。
なぜなら、
対応する頂点同士の順番になっていないから
だ。
こういうときは対応する頂点の順番で、
△ABCと△CDAにおいて
ってかいてあげよう。
先生によっては対応する順番でかかないと×ってひともいるから
きをつけてね。
証明問題でみちびいたことに「番号」をふろう!
たとえば、
AB = DC (仮定)・・・・・・(1)
といった感じで。
なぜ大事なのかというと、
結論をみちびく材料として使いやすくなるから
なんだ。
ただ単に、
以上のことより、△ABC ≡ △DACである
っていうよりも、
(1)、(2)、(3)より、△ABC ≡ △DACである
っていったほうが説得力があるからね。
番号をつけるのはタダ。無料さ。
番号のつけすぎで減点されないから大丈夫。
引用しやすいようにこまめに番号をつけよう!
証明問題の書き方にはたーくさんある。
先生によって書き方がちがう。
たぶん、誰を信じたらいいかわからなくなるはずさ。
そんな状況だからこそ、
先生流の書き方で証明問題をかいてあげよう!
ぼくが中学生のときも困惑したよ。
先生によっては、三角形の合同条件を、
ってかかないと×にするヒトもいたし。
だから、
担当の先生の書き方で証明をかいてあげること
が高得点をとる秘訣になってくる。
数学の先生の板書をしっかりとって、
テスト前に書き方をおぼえてみよう!
いや、ぜんぜん書き方がわからない!
ってときは、
証明問題の書き方の記事を参考にしてみて。
数学の証明問題はぶっちゃけむずい。
だけど、この記事で紹介した7つのコツで、
ちょっとだけラクになるはず。
やっかいな単元だけどがんばっていこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。ビタミンCがほしいね。
数学の証明を勉強していると、
仮定
とか、
結論
っていうムズい用語言葉がでてくるね。
日常生活で使わないから、
わけわからないよね??

そこで今日は、
「仮定」と「結論」という用語をわかりやすく解説していくよ。
よかったら参考にしてみてね。
〜もくじ〜
まずは仮定からみていこう。
意味を辞書(デジタル大辞泉)でしらべてみると、
1) 未定のこと、不確かなことを仮にこうと定めること。また、仮に定めた事柄。「今ここにコップがあると仮定してみよう」「仮定の上に立って物を言う」
2 ) 論理学などで、ある命題を導き出す推論の出発点におかれる前提条件。
ってかいてある。
数学の証明では2つめの意味がそれにあたるんだけど、正直よくわからないよね?。
あまりにも中学生にはむずかしすぎる・・・たぶん、大人にもむずい・・・
そこで、もう少し簡単にいってやると、
ある問題においてのみ、仮に正しいとされたこと
といえる。
えっ。これでもよくわらかないって!?
そうだな、たとえばつぎの問題があったとしよう。
例題
AB = AC である△ABCがあるとします。
この三角形が二等辺三角形であることを証明しなさい。
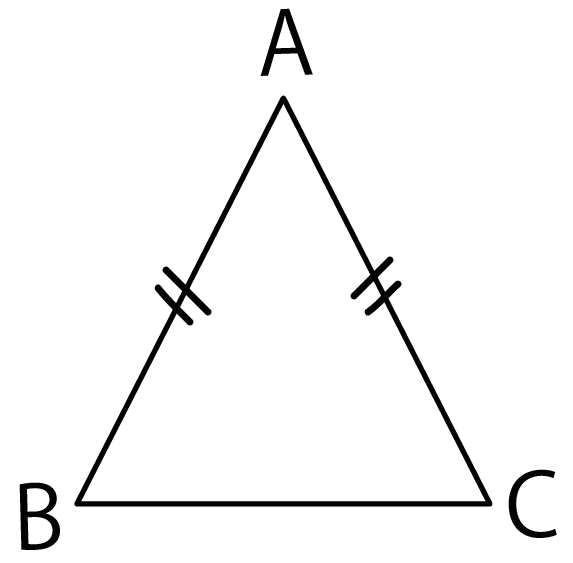
この問題のいっちゃんはじめに、
AB = AC である△ABCがあるとします。
ってかいてあるね。
じつはこの「AB = AC」はこの問題限定でいえること。
世界中に存在する△ABCのすべてが「AB = AC 」ってわけじゃあない。
AB = BCの△ABCもいるかもしれないし、
はたまた、
辺がぜんぜん等しくない△ABCもいるかもしれないね。
だから、
「AB = AC」は例題限定で正しいとしていることだから、
こいつは「仮定」なんだ。
どう?ちょっとスッキリしたかな?
結論は、
仮定をつかって正しいといえること
だよ。仮定がなければ結論をみちびけない。
たとえ、どんなに天才だとしてもね。
さっきの例題をみていみよう。
例題
AB = AC である△ABCがあるとします。
この三角形が二等辺三角形であることを証明しなさい。
この問題の仮定は、
AB = AC
だったね。
この仮定があるから、結論である「△ABCは二等辺三角形である」っていう結論がみちびけるんだ。
なぜなら、2つの辺が等しい三角形は二等辺三角形だからね。
もし、仮定がない問題だったら↓↓
例題
△ABCがあるとします。
この三角形が二等辺三角形であることを証明しなさい。
これはね、無理。無理だよ。
この問題には仮定がどこにもない。
△ABCが二等辺三角形であるって結論を導けるわけがないんだ。
「仮定」をつかってみちびける事実を「結論」という
ことをおぼえておこう。
「仮定」と「結論」は証明問題には必要不可欠なものさ。
なぜなら、証明とは、
与えられた仮定をつかって結論を論理的にみちびくこと
だからね。
「仮定」や「結論」がない証明問題はたとえるなら、
豚肉がない生姜焼きみたいなもんさ。
テスト前にもう一度復習してみてね。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。鼻呼吸したいね。
図形が合同のときってたまにあるよね。
そんなとき便利なのが、
記号をつかって合同をしめすこと
だ。
じつは、
≡
を使えば、

「2つの図形が合同である」といえるんだ。
たとえば、
図形1と図形2が合同のとき、
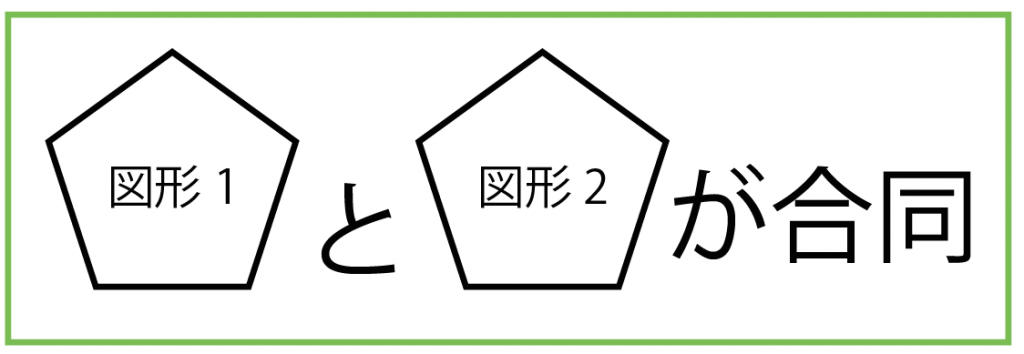
コイツらを「≡ 」でむすびつけてやる。
すると、
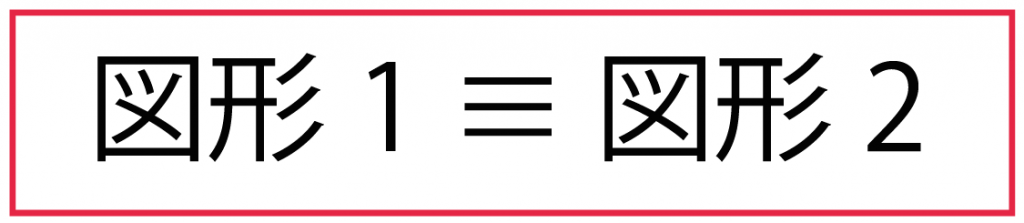
図形1 ≡ 図形2
みたいになるよ。
合同をあらわせるなんてむっちゃ便利じゃん!
すげえよ!!
・・・・・・・・
って祝いたい。
だけれども、一つだけ問題点があるんだ。
それは、
合同の記号をおぼえるのがムズいってことさ。
「合同」と「≡」っていう奇妙な記号をむずびつけられる??
答えはノー、だ。
誰もが四苦八苦するはず。
そこで今日は、
合同の記号の覚え方を2つ伝授するよ。
よかったら参考にしてみてね。
まずは王道の語呂をつかう方法だ。
チャンキーなフレーズで耳にやきつける方法さ。
合同の記号をおぼえるための語呂はずばり、
あの三兄弟はほぼ合同だ!
だよ。

えっ。
わけがわからないって??
語呂の、
あの三兄弟はほぼ合同だ!
「三」と「合同」に注目してほしいんだ。
そう、そうだよ。
これはまさに「合同」の記号は「≡」といってるようなもんだね。
「三」を「≡」におきかえてやればいいんだ。
3つ子の三兄弟をイメージできれば、
合同の記号を忘れることはないね。
2つ目はチョーマジメな覚え方だ。
なんと、合同な図形の性質をつかっておぼえていくよ。
合同な図形にはつぎの2つの性質があったね。
つまり、合同な図形たちには2つの「=」関係があるってことさ。

じつは、
この2つの「=」マークが合体すると、合同の記号「≡」みたいになるんだ。
えっ。
よくわからないって??
そうだな、ゆっくり近づけていこう。
おや、=記号のようすが?
トゥるトゥル、
トゥートゥー、
トゥートゥー、
トゥートゥー、
トゥリーン、
おめでとう! 2つの=は合体して≡になったね!
・・・・・・
って感じで、
2つの=記号をサンドイッチしたら、
≡になる
とおぼえておこう!
合同の記号の覚え方はどうだった??
困ったときは、
を思い出してみよう。
きっと「≡」の記号が頭に浮かんでくるはず。
そんじゃねー
Ken