こんにちは!この記事をかいているKenだよ。汗かきたいね。
一次関数の変域の求め方の基礎はわかった。
だけど、ときどき、
変域の応用問題ってでてくるよね。
たとえば、つぎのような問題さ。
y=-2x+bのxの変域がc≦x≦4のとき、yの変域が-5≦y≦5である。bとcを求めなさい。
いっけん楽勝にみえる。
だけどじつは、うっかりミスを誘うトラップ問題なんだ。
今日はこの変域の問題の解き方を3ステップで解説していくよ。
よかったら参考にしてみてね。
例題をいっしょにといていこう。
y=-2x+bのxの変域がc≦x≦4のとき、yの変域が-5≦y≦5である。bとcを求めなさい。
この手の問題はつぎの3ステップでとけちゃうよ。
まずは問題で登場する、
一次関数の傾きの符号をチェックしよう!
傾きが+なのか??
それとも、とんでもなくマイナスなのか??
さらっと調べてみよう。
例題の関数の、
y = -2x + b
に注目してみて。
こいつの傾きは「-2」。
あきらかにマイナスがついちゃってるよね??
ってことで、例題の傾きは負の数だ。
つぎは、
xが大きくなるとyはどうなるか??
を考えてみよう。
もし、一次関数の傾きが+のとき、
xが大きければ大きいほどyも大きいね?
だから、xが最大値になるとき、yも最大値になるってわけ。
逆に、傾きが -のとき、
xが大きければ大きいほどyは小さくなっちゃう。
だから、xが最大値のときはyは最小値になるわけさ。
つまり、これをまとめるとつぎのようになる↓↓
例題をみてみよう。
一次関数の傾きは「マイナス」だったよね??
xとyの変域から最小値・最大値をだしてみると、
になってるね。
んで、一次関数の傾きがマイナスだから、
になるんだ!
つまり、
y = -2x + b は、
の2点を通るんだ。
こんな感じで、
xとyの組み合わせをみつけるのが第2ステップだよ。
最後は、2つの座標を式に代入してみよう。
例題の直線は、
の2点を通るはずだったね??
こいつを直線の式、
y = -2x + b
さっそく、y = -2x + bに(4, -5)を代入すると、
y = -2x + b
-5 = -2 × 4 + b
b = 3
になるね。
つぎは、bの値がわかった一次関数の、
y = -2x + 3
に(c, 5)を代入してcを求めてみよう。
すると、
y = – 2x + 3
5 = – 2c + 3
c = -1
になるよ。
これで文字の正体がわかったね。
おめでとう。
一次関数の変域の問題はよく、
グラフをかけば解ける
っていわれる。
だけどね、ぶっちゃけグラフなんていらん。
傾きの符号をみて、xとyの組み合わせを考えればいいんだ。
応用問題におそれず挑んでいこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。換気は大事だね。
一次関数の変域の問題ってよくでるよね。
たとえば、つぎのような問題さ。
例題
1次関数y = -3x+7について、xの変域が -1 ≦ x ≦ 9のとき、yの変域を求めなさい。
一次関数の変域とかあきらかにむずそうだけど、
基本をおさえればチョー簡単なんだ。
今日はこのタイプの問題を攻略するためにも、
一次関数の変域の求め方がわかる3ステップ
を紹介するよ。
よかったら参考にしてみて。
3ステップで変域を求められるよ。
例題をいっしょにといてみよう!
1次関数y = -3x+7について、xの変域が -1 ≦ x ≦ 9のとき、yの変域を求めなさい。
まず、変域の端と端を代入してやろう。
たとえば、xの変域が○ ≦ x ≦ □だとしたら、
を一次関数に代入すればいいんだ。
例題でわかっているのはxの変域の、
-1 ≦ x ≦ 9
だね。
この変域の端っこの、
を一次関数 y = -3x + 7 に代入すればいいんだ。
x = -1 を代入すると、
y = -3x + 7
= -3 × (-1) + 7
= 10
になる。
一方、x = 9を代入してやると、
y = -3x + 7
=-3 × 9 + 7
= – 20
になるね。
これが第1ステップ!
さっき計算した2つの値のどちらが大きいのか??
を比べてみよう。
そして、
大きい値を右に、小さい値を左にかくんだ。
例題では、
の2つをゲットできたね??
こいつらを比べてみると、
明らかに10のほうがでかい。
-20のほうが小さいね。
だから、10を右に、-20を左にかいてみて。
これが第2ステップ!
最後は不等号で結んでみよう。
使う不等号は、
問題でわかってる変域と同じものを使うよ。
例題でいうと、xの変域は「≦」を使ってるよね??
だからyの変域も「≦」を採用するのさ。
例題をみてみよう。
「大きい値」と「小さい値」の間に「y」をかく。
そして、
「小さい値」・「大きい値」と「y」を「≦」で結んでやるのさ。
-20≦y≦10
これでyの変域が求まったよ。
おめでとう。
でもさ、なんで変域が求められるんだろう??
話がうますぎるよね。
じつは、ここだけの話なんだけど、
一次関数がまっすぐだからなんだ。
xの変域の端っこと端っこのy座標が、
yの変域の端っこと端っこになっているよ。
これは傾きがマイナスでも同じだね。
もし、一次関数が波だっていたり、
ギザギザしていたら変域はこのやり方だと無理。
なぜなら、変域の端っこ以外に、
最大値とか最小値がいるかもしれないからね。
一次関数がまっすぐだからこそ、変域の端っこが最大値・最小値になる
ってことを覚えておこう!
一次関数の変域の求め方は簡単。
の3ステップでいいんだ。
問題をといて変域に慣れていこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。鼻呼吸は大事だね。
中学数学でよく、
歯車の問題
ってでてくるね。もっとぶっちゃけいうと、
比例・反比例の利用
の問題でよくねらわれるんだ。
なぜだかしらんけど、よく歯車が登場するよ。
たとえば、つぎのような問題だ。
歯数がそれぞれ72、26の歯車A、Bがかみ合っている。歯車Aがx回転する間に歯車Bはy回転する。
yをxの式であらわし、比例しているか、反比例しているか答えなさい。
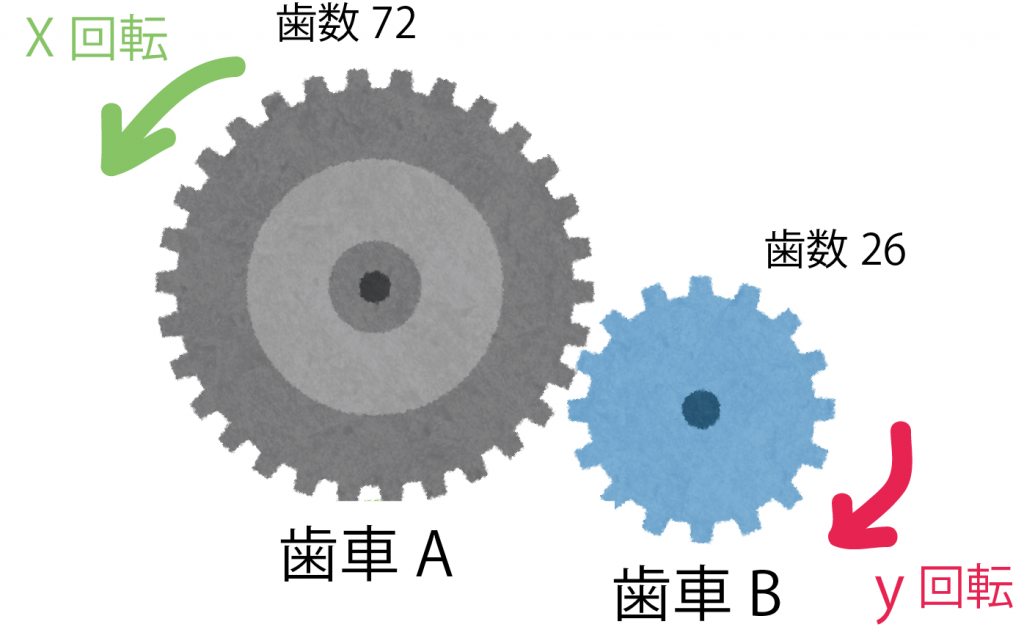
今日はこんな歯車問題にとまどわないためにも、
数学の歯車問題の解き方を4ステップで解説していくよ。
よかったら参考にしてみてね。
つぎの4ステップでとけちゃうよ。
例題をいっしょにといてみよう!
歯数がそれぞれ72、26の歯車A、Bがかみ合っている。歯車Aがx回転する間に歯車Bはy回転する。
yをxの式であらわし、比例しているか、反比例しているか答えなさい。

まず歯車の、
動いた歯数
を計算してみよう!
動いた歯数は、
(歯車についてる歯数)×(回転数)
で計算できるよ。
例題の歯車A・Bをみてみよう。
歯車Aは、
だったね??
ってことは、歯車Aの「動いた歯数」は、
動いた歯数(歯車A)
= (歯数)×(回転数)
= 72 x
になるね。
同じように、歯車Bの場合を考えてみて。
歯車Bは、
だ。よって、
動いた歯数(歯車B)
= 歯数×回転数
= 26y
になる。
これで第1ステップ終了さ!
つぎは方程式をつくってみよう!
かみ合っている歯車同士は、
動いた歯数が等しい
っていう性質があるんだ。この性質で方程式をつくってみよう。
例題をみてみると、
歯車A、Bがかみ合っている
ってあるね。
つまり、
歯車A・Bの動いた歯数が等しい
ってことなんだ。
※詳しくは「数学の歯車問題の基礎」を読んでみてね。
だから、
(歯車Aの動いた歯数)=(歯車Bの動いた歯数)
っていう方程式がつくれるよ。
実際につくってみると、
26x = 72y
になるね。

これが第2ステップ!
方程式をyについて解いてみよう。
えっ。
「yについて解く」の意味がわからんだって??!
そうだね。
yを左に持ってきて、xを右にどかして、yを裸にすればいいんだ。
例題でつくった方程式の、
72x = 26y
に注目してみよう。
yについて解いてみると、
72x = 26y
y = 72÷26 x
y = 13分の36x
になるね。
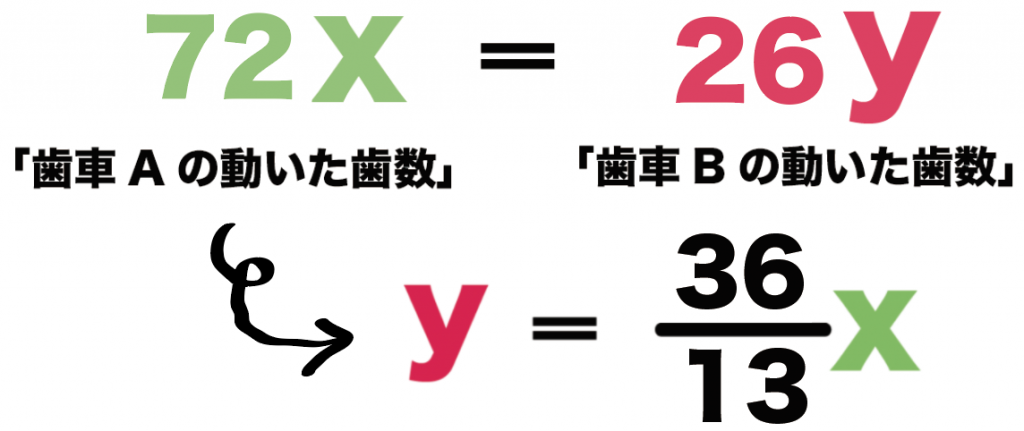
yをxの式であらわせたね。
あとすこし!
最後に、xの位置を確認しよう。
xが、
分子にあるか、
それとも、
分母にあるか
で比例か反比例かが決まってくるんだ。
っていう感じになるよ。

例題の式では、
xが分子の位置にあるよね??

ってことは、
この方程式は「比例」ってことになる。
どう?? 納得したかな??
数学で歯車の問題がでちゃった???
むずそうだって??
いや、そんなことない。
と
4ステップで攻略さ。
ガンガン歯車問題をといていこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。
一次関数の利用の問題ってムズい。
中でも、
動点の問題
が一番ヤッカイなんだ。たとえば、つぎのような問題だね。
タテの長さが4cm、横の長さが5cmの長方形ABCDの周上を、点Pは毎秒1cmの速さで、AからB、Cを通ってDまで移動します。
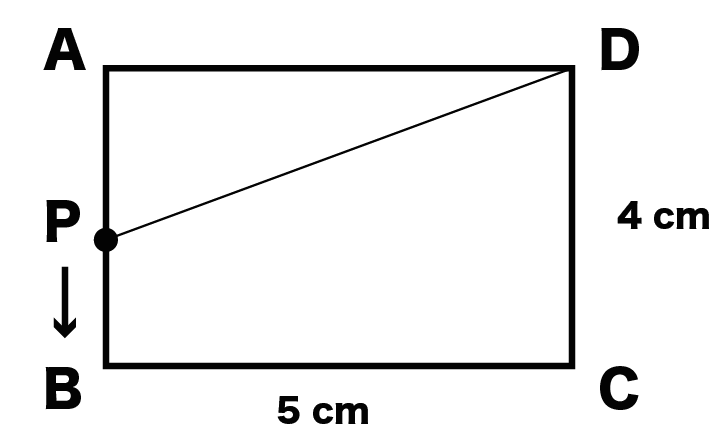
PがAを出発してからx秒後の△APDの面積をy cm²とするとき、yはxの変化にともなってどう変化するのか説明しなさい。
今日はこの動点の問題をわかりやすく解説していくよ。
よかったら参考にしてみてね。
問題のポイントは、
三角形の高さだけが変化していること
だ。
逆に、底辺はどんなに時が経っても動かない。
高さの変化をトラッキングすれば面積が計算できそうだね。
例題でいうと、
△APDの底辺ADは固定だね?
だって、AとDは動かないからさ。
Pの移動によって高さだけ変わっていくんだ。
しかも、高さの変化は点が辺を移動するたびに変わっていくよ。
例題でいうと、動点Pが、
にそれぞれあるときの3パターンだね。
今日はこの3つのフェーズごとに解説していくよ。
PがAB上を動いている場合だ。
このとき、△APDの高さは、
APの長さ
だよね??
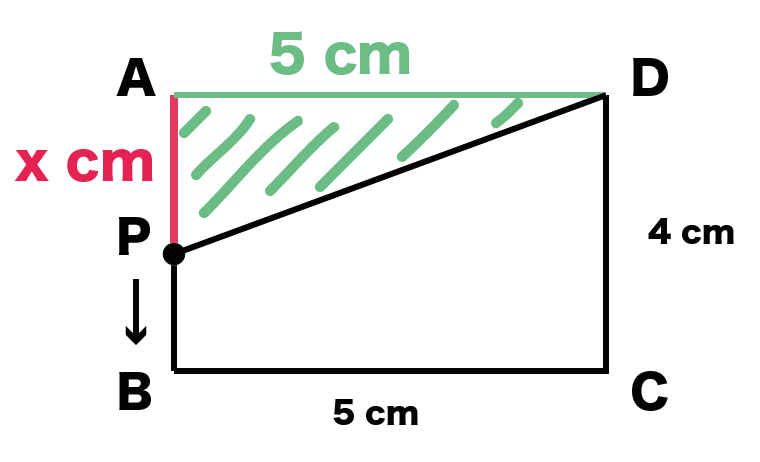
Pは1秒間にx cm動く。
APの長さはx秒後に「x cm」になっているはずだ。
よって、動点Pが辺AB上にあるとき(0 ≦ x ≦4)のとき、
△APDの面積は、
△APD = 底辺 × 高さ × 1/2
= 5 × x × 1/2
= 5/2 x
になるね。
ここまでの△APDの面積yの変化をグラフにしてみると、
こんな感じになる ↓↓
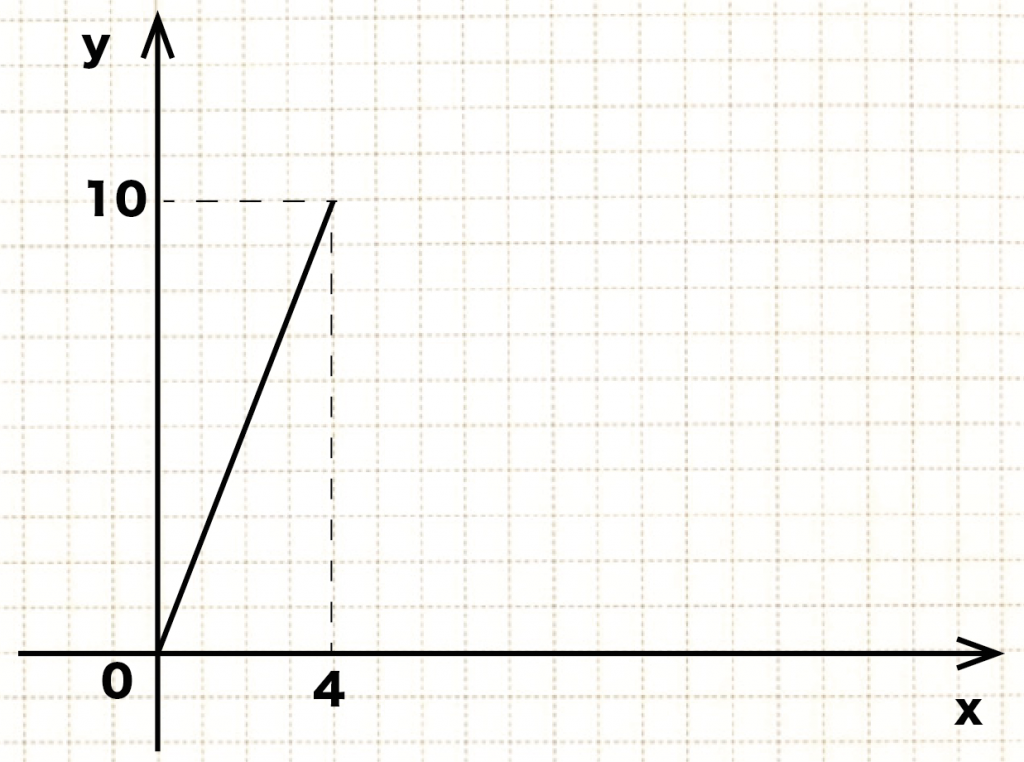
つぎは点Pが辺BCにたどり着いたケース。
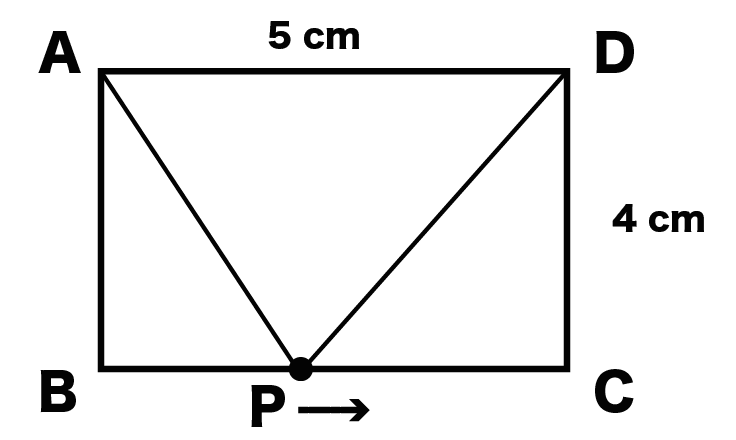
まだまだ動点Pの旅は続くんだ。辛いね。
PがBC上にあるときの△APDの高さって、
点Pから辺ADにおろした垂線になるよね?
垂線とADの交点をHとすればPHが高さってことだ。
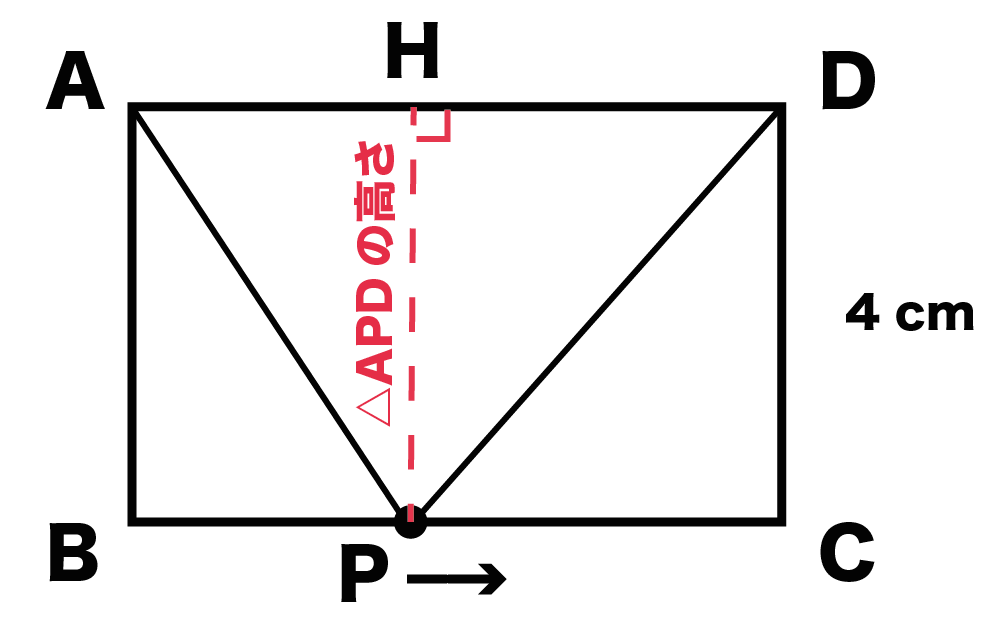
じつはこの高さって、
動点Pが左らへんにいても、
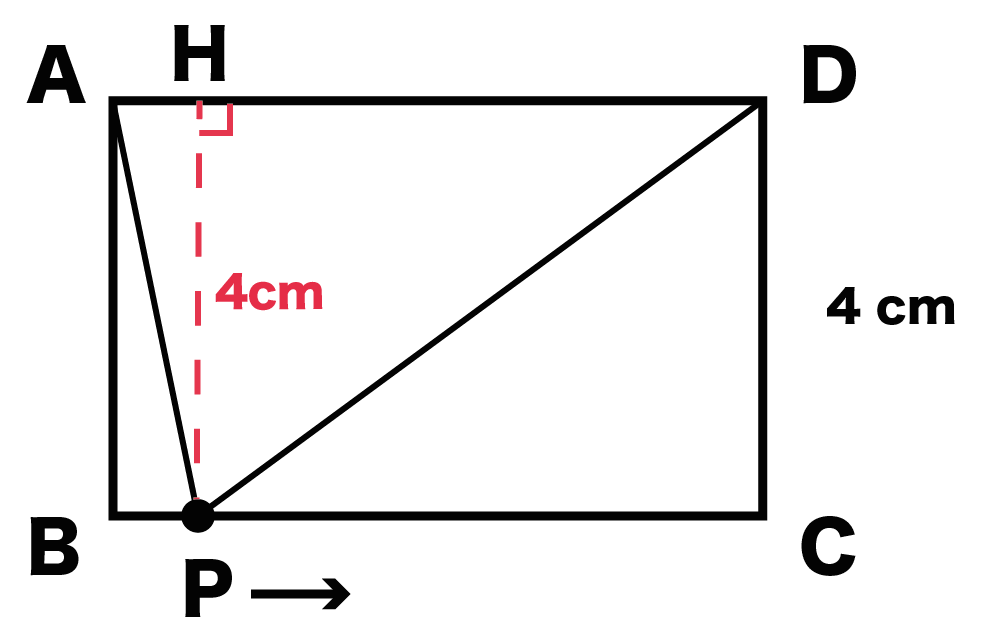
真ん中らへんにいても、
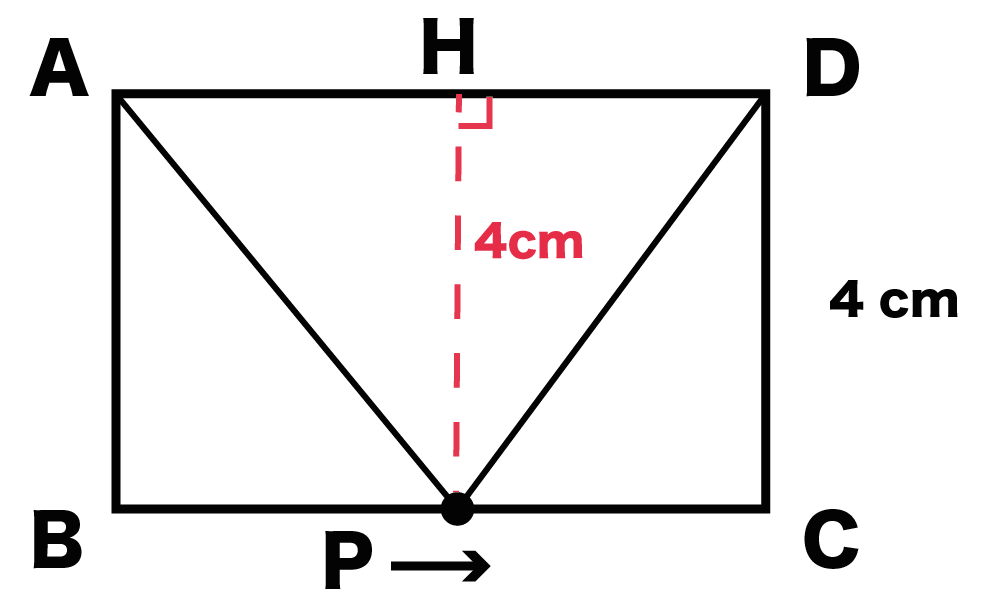
右のほうにいても、
変わらないんだ!
ぜんぶ辺AB・DCと同じ長さ(4cm)になるはず。
よって、動点Pが辺BC上にあるとき(4 ≦ x ≦ 9)、
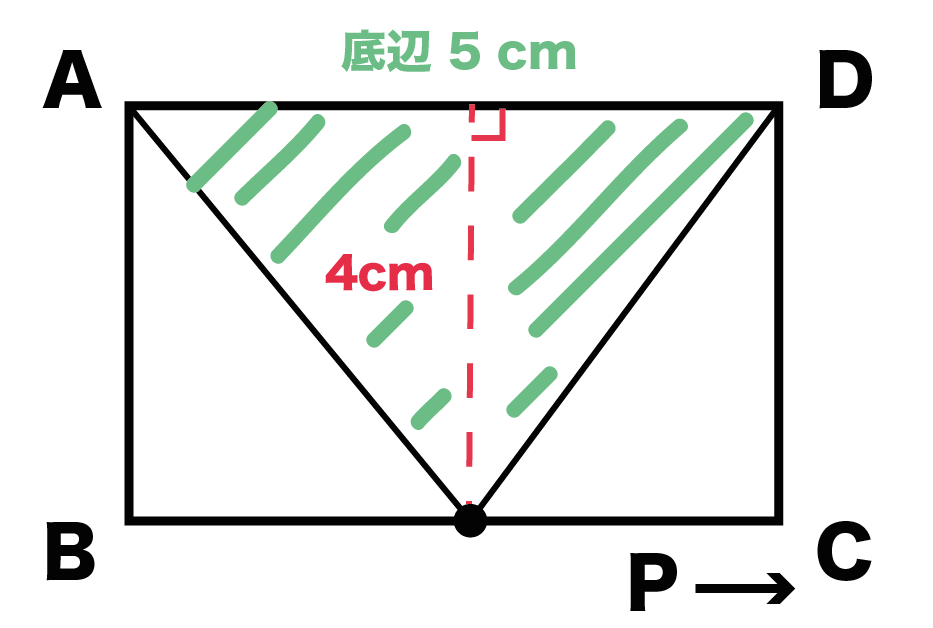
△APD の面積 = 底辺AD × 高さ × 1/2
= 5 × 4 × 1/2
= 10[cm²]
になるね。
つまり、動点PがBC上にあるとき、
△APDの面積はつねに一定というわけさ。
変数xがはいっていないからね。
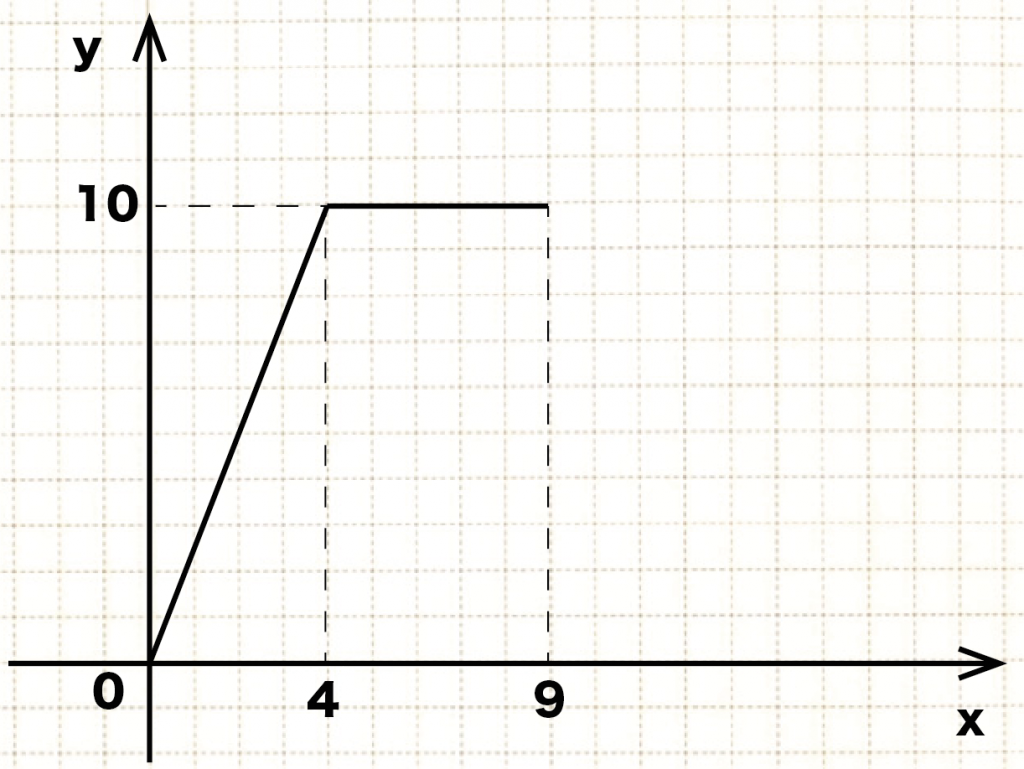
ここまで△APDの面積の変化をグラフにあらわすと、
こうなるね↓↓
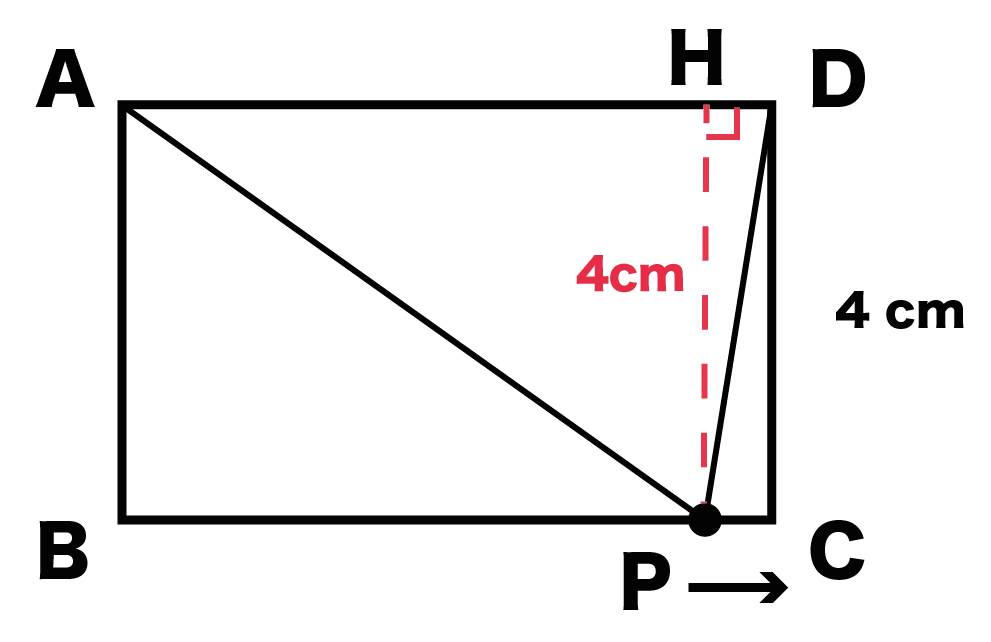
いよいよ最後のフェーズ。
Pが辺CDにさしかかった場合さ。
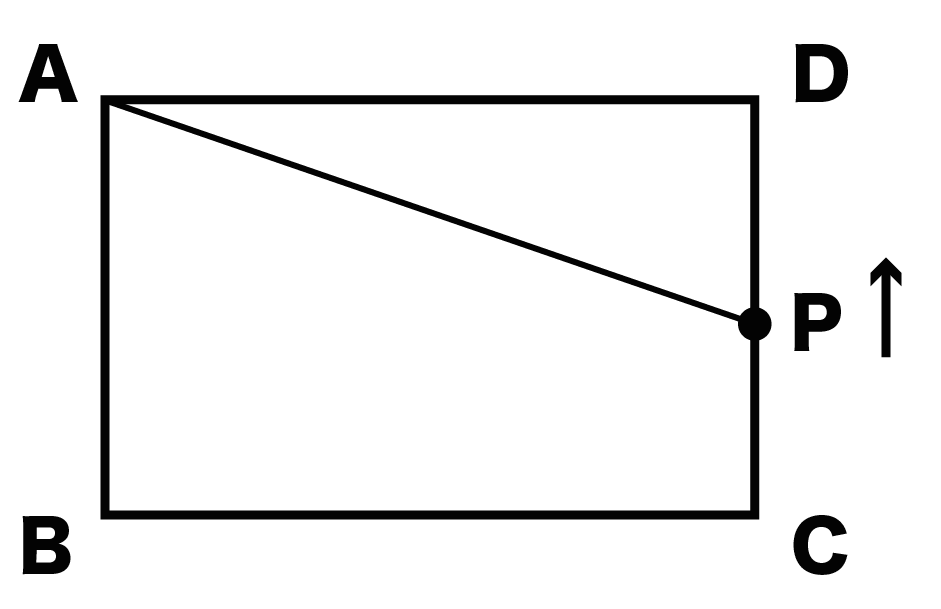
このときの△APDの高さって、
線分DPだよね?
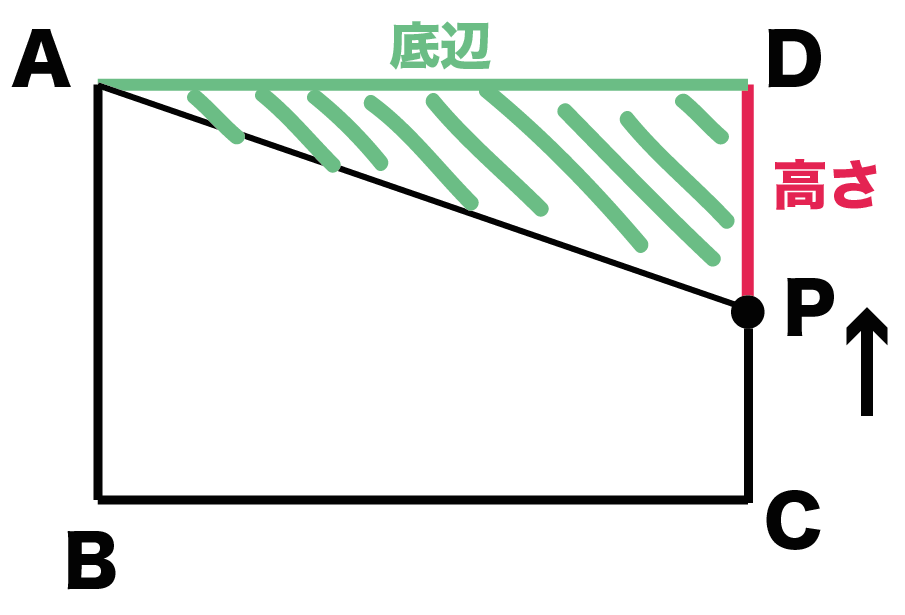
x秒後のDPの長さをだしてやれば、
△APDの面積yを式であらわせるってこさ。
このときの高さDPは、
「3つの辺(AB・BC・CD)」 – 「 Pが動いた距離」
で計算できるよ。
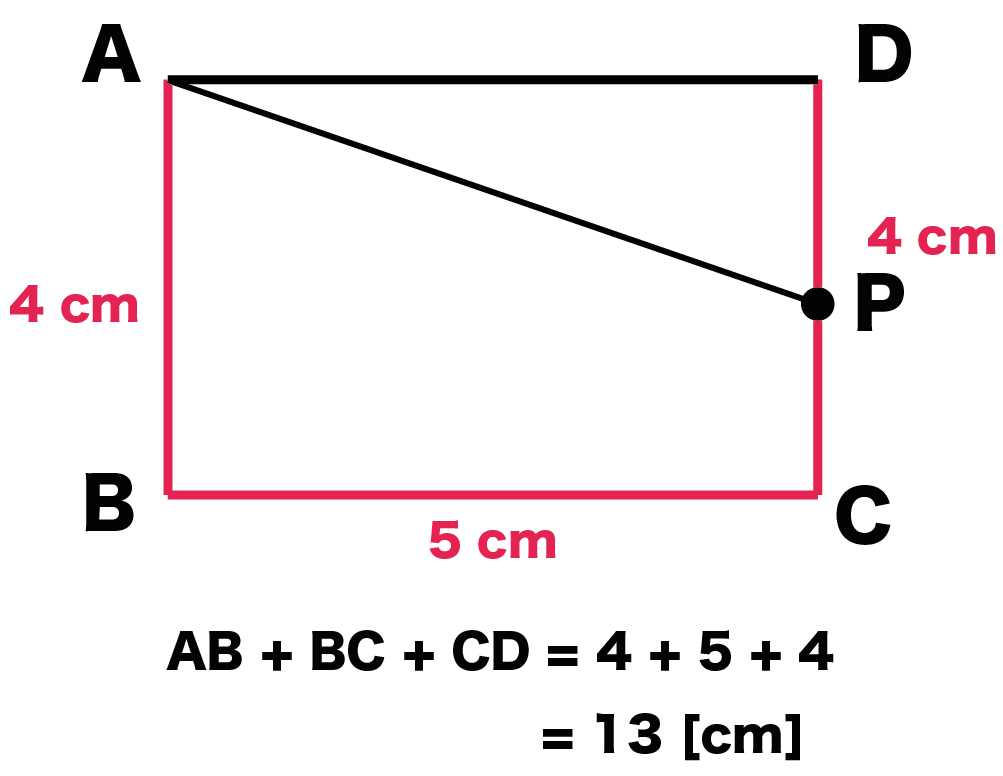
(3つの辺の長さ)= 4 + 5 + 4
= 13 [cm]
になる。
そんで、x秒後に「Pが動いた距離」は、
x [cm]
だね。
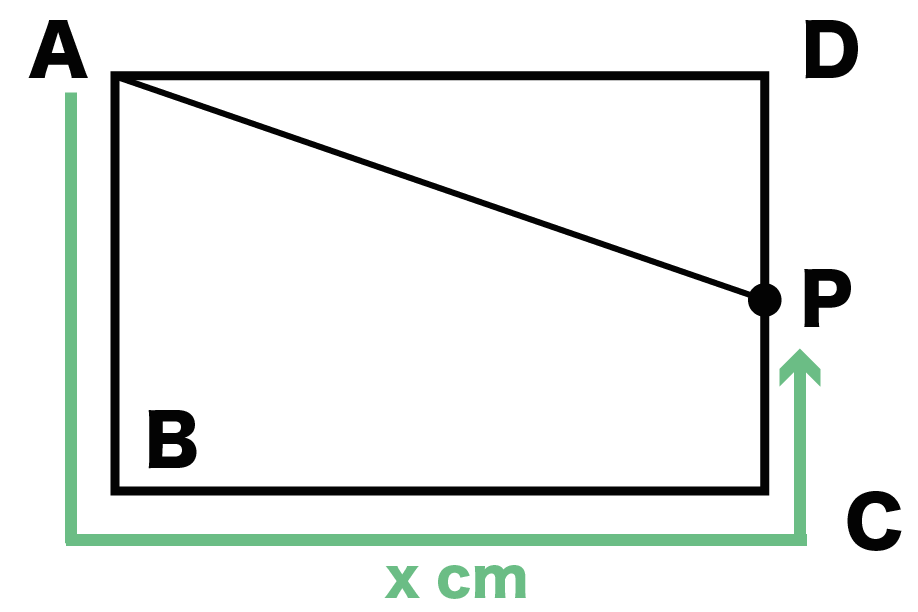
ってことで、
DPの長さは(3つの辺の長さ)- (Pが動いた距離)で求めることができるので、
13 – x
になるね。
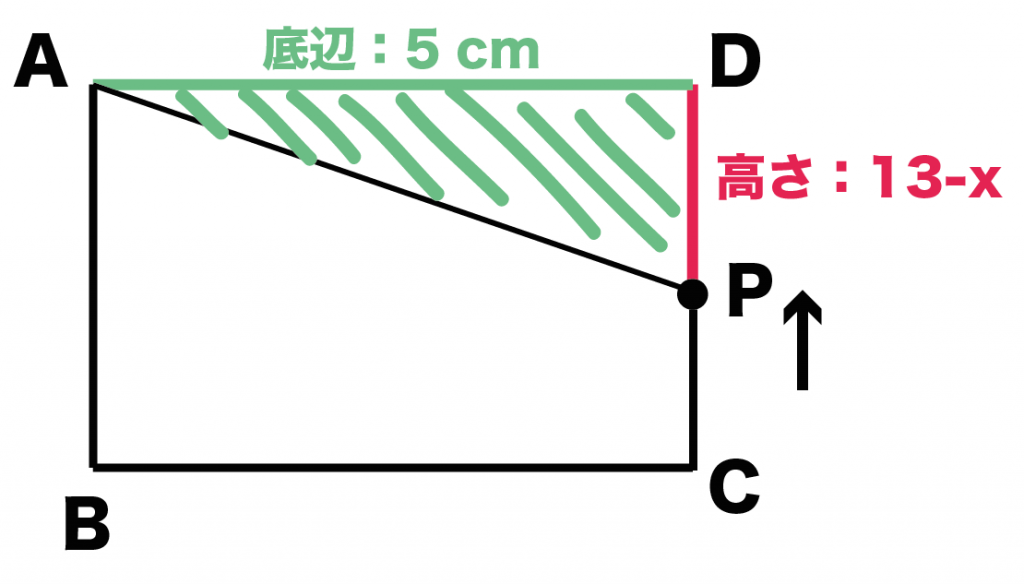
よって、Pが辺CD上を動くとき(9 ≦ x ≦ 13)、
△APDの面積 = 底辺AD × 高さDP × 1/2
= 5 × (13-x) × 1/2
= 5/2 (13-x)
となる。
よって、こいつをグラフに表してやると、
こうなるね↓↓
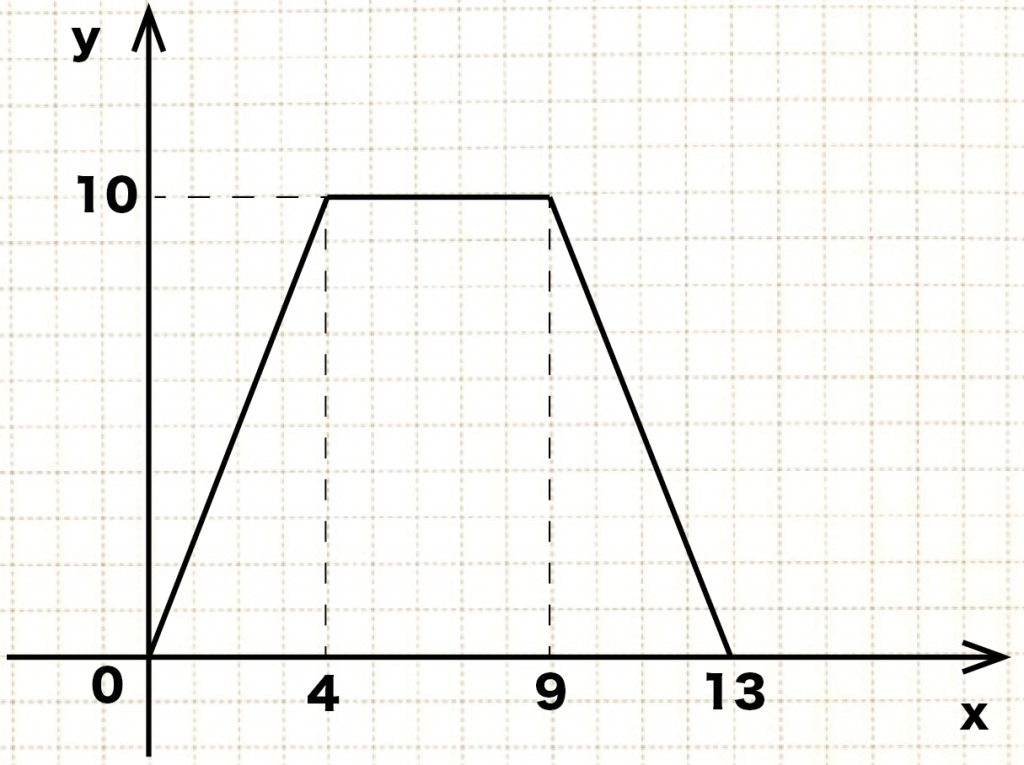
△APDの面積yをxであらわすことができて、
それをグラフにすれば完ぺきだ!
テストに出やすい問題だからしっかりおさえておこう。
動点の問題はどうだった?
フェーズごとに面積の変化が異なる
ってことさえ押さえておけば十分さ。
あとは、
どの辺が底辺・高さになっているのか??
ということに注意してみてね。
そんじゃねー
Ken
「一次関数の利用」はぶっちゃけ難しい。
だって、一次関数の応用問題だからね。
文章問題ばっかりだから、苦手意識もってるヤツも多いね。

今日は1次関数の利用の問題の解き方のコツを3つにしぼって
紹介するよ。よかったら参考にしてみてね。
一次関数の利用の問題でもっとも重要なのは、
どの値を「x」 「y」とおくか??
だ。これさえ間違えなければ、ぶっちゃけどうにかなる。
ってことで、
一次関数の利用での文字の置き方のコツ
というものをみていこう。
1つ目は、問題文の中に、
何をx・yと置いたらいいのか??
がかいてあるパターンだ。
こういうときは、
でてきた値をそのままx・yとおいてあげよう。
たとえば、つぎのような問題だね。
最近、クラスのマドンナに告白したらふられてしまったA君。

ふと、北に向かいたくなったので実家の自転車でひたすらこぎつづけました。
A君の自転車はロードバイク。
平均で分速400 mのスピードがでていました。A君がすすんだ距離をy m、自転車をこぎつづけた時間をx分とします。yはxの変化にともなってどう変化するでしょうか??
この手の問題はチョー簡単。
問題文の通りにy とxの値をあててやればいいんだ。
とすると、
y = 400x
みたいになるね。
流れに逆らわずに、そのまま文字でおいてあげよう。
2つ目のパターンは「時間によって値が変化する問題」だ。
こういう問題では、
とおいてやればいいんだ。
たとえばつぎのような問題だね。
疲れきったA君はマンガ喫茶にいきました。

基本料金が「500円」で、追加料金が10分ごとに180円かかります。
A君のおこづかい1000円で最大までいれる時間をしらべなさい。
この問題では、
A君がマンガ喫茶に支払う金額
が時間によって変化しているね。
長く引きこもるほど金がたくさん必要なわけさ。
よって、この問題では、
をxとyでおいてみよう。
仮に、1分1秒ごとに追加料金が加算されるとすると、
y = 180・x/ 10 + 500
= 18x + 500
こうなるね。
ちなみに、
y(料金)に1000円を代入してみると、
1000 = 18x + 500
18x = 500
x = 27.8
になるね。つまり、27分以上マンガを読み続けると1000円をオーバーしちゃうわけだ。
ちなみに、この漫画喫茶の料金体系は10分ごとに追加料金が発生するようになってるから、答えは最大で20分だね。
A君、ちょっとしか読めないね・・・
○○が◇◇の一次関数になる
ってかいてある問題もある。
こういうときは、
とおいて一次関数をつくってあげればいいんだ。
たとえば、つぎのような問題だね。
疲れきったA君は家にかえってカレーをつくることにしました。

母ちゃんに相談したところ、3人前のカレーをつくるには1700円、5人前のカレーをつくるには3500円かかると言われました。
カレーにかかる代金は、カレーを食べる人数の一次関数になっています。
このとき、8人前のカレーの料金を求めなさい。
この問題では、
カレーにかかる代金は、カレーを食べる人数の一次関数になっています。
ってかいてあるね。
だから、
とおいてみよう。
1次関数になるはずだからy = ax + bのカタチになるね。
この式に、
を代入してみよう。
すると、
1700 = 3a + b
3500 = 5a + b
っていう連立方程式ができるでしょ?
こいつを加減法でといてやると、
-1800 = -2a
a = 900
になる。aの値を元の式に代入すると、b = -1000がえられるね。
つまり、
このカレー1次関数は、
y = 900x – 1000
になるんだ。
8人前のカレーを食べる場合はxに8を代入すればいいから、
y = 7200 -1000
= 6200
になるね。
つまり、8人前のカレーは6200円でくえるってわけさ!
一次関数の利用はぶっちゃけむずい。
だけど、どんな問題にもヒントが隠れているんだ。
の3つのパターンを意識していれば問題ないよ。
あとは問題をときまくって慣れてみてね。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。うどん食い過ぎたね。
一次関数の問題に、
2直線の交点の座標を求める問題
ってやつがある。
たとえば、つぎのようなヤツね↓↓
直線 y = -x -3と y = -3x + 5の交点の座標を求めなさい。
このタイプの問題はゼッタイ期末テストにでる。
うん、ぼくが先生だったら出したいね。うん。
今日はこの問題をさくっととけるように、
二直線の交点の求め方を解説していくよ。
まずは基本をおさらいしよう。
連立方程式とグラフの記事で、
方程式をグラフにすると、
「2直線の交点」が「連立方程式の解」になっている
って勉強したよね?
今回はこれを逆手にとって、
「連立方程式の解」を計算して「交点の座標」を求める
ということをするよ。
例題をときながら勉強していこう。
直線 y = -x -3と y = -3x + 5の交点の座標を求めなさい。
つぎの3ステップでとけちゃうよ。
2直線で連立方程式をたてよう。
「方程式の解」が「交点の座標」になるはず!
例題の直線は「y = -x -3」と「y = -3x + 5」だったね。
こいつらを連立方程式にしてやると、
y = -x -3
y = -3x + 5
になるでしょ?
2つの一次関数をタテに並べてみてね。
1つの文字の方程式にすれば、
一次方程式の解き方で計算するだけでいいんだ。
例題では連立方程式の左辺が「y」で2つとも同じだね。
だから、
代入法をつかったほうが早そう。
上の式にyを代入してやると、
-x – 3 = -3x + 5
2x = 8
x = 4
になる。
これでxの解が求まったわけだ。
最後に「解」を「直線の式」に代入してみよう。
例題でいうと、
ゲットした「x = 4」を、
y = -x -3
y = -3x + 5
のどっちかに代入すればいいんだ。
とりあえず、xの係数が1の「y = -x -3」に「x = 4」を代入してみよう。
すると、
y = -x -3
y = -4 -3
y = -7
になる。
2直線の連立方程式の解は「直線の交点の座標」だったね?

ってことは、
この2直線の交点の座標は、
(x, y )= (4, -7)
になるってことさ。
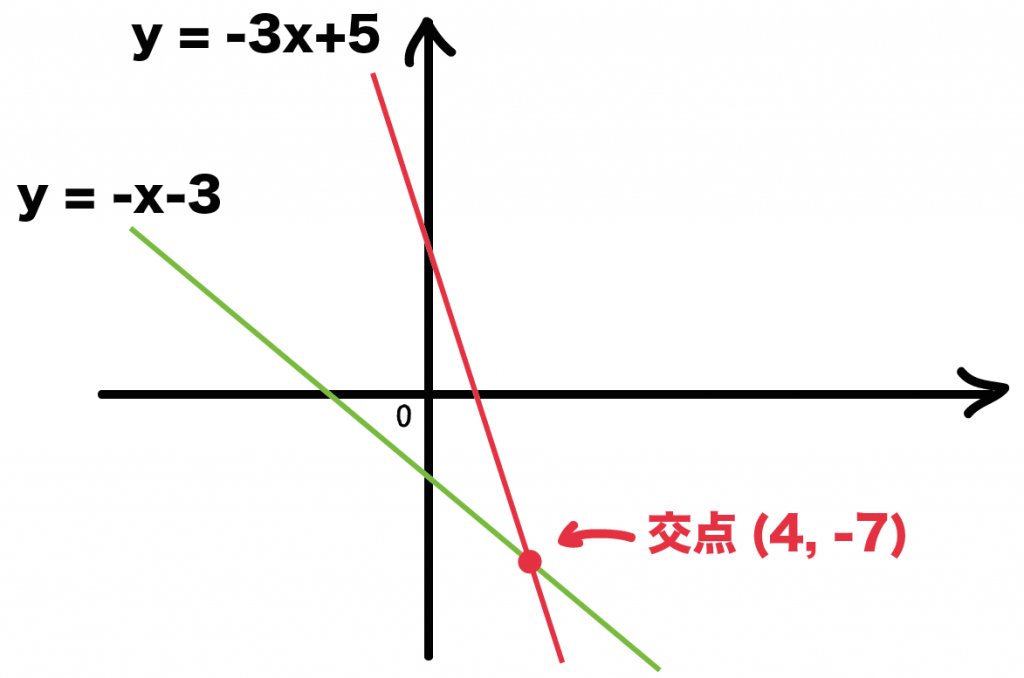
おめでとう!
これで二直線の交点の求め方をマスターしたね。
2直線の交点・・・? しらねえよ・・・・
ってなったとき。
連立方程式をたてて、それを解けばいいんだ。
そのxとyが交点の座標になるよ。
連立方程式の解き方を忘れたときはよーく復習してみてね!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。10円玉たまってるね。
「方程式」を「一次関数のグラフ」にする。
これが案外、むずかしい。
方程式なんか一次関数にみえないもん。
グラフをかくのもめんどくさそうだね。

そこで今日は、
「二元一次方程式」を「1次関数のグラフ」にする方法を2つ紹介するね。
よかったら参考にしてみて。
二元一次方程式って、
文字が2つある1次方程式
のことだよね。
この二元一次方程式をグラフにしてよ?
みたいな問題がちょくちょくでてくるんだ。
たとえば、つぎのような例題みたいにね↓↓
(1)3x + y = 7
(2)2x + 3y = 6
つぎの2つの書き方で攻略していこう!
1つ目の書き方は、
yについて等式を変形しちゃう方法だ。
等式の変形をつかって、
○○x + △y = ××
を、
y = ○○x + ××
に変形してやればいいのさ。
これは一次関数のカタチと一緒だね。
だから、一次関数のグラフの書き方をつかえばいいんだ。
この書き方は、
yの係数が「1」のときに使うのが便利だよ。
だって、xを移項するだけでいいからね。
例題でいうと、(1)の二元一次方程式だね。
3x + y = 7
をyについてといてやると、
y = -3x + 7
になる。
こいつは、傾き「3」、切片「7」の一次関数と同じ。
あとは一次関数のグラフの書き方通りにかくと、
こうなるね↓↓
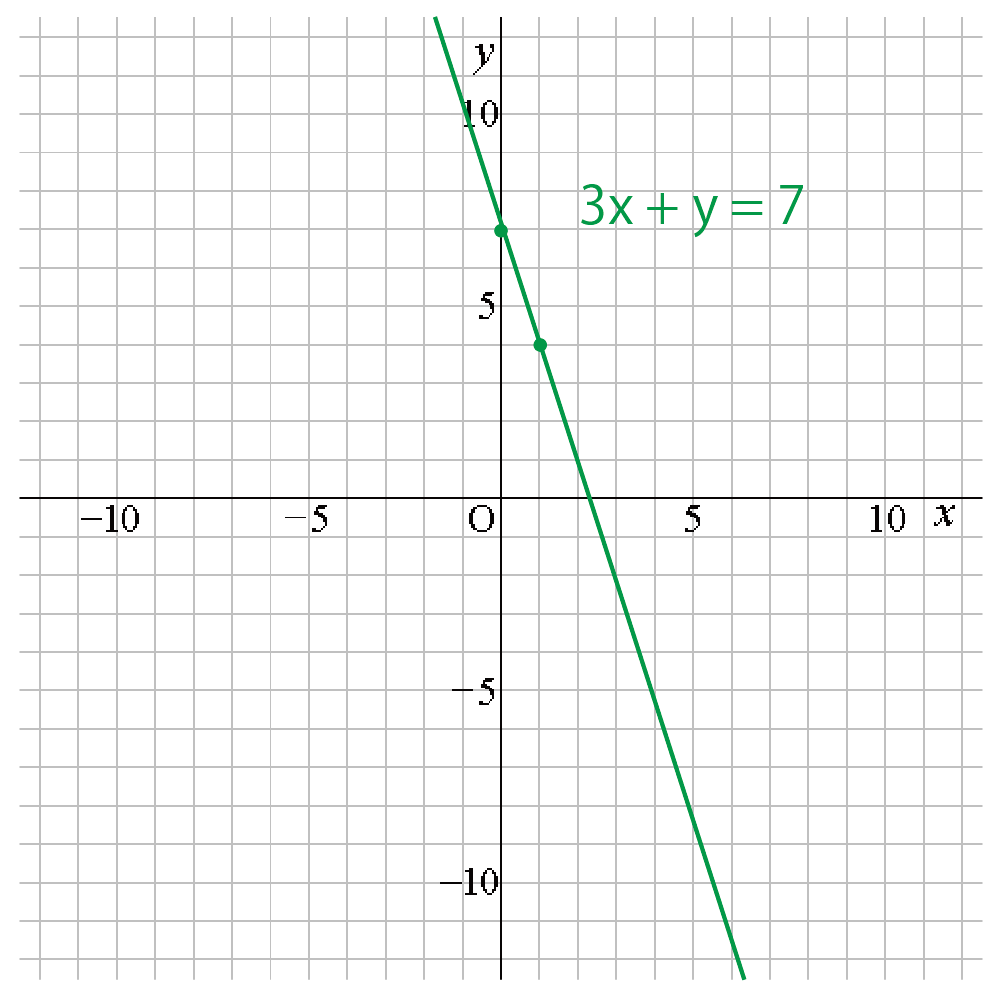
等式の変形ができればこっちのもんさ!
x・y軸との交点を求める方法だ。
方程式に、
を代入して、x・y軸との交点をさがせばいいんだ。
この書き方は、
yの係数が1より大きいときに便利だよ。
たとえば、例題の(2)の一次関数だね。
(2)2x + 3y = 6
x・y軸との交点をさがすために、
をそれぞれ代入してみよう。
x = 0のとき、
3y = 6
y = 2
になる。つまり、y軸との交点は(0, 2)ってわけさ。
また、y = 0のときは、
2x = 6
x = 3
になる。つまり、x軸との交点は(3, 0)ってわけだね。
2つの交点をむすぶとグラフがかけるよ。
こんな感じでね ↓↓
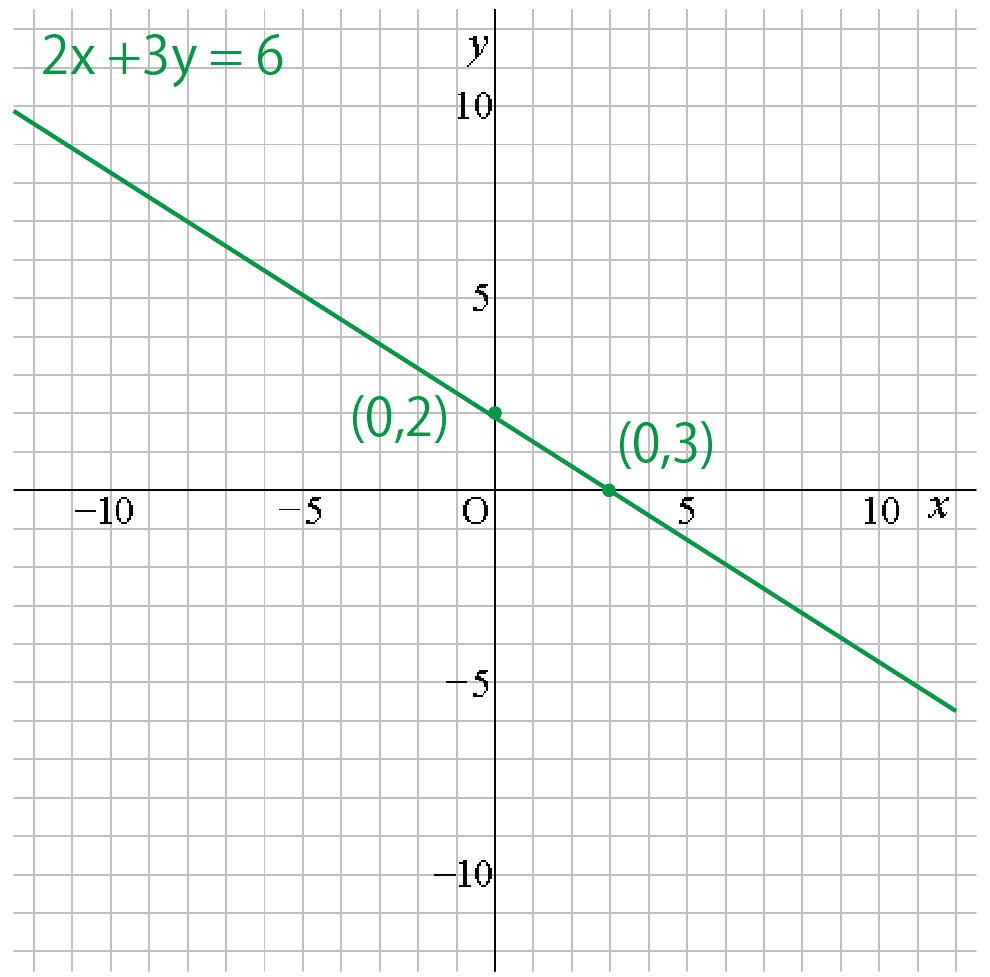
コツは、
yの係数によって書き方をかえる
ことだ。
たまにでてくる問題だからマスターしておこうね。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。洗濯物ためすぎたね。
一次関数の式を求める問題
ってけっこうあるよね。下手したら、3問に1問ぐらいは出るかもしれない。
テスト前におさえておきたい問題だね。

今日はこの「直線の式を求める問題」をわかりやすく解説していくよ。
よかったら参考にしてみてね^-^
まず、直線の式が計算できるケースを確認しよう。
つぎの4つの要素のうち、2つの値がわかっているときに式が求められるんだ。
たとえば、傾きと切片がわかっているとき、とか、座標と切片がわかっているとき、みたいな感じだね。

求め方のパターンをみていこう!
まずは一次関数の「傾き」と「切片」の値がわかっている場合だ。
たとえば、つぎのような問題だね。
例題
yはxの一次関数で、そのグフラの傾きは-5、切片は7であるとき、この一次関数の式を求めなさい。
このタイプの問題はチョー簡単。
一次関数の式「y = ax + b」に傾き「a」と切片「b」の値を代入するだけだよ。
例題での「傾き」と「切片」は、
だね。
だから、一次関数の直線の式は、
y = -5x + 7
になる。
代入すればいいだけだから簡単だね。
つぎは「傾き」と「座標」がわかっている場合だ。
たとえばつぎのような問題だね。
例題
yはxの一次関数で、そのグラフが点(2, 10)を通り、傾き3の直線であるとき、この一次関数の式を求めなさい。
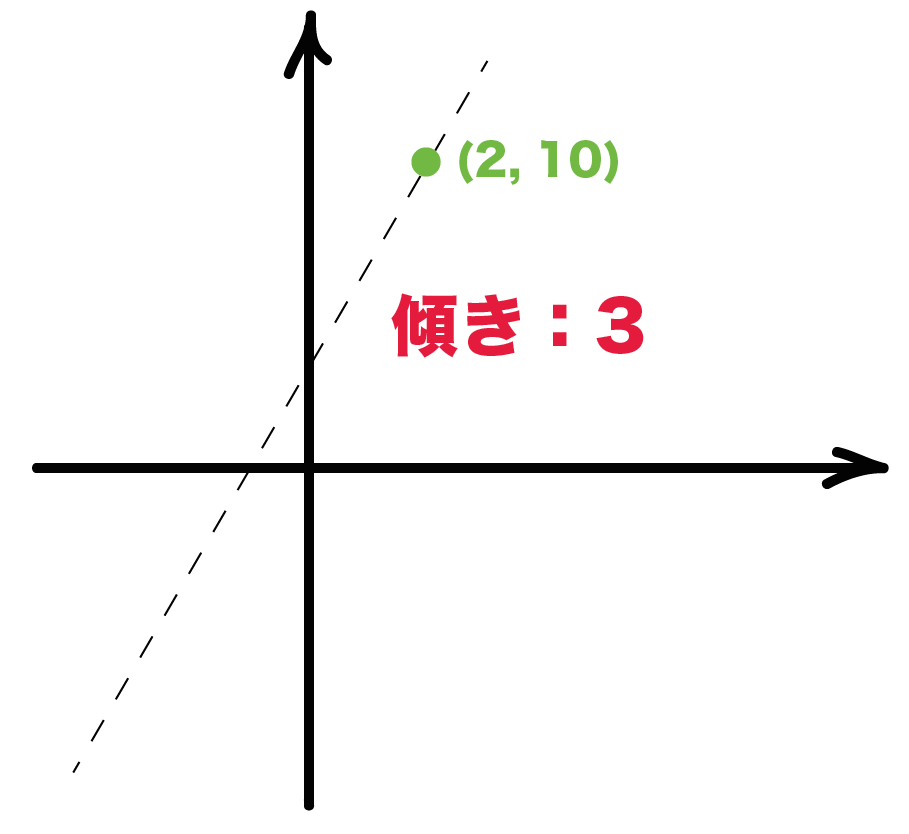
この手の問題も同じだよ。
一次関数の式「y = ax + b」に傾きaと、座標を代入してやればいいんだ。
bの方程式ができるから、そいつを根性でとくだけさ。
例題では、
っていう一次関数だったよね??
まずはaに傾き「3」を代入してみると、
y = 3x +b
になるでしょ? そんで、こいつにx座標「2」とy座標「10」をいれてやればいいのさ。
すると、
10 = 3 × 2 + b
b = 4
になるね。
つまり、この一次関数の式は「y = 3x + 4」になるよ!
こんな感じで、傾きと座標をじゃんじゃん代入していこう!。
つぎは「切片」と「座標」がわかっている問題だね。

たとえば、つぎみたいなヤツさ↓↓
例題
yはxの一次関数で、そのグラフが点(2, 11)を通り、切片3の直線であるとき、この一次関数の式を求めなさい。
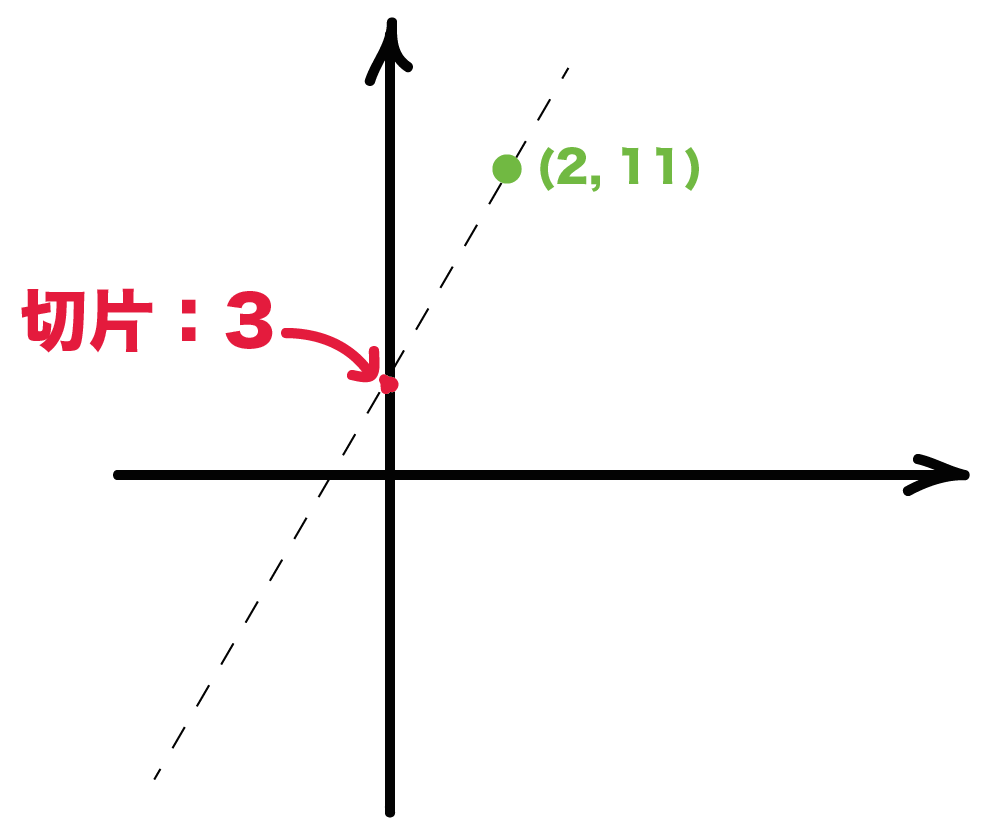
このタイプの問題もいっしょ。
一次関数の式「y = ax +b」に切片と座標を代入してやればいいんだ。
そんで、できた方程式を解いてやれば直線の式が求められるね。
例題では、
だったね?
切片の「3」をy = ax+bに代入してみると、
y = ax + 3
になるね。
そんでコイツに、
を代入してやると、
11 = 2a + 3
になる。
この方程式をaについて解いてやると、
11 = 2a + 3
2a = 8
a = 4
になる。
つまり、この一次関数の傾きは「4」ってことだ。
だから、
一次関数の式は「y = 4x + 3」になるね。
このタイプの問題も代入して方程式をとくだけさ!
最後は、直線が通る2点の座標がわかっている問題だ。
たとえば、つぎのような問題さ。
例題
つぎの一次関数の式を求めなさい。
グラフが、2点(1, 3)、(-5, -9)を通る直線である。
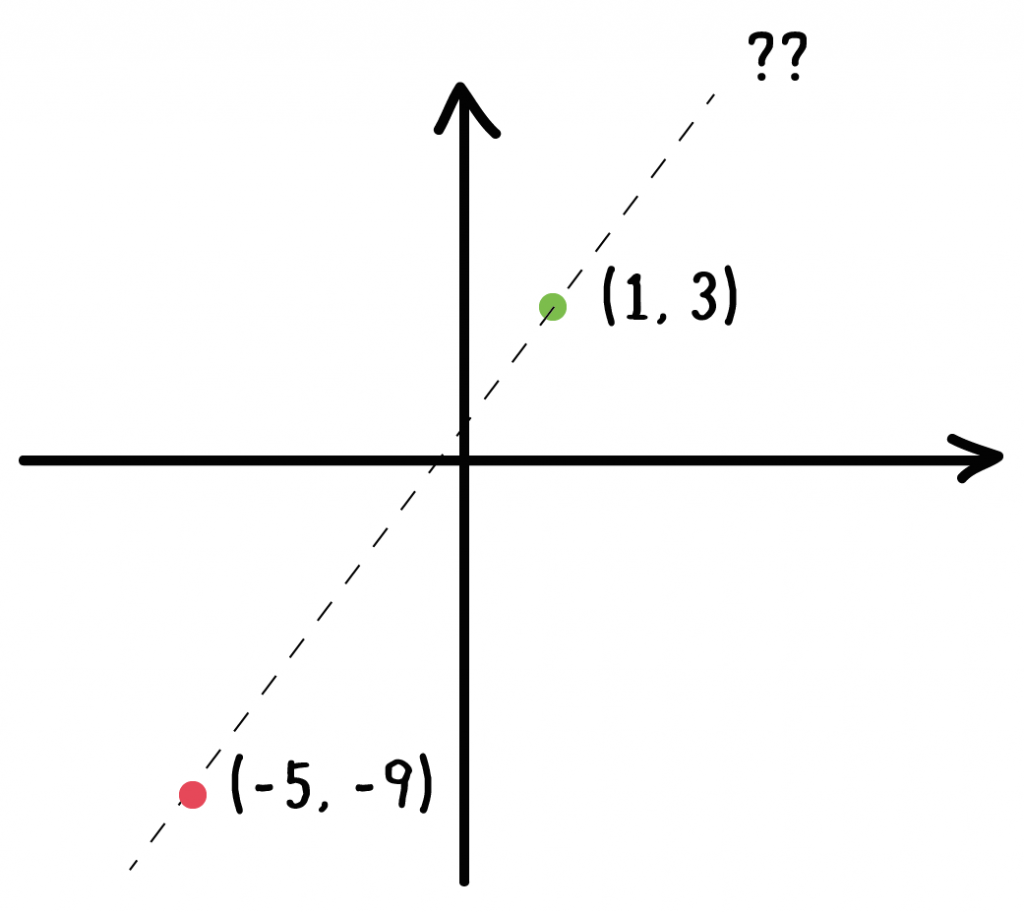
ちょっとめんどくなるけど、解き方はこれまでと一緒。
一次関数の式「y = ax + b」に2点の「x座標・y座標」を代入してやればいいのさ。
問題に慣れるまで練習してみてね。
直線の式を求め方はどうだった??
4パターンあるとか言っちゃったけど、
だいたいどれも解き方は一緒。
一次関数の式「y = ax + b 」に、
のうち2つを代入してやればいいんだ。
テスト前によーく復習してね。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。担々麺うますぎだね。
一次関数という単元は、
グラフの書き方がわかればどうにかなる。
もうね、ほんとね、どうにかなる。
だって、グラフの問題がたくさんでるからね。
グラフをかければ一次関数をマスターしたようなもんさ。

今日はそんな1次関数の攻略のカギをにぎる、
一次関数のグラフの書き方
を3ステップで紹介していくよ。
よかったら参考にしてみてね。
書き方の基本は、
グラフが通るであろう2点を結ぶ
ということだ。
なぜなら、
一次関数のグラフはゼッタイに直線になるからね。
2点をむすべば直線がかけちゃうんだ。
ってことは、
直線が通る2点をさがせばゲームクリアってわけ。
例題をといてみよう。
つぎの一次関数のグラフをかきなさい。
y = 3/5 x -2
つぎの3ステップでグラフがかけちゃうんだ。
「y軸」と「一次関数」の交点をうとう。
切片を「y座標」とする点を「y軸上」にとってやればいいんだ。
例題をみてみよう。
一次関数の切片は、
xもyもついていない項のこと
だったね。
例題の関数では、
「xもyもついていない項」って「-2」だよね?
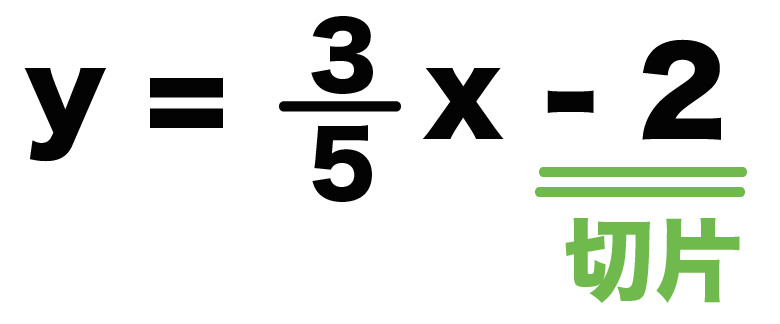
ってことは、コイツが切片だ。
この切片をy座標とするy軸上の点(0, -2)をうっちゃおう。
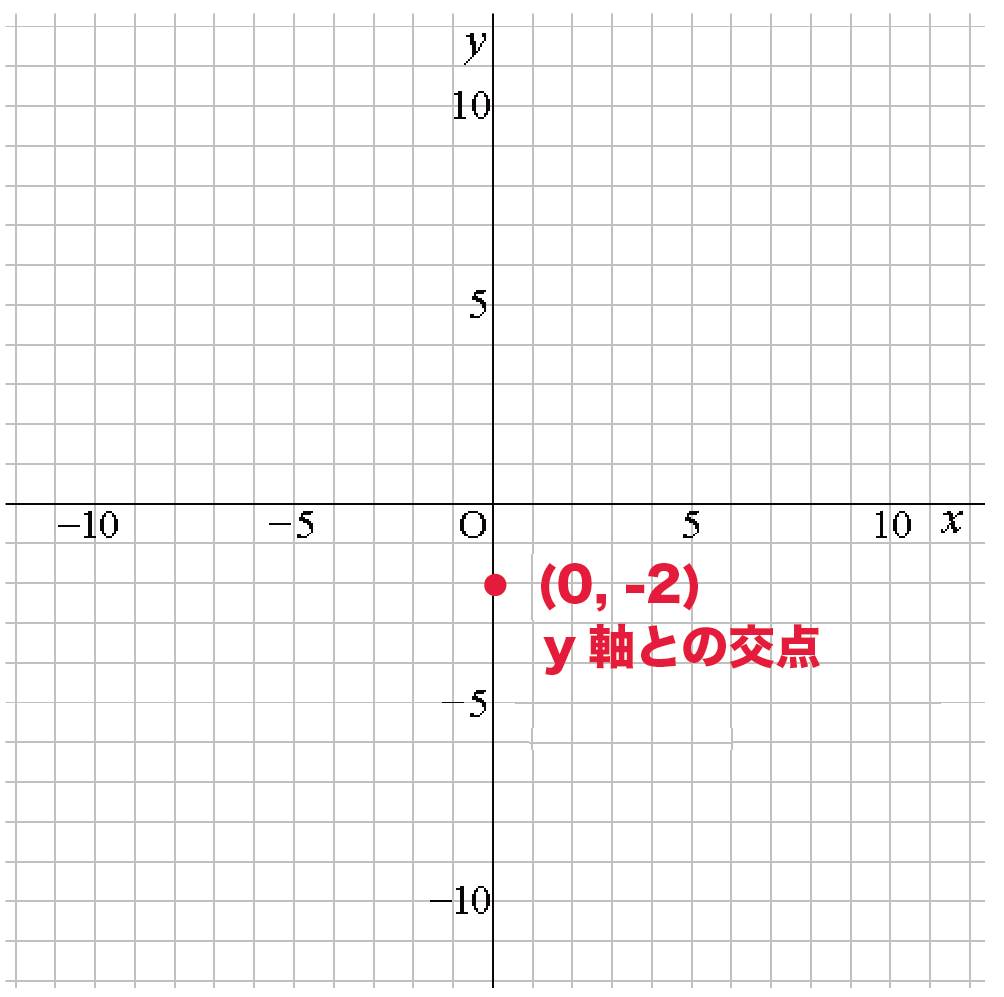
これが1つ目の点だ。
つぎは「xもyも整数になる点」を打とう。
xに適当な整数を代入して座標をだしてみて。
傾きが整数のときはxに「1」をいれてやればいいね。
ただ、例題みたいに傾きが分数の場合は、
「分母の数字」をxに代入してみよう。
xもyも整数の点がゲットできるはずさ。
例題をみてみよう。
傾きは3/5。
だから、xに分母の「5」を代入してみよう。
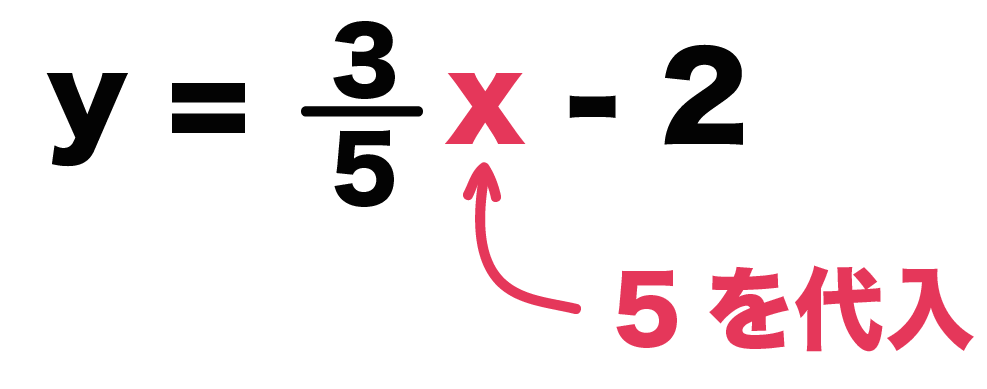
すると、
y = 3/5 × 5 -2
= 1
ってなるでしょ?
つまり、この一次関数は「整数の座標(5, 1)」を通るわけさ。
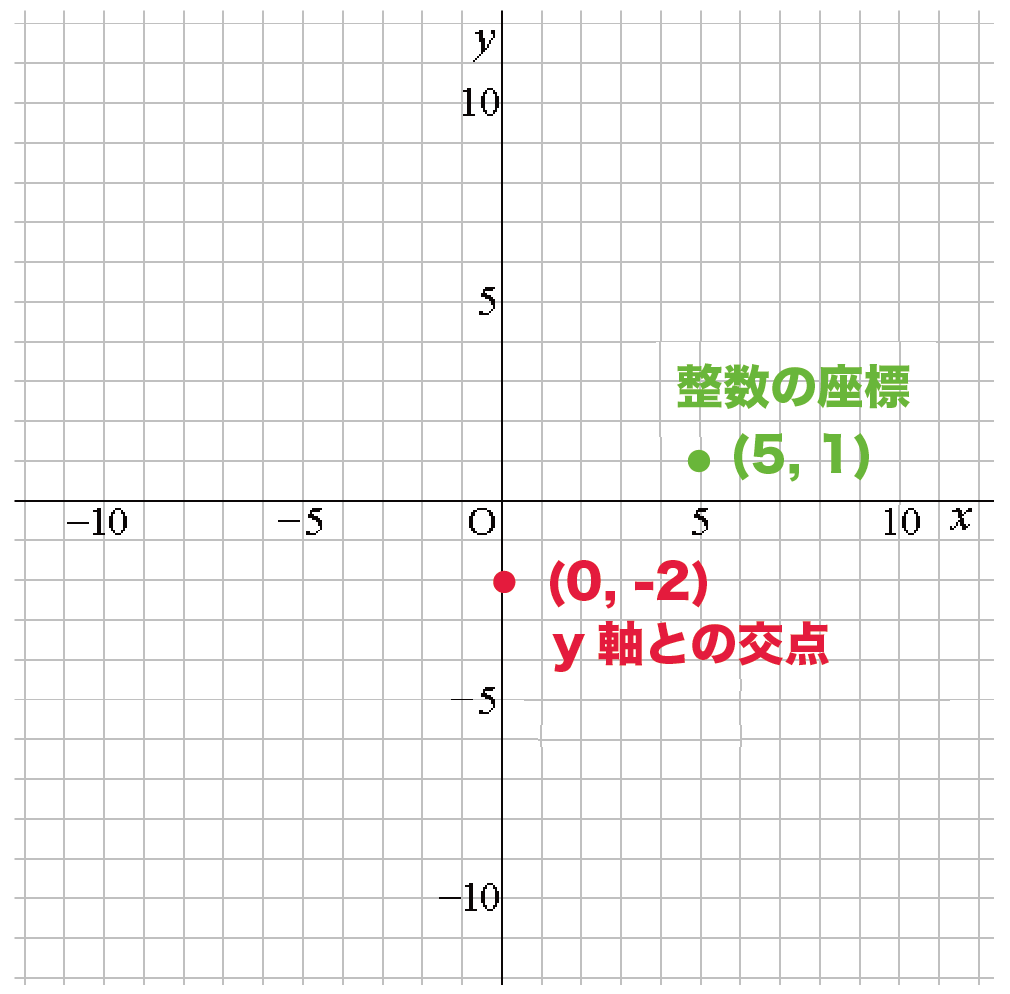
これで2点目がわかったね!
あとは2点をむすぶだけ。
定規で直線をひいてみよう。
できた直線が一次関数ってわけさ!
例題では、
をむすんでみよう。
すると、こんな感じになるっしょ? ↓↓
おめでとう!
1次関数のグラフがかけたね。
一次関数のグラフはむずかしくない。
をむすんであげればいいんだ。
あとは問題になれてみてね。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。自転車、ほしいね。
一次関数の切片(せっぺん)ってなんだろう??
よく耳にするけど、イマイチわからないよね。
教科書をみてみると、
直線y = ax+bとy軸との交点(0, b)のy座標bを、この直線の切片といいます。
ってかいてある。
正直ちょっとよくわからない。
コイツをわかりやすくいうと、
「1次関数」と「y軸」がまじわっている点の「y座標」ってことだ。
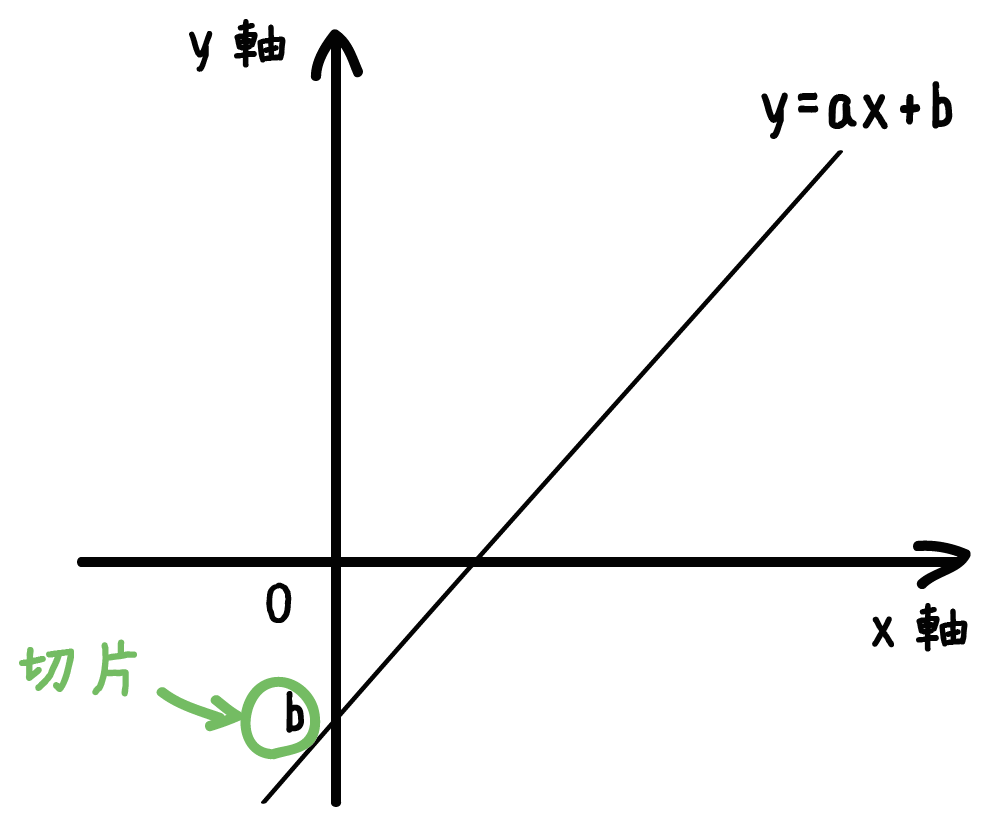
「せっぺん」って名前は取っ付きにくいけど、
意外とわかりやすいヤツでしょ??。
今日は「切片」の求め方を2つ紹介していくよ。
よかったら参考にしてみてね。
つぎの2つの求め方でゲットできるよ!
一次関数の中で「xでもyでもない項」をさがす方法だ。
数式見るだけで切片が求まるから簡単だね。
一次関数 y = ax + b の切片はずばり、
bの値
だ。
どんなにひねれくれていて、複雑な一次関数でも同じ。
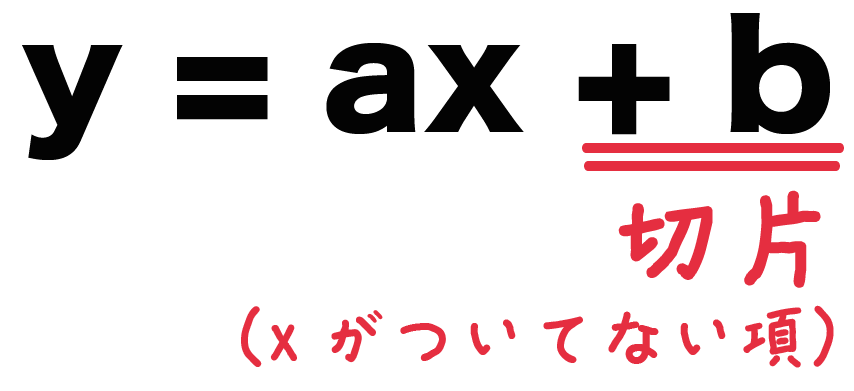
ってことは、
xもyもついていない項が切片
って言えそうだね。
だから、この「bの値」を数式からみつけてあげればいいわけさ。
たとえば、つぎの例題があったとしよう。
例題
直線 y = 7x – 2の切片を求めなさい。
切片は、一次関数で「xもyもついていない項」のことだったよね??
ってことは、
y = 7x – 2
で「xもyもついていない項」って「-2」だ。
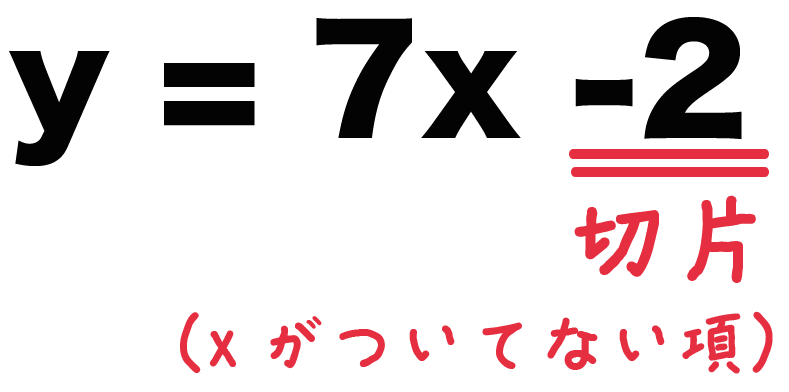
え。
そうそう。
つまり、
1次関数「y = 7x -2」の切片は「-2」なのさ。
グラフをかかなくても切片がわかるなんて便利でしょ??
グラフから切片を読み取る方法だ。
これはいたって簡単。
1次関数の直線がy軸とまじわっている点が「切片」だから、
交点をみつけるだけでいい。
ぶっちゃけ、1秒もかからないね。
たとえば、つぎのような問題だ。
例題
つぎのグラフの一次関数の切片を求めなさい。
※ x軸との交点(7, 0)、y軸との交点(0, 8)
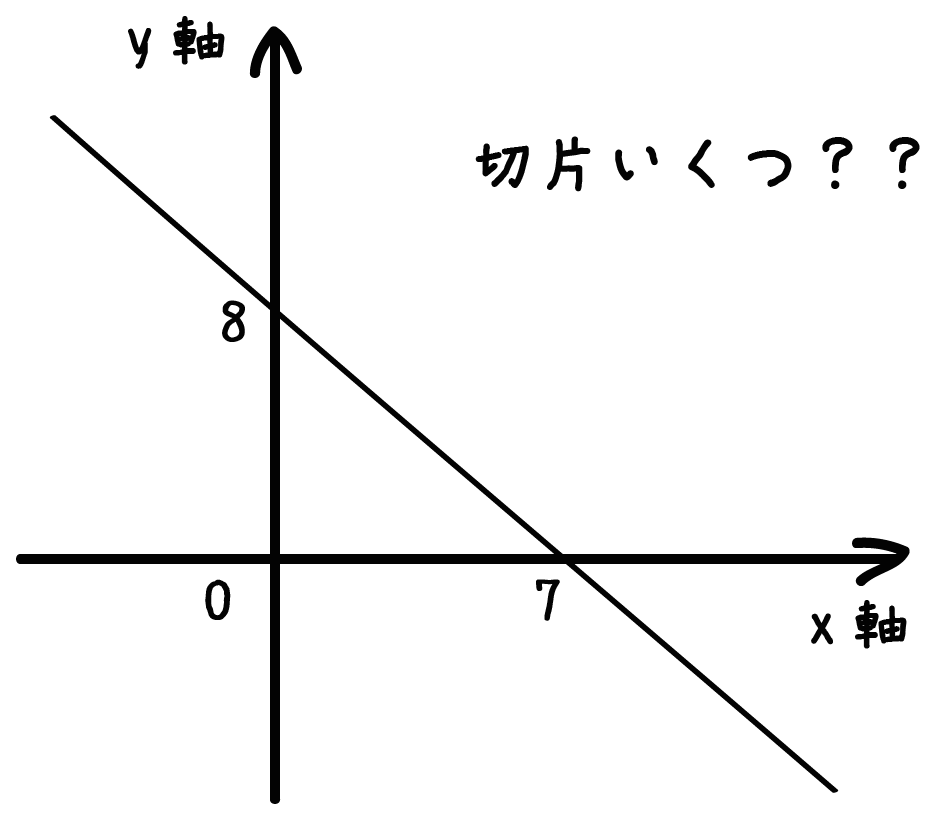
さっきも復習したけど、
切片って、
「1次関数」と「y軸」の交点の「y座標」のこと
だったよね??
グラフをみてみると、
y軸との交点は(0, 8)ってことがわかる。
だから、この関数の切片は「8」になるね。
なぜなら、交点のy座標は8だからね。
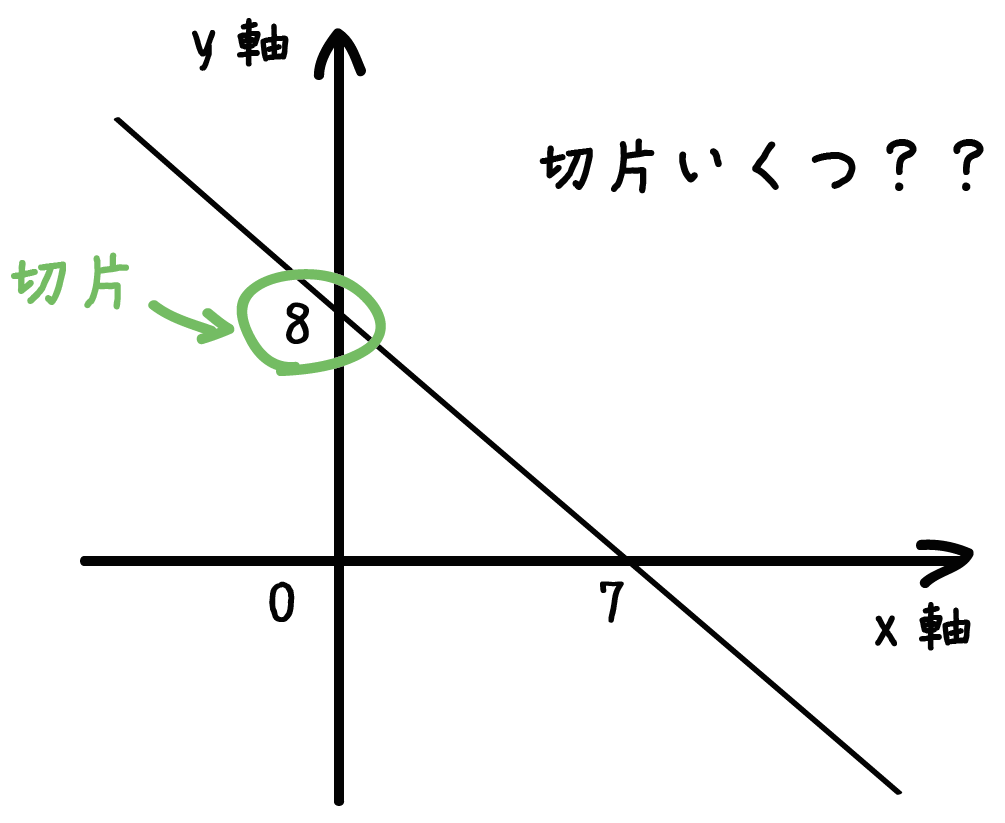
グラフをみるだけで切片がわかる。
チョー簡単な方法だね。
1次関数の切片は意外と簡単。
の2つでガンガン攻略できるよ。
あとはテスト前に問題に慣れておこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。パスタ、うまいね。
一次関数を勉強していると、
xの増加量を計算して?
とか、
yの増加量を求めねえと・・・
みたいなこと多いよね。
うん、これ、つらいよ。

今日はそんな事態にそなえて、
1次関数における「xの増加量」と「yの増加量」の求め方
を2つ紹介するよ。
増加量の求め方には2つのパターンがあるんだ。
1つ目のパターンは、
xとyの「変化前」と「変化後」の値がわかっているヤツだ。
たとえば、つぎのような問題だね。
xが3から6に変化したとき、yの値が8から-1になる一次関数があったとしよう。
このとき、xの増加量とyの増加量を求めなさい。
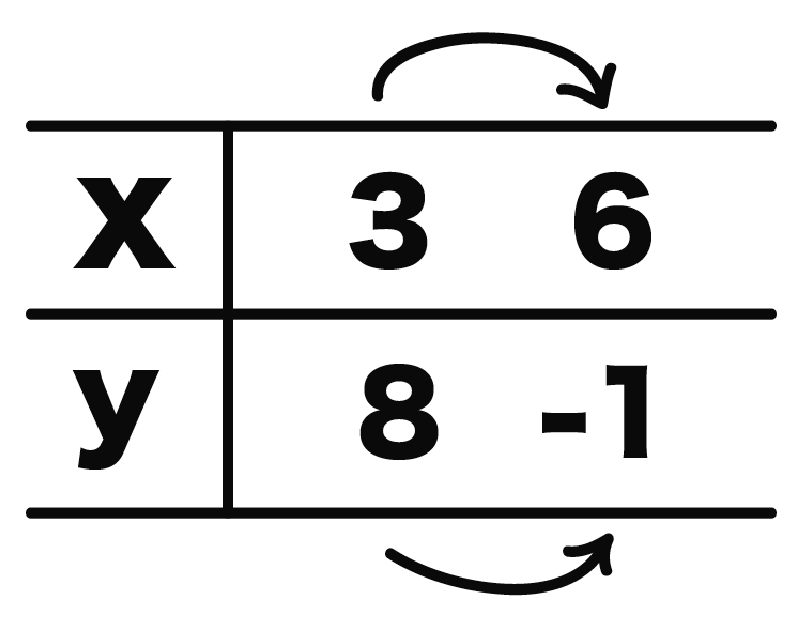
この問題では、
(変化後の値)- (変化前の値)
で計算してやればいいんだよ。
まずはxの増加量を求めてみよう。
xは「3」から「6」まで変化しているよね??
つまり、
ってわけだ。
これを、
(変化後の値)- (変化前の値)
で計算してやると、
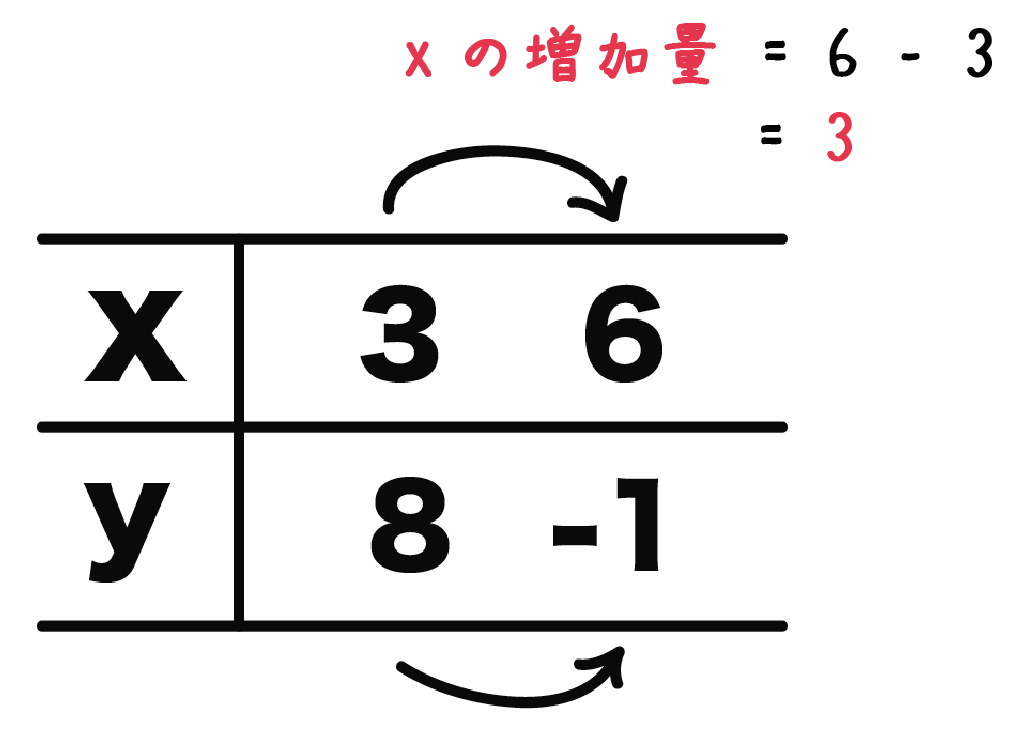
6 – 3
= 3
になるね!
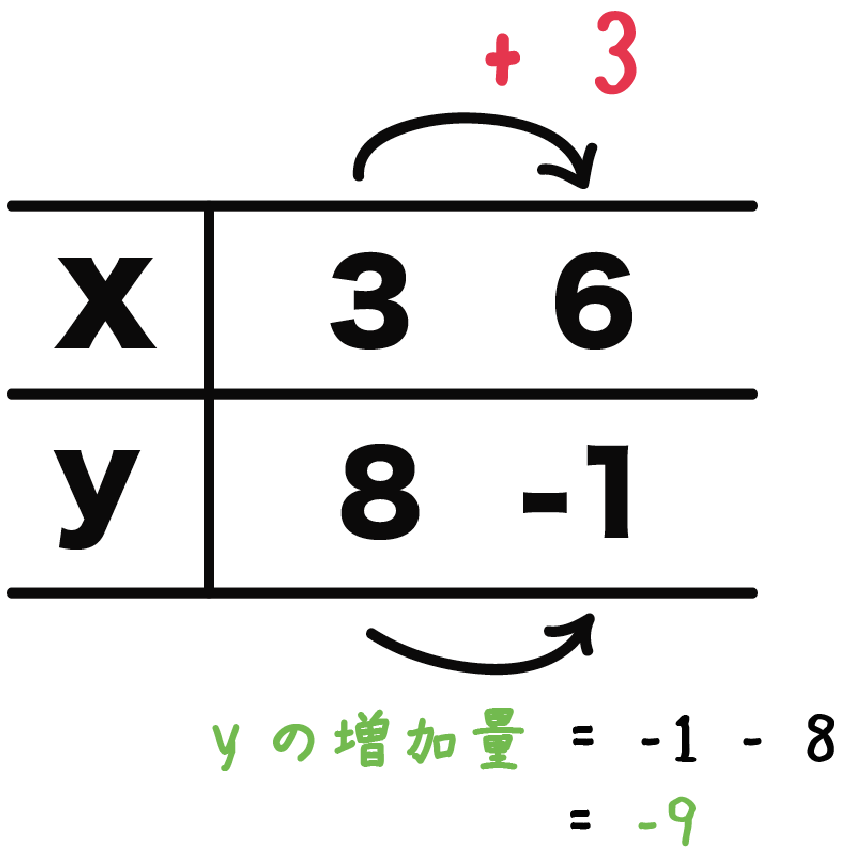
yの増加量も同じ方法で求められるよ。
(変化後の値)- (変化前の値)
だから、
(yの増加量)= -1 – 8
= -9
になるね。
これが一番シンプルな増加量の求め方。
基本だからしっかりおさえておこう。
2つめのパターンは、
1次関数の「変化の割合」と「増加量」がわかってるヤツだ。
わかってる「増加量」は「x」でも「y」のヤツでも構わないよ。
たとえば、つぎのような問題だ。
一次関数 y = 5x – 10000 で、xの増加量が2のとき、yの増加量を求めよ。
この手の問題は、
変化の割合 = (yの増加量) ÷ (xの増加量)
の公式をつかうよ。
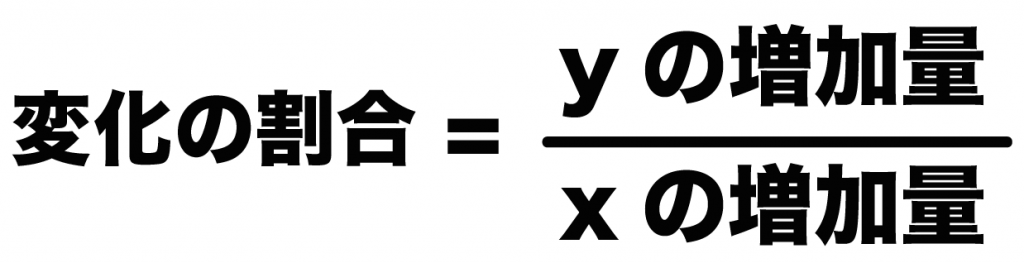
等式の変形で「yの増加量=」のカタチに変えてやると、
(yの増加量)= (変化の割合)×(xの増加量)
になるよね??
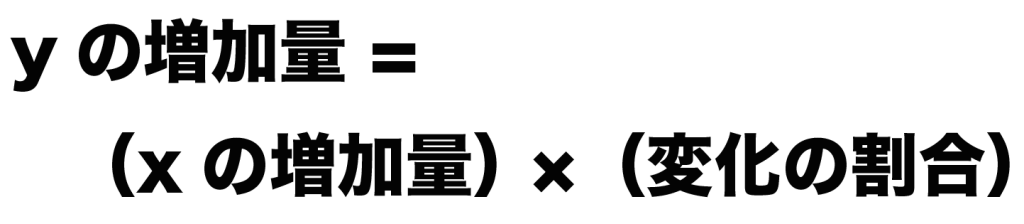
y = 5x -1000の「変化の割合」は「5」。
xの増加量は「2」。
ってことは、yの増加量は、
(yの増加量)=(変化の割合)×(xの増加量)
= 5 × 2
= 10
になるね。
公式を変形して計算するだけさ!
xの増加量も同じようにやってみてね。
一次関数でx・yの増加量を求める問題は、
の2パターン。
これでだいたいイケルね。
あとは問題をときまくって、一次関数の問題になれてみよう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。本屋にいきたいね。
一次関数の問題で、
変化の割合をもとめろ!!
ってヤツがよくだされる。
こいつは、変化の割合の公式、
(変化の割合)=(yの増加量)÷(xの増加量)
をつかえば攻略できるよ。
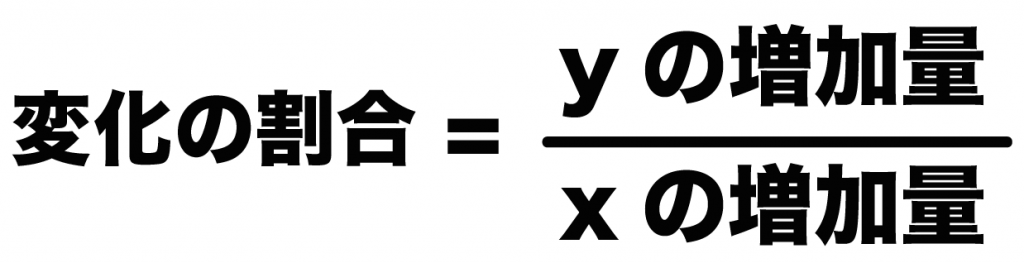
たとえば、
xの増加量が5のとき、yの増加量が25の関数があったとしよう。
こいつの変化の割合は、
(yの増加量)÷(xの増加量)
= 25 ÷ 5
= 5
になるんだ。
公式ならすぐ計算できちゃうでしょ??
今日はこの公式を使って、
1次関数の変化の割合の求め方
を3つのステップで解説していくよ。
テスト前に参考にしてみてね。
例題で「変化の割合」をもとめてみよう!
例題
xが3から6に変化したとき、yの値が8から-1になる一次関数があったとしよう。
この一次関数の変化の割合をもとめよ!
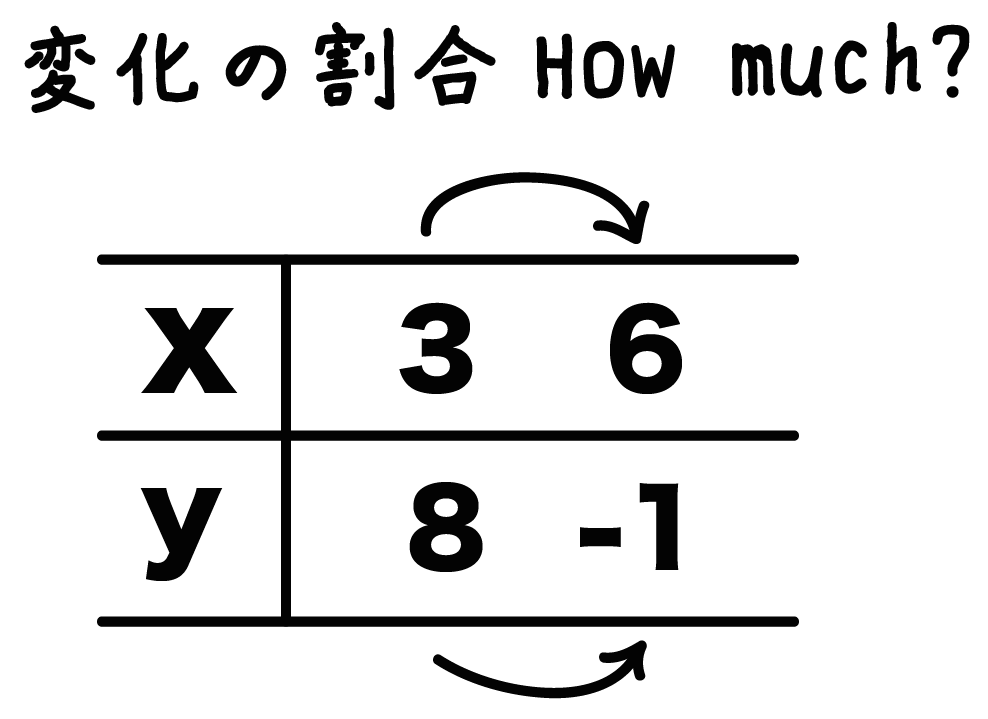
つぎの3ステップで攻略できちゃうよ!
まず「xの増加量」から計算しよう。
xの増加量の求め方は、
(変化の後のxの値)- (変化の前のxの値)
だ。
つまり、ゴール地点からスタート地点のxの値をひいてやればいいんだ。
例題では、
xの値は「3」から「6」 に変化したんだよね??
ってことは、このときのxの増加量は、
(変化の後のxの値) – (変化の前のxの値)
= 6 – 3
= 3
になるよ!
yの増加量をもとめてみよう!
「yの増加量」も「xの増加量」とおなじで、
(変化の後のyの値)- (変化の前のyの値)
で計算できるよ。
例題をみてみよう。
yの値は「8」から「-1」まで変化してるよね??
yの増加量を
(変化の後のyの値)- (変化の前のyの値)
で計算してやると、
-1 – 8
= -9
になるね。
yの増加量は「-9」ってことだよ。
勘の鋭いヤツはここで、
えっ。yの増加量がマイナスっておかしくね??
って思うはずだ。
ぶっちゃけ、暴動がおきてもおかしくない。
ここで覚えておいてほしいのは、
増加量がマイナス(負の数)になる場合もありえる
ということだ。
xとかyの増加量ってただの表記であって、
かならずしもプラスになっているとは限らない。
増加量というより、
xとyの「変化量」と捉えたほうがわかりやすいかもね。
xとyの増加量をゲットしたね?
あとは公式で計算してやるだけさ。
(変化の割合)=(yの増加量)÷(xの増加量)
を使ってみてね。
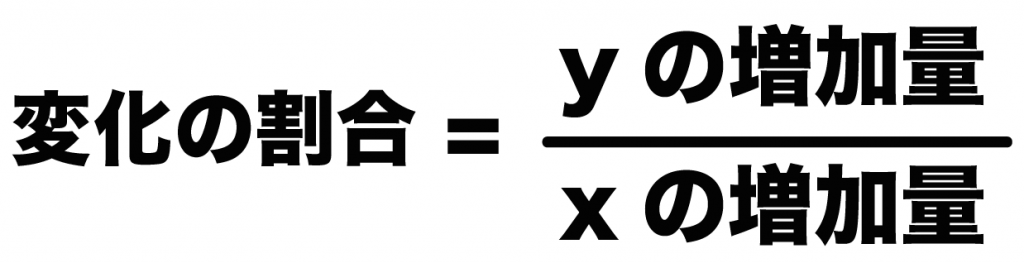
例題をみてみて。
xとyの増加量って、
だったよね??
こいつらを公式で計算してやると、
(変化の割合)
=(yの増加量)÷(xの増加量)
= – 9 ÷ 3
= – 3
になるよ。
変化の割合は「-3」になったね。
つまり、
この1次関数はxが1増えるごとに、yが3減る野郎だってことさ。
変化の割合の意味がイマイチ・・・・
ってときは、
一次関数の変化の割合の記事で復習してみてね。
変化の割合の求め方はわかった!?
(変化の割合)=(yの増加量)÷(xの増加量)
っていう公式で計算していこう。
問題をといて計算になれてみてね。
そんじゃねー
Ken