【連立方程式の利用】速さ・道のり・時間の文章問題の解き方
連立方程式の文章問題が苦手・・・!
中学生の連立方程式で厄介なのはやっぱり、
文章問題
だよね。
いわゆる連立方程式の利用っていう単元だ。
中でも狙われやすいタイプは、
「道のり・速さ・時間」についての文章題だ。
連立方程式を使った「道のり・速さ・時間」に関する文章問題
例えば、次のような問題↓
Aさんは、それぞれ何 mずつ進みましたか。
この問題は次の3ステップで解けるよ。
Step1. 図をかいてみる
まずはやってほしいのが、一旦、とりあえず、
図を書いて整理する
ってこと。
方程式の文章問題では、読んでもわかんなくて、ごっちゃになる時がある。
そういう時も落ち着いて、
問題の情報を「図」とか「絵」でかいてみるんだ。
うだうだ悩んでるよりも、図をかけば1歩進むことになるね。
今回の例題を整理してみると、こんな感じかな↓
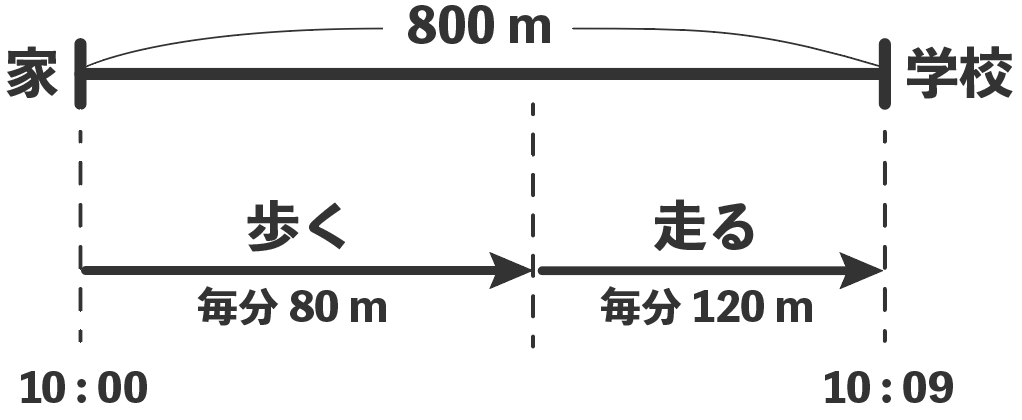
Step2. 「求めたいもの」を文字で置く
すべての文章問題ってわけじゃないけど、9割の文章題では、
「問題で求めたいもの」を文字でおくと解けるよ。
この例題では、
それぞれ何m進みましたか?
って聞かれてるね。
ということは、
- 毎分80 mで歩いた距離
- 毎分120 m で走った距離
を求めればステージクリアだから、こいつらをそれぞれ、
- 毎分80 mで歩いた距離 → xm
- 毎分120 m で走った距離 → ym
と置いてみよう。
これらをさっきの図に書き込むとこうなる↓
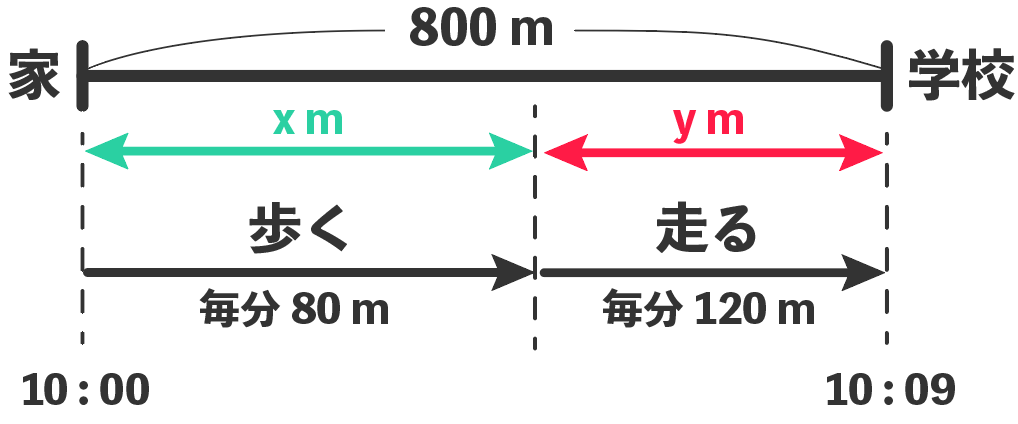
Step3. 1つ目の式をつくる(道のりについて)
まずは1つ目の方程式を作ろう。
連立方程式は「x」と「y」の2つの文字を使ってるから、2つ式が必要だね。
一番簡単なのが、
道のりに関する式だ。
さっき描いた図をみるとわかるけど、
「毎分80mの速さで歩いた距離」と「毎分120 mで走った距離」を足すと800mになるはずだね。
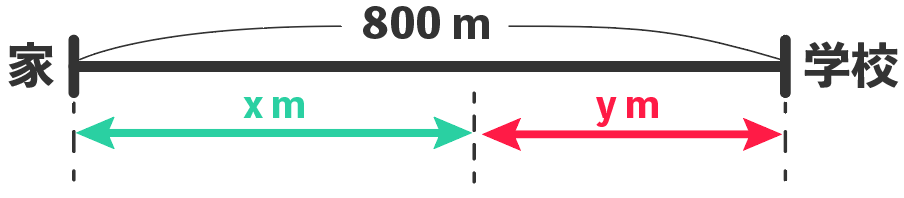
つまり、
x + y = 800
という式が作れるはずだ。
Step4. 2つ目の式をつくる(時間について)
もう1つは「道のり」じゃなくて「時間」についての等式を作ってみよう。
まず「Aさんが家から学校までにかかった時間」を求めてみる。
問題文によると、
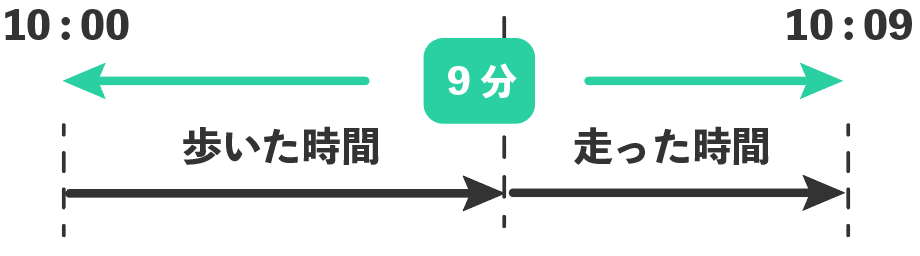
10時に出発して10時9分についた
とあるから、到着までの時間は9分だ。
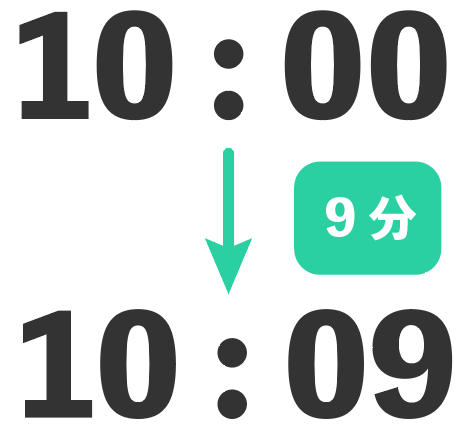
その「9分」に等しいはずなのが、
- 歩いた時間
- 走った時間
の合計。
つまり、
(毎分80 mで歩いた時間)+(毎分120 m で走った時間)= 9分
という式を作ればいいね。
「道のり・速さ・時間の公式」を使うと、
(時間) = (道のり)÷(速さ)
だから、「歩いた時間」と「走った時間」はそれぞれ、
- 歩いた時間 = 歩いた距離 ÷ 歩いた速さ
- 走った時間 = 走った距離 ÷ 走った速さ
になるね。
だから、
(毎分80 mで歩いた時間)+(毎分120 m で走った時間)= 9分
(歩いた距離 )÷ (歩いた速さ)+ (走った距離) ÷ (走った速さ) = 9分
x ÷ 80 + y ÷ 120 = 9
80分のx + 120分のy = 9
という式ができて、これが2つ目の等式になる。
Step5. 連立方程式を解く
最後に連立方程式を解いていこう。
Step4までで求めた連立方程式はこいつら↓
- x + y = 800
- 80分のx + 120分のy = 9
なんと、まさしく分数を含む連立方程式。
この手の問題は、
分数を消し去すことから始めよう。
分数が含まれているのは2つ目の式で、分数の分母は
- 80
- 120
の2つ。
こいつらの最小公倍数は240だから、240を両辺にかけてやると、次のようになる。
3x + 2y = 9 × 240
あとは加減法で解くだけ。
- x + y = 800
- 3x + 2y = 9 × 240
1つ目の式を2倍して、2つ目の式から引いてやると、
3x + 2y = 9 × 240
– ) 2x + 2y = 800 × 2
—————————–
x = 9 × 240 – 800×2
x = 560
と、xが出てくるはず。
このxを1つ目の式の
x + y = 800
に代入すると、
560 + y = 800
y = 240
と、yの値まで出てきたよ。
ここで冷静になって、xとyが何を表しているか考えると、
- 毎分80 mで歩いた距離 → xm
- 毎分120 m で走った距離 → ym
だったね。
ということで、この問題の答えは、
歩いた距離は560 m、 走った距離は240 m
になるんだ。
つまり、Aさんは歩いた距離が長くて、最後に少し走っただけになるね。
連立方程式の文章問題は図をかこう!とりあえず
こんな感じで、道のり・速さの文章題も情報を整理すれば大丈夫。
あとは「道のり・速さ・時間」の公式を理解して、それを使えば解けるはずだ。
これさえできれば、どんな速さの応用問題でも大丈夫。
「ちょっと連立方程式の解き方が危ういな・・・・」
と思ったら、
を復習してみよう。
そんじゃねー
Ken






