どーも、ぺーたーだよ。
図形と相似の単元で、
中点連結定理
を勉強していくよね。
えっ、忘れたって!?
中点連結定理を簡単にいってやると、
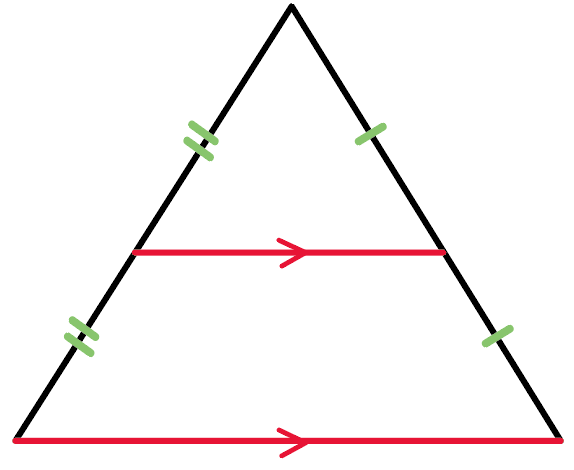
三角形の2辺の中点を通る線が、
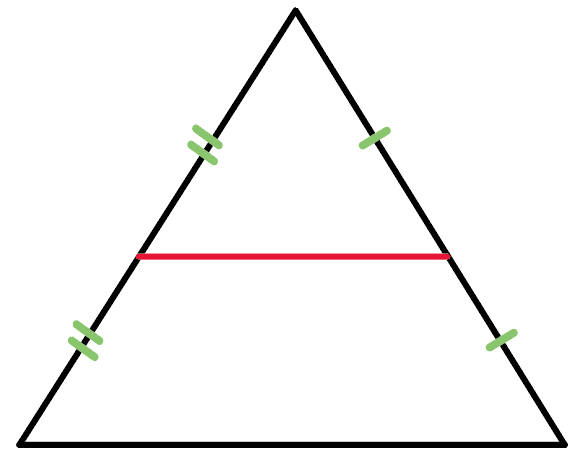
底辺に平行で、
なおかつ、
底辺の半分になってるよー
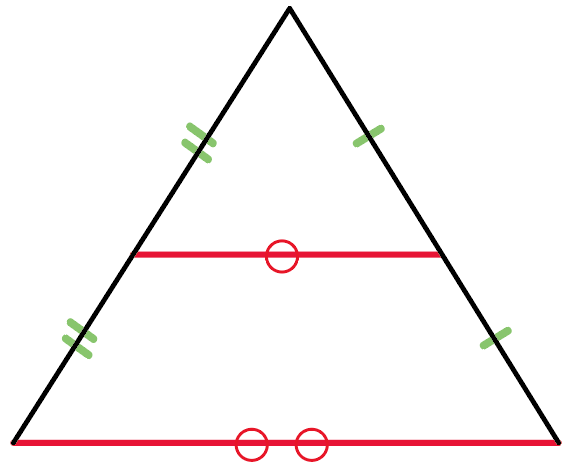
っていう定理なんだ。
けっこう便利なんだけど、
なんでそうなるの?
って思ったことはないかな?
思ったことがなくても、
中点連結定理を使えれば大丈夫なんだけどねw
ってことで、今日は、
なんで中点連結定理が使えるか??
を証明していくよ!
さっそく中点連結定理を証明していくよ。
3ステップで証明できちゃうんだ。
中点連結定理を証明するために、
つぎの、
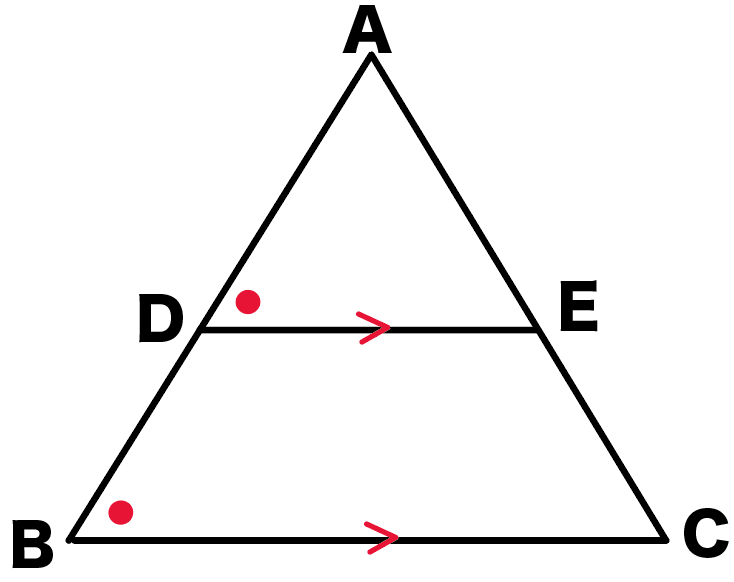
△ADEと△ABC
を思い浮かべてみて。
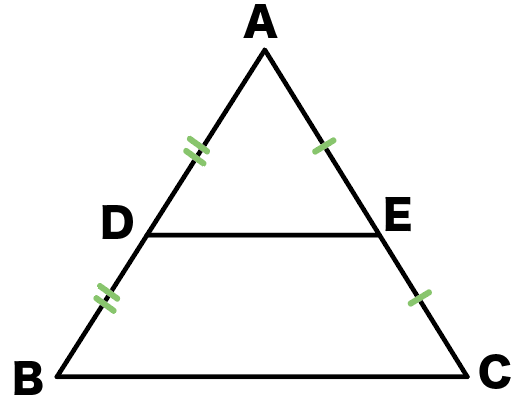
DとEはそれぞれ、ABとACの中点ね。
中点連結定理の証明のゴールは、
を証明することだよ。
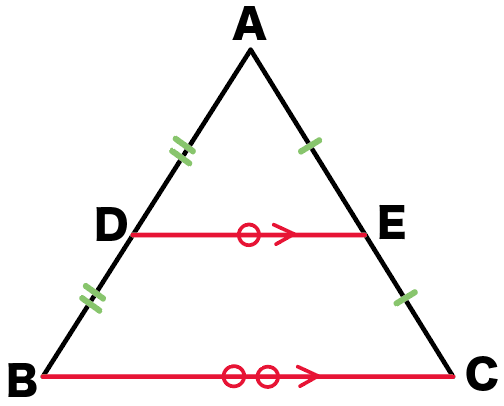
さっそく証明していこう!
まずは△ADEと△ABCの相似の証明だ。
D・Eはそれぞれの中点だから、
だよね??

ってことは、比であらわすと、
になるはずなんだ。
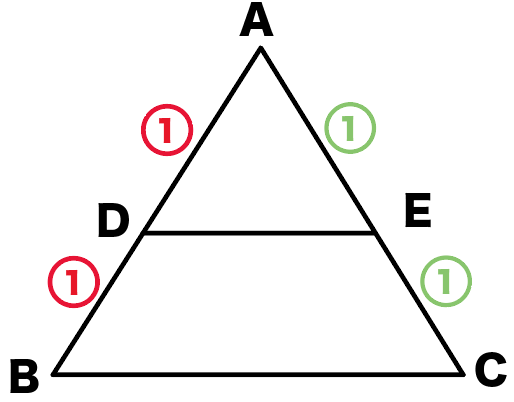
ADとDBの比を合わせると、
AD:AB=1:2…①
ACの比も同じ考え方でAEとECの比を合わせると、
AE:AC=1:2…②
になるね。
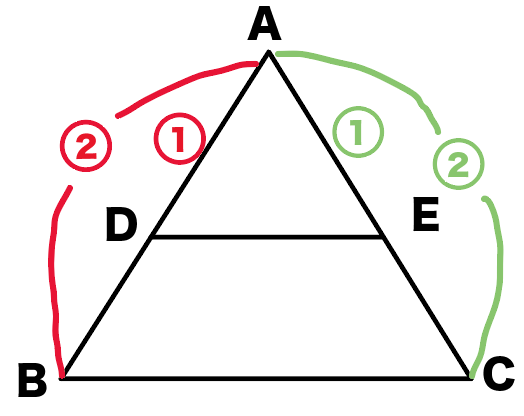
んで、
△ADEと△ABCは角Aを共有してるよね??
ってことで、
角DAE = 角BAC (共通)…③
だ。
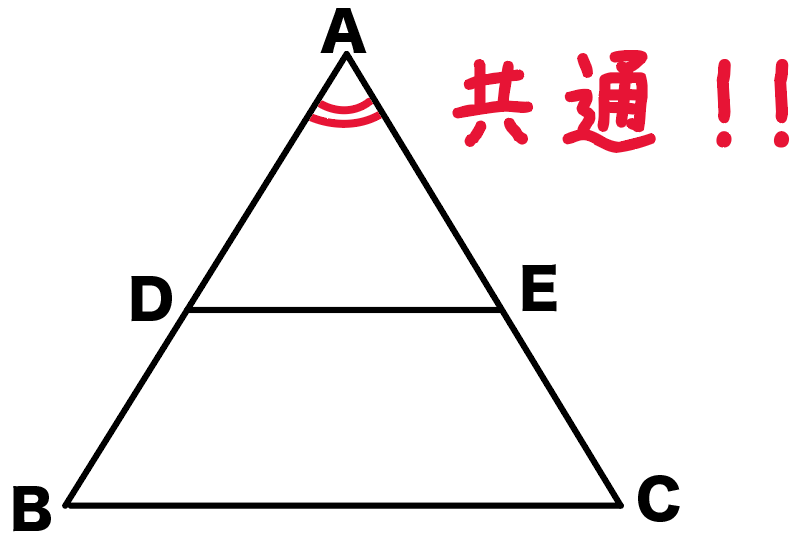
①、②、③より、三角形の相似条件の、
2組の辺の比とその間の角がそれぞれ等しいが使えるから、
△ADE∽△ABC
になるね。
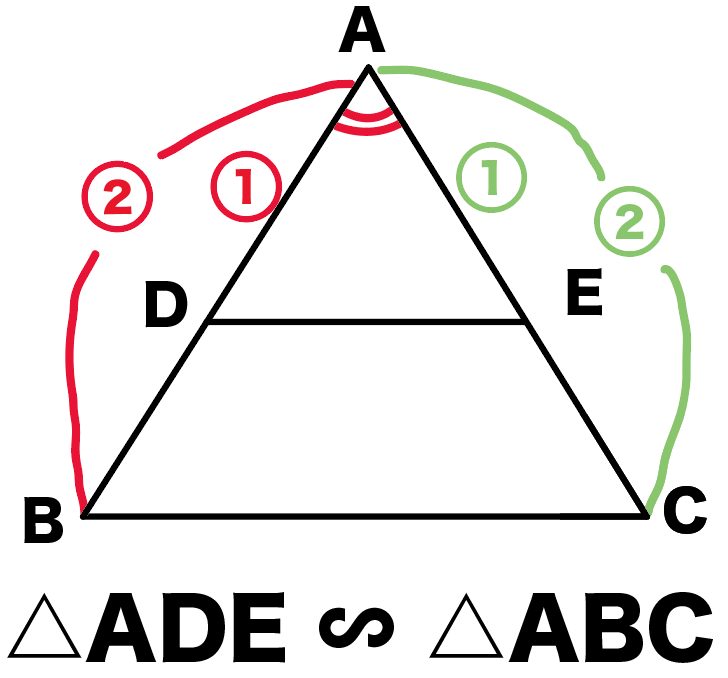
これで相似の証明はできた!
三角形の相似比を求めてみよう。
①のAD:AB=1:2より、
△ADEと△ABCの相似比は1:2になるよ。
なぜなら、
ADとABは対応してる辺どうしだからね。

つまり、
△ADEと△ABCの対応する辺の比は全て、
1:2になるはずなんだ。
ってことは、残りの対応する辺の、
DEとBCの相似比も1:2になるね。
DE:BC=1:2
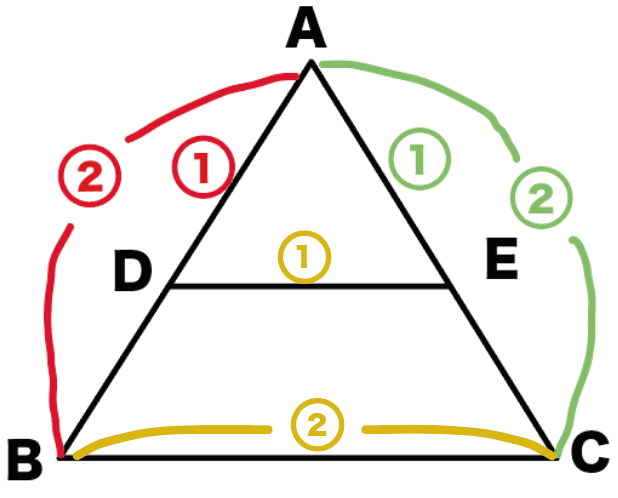
こいつを別の言い方をすると、
DE=1/2BC
ともできるよね。
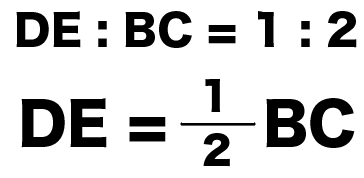
これでDEがBCの半分になるってことはわかったね!
あとは、
DEとBCが平行であること
を証明していこう。
これで中点連結定理の証明が完了するね。
平行の証明には、
同位角が等しいこと
をつかっていくよ。
△ADE∽△ABCだから、相似の図形の性質をつかうと、
対応する角はすべて等しいはずだね。
ってことは、
角ADE = 角ABC
がいえちゃうんだ。
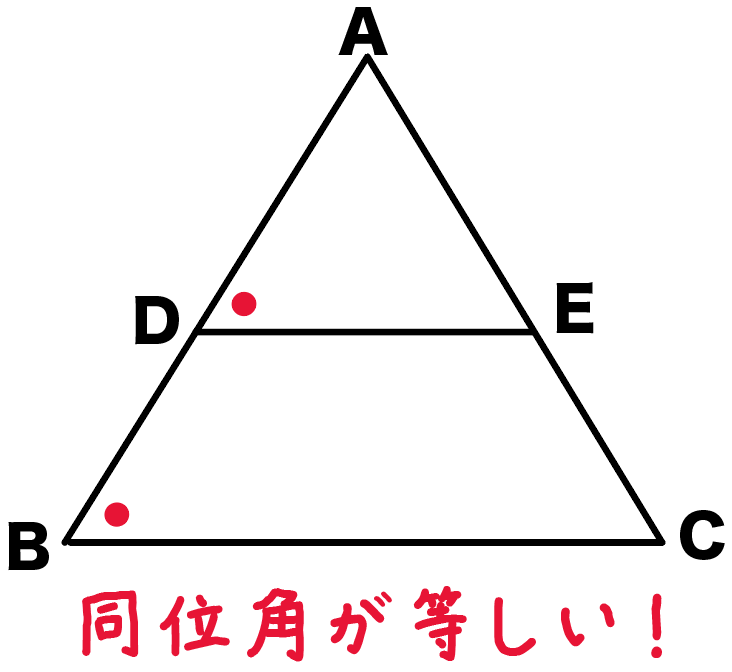
こいつらは、どうみても同位角。
同位角が等しいから、
同位角をつくってるDEとBCは平行
ってことがいえるんだ。
ってことで、
DE // BC
になるよ。
ここまでの3つのステップから、
DE//BC
DE=1/2BC
であることが言えるんだ。

おめでとう!
中点連結定理を証明できたね!!
ここまでで、中点連結定理は証明できたね??
べつに証明はできなくてもいいけど、
なぜ、中点連結定理がつかえるのか??
ということは、ふんわりでもいいから頭の片隅においておいてね。
じゃ、またね!
ぺーたー
こんにちは!ぺーたーだよ。
相似の単元の勉強はどうかな??
相似の証明問題だったり、
相似比を求める問題が出たり
あれこれ大変だね。
今日はもう1つ新しい、
相似比をつかった体積の比の求め方
を解説するよ!
ついでに表面積の比の出し方も説明するから、
セットで覚えてあげよう。
相似比から体積比をだすときは、
つぎの公式をつかってみよう。
それは、
相似比の3乗が体積比になるよ
っていう公式だ。
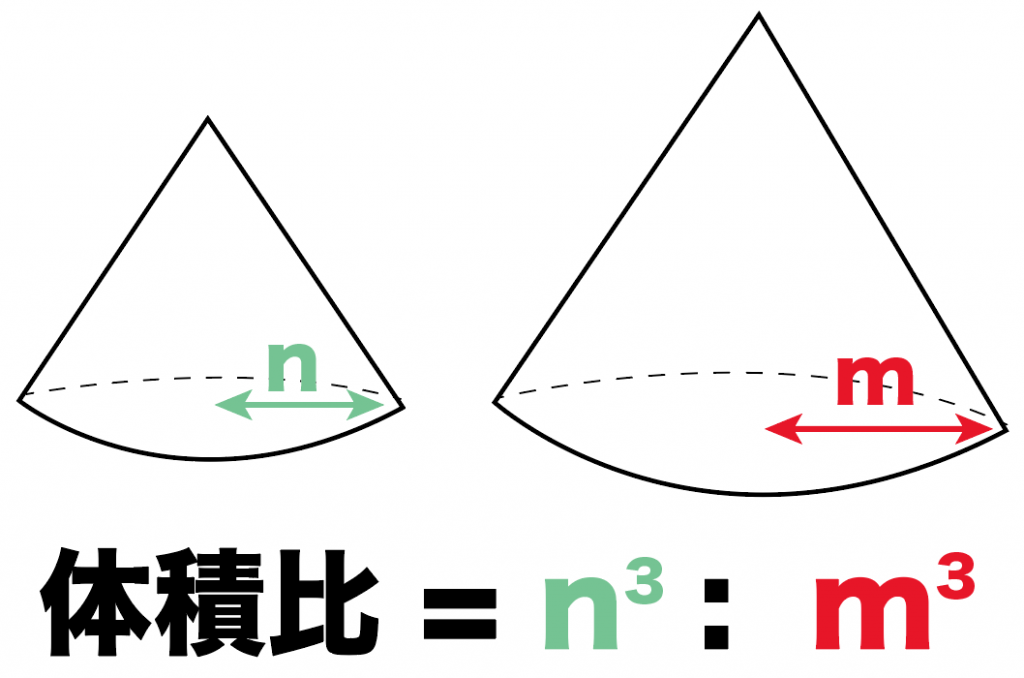
くわしくいうと、
2つの相似な立体があって、相似比がn:mのとき、
2つの立体の体積比は、
n^3 : m^3
になるってこと。
この公式で練習問題をといてみよう。
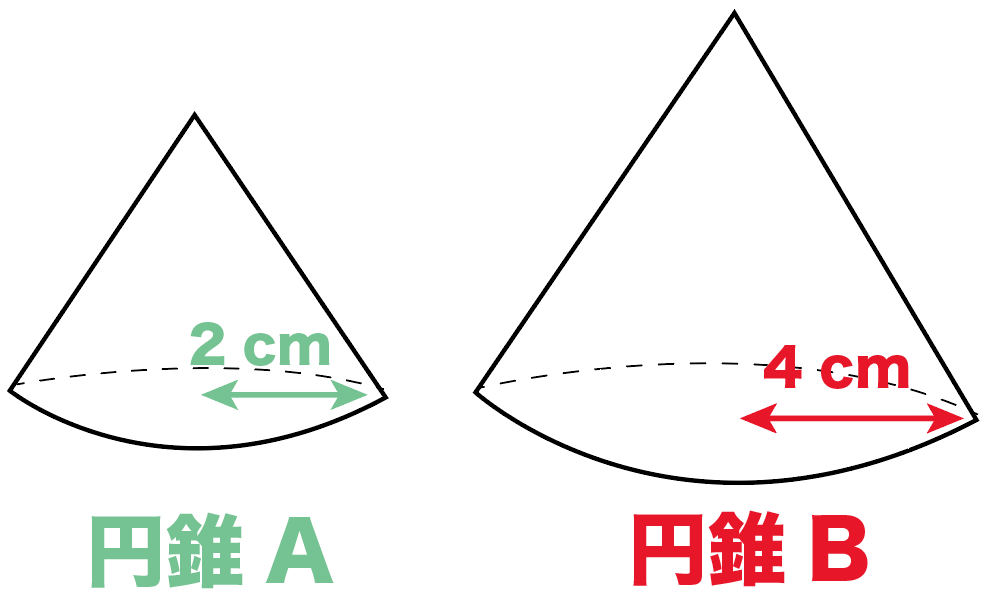
練習問題
次の円錐は相似の関係です。
体積比と表面積の比を求めてください。
この体積比の問題は、2ステップでとけちゃうんだ。
立体の体積比を求めるには、
相似比
が必要なんだ。
練習問題をみてみると、
2つの円錐は相似である
ってかいてあるね。
わざわざ相似を証明する必要ないからうれしい!
さっそく相似比を求めてみよう。
対応する辺を「半径」として、相似比をもとめてみてね。
2つの円錐の底面の半径はそれぞれ、
だったよね??
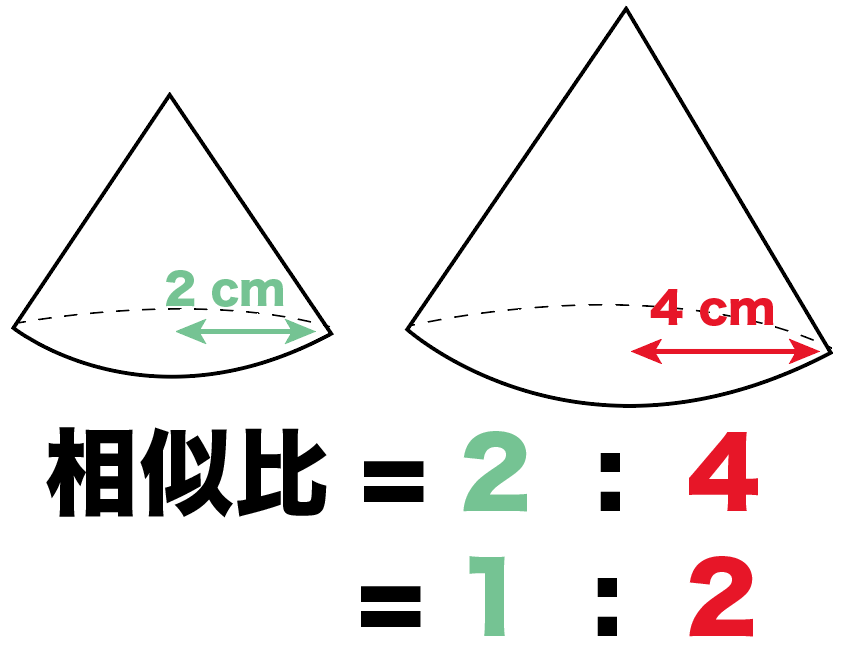
ってことは、こいつらの相似比は、
2: 4
= 1: 2
になるんだ。
相似比が出たら、
体積比はとっても簡単!
体積比の公式の、
相似比を3乗してやると体積の比になる
を使えばいいのさ。

練習問題でも体積比の公式をつかっていこう。
相似比は1:2っていうことがわかったね。
体積比はその相似比を3乗した、
1^3:2^3
= 1 : 8
になるね。
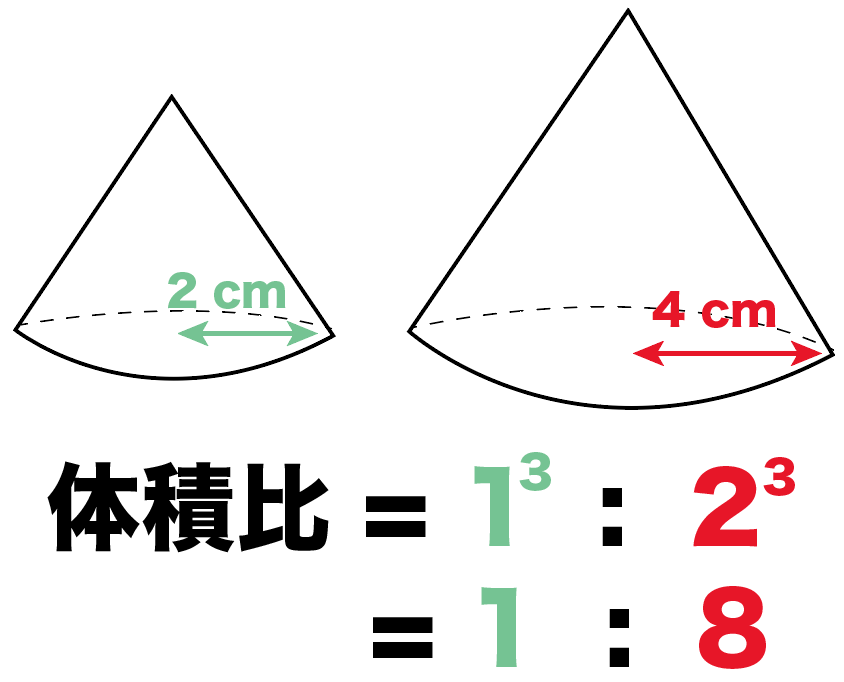
ってことで、
この2つの立体の体積比は「1 : 8」。
やったね!
えっ。
体積比は何の役にたつのかって??
じつは、体積比がわかると、
「ある立体の体積」から「べつの立体の体積」が計算できちゃうんだ。
たとえば、さっきの練習問題で、
円錐Bの体積が80 [cm^3]だったとしよう。
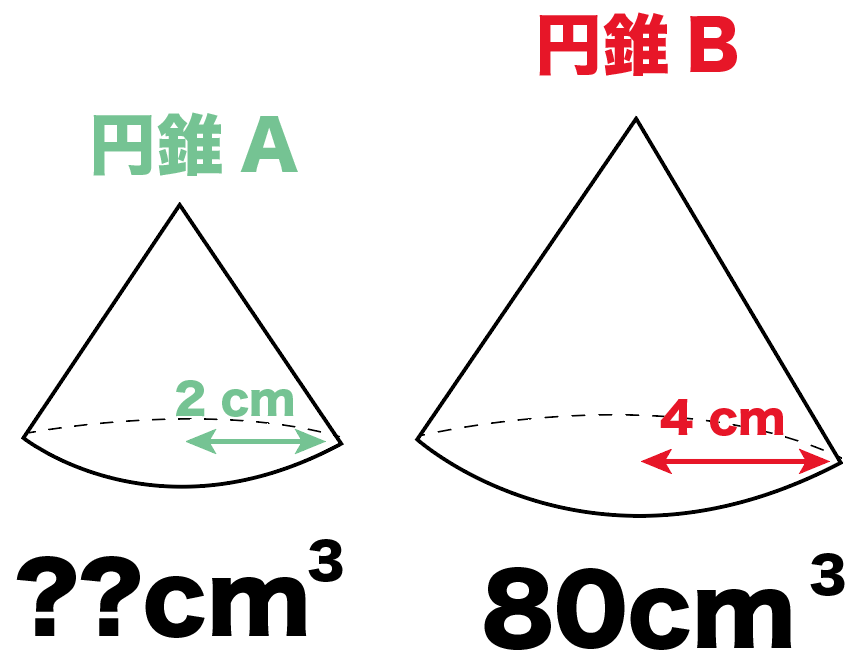
この2つの立体の体積比は、
1: 8だったよね??
ってことは、
「円錐Aの体積」は「円錐Bの体積」の8分の1。
ってことは、円錐Aの体積は、
(円錐Bの体積)×1/8
= 10 [ cm^3 ]
になるんだ。
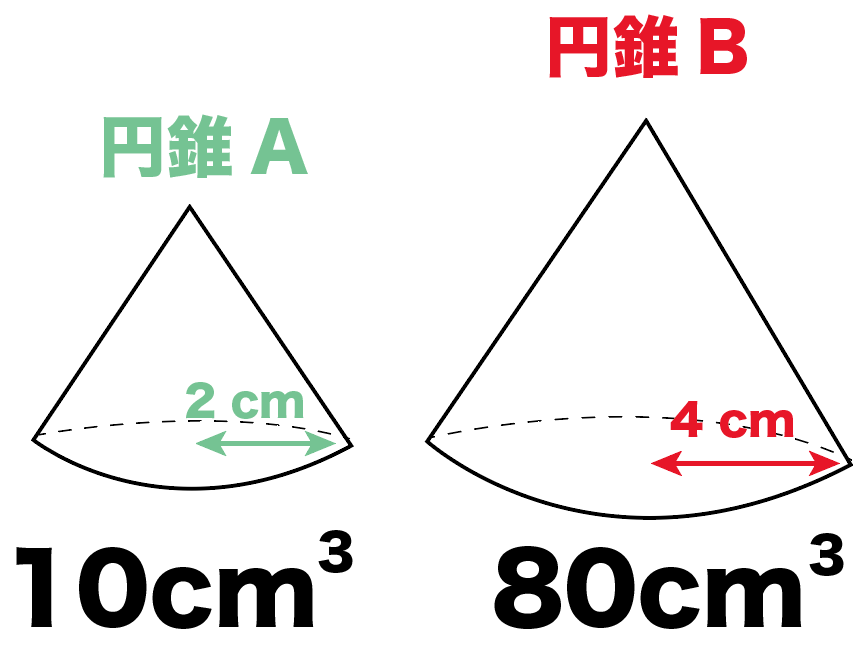
ね??
体積比をつかうと立体の体積がわかっちゃうんだ!
相似比から体積比が求められたね!
おめでとう・・・・・・!!
っていうのはまだはやい。
じつは、練習問題の最後に、
表面積の比も求めなさい
ってかいてあるじゃん?
せっかくだから、表面積の比も相似比から計算してみよう。
ずばり、表面積の比の求め方は、
面積比の求め方といっしょ。
つまり、
相似比の2乗の比になってるのよ。
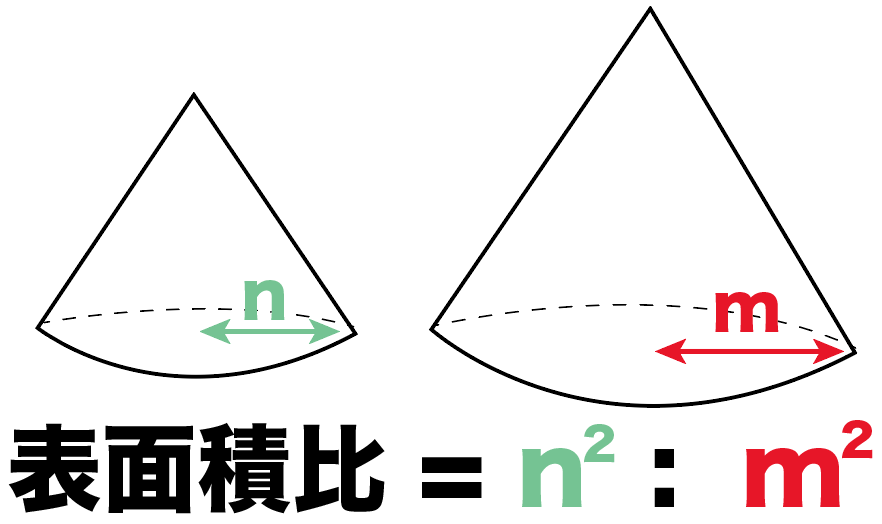
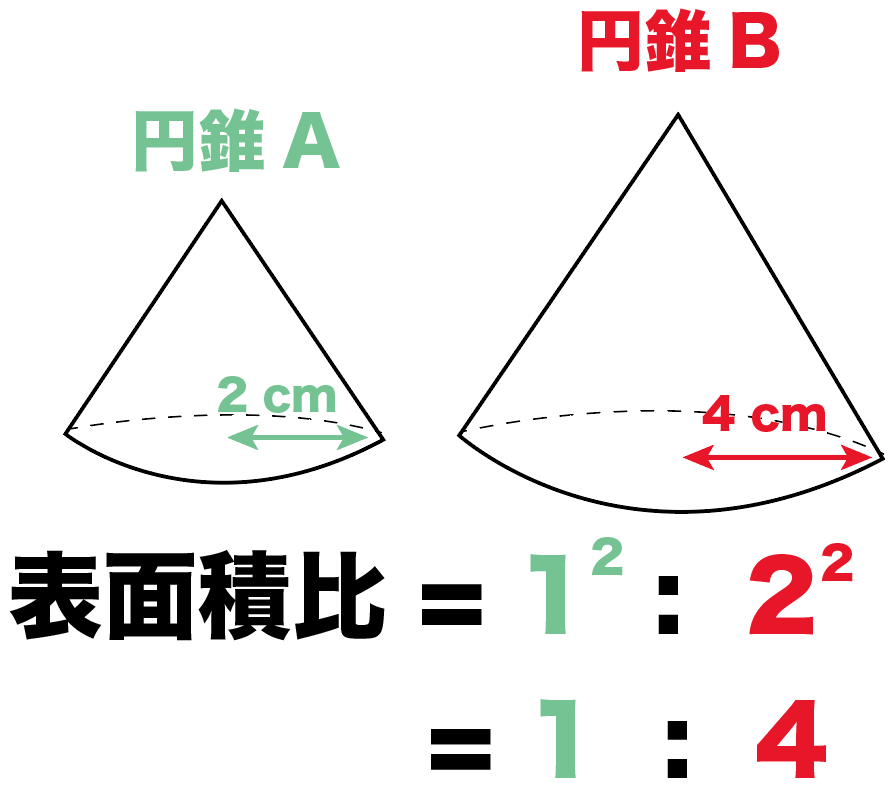
相似比が1:2の「円錐A・Bの表面積の比」は、
1^2 : 2^2
= 1 : 4
になるわけね。
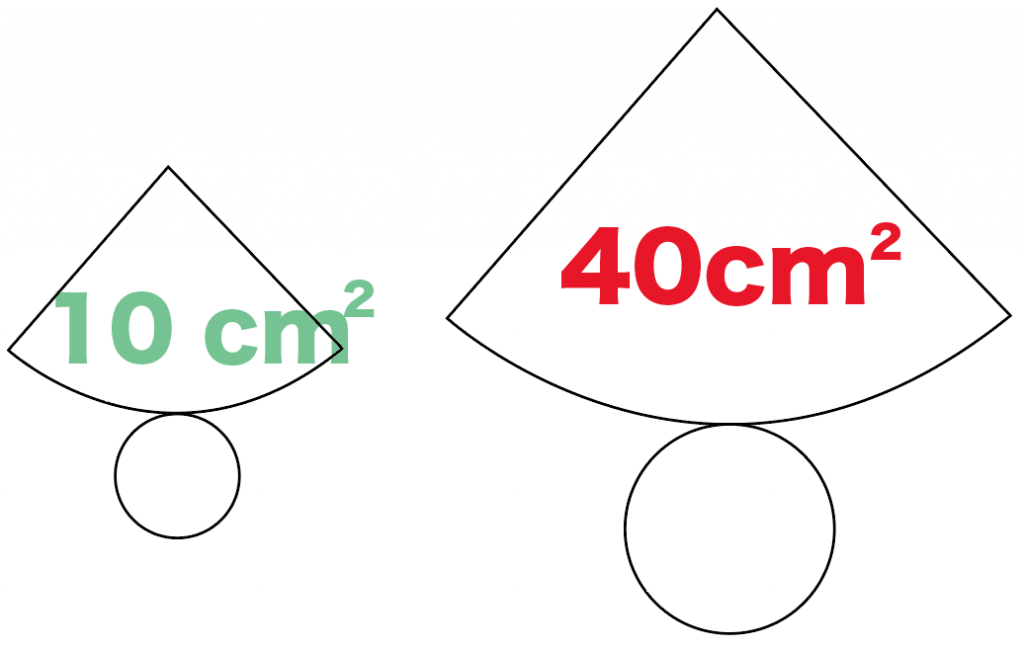
もし、円錐Bの表面積が40 [cm^2]だったら、
円錐Aの表面積は10 [cm^2]
になるわけだね。
おめでとう!
相似比から表面積の比も求められたね!
体積の比も、表面積の比も公式を覚えちゃえば楽勝。
しっかり公式を覚えてあげようね。
問題をときまくって段々なれていこう!
じゃあ、またね
ぺーたー
ある日、数学が苦手なかなちゃんは、
二次関数の利用の文章題に逆ギレしていました。
あー、もうやだ!!
なんで二次関数y=ax2でも、
文章問題でてくんだよ!?
あー、なるほどね、
うわあっ!?
先生か、びっくりした……
せっかく二次関数y=ax2に慣れてきたのに……
式が立てられないから、
解けないのかな?
!?
なんでわかるの?
先生って超能力者?
そういう人、結構いるよ。
1年、2年でも関数の文章題出てきたけどね
わたし苦手だった!
そんな文章題アレルギーっ子への朗報!
へっ?何??
えっ、そうなの?
そう!
基本のパターンを理解すれば……
じゃあ、二次関数の文章題を攻略しよう!
あれっ?
すごくやる気だね……
てへ!
二次関数の利用の文章問題には3パターンあるよ。
3つもあるんだ!
おもいやられるわ。
どれもわかりやすいから大丈夫!
順番にみていこう。
はい!!
1つめの文章題は、
xとyの表から式をよみとるだけ!
へ?
読み取るだけ??
そう!
たとえば、つぎのような問題ね。
練習問題1.
ボールが天から落ちています。
落下し始めてからの時間をx秒、
その間に落下する距離をymとします。
xとyの関係は以下の表の通りです。

このとき、
xとyの関係を式であらわしなさい。
xが1増えると、yが5増えて、
xが2増えるとyが20増え……
比例と全然違う!!
実は、これも比例なんだけどね。
じゃあ、1倍、2倍って考えてみよう。
xが2倍になると、yは4倍で、
xが3倍になると、yは9倍で……
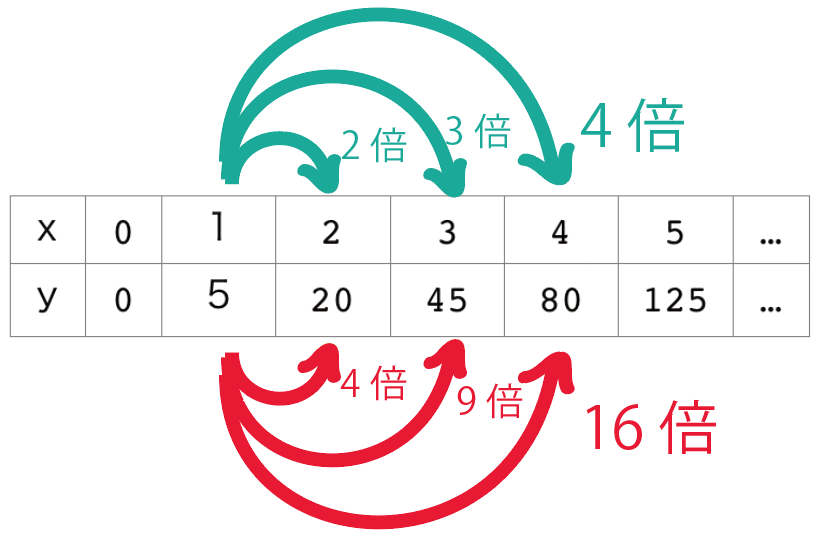
4,9,16って聞いて何か気付くことは?
あっ、何かの2乗になってる!!
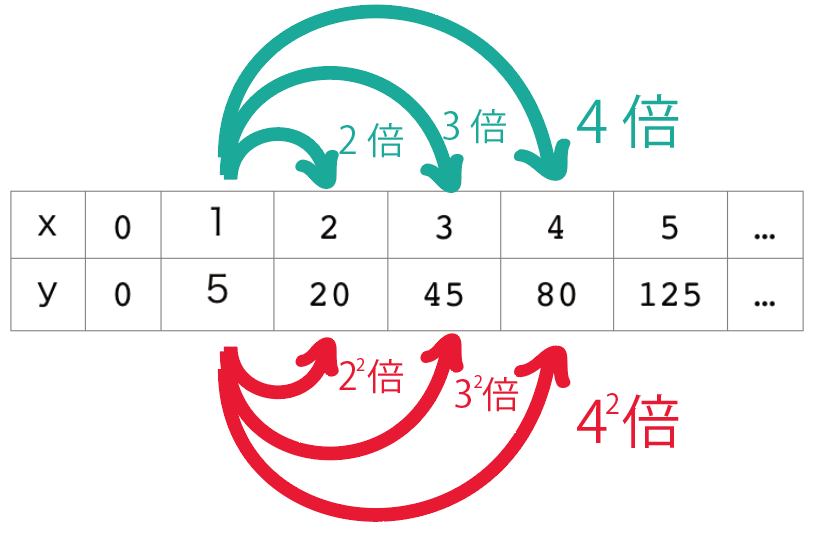
こんな関係のときに使うのが、
y=ax²!
なるほど!
この表の関数の式はどうなるかな?
xとyを「y=ax2」に代入すればよかったよね?
お、いいんじゃない?
x=1、y=5を代入して……
5=aになるから、y=5x²!
そう!
これで一つ問題が解けるようになった!
にやり
2つめの文章問題は、
二次関数y=ax2に代入するやつ。
代入かああ・・・
そうそう!
むずくないから大丈夫!
たとえば、つぎのような文章題だよ。
練習問題2.
振り子があります。
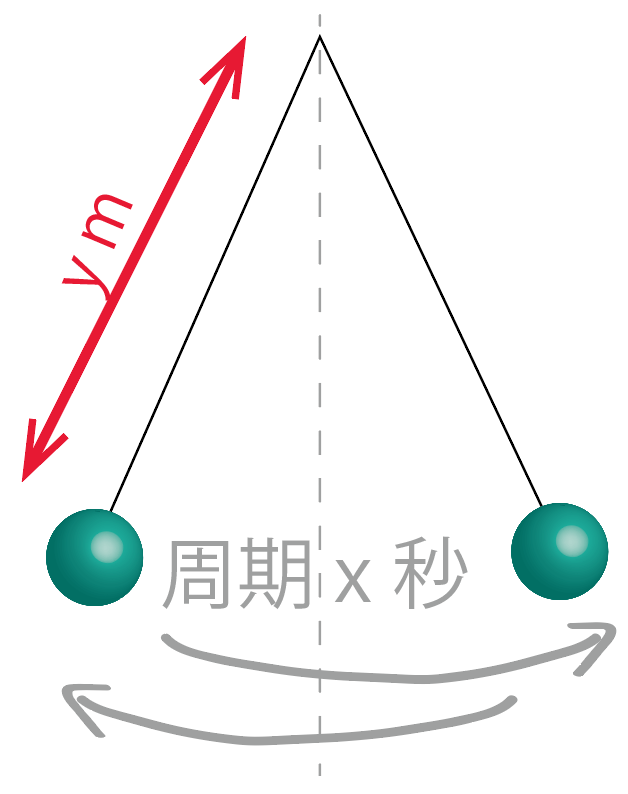
周期がx秒の振り子の長さをymとすると、
y=x²っていう関係になります。
周期が1秒の振り子の長さは何mでしょう?
振り子ってなんだっけ??
よく漫画ででてくるよ。
ワンピースでいうと、
ジャンゴ。
ポケモンでいうと、
スリーパーがもってるやつよ。
あ、あれか!
そこで、問題!
周期が1秒の振り子の長さは何mでしょう?
式に代入しちゃえばいいんだ!
周期はxだから、x=1を代入しよう。
y=x^2
= 1^2 = 1
になる!
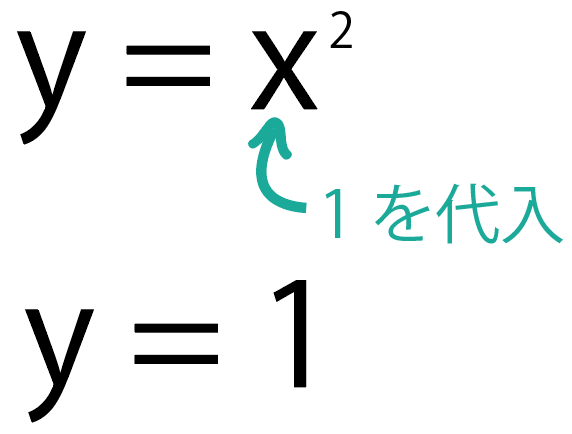
そう!だから、
振り子の長さ は1 m
になるよ!
いぇーい
二次関数y=ax2の変化の割合
をもとめる問題。
なんか、難しそう。
そんなことないよ!
たとえば、こんな問題!
練習問題3.
ボールが72mの坂を転がり始めてからの時間をx秒、
その間に転がる距離をymとします。
なんと、xとyには、
y=2x²という関係がありました。
このとき、1秒後から3秒後までの平均の速さを求めなさい。
また、xの変域もだしてね。
うわぁ、なんか、
文章題っぽい文章題でイヤだ。
でも、見て!
2次関数の式が問題に書いてある!
あっ、y=2x²のことかな?
そう。
もう一つ注目してほしいのは、
【平均の速さ】
どう注目すればいいの?
平均の速さは、
【変化の割合】と同じ意味を持っている!
え!なんで?!
じつは、このボール。
瞬間ごとにどんどん速さが速くなってるのよ。
だから、どっからどこまでの速さ
っていう平均の速さとらないと、
速さを特定できないわけよ。
なるほど・・・
まあようは、
二次関数の変化の割合
を求めればいいってことね。
そう!
解き方もおなじ!
おしい!
答え8だと、○がつかない!!
速さだから、
秒速8mだ!!
あ、
あと変域がのこってた
文章題の大切なポイント!
【実際にあり得る範囲が変域になる】
この問題だと、坂が72mしかないから、
この2次関数はy=72までしかない。
じゃあ、yの最小値はどこだろう?
0が一番小さいって覚えておくといいよ!
たしかに。
-1mとか、-2mって想像できない
じゃあ、yの変域は、0≦y≦72になるね。
xの変域を求めてみよう!
代入しちゃえばいいやつだ!
y=0のとき、x=0。
y=72のとき、
72=2x²
36=x²
x= ±6
ってあれ?
マイナスも出てきた!
そう!
でも、マイナスはあり得ないよね?
だって、秒数だもんん。
だから、
y=72のとき、x=6ってこと。
0≦x≦6だ!
そう、正解!
二次関数の利用って簡単かも!!
って思ってもらうのが、
今回の目的!
中学の二次関数はy=ax²しか出てこない。
基本のパターンが少ないんだ!
うんうん
レッツチャレンジ!
こんにちは!この記事をかいているKenだよ。犬なでたいね。
中3数学では、
相似
を勉強していくよ。
この単元を攻略するために知っておきたいのは、
三角形の相似条件
ってやつ。
これはどういうことかっていうと、
三角形が相似になるための条件
ってものなんだ。
つまり、相似条件を満たしていれば、
2つの三角形が拡大・縮小の関係にある
っていえるわけね。
大きくしたり小さくしたりすると重なるってわけ。
今日はこの、
三角形の相似条件をわかりやすく解説していくよ。
よかったら参考にしてみてね。
三角形の相似条件にはぜんぶで、
3つあるんだ。
使ってなれるのが一番だけど、
はじめは見ておぼえてみようか。
まずは一番使うことが多い、
2つの角がそれぞれ等しい
っていう三角形の相似条件。
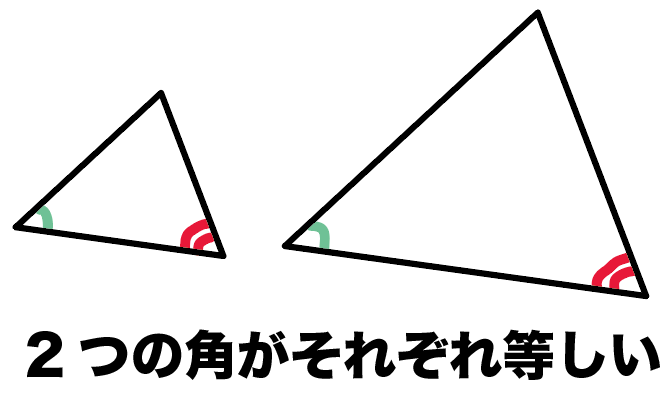
これは簡単にいっちゃうと、
2つの角が等しい三角形同士は相似
ってことがいえるの。
たとえば、そうだな。
つぎの△ABCと△DEFを思い浮かべてみて。
もし、こいつらの2つの角が、
ってかんじで等しかったとしよう。
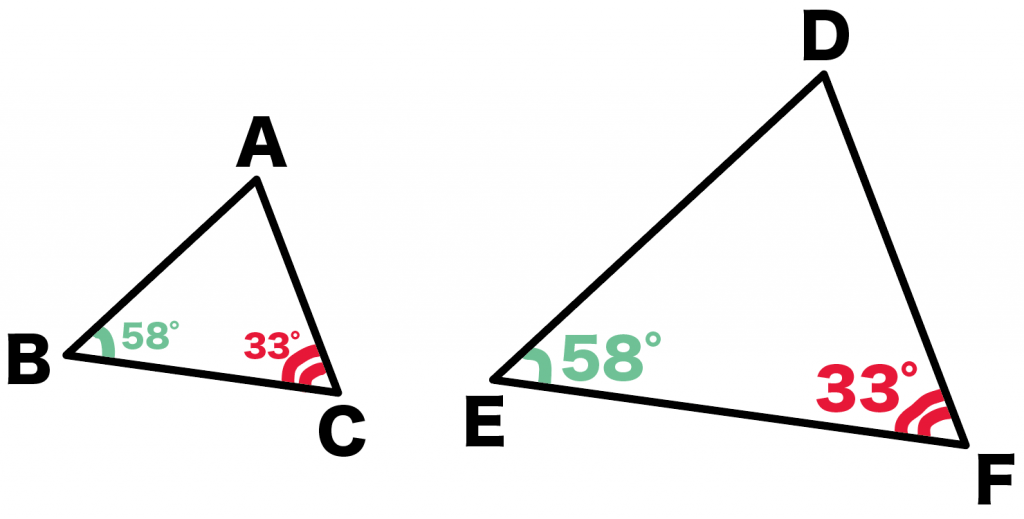
このとき、
△ABCと△DEFは相似な図形といえるんだ。
なぜなら、
2つの角がそれぞれ等しい
っていう三角形の相似条件をみてしてるからね。
の2つの角の組が等しいじゃん?
でもね、
もし、角Fがちょっと気まぐれで、
角F = 32°
になっちゃったとしよう。
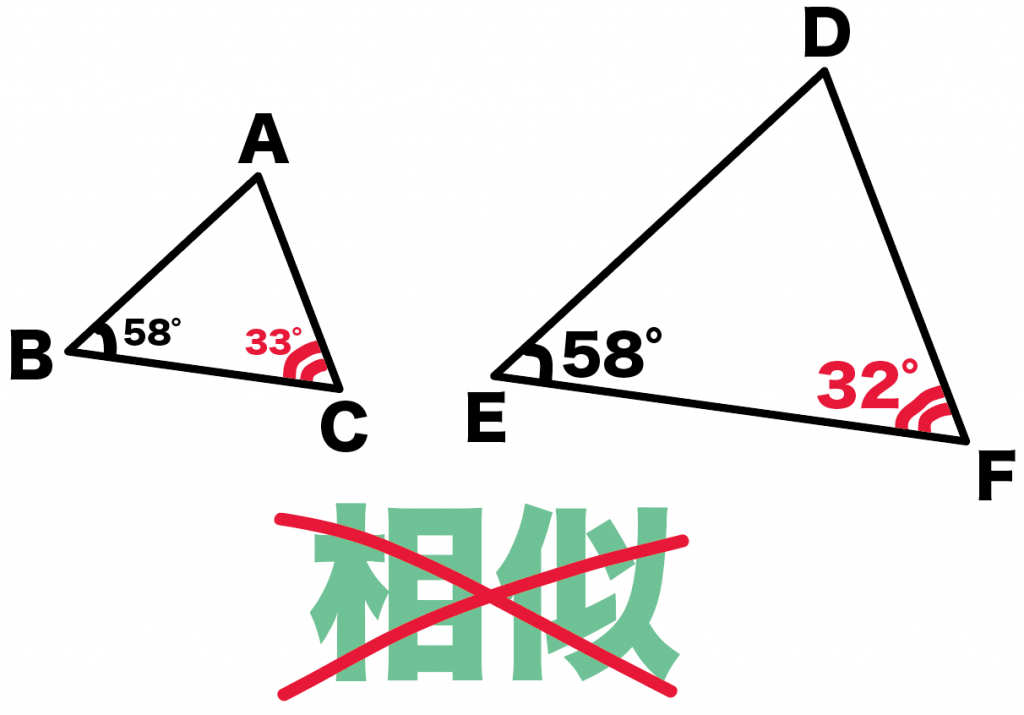
このとき、もうこいつらは相似なんかじゃない。
なぜなら、
1組の角(角Bと角F)しか等しくないからね。
こんなかんじで、
必ず2つの角が等しいかどうかチェックしようぜ。
2つめの三角形の相似条件は、
3組の辺の比がすべて等しい
ってやつだ。
対応する辺の比をそれぞれ計算してみて、
ぜーんぶ等しかったら相似っていえるんだ。
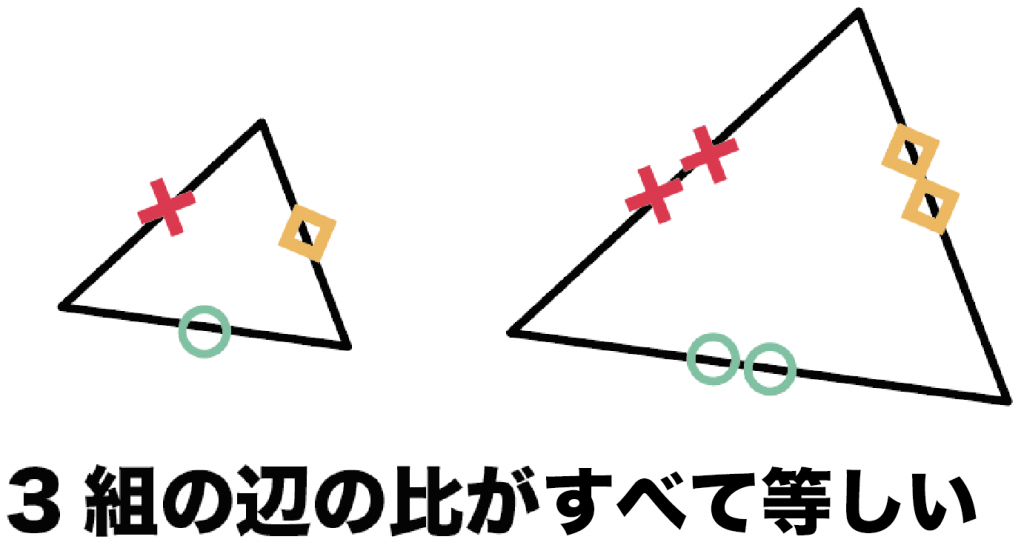
たとえば、△ABCと△DEFの辺の長さがそれぞれ、
だとしようか。
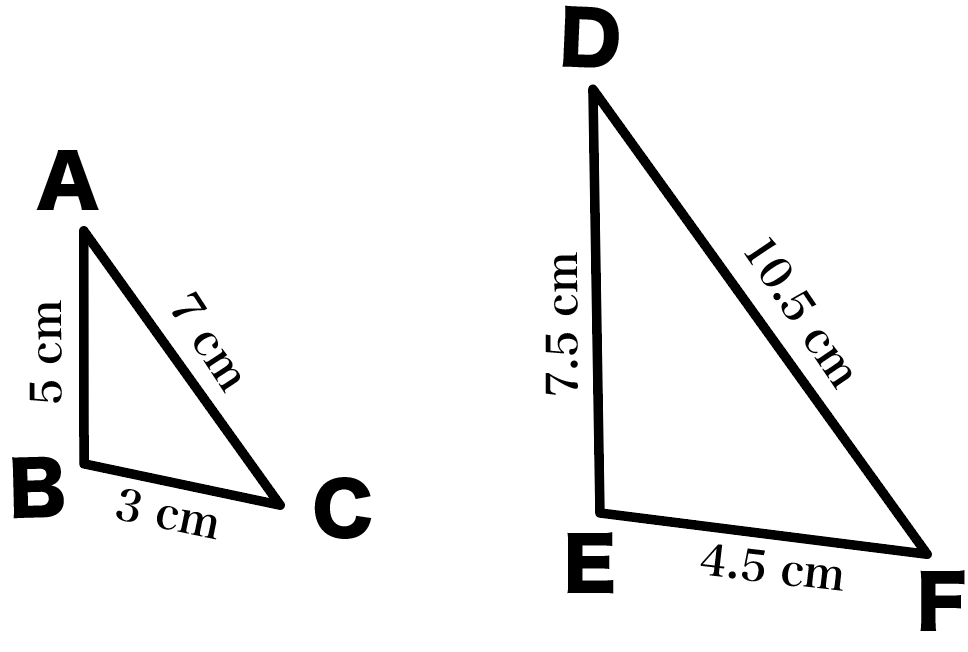
このとき、この2つの三角形たちは相似な関係にあるんだ。
なぜなら、
対応する辺どうしの辺の比がそれぞれ、
になってるからね。
ぜーんぶの対応する辺の比が「2:3」でいっしょ。
だから、
3組の辺の比がそれぞれ等しい
っていう相似条件をみてしてるっていえるわけ。
これはけっこうだるい相似条件だね。
最後の相似条件は、
2組の辺の比とその間の角がそれぞれ等しい
だ。
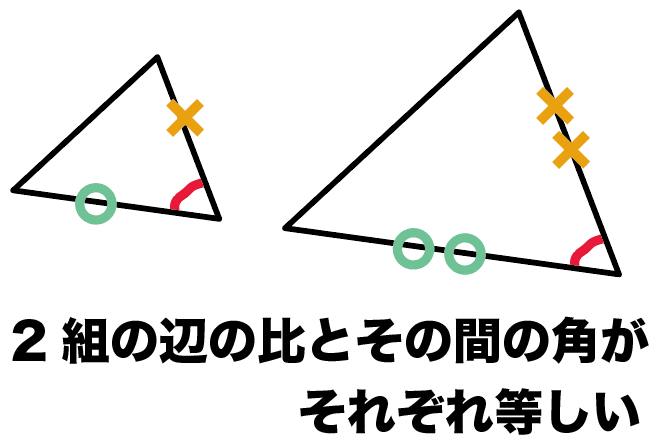
三角形の2つの辺どうしの比が等しくて、
なおかつ、
そいつらにサンドイッチされてる角まで等しい。
このとき、2つの三角形は相似であるっていえるんだ。
たとえば、△ABCと△DEFの2つの辺がそれぞれ、
だったとしよう。
んで、その2つの辺にはさまれてる角の、
が偶然、23°になってたとしよう。
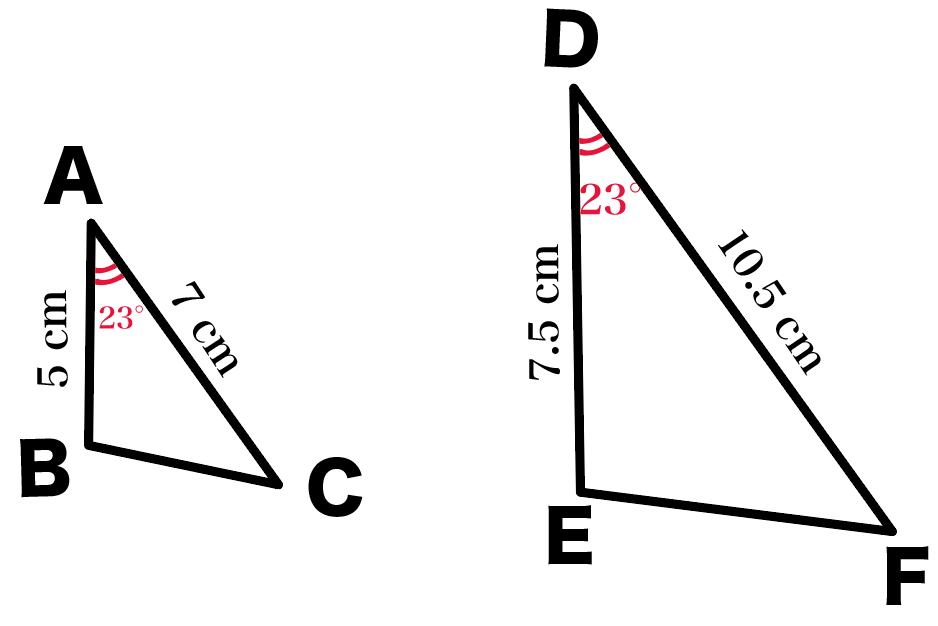
このとき、
△ABC ∽ △DEF
がいえるんだ。 なぜなら、
2組の辺の比が、
で等しくて、
なおかつ、その間にすっぽり収まってる、角Aと角Dが、
角A = 角D = 23°
になってるからね。
2組の辺の比とその間の角がそれぞれ等しい
っていう相似条件がつかえちゃうよ。
もし、もしも、だよ?
間にはさまってる角度が途中でごねて、
角D が 30°になっちゃったとしよう。
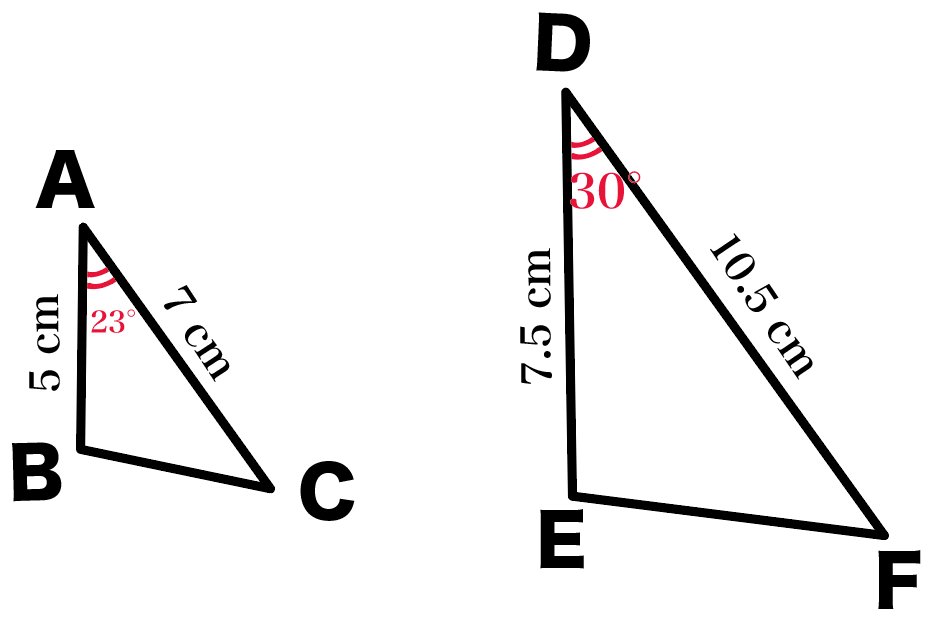
このとき、もうすでにこいつらは相似じゃなくなっちゃう。
なぜなら、2組の辺の比しか等しくないからね。
残念!!!!
えっ!?
三角形の相似条件がおぼえられないだって!??
そうだね。
そんなときは、
2組の角がそれぞれ等しい
っていう1番目の相似条件だけでもおぼえておこうw
なぜなら、
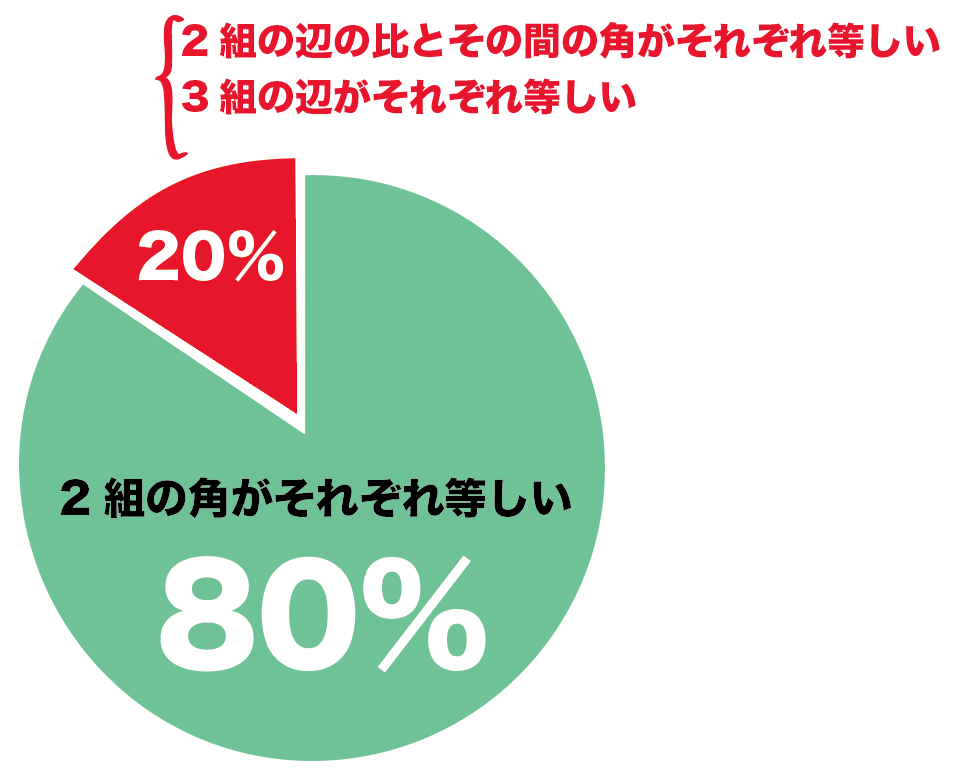
中学数学でつかう相似条件は、
だいたい80%が「2組の角がそれぞれ等しい」
だからね。
残りの相似条件の、
があとの20%をしめるってかんじ。
だから、
まあ、余裕がなかったら、
2組の角がそれぞれ等しい
だけでもおさえてね。
時間があるなら3つの相似条件をたたきこんでおこうぜ。
そんじゃねー
Ken
こんにちは!この記事をかいてるKenだよ。シロップはやさしいね。
中学数学では二次関数y=ax2を勉強するよね??
二次関数の問題にはたくさんあって、
放物線のグラフをかいたりしていくよ。
なかでも、テストにでやすいのは、
一次関数と二次関数の交点を求める問題
だ。
こんなふうに、
一次関数と二次関数y=ax2が交わっていて、
その交点を求めてね?
って問題なんだ。
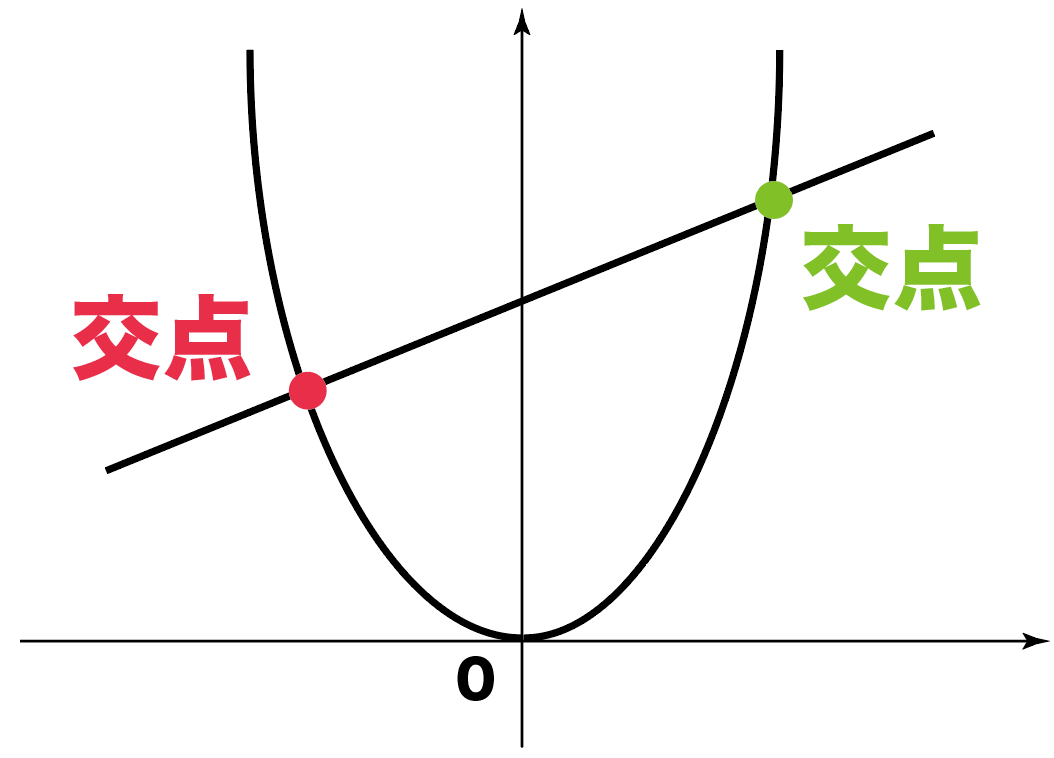
今日はこの問題の解き方をわかりやすく解説していくよ。
よかったら参考にしてみて。
さっそく交点をもとめてみよう。
たとえば、つぎの練習問題だね。
—————————————————————————–
練習問題
二次関数 y=x^2 と一次関数 y=x+6 の交点を求めてください。
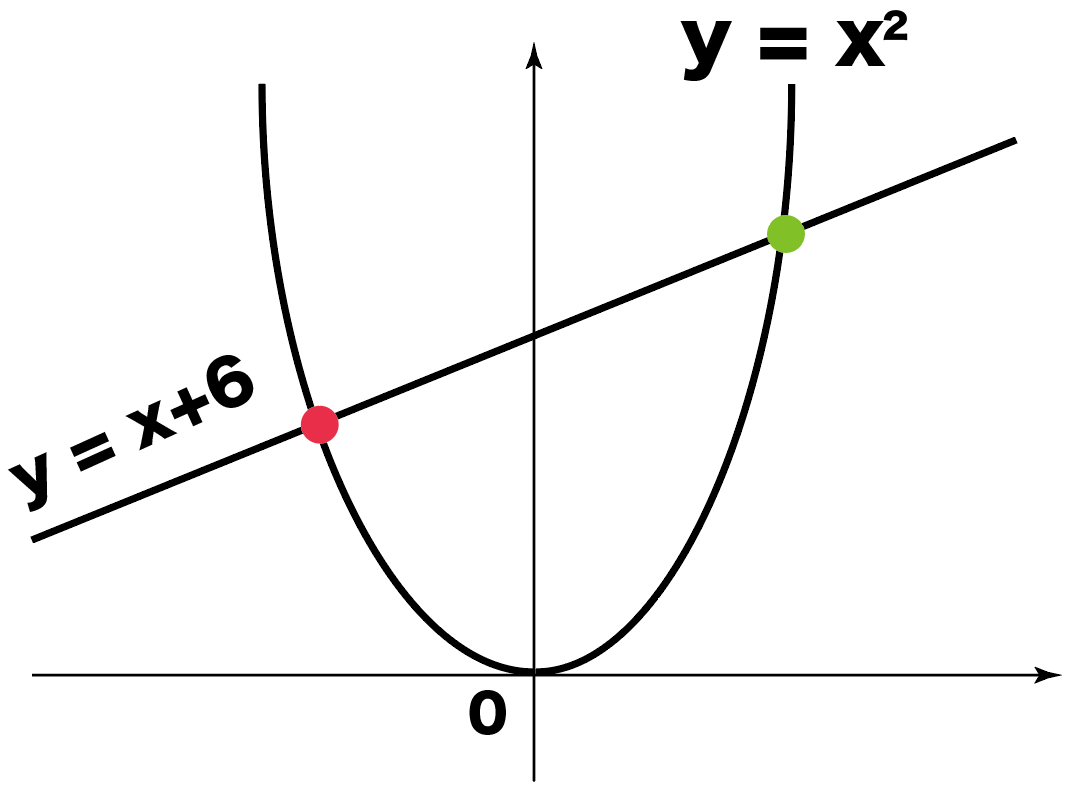
関数の交点を求めるには、
連立方程式をつくるのが一番。
一次関数のときにならった、
2直線の交点の求め方とやり方はおなじだね。
練習問題でも連立方程式をつくってみると、
こうなるね。
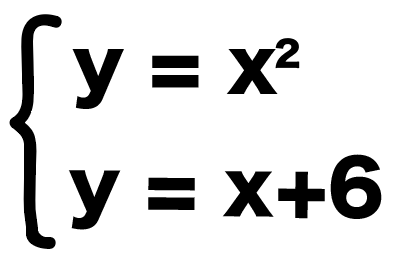
この2つの方程式から、xとyの値を求めていけばいいのさ。
さっそく連立方程式をといていこう。
連立方程式の解き方は、
の2つあったよね??
関数の交点を求めるときは、
代入法をつかっていくよ。
なぜなら、
「y =○○」になっていてyが代入しやすいからね。
つぎは二次方程式をといていこう。
二次方程式の解き方はたくさんあるけど、
どれをつかっても大丈夫。
練習問題の、
x^2 = x + 6
も解き方はいっしょ。
左辺にぜんぶの項を移項してみると、
x^2 – x – 6 = 0
になるね。
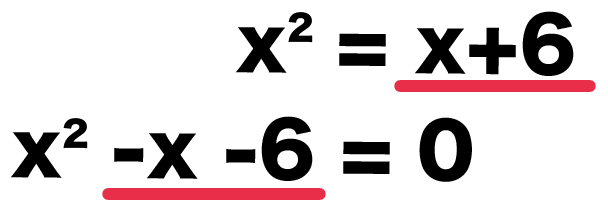
こいつを因数分解すると、
x^2 – x – 6 = 0
(x – 3) (x +2) = 0
になる。
あとは、どっちかが0になっていれば式がなりたつから、
この一次方程式をといてやると、
になるね。
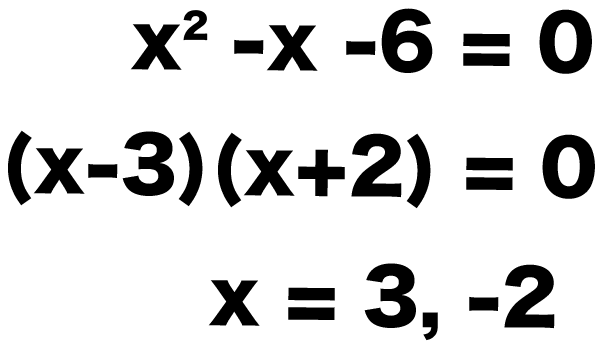
最後にxを関数に代入してみよう。
関数にxをいれるとy座標がわかるからね。
2つの交点のx座標が、
ってわかったよね??
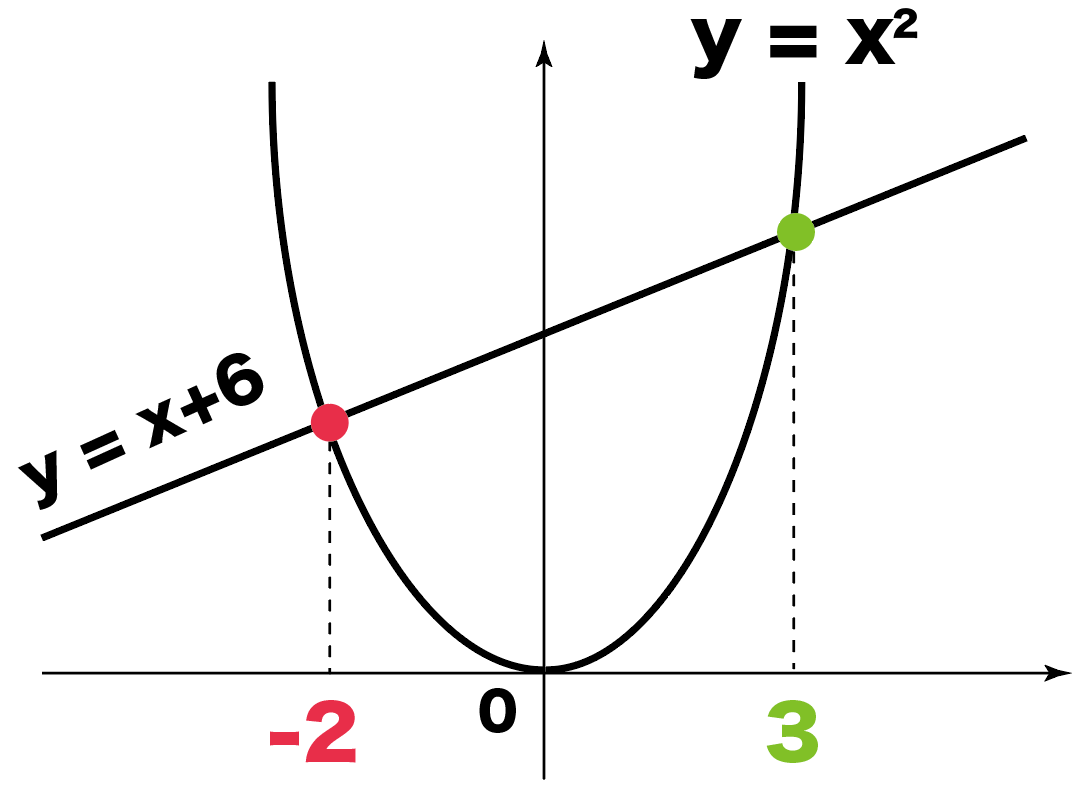
このx座標を、
「二次関数」か「一次関数」
のどっちかに代入するんだ。
今回は、そうだな、
簡単な一次関数「y=x+6」に代入してみよう。
すると、2つの交点のy座標は、
になる。
よって、2つの交点の座標は、
の2点になるね。
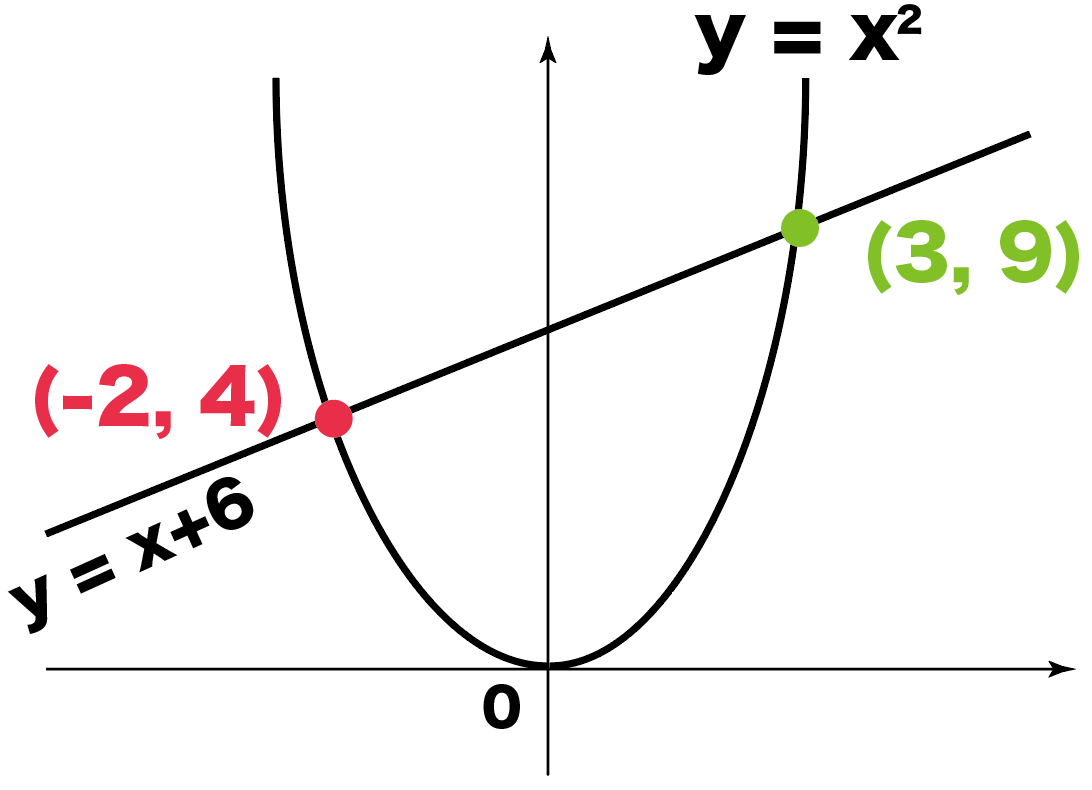
おめでとう!
これで一次関数と二次関数の交点が求められたね。
一次関数と二次関数の交点を求める問題はよくでてくるよ。
なぜなら、中学数学の総復習になるからね。
テスト前によーく復習しておこうね。
そんじゃねー
Ken
どーも、ぺーたーだよ。
中点連結定理をつかった証明問題はたくさん、ある。
なかでもよくでてくるのは、
平行四辺形であることを証明する問題
だ。
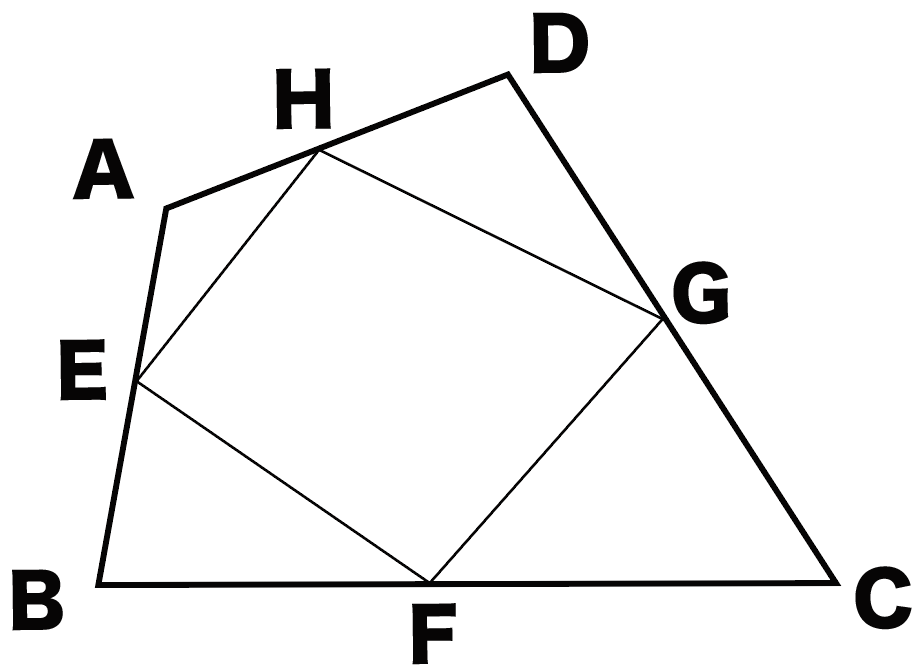
たとえば、つぎみたいな証明問題ね。
このとき四角形EFGHが平行四辺形になることを証明しなさい。
みんなけっこう難しいって
思ってるんじゃないかな?
今回はどうやって、
中点連結定理で平行四辺形を証明するのか
を3ステップで証明していくよ。
さっそく証明問題をといていくよ。
四角形ABCDの4辺AB、BC、CD、DAのそれぞれの中点をE、F、G、Hとする。
このとき四角形EFGHが平行四辺形になることを証明しなさい。

証明を始める前に1つだけやることがあるんだ。
それは、
対角線を1本かいてあげること!
そうするとこうなるね ↓↓
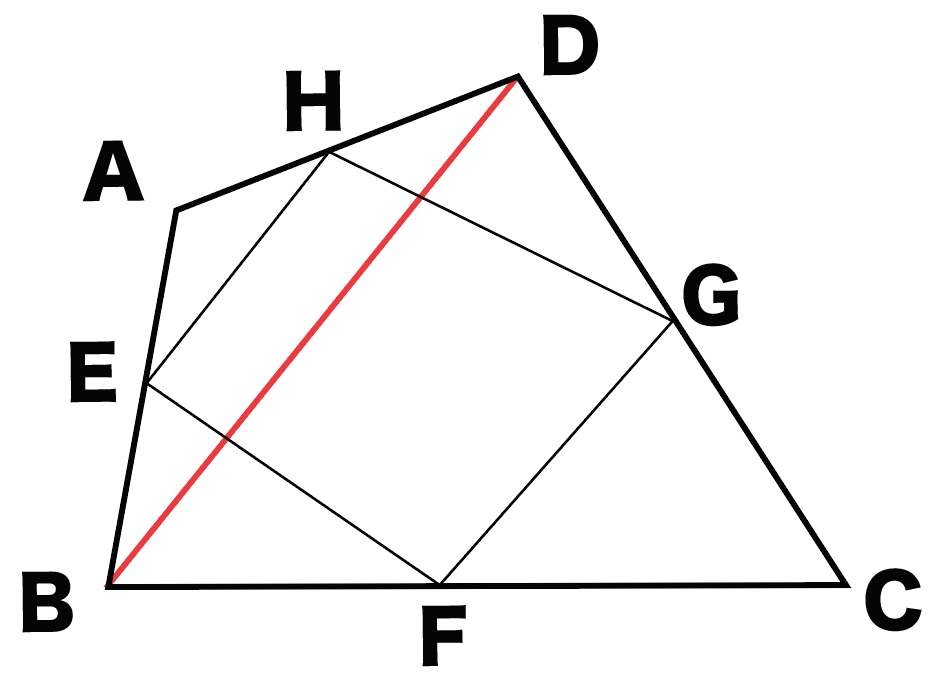
今回は、対角線BDをひいたけど、ACでも同じだからね。
対角線を引いたら、いくつか三角形が見えてくるよね?
練習問題でいうと、
の4つだね。

平行四辺形を証明するために
2組の三角形に分けてみてみよう。
まずは△AEHと△ABDに注目してみて。
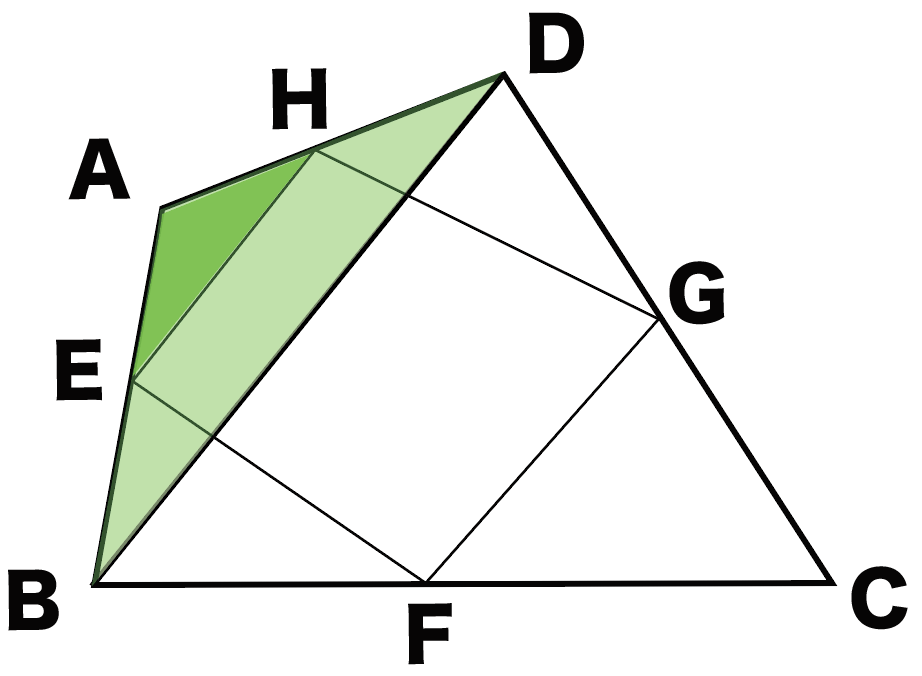
EとHはそれぞれ、
辺ABと辺ADの中点だよね??
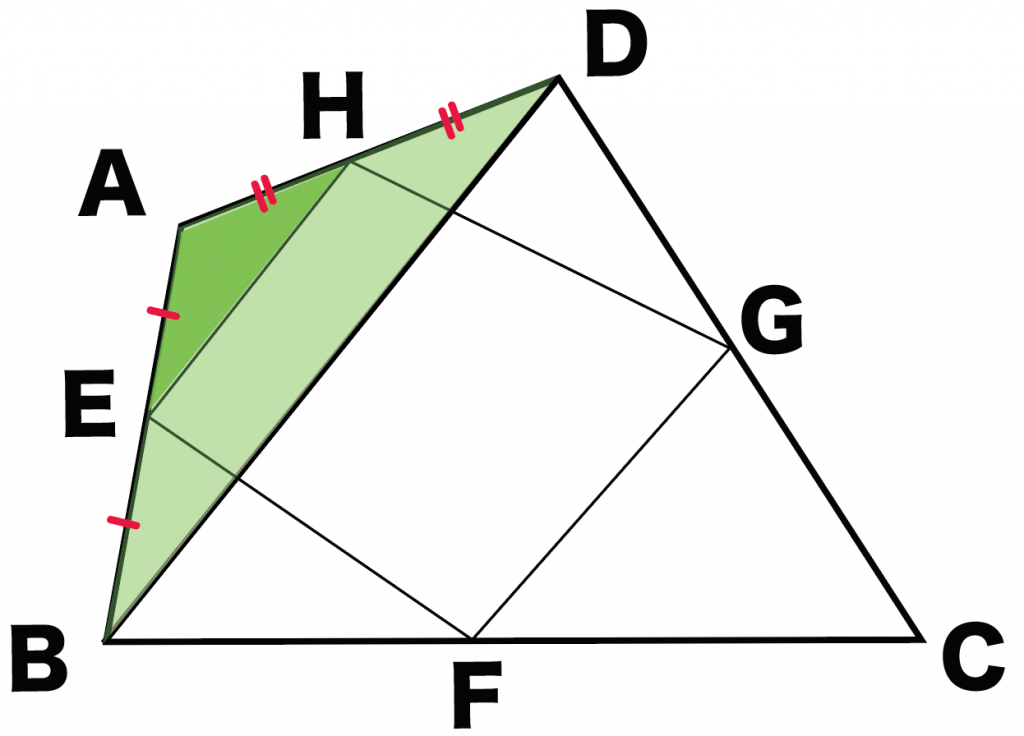
ってことは、中点連結定理をつかうと、
EH // BD・・・(1)
EH = 1/2 BD・・・(2)
がいえるんだ。
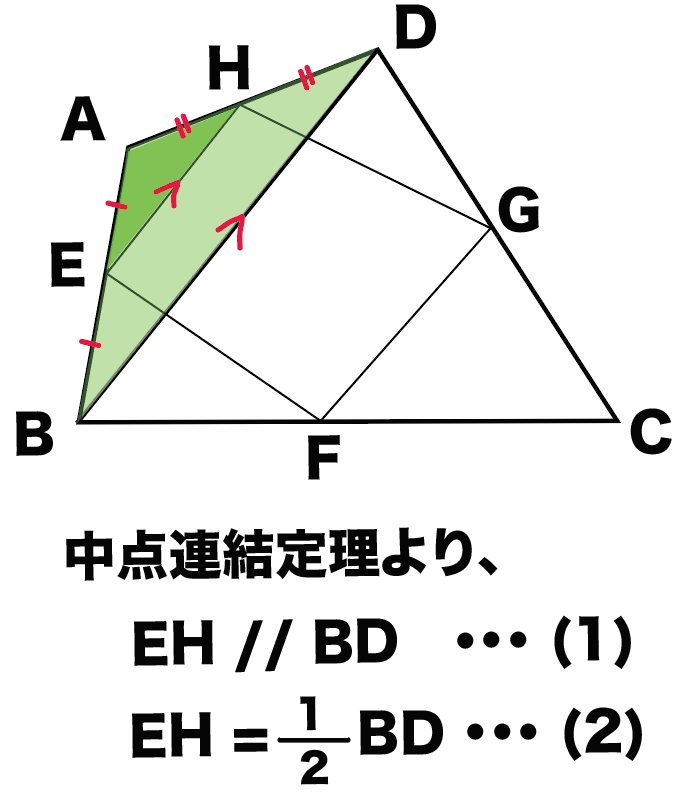
おなじことを△CGFと△CDBでもやってみよう。
FとGは、辺BGと辺DCの中点。
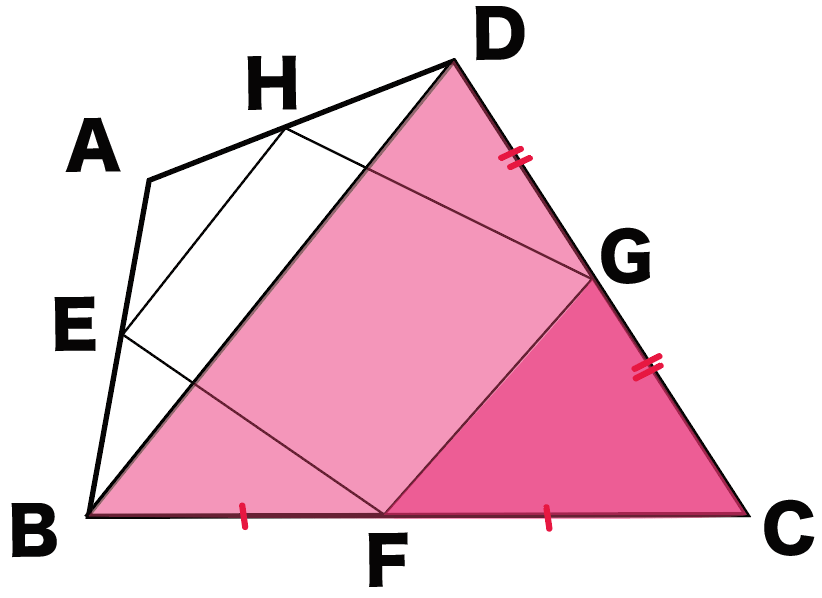
ってことで、中点連結定理がつかえるから、
FG // BD・・・(3)
FG = 1/2 BD・・・(4)
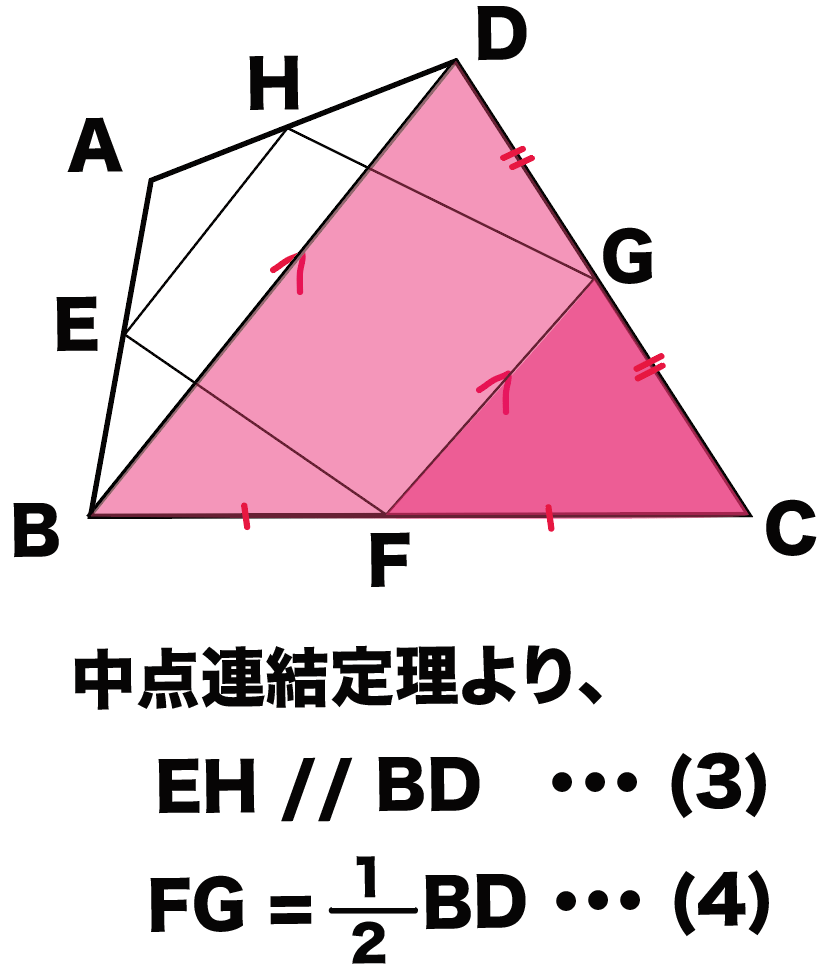
になるね。
最後は平行四辺形になる条件をつかうよ。
5つの条件を見なくても言えるかな?(。)
くわしくは平行四辺形になるための5つの条件をよんでみてね。
ちなみに、中点連結定理を使って平行四辺形を証明する問題は
1組の対辺が平行で長さが等しい
を使うのがほとんど。
今回もこの条件をつかうよ。
(1)と(3)から、
EH//BD//FGになるね。
つまり、
EH//FG・・・(5)
がいえるわけだね。
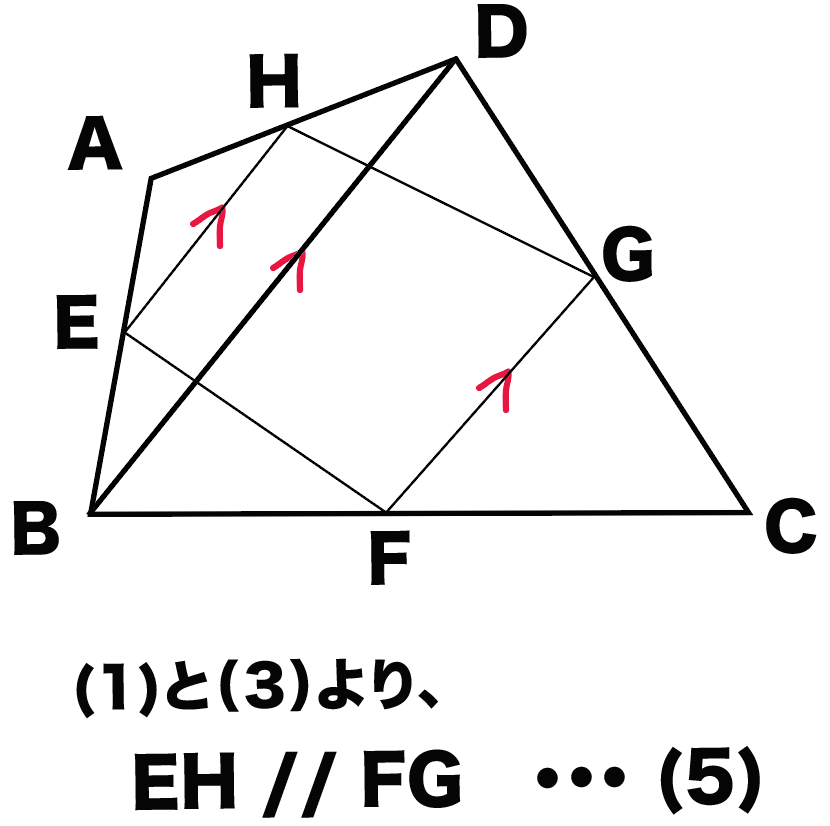
また、(2) と (4)から、
EH = FG = 1/2 BD・・・(6)
がいえるね。
EHとFGの両方がBDの半分になってるからさ。
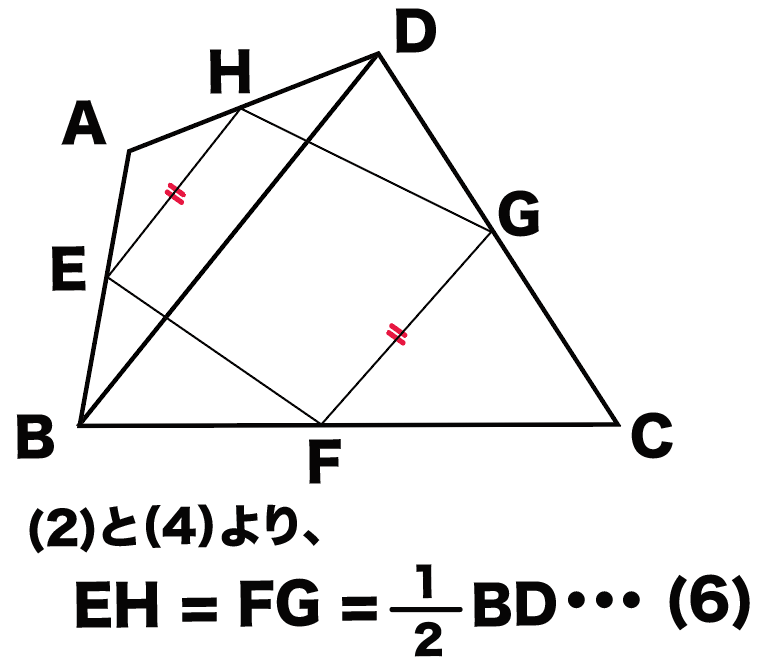
んで、
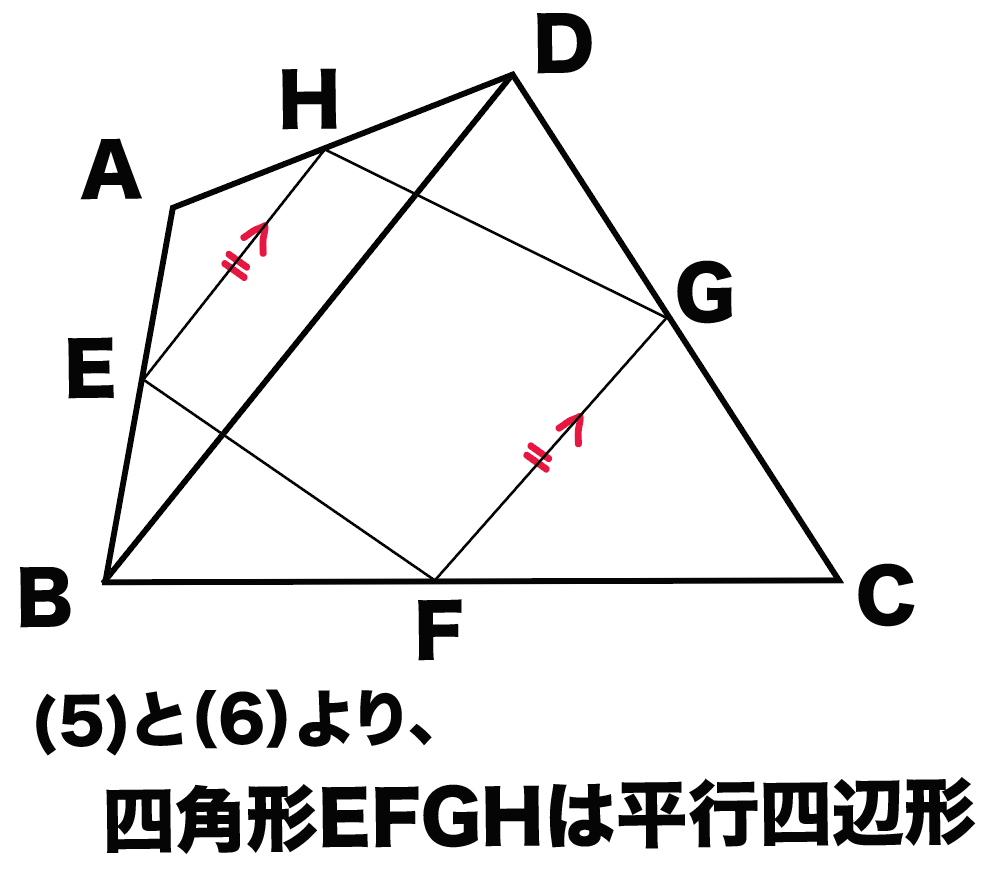
(5)と(6)より、平行四辺形になる条件の、
1組の対辺が平行で長さが等しい
がつかえるわけだね。
だから、
四角形ABCDは平行四辺形
ってわけ。
おめでとう!
これで証明おしまい!
中点連結定理をつかった平行四辺形の証明はどうだった??
この問題のポイントは、
対角線の補助線がひけるかどうか
だね。
平行四辺形を証明する問題は数をこなすのが一番!
おぼえるまで何回かといてみてね。
じゃあねー
ぺーたー
こんにちは!この記事をかいてるKenだよ。甘さを極めたね。
相似な図形で最後にでてくるのは、
相似の利用
っていうモンスターだ。
これはおもに、
相似を現実世界でもつかってみよう
というもの。
むちゃくちゃ実践的だから、
相似の証明より100倍ぐらいおもろいよ。
その相似の利用でよくでてくるのが、
縮図の問題
なんだ。
今日はこの問題を解説していくよ。
よかったら参考にしてみてね。
さっそく問題をといてみよう。
つぎの例題をみてみて。
映画「ザ・ウォーク」の主人公にまつわる問題なんだ。
練習問題
とある、むかし。
綱渡りで飯をくってる男が、いた。
野心が強すぎた彼は、ニューヨークの高層ビルに縄をかけて、
綱渡りしたいと思ってたのだ。
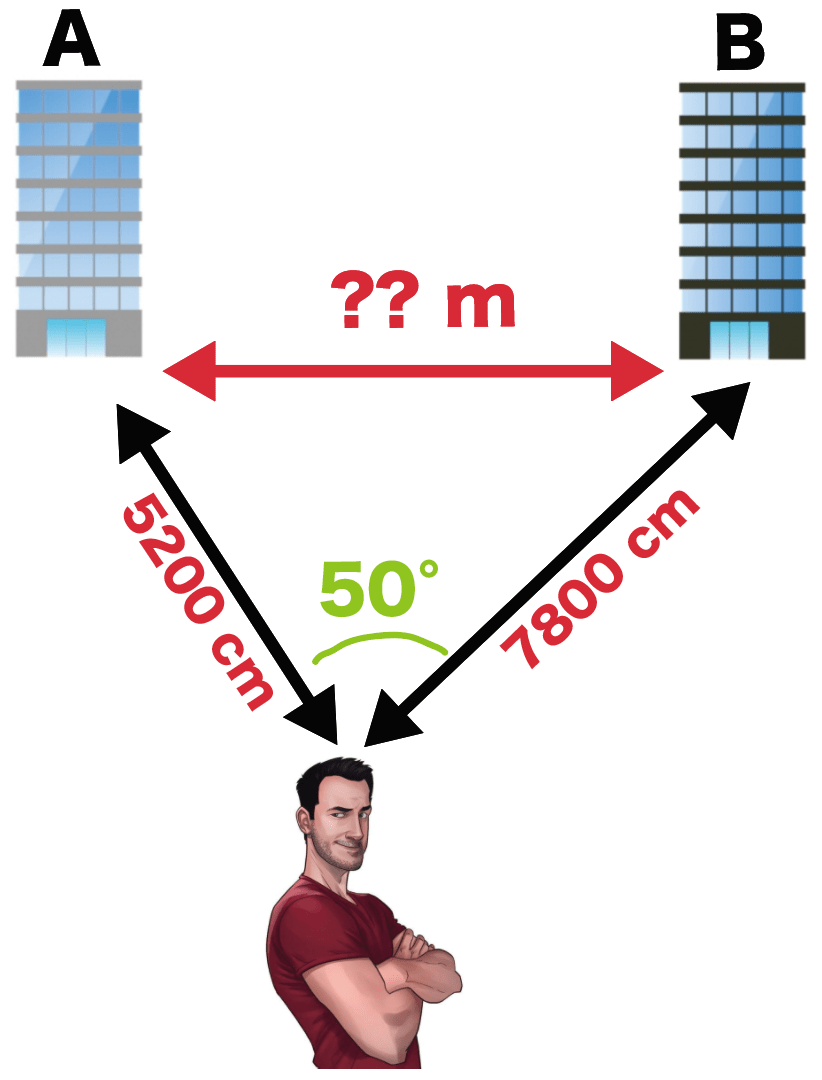
そこで、ビルとビルの間の距離を測らなきゃいけない。
縄をはらなきゃいけないからね。
ただ、いま彼がわかっているのは、
自分の現在地から2つのビルまでの距離
と、
角度
だけ。
だ。
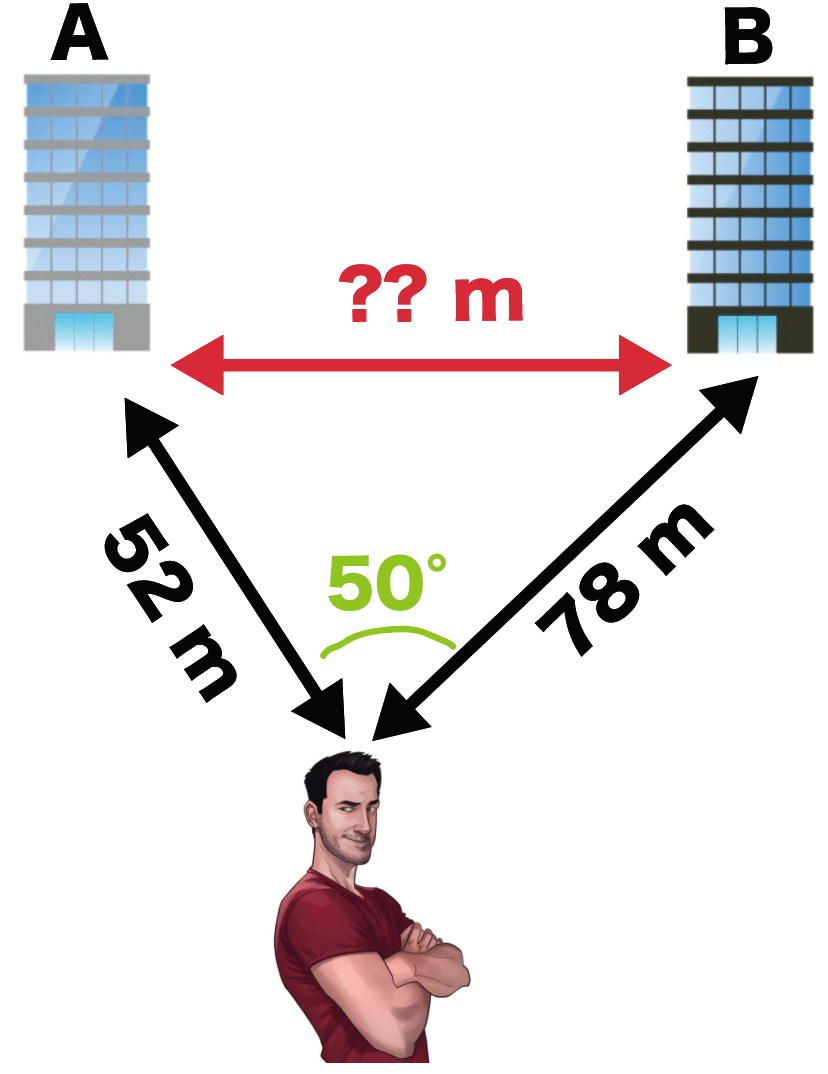
彼は縮図をつかって、
ビルの距離をはかることを思いついたのだった。
彼よりもさきに縮図でビル間の距離を計測しなさい。
ただし、400分の1の縮図をつかうこと。
この手の問題は3ステップでとけちゃうよ。
まずは縮図をかこう。
現実世界よりも小さい図をかけってことだね。
練習問題では、400分の1の縮図をつかえっていわれているから、
400分の1にした図をかいてみようか。
まずは、ビルまでの距離の、
をcmの単位になおしてみよう。
1m = 100cmだから、
だよね??
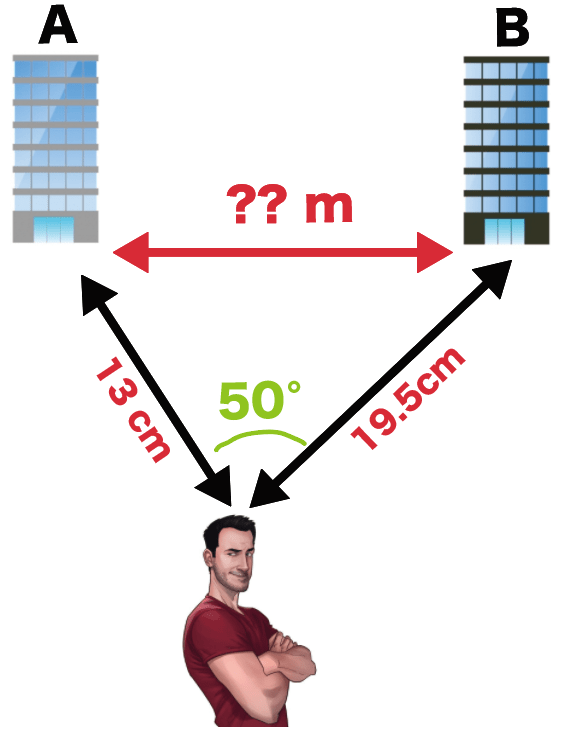
こいつを400分の1に小さくすると、
になる。
実際に縮図を作図してみよう。
まず男がいる地点を縮図上に点をうつ。

つぎに、適当な方向に13cmの線を、ひく。
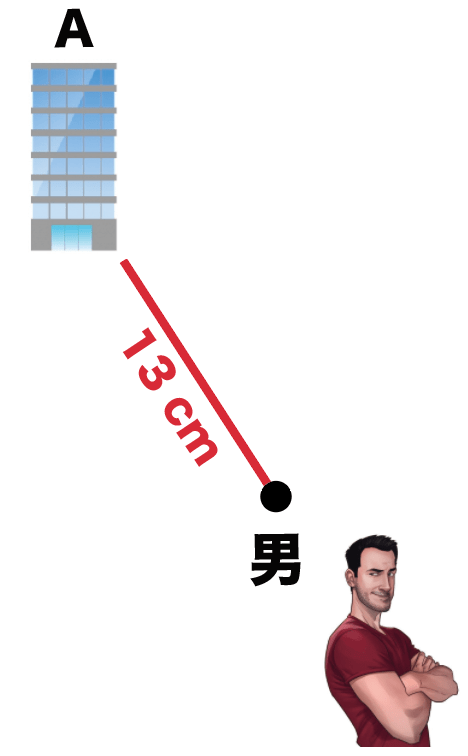
これは男からビルAまでの縮図上の距離だね。
つぎは分度器の出番。
分度器で男の点から50°をはかって、
適当に直線をひいてみよう。

そしたら、今度は男からビルBまでの縮図上の距離の、
19.5cm
をはかってあげる。
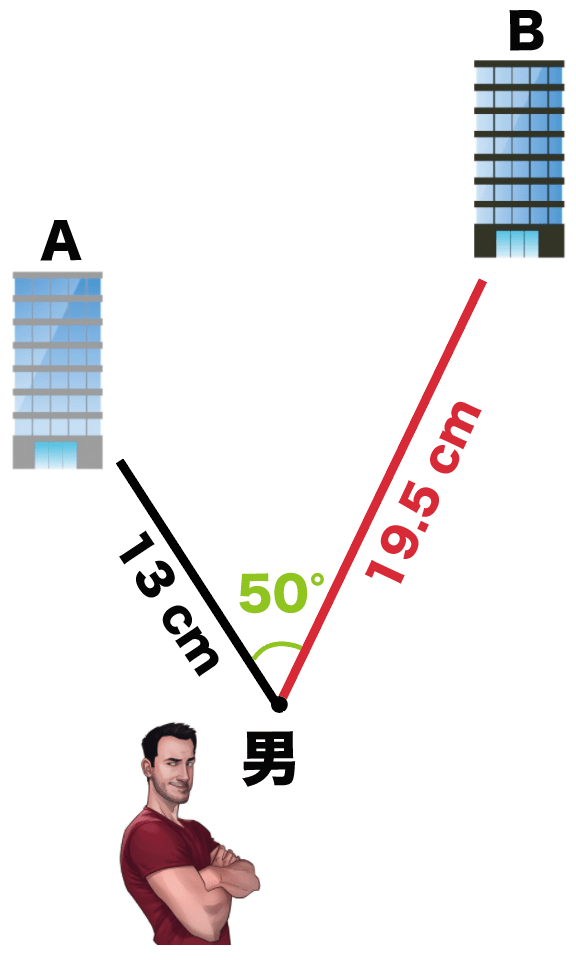
あとは、ビルとビルの間を線でむすぶだけ。
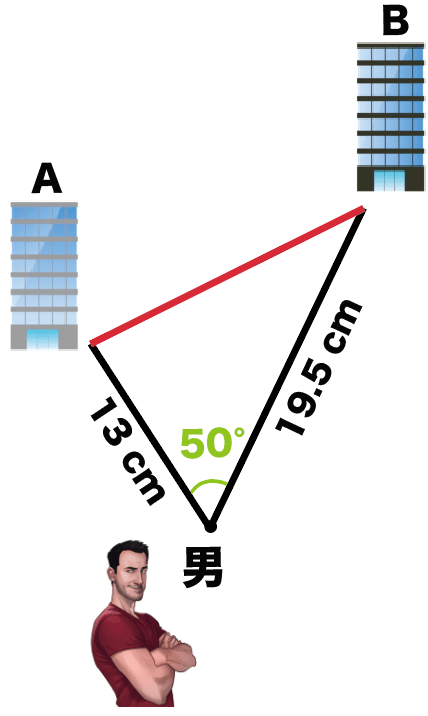
これで縮図の完成だ!
つぎは、縮図の長さをはかろう。
問題で求めたい長さ
をはかればいいんだ。
練習問題では、
ビルAとビルBの距離
だったよね??
縮図上で、2つのビルの距離をはかってみると、
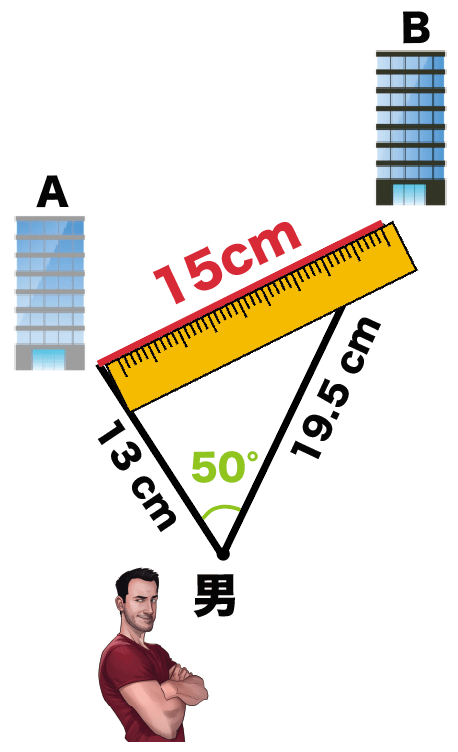
うわっ!
15 cm
になってるじゃん!!
最後はリアルな長さにもどしてあげよう。
つまり、
縮図の倍率をかければいいのさ。
今回の練習問題では、
400分の1の縮図だったね??
だから、縮図を400倍してやると、リアルな大きさになるわけよ。
ビルとビルの間は縮図上は15 cm。
こいつを400倍すると、
リアルな世界のビルとビルの距離になるんだ。
ってことで、リアルな世界のビル間の距離は、
15 × 400
= 6000 cm
= 60m
ってわけだね。
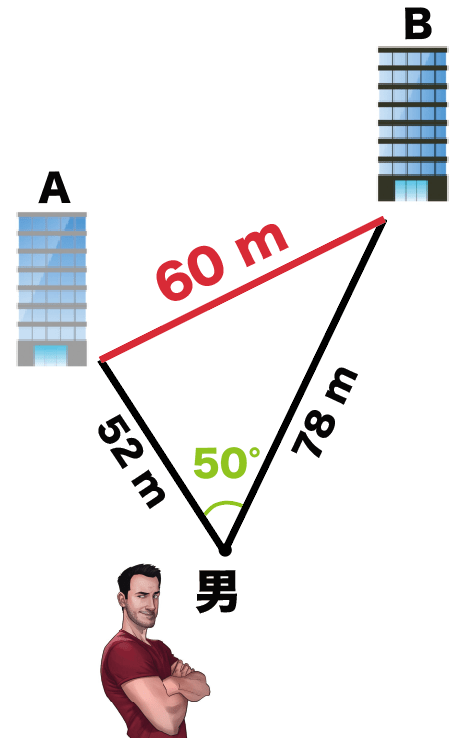
縮図からビルとビルの距離を求められたね。
あとは、60m以上の縄を買って渡るだけだ。

ふぁいつ!
相似の利用の縮図はどうだったかな??
ぶっちゃけ、相似の利用の縮図問題は、
作図の正確さ
が重要になるんだ。
分度器と定規で精密な作図をしてみてね。
それじゃあ!
Ken
ある日、数学が苦手なかなちゃんは、
相似と合同の違いがわからなくなってしまいました。

どっちも図形の問題だね。
いっとくけど、
相似と合同はべつものだよ。
えー!
でも、2つの図形を比べるとか、
ちょっと似てない?
どっちかわかんなくなる。
確かに、ちょっと紛らわしいかも。
違いを見つけていこう!
ういす!!
相似と合同の違いはつぎの3つかな。
3つもあるんだ!
たいへん!!
ゆっくりみていけば大丈夫。
それじゃあいくよー!
まずは言葉の意味から!
えっと・・・・
合同が「同じ」で、
相似が「似る」・・・・・?

うわ! ぴったり重なった!!
すげえ!
じゃあ相似は??
こんな感じで、形は一緒だけど、
大きさが違う!

なんか、拡大コピー見てるみたい。
そうだね!
小6で出てきた『拡大と縮小』を思い出せるといいね。
あー!あいつか!
対応している角度
と
辺の比
が等しくなっているんだ。
へー!
くわしくは、
相似な図形の性質を復習してみてね。
相似と合同では、
成立条件
に違いがあるよ。
せいりつじょうけん??
へー!
合同条件と相似条件ってことかな??
そうそう!
三角形の相似条件と合同条件をみてみよっか!

パッと見ただけじゃわからない…
じゃあ、
1つ目の条件を見比べてみよう!
1つ目?あっ!
相似は辺の「比」が等しいけど、
合同は辺の「長さ」が等しいとこかな!
そう!
図で表すとこんな感じ。
下の三角形は辺の比が1: 1: 1だから、
辺の比が等しい。
だから、相似っていえる!
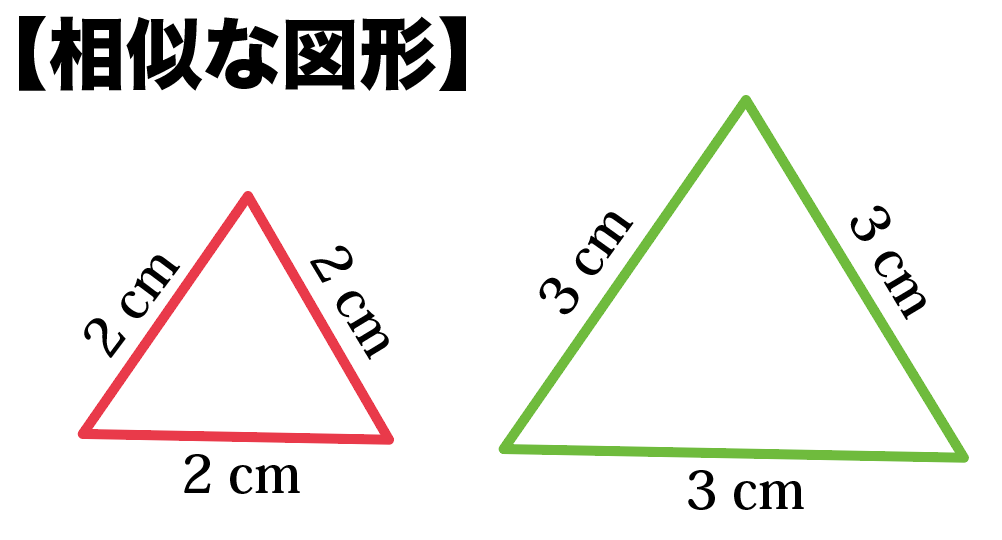
なるほど!
一方、
辺の長さがぜーんぶ等しかったら、
合同っていえるわけ。
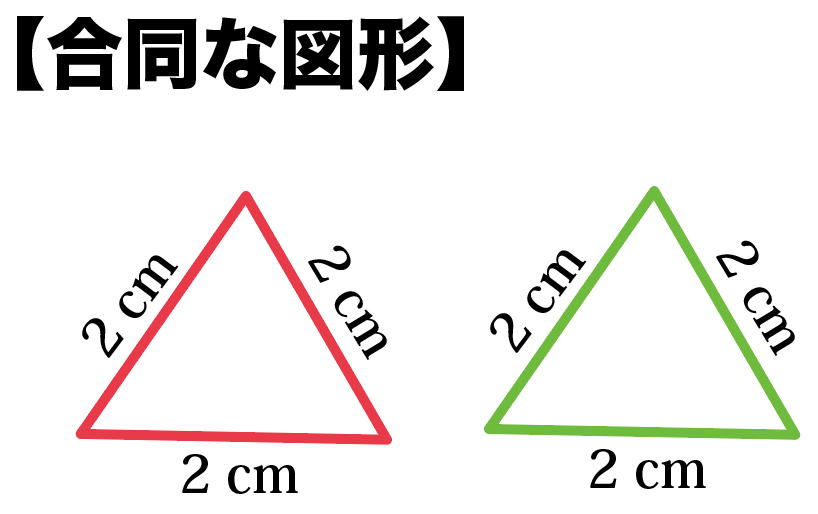
なるへ!
くわしくは、
「三角形の合同条件と相似条件の違い」
をよんでね。
記号の違いもある!
今回紹介する最後の違いだ!!
うす!!
相似と合同の記号のはつぎのやつだよ↓↓

めっちゃ違うじゃん!!
そうだね。
相似記号は、
アルファベットのSを横に倒したような記号。
合同記号は、
=に一本書き足したような記号
になっているね。
書き間違えないようにしようっと!
どう??
相似と合同の違いはわかったかな??
えっと、
『合同』は全く同じ図形だから、辺の長さまで同じ。記号は『≡』。
『相似』は似ている図形だから、辺の長さの比が一緒になる。記号は『∽』。
完ぺきじゃん!
『似ているけど同じじゃない』
それが『相似』だ!
やったあーー!
やあ、ぺーたーだよ。
中3になると、相似を勉強するよね。
覚えること多くて大変。
相似の証明したり、相似比を求めたり…ほんといろいろ。
中でもよくでてくるのが、
相似比から面積比を求める問題。
むずかしそうにみえるけど、公式さえ分かってれば大丈夫。
面積比は絶対に求められる!
今日はこの面積比の公式を紹介していくよ〜
面積比にはつぎの公式があるよ。
「面積比」は「相似比の2乗」になる
ってやつだ。
たとえば、△ABCと△A’B’C’の相似比が「n:m」だとしよう。
このとき面積比は、
n² : m²
になってるんだ。
せっかくだから、この面積比の公式をつかってみよう。
つぎの2つの三角形をイメージしてみて。
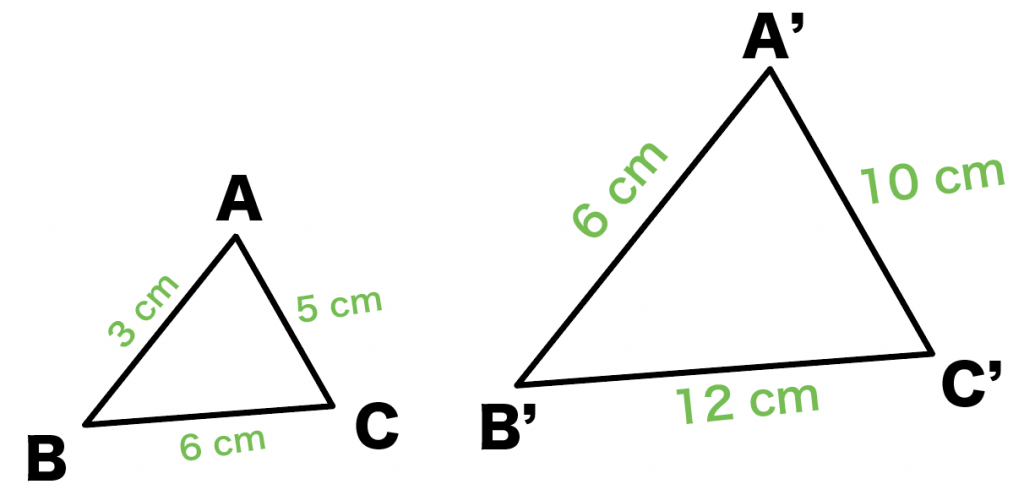
△ABCと△A’B’C’の辺の長さがそれぞれ、
と、
になってるよ。
この2つの三角形の面積比をだしてみよう!
公式なら2ステップで面積比だせちゃうんだ。
まず相似比を出してやろう!
相似比の求め方は覚えてる??
相似な図形同士の、
対応する辺の長さの比
を求めればよかったね??
今回でいうと、辺ABに対応する辺は辺A’B’。
AB=3cm, A’B’=6cmだから、
相似比は、
AB : A’B’
= 3: 6
= 1 :2
になるね。
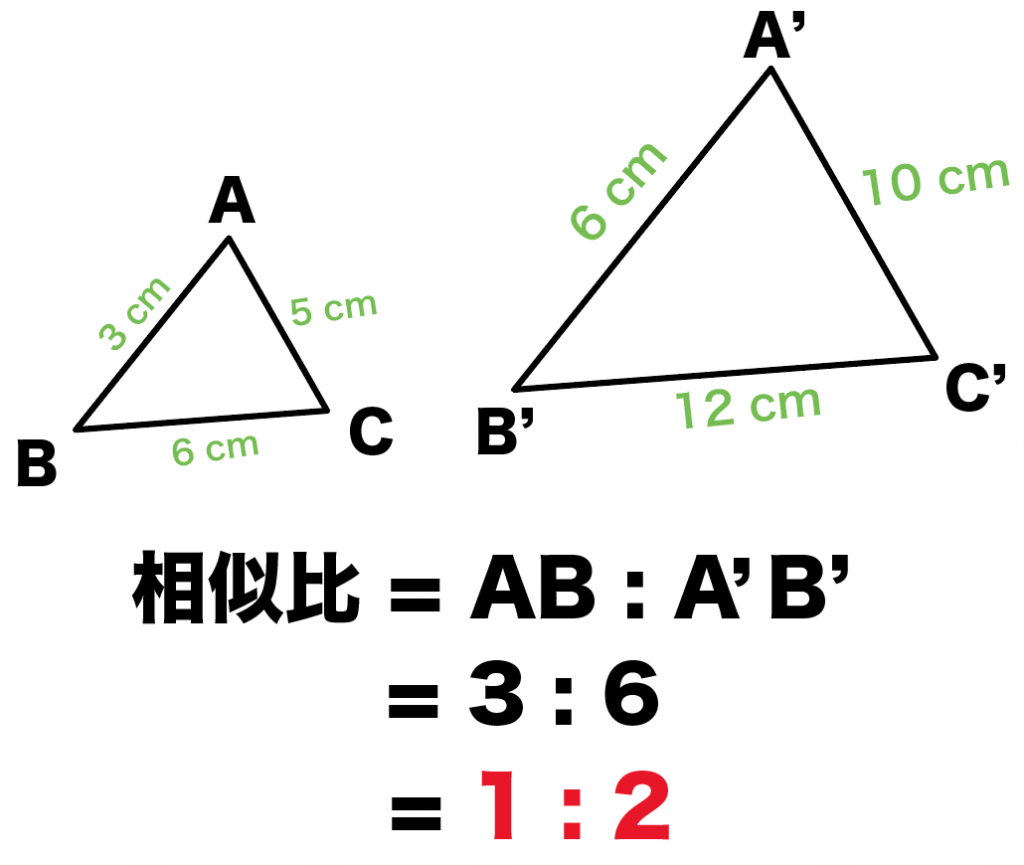
相似比が出ちゃえばあとは簡単。
相似比を2乗すれば面積比がでるってわけ。
△ABCと△A’B’C’の相似比は、
1: 2
だったね??
面積比は2乗してやった比の、
1² : 2²
= 1 : 4
になるはず!
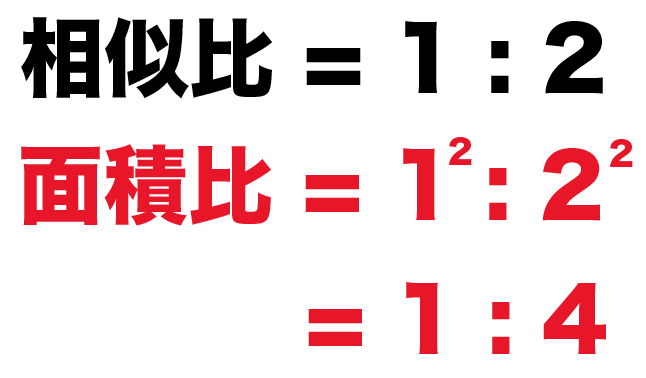
おめでとう!
相似比から面積比を計算できちゃったね。
面積比の公式でもう1つ問題を解いてみよう。
公式はつかっておぼえるのが一番!
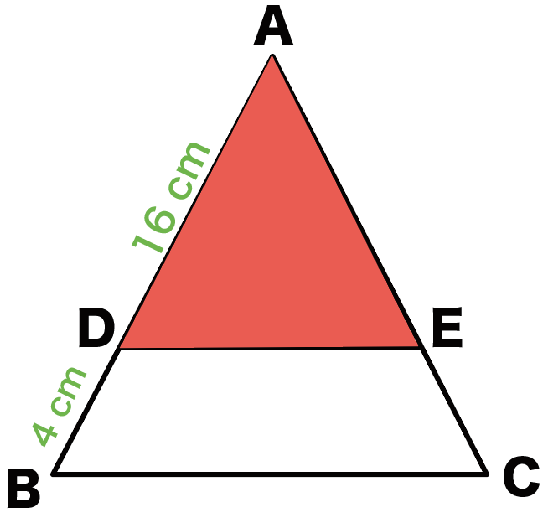
つぎの図の△ABCにおいて、AD = 16cm、DB = 4cmで、
△ADEと△ABCは相似です。
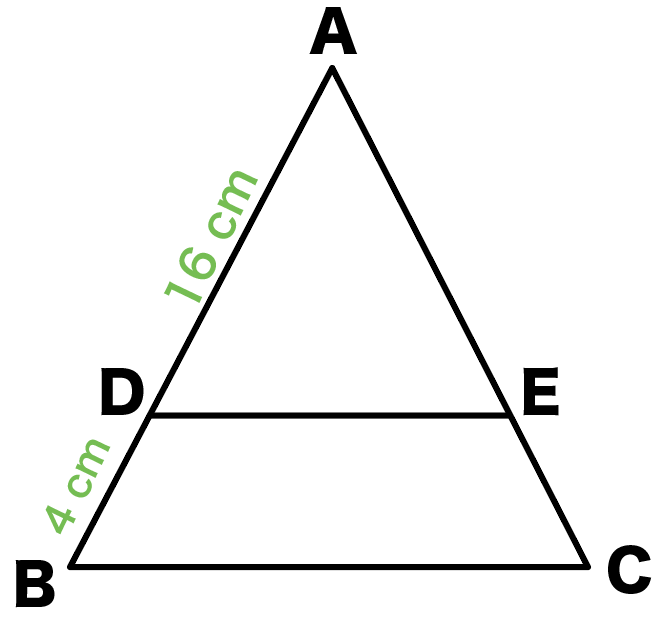
まずは相似比を求めるよ。
この場合、対応する辺は分かるかな?
色で分けるとこうなるよ!
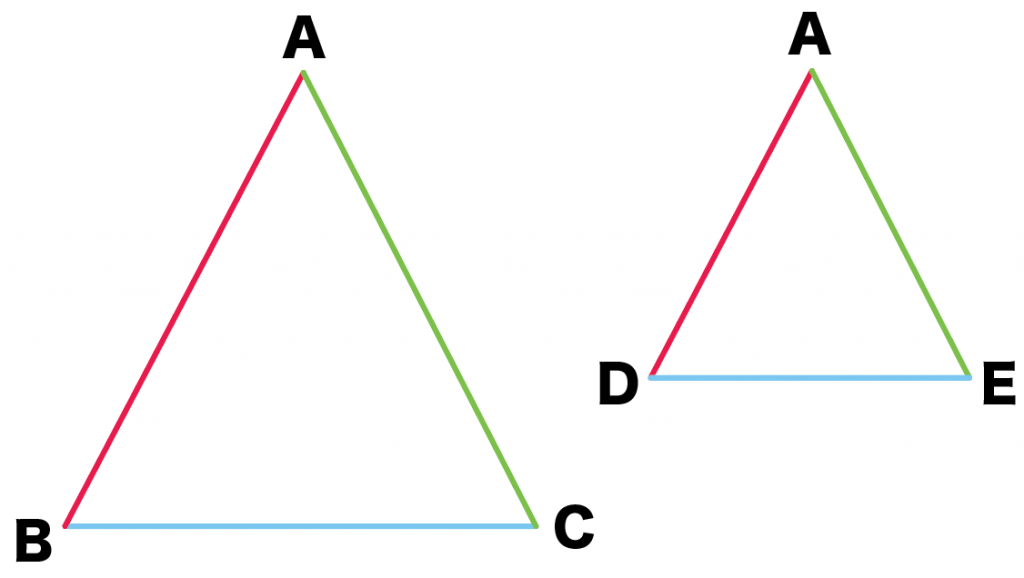
この問題では、ADの長さ(16 cm)が分かっているから、
赤色の辺を使って考えてみよう。
ABの長さはわかるかな?
そう、そうだね。
AB
= AD + DB
= 16 + 4 = 20
になってるはず。
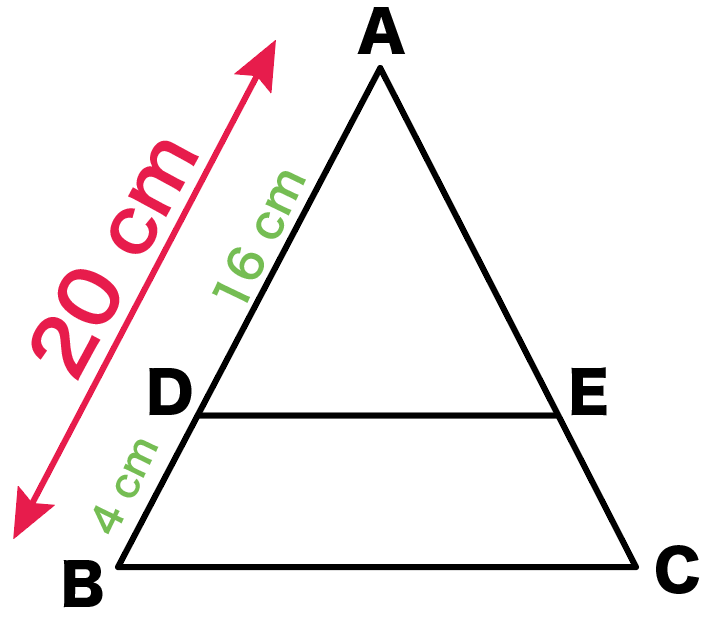
AD=16cm、AB=20cmだから、
相似比は…
△ADE : △ABC
= 16 : 20
= 4:5
だ!
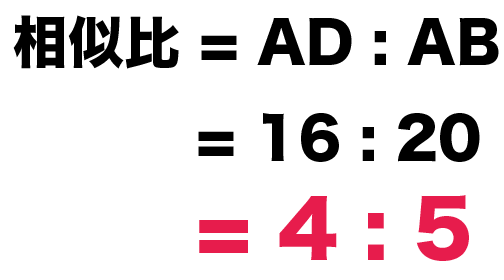
面積比はさっきの公式で一発!
面積比は相似比の2乗になる
だったよね??
この公式をあてはめると、
面積比
= 4² : 5²
= 16 : 25
になるね。

ってことで、答えは16:25!
最後は△ADEの面積だ。
さっきの面積比で求めていくよ。
△ADEの面積がわからないから、x[ cm²] とでもしておこう。
んで、
△ADEの面積:△ABCの面積 = 面積比
っていう比例式をつくってみようぜ。
だから、比例式は、
△ADEの面積:△ABCの面積 = 16 : 25
x : 50 = 16 : 25
になるね。
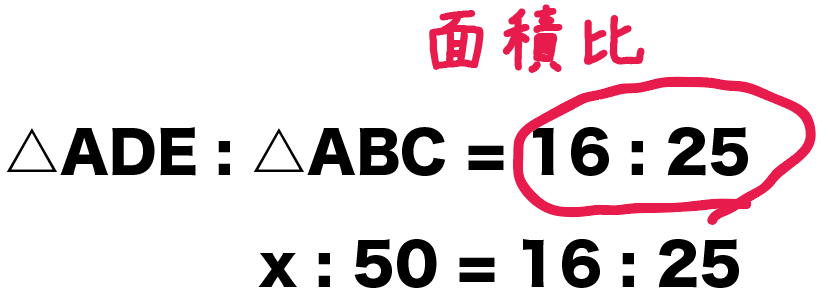
比例式の解き方でといてやると、
x : 50 = 16 : 25
25 x = 16×50
x = 32 [cm²]
になる。
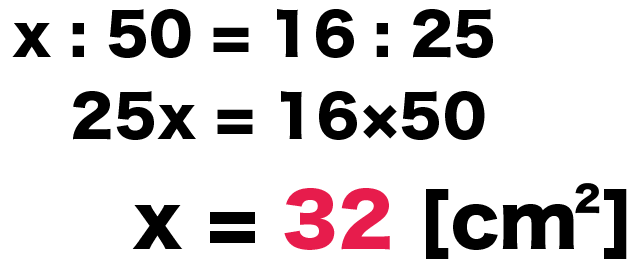
つまり、
△ADEの面積は32 [cm²]ってわけ!
相似比で面積比もとめられた??
相似比の2乗が面積比になる
っていう公式さえおぼえてれば怖くない。
面積比を求める問題はきっと大丈夫!
じゃ、またね!
ぺーたー
ある日、数学が苦手なかなちゃんは、
一次関数と二次関数のグラフをながめてました。
一次関数は久しぶりすぎて忘れかけてるし・・・・
二次関数はまだよくわからないところがある。
うわあっ!?
って、先生か。
びっくりした……
せっかくだから、
一次関数と二次関数グラフの違い
を見つけていこう!
復習もできるし一石二鳥??
そう!
さっそくみていこうー!
いぇーい
一次関数と二次関数のグラフの違いは3つあるよ。
3つもあるんだ!
やべえー
どれもわかりやすいから大丈夫!
順番にみていこう。
はい!!
まずは、一次関数と二次関数の、
「式」
を見比べよう!
あっ。
一次関数の式わすれちゃった・・・・
覚えてないのは仕方がない。
教科書見てみよう。

んー、違いかー!
bがあるかないかはわかったよ
もう一つの違いが注目ポイント!
あっ。
見つけた!
え!?
二次関数は、xが二乗になっている!
よく気付けた!
この2が二次関数の2なんだ!!
やったー!
つまり、
次数が違うってわけ!
へー
一次関数は一次式の関数、
二次関数は二次式の関数、
って覚えておくといいよ。
ってことは、もし、
三次式なら・・・
三次関数!?
そうそう!!
にやり
相似記号の2つめの覚え方は、
グラフのかたち
だね。
かたち・・・
そうそう!
一次関数と二次関数のグラフをみてみて。

まっすぐと、
曲がってる感じかな?
そうだね。
一次関数が直線で、
二次関数が曲線!
これは、わかりやすい!
あー!そうそう!
一次関数は直線、
二次関数は放物線、
っておぼえておこうね。
うす!
最後はyの値について!
なんか、難しそう。
そんなことないよ!
ヒントはグラフに隠れているから!
グラフ?
あっ、そうか!!
一次関数だとyはプラスにもマイナスにもなる!
おー
二次関数y=ax2だとどうなる??
二次関数y=ax2だと、
yの値がプラスだけのときや、
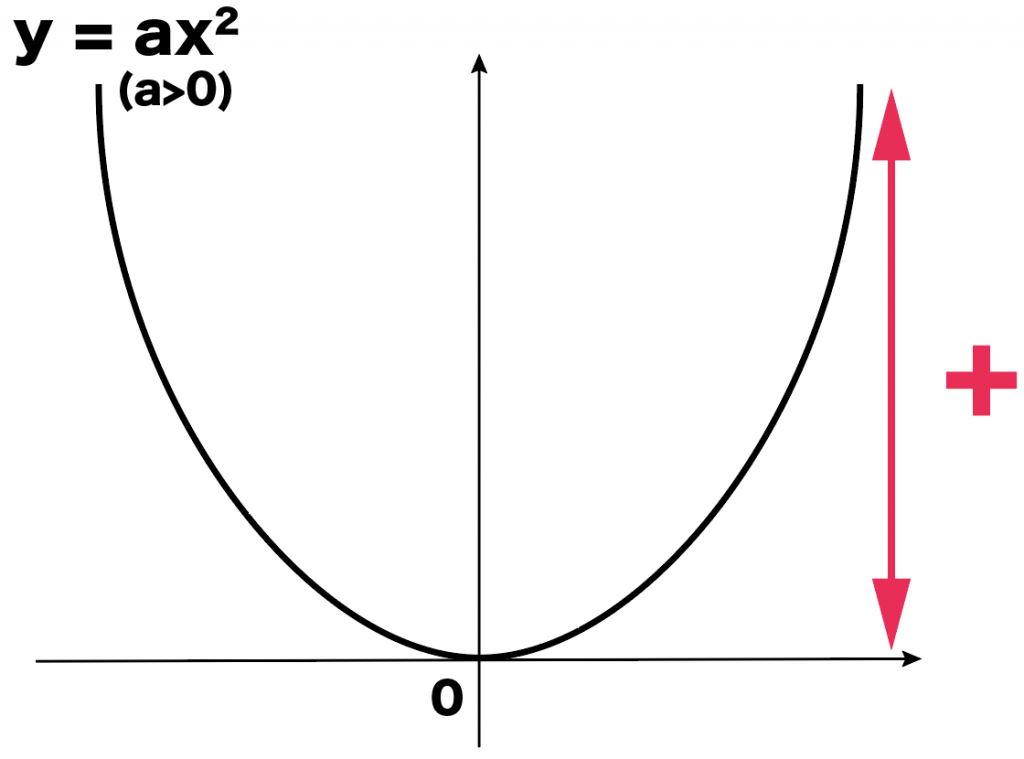
yの値がマイナスだけのときがある!
そうそう!
なんでだとおもうー?
えっと。。。
xが負の数でも二乗すると、
正の数になるから・・・?
そうそう!
例えば、y=x²だと……
あっ、やっぱりそうじゃん!
うん、そうそう!
なんか、直線が魔法で曲げられたのかと思った
……!?冗談、だよね?
半分くらいは。
けど、二次関数のグラフが曲線になるか知れてよかった。
じゃあ、いつものまとめをしよう!
一次関数と二次関数のグラフの違いは、
だったね??
一次関数のことも思い出せてきたかも。
よかった。
一次関数と二次関数が
一緒に出てくる問題もあるんだ。
えっ、どんな??
2つの関数の交点を求める問題があるんだよ
なんか、難しそう。
やり方さえ知っておけば怖くない。
こんな問題が出てきたときに、
一緒に考えていこう!
うす!
やあ、ぺーたーだよ。
二次関数のテストでよくでるのは、
三角形の面積を求める問題。
難しいからみんな嫌がるよね??
図形と関数のコラボとかやめてほしいけど、
テストに出てきちゃう。
何とか解けるようにしたいね。
そこで、今日は、
二次関数の三角形の面積の求め方
を3ステップを紹介するよ!
つぎの問題をといてみよう!
y = 1/2 x² のグラフ上に2点A, Bがあり、
それぞれのx座標は-4と2です。
直線ABとy軸の交点をCとするとき△AOBの面積を求めてください。
3ステップでとけちゃうよ。
まず座標を求めてみよう。
練習問題でいうと、
の3点の座標ね。
この問題では、それぞの点のx座標がわかってる。
だから、
二次関数にxを代入すればいいね。
y = 1/2 x²にそれぞれ代入すると、
になる。
ってことは、
になるはずだ。
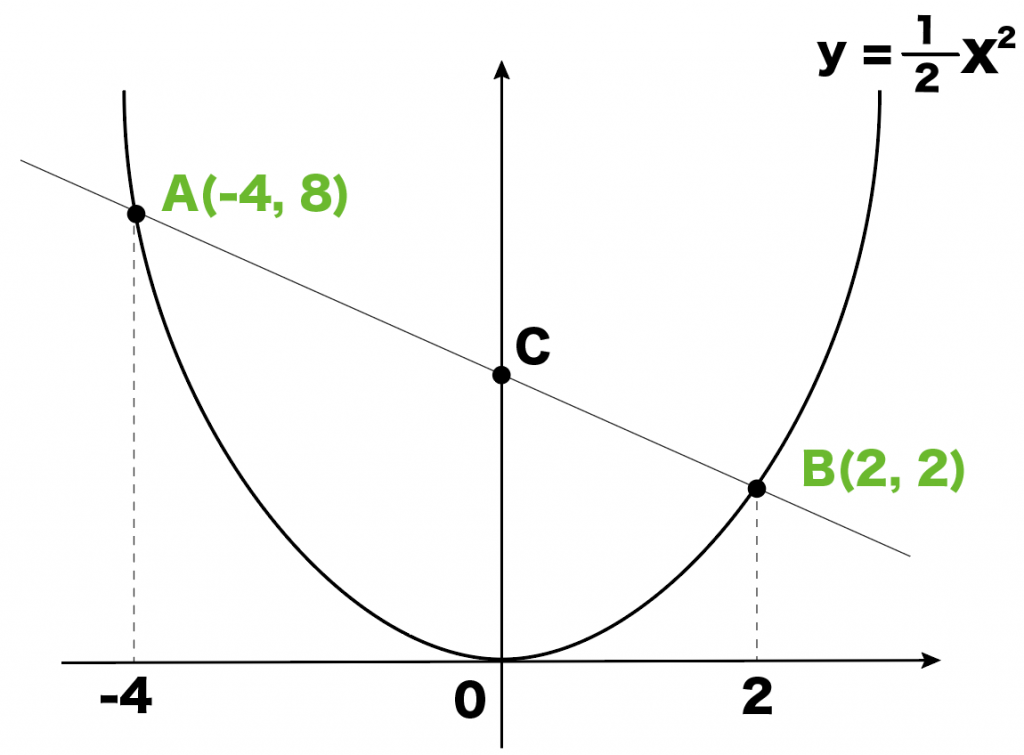
あとは点C。
こいつは、直線ABの切片だね??
直線ABの式がわかればCの座標もわかるってわけ。
直線ABの式は2点は、
だ。
y=ax+bに代入して連立方程式をつくると、
8 = -4a + b
2 = 2a + b
ってなる。
こいつをとくと、
になるね。
つまり、直線ABの式は、
y = -x + 4
になるんだ。
点CはABの切片だから、
C (0, 4 )になるね。
ちょっと長くなったけど、分かった座標を図に書き込むよ!
三角形の面積を2つにわけて考えてみよう。
練習問題では、
△AOBの面積
を求めたかったよね??
だがしかし、
そんな三角形見当たらない。
だから自分で、
△AOBを書き込むんだ。
すると、こんな三角形ができあがるよ!
さあ、これで三角形の面積を求めよう!
…と言いたいところなんだけど、このままだと難しいんだ。
なぜなら、
底辺も高さもわかってないからね。
じゃあどうすればいいの!?
よーく見ると三角形が見えてこない?
そう!
△AOBで見るんじゃなくて、
三角形を2つに分けて考えるんだ!
どう分けるかというと…
△COAと、
△COBでわけるんだ。
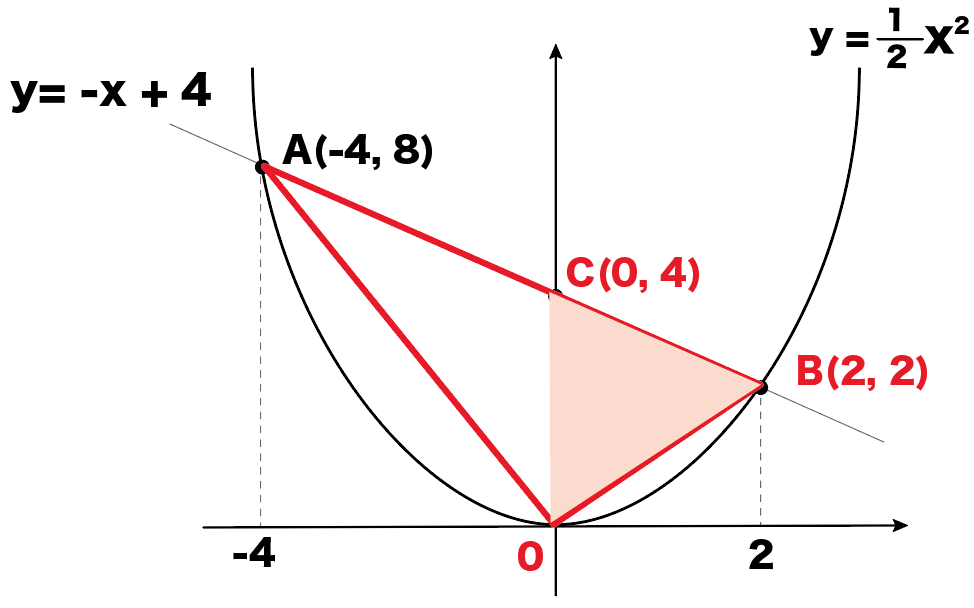
三角形の面積を計算しよう。
わけた2つの三角形の面積をそれぞれ計算すればいいのよ。
まず△COAの面積。
COを底辺、Aのx座標を高さとしてみてね。
Oのy座標は0、Cのy座標は4だから
底辺=4。
高さは「Aからy軸まで」の長さ。
つまり、Aのx座標のことだから、
高さ=4だね。
三角形の面積の公式は「底辺×高さ÷2」だったよね??
こいつで計算してやると、
△COA
= 底辺×高さ÷2
= 4×4÷2
= 8
になる。
次は△COB。
COを底辺、Bからy 軸までを高さと考えてみると、
△COB
= 底辺×高さ÷2
= 4×2 ÷2
= 4
になるね。
2つの三角形を足しちゃえば終わり!
練習問題でいうと、
△AOB = △COA + △COB
ってわけだね。
実際に計算してみると、
△AOB
= 8 + 4
= 12
になる。
だから答えは12なのさ。
大変だったね。お疲れさま!
二次関数で三角形の面積を求める問題は、
の2ステップで大丈夫。
難しいけど、慣れれば絶対に解けるようになるよ。
じゃ、今回はここまで。
じゃあねー
ぺーたー
ある日、数学が苦手なかなちゃんは、
相似の記号に出会いました。

相似の記号って、
へにょへにょ。
わかりにくい!
合同の記号は、
=に一本つけるだけでいいのに・・・

そう!それ!!
たしかにふにゃふにゃ。
わたしの彼氏みたい。
え!
先生恋人いたんですね?w
そりゃそうよ・・・・
ってとにかく。
今日はこの、
ふにゃっとした、
相似記号の覚え方を教えてあげる。
いぇーい
相似記号の覚え方は3つあるよ。
3つもあるんだ!
太っ腹!
うん。
私の腹は太くないけどね。
順番にみていこう。
相似記号の語源は、
「似ている」
っていう意味の英単語『similar』なんだ。
えー!
similarのsの字も混じってなくない?
いや。そんなことないよ。
相似記号の頭を右にかたむけると・・・・・・?

うわ!
Sが相似記号になった!!
無限大のマーク「∞」みたい。。
ほら、関ジャニ∞のやつ。

あ、ちょっと違うんだよね。
ポイントは2つのスキマ!
無限大『∞』
と
相似記号
を間違えないようにしよう!

はい!
相似記号の2つめの覚え方は、
かきまくる
だよ。
やっぱりそうなるんだ・・・
由来を知ったら、あとは書いて覚えるだけ!
でも、由来を覚えることはほんと重要!
なんで?
だって、
由来を意識しながら書けるからね。
覚えやすいんだ!
へー、そうなんだ。
漢字や英単語でも、同じことがいえる。
でも、相似記号のほうが1000%楽だね!
英単語覚えるよりは、簡単って思えてきた。
そう!その調子!
まず見ながら10回書いて、
今度は見ずに10回書こう!
うす!
最後の覚え方は、
つかいまくること。
慣れたら、
実際の問題に挑戦しよう!!
うす!!
じゃあたとえば、
したの2つの三角形が相似
って記号であらわしてみて。
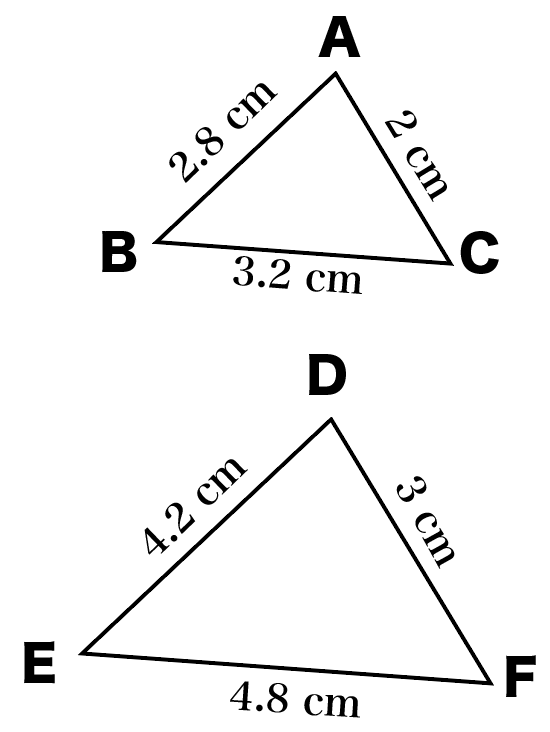
えっと・・・・・
あ、書き方教えてなかったね!
ルール伝えるね!
えっ、ルールがあるの?
(相似記号さえおぼえればいいと思ってた)
心の声が漏れてる!・・・、
まあ、そんなややこしくなくてね。
相似な図形のあいだに記号をかくだけ。
・・・・・・って、あ!
何かに気づいたみたいだね?
合同のときと同じ!
なるほど!
相似な図形で、
記号をサンドイッチ
すればいいですね!
そういえば、さっきより、
相似記号書くの上手になってきたんじゃない?

たしかに!!
この調子なら、次のテストまでには…!!
いいね!
その調子で相似を学んでいこう!
うす!