こんにちは!ぺーたーだよ。
円周角の定理とか円周角の定理の逆とか
もう慣れてきたかな?
円周角の定理って角度を求めるときにも使うんだけど、
相似を証明するときにも使えるんだ。
たとえば、つぎみたいな証明問題ね。
練習問題
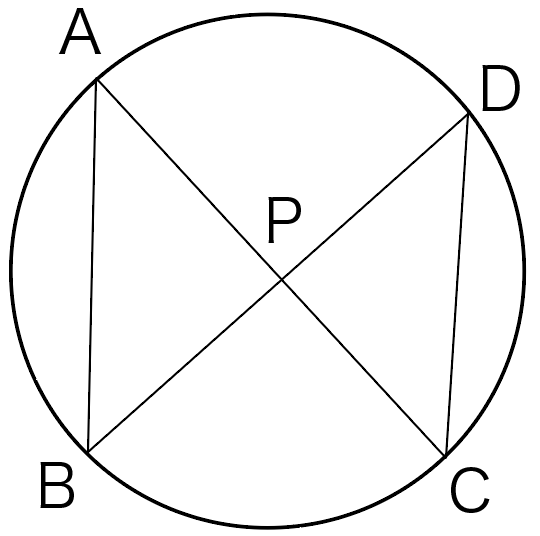
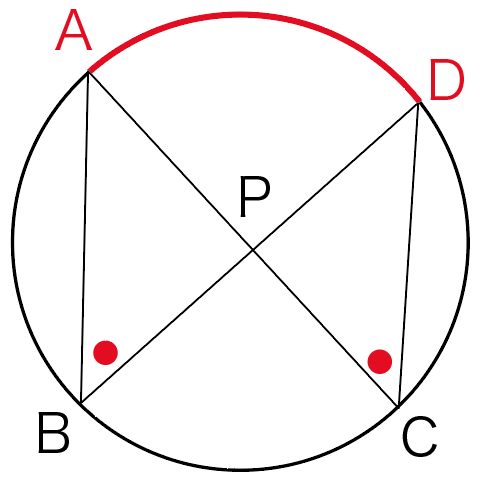
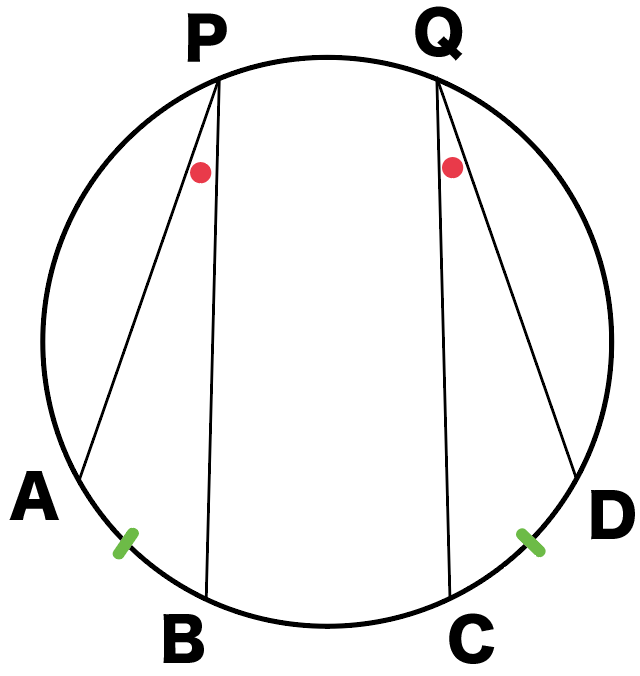
下の図のように、円周上に4点A,B,C,Dがあり、
ACとBDの交点をPとする。
このとき△ABP∽△DCPになることを証明せよ。
今日は、この問題を解説するよ。
証明に必要なことを復習しながら説明するから、
頑張ってついてきてね!
円周角の定理の証明問題はつぎの3ステップでとけちゃうよ。
さっきの練習問題をといていこう。
練習問題
下の図のように、円周上に4点A,B,C,Dがあり、
ACとBDの交点をPとする。
このとき△ABP∽△DCPになることを証明せよ。

証明問題に入る前に、
円周角の定理ってなんだったか、しっかり思い出しとこう!
円周角の定理は2つの性質があったね!
1つの弧に対する円周角の大きさは、
その弧に対する中心角の半分ってやつと、
同じ弧に対する円周角の大きさは等しいってやつだね。
くわしくは「円周角の定理」の記事を復習してみてね。
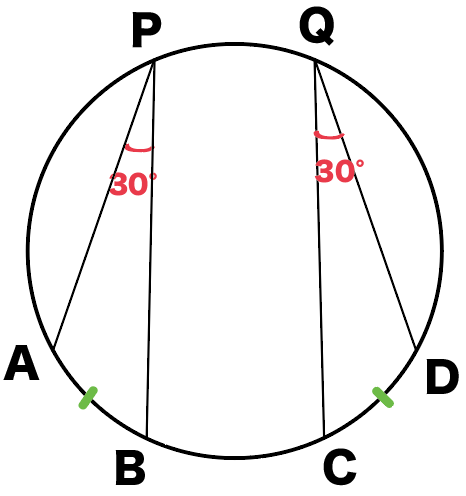
まず、さっき思い出した円周角の定理を使って、
等しい角がないか確かめてみよう。
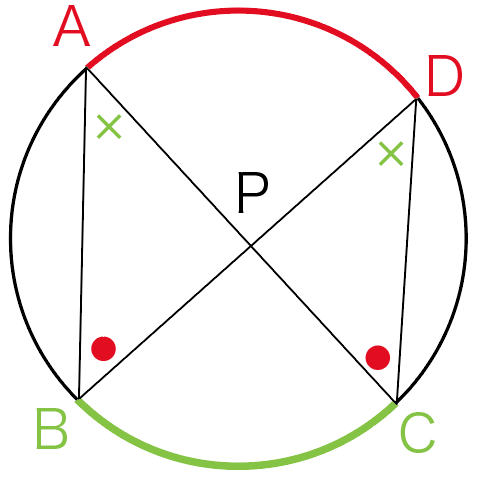
弧BCの円周角がどこになるかわかるかな?
そう。
∠BACと∠BDCだね!
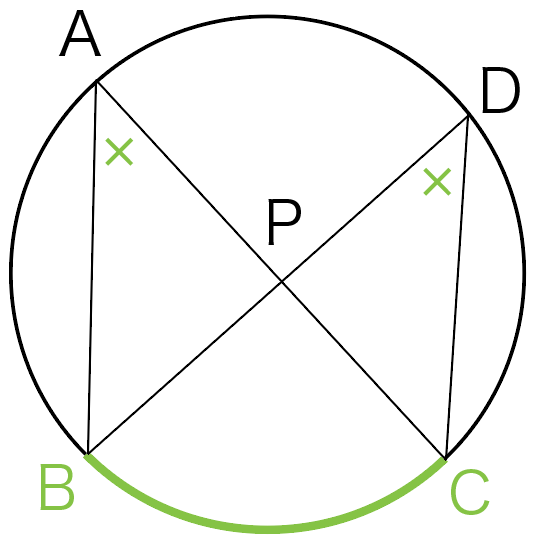
1つの弧に対する円周角は等しいんだから、
この2つの角は等しいってことになるね!
∠BAC=∠BDC…①
もう1つの角も円周角が使えるよ。
今度は弧ADで見てみようか。
さっきと同じように円周角を見つけてよう。
そうすると2つの円周角が見つかるね!
ってことは角の大きさは一緒だね!
∠ABD=∠ACD…②
つぎは相似条件で三角形の相似を証明しよう。
相似条件は、
だったね??
円周角の定理の証明では、十中八九、
2組の角がそれぞれ等しい
をつかうかな。
なぜなら、円周角の定理では辺の比が等しいことは証明しにくいからね。
角度が等しいことなら得意分野なんだ。
だから、まずは、
2組の角が等しいことがいえるかどうかを疑ってみよう。
練習問題をみてみて。
Step1で円周角の定理をつかったら、
がわかったよね??
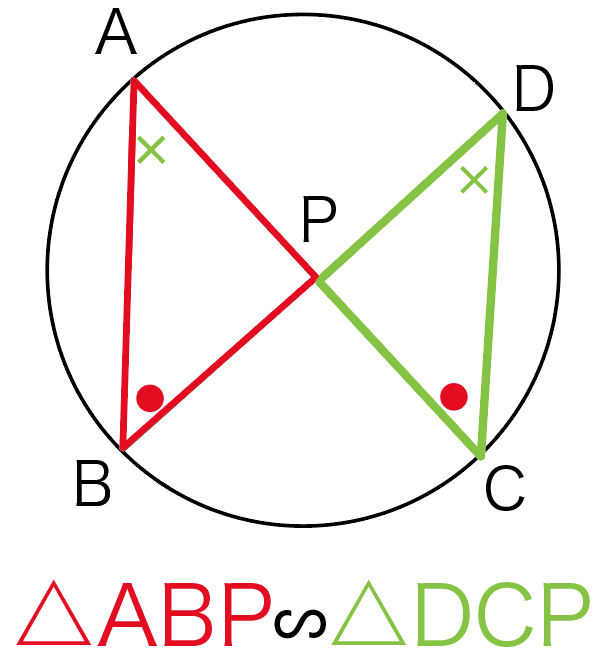
ってことは、
△ABPと△DCPにおいて、
2組の角が等しいことがいえるね。
よって、これは相似条件をみたしてるから、
△ABP∽△DCP
がいえるってわけね。
これで証明のゴールにたどり着けたね!
証明のゴールまでの見通しができたら、
あとは証明をかくだけ。
相似の証明の書き方を参考にしてね。
Step2までのながれをかいてみるとこうなるね↓↓
△ABPと△DCPについて、
円周角の定理より、同じ弧に対する円周角は等しいので、
∠BAC=∠BDC…①
∠ABD=∠ACD…②
①、②より、
2組の角がそれぞれ等しいので、
△ABP∽△DCP
ってかんじかな!
円周角の定理をつかった証明問題はどうだった??
基本的な解き方としては、
円周角の定理をつかって、
相似条件の「2組の角がそれぞれ等しい」の方向に持ち込む・・・
というのが基本かな。
今回紹介した証明問題は、基本的なものあったけど、
応用問題でも構造はいっしょ。
円周角については問題をたくさん解いて、
「こことここは円周角の定理で等しいな」
って見つけられるのが一番かな!
今日はこれでおしまい!
またね!
ぺーたー
ある日、数学が苦手なかなちゃんは、
面積比の公式をにらんでいました。

だああー!
何で面積比が求まるの?
意味不明!!
おっ!
相似比から面積比もわかるってやつだね。
相似比が面積比に……?
もっとわけわかんない……
よし、じゃあ今回は、
相似比と面積比のつながり
を見つけていこう!
相似比から面積比がだせる理由は、
つぎの2ステップをふむとわかりやすいよ。
へー!
2ステップなら楽勝じゃん!
そうそう!
いけるいける!
まずは、
正方形の面積比を考えてみよう。
何で?
面積比の公式をみちびきやすいからかな!
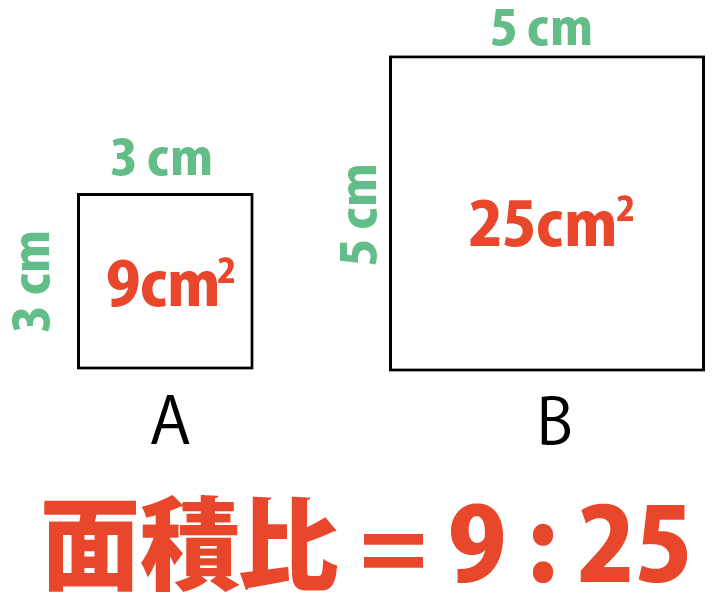
たとえば、
2つの正方形A・Bに注目してみて。
1辺の長さが3cmと5cmの正方形ね。
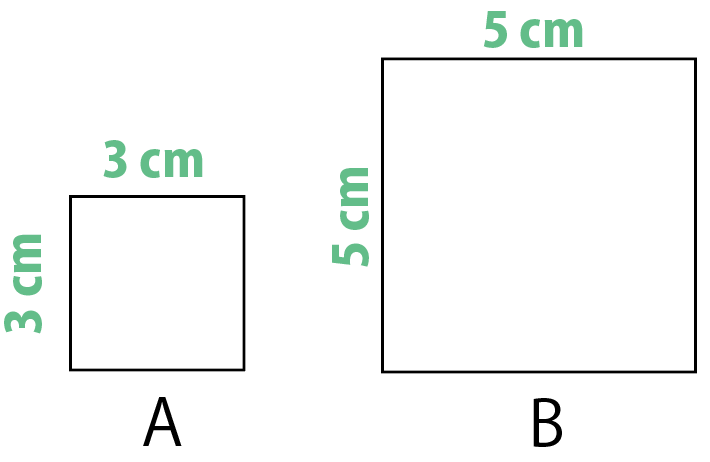
まずは、2つの正方形の面積を求めてみようか。
正方形の面積の公式をつかってね。
正方形の面積の求め方は、
一辺を2乗するだけだよね??
小さい正方形Aの面積は9㎠で、
大きい正方形Bは25㎠かな!
いいね。
次はそこから面積比を求めてみよう!
面積比は、
9:25
だ!
ここで、登場するのが相似比!
2つの正方形の相似比はいくつ??
えっと・・・
相似比は1辺の長さの比をとればいいから、
3:5かな!
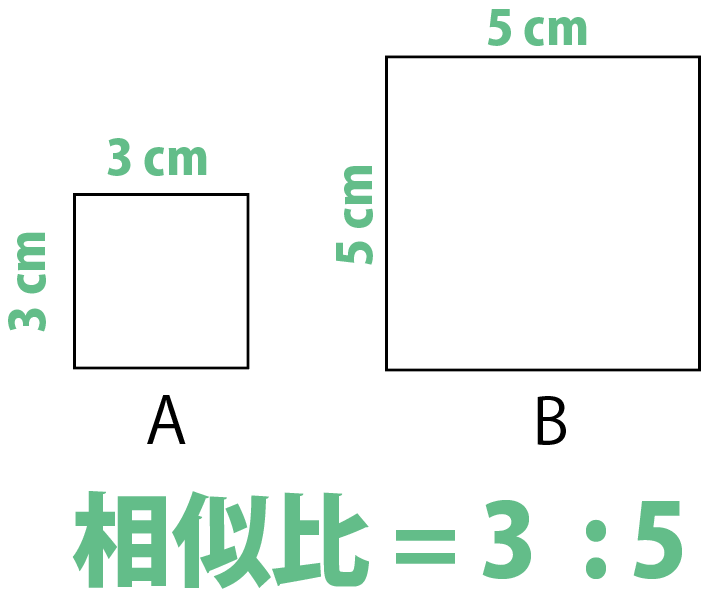
おっ。いいね。
相似比と面積比くらべると・・・??
あっ。
ああああああー
相似比の2乗が面積比になってない??
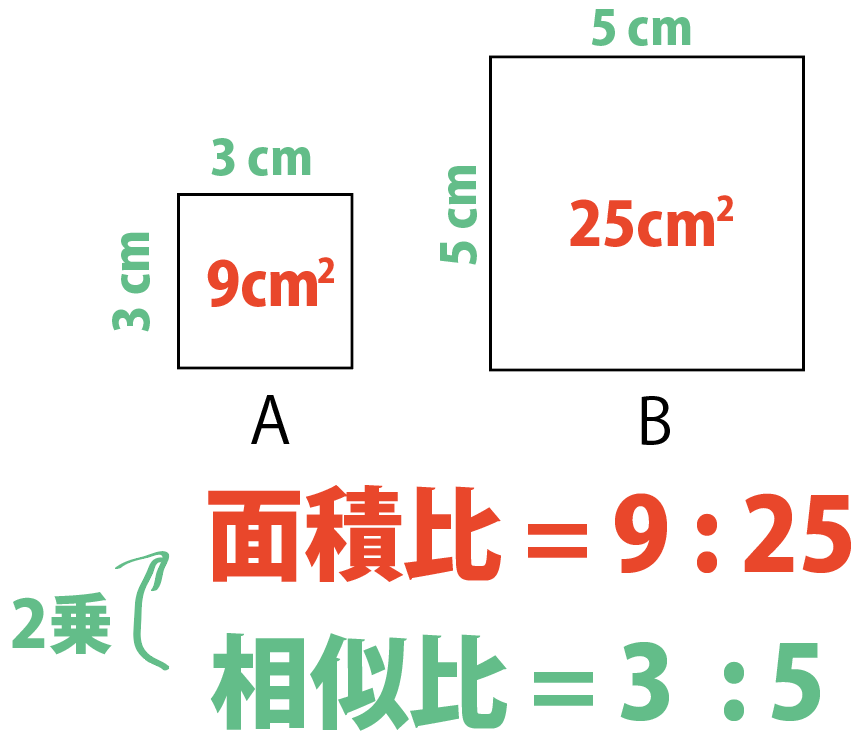
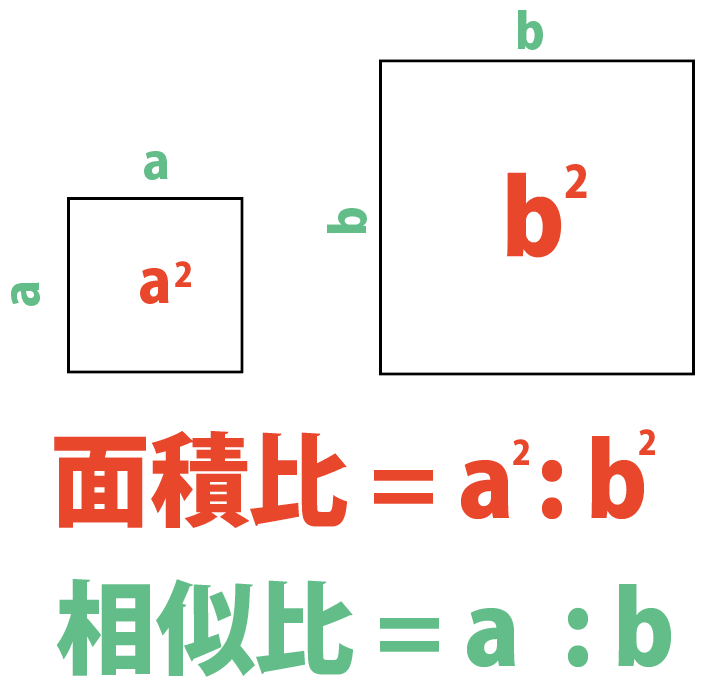
面積比はa²:b²になるんだ。
形は様々だけど、
どの図形も三角形に切り分けることが出来るんだ。
なるほど!
ってことは、
今度は三角形で考えろってこと?
鋭いね!
次は三角形で考えていくよ。
相似比がa:bの三角形。
それぞれの面積を求めよう。
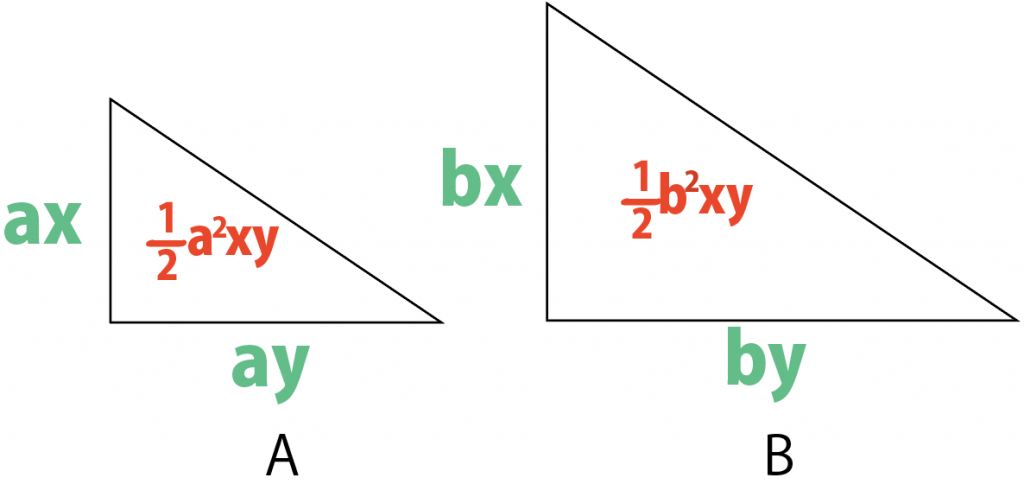
いいね。
ここで、2つの図形の面積を比べると……?
あっ、
面積比を簡単にすると、
a²:b²になる!
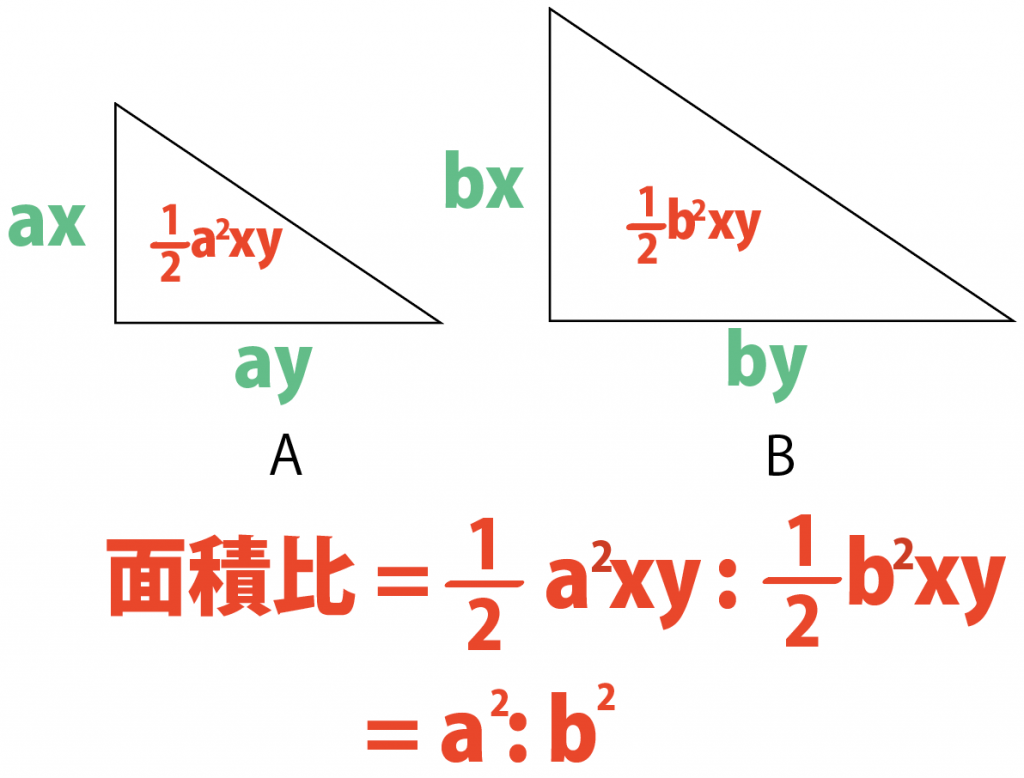
で、他の図形も分けて考えれば三角形と同じだから、
相似比がa:bなら、面積比はa²:b²って関係が当てはまるんだ!
そういうことか!
合点!!
どう?
何で相似比が分かると、
面積比を求められるのかが分かったかな?
の2ステップでいいんだ。
計算するとそうなるっていうのはわかったけど、
公式は覚えるの嫌だしそもそも覚えられない。
確かに、最初は慣れないし、何度も使うしかないね。
なんか、いい方法ないかな……
正方形を思い出すって手もあるよ。
何がいいかは人それぞれだね。
自分にあった覚え方を見つけてみよう!
ういす!
ある日、数学が苦手なかなちゃんは、
星がかけなくて困っていました。

だああー!
星かけねえええええ
おっ、苦戦してるね!
定規で一筆書きするといいよ。
へー!
やってみよっかなあー
わ!かけた!
でしょでしょ??
じつはね、
数学の問題には、
星形の角度を求める問題
があるんだ。
たとえば、こんな感じ↓↓
つぎの星形の角度のxを求めなさい。
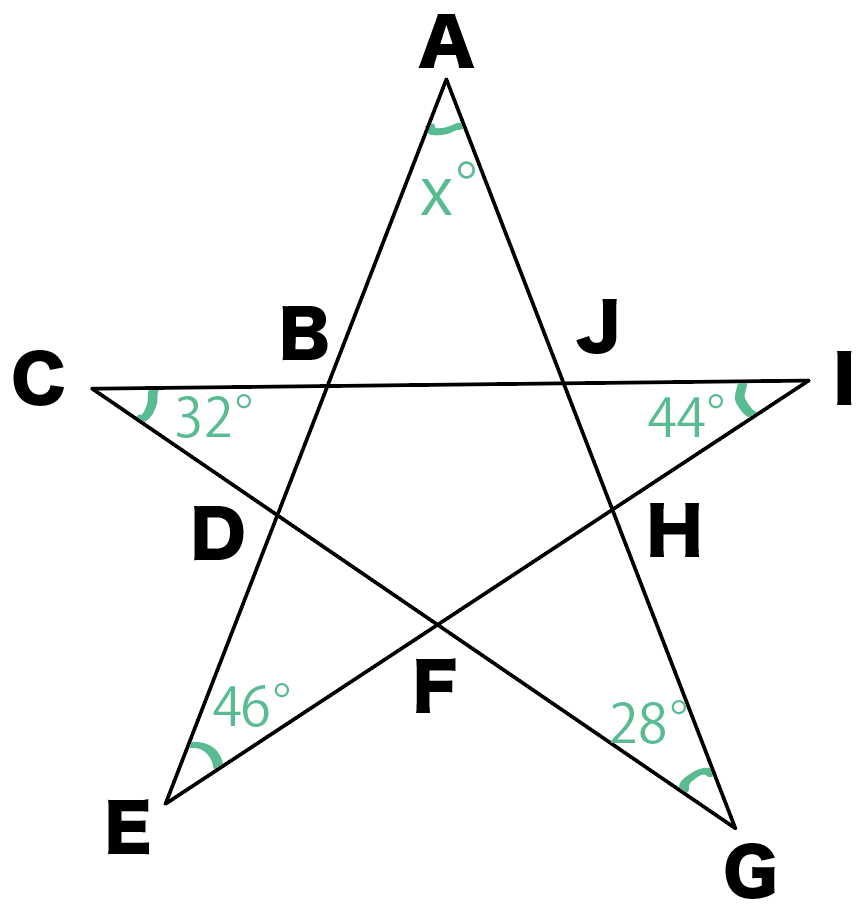
ひょえー!
雰囲気むずそーー
いや!
基本おさえちゃえば大丈夫。
いっしょにといていこう!
はい!!
星形の角度の求め方はつぎの3ステップだよ。
へー!
3ステップならできそう!
いけるいける!
それじゃあ、
さっきの星形の問題をといていこう。
つぎの星形の角度のxを求めなさい。

星形を、
「3つの三角形」
にわけて考えてみよう。
えっと・・・・
3つ??
そうそう。
星形の中に、
色んな図形が見えてこない??

三角形と….
あっ、
五角形もある!!
そう!
今回は、その中の3つの三角形に注目しよう。
練習問題でいうと、
の3つだね。
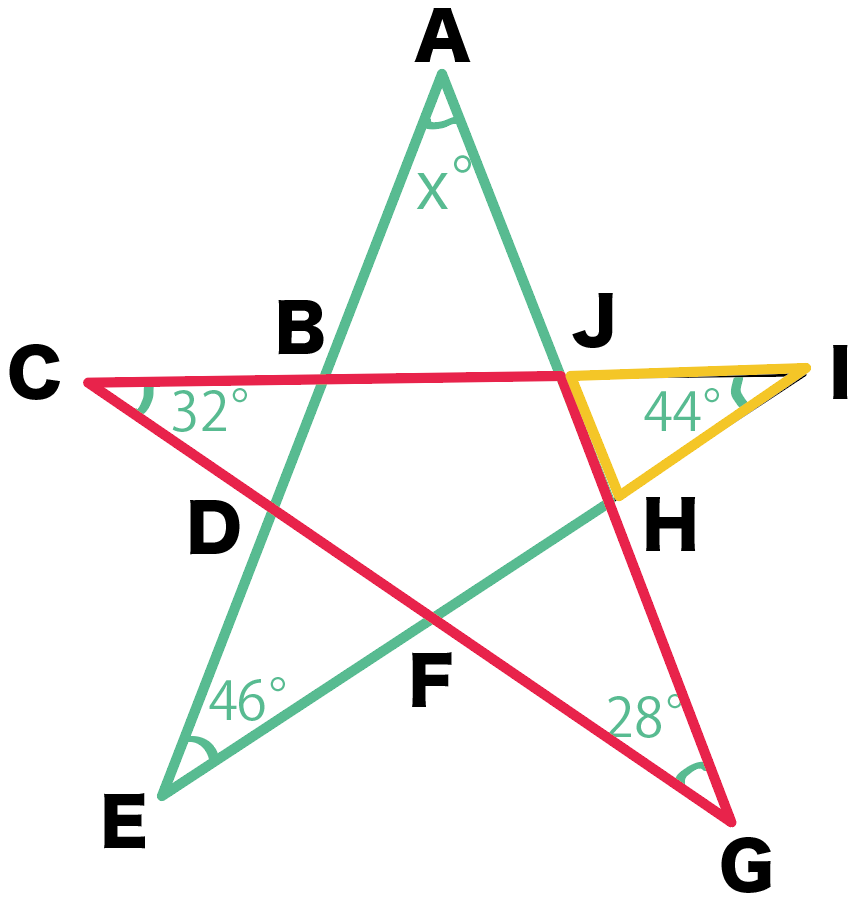
ひー
なんでその3つなんだろう?
それはね……
ひ、み、つ
えっ!
外角の定理ってなんだっけ??
っていう人もいると思って、
ちゃんと用意しといたよ!
さ、さすがすぎる!!
簡単にいうと、
三角形の内角を2つ足すと、
接してない外角になる
ってやつ。
下の図でいうと、
○と×をたしたら、
外角は「○+×」になるってわけ。
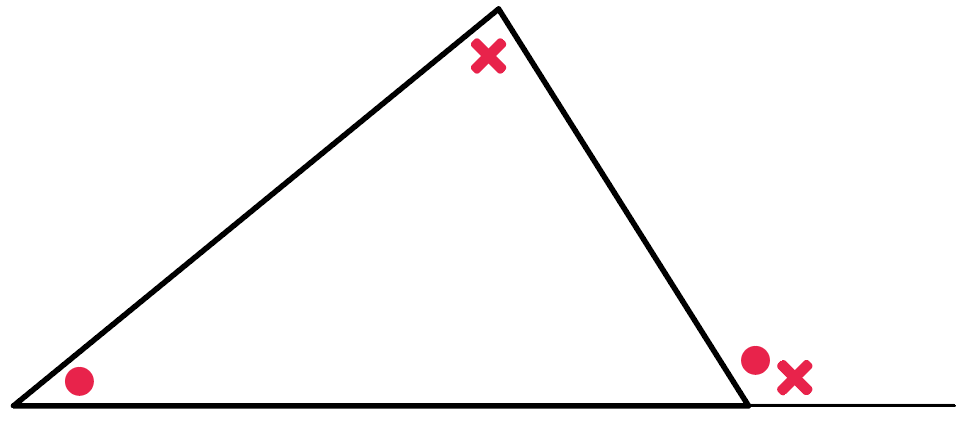
ああああああー
思い出してきたようなきがする!
これを星形の中の、
3つの三角形で考えてみよう!
外角になりそうなところ……
あっ、あった!
△AEHの外角は∠JHIだ!
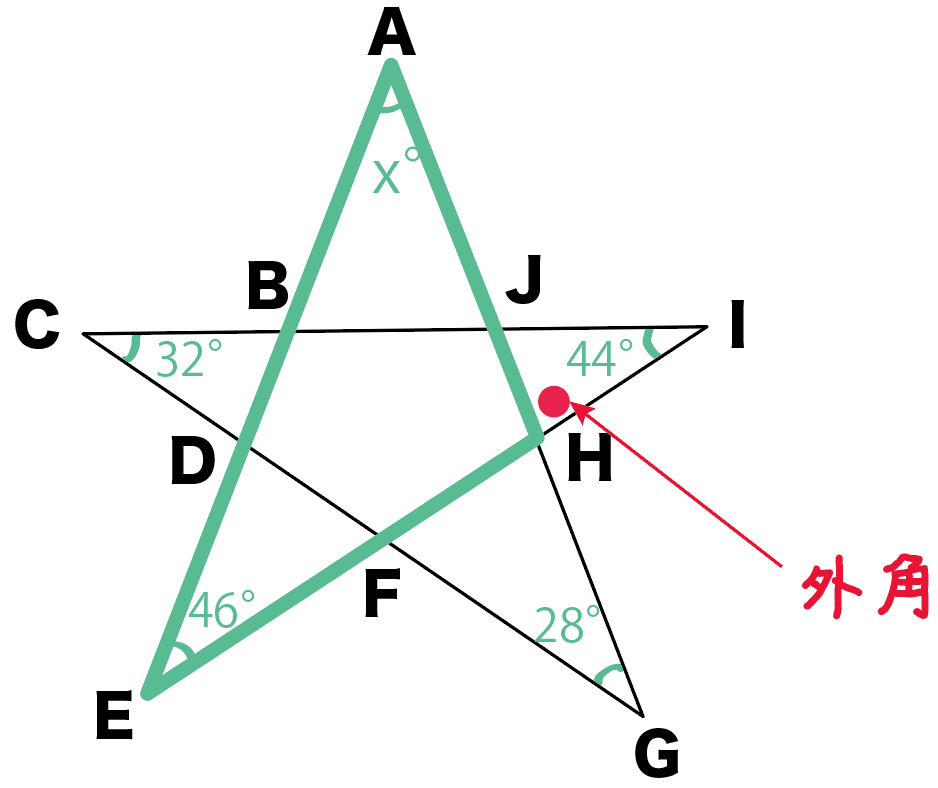
いいね。
△CGJでも同じように考えると……
あっ!
△CGJでいうと、∠HJIが外角になってる!
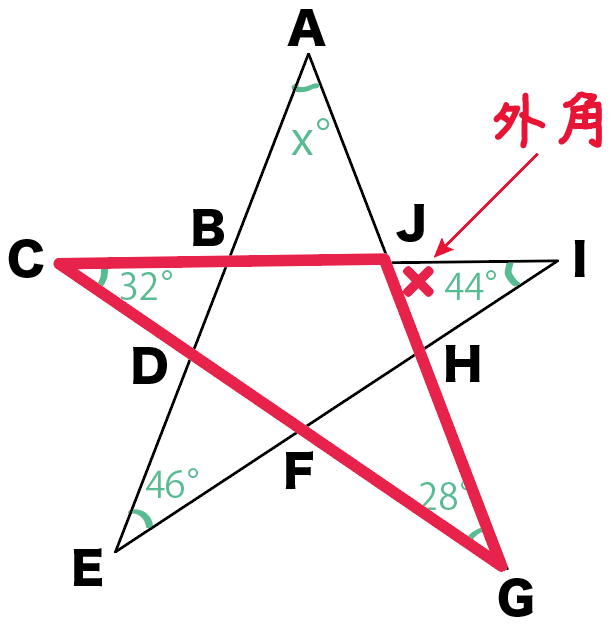
三角形の外角の定理で、
角を移動させるとどうなる??
えっと・・・・、
あっ。
小さい三角形に集まってない!??
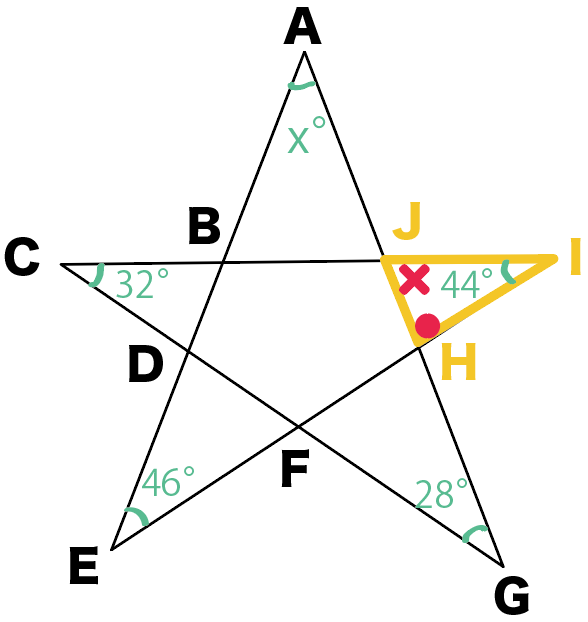
そう!
ぜんぶあわせて三角形の内角になってるね。
ということは??
三角形の内角の和は180度だから、
星の角度の和が180度になるってことだ!!
いいね!
じゃあ、角xはいくつ??
えっと・・・、
三角形の外角の定理をつかうと、
になる。
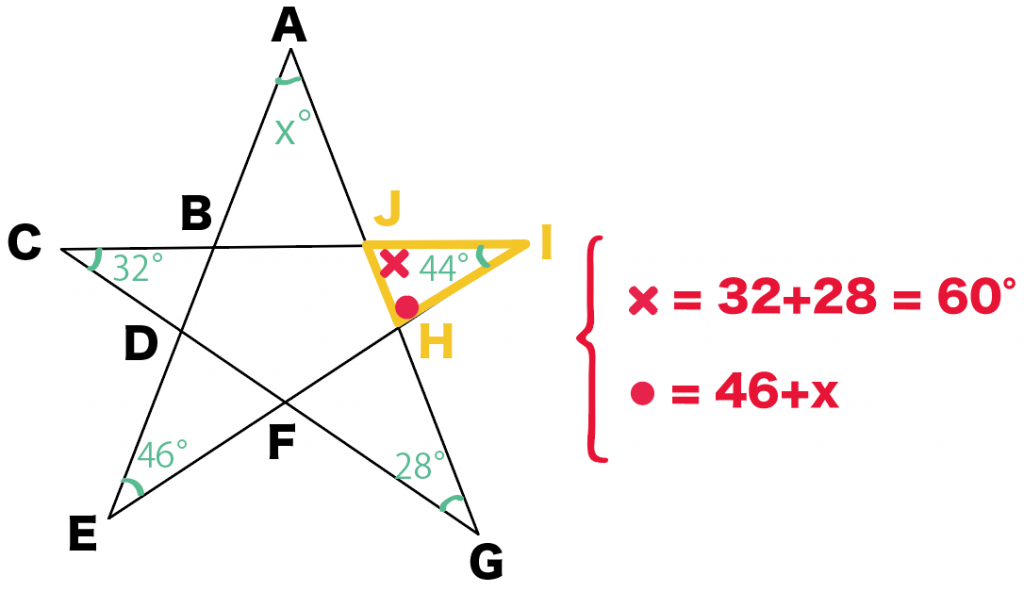
うんうん
だから、△HIJの内角は全部で180度だから、
(46+x) + 60 + 44 = 180
x = 30°
だ!
xは30°!
星形の角度の求め方はどうだったかな?
の3ステップだったね。
これなら、
他の問題も解けそうかも!!
いいね、このことを利用した問題は、
まだまだたくさんあるんだ。
最初はよく分かんなかったけど、
特徴さえわかっちゃえば、分かりやすいね!!
そう!
どんな問題でも、
初めては分かりづらい。
けど、一度理解すれば大丈夫。
色んな問題が解けるようになるよ!
はい!
ありがとうございました!
こんにちは!ぺーたーだよ。
中3数学の「円の性質」では、
を勉強してきたね。
今日はこいつらを使って、
円周角で角度を求める問題
にチャンレジしていこう。
円周角の定理をむちゃくちゃ使うから、
「まだよくわかんない…」っていう人は、
円周角の定理を復習してみてね。
さっそく、円周角で角度を求める問題をといていこう。
テストで役立つ3つの問題をいっしょにといてみよう。
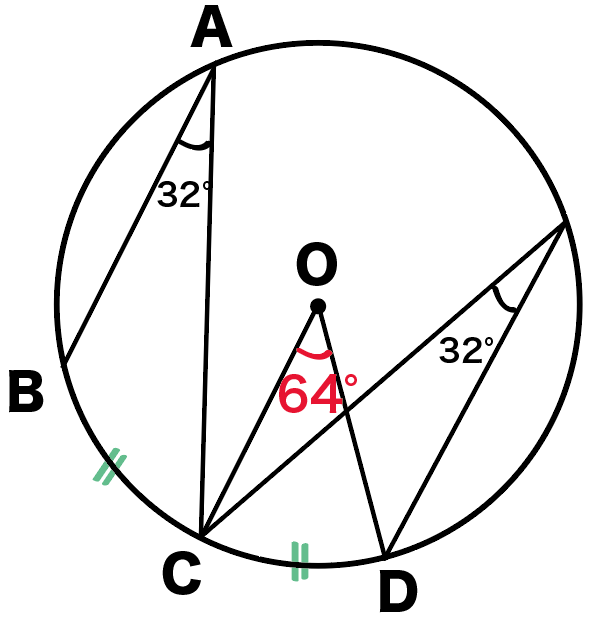
つぎの円Oにおいて角度xを求めなさい。
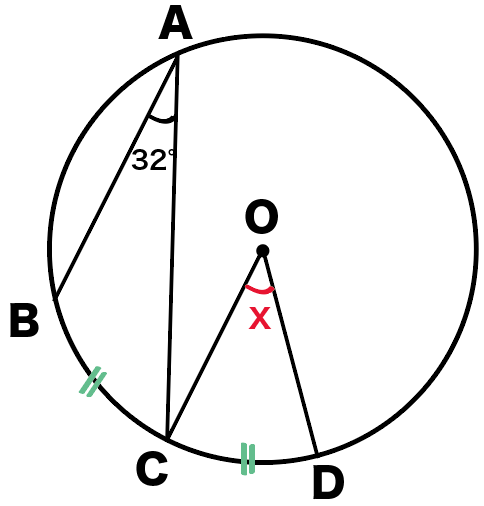
ただし、
孤BC = 孤CDとします。
この問題では、円周角の性質の、
1つの円で等しい弧に対する円周角の大きさは等しい
をつかっていくよ。
孤BC = 孤CDだから、
孤BCと孤CDがつくる円周角は等しいはずだね。
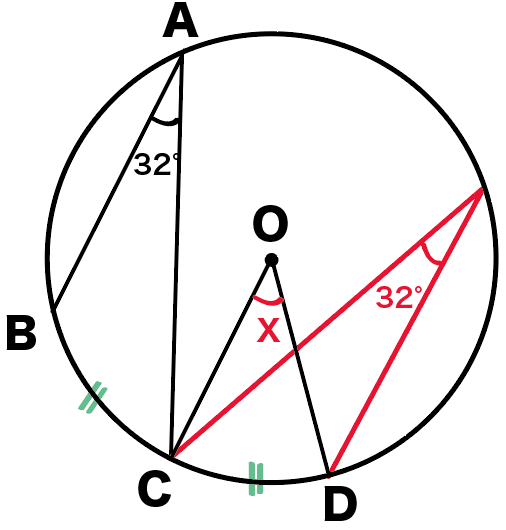
ってことは答えはもう簡単!
弧BCの円周角BACが32°だから、
弧CDの円周角も32°ってことだね!
でも、問題で求めたい角xは、
孤CDの円周角じゃなくて中心角だ。
円周角の定理より、
同じ孤の円周角を2倍すると中心角になるんだったね??
ってことは、角xは円周角32°を2倍した、
∠x = 64°
になるはず。
つぎの円Oにおいて角xを求めなさい。
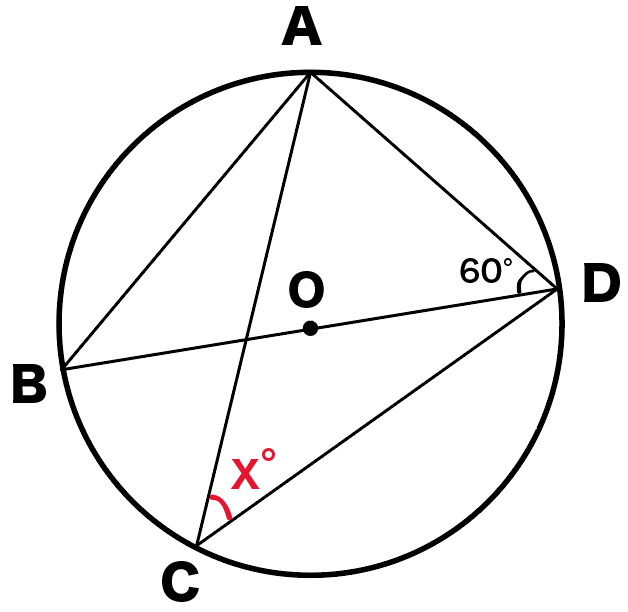
この問題では、
をフルフルにつかっていくよ。
まず、円周角の性質の、
半円の孤に対する円周角は90°
ってやつをつかってみよう。
円周角BADは半円に対する円周角だから、
∠BAD = 90°
になるね。
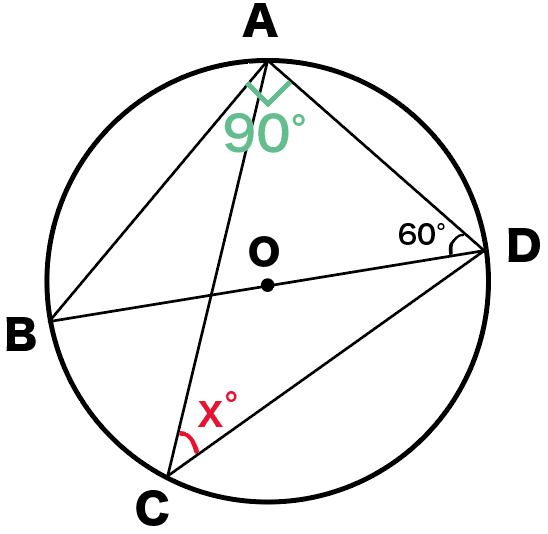
んで、ここで△ABDに注目してみよう。
三角形の内角の和は180°だったよね??
△ABDの内角のうちの2つの、
がわかってるよね??
ってことは、残りの内角の∠ABDは、
∠ABD
= (三角形の内角の和)- (∠BAD + ∠ADB )
= 180 – (90+60)
= 30°
になるね!
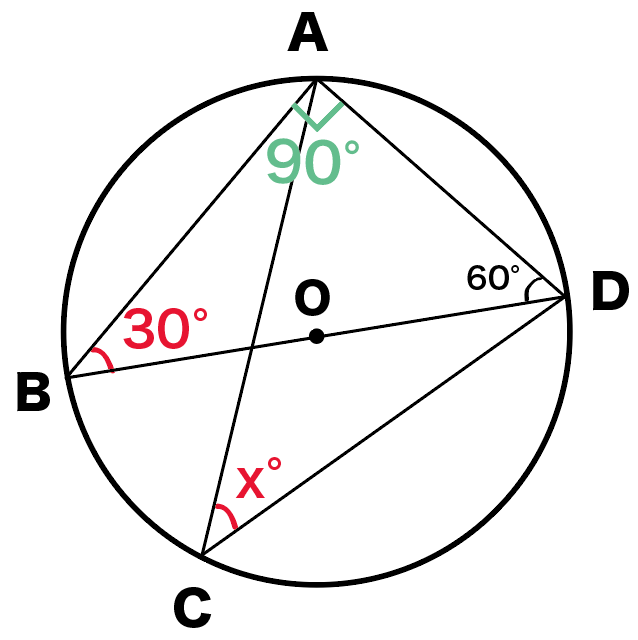
つぎは、円周角の定理をつかうね。
同じ弧に対する円周角は等しい
っていう定理をつかうと、
∠ABD = ∠ACD = 30°
になるね。
なぜなら、
両方とも孤ADに対する円周角だからね。
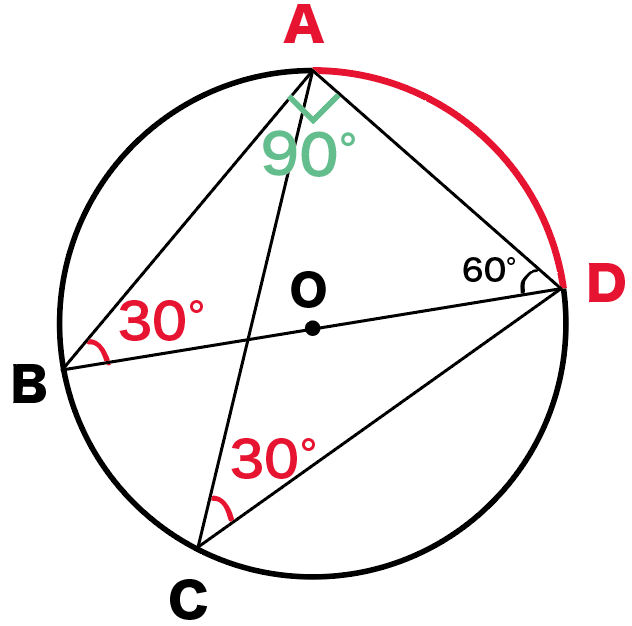
ってことで、
xは30°ね!
つぎの円Oにおいて∠xを求めなさい。
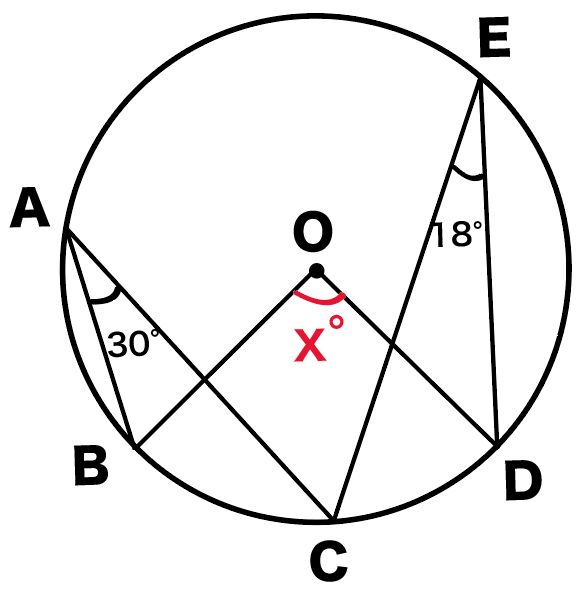
次はちょっと手ごわそうだねー。
こいつはこのままだと答えまで出すのは
難しいかもしれないね。
だから、自分で線を1本足してあげよう。
どこに付け足すかわかるかな?
そう。そうだよ。
AとDをむすんでみて!
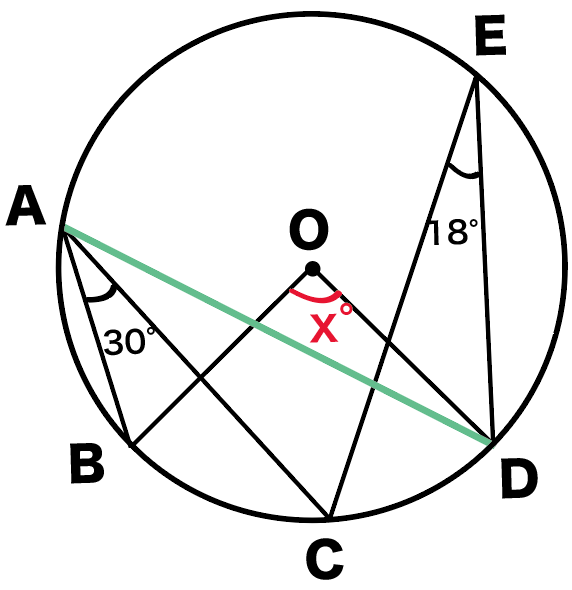
この1本の補助線が答えまで案内してくれるよ!
同じ弧の円周角は等しいんだったよね?
ってことは、
∠CED = ∠CAD = 18°
になるね。
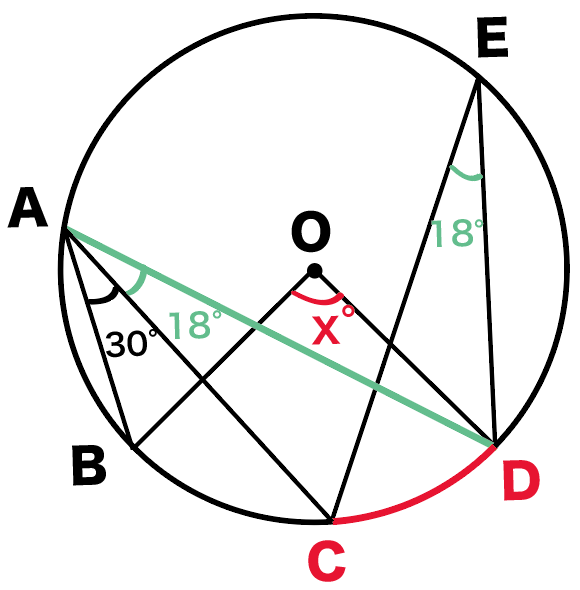
そうすると今度は、
∠BAD = 48°
になるね。
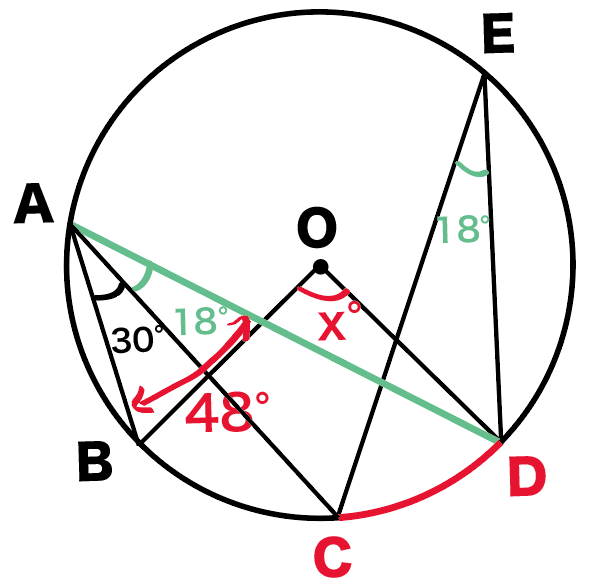
∠BADは求めたい∠BODの円周角。
ってことは、
円周角の定理の、
1つの弧に対する円周角の大きさは、
その弧に対する中心角の半分
ってやつをつかえばいいね。
すると、
x= ∠BAD×2
= 48°×2 = 96°
になるね!
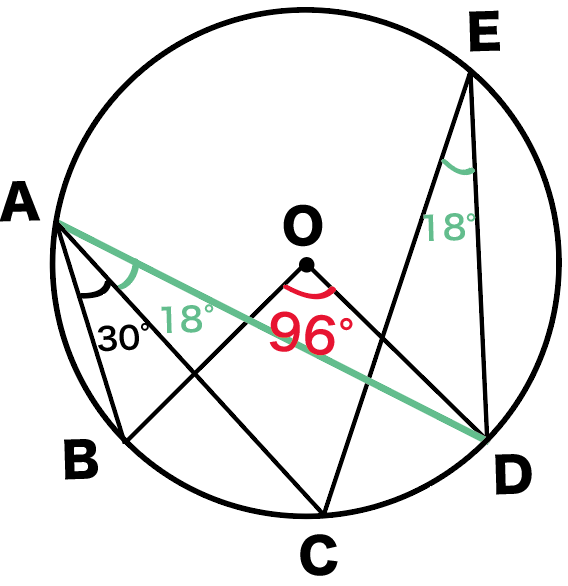
円周角の角度の問題はどうだった??
最初は慣れないかもしれないけど、
とけると面白いはず。
円周角を求める問題が出てきたら、
解いてみるといいね!
じゃあ、今日はここまで!
ぺーたー
こんにちは!ぺーたーだよ。
この前は、円周角の定理とはなにか??
ってことを勉強してきたよね。
今日はもう一歩ふみこんで、
円周角の性質
をまなんでいこう。
中学数学で勉強する円周角の性質は、
ぜんぶで3つ。
3つ覚えておけばいろんなとこで活躍するよ。
「できれば覚えておいてほしい」というよりは、
「絶対言えるようになってね!」っていう内容だね。
どんな性質なのか見ていこう!
中学数学で役に立つ「円周角の性質」はつぎの3つだよ。
それぞれ順番にみていこうか。
これは円周角の定理の復習。
円周角の定理に、
同じ弧を共有してる円周角はどれも等しい
っていうやつがあったよね。
これはね、円周角の問題を解く時によくでてくるから、
絶対におさえておきたい性質だね。
たとえば、つぎの円Oがいたとしよう
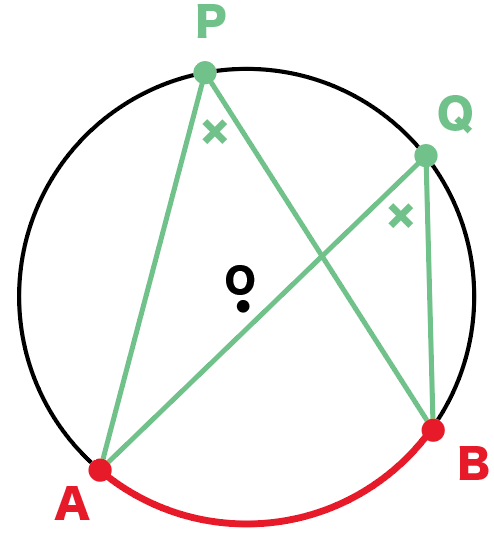
このとき、
角APBと角AQBは、
弧ABの円周角だよね??
さっきでてきた円周角の定理をつかうと、
角APB = 角AQB
ってことがいえるんだ。
たとえば、角APBが50°だとすると、
角AQBもおなじ50°になるわけ。
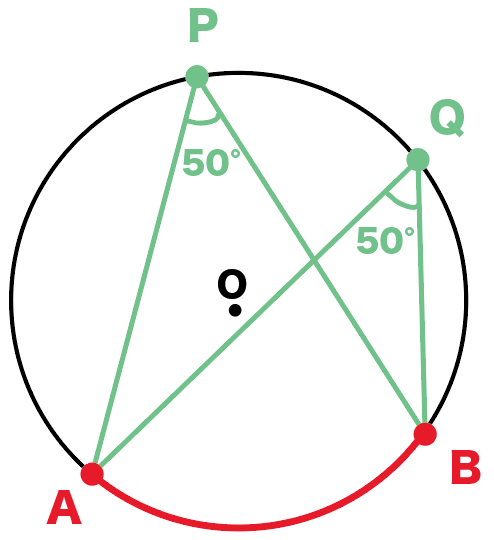
これは円周角の問題では絶対に知っておきたい性質だね。
2つ目の円周角の性質は、
等しい弧の円周角は等しいよ
ってやつね。
円周角の問題でむちゃくちゃよく使うよ。
たとえば、つぎの下の円をイメージしてみて。
円周上に弧ABと弧CDがあるよね。
それぞれ円周角∠APB、∠CQDがあるけど、
2つの弧の長さが等しいとき(弧AB=CD弧)、
円周角も同じ大きさになるっていう性質だよ。
つまり、
∠APB=∠CQD
がいえるんだ。
だから、
∠APB=30°だとしたら、
∠CQDも30°になるってわけ。
この円周角の円周角の性質はちらっとでてくることがあるよ。
よく復習しておこう。
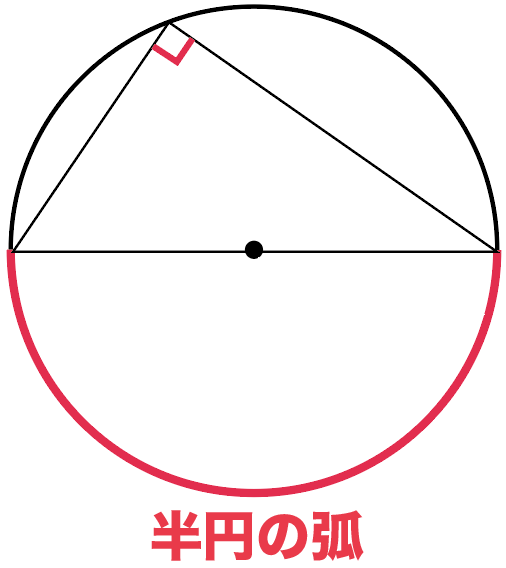
いよいよ最後の円周角の性質。
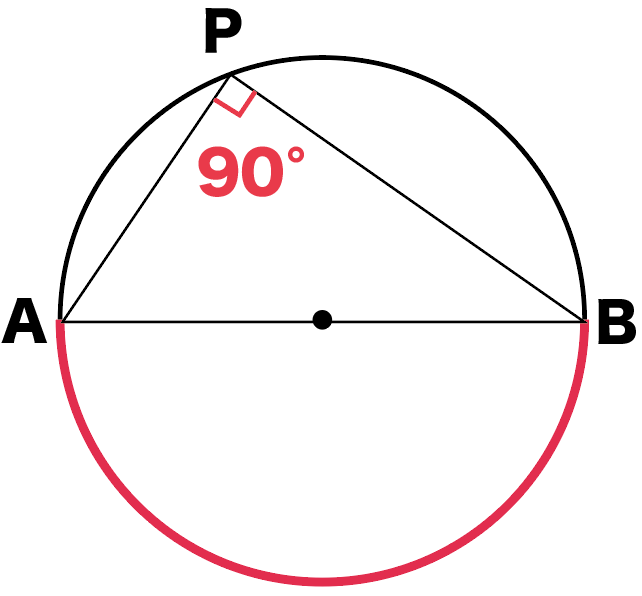
もし、弧が半円のやつだったら、そいつの円周角は、
90°になる
っていう性質だね。
「えっ、そうなの!?」
ってびっくりする人もいるかもしれない。
これも、知っているのと知らないのとでは
問題を考えるときに大きな違いが出てくるから
ぜひ覚えておきたいところだね!
図で表すとこんな感じだ。
たとえば、下の円Oを想像してみて。
直線ABは中心Oを通ってるから、
円の直径になってるよね。
直径ABで円を切ると半円になるから、
弧ABは半円の弧になってることがわかる。
よって、
半円の弧に対する円周角の角APBは90°になってるわけ。
えっ。なんで半円の弧に対する円周角が90°になるのかって??
って人のために、
なぜ、半円の孤に対する円周角は90°になるのか
を説明しておこう。
って言っても、これ自体はめちゃ簡単。
円周角の定理をつかえば説明できちゃうんだ。
半円の弧に対する中心角
に注目してみて。
さっきの弧ABに対する中心角をみてみると、
直線ABがつくる180°
であることがわかるね。
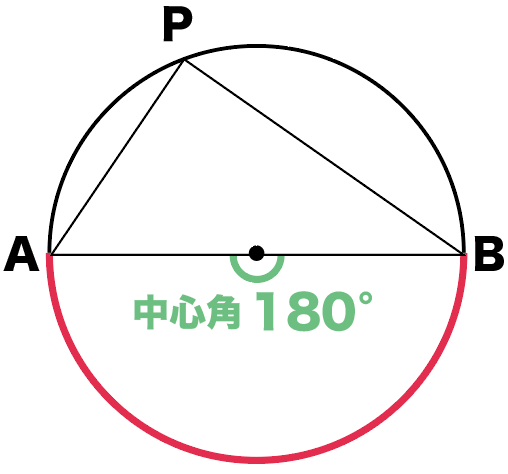
で、あとは円周角と中心角の関係を思い出そう。
1つの弧に対する円周角の大きさは、その弧に対する中心角の半分である
だったから、
中心角の半分の大きさが円周角になるんだ!
で、中心角の∠AOBって180°だよね?
その半分が円周角なんだから、
円周角の∠APB=90°になるんだ!
これで説明終わりだよ。
意外と簡単だったでしょ?(。)
円周角の性質はどうだったかな??
ここで出てきた性質は問題を解く上では必須。
絶対忘れないようにしてね!
この円周角の性質と同じぐらい大事なのは、
だね。こっちも忘れかけてたら復習してみてね。
じゃあ、今日はこのへんで。
またね!
ぺーたー
やあ、ぺーたーだよ。
中3数学もいよいよ大詰め。
いよいよ、
円の性質っていう単元
を勉強していくよ。
今日は、この単元でいちばん大事な、
円周角の定理とはなにか??
をまとめてみたんだ。
計算や証明で使ったりするから、しっかりおさえてあげてね。
= もくじ =
円周角の定理を理解するためにはまず、
の2つの意味を知らないとね。
まず円周角からだ。
円周角とはなんだろう??
Wikipediaをみてみると、
ユークリッド幾何学においてある円周上の一点から、この点を含まない円周上の異なる二点へそれぞれ線分を引くとき、その二つの線分のなす角のことである。
ってかいてある。
これはちょっとむずかしいw
正直、ユークリッドとかわけわからんよね。
円周角をもうちょっと簡単にいってあげると、
「円周上の1点」と、
そいつと被らない円周上の2つの点を、
線分でむすんだときに、
できる角度のことを、
円周角(えんしゅうかく)
とよんでいるんだ。
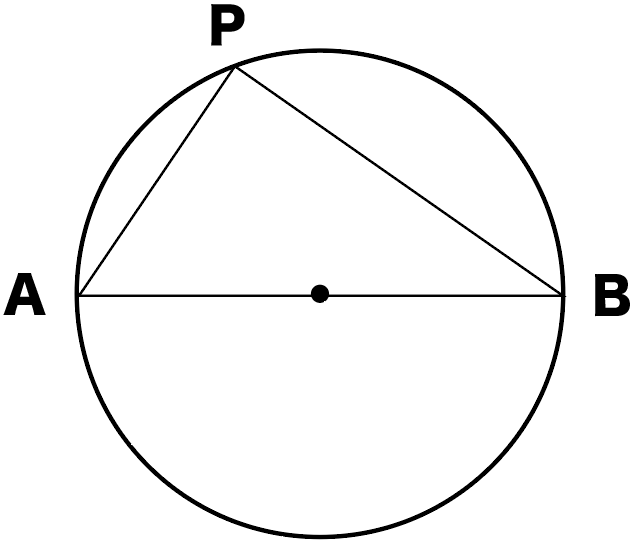
たとえば、つぎの円Oがあったとしよう。
円周上の点をA・B・Pとするよ。
このとき、
∠APBを弧ABに対する円周角
っていうんだ。
こんなかんじで、円周角には、
弧○○の円周角
というかんじで、どこかの弧に属してるってわけ。
つぎは中心角。
中心角を数学用語集でしらべてみると、
弧の両端を通る2つの半径の作る角
らしいね。
これはわかりやすい。
「円の弧」の、
「両端を通る2つの半径」が、
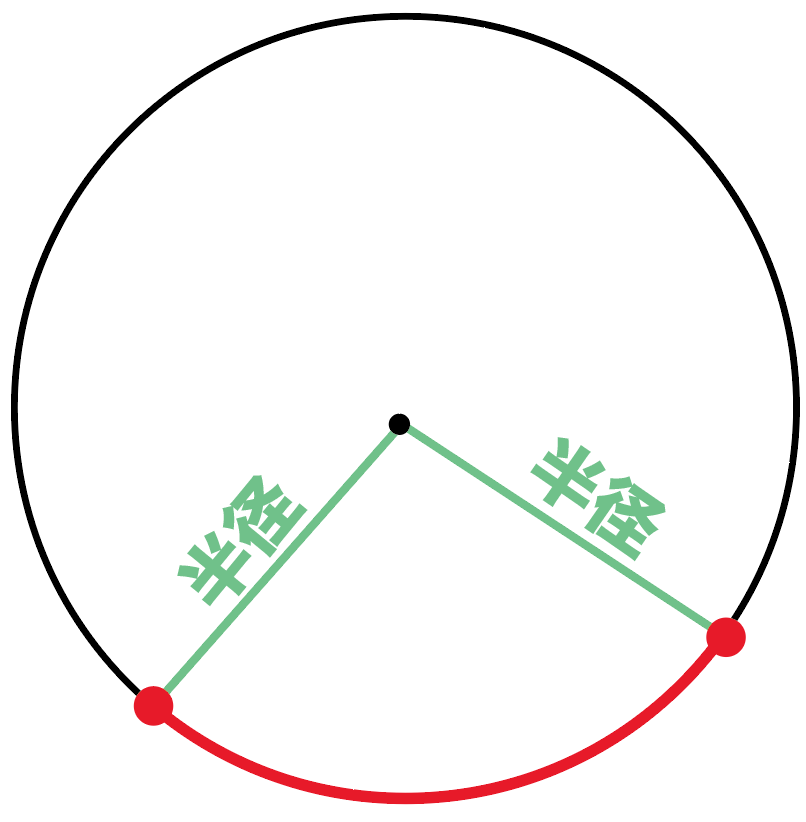
つくる角を、
中心角(ちゅうしんかく)
というんだ。
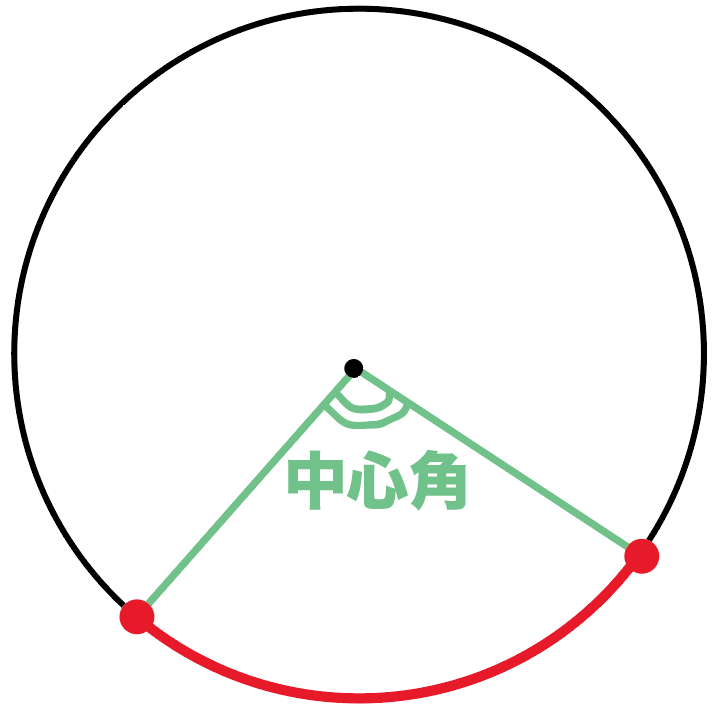
たとえば、下の円Oだったら、
∠AOBが弧ABに対する「中心角」
ってわけね。
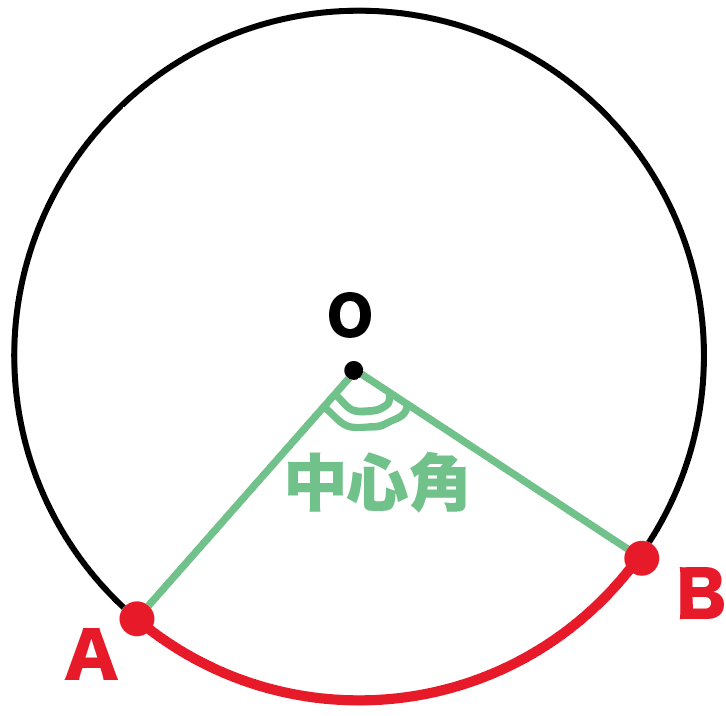
中心角も円周角とおなじように、
弧○○っていうかんじでどこかの弧に属しているよ。
円周角と中心角の違いはOKかな?
この2つの違いはしっかり理解しておいてね!
円周角の定理は、
円周角の決まりみたいなもんだ。
大切だからきっちり覚えてね!
円周角の定理は2つの性質があるよ。
つまり、
の2つの円周角の定理があるんだ。

どっちも、
「同じ弧に対する」
っていう条件が含まれてることに注意ね。
まずは、円周角と中心角の性質からだね。
1つの弧に対する円周角の大きさは、
その弧に対する中心角の半分である
っていう定理なんだ。

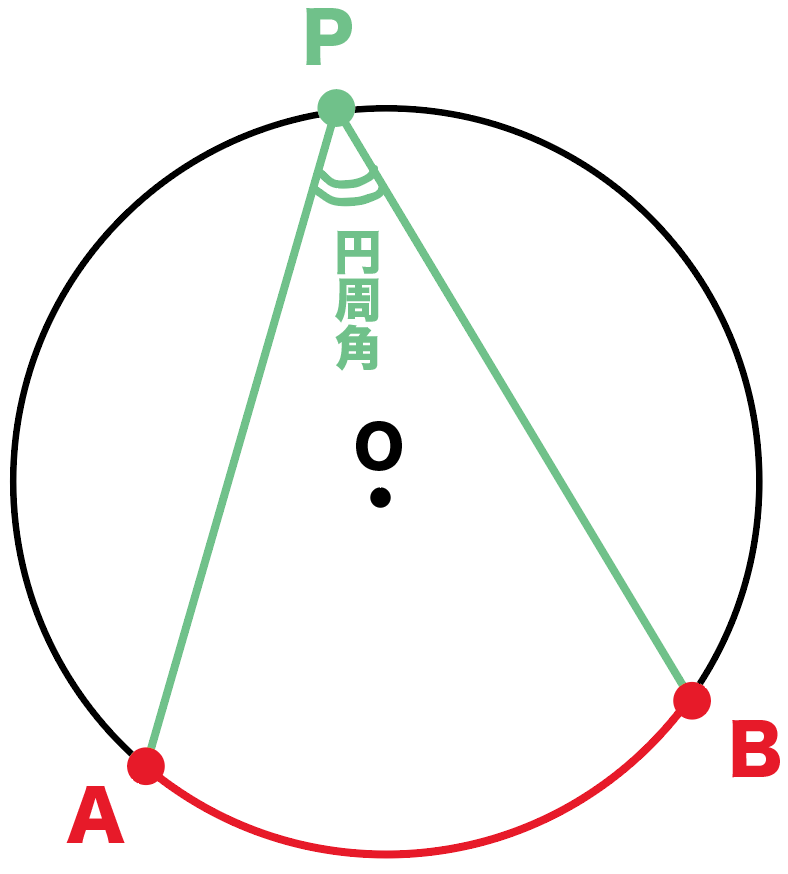
たとえば、つぎのような円Oがあったとしよう。
このとき、円周角APBは中心角AOBの半分になるんだ。
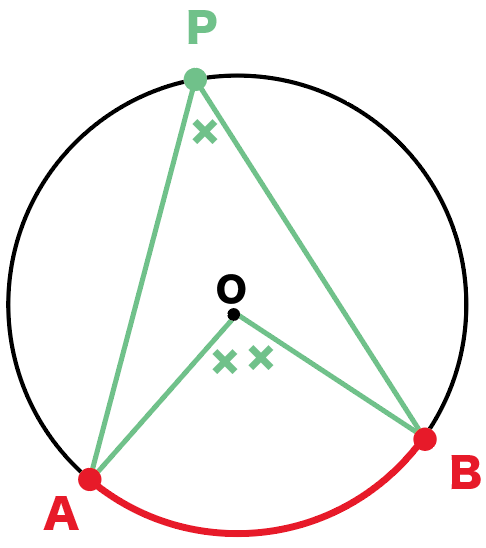
式であらわしてやると、
角APB = ½ 角AOB
になるね。
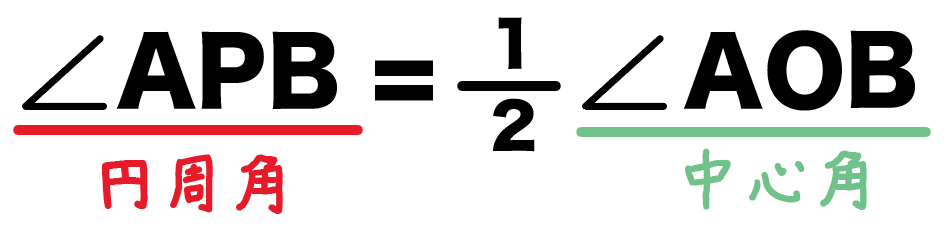
これが、円周角の定理のうち、
同じ弧に対する円周角と中心角の関係ってやつね。
だから、もし、円周角APBが「50°」だとしたら、
中心角AOBは「100°」になるってわけだね。
つぎは、円周角の性質だね。
なんと、同じ弧の円周角ならすべて等しいんだ。

この定理でも、
“同じ弧に対する”
っていう点に注意してね。
たとえば、下の円Oをみてみて。

もし、弧ABに対する円周角APBが「50°」だとしたら、
∠AQB = 50°
になるはずなんだ。

なぜなら、
両方とも弧 ABの円周角だからね。
円周角の定理がどんなものかわかったかな?
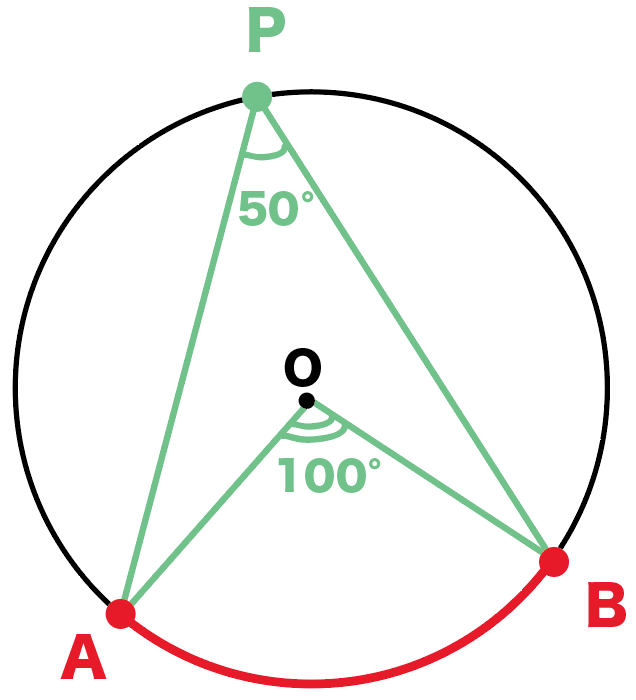
最後に円周角の定理を使った例題を解いてみよう。
次の図の∠xの大きさを求めてみて。
こいつはそんなに難しくないかもね!
1つの弧に対する円周角の大きさは等しいから、
∠APB = ∠AQB
になるんだ。
だから∠x=36°だね!
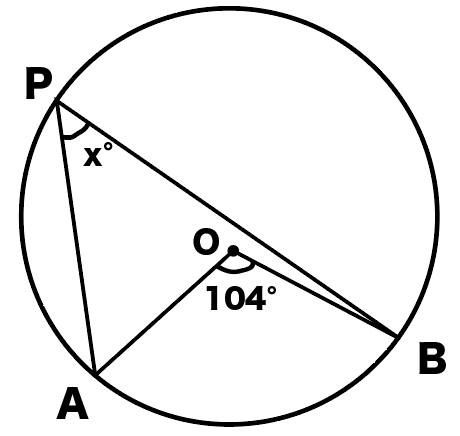
この問題は解けそうかな?
弧ABの円周角がx、∠AOBが弧ABの中心角
っていうことを見抜けると答えが出るよ。
そうすると円周角の定理の、
1つの弧に対する円周角の大きさは
その弧に対する中心角の半分である
をあてはめてやって、
∠x=104÷2
=52
ってことで、
答えは52°だね!
どうだったかな?
円周角の定理がどんなものか
理解できたかな?
どこが円周角で、どこが中心角なのか
ぱっぱと頭の中で分かるようになるのがカギだね。
円周角の定理を使った問題をくりかえしやってみてね。
最初にも言ったけど、証明問題でも活躍するから覚えといてね!
じゃあ、お疲れ!またね!
ぺーたー
こんにちは、Drリードだよ。
相似でいちばんやっかいなのは、
相似の証明の問題
だね。
これは文字通り、
ある図形が相似であること
を証明しなきゃいけない問題なんだ。
テストによくでてくるから完ぺきにしておこう。
前回の記事では「相似の証明問題の書き方」を勉強してきたよね??
今日は、もう一歩踏み込んで、
相似の証明問題でよくでてくる3つのパターン
を勉強していくよ。
テスト前に参考にしてみて。
相似の証明には基本の3パターンがあるよ。
それぞれの特徴と証明の進め方を確認していこう。
図形を見て、
「あっ,○○○タイプだっ」
てわかるようになれば一安心だね。
1つめによくでてくる証明問題のパターンは、
リボン型の図形
だ。
この問題の図形は、文字通り、
リボンの形
をしているよ。

たとえば、つぎのような問題だね。
証明問題1.
つぎの△AODと△COBが相似であることを証明しなさい。
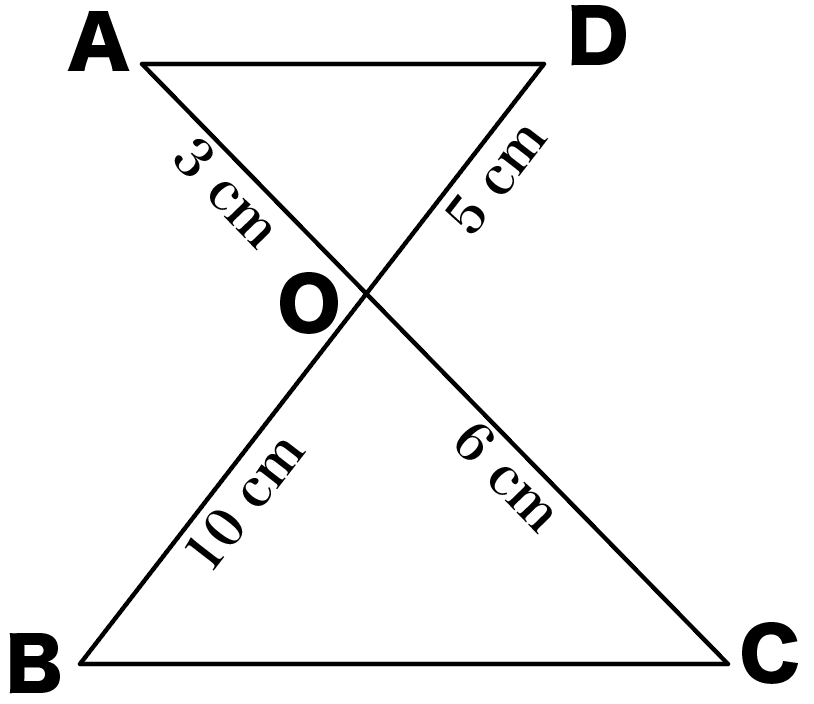
この問題の場合、2つの辺の長さがわかっているね。
あとはどの相似条件にあてはまるかだ。
2つの辺がわかっているから、つぎの相似条件のどっちかにあてはまるはずだね。
1つめの相似条件にあてはまるためには、
ADとBCの長さ
が必要になってきちゃうね。
これはたぶん、おそらく、無理!
超能力ならいけそうだけどね。
ってことで、2つめの相似条件の、
2組の辺の比とその間の角がそれぞれ等しい
が使えそうだ。
これなら、長さがわかってる2つの辺にはさまれた、
の大きさが等しいってわかるからね。
だって、対頂角だから等しいんだもん。
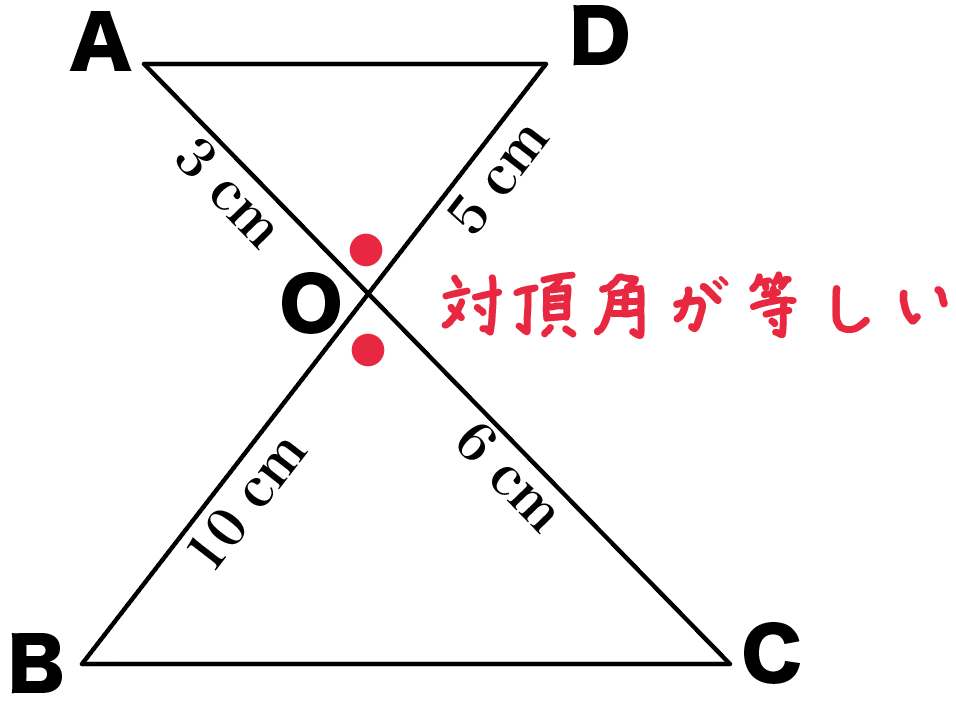
ってことで、
になるから、相似条件の、
2組の辺の比とその間の角がそれぞれ等しい
がつかえそう。
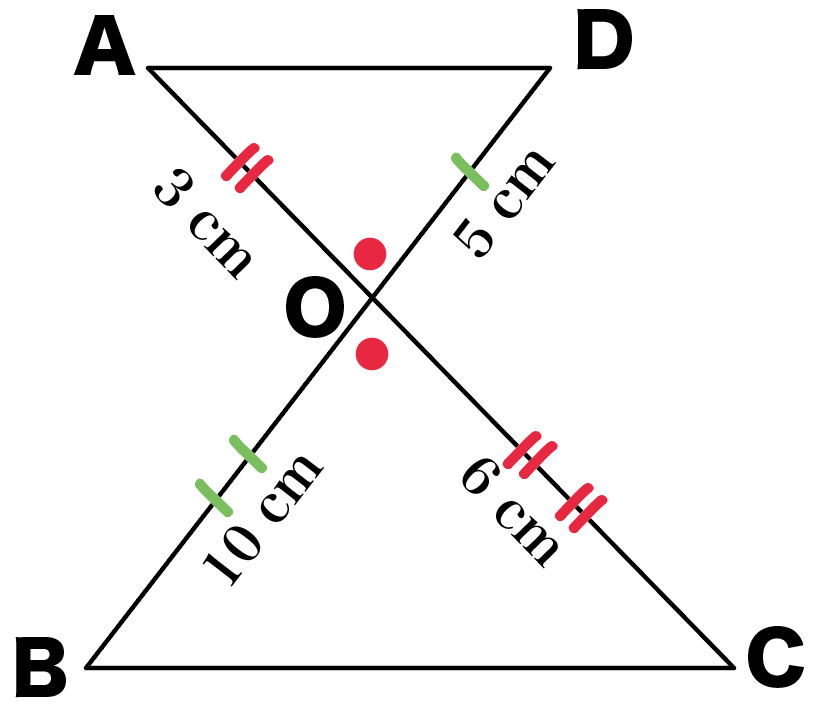
以上をふまえて、相似の証明の書き方通りにかいてやると、
仮定から、
AO:CO = 3 : 6 = 1 : 2 ・・・①
DO:BO = 5 : 10 = 1:2 ・・・ ②
対頂角は等しいので、
∠AOD = ∠COB・・・ ③
①②③より、
2組の辺の比とその間の角がそれぞれ等しいので、
△AOD ∽ △COD
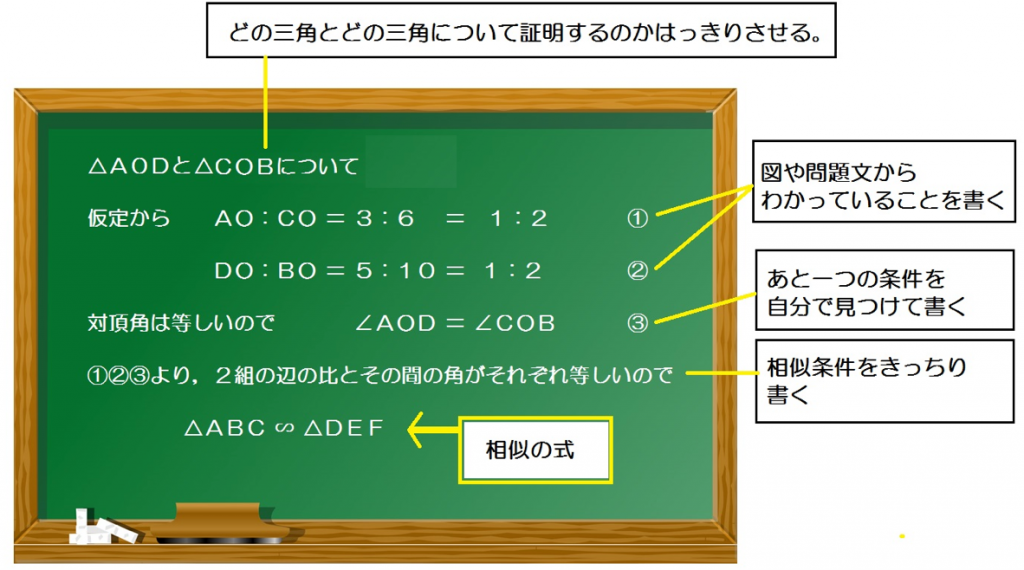
になるね。
つぎの相似証明問題のパターンは、
ひねくれ回転型
だ。

これは文字通り、
図形が回転していて、相似がみえにくくなってる問題ね。
たとえば、相似なイラスト同士だったら回転していても、
どことどこが対応するかわかりやすいよね。
特徴があるんだもん。

でも図形だと、そうはいかない。
向きが変わるだけでわからなくなっちゃうんだ。
たとえば、つぎのような証明問題。
証明問題2.
つぎの図形のなかから相似な図形をさがして、
その相似を証明しなさい。
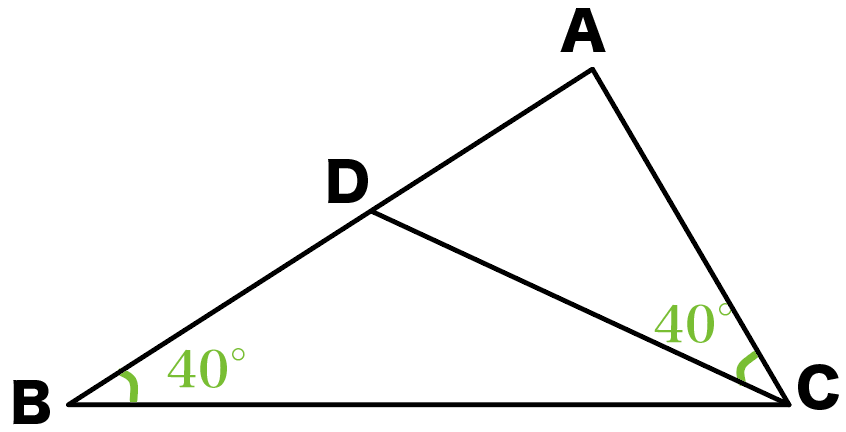
このタイプの証明問題では、
面倒でも別々に切り離して、
対応する辺や角度を確認してみるといいよ。
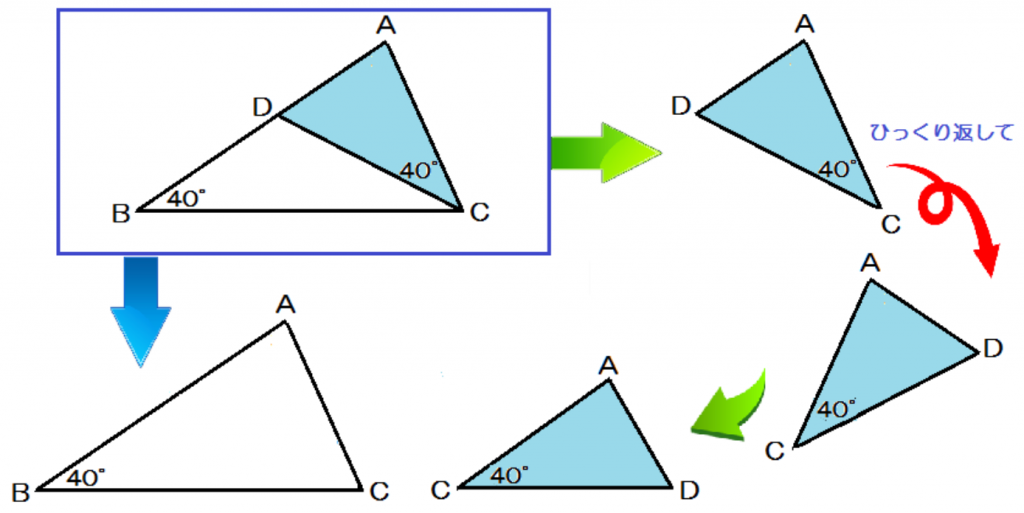
すると、
△ABCと△ACDが相似ってことがわかるね。
なぜなら、
になって、2組の角がそれぞれ等しいっていう相似条件がつかえるからね。
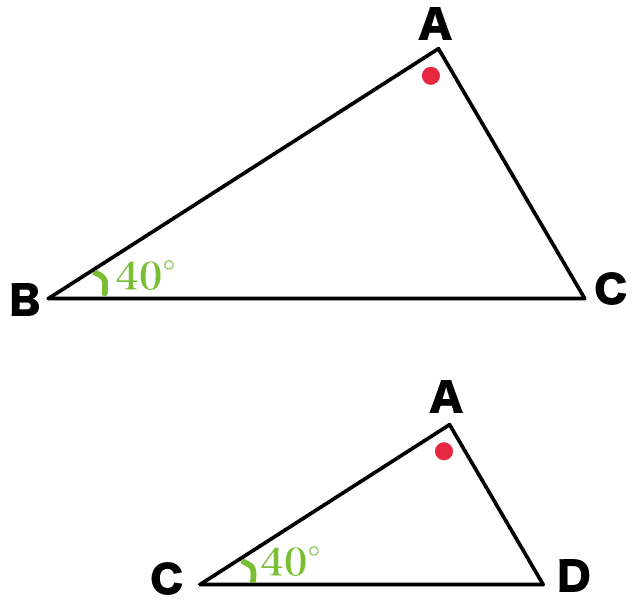
えっ。図形を回転させるのがむずかしいって!??
そんなときは、
対応する辺や角を大きさ順に、
「大中小」とか「長中短」とか
っていう順序をつけるといいよ。
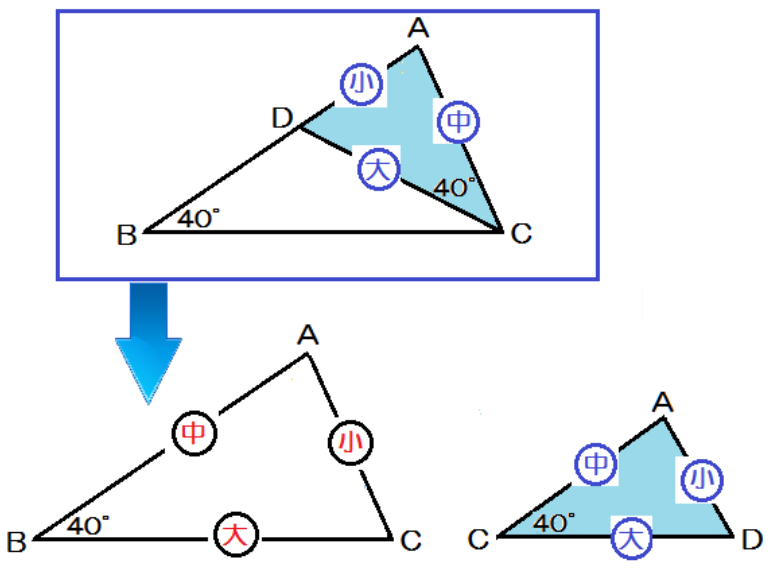
こんなかんじで、ひねくれて回転している図形をなんとかして、
対応する辺の順番にそろうように回転させてみてね。

実際に証明をかいてみると、こんな感じになるよ↓↓
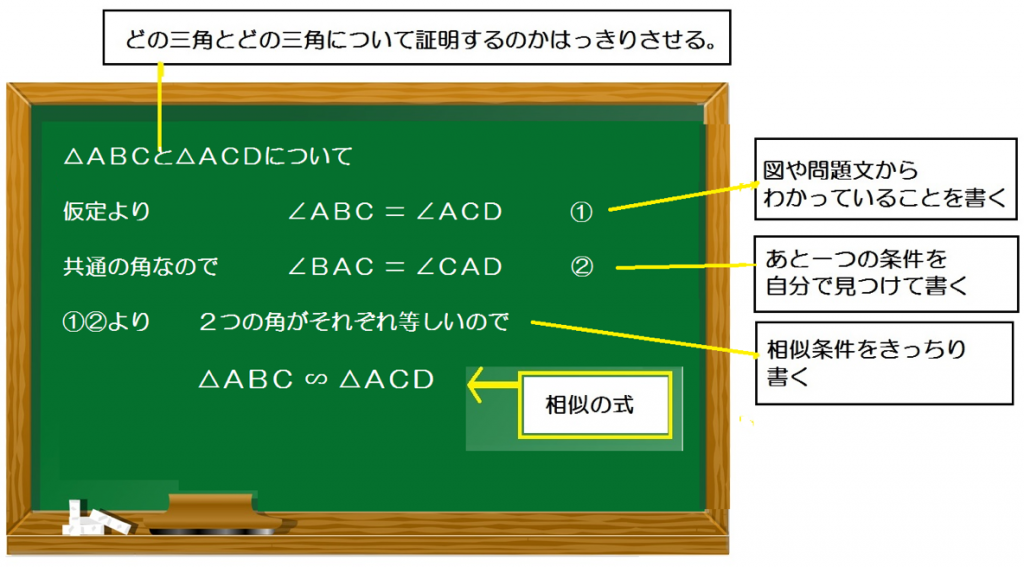
△ABCと△ACDについて
仮定より
∠ABC = ∠ACD ・・・ ①
共通の角なので、
∠BAC = ∠CAD・・・②
①・②より、
2つの角がそれぞれ等しいので、
△ABC ∽ △ACD
最後の相似の証明のパターンは、
直角三角形で垂線がおろされてる問題
だ。

たとえば、つぎの相似の証明問題だね。
証明問題3.
つぎの図形のなかから相似な図形をさがして、
相似であることを証明しなさい。
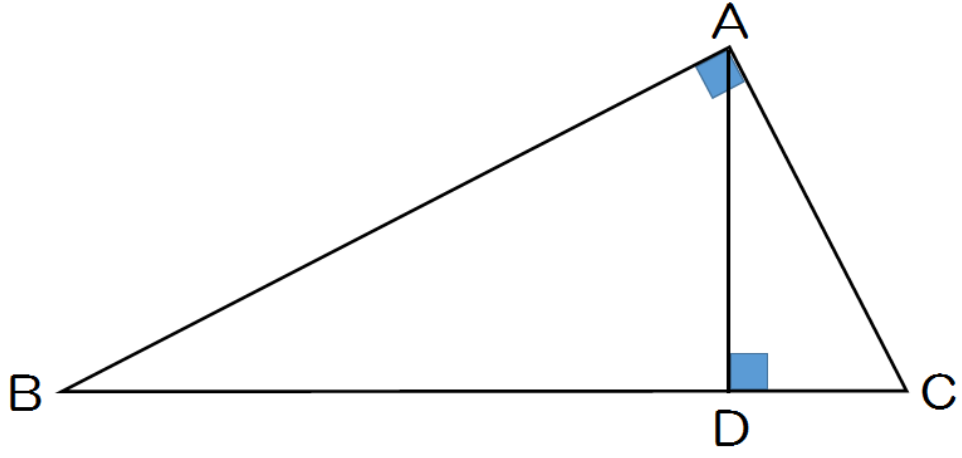
このさっきの相似の証明問題とおなじ。
対応する辺・角が重なるように回転させればいいんだ。
わかりやすいように、△ABDを△ABCの外にとりだして回転させてみると、
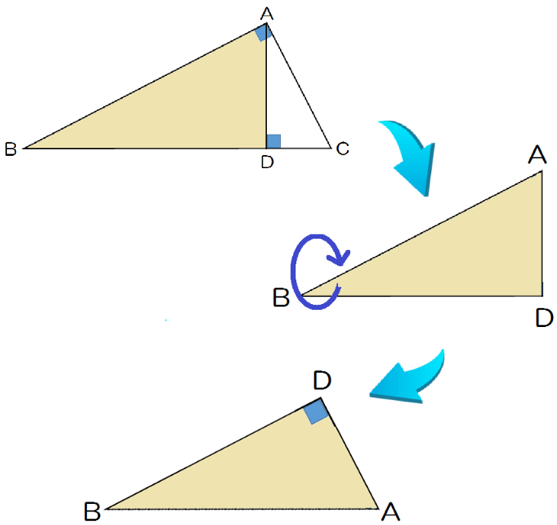
あら!
△ABCと△DBAが相似っぽい!
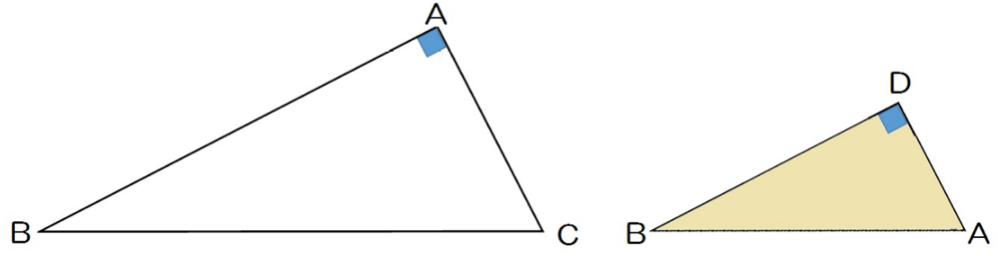
なぜなら、
だからね。
2組の角がそれぞれ等しい
っていう相似条件が使えることになるんだ。
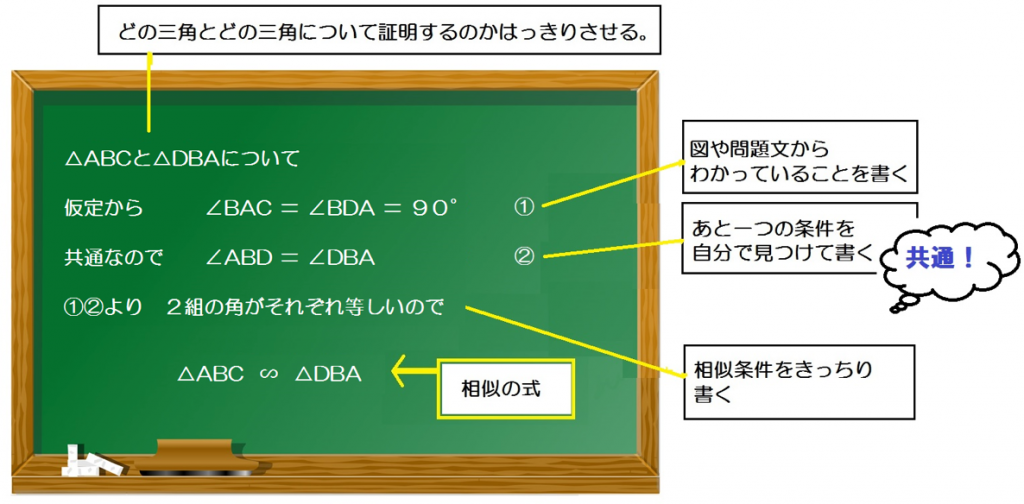
この証明をちゃんとかいてやると、こうなるよ↓↓
△ABCと△DBAについて
仮定から、
∠BAC = ∠BDA = 90°・・・①
共通なので、
∠ABD = ∠DBA・・・②
①②より、
2組の角がそれぞれ等しいので
△ABC ∽ △DBA
相似の証明問題はめんどくさそうにみえるけど、じつは、
どの問題もよく似ていて、
パターンがみえるんだ。
なれるまでたくさん相似の証明問題をといてみよう。
それじゃあ!
Drリード
どうも、Drリードだよ。
中3数学の図形では、
図形と相似
を勉強してくよね。
この単元のなかでもやっかいなのが、
相似の証明問題
だ。
まず、証明とか苦手なのに、
図形の相似を証明しなきゃいけないときてる。
正直、きちいね。
でもね、じつは、
相似の証明問題には書き方のルールがあるんだ。
これならどんな相似の証明問題もイチコロさ。
相似証明問題の書き方を紹介していく前に、
2つのことをやっておこう。
つぎの相似の証明問題で練習してみようね。
つぎの2つの三角形が相似であることを証明しなさい。
ただし、
とします。
まずは、
問題でわかってる条件(仮定)
を図にかきこんでみよう。
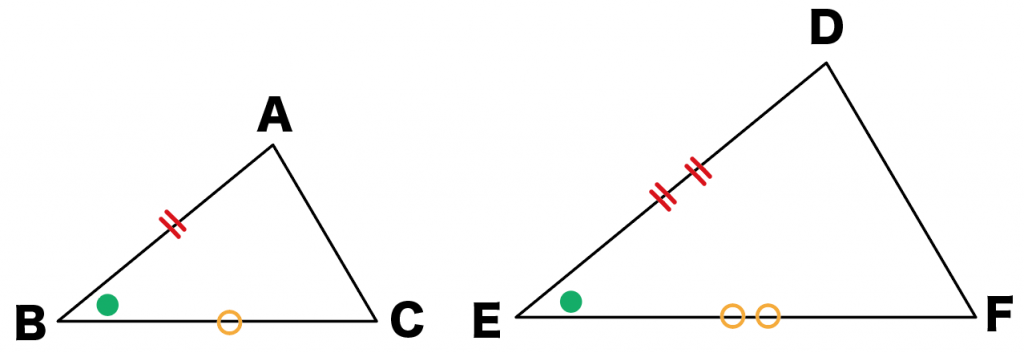
練習問題では、
がわかってたよね??
さっそく書き込んでやると、こうなる↓↓
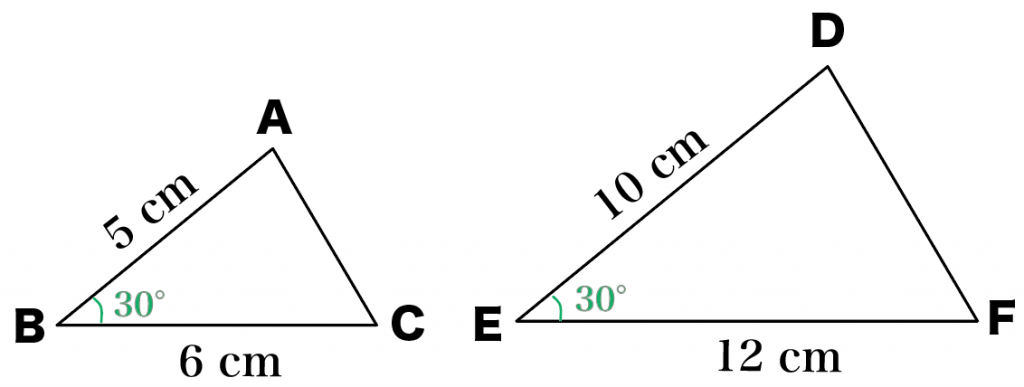
んで、
同じ角度・辺の長さ同士に、「同じ印と色」をつけてやると、
こうなるね↓↓
つぎは、相似な三角形をさがそう。
三角形の相似条件にあてはまる2つの三角形をさがせばいいのさ。
念のため、三角形の相似条件を確認しておくと、
だったよね??
ってことで、練習問題をみてみると、
2組の辺の比とその間の角がそれぞれ等しい
がつかえそうってことに気づかない??

だって、三角形の2組の辺の比が、
で両方1:2で等しいし、
その間にはさまってる角の、
が両方30°になってるからね。
えっ。簡単すぎるって??!
本番の証明問題はもっと複雑でみつけにくいよ。
まだまだ油断大敵。
それじゃあ、相似の証明を実際にかいてみよう。
書き方はつぎの3ステップ。
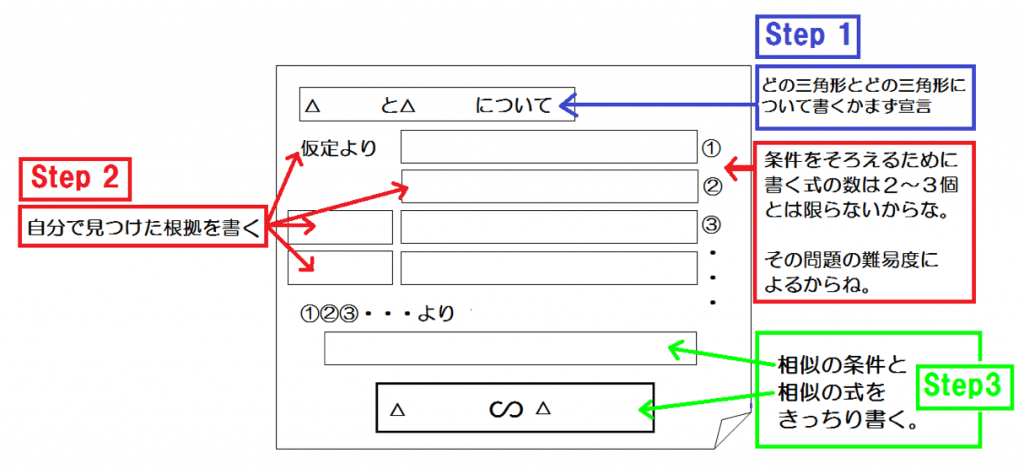
まずは、どの図形で相似を証明するのかを宣言しよう。
相似の証明問題では、おもに、
準備でみつけた「相似になりそうな三角形」を宣言することが多いね。
練習問題では、
△ABC と△DEFが相似疑惑だったよね??

だから、証明のいちばん最初に、
△ABCと△DEFについて、
って宣言すればいいんだ。
つぎは、
図形が相似になる根拠をかいていこう。
図や問題文からわかってることをかけばいいよ。
相似条件にあてはまる根拠をかいていけばいいのさ。
まずは、仮定からわかることを書いていこう。
問題文の中に書かれていることを数式にしてみよう。
練習問題では仮定として、
がわかってたよね??
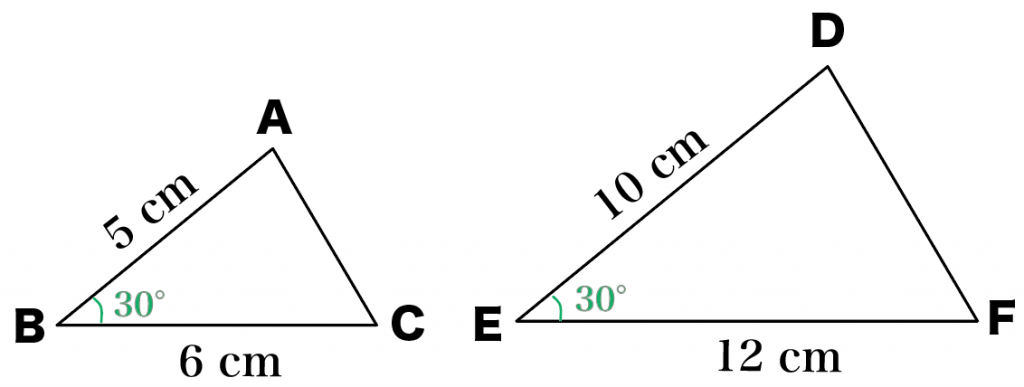
この仮定だけで相似条件でつかえそうだから、
証明の根拠はこれだけでいいんだ。
相似の証明の最後では、
なぜ、相似がいえるのか??
という相似条件と、
宣言した図形が相似であること
を記号であらわしてみよう。
練習問題で言うと、
△ABCと△DEFが相似になってたね??
つかった相似条件は、準備でもみてきたように、
2組の辺の比とその間の角がそれぞれ等しい
だ。
これにより、
△ABC ∽ △DEF
がいえるってかけばいい。
これで相似の証明はおわり!
それじゃあ、この書き方で相似の証明をかいてみよう。
こんなかんじになるよ↓
△ABCと△DEFについて
仮定より、
AB:DE = 5:10 = 1:2 ・・・①
BC:EF = 6:12 = 1:2 ・・・②
∠ABC = ∠DEF ・・・③
①②③より、
2組の辺の比とその間の角がそれぞれ等しいので、
△ABC ∽ △DEF
最後にもう一度復習しておこう。
相似の証明問題を書く前の準備は、
だったね。
んで、相似証明問題の書き方は、
の3ステップ。
これで何とか道は開けるよ。

何がわかっていて、あと何がわかれば、
相似の条件がそろうのか考えてみよう。
証明を書き始める前にしっかり用意してね。
次は「相似の証明問題でマスターしておきたい3つのパターン」について話す予定だよ。
相似の証明を極めたいやつは読んでみてくれ。
それじゃあ
Drリード
ある日、数学が苦手なかなちゃんは、
平行線と線分の比の証明問題に出会いました。
証明問題.
下の図形において、DE//BCです。
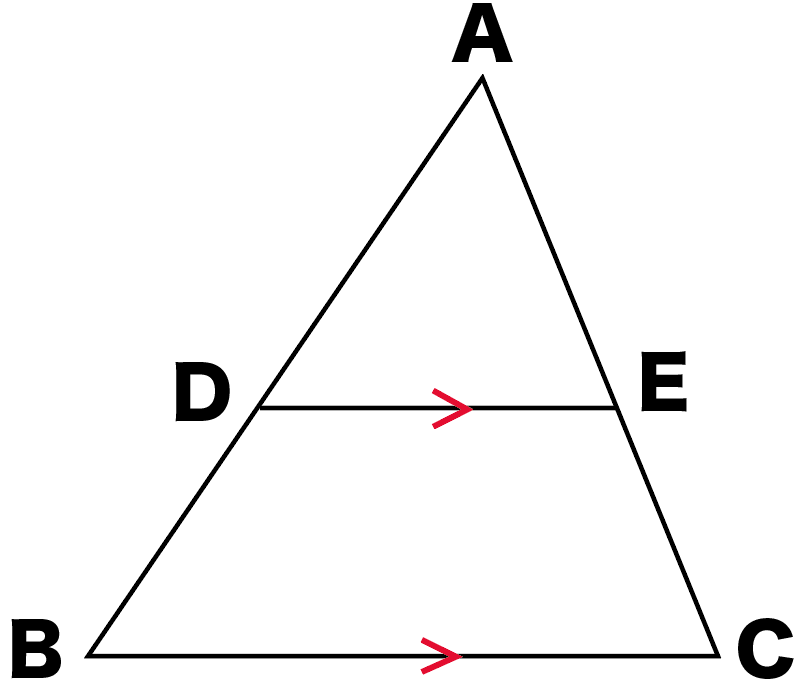
つぎの2つのことを証明しなさい。
平行線と線分の比の証明??
あー、もうやだ!!
平行って、
わたしと数学みたい!
決して交わることのない者同士……って、
少しは歩み寄ろ?ね?
うわあっ!?
先生か、びっくりした……
だって、
今日の授業もわかんなかった。
平行だと線分の比が……
みたいな。
いきなり、
平行線と線分を語られても困るよね。
今日は、
平行線と線分の比について考えていこう!
うす!
平行線と線分の比の証明は、
2つあったよね??
まず1つめの、
AB : AD = AC : AE = BC : DE
を証明していこうか。
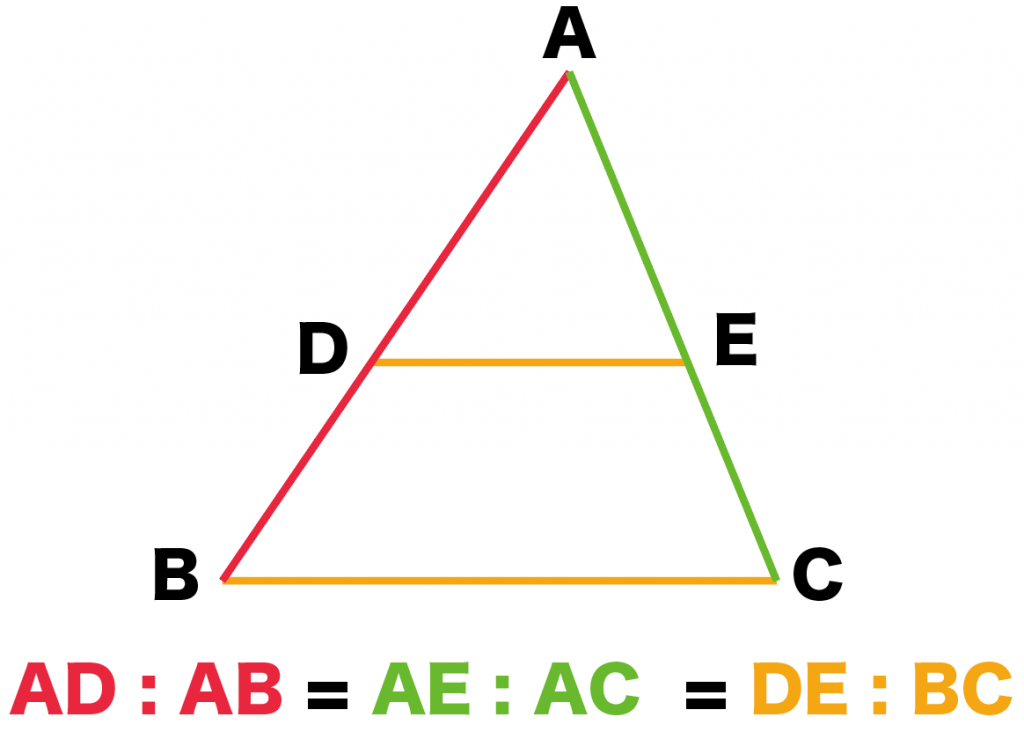
色分けしてあると、
わかりやすい!
うん、
自分でも描いてみると覚えやすいよ。
この証明のゴールはなんだっけ??
DEとBCが平行だと、
AD:AB
=AE:AC
=DE:BC
ってこと?

そう!
辺の比を証明したいってことね。
こういうときは、
相似を使おう!
相似ってことは、
二つの図形を比べるの?
そう。
この場合なら、
△ABCと△ADEだね!
うーん、
DEとBCが平行
が仮定かな?
「DE//BC」
って問題にかいてあるから!
おっ、いいね!
その仮定をつかって、
△ABCと△ADEの相似
を証明できるかな??
うーん、あ!
おっ!
なにか降りてきたかな?
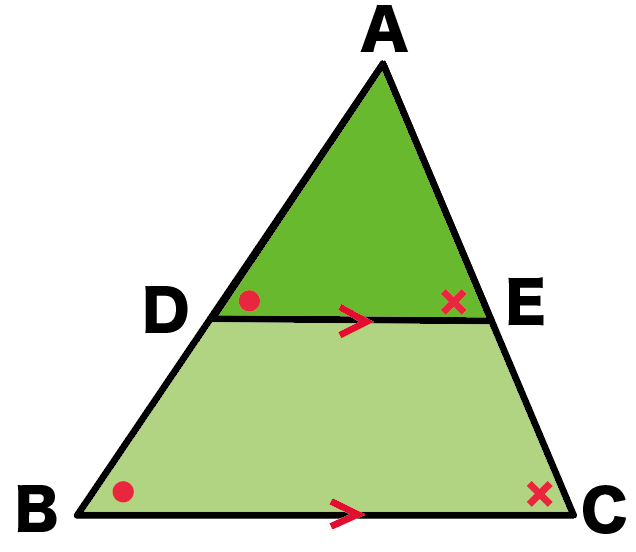
相似条件はなにをつかう??
2組の角がそれぞれ等しいかな!
同位角で対応する2つの角が等しいし
お、
今日はキレっキレっだねー
その通り!
わーい
実際に証明をかいてみよう。
証明のネタを集めたし
うす!
でもちょっと怖い……
うす!
うーん、
こんな感じかな・・・?
【証明】
仮定より、
BC//DE … ①
△ABCと△ADEで、
①より同位角が等しいので、
∠ABC=∠ADE…②
∠ACB=∠AED…③
②・③より、
対応する2つの角が等しいので、
△ABC∽△ADE
相似な図形では、対応する辺の比がそれぞれ等しいので、
BC:DE=AB:AD=AC:AE
お、やるねー!
やった!
おっと。
これでおわりじゃないよ!
平行線と線分の比は、
もう1つあったよね??
AD : DB = AE : EC
ってやつか!!
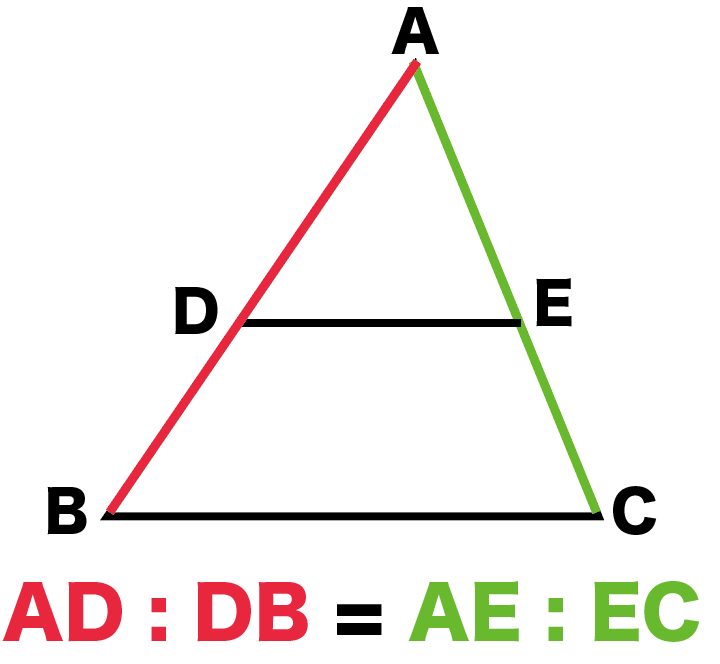
そうそう!
うーん・・・・・
わ、わからない!
どうしたら証明できるの!?
図形は困ったら、
補助線を引くことが大切なんだ。
補助線?
そう!
Eから、ABと平行な直線を引いてみて。
平行線とBCの交点をFとするんだ。
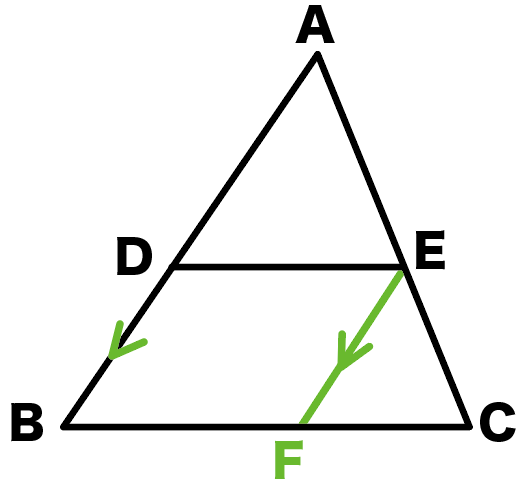
ひ、ひけた!
どう??
相似な図形がみえてこない??
あああ!
△ADEと△EFC!!
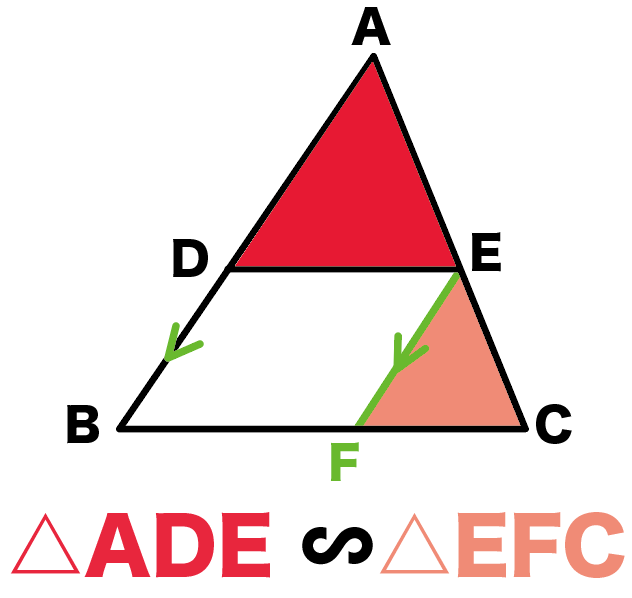
なんで??
AB//EFだから、
同位角が等しいことがつかえる!!
だ。
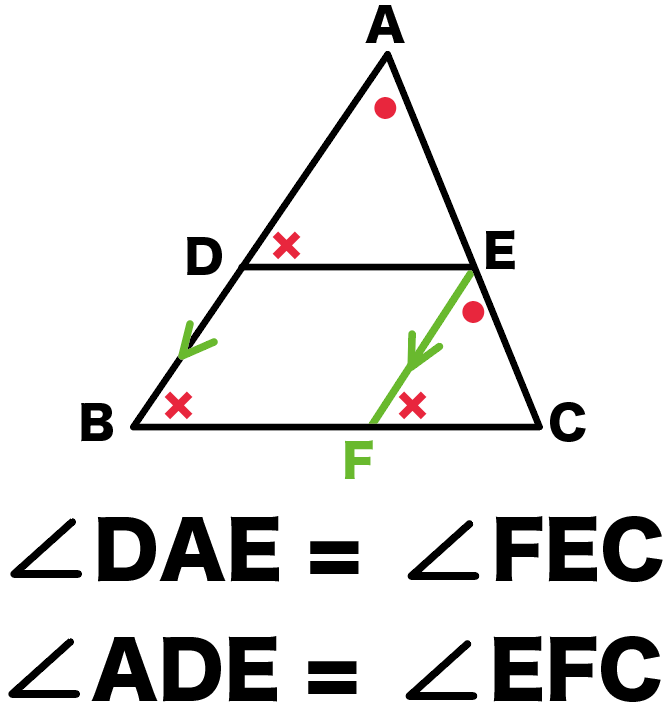
お、いいねー!
相似条件の、
2組の角がそれぞれ等しい
を使うわけね。
じゃあ証明かいてみてー
ういす!
【証明】
EからABに平行に引いた直線と、
BCとの交点をFとする。
仮定より、
BC//DE …①
AB//EF …②
△ADEと△EFCで、
①より同位角が等しいので、
∠ACB=∠AED…③
同様に、AB//EFより同位角が等しいので
∠ABC=∠ADE…④
また、BD//EFより、
∠ABC=∠EFC…⑤
④・⑤より、
∠EFC=∠ADE…⑥
対応する2つの角が等しいので、
△ADE∽△EFC
相似な図形では、
対応する辺の比がそれぞれ等しいので、
AE:EC=AD:EF…⑦
また、四角形DBFEは、
①、②より平行四辺形で
向かい合う辺の長さが同じなのでBD=EF…⑧
⑦・⑧より、
AE:EC=AD:DB
できたぜ!姉御!
おっ。
やるじゃああん
平行線と線分の比の証明も楽勝!
って思ってもらうのが、
今回の目的!!
証明のいいところは、
多少言葉の言い回しが違っても、
正解になるところ!
筋が通っていればいいのよ。
うんうん
証明は、
とにかく書いてみよう。
おかしくてもなんとかなる。
はい!
七転び八起きですね!
ということで、
今回のポイントをまとめよう。
証明はなれれば大丈夫。
解けば解くほど上達するよ。
おまけの問題を作ってみたよ〜
【おまけ】
BC:DE=AB:AD=AC:AE なら、BC//DEとなる証明をしてみよう!
といてみます!
こんにちは!ぺーたーだよ。
相似の単元では、
相似条件とか、
相似の証明とか、いろいろ勉強してきたね。
今日は ちょっと新しい、
平行線と線分の比のから辺の長さを求める問題
について解説していくよ。
たとえば、つぎのような問題ね↓
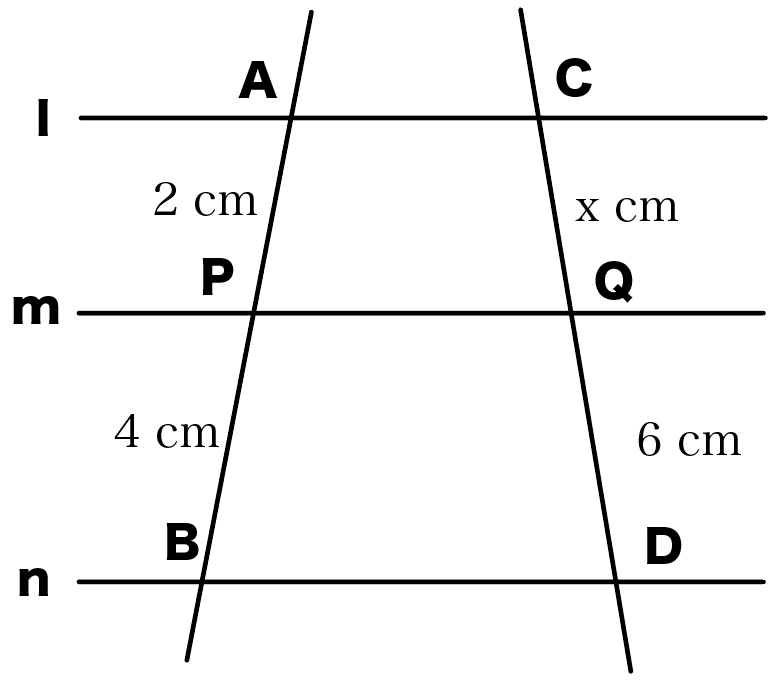
平行線とか線分がたくさんあって、ちょっと難しそうだね。
だけど、慣れちゃえば簡単。
「これはできるぜ!」っていうレベルになっておこう。
次の段階に分けて説明してくね。
目次
問題をとく前に、
平行線と線分の比の性質を思い出そう。
3つの平行な直線(l・m・n)
と
2つの直線が交わる場面をイメージしてね。
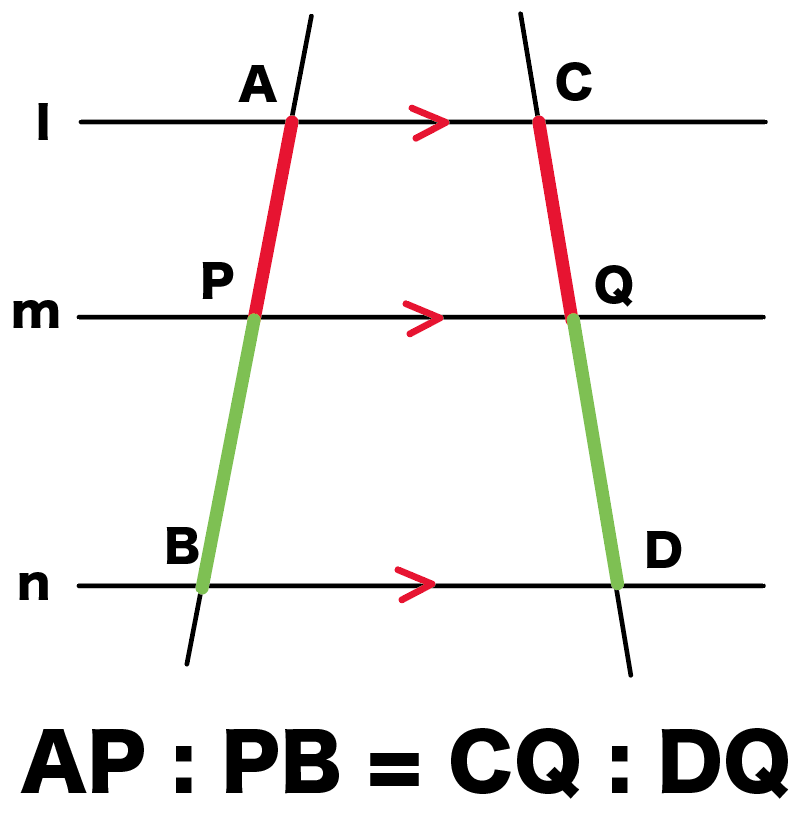
このとき、
AP:PB=CQ:QD
が成り立つんだ。
つまり、
平行線にはさまれた、
向かいあう線分の長さの比が等しい
ってわけね。
これさえおさえておけば大丈夫。
平行線と線分の比の問題もイチコロさ!
さっそく、平行線と線分の比の問題を解いてみようか。

この手の問題は3ステップでとけちゃうよ。
平行線と線分の比がつかえる線分を見極めよう!
平行線にはさまれた線分のセット
をさがせばいいってわけね。
練習問題でいうと、
で平行線と線分の比がつかえそうだ。
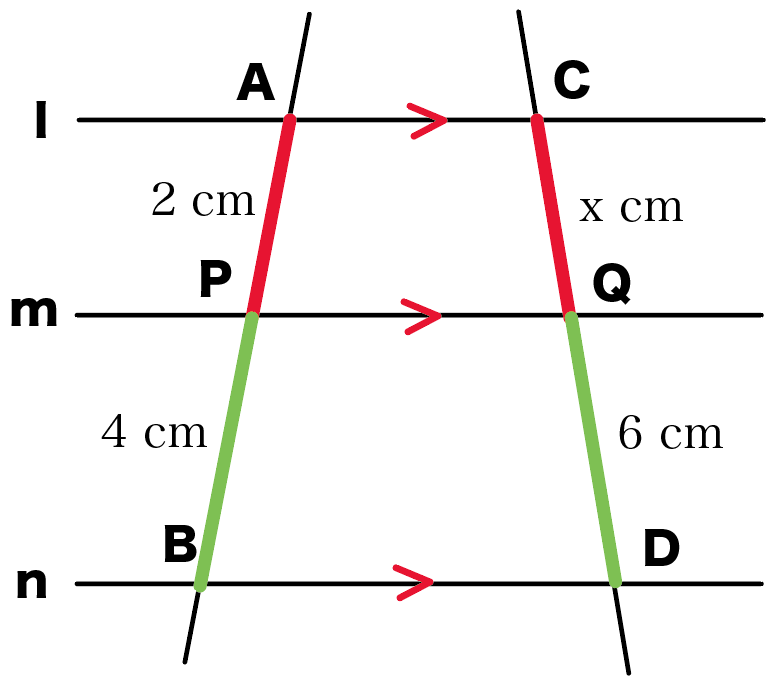
なぜなら、こいつらは、
3本の平行線(l・m・n)にはされまれてるからさ。
あきらかに3本の平行線に囲まれてる。
平行線と線分の比の性質で比例式をつくってみよう。
平行線と線分の比の性質は、
2つの直線が、3つの平行な直線と交わるときAP:PB=CQ:QD
だったね??

だから、練習問題でいうと、
AP : PB = CQ : DQ
2 : 4 = x : 6
っていう比例式ができるはず!
つぎは、比例式をといてみよう。
練習問題でつくった比例式は、
2 : 4 = x : 6
だったよね??
比例式の解き方の「内項の積・外項の積」で解いてやると、
2 : 4 = x : 6
4x = 2×6
4x = 12
x = 3
になるね。
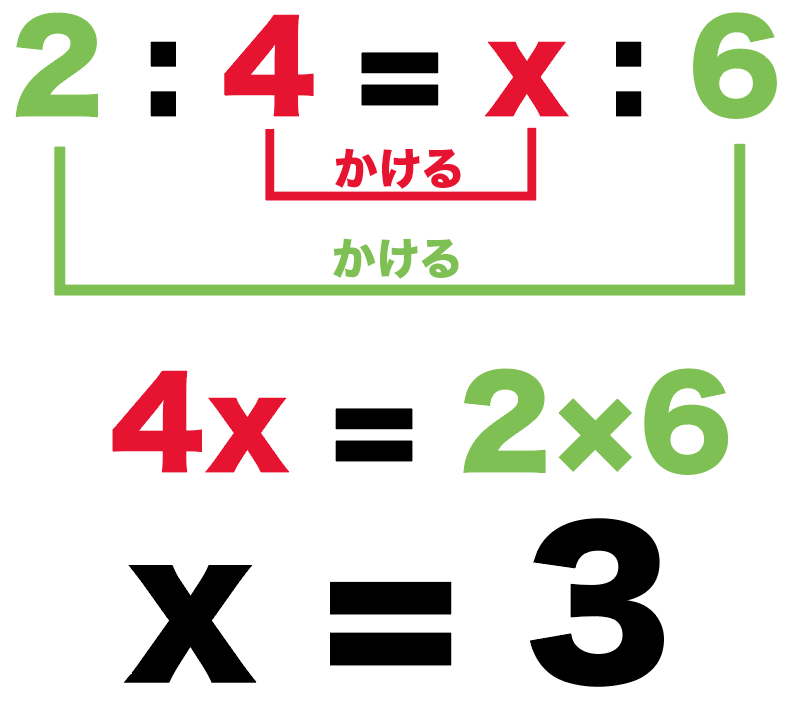
つまり、
求めたかったCQの長さは「3 cm」ってこと。
やったね!
平行線と線分の比の性質もだいたいわかったね。
あとは練習問題でなれてみよう。
今日はテストにでやすい問題を2つ用意したよ。
平行線と線分の比の問題になれてみようぜ。
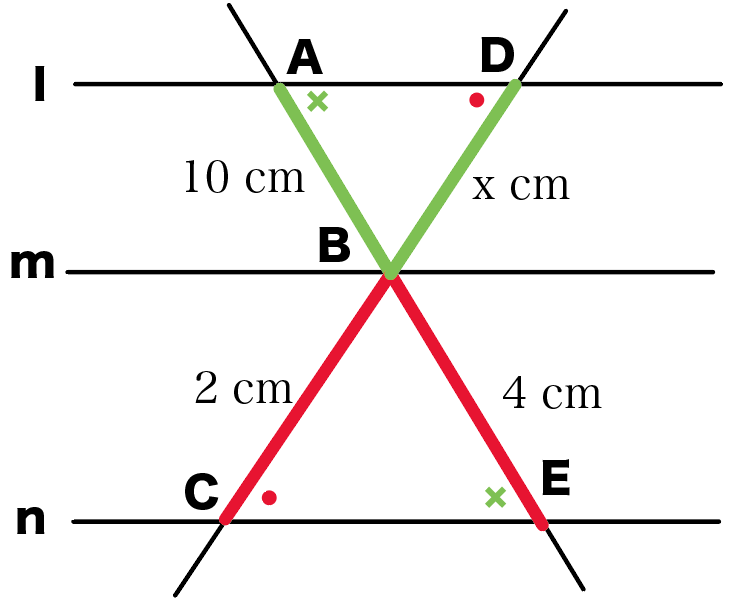
l//m// nのとき、xの大きさを求めなさい。
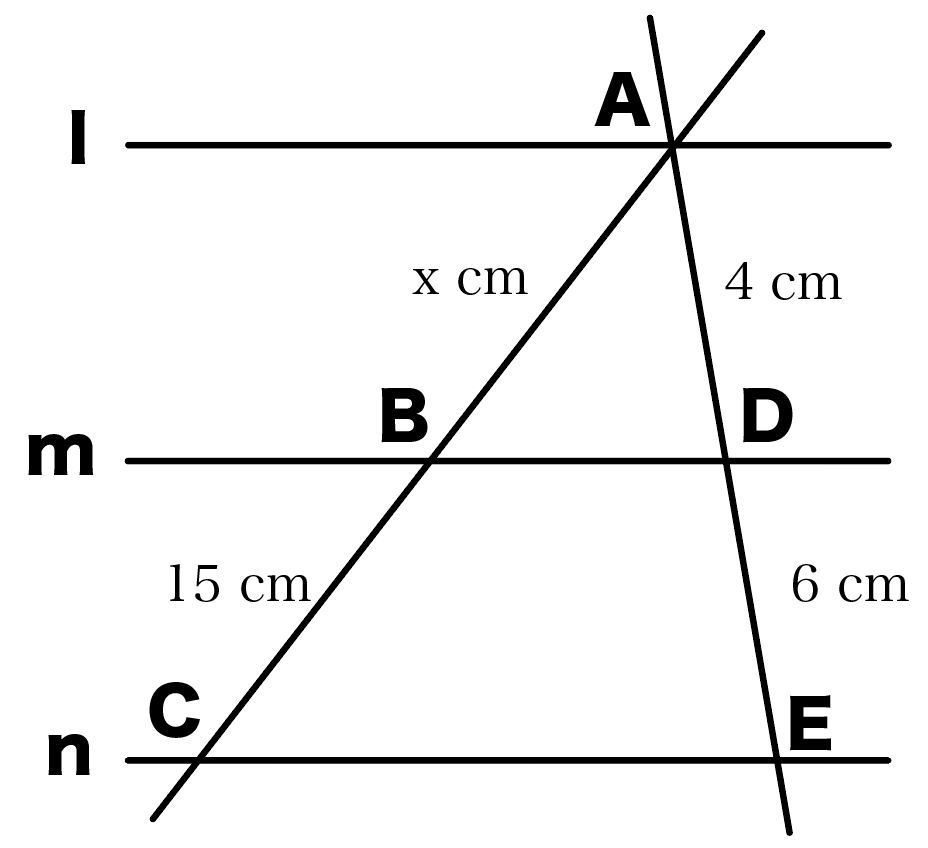
この手の問題は、
AB : BC = AD : DE
という平行線と線分の比をつかえば一発さ。
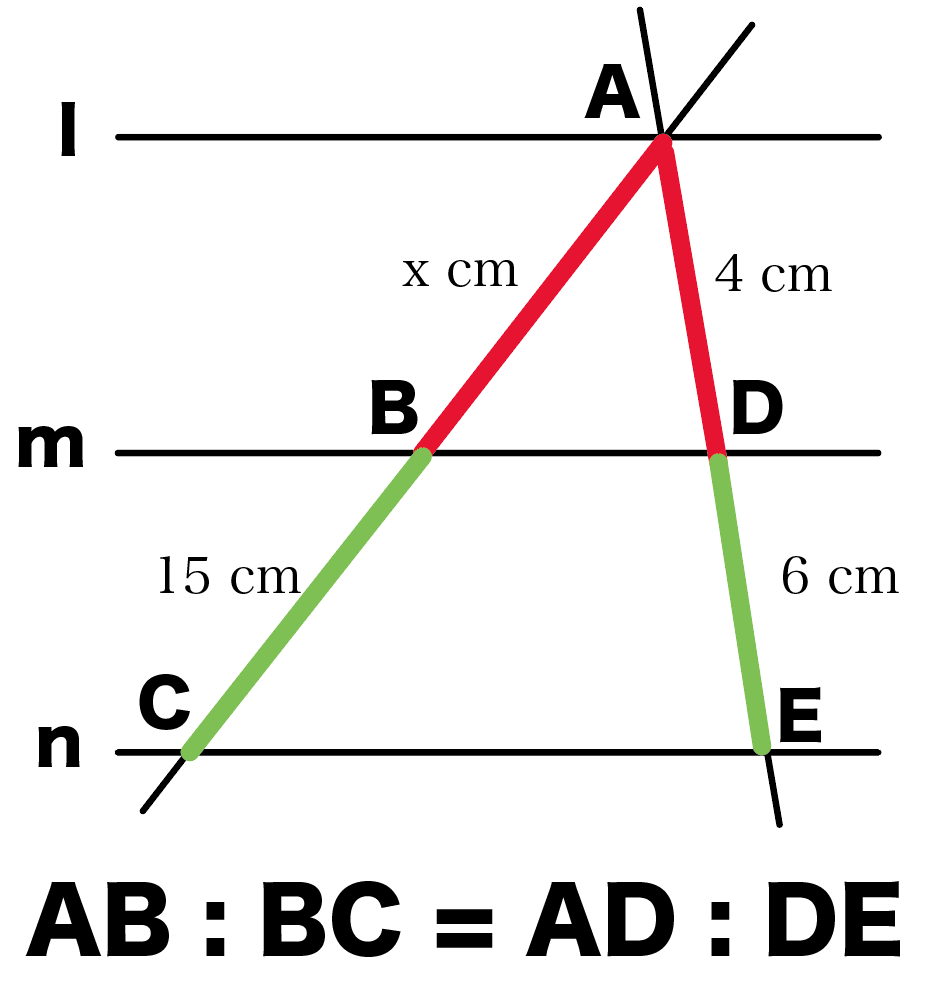
これは、△ABDと△ACEが相似だから、
対応する辺の比が等しいことをつかってるね。
えっ。
なんで相似なのかって??
それは、同位角が等しいから、
がいえるからなんだ。
三角形の相似条件の、
2組の角がそれぞれ等しい
がつかえるし。
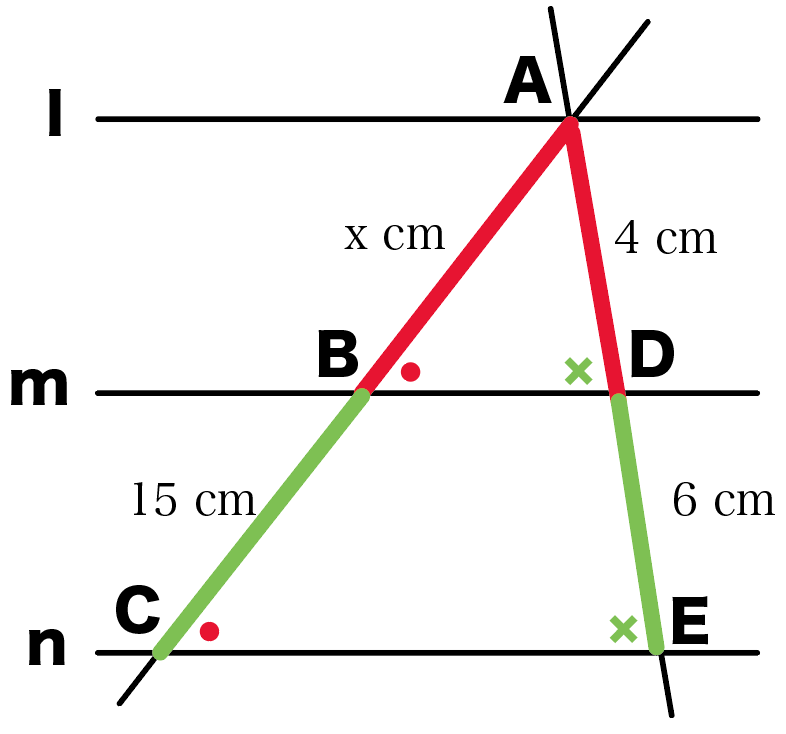
さっそく、この比例式をといてやると、
AB : BC = AD : DE
x : 15 = 4 : 6
x = 10
になるね。
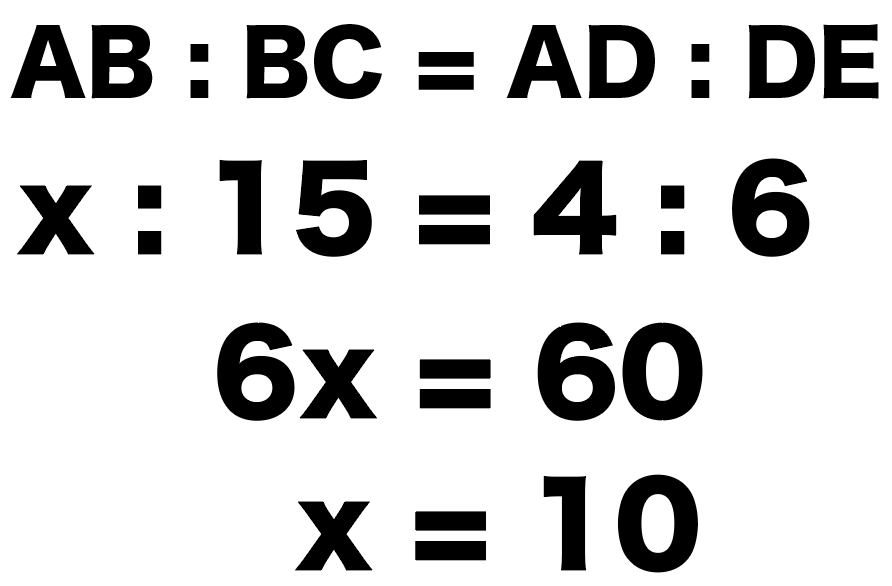
ってことは、ABの長さは、
10cm
になるってこと!
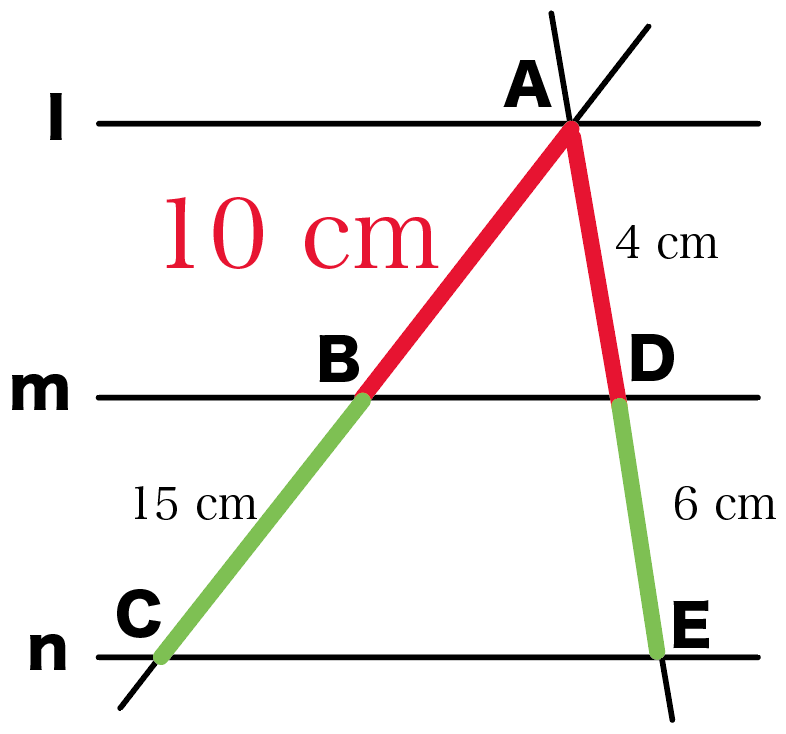
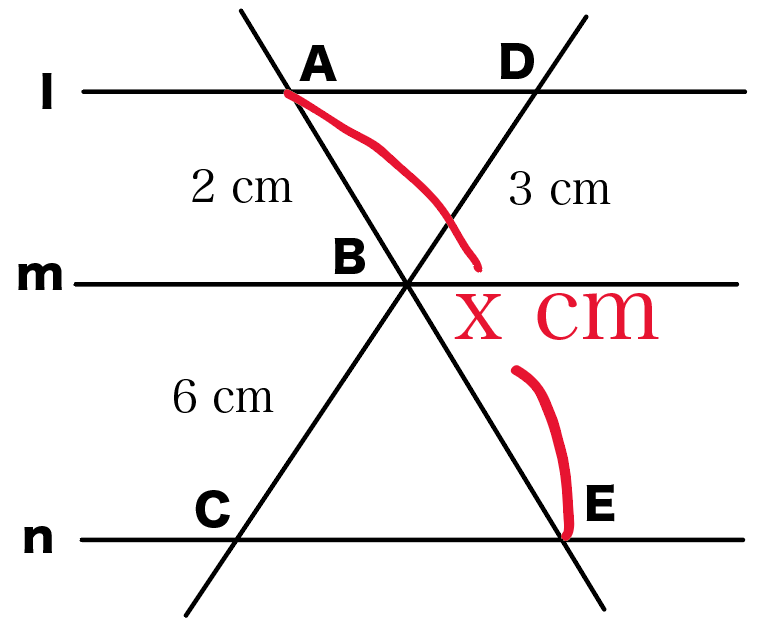
l//m// nのとき、xの大きさを求めなさい。
今度は直線がクロスしている問題だ。
対応する部分に色を付けるとこうなるよ。
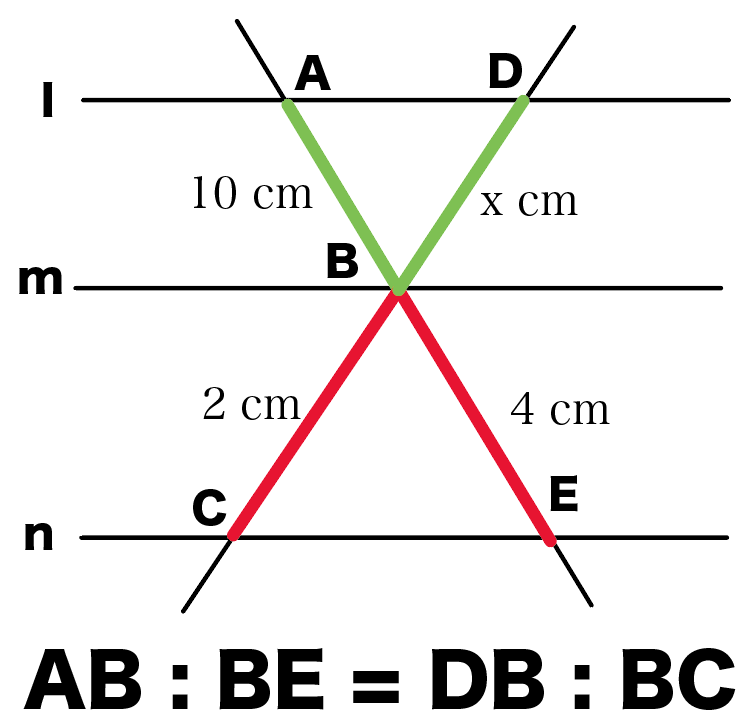
なぜなら、これもさっきと同じで、
△ABDと△EBCの相似をつかってるから使えるんだ。
l・m・nがぜーんぶ平行だから、
錯角が等しいことがつかえるね。
だから、
2組の角がそれぞれ等しい
っていう三角形の相似条件がつかえる。
比例式をといてやると、
AB : BE = DB : BC
10 : 4 = x : 2
4x = 20
x = 5
になるね。
平行線と線分の比の問題は、
対応する辺の比をいかにみつけるか
がポイント。
最後の最後に練習問題を1つ!
練習問題
l//m// nのとき、xの大きさを求めなさい。
どう?とけたかな??
解答はここをみてみてね。
それじゃあ、また。
ぺーたー
ある日、数学が苦手なかなちゃんは、
三角形の角の二等分線の定理の証明
に出会いました。
AB:AC = BD:DC であることを証明しなさい。
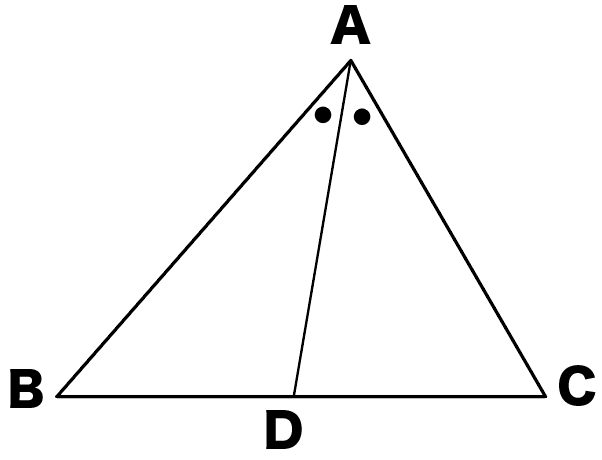
証明なんか、嫌いだ!
何で?
文章書くのむずい。。
確かに。
でも、数学の証明もやっぱり数学なんだ。
へっ?
どこが?
うーん、
スタートとゴールが明確なとこかな。
例えば計算問題だと?
問題を解くと、
答えにたどり着くってこと?
そう、証明も同じ。
証明すること
を見つけるのがスタートで、
証明できたらゴール!
ってこと。
道のり長そう……
ま、ってわけで。
二等分線の定理の証明のついでに、
証明にもなれちゃうおう。
この定理は知っておくと後々便利だよ。
……って言われても。。
三角形の二等分線の定理の証明は、
の5ステップだよ。
へー!
5つでいいんだね。
そうそう!
あっというまだよ!
それじゃあいくよー!
以下の図で∠BAD=∠CADのとき、
AB:AC = BD:DC であることを証明しなさい。

証明のために補助線をひこう!
証明の種をみつけるんだ。
えっと・・・・
補助線ってなに??
問題を解くのを
助けてくれる線だよ!
誰かが引いてくれるわけじゃないのかな……
そう!
残念ながら、
自分でひかなきゃいけないんだよね。。
ひー
今回ひく補助線は2本!
まず、ADをのばしまくる。
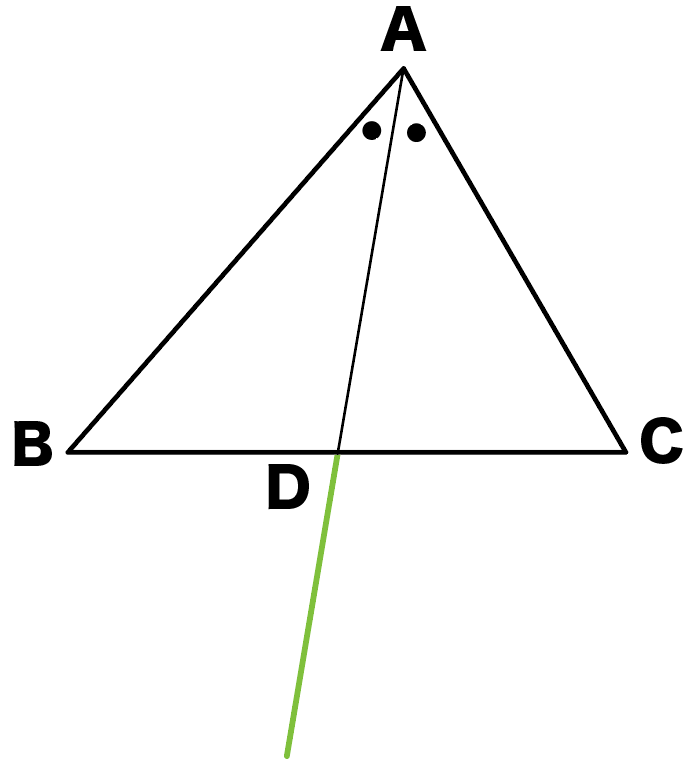
ほい!
もう一本は、
ABと平行で、
Cを通る直線をひくんだ。
この直線
と
ADの延長線との交点
をEとしよう。
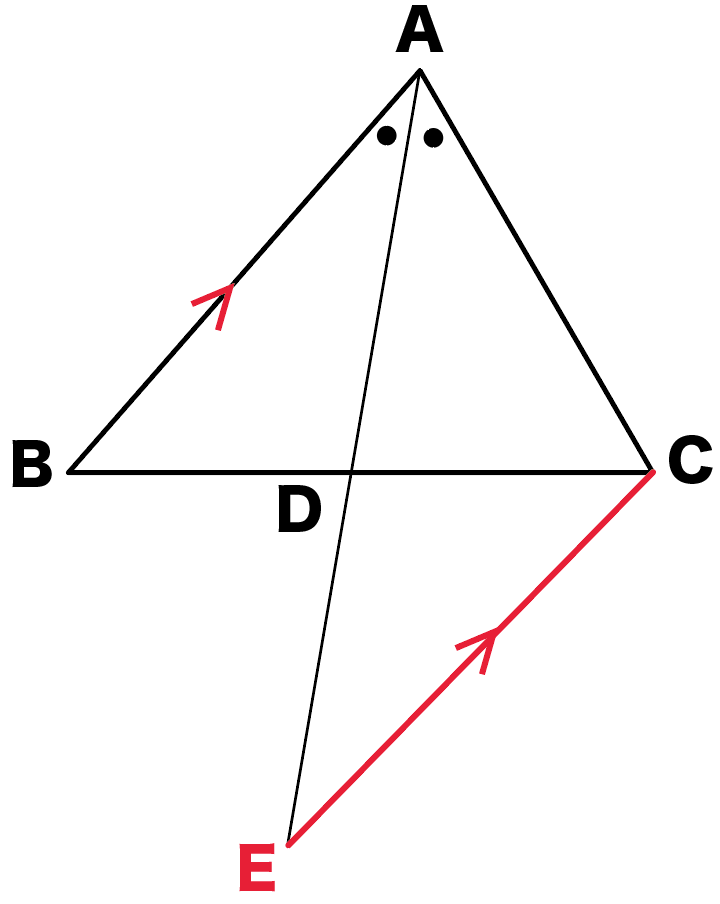
かけた!
書いた前後の変化を考えてみよう!
んー……、
あっ!三角形が増えてる!
そうだね。
いいところに気づいた!
増えた三角形
と
元の三角形
を見比べると……?
んー……、あっ!
相似な図形をみつけてみて!
△ABDと△ECDかな??
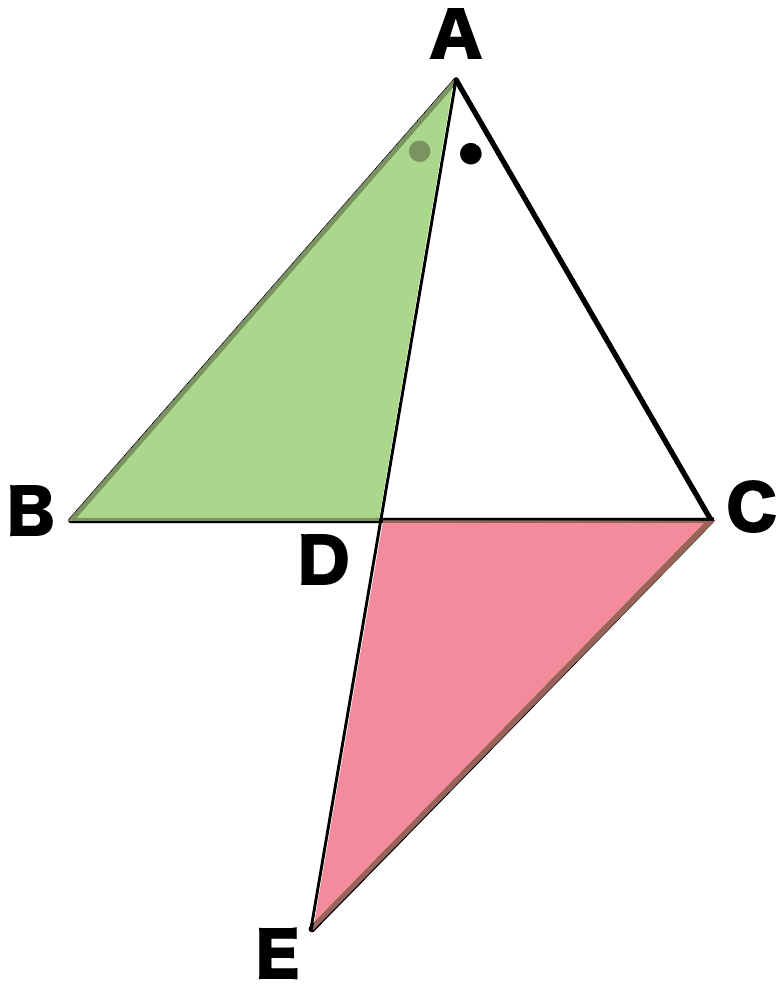
いいね!
覚えた相似条件と照らし合わせてみよう!
そ、相似条件…(遠い目)
ってなる人のために、
ちゃんと用意しといたよ!
さすがは先生!
生徒のこと分かってる!!
できれば3秒で覚えてほしいけど、
慣れるまで書いておぼえてね。
えっと、この場合は……
注目ポイントは、
平行線!
あっ!
錯角だ!!
そうだね。
錯角が等しいから、
だね。
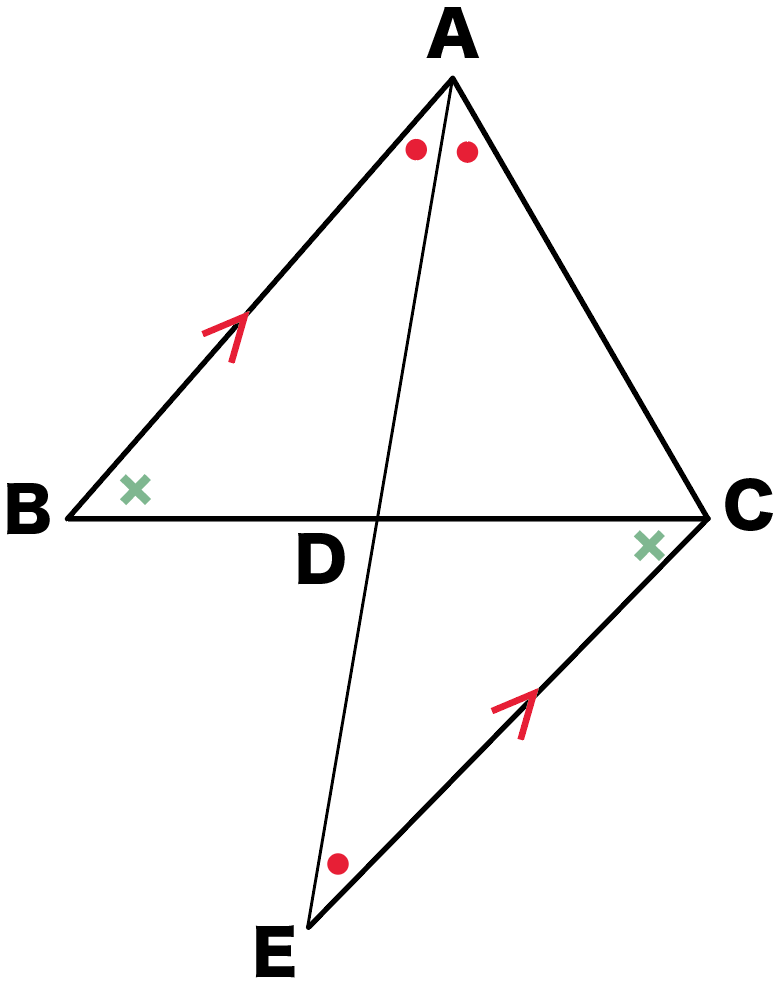
ってことは、
相似条件の3つめの、
2組の角がそれぞれ等しい
を使えばいいんだ!
そう!その調子!
△ABDと△ECDが相似
ってわかったから……
AB : CE = BD : DC・・・(1)
だ!!
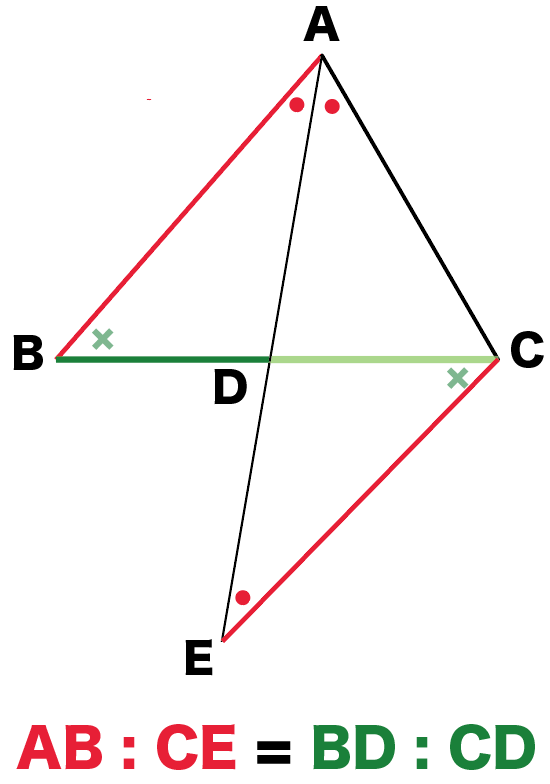
そうそう!
つぎは、
二等辺三角形をさがしてみて!
にとうへんさんかくけい??
二等辺三角形になるための条件はおぼえてるー?
あ、
底角が等しくなる
じゃなかったっけ!?
お、それもあるね!
じゃあその条件つかおう。
二等辺三角形みつけられるかな??
あ!
∠CAE=∠CEAだから、
△ACEは二等辺三角形だ!!
ってことは、
AC = CE ・・・ (2)
になる。
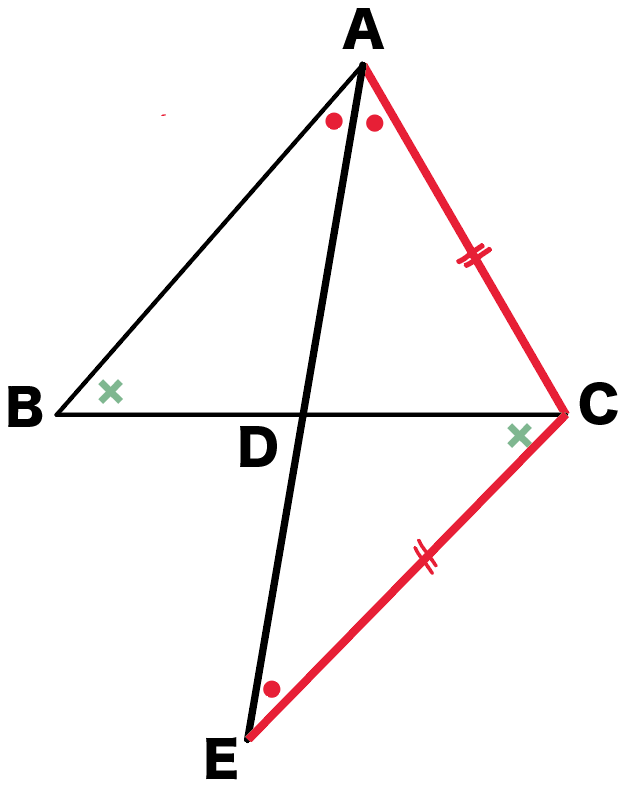
お、いいねー!
(1)と(2)から何が言える??
AB : EC = BD : DC・・・(1)
AC = CE ・・・ (2)
だから、、
あ。
AB : AC = BD : DC
ってことか!
そう!
これで証明したいことが見つけられたね!
やったー!
これで……
終わらないよ。
これから証明書くからね!
ひょええええええええ
つぎは証明をかくよ。
いよいよね。
ういっす……
手順は簡単!
って感じだよ!
書けそうなとこからで大丈夫!
CからABに平行に引いた直線と、
ADとの交点をEとします。
△ABDと△ECDにおいて、
錯角が等しいので、
∠ABD=∠ECD…①
∠BAD=∠CED…②
①,②より、
対応する2つの角が等しいので、
△ABD∽△ECD
また、相似な図形では、
対応する辺の比が等しいので、
BD:DC=AB:CE
△ACEは二等辺三角形なので、
AC=CE
よって、
BD:DC=AB:AC
できた!!
どう??
おー!
やるじゃーーん
今までのことを書いた
って感じかも!!
いいね。
自分で見つけたことを証明に書けばいいの。
証明は準備ができれば、
難しいってわけではないんだ。
証明マスターになった気がする
そう、その調子!!
挑戦してるうちに慣れてくるよ。
おつかれさま!
三角形の角の二等分線の定理の証明は、
の5ステップだったね??
難しいけど、
何度も挑戦してみようかな。
そう!その意気だよ!
うっす!
こんにちは、Drリードだよ。
ここまで相似な図形を勉強してきたよね。
相似の記号もおぼえたし、
相似比も求められるようになった。

今日はね、もう一歩踏み込んで、
相似な図形同士がもつ性質を勉強していこう。
相似な図形たちはどんな性質をもっているんだろう??
さっそく相似な図形の性質を紹介しよう。
つぎの性質があるんだ。
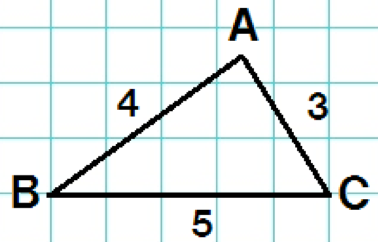
つぎの△ABCを想像してみて。
こいつを2倍に拡大してみよう。
スマホやタブレットの画面で、
「ピンチ」して2本指で画面を拡大したことあるよね?

その調子で、△ABCも拡大してみると、
ほれ!
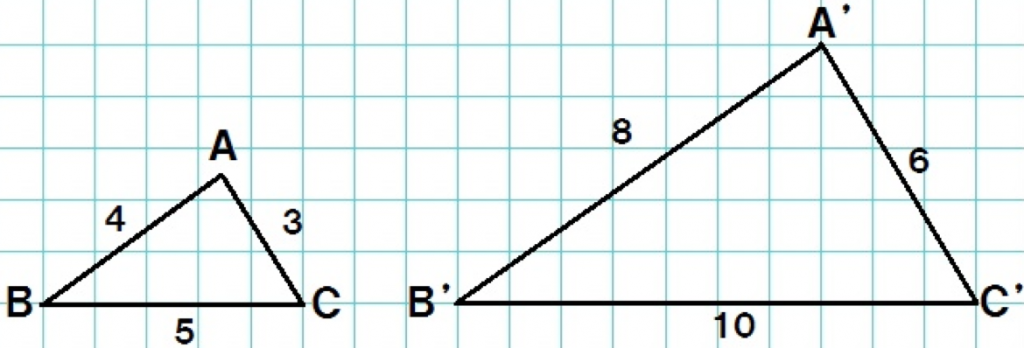
△ABCの2倍の△A’B’C’のできあがりさ。
この2つの三角形をつかって、
相似な図形の性質を確認していこうか。
相似な図形の性質の1つめは、
対応する線分の長さの比が等しい
ってやつだ。
つまり、ぜんぶの辺の比が同じになってるって性質ね。
それじゃあ、
「△ABC」と「2倍に拡大した△A’B’C’」の、
対応する辺を確認していこう。
対応する辺はそれぞれ、
だね。
色でわけてみたよ↓↓
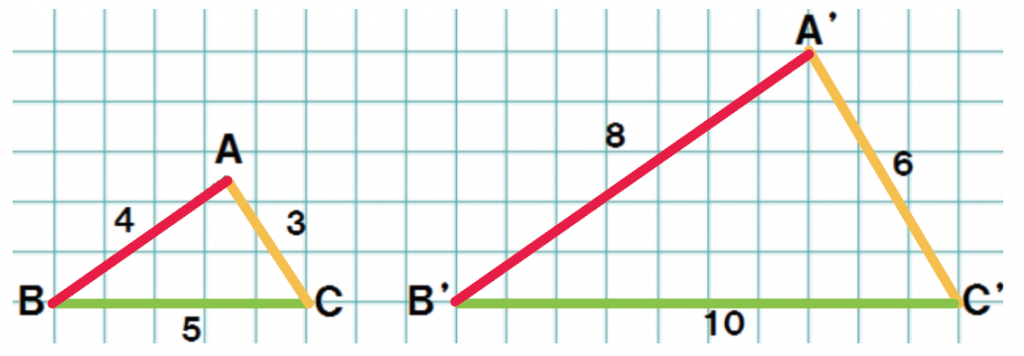
対応する辺の長さについて調べみると、
うんうん、
△A’B’C’ の辺の長さは△ABCの辺の2倍になってるね。
辺の長さの比を書くと、
になってるね。
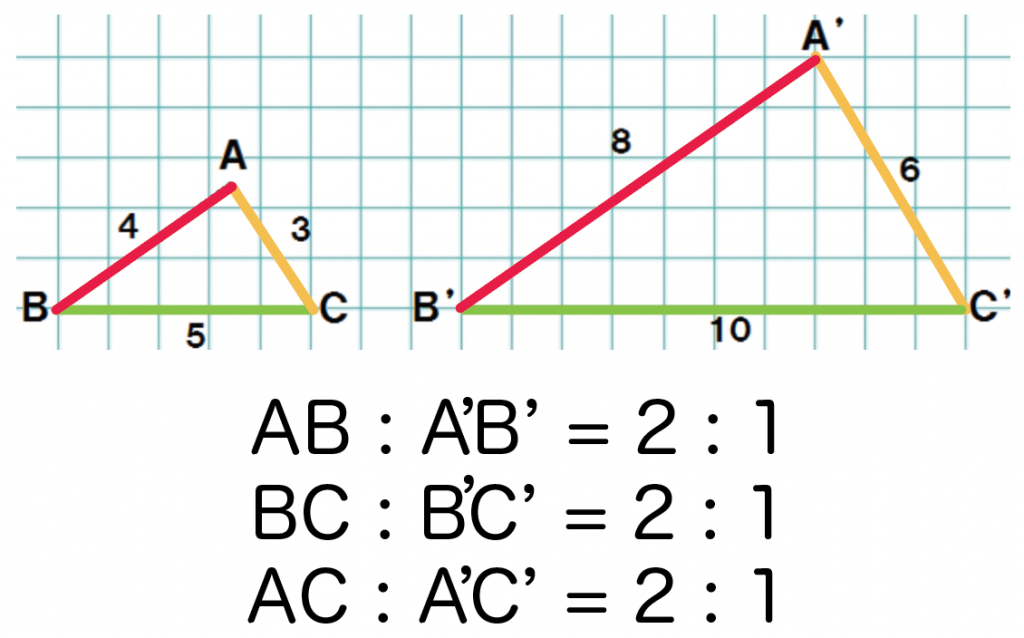
あ!
ぜーんぶの比が2: 1になっとるやん!
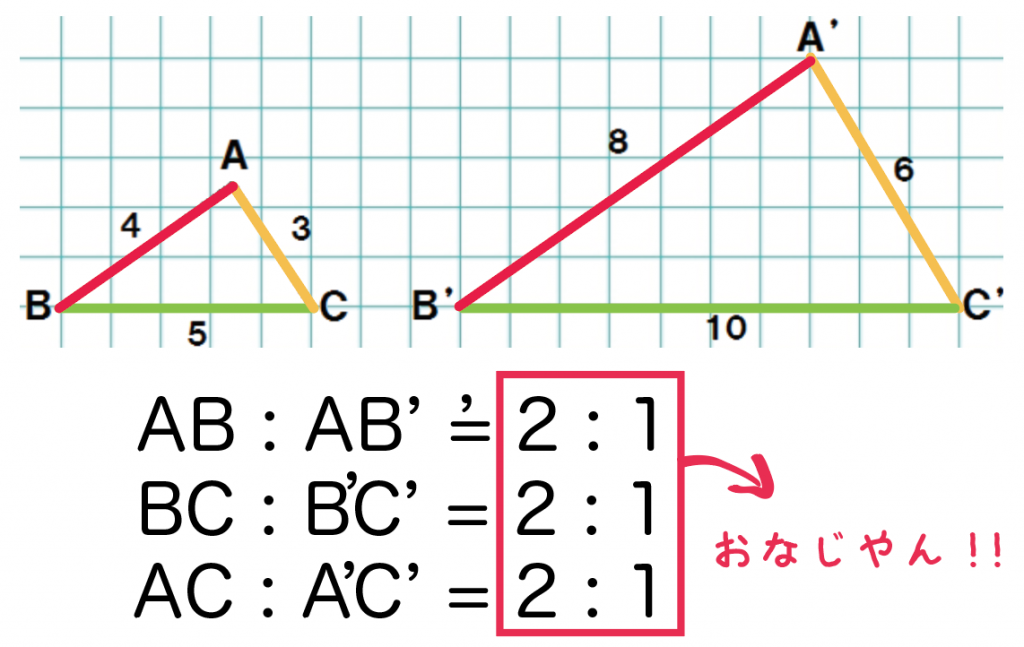
ってことは、
対応する辺(線分)の長さの比はすべて等しい
っていえるね。
これが相似な図形の1つめの性質だ。
2つめの相似な図形の性質は、
対応する角の大きさが等しい
ってやつね。
簡単にいってやると、
相似な図形の角度はぜんぶ等しいよ!
ってこと。
ためしに、△ABCと△A’B’C’をみてみようか。
実際に分度器で角度をはかってみると、
うわ!
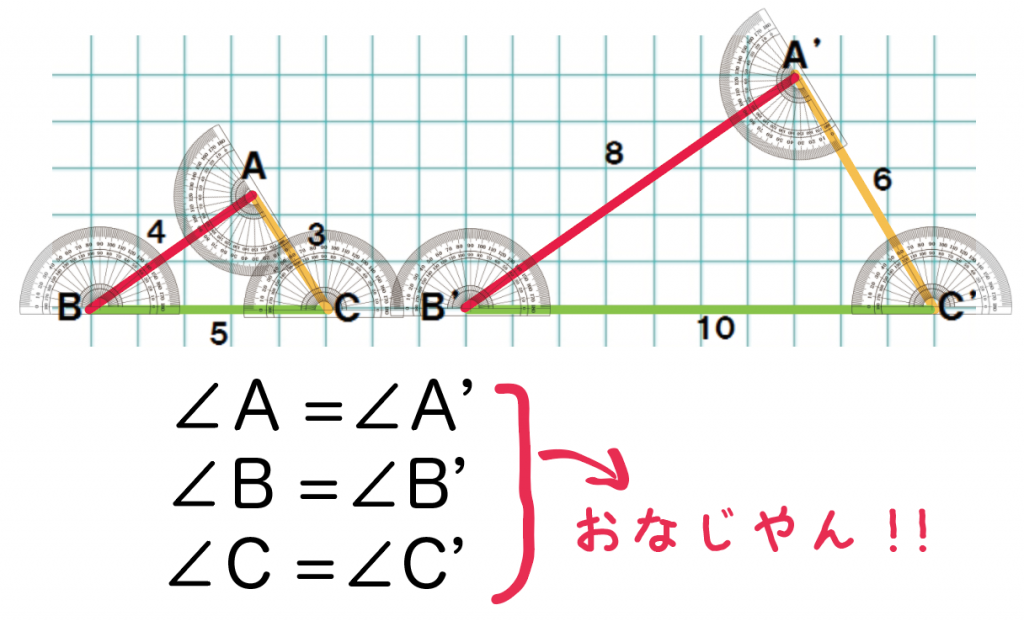
いっしょじゃん!
対応する角たちが等しくなってる!!
えっ。うさんくさいって??
そういうときは、2つの図形をかさねてみて。
ほら?
きれいに重なるでしょ?
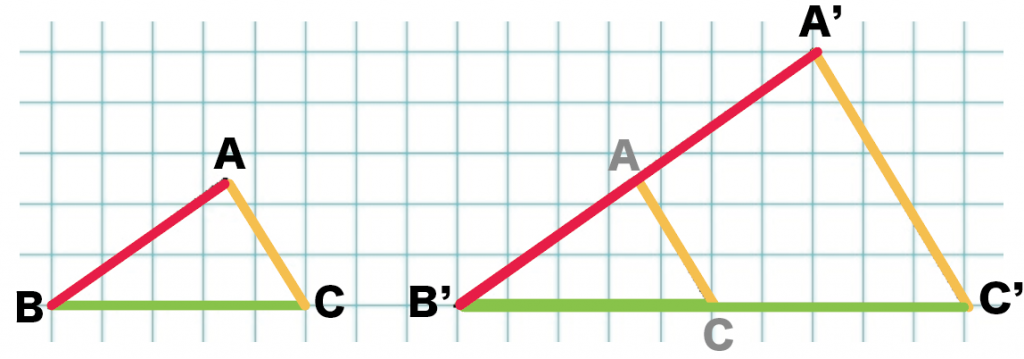
こんなかんじで、
2つの相似な図形の角度は、
ぜーんぶ等しいっていう性質があるんだ!
相似な図形の性質を忘れないように復習しておこう。
相似な図形の性質は、
の2つだったね??

この2つの性質は基本中の基本。
相似な図形を見たときに,
「あ,こことここの角度同じ!」
「相似だから,こことここの比が同じ!」
って気がつくことが大事。
相似の基本的なことだけど、重要だよ。
性質を必ず頭に叩き込んでおこう。
それじゃあ、
Drリード