こんにちは!この記事を書いているKenだよ。電気最高。
中学3年生になると、
三平方の定理
を勉強していくよね??
この定理は今から2500年ぐらい前に活躍した「ピタゴラス」っていう数学者が発見した定理だから、
ピタゴラスの定理
とも呼ばれてるやつね。
発見者の名前がついてるわけ。
この三平方の定理(ピタゴラスの定理)とは何かっていうと、
直角三角形の3つの辺の関係を表した公式
なんだ。
もうちょっと具体的にいうと、直角三角形には、
斜辺の2乗は、直角をはさむ辺を2乗して足したものと等しい
っていう関係があるんだ。
たとえば、斜辺の長さがc、その他の辺の長さがa・bの直角三角形ABCがあっとすると、
a² + b² = c²
っていう公式が成り立っているんだ。

たとえば、斜辺の長さが15cm、その他の辺の長さが12cm、9cmの直角三角形ABCをイメージしてみて。
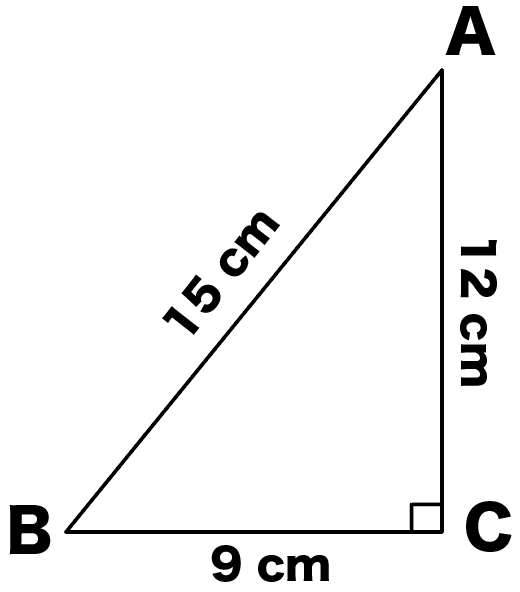
斜辺ABの2乗は、
AB²=15² = 225
一方、その他の辺のBCとACの2乗して足してみると、
AC²+ BC²
= 12² + 9² = 144 + 81 =225
だね!
おっ。両方225になって等しくなってんじゃん!
ピタゴラスの定理の公式すごいな。。
>>三平方の定理(ピタゴラスの定理)の証明はこちら
でもさ、
三平方の定理(ピタゴラスの定理)の公式のすごさがいまいちわからないよね??
ぜんぜん生活に役に立ったないじゃん!
って思ってない??
じつは、三平方の定理(ピタゴラスの定理)のすごいところは、
直角三角形の2辺の長さがわかれば、残りの辺の長さがわかる
ってところなんだ。
たとえば、斜辺の長さ13cm、その他一辺の長さが5cmの直角三角形DEFがあったとしよう。
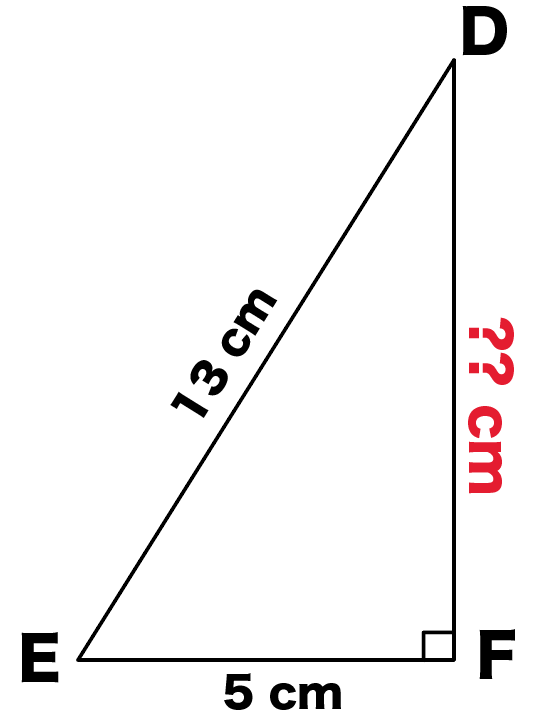
DFの長さって問題にも書いてないし、誰も教えてくれてないよね??
でも、大丈夫。
三平方の定理(ピタゴラスの定理)を使えば求められるんだ。
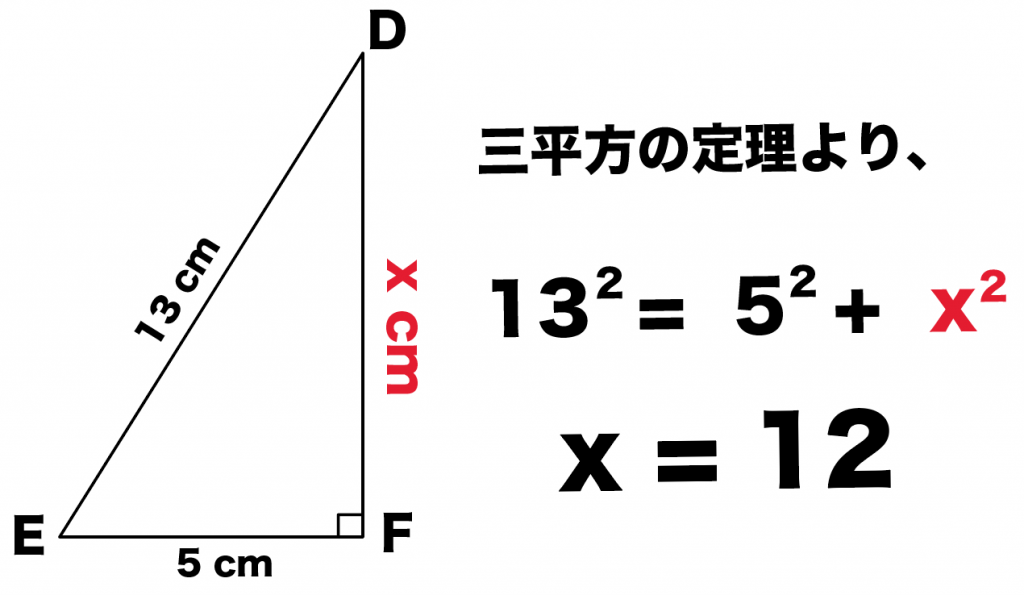
DFの長さをxcmとして、三平方の定理(ピタゴラスの定理)に代入してみると、
13² = 5² + x²
x = 12
あら不思議!
長さがわからない直角三角形の辺を求めることができたね。
>>三平方の定理(ピタゴラスの定理)の計算問題にチャレンジ!!
三平方の定理(ピタゴラスの定理)の公式はめちゃくちゃ便利。
この公式なら、
だって計算できちゃうんだ。
入試問題や定期テストでむちゃくちゃよく出てくる定理だから、しっかりと覚えておこうね。
そんじゃねー
Ken
中学生なると、
勉強が苦手という生徒さんが増えますよね?
今日はそんな中学生から通える学習塾をまとめてみました。
まとめた学習塾は、
中学生でも通える
で、
東京都多摩市から通える
です。
東京都多摩市で学習塾 をお探しの方はよかったら参考にしてみてください。

コース:「高校受験コース 」
頻度:要問い合わせ
料金:要問い合わせ
アクセス:永山駅 徒歩10分
住所:東京都多摩市諏訪3-14-10 ホワイトハウス2F【地図】
塾のURL:http://gakujikai.com/
多摩・稲城地域に根付いた難関突破進学塾。
少人数制のクラスで、科目別にベテランのプロ講師が指導しています。
入塾生の内申は平均25点アップしており、毎年多くの生徒を進学校に輩出しています。
1クラス定員8名の少人数編成で授業を行っています。
一方的に説明をするのではなく、Q&Aを取り入れながら授業を進めていきます。
生徒との距離は近く、自由に質問ができるアットホームな雰囲気の学習塾です。
中学3年生の塾生のほとんどが5教科で内申を2~3以上アップさせています。
大手学習塾のようにアルバイト講師ではなく、教科別専任講師による指導なので、学習効果が大いに期待できます。
病気で欠席したり宿題を忘れたりした後には、必ず補習を組んで下さり、熱心に指導していただきました。学習があまり好きではない子でしたが、粘り強く対応していただいたので、力がついたのだと、夫婦共々感謝しています。
レベルの高い私立高校への進学実績を多くもっており、受験対策情報を提示しながら懇切丁寧に面談いただき、志望校を絞っていくことができました。感謝しています。
学校生活が忙しい中、休まずに通っているので、本当にいい環境の塾のようです。先生がさまざまな角度からフォローしてくださっているようです。
本人の生活にあわせてフォローしてくださり、無理なく学習に取り組むことができたと思います。高校の受験をあわせて、しっかりとした指導のおかげで第1志望に合格することができました。

コース:「四葉プラン(1対4) 」
頻度:要問い合わせ
料金:要問い合わせ
アクセス:小田急多摩線 唐木田駅 徒歩3分
住所:東京都多摩市唐木田1-7-1-102 グリーンドエル唐木田【地図】
塾のURL:http://i-iroha.com/
小学1年生から大学受験生までを対象とした個別指導塾。
授業の予習・復習から難関校の受験対策まで、生徒1人ひとりに合わせた指導を行っています。
不登校や特別支援学級の生徒を対象とした授業プランも用意されています。
講師の質を高く保っていることが特徴です。
研修カリキュラム後、修了試験において充分に適性があると認められた者のみが授業を担当できるシステムとなっています。
講師・保護者・生徒が相互に連携できるメールシステムを導入しています。
宿題のことでちょっと質問したいときなど、さまざまな場面でメールのやり取りが可能となっています。
また、月1回の「いろはレポート」では、生徒の成長記録や改善点、今後の方向性などを記載して保護者に報告するようにしています。
とても勉強嫌いなので、どこか良い塾が無いかと探していましたら、ここが評判も良かったので入塾してみました。
なんと勉強の仕方が判った見たいで、その後成績が上向いたので、気を良くして行っているのがとても良かったです。

コース:「課題自習コース 」
頻度:要問い合わせ
料金:要問い合わせ
アクセス:聖蹟桜ヶ丘駅 徒歩9分
住所:東京都多摩市関戸4-9-10-1F【地図】
塾のURL:http://www.tama-robert.com/
指導実績40年以上の地元に根ざしたアットホームな学習塾。
生徒1人ひとりの個性を磨き・鍛え・向上させるという考えに基づき、子どもたちが勉強面・精神面で大きく成長できるよう親身に指導しています。
とても家庭的な塾なので、卒業してからも多くの生徒が訪れています。
課題自習コースでは、自習を通して学習習慣を定着させていきます。
いつでも質問や相談ができ、生徒1人ひとりに合わせて課題内容や自習回数を決めていくようになっています。
学校の宿題ワークや公文、学研チャレンジなどを進めることも可能です。
家庭的な塾で、人間味あふれる親身な指導をしています。
勉強のやり方や学ぶ姿勢、学習リズムがしっかりと身につくことが魅力であり伝統です。
私もここの卒業生です。かなり前ですが…
昔ながらの学習塾で、先生が親身になって進路相談や
勉強を見てくれました
自習室もあり、授業のない日も来て学習している子が多かったです
家だと気が散りますからね~
コース:「中学3年生コース 」
頻度:100分授業週2回
料金:21000円
アクセス:永山駅 徒歩11分
住所:東京都多摩市馬引沢 1-8-7-2F【地図】
塾のURL:http://www.treppe-tama.com/
「怒られなくても、ひとりで勉強ができるようになる教室」を理念としている1対2形式の個別指導塾。
各教科ごとに適切な勉強の仕方や、テストでの点の取り方をしっかりと教えてくれるので、成績が伸び悩んでいる生徒におすすめです。
学年を問わず中学1年生の内容からスタートし、しっかりした足場づくりを行います。
後戻りをして勉強をするのがこわいと思うかもしれませんが、成績が伸び悩む原因にもなります。
しっかり理解できている単元はスピードアップで進めるので、学習時間を無駄にすることはありません。
授業は「授業60分+休憩10分+宿題30分=100分」で構成されています。
他塾との大きな違いは、家でやる宿題のほかに、教室で残ってやっていく宿題が出題される点です。
このちょっとした工夫で、学習内容が忘れにくくなり、確実に成績をあげることができます。
口コミはありません(口コミを書いてみる)
コース:「中学2年生 受験3科クラス 」
頻度:70分授業×2 週3回
料金:28000円
アクセス:多摩センター駅徒歩17分
住所:東京都多摩市落合3-13-1【地図】
塾のURL:http://housuu.net/
1948年に創立された小・中学生を対象とする地域密着型の学習塾。
生徒1人ひとりを大切にした指導で、「自学自習」ができる生徒を育てます。
集団授業を基本に、臨機応変に個別対応を取り入れています。
定期テスト対策に力を入れており、テスト1ヶ月前から週6日で「9教科対応のテスト勉強会」を実施し、習った分野が身につくまで何度も復習をします。
平常点に直結する宿題・課題・提出物に関しても、提出忘れがないようしっかりとチェックし、内申アップにつなげます。
毎回漢字テストを行い、語彙を増やすとともに、文法の練習や良書の読書を行っています。
学習意欲がない、成績が伸びない生徒のほとんどが、「問題文に何が書かれているか」を読み解く段階で苦戦し、つまづいているからです。
口コミはありません(口コミを書いてみる)
東京都多摩市の学習塾のまとめはいかがでしたか??
最後に紹介した学習塾をまとめてみました。
(永山駅 徒歩10分)
多摩・稲城地域に根付いた難関突破進学塾。
少人数制のクラスで、科目別にベテランのプロ講師が指導しています。
(唐木田駅 徒歩3分)
小学1年生から大学受験生までを対象とした個別指導塾。
教科書の予習・復習から難関校の受験対策まで、生徒1人ひとりに合わせた指導を行っています。
(聖蹟桜ヶ丘駅 徒歩9分)
指導実績40年以上の地元に根ざしたアットホームな学習塾。
生徒1人ひとりの個性を磨き・鍛え・向上させるという考えに基づき、親身に指導しています。
(永山駅 徒歩11分)
1対2形式の個別指導塾。
各教科ごとに適切な勉強の仕方、点の取り方をしっかりと教えてくれるので、成績が伸び悩んでいる生徒におすすめです。
(多摩センター駅徒歩17分)
小・中学生を対象とする地域密着型の学習塾。
生徒1人ひとりを大切にした指導で、「自学自習」ができる生徒を育てます。
それでは!
こんにちは!この記事を書いてる Kenだよ。遺跡が呼んでるね。
標本調査ってむちゃくちゃ便利。
安くて早いし!
だけど、1つだけ気をつけなきゃいけないことがあるんだ。
それは、
標本を無作為(ランダム)に選ばなきゃいけないってこと。
好き嫌いで選んでもいけないし、賄賂を受けとってもダメ。
完全に無作為、つまり、ランダムに標本を選んであげないといけないんだ。
そこで今日は、いつでも標本調査ができるように、
無作為に抽出する方法
を3つにしぼって紹介するよ。テスト前に参考にしてみて。
母集団から標本を無作為に抽出する方法を紹介していくよ。
中学の数学の授業でならう方法はつぎの3つ。
まず一番簡単な方法が、
乱数さいを振る
っていう方法だ。
これはいたって簡単。
0から9までの10つの数字がかかれた「乱数さい」を、何も考えずに振ってやればいいだけ。
ぶっちゃけ、すごろくでサイコロを振るのと同じだね。
たとえば、乱数さいを何も考えずにカジュアルに振ってみて、
0と9
が出たとしよう。
このとき、無造作に抽出できた数字は「09」、
つまり、
9
っていう乱数がゲットできたわけね。
この場合、データ番号9のやつが調査されるんだね。
乱数さいのデメリットとしては、
乱数さいが手に入りにくい
ってことぐらいかな。
スーパーにも売ってなさそうだし、文房具屋にも置いてなさそう。
東急ハンズに行けばいいのかな?
>>詳しくは「乱数さいの振り方」を読んでみて
つぎは、乱数表を使う方法だ。
これは名前の通り、乱数がむちゃくちゃいっぱい書いてある表のことだね。
乱数表の使い方もそんなに難しくない。
まず、表のどっからでもいいから、適当に数字を選ぶ。
たとえば、誕生日が5月11日だったら、
5行目11列の数字を選ぶ
みたいな感じでね。
んで、あとは右か左か上か下に、乱数が必要なだけ選んでみればいいんだ。
乱数表を使うデメリットとしては、
目が疲れる
ぐらいかな。
該当する列と行の乱数を追うのはちょっと目を駆使するね。
まあでも、乱数表っていうアイテムさえあればいつでもどこでも無作為に抽出できるのはマジ助かる。
最後の方法は、
エクセルの関数で乱数を生み出す方法
だ。
ちょっと理解するのが難しいけど、一回マスターしちまえばこっちのもの。
ちょっとエクセルを立ち上げてみて。
※エクセルがない子は「スプレッドシート」でも大丈夫。
エクセルの1マスに、
=RANDBETWEEN(1, 100)
っていう呪文を書いてみて。
そうすると、あらふしぎ!
そのマスに、1から100までの乱数が出てくるはず!
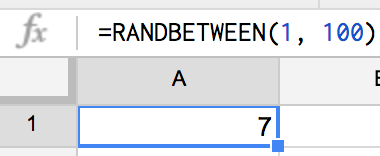
さっき入れてみたら、
7
が出てきた!
すげえな!エクセル!
こんな感じで、エクセルのマスに呪文を入れるだけで無作為に乱数を抽出できるのさ。
まだ試したことなかったらやってみてね。
この方法のデメリットは、
むずかしいエクセルの関数を覚えなきゃいけないところかな。
エクセル関数は1文字でも間違えるとエラーが出てきちゃう。
正確に書いてあげるのが最大のコツだ!
>>詳しくは「エクセルで乱数を抽出する方法」を読んでみて
母集団から標本を無作為に抽出する方法はいろいろあるね。
中学数学で勉強する方法はつぎの3つ。
テストに出てくるかもしれないから、
よ〜く復習しておいてね。
そんじゃねー
Ken

標本調査では、
母集団から無作為に標本を抽出する
ってことがすごく大事。
そうじゃないと、標本調査の結果がしっかり出てこないからね。
標本をランダムに抽出する方法はいくつかあるんだけど、今日はその内の1つの方法の、
乱数表の使い方
を紹介するよ。
授業でならったけど使い方イマイチ・・・・・ってときに参考にしてみてね。
まず乱数表とは何か??を復習しようか。
乱数表とはズバリ、
0から9までの10つの数字をランダムに縦横に並べた表のこと
なんだ。
乱数表では驚くべきことに、
縦、斜め、横、どの方向をみてもランダムに10つの数字が記載されてるよ。
0から100までの数字をランダムに選びたいときは大抵、
2つの数字がセットになって1桁〜2桁の数字をあらわすことになってるんだ。
実際に乱数表を使ってランダムな数字を選んでみよう。
乱数表の使い方はつぎの2ステップ。
今回は練習だから、乱数表で 3つの数字をランダムに選んでみて。
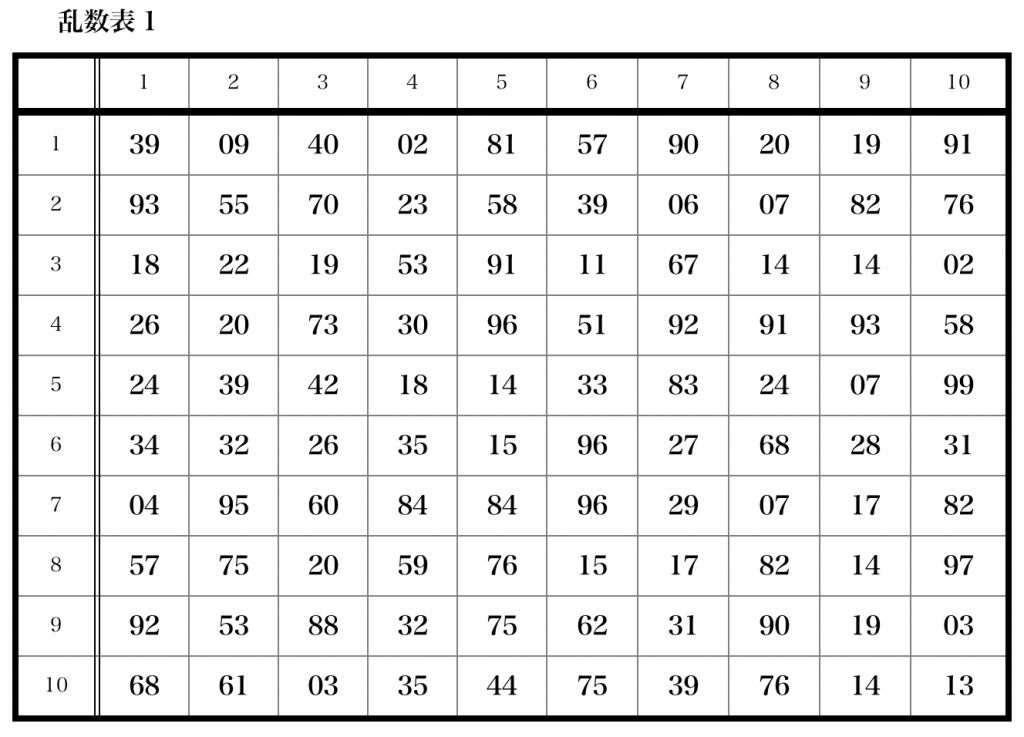
乱数表(桃ソロ著)の位置No.6803より引用
乱数をとりはじめる「列と行」を選んでみよう。
最初に選ぶ数字はどれでもオッケー。
自分の誕生日を使ってもいいし、出席番号をでもいいんだ。
今回は、レミオロメンの「3月9日」っていう楽曲にちなんで、
3行9列目の数字
から乱数を選んでみよっか。
さっきの乱数表でいうと、
14
がそれにあたるね。
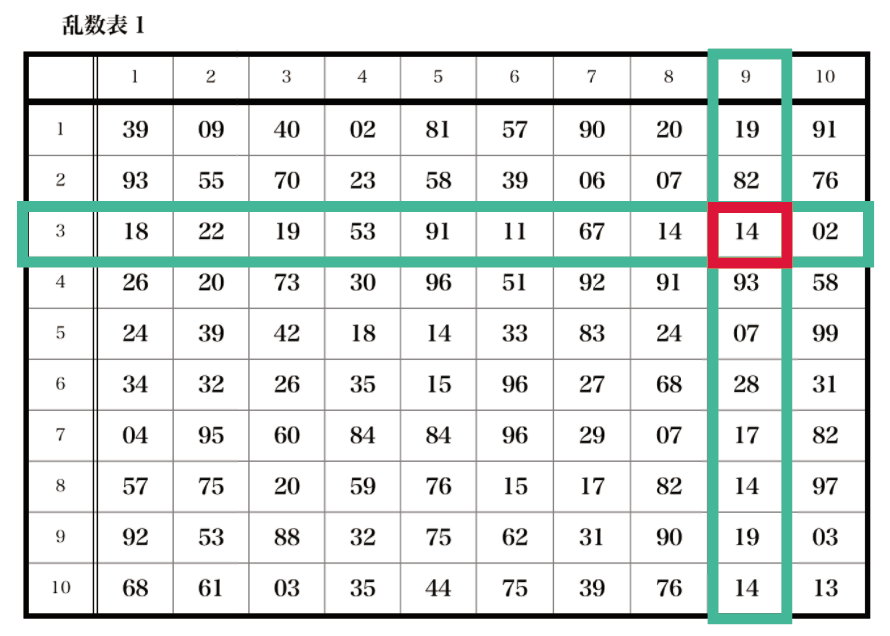
これで1つ目の乱数ゲット!
最初の数字を始まりとして、好きな方向に必要なだけ数字をとってみよう。
今回は、個人的に下が好きだから、下に進んでみようっか。
3つの乱数が必要だから、あと2つの乱数を選ばないといけないね。
3行9列目から下に2つ数字をピックアップしてみると、
っていう2つの数字があるね。
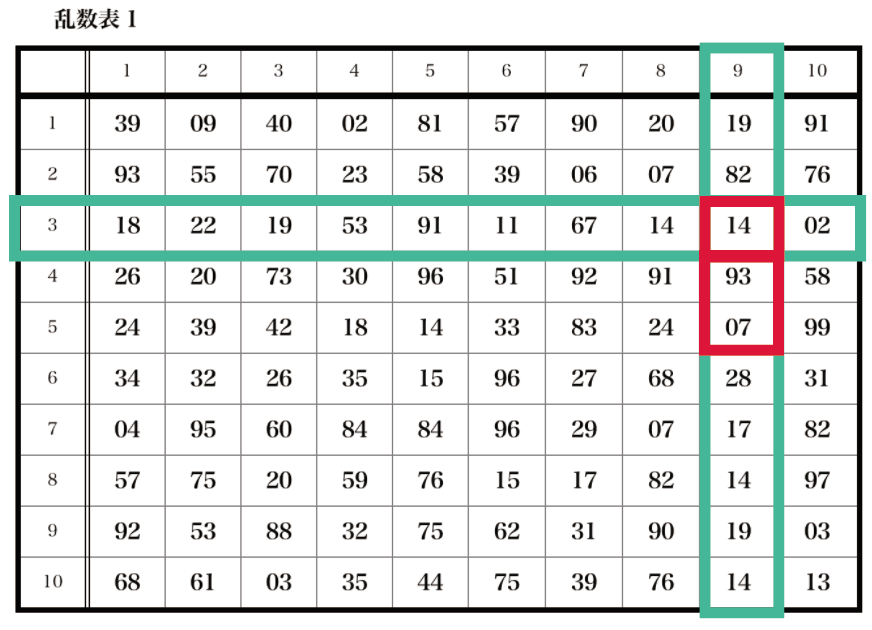
ってことで、今回選ぶことができた3つの乱数は、
の3つだ。
無事に乱数表を使って乱数を抽出できたね。
乱数表の使い方はどうだったかな??
乱数さいを振るのと同じぐらい簡単だったよね?。
ただ、好きな行と列を選んで好きな方向の数字をピックアップすればいいだけだからね。
乱数表を使ってガンガン乱数をゲットしていこう。
そんじゃねー
こんにちは!この記事を書いてるKenだよ。変換は使いようだね。
母集団から標本を選ぶときって、
無作為(ランダム)に選ばないといけないよね??
無作為に抽出する方法はいくつあって、
乱数さいを振ったり、
乱数表を使ったりするよ。
そうすれば、ランダムな数字が得られて、無事に標本を取り出すことができるんだ。
だけどね、しかし、ね。
ぶっちゃけ、こいつらの方法は、
めんどい。
サイコロ買わないといけないし、乱数表とか目が疲れそうだし。
えっ。
もっと簡単に乱数(ランダムな数)をゲットする方法はないのかって??
じつはあるんだ。
それは、
エクセルを使って乱数を得る方法
だ。
1~100までの数字をランダムに作る方法を勉強していこう。
Googleスプレッドシートで軽く練習してみるといいよ。
1秒ぐらいでエクセルで乱数をゲットできる方法。
それは、
= INT(RAND()*100)+1
とエクセルのセルに打ち込む方法だ。
試しに、Googleスプレッドシートに入力してみると、
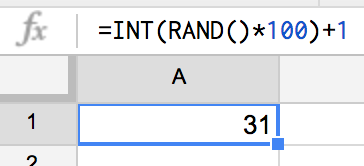
うわっ。
31っていうランダムな数字が得られてる!
しかも、1~100までにおさまってるじゃん?
超便利だな、この呪文・・・・・・
でもさ、この呪文、
便利すぎて怖いよね??
ちょっとあまりにもうまく行きすぎだから、
なぜ、INT(RAND()*100)+1 で乱数が得られたのか?
をみていこうか。
まず最初は、
RAND ()
に注目してほしい。これは、
0以上で1より小さい数字をランダムにゲットできる関数
なんだ。

試しに、エクセルに「=RAND()」って入れてみると、
0.0252561728
って感じで0以上で1より小さい数字が出てくるね。
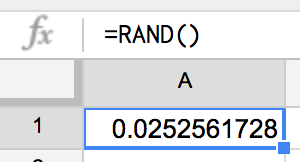
つぎに、その後ろの「*100」は「×100」って意味。
さっきの「0以上1より小さい数字」を100倍してるってわけ。

すると、
あら、
今度は0以上で100より小さい数が出てきた!
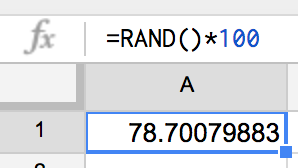
それもそのはず。
0以上で1より小さい数字が出てくる関数を100倍してるからね。
あっ、でも小数点とかうざいな・・・・
つぎに出てくるのが、
INT関数
っていうエクセルの関数だよ。
これは、
ある数値を「一番近い整数」に切り捨ててくれる関数なんだ。
たとえば、3.14っていう数字をINT関数に入れてみると、
3
になるね。
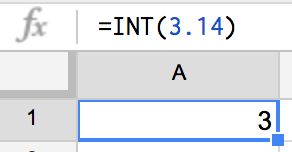
だから、この INT関数を使ってやると、
RAND()*100
でうざかった小数点以下の数字を消し去ることができるんだ。
試しに、
=INT(RAND()*100)
を入れてみると、
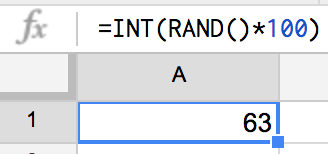
おおー!
うざい小数点以下消えてる!
これで乱数ゲットできたんじゃないかな・・・・
いや、まだ早い。
じつは、
=INT(RAND()*100)
に1を足さないと1~100までの数をランダムにゲットできないんだ。
なぜなら、
RAND関数で得られる数字は「0以上で1より小さい」だったからね。
それを100倍したら、
0以上で100より小さい数
になっちゃう。
つまり、
0が出てきちゃう可能性あるし、100は絶対に出てこないってことになっちゃう。
これに1を足してやると、
0が出てくる心配はないし、100が出てきてくれるようになるよ。
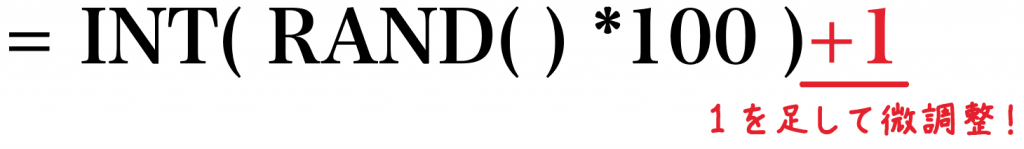
最後に1を足すのを忘れずに!
これでエクセルで1から100の乱数を得られるようになったね。
ここまで、
=INT(RAND()*100)+1
っていう謎の呪文を解説してきたけど、じつは、
もっと簡単に乱数を得られる関数がエクセルに存在しているんだ。
それは、
RANDBETWEEN関数
ってヤツ。
ちょっと名前が長いけど、RANDBETWEEN()のカッコの中に、
=RANDBETWEEN(最小値, 最大値)
って書いてあげると、
最小値から最大値までの範囲内の乱数が出てくるんだ!
ためしに、
= RANDBETWEEN(1, 100)
って入れてみると、
うわっ!
7っていう乱数が得られてる!

こりゃ便利すぎるぜ!
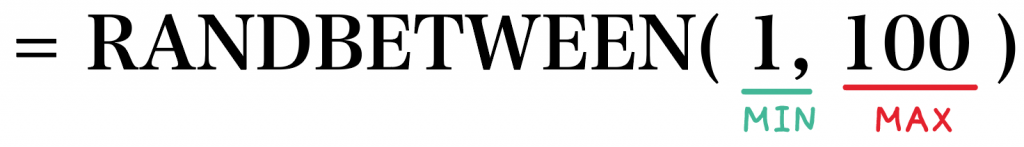
エクセルで乱数を得る方法はどうだった?
1から100の乱数をゲットする方法は2つあったね。
どちらか好きな方をエクセルのマスに入れてみてね。
きっと望み通りの乱数が出てくるはずだ。
そんじゃねー
Ken
こんにちは!この記事を書いているKenだよ。エンジンに着火したね。
標本調査では、母集団から標本を「ランダムに」取り出さなきゃいけないよね??
ランダム、
つまり、
無作為にどうやって標本を選べばいいんだろうね?
じつは、母集団から標本を無作為に抽出する方法の1つに、
っていう特殊なサイコロを使う方法があるんだ。
今日はこの「乱数さい」っていうアイテムの使い方をわかりやすく解説してみたよ。

よかったら参考にしてみてね。
= もくじ=
まず、
乱数さいってどんなやつ??
ってことからみていこうね。
乱数さいは、
0から9までの10つの数字が2つずつ書かれた特殊なサイコロ
のこと。
このサイコロは、出る目の確率を全部等しくするために、
正二十面体
になっているんだ。
普通のサイコロだと1~6までの6つの数字しか書いてないし、
0~9の数字を1面ずつに書いたサイコロだと、正多面体じゃないから出る目の確率を平等にするのは難しい。(実際にあるみたいだけどね)
だから、0~9までの10つの数字を2つずつ書いた正二十面体が採用されてることが多いんだ。
それじゃあ、
乱数さいってどう使うんだろうね??
使い方はいたって簡単。
乱数さいをね、ふればいいんだ。
ころっとね。
たとえば、0~100までの数字をランダムに選びたいときは、
乱数さいを2回ふればいい。
すると、
っていう感じで0~9までの数字が2つゲットできるね。
もし、
だったら、ランダムに乱数さいを使ってランダムに選んだ数は、
92
になるってわけ。
乱数さいを使って、実際に母集団から標本を無作為に抽出してみよっか。
そうだなあ、シチュエーションとしては、
0~100までの出席番号の生徒からランダムに3人選ばなきゃいけない場面を想像してみて。
まず、乱数さいを1回振ってみると、
0
つぎは、
9
。
2つの数字を組み合わせると、
09
だね。
ってことで、「出席番号9番」の生徒を選べばいいわけ。
同じように乱数さいを2回ずつ振ってみると、
っていう4つの数字をゲットできた。
ってことは、今回ランダムに抽出できた生徒の出席番号は、
の3つだ。
この3つの出席番号に該当する生徒は、
の3人。
調査に協力してね!
乱数さいを使えば、母集団から標本を好きなだけ取り出せるね。
まあ、乱数さい振り続けるのは面倒だけどねw
乱数さいの他にも無作為に抽出する方法として、
なんて方法があるよ。
よかったら試してみてね。
そんじゃねー
Ken
こんにちは!この記事を書いてるKenだよ。キーボード強打したね。
標本調査の問題でよく出てくるのは、
標本のデータから母集団を推測する
っていうタイプね。
たとえば、つぎのような問題。
練習問題
Aさんが通う中学校では好きなテレビ番組のアンケート調査が行われました。
全校生徒1200人のうち、100人を無作為に抽出して行った調査では、
17人がアニメ「フニャッとモンスター」を視聴していました。

それでは、実際に全校生徒のうち何人が「フニャッとモンスター」をみたと推測できますか?
今日はこの標本問題の解き方をわかりやすく解説していくよ。
よかったら参考にしてみて。
標本問題の問題の解き方の基本は、
ある性質を持っている「もの」や「人」が含まれる比率が「母集団」と「標本」で等しい
っていう式を作ればいいんだ。

たとえば、さっきの練習問題でいうと、
無作為に抽出した100人の中で「フニャッとモンスター」を視聴した人が含まれる比率
と
全校生徒1200人の中で「フニャッとモンスター」をみた人の割合
が等しいっていう比例式を作るのさ。

えっ。全然ピンとこないだって?
それじゃあ、さっきの練習問題を一緒に解いていこうか。
練習問題
Aさんが通う中学校では好きなテレビ番組のアンケート調査が行われました。
全校生徒1200人のうち、100人を無作為に抽出して行った調査では、
17人がアニメ「フニャッとモンスター」を視聴していました。
それでは、実際に全校生徒のうち何人が「フニャッとモンスター」をみたと推測できますか?
つぎの3ステップで問題が解けちゃうよ。
問題で求めたいものをxとおいてみよう。
白玉の数を求めたかったら、白玉の数をx個、
腐ったミカンの数を知りたかったら、腐ったミカンをx個とすればいいわけね。
今回の練習問題では、
全校生徒の中で「フニャッとモンスター」をみた人数
を求めたかったよね??
だから今回は、
全校生徒の中で「フニャッとモンスター」をみた人数 = x人
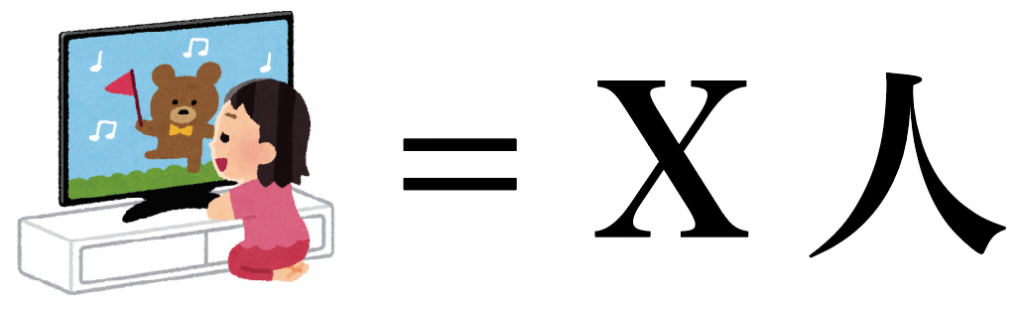
とおいてみたよ。
つぎは比例式をつくってみよう。
標本調査の問題でつくる比例式はだいたい、
(母集団での比率)=(標本での比率)
ってすればいいよ。

今回の練習問題でいうと、
(全校生徒の中で番組をみた比率)=(100人の中で番組をみた比率)
っていう式をたてるんだ。

全校生徒の中で「フニャッとモンスター」をみた人数 をx人としたから、
(全校生徒数): (みた人数)= (無作為に選んだ100人):(番組をみた17人)
1200 : x = 100 : 17
っていう比例式が完成するね。
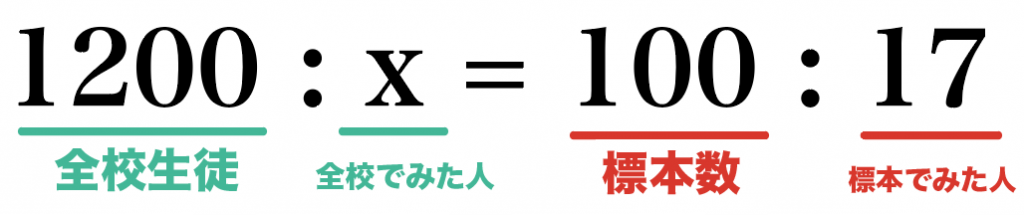
あとは比例式をとくだけ。
えっ。
比例式の解き方がわからない??
比例式の解き方の基本は、
内項と外項の積
だったね??
ようは、「内側にあるもの」と「外側にあるもの」同士をかけて等式にすればいいんだ。
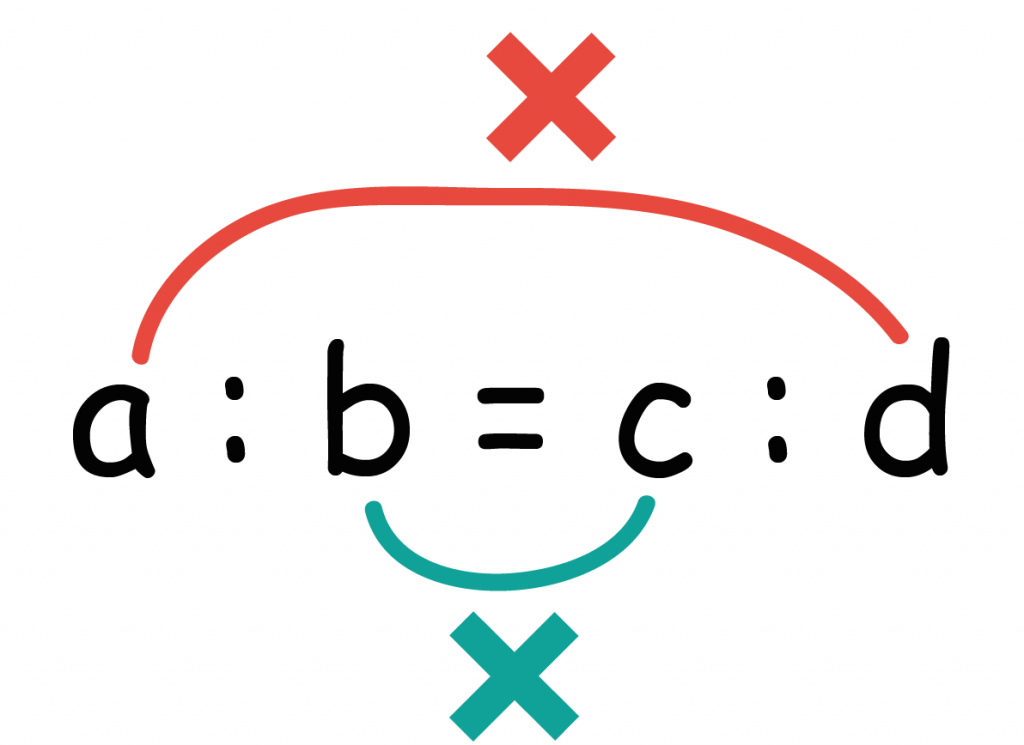
>>詳しくは「比例式の解き方」を読んでみてね。
練習問題でできた比例式は、
1200 : x = 100 : 17
だったね?
こいつを内項の積・外項の積で解いてやると、
1200 : x = 100 : 17
100x = 1200×17
x = 204
ってなるね。
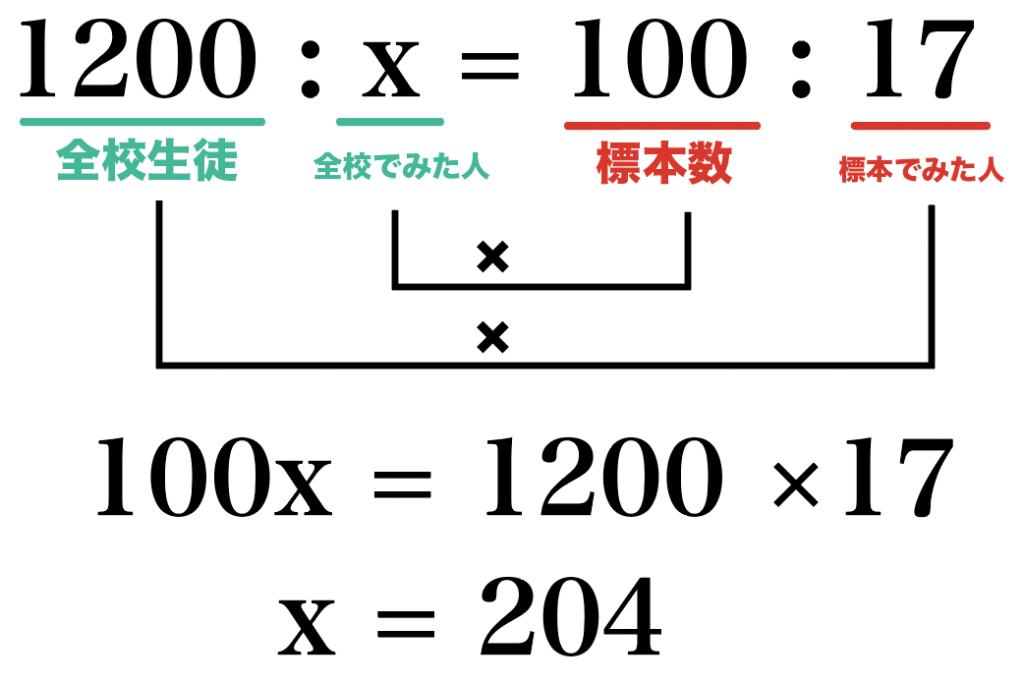
つまり、この標本調査から全校生徒1200人のうち、だいたい204人が「フニャッとモンスター」をみたんじゃないか?
って推測できるんだ。
全校生徒にアンケート取らずに、100人にアンケートしただけだから、かなり楽になってるね。
標本調査って早くて便利。あくまでも推測でしかないけどね。
標本調査の問題の解き方はどうだったかな??
つぎの3つのステップで簡単に解けるってわかったね。
定期テスト前によーく復習しておこう。
そんじゃねー
Ken
こんにちは!この記事を書いているKenだよ。フォルダは怖いね。
中3数学の標本調査を勉強していると、
っていう2つの言葉が出てくるよね??
母集団っていう漢字むずかしいし、
標本とか言われても昆虫の標本しか思い浮かばない・・・・
そこで今日は、
母集団と標本の意味をわかりやすく解説してみたよ。
よかったら参考にしてみて。
さっそく、母集団と標本の意味を解説していこう。
母集団と標本は「標本調査」っていう、ある集団・グループの性質を調べる方法で使われる言葉なんだ。
>>詳しくは「全数調査・標本調査の違い」をみてね
標本調査とは簡単に言ってしまうと、
グループの一部だけをランダムに選んで調べて、全体の性質を推測する
っていう方法だったよね?
たとえば、八百屋さんにおかれている大根の性質を調べたいとしようか。
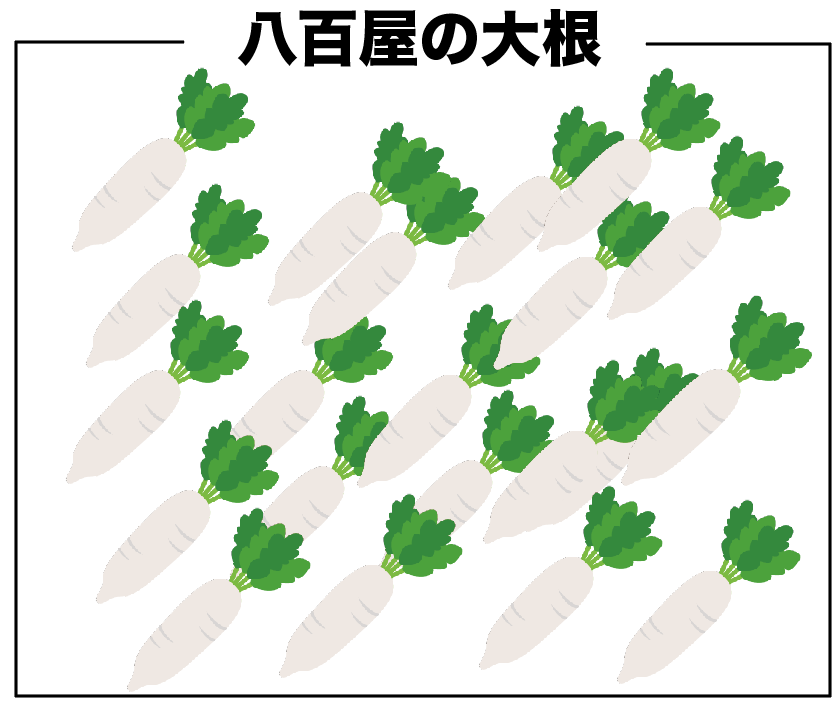
このとき、八百屋さんにおいてある大根をすべて調べるんじゃなくて、
一部の大根だけを調べて、ぜんぶの大根の性質を推測するのが「標本調査」なんだ。
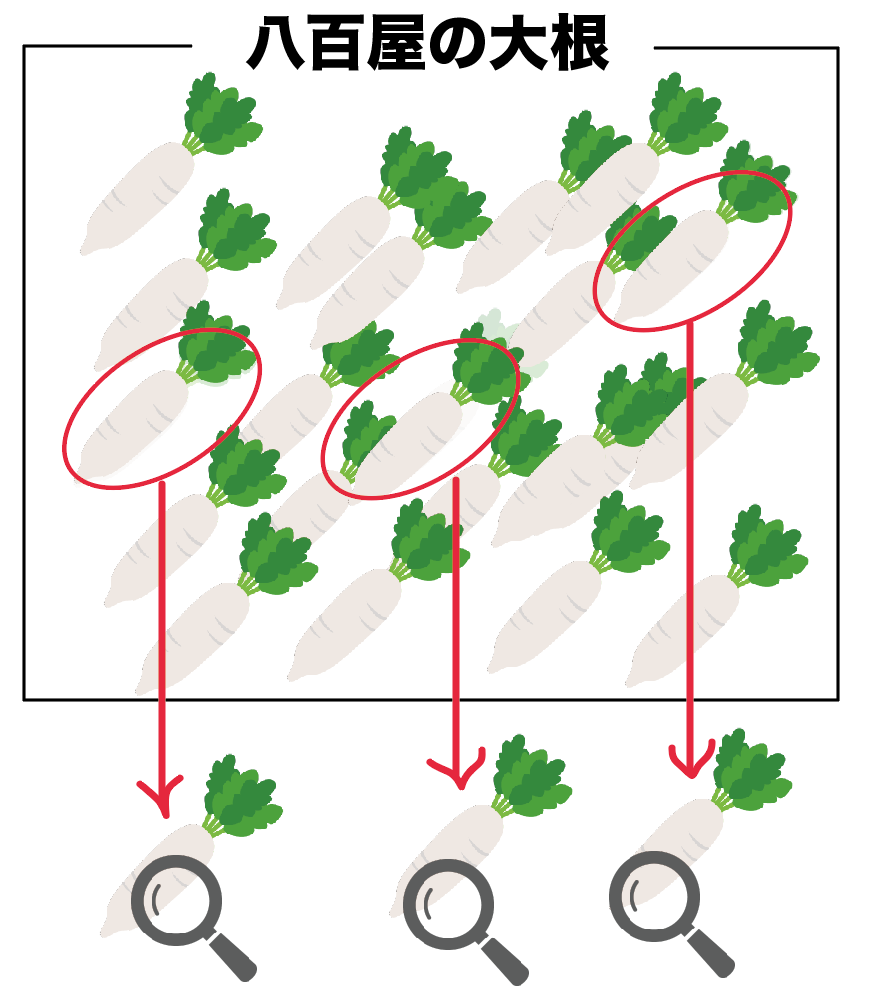
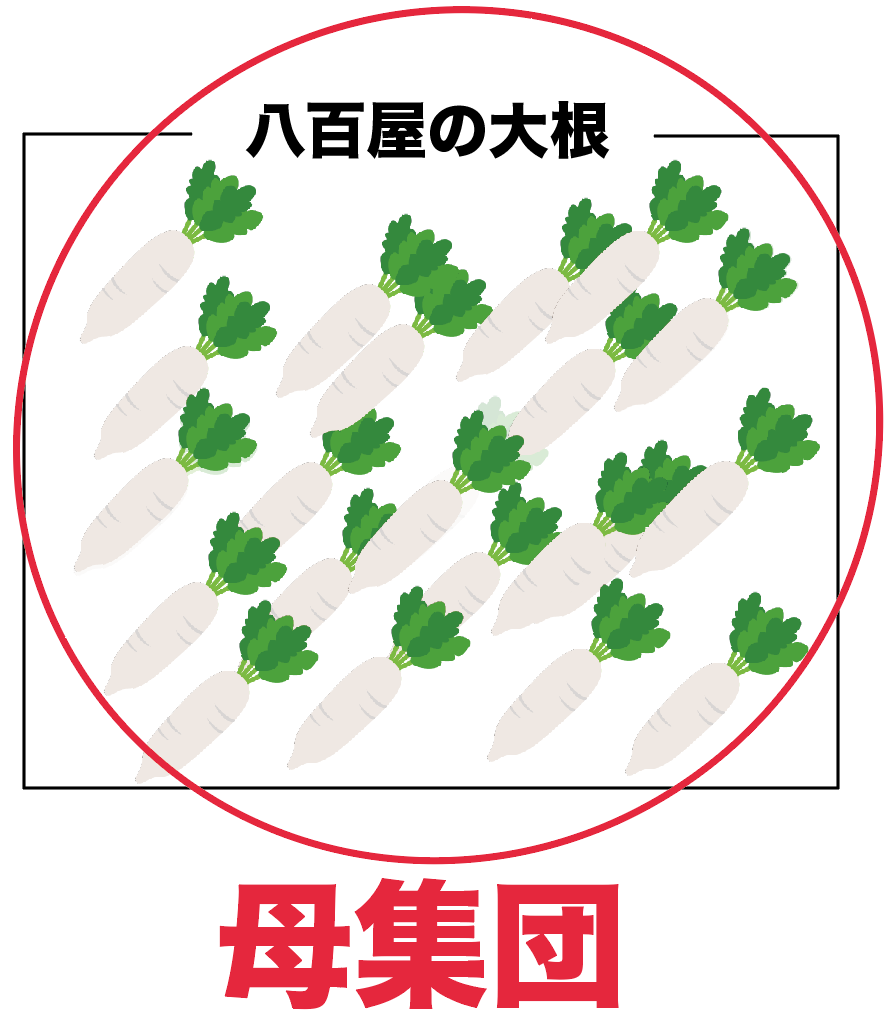
んで、母集団とは、
標本調査をしたときに調べたグループ全体
のことだよ。
さっきの例でいうと、八百屋さんの大根ぜんぶのことね。
一方、標本とは、
標本調査をしたときにグループから取り出した一部のこと
なんだ。
さっきの例でいうと、
八百屋さんの大根から選んだいくつかの大根のことね。
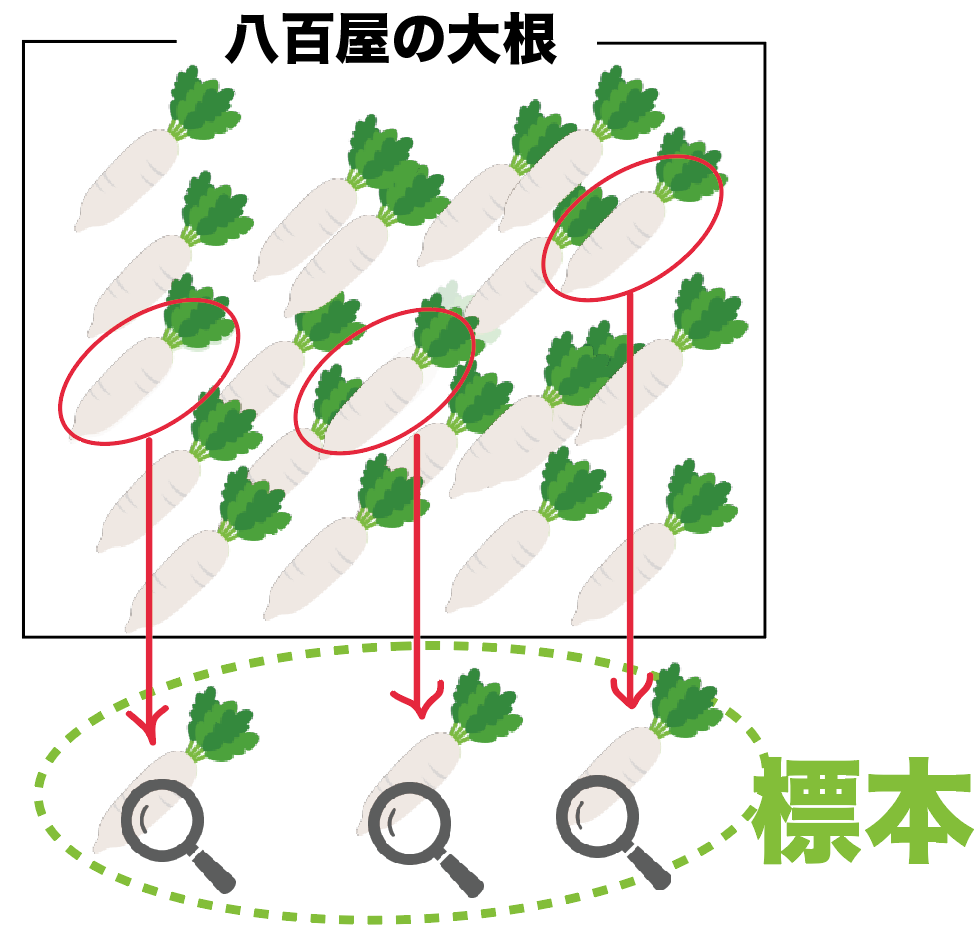
こんな感じで、
標本調査で調べるグループ全体のことを「母集団」、
調べるためにピックアップしたやつらを「標本」っていうんだ。
テストに出やすいから頭の片隅に置いておいてね。
もっと母集団と標本の理解を深めるために、3つの標本調査の例を見てみよっか。
テレビ番組の視聴率を調べる方法は、標本調査を使ってるよ。
テレビの視聴率はざっくりいうと、
「日本全国のテレビ視聴率」を調べるために、いくつかの世帯をランダムにピックアップして視聴状況を調べているんだ。
この標本調査の場合、母集団は、
日本に住んでいる人たち
で、
標本は、
視聴率計測に選ばれた世帯
ってことだね。

つまり、テレビの視聴率は日本の全部のテレビの視聴状況をぜーんぶ調べてるわけじゃないってことね。
全部調べるの大変そうだもんね。
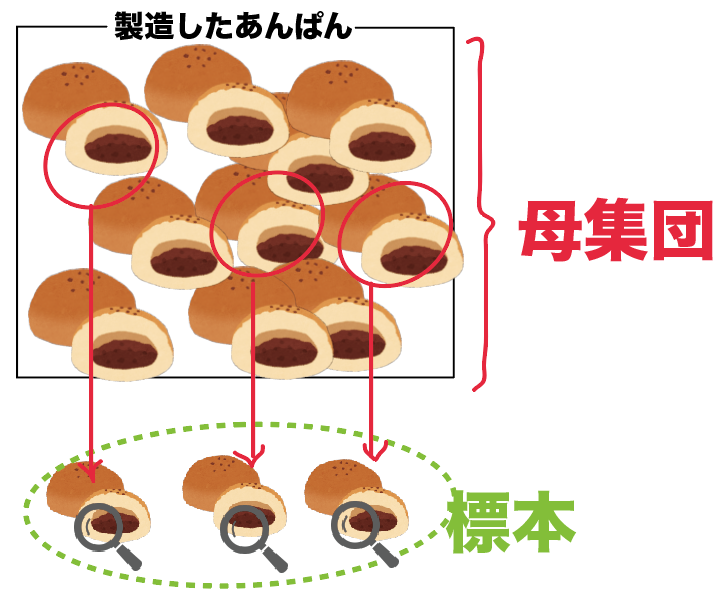
つぎは、あんぱんの製造工場での品質検査。
工場で作っているあんぱんの数はおよそ数千。
ぜんぶのあんぱんを調べた方が安全だけど、一度調べたあんぱんは商品として扱われなくなっちゃうんだ。
なぜなら、検査するためには薬品を使ったり、パンを切り刻んだりするからね。
ぜんぶ調べてたらあんぱんを全然出荷できなくなっちゃうじゃんね。
そこで、あんぱんの品質検査では標本調査を使うよ。
つまり、
作ったぜんぶのあんぱんの品質を検査するために、一部のあんぱんをランダムに選んで調査する
ってわけ。
この標本調査の例でいうと、
「作ったぜんぶのあんぱん」が「母集団」、
検査のためにピックアップした一部のあんぱんを「標本」というんだ。
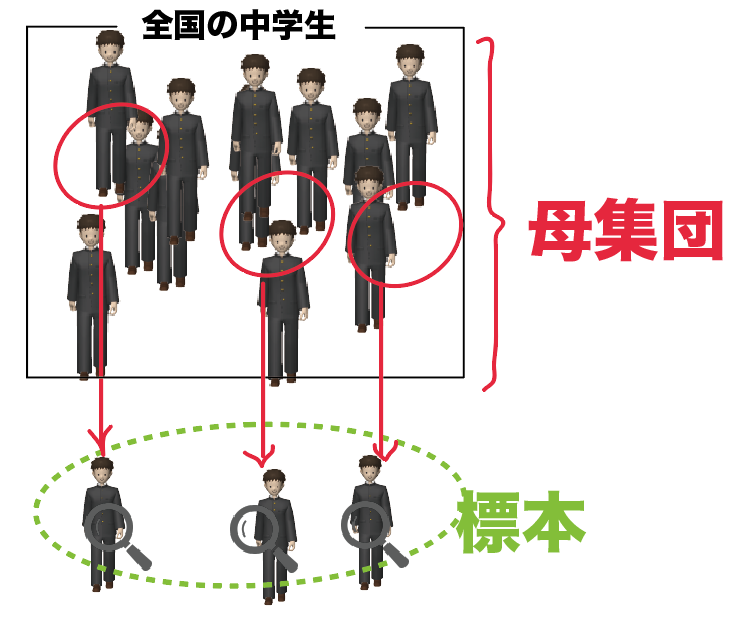
つぎは中学生の学習状況調査。
日本全国の中学生がどれくらい勉強しているのかを調べちゃうってわけね。
日本全国の中学生全員にアンケート取るのが一番正確だけど、
全員に聞きまくっていたら骨が折れまくるよね。
だから、
一部の中学生をランダムに選んで調査するんだ。
この標本調査では、
日本全国の中学生が「母集団」で、
調査のためにテストを受けてもらう中学生たちを「標本」というんだ。
母集団と標本の意味はピンときたかな??
こいつらは標本調査で使う用語で、
のことね。
標本調査の具体例を実際に考えてみて、
母集団と標本はどれなのか??
って考える癖をつけてみてね。
そんじゃねー
Ken
こんにちは!この記事を書いてるKenだよ。背骨をリセットしたいね。
あるグループや集団について調査したいとき、
君ならどうする??
たとえば、
クラスで人気のYoutubeチャンネルを調べたいときとか、
ね。
たぶん、いろいろあると思うんだ。
じつは数学界ではグループを調べる方法は2つあるんだよ。
ざっくり言っちゃうと、
全数調査は「調べたいグループ内のすべての奴らをしらべる方法」で、標本調査は「グループの中からいくつかのやつを選んで調査する方法」なんだ。
この2つの調査方法を表にまとめてみたよ。
| 使うとき | メリット | デメリット | |
|---|---|---|---|
| 全数調査 |
|
調べた結果は真実 | めんどくさい。金と時間かかる |
| 標本調査 |
|
早くて安い調査方法 | あくまでも推測 |
今日はこの、
全数調査と標本調査の違いをくわしく勉強していこう。
まず1つ目の調べ方は、
全数調査
ってヤツね。
これは、
あるグループに入ってる人や物をすべて調べる
っていう調査方法なんだ。
たとえば、 グループ1っていう集団の中に、
の5人がいたとしよう。
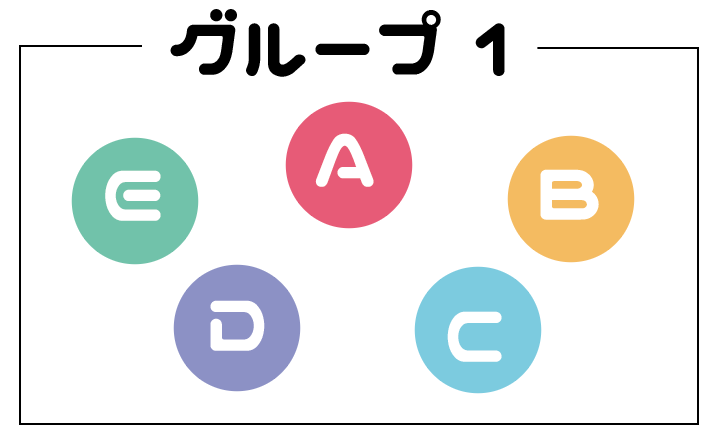
こいつらの何かを調べたいときに、
の5人ぜんぶ調べるのが全数調査なんだ。

でもさ、
いつもグループのぜんぶのデータを調べたら疲れちゃうよね?
だから、全数調査はつぎの2つのときに使うことが多いよ。
グループに属しているすべてのやつらを調べなきゃいけないとき。
こういうときは文句言わず、
全数調査
を採用しよう。
たとえば、
クラスの健康診断。

学校であるよね??
体重や身長を測ったり、視力をチェックしたりするヤツ。
あれは全数調査で、クラス全員の健康状態を調べなきゃいけないんだ。
なぜなら、
クラス全員の健康状態をチェックする必要があるからね。
クラスのみんなのほとんどが健康っていうよりも、
クラスのみんなが一人漏らさず健康であることの方が重要なんだ。
こういう風に、グループ内のデータをすべて調べなきゃいけないときは、
全数調査を使うよ。
【その2. グループに入ってるやつの数が少ないとき】
グループの大きさがすごく小さいときにも全数調査を行うね。
たとえば、家族の3人が好きなテレビ番組を調査するときとかね。

この場合、
家族っていうグループが全部で3人しかいないから、全員調べるのは超楽勝。
こういうときは全数調査でグループを調べよう。
えっ。全数調査にいいところはあるのかって??
そうだね。
じつは全数調査にはつぎの2つのメリットがあるんだ。
全数調査ではグループ内のすべてのものや人のデータを取るから、
データはすべて真実。
データの取り間違いとかはあるかもだけど、本当に全部調べちゃうから推測とかがまるでない。
100%真実なんだ。
全数調査は、グループの全員のデータを取るから、
むちゃくちゃ情報量が多いね。
ゲットできる情報が多くていろんなことを考えることができるんだ。
でも、全数調査にもよくないところがあるよ。
それは、
調べるのがむちゃくちゃ大変
ってこと。
グループのサイズが大きければ、すべてのデータを調べるのは至難の技。
金がかかるし、
時間もかかって、
調査自体が遅くなっちゃうんだ。
日本国勢調査って言って、日本に住んでる人のデータを全部調べる全数調査を行なっているんだけど、
この調査を終わらせるためには、
すごい時間がかかるよね?
日本には1億人以上住んでるからまじ骨が折れそうだ。
だけど、日本に住む全世帯のデータを調べなきゃいけないから、金と時間をかけてでも全数調査を行なっているわけだね。
こんな感じで、
全数調査にもデメリットがあるってことを頭に入れておいくれ。
つぎは、
標本調査。
標本調査とはズバリ、
グループの一部の奴らを無作為にピックアップして調べる
っていう方法なんだ。
たとえば、 グループの中に、
っていう5人がいたとしたら、そのうちの2人をランダムに選んで、
になったとしよう。
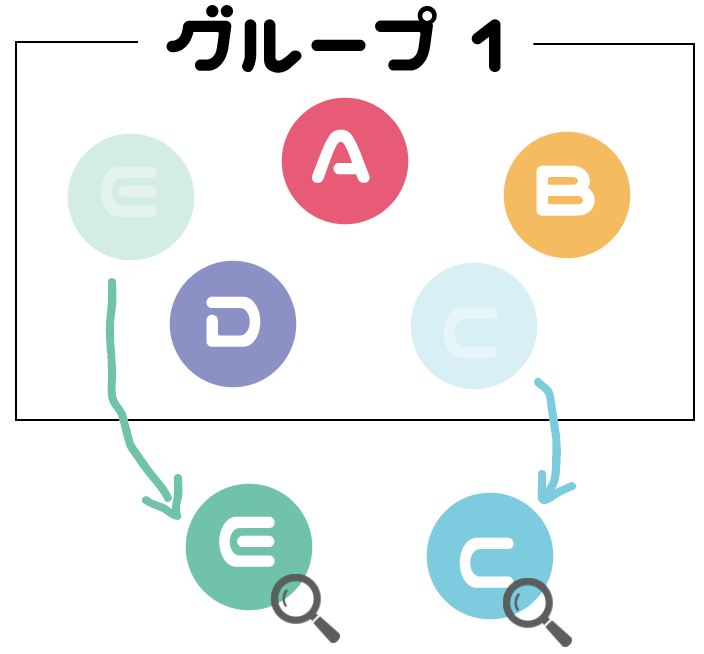
この二人のデータを調べて、グループ1の性質を推測するって方法が、
標本調査なんだ。
標本調査はつぎの2つのときに役に立つよ。
グループの中の全員調べたいけど、調べるのがめんどくさいとき。
こういうときは、
標本調査を使うよ。
たとえば、テレビの視聴率を調べるときかな。
テレビの視聴率を調べるためには、
見る人の性別や年齢、家族構成などのデータを集める必要があるよね?
あと、視聴率を計測する機械も取り付けなきゃいけない。
これを日本の全国民に対してやっていたら日が暮れちゃうわけだ。
そこで、こういう面倒なときは、
一部の人をランダムに選んで調べるんだ。
テレビの視聴率はランダムにピックアップした世帯がみている番組の視聴時間を調べているよ。
これによって、
その番組が日本でどれくらい見られているのか?
ってことを推測してるんだよ。
つぎは、
グループの中の奴らを全部調べてはいけないときね。
「えっ。そんなときある??」
って思うかもしれないけど、結構あるんだ。
たとえば、牛乳の製造工場で給食の牛乳の品質を調べるとき。
こういうときは標本調査を使うよ。
なぜなら、
全部の牛乳を調べたら、学校のみんなが飲む牛乳がなくなっちゃうからね。
牛乳をチェックするときには薬を入れたり、
スプーンを入れたり、
温度計を入れたり、
加熱したりと、
牛乳をガンガンいじりまわすから、一度調査した牛乳はもう飲めなくなっちゃう。
だから、全部は調べちゃいけないってわけ。
こういうときは一部の牛乳だけを選んで調べて、全部の牛乳の品質をチェックするんだ。
標本調査のいいところってズバリ、
早くて安いところ。
グループ内の全部のデータを調べなくていいから、手間がかからないんだ。
グループの大きさがでかいときにこの調査方法は有効だ。
標本調査のよくないところは、
調査結果があくまでも推測でしかない
ってこと。
グループの中の全員について調べてるわけじゃないからね。
全員について調べた場合の全数調査と、
一部だけを調べて推測した標本調査では結果がちょっと異なるはずなんだ。
完全にぴったり一致してるデータは得られないってわけ。
テレビの視聴率もそうで、
あれも完璧に正確な視聴率ってわけじゃない。
あくまでも推測でしかないのが標本調査のデメリットだ。
全数調査と標本調査の違いはどうだったかな??
最後に違いを表で復習しておこう。
| 使うとき | メリット | デメリット | |
|---|---|---|---|
| 全数調査 |
|
調べた結果は真実 | めんどくさい。金と時間かかる |
| 標本調査 |
|
早くて安い調査方法 | あくまでも推測 |
標本調査の基本的なところだから、テスト前に復習しておいてね。
そんじゃねー
Ken
こんにちは!この記事を書いてるKenだよ。ビタミンEが欲しいね。
図形の相似を勉強していると、
相似の中心
という言葉が出てくるよね??
相似って言葉でもちょっと怪しいのに、それの中心??
ちょっとね、正直わけがわからない。
そこで今日は、相似の中心を使って拡大図をかく方法をわかりやすく解説してみたよ。
よかったら参考にしてみてね。
つぎの5つのステップで拡大図がかけちゃうんだ。
試しに、つぎの△ABCの2倍の拡大図をかいてみようか。
まず相似の中心を決めよう。
問題ですでに相似の中心がかかれているときは飛ばしてもいいよ。
△ABCではまだ相似の中心がなかったよね??
だから、適当にポチッと点を打ってあげてね。
これが第一ステップ。
つぎは、「図形の頂点」と「相似の中心」を直線で結んでみよう。
相似の中心をOとすると、
の線分を引けばいいってことね。
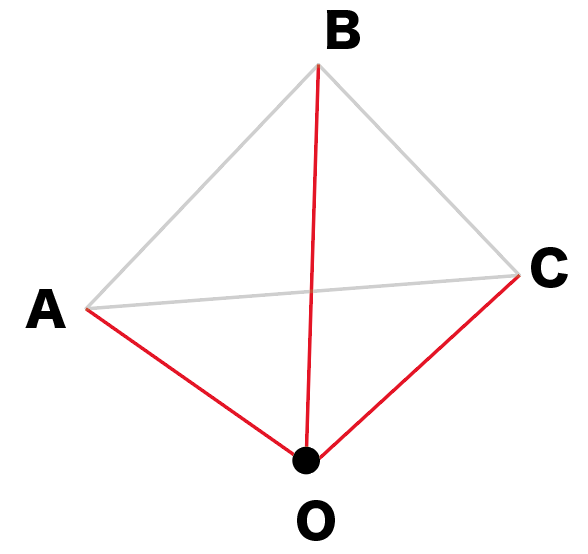
点を結ぶだけだから楽勝だぜ。
「相似の中心」と「頂点までの距離」を測ってみよう。
さっきかいた線分の長さを測るだけ!
定規でさっきの線分の長さを測ってみると、
になった!!
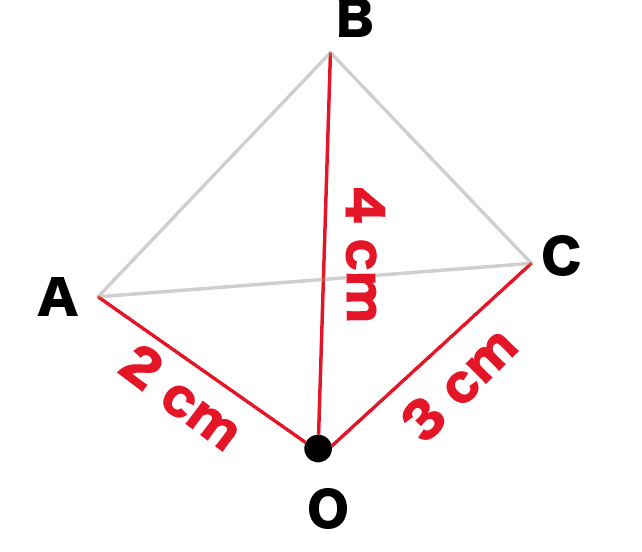
えっ。都合が良すぎるって?!
これはしょうがない。
定規で測ったらこうなったんだもん。
つぎは「倍率の分だけ」線分を伸ばしてみよう。
3倍の拡大図なら3倍、
100倍の拡大図なら100倍に伸ばしてみればいいんだ。
△ABCでは2倍の拡大図をかきたかったから、
をそれぞれ2倍に伸ばしてみよっか。
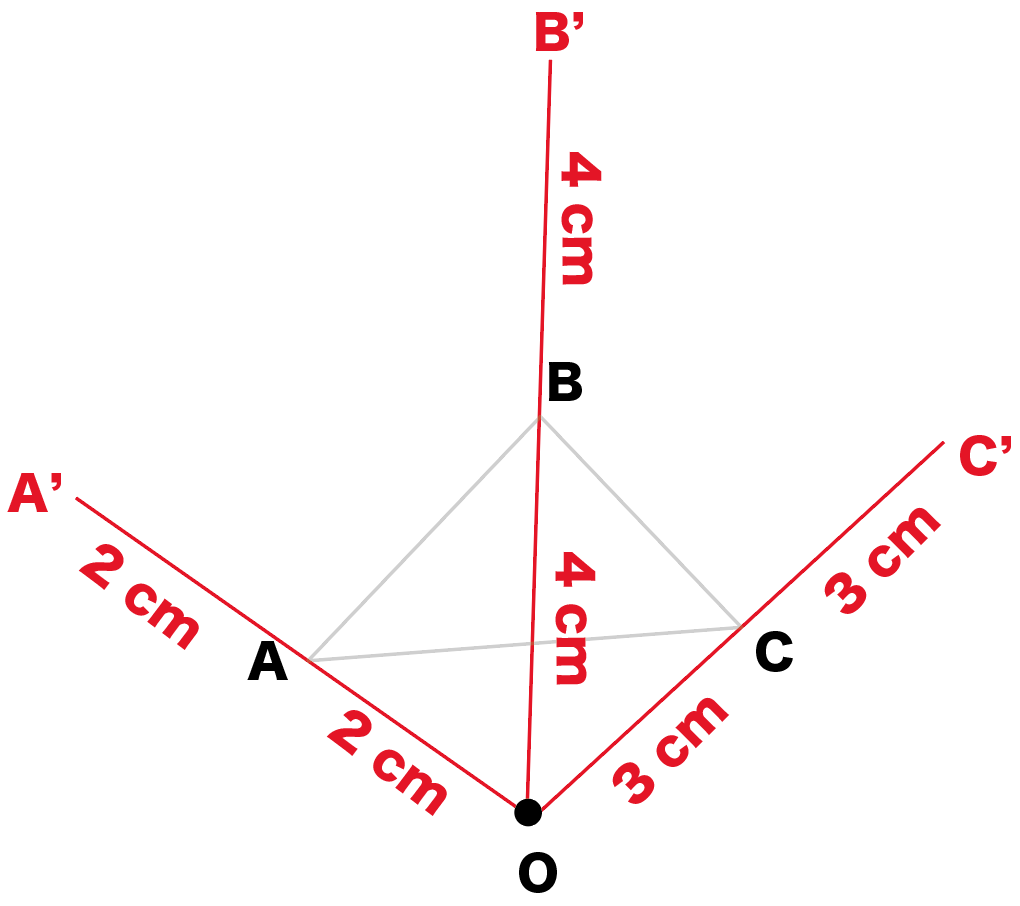
伸ばした線分の先っちょをそれぞれ、
とするよ。
最後に、新しくできた頂点を結んでみよう。
結んでできた図形が拡大図だよ。
△ABCの例でいうと、
を結んでやればいいね。
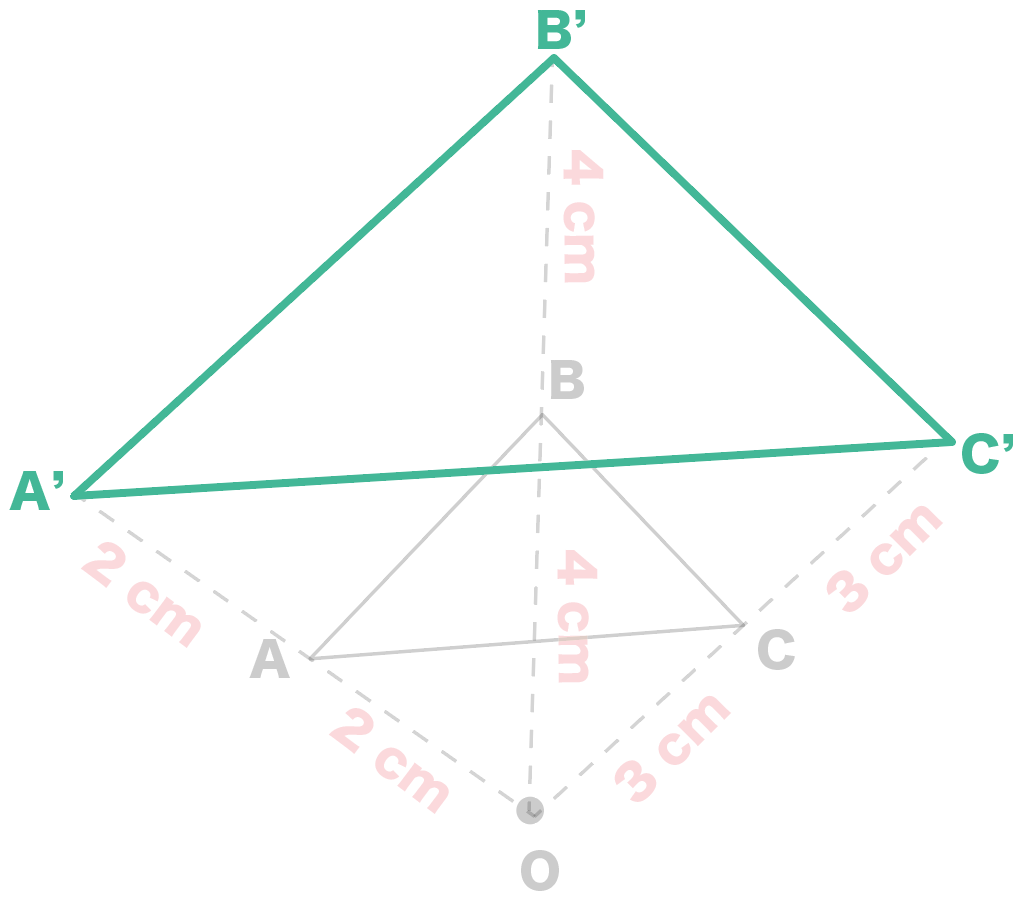
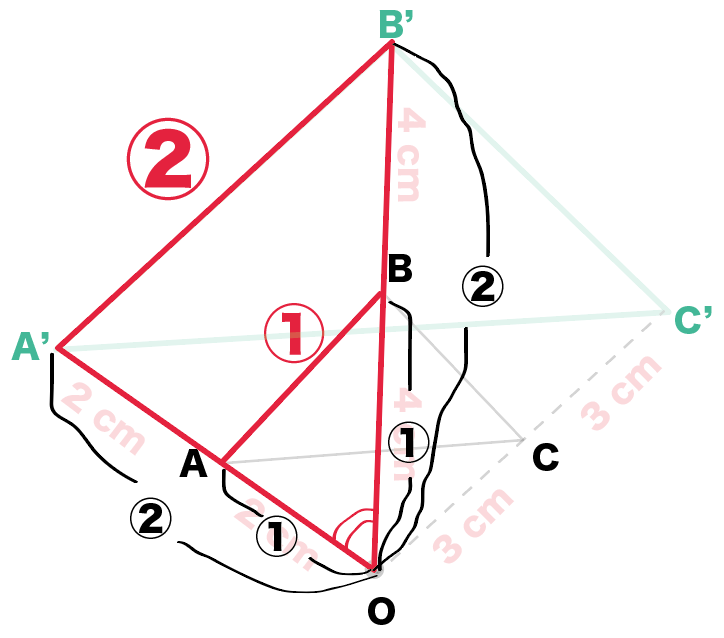
新しくできた△A’B’C’が△ ABCの2倍の拡大図だ!
こんな感じで、
「相似の中心」から「各頂点までの距離」の比が等しいとき、
2つの図形は、
相似の位置にある
っていうんだ。
んで、相似の位置にある図形たちは相似になっているよ。
今回の例でいうと、
△ABCと△ A’B’C’は相似の位置にある
って言えるわけね。
なぜなら、
になっていて、相似の中心Oから各頂点までの距離の比が等しくなってるからね。
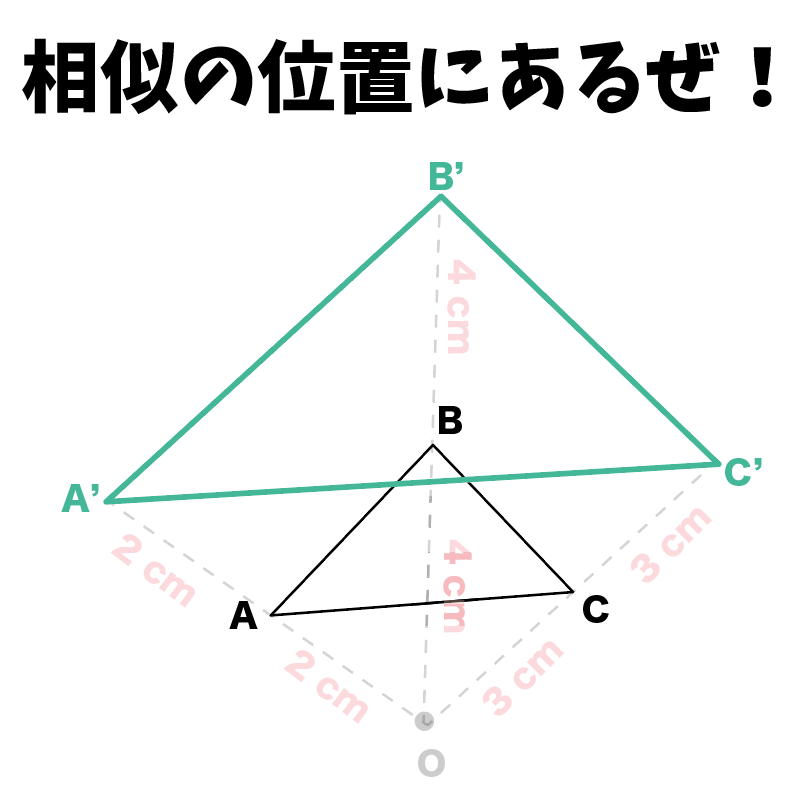
でもなぜ、相似の位置にある図形同士が相似なんだろうね??
その理由は、
平行線と線分の比を使うとわかるよ。
さっきの例でいうと、△OA’B’と△OABに注目してみて。
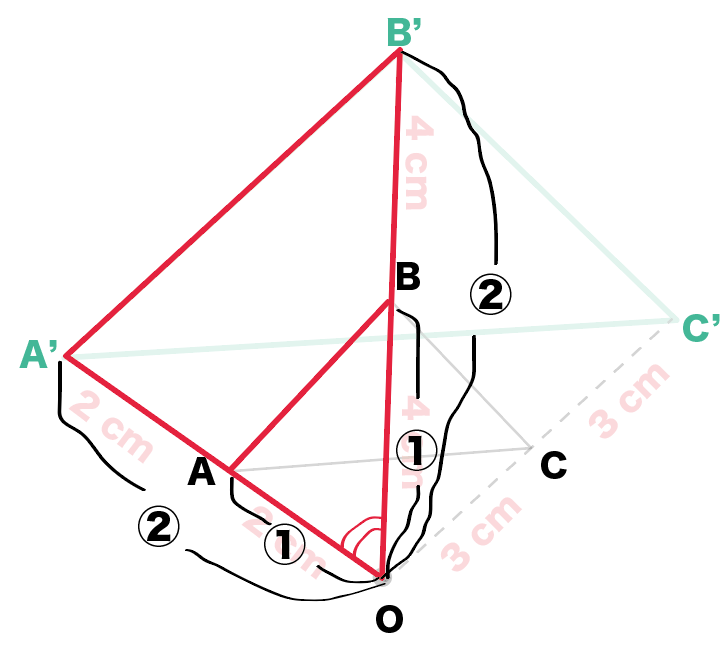
OA: OA’ = OB : OB’ = 1 :2
になってるよね??
しかも、
∠AOBは共通。
「2組の辺の比とその間の角がそれぞれ等しい」っていう相似条件が使えるから、
この2つの三角形は相似になってるわけだ。
対応する辺の比が等しいはずだから、
AB : A’B’ = 1 :2
になるね。
こんな感じで他の辺に対しても同じようにやってみると、
になってるんだ。
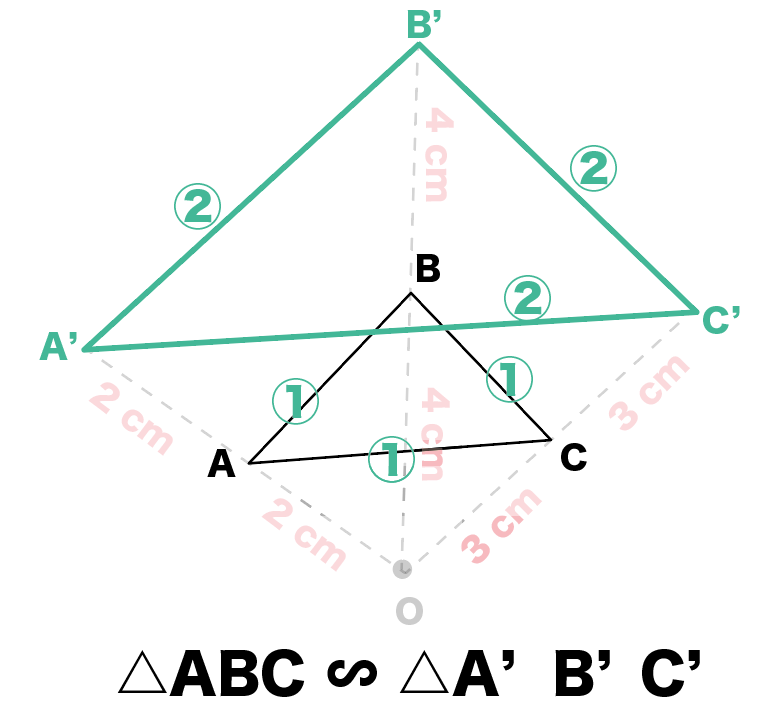
よって、△ ABCと△ A’B’C’の3組の辺の比が1:2でそれぞれ等しいから、
△ ABC∼△ A’B’C’
が言えるんだ。
どう?ちょっとスッキリしたかな?
相似の中心を使ってしまえば、拡大図のかきかたも簡単。
の5ステップでいいんだ。
相似の中心を使いまくるのもいいけど、
なぜ、相似の中心を使えば拡大図がかけるのか?
ってこともおさえておいてね。
そんじゃねー
Ken
こんにちは!Dr.リードだぞいっ。
今回のテーマは三平方の定理(ピタゴラスの定理)だ。
聞いたことあるかな?
紀元前572年ごろのギリシア人のピタゴラスさんが発見したから「ピタゴラスの定理」っていうんだな。
今日はその三平方の定理(ピタゴラスの定理)の使い方じゃなくて、
なぜ、三辺平方の定理が使えるのか?を証明していくぞ。
三平方の定理の証明法は100以上、いやもっとそれ以上あるといわれている。
中でも、中学生にも分かりやすい4つの証明を紹介していくぞ。
今回は姉上といっしょに三平方の定理(ピタゴラスの定理)の証明をみていこう。

まず1つ目の証明は、
小さな直角三角形二等辺三角形
を使った証明だ。
直角三角形を4枚合わせると、
正方形になるよな?
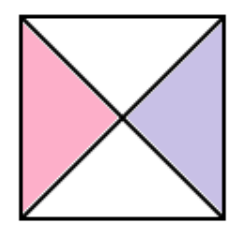
んで、この正方形をもっとつなぎ合わせると、もっとでかい四角形ができるね。
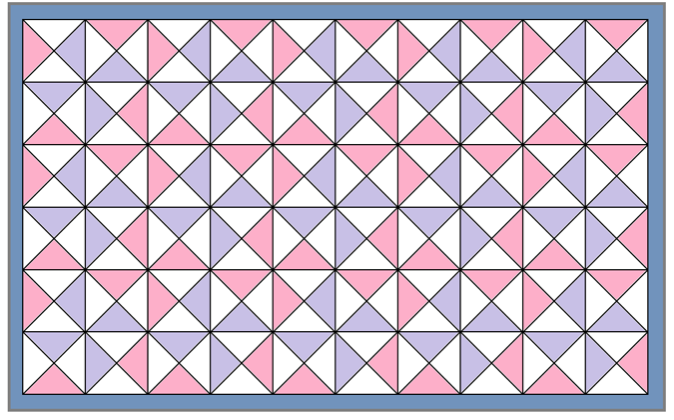
この証明では、パッチワークみたいな感じで、小さい直角二等辺三角形を使っていくぞ。
まずは、中ほどにピンクの生地8枚使って、直角三角形を作ってくだされ。

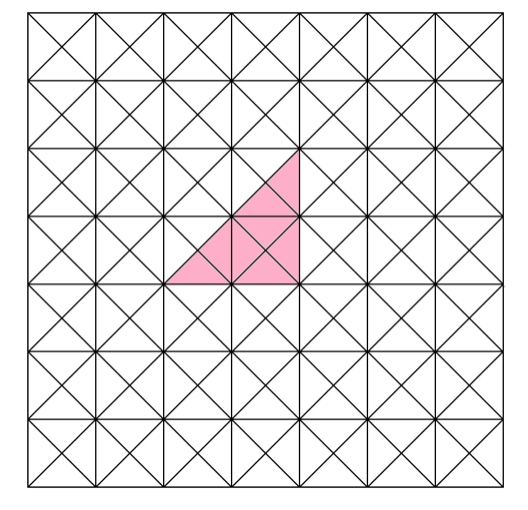
ついでに3種類、イエロー、パープル、ミントグリーンも使って、ピンクの三角形の各辺がくっついた正方形を作ってくだされ。
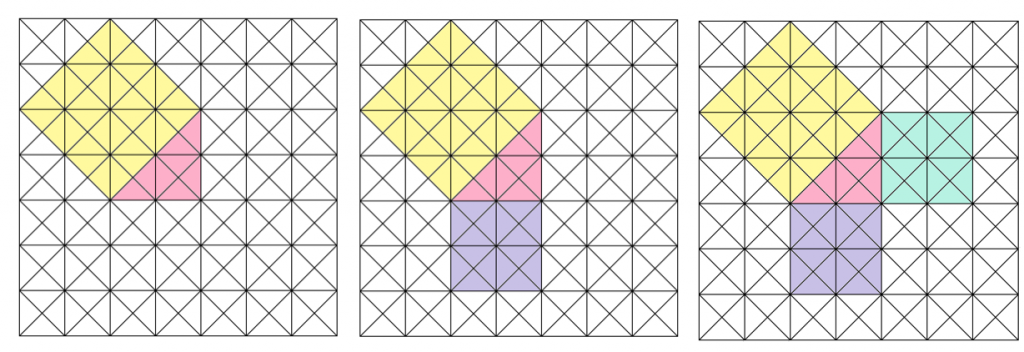
それぞれの色にふくまれる直角二等辺三角形の数を数えてみよう。
「黄色の枚数」と「パープル+ミントグリーン」の枚数が一緒ってことに気づくかな?
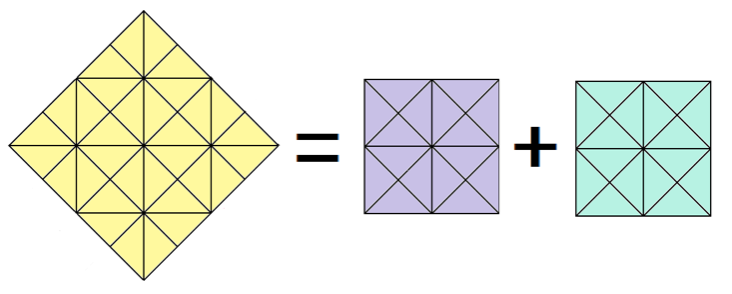
黄色い正方形の1辺をb、
パープル・ミントグリーンの正方形の1辺をaとすると、
b² = a² + a²
になってるはずだね。
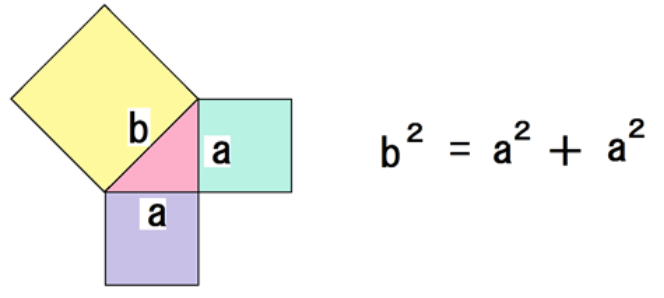
このことから、
赤の直角二等辺三角形の斜辺の2乗が、他の2辺の2乗の和になってる
って言えるね。
おお、これって三平方の定理じゃん!!
つぎの三平方の定理(ピタゴラスの定理)証明は、
の2つを使っていくよ。
こんな感じのパッチワークを想像してくれ。
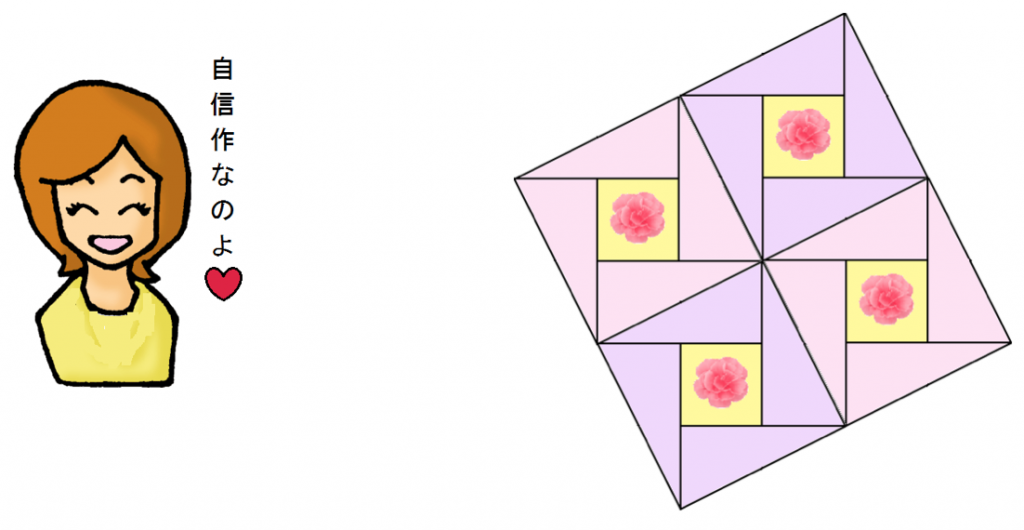
これの一番基本となるピースに注目。
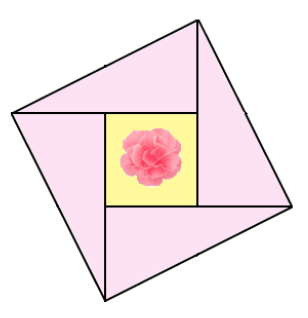
今回は、この、
が合体して正方形になってる図形を使っていくんだ。
1つの直角三角形の辺の長さをそれぞれ、
としてやろう。
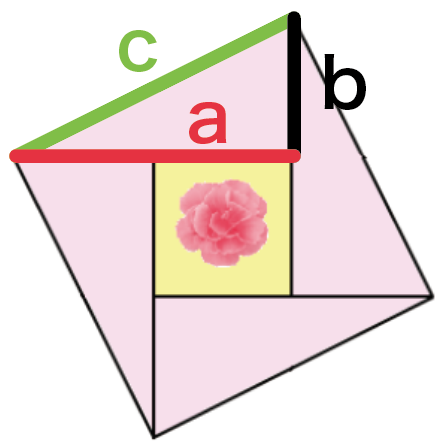
まず、下のようにピンクの三角形を右下へ動かしてみる。
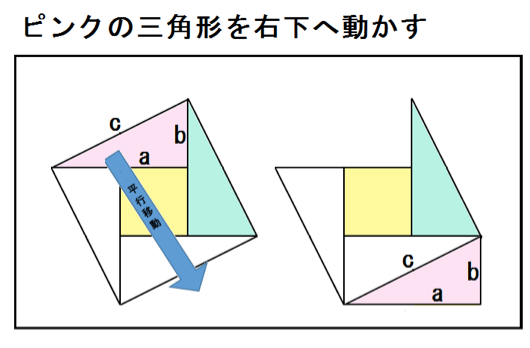
つぎは、水色の三角形を左下へ動かしてみる。
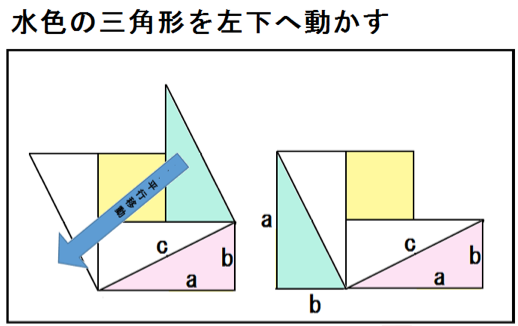
ここで、こいつを2つの正方形、
に分けてみると、
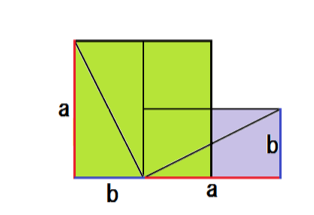
こいつの面積は、
a² + b²
になるよね?
んで、もともとは1辺がcの正方形だったはずだから、
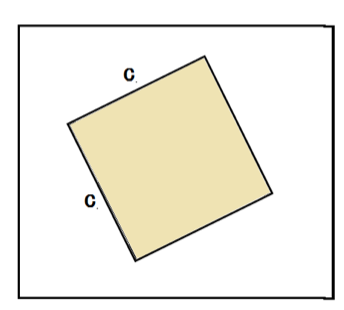
c² = a² + b²
っていう式が成り立つね。
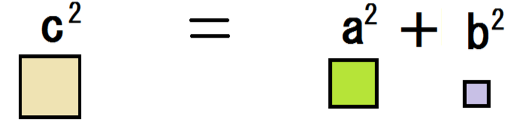
ここで、左上の基本のピンクの直角三角形に注目てしてみて。
cは斜辺、aとbはその他の2辺の長さになってるよね?
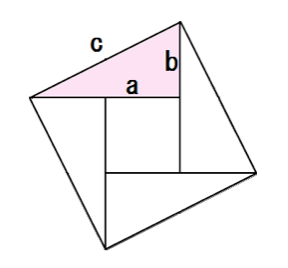
おお、みごと、三平方の定理の式になりました。

つぎの三平方の定理(ピタゴラスの定理)の証明は、
正方形を2つ使うパターン。
の2つの正方形をイメージしてみよう。
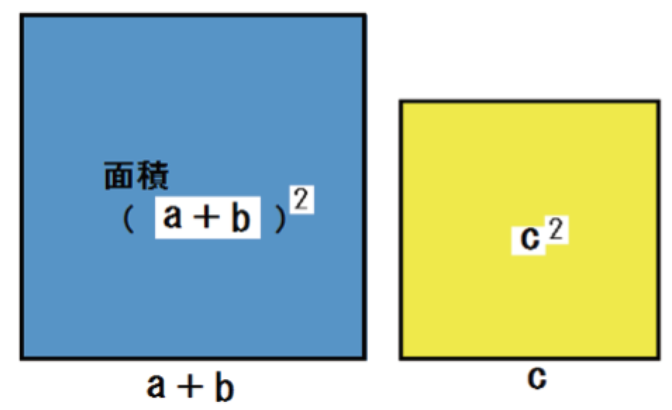
こいつをこんな風に重ねてみた。
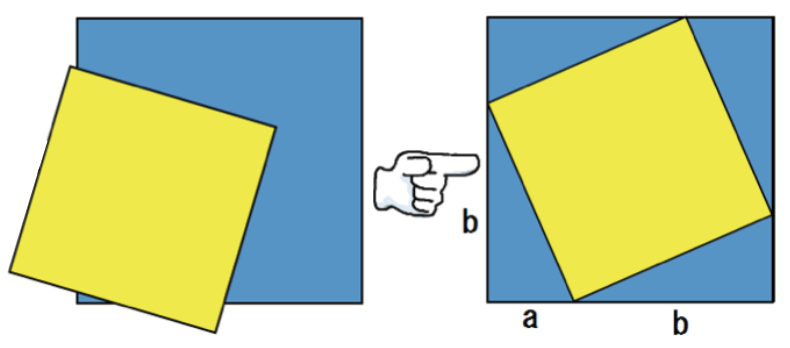
それぞれの面積を出すと、
真ん中の黄色い正方形は、青い正方形から4つの直角三角形を引いたものだから、
c² = (a+b)² -2ab
c² = a²+2ab +b² -2ab
c² = a²+b²
1つの直角三角形でみると、
cは斜辺でaとbはその他の辺だね。
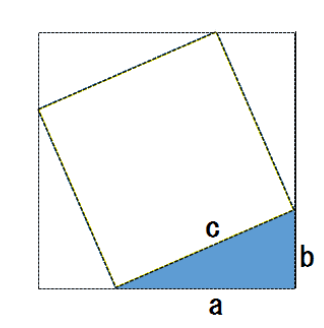
おお、これも見事三平方の定理の式になったぞ。
相似の証明を使って、三平方の定理を証明することもできるんだよ。
つぎのような直角三角形△ABCがある。
Bから辺ACに垂線を下ろし、交点をDとするね。
AD = x 、DC = y としておく。
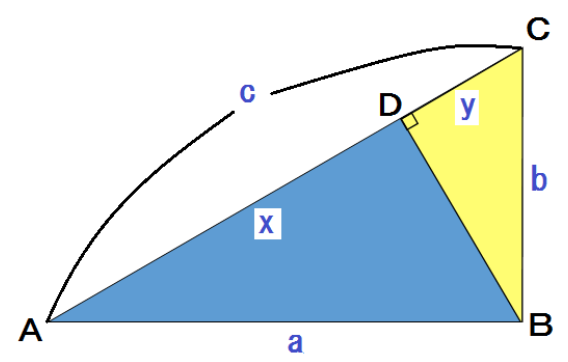
見やすいように図形をバラバラにすると、
相似な三角形が3個も隠れてるんだ。
△ABCと△ADBについて、
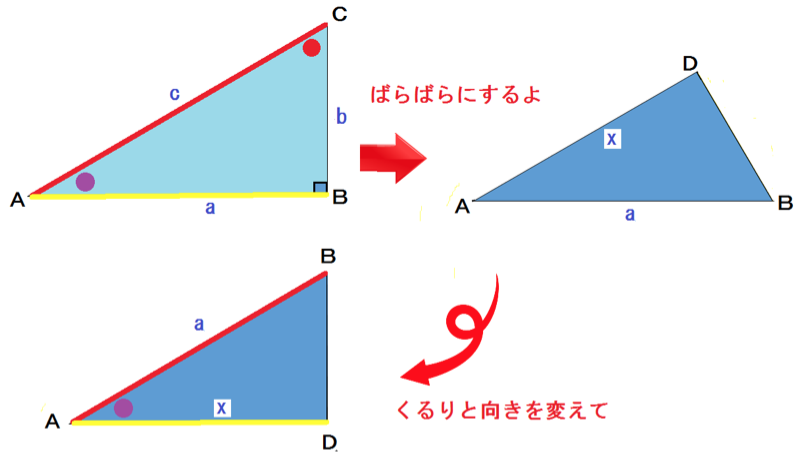
仮定より、
∠ABC = ∠ADB = 90°・・・①
また、
∠CAB = ∠BAD(共通)・・・②
①②より、
2組の角がそれぞれ等しいので、
△ABC∼△ADB
よって、対応する辺の比はそれぞれ、
c : a = a : x
a² = cx・・・③
になる。
また、
△ABCと△BDCについて、
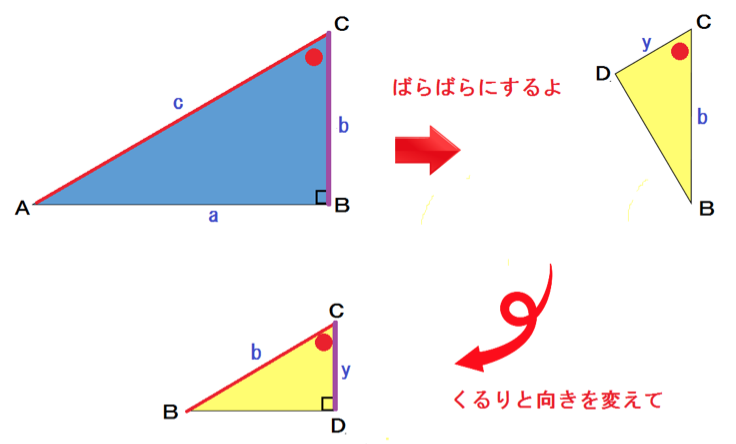
仮定より、
∠ABC = ∠BDC = 90°・・・④
また、
∠CAB = ∠BAD(共通)・・・⑤
④⑤より、
2組の角がそれぞれ等しいので、
△ABC∼△BDC
よって、対応する辺の比はそれぞれ、
c : b = b : y
b² = cy・・・⑥
になる。
③+⑥を計算すると、
a² + b² = cx + cy
a² + b² = c (x + y)
a² + b² = c²
おお、これも見事三平方の定理の式になったぞ。
三平方の定理(ピタゴラスの定理)の証明はどうだっかな?
勉強したのは4つだったね。
しっくりきたやつを覚えておこう。
ピタゴラスは数学者じゃなくて、ピタゴラス学派っていうギリシャの宗教教団のリーダーだったんだ。
数学者・哲学者・音楽家と様々な顔を持っていたらしいよ。
なかなかやるな、ピタゴラス。

それじゃあ!
Dr.リード
こんにちは!この記事をかいてるKenです。良薬は苦しだね。
直角三角形の辺の比の問題でよく出てくるパターンの1つに、
3: 4: 5の直角三角形
っていうのがあるんだ。
これは文字通り、
3つの辺の比が3:4:5になってる直角三角形のことね。
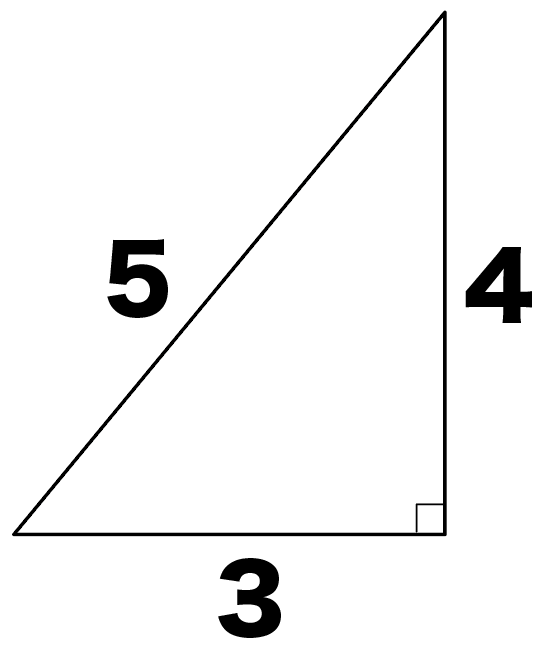
たとえば、辺の長さが、
になってる直角三角形。
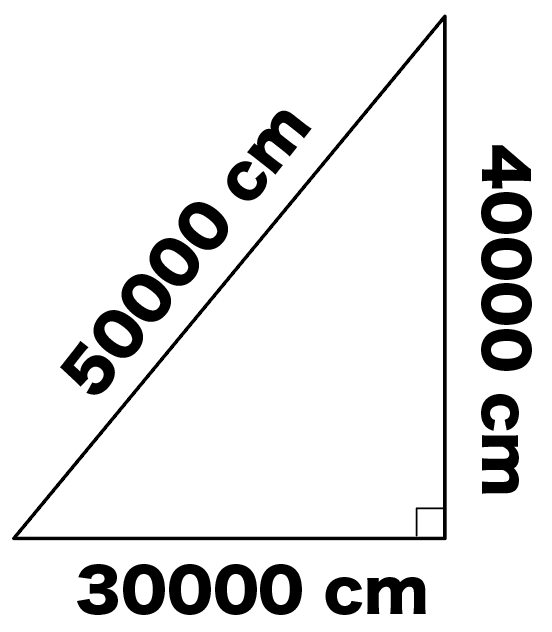
辺の長さの比を取ってみると、
30000 : 40000 : 50000
= 3 : 4 :5
になってるでしょ??
今日はこんな感じで、
3:4:5の直角三角形の辺の長さを求める問題
の解き方紹介していくよ。
よかったら参考にしてみてね。
3:4:5の直角三角形の辺の比の問題は3種類あるよ。
一つ目のパターンは、
斜辺以外の辺の比が3:4の問題だね。
直角三角形の辺の比を使えば、三平方の定理より早く解けちゃうんだ。
たとえば、つぎのような練習問題ね。
練習問題
直角三角形の辺の長さxを求めなさい。
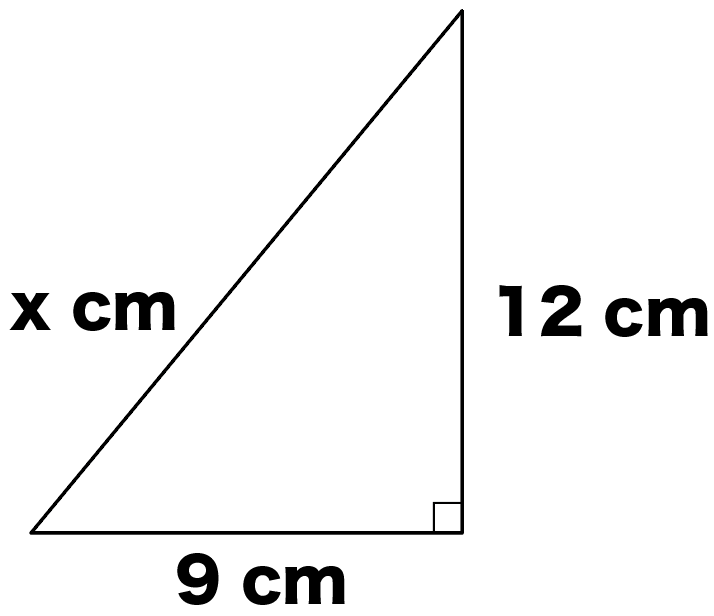
直角三角形の斜辺以外の辺の比をみてみると、
9 : 12
= 3 : 4
になってるよね??
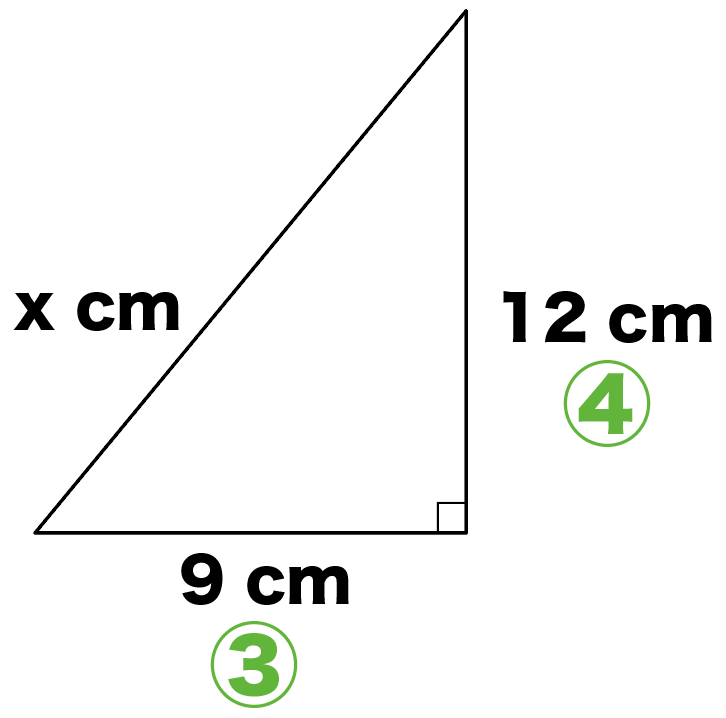
ってことは、これは紛れもなく3:4:5の直角三角形。
この手の問題では、
「1番小さい辺の長さ」に3分の5をかければ斜辺の長さを計算できるんだ。
なぜなら、
(斜辺の長さ):(1番小さい辺の長さ)= 5 : 3
になってるはずだからね。
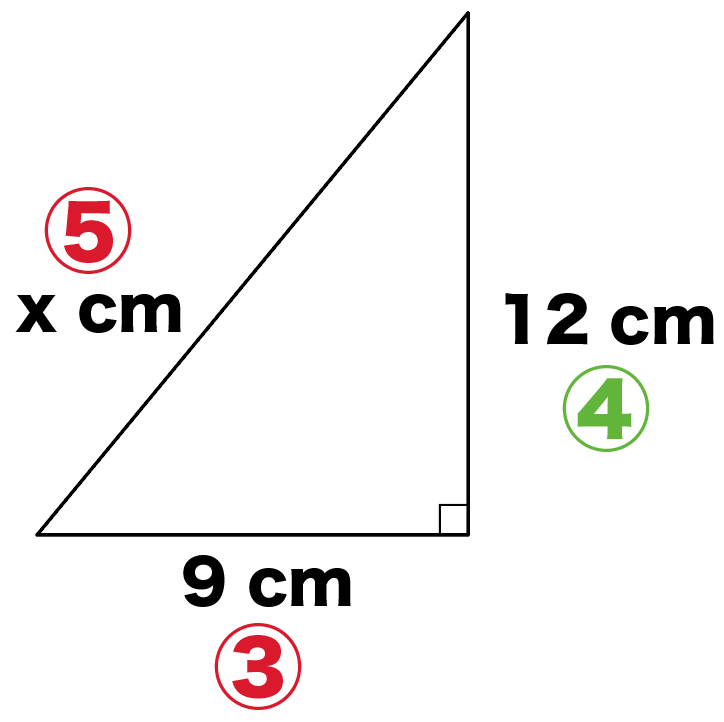
ってことで、1番小さい辺の「9 cm」に3分の5をかけてやると、
9× 5/3
= 15 cm
に斜辺はなるね。
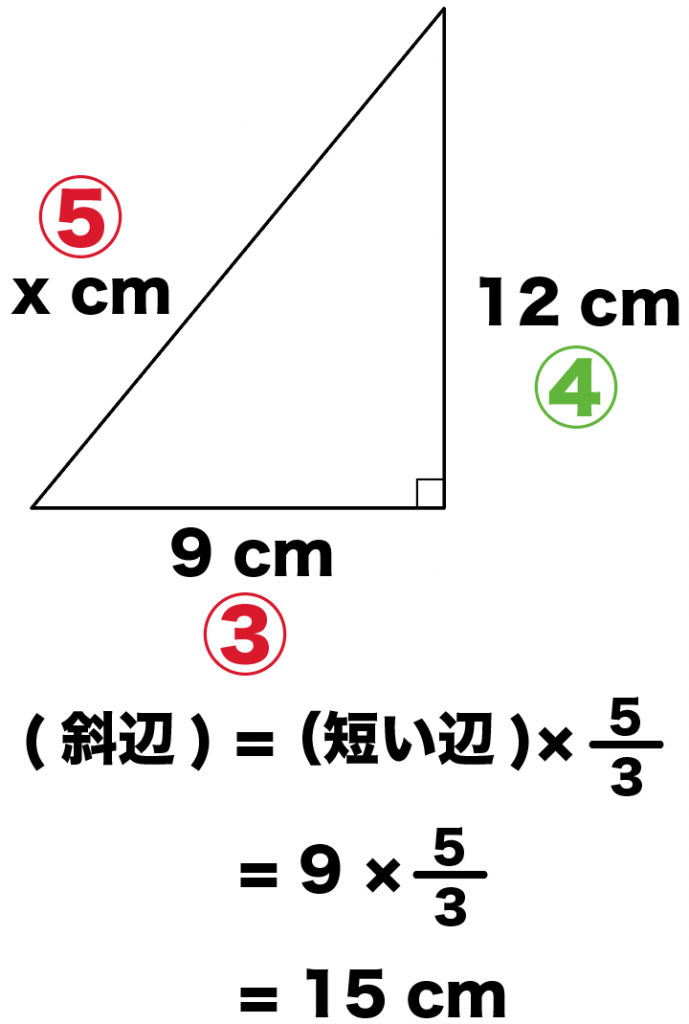
三平方の定理を使うより早くて簡単だ。
つぎは「斜辺」と「その他の辺」の比が5:4の問題ね。
練習問題
つぎの直角三角形の辺の長さxを求めなさい。
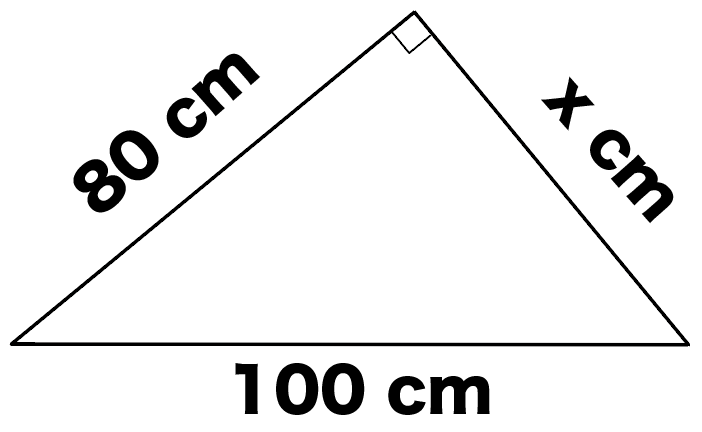
この問題では、「斜辺」と「もう1辺の長さ」の辺の比が、
100 : 80
= 5 : 4
になってるよね??
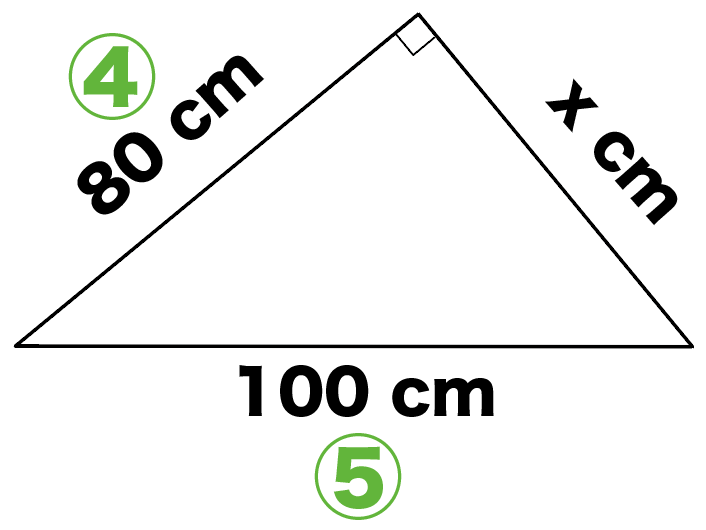
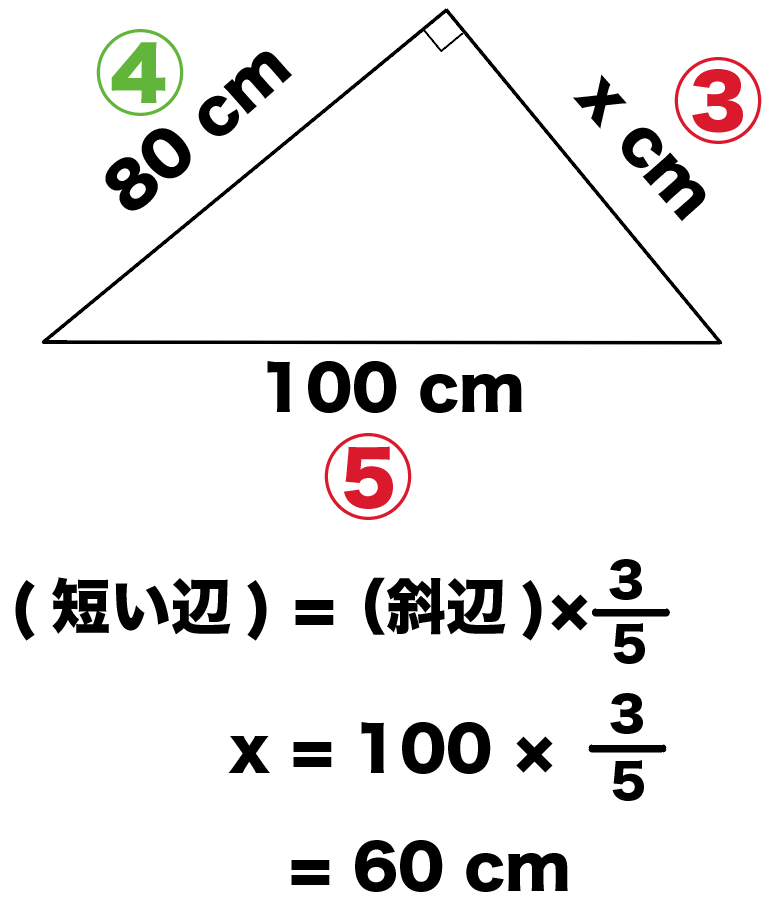
ってことは、直角三角形の辺の比は3:4:5になるはずだから、
「斜辺の長さ」に5分の3をかければ残りの辺の長さを計算できちゃうね。
ってことで、残りの辺の長さxは、
x = 100×5分の3
= 60 cm
になるね。
最後は、「斜辺」と「その他の辺」の比が5:3になってる問題ね。
たとえば、つぎのようなやつ。
練習問題
つぎの直角三角形の辺の長さxを求めなさい。
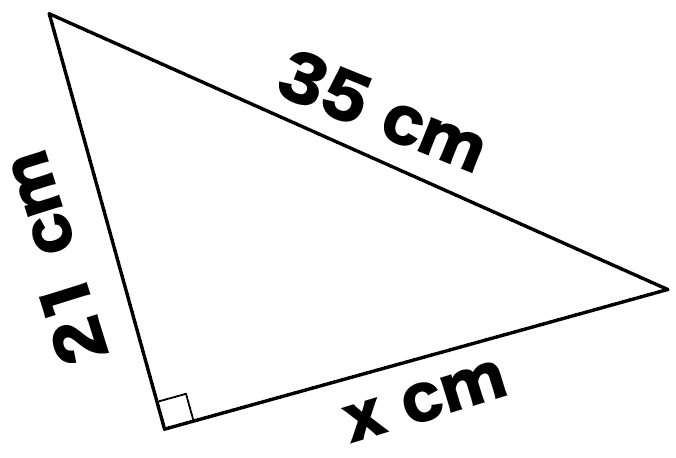
直角三角形の「斜辺」と「その他の一辺の長さ」の比を出してみると、
35 : 21
= 5 : 3
になってるよね?
ってことはこの直角三角形も3:4:5のタイプ。
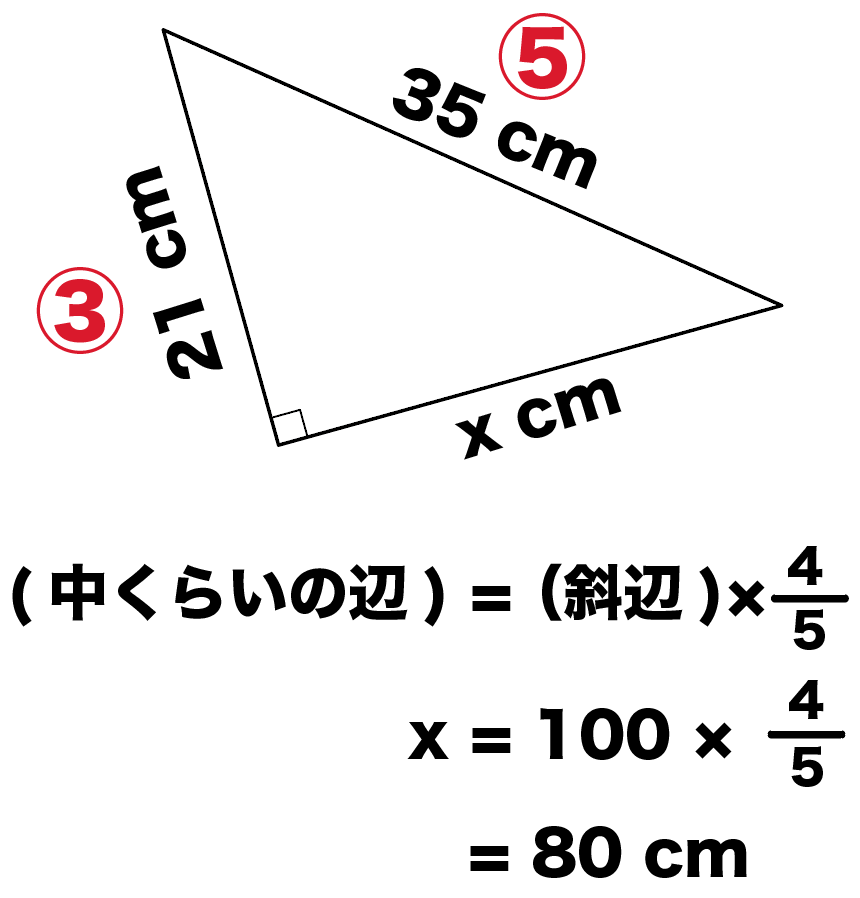
斜辺と残りの辺の長さの比は、
5: 4
になってるはずだから、斜辺に5分の4をかければ辺の長さが出てくる。
実際に計算してみると、
x = 35×4/5
= 28 cm
になるね。
辺の比が3:4:5の直角三角形の問題はどうだったかな??
全部で、
の3パターンあったけど、やってることは全部一緒。
3:4:5の辺の比を使って分数の掛け算すればいいのさ。
コツは、
辺の比が3:4:5になってることをいかに早く見つけるか
だ。
問題をたくさんといて解き方に慣れていこう。
そんじゃねー
Ken