「代表値の求め方」を教えてほしい！！
こんにちは、かまぼこにはまっているKenです。
「資料の活用」で「代表値」がでてきますよね！？？
代表値に関しては「中学数学で勉強する「代表値」とは？？」という記事で解説しました。
よかったら参考にしてくださいね。
今日はもう一歩踏み込んで、
代表値の求め方
を徹底解説します！！
中学数学で役立つ3つの「代表値の求め方」
3つの代表値「平均値」、「中央値（メジアン）」、「最頻値（モード）」の求め方を確認していきます。テスト前にチラ見してください。
代表値1. 「平均値の求め方」
代表値の1つである「平均値」。
平均値の求め方は以下の式であらわせます。
度数分布表では「階級値」をつかって平均値を計算しましょう！
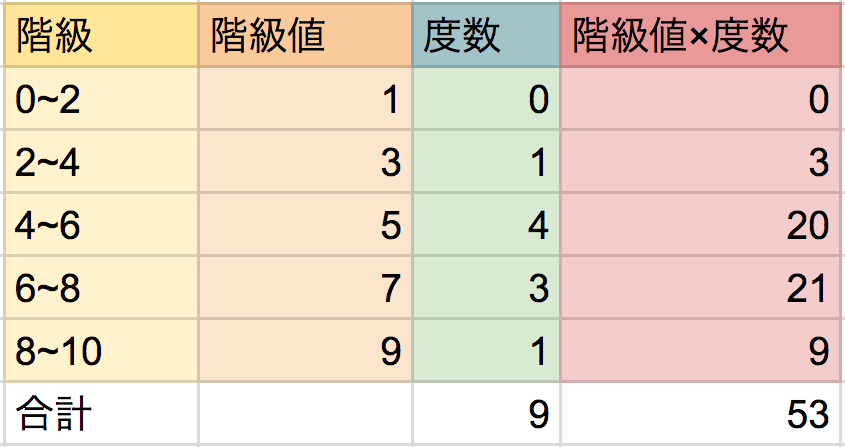
よって、「階級値×度数」を「データの合計数」でわると5.89という平均値が得られます。
平均値は3つの代表値の中で唯一、計算する値です。計算ミスをしないように気をつけましょうねー。
詳しくは平均値の求め方を読んでみてください。
「度数分布表から平均値を求めたいんだよ！」
というときはこちらの「度数分布表から平均値を求める方法」を読んでみましょう。
代表値2. 「中央値（メジアン）の求め方」
中央値、通称「メジアン」。
中央値とは、
データを大きい順に並べたときに真ん中になっているもの
です。中央値を求めるにはデータの並べかえが必要なのです。大きい順に！！
つぎのデータをみてみましょう。
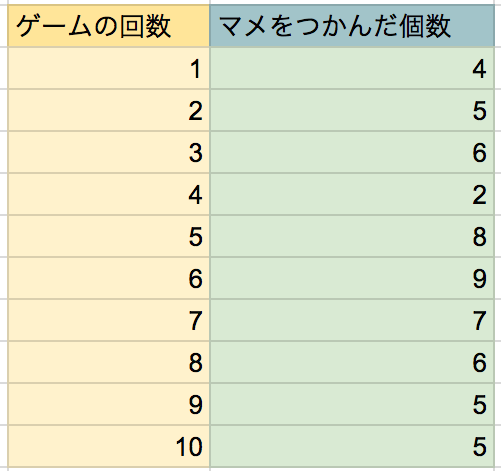
「マメをつかんだ個数」は大きい順に並んでません。むちゃくちゃな順番です。
これを大きい順に左から並べてやると、
「5」と「6」が真ん中のデータであることがわかりますね！
真ん中の数が2つある場合は、その平均が中央値となるので、この例でいうと、
(6+5)÷2
= 5.5
が中央値になりますね。この例のように、データの総数が偶数のときは真ん中の2つの数字の平均をとってあげましょう。
では、
データ数が奇数になったときは中央値はどうなるのでしょうか？
たとえば、
8, 7, 6, 6, 5, 5, 5, 4, 2
というデータが得られたとしましょう。
この場合は真ん中のデータの「5」がそのまま中央値（メジアン）になりますね。
詳しくは「中央値の求め方」を読んでみてくださいね。
代表値3. 「最頻値（モード）」の求め方
最後の代表値は「最頻値（モード）」。
最頻値とは、
データの中でもっとも頻繁にでてくる数字のこと
です。最頻値では、データの全体をながめる技術が必要です。さらーっとみていちばん多いデータの値をチョイスしましょう。
ただ、ミスを防ぐためにデータを大きい順に並び替えるのも1つの手です。
この場合、「5」というデータがいちばん多く含まれているので、
最頻値は「5」！！
ということになります。
詳しくは最頻値の求め方を読んでみてくださいね。
「代表値の求め方」は大丈夫！
以上で「代表値の求め方」は終了です。
- 平均値の求め方
- 中央値（メジアン）の求め方
- 最頻値（モード）の求め方
をしっかりマスターして「資料の活用」であばれちゃいましょう！！
それでは！
Ken
＜＜関連記事＞＞
- 中1数学の「資料の活用」を攻略する3つのコツ
- 【資料の活用】度数分布表の「階級・度数」ってなに？？
- 【中学数学】3分でわかる！相対度数の求め方
- 【中学数学】3分でわかる！平均値の出し方
- 【中学数学】3分でわかる！「階級値」ってなに？？
- 【中学数学】有効数字の1つの計算方法と考え方
