小数と分数が含まれちゃってる方程式は？？ 「一次方程式」には色々なタイプがあるけど、中には 分数と小数の両方を含む厄介な奴 がいるんだよね。   例えば次のような問題さ。 次の方程式を解け。 $$\frac{x…

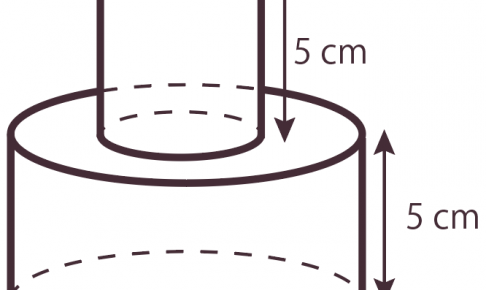
円柱を2つ重ねた立体の表面積だと・・・？ 立体の問題ではこんな問題もあるっぽいよ。   次の立体の表面積を求めよ。   なんと、 円柱を2つ重ねた立体 の登場だ。 しかも「表面積」を求めろ、と。 &n…

  一次方程式で出てきやすいのが かっこ（） がついたバージョン。   例えばこんなやつかな↓ 次の方程式を解いて。 $$5 ( x + 1 ) = 3 ( 2x -3 )$$ 解き方は次の3ステップ…

食塩水の文章問題で混ぜてきたらどうする？ 食塩水の問題は、食塩水ってだけで厄介だけど、たまに、 混ぜる系の文章問題 が出てくるんだ。 例えばこんな感じ↓ 12%の食塩水を600g用意し、そこからある食塩水をくみ出してから…

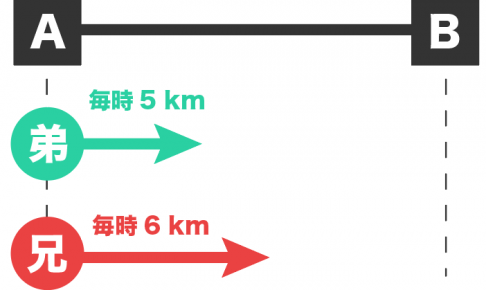
方程式の文章問題には「早く着いちゃったパターン」がある？？   世界にはいろんな一次方程式の問題があるけど、やっぱり厄介なのが、 道のり・速さの文章問題だね。 これまで 追いついちゃった問題 移動手段を変えるパ…

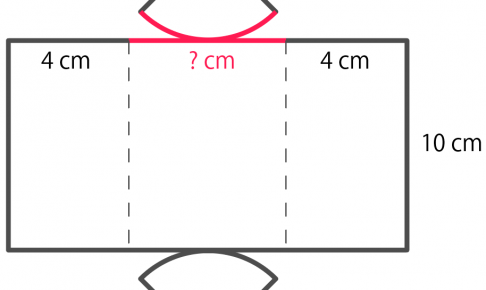
底面の扇形の立体の表面積を求めたい！ こんにちは！この記事を書いているKenだよ。博物館、ハマったね。   世の中にはいろいろな立体が存在しているけど、中には 扇形が底面の立体 もあるみたいだね。 例えばこんな…

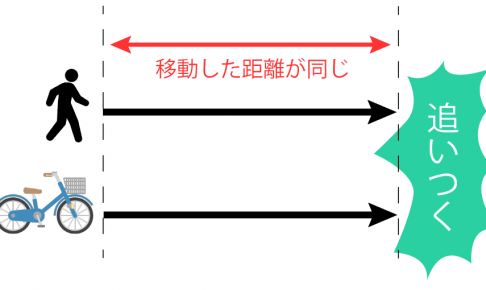
また方程式の文章題で速さの問題？？ こんにちは！この記事を書いているKenだよ。蒸しパン、呼んでるね。   方程式の文章題では「速さ・道のりの問題」は出やすい。 前回は「追いつく系」の文章題を解いたけど、もう一…

一次方程式の文章題で速さの問題がムズイ！ こんにちは！この記事を書いているKenだよ。洗った、ね。   一次方程式の文章題にはいろんなパターンがあるけど、中でも出やすいのが、 速さ・道のりの文章問題。 例えば、…

文房具屋にノートを買いに出かけるだと？ こんにちは！この記事を書いているKenだよ。干した、ね。   中1で勉強する「一次方程式の文章問題」には色々なパターンがでてくる。 道のり・速さの問題だったり、割合の問題…

長椅子の文章題でてきちゃった！ こんにちは！この記事を書いているKenだよ。どら焼き、品切れだね。   一次方程式の文章問題にはいろんな種類がある。 中でも、なんか知らんけどよく出てくるのが、 長椅子の文章問題…

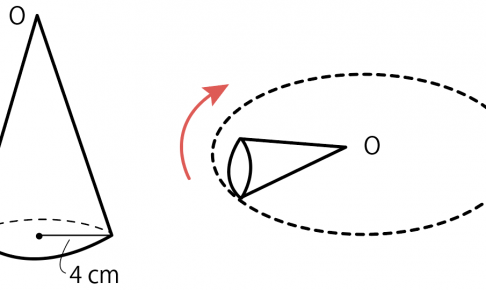
円錐が転がる問題の解き方を教えてほしい！ この記事を書いているKenだよ。下痢に、勝ったね。   中学数学ででてくる円錐の問題には 円錐の表面積の求め方 円錐の側面積の求め方 円錐の体積の求め方 円錐の高さを求…

tomo（旧Qikeru）の中学1年生の数学の記事をまとめました。   Chapter1. 正の数・負の数 数学の基本中の基本。プラスマイナスをマスター！   正負の数 負の数の例 マイナスかけるマイ…

円周率の求め方・出し方ってどうやるの？？ こんにちは！この記事をかいているKenだよ。ゴミ袋は必須だね。   中学数学で図形を勉強していると、 円周率 をたくさん使うよね？？ たとえば、円の面積や球の体積を計算…