連立不等式の文章題の解き方がわかる3ステップ

前回「連立不等式の解き方」を見てきたよな。
今日はもう1歩踏み込んで、
連立不等式の文章題
を解いてみよう。
例えば次の問題だ。
あるところに所持金が1500円の男がいました。その男はマスターから買い物を頼まれ、リンゴとレモンを調達せねばなりません。
近所のスーパーではリンゴが150円、レモンが100円でした。
マスターは合計で10個のリンゴとレモンが欲しいようです。そして「リンゴの方が好きなのでリンゴの方が多く買ってきてほしい」という要望もありました。さてこの男性はリンゴを何個買えばいいでしょうか。

連立不等式の文章題の解き方がわかる3ステップ
それじゃあ早速この文章問題解いていくぞ。
連立等式の文章題の解き方は次の3ステップだ。
1. 「求めたいもの」を文字でおく
まず最初に、
文章内で求めたいものを文字($x$)でおこう。
この鉄則は、一次方程式の文章題でも、連立方程式の文章題でも、二次方程式の文章題でも同じだ。
例の文章題をみると、最後の方に
さてこの男性はリンゴを何個買えばいいでしょうか
って書いてある。つまり、
男が買わねばならないリンゴ数
を求めなきゃいけないな。
ってことで、
男が買わねばならないリンゴ数 = $x$個
としてみよう。
2. 不等式を2個つくる
求めたいものを文字に置いたら、次は不等式を作っていくぞ。
連立不等式は、2つの不等式を用意すれば解けるな。
不等式とは、
2つの等しくない数の関係を表すもの
だった。
だから、文章から「2つの等しくない数量」を探すんだ。
1つ目は、合計金額について。
リンゴとレモンを買った合計金額は所持金の1500円より小さくないと買えないよな。
つまり、
(リンゴとレモンを買った合計金額)<(所持金の1500円)
という不等式が成り立つ。
2つ目の大小関係はリンゴとレモンの個数だ。
リンゴとレモン10個合計で必要なんだけど「リンゴのほうが多く」買わないといけないんだ。
つまり、
(リンゴの数)>(レモンの数)
という不等式になりそうだ。
って感じで、不等式を2つ立てていくぞ。
すると、次のような連立不等式になる。
$$\begin{cases} 150x+100(10-x)<1500 & \\ x>10-x & \end{cases}$$
3. 連立不等式を解く
あとは不等式の基本的な解き方に基づいてとくだけ。
連立不等式では、
複数の不等式の解の共通範囲を求めればよかったな。
例題で作った2つの不等式を解いてみると、次のようになる。
(1つ目)
$$150x+100(10-x)<1500$$
$$150x+1000-100x<1500$$
$$50x<500$$
$$x<10$$
(2つ目)
$$x>10-x$$
$$2x>10$$
$$x>5$$
つまり、連立不等式はこうなる。
$$\begin{cases} x<10 & \\ x>5 & \end{cases}$$
んで、共通範囲を視覚的にあぶりだすために数直線を書く。
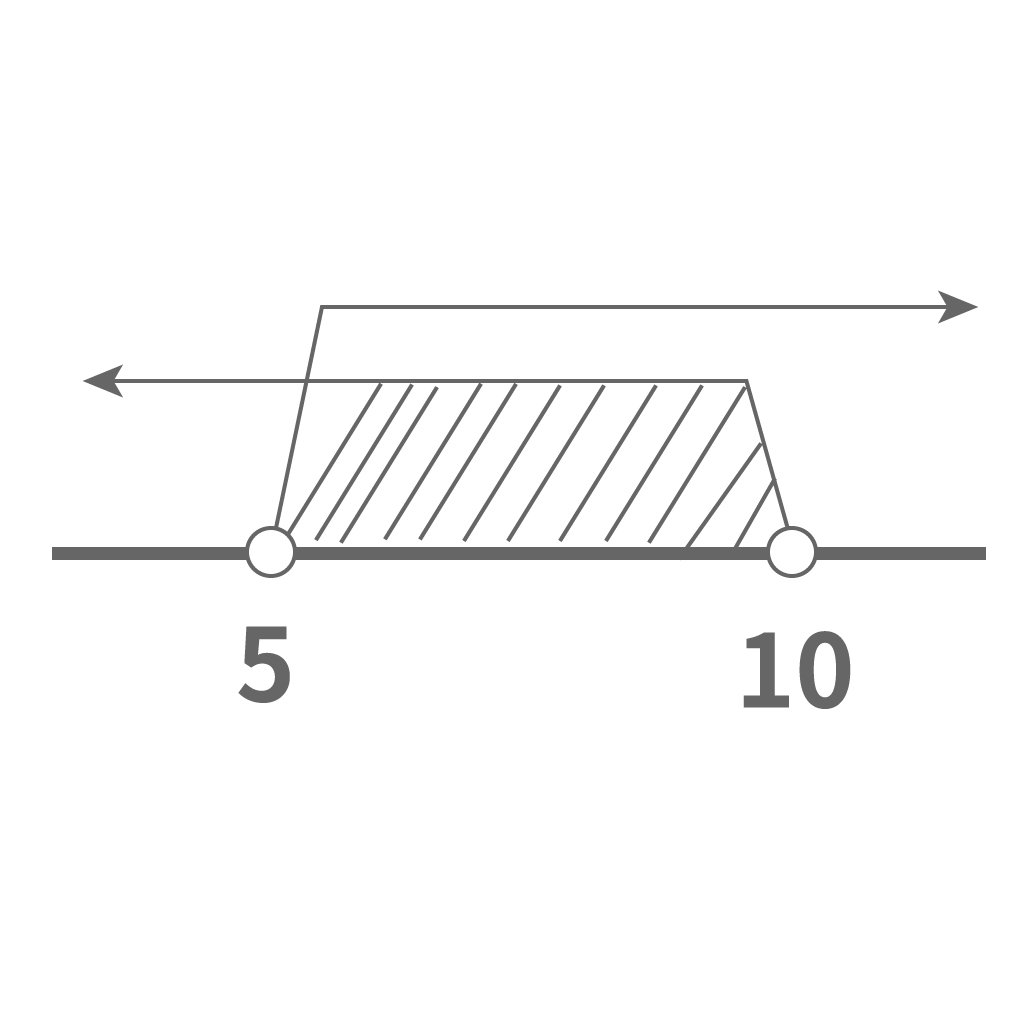
うん、つまり2つの不等式の共通範囲は次のようになる。
$$5<x<10$$
$x$はリンゴの個数だったな。
リンゴの個数は小数と分数とかでもない、正の整数だ。
つまり、リンゴの個数は6〜9個のいずれかでオッケーってわけだ。
こんな感じで、連立不等式の文章題だろうが、文章題攻略の基本は変わらねえ。
「求めたいものを文字でおく」という基本さえ間違えなければ、こっちのもんさ。

それじゃあな!



