一次方程式の文章題で速さの問題がムズイ！
こんにちは！この記事を書いているKenだよ。洗った、ね。
一次方程式の文章題にはいろんなパターンがあるけど、中でも出やすいのが、
速さ・道のりの文章問題。
例えば、次のようなやつだ↓
AさんはBさんの家を出発して自宅に向かいました。Aさんの忘れ物に気づいたBさんは、Aさんが出発してから10分後に自転車で追いかけました。Aさんの歩く速さを60㍍、Bさんの自転車の速さを分速160㍍とするとBさんがAさんに追いつくのはAさんが出発してから何分後か？
よーく読んでみると、
「誰か」が「誰か」に追いついているよね？
例題では「Bさん」が「Aさん」に追いついちゃってるね。
この手の「追いつく系」の速さの文章問題は次の3ステップで解けるよ。
Step1. 求めたいものをXでおく
まずは方程式の文章問題のセオリー通り、
求めたいものを「x」と置こう。
この問題では、
BさんがAさんに追いつくのはAさんが出発してから何分後か
を求めたいから、その「BがＡに追いつく時間」をAが出発してからx 分後としようぜ。
Step2. 等しい関係を見つける
次は「等しい関係にあるもの」を探してみよう。
追いついちゃう系の問題では、何が等しいのかというと、
2人が移動した距離
だ。
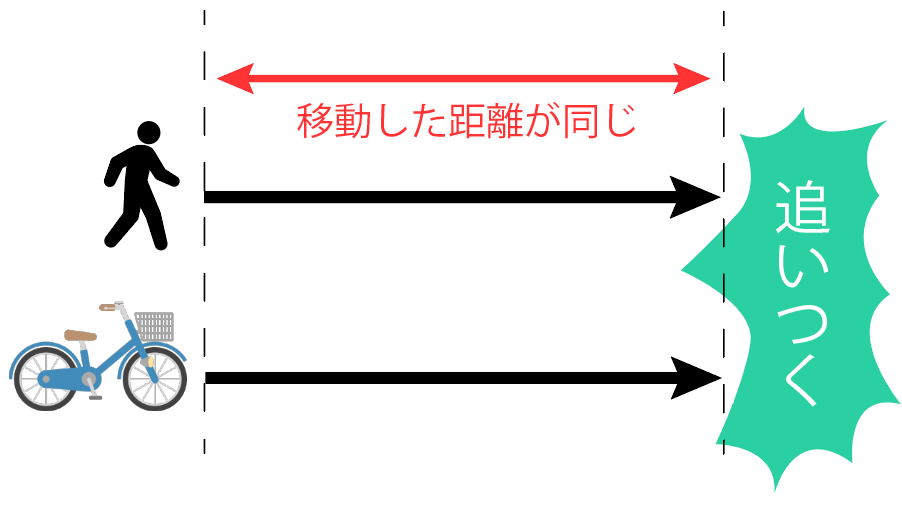
つまり、「追いつかれた人」と「追いついた人」が同じ距離移動しているはず。
例題だと、
（Aが移動した道のり）＝（Bが移動した道のり）
という等式が作れそうだ。
速さの公式を使うと「道のり」は、
速さ×時間
で計算できたね。
つまり今回の方程式は、
（Aが移動した道のり）＝（Bが移動した道のり）
（Aの速さ） ×（Aが移動した時間）＝（Bの速さ） ×（Bが移動した時間）
60 x ＝ 160 （x-10）
になる。
なぜ「Bの移動時間」が（x-10）なのかというと、BはAよりも10分後に出発しているからさ。
Aの移動時間x分から10分差し引かないといけないんだ。
Step3. 方程式を解く
あとは方程式を解くだけ。
60 x ＝ 160 （x-10）
ちょっと厄介なのが「かっこ」がついてるところかな。
「かっこ」が付いているなら分配法則で外してから解くといいよ。
実際に解くと、
60 x ＝ 160 （x-10）
60x = 160x – 1600
100x = 1600
x = 16
となる。
xは「Aが出発してから追いつかれるまでの時間」を表していたから、文章題の答えは、
16分だね。
こんな感じで、追い付く系の速さの文章題では、
「追いつかれた人」と「追いついた人」の移動した道のりが等しい
という方程式を作ればOK。
次は「移動手段を変える系の文章題」を解いていこう。
そんじゃねー
Ken
