方程式の文章問題には「早く着いちゃったパターン」がある？？
世界にはいろんな一次方程式の問題があるけど、やっぱり厄介なのが、
道のり・速さの文章問題だね。
これまで
を勉強してきたけど、もう一個、今日は文章問題にチャレンジしてみよう。
それは、
どっちかが早く着いちゃったパターン
だ。
例えば次のような問題 ↓
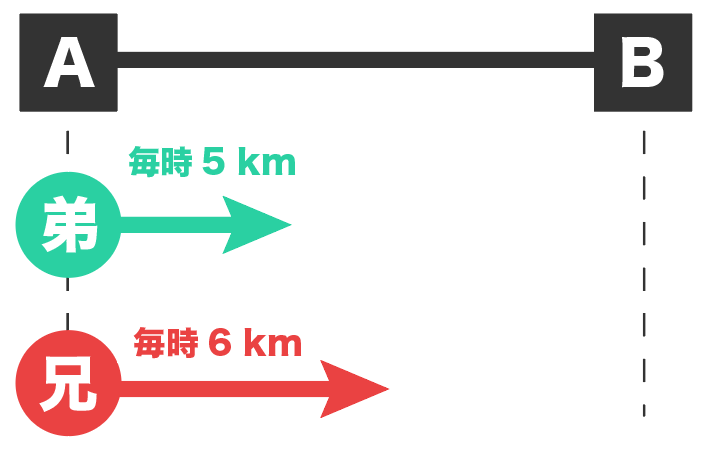
この文章題では、兄が弟よりも速く移動しちゃってるから、
兄が弟より14分早く到着している。
うん、これがまさしく「早く着いちゃった系の速さの文章題」だ。
早く着いちゃった道のり・速さの文章問題の解き方
3ステップを踏めば解けるはずだよ。
「求めたいもの」をXとおく
この問題でも「方程式の文章題の鉄板セオリー」が使えるね。
それは、
求めたいものをXとおく
だ。
例えば、例題では、
Ａ町からＢ町までの道のりを求めなさい
と言ってるよね？
だから「Ａ〜Ｂまでの道のり」を「x km」と置けばいいんだ。
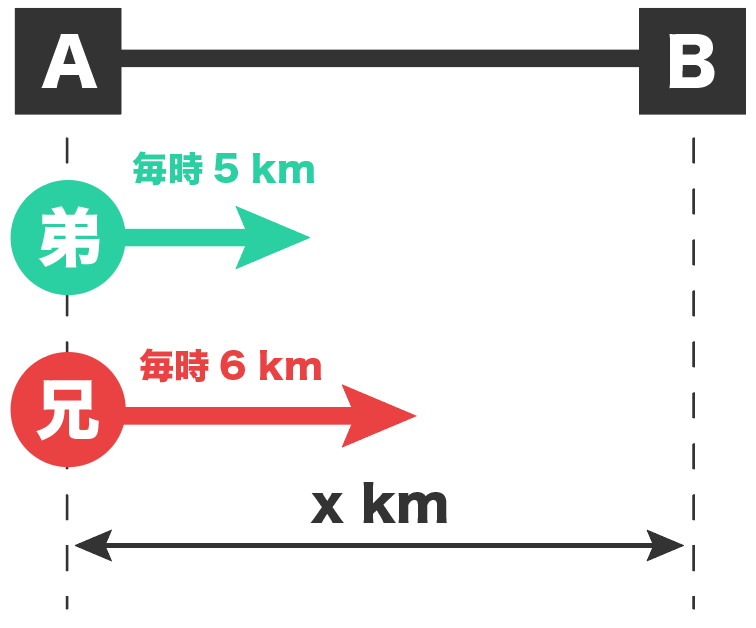
求められそうなやつを探す
ここで冷静になって、道のり・速さの公式を思い出そう。
速さの公式は、
（道のり）÷（速さ）＝ （移動にかかった時間）
だったよね。
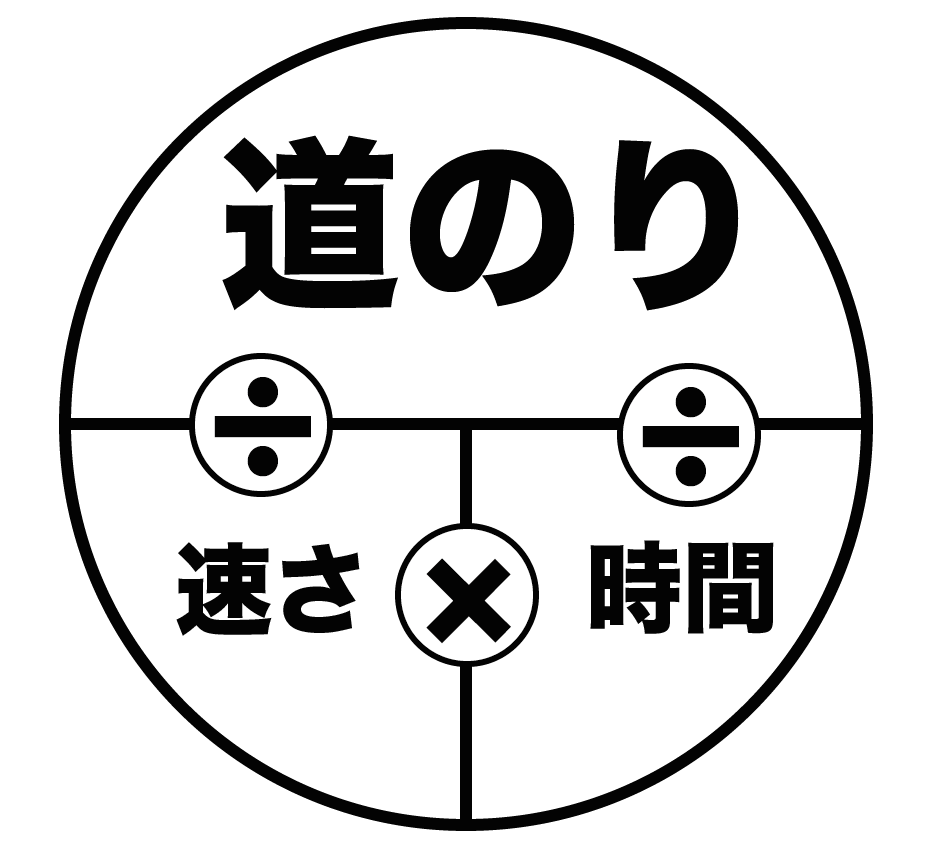
公式を使うと、何が求められそうか見てみよう。
文章題では、
兄と弟の速さ
が分かっていて、かつ、さっき「A〜Ｂの距離」を「x」にしたよね。
ということは、現段階で
- 道のり
- 速さ
がわかってるってこと。
この2つで「道のり・速さの公式」を使うと、
弟と兄が「AからＢまでの移動」にかかった時間
が計算できそうだ。
等式を作る
ということで、公式で計算できそうな「移動にかかった時間」で等式を作ってみよう。
が、しかし、だよ？
ここで問題がひとつ発生だ。
それは、
兄と弟の移動時間が等しくない
ってこと。
問題文には、
兄のほうが14分早く着きました
って書いてあるよね。
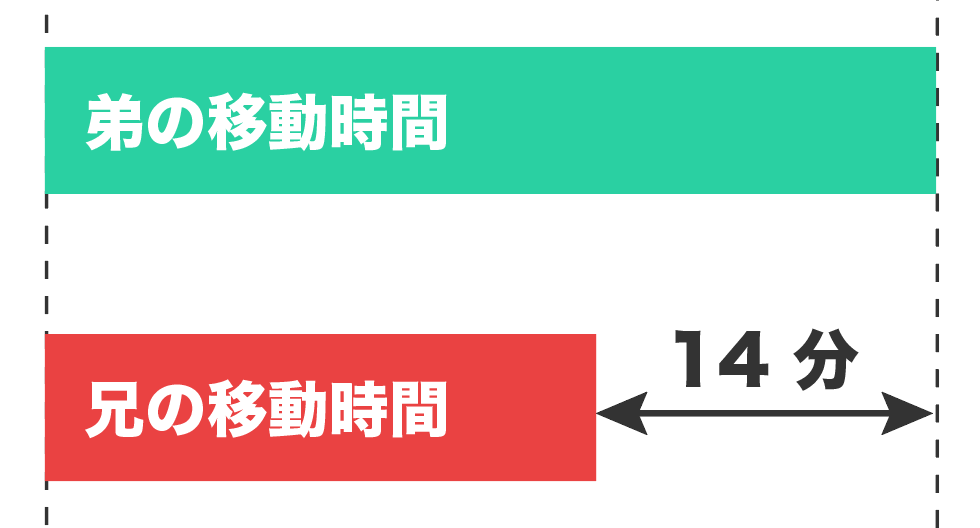
兄と弟のかかった時間を等しくさせるためには、
兄の時間に「早く着いて余った時間」を足せば「弟の移動時間」に等しくなるはず。
つまり、
（弟の移動時間）＝（兄の移動時間）＋（早く着いて余った時間）
という等式を作ればいいことになる。
速さの公式によると、
（道のり）÷（速さ）＝ （移動にかかった時間）
だったから「A〜Bまでの道のり」を「x km」とすると、
x ÷ 5 ＝ x ÷ 6 ＋14分
になる。
ただし、ここで注意したいのが「時間の単位」だ。
公式で求めた「x ÷ 5 」とか「x ÷ 6」とかの単位は「時間」。
なぜなら、道のりの単位は「km」で、速さの単位は「毎時km」だったからだね。
等式を成り立たせるためには、
「14分」の単位を「分」じゃなくて「時間」に直せばいいんだ。
そのために、14を60で割ればいいね。
ってことで、さっきの等式は
（A〜Ｂの道のり）÷（弟の速さ）＝（A〜Ｂの道のり）÷（兄の速さ）＋14分
x ÷ 5 ＝ x ÷ 6 ＋14÷ 60
5分のx = 6分のx + 60分の14
になる。
方程式を解く
あとは解くだけ。
5分のx = 6分のx + 60分の14
は「分数を含む方程式」。
分母の最小公倍数を両辺にかけて分数を消せばいいね。
今回の方程式では、
- 5
- 6
- 60
という3つの分母で、こいつらの最小公倍数は60。
ってことで、両辺に60をかけてみよう。
すると、
5分のx = 6分のx + 60分の14
12x = 10x + 14
2x = 14
x = 7
となる。
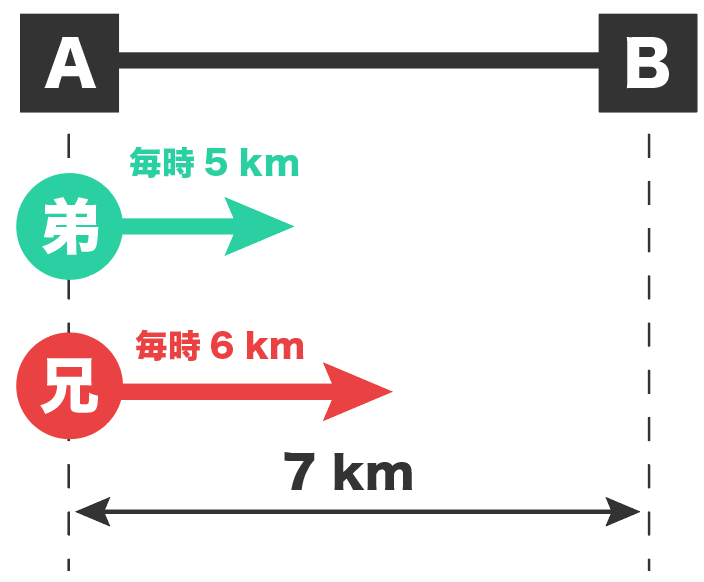
xは「ＡからＢまでの道のり」としていたから、
ＡからＢは 7 km 離れている、とわかったね。
こんな感じで、「どっちかが早く着いちゃった文章題」でもやることは一緒。
- 求めたいものを文字で置く
- 方程式を作る
- 解く
でいいんだ。
テストに出やすいからよーく復習しておこう。
そんじゃねー
Ken
