こんにちは!この記事をかいてるKenだよ。ダーツ、始めたね。
中学理科の「身のまわりの現象」では、
とかを勉強してきたけど、もう1つ勉強する現象があるんだ。
それは、
力
だ。

でも「力」と言ってもイマイチピンとこないよね?
感覚的にはわかってはいるけど、実際に力が何か説明しろって言われてると困る。
今日はこの記事で、
「一体、力にはどういうはたらきがあるのか?」
をみていくことで、力の正体を掴んでいこう。
中学理科で勉強する力のはたらきには、次の3つのものがあるよ。
今回は、この「力のはたらき」をカラーボールを使って解説していこう。

まずは、力のはたらきのうち、
物体の形を変える
ってやつだ。
カラーボールをムギュッと握るシーンを想像してほしい。
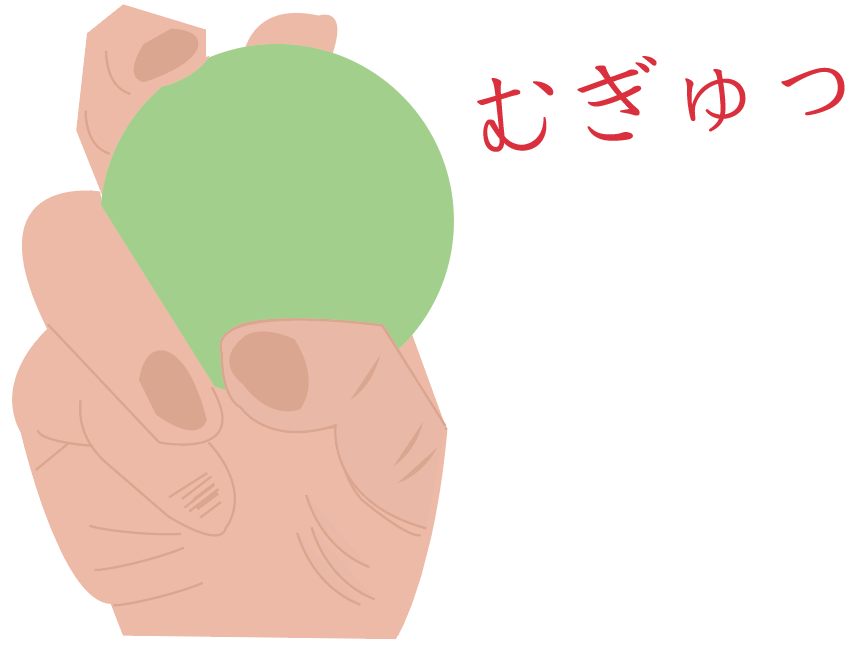
このように握力全開でカラーボールを握ってみると、カラーボールがへこむよね?
ちょうど指のあたりに食い込む感じで。
この時、カラーボールの形に注目すると、元の形から変形してしまってると思うんだ。

こんな感じで「力を及ぼしたものの形を変形させる」というはたらきが力にはあるよ。
次は、
物体の運動の状態を変える
っていう力のはたらきだ。
物体の運動の状態を変えるとは、
静止している物体を動かしたり、動いてる物体を止めること
だね。
またまたカラーボールを想像してくれ。
完全にとまっているカラーボールがあるとしよう。

こいつを少し蹴ってみる。

すると、蹴った方向に動き出すよね?
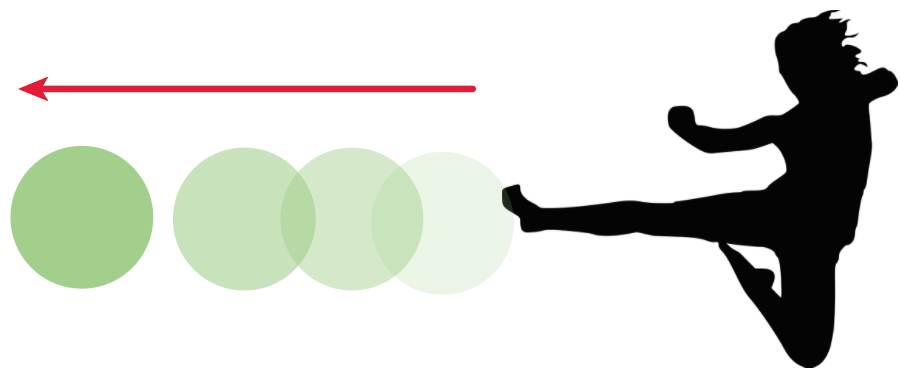
つまり、力を加えたことにより、ボールの運動の状態が、
静止→動く
というように変化しているんだ。
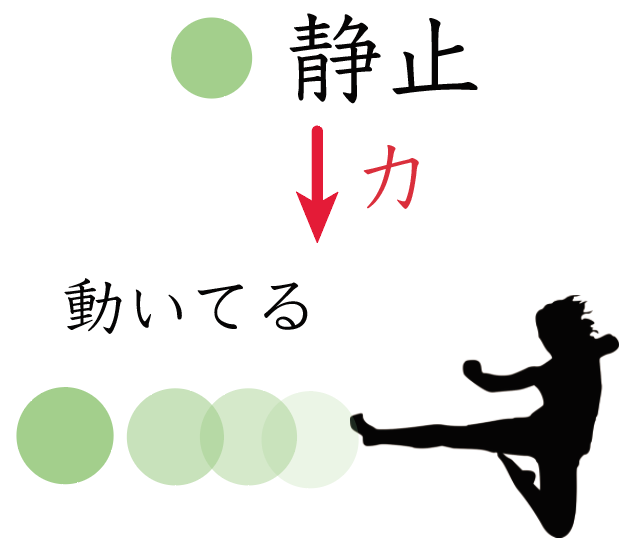
これが力のはたらきの2つ目の「物体の運動の状態を変える」ってやつね。
最後の力のはたらきは、
物体を支える
ってやつだ。
これは文字どおり、どういうことかいうと、力を使うことで何かなんでもいいから支えるってわけだ。
例えばさっきのカラーボール。
こいつを手のひらにひょこっと載せてみよう。
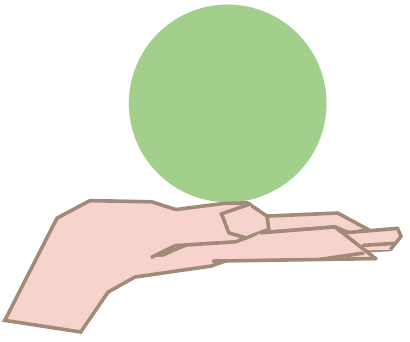
うまく載せてやればカラーボールは手の上で静止するはずだ。君の手は、カラーボールを支えてることになる。
もし、手をうっかり放してしまえば、カラーボールは地面に落下していき痛い思いをするだろう。
こんな感じで、力を働かせることでとある物体を支えることもできるんだ。
以上が中学理科で勉強する力のはたらきだよ。
この3つさえ覚えておけば問題ないね。
力のはたらきを覚えると、力の正体がうっすらとわかってくるはずだ。
次は中学理科で勉強する「力の種類」を勉強していこう。
そんじゃねー
Ken
こんにちは!この記事を書いてるKenだよ。眠眠、打破したいね。
中1理科の音の世界でよく出てくるのは、
花火の打ち上げ地点までの距離を計算する問題だ。
たとえば、次のような問題だね。
ある日、花火を鑑賞していたら、花火が光ってから、「ドン」というと効果音が5秒後に聞こえました。さて、花火の打ち上げ地点までの距離を計算してください。ただし、音の速さは毎秒340mとする。

この花火の問題をクリアするには、次の4つの基本と、1つの解き方を押さえておけば大丈夫。
まずは花火問題の基本中の基本だ。
簡単に言ってしまうと、花火というやつは、
の2つの要素にわけられるんだ。

そして、花火の光と音の速さに注目してみると、
花火の光は、音よりものすごく速い。
どれくらい光が速いのかというと、1秒で地球を7.5周するほどなんだ。

一方、音はそれほど速くなくて、
1秒で東京タワーのてっぺんまで登れるぐらいだね。

音もウサインボルトと比較するとなかなかはやいけど、やはり、世界を7.5周もする光とは比べ物にならないほど遅いんだ。
ってことで、花火の光は一瞬で、みんなの目に到達するんだけど、音はちょっと時間がかかる。
だから、
花火が光ってから音がするまでの時間、音が進んだ距離
が花火打ち上げ地点までの距離になってくるんだ。
それじゃあ、さっきの例題を解いてみよう。
ある日、花火を鑑賞していたら、花火が光ってから、「ドン」というと効果音が5秒後に聞こえました。さて、花火の打ち上げ地点までの距離を計算してください。ただし、音の速さは毎秒340mとする。

次の計算式を使えば一発で花火の打ち上げ地点までの距離を計算できるよ。
(花火が光ってから音が聞こえるまでの時間)x(音の速さ)
なぜなら、光は一瞬で目に到達するけど、音はちょっと遅くて、光と音には時差があるからね。
その時差に音の速さをかけて、音が進んできた道のりを計算しようという魂胆さ。
今回の例題では、
だったよね??
これらのデータから、花火の打ち上げ地点までの距離を計算してやると、
になる。
つまり、花火はその観測者が立っている地点から1700m(1.7km)離れてるってわけ。
花火の距離の問題は案外テストに出てきやすいから、よーく復習しておこう。
また、花火の距離の問題と似ているのが雷の距離を求める問題。
計算の仕方は全くと言っていいほど同じだから雷の問題も解いてみてね。
そんじゃねー
Ken
こんにちは!この記事を書いてるKenだよ。メープルが攻めてくるね。
中1理科の「身のまわりの現象」という単元では、
「音」についても勉強して行くよね?
その中でも、問題として取り上げられやすいのが、
雷までの距離を求める問題だ。
たとえば、次のような感じ↓
雷が光ってから4秒後にゴロゴロという音がなりました。音の速さを毎秒340mとするとき、雷が落ちた地点までの距離を計算しなさい。

この手の雷問題は、
4つの基本
と
1つの計算手順
で簡単にクリアできちゃうんだ。
まずは雷の基礎から勉強していこう。
雷までの距離を求める問題では、次の4つのことをおさえておけばいいね。
まず、雷の正体が何者かってことだ。
この距離を求める問題では、
雷は、
っていう2つからできていると考えていいよ。

音と光だけだから、何もビビることはないね。
雷の要素の1つの光。
1つおぼえておいて欲しいのが、
光の速さはむちゃくちゃ速い
ってこと。

数字にすると、1秒間に30万キロメートルも進んでしまうほど速いんだ。
想像しやすいように地球規模で考えてみると、光は1秒間に地球を7.5周もしてしまうほど速い。

もう、異次元すぎて、光が体育祭に出ちゃったら新記録を叩き出しまくるだろうよ。
ただ、もう1つの雷の音は、光に比べるとちと遅い。
気温とかにもよるんだけど、音の速さは約、
毎秒340m
なんだ。
340mっていうと、だいたい東京タワーの麓からタワーのてっぺんまでの距離だね。

音は1秒間でこれだけの距離を進むんだ。
人間たちと比べると速い方なんだけど、どうしても光と比べると遅く感じちゃうね。あっちは地球7.5周だもの。
ってことで、雷の光はむちゃくちゃ速いから、雷がどんなに離れていようが、
雷が発生した瞬間に光が、ぼくらの目に到達するんだ。
そこには時差はないと考えていい。
ただ、雷の音はちょっと違う。
一瞬で耳に到達するほど圧倒的に早くないから、雷の光よりも遅れて耳に入るんだ。
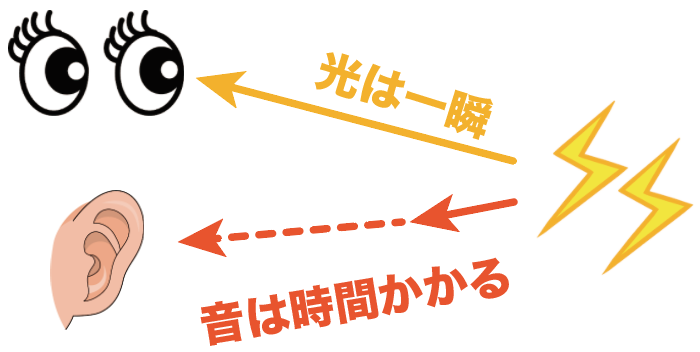
だから、雷の光が見えた瞬間から、雷の音が耳に届くまでの時間、音が頑張ってこっちに向かってくるわけだ。
さて、ここまでで雷の問題の基礎は終わり。
せっかくだから雷の距離の求め方の問題を解いていこう。
雷が光ってから4秒後にゴロゴロという音がなりました。音の速さを毎秒340mとするとき、雷が落ちた地点までの距離を計算しなさい。
この手問題の解き方は簡単。
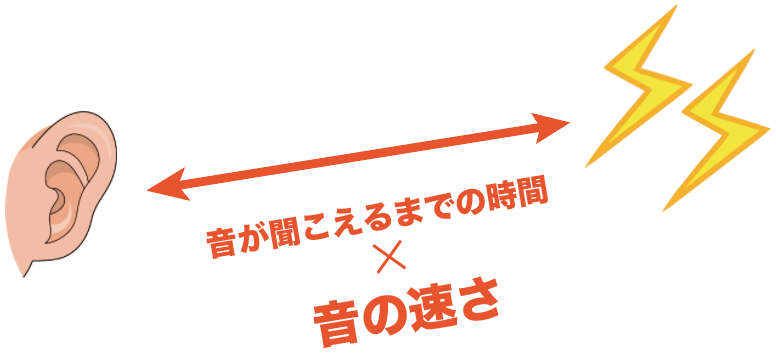
雷が光ってから音が到達するまでの時間に、音の速さをかければいいんだ。
公式っぽく表すと、
(雷までの距離)=(光ってから音がなるまでの時間)x(音の速さ)
だ。
なぜなら、雷の光は一瞬で目に到達するけど、雷の音はちょっと遅れて音の速さで耳にやってくるからなんだ。
つまり、音が移動した距離だけ観測者と雷が離れているってことがわかるのさ。
今回の問題でいうと、光ってから4秒後に雷の音が聞こえたよね??
今回は音の速さを毎秒340mとしてるから雷までの距離は、
340 x 4 = 1360 m
になるね。
計算簡単!
こんな感じで、雷までの距離を求める問題が出ても落ち着いて基本を整理して、計算問題をクリアしていこう!
そんじゃねー
Ken
こんにちは!この記事を書いているKenだよ。オレンジで補給してるね。
中1理科の身のまわりの世界では、
音
についても勉強していくよ。
その中でも重要なキーワードとなってくるのが、
っていう5つの用語だ。
今日は中学理科で勉強する音の世界を完全制覇するために、音の基礎となるこれらの用語を勉強していこう。
まずは、
っていう2つの用語から見ていこう。
音源とは、
音を発している物体のことだ。

「発音体」は音源の別名で、2つの言葉は同じものを指しているよ。
食料と食べ物の関係に近いかな。
んで、この音源・発音体は、音を出すときに、
必ず振動しているっていうことが重要だ。
たとえば、タンバリンを思い浮かべてほしい。
このタンバリンの音源はこのベルみたいな鈴だ。
タンバリンを鳴らしたときのこのベル部分を拡大してみると、こんな感じで振動しているってわけ。
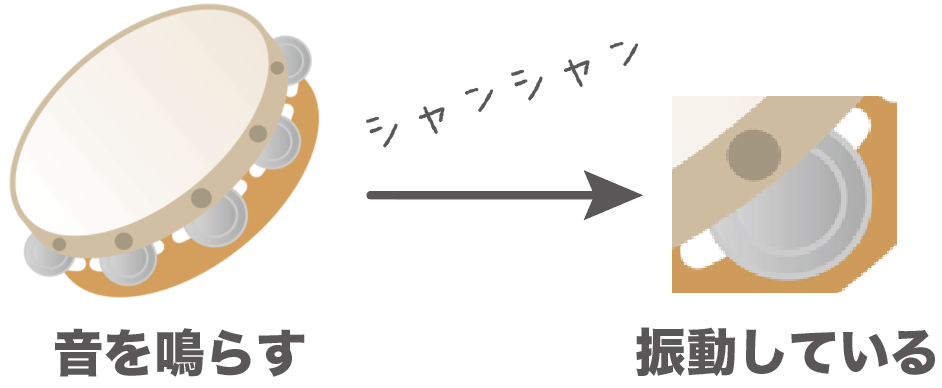
もし、このベル部分を手で押さえつけて振動しないようにしちゃうと、タンバリンが音を発しなくなっちゃうんだ。
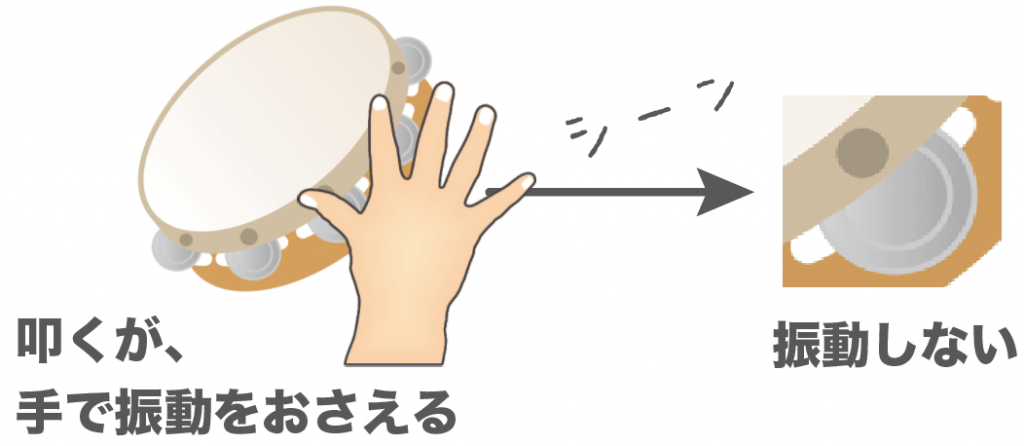
なぜなら、ベルの振動を手で止めてしまったからね。
こんな感じで、音源とは音を発する物体なんだけど、それと同時に、音を出すときは振動しているってことを頭に置いておいてくれ。
続いては、振幅(しんぷく)だ。
振幅とは、
振動の中心からの距離のこと
なんだ。
振幅が大きいほど振動の波の大きさが大きくなって、大きな音になるんだ。
たとえば、タンバリンのベル部分が次のように振動していたとしよう。
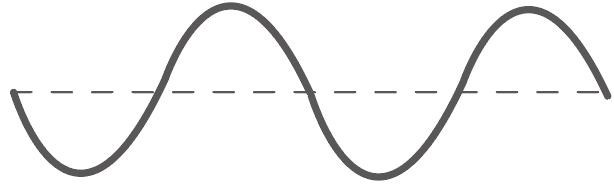
このとき、振動の中心からの距離のこの部分が振幅だ。
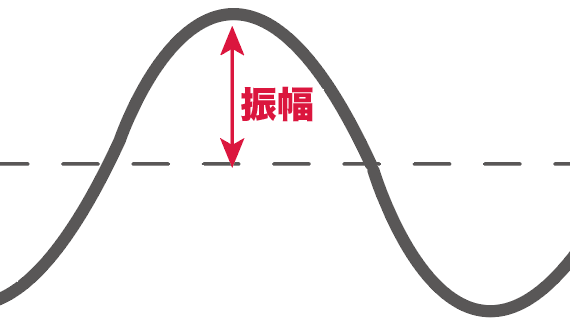
振動の中心から山のてっぺんまでの長さと覚えておけばいいね。
音の振幅は「音の大きさ」をあらわしているから、
振幅が大きくなればなるほど大きい音になるし、
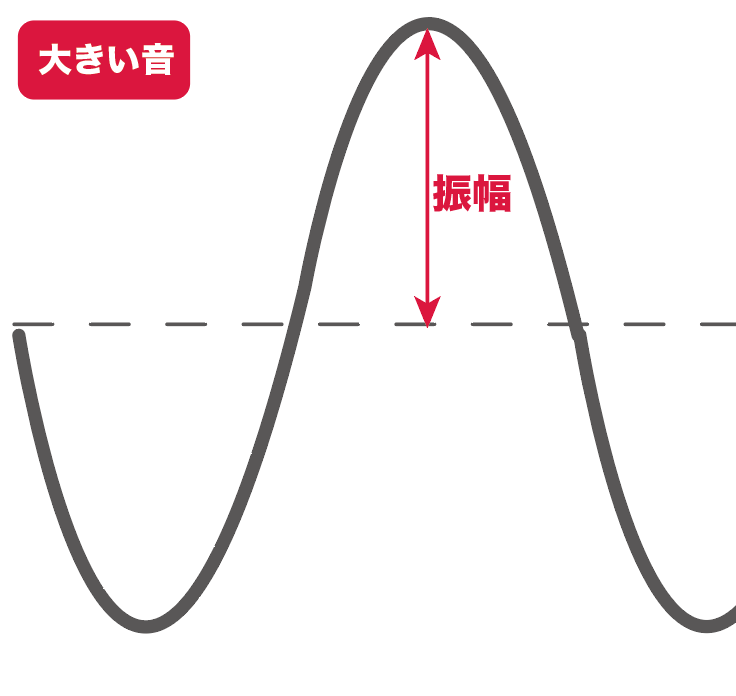
逆に振幅が小さければ小さいほど小さい音になるってわけ。
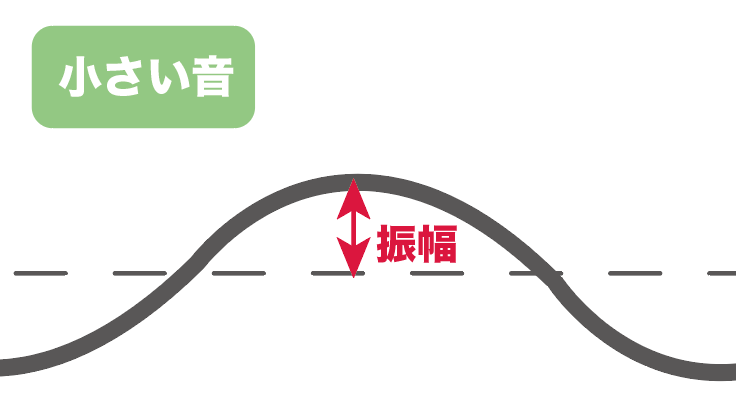
次は振動数(しんどうすう)だ。
振動数は、
音源が1秒間に振動する回数のこと
なんだ。
たとえば、タンバリンの振動が1秒間にこんな感じで振動していたとしよう。
このとき、2回同じ振動を繰り返してるから、振動数は2ってことさ。
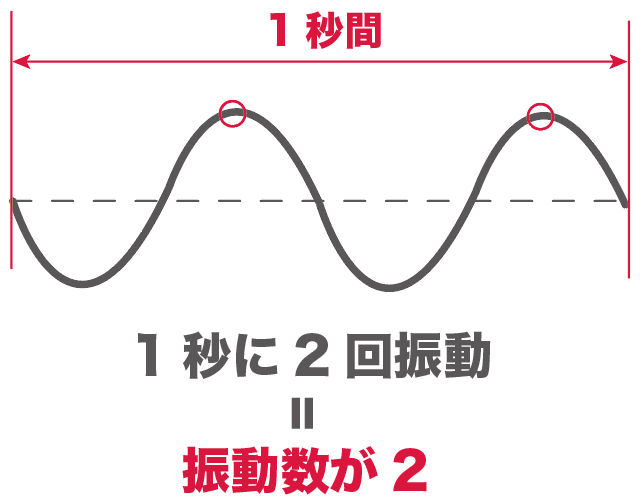
この振動数が大きくなればなるほど、音が高くなって、
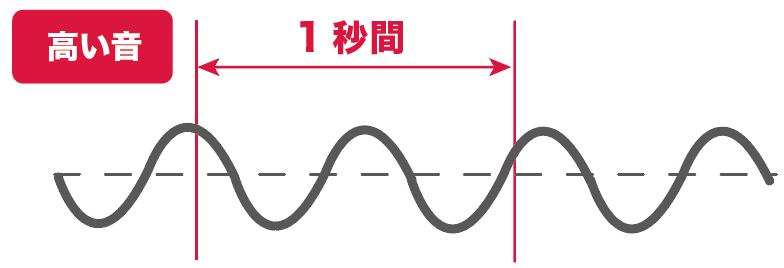
小さくなればなるほど音が低くなるわけね。
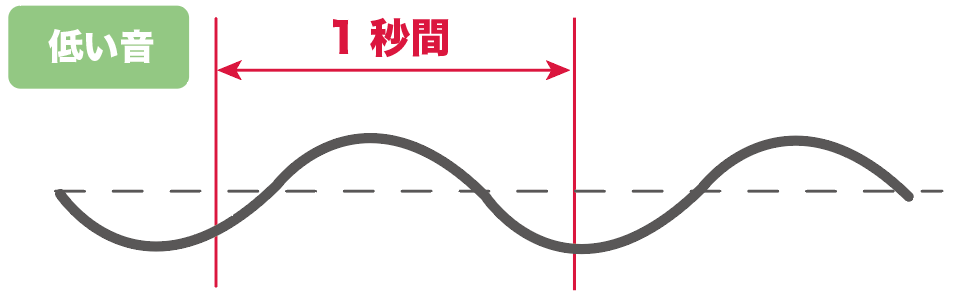
振動を山に例えるなら、1秒間あたりの振動数は山の数だ。
山の数が増えれば増えるほど振動数は大きいことになる。
じゃあ、「ヘルツ」って何かっていうと、
振動数の単位のことだ。
つまり、さっきのタンバリンが1秒間に2回振動していたら、
このタンバリンの振動数は「2ヘルツ」ってことになるのね。
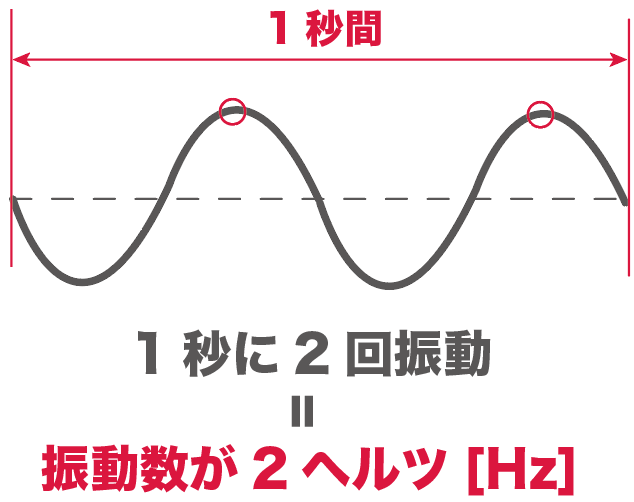
ちなみに、この「ヘルツ」っていう単位を英文字で表してやると、
Hz
になるよ。
ヘルツ=Hz
ってわけね。
以上が、「音源・発音体・振幅・振動数・ヘルツ」だよ。
最後に復習しておこう。
音源とは、音を発する物体のことで、音を出すときには振動していて、

別名を発音体ともいう。
音源が振動しているとき、振動の中心からの幅のことを「振幅」って言って、音の大きさをあらわしているね。

1秒間あたりに振動する回数を振動数っていって(単位はヘルツ)、振動数が大きければ大きいほど高い音になる。

音の基本をマスターしたら花火の距離を計算する問題に挑戦してみてね。
そんじゃねー
Ken
こんにちは!この記事を書いているKenだよ。風で乾かしたね。
中学理科では凸レンズについて詳しく勉強してきたよね??
時々、凸レンズに関する問題で、
焦点距離を求める問題
っていうのが出題されるんだ。
高校物理になると、焦点距離を求められる公式を習うんだけど、中学理科では範囲外だから勉強しない。
じゃあ、一体、中学理科ではどうやって凸レンズの焦点距離を求めたらいいんだろうね??
中学理科では主に次の2つのパターンの焦点距離を求める問題が出題されるよ。
早速、それぞれ解き方を見ていこう。
まずは、凸レンズでできる実像が物体と同じ大きさになってる問題。
たとえば、次のような感じ。
りんごを凸レンズから50cmの位置に置いたら、このりんごと同じサイズの実像ができた。じゃあ、この凸レンズの焦点距離はいくつですか??
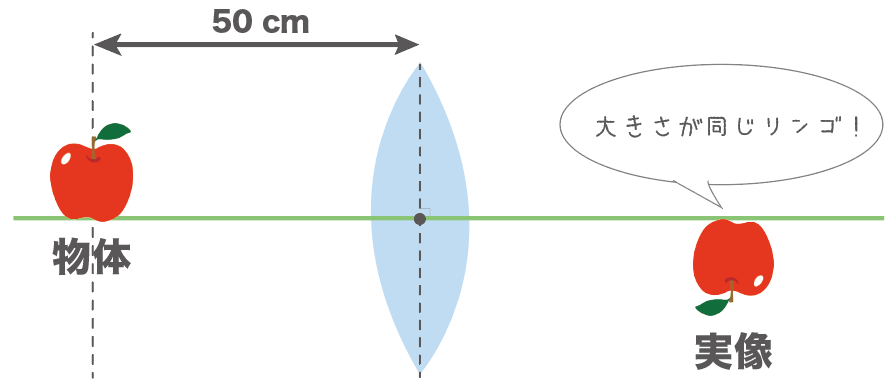
っていう問題だ。
このタイプの問題は、
焦点距離がちょうど2倍になる位置に物体を置くと、実像が物体と同じ大きさになる
っていう実像と焦点距離のルールを使ってあげれば解けるはず。
今回は、凸レンズから50cmの位置にりんごを置いてあげたよね??
実像がちょうど同じ大きさになってるから、この50cmの地点は「焦点距離の2倍の位置」だ。
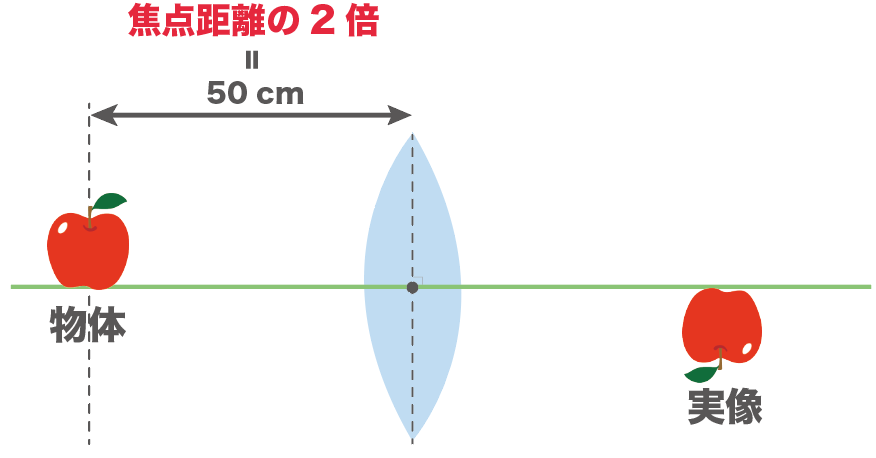
50cmで焦点距離の2倍の位置ってことは、焦点距離はその半分。
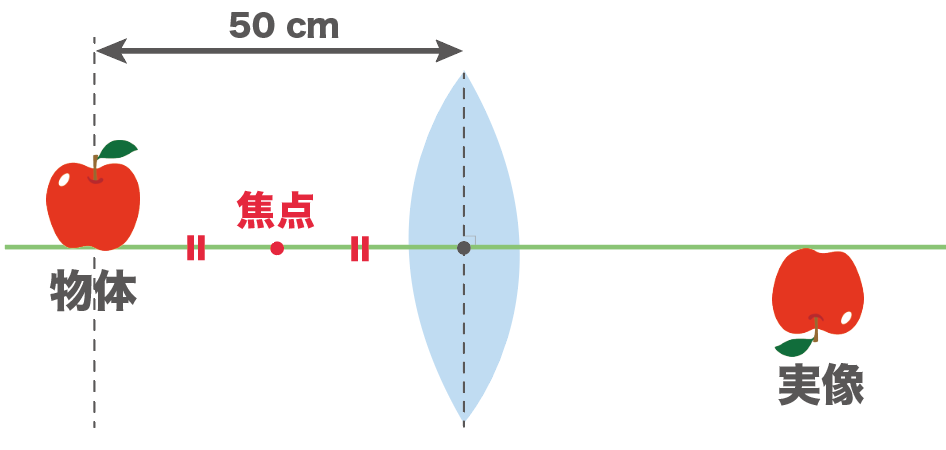
つまり、
25cm
が焦点距離ってわけ。
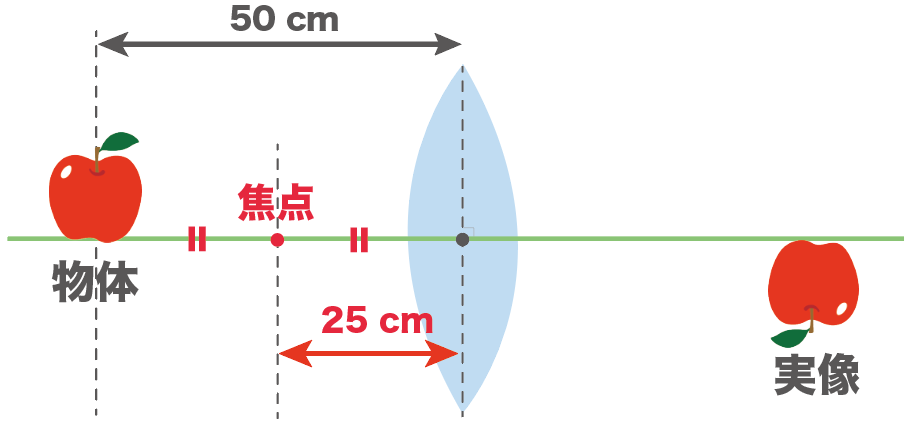
この手の問題では、物体を置いた位置の凸レンズからの距離をちょうど半分にしてやればいいのね。
続いて、
というパターンの問題だ。
たとえば、次の練習問題を解いてみよう。
りんごを凸レンズの前に置いてあげたら、スクリーンにくっきりと実像がうつった。さて、この凸レンズの焦点距離はいくつ??
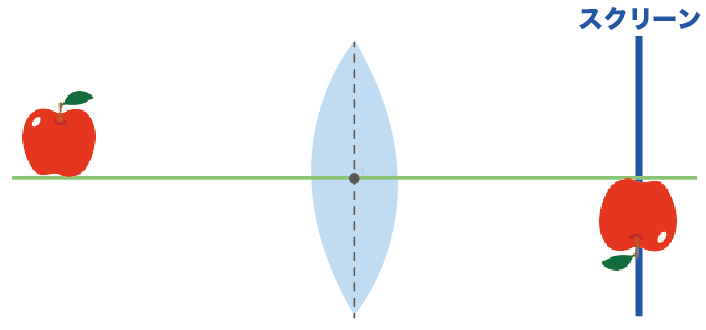
この手の問題は、次の3ステップで解いてみよう。
まずは、物体から出ている光のうち、凸レンズの中心を通る光をかいてあげよう。
スクリーンにぶつかるまで伸ばしてね。
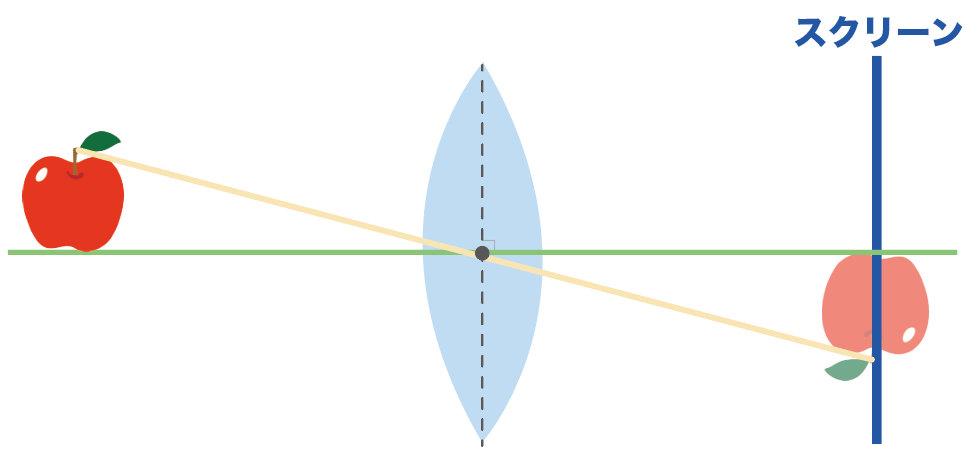
凸レンズの軸に平行な光の道筋をかいてあげよう。
軸に平行な光は、凸レンズを通過すると、凸レンズの焦点を通るんだったね??
んで、今回の問題では、ちょうどスクリーンの位置でくっきりとした実像ができてるんだ。
ってことは、凸レンズを通る平行な光は屈折して、さっきかいた凸レンズの中心を通る光とスクリーンが交わっている点を通るはず。
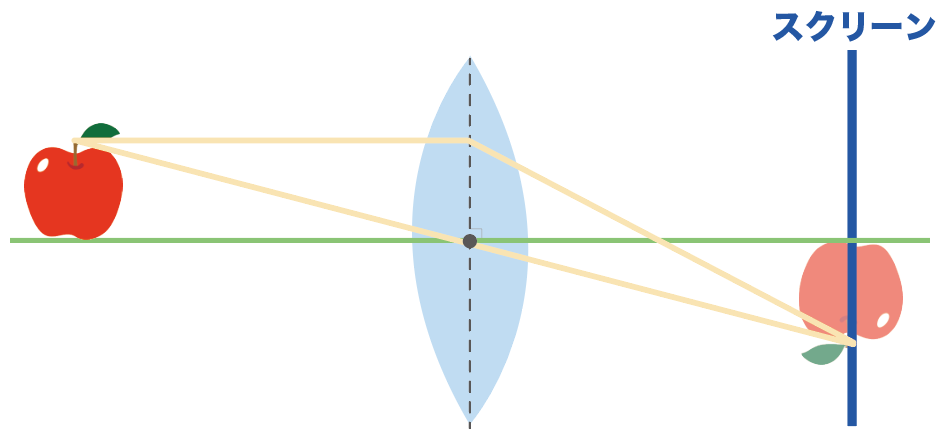
あとはもうね、力技。
さっきかいた凸レンズの軸と平行な光と、凸レンズの軸の交点が焦点になるはず。
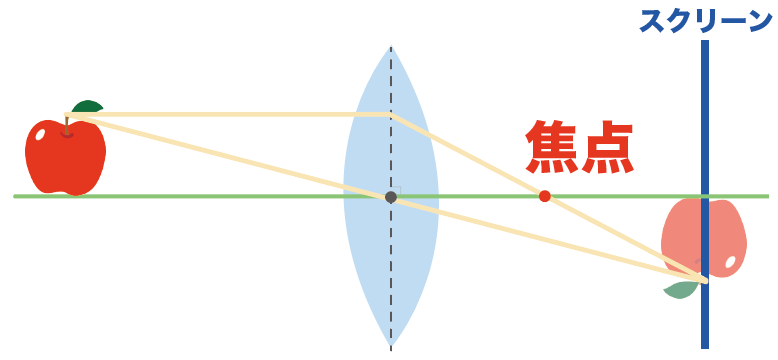
だから、この交点から、凸レンズまでの距離を定規かなんかで距離を測ってあげればいい。
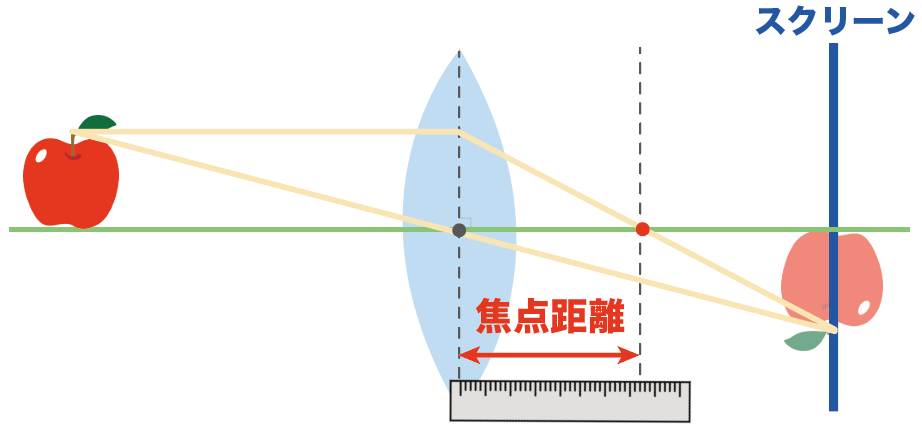
問題でマス目があるときは、マス目を使えばよしだ。
さっきのリンゴの問題では、焦点距離を定規で測ってみるとちょうど10cmだったよ。
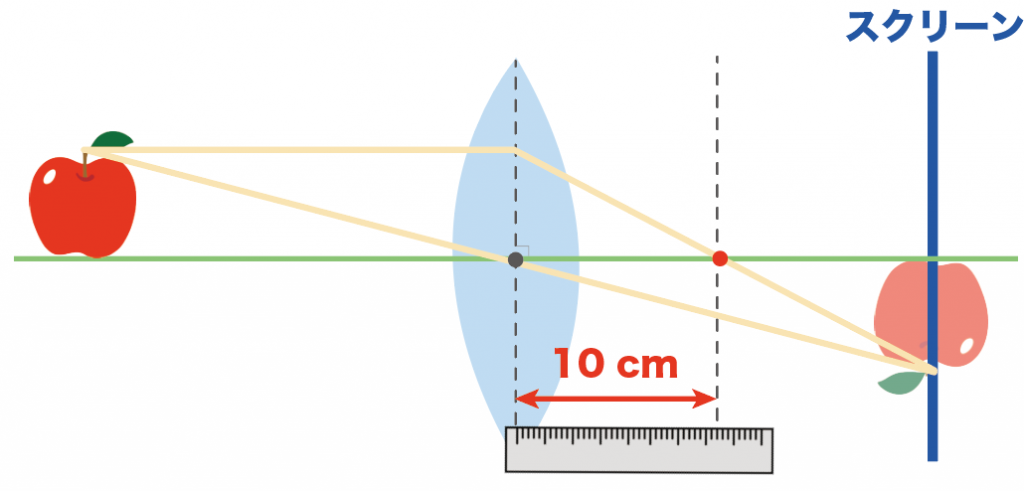
ってことで答えはこの凸レンズの焦点距離は10cmだ。
以上が凸レンズの焦点距離の求め方だったね。
焦点距離の求め方の公式は高校物理じゃないと勉強しないけど、怖がらなくて大丈夫。
の2種類の問題の解き方さえマスターしておけばこっちのもの。
テスト前によーく復習しておこう。
そんじゃねー
Ken
こんにちは!この記事を書いているKenだよ。椅子、チェンジしたね。
中1理科の光の世界っていう単元では、
凸レンズについて詳しく勉強していくよね??
中でもテストに狙われやすいのが、
凸レンズに見える虚像の作図問題だ。
凸レンズの実像の作図問題は前回マスターしたから、あとは虚像の問題さえ解ければ完璧だ。テストの点数は上がるし、クラスでは、たぶん、モテる。
そこで今日は、この凸レンズの虚像に関する作図問題の解き方をわかりやすく復習していこう。
まずは、虚像の作図問題を解く前に、
凸レンズに見える虚像とはなにか??
ということを復習して行こう。
虚像について理解するには、次の3つのことを押さえておけば大丈夫。
まずは凸レンズに虚像が見える条件。
虚像を見たい物体を、
凸レンズと焦点の間に置かないといけないんだ。
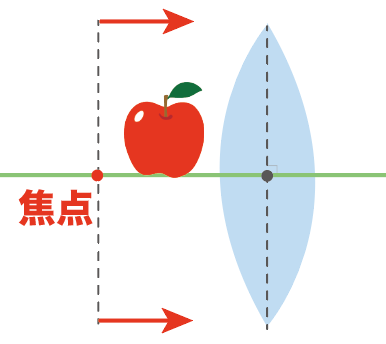
すると、どうだろう??
焦点よりも外側に物体を置いていたときにうつっていた実像が見えなくなっちゃったね。
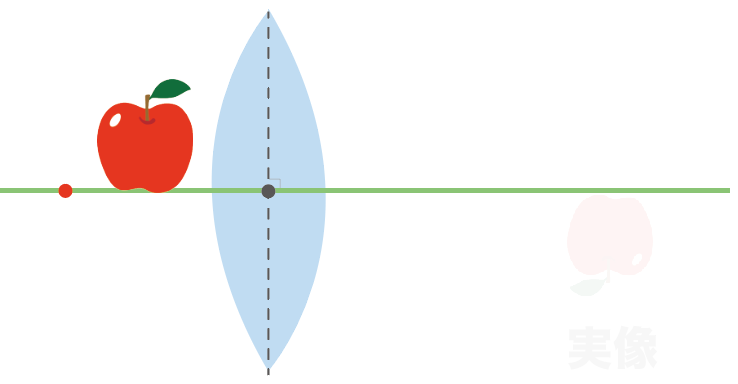
ど、どこ行った!?
「あれ、実像どこ行ったんだろうな・・・・」
と意気消沈しながら凸レンズを物体とは逆側からのぞいて見ると、
物体よりも大きな、上下左右反転していない像
が見えるはずだ。
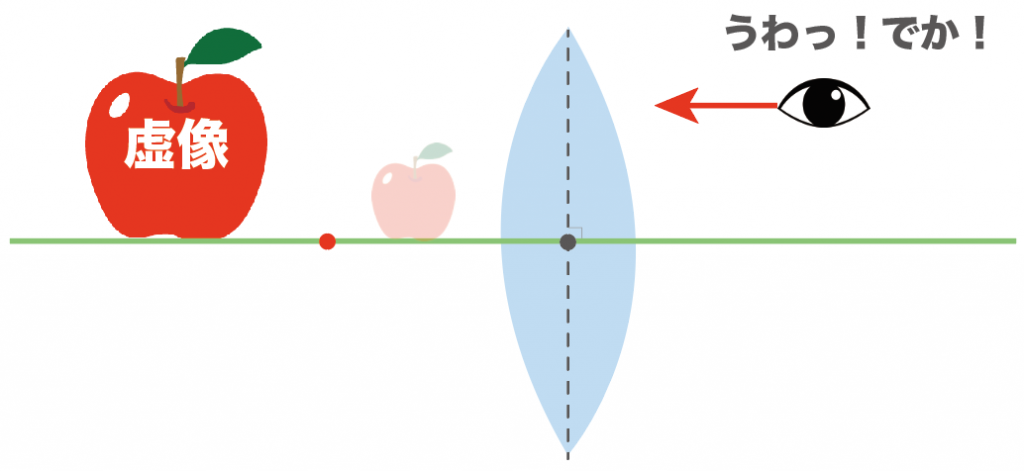
この像のことを、
虚像(きょぞう)
と呼んでいるんだ。
お次は、凸レンズに見える虚像を作図する問題を一緒に解いていこう。
矢印みたいな物体が、凸レンズの焦点よりも内側に置いてあります。このとき、凸レンズを通して見える虚像を作図しなさい。
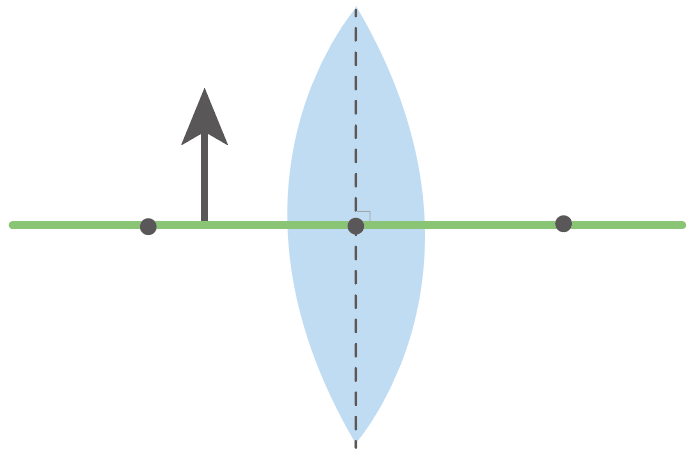
この手の問題は、次の4ステップで解けちゃうよ。
まずは、物体から出る光のうち、凸レンズの軸に平行な光の道筋をかいてあげよう。
凸レンズの光の進み方のルールでは、
凸レンズの軸に平行な光は、逆側の焦点を通る
だったね??
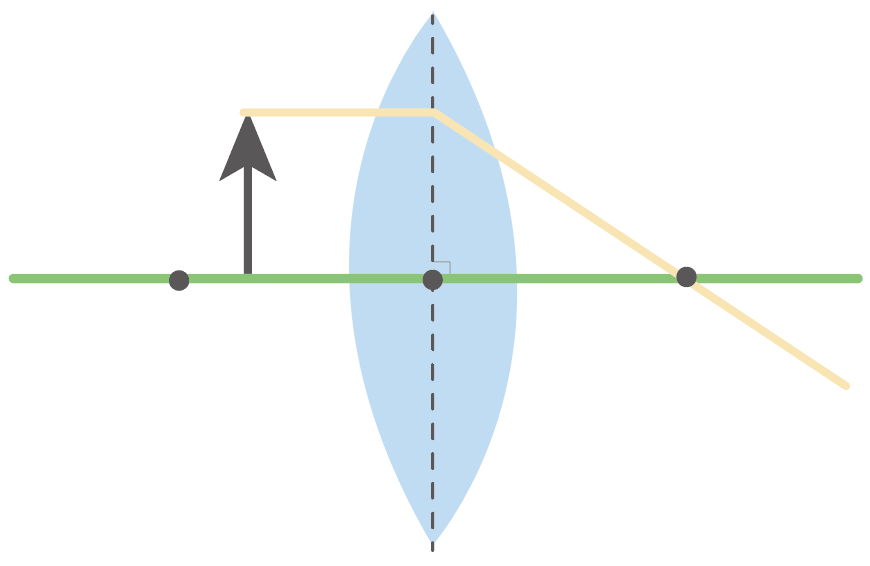
次は、凸レンズの中心を通る光。
凸レンズの光の進み方によると、レンズの中心を通る光は、
そのまままっすぐ進むんだったね??
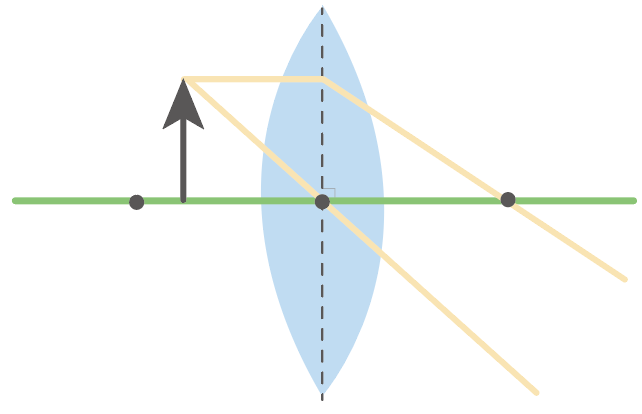
あとは、2つかいてみた光の道筋を延長してやるんだ。
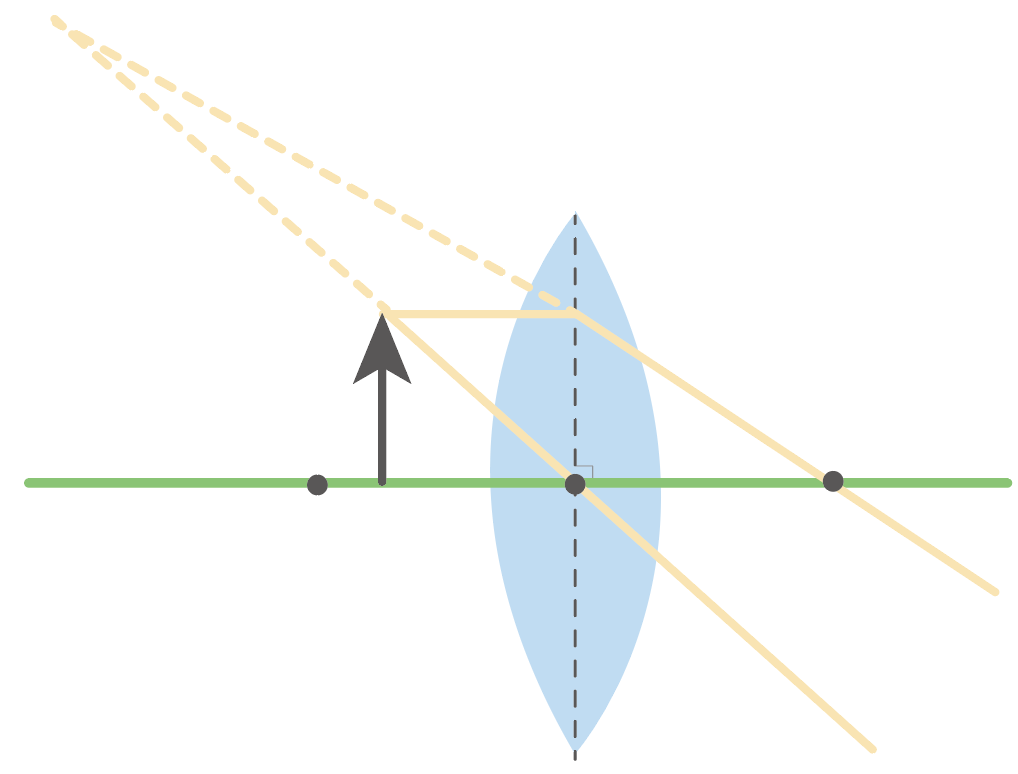
すると、たぶん、どこかで2つの光の道筋が交わるはず。
2つの光の交点が見つかったかな??
ここに、光の道筋がスタートしているパーツをかいてあげよう。
例でいうと、矢印の頭だね。
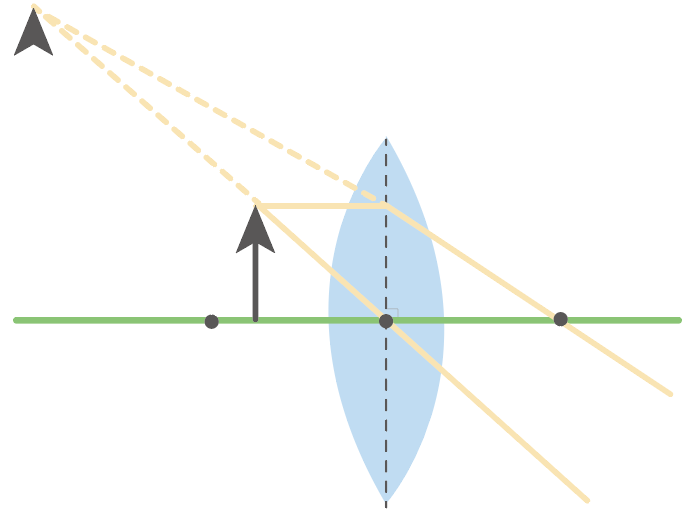
矢印の頭の位置が確定したら、そのまま矢印の足を下に下ろして、矢印を完成させてやろう。
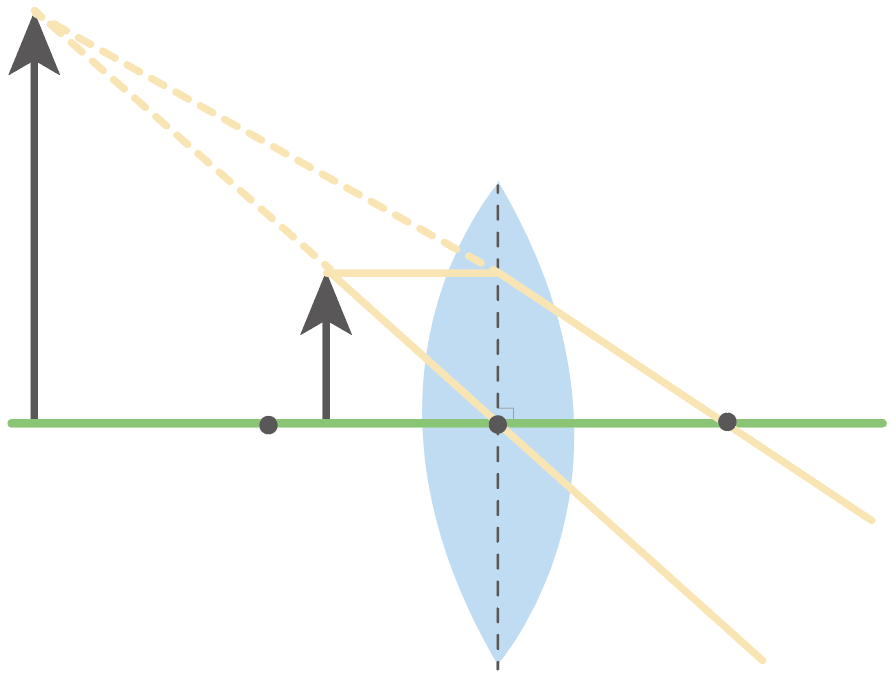
これで作図完了だ!
虚像が元の物体よりも大きくなっていればオッケー。
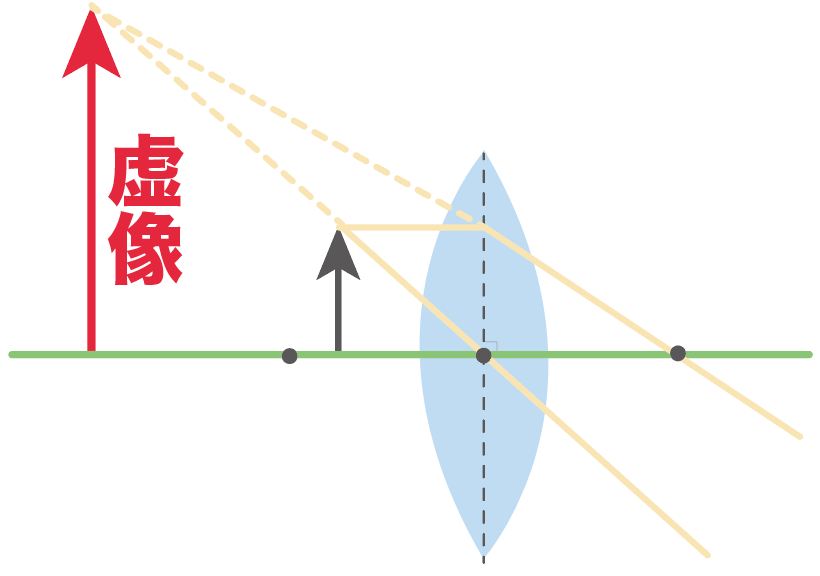
以上が、凸レンズの虚像の作図問題の解き方だったね。
の4ステップで解けちゃうね。
凸レンズの虚像の作図問題をマスターしたらついでに「凸レンズの実像の作図問題」も習得しておこう。
そんじゃねー
Ken
こんにちは!この記事を書いているKenだよ。コーヒー、ドリップしたね。
中1理科の光の世界の単元で一番の山場。
それは、凸レンズの作図問題だよね。
作図問題と聞くと難しそうに聞こえるけど、これまで勉強してきた2つの基本である、
を押さえておけば解けるはずなんだ。
今日は、その凸レンズの作図問題の中でも、
実像
を作図する問題を一緒に解いていこう。
レンズに映って見えるものや、レンズを通してスクリーンに映しだせるものを「像(ぞう)」と呼んでたね?
この像の中でも「実像」は、
物体から飛び出た光が凸レンズの逆側で1点に集まってできる像のこと
を言うんだ。
しかも、上下左右が逆向きの像。
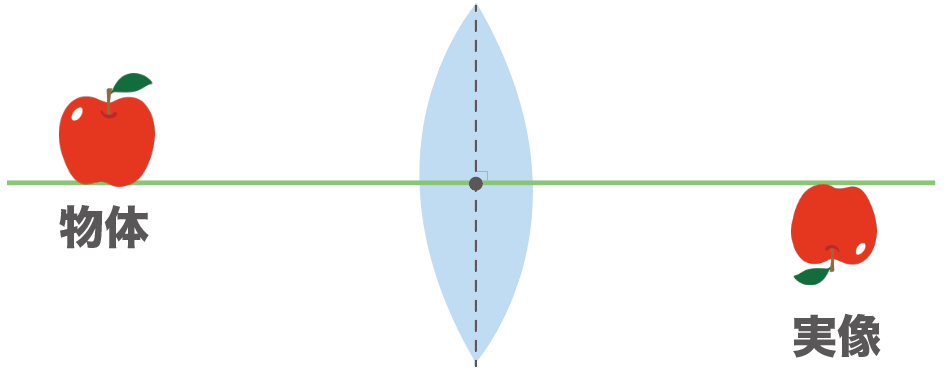
たとえば、りんごの実像を映し出してみたとすると、こんな感じでへたが下向きになって映し出されるはず。
これが実像。
でもでも、凸レンズに24時間365日どこでも実像がうつるわけじゃない。
じつは、
凸レンズの焦点よりも外側にうつす物体を置いた時だけ
なんだ。
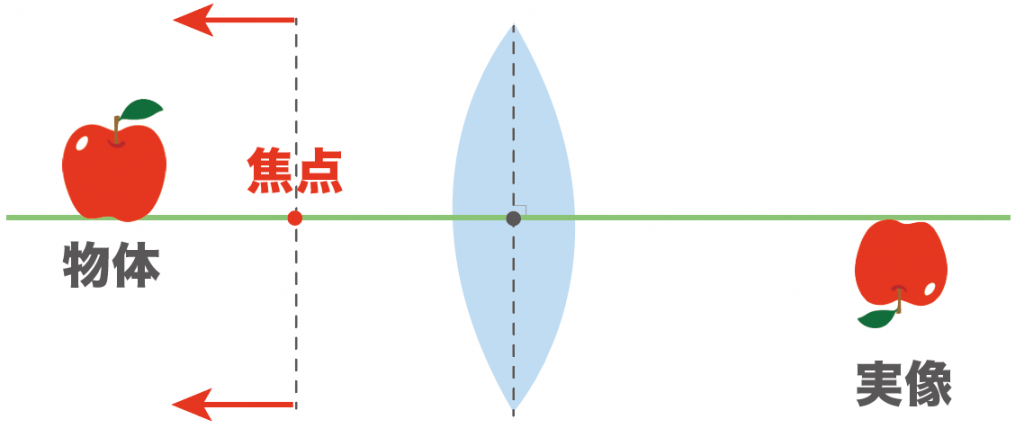
焦点の上に置いたり、
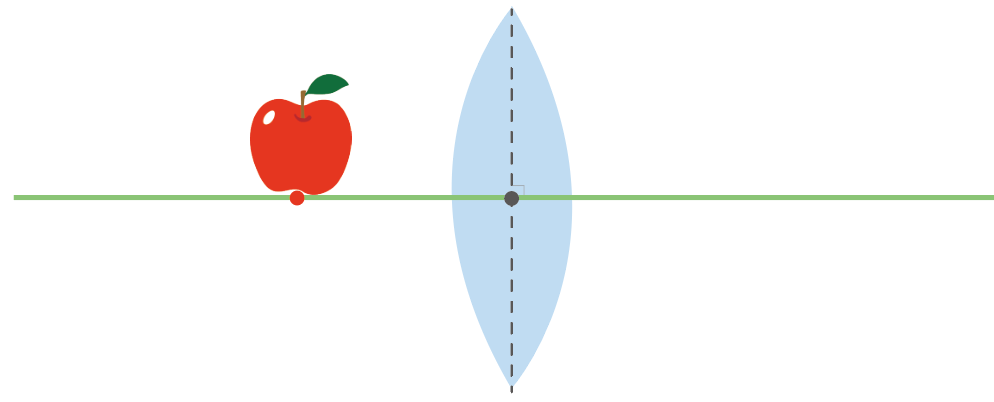
焦点よりレンズに近い位置に物体を置いても、実像はできないってわけさ。
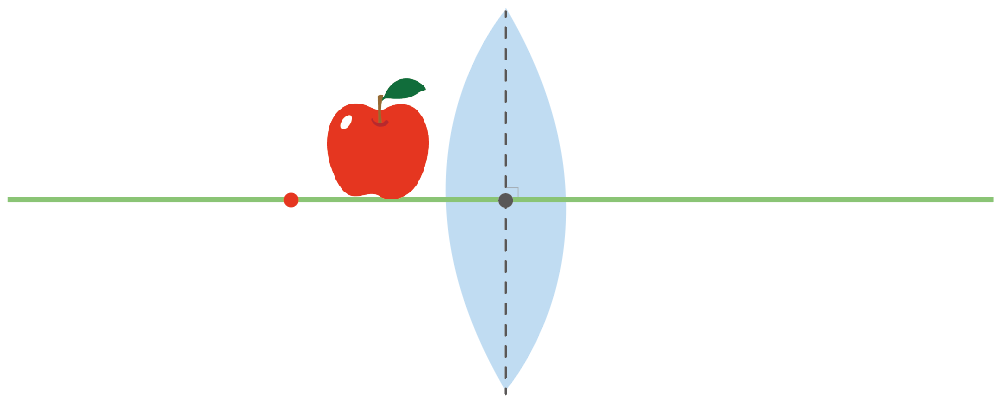
それじゃあ凸レンズにできる実像を作図する問題を解いていこう。
凸レンズの焦点の外側に、こんな感じで矢印の物体が置かれている時、この凸レンズによってできる実像を作図しなさい
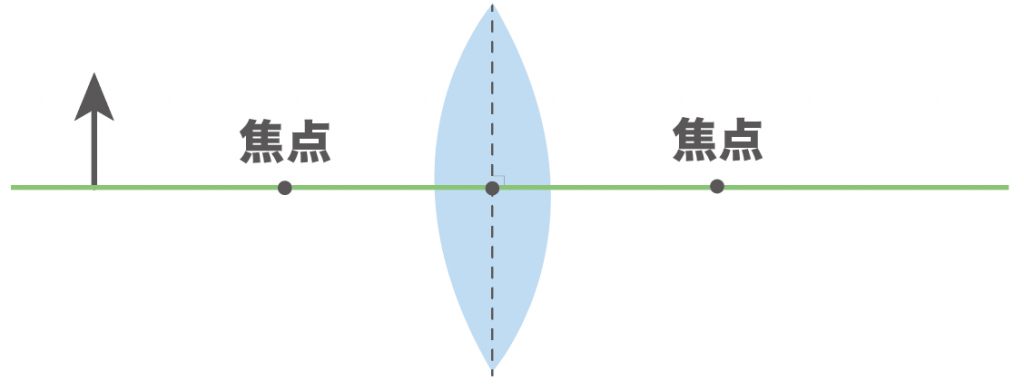
このタイプの作図問題は次の3つのステップを踏めば大丈夫。
凸レンズの中心を通る光を書いてみよう。
物体の頭から出た光のうち、凸レンズの中心を通る光だけかくんだ。
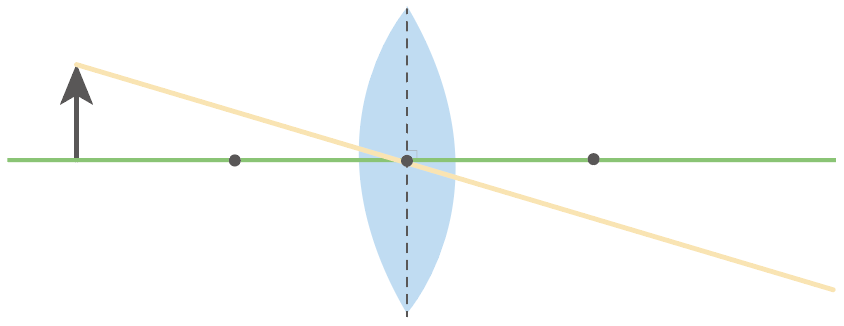
凸レンズの光の進み方で勉強したように、凸レンズの中心を通る光はそのまままっすぐ進むんだったね??
まっすぐな光の道筋の線を引ければオッケー。
続いて、凸レンズの軸に平行な光をかいてみよう。
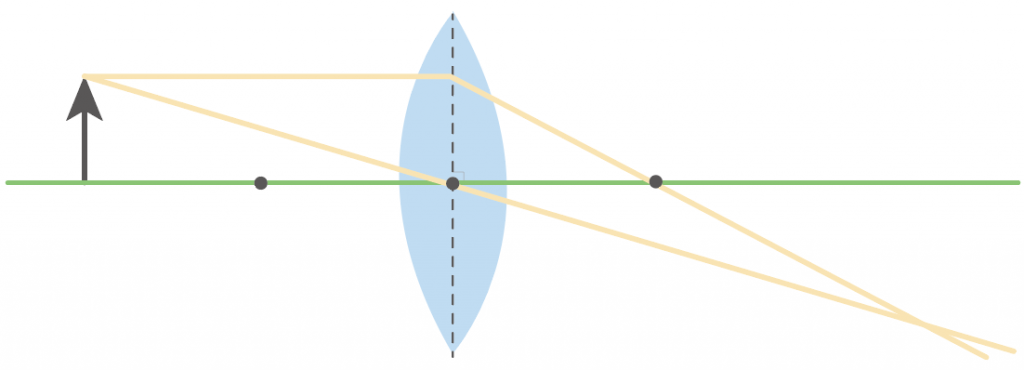
このタイプの光は、
凸レンズにあたると焦点を通過するんだったね?
最後に、凸レンズの焦点を通った光の道筋をかこう。
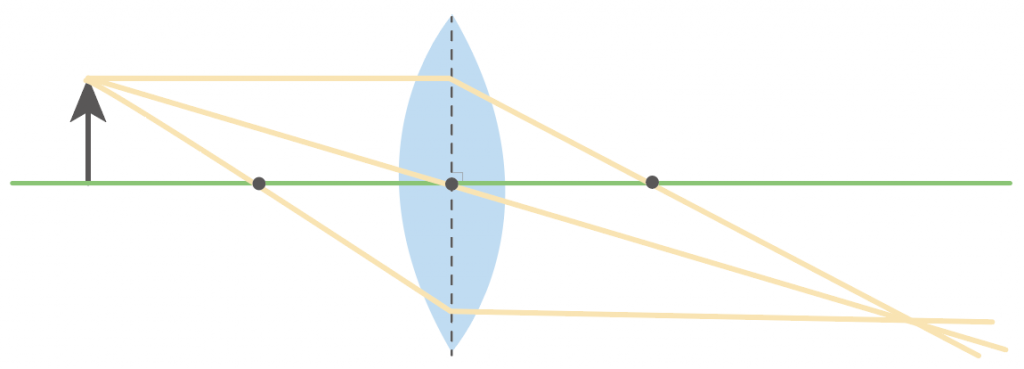
凸レンズを通過した後に、レンズの軸に平行しなきゃいけないから作図が難しい。
Step2までに引いた2つの光の道筋の交点を目指すとかきやすくなるよ。
ここまで3つの光を作図してきたけど、たぶん、うまく作図できると3つが一点で交わってるんじゃないかな。
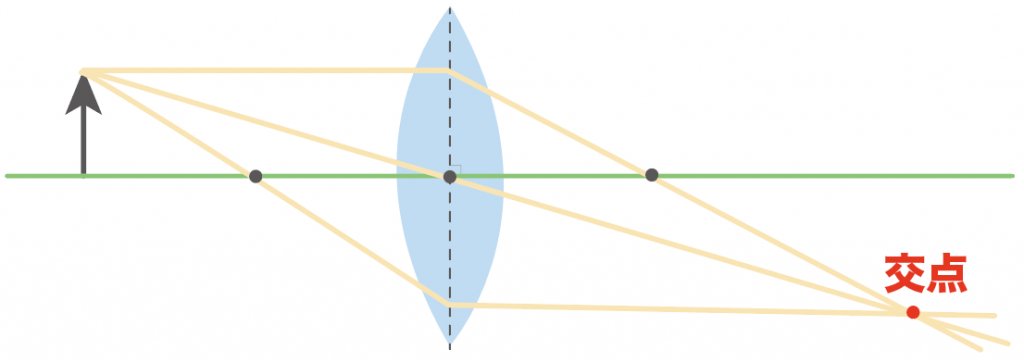
そのとき、交わっている交点には、光がスタートした地点のパーツを書いてあげよう。
今回は、矢印の物体の頭から光を発射したから、矢印の頭のてっぺんがこの光の道筋の交点にくるはず。
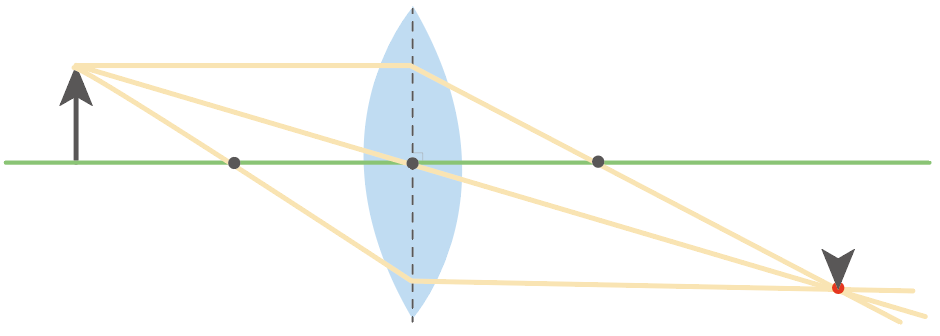
そしたら、そのほかのパーツの残りも描いてあげよう。実像だから上下左右逆さまになってるね。
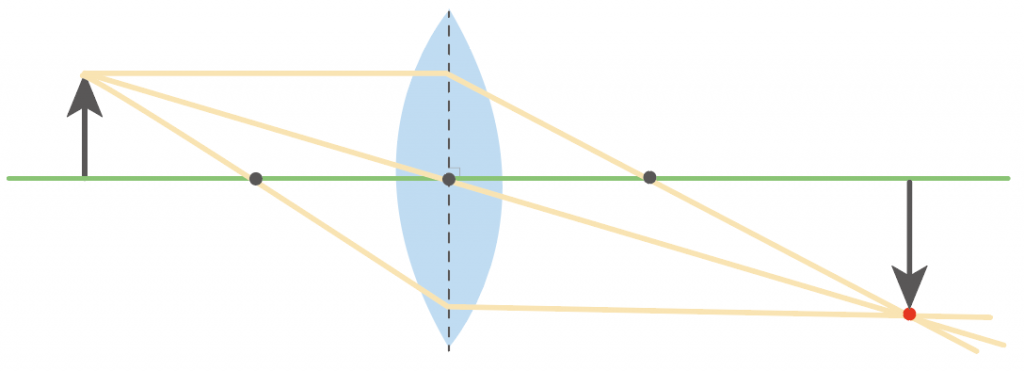
あとは凸レンズの実像について知っておくと便利なことを2つばかり紹介するよ。
焦点距離のちょうど2倍の地点に物体をセッティングしてやると、凸レンズでできる実像は、本物の物体の大きさと同じになるよ。
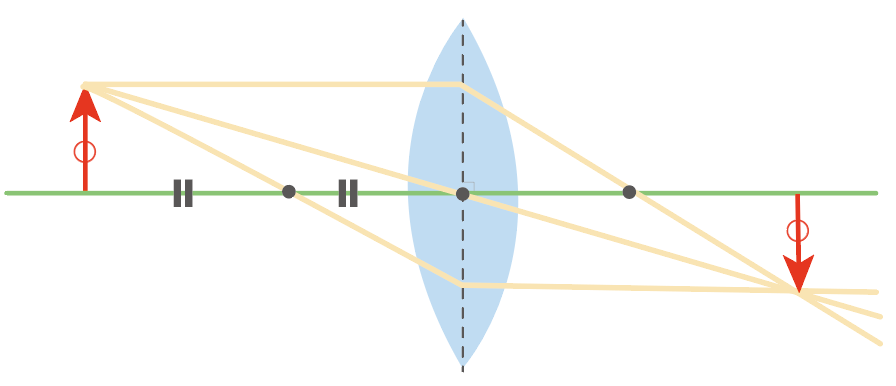
あくまでも大きさだけだから、向きは左右上下逆になってるのは変わらないけどね。
もし、物体の位置を焦点距離からもっと遠ざかるようにセッティングすると、
実像がもっと小さくなるんだ。
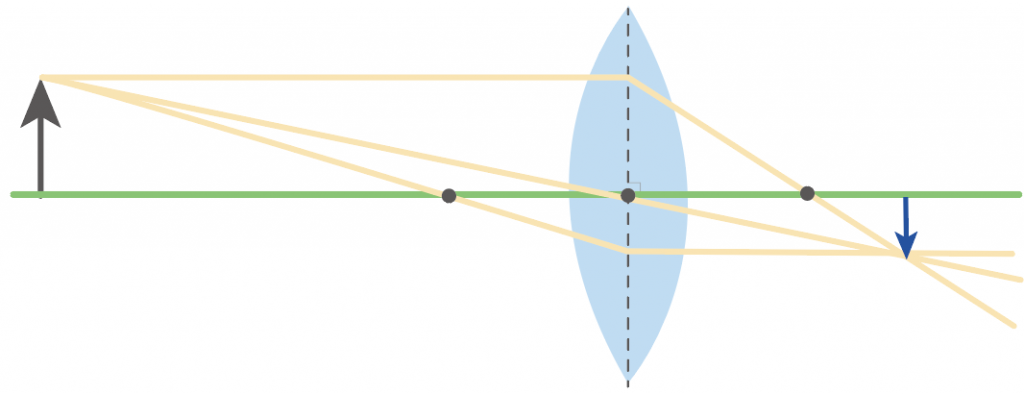
逆に、焦点の位置に物体を近づけると実像は大きくなるけどね。
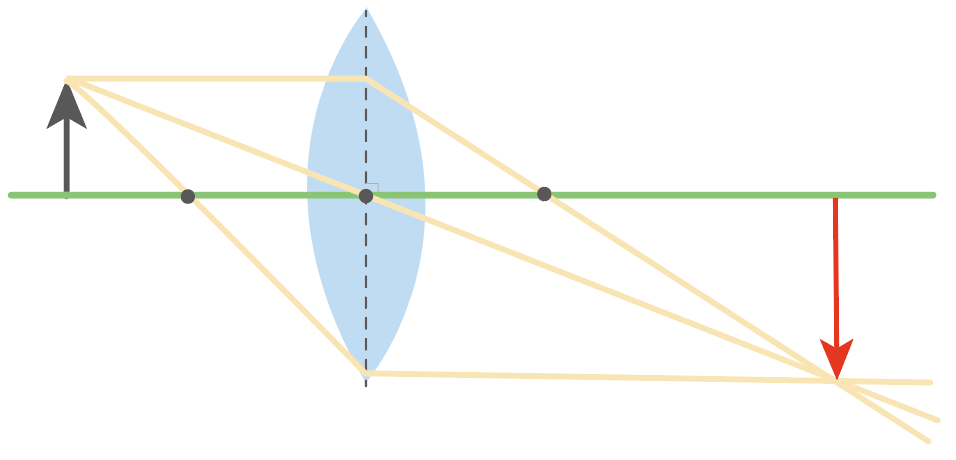
ただ、焦点の位置ぴったりに物体をセッティングすると、何も見えなくなることに注意してね。
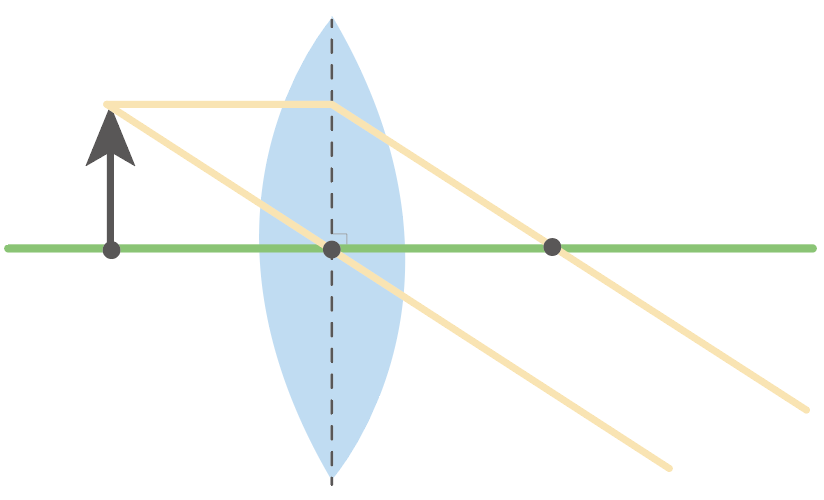
以上が、凸レンズにできる実像を作図する問題の解き方だよ。
さえ押さえて、落ち着いてテストに臨めば解けるはず。
実像の作図問題をマスターしたら次は虚像の作図にチャレンジしてみよう!
そんじゃねー
Ken
こんにちは!この記事を書いているKenだよ。はちみつ、ゆずだね。
中1理科の光の世界の単元では、
凸レンズの作図問題
がよく出題されるよね。
その作図問題を制覇するために知っておきたいことの1つとして、
凸レンズの光の進み方があるよ。
つまり、
凸レンズを通った光の道筋がどう変化するのか??
っていうルールのことね。
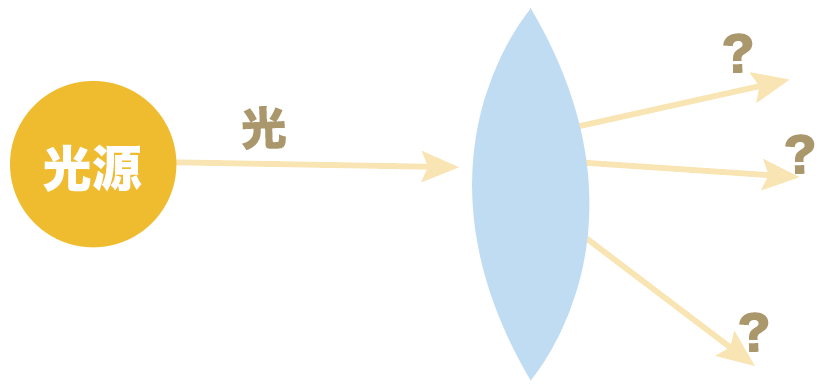
今日はこいつの基本をみっちり押さえていこう!
凸レンズに光が当たったとき、どう道筋を変えるんだろうね??
まず、1つ目のルール。
凸レンズの軸に平行な光の道筋は焦点を通るんだ。
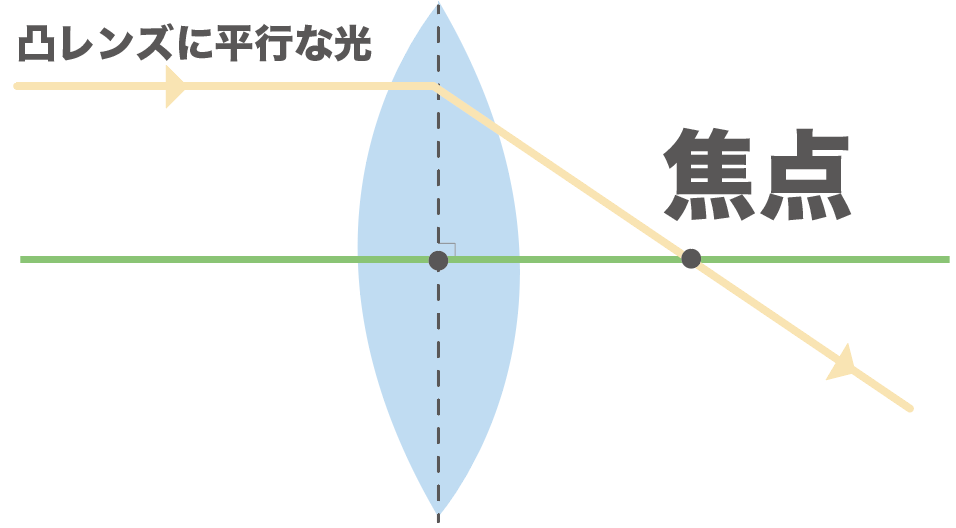
「凸レンズの軸」は凸レンズの中心を通る、凸レンズの中心線に垂直な直線のことだったよね??
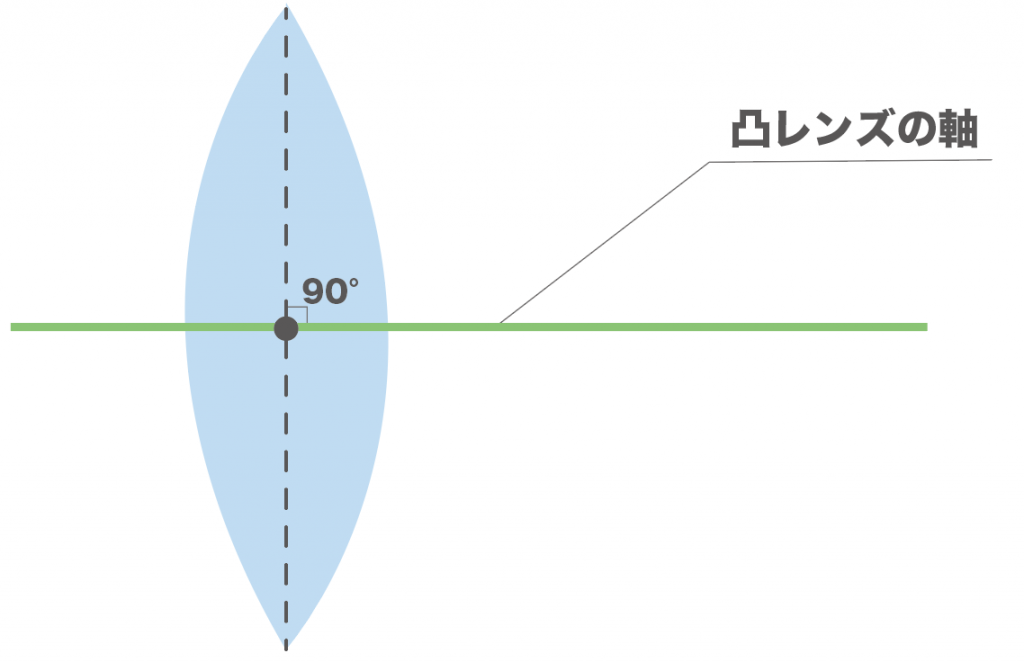
こいつに平行な直線をどこから凸レンズに当てても、必ず逆側の焦点を通るようになっているんだよ。
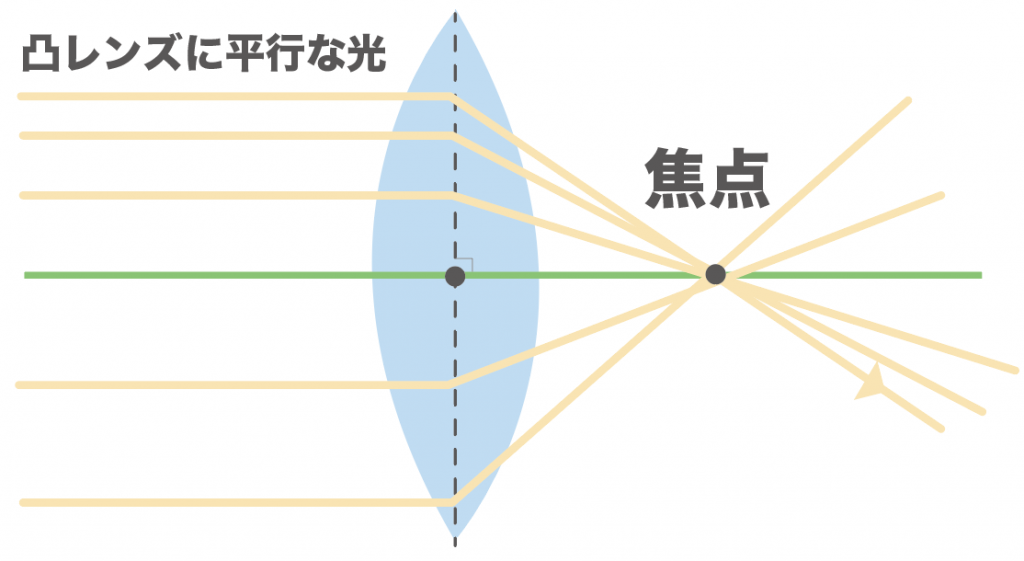
次は凸レンズの中心を通る光のルールね。
光の進み方のルールはシンプルで、
凸レンズの中心を通る光はそのまま直進するんだ。
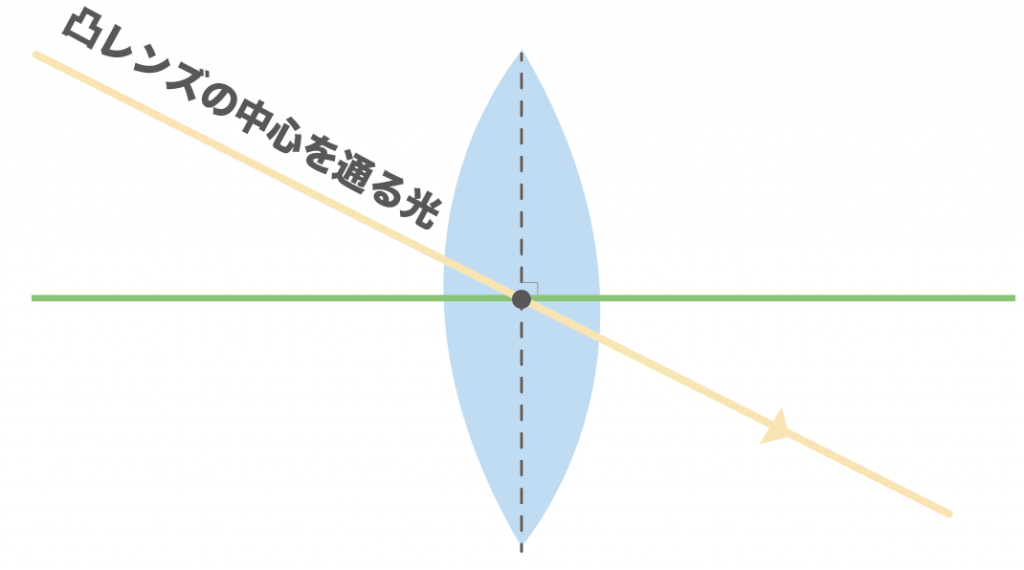
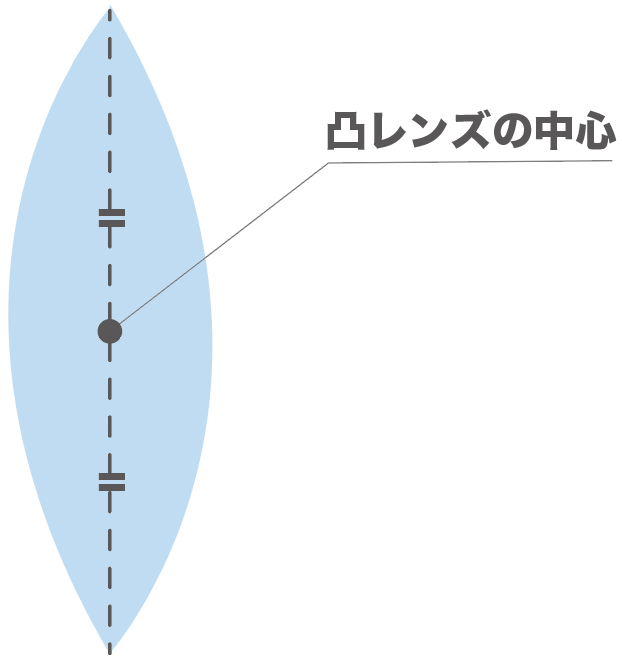
「凸レンズの中心」って、
凸レンズの中心線の中点のこと
だったよね??
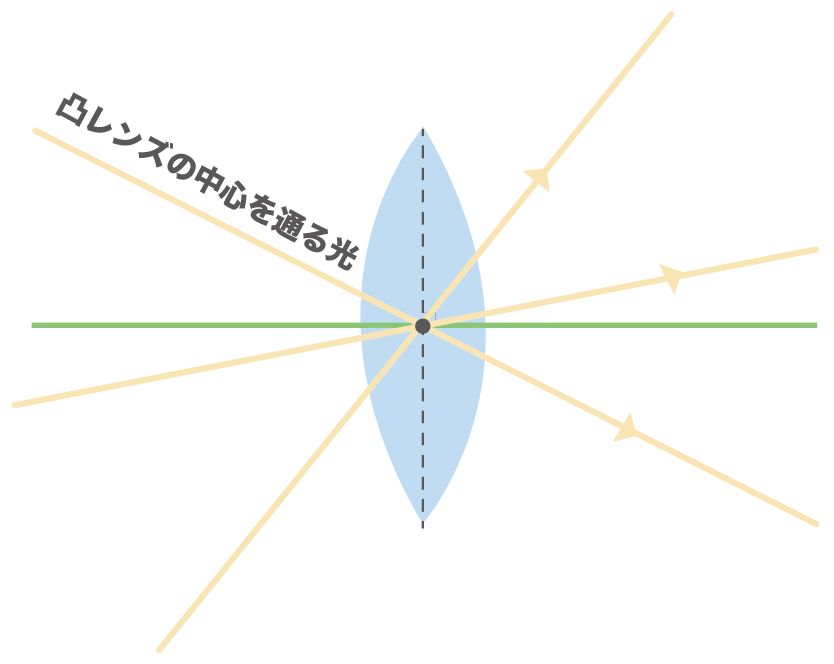
この凸レンズの中心を通る光なら、どこから、どの角度から当ててもまっすぐと進んでいくんだ。
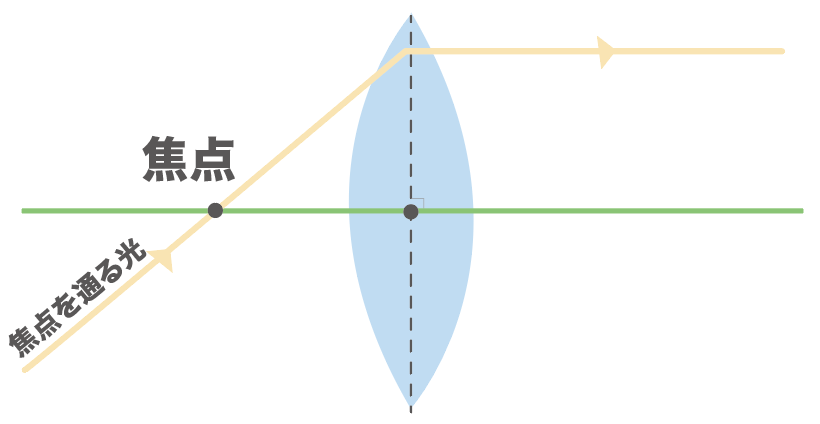
これはルール1の逆だね。
凸レンズの焦点を通った光が凸レンズを通過すると、凸レンズの軸に平行に進むんだ。
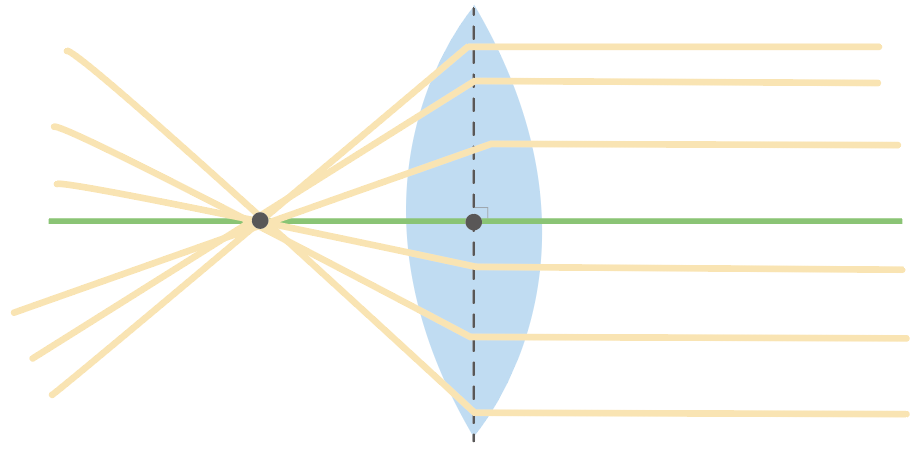
これまでのルールと一緒で、どこからどの角度から凸レンズに光を当てようが関係ない。
焦点を通ってしまえば凸レンズの軸に平行に進むようになってるんだ。
以上が、凸レンズの光の進み方のルールだったね。
という3つを押さえておけば大丈夫。
この基本を押さえて凸レンズの作図問題を倒していこう!
もし、凸レンズの専門用語がわからなすぎて理解できない!
っていうときは、「凸レンズの基本名称」で復習してみてね。
そんじゃねー
Ken
こんにちは!この記事を書いてるKenだよ。アルフォート最高。
中学理科の光の世界の単元では、
凸レンズに入った光がどう進むのか??
ってことをなぜか深く勉強していくよ。
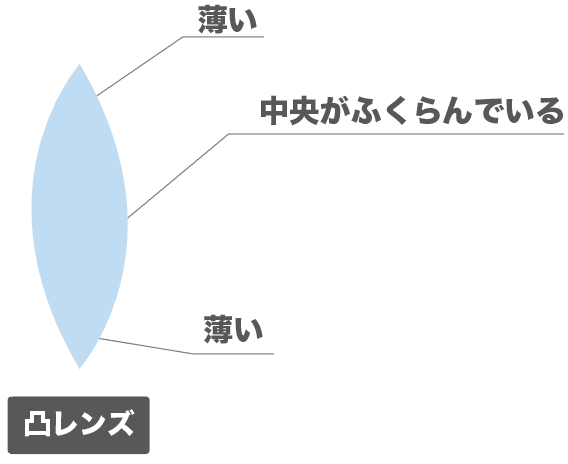
凸レンズとは、虫眼鏡にも使われているレンズのことで、

中央が膨らんでいて、周辺に向かうほど薄くなるレンズのこと
だったね。
んで、中学理科では、この凸レンズの光の進み方の作図とか、実像とか虚像とか、いっぱい厄介なことを勉強していくんだ。残念ながら。
ただ、これらの勉強って、
凸レンズの性質や名称の基本さえ押さえておけばかなり簡単。
名前を覚えてしまえば凸レンズの基本ルールが言ってることがわかるようになるからね。
ってことで、今日は今後、凸レンズを勉強していくにあたって苦戦しないように、凸レンズの基本の名称をマスターしていこう。
凸レンズについていっぱい専門用語が出現してくるけど、だいたい次の5つの名称を押さえておけば問題ないかな。
まずは「凸レンズの中心線」ってやつだ。
これは凸レンズが薄くなっている端っこと端っこを結んだ線のことね。
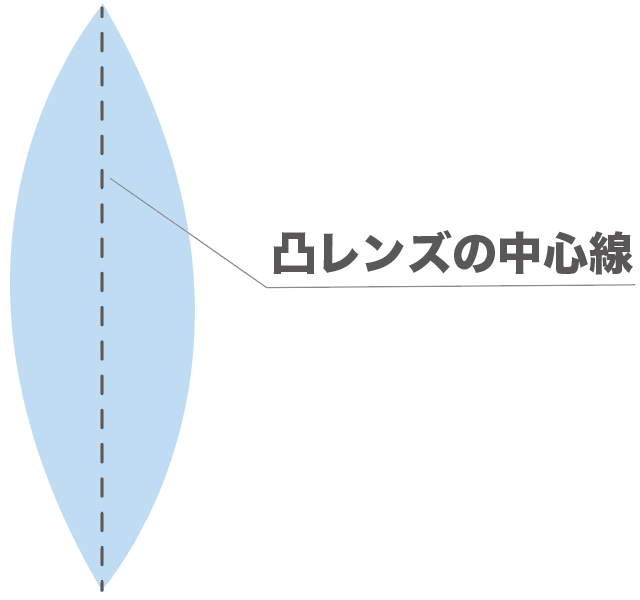
大抵、凸レンズは線対称になっているから、この中心線で凸レンズを折りたためば重なることになる。
これが凸レンズの中心線。
続いては、凸レンズの中心だ。
これは、
凸レンズの中心線の中点のこと
だ。

端っこから端っこまでの距離が等しい点のことだね。
凸レンズの中心は中心線上にあるんだ。
たとえば、凸レンズの端っこをA、Bとして、レンズの中心をOとしてやると、
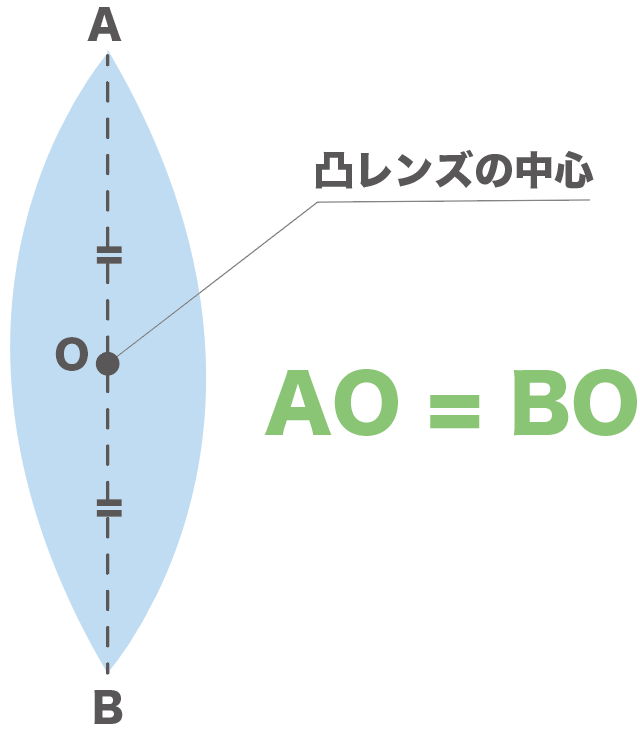
AO = BO
になるわけだ。
凸レンズの中心線に垂直で、なおかつ、凸レンズの中心を通る直線のことを、
凸レンズの軸
って呼んでるよ。

凸レンズに凸レンズの軸に平行な光を当ててやったとする。
このとき、じつは、
光が屈折して1点に集まるようになってるんだ。
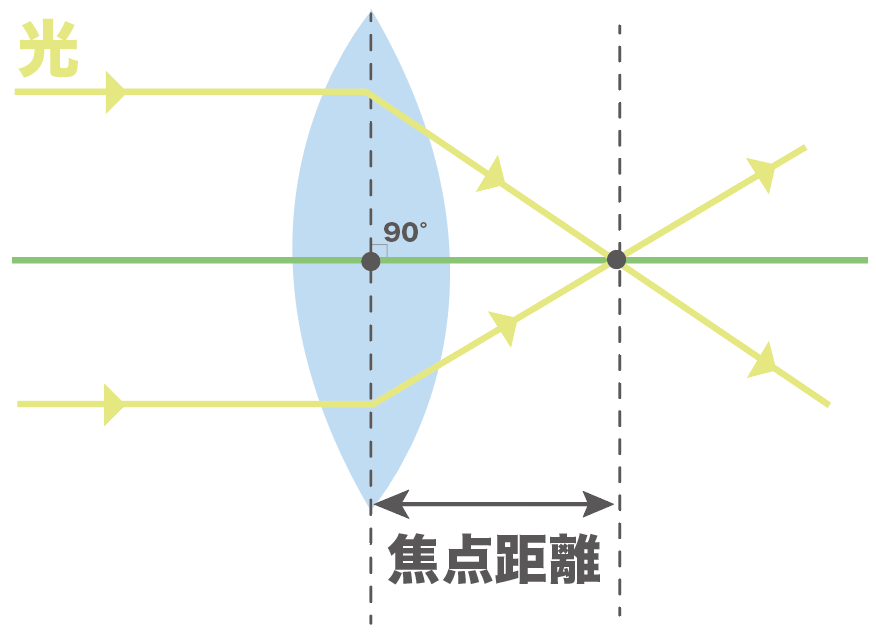
この凸レンズの軸に平行な光たちが集まる点のことを「焦点(しょうてん)」って呼んでるよ。
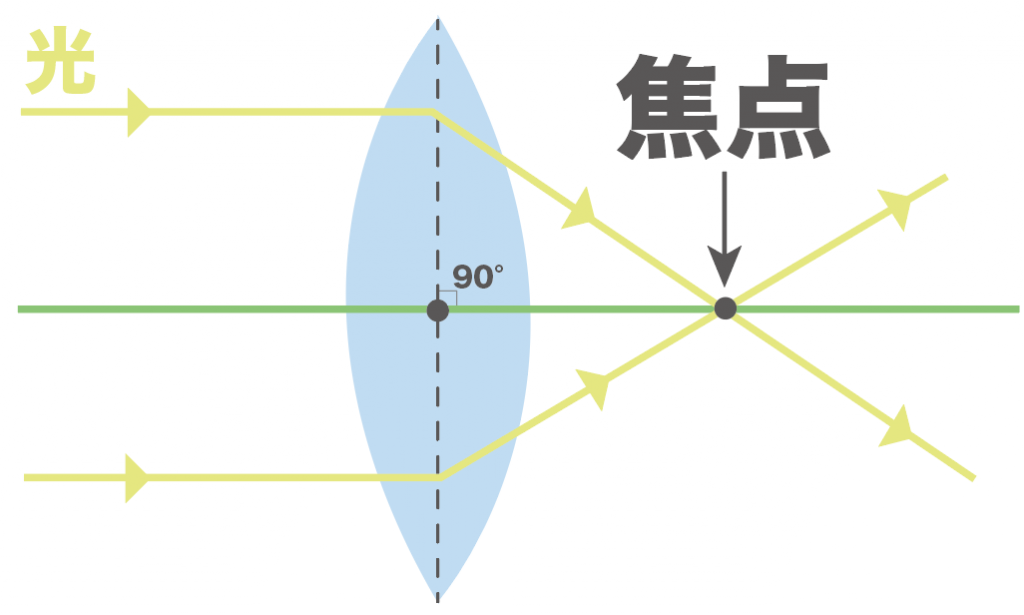
んで、凸レンズの中心から焦点までの距離のことを、
焦点距離
って呼んでるんだ。
なるほどね〜〜
以上が凸レンズの基本の名称たちだね。
最後に復習しておこう。
凸レンズの薄い端っこと端っこを結ぶ線を「凸レンズの中心線」、

凸レンズの中心線の中点を「凸レンズの中心」、

さらに、凸レンズの中心線に垂直で、かつ、凸レンズの中心を通る直線を「凸レンズの軸」というんだったね。

凸レンズの軸に平行な光を当てた時、光が集まる点を焦点、凸レンズの中心から焦点までの距離を「焦点距離」と覚えておこう。

そんじゃねー
Ken
こんにちは!この記事を書いてるKenだよ。鳩、目があったね。
中学1年例の光の世界の単元では、いくつか重要な事柄を勉強してきたね。
今日はもう一つ重要な光の現象を紹介するよ。
その名も、
全反射(ぜんはんしゃ)
というやつだ。
ってことで、全反射をわかりやすく復習していこう。
まずは全反射が起こるシチュエーションから。
全反射が起こるのは、水やガラスなどの透明な物体から、空気中へ光が通るときなんだ。
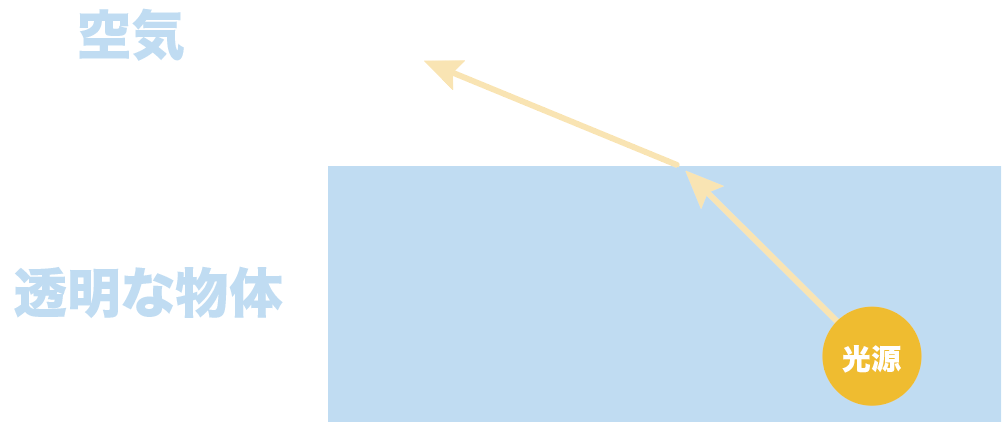
その逆の、空気から透明な物体へ光が入ってくるときは全反射は起きないと覚えておいてね。
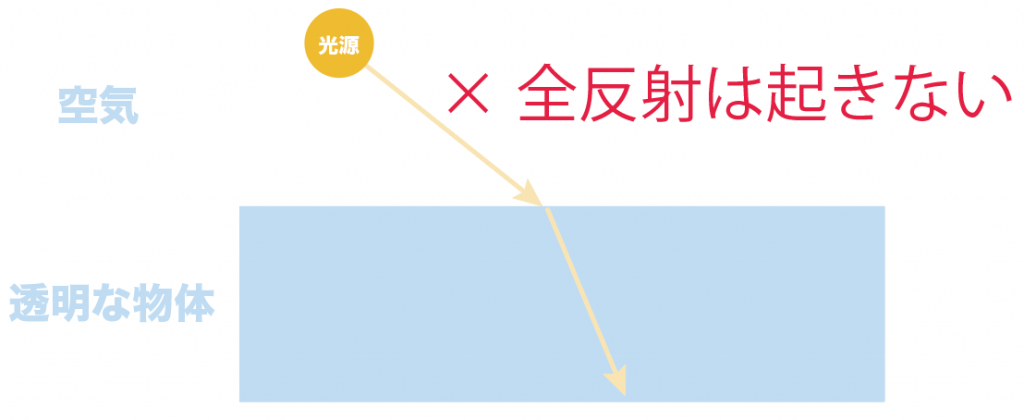
んで、このシチュエーションのとき、何が起こるのかを見てみよう。
全反射とはズバリ、
入射角を大きくしていくと、光が屈折しないで反射してしまう現象のことだ。

透明な物体から空気中に光が飛び出さず、また透明な物体の方向へ跳ね返されてしまうわけ。
ここで、光の屈折の法則を思い出して欲しい。
光の屈折の法則によると、
透明な物体から空気へ光が通るとき、屈折角は入射角よりも大きい
って習ったよね??
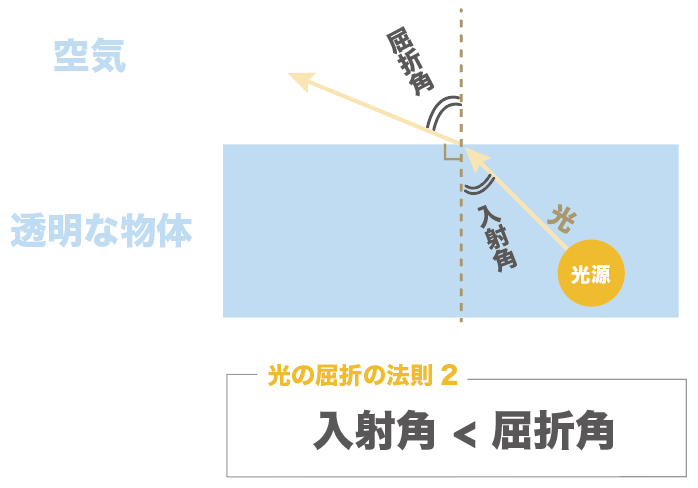
だから、入射角をどんどん大きくして、
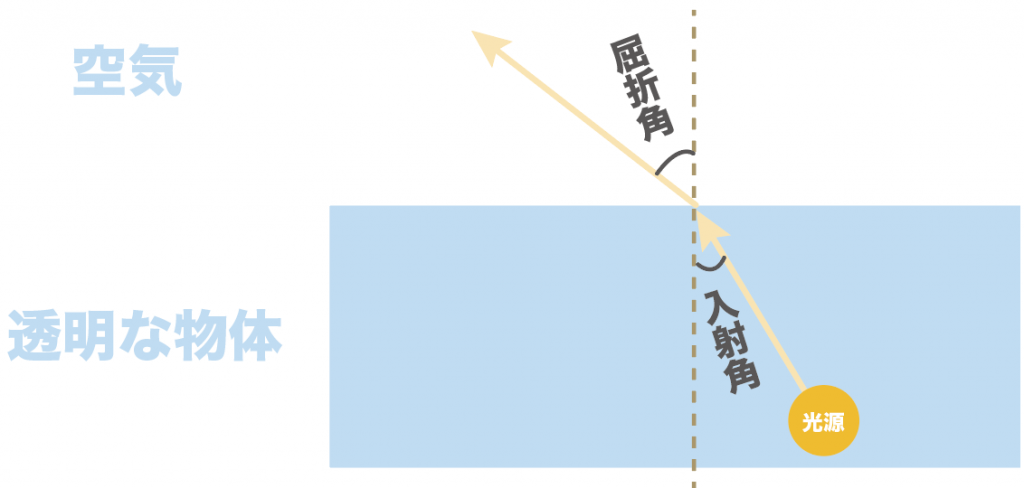
徐々に90度に近づいてくると、
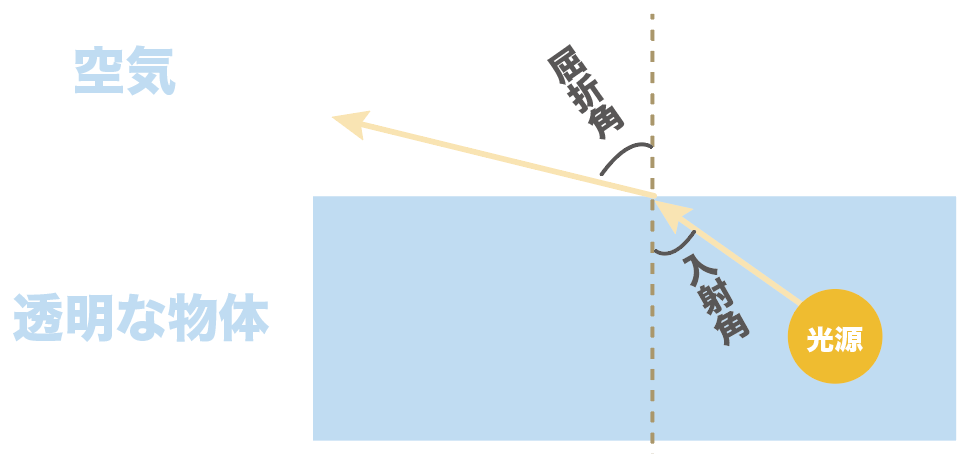
入射角よりも屈折角の方が先に90度に達してしまうんだ。
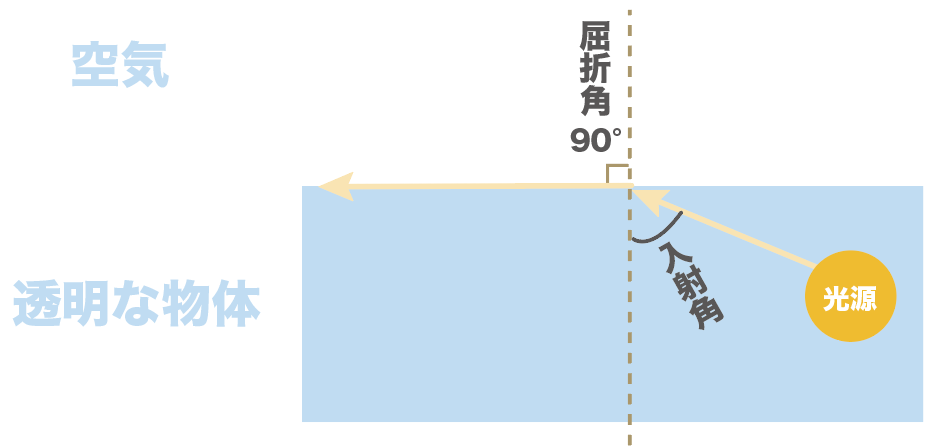
屈折角が90度ってことは、透明な物体と空気の境界面と平行に光が進んでいくことになるよね??
それよりも入射角を大きくして屈折角が90度より大きくなると、光は境界面を飛び越えて空気へ行けなくなっちゃう。
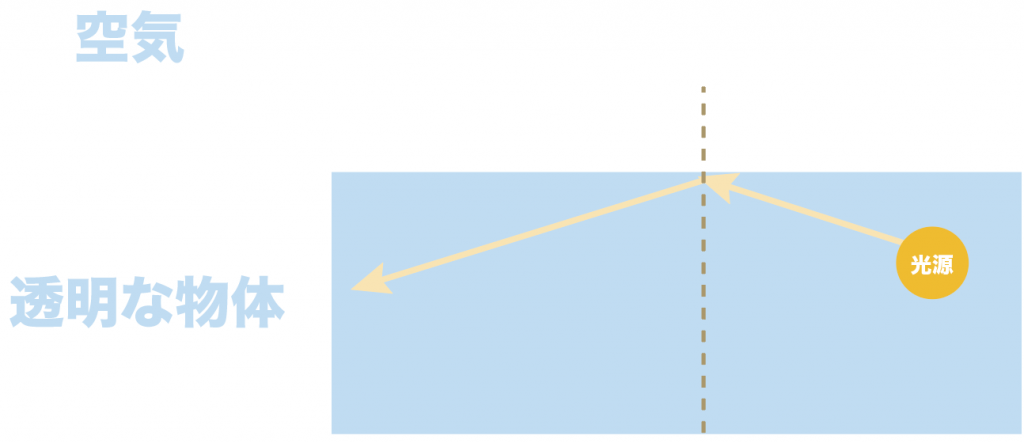
これが全反射だ。
一度全反射になると、光の道筋には「光の反射の法則」が適用される。
どういうことかっていうと、
入射角と反射角が等しい
ってことさ。
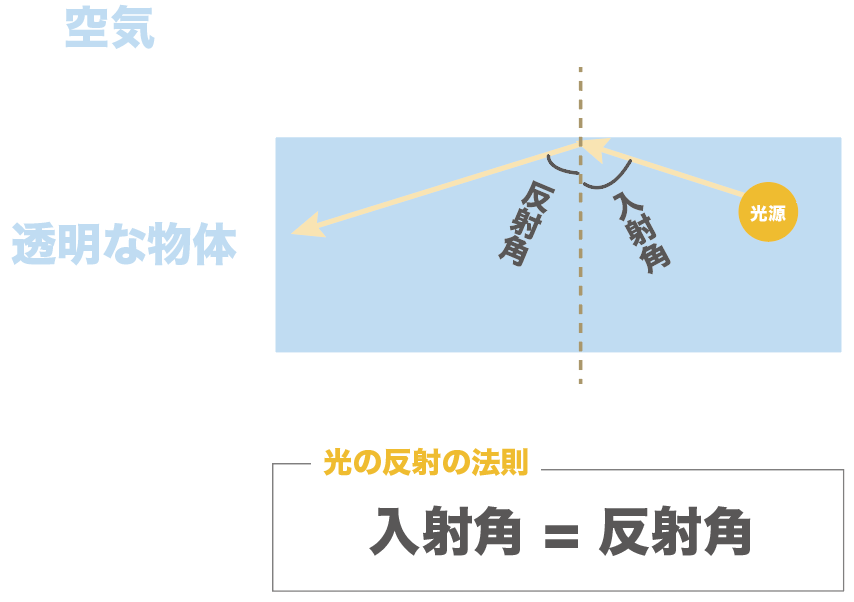
もはや屈折してないから屈折角じゃなくて名前が反射角になってる点に注意してね。
以上で全反射の概要終わり!
テストにも出やすいからよーく復習しておこう!
そんじゃねー
Ken
こんにちは!この記事を書いているKenだよ。麦茶、冷えてるね。
中1理科では「光の屈折」という光の性質を勉強してきた。
光の屈折の法則とは簡単にいうと、
光がある透明な物体を通過すると、光の道筋が曲がる
というものだったね。
>>詳しくは「光の屈折」を参照
この光の屈折の効果を確認できる実験として、よく、
コップにコインを入れて、水を注ぐと浮かび上がって見える
というものが実施されるね。
どういう実験か具体的に見ていこう。
まず、何も入ってないからのコップがあるとしよう。
こいつにコインをチャリーンと入れる。
この状態だと、コップのふちに隠れて外からはコインが見えないはず。
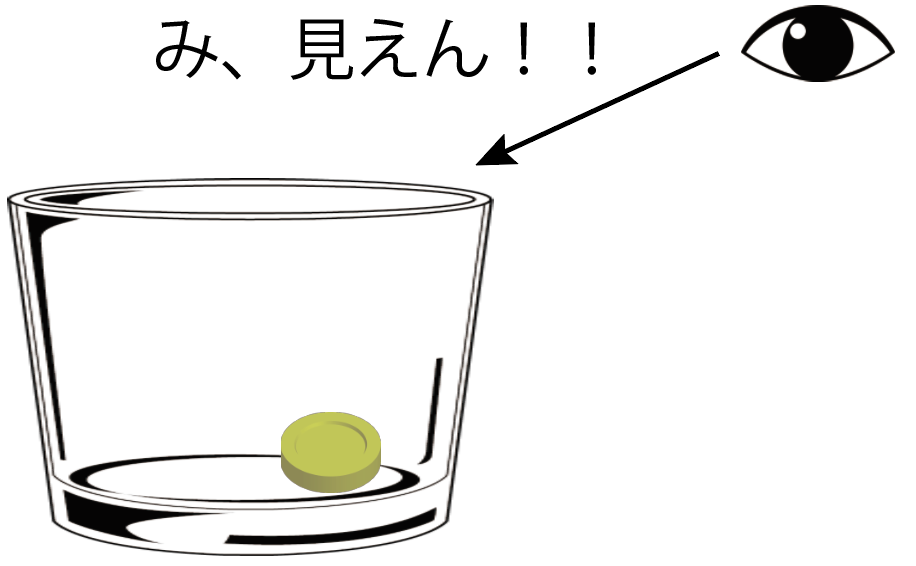
ここで、コップに水をドボドボ注いでみよう。
すると、どうだろう??
さっきまで見えなかったコインが浮き出て見えるようになってるじゃないか!
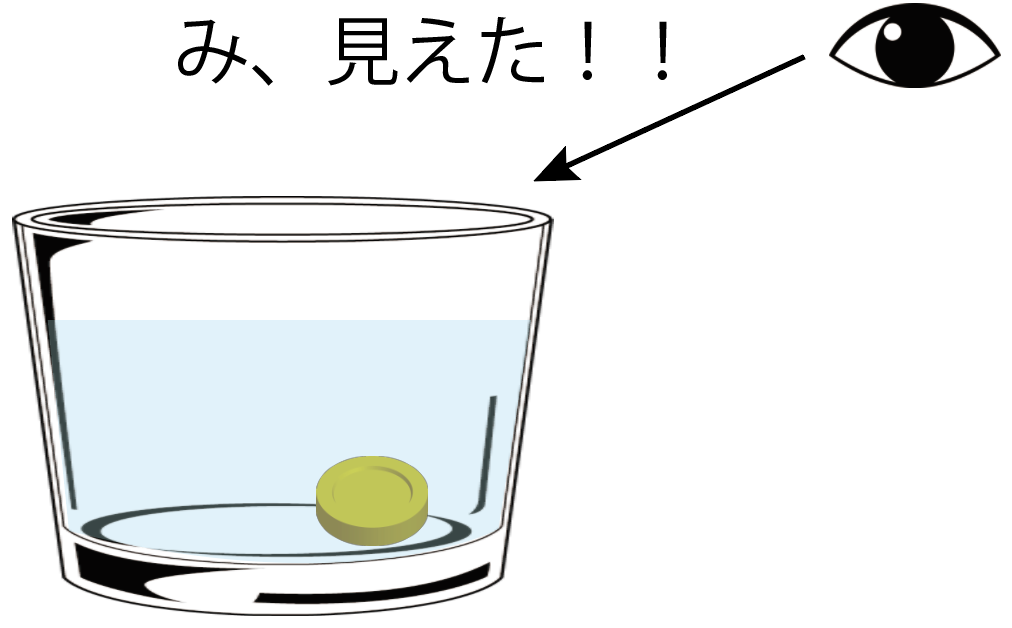
実際にリアルの世界でも実験してみても、やっぱり浮かび上がって見える。
こ、これはどういうことなんだ?!
それじゃあ、なんで水を入れた途端にコインが浮かび上がって見えるんだろうね??
じつはその理由は、
光の屈折の法則
にあるんだ。
水を入れないと、このコインからの光が目に届かない。
光が目に届かないと、目がコインが見えたっていう指令を脳に送らないから、結果的にいくら踏ん張っても見えないまま。
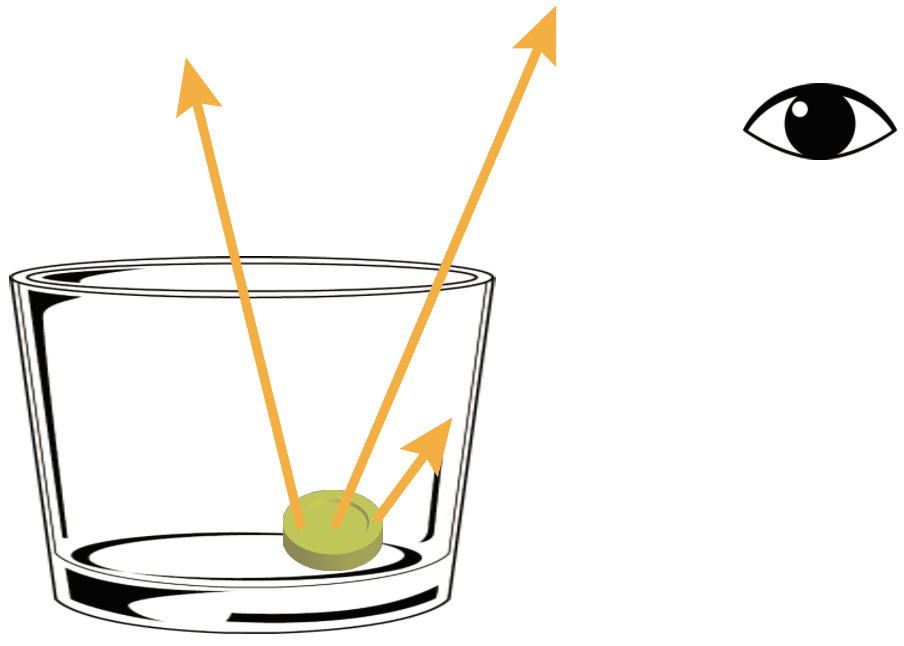
水を入れると、コインからの反射した光が屈折して、無事に目に届くようになるんだ。
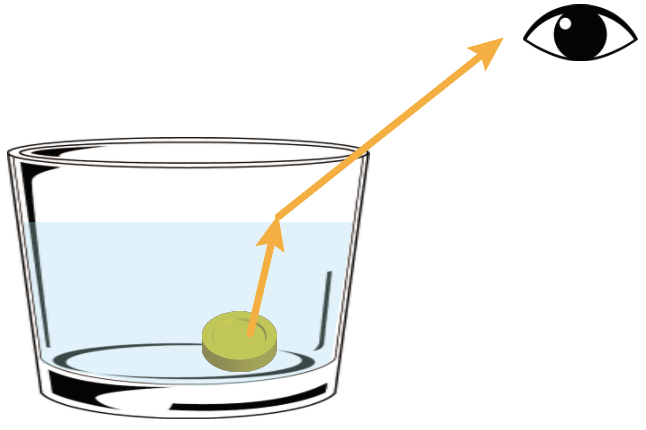
だから、コインは実際の位置ではなくて、目からすると、屈折した光の延長上に見えることになるってわけ。
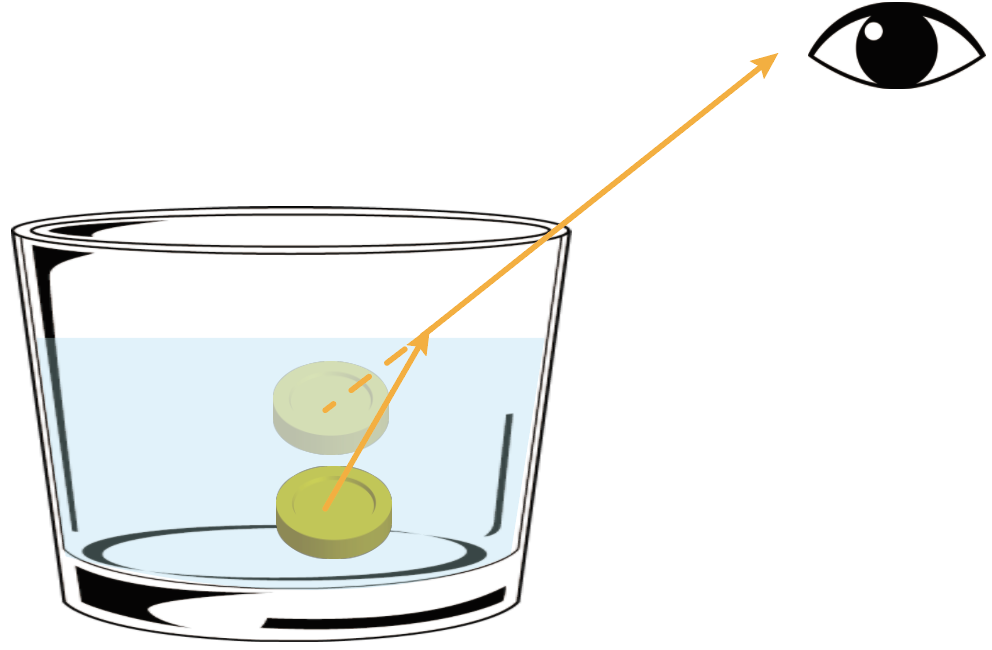
光の屈折の法則さまさまだ。
じつは、このコインが浮かび上がる実験はテストでも狙われやすいんだよ。
たとえば、次のような作図問題がよく出題されるかな。
水が入ったコップにコインを入れると浮かび上がって見えた。
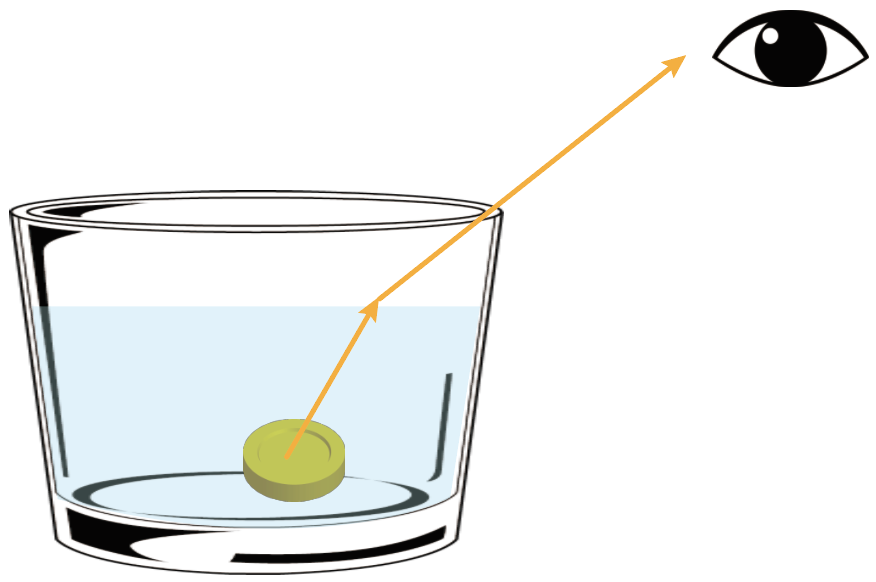
コインの中央からの光が図のように屈折して目に入る時、コインが浮かび上がって見える位置を作図してください。
という問題。
こういう問題では、屈折した光の道筋を逆方向にまっすぐ延長させればいいんだ。
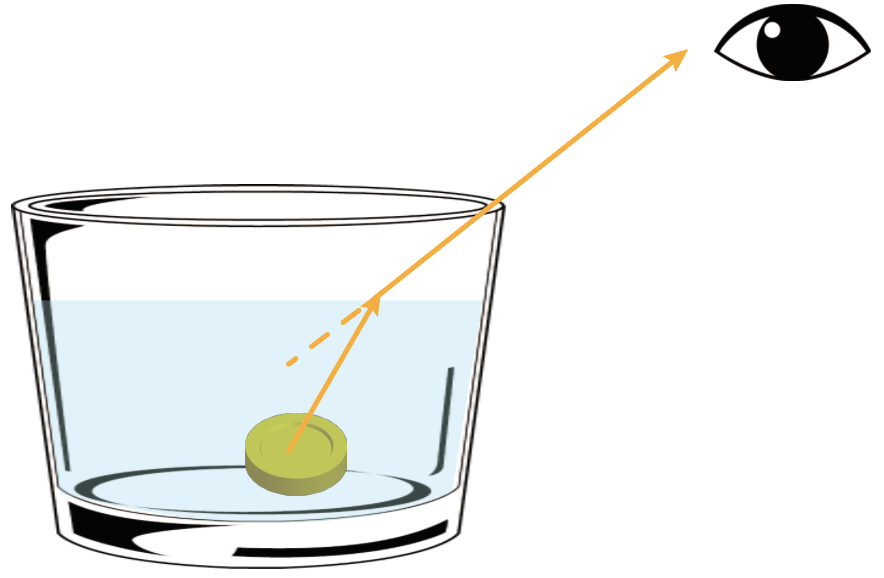
まっすぐ延長線をかくために定規を使ってやろう。
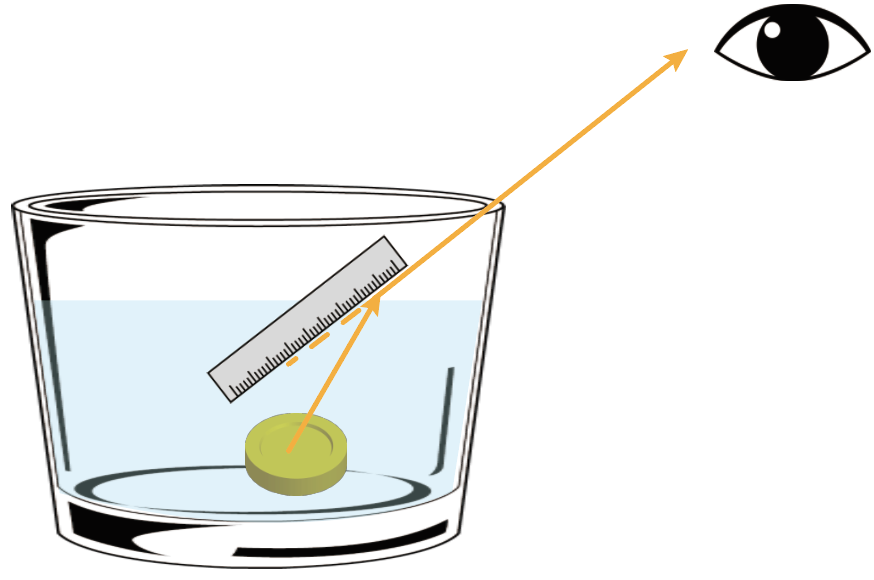
その延長線上にコインが見えているはずだから、だいたい元のコインの位置の真上にコインを作図してやればオッケー。

この手の問題はよくテストに出るから復習しておこう!
そんじゃねー
Ken
こんにちは!この記事を書いているKenだよ。のど飴、100個ぐらい欲しいね。
中学1年生の理科では、
光の屈折の法則
を勉強していくよ。
この法則とはズバリ、
光が空気中から透明な物体に入るとき、入射角の方が屈折角より大きくなる。
逆に、透明な物体から空気中に光が入ってくるとき、屈折角の方が入射角より大きくなる。
というやつだったね。
えっ。
「屈折角」とか「入射角」とか意味がわからないだって!?
今日はそんな光の屈折の法則を完璧に忘れちゃったときのために、一からわかりやすく覚え方まで解説してみたよ。
よかったら参考にしてみて。
まずは、光の屈折の法則で出てくるキーワード、
の2つの意味を確認していこう。
これらの2つの言葉はすべて、
空気中から透明な物体へ光をあててみたり、
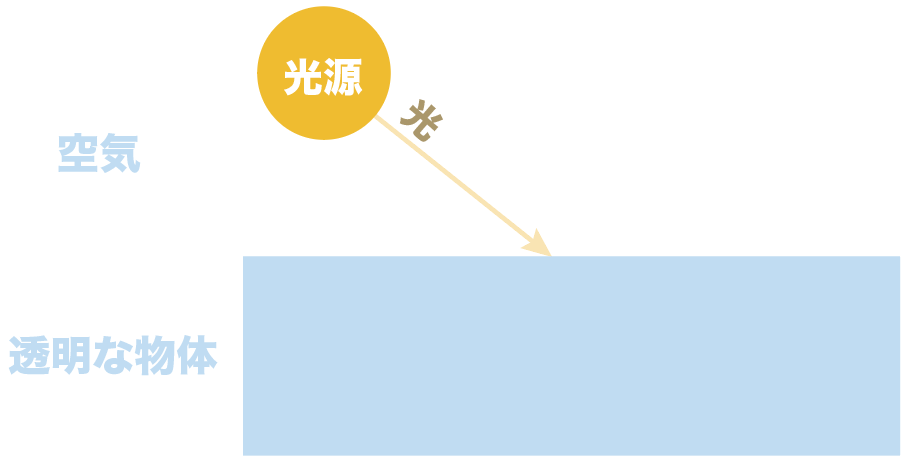
逆に、透明な物体から空気中へ光を当ててみたり、

っていうシチュエーションで使う言葉だよ。
あんまりイメージ湧かないかもしれないけど、この状況で出現する用語だと認識しておいてね。
入射角とは、
入ってくる光の道筋と境界面に垂直な線との角度のこと
なんだ。
ここでいう「境界面」とは、
の境目のことね。

入射角っていう言葉は「光の反射の法則」でも出てきたから馴染みあるかもね。
たとえば、空気から透明な物体(半円レンズ)に光を入れたときは、この角度が入射角になるよ。
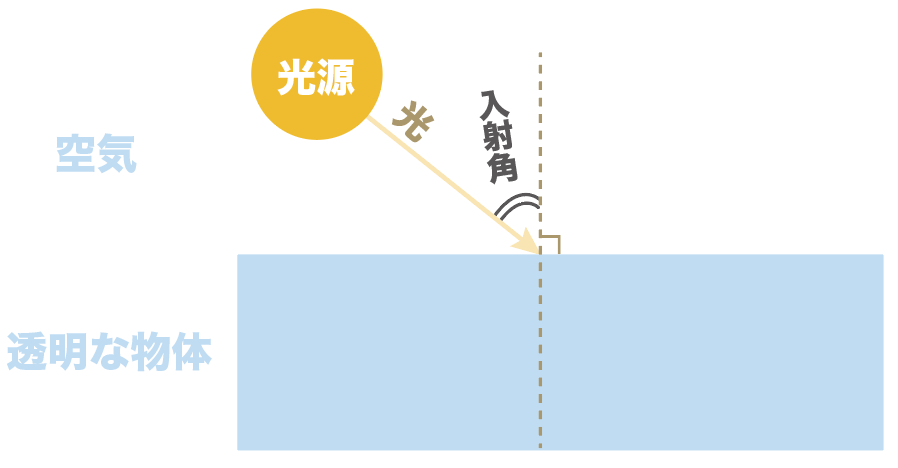
逆に、透明な物体から空気に光を入れた場合はこっちが入射角だけどね。
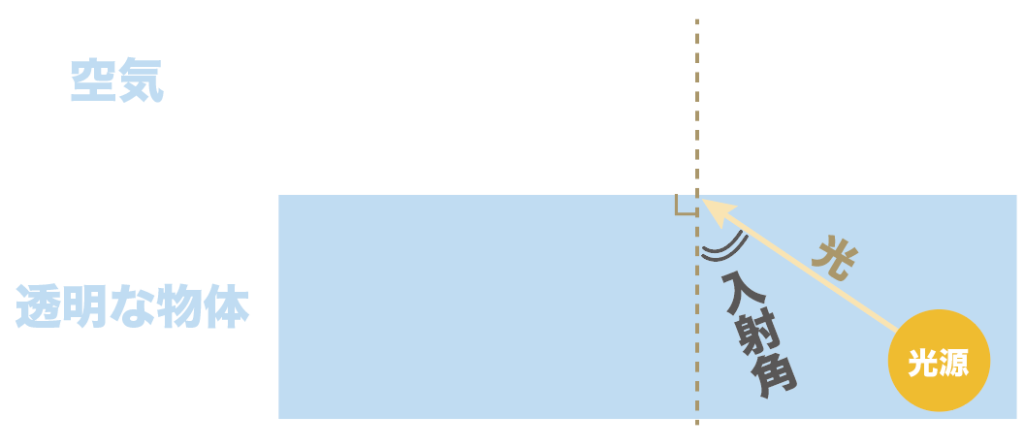
屈折角とは、
出ていくときの光の道筋と境界面に垂直な線との角度のこと
なんだ。
出ていくときの道筋はまっすぐじゃなくて屈折(曲がる)から、屈折角と呼ばれているんだ。
たとえば、空気から透明な物体(半円レンズ)に光を入れたときは、ここが屈折角。
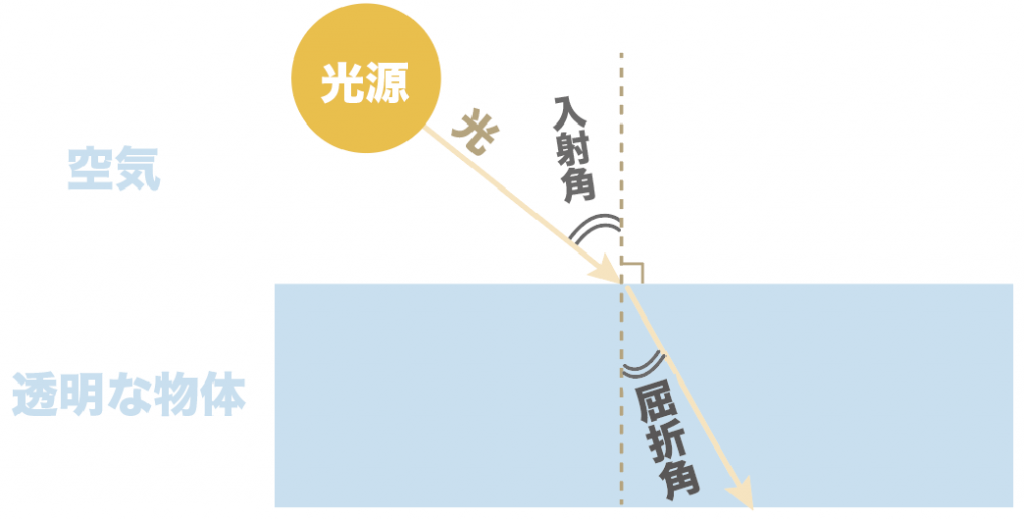
逆に、透明な物体から空気に光を入れたときは、ここが屈折角になるのね。
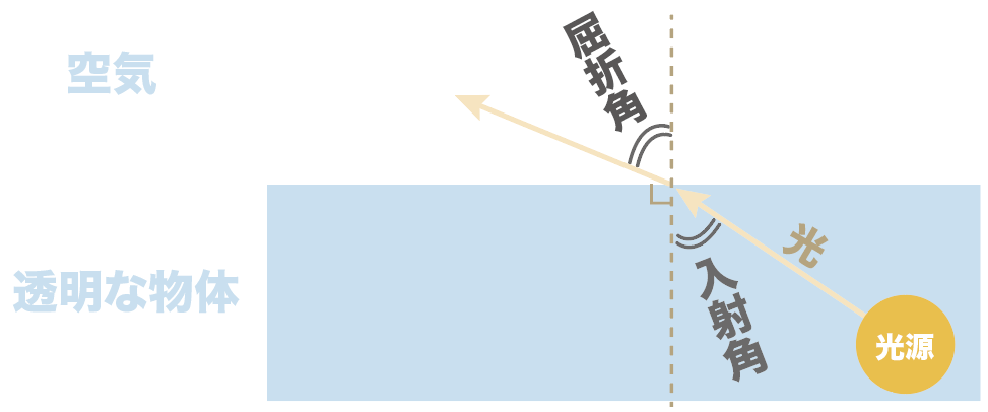
さて、入射角と屈折角の意味がわかったから、光の屈折の法則に戻ってみようか。
光の屈折の法則とは、
光が空気中から透明な物体に入るとき、入射角の方が屈折角より大きくなる。
逆に、透明な物体から空気中に光が入ってくるとき、屈折角の方が入射角より大きくなる。
だったね。
つまり、光の入り方が、
っていう2つのパターンのときの、入射角と屈折角の関係を表した法則なんだ。
それぞれのパターンについてみていこう。
まず、空気中から透明な物体に光が入るときのパターンね。
このとき、光の屈折の法則によると、
入射角の方が屈折角より大きくなるんだ。
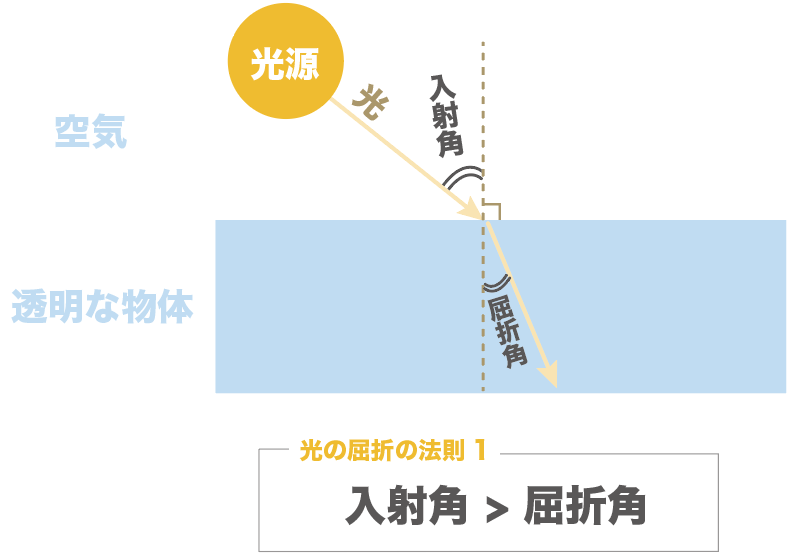
不等号で表すとこうなるよ↓↓
入射角>屈折角
今度は、逆に、
透明な物体から空気中に光が入ってくるパターンね。
この場合は、
屈折角の方が入射角より大きくなるんだ。

不等号であらわすと、
入射角 < 屈折角
つまり、どういうこと言ってるのかというと、
空気中から透明な物体に入れたり、その逆のことをすると、
入れた光はまっすぐ進むんじゃなくて境界面で曲がって光の道筋が変化するよ
ってことを言ってるわけね。
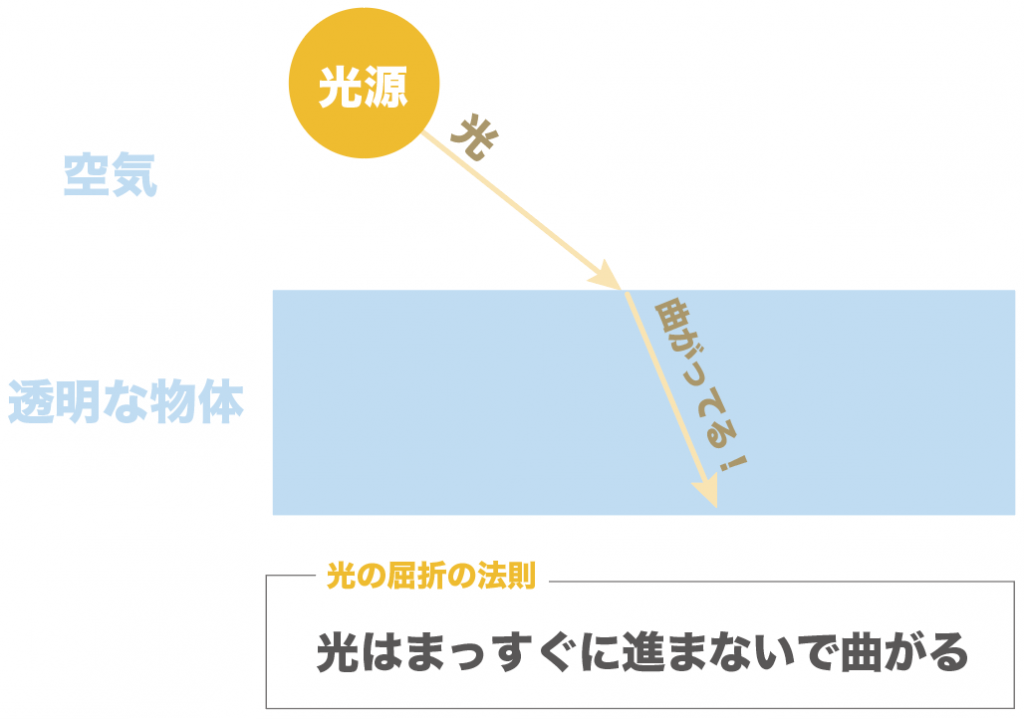
だいたい光の屈折の法則はわかって来た。
だけどさ、
この光の屈折の法則って覚えづらくない??
どっちのパターンの時に、入射角が大きくなるとか屈折角が小さくなるとか、もうね、勘弁して欲しいよ。
そんなときは次の光の屈折の法則の覚え方を使ってみて。
ヤクザの事務所に乗り込む親父をイメージしてくれ。
覚え方はズバリ、
入り口では屈しなかった親父も、帰りは屈してしまった
だ。
ここでは、ヤクザの事務所を「透明な物体」、事務所の外側を「空気」としているよ。
さすがに頑固でマッチョな親父も組織的なヤクザには勝てなかったみたいね。
行き(空気中から透明な物体へ)は、屈しなく、入射角の方が大きかったんだけど、
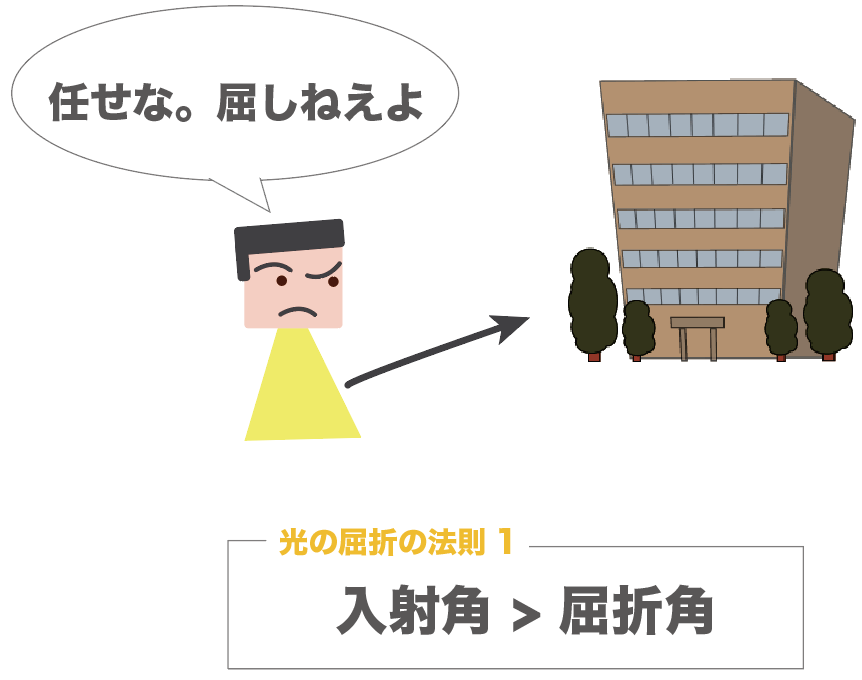
帰り(透明な物体から空気中へ)は、屈してしまい、屈折角の方が大きくなってしまったんだ。
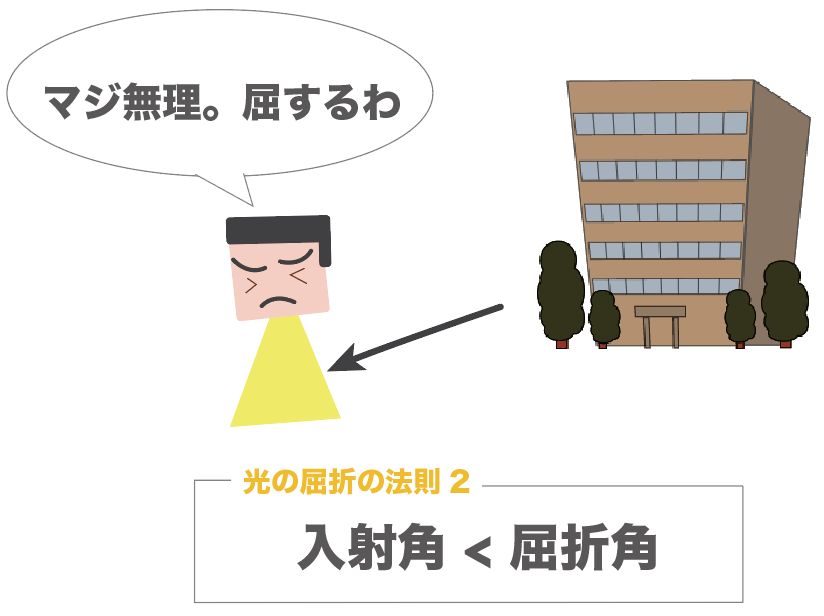
光の屈折の法則では、
の大小だけを語っている法則だから、2つのパターンにおいてどっちの角度の方が大きくなるってことを覚えておけばいいね。
そんじゃねー
Ken