みんな元気?「そら」だよ(^_-)-☆

今日は中学3年生で勉強する、
「2乗に比例する関数」
にチャレンジしていくよ。
この単元ではいろいろな問題が出てきて大変なんだけど、
まずは、一番基礎の、
2乗に比例する関数とは何もの??
を振り返っていこうか。
=もくじ=
中学3年生で勉強する関数は、
y = ax²
ってヤツだよ。
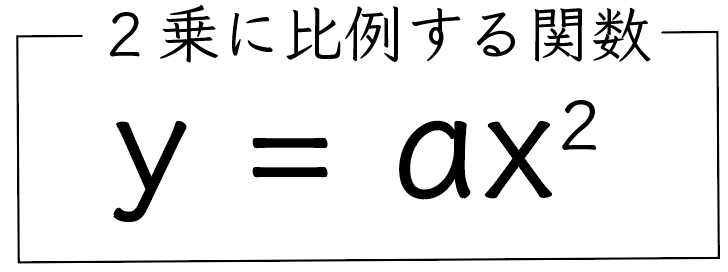
1年生で習った比例y=axの兄弟みたいなもんだね。
xが2乗されてる比例の式だ。
この関数にあるxを入れてやると、
2乗されて、それにaをかけたものがyとして出てくるんだ。
たとえば、aが6の場合の、
y = 6x²
を考えてみて。
このxに「3」を入れてみると、
「3」が2回かけられて、そいつにaの「6」がかかるとyになるよね?
だから、x = 3のときは、
y = 6×3×3 = 54
になるね。
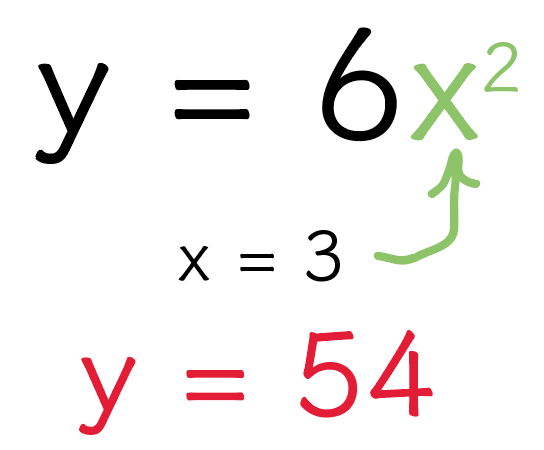
こんな感じで、
関数がxの二次式になっている関数を、
2乗に比例する関数
って呼んでいるんだ。
2乗に比例する関数って形がすごいシンプル。
覚えなきゃいけない言葉も少ないんだ。
たった1つでいいよ。
それは、
っていう言葉。
これは中1で勉強した比例の「比例定数」と同じだよ。
2乗に比例する関数の中で、
xがいくら変化しても変わらない数を、
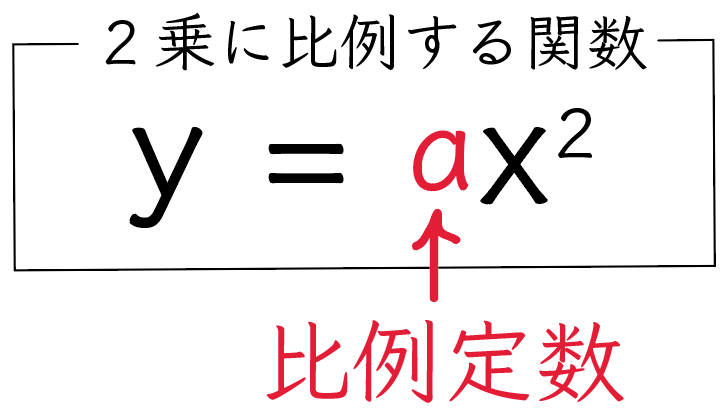
比例定数
って呼んでるんだ。
y=ax²
の関数の式だったら、
a
が比例定数に当たるよ。
y = 6x²
だったら、「6」が比例定数ってわけだね。

問題でよくでてくるから、
2乗に比例する関数の比例定数をいつでも出せるようにしておこう。
じゃ、2乗に比例する関数のグラフを描いてみよう!
y = ax²のa、x、 yを表にまとめてみよっか。
比例定数aの値が、
の4パターンの時のグラフをかいてみるね。
>>くわしくは二次関数のグラフのかき方の記事を読んでみてね。
まず、xとyが整数になる時の値を考えてみると、
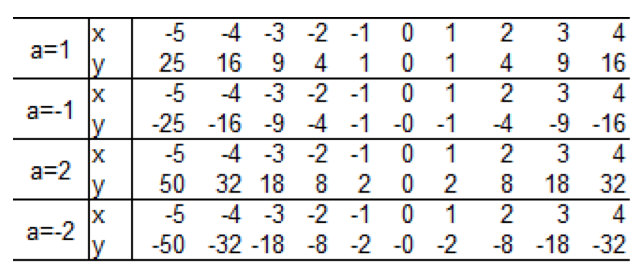
こうなる。
これを元に二次関数のグラフをかいてやると、
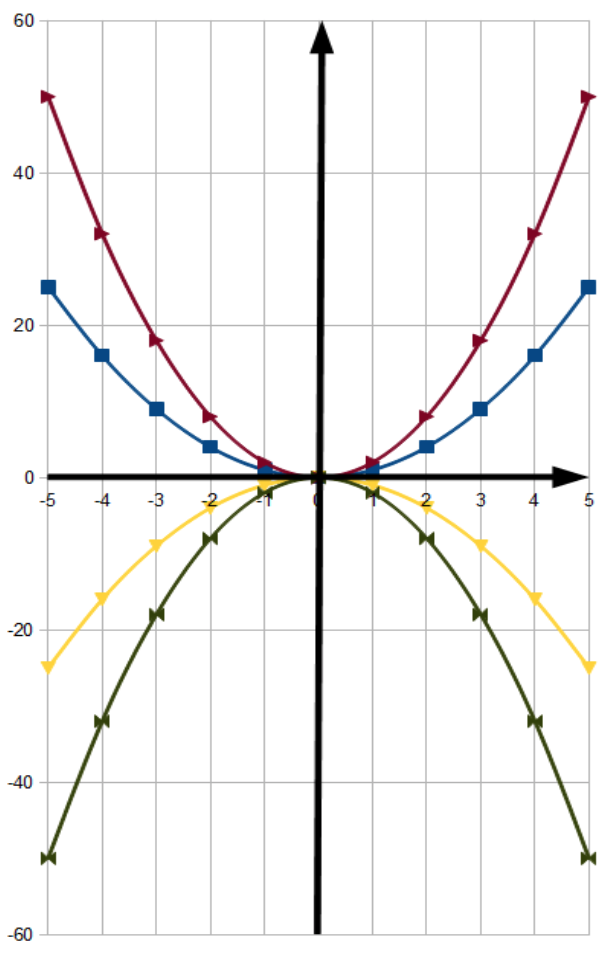
こうなるよ。
なんか山みたいでしょ?
こういうグラフを「放物線」と読んでるんだ。
グラフの特徴としては、
っていうのがあるよ。
>>くわしくは放物線のグラフの特徴の記事を読んでみてね。
2乗に比例する関数はどうだったかな?
基本は1年生のときの比例と変わらないよね?
おさえておくべきことは、
の3つ。
基礎をしっかり復習しておこう。

そんじゃねー
そら
やあ、 Dr. リードだよ!!
今日は平行線にはさまれた線分の比の定理を証明するよ。
つぎの2つの定理を証明していくんだ。
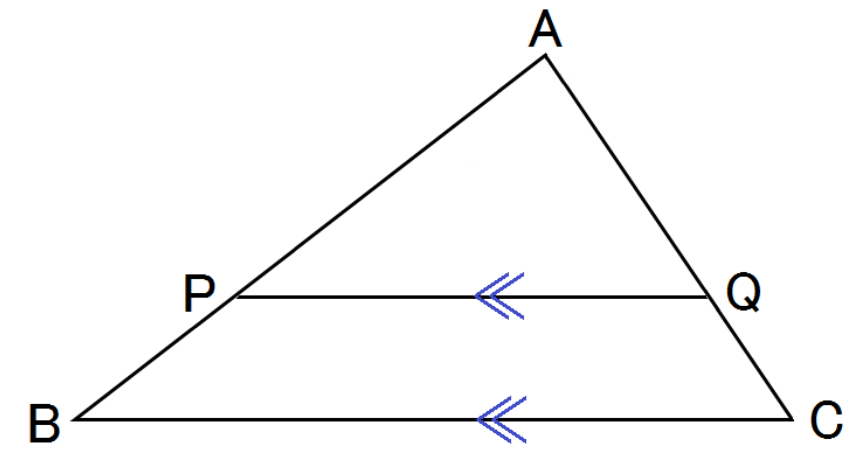
△ABCの辺AB・AC上の点をそれぞれP・Qとするとき、
ところで、今日はケーキを用意したぞ。
最近よく頑張ってるみたいだし。
ごほうびだ。
ちょっと注目して欲しいんだけど、
スポンジとクリームが見事な平行線をつくってるだろ。
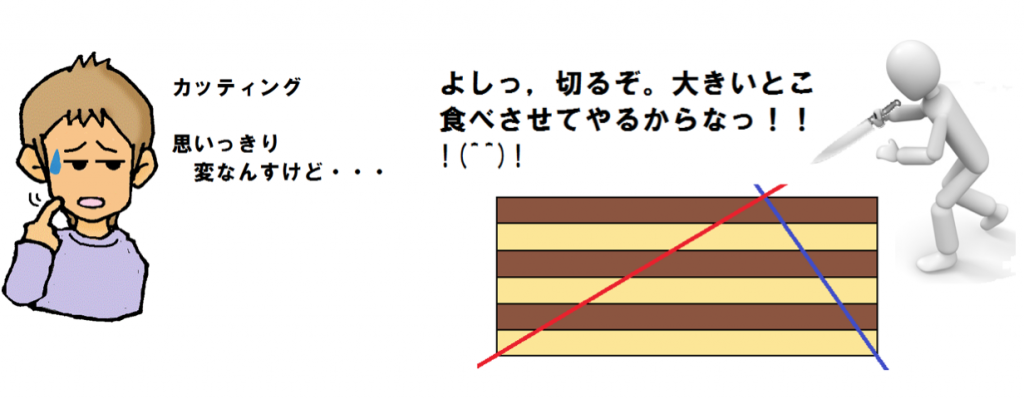
「クリーム」と「スポンジの切り口」の長さは左側でも右側でも、
それぞれ一緒だろ?
よ~く目に焼き付けといてくれよ。
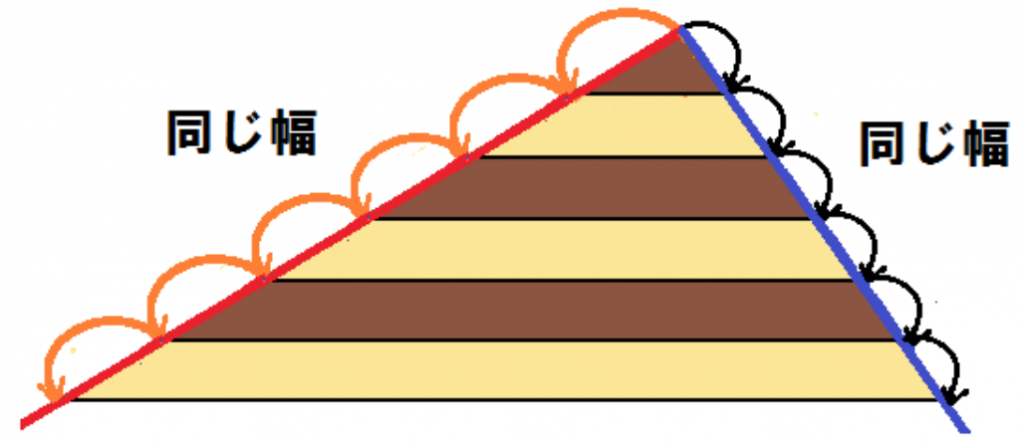
平行線と線分の比の定理を忘れそうになったときは、
カットしたケーキをイメージしてくれよな。
さっそく、2つの定理の証明をしていくぞ。
平行線と線分の比の証明の1つめ。

△ABCの辺AB・AC上の点をそれぞれP・Qとするとき、
PQ//BCならば、 AP:AB = AQ : AC = PQ : BC
こいつはズバリ、
で2つの三角形の相似を証明をしていけばいいのさ。
以下、証明な↓↓
△ABCと△APQにおいて、
PQ∥BCなので、
∠ABC = ∠APQ (平行線の同位角は等しい)①
∠ACB = ∠AQP (平行線の同位角は等しい)②
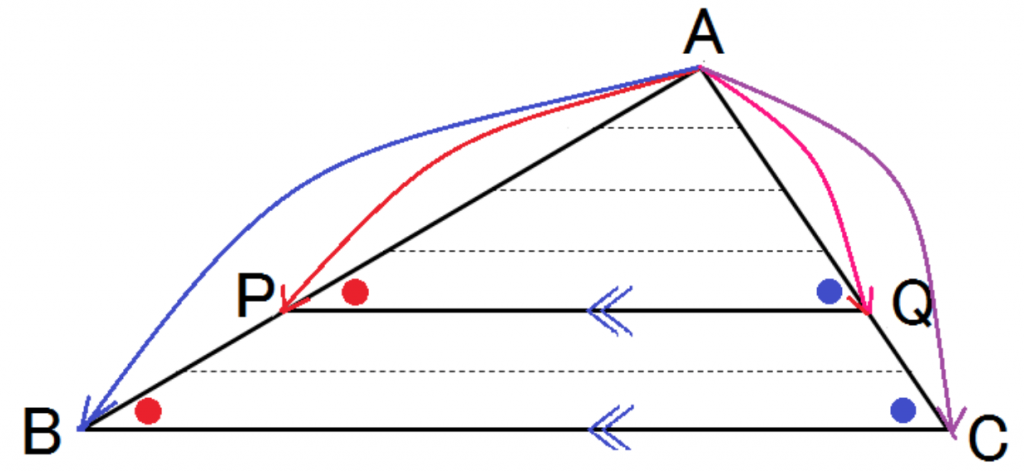
①・②より、
2つの三角形の2組の角がそれぞれ等しいので、
△ABC ∽ △APQ
よって、PQ∥BCならば、
AP:AB = AQ:AC = PQ:BC である。
2つの三角形の相似を証明するだけだから簡単だね。
つぎは2つ目の平行線と線分の比の証明だ。

△ABCの辺 AB、AC上の点をそれぞれ点をP・Qとするとき、
PQ // BCならば、
AP : PB = AQ : QC
を証明していけばいいんだね。
まず、補助線を引くぞ。
点Pを通り辺ACに平行な直線PRを引いてみるよ。
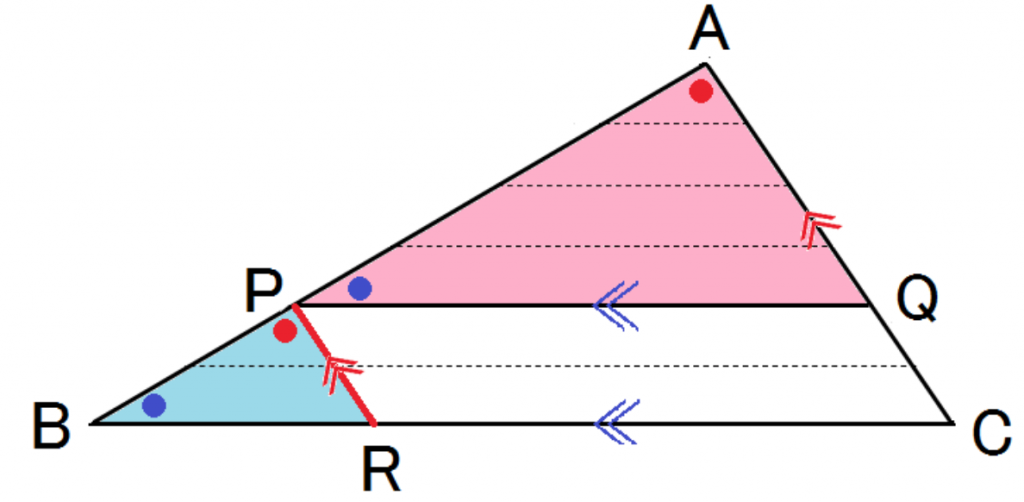
以下、証明な↓↓
△APQと△PBRについて、
PQ∥BCなので、
∠APQ=∠PBR(平行線の同位角は等しい)①
PR∥ACなので、
∠APQ=∠PBR(平行線の同位角は等しい)②
2つの三角形の2組の角がそれぞれ等しいので
△APQ ∽ △PBR
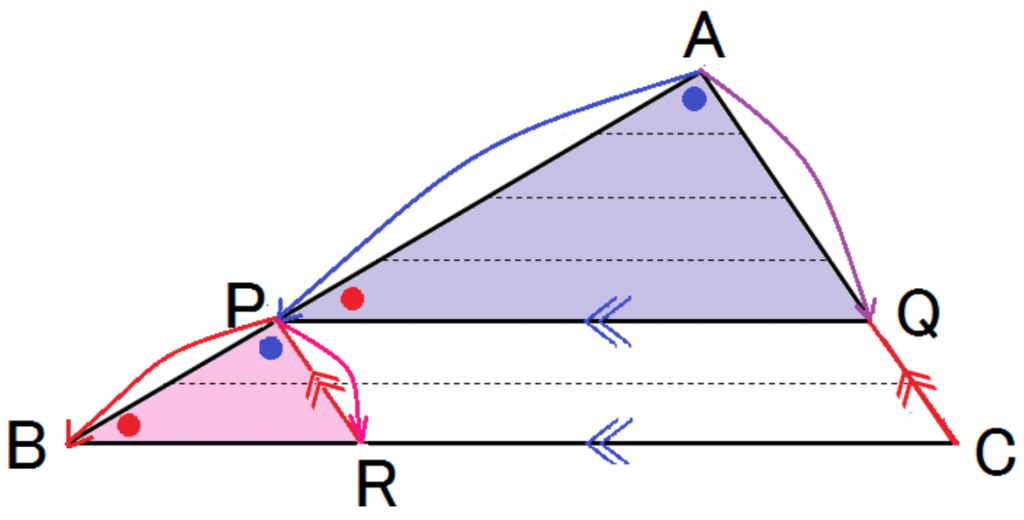
よって、AP:PB = AQ:PR・・・ ③
また,PQ∥BC,PR∥ACなので、
四角形PRCQは平行四辺形で、
PR = QC・・・④ (平行四辺形の向かい合う辺の長さは等しい)
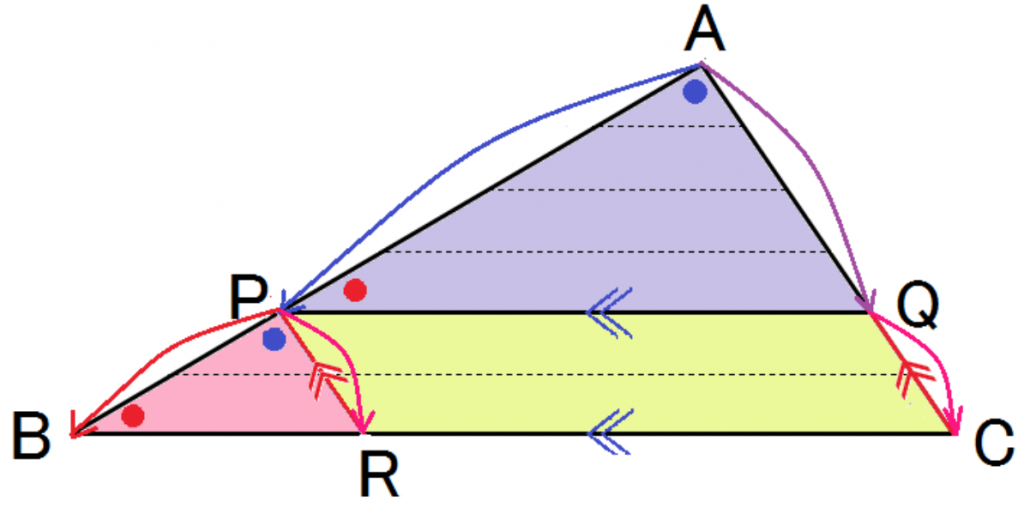
③と④より、
AP:PB = AQ:PR = AQ:QC
やった!
平行線と線分の比の証明もできるようになったね。
平行線と線分の比の証明はどうだったかな?
定理①はすぐ思い浮かぶけど、定理②は忘れちゃいがち。
2つの定理に共通してるのは、
同位角をつかって三角形の相似を証明する
ってこと。
しっかり覚えてくれよ。ケーキだよ。ケーキ。
今回はここまでね。
じゃ、お茶にしよう。


Dr.リード
やあ、がんばってるかい? Dr.リードだよっ。
相似の勉強もそろそろ終盤戦だ。
年間スケジュール達成のため、学校でもさらーっと流すことが多い。
そのペースに流されることなく、じっくり取り組んでほしいぞ。
今日のトピックは、
相似な立体同士にみられる性質
だ。
さっそく、相似な立体同士の性質を3つ紹介していくよ。
まず1つ目の性質は、
相似な立体同士の線分の長さの比は等しい
ってヤツだ。
立体じゃなくて、平面図形の相似の性質があったよね?
それと同じさ。
たとえば、りんごジュースを買いにいったとしよう。
リードのジュースは君のより3倍でかい。
重いぞ。
飲みごたえたっぷりだ。
お得な3倍サイズって書いてあったんだよ。
ってことは、
は拡大縮小の関係になってるから、相似だよな。
で、対応する縦、横、高さの比を比べてみる。
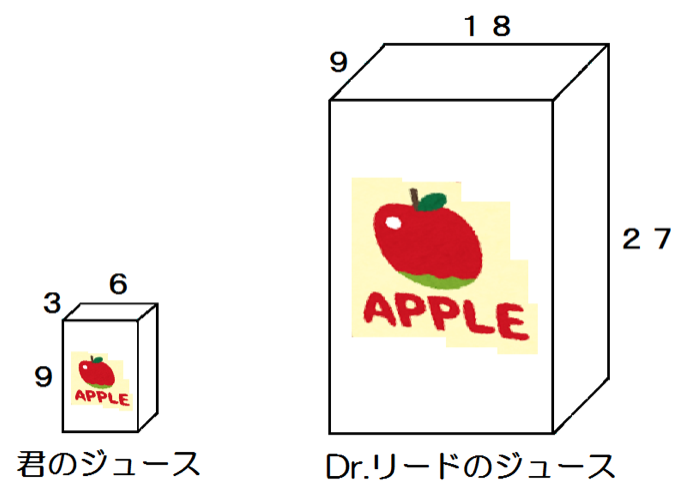
まっ、当たり前だけど、平面図形と同じで、対応する辺の比は同じだったぞ。
どの辺の長さも3倍になってるね!
こんな感じで、
相似な立体同士は各辺の相似比が一緒なんだ。
次の相似な立体の性質は、
表面積の比は相似比の2乗になる
ってヤツだ。
たとえば、次の立方体が2つあったとしよう。
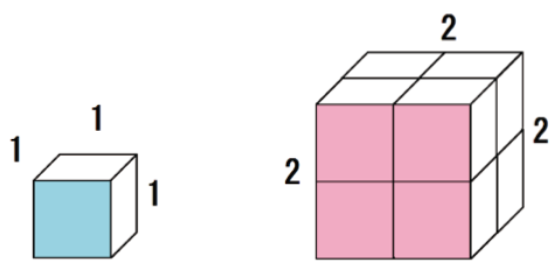
立体の相似比は1:2だから、表面積比はその2乗で、
1 : 4
になるってわけ。
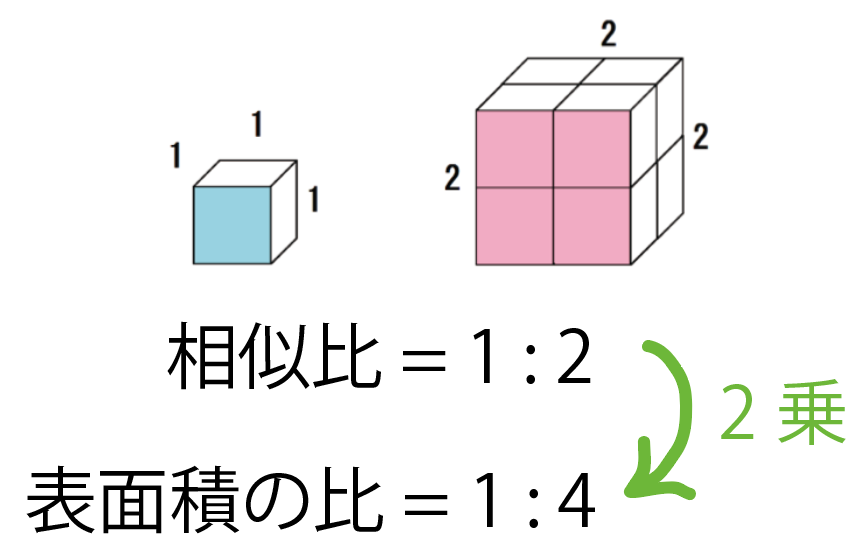
本当かどうか確かめよう。
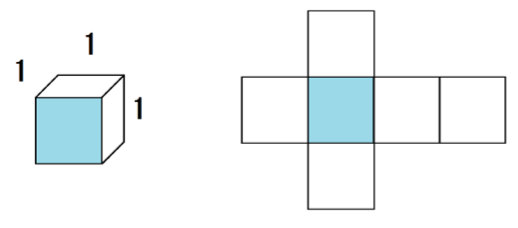
表面積だから、展開図も書いてたしかめてみるな。
1×1×1の立方体の1つの面の面積は1 cm²。
よって、表面積は、
1×6 =6 cm²
だ。
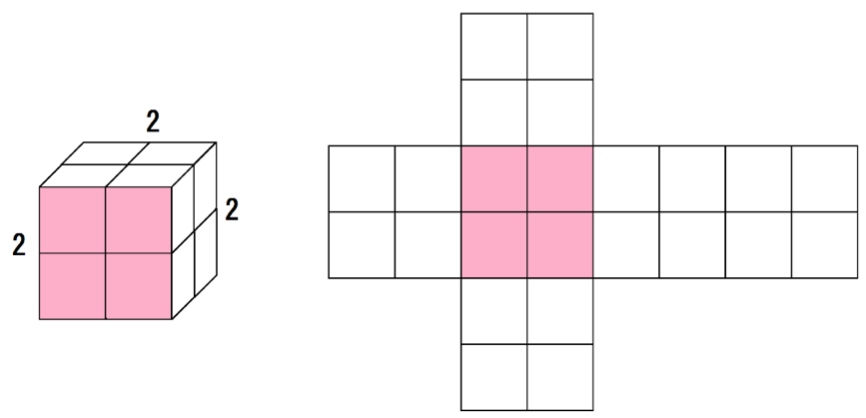
一方、相似比2倍の立方体はどうだろう??
立方体の1つの面の面積は4 cm²。
よって、表面積は、
4×6 = 24 cm²
になるね。
よって、表面積の比は、
6: 24 = 1 : 4 = 1² : 2²
相似な立体同士の表面積の比は、相似比1:2の2乗になってるね。
えっ。
相似比が1:3の場合でも表面積の比は1:3なのかって?!
疑い深いならたしかめてみようか。
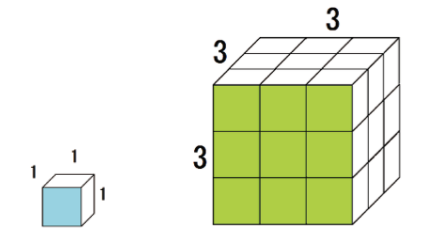
立方体の各辺が3倍になるとだな、
2つの立体の相似比は、
1 : 3
になるね?
1つの面の面積は、
3×3 = 9 cm²
よって、表面積は、
9×6 = 54 cm²
1辺の長さが1cmの立方体との表面積の比は、
6 : 54
= 1: 9 = 1² : 3²
になるね。
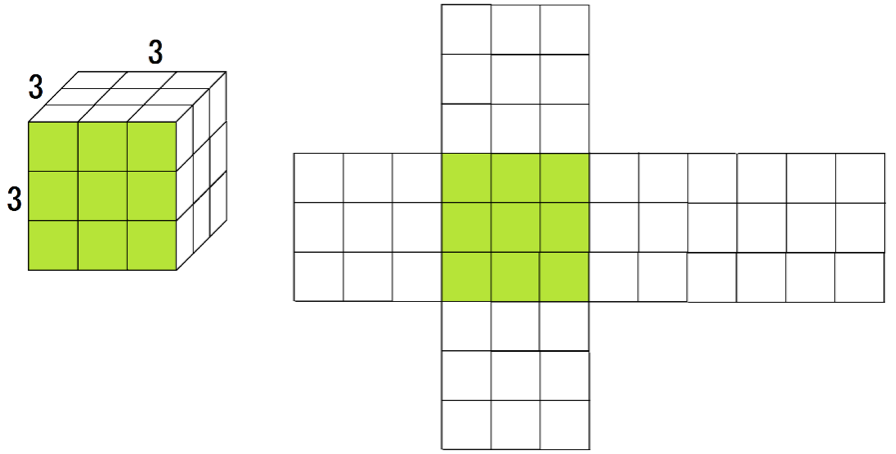
ねっ、今回も相似比の2乗になったぞ。
しかし、永遠に何倍何倍って確かめるわけにもいかんわな。
何倍かわからんがとりあえず、
「k倍」ってことにしてみるぞ。

1辺の長さが、
の直方体で考えてみよう。
これをk倍してみると、
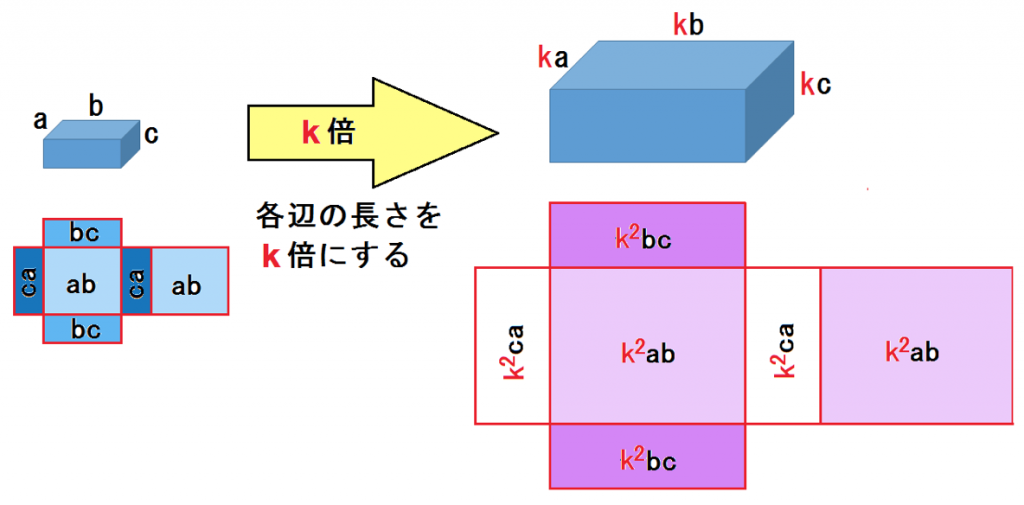
じゃーん!!!
やっぱり相似比の2乗になったね。
ってことで、相似な立体同士の表面積の比は相似比の2乗になってるんだ。
最後の性質は、
相似な立体同士の相似比と体積比の関係だ。
おっ、なんかもうわかってる感じだな。
そう。
体積比は相似比の3乗になるんだ。
たとえば、さっきの3つの立方体をみてみよう。
相似比が1:2の立方体の体積比なら、
1³: 2³ = 1 : 8
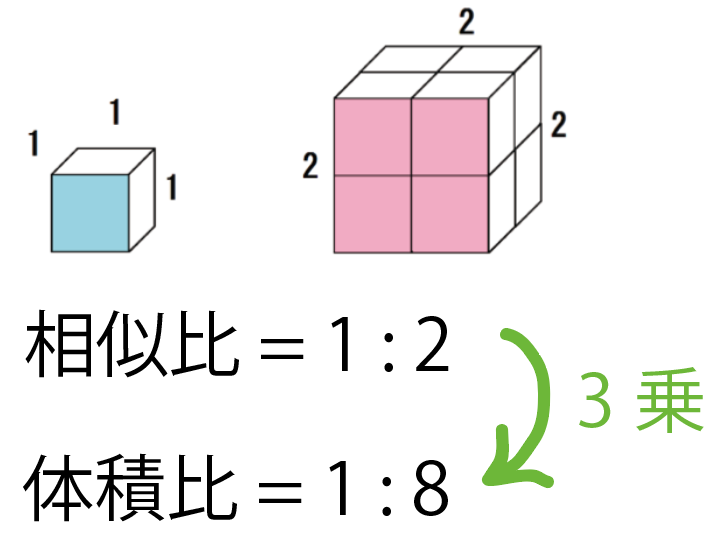
相似比が1:3の立方体なら、
体積比 = 1³ : 3³ = 1 : 27
になるってわけ!
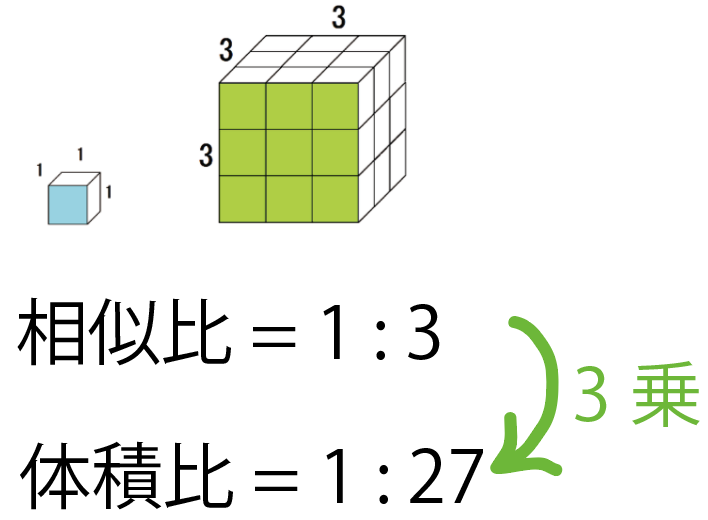
念のため、k倍のも確認すると、
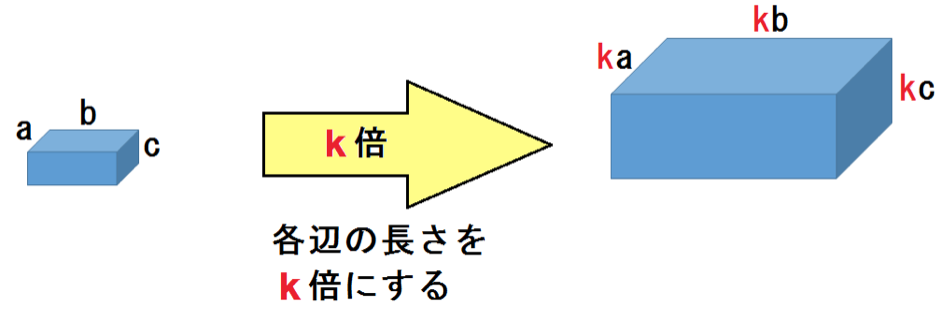
体積比
= abc : k³abc = 1 : k³
になるね。
ほいっ、確認完了だ。
相似な立体どうしの3つの性質を頭に入れとこう!
表現を変えると、
相似な立体の相似比が m : nならば、
表面積比は m² : n²、
体積比は m³ : n³、
ご存じ、ロシア土産の定番「マトリョーシカ人形」。
1900年のパリ万博には出品されていたらしいね。
マトリョーシカ人形は一説では日本の「入れ子」に起源をもつという説や、ロシアの木工品だとか、諸説あるでござる。
相似な立体のどうしの性質を面白おかしく記憶にとどめてもらうために、ご出演願ったよ。

それじゃあな!
Dr.リード
Dr.リードだよっ。
円周角の定理の使い方にも慣れてきたかな?
今日はな、
円周角の定理の証明
を解説していくぞ。
つまり、
なぜ、円周角の定理が使えるのか??
ってことを暴いていくわけだ。
別に知らなくてもいいけど、知っておいた方がスッキリするだろ?
今日は長い長い話になる。
ピザでも食べながら行ってみよう!


「円周角の定理」を証明していくぞ。
3点A・B・Pがある円Oを想像してくれよな。
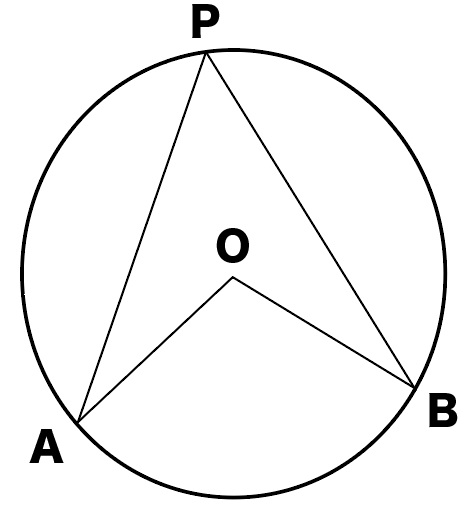
円周角と中心角の位置関係はつぎの3通りある。
それぞれの場合を証明していけばいいんだ。
まずは点P がOBの延長上にきてる場合ね。
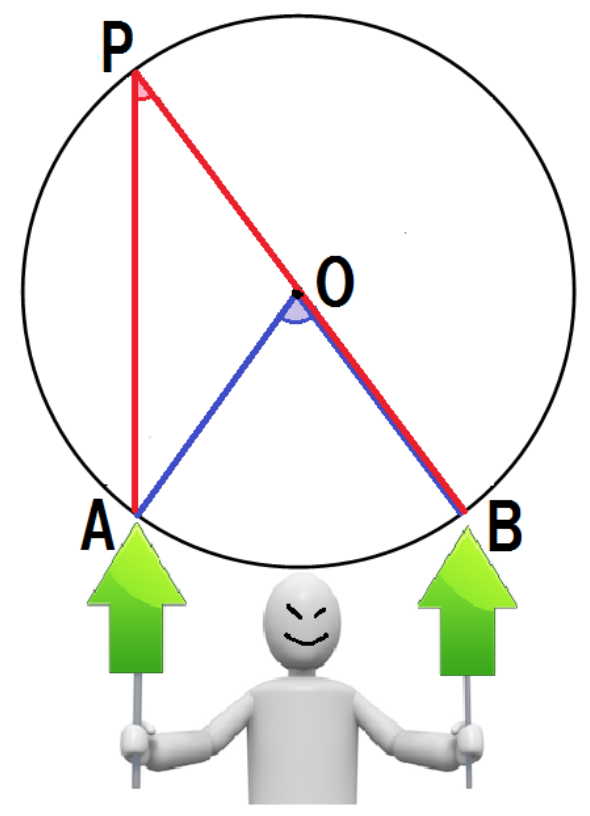
このパターンでは、
をうまく使っていくよ。
えっ。三角形の外角の定理なんて忘れた?!
三角形の1つの外角はそれと隣り合わない2つの内角の和に等しい
っていう定理だったね。
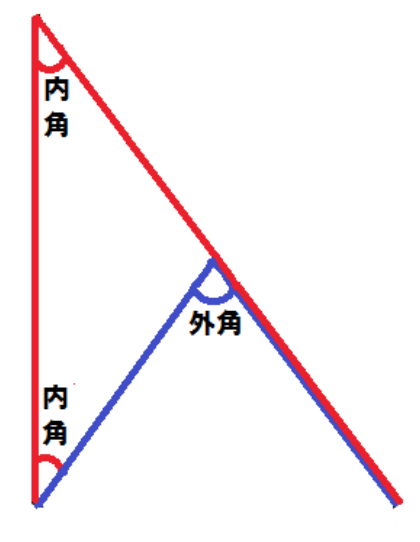
こいつをうまく使って証明してみよう。
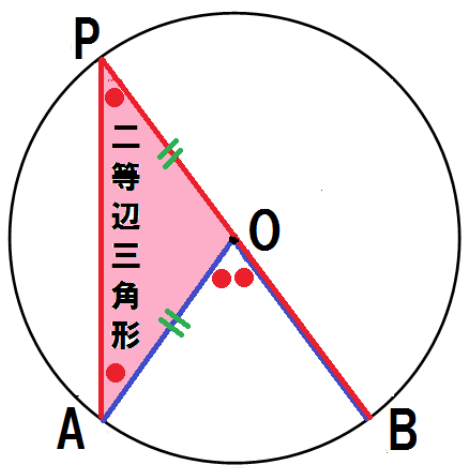
OP・OAはそれぞれ円Oの半径だから、
OP = OAよって、△OPAはOP = OAの二等辺三角形である。
二等辺三角形の底角は等しいから、
∠OAP = ∠OPA ・・・ (1)三角形の外角の定理より、
∠AOB = ∠OAP + ∠OPA・・・(2)
(1)、(2)より、
∠APB = 1/2∠AOB
「二等辺三角形の性質」と「外角の定理」を知ってれば証明できるね!
さあ、サクサク行くぞ。
つぎは、
中心Oが円周角の内部におさまってる形だ。
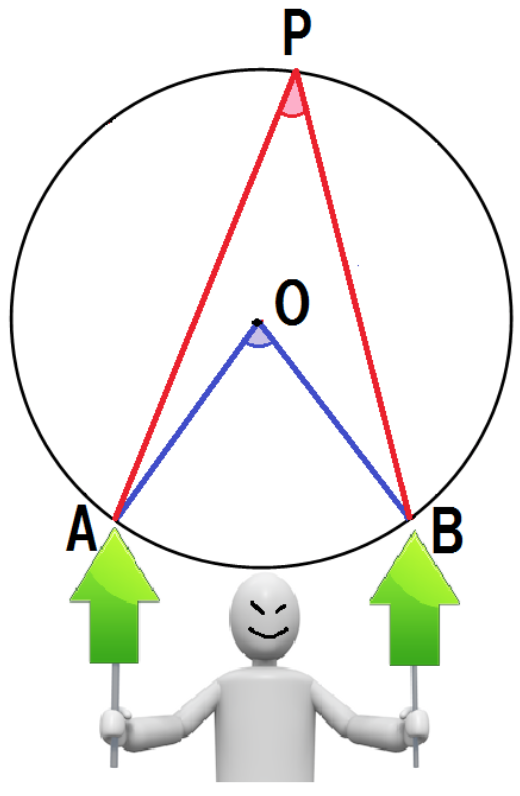
補助線を緑で引いていくぞ。
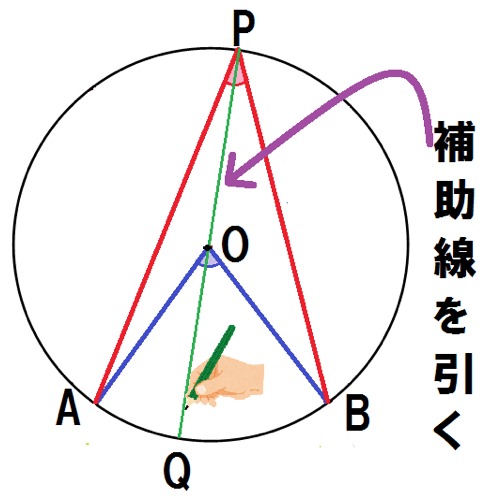
点Pと中心Oを結び延長して、交点をQとしよう。
中心を通るから、PQは円Oの直径ってことになるね。
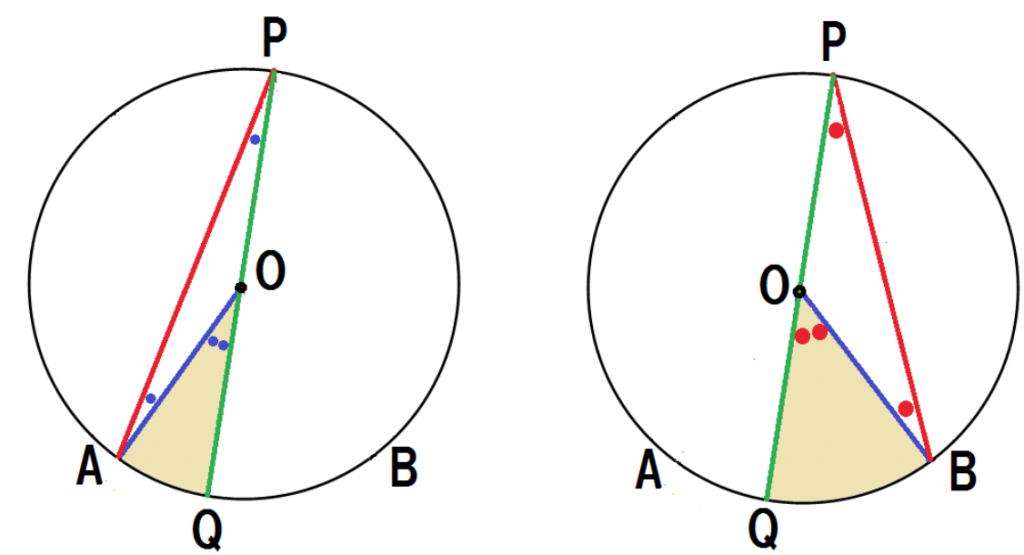
上の図みたいに補助線を中心に2つの図形に分けてみて。
の順番で証明していくよ。
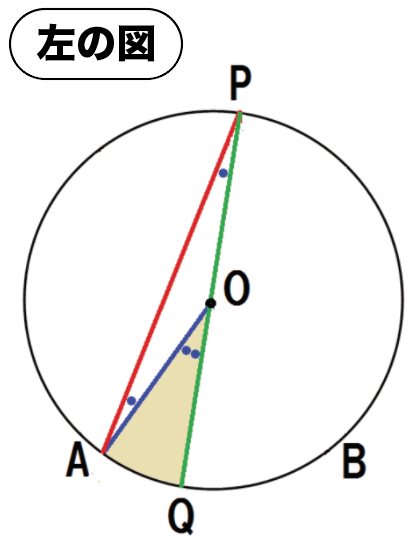
OP・OAはそれぞれ円Oの半径だから、
OP = OA
よって、△OPAはOP = OAの二等辺三角形である。
二等辺三角形の底角は等しいから、
∠OAP = ∠OPA ・・・ (1)
三角形の外角の定理より、
∠AOQ = ∠OAP + ∠OPA・・・(2)
(1)、(2)より、
∠APQ = 1/2∠AOQ・・・(3)
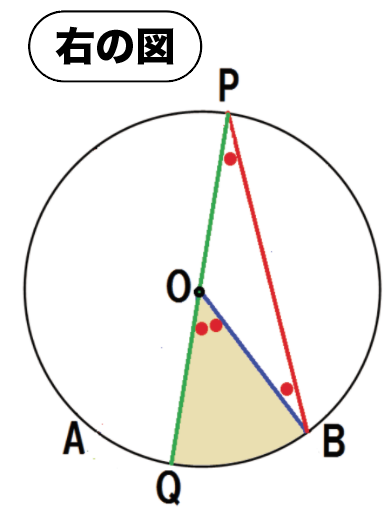
OP・OBはそれぞれ円Oの半径だから、OP = OB
よって、△OPBはOP = OBの二等辺三角形である。
二等辺三角形の底角は等しいから、
∠OBP = ∠OPB ・・・ (4)
三角形の外角の定理より、
∠BOQ = ∠OBP + ∠OPB・・・(5)
(4)、(5)より、
∠BPQ = 1/2∠BOQ・・・(6)
で,右半分の図と左半分の図を元通りに重ね合わせると,
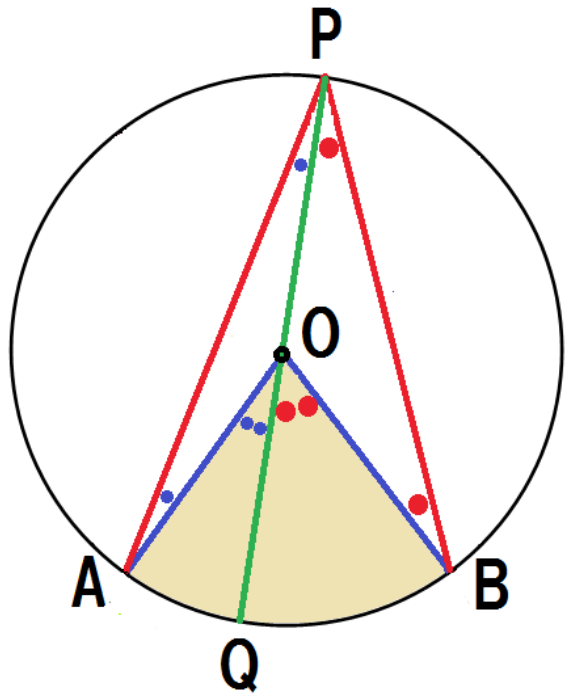
(3)+(6)より、
∠APQ +∠BPQ= 1/2∠AOQ + 1/2∠BOQ
よって、
∠APB = 1/2∠ AOB
よって、
円周角∠APBは中心角∠AOBの半分である。
最後は、
中心Oが∠APBの外にあるパターンね。
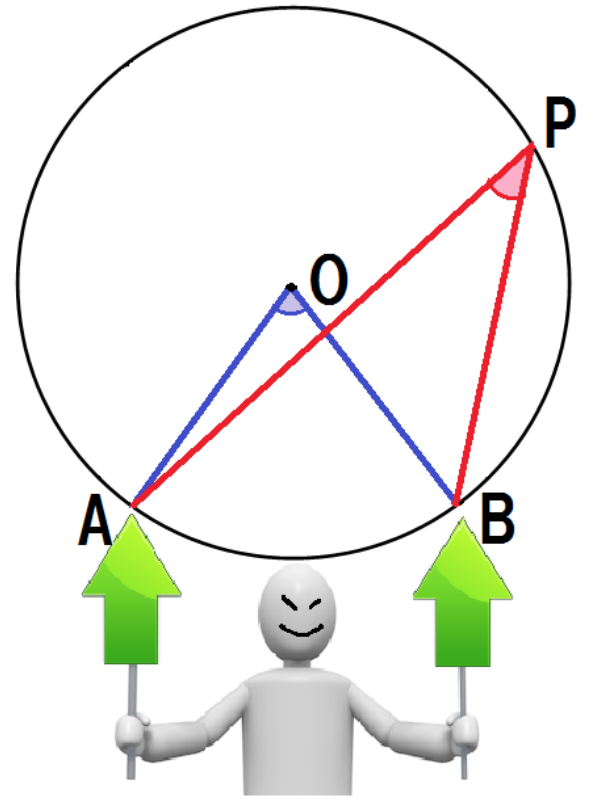
またまた補助線引くよ。
OPを延長した線分と円周の交点をQとするぞ。
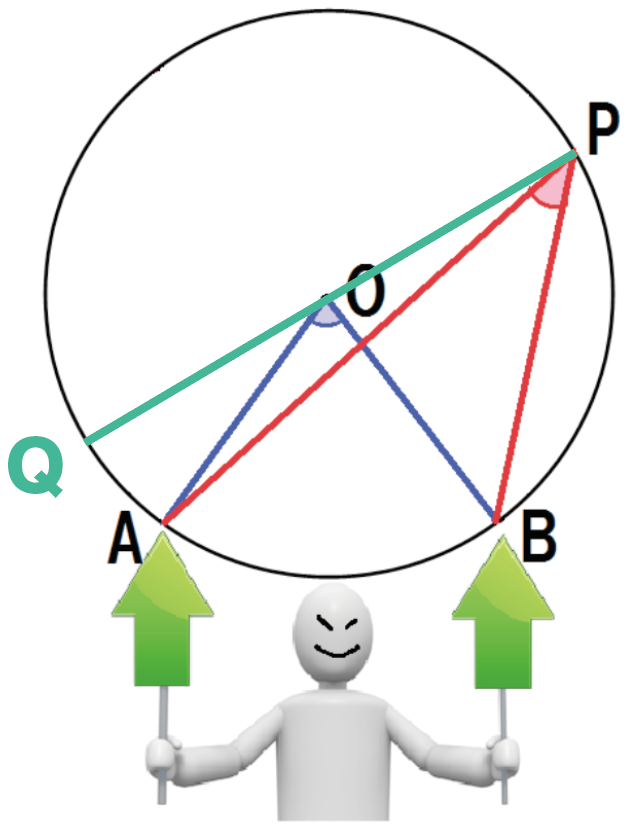
ややこしいから、目を皿のようにして見とけよ!

同じように図形を分解して、見やすくしてみるね。
重なりをバラバラにして、
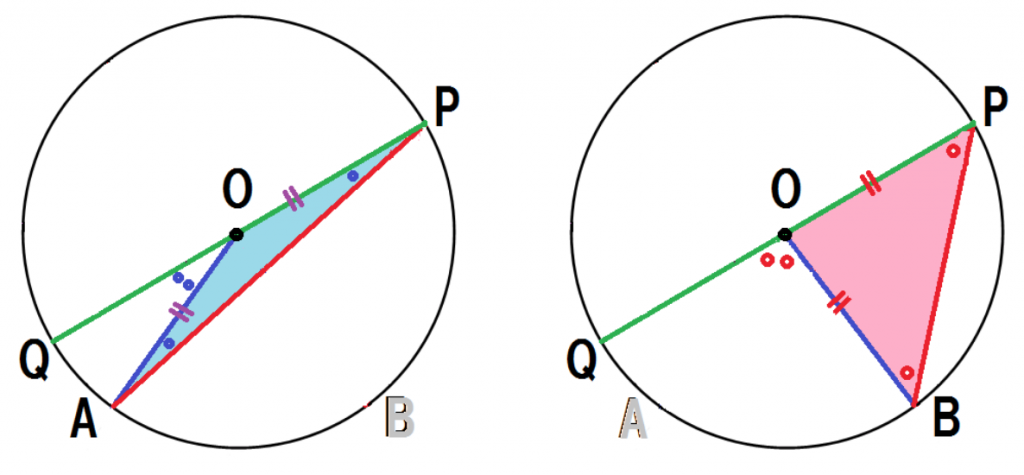
左と右でそれぞれ分けて考えてみるよ。
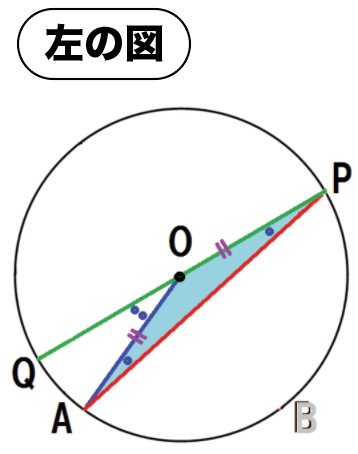
OP・OAはそれぞれ円Oの半径だから、
OP = OA
よって、△OPAはOP = OAの二等辺三角形である。
二等辺三角形の底角は等しいから、
∠OAP = ∠OPA ・・・ (1)
三角形の外角の定理より、
∠AOQ = ∠OAP + ∠OPA・・・(2)
(1)、(2)より、
∠APQ = 1/2∠AOQ・・・(3)

OP・OBはそれぞれ円Oの半径だから、
OP = OB
よって、△OPBはOP = OBの二等辺三角形である。
二等辺三角形の底角は等しいから、
∠OBP = ∠OPB ・・・ (4)
三角形の外角の定理より、
∠BOQ = ∠OBP + ∠OPB・・・(5)
(4)、(5)より、
∠BPQ = 1/2∠BOQ・・・(6)
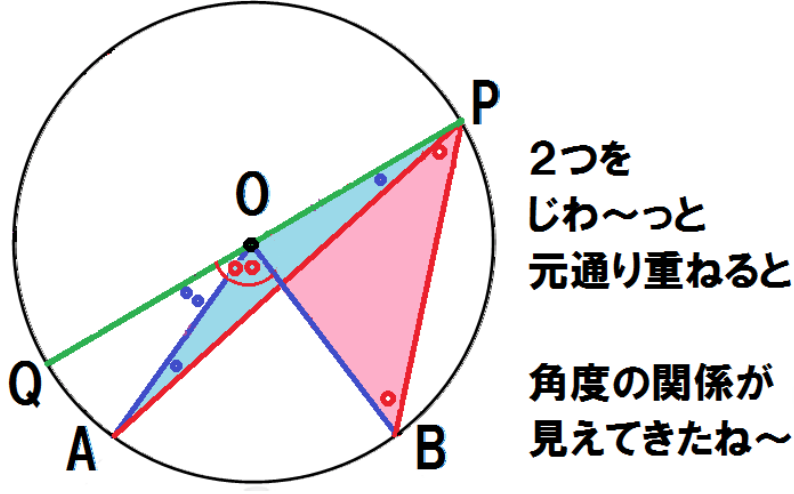
(3)・(6)より、
∠BPQ -∠APQ = 1/2∠BOQ – 1/2∠AOQ
よって、
∠APB = 1/2∠AOB
よって、
円周角∠APB は∠AOBの半分である。
円周角の定理の証明はどうだったかな??
つぎの3パターンの証明ができればよかったよね?
3パターンとも証明しちゃったんだから使いホーダイ。

円周角の定理を心気なくガシガシ使っていこう。
じゃあな。
Dr.リード
ある日、数学が苦手なかなちゃんは、
円周角の定理の逆をつかった問題が解けなくて困っていました。
練習問題
四角形ABCDで、∠x、∠yの大きさを求めなさい。
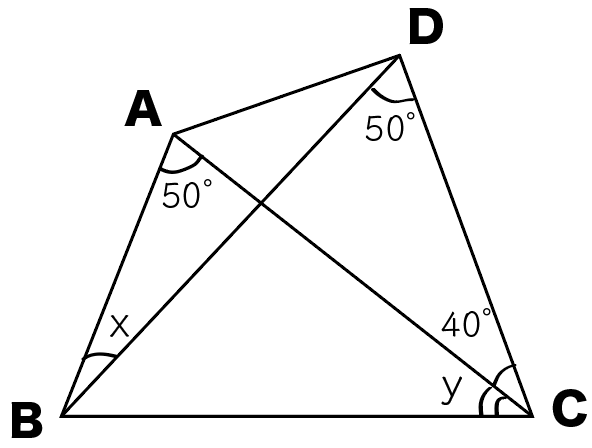
どうしよう……
どうしたの?
困ってそうだね。
やらないと友だちと遊びに行けない……
なるほど。
それは困ったね
でしょ?
この問題、角度いっぱいわかるのにムズイ!
えーっと、ふむふむ。。
おっ、これはっ……!?
これは……?
円周角の定理の逆を使えば一発さ!
え?
練習問題
四角形ABCDで、∠x、∠yの大きさを求めなさい。
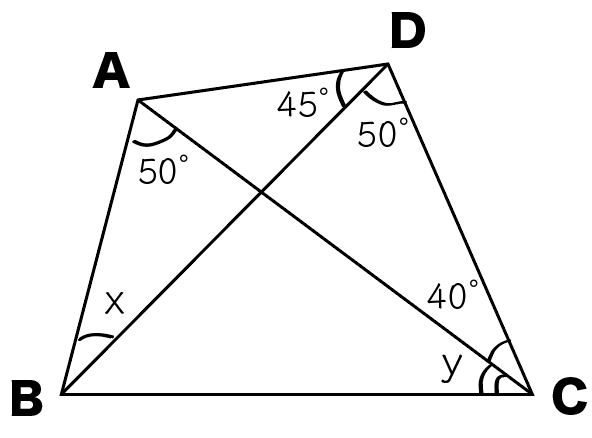
この問題では、
円周角の定理の逆をつかえばいいんだ。
えっと。。。
円周角の定理の逆ってなんだっけ?
そんなときのために用意しておいたよ
☆円周角の定理の逆☆
2点C・Pが直線ABについて同じ側にあるとき、
∠APB=∠ACBならば4点A、B、C、Pは同じ円周上にある。
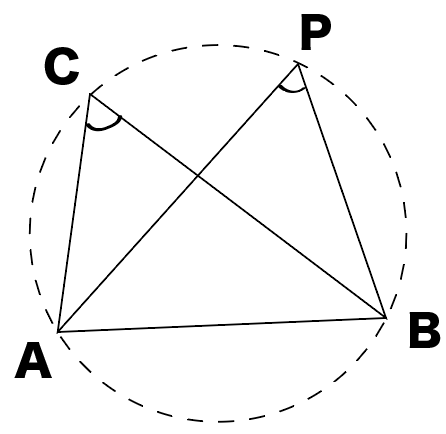
この前習ったやつだ!
だよね。
「円周角の定理の逆」を使えば2ステップで解けちゃうんだ。
図形の点が同じ円周上にあるか確認しよう!
円周角の定理の逆を使ってね。
すぐに見つける方法ないの?
同じ大きさの角を見つけることかな!
同じ50度の角が2つある!!
そう!
記号で書いてみると?
∠BAC=∠BDCでしょ?
おっ、いい感じ!
円周角の定理の逆を使ってやると、
4点A・B・ C・Dは同じ円上にあることがわかるね〜
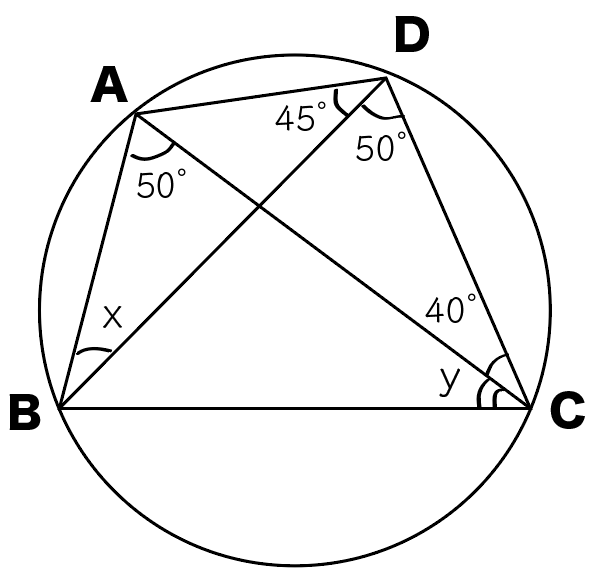
同じ弧の円周角をみつけよう!
同じ弧ADの円周角みっけ!
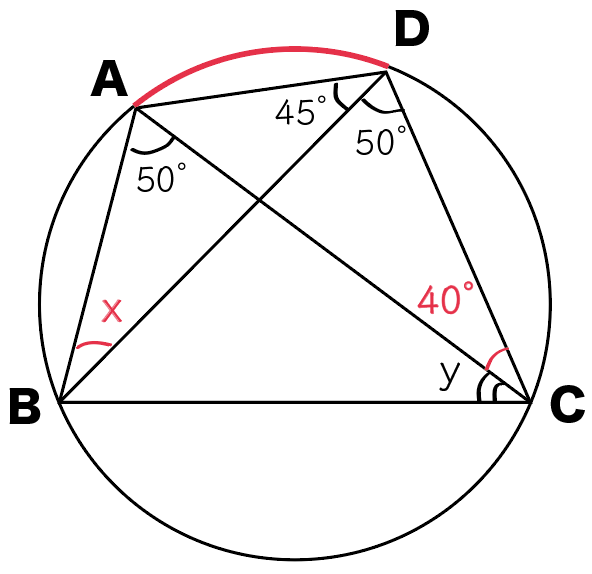
だから、
∠ABD = ∠ACD
x = 40度
になるね。
あとは、
∠ADCと∠ACB!
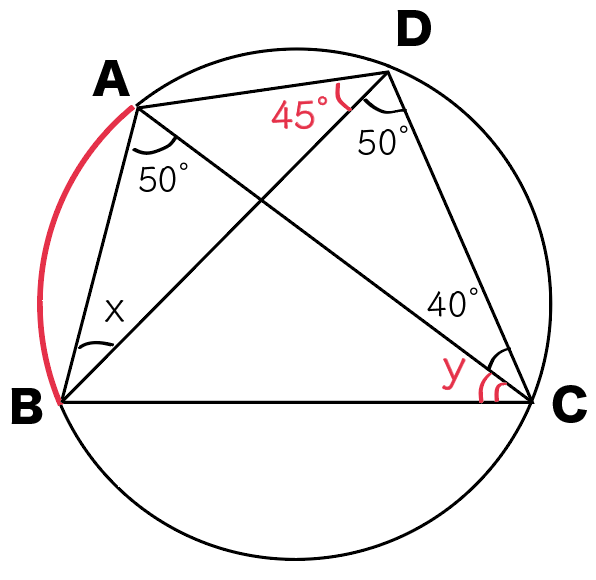
いい感じだね。
∠ADC=∠ACB
y = 45度
だ!
やったー!
円周角の定理の逆なら2ステップで解けちゃうね。
すぐ解けちゃうかも!!
でしょ?
1回使いこなせれば簡単!
たしかに!!
よしっ、解こう……!
あっ、友だちとの約束!!
時間をうまく使って問題を解いてみよう!!
うす!
ある日、数学が苦手なかなちゃんは、
円周角の定理の逆の証明がかけなくて困っていました。
円周角の定理の逆を証明してみよう!
いきなり証明って言われても……
いったん分かると便利!
いろんな問題に使えるんだよな。
円周角の定理の逆って、
そんなに便利なの?
まあね。
円の性質の問題では欠かせないよ。
円周角の定理すら覚えてないのに……
そんなときのために!!
円周角の定理をサクッと復習しよう。
【円周角の定理】
1つの円で弧の長さが同じなら、円周角も等しい
∠ACB=∠APB
なるほど!
少し思い出せた!
【円周角の定理の逆】
2点P、 Qが線分ABを基準にして同じ側にあって、
∠APB = ∠AQB
のとき、
4点ABPQは同じ円周上にある。
ちょっとわかった気がする!
その調子で、
円周角の定理の逆の証明をしてみようか。
はい!!
さっそく、
円周角の定理の逆を証明していくよ。
どうやって?
証明するの?
つぎの3つのパターンで、
角度を比べるんだ。
つぎの円を思い浮かべてみて。
点Pが円の内側にあるとき、
∠ADBと∠APBはどっちが大きい?
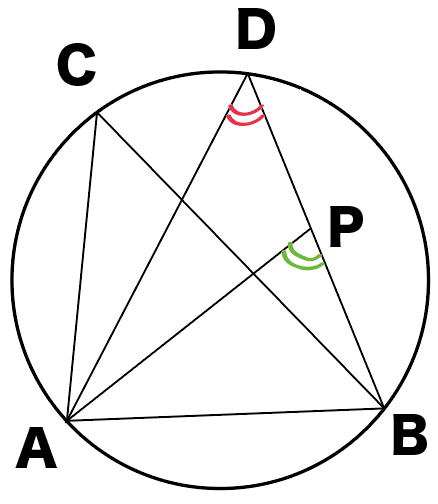
そう!
点 Pが円の外にあるときは?
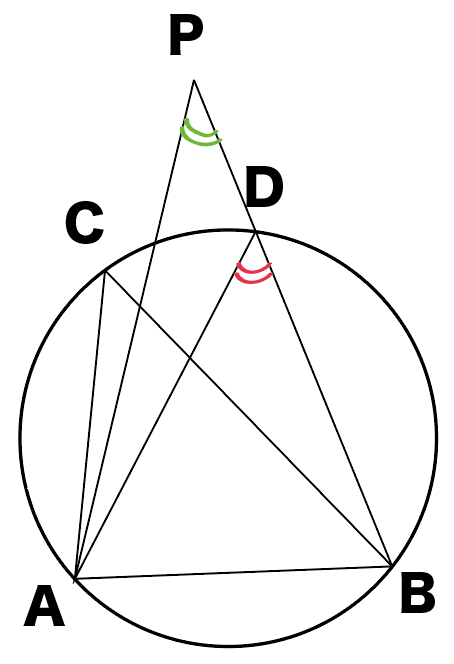
∠ADBの方が大きい!
そうだね!
今わかってることを書いてみよう!
点Pは円の内側になると、
∠ADB<∠APB
になって、
点Pが円の外側になら、
∠ADB>∠APB
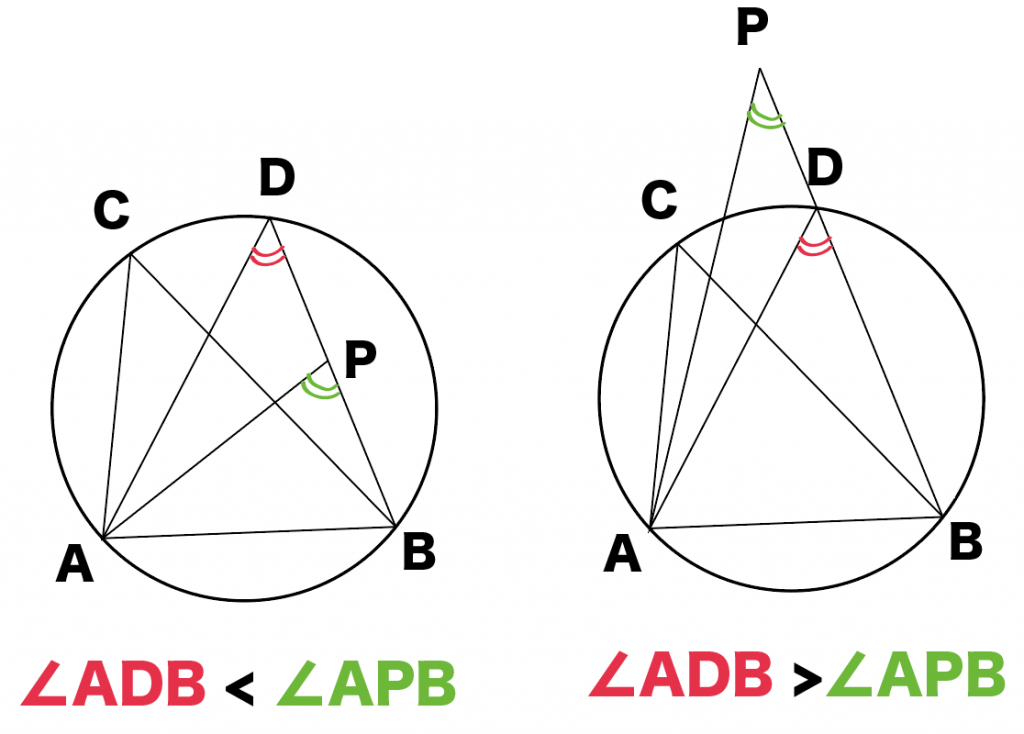
おっ、いい感じだね!
点Pが円上のとき、
∠ADB=∠APB
じゃん!
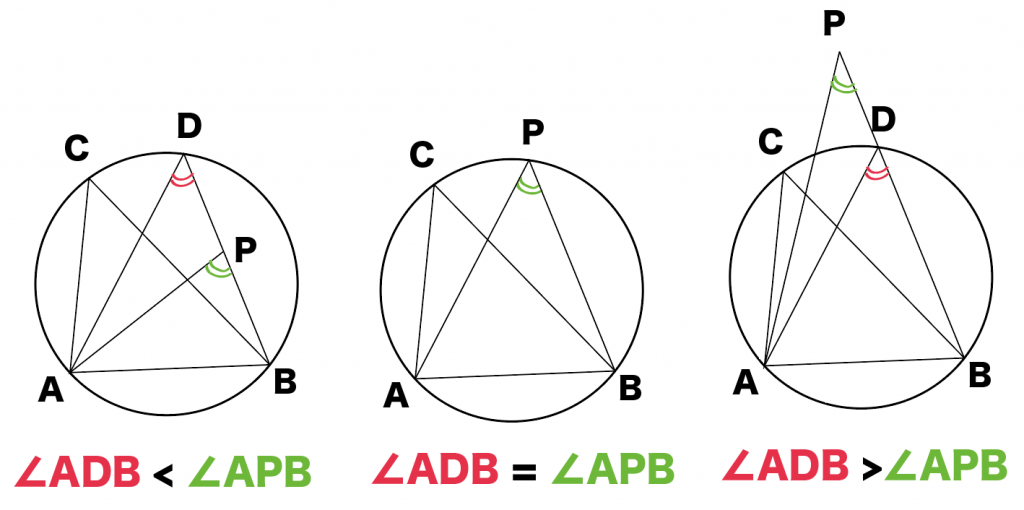
そういうこと!
点 Pが円の内側に入っちゃったり、
円の外側に出ちゃったりすると、
角度は等しくなくなっちゃうよね。
はい!
点 Pが円周上にあるときだけ、
2つの角度が等しくなるってわけ。
なるほど!
ってことは、これが証明なんだ。
そう。
円周角の定理の逆の証明はこれでok。
いつもの証明よりは楽だったかも。
円周角の定理の逆の証明はどうだったかな?
3つの円のパターンを比較すればよかったね。
図を見れば当たり前のことだったなあ
いうねえ
やってみると分かりやすかった!!
まずはあきらめず挑戦してみて!
うす!
どうも!ぺーたーだよ。
中3数学では、
三平方の定理(ピタゴラスの定理)
っていう単元を勉強するよ。
この章が終われば、中3年の数学はほぼ終わり。あともう少し頑張って勉強していこうね。
今回はこの三平方の定理を使った計算問題のうち、
よく出てくる問題の解き方
を3つ紹介するよ。
よかったら参考にしてみて。
=もくじ=
まず問題を解く前に、
三平方の定理(ピタゴラスの定理)を復習しておこう。
これがわからないと問題解けないからね。
三平方の定理(ピタゴラスの定理)とはズバリ、
直角三角形の各辺同士の関係を表した公式
だったよね??
具体的にいうと、
直角三角形の直角を挟む2辺の長さをa、b、
斜辺の長さをcとおくと、
$$a² + b² = c²$$
になるってやつね。

三平方の定理は直角三角形のときに使える
っていうことがとっても大事だよ。
慣れてないと、ふつうの三角形でも使っちゃう人がいるからね。
早速、三平方の定理(ピタゴラスの定理)を使って問題を解いていこう。
今回紹介する問題は次の3つね。
まず三平方の定理(ピタゴラスの定理)を使って、
直角三角形の斜辺を計算する問題
を解いていくよ。
例えば、次のような問題ね。
練習問題1.
次の直角三角形ABCのxの長さを求めなさい。

この問題は直角三角形の斜めの辺、
つまり「斜辺の長さ」を求める問題だ。
三平方の定理はa² + b² = c²だったね。
今は斜辺がx、底辺と高さが3cm、1cmだから、
$$3² + 1² = x²$$
っていう式が成り立つんだ。
あとはこいつを計算してみよう。
$$3² + 1² = x²$$
$$9 + 1 = x²$$
$$x² = 10$$
$$x = ±\sqrt{10}$$
辺の長さがマイナスになることは絶対にないから、
$$x =\sqrt{10}$$
ってことね。

これが一番ベーシックな計算問題だ。
じゃあつぎ行ってみよう!
次は斜辺以外がわからないパターンだね。
例えば、つぎのような計算問題。
練習問題2.
次の直角三角形ABCのxの長さを求めなさい。

この問題では、斜辺の長さがすでにわかってるね。
まあ、こいつも三平方の定理(ピタゴラスの定理)で計算をすればよくて、
$$4² + x² = 6²$$
$$x² = 20$$
$$x = 2\sqrt{5}$$
になるね。

最後はちょっと難しい問題。
直角三角形の中に、直角三角形がいる??
っていう問題なんだ。
練習問題3.
次の直角三角形ABCのxの長さを求めなさい。

この問題はいくつか段階を追って答えを出すんだ。
まず△ADCに注目。
こいつは直角三角形だよね??
ってことは、三平方の定理で残りの辺の長さが求められるんだ。
斜辺が2√5㎝、高さが4㎝だから、
$$y² + 4² = (2\sqrt{5})²$$
$$y = 2$$
になるね。

図で表すとこうなる。

じゃ、次は大きい△ABCに注目。
BCの長さをzとすると、
x㎝を求めるには、z㎝からyの2㎝引けばいいよね?
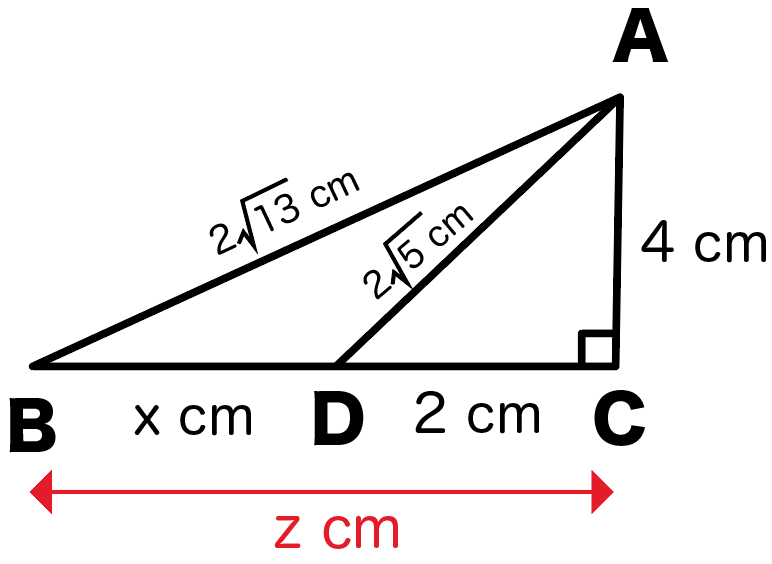
だからzの値が出れば答えまでもう少し!
直角三角形だから三平方の定理(ピタゴラスの定理)が使えるんだ。
斜辺が2√13cm、高さが4㎝だから、
$$z² + 4² = (2\sqrt{13})²$$
$$z = 6$$
になるね。
ってことは、xcmの長さは、そこからyの2cmを引いてやって、
$$x = 6 -2$$
$$= 4$$
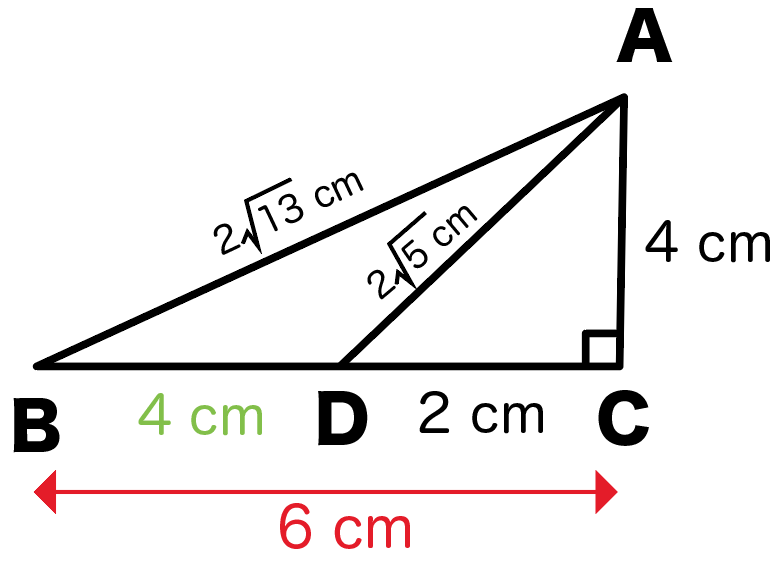
答えは4cmだ!
お疲れ!
三平方の定理(ピタゴラスの定理)の計算問題はどうだったかな??
今回マスターした計算問題の解き方は次の3つだったね。
三平方の定理の問題は解きまくってマスターしていこう。
またねー
ぺーたー
こんにちは!ぺーたーだよ。
今日は三平方の定理を使って、
座標上の2点の距離を計算する方法を勉強していこう!
関数が苦手な子は、
「えー、絶対やだ!」
とか思っちゃうかもしれないけど、
三平方の定理がしっかりわかっていれば、そんなに難しくないよ。
頑張ってやってみよう!
三平方の定理を使えば、2点間の距離は3ステップで計算できるよ。
次の例題を一緒に考えてみよう。
練習問題
2点A(-1,5), B(2,1)の間の距離を求めてください。
まずは座標と点を図にしてみて。
図がかかれてたらスキップしてもOKだけどね
練習問題でも図をかいてみようか。
まず、 座標軸をスラーっとかいてあげて、

2点の座標をポチッと打ってあげる。

だいたいこんな感じだよね。
直線ABを長さを求めるのが目標だ。
次は三平方の定理を使うために、
直角三角形を作ってみよう。
「求めたい2点の距離」を斜辺とする直角三角形を作ればいいのさ。
練習問題をみてみて。
ABを斜辺とする直角三角形を作るには、
2点から垂線を引いてやればいいね。
まず、Aからy軸と平行な垂線をひいてみて。
要はAから縦方向に線をひくんだ。

それがかけたら、Bからx軸に平行な垂線をひいてみて!
つまり、横方向の垂線ってことね。

そしたら、
2つの垂線の交点をCとしよう。
Cの座標はAのx座標、Bのy座標と同じだから、
(-1,1)
ってわけさ。

これで、 ABを斜辺とする直角三角形ABCがかけたね。

最後は三平方の定理で斜辺を求めるだけ!
練習問題では、
ACは2点のy座標の差、
BCはx座標の差だよね??
つまり、
になるはず。

あとはABをxとおいて、三平方の定理で計算すればいいね。
4²+3²=x²
こいつを計算すると、
x = 5
になる。
つまり、
AB = 5ってこと。

だからこの座標上の2点の距離は、
5
になるってことね。
おめでとう!
座標の2点間の距離はゲットできたかな??
最後に解き方を復習しておこう。
難しい作業もないから頑張ればできるはず。
グラフは書いた方がわかりやすいから忘れずに。
これでおしまい!
ぺーたー
どーもー!ぺーたーだよ。
立方体の対角線の長さの求め方には公式があるって知ってたかな??
立方体の1辺の長さをaとすると、
√3 a
で対角線の長さが求められるんだ。

つまり、
立方体の辺の長さに「√3」をかけるだけでいいんだ。
たとえば、1辺の長さが4cmの立方体があったとしよう。
すると、この対角線の長さは、
4√3
になるってわけ。

ね??すごい簡単な計算公式でしょ??
でもさ、ちょっと待って。
立方体の対角線の公式が簡単ってのはわかったけどさ、
なんでこの公式が使えるんだろう!??
って思わない??
公式忘れたら一発KOだよね。
そこで今日は、
公式を使わないで立方体の対角線の長さを出す方法
もみていくよ。
さっきの1辺が4cmの立方体の対角線の長さを出していこう。

だいたい直方体の対角線の長さの求め方と一緒なんだけどねw
まずは立方体の底面の対角線の長さを求めてみよう。
さっきの立方体でも底面に対角線を書き込んでみて。

△FGHに注目してみると、
この三角形は直角三角形ってことがわかるね。
ってことは三平方の定理が使えるはず。

△FGHを抜き出すとこんな感じだ。
この直角三角形で三平方の定理を使ってみよう。
斜辺をxとしておくと、式はこうなるね。
4²+4²=x²
こいつを計算すると、
x = 4√2
になるね。

三平方の定理を使って対角線を求めたけど、
別のやり方でも求めることができるんだ。
△FGHって直角二等辺三角形だよね。
直角二等辺三角形の比って覚えてるかな?
1:1:√2
ってやつだよ!

こいつをこの問題に当てはめると、
4㎝の辺と斜辺の比が「1:√2」だから、
4:x=1:√2
っていう比の式が立てられるんだ。

計算はこっちのほうがずっと楽だね!
次は立方体の対角線が計算できそうな直角三角形を見つけよう。
具体的にいうと、
を辺に持つ直角三角形だね。
さっきの立方体でいうと、
直角三角形AEGのこと。

なぜなら、
になってるからね。
次は立方体の対角線を求めていくよ。
さっき見つけた直角三角形で三平方の定理を使えばいいのさ。
奥行きがあってわかりにくいかもしれないから、
△ AEGの部分を抜き出してみるよ。

2辺の長さがわかってるから三平方の定理を使ってみよう。
AEは立方体の辺だから4㎝、AGを y cm とすると、
4²+(4√2)²=y²
になるね。
これをyについて解くと、
y = 4√3
になる。

ってことで、この立方体の対角線 AGの長さは「4√3 cm」になるのさ。

どう??できたかな??
立方体の対角線の長さの求め方は、
の3ステップだったね??
最初にも言ったけど、立方体の対角線の求め方は、
直角三角形の対角線の求め方とだいたい一緒。
どっちかできれば空間図形の対角線は大丈夫だね。
今日はこれでおしまい!
またねー
ぺーたー
どーもー!ぺーたーだよ。
今日は、
「円」と「三平方の定理」を合体させた問題の説明をするよ。
その一つの例として、
円の弦の長さを求める問題
が出てくることがあるんだ。
たとえば、次のような問題だね。
練習問題
半径6cmの円Oで、中心Oからの距離が4cmである弦ABの長さを求めなさい。

弦っていうのは、弧の両端を結んでできる直線だったね。
ここでは直線ABが弦だよ。
この「弦の長さ」を求めてねっていう問題。
この問題を今日は一緒に解いてみよう。
自分のペースでついてきてね!
弦の長さを求める問題は次の3ステップで解けちゃうよ。
練習問題
半径6cmの円Oで、中心Oからの距離が4cmである弦ABの長さを求めなさい。

まずは、
「弦の端っこ」と「円の中心」を結んで、
直角三角形を作っちゃおう。
練習問題では、
AからOへ、BからOへ線を書き足したよ。

弦ABとOの交点をHとすると、
△AOHは直角三角形になるよね?

これで計算できるようになるんだ。
次は、直角三角形で「三平方の定理」を使ってみよう。
練習問題でいうと、
△AOHは直角三角形だから三平方の定理が使えそうだね。

三平方の定理を使って残りの「AHの長さ」を出してみようか。
こいつに三平方の定理に当てはめると、
4²+x²=6²だから
16+x²=36
x²=3²-16
x²=20
x>0より
x=2√5
になるね。

だから、AH=2√5㎝になるってわけ。
あとは弦の長さを求めるだけだね。
弦の性質を使ってやればいいのさ。
弦の性質についておさらいしておこう。
円の中心から弦に垂線をひくと、弦との交点は弦の中点になる
って性質だったね。
「えっ、そんなの聞いたことないんだけど」
って人もいるかもしれないけど、意地でも思い出してほしいね。
∠AHO=90°ってことは、OHは垂線ってことだね。
だから、弦の性質を使うと、
Hは弦ABの中点なんだ!

ABの長さはAHの2倍ってことだから、
AB = 2AH
=2√5×2=4√5
つまり、
弦ABの長さは 4√5 [cm] になるんだね。

おめでとう!
弦の長さの問題はどうだったかな??
の3ステップでじゃんじゃん弦の長さを計算していこう。
じゃあ今日はこれでおしまい!
またね!
ぺーたー
こんにちは!ぺーたーだよ。
三平方の定理を使うと、
直方体の対角線の長さの公式を導けるって知ってた??
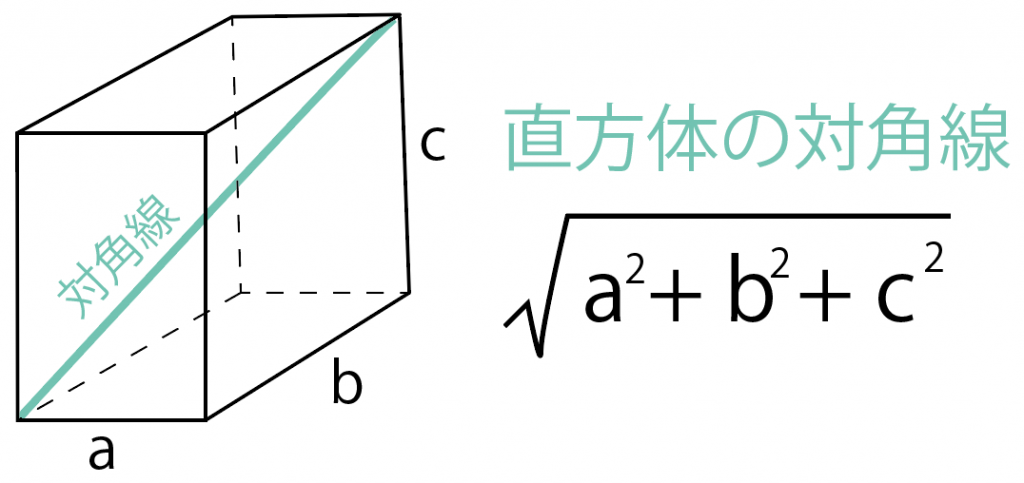
実は、対角線の長さには次の公式があるんだ。
直方体のそれぞれの長さを、
とすると、対角線の長さは、
√(a² + b² + c²)
になるよ。
たとえば、
の直方体があったとしよう。
こいつに直方体の対角線の公式を使ってやると、
対角線
= √(a² + b² + c²)
=√(3² + 4² + 5²)
= 5√2
になる。
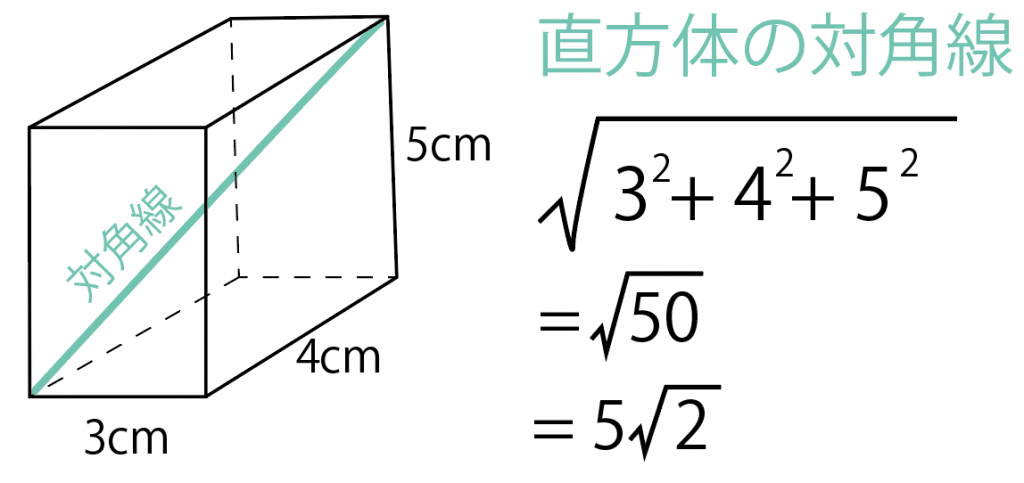
どう??
すぐに直方体の対角線の長さ求められたでしょ??
でもね、公式を使うときには、
なぜその公式が使えるのか??
を知っておくといいよ。
公式を忘れても大丈夫なようにね。
だから今日は最後に、
公式を使わずに直方体の対角線を求めてみよう。
さっそく、公式なしで直方体の対角線の長さを出してみようか。
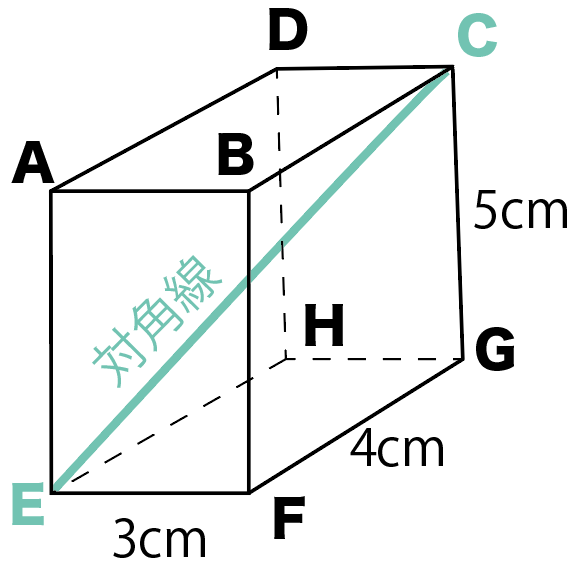
この問題では、対角線ECを求めてみよう。
まず最初は、
底面の対角線を引いてみよう。
なんでそんなのひかなきゃいけないの?
って思うかもしれないけど、
その理由はあとでわかるからちょっとがまんしてね!
底面に対角線をひくとこうなるね。
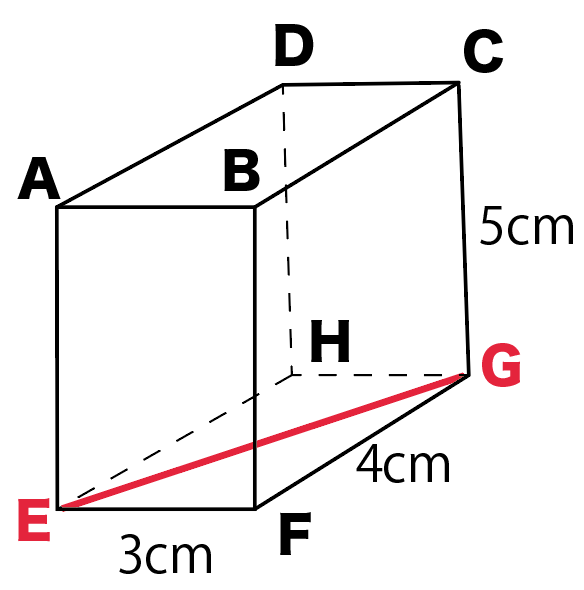
対角線ECを求めるために、
底面の対角線はEG
を引くってことね。
次は、底面の対角線の長さを計算してみよう。
えっ。
どうやって出すのかって??
こういうときは、
底面にできた三角形に注目してみて。
さっきの直方体でいうと、
△EFG
だね。
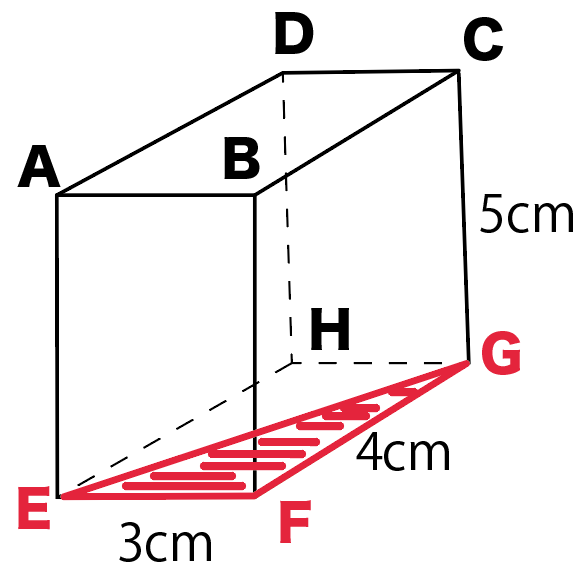
この三角形は上から見るとわかると思うけど、
直角三角形になってるよね。
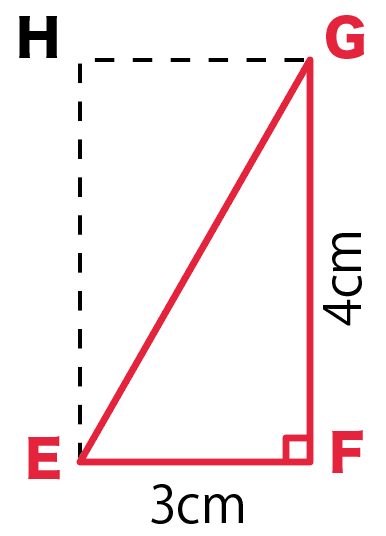
てことは、
三平方の定理で「斜辺EGの長さ」を求めることができるんだ。
三平方の定理を使ってやると、
EG² = EF² + FG²
EG² = 3² + 4²
EG = 5 cm
になるね。
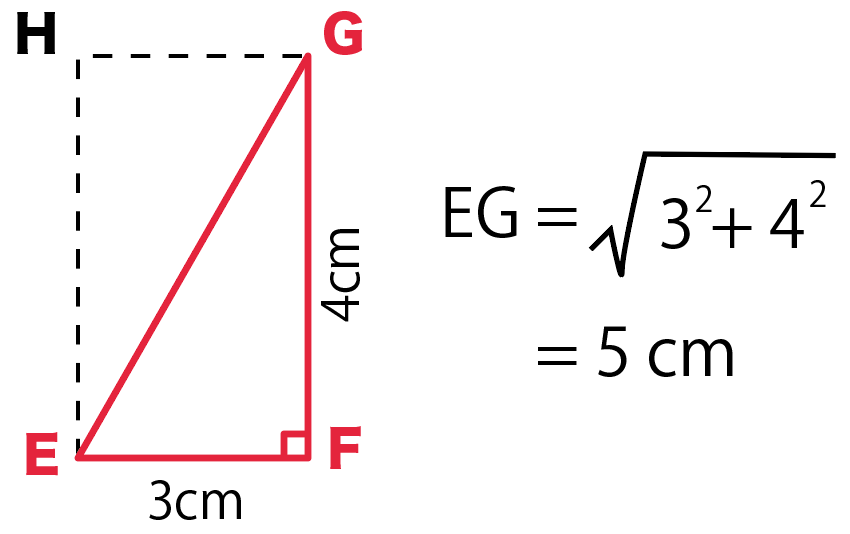
いよいよ本題の直方体の対角線の長さを求めるよ。
まず、求めたい直方体の対角線をさっきの図に書き込んでみよう。
対角線を書き込んだことで、また新しい三角形ができるよね??
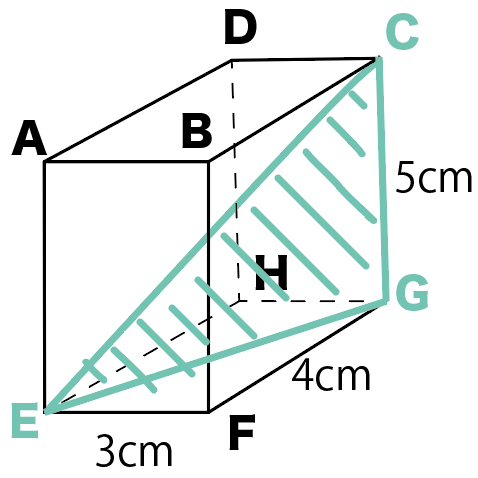
直方体の高さの辺と、底面の対角線でできる直角三角形ECGだ。
この三角形を取り出すと下みたいになるよ。
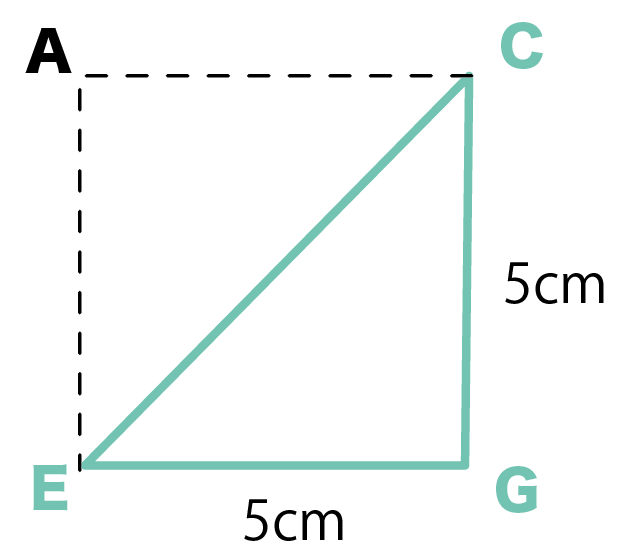
ここで、さっき求めた底面の対角線を使うんだ。
底面の対角線EGは5㎝だったね。
こいつを先に出しておかないと、うまく式が立てられず、計算できないんだ。
だから、底面の対角線を求めておくのはとっても大事ってわけ!
さっきと同じように三平方の定理を使うと、斜辺 ECの長さは、
EC² = CG² + FG²
EC² = 5² + 5²
EC = 5√2 cm
になるね。
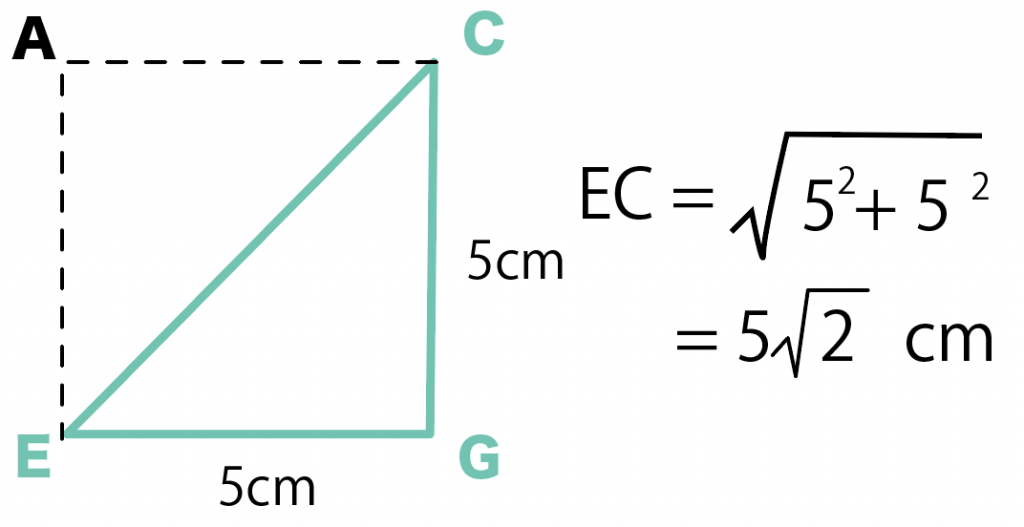
つまり、
この直方体の対角線の長さは「5√2 cm」になるってわけ!
直方体の対角線の求め方はわかったかな?
の2ステップでオッケー。
都合のいい直角三角形を見つけて、三平方の定理を使えれば全く問題ないね。
じゃあ、今日はここまでにしようか。
またね!お疲れさま!
ペーター
やあ,Dr.リードだぞいっ!!
円周角の定理は頭に入ったよな!!
だよな!
円周角の定理はおぼえるだけじゃだめだ。
実際に、いろんな問題を解いてみることが大事なんだ。
円周角の問題を解くコツは、
でっかく自分で図をかいてみること。
問題集の円なんて、小さすぎて見にくいだろ??
これだと考えにくいから、
ノートや別の紙にお皿くらいでっかく描いて考えてみるといいな。
そうそう。でっかくでっかく。
中華料理のターンテーブルみたいにさ、くるくる回しやすいだろ?

今日は、テストにでやすい円周角の求め方を3パターン紹介していくぞ。
円周角の求め方は意外とシンプルでわかりすいんだ。
まずは、円周角の定理を使った求め方だね。
円周角の定理は、
の2つだったよな?
忘れたら円周角の定理の記事で復習しような。
それじゃあ円周角の問題を解いていくぞ。
次の角xを求めなさい。
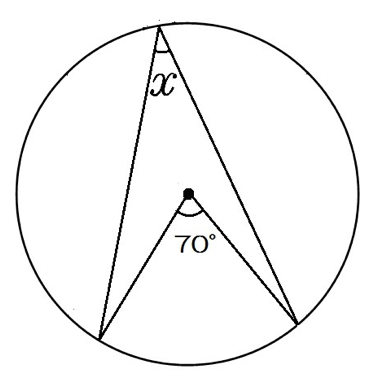
この問題では円周角の定理の、
1つの弧に対する円周角の大きさは、その弧に対する中心角の半分である。
を使っていくぞ。
円周角は中心角の半分。
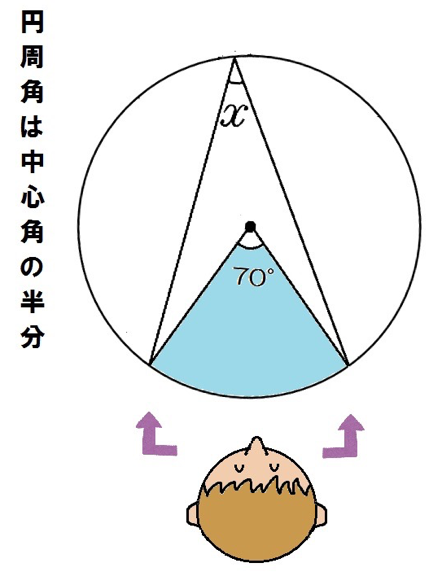
だから、xは35°だ。
次の角xを求めなさい。
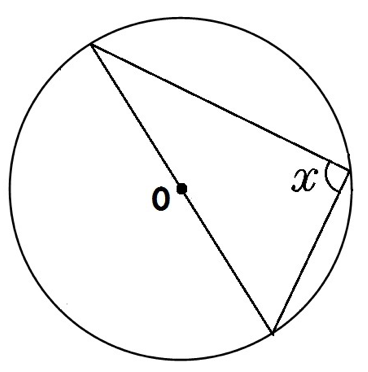
この円周角の求め方もさっきと同じ。
同じ孤に対する円周角は中心角の半分。
この円は円の半分だから、中心角は180°。
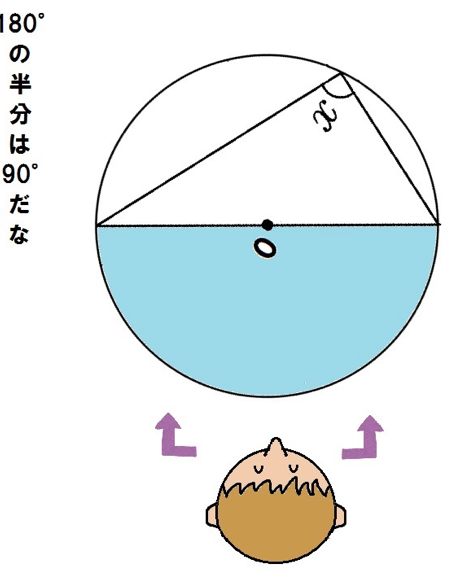
よって、円周角のxは90°。
これも基本通り。
直径に対する円周角は90° はよくでてくるぞ。
次の角xを求めなさい。
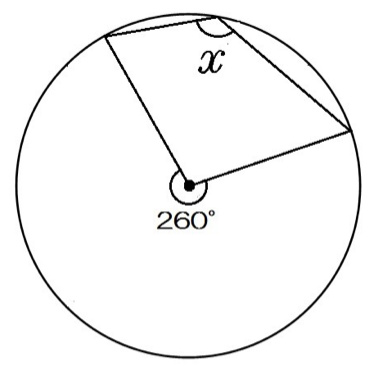
この問題も同じさ。
中心角が260度だから、円周角xはその半分で
130度。
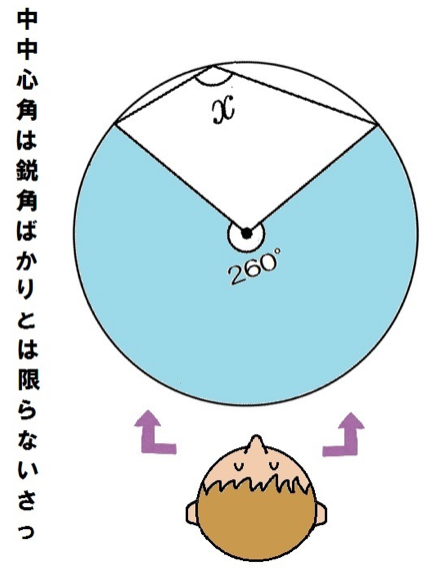
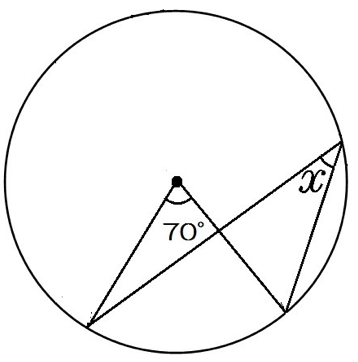
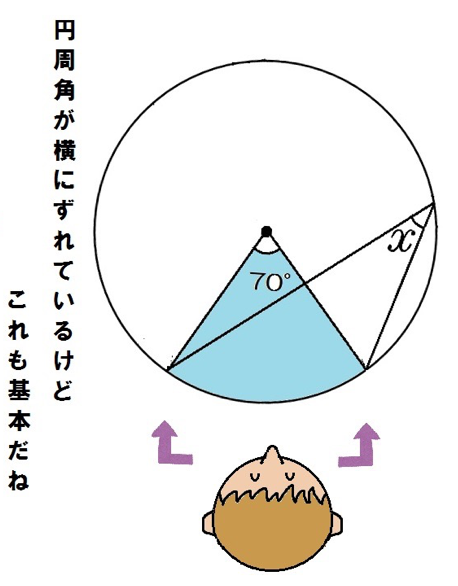
円周角の頂点が中心角からずれてるパターン。
基本の求め方は同じだぞ。
円周角は中心角70°の半分だから35°だ。
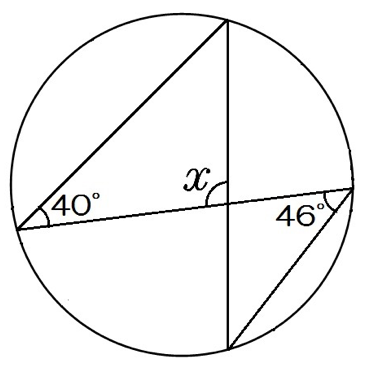
リボンタイプの問題っておぼえておくといいよ。
中心角はかかれてない。
この問題では、
同じ弧の円周角はどこも同じってことを利用する。
角xは、
180-40-46=94°
になるね。
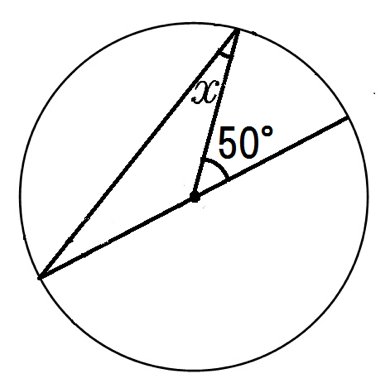
げっ、円周角じゃないとこきかれてるじゃん。
でも中心角を頂角にする三角形が「二等辺三角形」ってことを利用すると・・・
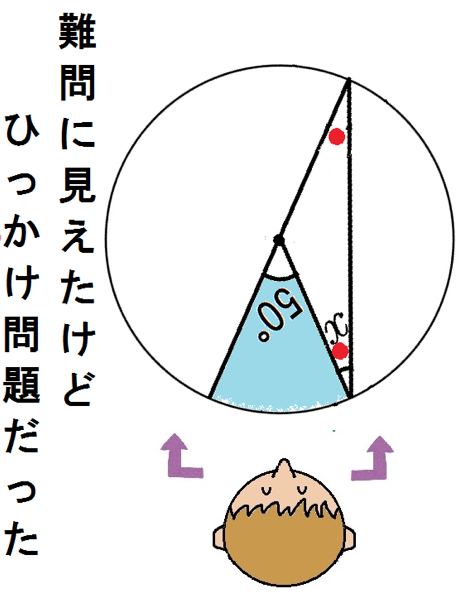
つまり50°の半分、25°が円周角だね。
二等辺三角形の底角は等しいからxも25°。
次はちょっと難しい問題。
補助線を引かないと円周角が求められないやつだ。
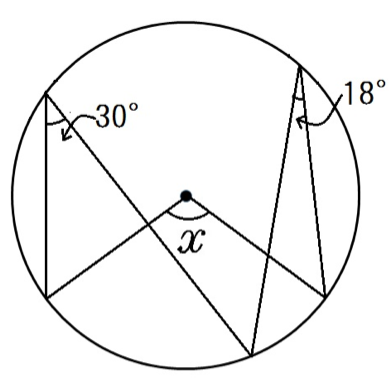
さあ、補助線を引くぞ。
中心角を2つに分けられる補助線を引けばいいんだ。
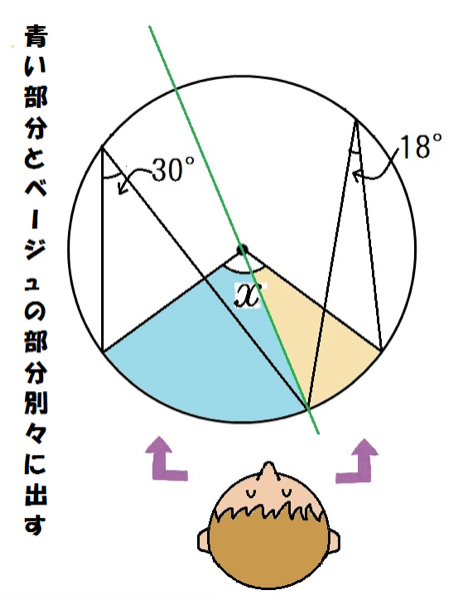
補助線さえ引けたら,円周角の問題が2つドッキングしてるだけなんだよね。
青いほうが円周角の2倍だから60°。
ベージュのほうが円周角の2倍で36°。
合計でxは96°だ。
補助線引けないと手も足も出ないが、コツさえつかめばだいじょうぶ。
最後は、中心角・円周角出したその先がある問題。
もうひと踏ん張りのパターンだ。
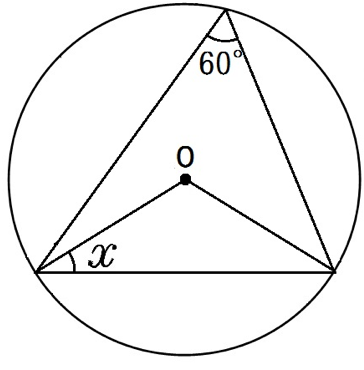
円周角60°ってことは、中心角は2倍の120°。
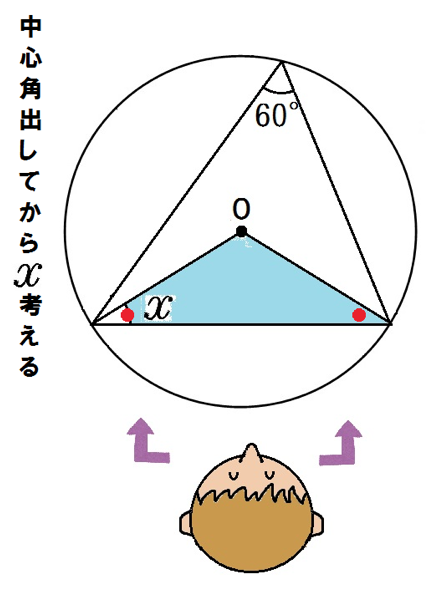
水色の三角形は二等辺三角形だから底角は等しい。
よって、底角のxは、
(180-120)÷2=30
になるぞ。
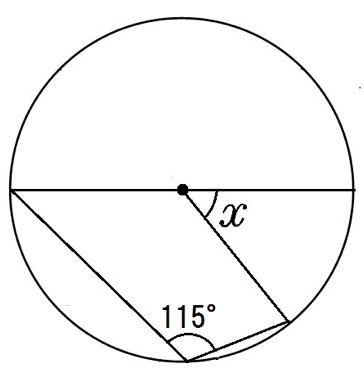
円周角115°だから、赤い中心角は2倍の230°。
紫のとこは、
360-230=130°
だから、求めるxは、
180-130=50°
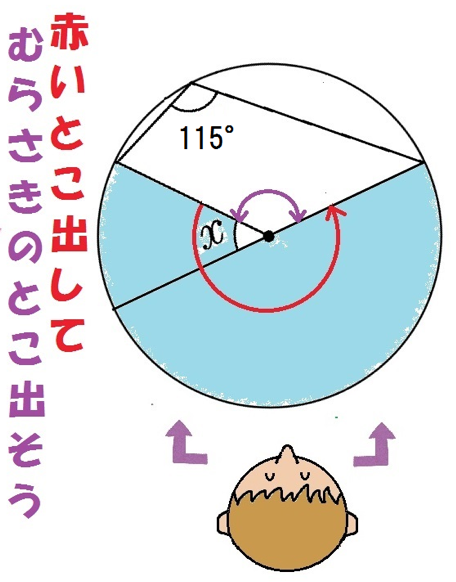
うんうん。
みるからに50°だ。
円周角の求め方はパズルみたいだね。
変に難しく考えなくて大丈夫。
あとは円の見方を変えたりするぐらいかな。
テストによく出てくるから復習しておこうぜ。
じゃ、おつかれさん。
一緒に中華料理でも食うかな!
Dr.リード
