3分でわかる!円周角の定理とはなんだろう??
円周角の定理とはなんだろう?!?
やあ、ぺーたーだよ。
中3数学もいよいよ大詰め。
いよいよ、
円の性質っていう単元
を勉強していくよ。
今日は、この単元でいちばん大事な、
円周角の定理とはなにか??
をまとめてみたんだ。
計算や証明で使ったりするから、しっかりおさえてあげてね。
= もくじ =
- 円周角・中心角とは??
- 円周角の定理とは??
- 円周角の定理をつかった練習問題
円周角・中心角とはなにもの??
円周角の定理を理解するためにはまず、
- 円周角
- 中心角
の2つの意味を知らないとね。
まず円周角からだ。
円周角とは?
円周角とはなんだろう??
Wikipediaをみてみると、
ユークリッド幾何学においてある円周上の一点から、この点を含まない円周上の異なる二点へそれぞれ線分を引くとき、その二つの線分のなす角のことである。
ってかいてある。
これはちょっとむずかしいw
正直、ユークリッドとかわけわからんよね。
円周角をもうちょっと簡単にいってあげると、
「円周上の1点」と、
そいつと被らない円周上の2つの点を、
線分でむすんだときに、
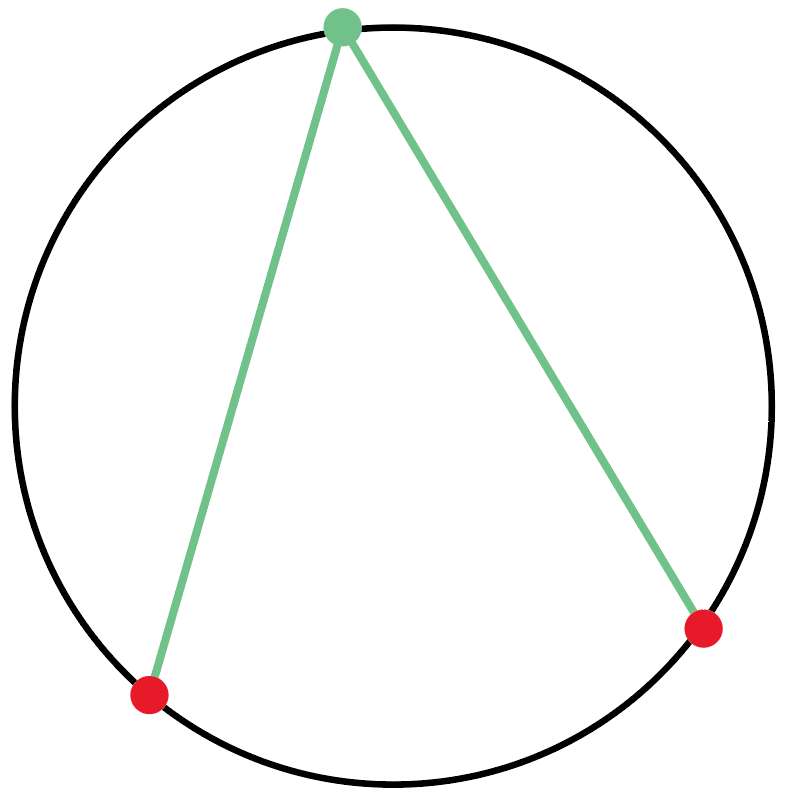
できる角度のことを、
円周角(えんしゅうかく)
とよんでいるんだ。
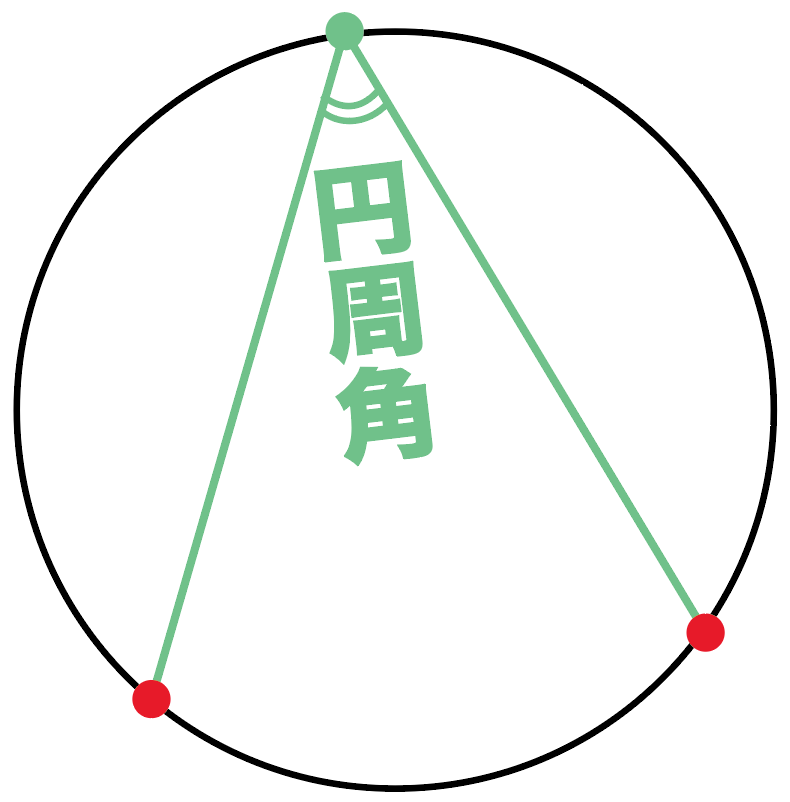
たとえば、つぎの円Oがあったとしよう。
円周上の点をA・B・Pとするよ。
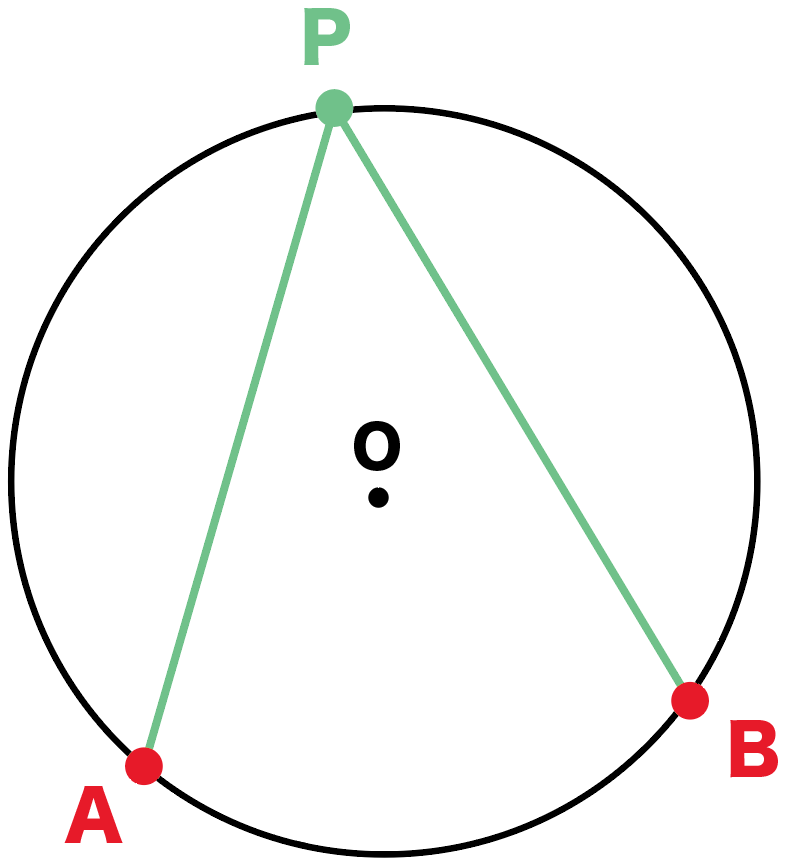
このとき、
∠APBを弧ABに対する円周角
っていうんだ。
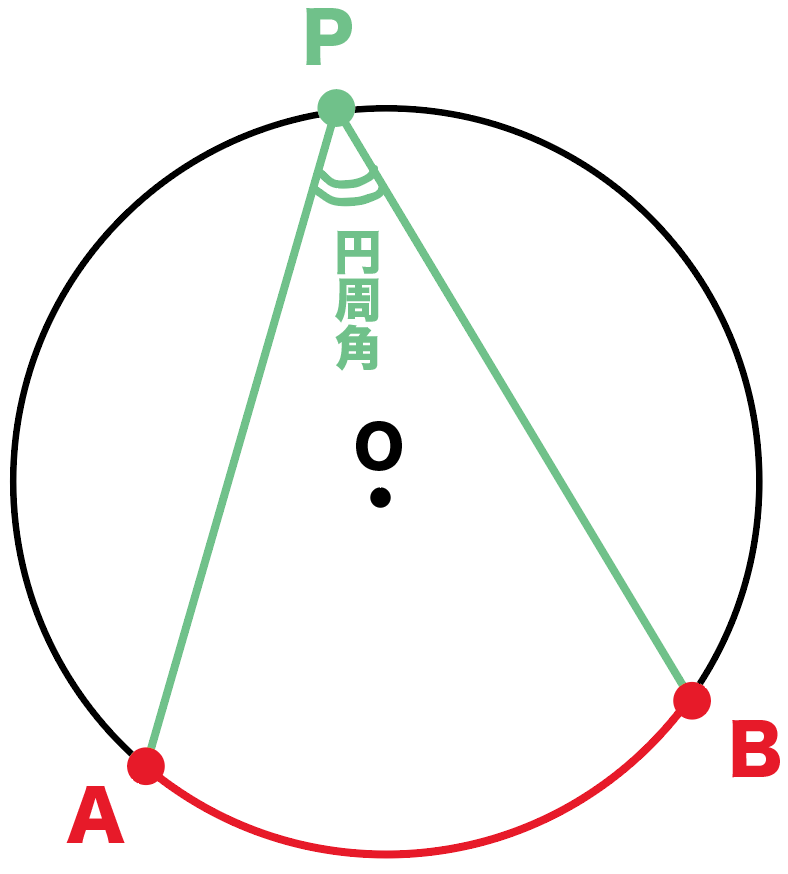
こんなかんじで、円周角には、
弧○○の円周角
というかんじで、どこかの弧に属してるってわけ。
中心角とは??
つぎは中心角。
中心角を数学用語集でしらべてみると、
弧の両端を通る2つの半径の作る角
らしいね。
これはわかりやすい。
「円の弧」の、
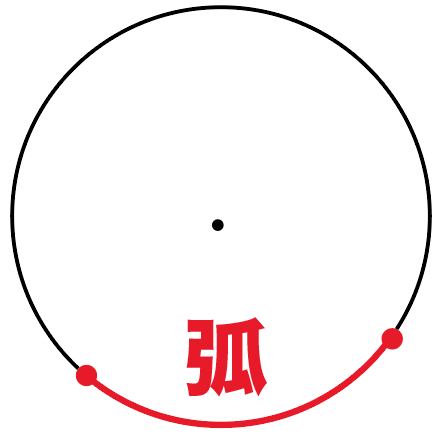
「両端を通る2つの半径」が、
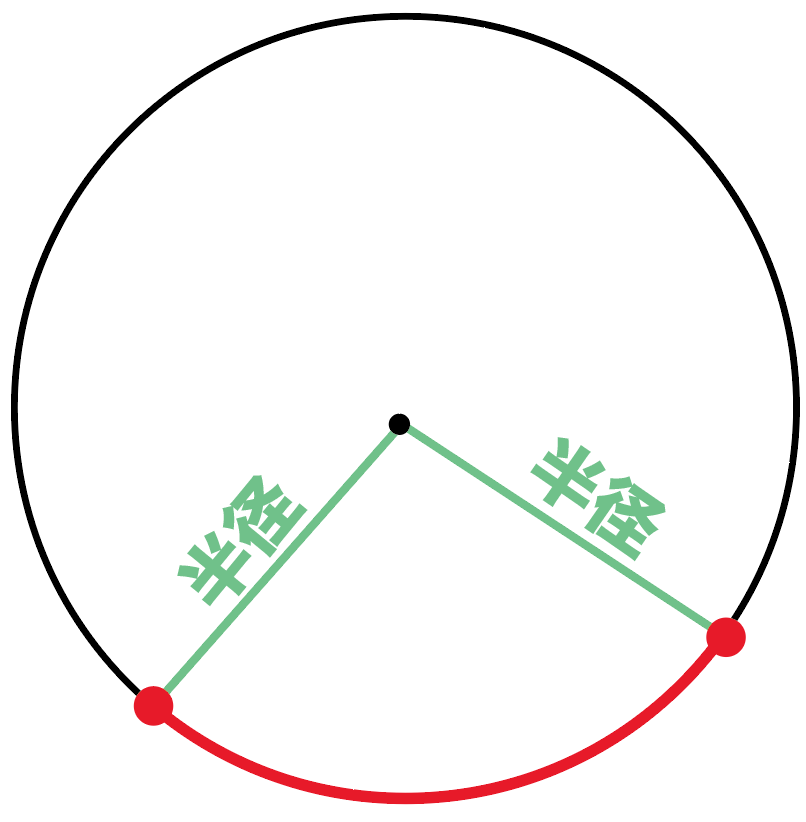
つくる角を、
中心角(ちゅうしんかく)
というんだ。
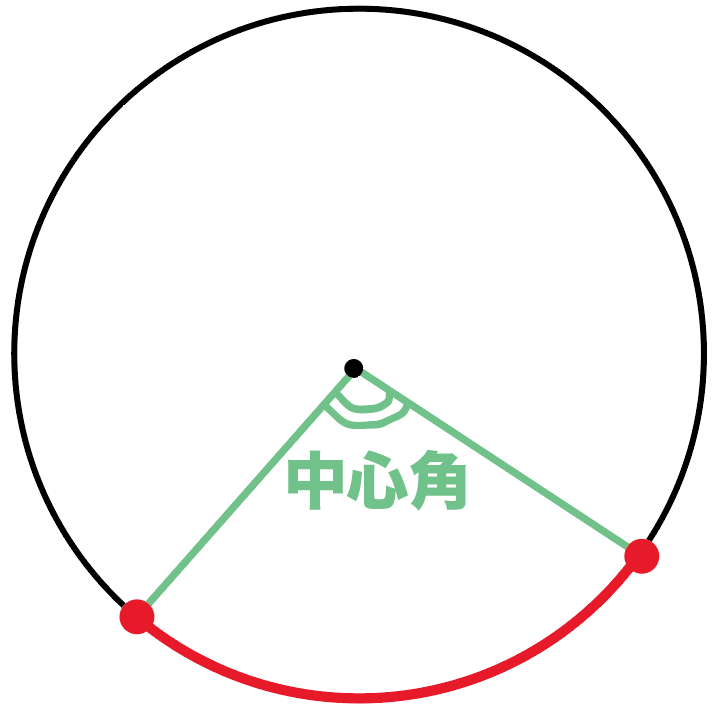
たとえば、下の円Oだったら、
∠AOBが弧ABに対する「中心角」
ってわけね。
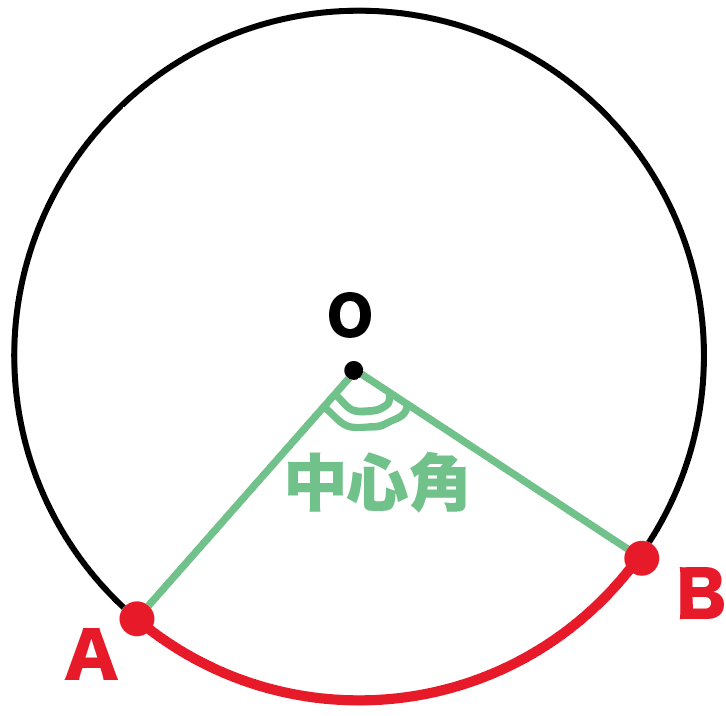
中心角も円周角とおなじように、
弧○○っていうかんじでどこかの弧に属しているよ。
円周角と中心角の違いはOKかな?
この2つの違いはしっかり理解しておいてね!
円周角の定理とはなにもの??
円周角の定理は、
円周角の決まりみたいなもんだ。
大切だからきっちり覚えてね!
円周角の定理は2つの性質があるよ。
- 1つの弧に対する円周角の大きさは、その弧に対する中心角の半分である。
- 同じ弧に対する円周角の大きさは等しい。
つまり、
- 同じ弧に対する「円周角」と「中心角」の関係
- 同じ弧に対する「円周角」と「円周角」の関係
の2つの円周角の定理があるんだ。

どっちも、
「同じ弧に対する」
っていう条件が含まれてることに注意ね。
定理1. 「円周角は中心角の半分」
まずは、円周角と中心角の性質からだね。
1つの弧に対する円周角の大きさは、
その弧に対する中心角の半分である
っていう定理なんだ。
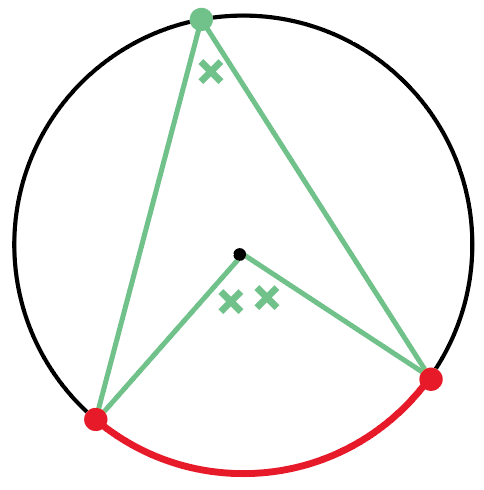
たとえば、つぎのような円Oがあったとしよう。
このとき、円周角APBは中心角AOBの半分になるんだ。
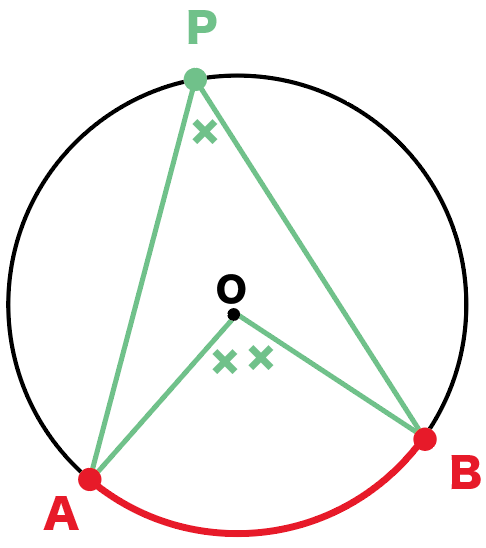
式であらわしてやると、
角APB = ½ 角AOB
になるね。
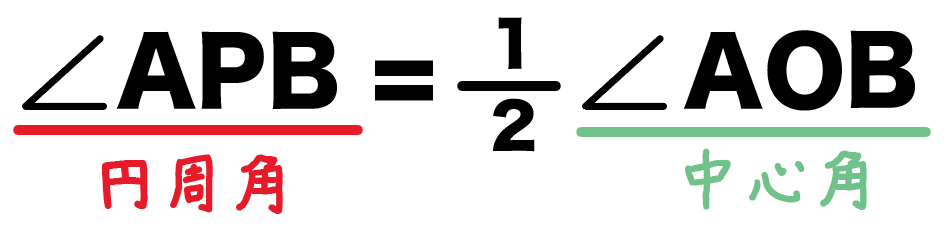
これが、円周角の定理のうち、
同じ弧に対する円周角と中心角の関係ってやつね。
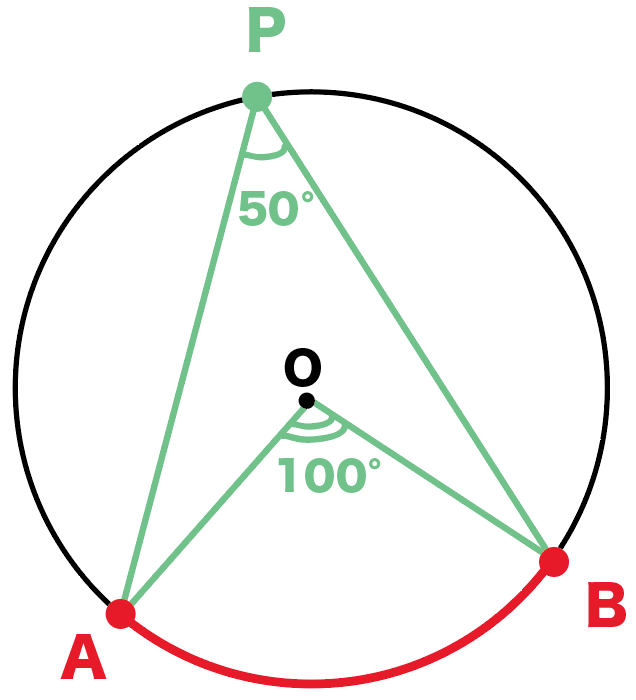
だから、もし、円周角APBが「50°」だとしたら、
中心角AOBは「100°」になるってわけだね。
定理2. 「同じ弧に対する円周角は等しい」
つぎは、円周角の性質だね。
なんと、同じ弧の円周角ならすべて等しいんだ。
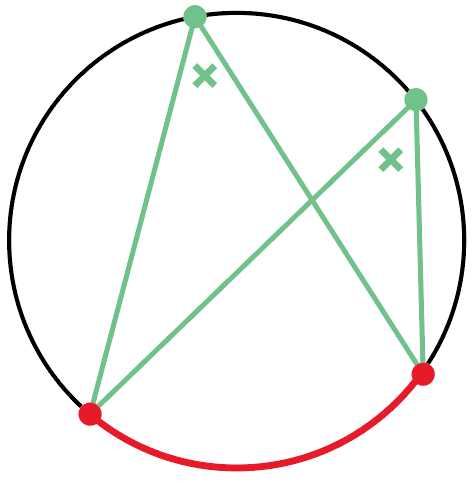
この定理でも、
“同じ弧に対する”
っていう点に注意してね。
たとえば、下の円Oをみてみて。
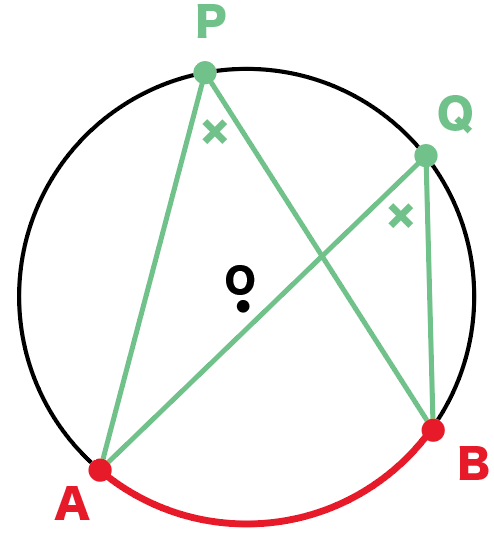
もし、弧ABに対する円周角APBが「50°」だとしたら、
∠AQB = 50°
になるはずなんだ。
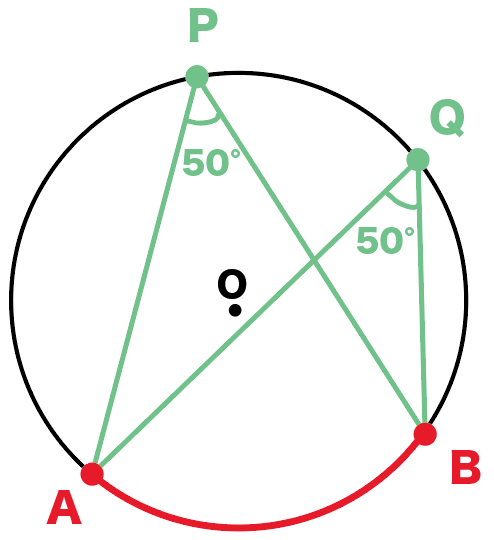
なぜなら、
両方とも弧 ABの円周角だからね。
実践問題でなれよう!円周角の定理
円周角の定理がどんなものかわかったかな?
最後に円周角の定理を使った例題を解いてみよう。
次の図の∠xの大きさを求めてみて。
練習問題1.
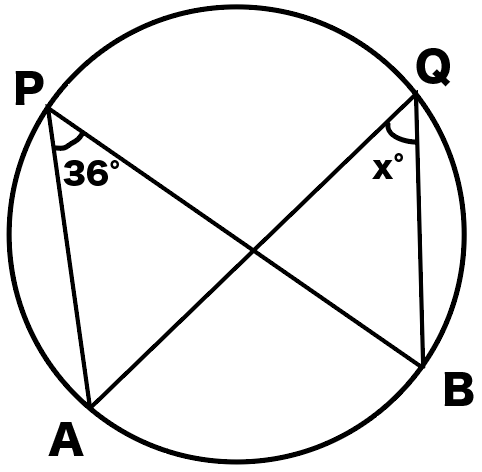
こいつはそんなに難しくないかもね!
1つの弧に対する円周角の大きさは等しいから、
∠APB = ∠AQB
になるんだ。
だから∠x=36°だね!
練習問題2.
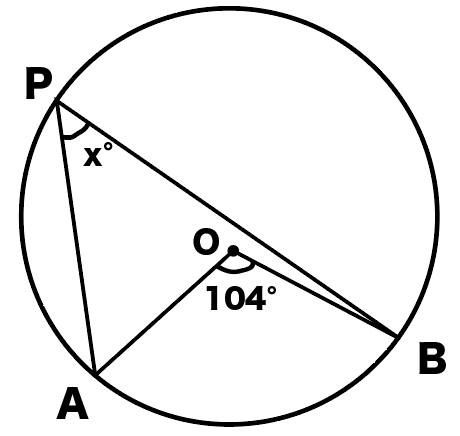
この問題は解けそうかな?
弧ABの円周角がx、∠AOBが弧ABの中心角
っていうことを見抜けると答えが出るよ。
そうすると円周角の定理の、
1つの弧に対する円周角の大きさは
その弧に対する中心角の半分である
をあてはめてやって、
∠x=104÷2
=52
ってことで、
答えは52°だね!
まとめ:円周角の定理はしっかり覚えよう!
どうだったかな?
円周角の定理がどんなものか
理解できたかな?
どこが円周角で、どこが中心角なのか
ぱっぱと頭の中で分かるようになるのがカギだね。
円周角の定理を使った問題をくりかえしやってみてね。
最初にも言ったけど、証明問題でも活躍するから覚えといてね!
じゃあ、お疲れ!またね!
ぺーたー


