こんにちは、この記事をかいているKenだよー。コーヒーは何度飲んでもうまいね。
「円とおうぎ形」という単元では、
という2つの図形について勉強していくよ。
前回まで、
っていう2つの公式をマスターしてきたね。
今日は、「扇形の面積」について詳しく勉強していこう。
「面積の求め方の公式」をおぼえていればテストでも楽勝さ。
~もくじ~
「おうぎ形の面積の求め方」はつぎの公式であらわされるんだ。
半径をr、面積をS、円周率をπ、中心角をαとすると、
S = πr² × α / 360
になるんだ。
つまり、
円周率×半径×半径×中心角÷360
ってわけさ。
たとえば、半径3cm、中心角が90度の扇形があったとしよう。扇形の公式をつかってやれば、
S = 3×3×π×90/360
= 9π/4
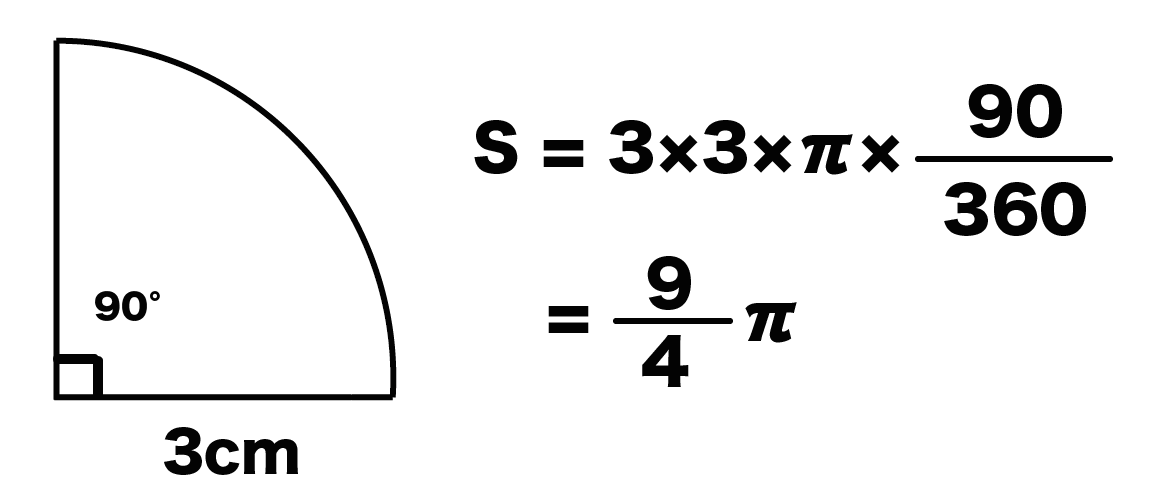
になるんだ。どんな扇形の面積でもバッチコイだね!!
扇形の面積の求め方はあんまり難しくない。シンプルさ。
ただ、半径rの「円の面積」に「おうぎ形パワー」をかけているだけなんだ。
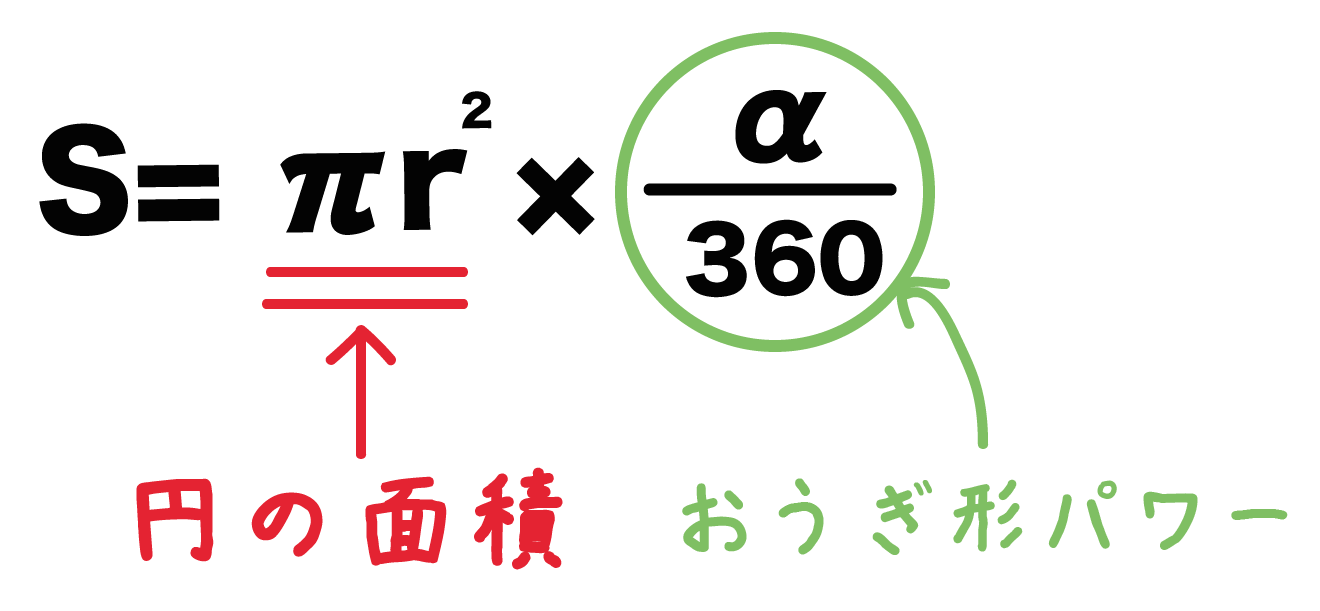
ここでいう「おうぎ形パワー」っていうのは「扇形の大きさ」をあらわしている指数のことさ。
扇形が大きければ大きいほど大きくなる。
おうぎ形パワーとは、
「同じ半径の円」に対して「扇形」がどれくらいの割合になっているか??
ということを表したものなんだ。
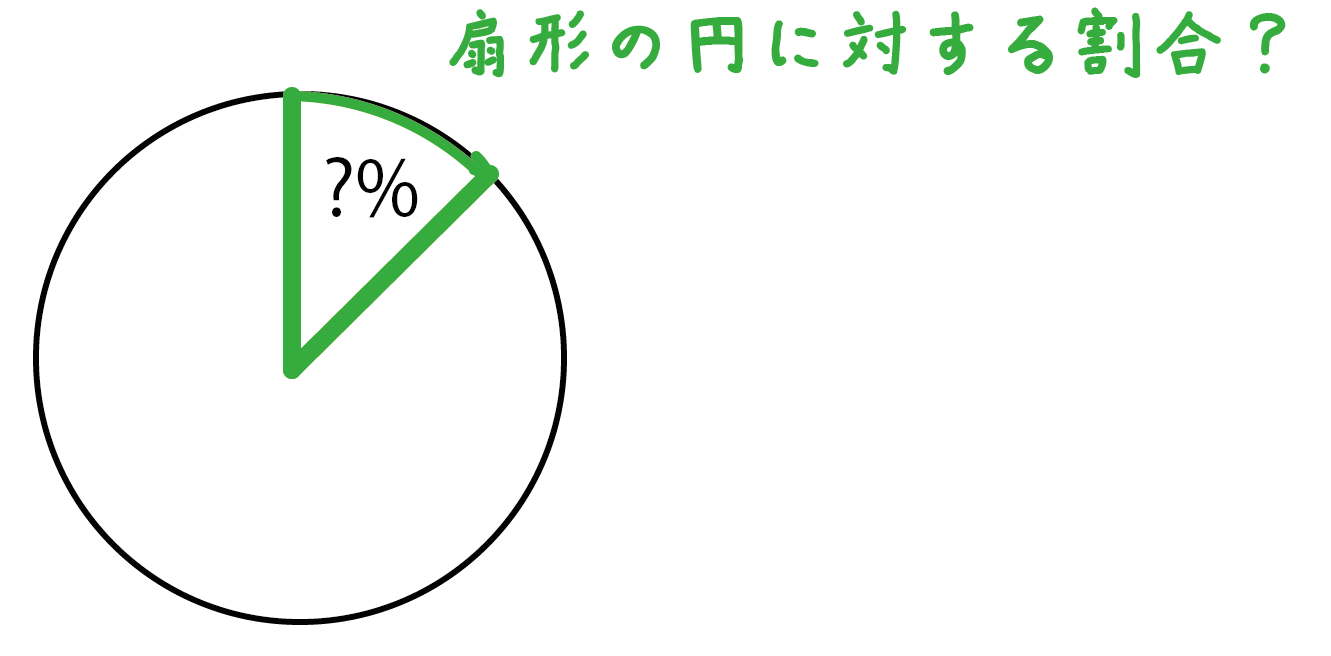
この割合を計算するためには、
「扇形の中心角」が360°中どれだけ大きいか??
ということをみればいい。だって、円の中心角はぐるっと回った360°だからね。
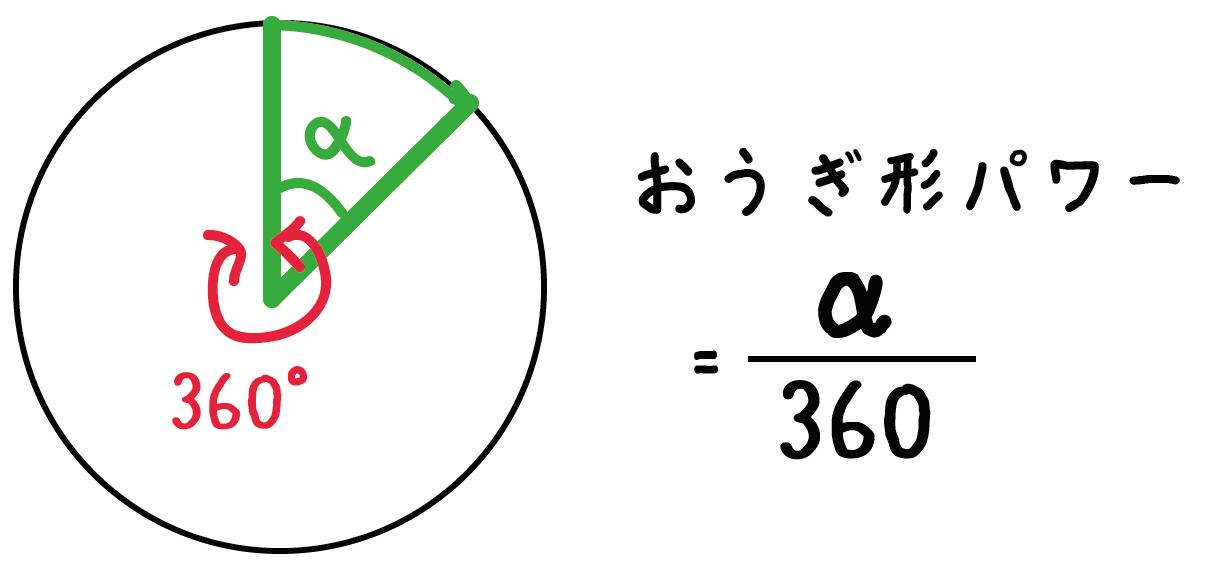
だから、おうぎ形パワーは中心角αを360°でわった、
α/360
になるんだ。
これはなんという偶然か、ピザを切り分けるときと一緒。
一枚まるまる1200kcalのピザがあったとしよう。こいつを6枚に切り分けると、カロリーはその1/6の200kcalになるでしょ??
これは一枚のピザにたいしてどれぐらいの大きさをしているか、ということを表しているんだ。
「扇形の面積の公式」を忘れたら「ピザ」を思い出そう。
扇形の面積の求め方はどうだった??
円の公式に毛がはえたようなもんだから、頑張れば覚えられそうだね。
S = πr² × α / 360
「円とおうぎ形」がテストにでるときに確認したいね。
おうぎ形の面積をマスターしたら次はおうぎ形の中心角を求めてみよう!
そんじゃねー
Ken
こんにちは、この記事をかいてるKenだよ。チョコレートに惚れ直したね。
「円周の長さの公式」ってなかなか覚えられない??
教科書には、
「円周の長さ = 直径 × 円周率」
っていう計算式が公式としてのっているね。
たとえば、直径3cmの円があったとすると、円周の長さは、
3 × 3.14 = 9.42[cm]
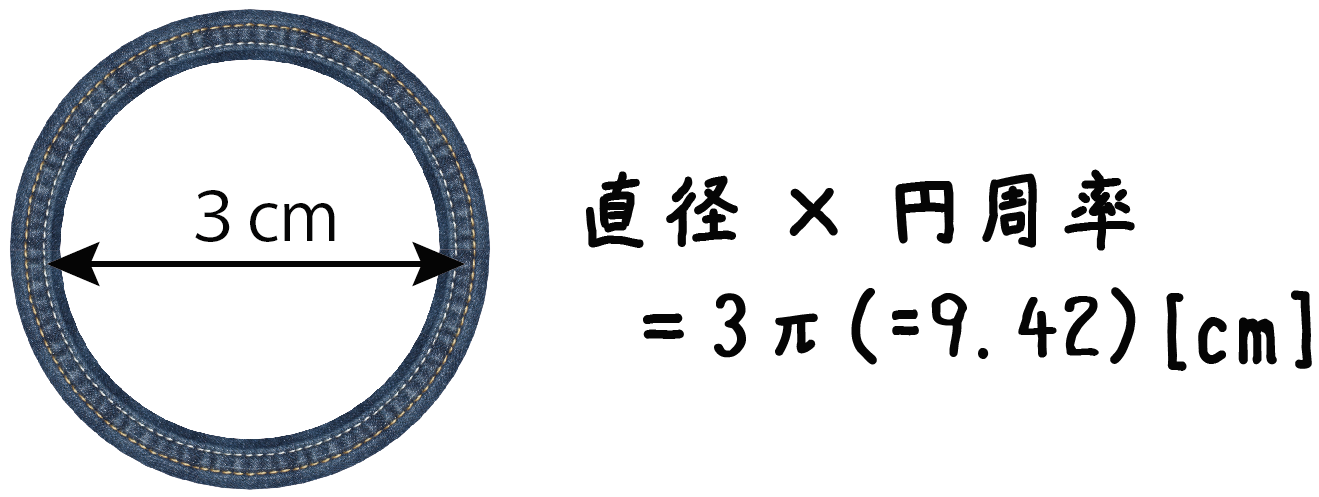
になる。つまり、この円をハサミで切ってあげると、
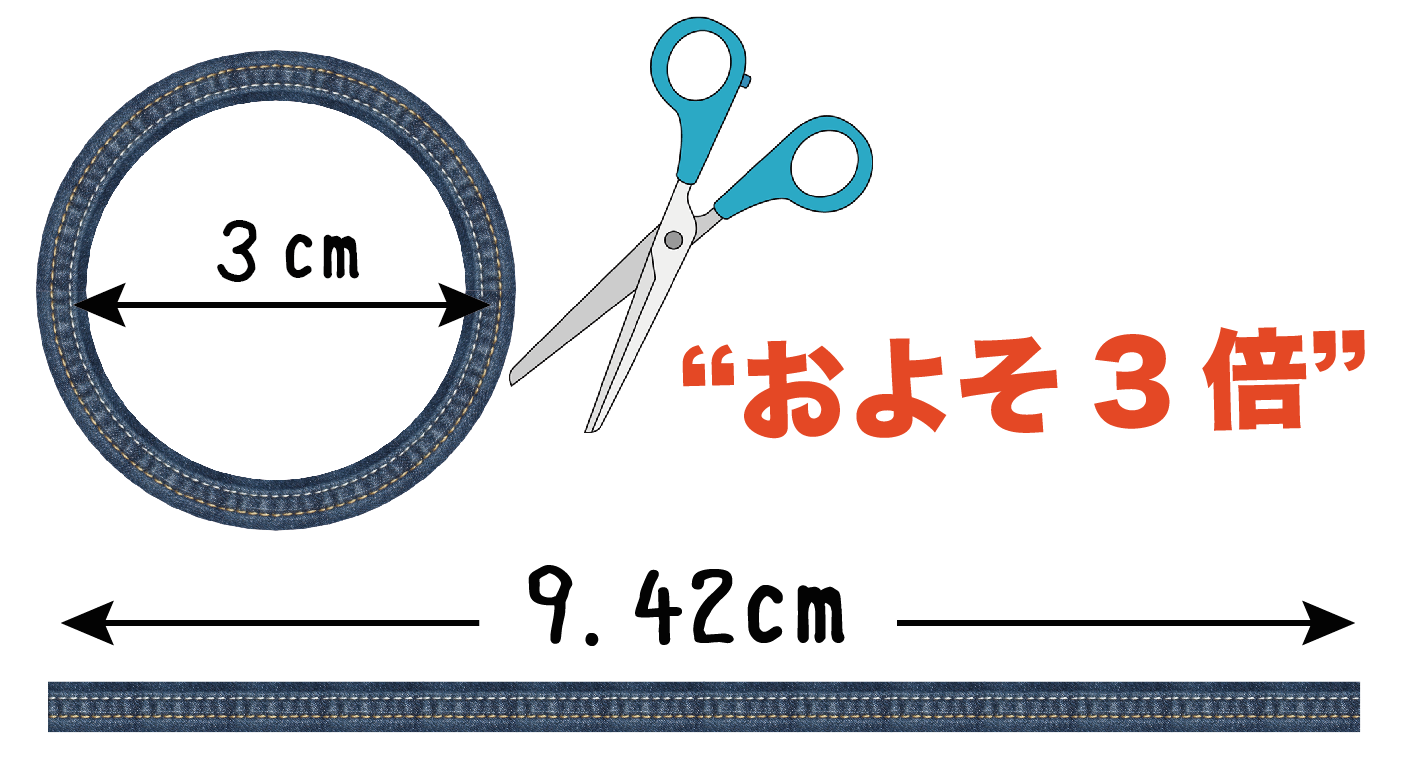
おおよそ、直径の3倍ぐらいの長さになっているってことだ。
直径と円周率をかけるだけ。
チョー便利な計算公式。だけど、どうやって覚えたらいいんだろう!??
「円周の長さの公式」をおぼえるためには何もいらない。
語呂合わせも裏技も必要ない。
円周率の意味を思い出すだけ
で円周の長さを求めることができるんだ。
円周率の意味って、
「円周の長さ」が「直径」の何倍になっているかを表した数値
だったよね??
つまり、直径に円周率をかけるだけで「円周の長さ」を求めることができるんだ。
だって、円周率って「直径」の「円周」に対する比のことだからね。
だから、
円周の長さ = 直径 × 円周率
っていう公式はある意味当たり前のこと。
円周率の意味さえおさえておけば、どうってことない公式さ。
ここまでは算数でも勉強してきた。
ここからは「中学生の数学」を勉強していこう。
中学数学でのあたらしいミッションは、
「円周の公式」を文字式であらわす
ということ。
なぜこんなことをするのかというと、文字式であらわしたほうが断然かっちょいいからだ。うん。ぜったいそう。
中学では次のように「円周の長さ」の公式をあらわすことにしているよ。
l = 2πr
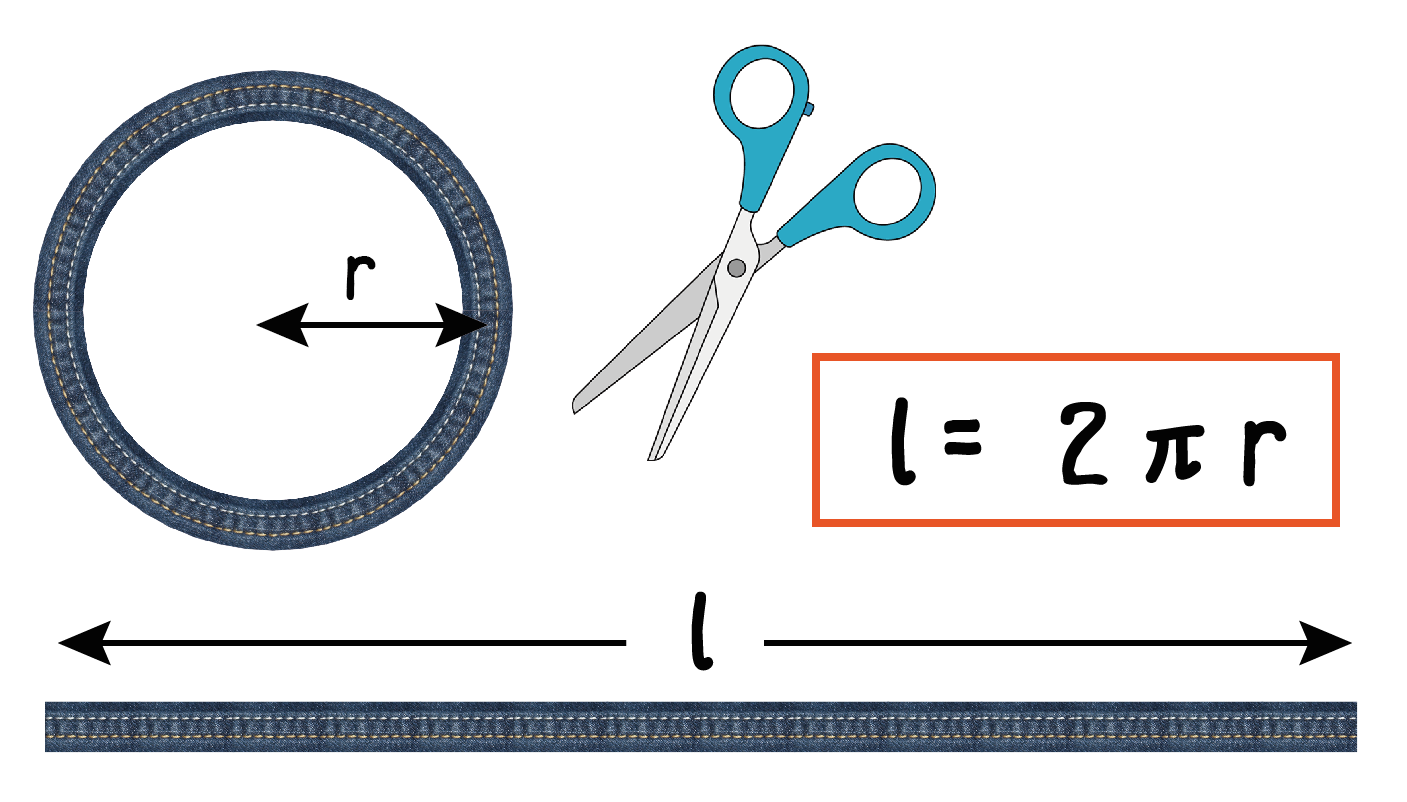
「r」という文字が「円の半径」であることに注意してね。直径は半径の2倍で「2r」になるんだ。だから、
円周の長さ = 直径 × 円周率
っていう公式を「r」と「l」と「π」であらわしてやると、
l = 2πr
になる。
「π」はどの文字よりも優先して先に書いてあげてね。
円周の公式はシンプルだけど意外に忘れやすい。
円周の公式を忘れたら、「円周率の意味」をおもいだしてみてね。
「l = 2πr」でバンバン円周の長さを計算していこう!
そんじゃねー
Ken
☆1分でわかる!円周の求め方を動画にしてみたよ☆
よかったらみてみてね↓↓
こんにちは、この記事を書いてるKenだよー。ひさしぶりに服を買ったね。
「円とおうぎ形」っていう単元に入ると、
円の面積を求めろおお!
っていう問題がたくさんでてくるんだ。
だって、ここでは「円」と「おうぎ形」が主役だからね。めんどうだけど、しょうがないね。
だけれども、一度公式をおぼえてしまえば、あとは公式の通りに計算するだけでいい。
ってことは、
円の面積の公式を一度おぼえて忘れなければいいってことなんだ。

今日は、「円の面積の求め方」の公式を一生忘れないようにするために便利な、
円の面積の公式の覚え方
を紹介するね。
テスト前に参考にしてみてー
小学校で「円の面積の求め方」の公式を勉強してきたよね??
たしか、
円の面積 = 半径 × 半径 × 円周率
ってならったはずだ。
たとえば、半径3cmの円がいたとすると、コイツの面積は、
3×3×3.14 = 28.26[cm2]
になるんだったね??
円の面積 = 半径 × 半径 × 円周率
っていう公式さえ覚えていればどうにかなるけど、これを忘れるとイタい。あせる。テストでいい点はとれない・・・・
どうしよ・・・・
公式を覚えられない中学生のために、裏技を開発してみた。
いわゆる、語呂、というやつだ。
フレーズを暗記するだけで「円の面積の求め方」を覚えられるというわけ。
これは心強いね。
とりあえず、
ラーメン屋に2人で行ったときのシチュエーションを想像してくれ。

http://www.kome100.ne.jp/main/contents/cec/f-ccc1/f-cpd1/f-cqb1/IPA-ccc660.htmより
友だちと2人で、だ。2人で。
さっそく美味そうなラーメンを注文し、2人同時にラーメンを食べ始めたんだ。

すると、
一緒にきていた友だちのラーメンを食べるスピードが異様に速い。
速すぎるじゃないか。

あまりの驚きを隠せないキミ。
そこで、ついつい耐えきれなくなって、次の「衝撃のツッコミ」を入れたんだ。

ラーメン食うの、は、はえよ!!
って。
え。ふつうの「ツッコミ」にみえるって??
たしかにそうだ。円の面積の公式なんかとぜんぜん関係ないようにみえる。
だがしかし、このフレーズに重大なヒント・手がかりが隠されているんだ。
もう一度、さっきの名台詞を確認してみると、
ラーメン食うの、は、はえよ!!
そろそろ、キーワードに気づいたかい??
そうだ。
じつは、
(円のめんせき)= (はんけい)×(はんけい)×(えんしゅうりつ)
っていう円の公式にでてくるキーワードの頭文字と偶然に一致している。
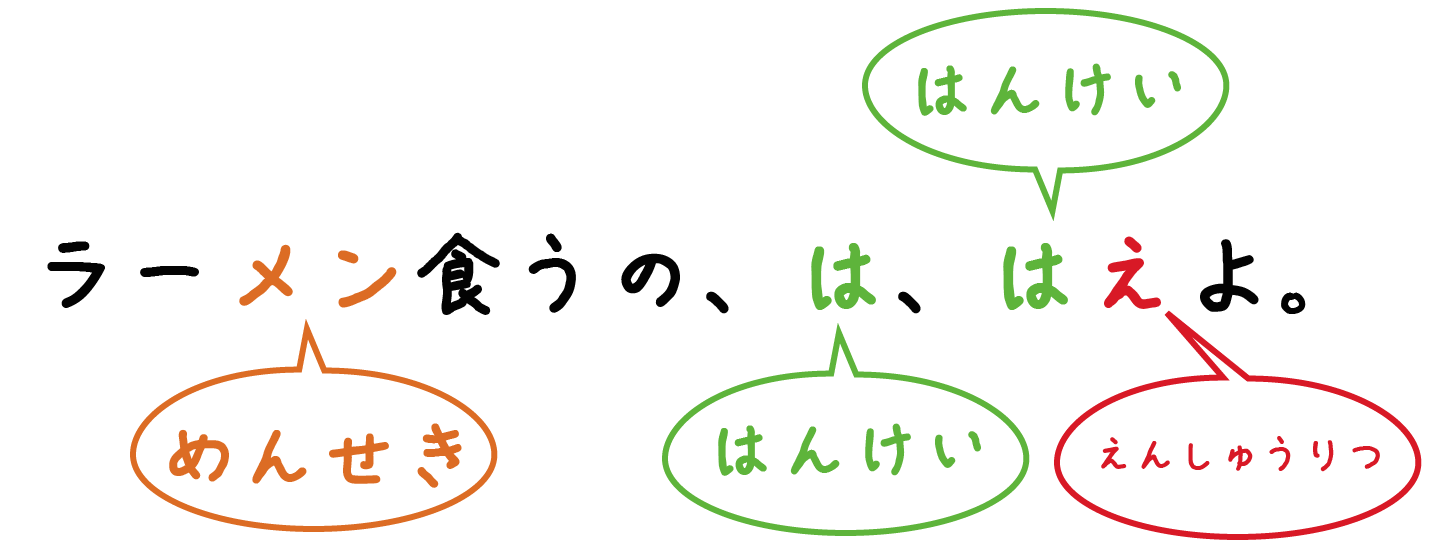
ラーメン屋のシチュエーションを頭に浮かべるだけで、円の面積の公式が覚えられるんだ。
ね? クソ便利じゃない??。
「円の面積の求め方」の公式も大丈夫。
あとはテスト中にラーメン屋のシーンを思い浮かべるだけさ。
あ、でも、中学校の数学では「円の面積の公式」はもう少しカッコいいのを使うよ。
言ってることは同じなんだけど、文字式で公式をあらわすことにしてるんだ。
円の面積を「S」、半径を「r」、円周率をπとすると、

S = πr^2
ってあらわすことができるんだ。やってることは、
面積=半径×半径×円周率
と同じこと。ただ、「円の面積の公式」を文字式であらわしているだけだよ。
なぜ面積がSなのかというと、「面積」を英語にすると「Surface」になるからだ。おなじように、半径がrなのも英語の「radius(半径)」からきてるんだ。
テストで忘れそうになったらラーメン屋の風景を思い浮かべてね。
「円の面積の公式」は導きだすのはちょっとむずかしい。
だから、公式をおぼえておくと、むちゃくちゃ便利なんだ。
ラーメン食うの、はっ、はえよ!!
っていう「ツッコミ」を忘れずにテストにのぞみたいね。
そんじゃねー
Ken
こんにちは、この記事をかいているKenだよ。メガネ探知機がほしいね。
今日から「円とおうぎ形」を勉強していくよ。この単元でいちばん出現するのは、
そう、
円
だ。
円。まるっこい奴のことさ。
教科書によると、
中心Oと円周上の点を結ぶ線分の長さは、円周上の点をどこにとっても等しく、この円の半径になります。
って書いてあるね。
つまり、ただ丸っぽいだけじゃなくて、中心から等しい距離に線をかきまくってできる図形のことなんだ。
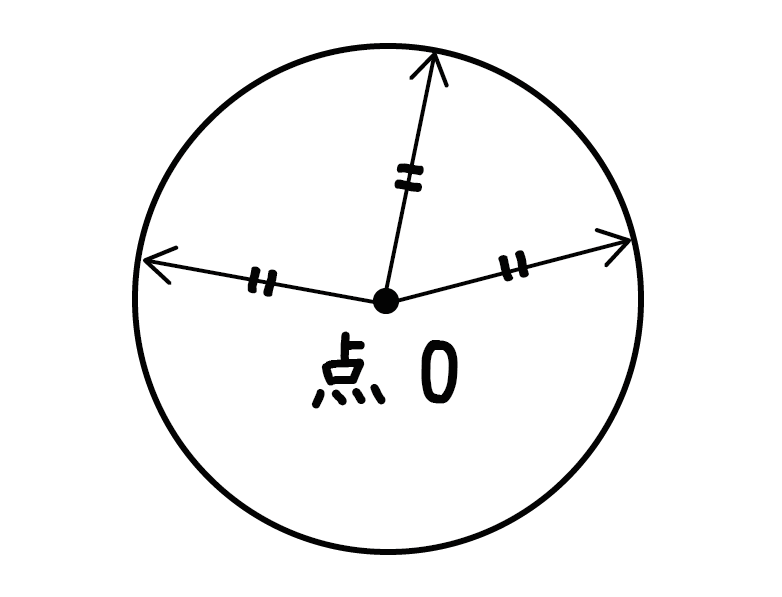
これが「円」だ。
この円について勉強していく上で、知っておくべき用語の1つに、
円周率
っていうものがある。これがむちゃくちゃ重要。円周率を知らないとテストで一問も解けないままゲームセットになっちまうんだ。

それじゃあ、円周率の意味とはなんだろう!??
教科書で「円周率の意味」を確認してみよう。中1数学の教科書には、
円周の直径に対する割合です
って説明があるね。円周の直径に対する割合?? えっと・・・ちょっと意味がよくわからないよね。うん、堅苦しい。
もっとわかりやすくいうと、円周率とは、
円周(円のまわりの長さ)が直径の何倍になっているか
ということを表した数字なんだ。小学校のとき、円周率は約3.14って習ったでしょ?? つまり、
円周は直径のだいたい3倍の長さになっているよ。
ってことなんだ。
たとえば、直径1cmの円があったとしよう。
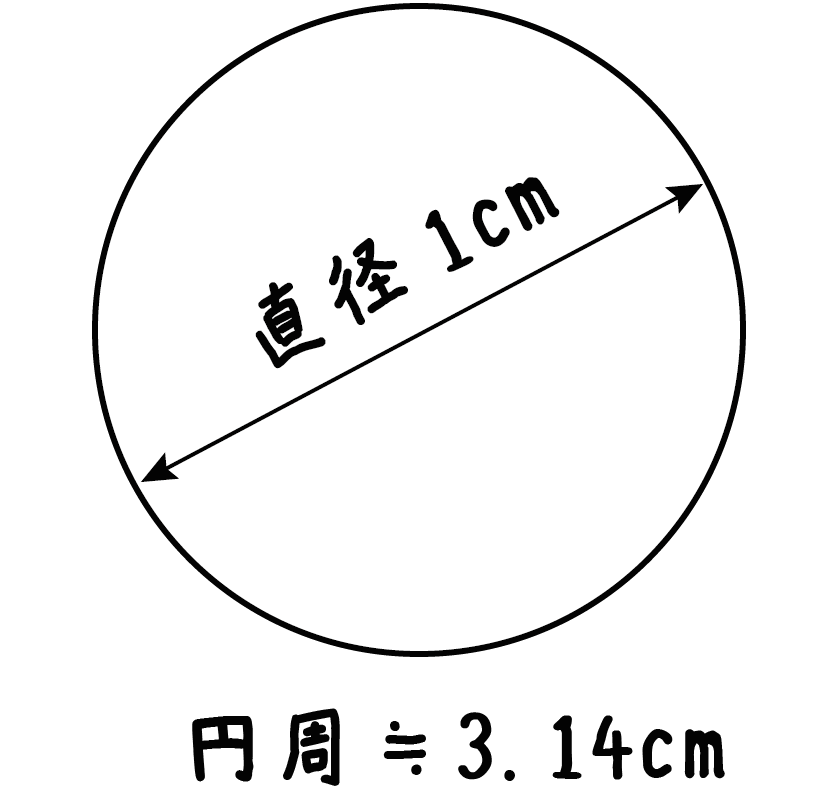
この円周の長さはだいたい3.14cmってことになるわけ。
じつは、この円周率っていうのはむちゃくちゃすごいことなんだ。
なぜかっていうと、
円の大きさを変えても円周率は変わらないからね。たとえば、「小さい円」でも「大きい円」でも決まって、直径の3.14倍が円周の長さになっているんだ。
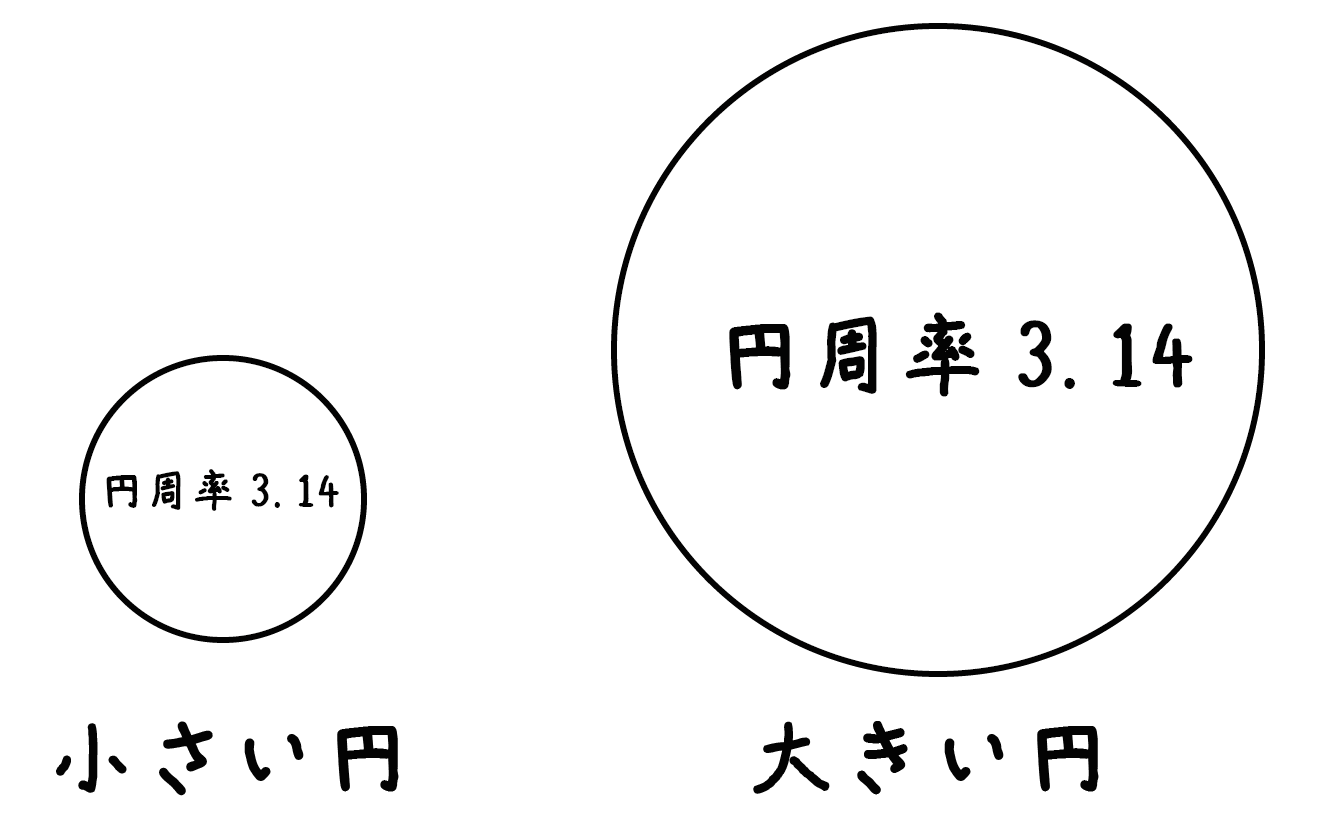
どんなに大きさを変えても「直径」と「円周の長さ」の関係が変わらない。
これってスゴイよね?? もはや地球の神秘のひとつといってもいいぐらいさ。
小学校の算数では、
円周率は3.14である
って教わってきたよね。
だけれども、超厳密にいってしまえば、円周率は3.14じゃあない。
円周率は無限につづく終わりがない数字(無理数)なんだ。
3.14のつづきをちょっと書いてみると、
3. 1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502….
こんな感じで無限につづいていくんだ。
マジ、終わりがない。
円周率って3.14に近い数字だけれども、3.14ではないんだ。でも、いちいち円周率を長く書いていたらテスト用紙がいくらあっても足りない。
そこで中学数学では、
ギリシャ文字のπ(パイ)
を円周率としてあげることにしたんだ。パイって食べるお菓子のことでもないし、ドラゴンボールにでてくるタオパイパイでもない。
したがって、
円周の長さは直径のπ(パイ)倍である
ってことが言えるね。
円周率の意味についてちょっとスッキリしたかな??
次回はいよいよ円の面積・円周の長さの求め方についてみていこう。
そんじゃねー
Ken
こんにちは、この記事を書いてるKenだよ。まんじゅうを食べたいね。
ここまで2つの「基本の作図」、
をみてきたね。もうじっさいに作図してみた!??
うん、
うん。
オッケーそうだねw

今日は、「基本の作図」で最後の、
「垂線」の書き方
をわかりやすく解説していくよ。テスト前に参考にしてみてね。
~もくじ~
垂線の作図問題って色々ありそうだよね??
だけど、だいたい次の2つしかないんだ。
それは、
の2種類だ。
ちょっとわかりにくいので、図であらわしてみよう。
基本的に垂線の作図問題って、
つぎの直線に垂線をひいておくれ!

って奴なんだ。
だけれども、なーんにも問題に指定がないと、どこに垂線をかいても正解になっちゃうよね??
左寄りにかいてもいいし、別に真ん中にかいたっていい。
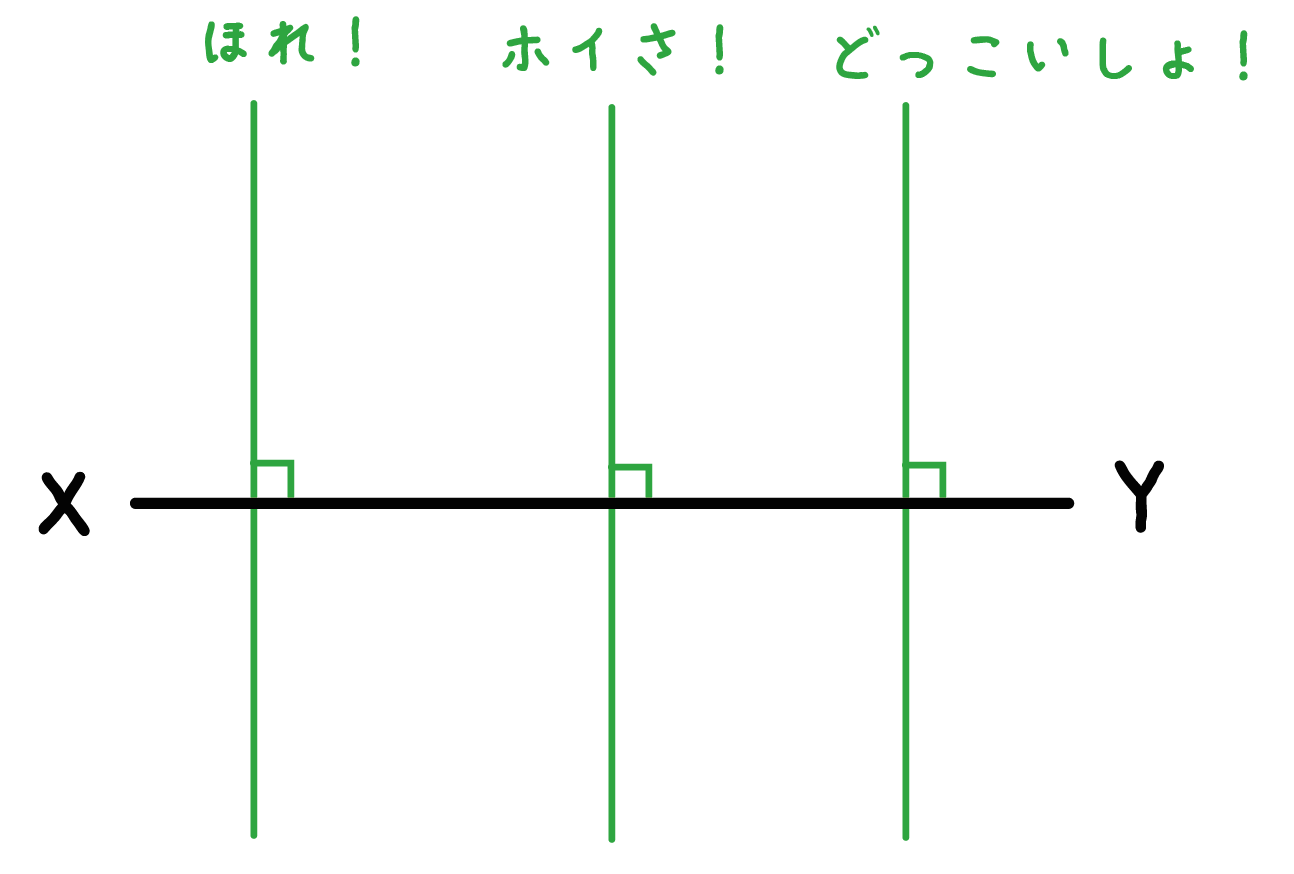
だから、たいていの「垂線の作図問題」では、
この点を通る垂線をかいてね。
っていう垂線がとおる「ある点」が指定されてあるんだ。
この「ある点」の位置が、
「直線上にある」のか、
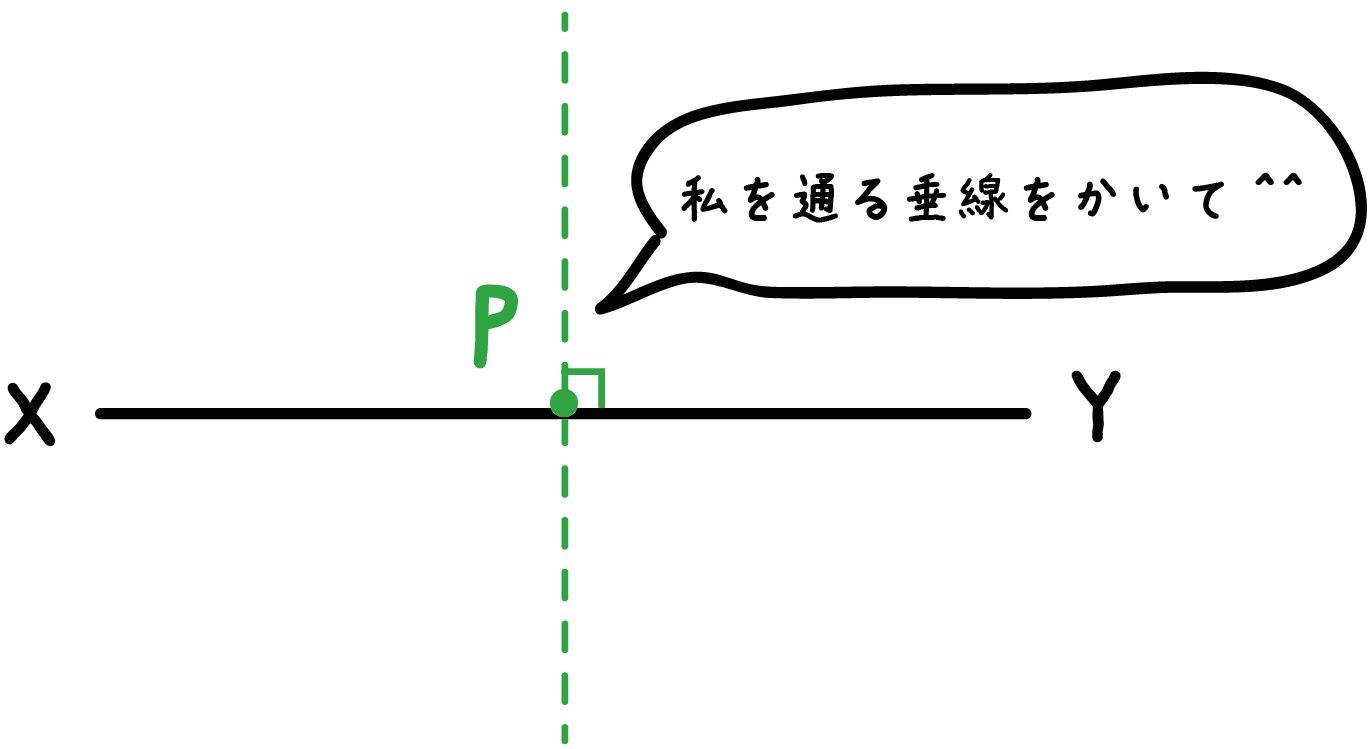
それとも「直線上にない」のか。
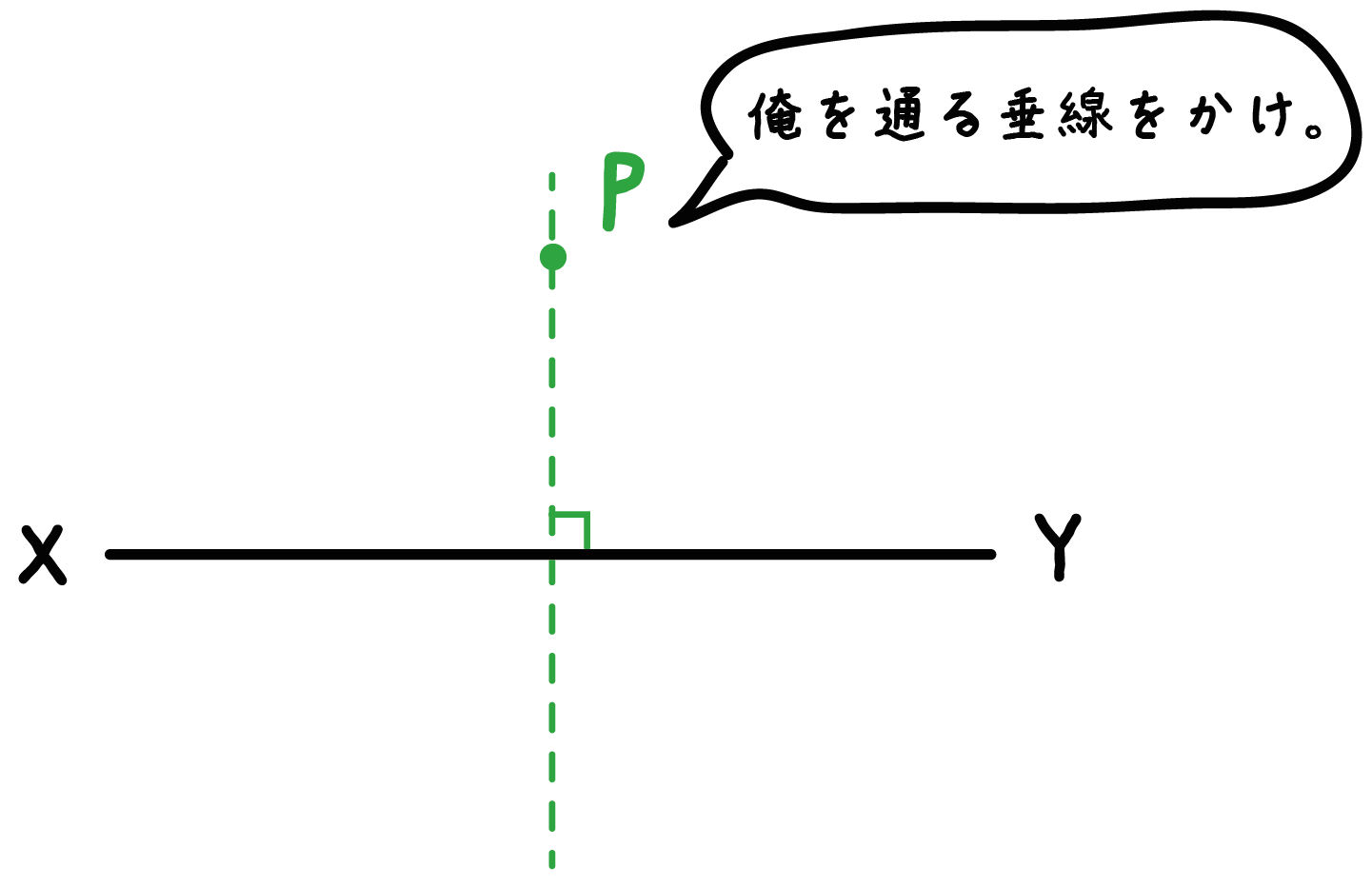
それによって、問題が2種類あることになるんだ。
作図の問題は2種類あるからビビるけど、垂線の書き方は2つのパターンとも一緒。
安心してね。
今日は2つめの、
「直線上にない点」を通る垂線の作図
をみていこう。

垂線の作図のために、
の2つのアイテムを用意してから始めてねー!
まずコンパスを適当に開いちゃおう。
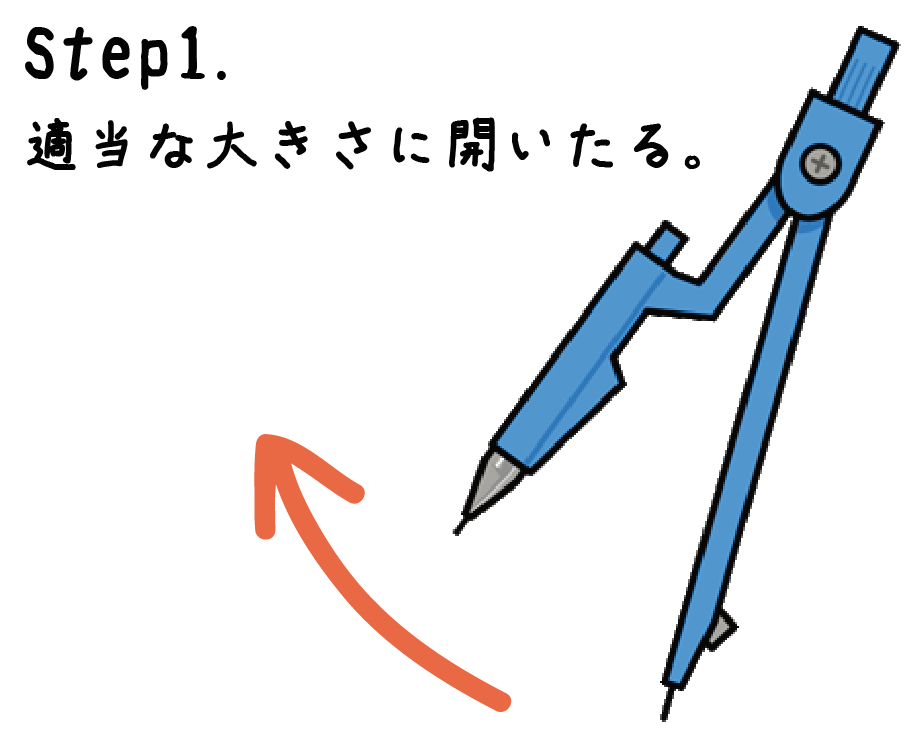
開く大きさはどうでもいいんだけど、一つだけ守ってほしいことがある。
それは、
点Pから円をかいたら直線XYに触れるだけ開く
ということだ。いくら円をかいても直線に触れなかったらダメ。
これは忘れないようにしよう。
つぎは、コンパスの針を「垂線が通る点」のうえにおいちゃおう!
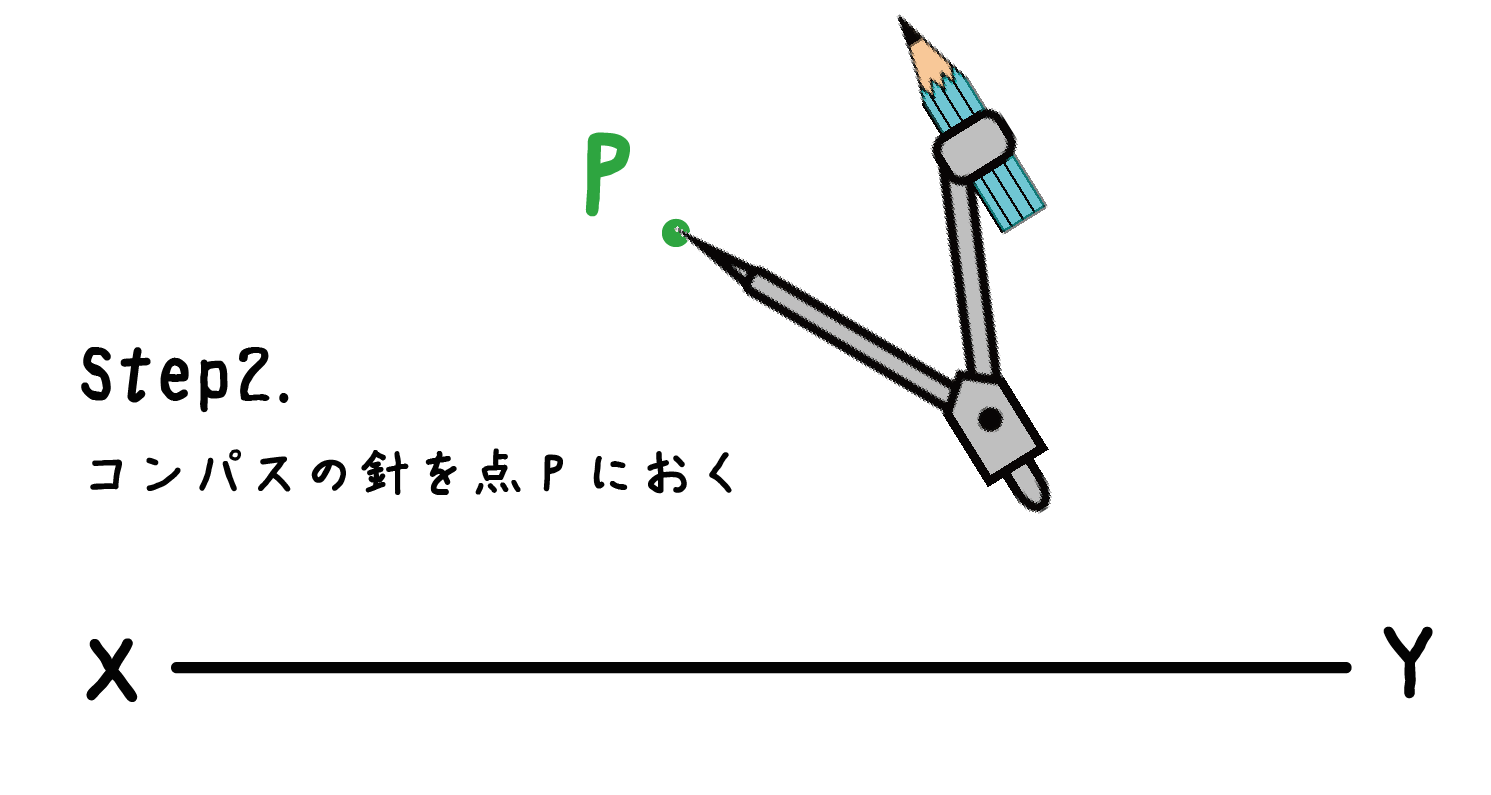
この例題でいえば、点Pの上ってことだね。
コンパスの針は動かないようにして、円をかいてみよう。
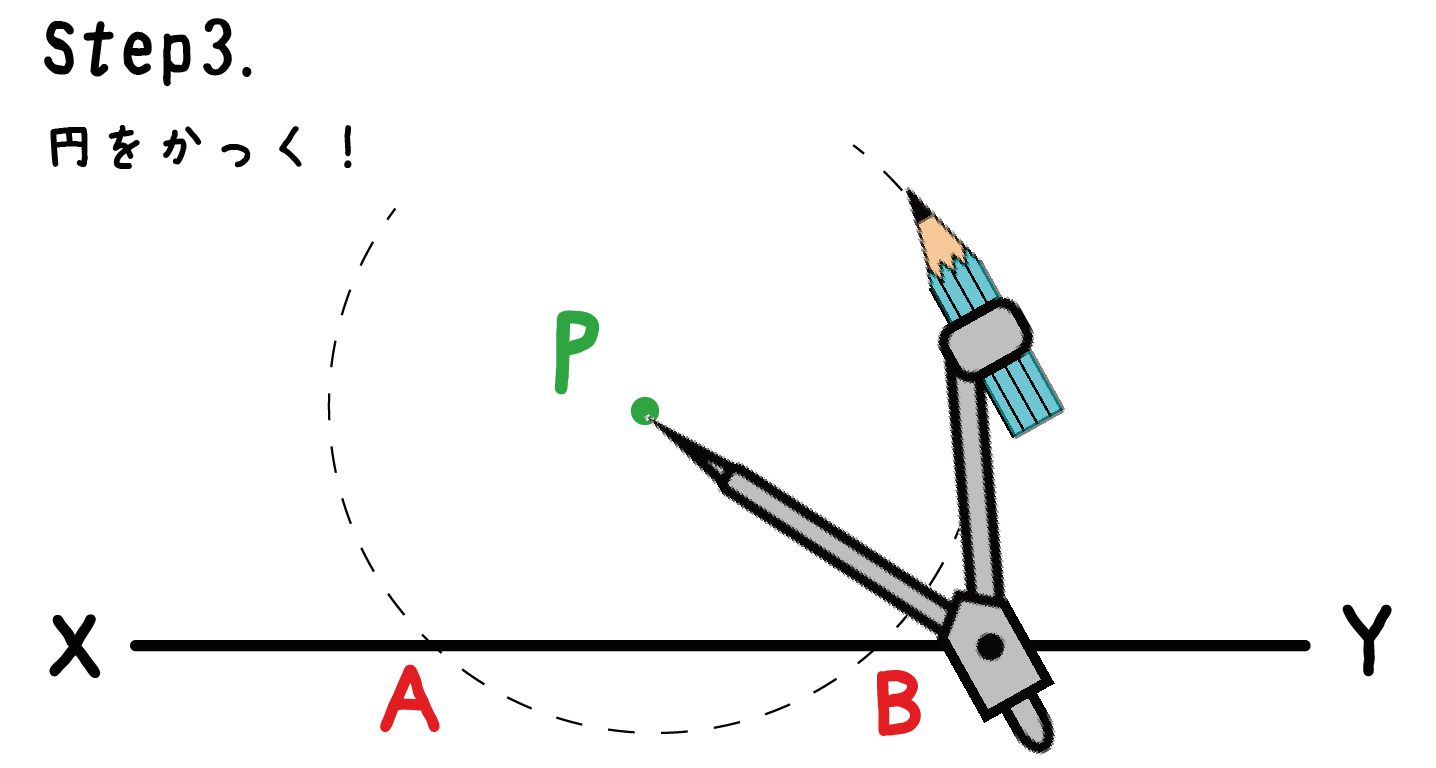
ここでは丸々ひとつの円をかく必要はないよ。
「直線」に「円」の交点が2つできればそれでいいんだ。
例題では、点AとBという2つの交点ができてるでしょ??。
どちらかの交点にコンパスの針をおいてほしい。
そんで、ちょっとだけ円をかくだ。こんな感じでね↓↓
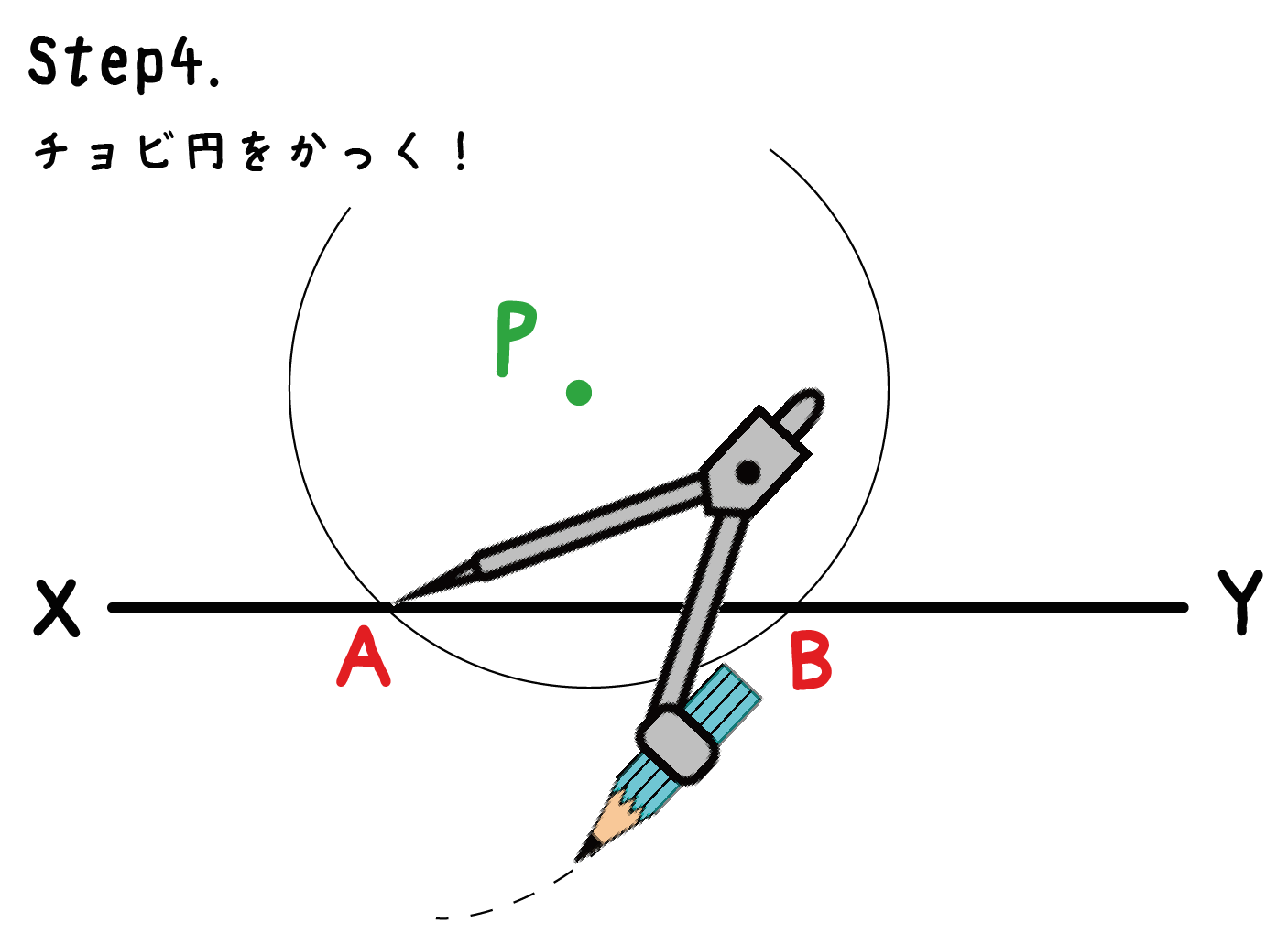
例題でいうと、点Aに針をおいてちょっとだけ円をかいているね。
このチョビ円がかき終わったら、今度は点Bで同じことをするんだ。つまり、チョビ円をかくってことね。
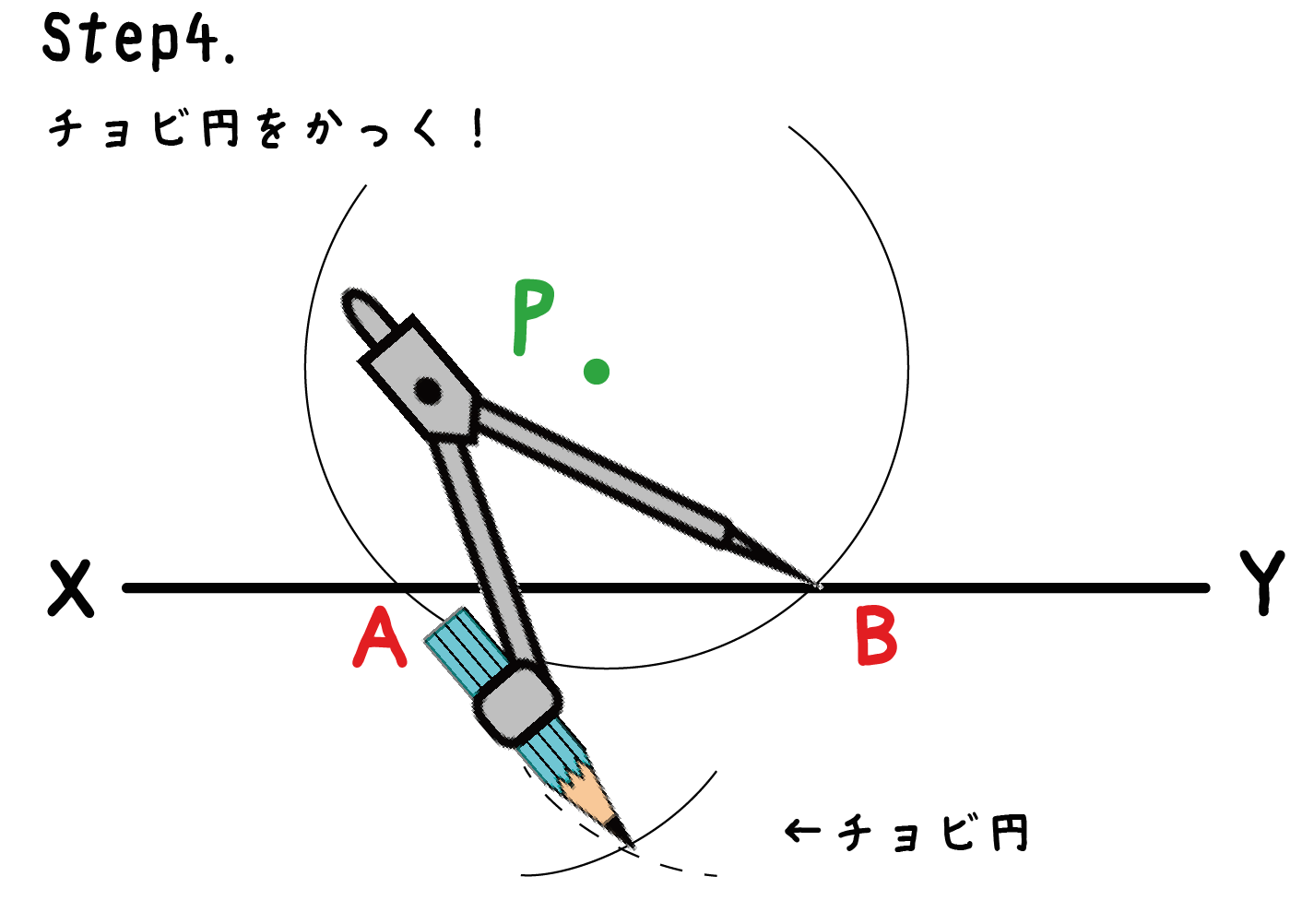
このように、新しくできた交点を中心に2つの「チョビ円」をかくんだ。
チョビ円同士が交わっていれば問題なしさ!
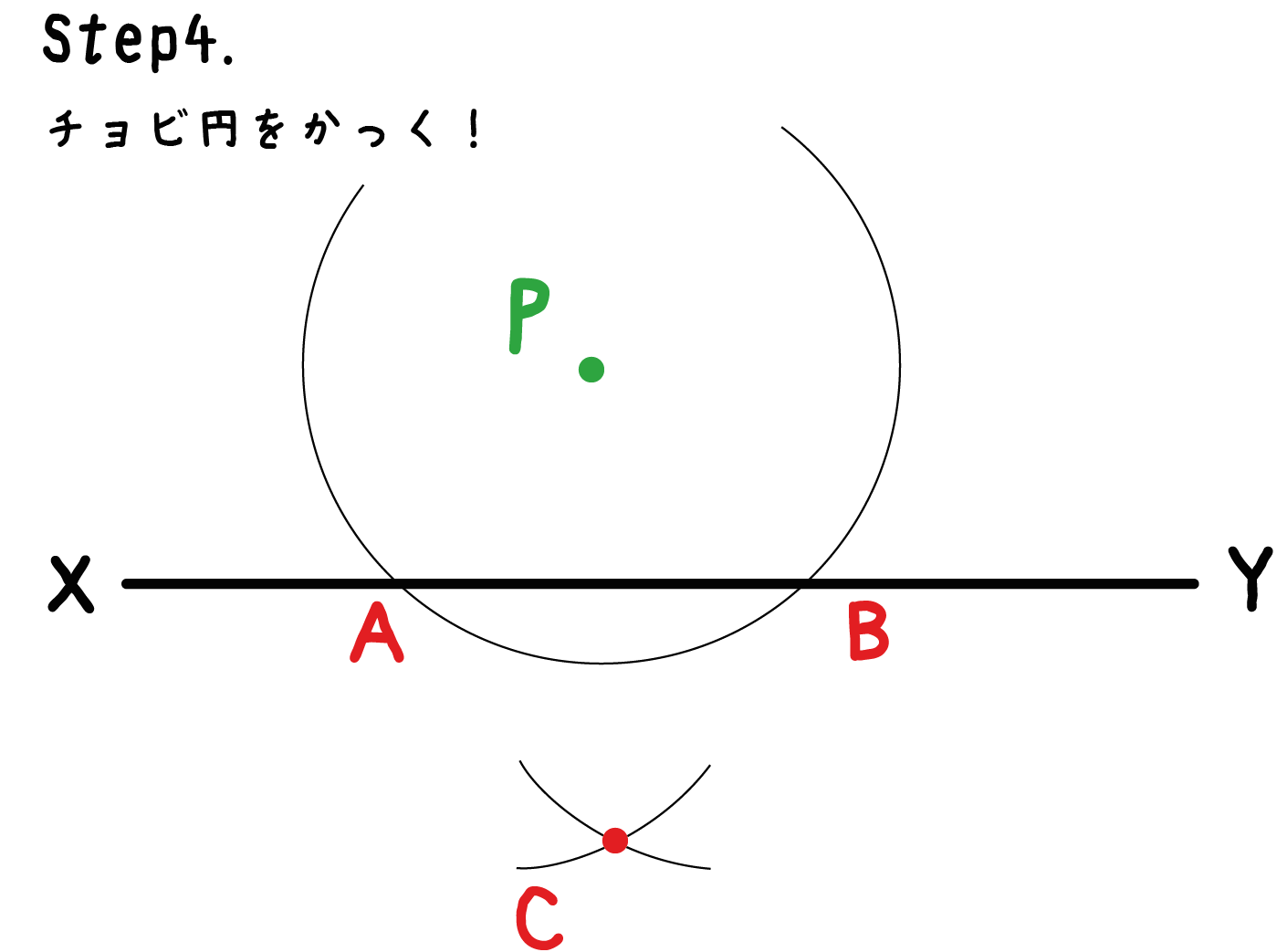
いよいよ最後のステップだ。
「垂線がとおる点」と、Step4で誕生した「チョビ円の交点」を結んであげよう。
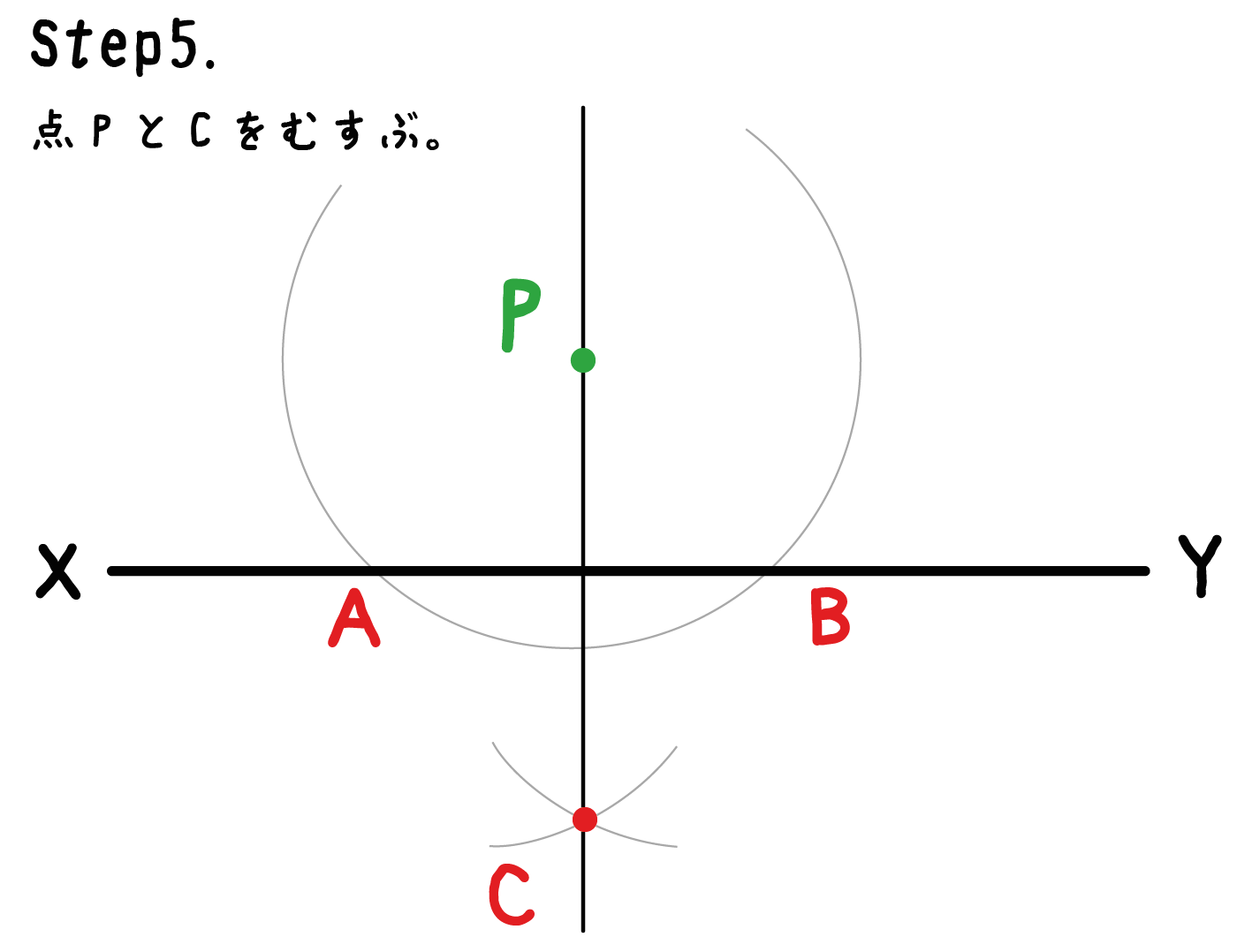
例題でいうと、点Pと点Cを結ぶことになるね。
この2つの点をむすんで生まれたのが「垂線」だ。
ちょっとかっこよくいえば、
点Pをとおる直線XYの垂線
ってことになる。やったね!
垂線の書き方はどうだったかな?!
コンパスと定規をつかっちゃえばカンタン。たった5つのステップでいいんだ。
テストにでてくるからよーく復習しておいてね。
これで中1数学で勉強する3つの「基本の作図」、
をマスターしたね!おめでとう!!
次回はいよいよ「円とおうぎ形」の単元にはいっていくよー。
そんじゃねー
Ken
こんにちは、この記事を書いてるKenだよー!筋トレにはまってるね。
中1数学で勉強する「基本の作図」は、
の3つがある。どれもテストに狙われやすいから覚えておきたいね。

今日は2つめの、
角の二等分線の書き方・作図
をわかりやすく解説していくね。テスト前に確認してみてくれ。
~もくじ~
さっそく、角の二等分線の作図を勉強していこう。
つぎの問題をときながらみていくよ。
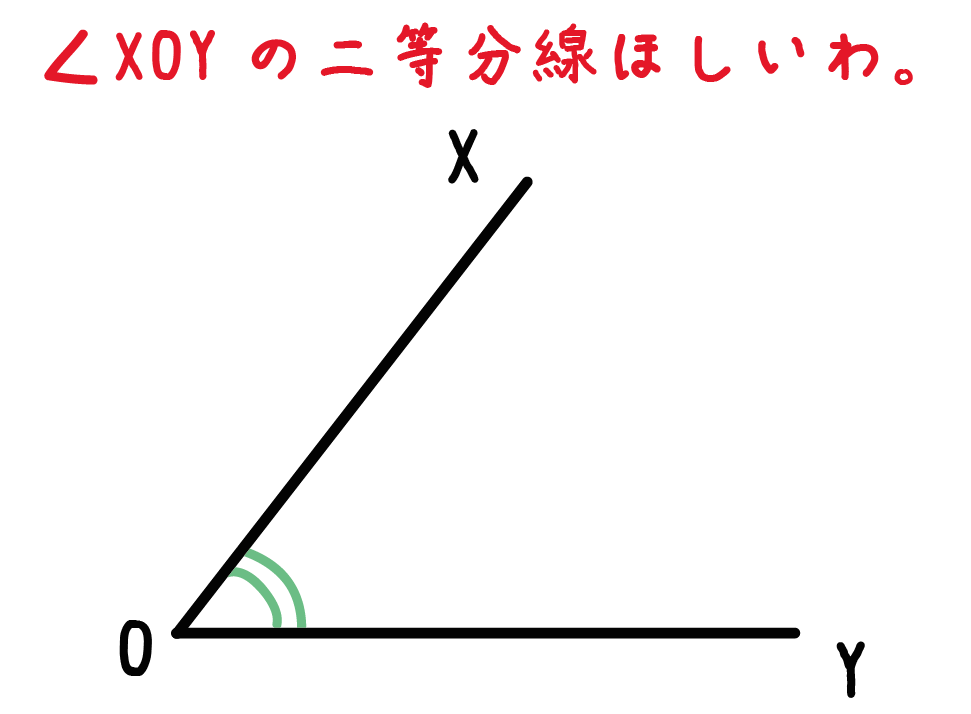
角の二等分線の作図に必要なアイテムは、
の2つだ。準備はいいねー?!
まずは手にもっているコンパスを適当に開いちゃおう。

コンパスの開き具合はマジで自由。
円をかきやすいぐらいにコンパスを開いてみてね。
コンパスを開いたね?! それじゃあそのコンパスの針を頂点においちゃおう!
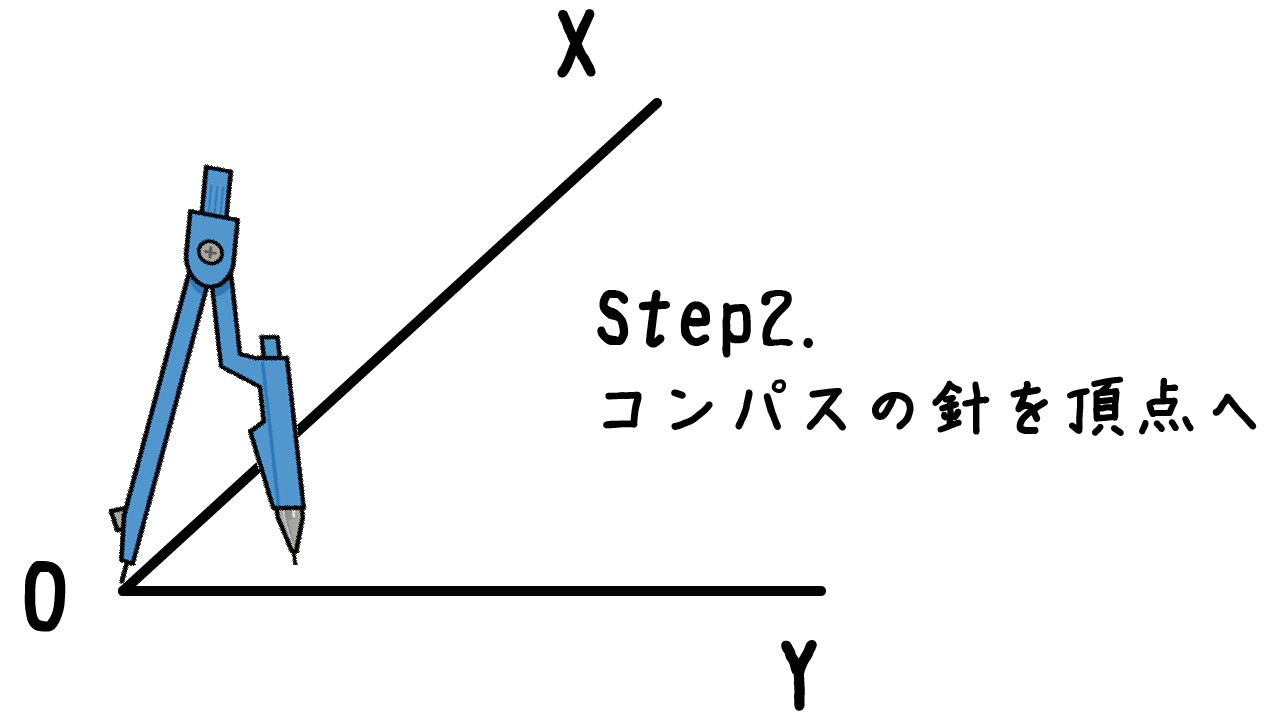
ここでいう頂点というのは、
「角の二等分線」をかきたい角がある頂点のこと
だよ。例題でいうと点Oがそれにあたる。
だって、点Oは角XOYの頂点になってるでしょ??
コンパスの針をおく点を間違えないようにしよう。
そのまま半円をかいてあげよう!
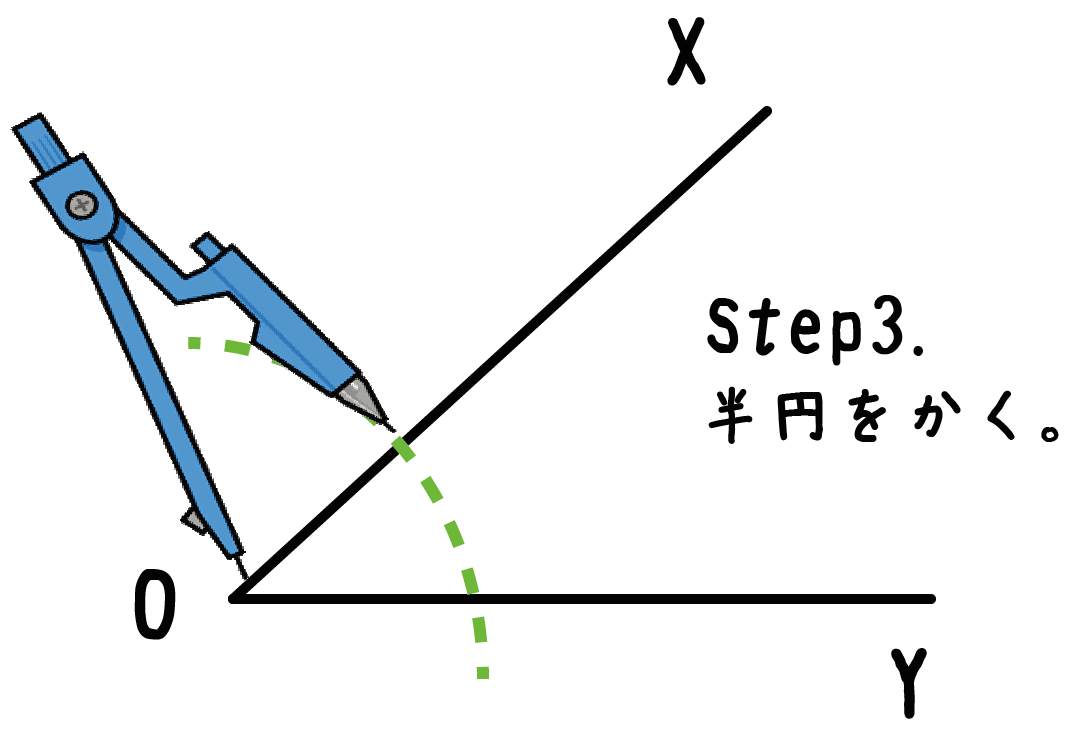
別にぜんぶの円をかいてもいいし、半円より小さくてもいいんだ。
重要なのは、
角をつくっている2つの線分と円がまじわっているかどうか。
この問題の例でいえば、線分OXと線分OYと円が交わっていればOKだよ。
Step3で2つの交点ができたよね?? 例題でいうと点PとQがそれにあたる。
つぎはこの交点をいかしていくよ。
新しくできた2つの交点のうちの1点にコンパスの針をおこう。つまり、点PかQだね。
そして、ちょこっとだけ円をかくんだ。
こんな感じで↓↓
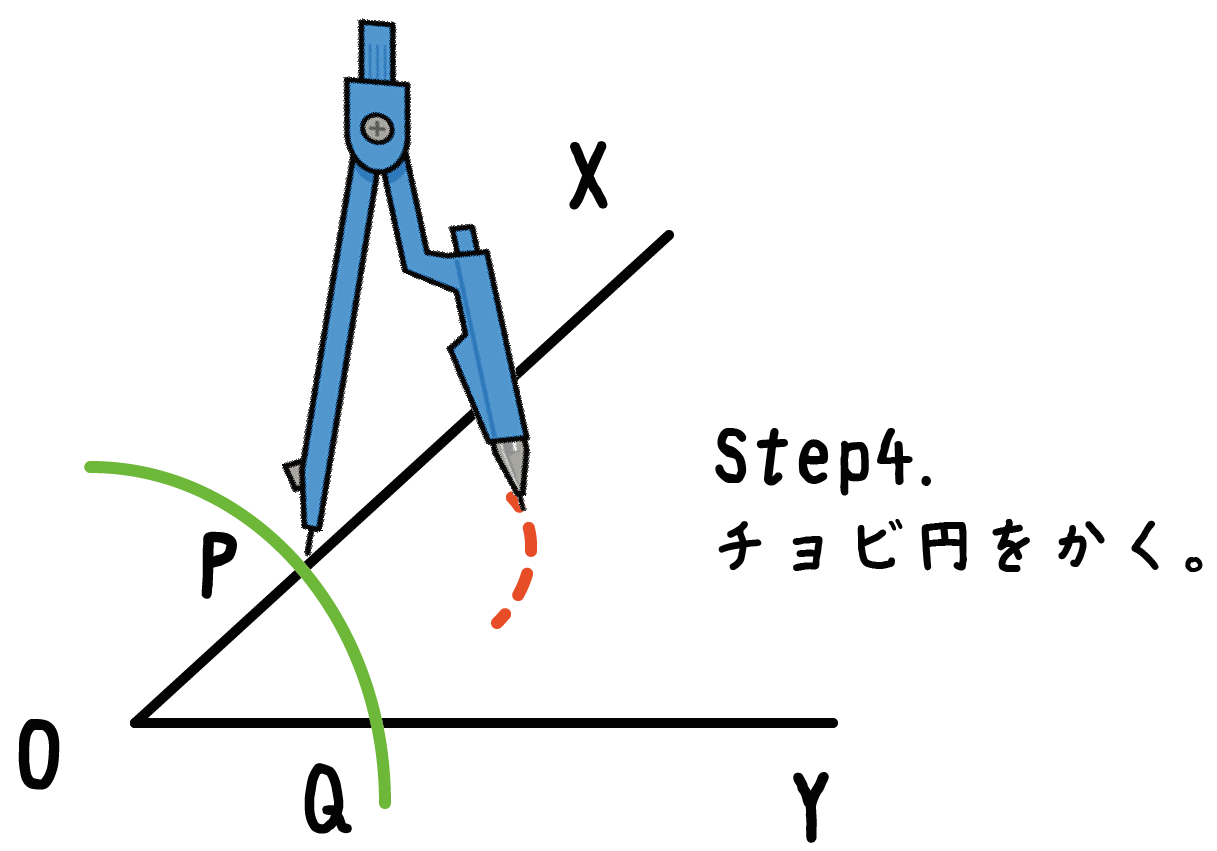
コンパスの開き具合はそのままでもいいし、変えてもいいよ。
これができたら、もう一個の交点を中心にも同じことをしてあげよう。
こんな感じだ↓↓
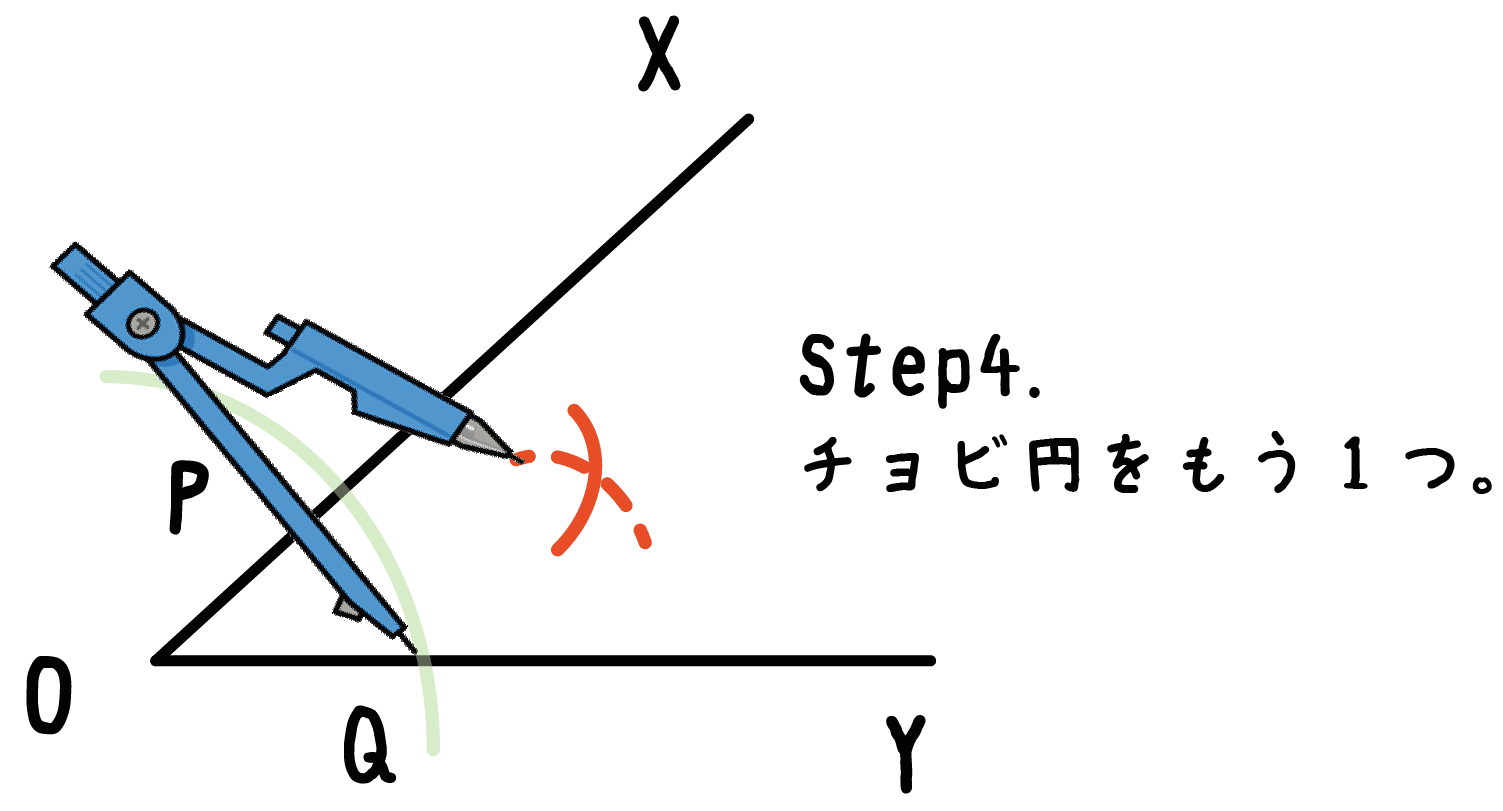
2つのチョビ円がまじわっていれば大丈夫だよ。
いよいよ最後のステップだ。
Step4でつくった「チョビ円」の交点と、角をもっている頂点を結んであげるんだ。
例題でいえば、点Rと点Oを結ぶことになるね。
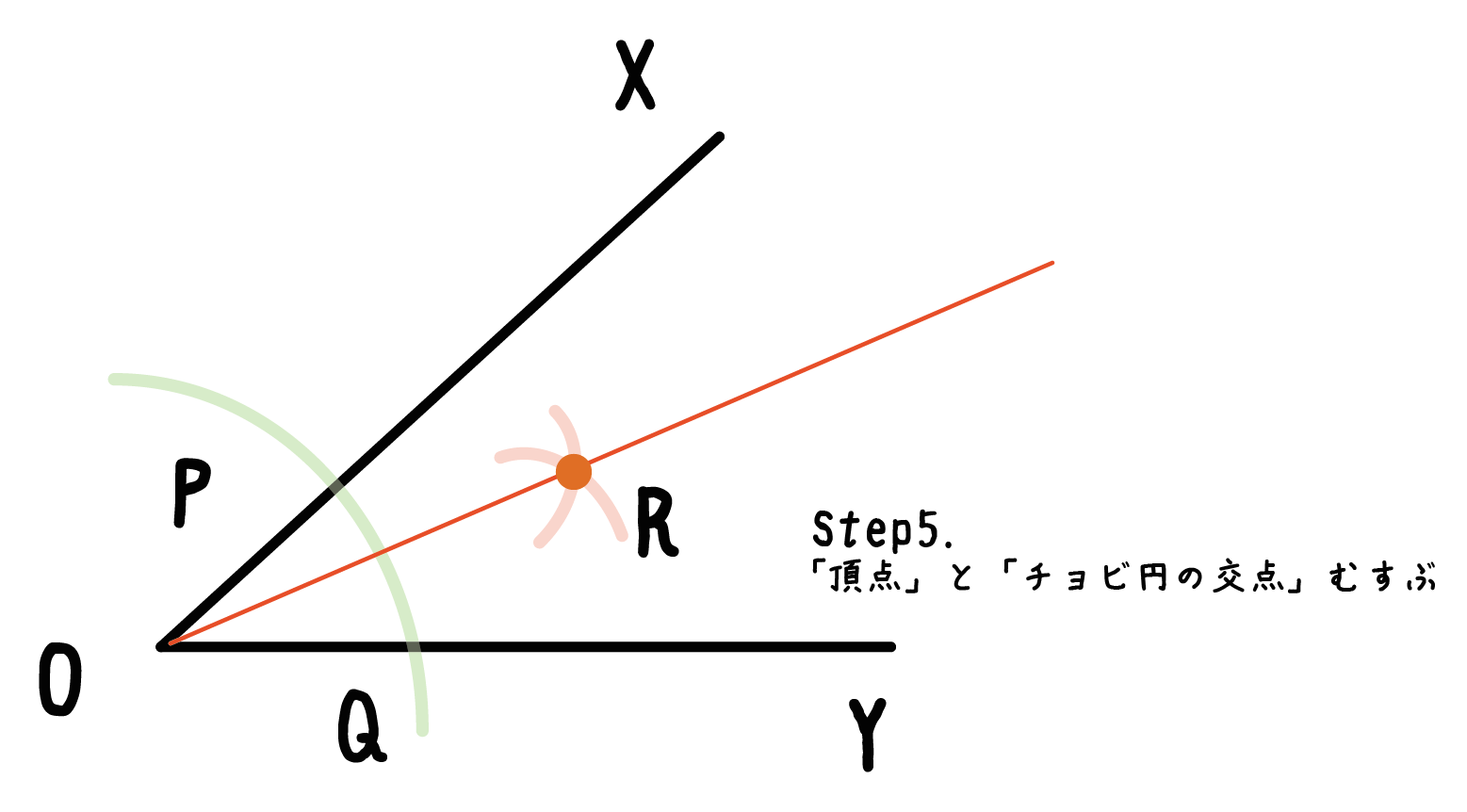
これによってできた直線が「角の二等分線」だよ。
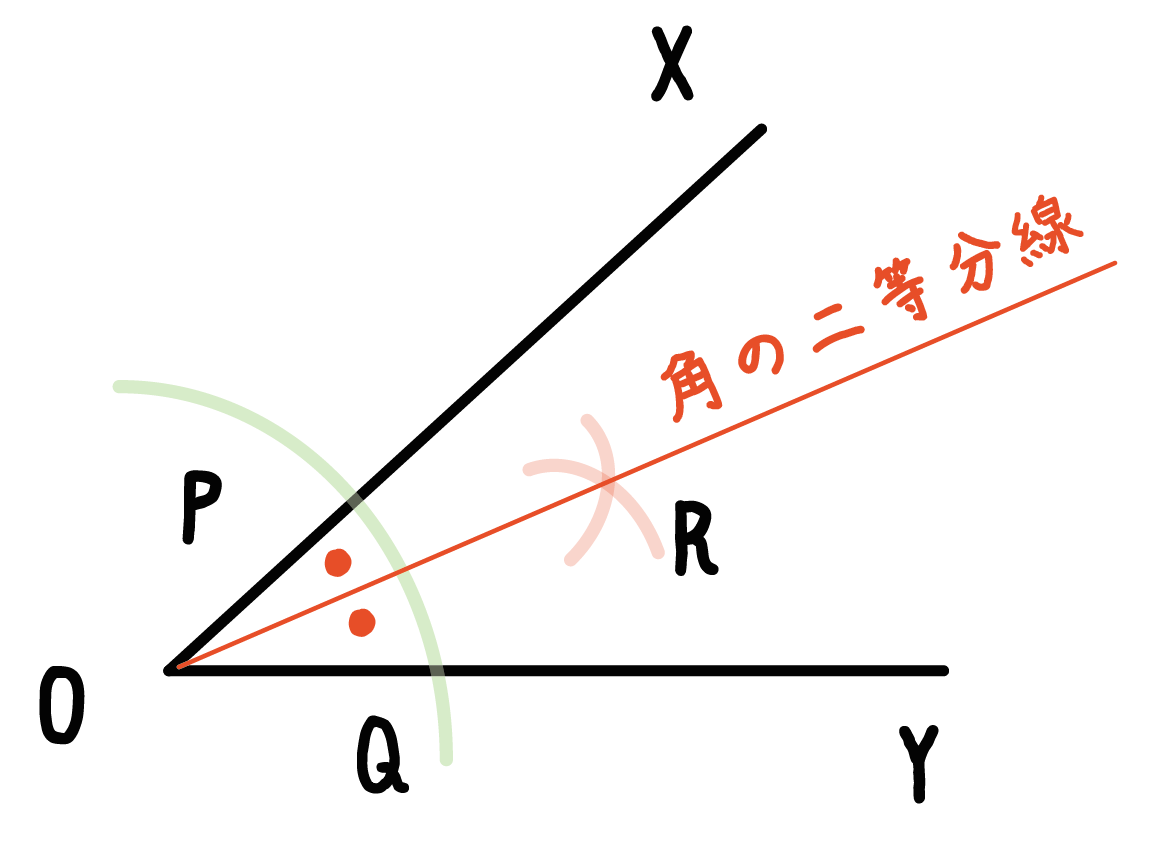
やったね!! 。
角の二等分線の書き方は意外とシンプルだったでしょ?!?
でも、つぎのことを考えてほしいんだ。それは、
なんでこの書き方で「角の二等分線」が作図できるのか??
ということ。テストでは書き方さえ覚えておけば、ぶっちゃけどうにかなる。
ただ、数学をもっと面白く勉強するためには、その作図方法がどうして使えるのか、ということを知っておいたほうがいいんだ。
そのほうがゼッタイ楽しいよ。
それじゃあ、なんでさっきの書き方で角の二等分線が作図できるんだろう??
その答えは、
まったく姿、かたちが同じ三角形が2つできるからさ。下の図いうと「1」と「2」の三角形だね。
つまり、「三角形OPR」と「三角形OQR」だ。
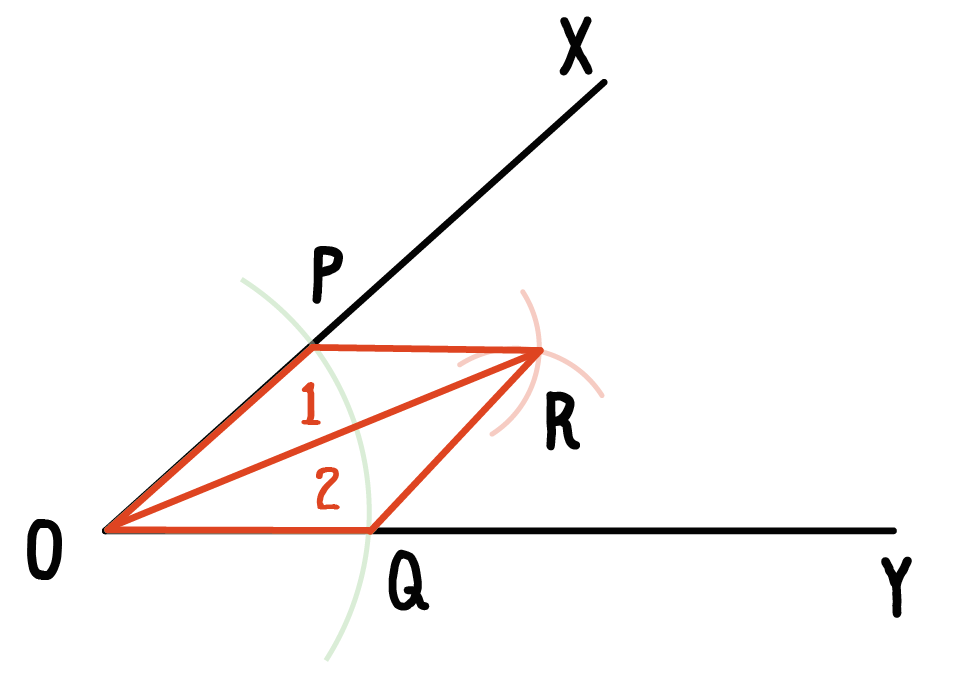
なぜ、この2つの三角形の姿カタチが同じになるのか??
これは中2数学で勉強する「三角形の合同条件」を知らないいけない。だから、ここでは無視するよ。
ってこで、
三角形OPR (1)と三角形OQR(2)の姿がまったく同じ。
だから、対応する角度である、
角PORと角QORは等しい
ってことになるんだ。
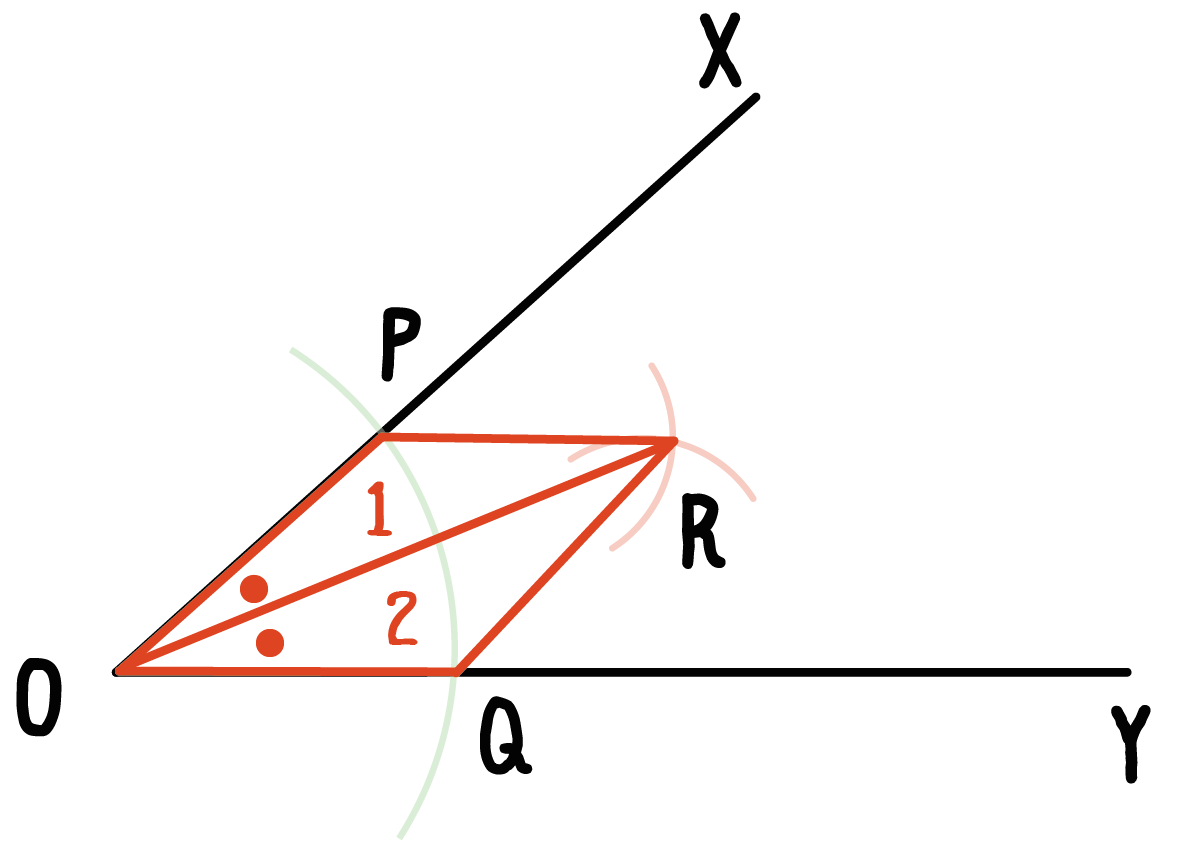
どう??ちょっとスッキリした??。
角の二等分線の書き方はどうだったかな??
テストで狙われやすいところだから、しっかりと復習しておこう。
作図は練習が大事だから、コンパスと定規で今から実際に「角の二等分線」をかいてねー!
そんじゃねー
Ken
こんにちは、ドライマンゴーにはまってるKenだよー!
中1の平面図形でマスターしておきたいのは「基本の作図」。
先生たちは作図の問題をテストに出したがるんだ。
だって、カンニングしてもよくわからない問題だからね。作図の練習をしていないとゼッタイに解けないのが特徴だ。

そこで今日は、平面図形でもっともねらわれやすい、
垂直二等分線の書き方・作図方法
を4ステップで解説していくね。
垂直二等分線の作図とかよくわかんねーってときは参考にしてみて。
~もくじ~
垂直二等分線の書き方をマスターするために1つだけ知っておくべきことがある。
それは、
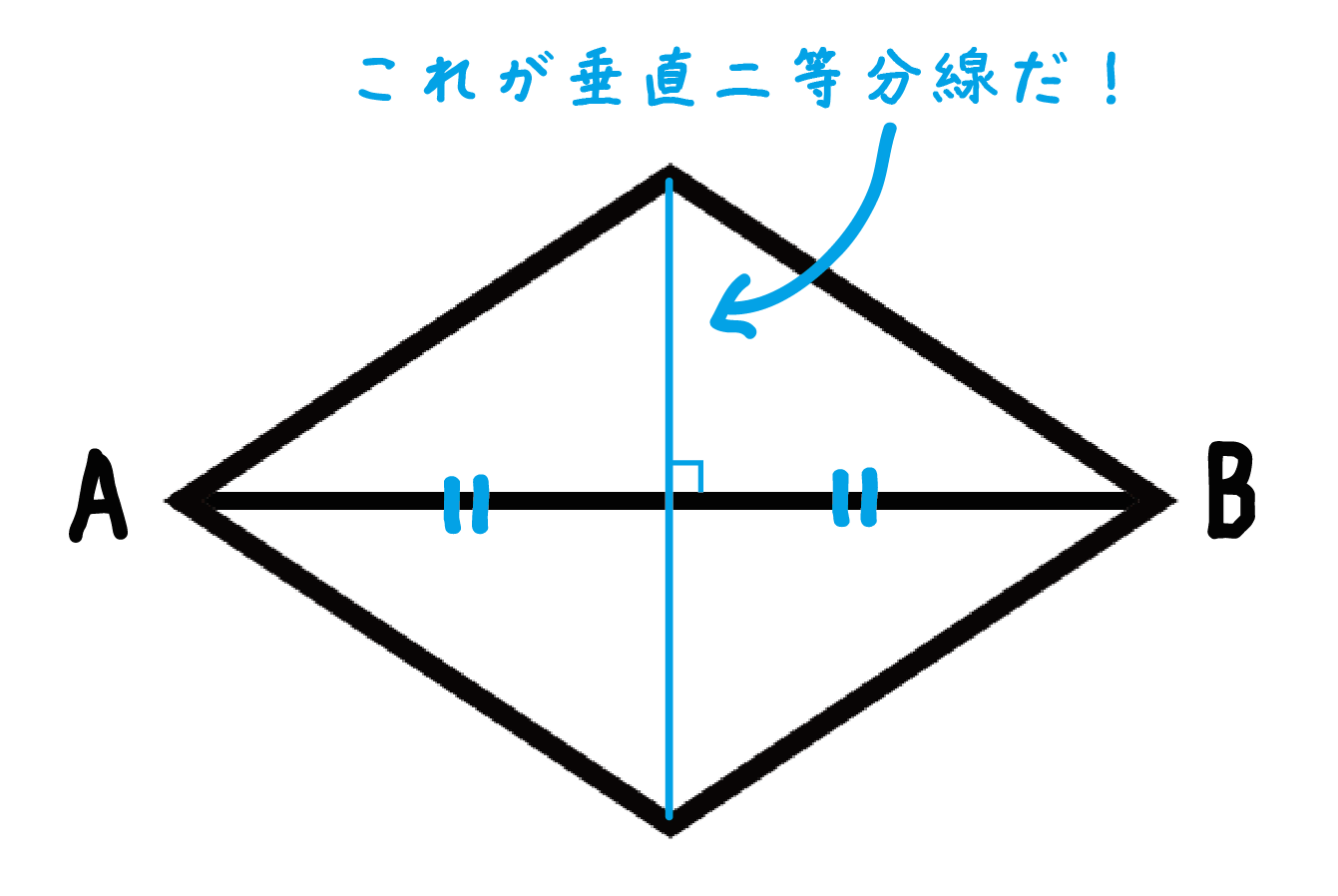
ひし形の対角線の性質
だ。

「ひし形」といえば、
4本の辺の長さが全て等しい四角形
のことだったね (Wikipediaより)。
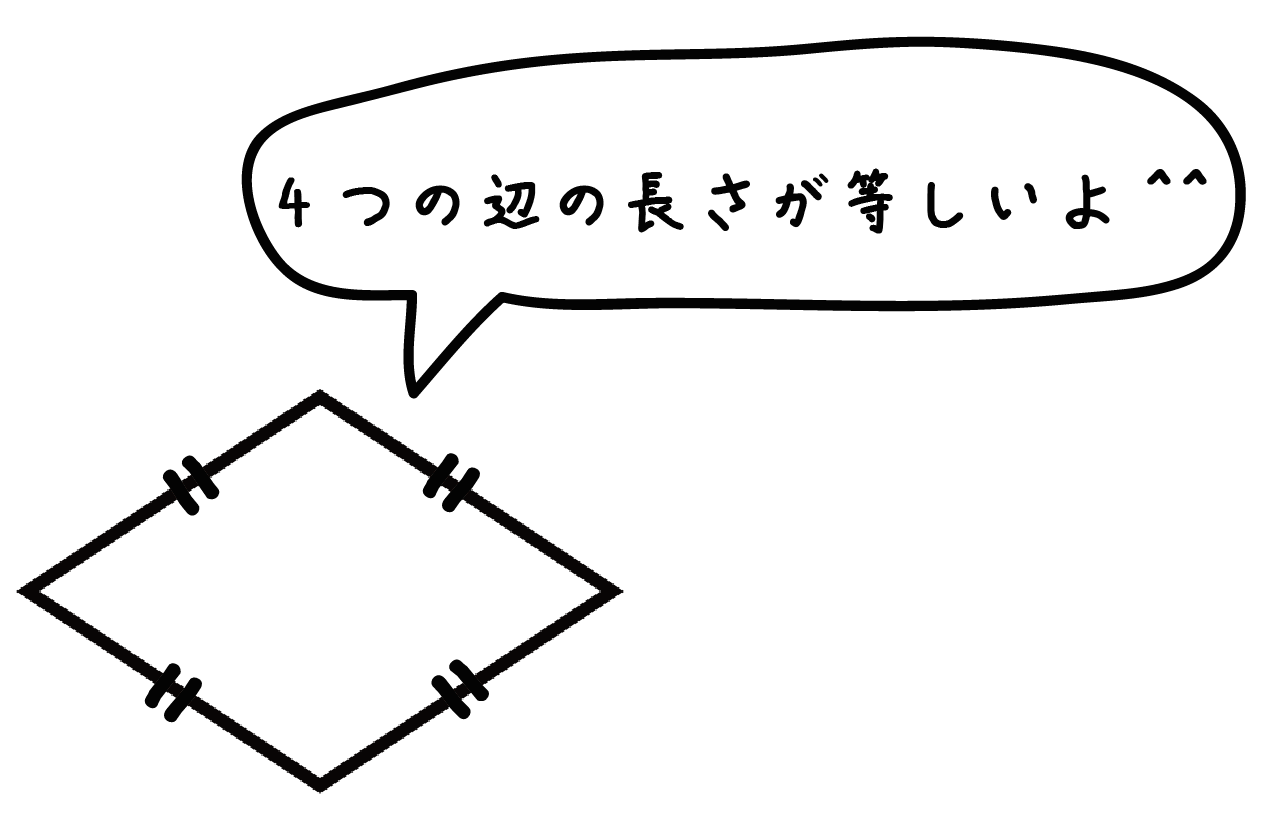
じつは「ひし形」には「ある性質」が備わっているんだ。それは、
対角線がそれぞれの中点で垂直に交わる
というものさ。
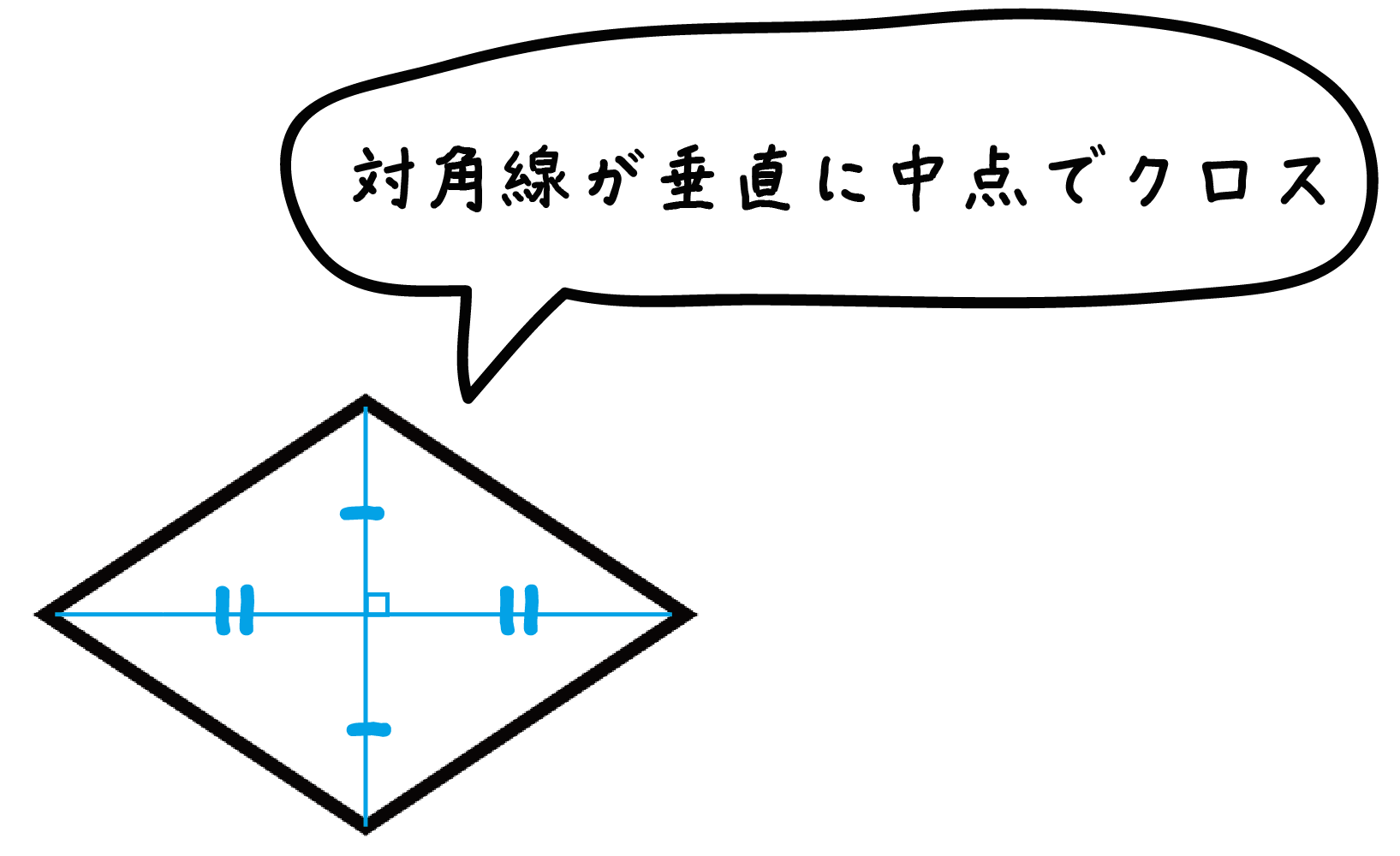
垂直二等分線の作図では、
ひし形の「対角線の性質」を利用してあげればいいんだ。
たとえば、
線分ABの垂直二等分線を作図しなさい。
という作図問題があったとしよう。

さっきの「ひし形の対角線の性質」を応用するためにはどうしたいいかな??
答えはいたってカンタン。
この線分ABを「ひし形」の対角線のうちの1つにしてやればいいんだ!
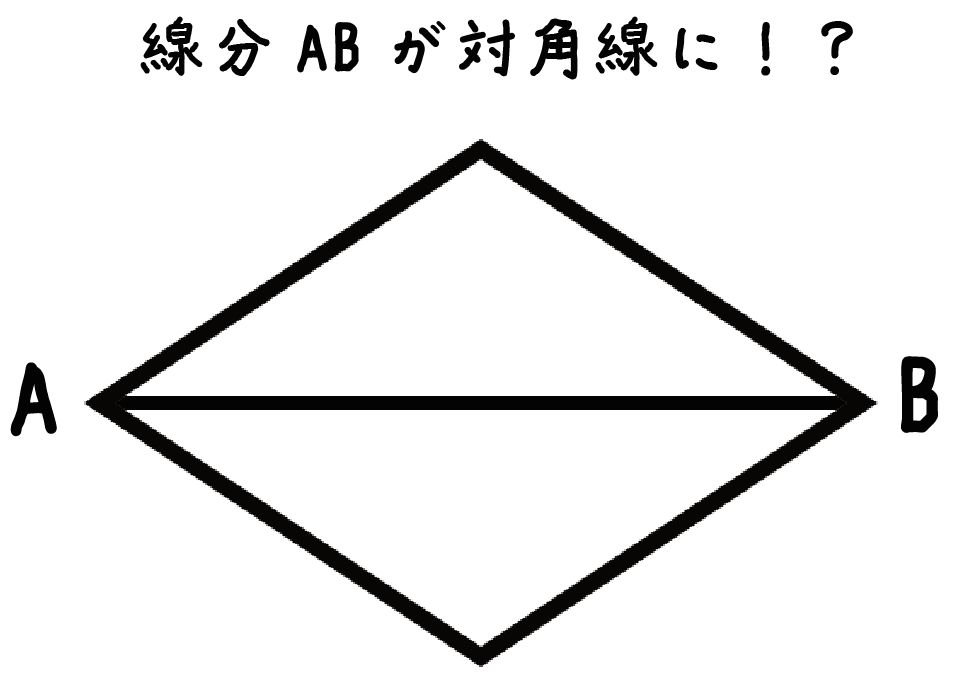
そんで、「もう1つの対角線」が「線分ABの垂直二等分線」ってことになるよね。だって、2本の対角線は中点で垂直に交わるからさ。
垂直二等分線をかくためにはお金はかからないし、特別な知識だっていらない。
必要なのはこの「ひし形」の対角線の性質だけなんだ。
どう??垂直二等分線が書けるような気がしてきたでしょ??
いよいよ、垂直二等分線の書き方をみていこう。
たった4ステップで作図できちゃうんだ。さっきの、
線分ABの垂直二等分線を作図しなさい。そしたらクッキーやるわ。
っていう例題をといていこう!

作図に必要なアイテムは、
の2つだよー!
1つめのステップはコンパスの足を適当な大きさに開くことだ。

ここでは何をしてるかっていうと、
ひし形の辺の長さを決めているんだ。いわば、垂直二等分線を作図するための準備フェーズだ。
コンパスを開く大きさは線分ABの半分よりちょいデカめがベストだよ。
さっき開いたコンパスを閉じないでね。
そのままの状態で点Aを中心に半円かいてあげるんだ。
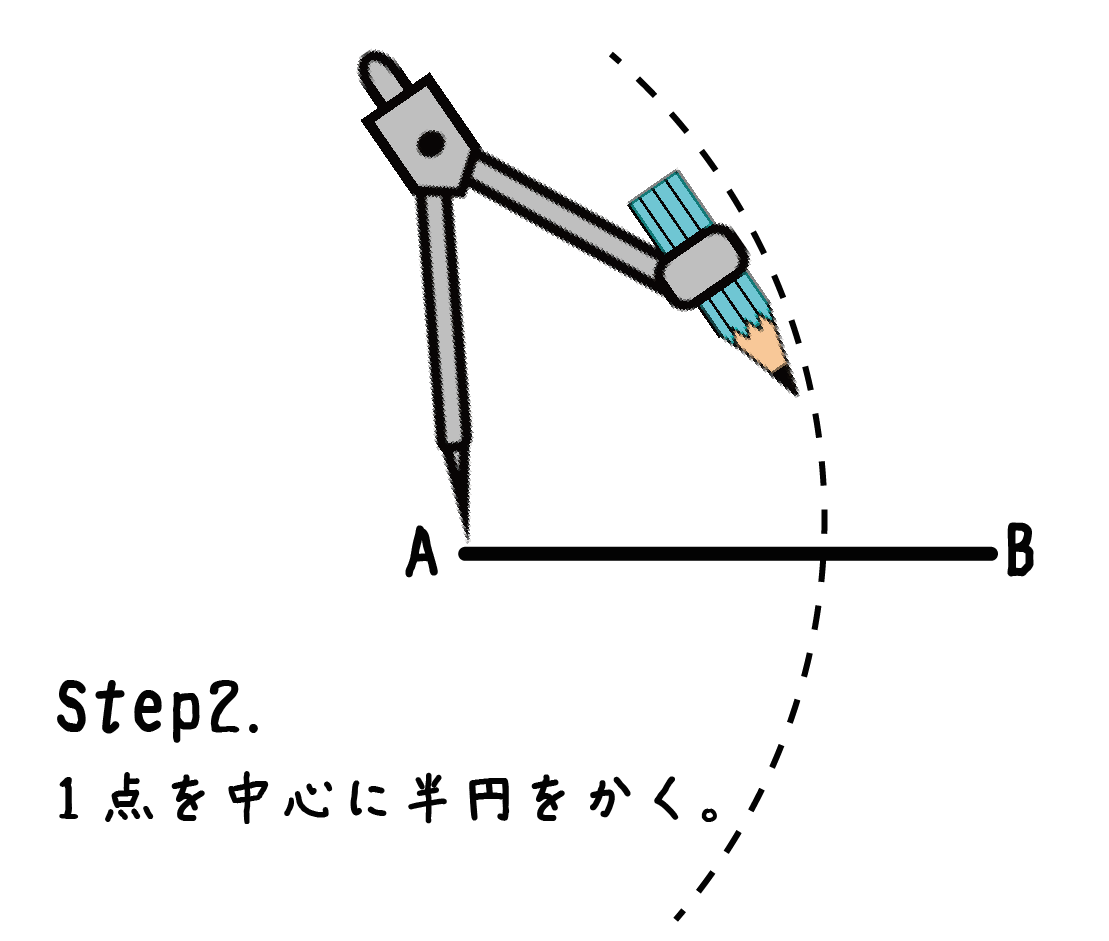
円をぜんぶ書かなくても大丈夫だよ。半分でいいんだ半分で。
Step2と同じことを反対側の点Bでもやってあげよう。
つまり、点Bを中心に半円をかくということだね。
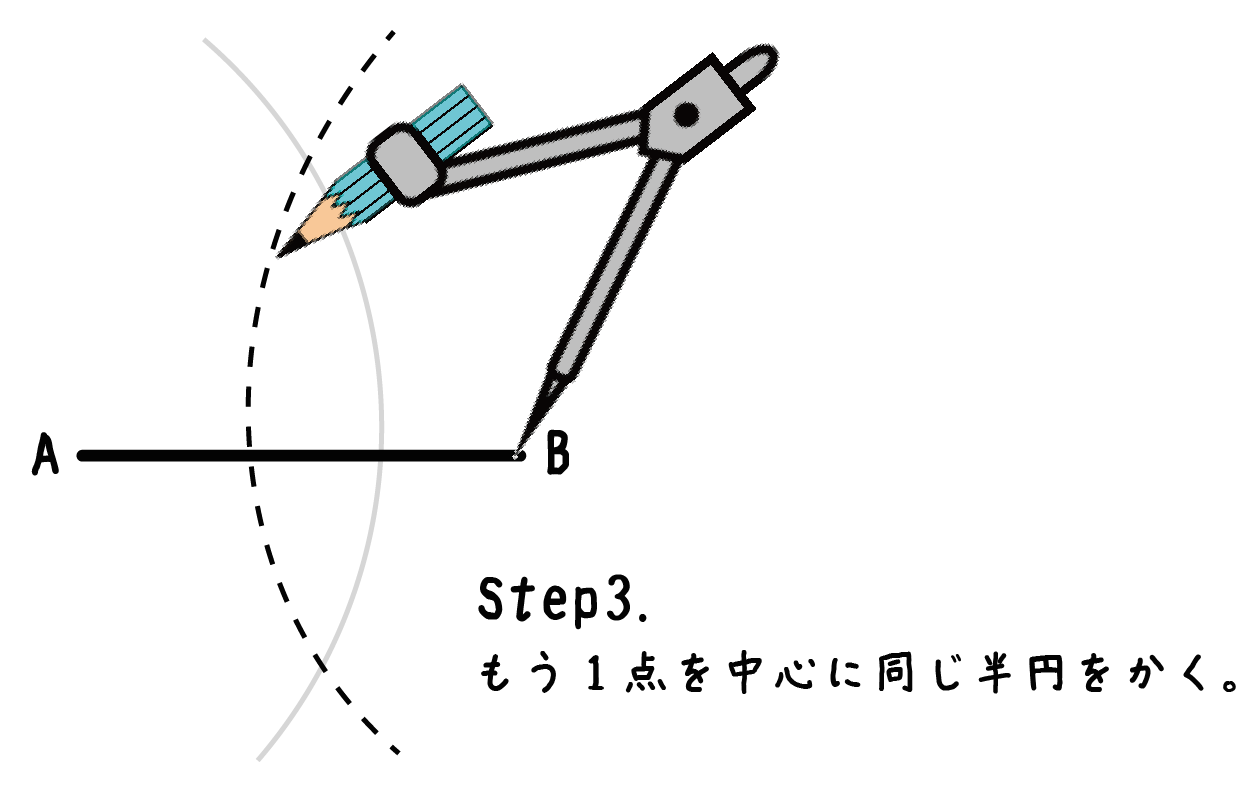
半径は変えずにそのままで書き終えちゃおう!
いよいよ最後のステップだ。Step3までにかいた2つの半円があるだろう??
その交点を結んでしまえばいいんだ。2つの点を結んでできた直線が、
「線分ABの垂直二等分線」
になるよ。
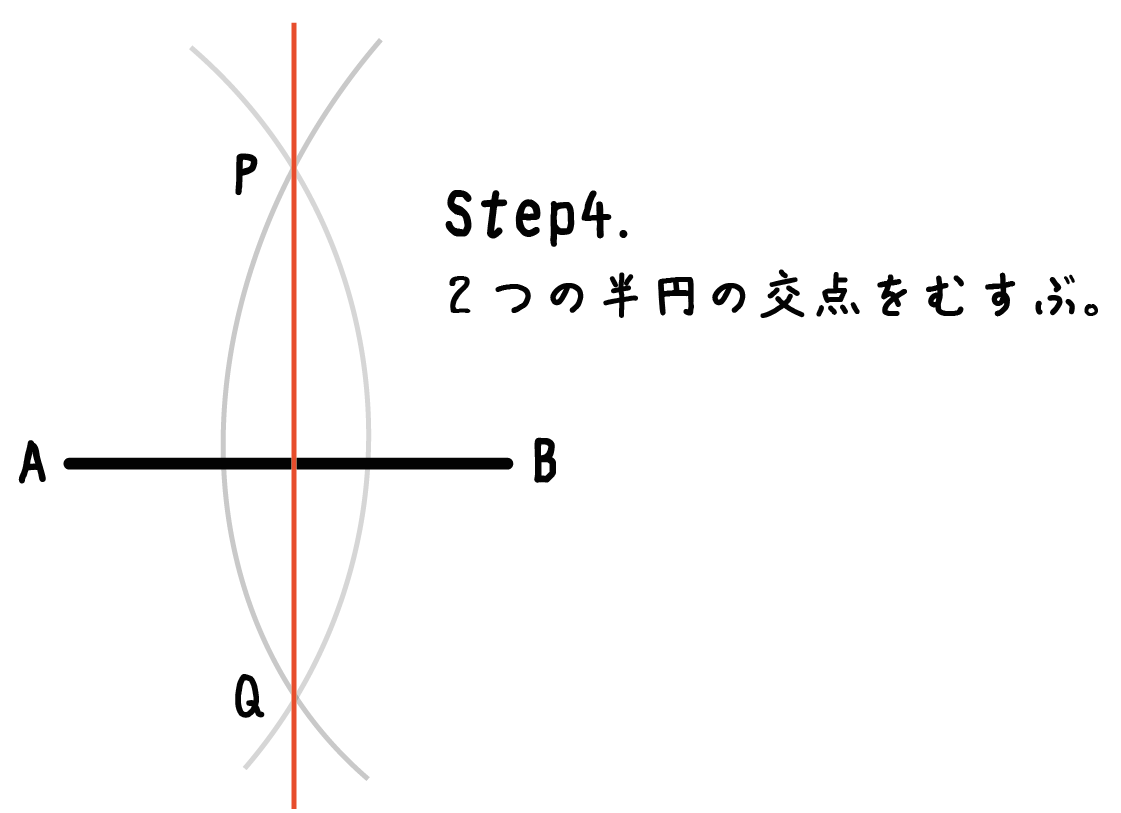
さっきの例でいえば、交点の「点Pと点Q」をむすんであげるんだ。
定規で直線をひいてあげよう。
この直線がなぜ線分ABの垂直二等分線になるのか??
それは、四角形APBQが「ひし形」になっているからさ。
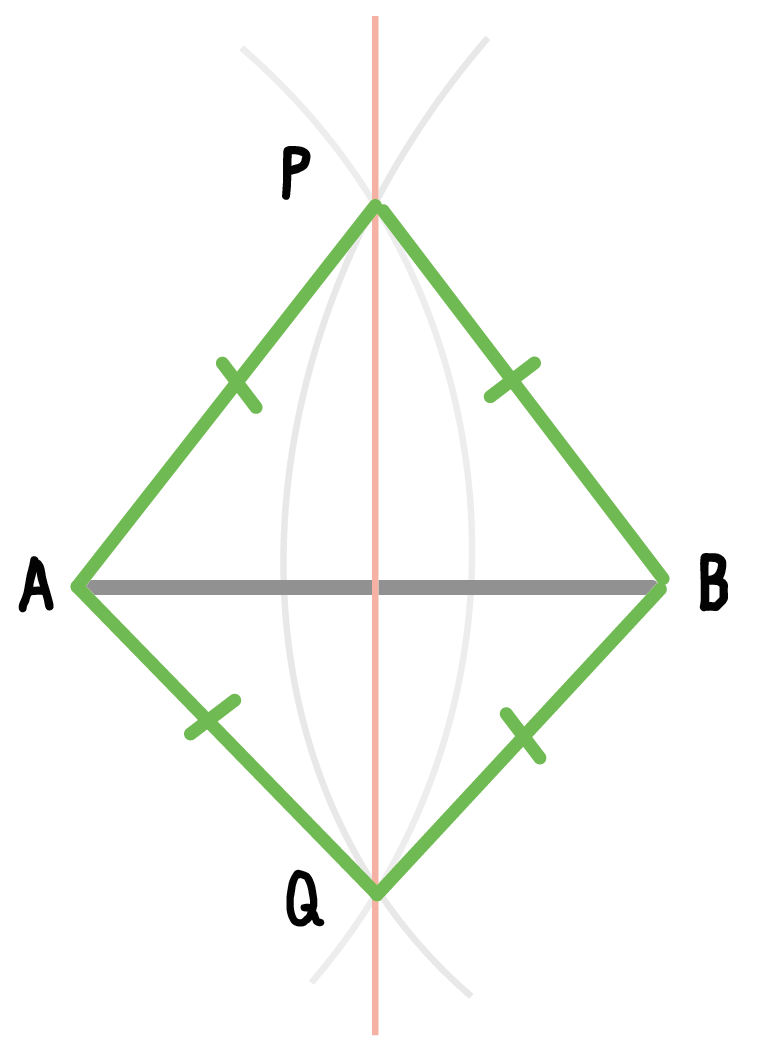
そんで、線分AB・PQが「ひし形の対角線」になっているでしょ??
だから、線分ABと交わる線分PQが「垂直二等分線」なんだ。
どう??すっきりした??
垂直二等分線の書き方はどうだった??
テストによくでてくるのでしっかり押さえておこう!
作図のやり方がわかったら実際にかいて練習してみてね。
作図は馴れでどうにかなる!!。
そんじゃねー
Ken
こんにちは、この記事を書いているKenだよ。インドカレーにはまったね。
中1数学の平面図形でややこしい数学用語がでてくる。
それは、

「線」と「点」っていう一文字しか違わないね。
テストで出されたら、点対称と線対称がごっちゃまぜになっちゃいそう!こりゃ大変!!
だから、今日はテストに備えて、
線対称と点対称の違いを3つわかりやすく解説するね。よかったら参考にしてみて。
線対称と点対称には3つの違いがあるんだ。
線対称と点対称の図形では「図形の移動方法(作り方)」が異なるんだ。
平面図形の移動方法っていう記事で、図形の移動には3種類あるって勉強したよね??
それで、線対称と点対称は「ちがう移動方法」によってできる図形たちなんだ。
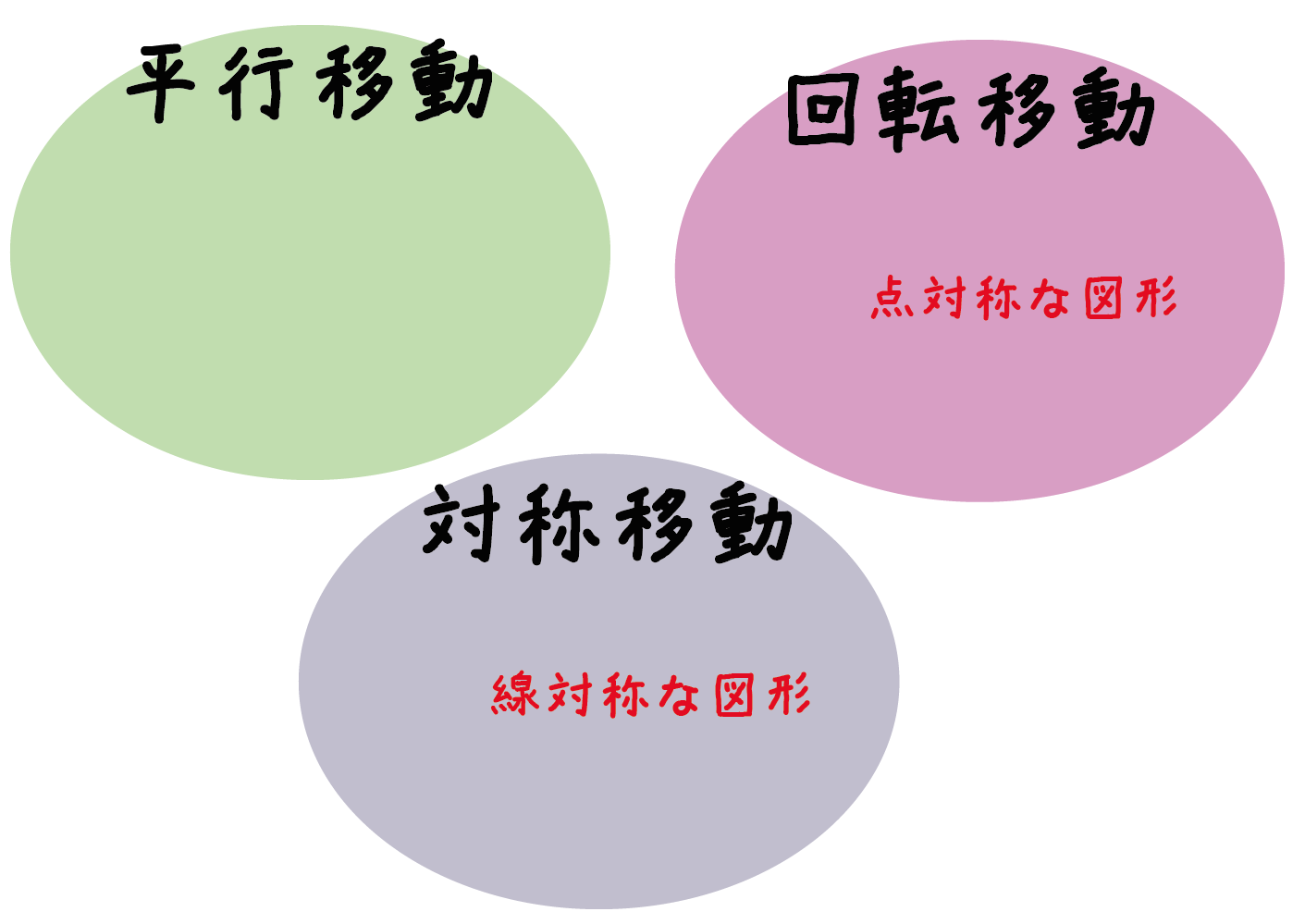
だから、線対称と点対称の図形って言葉は似てるけど、
作り方(図形移動の種類)は異なっていることを覚えておこう!
線対称と点対称させた図形って似ていてまちがいやすい。
しかも、点対称と線対称っていう名前まで似ている。余計ごっちゃまぜにしちゃいそうだね?
そこで、線対称と点対称をみわける1つのポイントを覚えていると便利だ。
それは、
図形が上下・左右どちらに逆さまになっているかどうか
なんだ。
わかりやすくするために、きもいイラストを線対称・点対称させたとしよう。
線対称のときは、おかまが左右方向に反転したようになるけれど、
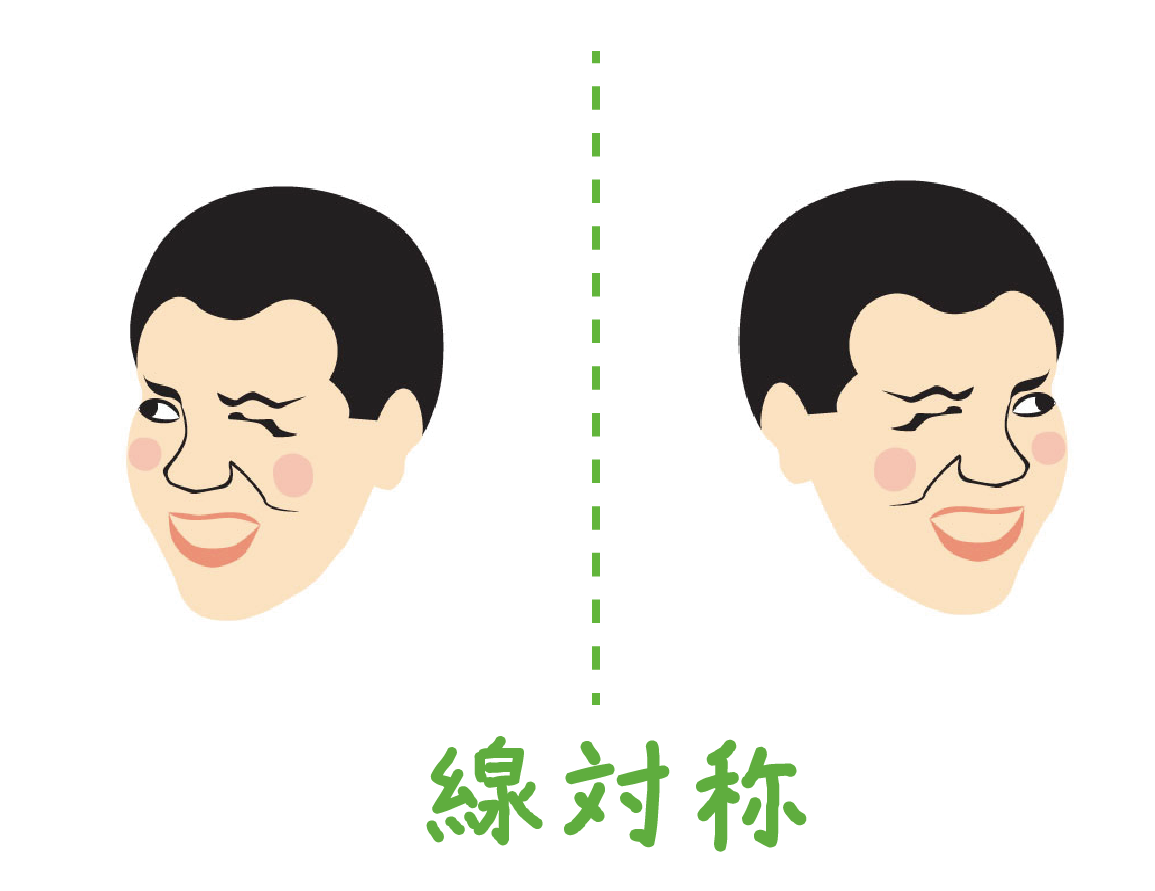
点対称のときは、おかまの顔の上下が反転する。頭に血がのぼってそうでしょ?。

だから、図形移動がおわったあとの形をみて一発で判断できるってこと。
図形がどの向き(上下 or 左右)に反転しているか確認するだけでいいからね。
最後は、何が中心になっているかが違うということ。じつは、
「対称の前にくる文字」によって、
何を中心に対称移動させたものなのか、ということが異なってくるんだ。

線対称なら「対称」って文字の前に「線」がついてるでしょ??
ってことは、こいつは「線」を中心に対称になった図形なんだとわかる。

一方、点対称なら「点」が「対称」の前についているから、
点を中心にして対称にさせた図形なんだってことを覚えておこう。

だから、もし問題文のなかに「線(対称の軸)」をみかけたら、そいつは「線対称の問題」だと疑ってかかっていいし、

もし「点(回転の中心)」をみつけたら「点対称の問題」とおもって全力をつくそう。

ここまで見てきた線対称と点対称の違いはどうだった??
線対称と点対称をすぐに見分けるためにこいつらは使えるけど、ソレ以外のときはあまり役に立たない。
ソレ以外のときというのは、
の図形を書け!っていわれたときだね。
こういうときは「【線対称の作図】4つのステップでわかる!対称移動の書き方」や「【平面図形】5ステップでできる!点対称移動の作図・書き方」で作図をクリアしちまおう!
そんじゃねー!
Ken
こんにちは、この記事をかいているKenだよ。コーヒー豆が好きだね。
前回まで、
っていう3つの図形移動を勉強してきたね。もう正直、図形なんて移動させたくないでしょ??。
だけど、今日はもう1つだけ知っておくべきことがあるんだ。

それは、
点対称移動の書き方・作図
というやつさ。
点対称移動ってきくと、
また図形移動が増えんのかよ?!? ざけんな!
っていいたくなるよね。
だけど、点対称移動は回転移動の一種なんだ。
回転移動にもいろんなやつがいて、そのうちの1人だと考えてもらって構わない。
たとえば、「回転移動の図形をあつめたクラス」があったとしたら、点対称移動はこころせましと座っているうちの一人。

クラスにもいろんな奴がいると思うけど、回転移動のクラスだって同じさ。
それじゃあ、どんな奴が点対称移動になるのかって気になるよね??
じつは、
回転移動のうち、
回転角度が180°のものを「点対称移動」って呼んでいるんだ。
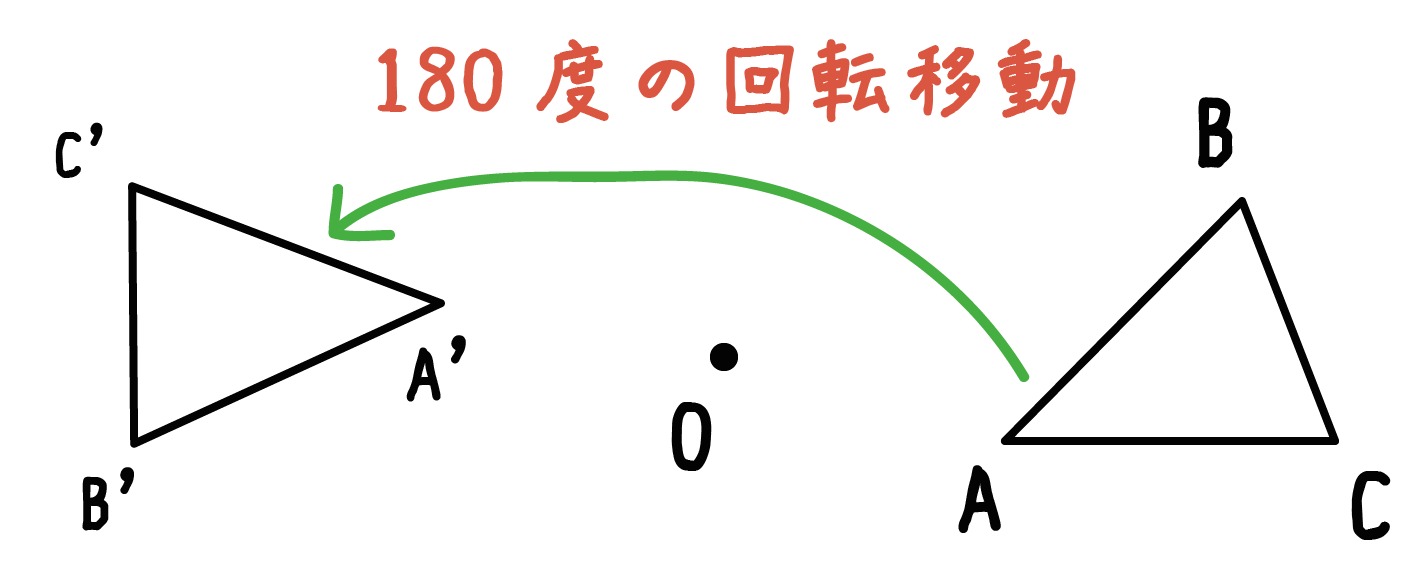
ちょっと点対称の正体がわかったでしょ??
つぎは点対称移動の書き方をみていこう!
点対称移動の作図をマスターするためには、
点対称移動の図形の性質
をおさえておくべきなんだ。平行移動でも回転移動でもそうだったように、性質を知っていると移動方法がわかってくるんだ。
教科書では、
点対称移動では、対応する点と回転の中心はそれぞれ1つの直線上にあります。
って書いてあるね。つまり、
「対応する点」をむんでできた直線の上に「回転の中心」があるってことになる。
たとえば、三角形ABCを回転の中心Oで点対称移動させたとしよう。
点対称移動後の三角形A’B’C’とすれば、
線分AA’、BB’、CC’には必ず「回転の中心O」がふくまれているんだ。
この性質を使ってガンガン点対称移動させまくろう!!
それじゃあ、点対称移動の書き方をみていこう。
三角形ABCを「回転の中心O」で点対称移動させよ!
っていう例題をつかって解説していくね。

最初に、「1つの頂点」と「回転の中心」を直線でむすんであげよう。
たとえば、三角形ABCの「頂点A」と「回転の中心O」って感じで↓↓
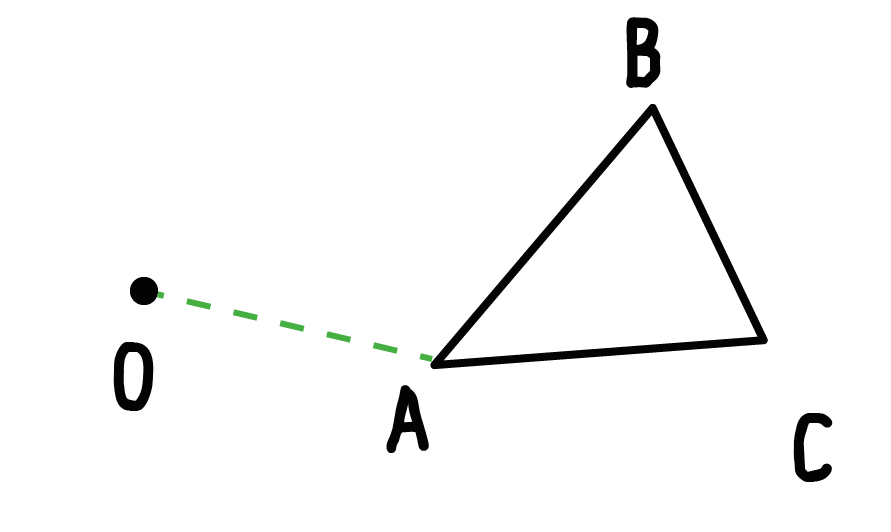
定規をつかってむすんであげてね。
つづいては、さっきできた新しい線分の長さを測ってあげよう。
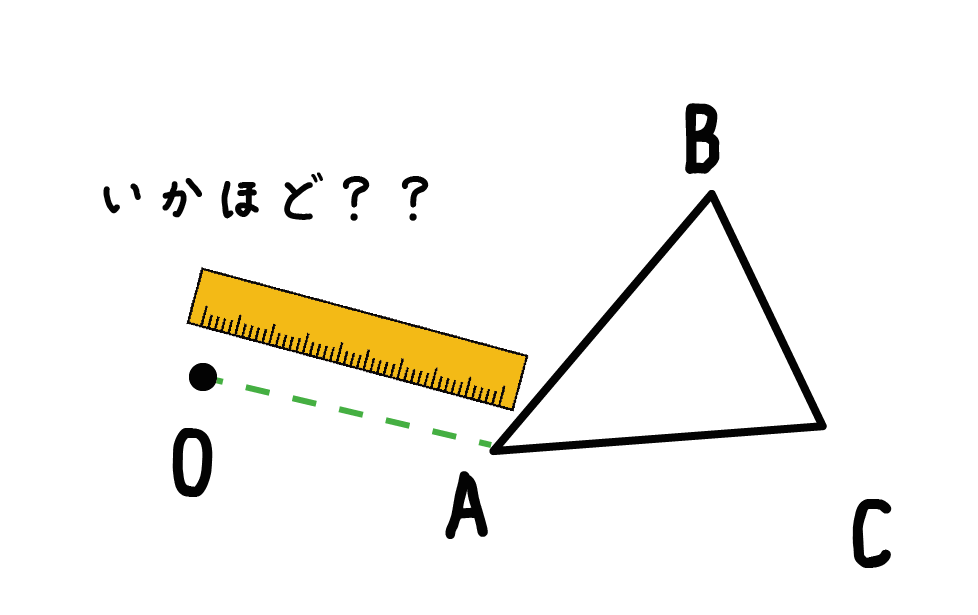
つまり、「図形の頂点」と「回転中心の距離」をはかるってことだね。
こいつを定規でびしっと測ってやろう。
つぎは、さっき作った新しい線分を伸ばしてあげよう。
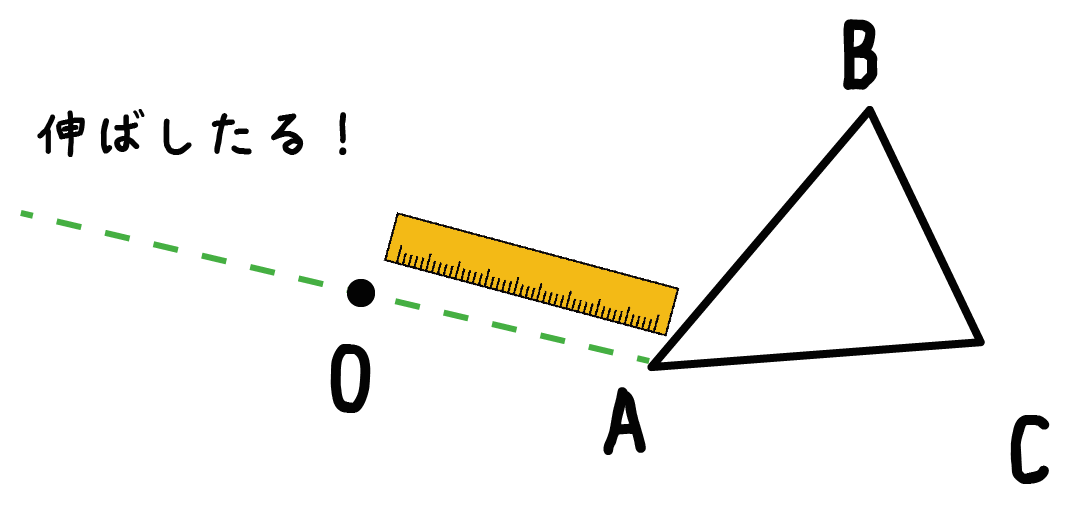
線分を伸ばす方向は移動させる図形とは逆側だ。
ぐんぐん適当にのばしておこう!
つぎは、伸ばした直線の長さを決めてやるフェーズだ。
ステップ2ではかった長さだけ、回転の中心Oから離れたところで点をうつんだ。
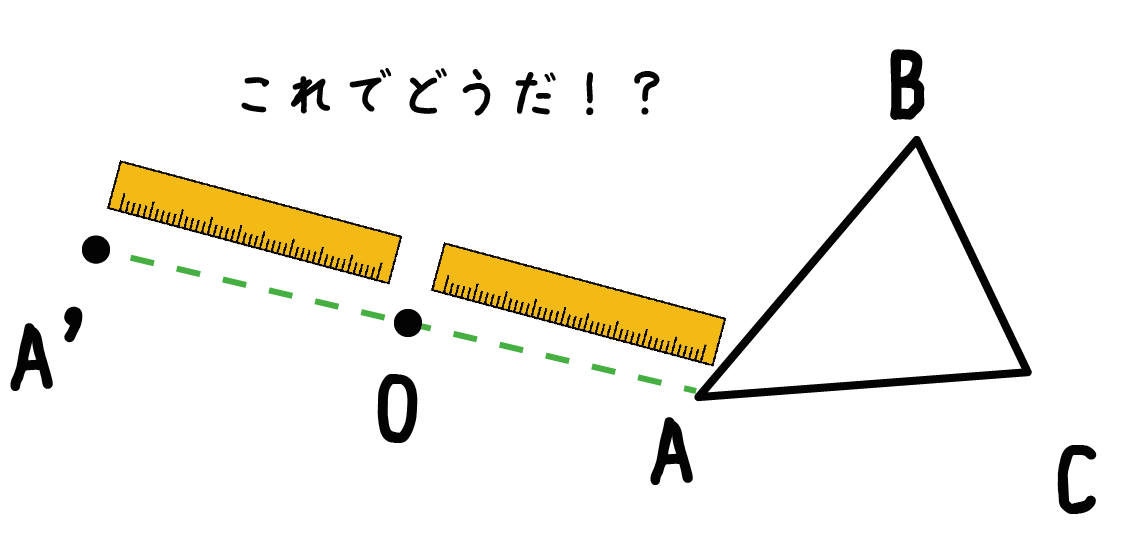
例題でいうと、点A’がそれにあたる。
これが三角形ABCの頂点Aに対応するA’になるね。
ここまでのステップを他の頂点でもやってみよう!!
例題でいうと、残りの頂点BとCだね。
こいつらもAと同じように、結んだり点を打ったりすると、
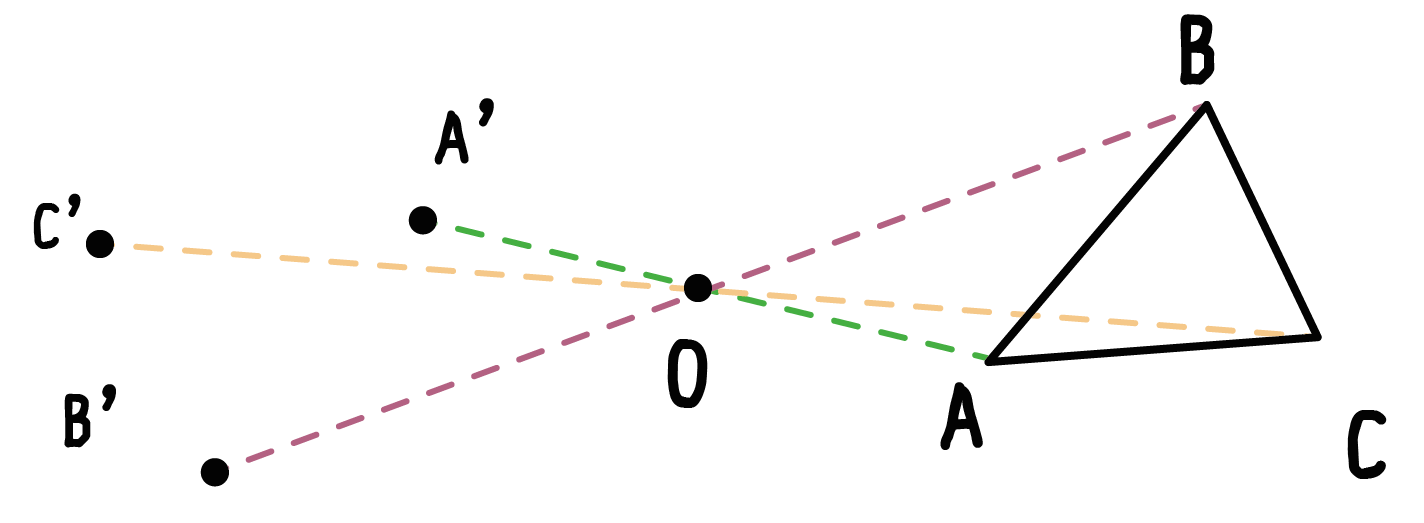
こうなるね。そんで新しくできた移動後の頂点たち(A’、B’、C’)をむすんであげると、
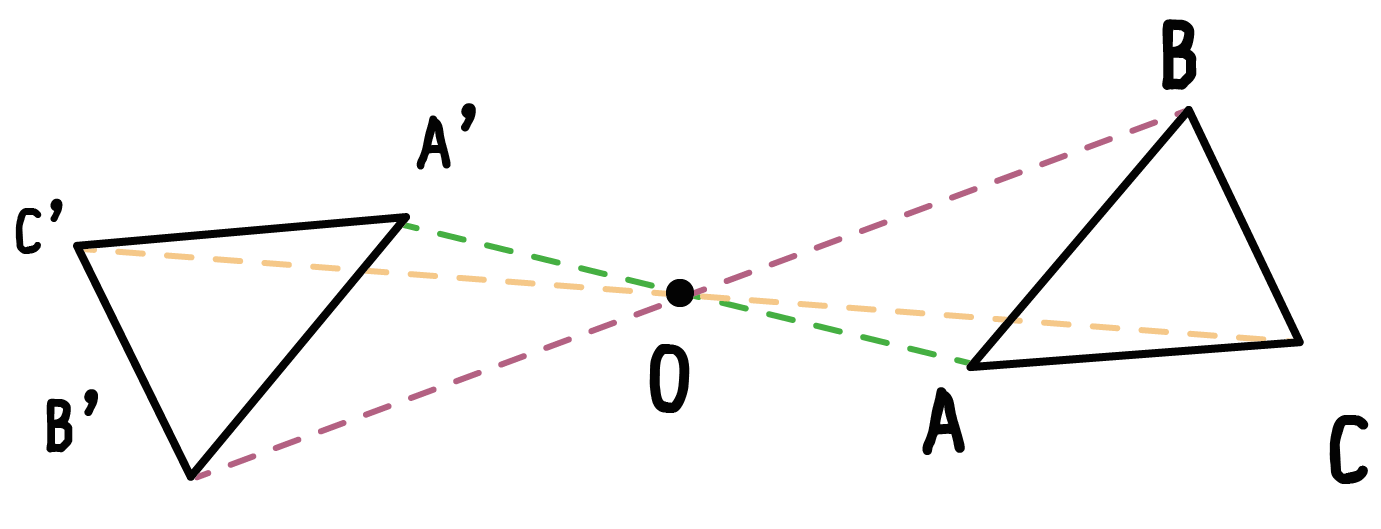
点対称移動したあとの三角形A’B’C’があらわれるでしょ??
これで点対称移動はおしまい!
ふう、疲れたー
点対称移動は回転移動のうちの1種。
だから、とくに新しいことを覚える必要なんてない。
ただ、回転移動と同じ方法で作図するのはちょっと疲れるんだ。
めんどくさがり屋な奴こそ、点対称移動の書き方をおぼえておこう。
つぎは点対称と線対称の違いについて書いてみるねー!
そんじゃねー
Ken
こんにちは、目玉焼きが得意なKenだよー!今日も一緒に中学数学の勉強をはじめよう!!
図形の移動方法のうち、
という2つの移動方法についてみてきたね。
今日は、残りの「対称移動(線対称)」の書き方を勉強していこう。

これをマスターしちまえば、図形の移動をすべて網羅したことになる。
数学のテストで高得点は間違いないさ。
~もくじ~
対称移動の書き方を勉強する前におさえておきたいことが1つある。
それは、
対称移動(線対称)の図形の性質だ。教科書によると、線対称の図形には、
対応する点を結んだ線分は、対応の軸と垂直に交わり、その交点で二等分される
って書いてあるね。
たとえば、三角形ABCを「対称の軸(直線m)」で対称移動させたとしよう。
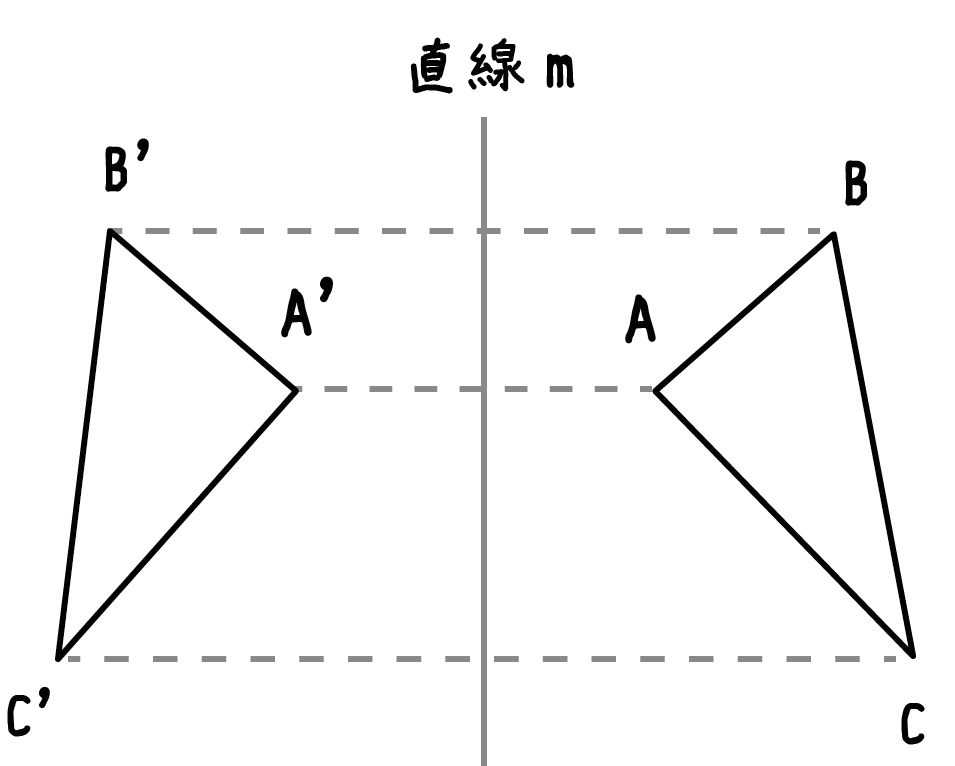
このとき、直線mと「対応する点を結んだ線分」たちは垂直に交わっていて、
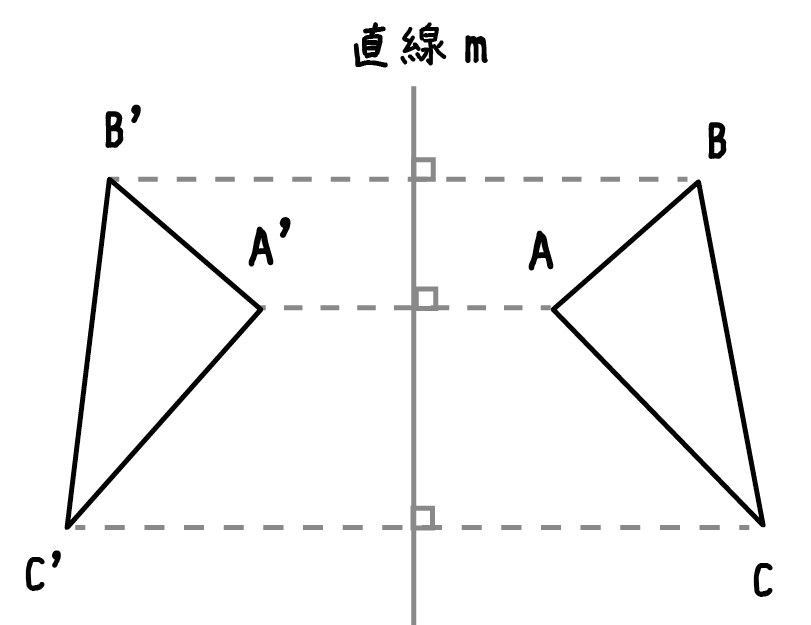
交点が2点の中点になっているということなんだ。
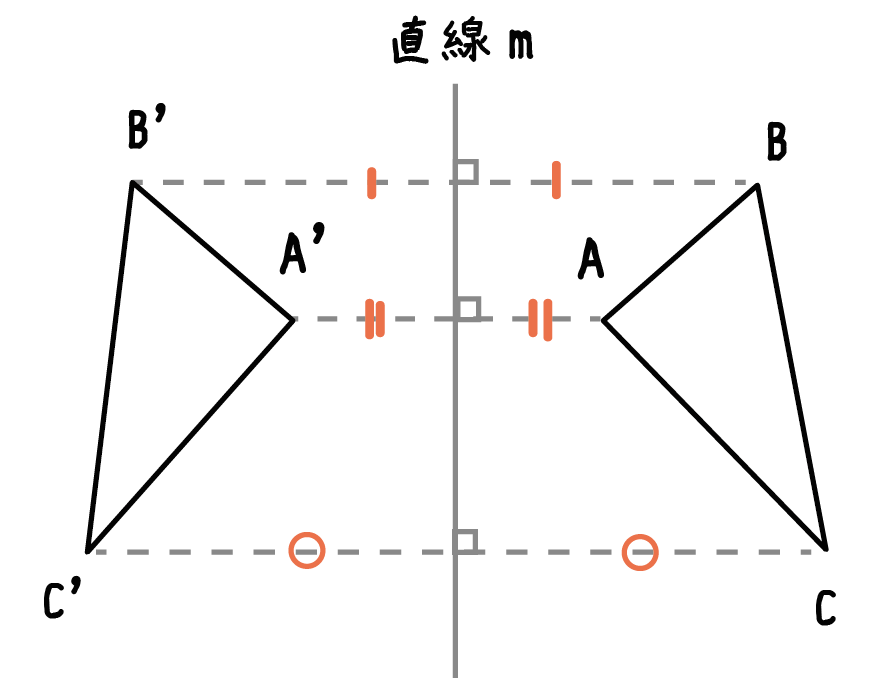
この対称移動の性質をおさえれば書き方もわかってくるよ!!
さっそく、線対称の書き方をさらっとみていこう。
最初にやるべきことは、
対称移動させる図形の頂点を1つ選ぶことだ。
そして、
その頂点から「対称の軸」へテキトーに垂線をおろしてみよう!
さっきの例だったら、
点Aから直線mにこんな感じで垂線をひいてみるってこと↓↓
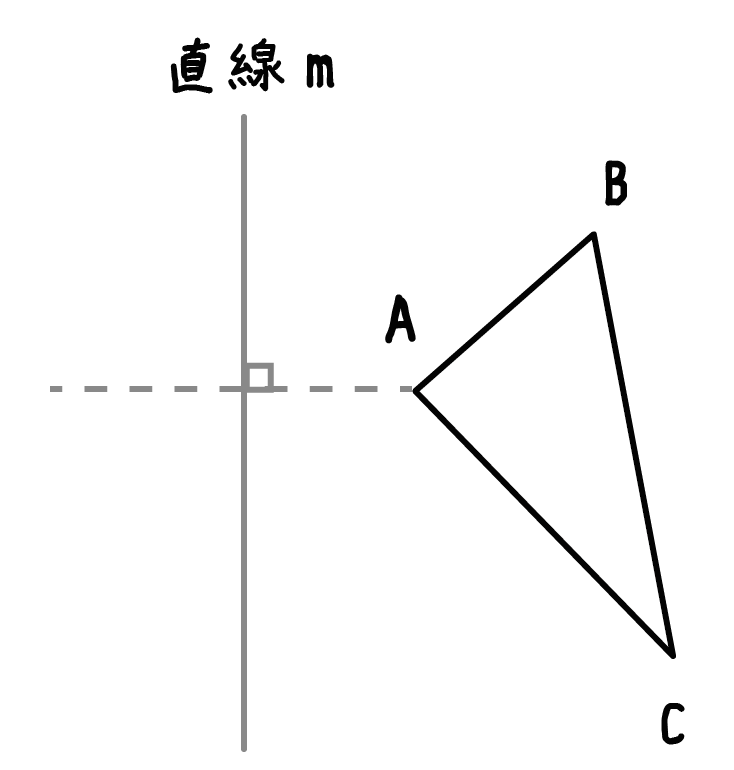
垂線をかくためには、
っていう3つのアイテムのいずれかを使ってあげればいい。どれか好みのものをピックアップしてくれ!
つぎは、
「対称の軸」と「頂点」の距離を測ってあげよう。
線と点の距離は、
点から線におろした垂線の長さ
だったよね??
だから、これも同じ。垂線の長さをはかってあげよう。
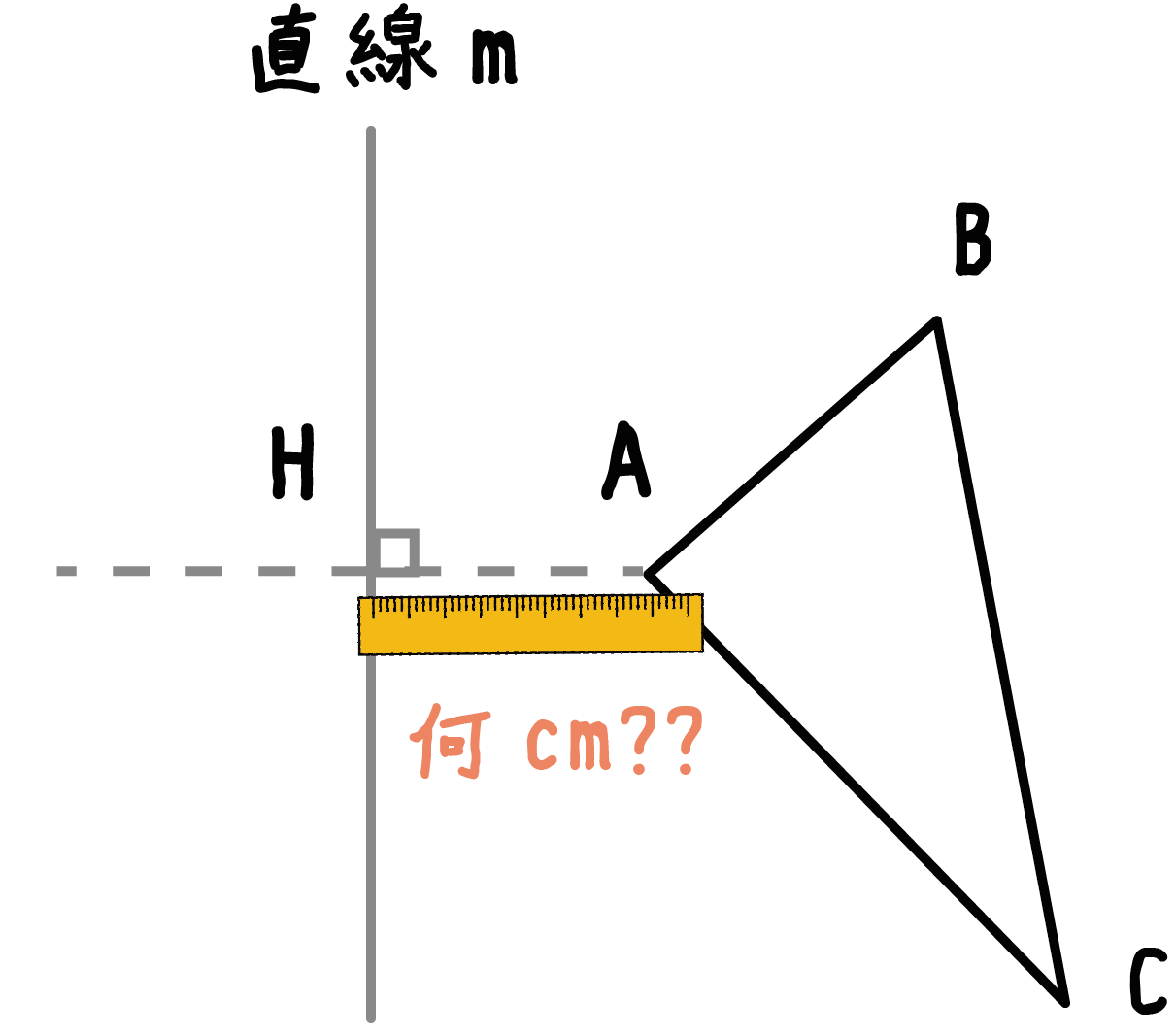
垂線と「対称の軸」の交点をHとしてやると、線分AHの長さがそれにあたる。
定規でも使ってAHの長さを測ってみよう!!
ステップ2でゲットしたつかった線分の長さを使うよ。
さっき測った線分の長さだけ、図形とは逆側の垂線上に点をうってやるんだ。
ちょっと言葉ではむずかしいので図をみてみよう。
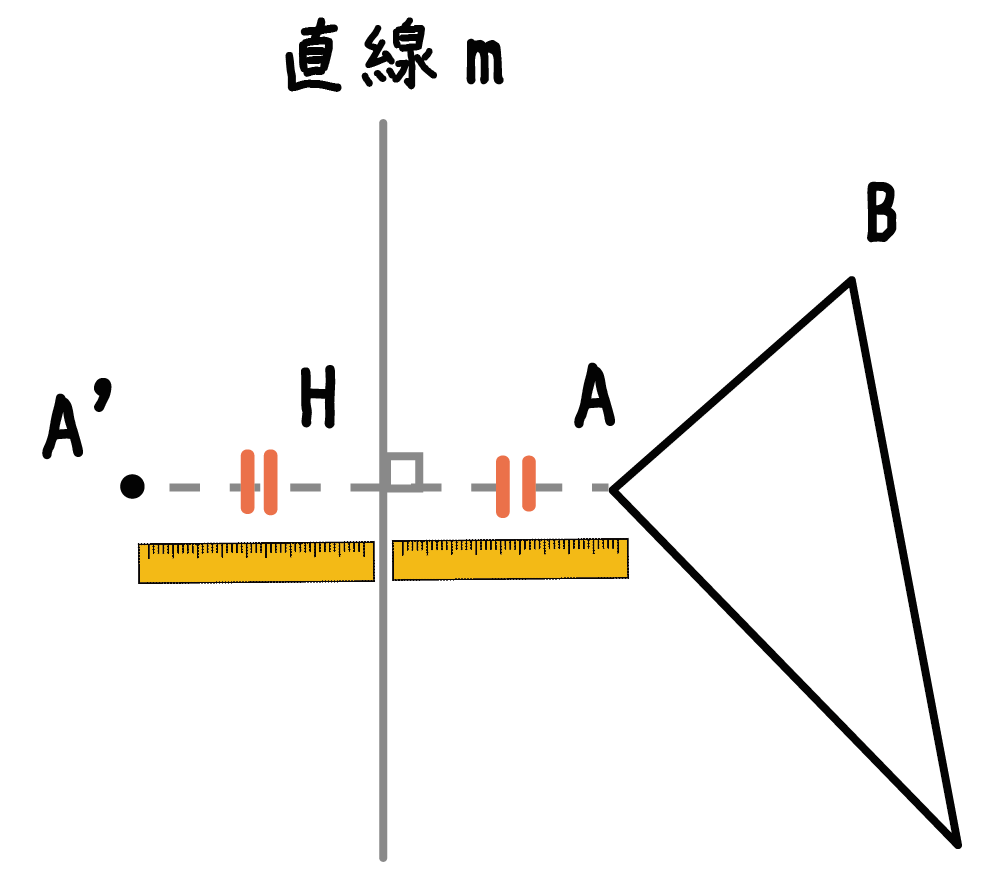
三角形ABCとは逆側に点A’をうつ。
そして、その点は垂線上に点Hから「さっき測った長さ分」はなれた位置だ。
コンパスでも定規でもいいから、必ずAHとA’Hの距離が等しくなるようにしよう!!
あとはここまでの手順を他の頂点でもくり返すだけ。
例題でいうと、点Bと点Cの場合だね。
すると、こんな感じで3つの点がうてるはずだ(点A’、点B’、点C’)↓↓
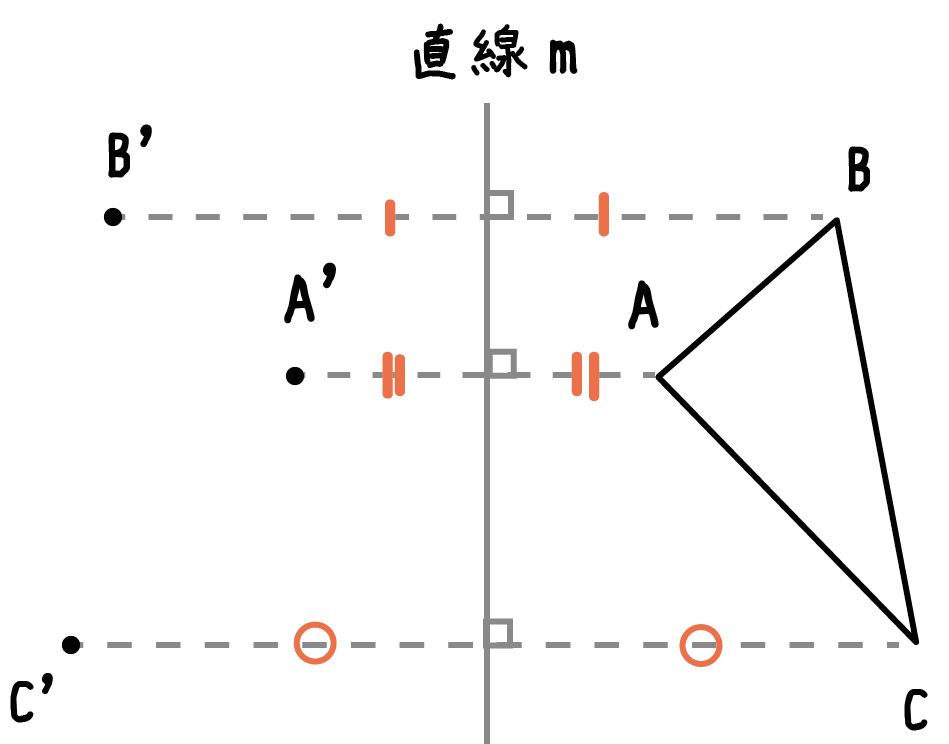
「対応する点」をすべて打てたらこっちのもの。
あとはこいつらを結んでやるだけさ。

これで対称移動(線対称)は完了だ。
書き方に4つもステップがあったけど、ゆっくりやれば間違えないはず!
以上が対称移動の書き方だ。
これでやっと、
っていう3つの図形移動をマスターできたね。
次回はちょっとややこしい「線対称と点対称の違い」について解説していく。よかったら確認してみてね。
そんじゃねー!
Ken
こんにちは、この記事を書いているKenだよ。コーヒーは一日一杯までだね。
中1数学の平面図形で勉強する図形の移動には、
の3種類があるって勉強してきたね。どれもテストで狙われやすいやつばっかだけど、一つ一つ順番にみていこう。

今日は2つめの「回転移動」の書き方をわかりやすく解説していくね。
テスト前に参考にしてみてね。
回転移動では回転移動の性質を使うと一発で終わるんだ。
教科書によると、
対応する点は、回転の中心からの距離が等しく、回転の中心と結んでできた角の大きさはすべて等しい
という性質があるって書いてある。
これはどういうことなんだろう??
たとえば、点Oを「回転の中心」として三角形ABCを回転移動させてやるとしよう。
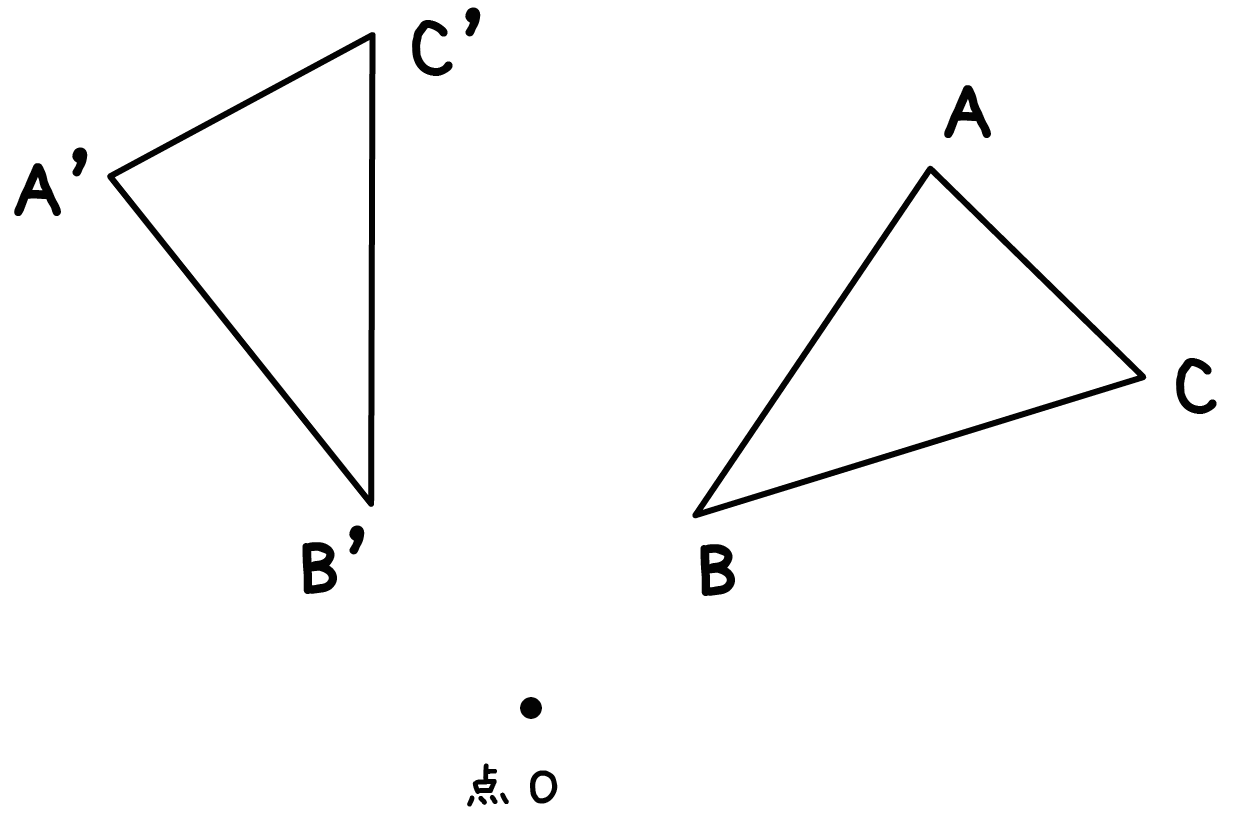
このとき、対応する点BとB’は、
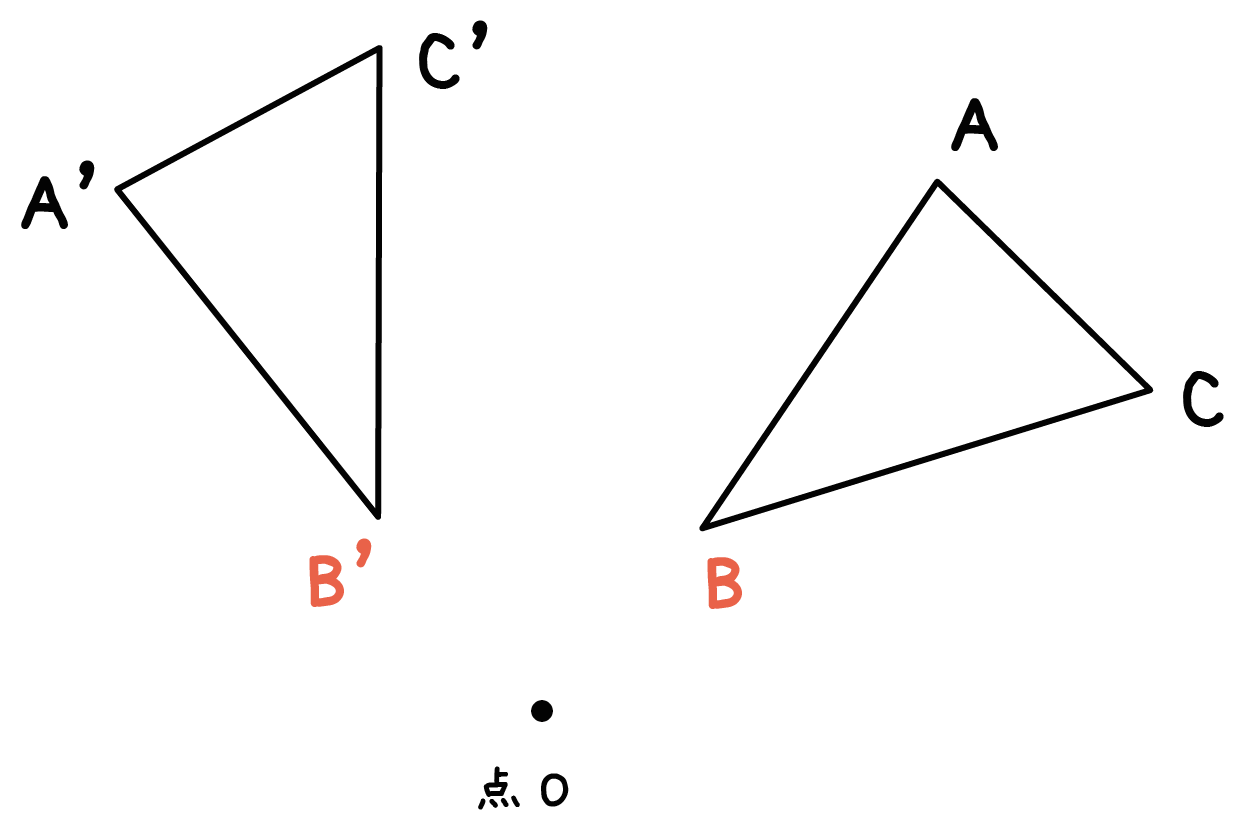
回転中心Oからの距離が等しい ( 線分OB=線分OB’)。
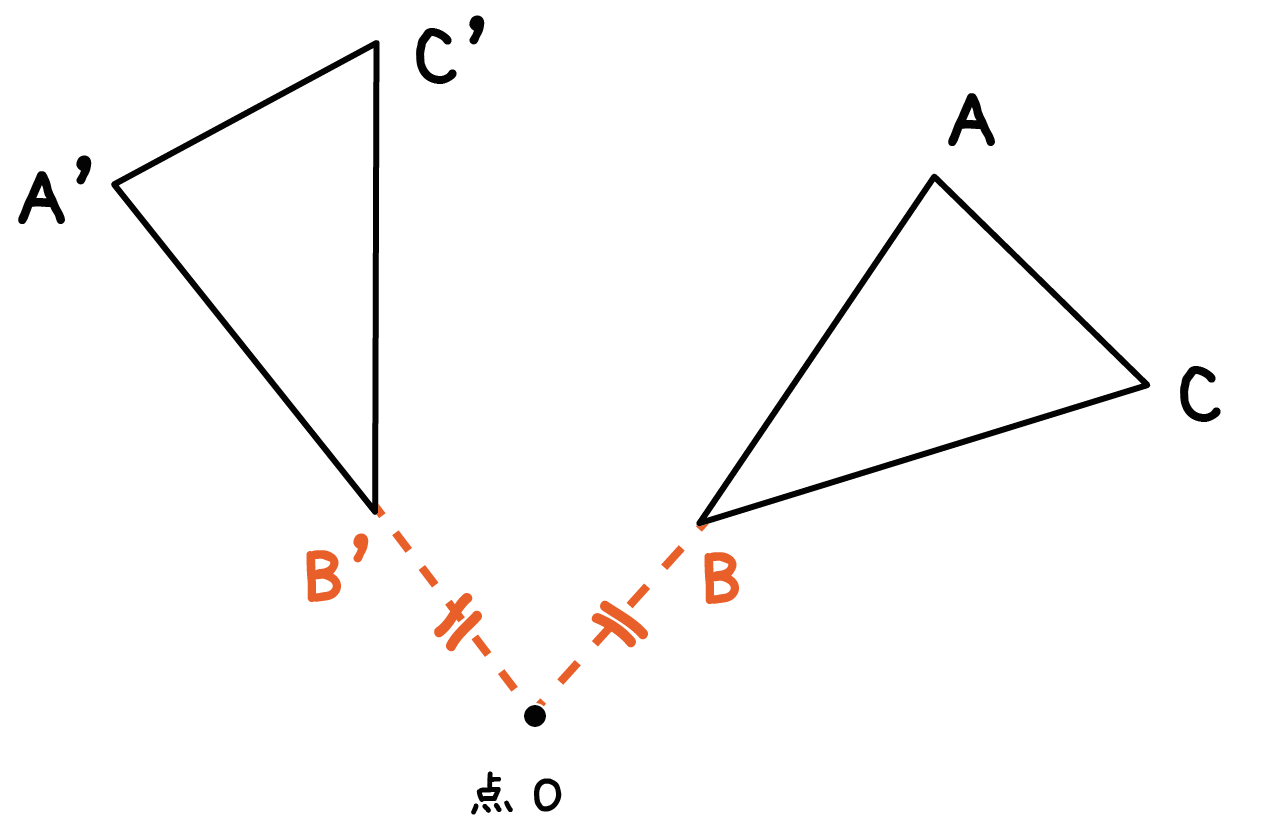
さらに、回転の中心と結んでできた角の大きさ(角BOB’)は、
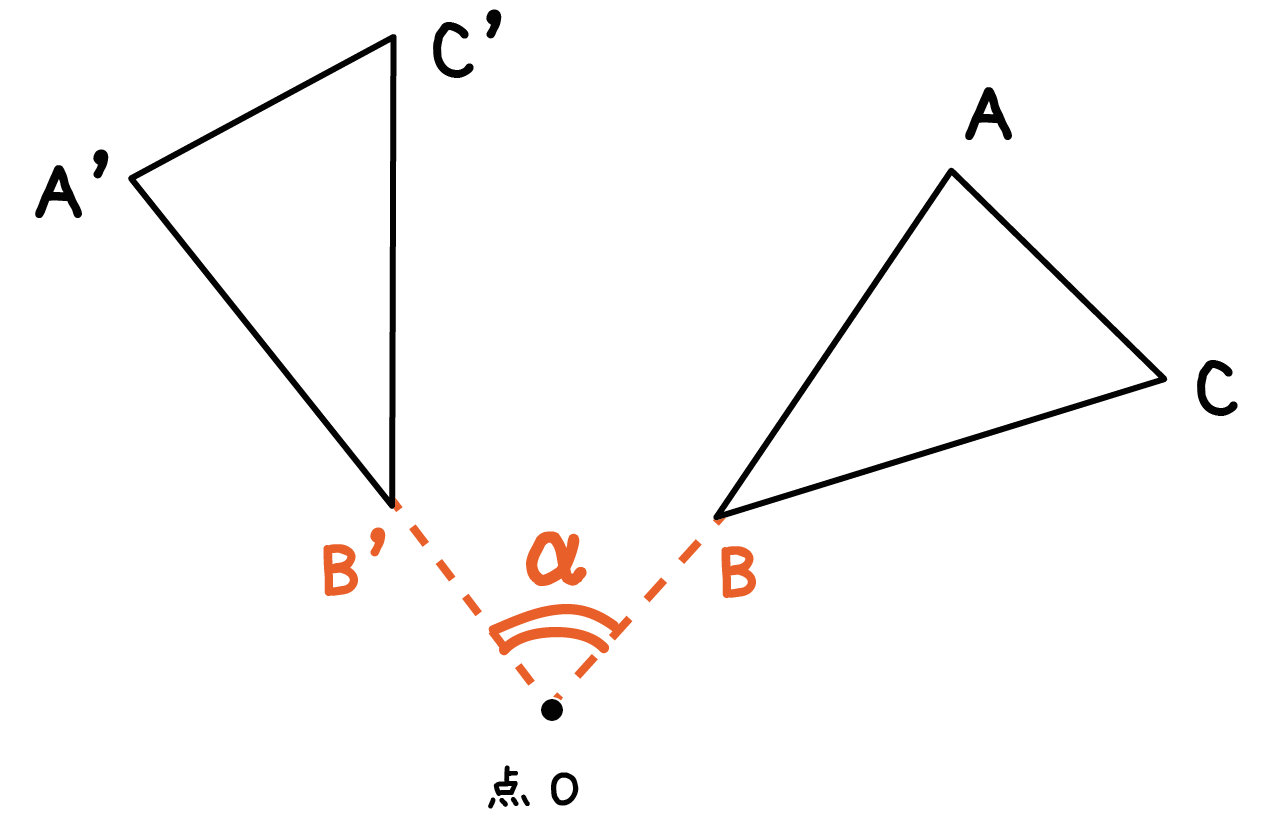
他の頂点の場合のそれとすべて等しい (角BOB’ = 角AOA’ = 角COC’)ってことなんだ。
これが回転移動した図形の性質だね。
こいつらをウマくつかってやれば、自由自在に回転移動できるようになるよ。
それじゃあ、さっそく回転移動の書き方を解説していこう。
よーくみてみると、回転移動はつぎの5つのステップで書けることがわかる。
「回転の中心」と「1つの図形の頂点」を結んであげよう。
そして、あたらしい線分をつくってあげるんだ。
たとえば、
三角形ABCをOを中心に反時計まわりに90°回転移動させよ!
っていう問題があったとしよう。
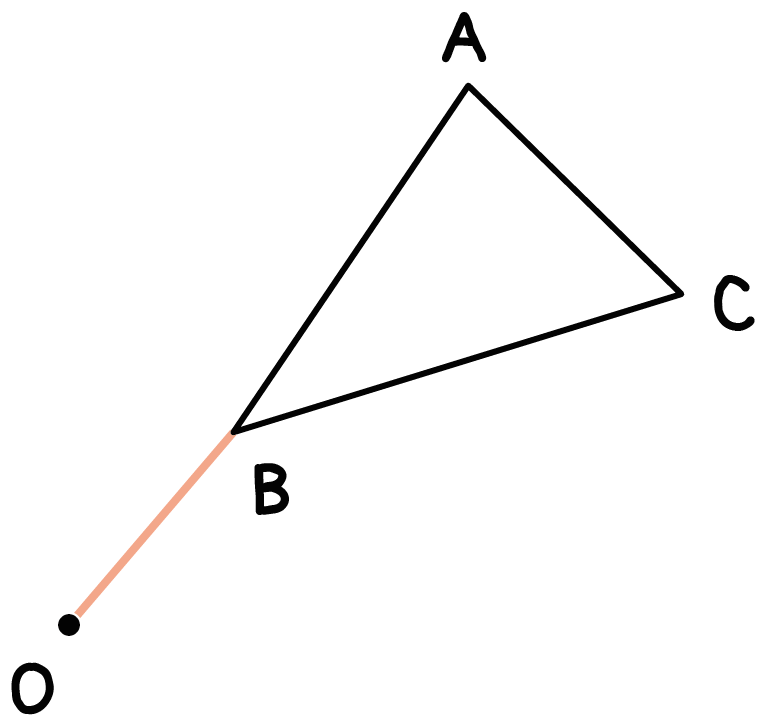
この場合なら、OとBを結んで線分をOBをつくってあげるって感じ。
これが第一ステップさ。
つぎは、コンパスの出番だ。
ステップ1でつくった線分を半径として、回転の中心から「孤」を書いてみよう!
コンパスの針を「回転の中心O」において、
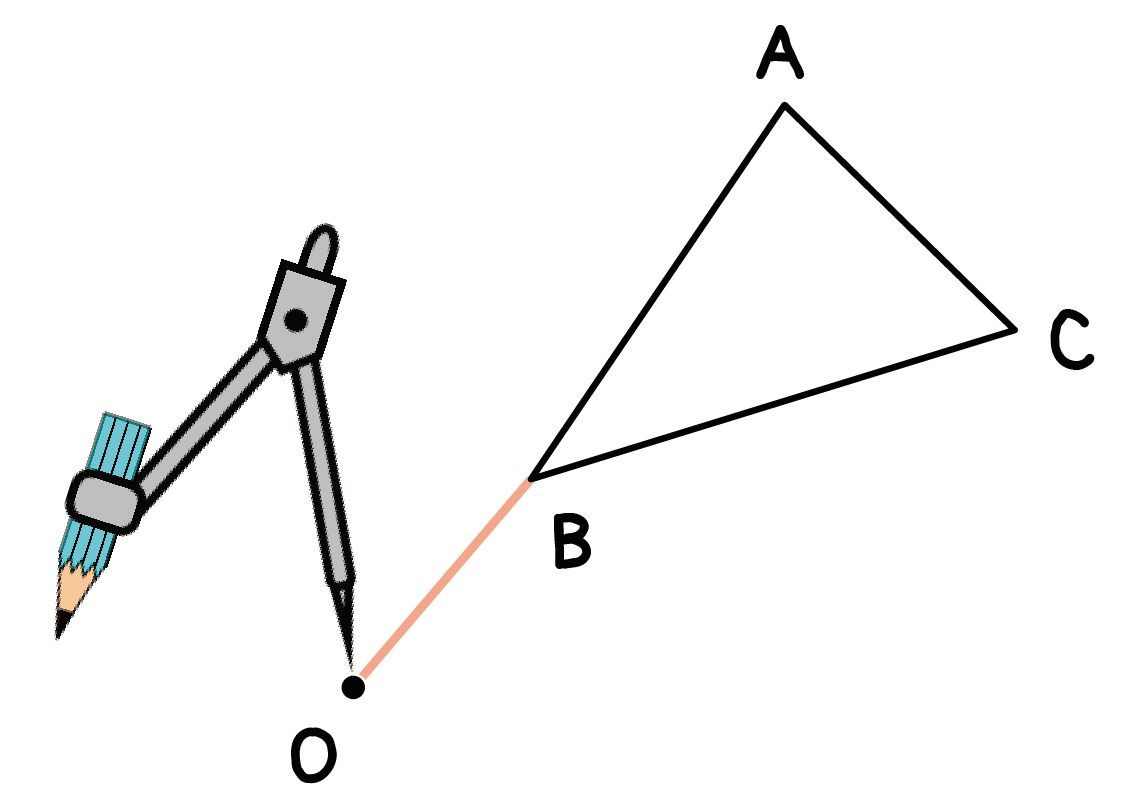
コンパスの鉛筆側を頂点Bにあわせ、
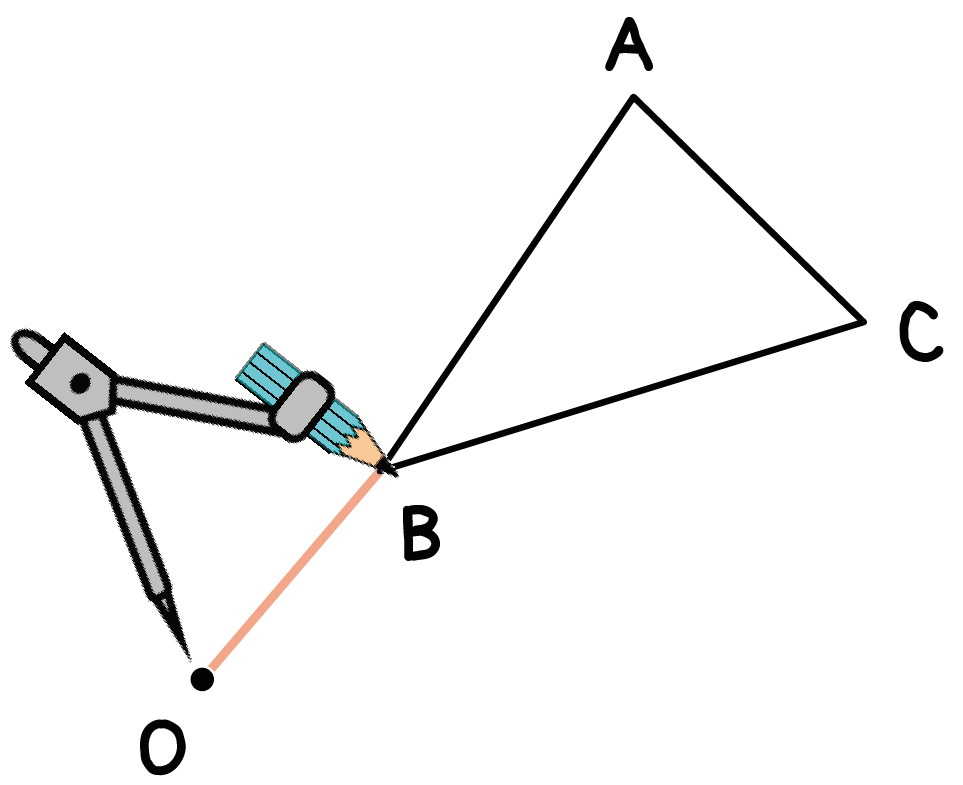
反時計回りに90°以上の孤をてきとーに書いてあげよう。
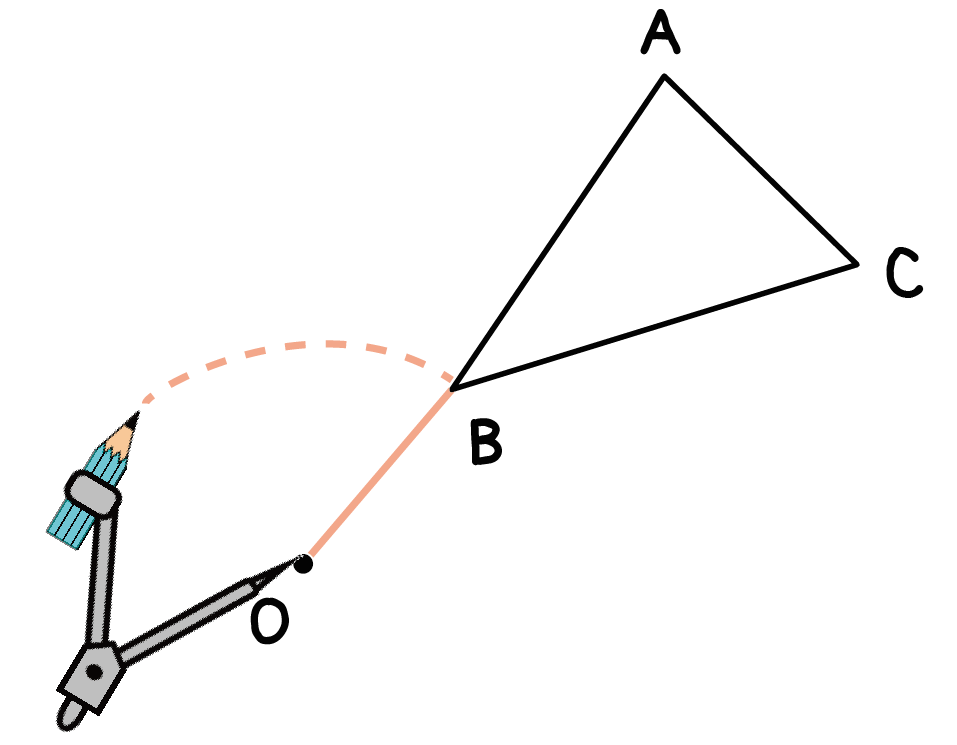
つぎは、回転させる角度をはかっちゃおう。
この例題では、反時計まわりに90°図形を回転移動させる問題だから、
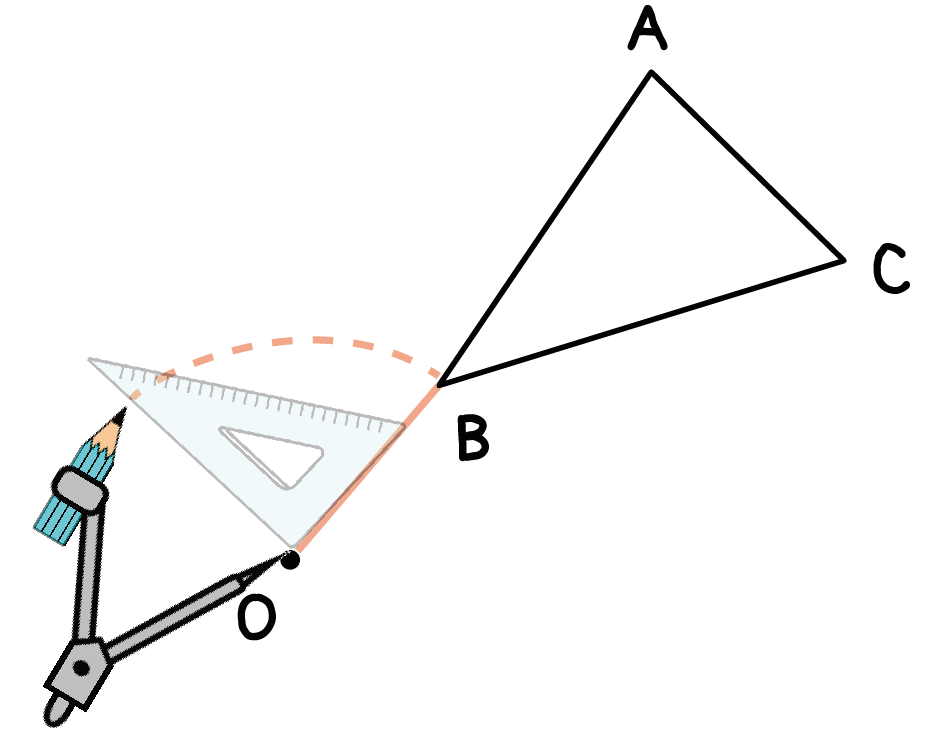
孤の半径となっている線分OBから反時計回りに90°の角度をはかってあげよう。
角度を測る方法としては、
などがあるよ。もし、分度器を使うな!って問題でいわれたら、三角定規とコンパスでねばってみよう!!
回転させる角度を測った??
あとは、その角度上の孤に「点」をうってあげるだけ。
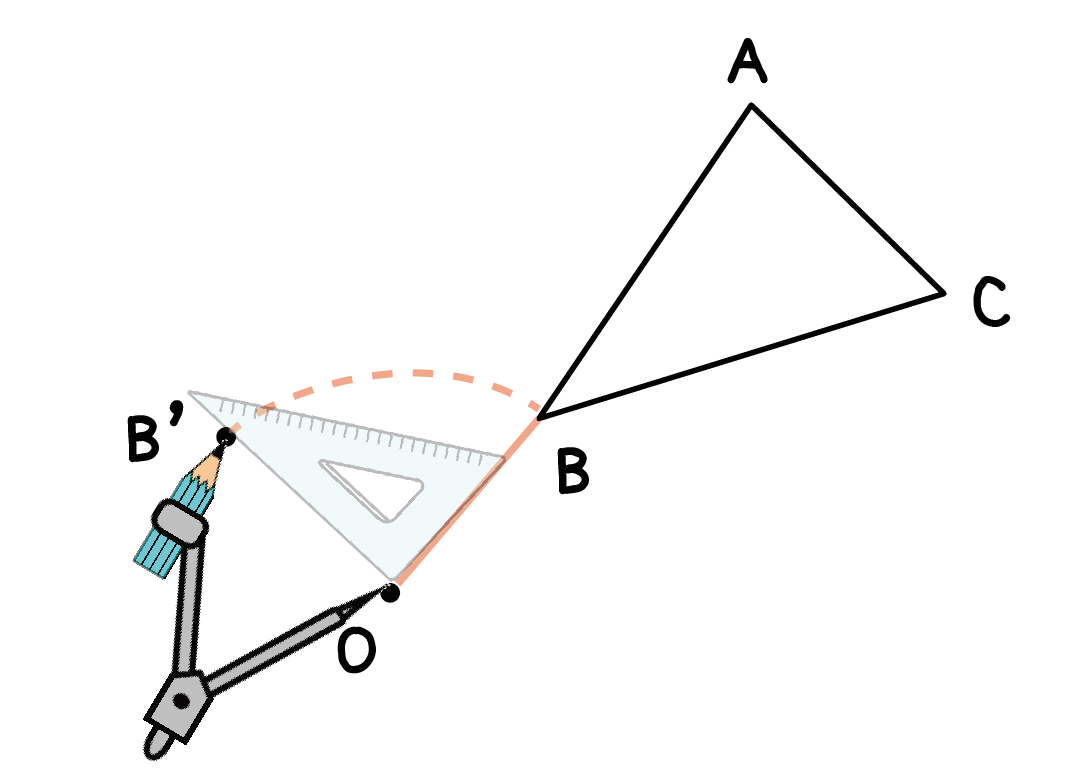
さっきの例でいえば、
孤の90°の角度上に点B’がうてる。
同じ手順をのこりの頂点でもやってみよう。
この例題だと、点AとCだ。
点Bと同じように、
という動作を繰り返せばいいんだ。
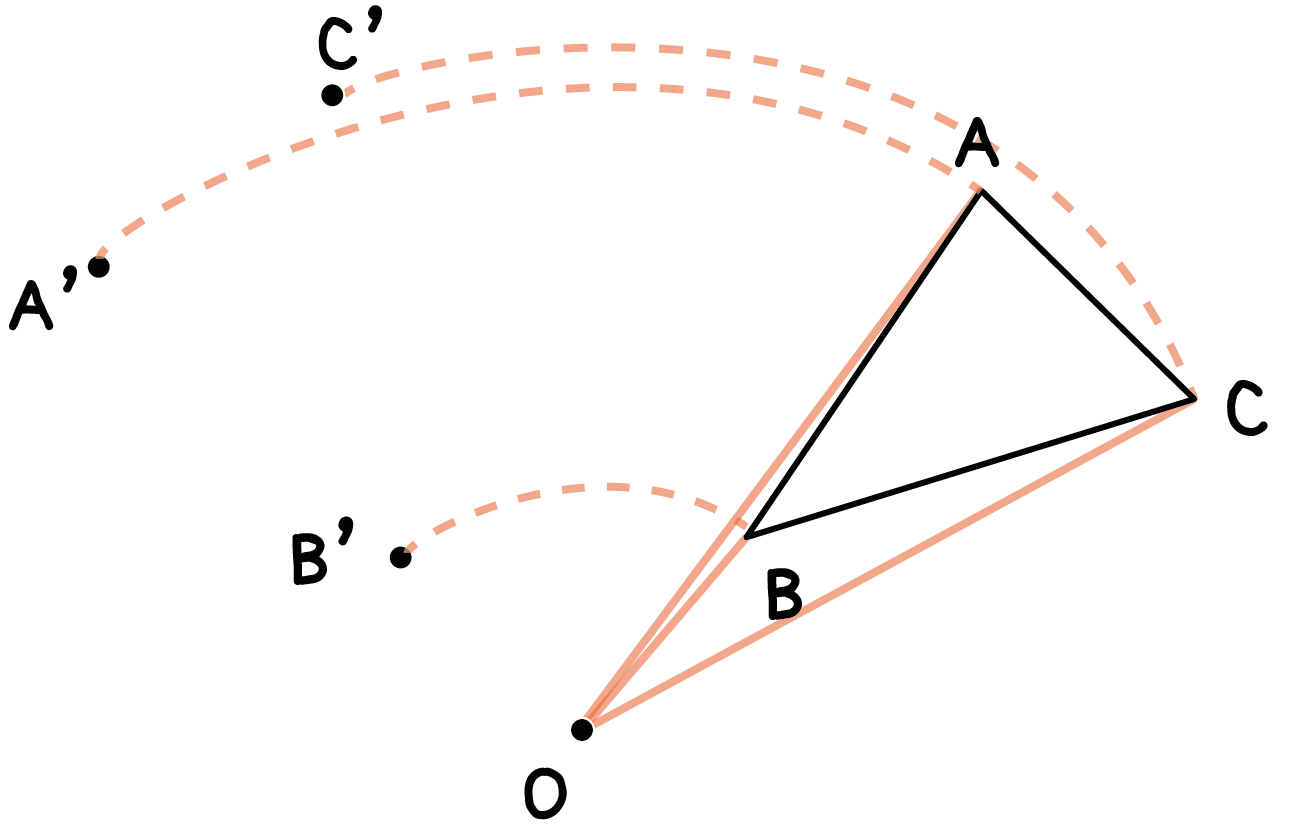
そんで、ぜんぶ書き終えたら結んでみよう!
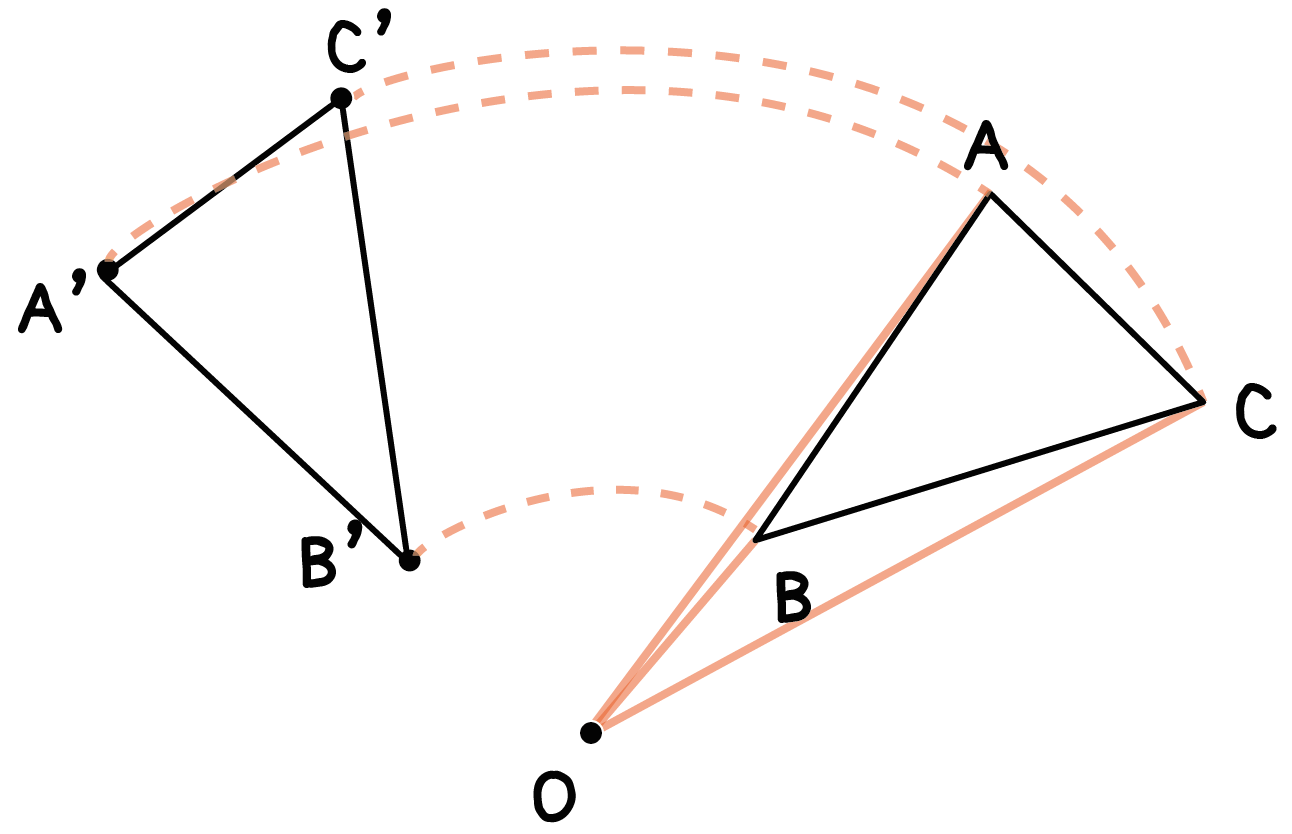
この新しくできた三角形A’B’C’が「回転移動した図形」だ!
やったね! 疲れたー
回転移動の書き方はどうだった???
コンパス、三角定規、分度器っていう3つのアイテムでチョちょいのちょい。
テストでも落ち着いて図形を移動させていこう!
次回は対称移動の書き方を解説していくね。
そんじゃねー
Ken
こんにちは、この記事を書いているKenだよ。メガネふきが欲しいね。
「図形移動」の方法って次の3つあったよね。
こいつらを「【中1数学】平面図形で勉強する「図形の移動」3つのまとめ」でだいたい確認してきたけれど、図形の移動を知っているだけじゃ問題は解けない。
じつは、
作図方法を知っていないとテストで点数はとれないんだ。

だから今日は、
平行移動の書き方・作図
をわかりやすく3つのステップで解説していくね。テスト前に参考にしてみてね。
~もくじ~
平行移動のために使うことはたった1つ。
それは、
平行移動した図形の性質だ。
平行移動した図形同士には、
対応する点を結んだ線分は、それぞれ平行で、その長さは等しい
という性質があるね。これは教科書にのっていることだ。
たとえば、三角形ABCを平行移動させたとすれば、
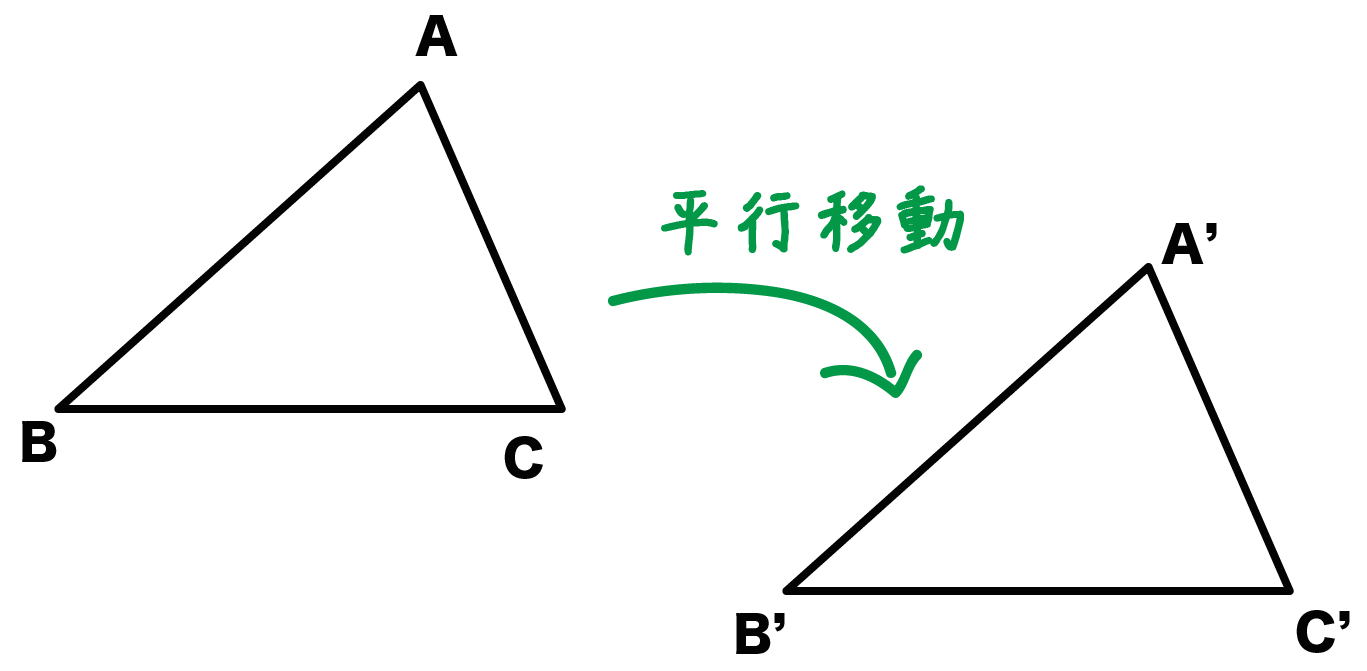
対応する点同士である、
を結んだ線分たちは、
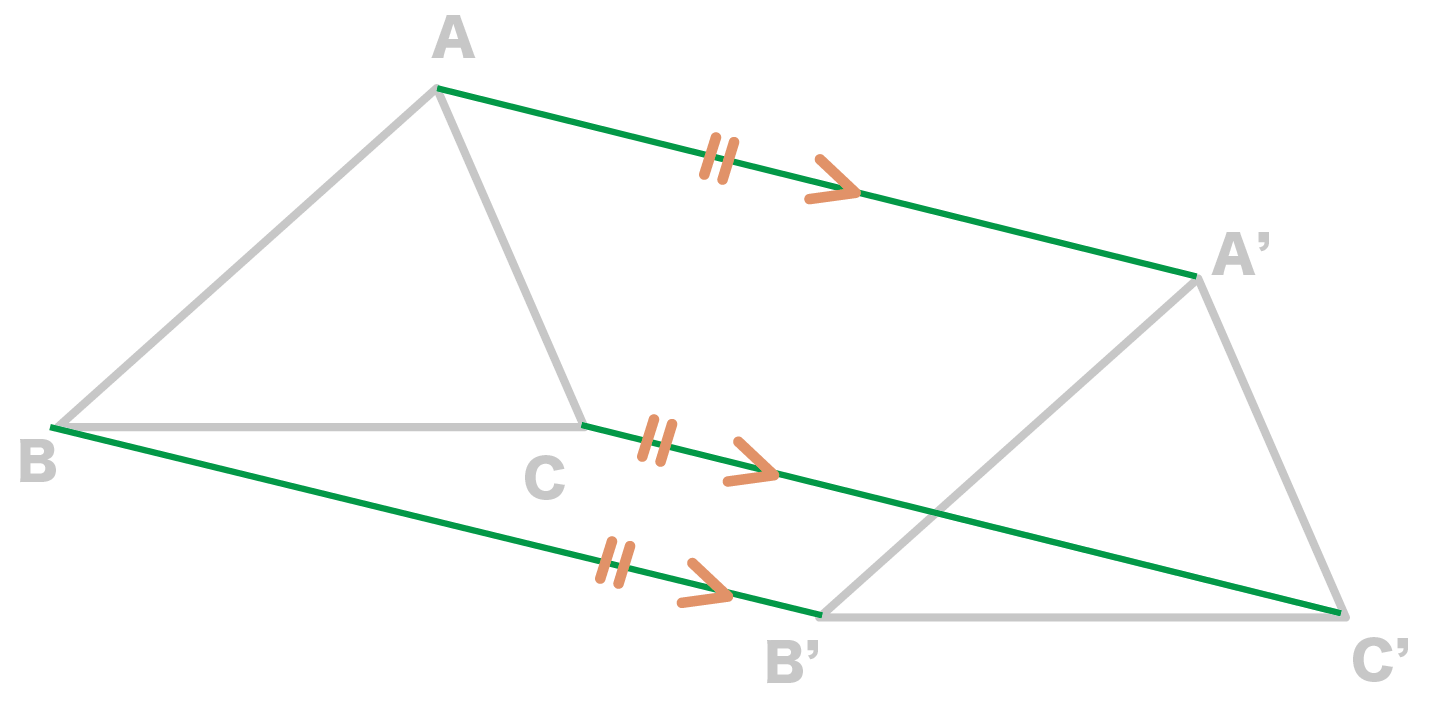
という性質があるんだ。
これをつかえば作図がつぎの5ステップでできるよ。
つぎのような作図問題が出されたとしよう。
問題:三角形ABCの頂点Aを点Pに移すように平行移動した図をかいてね。
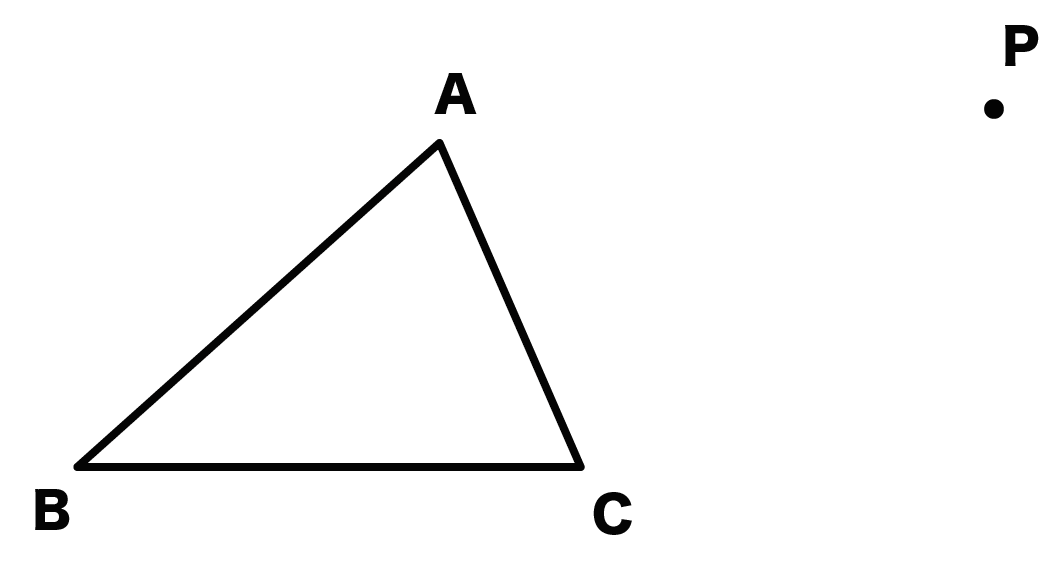
これをもとにしながら平行移動の書き方を解説してくね。
まず、対応する2つの点を結んでしまおう!
ここでいう「対応する点」とは、
「移動する前の点」と「移動後の点」
のことだ。さっきの問題でいうと、点Aと点Pがそれにあたるね。
ってなわけで、
対応する点AとPをむすんで線分APをつくっちゃおう!
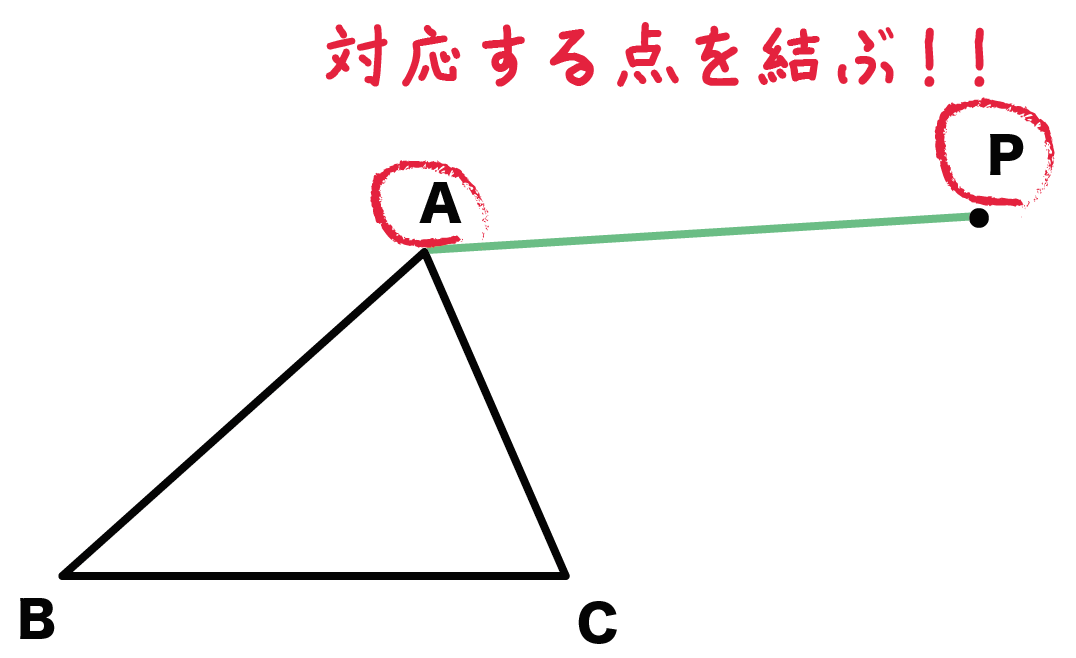
これが平行移動の作図の第一ステップさ。
次に、さっき引いた線分の平行線を残りの頂点からひいてあげよう!
この問題では点BとCから線分APとの平行線をひくってことだね。
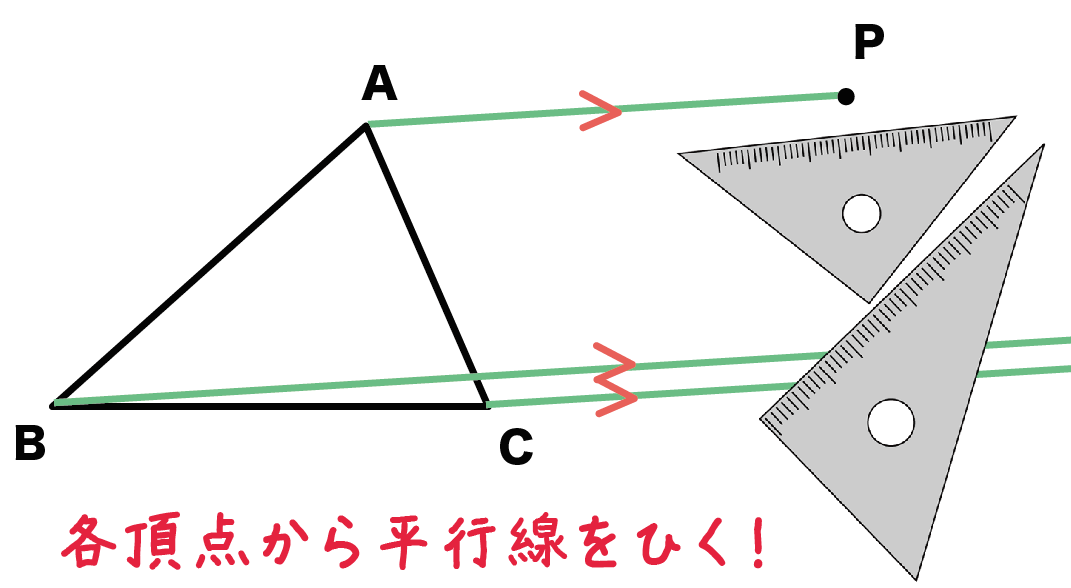
平行線をひくときはコンパスでも三角定規でもかまわない。
ただ、勘やひらめきで平行線をかかないようにしよう。
>>平行線の書き方はコチラ!!
つぎに、対応する点を両端とする「線分の長さ」をはかろう!!
ここでは線分APの長さってことだね。
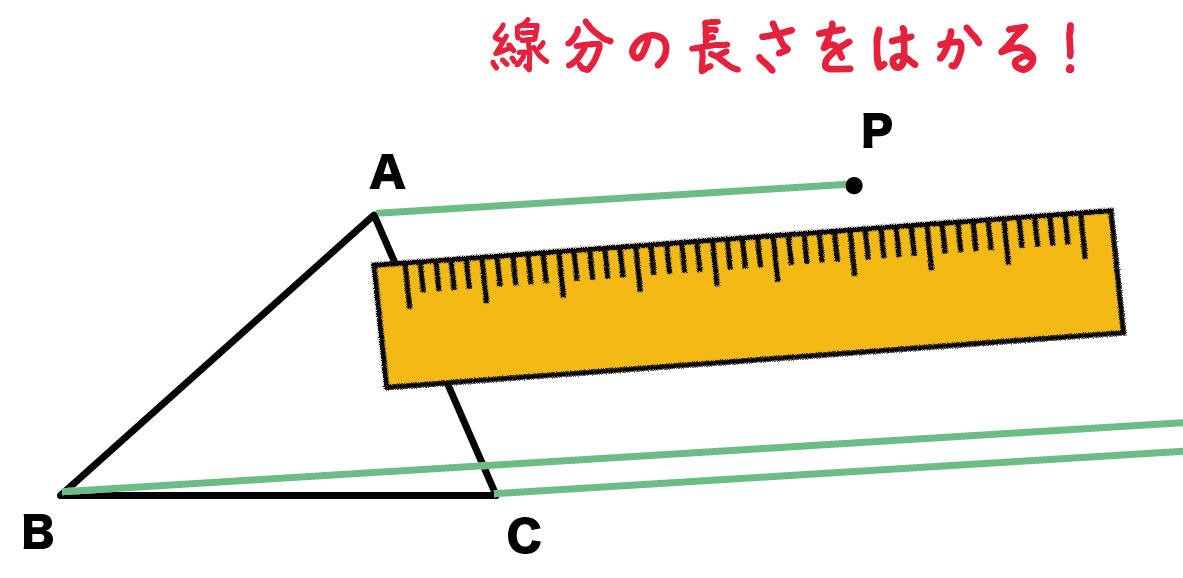
新しくできた線分に定規をあてるだけ。ゆっくり落ち着いてね。
ステップ3で測った長さを使うよ。
平行線上に、各頂点からその長さ分はなれたところに点をうつんだ。ちょっと言葉じゃ説明しずらいから下の図をみてくれ。
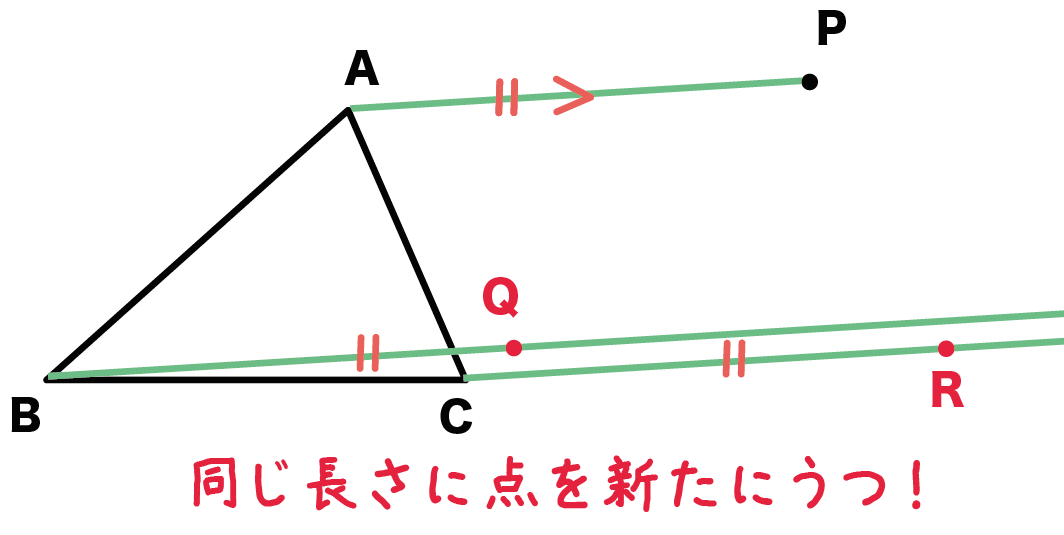
つまり、
AP = BQ = CR
となる新しい点Q・点Rを2つの平行線上にうつんだ。
これが第四ステップ。あと1つだね。
最後のステップはとってもカンタン。
ステップ4まで苦労して打ってきた点同士を結ぶだけだ。
さっきの例でいうと、
だね。そんで、点Pはもともと問題であたえられていた移動後の頂点。
だからこれも結んであげる。
そうすると、
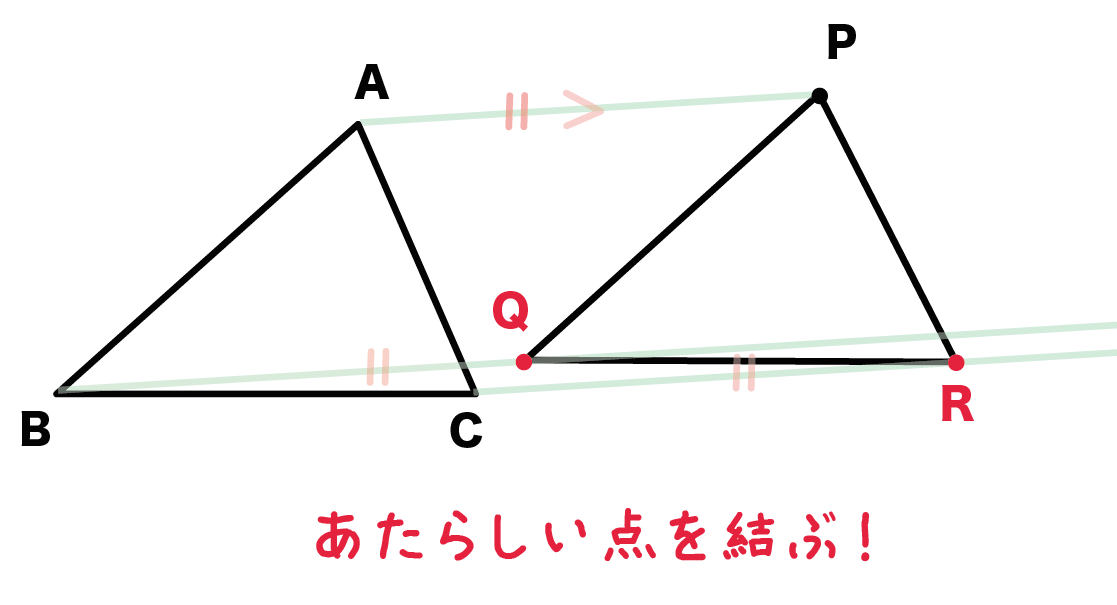
こんな感じで、
平行移動した三角形PQRが書けるんだ。
案外、平行移動の作図もカンタンそうでしょ!??
ここまでみてきた平行移動の作図はどうだった??
5つのステップでゆっくりかけば大丈夫。
あせって間違えるより確実に問題に答えたいね。
つぎは「回転移動の作図」について解説してくねー!
そんじゃねー
Ken