こんにちは!この記事をかいているKenだよ。みかんを5つ買ったね。
玉を取り出すときの確率の問題。
けっこうでてくるよね。
たとえば、
赤玉が2個、白玉が4個入った袋から1回だけ玉を取り出す問題
とかね。
今日はこのタイプの、
玉の確率の問題でつかえる公式
を紹介していくよ。
よかったら参考にしてみてー
さっそく公式を紹介するね。
1回玉を取り出したとき、ある色の玉がでる確率は、
(その色の残りの玉数)÷(全部の残りの玉数)
で計算できちゃうよ。
たとえば、つぎの例題をといてみよう。
例題1
赤玉が2個、白玉が4個入った袋から1回だけ玉を取り出すとき、赤玉をひく確率を求めてください。
このとき、
だね?
公式をつかうと、
(赤玉の残りの数)÷(ぜんぶの玉の残数)
= 2÷6
= 3分の1
になるんだ。
どう??簡単でしょ?
えっ。
玉を1回だけじゃなくて、2回以上取り出したい?!?
2回以上取り出す時は、くじ引きの確率と一緒。
(1回目の玉の確率)× (2回目の玉の確率)×(3回目の玉の確率)・・・
みたいに、
玉をひくごとの確率をかけていけばいいんだ。
たとえば、つぎの例題をといてみよう。
例題2.
赤玉が2個、白玉が4個入った袋から連続で2回玉を取り出すとき、すべて赤玉をひく確率を求めてください。
さっきの計算式で確率をだせちゃうね。
つまり、
(1回目の玉の確率)× (2回目の玉の確率)
ってわけ。
1回めに赤玉をひく確率は、
(赤玉の残数)÷(全玉数)
= 2 ÷ 6
= 3分の1
になるね。
2回目は赤玉が1つなくなった袋から玉をひくよね??
だから、2回目も赤玉をひく確率は、
(赤玉の残数)÷(全玉数)
= 1 ÷ 5
= 5分の1
になるわけだ。
よって、2回連続で赤玉を引く確率は、
(1回目の確率)×(2回目の確率)
= (3分の1) × (5分の1)
= 15分の1
になる。
おめでとう!
これで玉の確率を計算できるね。
玉の確率は一見むずかしい。
だけど、
(ある色の残り数)÷(ぜんぶの残り数)
さえ計算すれば大丈夫。
あとは問題をたくさんといてみよう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。グレープフルーツは常備だね。
当たりくじをひく確率って、
(当たりくじの本数 )÷(残りの本数)
だったよね??
たとえば、5本中1本当たりのくじがあったとしよう。
当たりくじがでる確率は、
(当たりくじの本数:1)÷(残りのくじ本数:5)
= 5分の1
になるんだ。
だけどさ、
この公式って、
くじを1回しか引かない問題でしか使えないよね??
これじゃあ、2回以上ひく問題はとけないね!
そこで今日は、
2回以上くじを引くときの確率の求め方を解説していくよ。
よかったら参考にしてみて。
確率の求め方はつぎの公式だよ。
(1回目のくじ引きの確率)×(2回目のくじ引きの確率)×(3回目のくじ引きの確率)・・・
たとえば、「当たりくじを連続でひく確率」だったら、
(当たりくじの残り本数)÷(残りくじ本数)
をかけていけばいいね!
たとえば、つぎの例題をといてみよう。
例題
10本中3本が当たりくじのくじ引きがある。3回ひいて連続で当たりがでる確率を計算してください。
こいつは2ステップでとけちゃうんだ。
1回目は、
のくじが箱にはいってるよね??
だから、
(当たりくじ数)÷(残りのくじ数)
= 3÷10
= 10分の3
になるよ!
2回目は、当たりくじを1本ひいたあとだ。
1本当たりくじが消えているはず。
だから、箱の中には、
が残ってるよね??
このとき、当たりくじをひく確率は、
(残当たりくじ数)÷(残りの全くじ数)
= 2÷9
= 9分の2
になるんだ。
おなじように考えると、3回めに当たりくじをひく確率は、
が箱にのこっている。
だから、3回目に当たりをひく確率は、
(残当たりくじ数)÷(残すべてのくじ数)
= 1÷8
= 8分の1
になる。
あとは公式通りに、
(1回目のくじ引きの確率)×(2回目のくじ引きの確率)×(3回目のくじ引きの確率)
を計算するだけ。
になったから、
(3回連続で当たりくじを引く確率)
=(1回目のくじ引きの確率)×(2回目のくじ引きの確率)×(3回目のくじ引きの確率)
= (10分の3)×(9分の2)×(8分の1)
= 120分の1
になるよ!
おめでとう!
これで2回以上くじを引く問題も攻略だね。
くじ引きの確率問題はどうだったかな??
2回でも3回でもくじ引きをひいても大丈夫。
あとは公式になれていこう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。すた丼くいたいね。
ある日。
くじ引きに参加したとしよう。
一等賞はディズニーリゾートのペアチケット。
チャレンジャーはAさん、Bさん、キミの3人だ。
当たりくじは10本中1本。
しかも、1人1回しかくじを引けないんだ。
当たりをひくのはむずそうだね・・・・・
そんな状況にいたとしよう。
そこでキミは、
どの順番なら当たりくじをひきやすいのか??
って思うよね?
最初にくじをひいたほうがお得なの??
それとも、
ライバルにはずれを引かせてやるのがいいのか。。
むちゃ迷うね。。。
だけど、残念ながら、
どの順番で引いてもおなじ確率になるんだ。
だから、くじ引きの順番を争っても意味がない。
順番はゆずっても大丈夫。;
なぜ、くじ引きに順番は関係ないんだろう??
もやもやするね。
順番ごとに確率を計算してみよう。
もし、1番目にくじをひいたときを考えよう。
1番目にひくとき、
が箱にはいってるはず。
くじ引きを1回ひいたときの確率の求め方で計算してみよう。
だから、当たりじをひく確率は、
(当たりくじの本数)÷(残りのくじ本数)
= 1÷10
=10分の1
になる。
つぎは2番目にくじを引いたときの確率。
当たりくじの確率ってどれくらいなんだろう??
2番目にくじをひくときは、
を計算してみて。
一人目がはずれくじを引く確率は、
(はずれくじの残本数)÷(すべてのくじの残本数)
= 9÷10
= 10分の9
だね。
そして、2人目のキミが当たりくじを引く確率は、
(当たりくじの残本数)÷(すべてのくじの残本数)
= 1÷9
= 9分の1
になるんだ。
よって、1人目がハズレで2人目が当たりくじをひく確率は、
(一人目がはずれくじを引く確率)×(2人目が当たりくじを引く確率)
= (10分の9 )×(9分の1)
= 10分の1
になるね。
これはさっきの確率といっしょ!
くじを最後にひく確率を求めよう。
計算方法は、
2回以上くじをひいた場合の計算方法をつかえばいいんだ。
(一人目がはずれくじを引く確率)×(2人目もはずれくじを引く確率)×(3人目で当たりくじをひく確率)
を計算していくよ。
一人目がはずれくじを引く確率は、
(はずれくじの残本数)÷(すべてのくじの残本数)
= 9÷10
= 10分の9
二人目がはずれくじを引く確率は、
(はずれくじの残本数)÷(すべてのくじの残本数)
= 8÷9
= 9分の8
3人目のキミが当たりくじを引く確率は、
(当たりくじの残本数)÷(すべてのくじの残本数)
= 1÷8
= 8分の1
になる。
よって、
1~2人目がハズレで3人目で当たりくじをひく確率は、
(1人目がはずれくじを引く確率)×(2人目がはずれくじを引く確率)×(3人目で当たりくじを引く確率)
= (10分の9 )×(9分の8)×(8分の1)
= 10分の1
になるね。
こいつもさっきと同じ確率だね!
つまり、
どの順番でも確率はおなじってことだ。
どう??しっくりきたかな??
くじ引きの確率は順番なんて関係ない。
これを知っているとかなり便利。
くじ引きに冷静に参加できるからね。
中学数学でもたまにでてくるから、しっかりおさえておこう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。オレンジは目覚めにいいね。
中学数学の確率でたまーに、
くじ引きの問題
ってあるよね??
たとえば、
6本のうち当たりくじが4本あるとき、当たりくじをひく確率を求めなさい。
っていう感じで。

こういう問題はむずかしそう。
だけど、公式をつかえば5秒で確率を計算できるんだ。
つぎの公式で計算できるよ。
(当たりor はずれを引く確率)
=(当たりorはずれの本数)÷(残りのくじ本数)
あ、くじを1回引く場合だけどね。
たとえば、6本のうち2本が当たりくじだとする。
くじを1回ひいて「当たりくじ」がでる確率を求めてみよう。
だよね。
公式をつかってやると、
(当たりくじを引く確率)
=(当たりくじの本数)÷(ぜんぶのくじ数)
= 2 ÷ 6
= 3分の1
になるんだ。
「当たりくじの数」を「残りのくじ数」でわるだけ。
簡単でしょ!?
でもさ、なんで公式が使えるんだろう??
ちょっと怪しいよね。。
この公式がつかえる理由は、
1つ1つのくじ引きを区別しているから
なんだ。
「当たりくじ」たちはすごく似ている。
ぶっちゃけ、どれも同じ。
だけど、確率を計算するときは同じじゃだめなんだ。
こいつらを区別しないといけない。
たとえば、
みたいな感じでね。
当たりくじだけじゃなくて、はずれでも同じ。
見た目は同じだけど、別ものとしてあつかってやろう。
だから、「当たりくじのひき方」だったら、
の2通りがあるはず。
ぜんぶのくじ引きは、6通りのひきかたがある。
だから、確率の公式をつかってやれば、
(当たりくじの場合の数)÷(すべてのくじ引きの場合の数)
= 2÷6
=3分の1
になるんだ。
おめでとう!
くじ引きの確率もマスターだね。
くじ引きの確率の問題??
おそれることはない。
ただ、公式で計算すればいいんだ。
くじの1つ1つが区別されるっておぼえておこう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。コイン、ほしいね。
コインの確率の問題ってでてくるよね??
具体的にいうと、
〜枚のコインを投げて○○が△△回でる確率を求めなさい
ってやつだ。
コインの確率がわかると便利。
勝負やゲームに強くなる。
テストの点数もあがる。
いいとこづくしなんだ。
今日はコインの確率を一瞬で計算できる公式を紹介していくよ。
よかったら参考にしてみて。
コインの枚数をn、求めたいコインの場合の数をaとしよう。
このときのコインの確率は、
a÷2^n
で計算できるんだ。
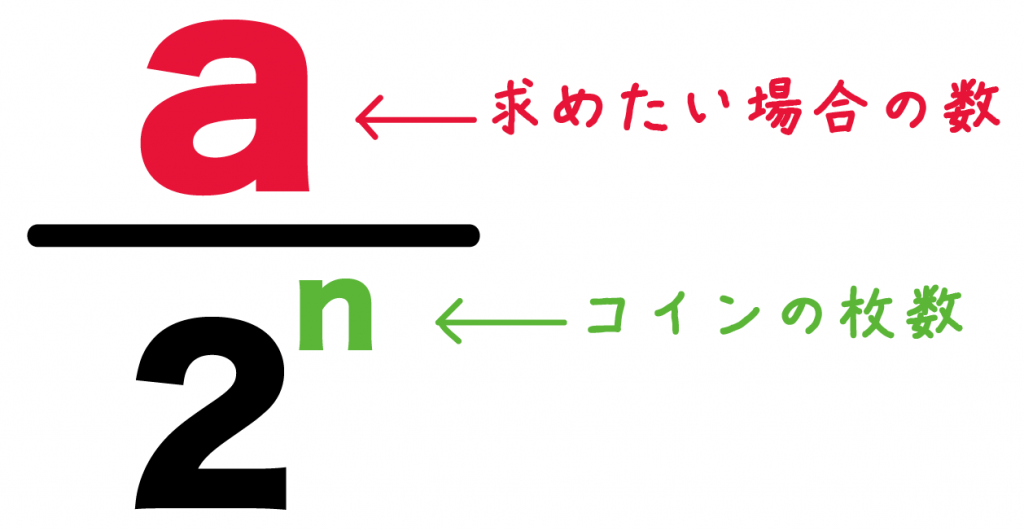
「コインの枚数」と「ある場合の数」さえわかればいいってことだね。
たとえば、つぎの例題をといてみよう。
例題
3枚のコインをなげてすべて表になる確率を計算しなさい。
3ステップで確率を計算できちゃうよ。
まず樹形図をかこう。
出る目は「表」か「裏」のどちらかだよね??
だから樹形図はこうなるはず↓↓
※ 樹形図の書き方を参考にしてみてね。
求めたい場合の数をしらべてみよう。
例題では、
3枚のコインがすべて表になる確率
を計算したかったんだよね??
さっきの樹形図をみてみよう。
「3枚すべてのコインが表になる場合の数」は、
1通りしかないね。
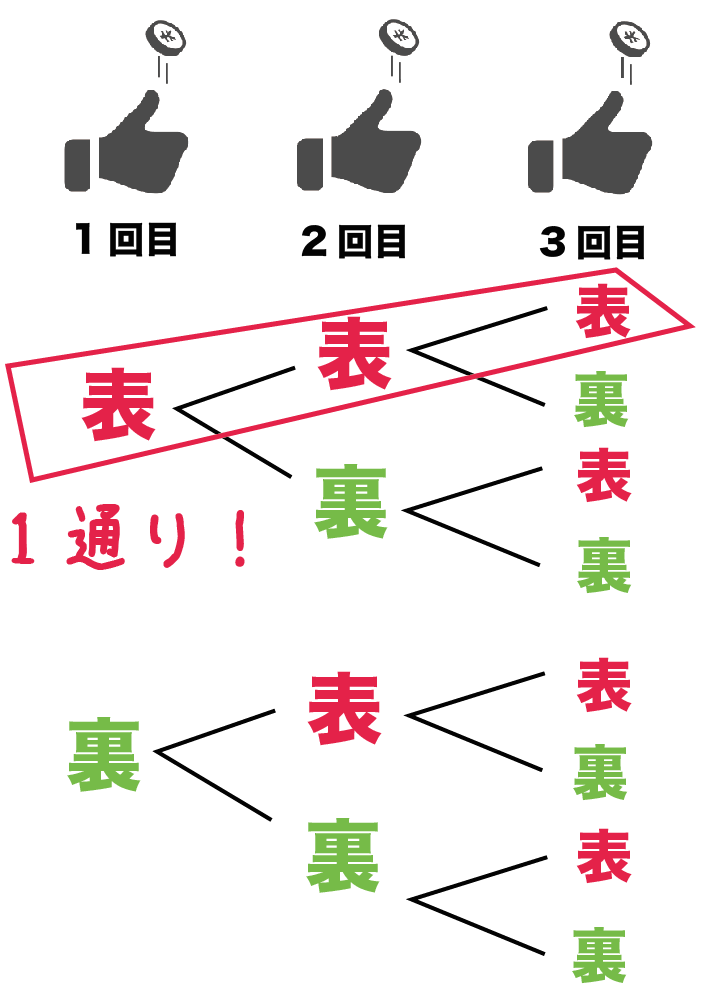
うん、どうみても1つだ。
公式をつかおう。
例題では、
コインの枚数が「3」、表になる場合の数は「1」。
だから、コインの確率公式をつかってやると、
(すべて表になる場合の数)÷(2のコインの枚数乗)
= 1÷2^3
= 1/8
になるね。
おめでとう!
これでコインの確率もマスターだね。
コインの確率は簡単。
の2つさえわかればいいからね。
あとは公式で計算してみよう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。コーヒー豆買いたいね。
中学数学の確率で、
サイコロの問題
ってけっこうでてくる。
たとえば、サイコロを2つふって目の和が4になる確率を求めよ!とかね。
たまに3つサイコロなげるときもある。
サイコロの確率ってめんどくさいから、
公式があったらいいのになあ・・・・・・
とか思ってない??
今日はそんなキミのために、
中学数学でつかえるサイコロの確率問題の公式
をわかりやすく解説していくよ。
よかったら参考にしてみて。
サイコロをn個ふったときの確率の公式は、
(あるできごとの場合の数)÷(6のn乗)
で計算できちゃうよ。
たとえば、サイコロを2つふって、目の和が8になる確率を求めよう。
2つのサイコロの確率の場合の数は
「表」をかいて求めるんだったね??
「目の和が8になる」場合の数をかぞえてみると、
5通りであることがわかる。
また、サイコロは2つ振っているね。
公式をつかってみると、
(目の和が8になる場合の数)÷(6の2乗)
= 36分の5
になるね!
サイコロの数nを代入して、場合の数を数えるだけ。
すぐに確率を計算できちゃう。
だけどさ、
なんでこの公式つかえちゃうんだろう??
簡単すぎてちょっと怖いよね。
じつはこれ、確率の求め方の公式をつかっているんだ。
を代入してるだけ。
えっ。
なぜ6^n通りになるのかって?!?
じつは、1つのサイコロに目が6つあるからなんだ。
だから、n個のサイコロをふったときには、
6をn回かけた場合の数があるんだ。
どう??スッキリしたかな??
サイコロの確率の公式はどうだったかな??
サイコロの数を数えて、
樹形図や表で場合の数をゲットするだけ。
実践問題で公式をつかっていこう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。水、うまいね。
3つのサイコロの確率の問題ってたまにでてくる。
サイコロが2つの確率ならけっこう簡単だったね。
だけど、
サイコロが1つ増えたらちょームズくなるんだ。

なぜなら、
サイコロ3つだと表がかけないからね。
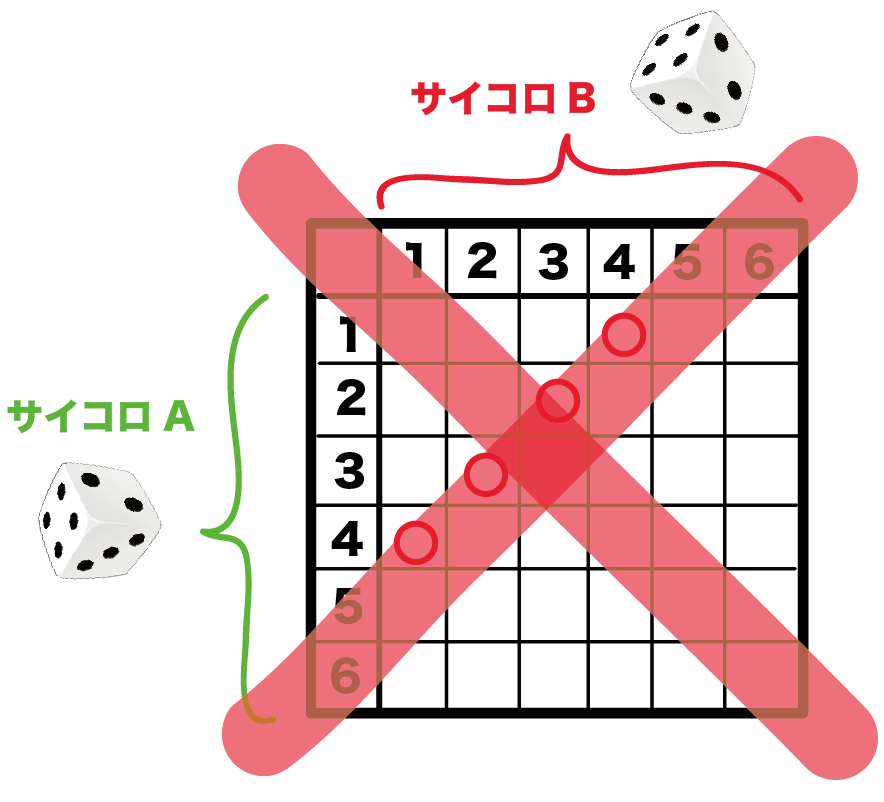
今日はこのやっかいな
「3つのサイコロの確率の問題」の解き方をわかりやすく解説していくよ。
よかったら参考にしてみて。
サイコロ3つの確率の問題は3ステップでとけちゃうよ。
例題をといてみよう。
3つのサイコロを同時に振ったとき、目の和が5になる確率を求めよ。

樹形図をかいてみよう。
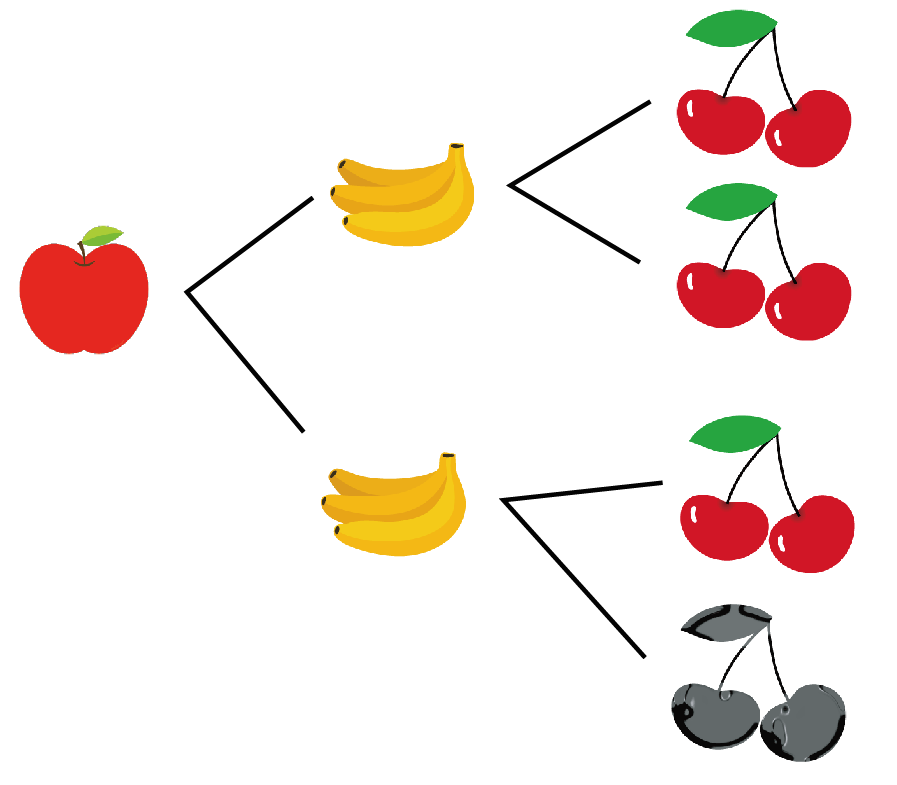
中学数学では樹形図で場合の数をかぞえていくんだ。
例題では、
3つの目の和が5になる
場合の数をしらべなきゃいけないね。
3つのサイコロを、
としてみよう。
樹形図で「3つの目の和が5になる」場合の数をかぞえてみると、
ぜんぶで6通りありそうだね!
ぜーんぶの目の場合の数をしらべよう。
サイコロ1つの目のパターンは6つ。
ってことは、サイコロを3つ同時にふったときの目の出方って、
6×6×6
= 216
になるはずだね。
最後に確率の公式で計算してみよう。
「樹形図でかぞえた場合の数」を「すべての場合の数(216)」でわればいいんだ。
例題だと、
だったね??
ってことは、
サイコロ3つの目の和が5になる確率は、
(サイコロの目の和が5になる場合の数)÷(すべての場合の数)
= 6÷216
= 36分の1
になるね。
おめでとう!
3つのサイコロの確率をマスターしたね。
3つのサイコロの問題は正直、
近道がない。
ガッツと樹形図のスキルが必要だね。
問題をガンガンといてなれていこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。茶漬け最高。
中学数学では、
サイコロの確率を求める問題
ってよーくでてくる。
いちばん出やすいのが、
サイコロを2つふったときの確率の問題
なんだ。
サイコロが2個もあるなんて無理。。。。
と思うかもしれないけど、じつはこれが簡単。
解き方さえおぼえておけば大丈夫なんだ。
今日は、この「2つのサイコロの確率の求め方」をわかりやすく解説していくよ。
よかったら参考にしてみて。
2つのサイコロの確率問題は簡単。
3ステップでとけちゃうんだ。
例題をいっしょにといてみよう!
2つのサイコロを同時になげたとき、目の数の和が5になる確率を求めてください。
まず、
7 × 7マスの表
をかいてみよう。
そしたら、
横1行に1~6の数字を右詰めでいれる。
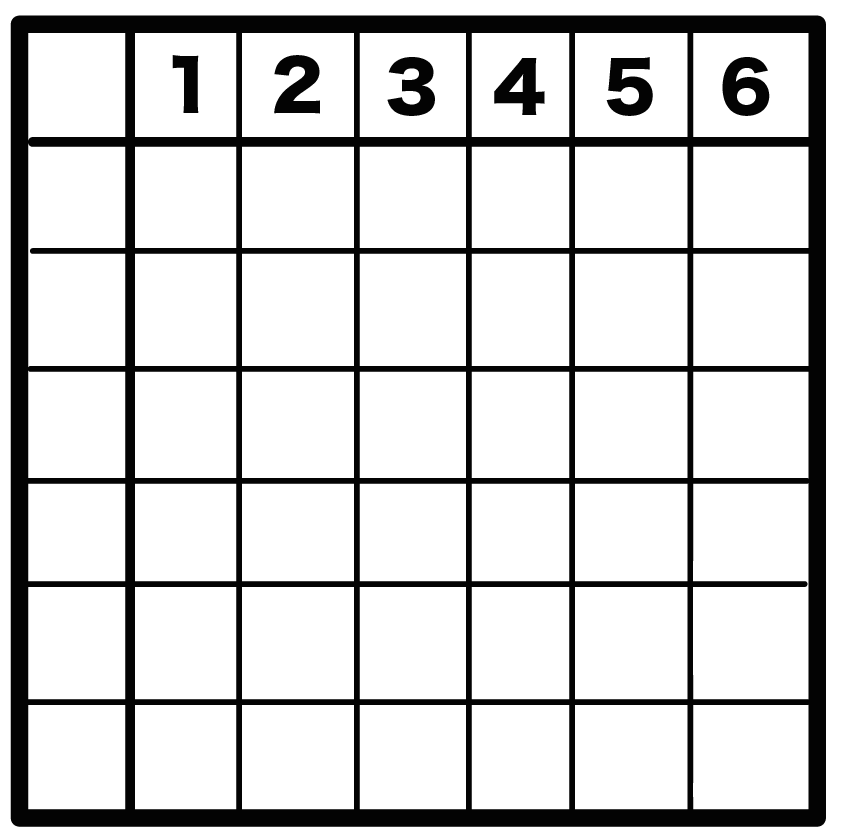
縦1行にも1~6の数字を下詰めでかいてみよう。
こんな感じになるね↓↓
この表は、
をあらわしているよ。
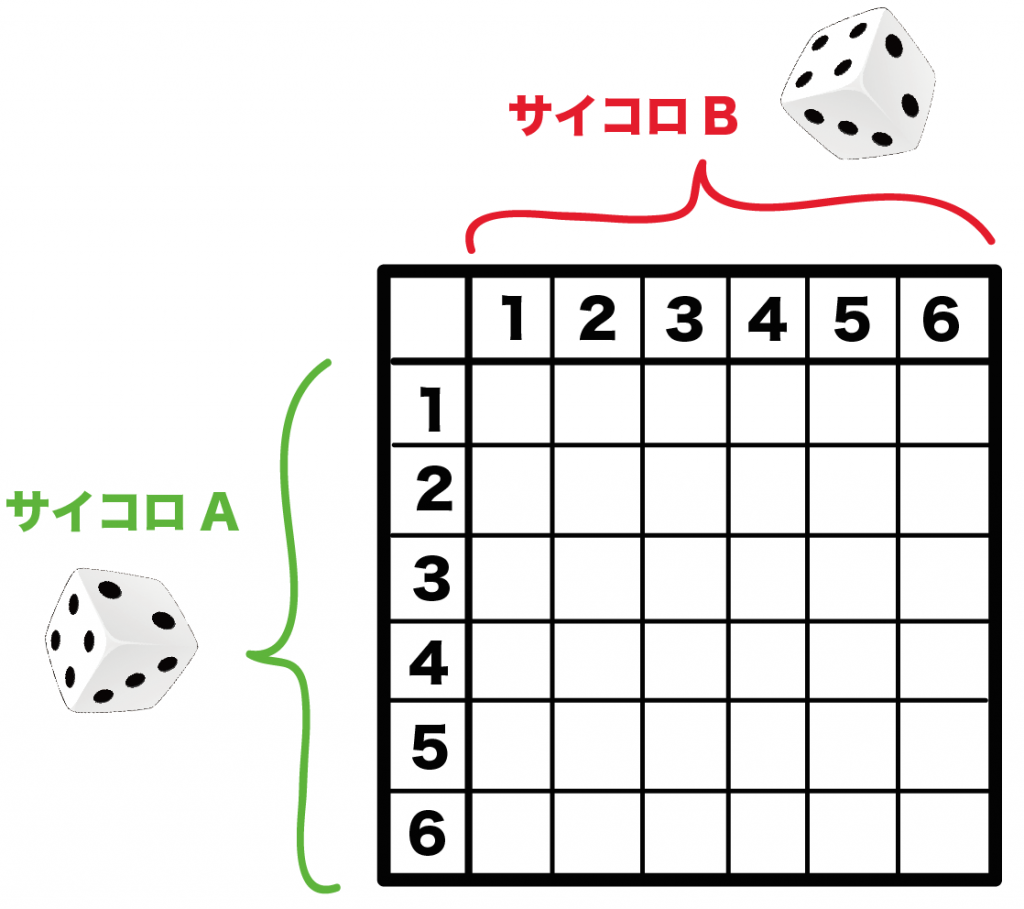
たとえば、
サイコロAが2, サイコロBで4がでたとしよう。

このとき、○をつけたところにあてはまるってわけ。
つまり、1通りしかないってことだね。
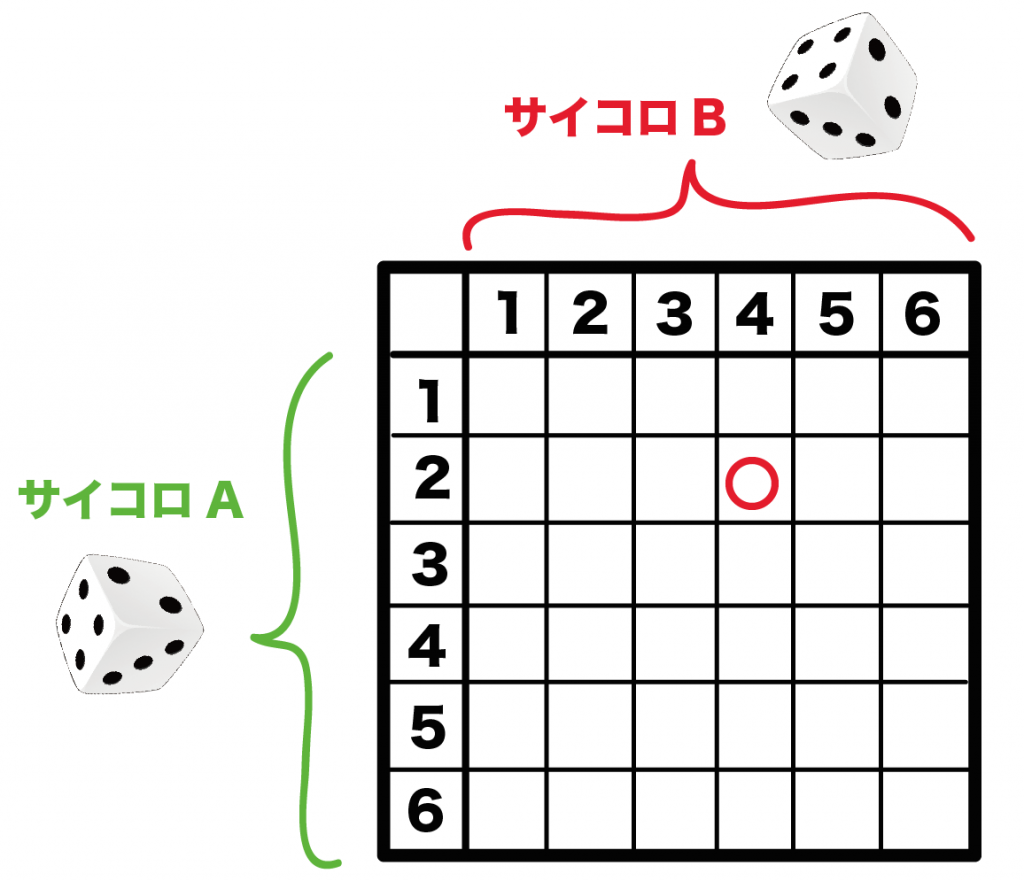
2つのサイコロの場合の数を一瞬で数えられちゃうんだ。
ガンガン使っていこう!
サイコロの表をかいたね??
つぎは、表の中に○をつけていこう。
求めたい目のパターンを数えればいいんだ。
たとえば例題では、
2つの目の和が5になる確率
を求めたかったよね?
サイコロAとBの目の和が5なるところに○をつけてみよう。
ぜんぶで○が4つだね??
目の和が5になる場合の数は「4」ってことだよ。
場合の数がわかったね??
あとは公式で確率を計算するだけ。
確率の求め方の公式って、
(Aがおきる確率)=(Aが起きる場合の数)÷ (すべての場合の数)
だったよね??
2つのサイコロの確率でいうと、
(表の○の数)÷ (すべての場合の数の36)
になるね。
例題でいうと、
になったね?
だから、
(2つのサイコロの目の和が5になる確率)
=(○をつけた数)÷(全部のマス数)
= 4 ÷ 36
= 9分の1
になるんだ。
おめでとう!
これでサイコロ2個の問題も楽勝だね!
2つのサイコロの問題??
まず表をかいて、○をつける。
で、
○の数を36でわればいいんだ。
解き方はわかりやすいから点を稼いでいこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。焼き肉は週一でいいね。
サイコロを2個以上投げたとしよう。
このとき、「ぜんぶ同じ目になること」を「ゾロ目がでる」ってよんでいるよ。
たとえば、サイコロを4つふったとしよう。
ぜんぶの目が4になったら「ゾロ目」がでたっていうんだ。

ゾロ目をだすといいことばかりだ。
ボーナスがもらえたり、ワープできたりと、かなりお得。
それだけめずらしくてラッキーってことなんだ。
だからこそ、
サイコロでゾロ目がでる確率
ってむちゃくちゃ気になるよね?
今日は、
サイコロをふってゾロ目がでる確率を3秒で計算できる公式
を紹介していくよ。
よかったら参考にしてみて。
サイコロの数をnとしよう。
ゾロ目になる確率は、
6/6^n
になるよ。

ただし、nは2以上にかぎるけどね!
たとえば、サイコロ4つのゾロ目の確率を計算してみよう!

サイコロの数は4だから、
「n」 に「4」を代入すればいいわけだ。
すると、
(4つのサイコロでゾロ目がでる確率)
= 6 ÷ 6^4 = 1/ 216
になるはず。
つまり、
1/216っていう確率で、
「3の目」が4つでるかもしれないし、

「1の目」が4つでるかもしれないんだ。

どう??簡単な公式でしょ??
でもさ、
なぜゾロ目の確率が計算できるんだろう??

nに「サイコロの数」をいれるだけ。
簡単すぎる。
ぜったいあやしいよね??。
だから、
なぜゾロ目の確率公式がつかえるのか???
っていうことを確認していこう。
サイコロを何個ふっても、
「ゾロ目がでる場合の数」って「6」なんだ。
なぜなら、
サイコロの目が同じになる場合の数は1~6で1つずつだからね。
だから、1000個サイコロをふろうが、1万個サイコロをなげようが、
ゾロ目になる場合の数は6通りになるんだ。

あとは分母の、
すべての場合の数を求めるだけ!
6のn乗
だったね??
なぜなら、1個のサイコロは6通りの目をもっているからね。
n個のときは6をn回かけると場合の数になるんだ。
だから、n個のサイコロをふったときにゾロ目がでる確率は、
6/6^n
になるよ。
どう?スッキリしたかな!?
サイコロでゾロ目がでる確率の公式は簡単。
n個サイコロをふったとすれば、
6/6^n
の公式で計算できちゃうんだ。
じゃんじゃん計算していこう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。散歩は大事だね。
中学数学の確率で重要なのは、
場合の数の調べ方
だ。
「場合の数」さえ数えられれば大丈夫。
あとは確率の公式にいれるだけだからね。
「場合の数の調べ方」さえおぼえれば、
確率マスターになれるわけさ。
今日はそんな確率で大切な、
場合の数の調べ方を2つ紹介するよ。
よかったら参考にしてみて。
中学数学ではおもに、
樹形図で場合の数を調べていくよ。
調べ方はつぎの2つさ。
つぎの例題をときながら解説していくよ。
例題
3・4・8がかかれたカードが3枚ある。こいつらを並べて3ケタの数字をつくるとき、偶数になる確率を求めよ。
このとき、樹形図はつぎのようになるね。
※詳しくは「樹形図の書き方」をよんでみてー!
まずは「すべての場合の数」をしらべよう。
これは確率の計算で分母にくるやつだね。
調べ方はとっても簡単。
樹形図のいちばん右をぜんぶ数えればいいんだ。
例題でいうと、いちばん右には6つの実がなっているよね??
だから、
すべての場合の数は「6通り」になるんだ。
樹形図のいちばん右をかぞえると「すべての場合の数」になる
って覚えておこう。
今度は「あるできごと」の「場合の数の調べ方」だね。
これは確率の公式の分子にくるやつだ。
この調べ方はちょっとむずかしい。
なぜなら、あてはまる場合の数を樹形図から選ばないといけないからね。
たとえば、さくらんぼが腐ってる場合の数をしらべたいとき。
このとき、樹形図をばーーってみてみよう。
さくらんぼが腐ってそうな場合の数をみつけるんだ。
ざっと見た結果、
緑でかこった1通りしかないね。
こんな感じで場合の数を数えればいいんだよ。
例題をみてみよう。
例題で求めたいのは、
3ケタの数字が偶数になる確率
だったよね??
樹形図でかぞえてみると、
4通りある!
よって、
(3ケタの数字が偶数になる確率)
= (偶数になる場合の数)÷(すべての場合の数)
= 4÷6 = 2/3
になるね。
おめでとう!
これで場合の数の調べ方をマスターしたね。
中学数学では基本的に、
樹形図で場合の数をしらべていくよ。
の2つさえ調べられればこっちのもの。
あとは、公式で確率を計算するだけだね。
じゃんじゃん調べていこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。小腹がすいたね。
中学数学の確率で便利なのは、
樹形図
というアイテムだ。
樹形図とは文字通り、
樹の形みたいに枝分かれしている図のことだよ。
ちょうど下みたいな図だね↓↓
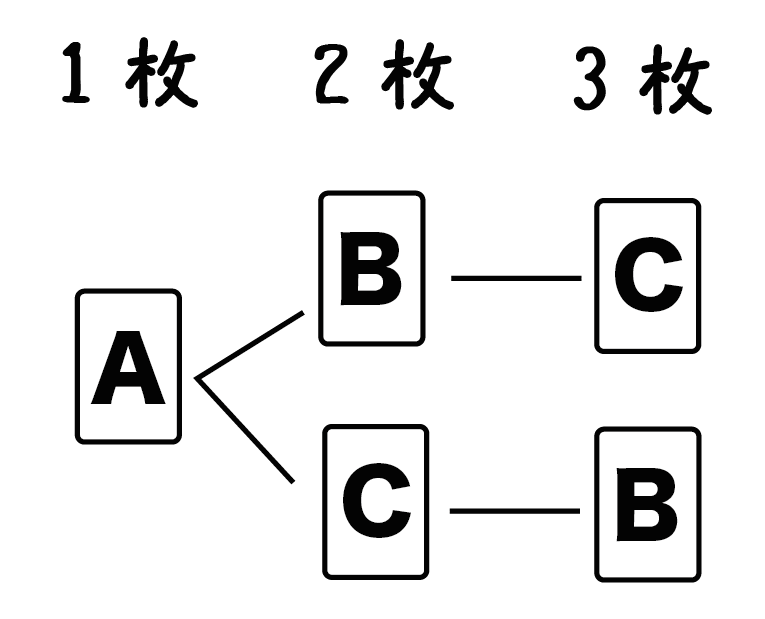
どう??樹の枝みたいでしょ??
中学生が勉強する確率では、
「樹形図」をつかって場合の数をかぞえていくんだ。
確率では樹形図がむちゃ重要ってわけ。
さっそく樹形図をかいていこう。
3ステップでかけちゃうんだ。
つぎの例題をときながら解説していくよ。
例題
3・4・8がかかれたカードを3枚ならべてできる整数の場合の数を求めなさい。
まずは何回挑戦できるかかいてみよう。
つまり、
トライアル数ってわけ。
コインを3回なげるんなら「3」、
くじ引きを2回ひけるなら「2」がトライアル数だね。
例題のトライアル数は「3」。
なぜなら、
カードを3枚並べられるからさ。
もちろん、カードを4枚ならべるなら「4」、
120枚並べるなら「120」がトライアル数だ。
このトライアル数をヨコにずらーっと書いてみよう!
まずは一回目のトライアルでどうなるか考えてみよう。
コインだったら表か裏か。
くじ引きだったら当たりか・はずれだね。
例題で1枚目になるのは、
のいずれかのカードだね??
つまり、
1枚目は3枚のどれかってわけ。
だから、「1枚」の下に「3」「4」「8」の3通りをかいてあげよう。
つぎは、前回のトライアルの結果をふまえてどうなるか??
ってことを考えてみよう。
1回目が終わったら、1回目をふまえて2回目。
2回目が終わったら、1・2回目をふまえて3回目
の結果を予想するんだ。
例題でいうと、
1回目のトライアルの後、残されたカードは2枚。
1枚目に4がくると、
つぎは「3」か「8」の結果になる。
おなじように「3」と「8」がきている場合を考えると、
こんな樹形図になるはず↓↓
同じように、3回目の結果も予想してみよう。
2枚カード並べたら残り1枚だね。
つまり、残っているカードを並べるだけってことだ。
だから、3枚目も加味するとこうなるはず↓↓
おめでとう!これで樹形図は完成だね。
すべてのカードの並び方は6通りってわけ!
樹形図の書き方はどうだったかな??
ポイントは、
前のトライアルの結果をふまえること。
これにつきるね。
1回目のトライアルが終わったら2回目はどうなるのか。
これをイメージしてみよう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。チャーハンは万能だね。
確率の問題ってむずいよね??
場合の数をかぞえたり、
樹形図をかいてみたり・・・・
なんだろう、
大忙しだ。
っていうか、解き方がよくわからないときが多いはず。
そこで今日は、
中学数学でつかえる確率問題の解き方を5ステップで解説していくよ。
テスト前に参考にしてみてね。
確率の問題は5ステップでとけるよ。
つぎの例題で解き方を解説していくね。
例題
A・B・Cの3枚のカードを並べるとき、BとCが隣り合わせになる確率を求めよ。
まず樹形図をかいてみよう。
中学数学では場合の数を調べる方法は、
樹形図しか、ない。
だから、
めんどいかもだけど樹形図をかいてみよう。
カードA・B・Cの並べ方はつぎのようになるよ。
樹形図から「すべての場合の数」を調べよう。
いちばん右の「実の数」を数えればいいんだ。
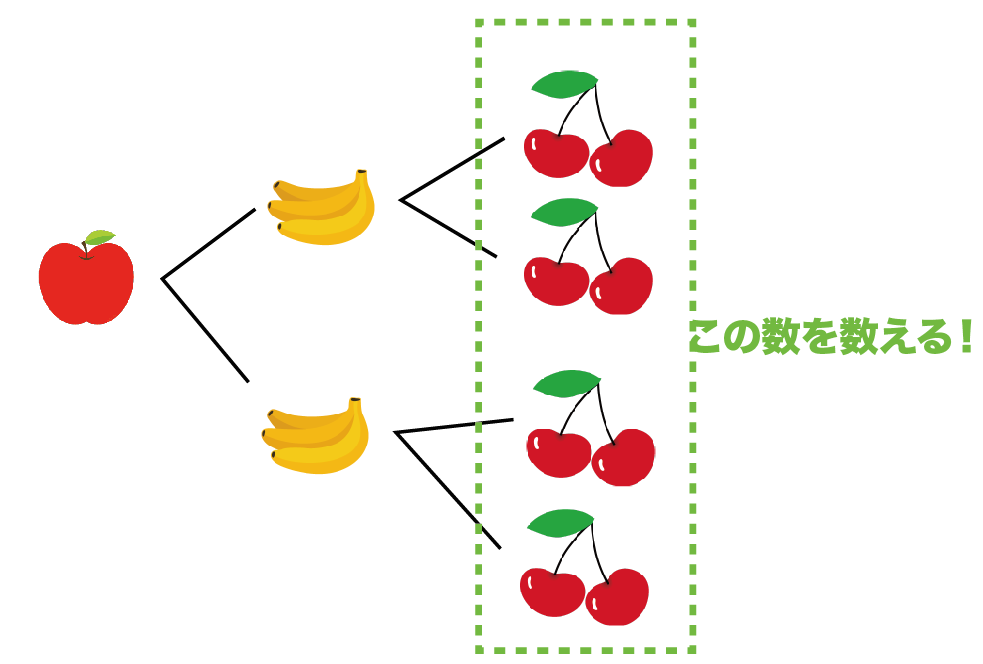
例題の樹形図では「6」だね??
つまり、
すべての場合の数は「6通り」あるってことさ。
「求めたいことがら」の場合の数をしらべよう。
例題でいうと、
BとCが隣り合わせになる場合の数
をしらべればいいんだ。
樹形図をみてみると、
4通りってことがわかるね。
あとは確率の公式で計算するだけ。
あることがらAが起きる確率は、
(Aが起きる場合の確率) = (ことがらAが起きる場合の数)÷(すべての場合の数)
だったよね??
これを使おう。
例題でいうと、
だ。
ってことは確率の計算式をつかえば、
(BとCが隣り合わせになる確率)
=(BとCが隣り合わせになる数)/(すべての場合の数)
= 4/6
になるはず。
最後に約分しよう。
約分しなくても間違えじゃない。
だけど、先生によっては×にされるかもしれない。
約分して分数を簡単にしよう。
例題の確率は、
6分の4
だったよね??
こいつを約分すると、
3分の2になる。
これがきれいな確率の答えだよ。
帰るまでが遠足
ってよくいうよね。
だけど、確率では、
約分までが確率だよ。
もう一度約分できるか疑ってみよう!
そんじゃねー
Ken