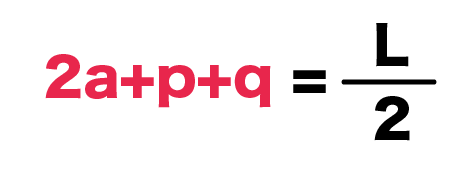【式の計算の利用】図形の証明問題の解き方がわかる4ステップ
式の計算の利用の図形の証明??
こんにちは!この記事をかいているKenだよ。にんじんはゆでたいね。
中3数学では、
式の計算の利用
って単元を勉強していくよ。
因数分解の公式をふつうの計算問に使ってみたり、
いろいろな証明にチャレンジしたりするんだ。
そんな中でも、よく質問をうけるのが、
図形の証明問題
だ。
たとえば、つぎのような証明問題だね。
例題
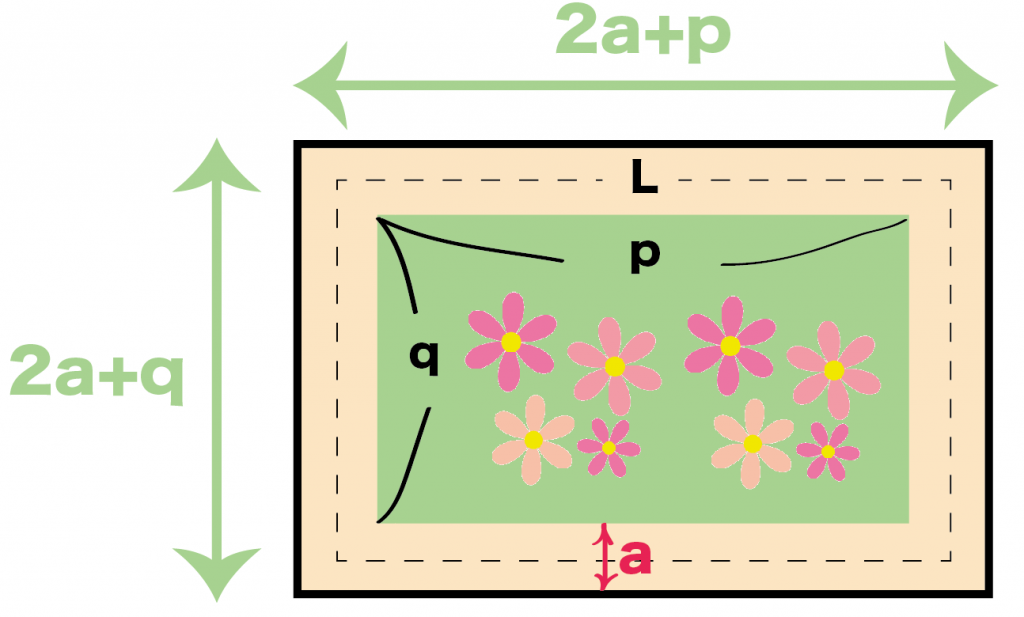
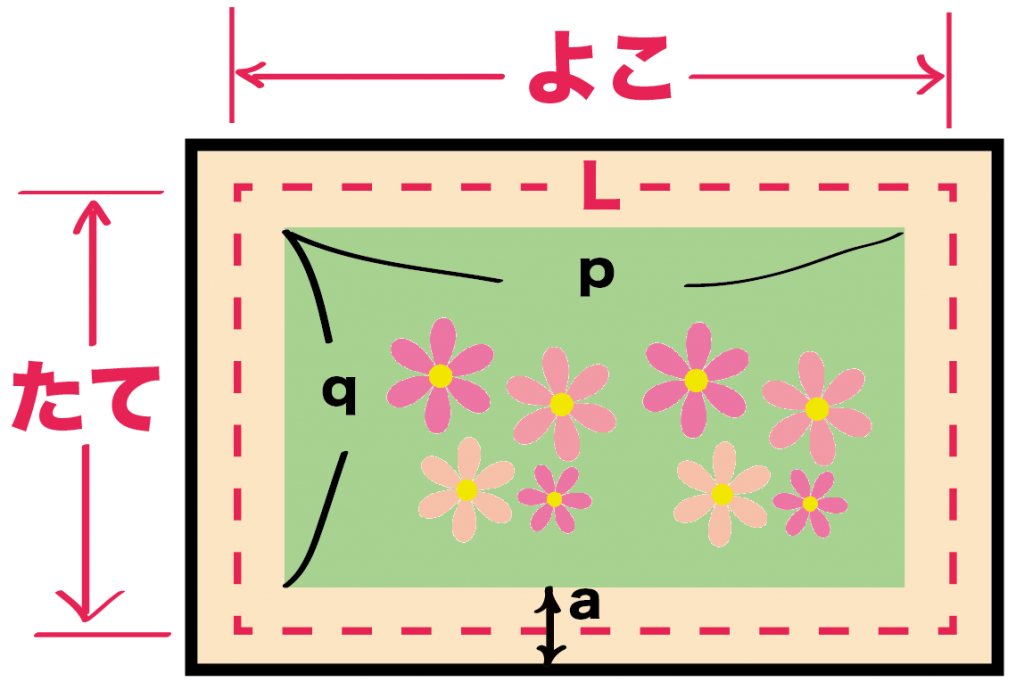
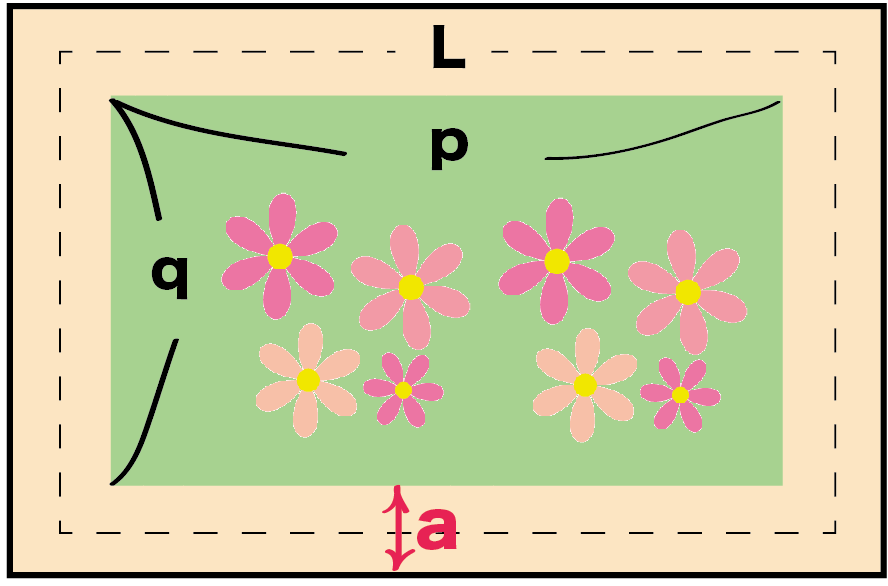
タテの長さがp、横の長さがqの長方形の花壇がある。道幅をa、道のちょうど真ん中をとおる線の長さをLとする。道の面積をSとするとき、
S = aL
となることを証明しなさい。
今日はこのタイプの問題を攻略するために、
式の計算の利用の図形証明問題の解き方
を4ステップで解説していくよ。
よかったら参考にしてみてね。
式の計算の利用の図形の証明がわかる4ステップ
4ステップでとけちゃうよ。
- 道幅の面積をだす
- 道の真ん中を通る線Lをだす
- 道幅の面積を因数分解
- 代入する
例題をいっしょにといてみよう!
例題
タテの長さがp、横の長さがqの長方形の花壇がある。道幅をa、道のちょうど真ん中をとおる線の長さをlとする。道の面積をSとするとき、
S = al
となることを証明しなさい。

Step1. 道幅の面積をだす
道幅の面積Sを計算してみて。
S以外の文字で面積をあらわせばいいんだ。
道幅の面積は、
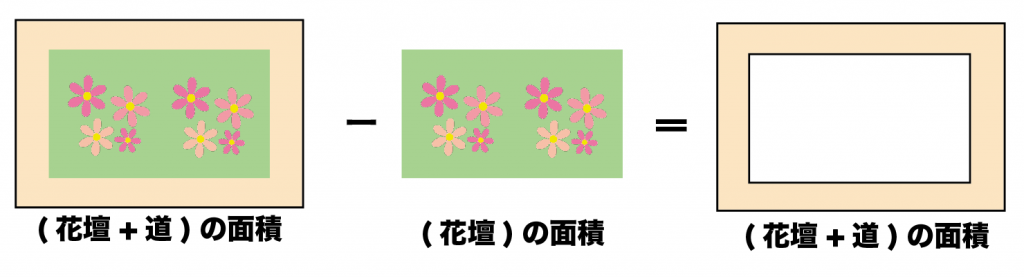
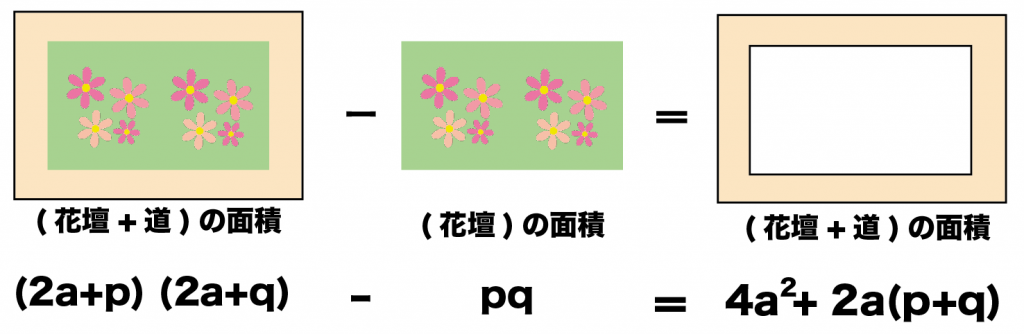
(「花壇+道」の面積)- (花壇の面積)
で求められるよ。
「全体の面積」から「花壇の面積」をひいちまえばいいってわけ。
例題でもまずは、
- (花壇+道)の面積
- 花壇の面積
を計算してみよう。
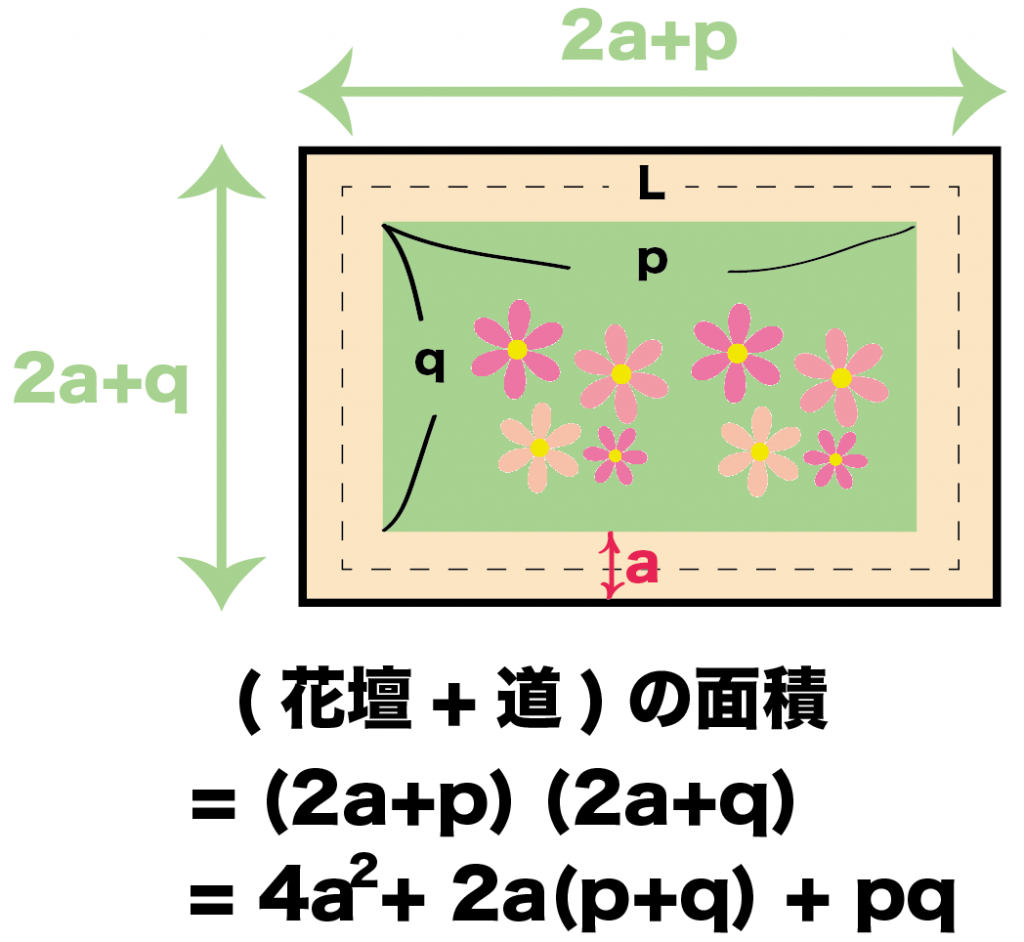
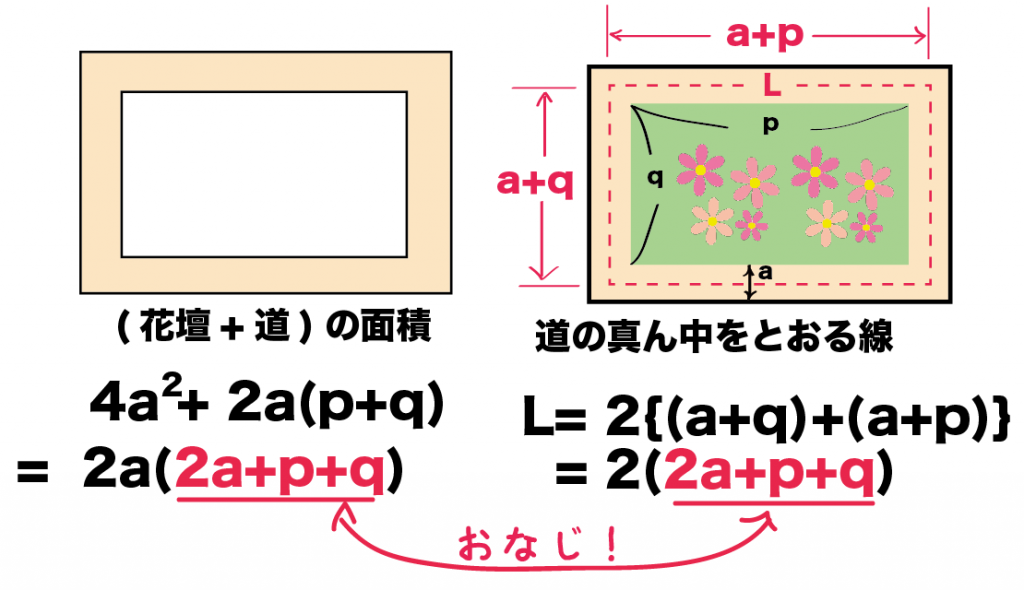
まず、(花壇+道)の面積だね。
タテ・横の長さは、
- よこ:2a+p
- たて:2a+q
になってる。
だから、この長方形の面積は、
たて×よこ
= (2a+p)(2a+q)
= 4a^2 + 2a(p+q)+pq
になるんだ。
うまく乗法の公式で展開してね。
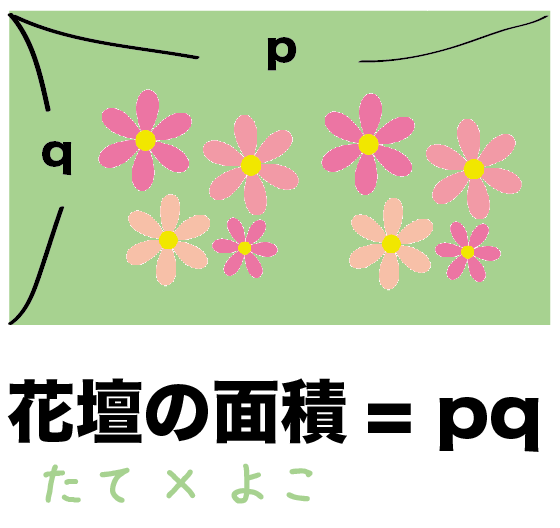
つぎは花壇の面積。
花壇は、
- たて: q
- よこ: p
の長方形だね。だから、こいつの面積は、
(花壇の面積)
= たて×よこ
= pq
になるね。
よって、道幅の面積Sは、
S = (花壇+道の面積)- (花壇の面積)
= 4a^2 + 2a(p+q)+pq – pq
= 4a^2 + 2a(p+q)
になる!
Step2. 道幅の真ん中の線の長さ(L)を求める
つぎは「道の真ん中を通ってる線」の長さだ。
例題では、
2×(道の真ん中のタテ+道の真ん中のよこ)
で求められるよ。
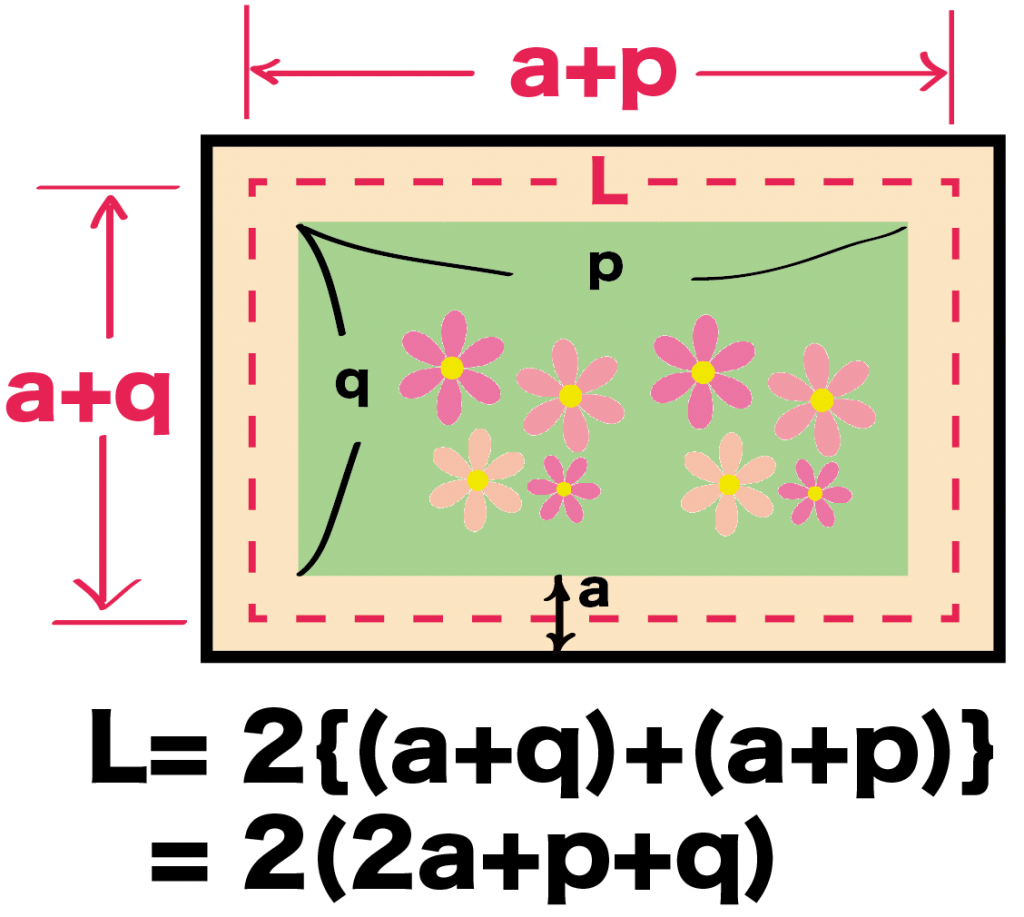
- 道の真ん中のたて= a+q
- 道の真ん中のよこ= a+p
になってるから、
道の真ん中の線のぜんぶの長さLは、
L =2×(道の真ん中のタテ+道の真ん中のよこ)
= 2×(a+q+a+p)
= 2 (2a + p + q)
になるね。
Step3. 道幅の面積を因数分解
道幅の面積Sを因数分解してみよう。
共通因数でくくってもいいし、
因数分解の公式をつかってもいいよ。
例題の道幅の面積Sは、
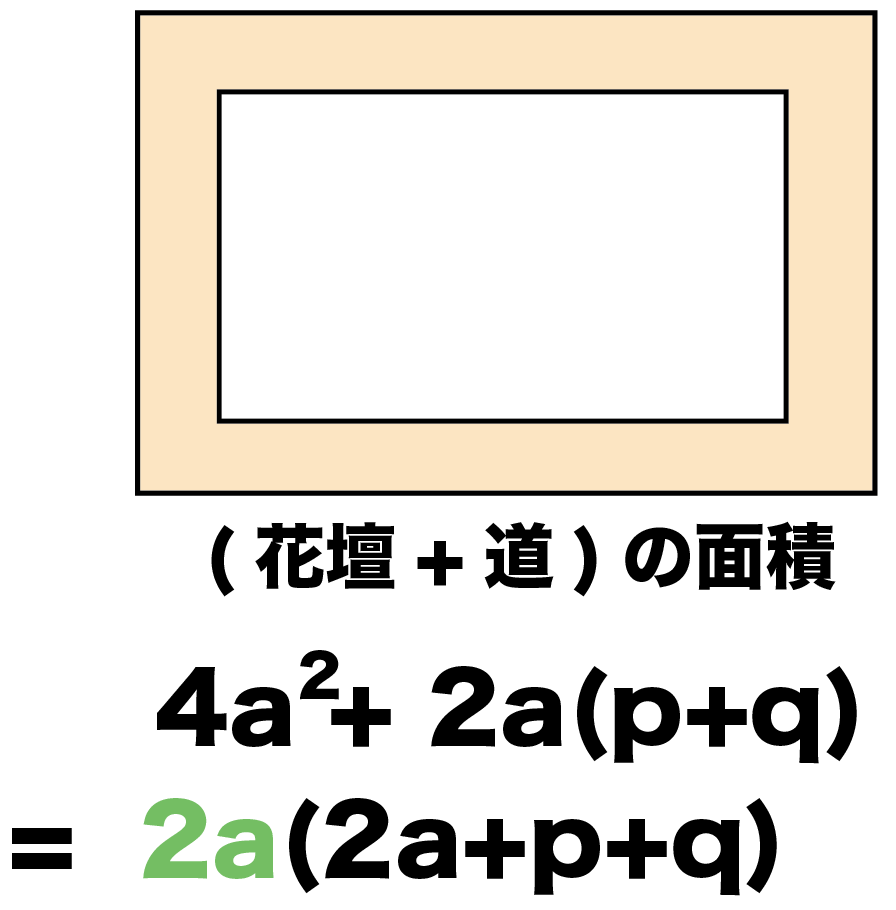
S = 4a^2 + 2a(p+q)
だったよね??
こいつを共通因数2aで()くくってやると、
S = 2a(2a+p+q)
になるはず。
これで因数分解は終了さ。
Step4. 代入する
「道幅の面積S」に「道の真ん中を通る線L」を代入しよう。
Step2で求めたLは、
L = 2 (2a + p + q)
だったよね??
じつは、この、2a+p+qに注目してほしいんだ。
これ、Sを因数分解してできた文字といっしょだね。
だから、もし、
Lの式を(2a + p + q)についてとければSに代入できそうだね。
さっそく、Lの式を(2a+p+q)についてとくと、
2a + p + q = L÷2
になるね。
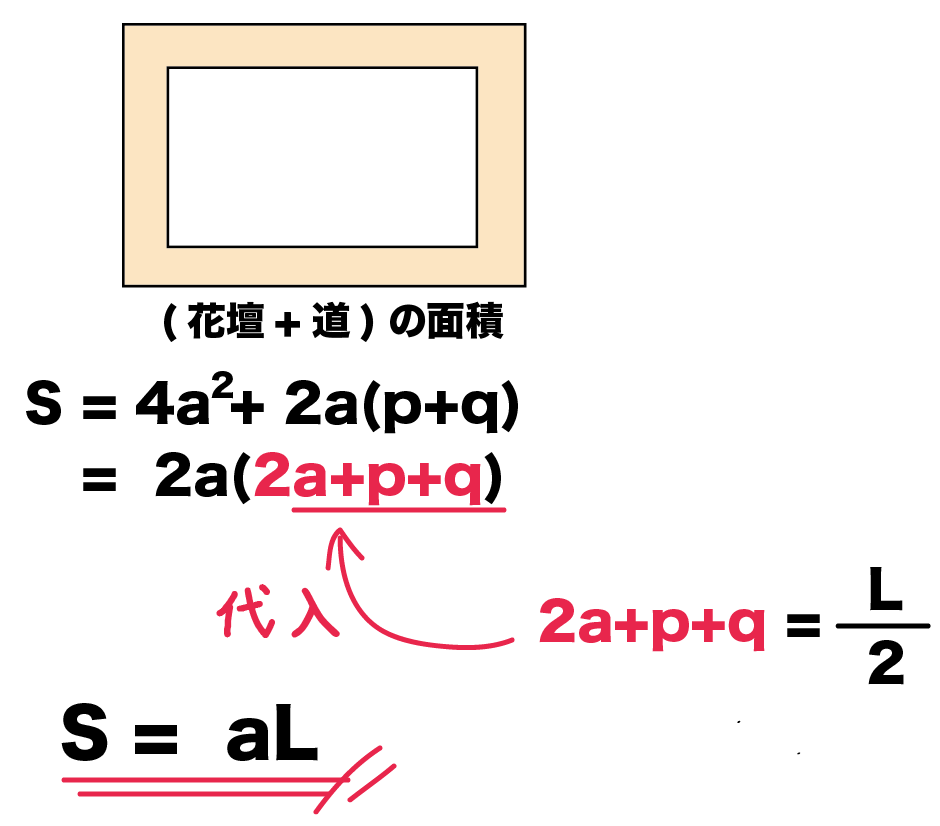
これを道幅面積Sの式に代入すると、
S = 2a(2a+p+q)
= 2a × L÷2
= aL
になるね!
これで「S = aL」を証明できちゃったね!
まとめ: 式の計算の利用の図形の証明は「展開」と「因数分解」で突破!
式の計算の利用??
花壇とか道幅とかめんどそう??
だけどね、使ってるのはシンプルにこの2つなんだ。
- 展開の公式
- 因数分解の公式
基本をおさえて証明を撃破していこう!
そんじゃねー
Ken