【高校数学】実数の意味とは何かわかりやすく解説してみた〜見分け方もマスター〜

高校数学で二次方程式を勉強していると、3秒に1回ぐらい目にするのが
実数(じっすう)
という言葉だ。
一体この「実数」とはどんな数なのか??
今日はその実数の意味をわかりやすく解説していくぞ。
実数の意味とはわかりやすく言うと?
ズバリ実数とは、
有理数と無理数を合わせた数のこと
だ。
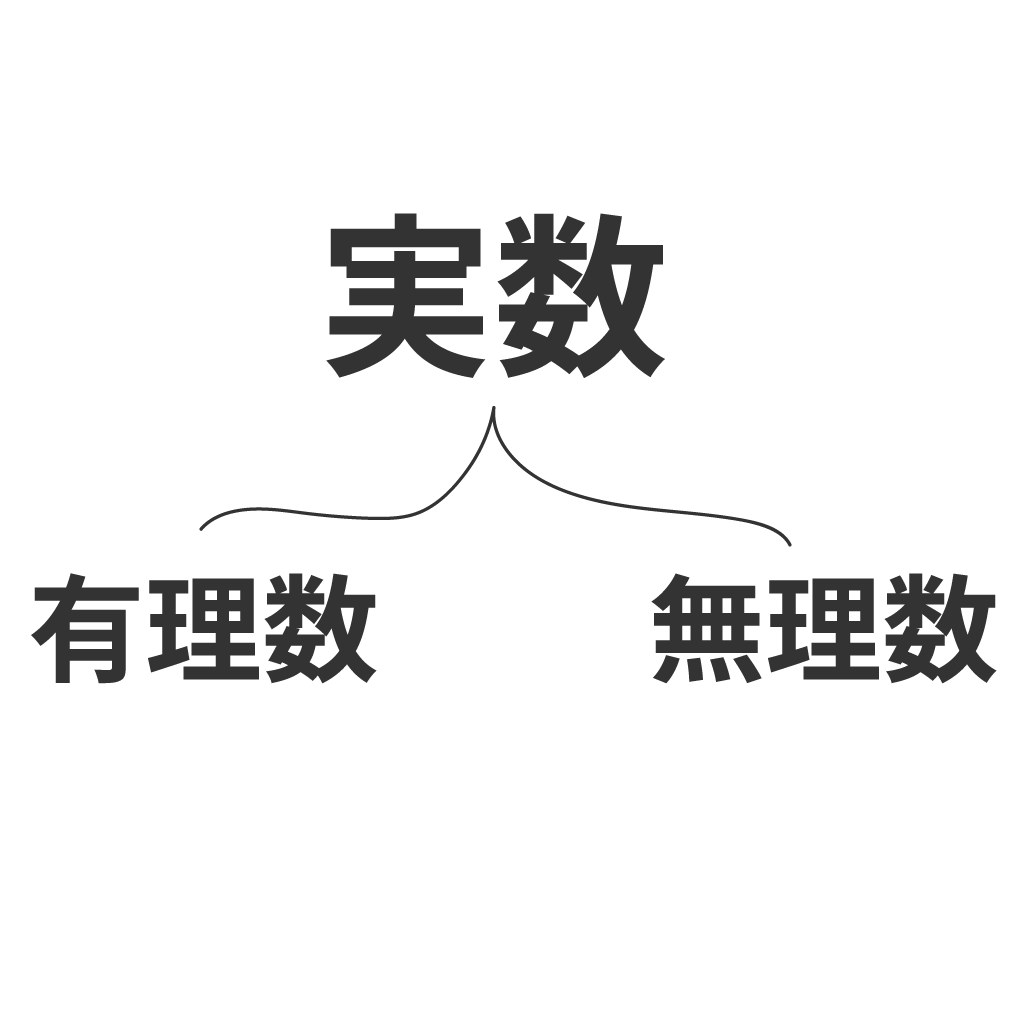
有理数と無理数は中学数学で勉強してきたよな?
ちょっと目が泳いだやつもいるだろうから、念のために復習しておこうか。
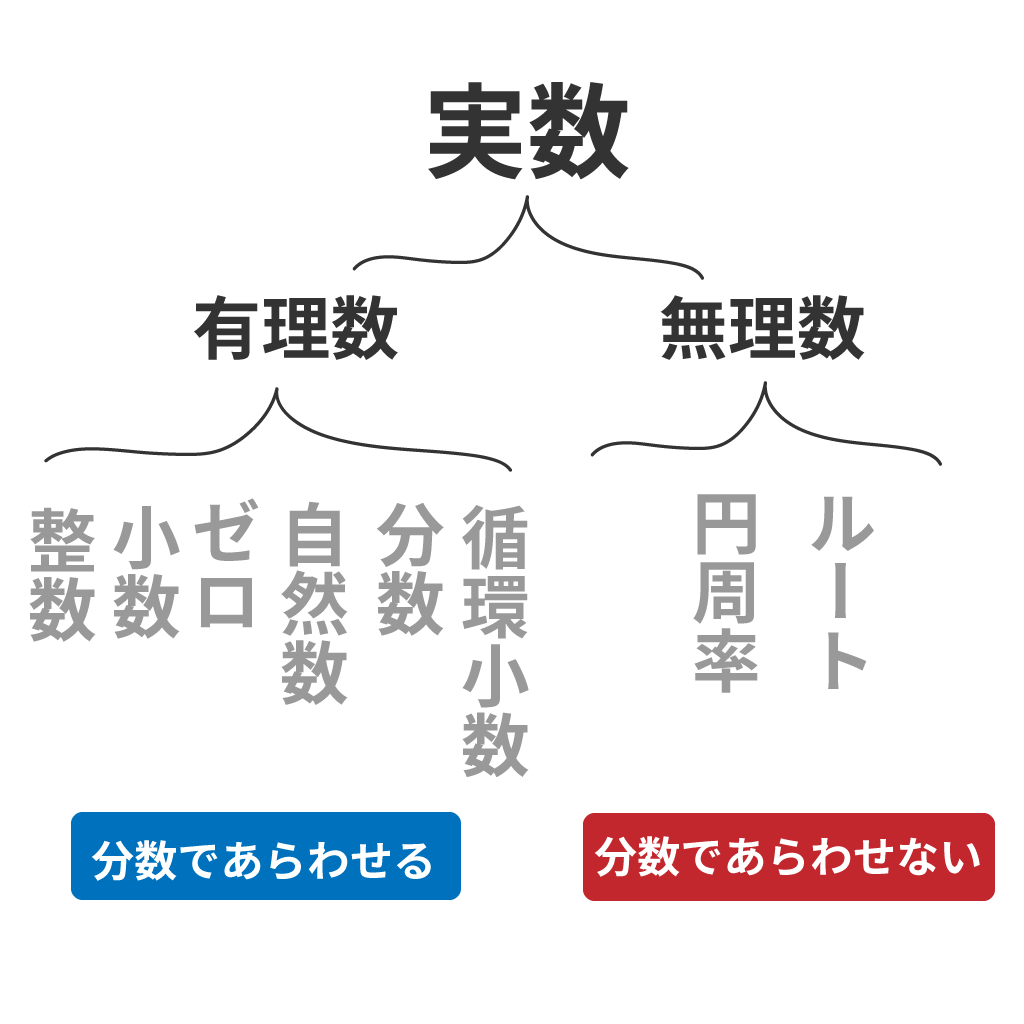
有理数とは、
分数で表せる数
だったな。
例えば、有理数の具体例には次のやつがあるぞ。
- 整数
- 有限小数
- 自然数
- 0
- 循環小数
どいつもこいつも頑張れば分数で表すことができるからな。
一方、無理数とは、
分数で表せない数のこと
だ。例えば、平方根(ルート)とか、円周率のπバイとか、そういった数は無理数だったことを思い出してくれ。
この無理数というやつは、
循環しない無限小数
だったこともついでに思い出してくれよな。つまり、無理数というやつは、小数点の続き方に規則性がないんだ。
たとえば、円周率πは、
3.1415926535…..
と無限に続いていくが、その続き方に規則性はない! だから、円周率を暗記することが一発芸になりうるわけさ。規則性あったら暗記するの楽だもんな。
という感じで、ここまでの流れをまとめておこう。
実数とは、
有理数と無理数を合わせた数
だから、
有理数も実数だし、無理数も実数なんだ。
実数以外の数なんてあるの?
でも、こう思っちゃいないか。
「私の知ってる、想像できるすべての数は実数なのかも…」
さすが、鋭いな。
実数というものは、
実際に存在するすべての数なんだ。だから、お前が頭で想像できる数字っていうのは、だいたい実数だ。
それじゃあ、実数以外の数なんてあるのか??
実際に存在していない「幻の数」なんてものは、この世にあるんだろうか。
じつは、人間の数学界では、そんな実数ではない幻の数があるんだな。
例えば、これから先、数学を勉強し続けたら巡り合うことになる
虚数(きょすう)
ってものがある。
虚数は、実際に存在しない数の具体例の1つだ。
その虚数の具体例をあげよう。
$$\sqrt{-1}$$
つまり、2乗したら「-1」になる数だ。
よーーく考えてみろよ、そんなのありえないよな?
だって、ある数に2乗、つまり2回かけたら、絶対正の数になっちまうからな。
ある数がプラスだろうとマイナスであろうと、2回かけたら答えはプラスだ。
なのに、2乗してもマイナスになる・・・・数・・・・なんて絶対にありえねえ!
でも、人間界ではそんなありえない数を無視せず「虚数」と名付けたんだ。
こんな感じで、人間の数学界では実数以外の数も取り扱っていくことを頭に入れとこう。
実数の見分け方
実数以外の数も数学界にあるとなると、
実数の見分け方
が気になってこないか??
そこで、そんなお前らのために、とっておきの実数の見分け方を伝授してやる。
それは、
数直線でその数がありそうなところを指で示せたら実数!
という見分け方だ。

例えば、0。
0の位置は数直線でここら辺ってわかるよな。
負の数の- 3とかもあそこら辺だし、分数の$\frac{1}{3}$もあそこら辺だろう。
無理数の円周率π・・・・・もいける。
だいたい3.14だからあそこら辺だし、ルートの2だって「ひとよひとよにひとみごろ」で1.4付近だとわかる。正確じゃなくてアバウトでいいんだ。
とにかく、その数がありそうなところを、数直線上で指で示せたら、そいつは実数だと覚えておこう。
さっき紹介した虚数の「$\sqrt{-1}$」。
こいつが数直線でありそうなところは・・・・・ないよな。
うん、いくら目に力を入れても到底浮かんでこねえ。
こんな感じで、ある数が実数かどうか問われたら、数直線を想像するんだ。
そして、その数がありそうなところを矢印で示せるかで見分けていこう。

それじゃあ!



