【高校数学 I 】二次関数の対称移動の公式（基本編）

クマシロ

よう、消しゴムの妖精のくましろだ。

高校数学では二次関数を平行移動してきたな。

tomo

2024.07.15

二次関数を平行移動させて重ねて一致させる問題の解き方

https://text.tomo.school/overlapping-quadratic-functions

よう、消しゴムの妖精のくましろだ。認証、待ちだわ二次関数

y = a x^{2} + b x + c

ってさ、いろんな形してるよな。こんなんだって、あんなのだってあるだろうし。じつは、この二次関数のグラフの形は、

a

の大きさによって変化するんだ。

a

が大きければを狭い開き具合になるし、逆に小さければ、緩やかな開き具合になるってことよ。ということは、

a

が同じ二次関数ならば、生えてる場所が同じだけで放物線の形は一緒。ということは、ということは。

a

が同じ二次関数ならば、片方の二次関数を平行移動させれば、もう1つ...

だが、しかし。

高校数学は二次関数を平行移動するだけじゃおさまらねぇ。

なんと、

二次関数を対称移動させてくんだ。

対称移動とは復習すると、

ある直線を軸として折り返して移動させること

だったよな。

例えば、このこのような放物線があったとしよう。

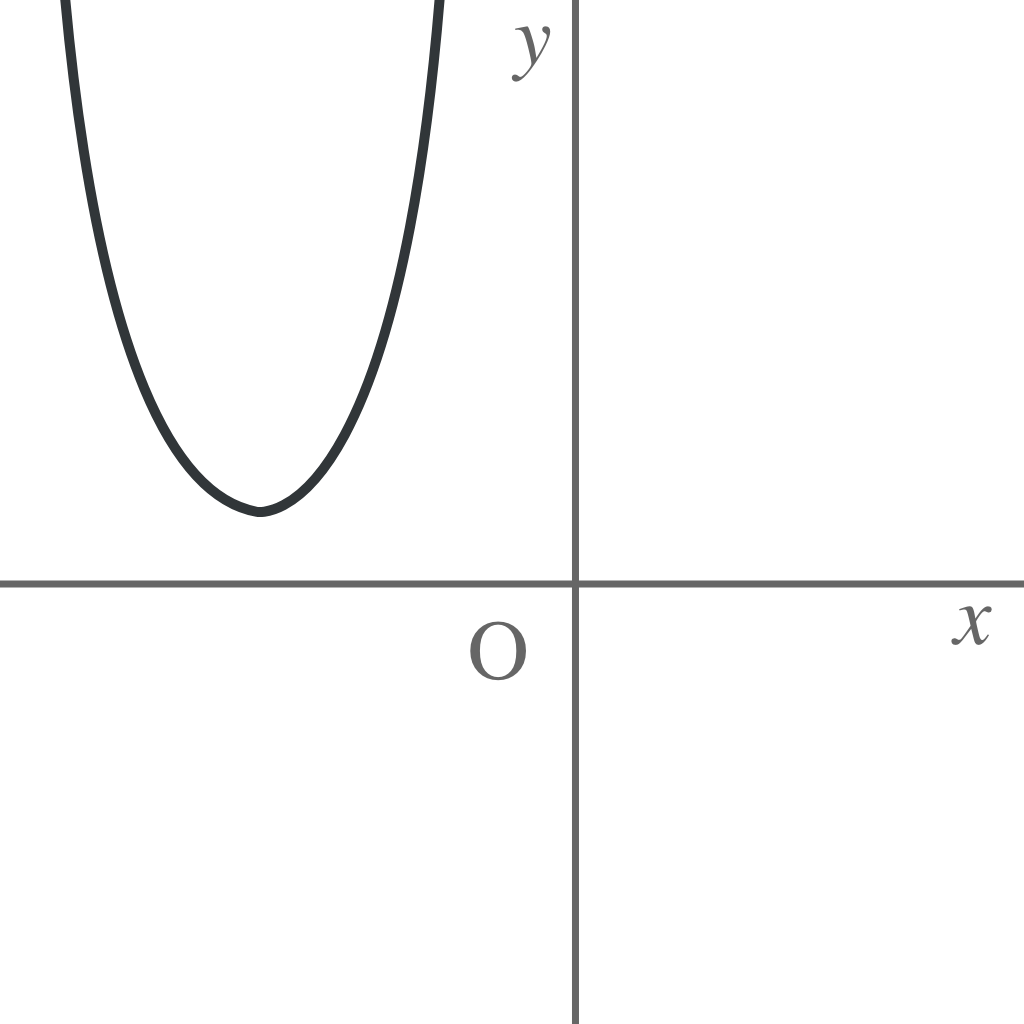
x軸に対して対称移動させたら、こうなって、

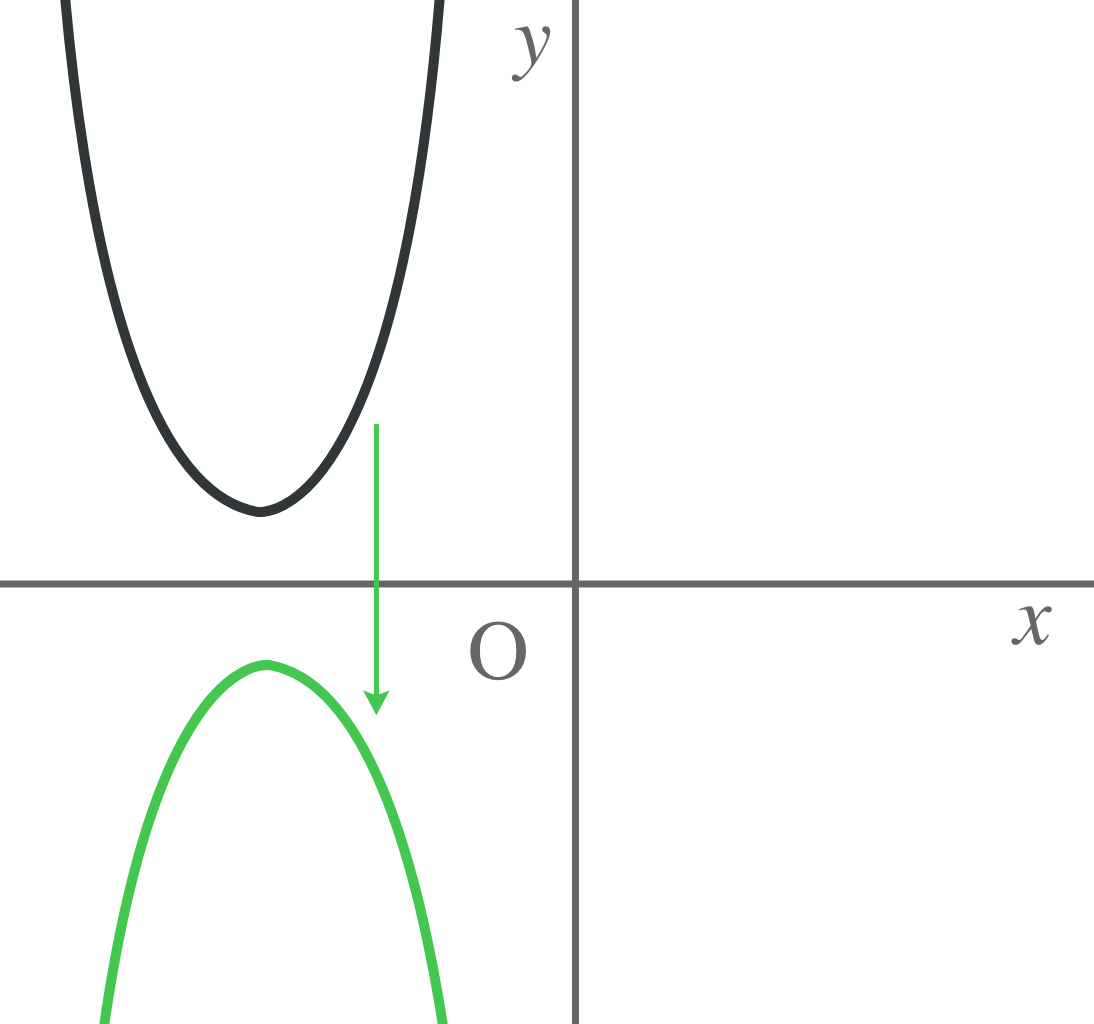
$y$ 軸に関して対称移動させらこのようになる。

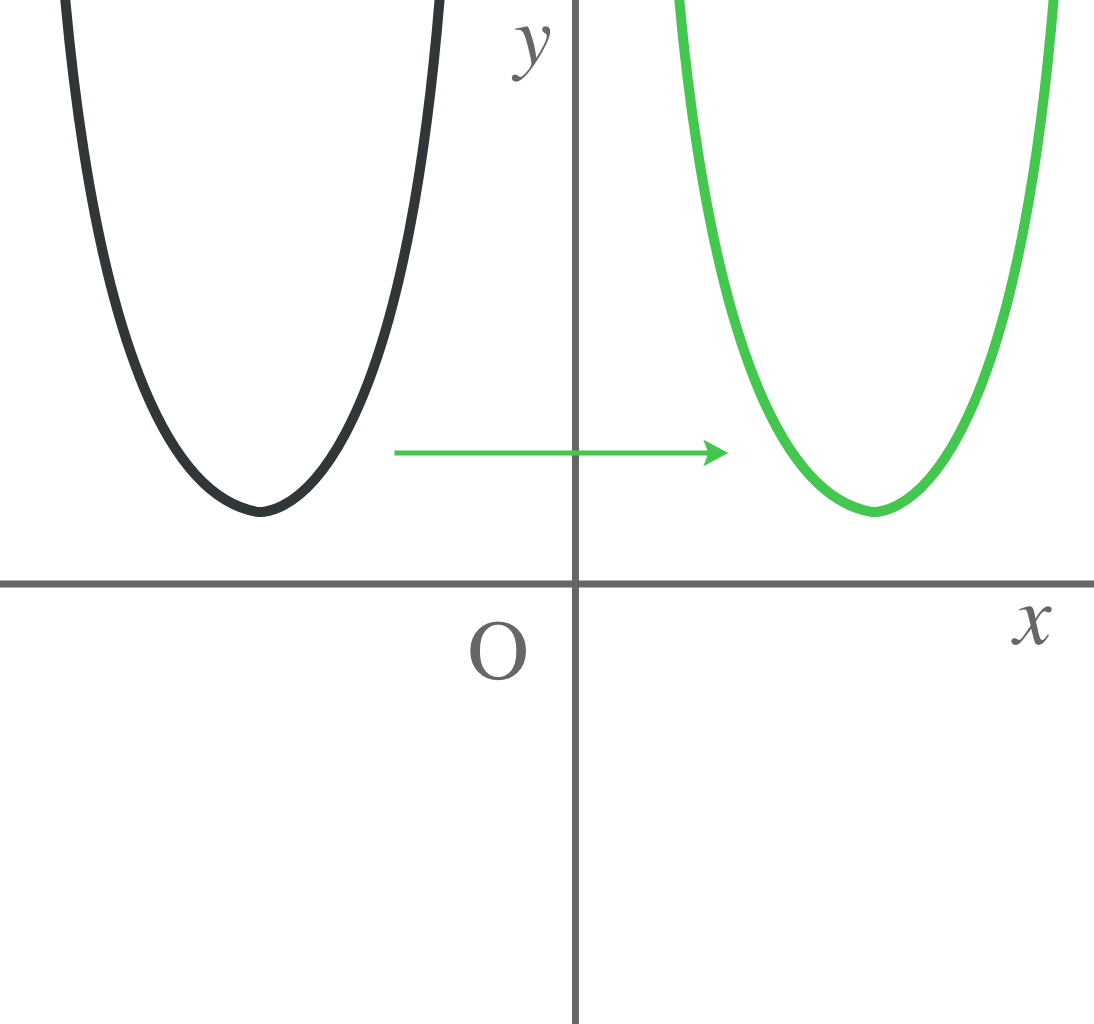
原点に対してだったら、次のようになる。

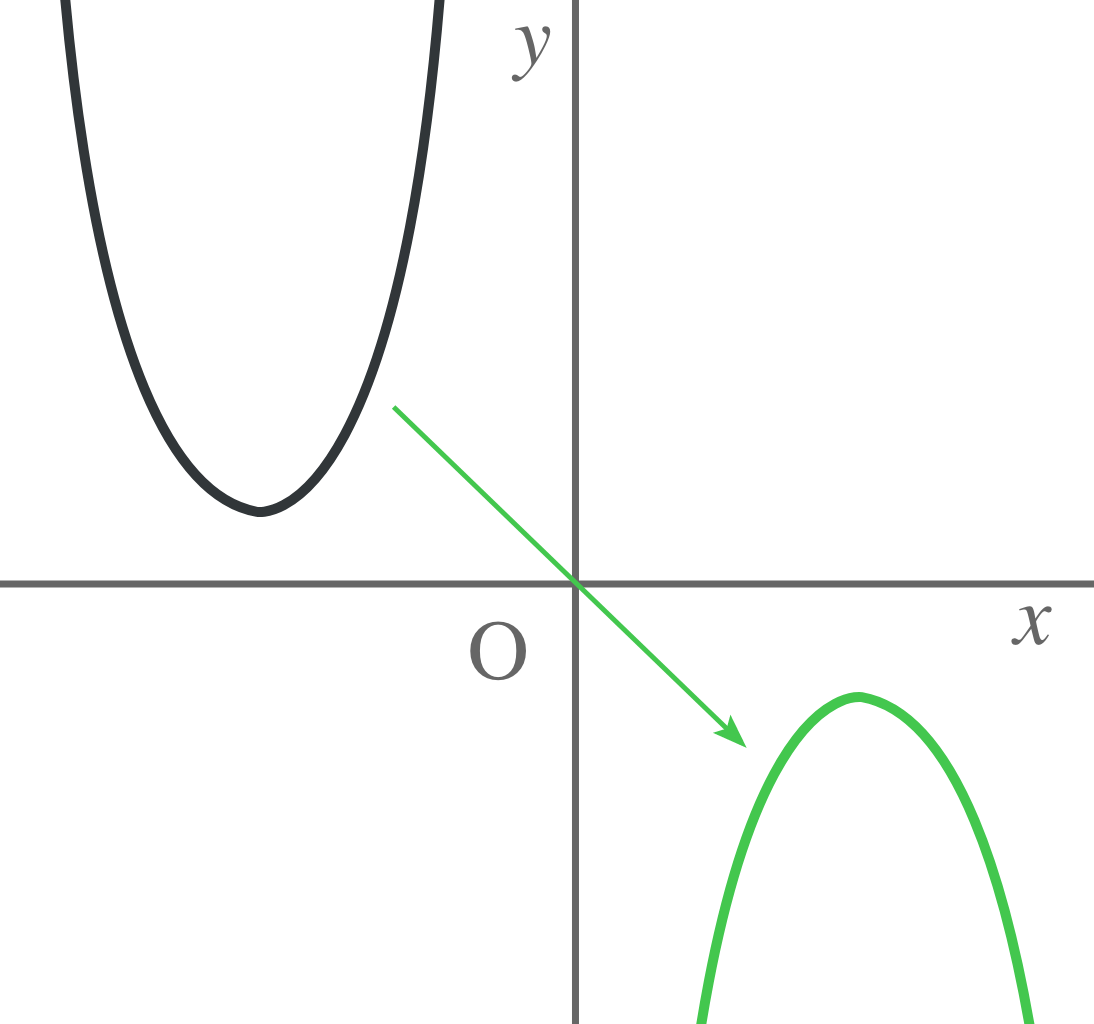
つまり、対称となる直線を折り目として座標平面をおった時に重なる放物線が、対称移動した結果できる放物線ってわけよ。

ここではその二次関数の対称移動のうち、基本の公式を紹介するぞ。

基本の公式は次の3パターンだ。

$x 軸について対称移動$
$y 軸について対称移動$
$原点について対称移動$

この3パターンマスターするため、ここでは

$y = 2 x^{2} + 5 x + 1$

という二次関数をそれぞれのパターンで対称移動させていこうな。

$x$ 軸に関して対称移動させる方法

まず $x$ 軸だな。

$x$ 軸に関して放物線を対称移動させる、ってことは次のようになるんだ。

この図からわかる通り、

$y$ の値の符号が逆転しているな？

一方で、 $x$ の値は対称移動させても同じ、ってこともわかるはずだ。

ということで、放物線 $y = 2 x^{2} + 5 x + 1$ をx軸に関して対称移動させてやった場合、

$y$ の値の代わりに $- y$ を代入してやればいいわけだ。

さっきの二次関数 $y = 2 x^{2} + 5 x + 1$ でいうと、x軸に関して対称移動させると次のようになるな。

$y = 2 x^{2} + 5 x + 1$

$- y = 2 x^{2} + 5 x + 1$

$y = - 2 x^{2} - 5 x - 1$

$y$ 軸に関して対称移動させる方法

続いて、 $y$ 軸に関して対称移動させるぞ。

安心しろ。

$x$ 軸に関する対称移動と同じ考えで充分だ。

放物線を $y$ 軸に関して対称移動させたら、次の図のようになるよな。

$x$ の符合が逆転する一方、今度は $y$ がそのまま同じってわけよ。

ゆえに、二次関数の式の $x$ の代わりに $- x$ を代入した二次関数を求めりゃいいのな。

さっき見てきた二次関数 $y = 2 x^{2} + 5 x + 1$ を $y$ 軸に関して対称移動させると、次のようになる。

$y = 2 x^{2} + 5 x + 1$

$y = 2 (- x)^{2} + 5 (- x) + 1$

$y = 2 x^{2} - 5 x + 1$

原点に関して対称移動させる方法

最後は原点に関して対称移動させる方法だ。

原点に関して放物線を対称移動させると、次の図のようになる。

話が原点に及ぼうが、ビビることはないぞ。

原点の場合、

$x$ 軸と $y$ 軸に関してそれぞれ対称移動させる方法を融合させればいいんだ。

つまり、 $x$ 軸に関して対称移動させた後、 $y$ 軸に関して対称移動。

この2ステップを踏んでやれば、気づいたら結果的に、原点に関して対称移動させたことになるのさ。

「原点に関して対称移動」とはつまり、

$x$ と $y$ の両方の符合を逆転させればいいってわけよ。

もはやお馴染みとなった二次関数 $y = 2 x^{2} + 5 x + 1$ を原点に関して対称移動させるぞ。

$x$ と $y$ の代わりに $- x$ と $- y$ を代入してやればいいんだ。

すると、こうなる。

$y = 2 x^{2} + 5 x + 1$

$- y = 2 (- x)^{2} + 5 (- x) + 1$

$- y = 2 x^{2} - 5 x + 1$

$y = - 2 x^{2} + 5 x - 1$

これで原点だろうが、二次関数を対称移動できるようになったな！

以上、二次関数を対称移動させる方法だ。

$x$ と $y$ の符号を変えるだけだから、そんな難しいことなかったな。

だが、ここまでは基本技だ。組体操でいうと、サボテンってとこだな。

クマシロ

次は二次関数の対称移動の応用問題を一緒に解いていこう。

それじゃあなぁ！

x軸に関して対称移動させる方法

y軸に関して対称移動させる方法

原点に関して対称移動させる方法

$x$ 軸に関して対称移動させる方法

$y$ 軸に関して対称移動させる方法