二次関数を平行移動させて重ねて一致させる問題の解き方

クマシロ

よう、消しゴムの妖精のくましろだ。認証、待ちだわ

二次関数$y=a{x}^2+bx+c$ってさ、 いろんな形してるよな。

こんなんだって、

あんなのだってあるだろうし。

じつは、この二次関数のグラフの形は、

$a$の大きさによって変化するんだ。

$a$が大きければを狭い開き具合になるし、

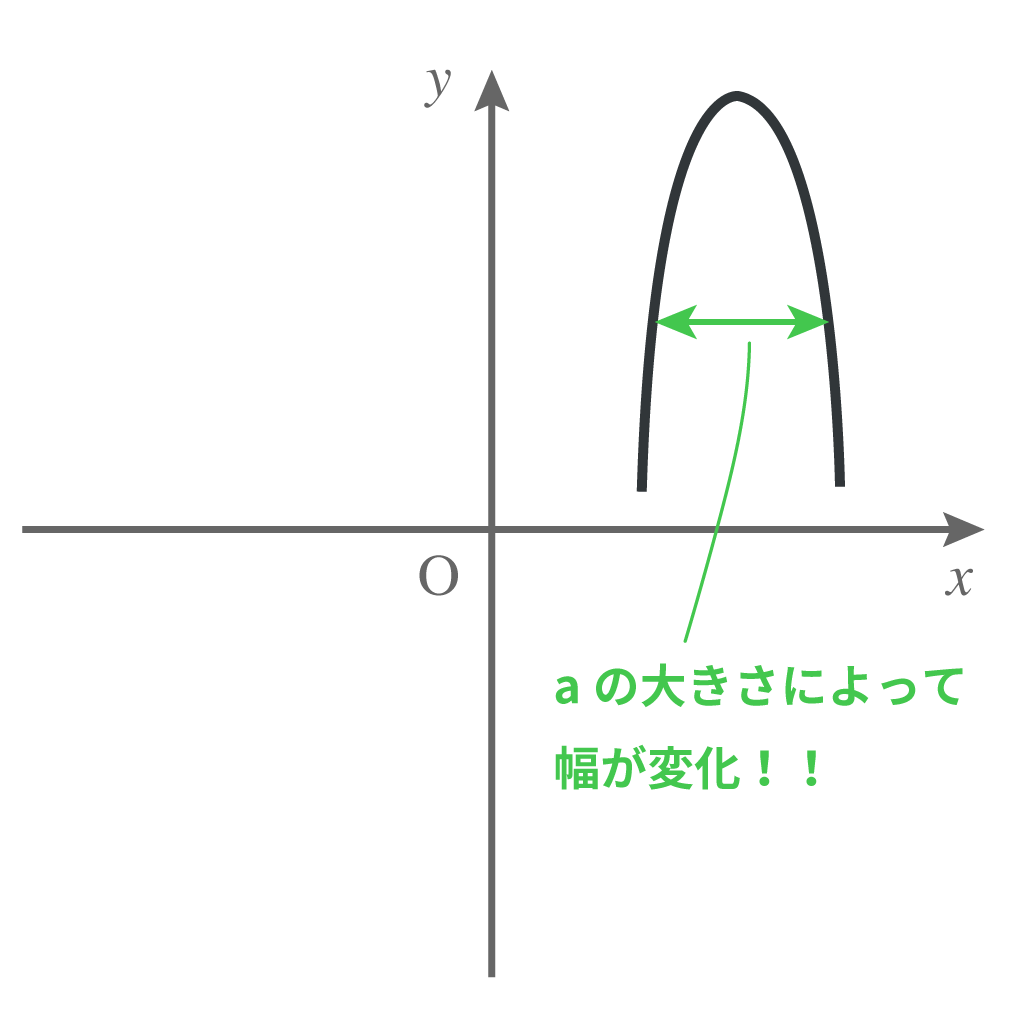
逆に小さければ、緩やかな開き具合になるってことよ。

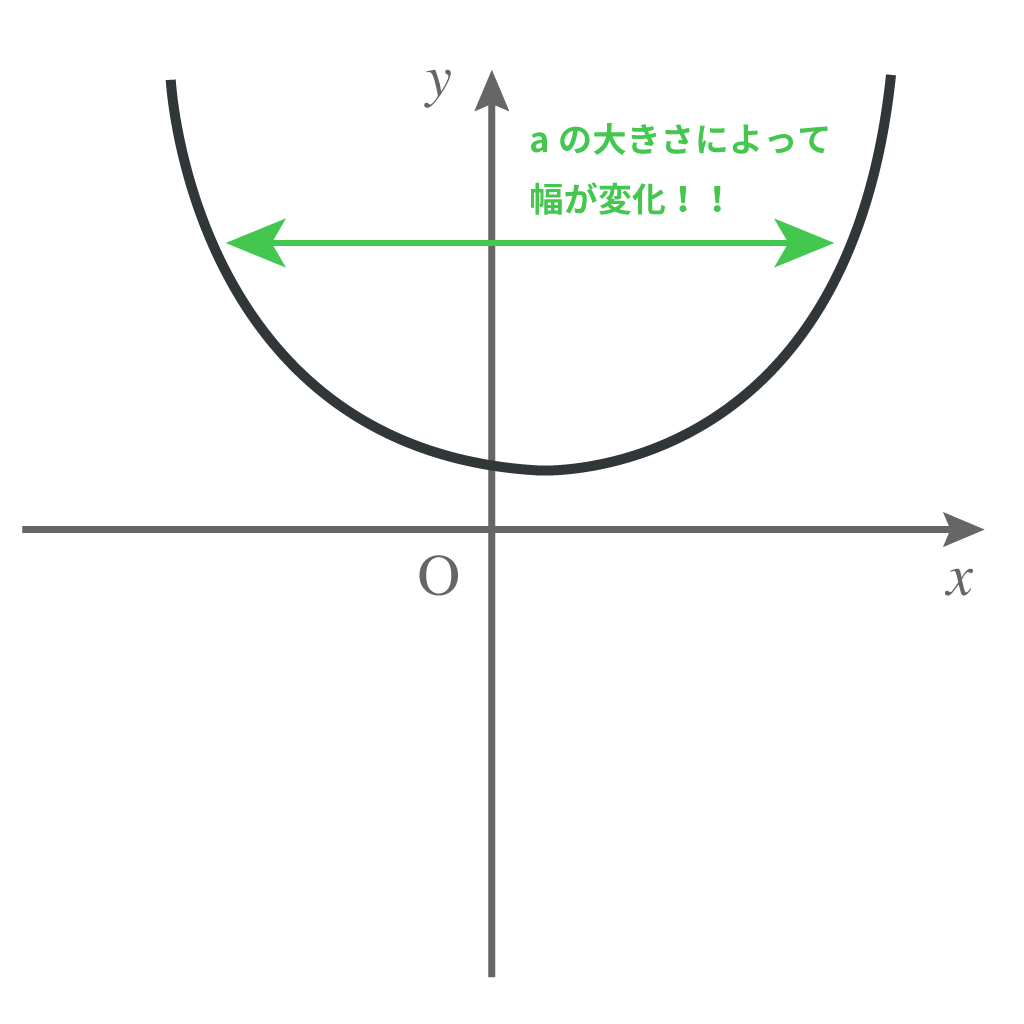
ということは、$a$が同じ二次関数ならば、生えてる場所が同じだけで放物線の形は一緒。

ということは、ということは。

$a$が同じ二次関数ならば、片方の二次関数を平行移動させれば、もう1つの二次関数に重ねて一致させられるわけだ。

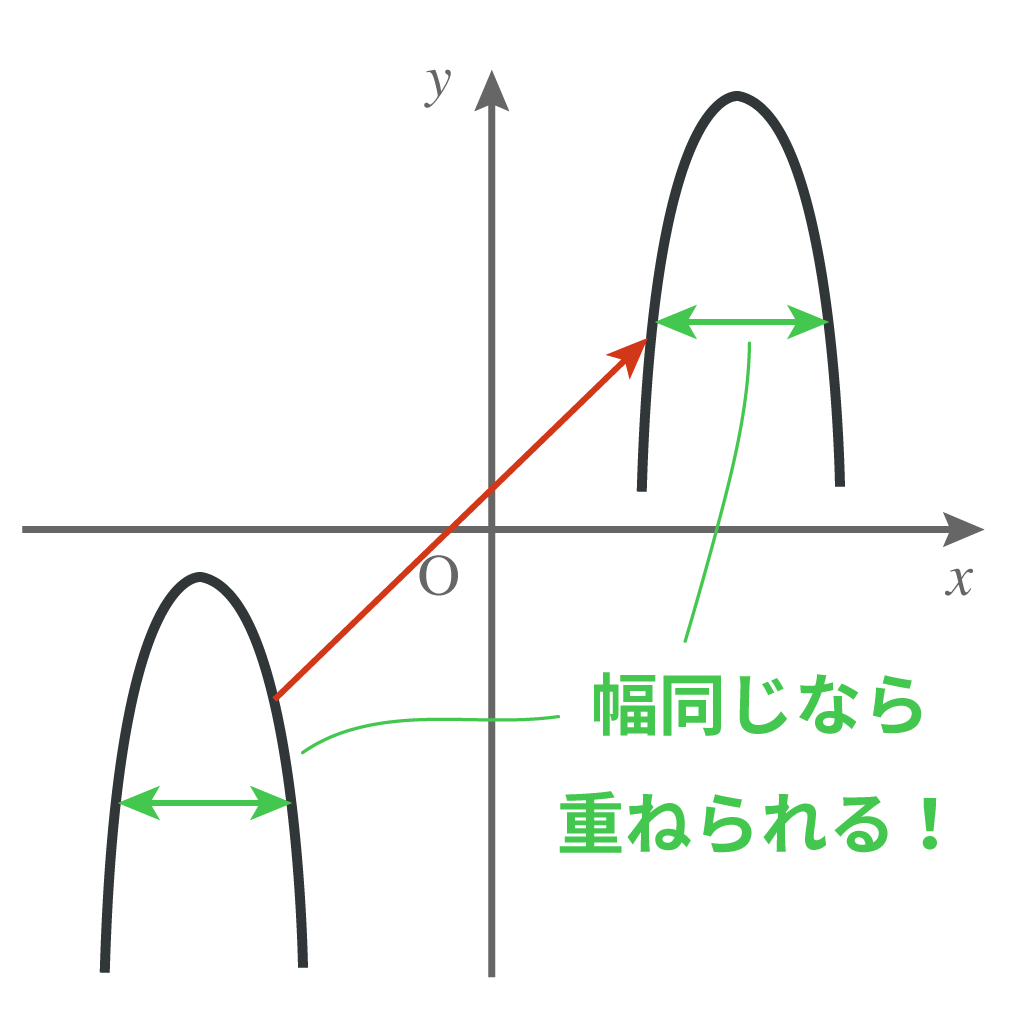
どうだ？

やってみたくなっただろう？

この好奇心を先読みしてたんだろうな、きっと。

高校数学では、

二次関数を平行移動させて重ねる・一致させる問題がよく出てくるんだ。

たとえば、次の問題な。

今日はこの問題の解き方を勉強していこう。

二次関数を平行移動させて重ねて一致させる問題の解き方

この手の問題の解き方が次の3ステップだ。さっきの例題を一緒に解いていくぞ。

それぞれの二次関数を平方完成

まずはお馴染みとなった動作からだな。

2つの二次関数をそれぞれ平方完成させて頂点を求めよう。

tomo

2024.07.07

平方完成で二次関数の軸と頂点を求める方法

https://text.tomo.school/quadratic-function-axis-vertex-square-completion

 よう、消しゴムの妖精のくましろだ。 前回、二次関数の軸と頂点の基本の求め方を勉強してきたよな。 これでこの基本形、$$y=a(x-p{)}^2+q$$になっている二次関数の軸と頂点なら容易にゲットできるようになったわけだ。でもさ、いつでも、どんなときも、この基本形に二次関数なってるわけはないよな？例えば、次の二次関数を見てくれ。$$y=5x^2+2x+4$$この二次関数、基本形にぜんぜんはまってないよな。そんな二次関数の軸と頂点を求めるのは諦めるしかないのか？ いや、そんなことは無い。これから紹介する、平...

二次関数の軸・頂点を求める公式を覚えているやつは、このステップをスキップしてもいい。

tomo

2024.07.09

【高校数学 I 】二次関数の軸と頂点を求める公式と覚え方

https://text.tomo.school/formula-axis-vertex-quadratic-function

 よう、消しゴムの妖精のくましろだ。 前回、平方完成で二次関数の軸と頂点を求めるやり方、勉強してきた。 でもさ、毎回平方完成してしないとなんて、大変不便だよな。そんなことを思っちゃったお前に朗報だ。じつはな、二次関数の軸と頂点を求める3秒で求められる公式があるんだ。 それは次のものだ。$y=a{x}^2+bx+c$ という二次関数があったとしよう。このとき、$\mathrm{軸}=-\frac{b}{2a}$$\mathrm{頂}\mathrm{点}(-\frac{b}{2a},-\frac{b^2-4ac}{4a})$なんだ。 例えば、次の二次関数があったとしよう。$$y=2x^2+5x+17$$この二次...

公式を忘れた、もしくは、平方完成力に自信があるやつは、このステップからやっていこう。

さっきの例題で、2つの二次関数をそれぞれ平方完成させるぞ。

$y=3x^2+5x+7$

$y=3(x^2+\frac{5}{3}x)+7$

$y=3\{(x+\frac{5}{6}{)}^2-\frac{5^2}{6^2}\}+7$

$y=3(x+\frac{5}{6}{)}^2-\frac{25}{12}+7$

$y=3(x+\frac{5}{6}{)}^2-\frac{59}{12}$

$y=3x^2-11x$

$y=3x^2-11x$

$y=3(x^2-\frac{11}{3})x$

$y=3\{(x-\frac{11}{6}{)}^2-\frac{{11}^2}{6^2}\}$

$y=3(x-\frac{11}{6}{)}^2-\frac{121}{12}$

頂点を求める

平方完成は無事に通過したな？

次はこの形から二次関数の頂点を求めていくぞ。

二次関数の基本形「$y=a(x-p{)}^2+q$」の頂点は、

$$\mathrm{頂}\mathrm{点}(p,q)$$

だったよな。

だから、例題の2つの二次関数の頂点は次のようになる。

$y=3x^2+5x+7$の頂点

平方完成すると、$y=3(x+\frac{5}{6}{)}^2-\frac{59}{12}$になるから、

$(-\frac{5}{6},\frac{59}{12})$

$y=3x^2-11x$

平方完成すると、$y=3(x-\frac{11}{6}{)}^2-\frac{121}{12}$になるから、

$(\frac{11}{6},-\frac{121}{12})$

頂点の求め方の公式を覚えていたやつは、公式に$a\mathrm{・}b\mathrm{・}c$を代入して二次関数の頂点をそれぞれ求めておくれ。

頂点が求めれば公式を使うが何しようがオッケーだ。

頂点の差を求める

最後に、2つの頂点の差を見つけてゲット。

その頂点のズレを埋めてやるように、二次関数を平行移動させてやればグラフが一致するはずさ。

ここでのコツは、

座標平面に書き出す！

だ。実際に書いてみると見えてくるものもあるのさ。

さて。

1つ目の二次関数の頂点を、2つ目の二次関数の頂点に、一致させるためにはどうすればいい？？

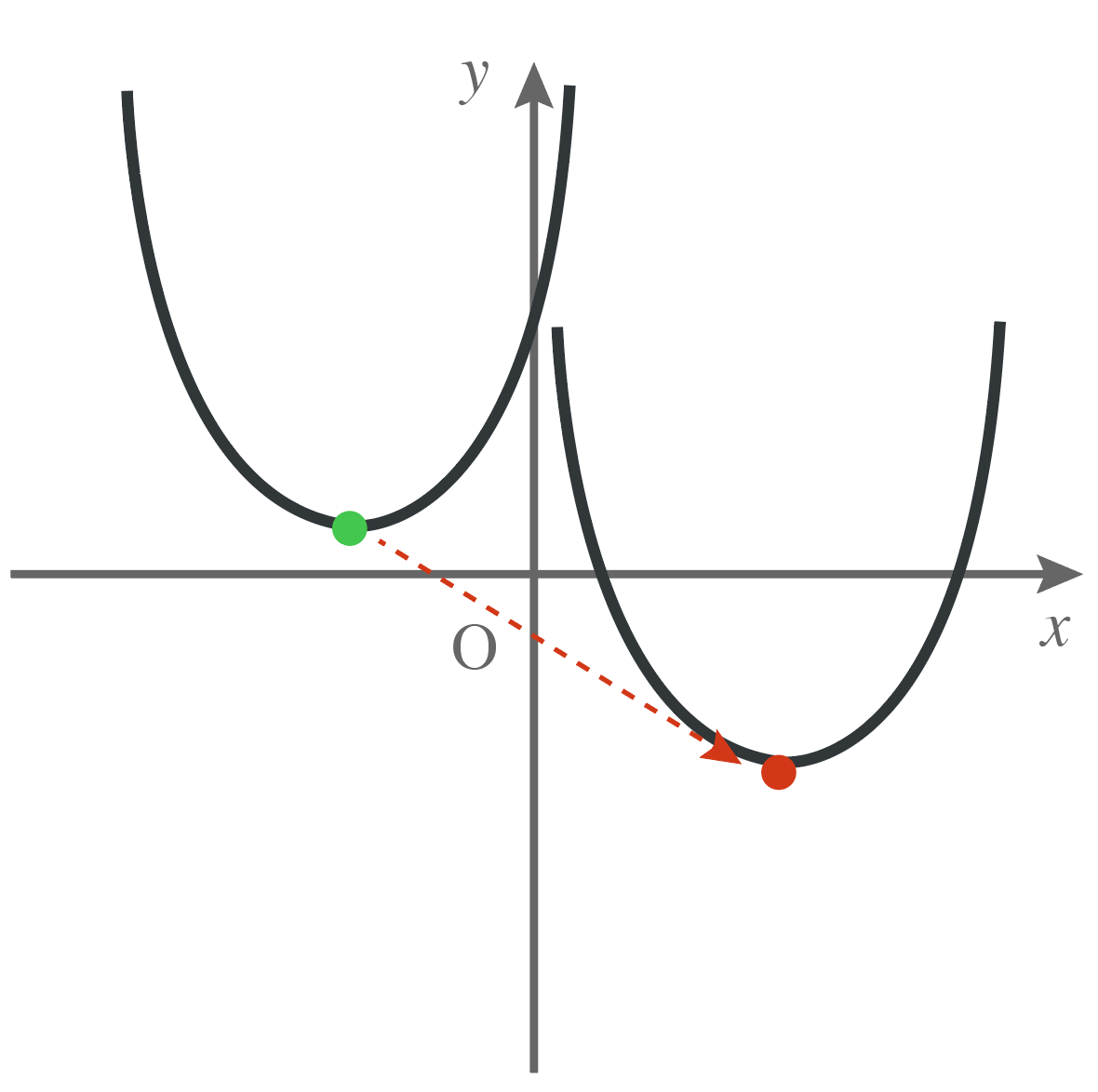
そう、

（2つ目の二次関数の頂点 ）と（1つ目の二次関数の頂点）の差の分だけ移動させりゃいいよな。

つまり、

（2つ目の二次関数の頂点 ）-（1つ目の二次関数の頂点）

の分だけ、移動させりゃ、2つの二次関数は一致するはずだ。

例題の二次関数の頂点たちは、

• 1つ目の頂点：$(-\frac{5}{6},\frac{59}{12})$
• 2つ目の頂点：$(\frac{11}{6},-\frac{121}{12})$

だったよな？

（2つ目の二次関数の頂点 ）-（1つ目の二次関数の頂点）

を$x\mathrm{・}y$座標それぞれ計算してやろう。

$x$座標

$\frac{11}{6}-(-\frac{5}{6})$

$=\frac{16}{6}$

$=\frac{8}{3}$

$y$座標

$\frac{121}{12}-\frac{59}{12}$

$=-\frac{180}{12}$

$=-15$

ってことで、$x\mathrm{方}\mathrm{向}$に$\frac{8}{3}$、$y\mathrm{方}\mathrm{向}$に$-15$移動させれば2つの二次関数は重なるはずさ。

以上、二次関数を平行移動させて一致させる問題の解き方だ。

解けるようになったな？

クマシロ

次は3点を通る二次関数の求め方を勉強していこう。

そじゃぁなぁ！