平方完成で二次関数の軸と頂点を求める方法

クマシロ

よう、消しゴムの妖精のくましろだ。

前回、二次関数の軸と頂点の基本の求め方を勉強してきたよな。

tomo

2024.06.16

【高校数学 I 】二次関数の軸と頂点の求め方（基本編）

https://text.tomo.school/quadratic-function-axes-vertices

よう、消しゴムの妖精のくましろだ。東か南か・・・南だな高校生では中学数学と同じように二次関数を勉強していくぞ。二次関数とは復習すると、

x

の次数が「2」の関数だったよな。中学数学では

y = a x^{2}

っていう二次関数を集中的に勉強してきたことを思い出してくれ。ここで思い出して欲しいのは軸頂点放物線というキーワードだ。二次関数のグラフは、物体を真上に投げたときに描かれる線のように変化するから「放物線」といって、左右対称になっていたな。そして、こ...

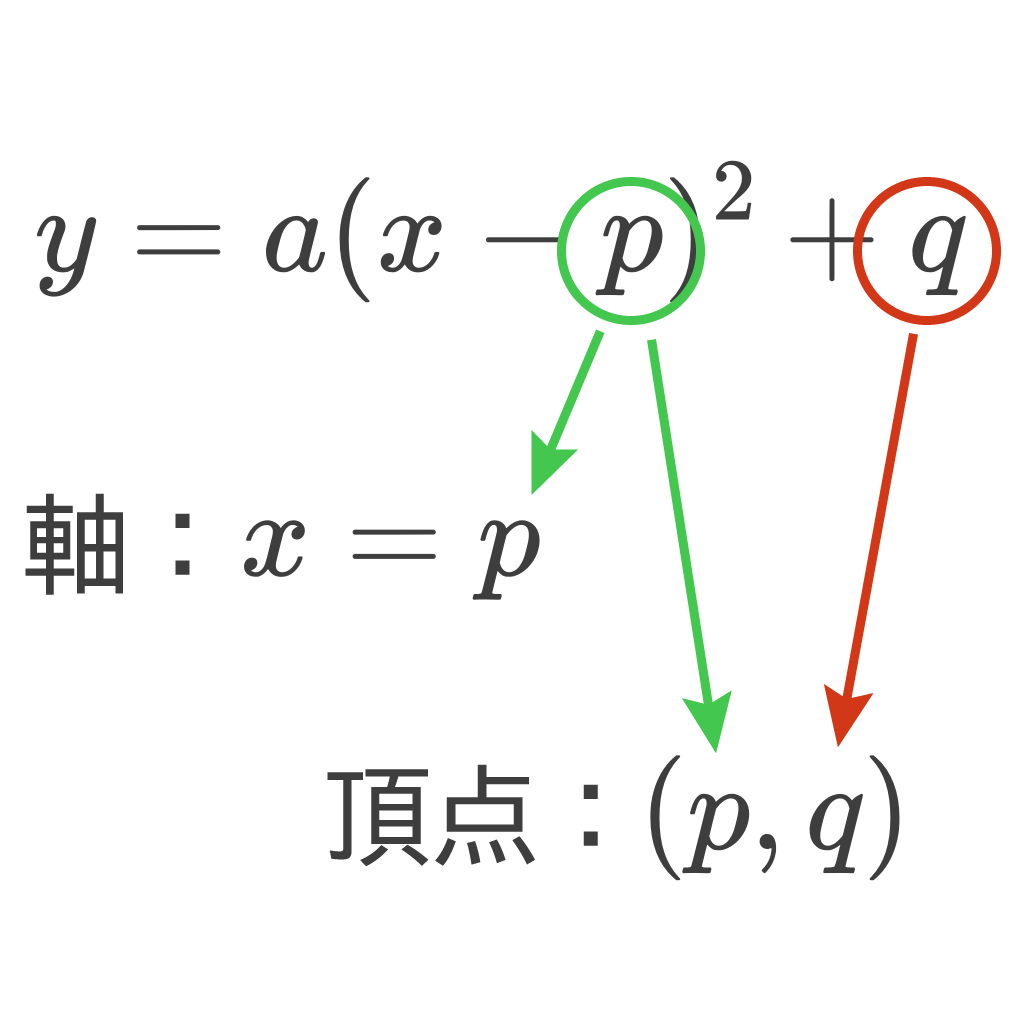
これでこの基本形、

$y = a (x - p)^{2} + q$

になっている二次関数の軸と頂点なら容易にゲットできるようになったわけだ。

でもさ、いつでも、どんなときも、この基本形に二次関数なってるわけはないよな？

例えば、次の二次関数を見てくれ。

$y = 5 x^{2} + 2 x + 4$

この二次関数、基本形にぜんぜんはまってないよな。

そんな二次関数の軸と頂点を求めるのは諦めるしかないのか？

いや、そんなことは無い。

これから紹介する、

平方完成による二次関数の軸と頂点の求め方

を使えば、どんな二次関数が来ても軸と頂点を求められるようになるんだ。

平方完成を使った二次関数の軸と頂点の求め方

えっ。

平方完成ってなにー？

だと・・・？

平方完成は中学数学の二次方程式で勉強した内容だったな。

tomo

2016.08.27

平方完成による二次方程式の解き方がわかる3ステップ

https://text.tomo.school/completing-square-equation

平方根の二次方程式の解き方ってどうやるの？？こんにちは！Drリードだよ。二次方程式の解き方にはたくさん種類があったね。今日はもう1つ解き方を勉強していくよ。その名も、平方完成をつかった二次方程式の解き方だ。この解き方は、因数分解できなくて、なおかつ、解の公式を忘れたときに使える解き方なんだよ。絶望的な状況をすくってくれるのが平方完成ってわけ。平方完成による二次方程式の解き方3ステップつぎの2次方程式の問題をといていこうか。平方完成をつかった二次方程式になれるためにね。 ...

平方とは「2乗」、同じ数を2回かけることを意味する。

つまり、「同じ数を2回かける」形になっていないものを、強引に「同じ数を2回かける」形にするのが平方完成だ。

忘れちまったやつは復習よろしくな。

さて、早速、二次関数の軸と頂点の求め方を平方完成でやってみるぞ。

さっき出てきた二次関数の例題の二次関数の軸と頂点を一緒に求めてみよう。

$y = 5 x^{2} + 2 x + 4$

次の4ステップだ。

$x^{2}$ の係数でくくる

まずは下準備だな。

二次関数の中で、

$x^{2}$ の係数

に注目してくれ。

つまり、 $x^{2}$ の前についてる数字だな。

この $x^{2}$ の係数で「 $x$ がついている項たち」をかっこでくくってやるんだ。

例題の二次関数に注目するぜ。

$y = 5 x^{2} + 2 x + 4$

$x^{2}$ の係数は・・・・

だな。で、「 $x$ がついている項たち」は

$5 x^{2}$
$2 x$

の2つだ。

ってことで、こいつらを「 $x^{2}$ の係数」の5でくくると、こうなる。

$y = 5 x^{2} + 2 x + 4$

$y = 5 (x^{2} + \frac{2}{5} x) + 4$

えっ、 $x^{2}$ の係数が「1」ならどうしたらいいかって？

その場合は、このステップを飛ばしてオッケーだ。次にいこう。

平方完成する

下準備終了。ってことで、早速平方完成やっていくぞ。

ポイントは、

$x$ がついている項だけで平方完成するってことだ。

さっきの例の二次関数では、

$(x^{2} + \frac{2}{5} x)$

だな。

それ以外の「 $x$ がついていない定数項」は脇に置いてスルー！

ってことで、 $(x^{2} + \frac{2}{5} x)$ を平方完成するぞ。

$y = 5 x^{2} + 2 x + 4$

$y = 5 (x^{2} + \frac{2}{5} x) + 4$

$y = 5 {(x + \frac{1}{5})^{2} - \frac{1}{25})} + 4$

もろもろ計算する

さて、完成した平方（ $(x + \frac{1}{5})^{2}$ ）はそのまま保存だ。

それ以外の項たちを計算してきれいにまとめるぞ。

すると、次のようになる。

$y = 5 {(x + \frac{1}{5})^{2} - \frac{1}{25})} + 4$

$y = 5 (x + \frac{1}{5})^{2} - \frac{1}{5} + 4$

$y = 5 (x + \frac{1}{5})^{2} + \frac{19}{5}$

軸と頂点を求める

これで、二次関数が基本形 $y = a (x - p)^{2} + q$ になったよな。

後はこの基本形から、

にあたる数を探し、その情報から軸と頂点の式に $p$ と $q$ を代入すればいいんだ。

さっきの例の二次関数に戻るぞ。

$y = 5 (x + \frac{1}{5})^{2} + \frac{19}{5}$

それぞれ $p$ 、 $q$ は次のようになる。

$p = - \frac{1}{5}$
$q = \frac{19}{5}$

ゆえ、軸（ $x = p$ ）と頂点（ $(p, q)$ ）は次のようになる。

軸： $x = - \frac{1}{5}$
頂点： $(- \frac{1}{5}, \frac{19}{5})$

以上が、平方完成を使った二次関数の軸と頂点の求め方だ。

この方法をマスターしておけば、どんな二次関数がきても、軸と頂点を求められるんだ。

ここは先生が大好きで、テストでも出やすい。

踏ん張って、軸と頂点の求め方の平方完成バージョンを習得しような。

えっ。

いちいち平方完成しなきゃいけないなんて・・・・ちょっと・・・・

だと？

クマシロ

そんなお前のために、次は公式を使った二次関数の軸と頂点の求め方を紹介するぞ。

それじゃあなぁ！

平方完成を使った二次関数の軸と頂点の求め方

x2の係数でくくる

平方完成する

もろもろ計算する

軸と頂点を求める

$x^{2}$ の係数でくくる