【高校数学 I 】二次関数の軸と頂点の求め方（基本編）

クマシロ

よう、消しゴムの妖精のくましろだ。東か南か・・・南だな

高校生では中学数学と同じように二次関数を勉強していくぞ。

二次関数とは復習すると、

$x$ の次数が「2」の関数

だったよな。

中学数学では

$y = a x^{2}$

っていう二次関数を集中的に勉強してきたことを思い出してくれ。

tomo

2016.08.31

二次関数y=ax2の放物線にみられる5つの特徴

https://text.tomo.school/parabola-characteristic

二次関数y=ax2の放物線ってなに？？ある日、数学が苦手なかなちゃんは、放物線に出会いました。うっわ・・・・二次関数y=ax2のグラフ。。。放物線？ほーぶつせんほーぶつせんほーぶつせん・・・・・なにを呪文となえているの？あっ、先生！2次関数で『ほーぶつせん』が出てきたんだけど、よくわからなくて。なるほど！『放物線』のことだね。ひらがなだとわかりづらい。漢字を見てみよう。放る、物、線？そうそう！『放った物の線』何か、物を放るの？？そう！例えば、ボールを斜めに投げるとどう？ &n...

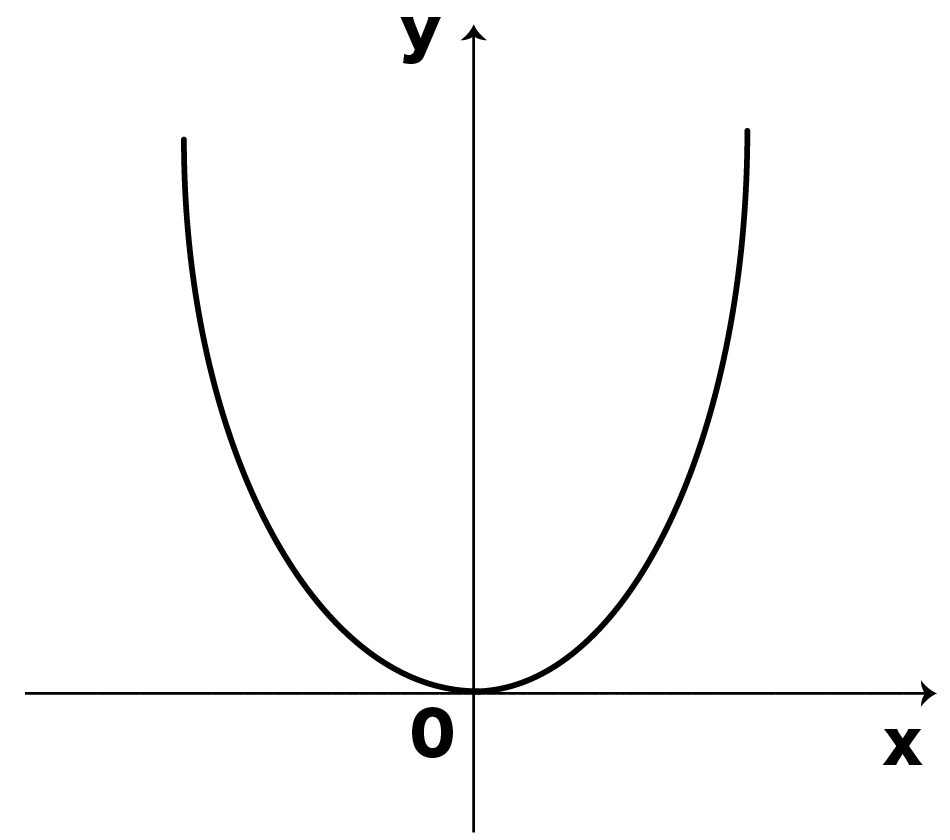
ここで思い出して欲しいのは

軸
頂点
放物線

というキーワードだ。

tomo

2016.08.24

【中3数学】放物線の頂点と軸とはなにもの？？〜高校数学につながる3つのお話〜

https://text.tomo.school/parabola-axis

放物線の頂点と軸ってどこのなの？？ある日、数学が苦手なかなちゃんは、放物線に出会いました。うっわ・・・・二次関数y=ax2のグラフ。。。放物線わけわかんない泣おっす！あ！ゆうき先生だ！お、放物線みてるね。うす！放物線には、いろいろな名前があるの知ってたかな？？放物線の軸放物線の頂点とか。ちょうてん・・・・じく・・・・・意味がつながるから、漢字で覚えたほうがいいよ。ですよね！でも、聞き慣れない言葉だと、どうしても・・・・・・気持ちはわかる！じゃあ、『軸』はどう？もしか...

二次関数のグラフは、

物体を真上に投げたときに描かれる線

のように変化するから「放物線」といって、

左右対称になっていたな。

そして、この対称の軸、つまり、放物線を重なるように折りたたんだときの折り目を「軸」。

この軸と放物線の交点を「頂点」といったことを思い出してくれ。

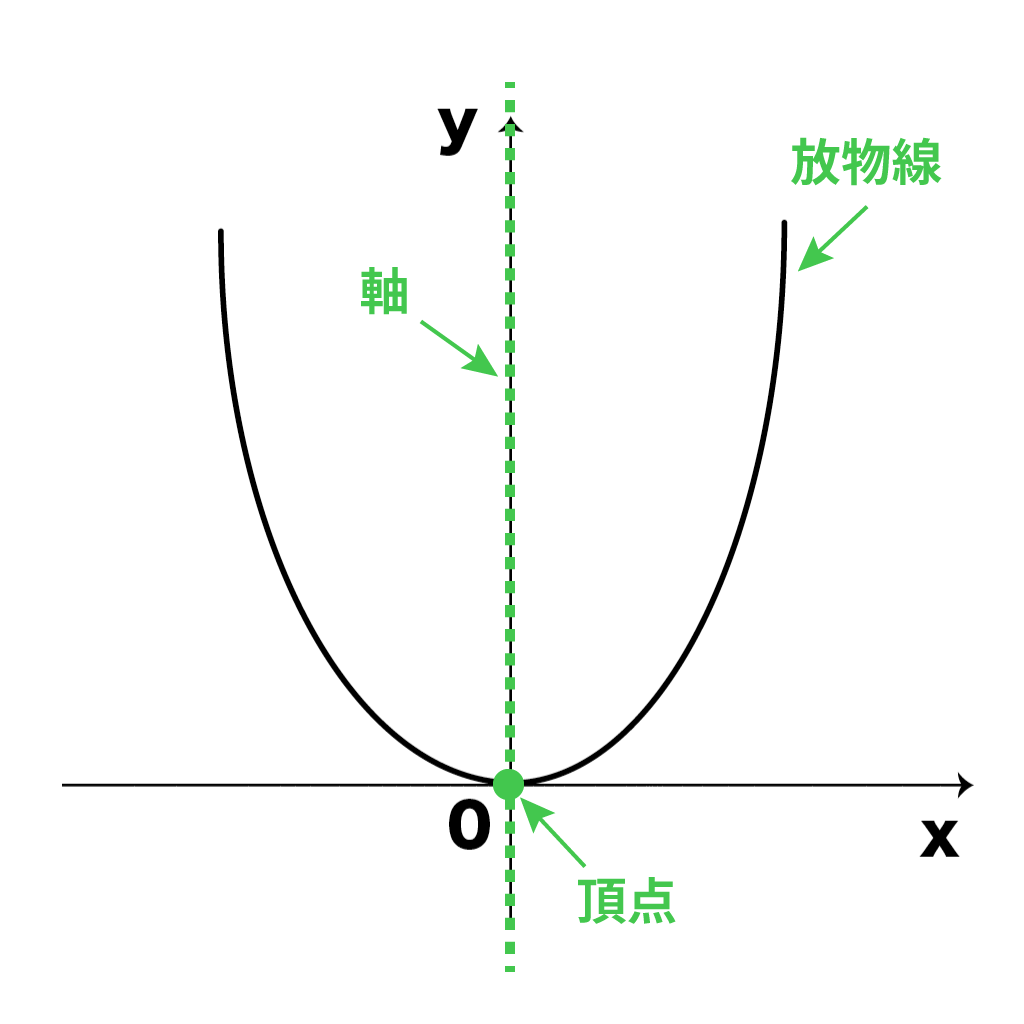
中学数学では、原点(0,0)に頂点がある二次関数を取り扱ってきた。

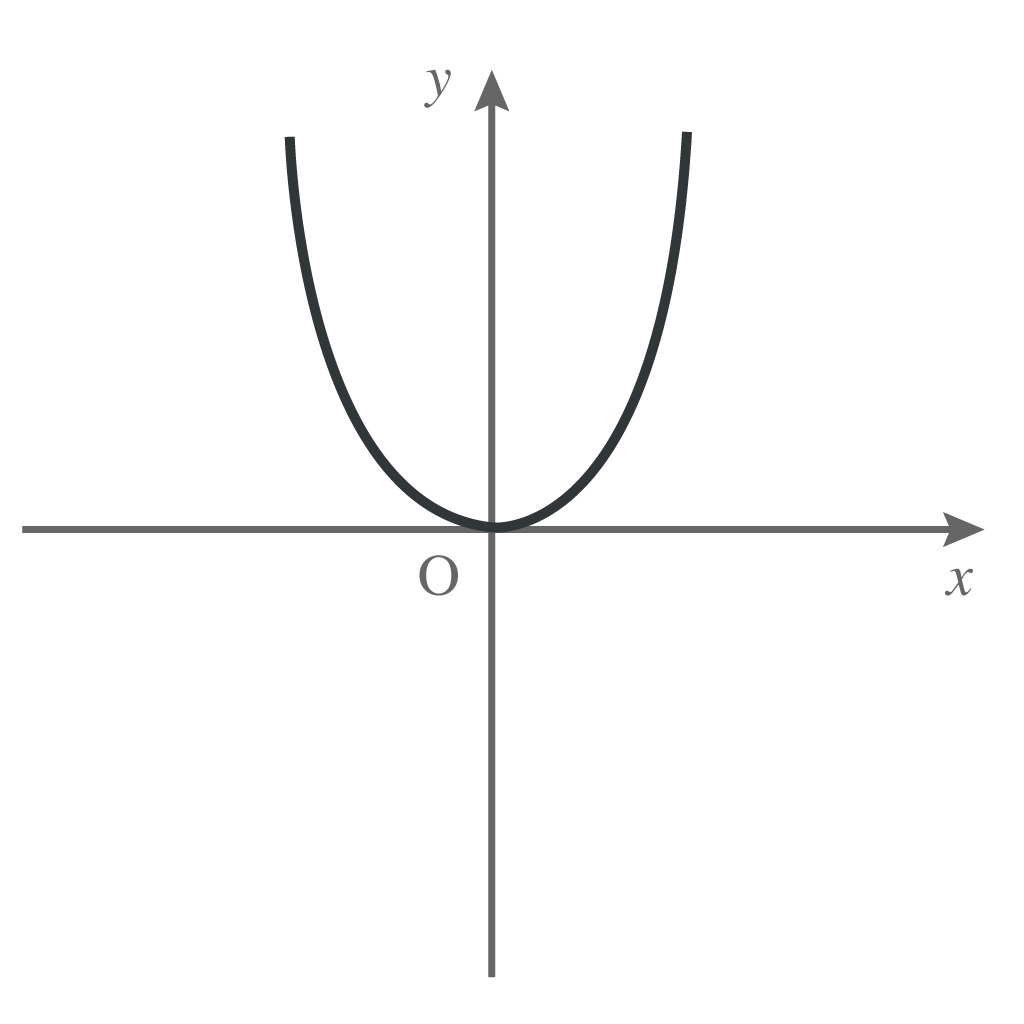
だが、高校数学では、放物線が原点から解き放たれちまったんだな。

こんなんとか、

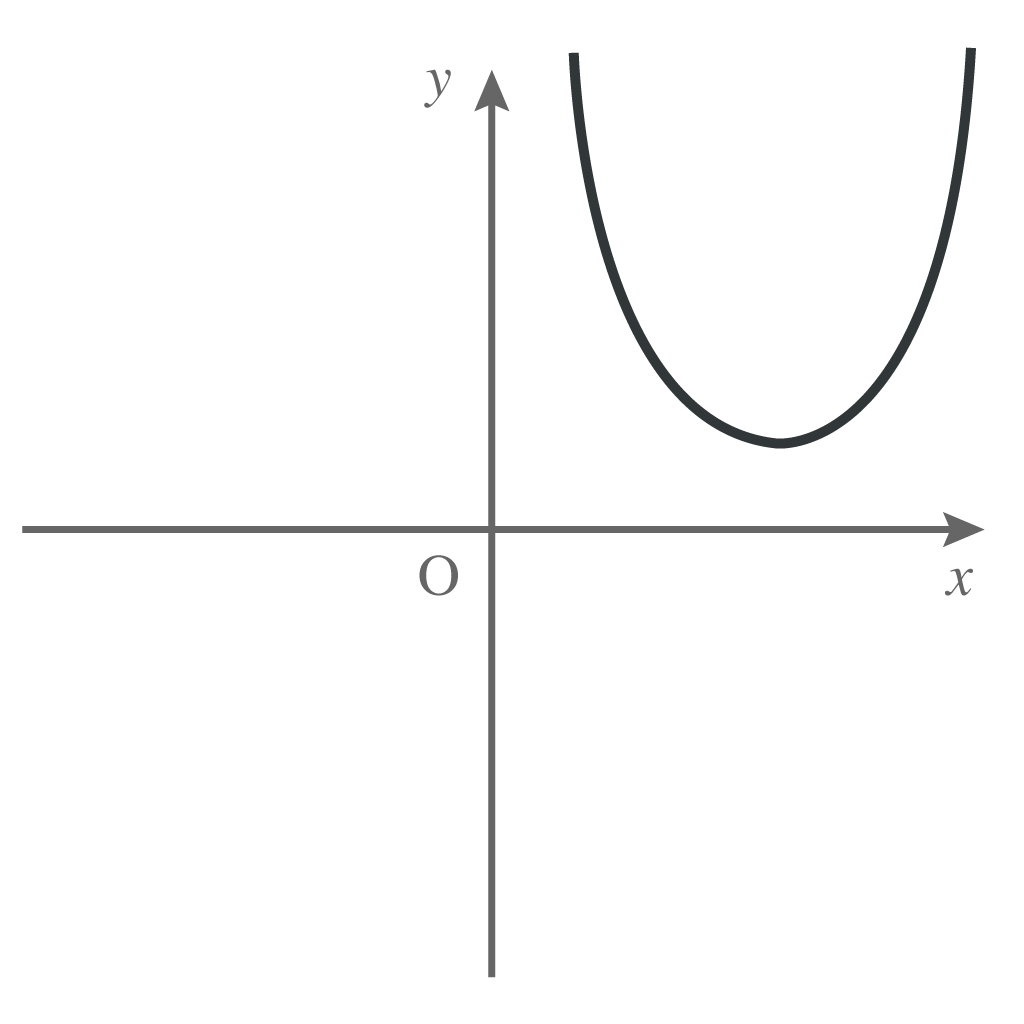
あんなんとか、

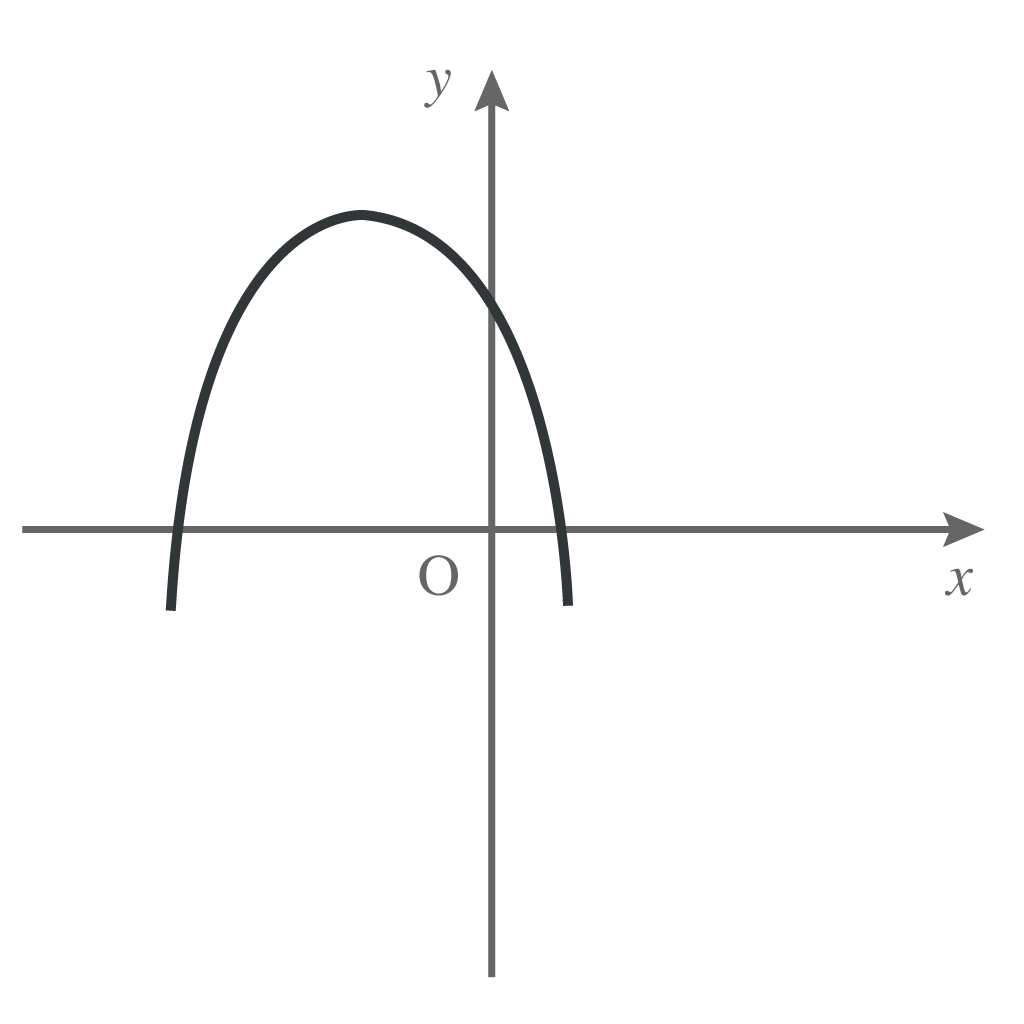
そういった二次関数を勉強していくんだ。

高校数学では、これらの自由になった放物線の軸と頂点を求めていくぞ。

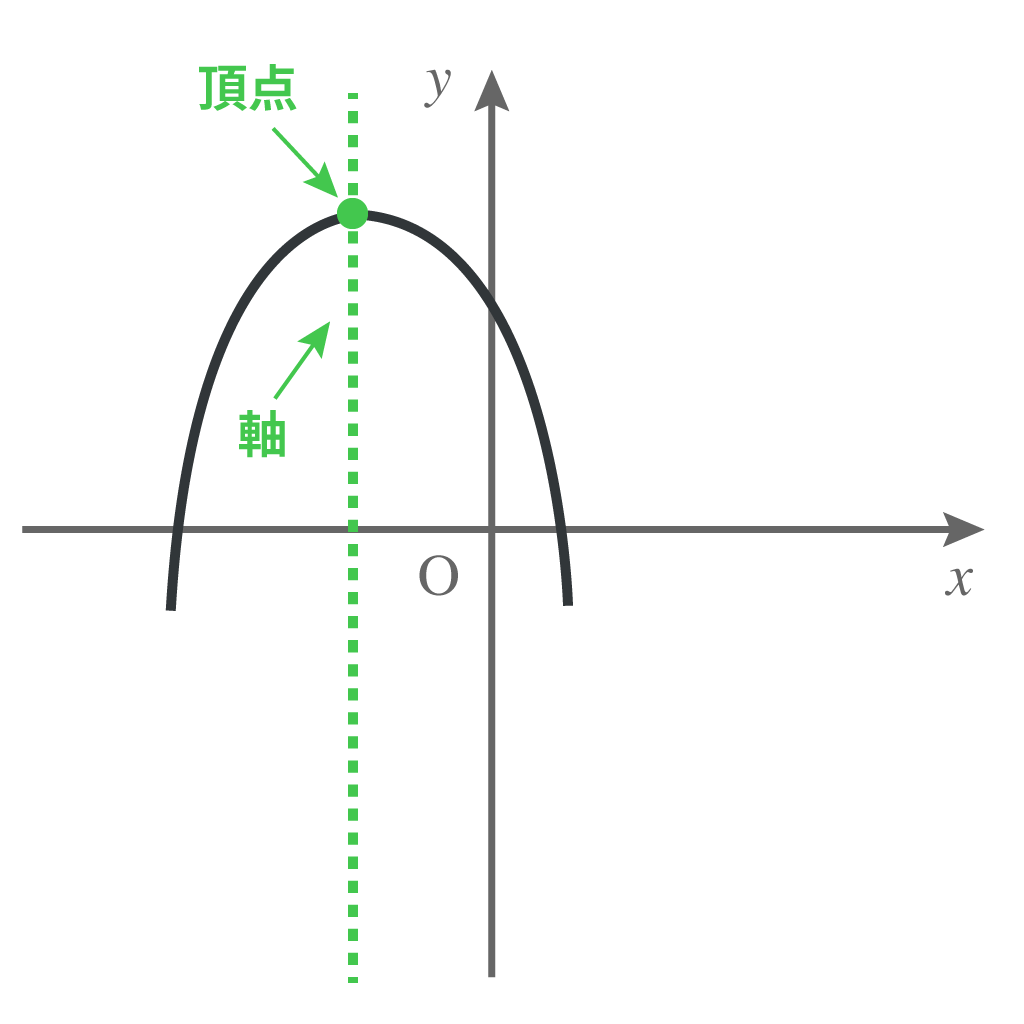
ってことで、ここではその二次関数の軸と頂点の求め方の基本技をマスターしようぜ。

二次関数の軸と頂点の求め方の基本

二次関数の軸と頂点の求め方の基本を習得していこう。

とあるところにな、偶然、二次関数の、

$y = a (x - p)^{2} + q$

がいるとしよう。

この放物線の軸は、

$x = p$

頂点は、

$(p, q)$

になるんだ。

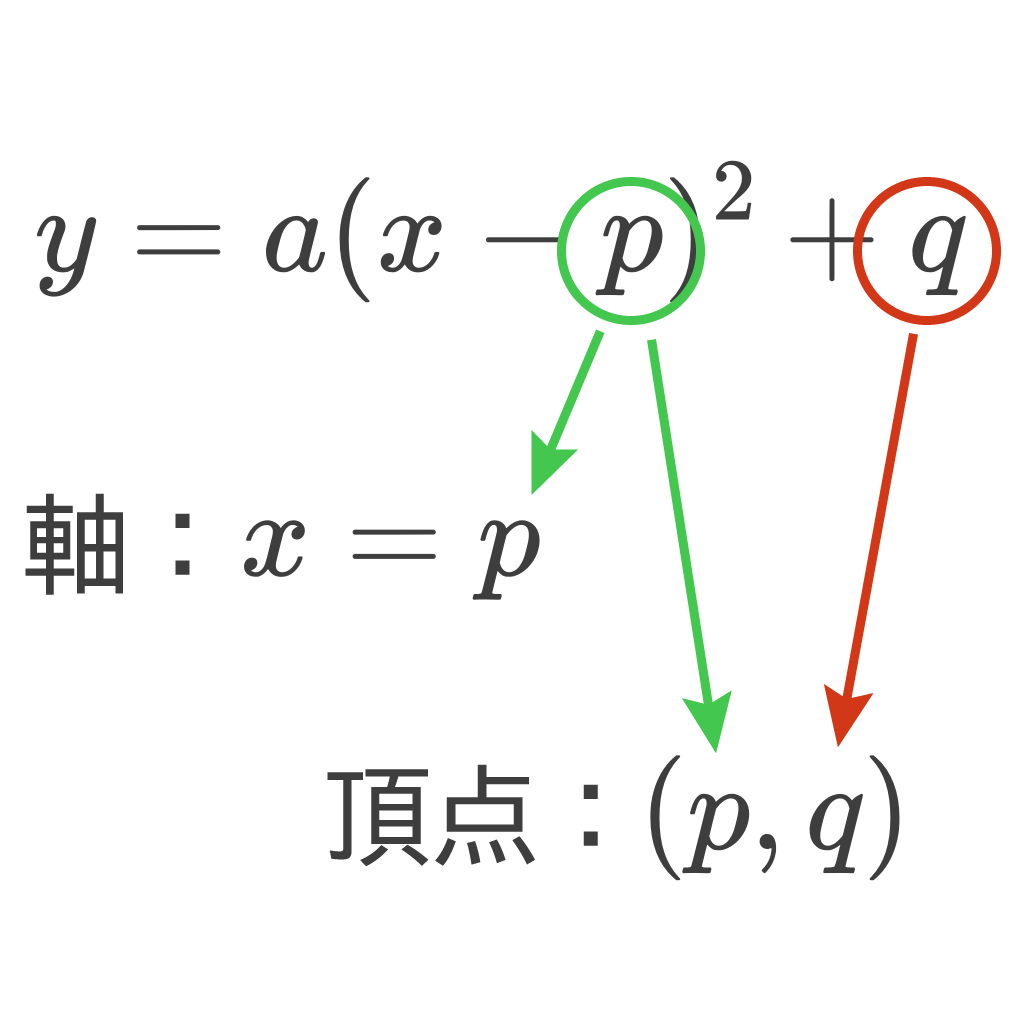
これが軸と頂点の求め方の基本だ。

つまり、二次関数の $p$ と $q$ にあたる数を探してやればいいんだな。そしたら、その $p$ と $q$ を使って軸と頂点をゲットさ。

例えば、

$y = 3 (x^{2} - 5) + 7$

という二次関数があったとしよう。

この二次関数は偶然、さっき出てきた

$y = a (x - p)^{2} + q$

という形だな。偶然な。

で、この式から

どの数字が $p$ と $q$ になっているか確認すりゃいいってことよ。

冷静に凝視すると、この関数では

$p = 5$
$q = 7$

だな。

だから、軸（ $x = p$ )は

$x = 5$

になる。で、頂点 $(p, q)$ は

$(5, 7)$

になるわけだ。

なぜ二次関数の軸と頂点の求め方の公式が使えるの？

よし、ここまでで二次関数の軸と頂点の求め方の基本はわかったな。

でもさ、なんでこの公式使えるんだろうな？

いくらなんでも怪しすぎやしねか？

pがプラスならまだしも、マイナスついちゃってるもんな。

さて。ここで、

$y = a (x - p)^{2} + q$

という二次関数に注目しよう。

こいつは、原点が頂点の二次関数「 $y = a x^{2}$ 」からはx軸方向にp、y軸方向にqだけ頂点がずれているんだ。

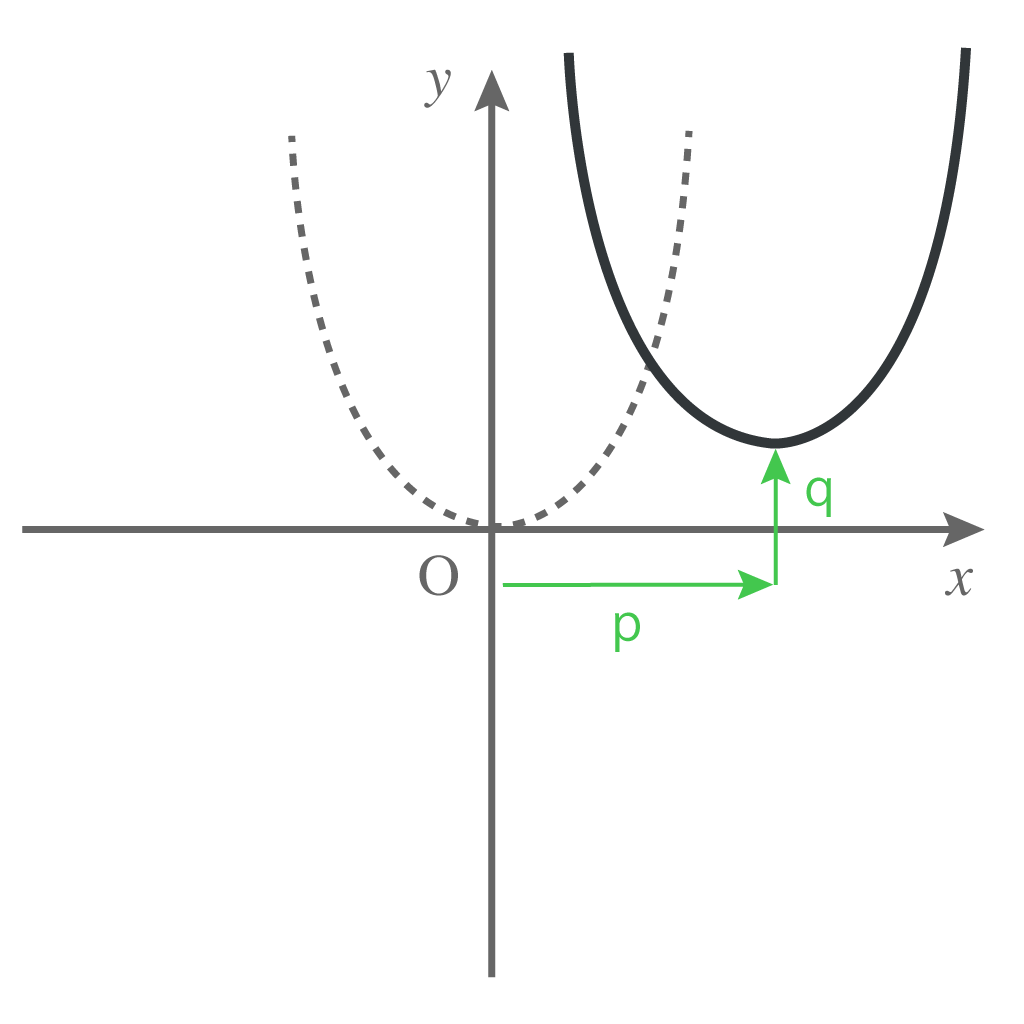
つまり、「 $y$ = $a x^{2}$ 」をx軸方向にp、y軸方向にqだけ平行移動させたらこの式になるってことよ。、

それじゃなぜこうなるのか？

ここで深呼吸して、冷静に図を書いてみるぞ。

まず原点を頂点する $y = a x^{2}$ という二次関数があるとしよう。

その中の1つの点を

$(x, y)$

とする。

この $(x, y)$ をx軸方向にp、y軸方向にqだけ平行移動させてやろう。

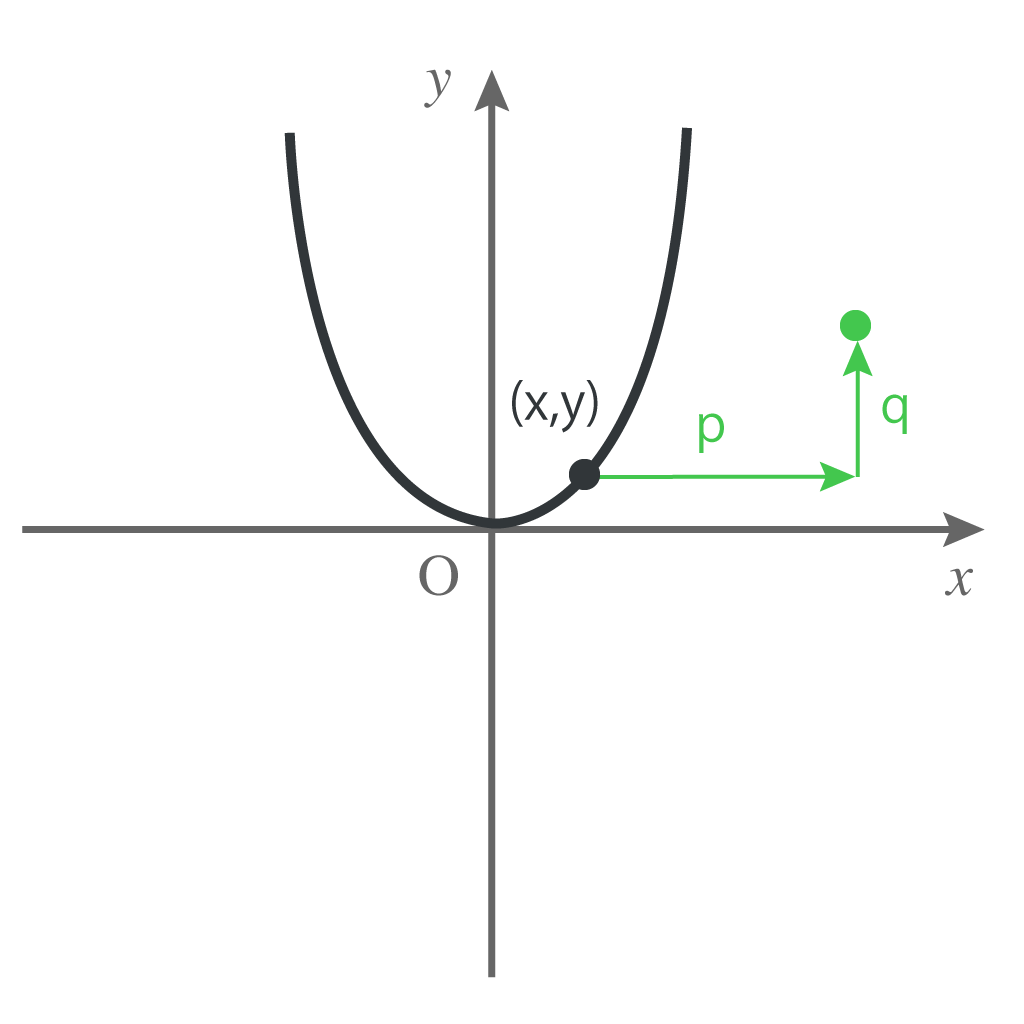
そうすると、

$(x + p, y + q)$

になるよな。

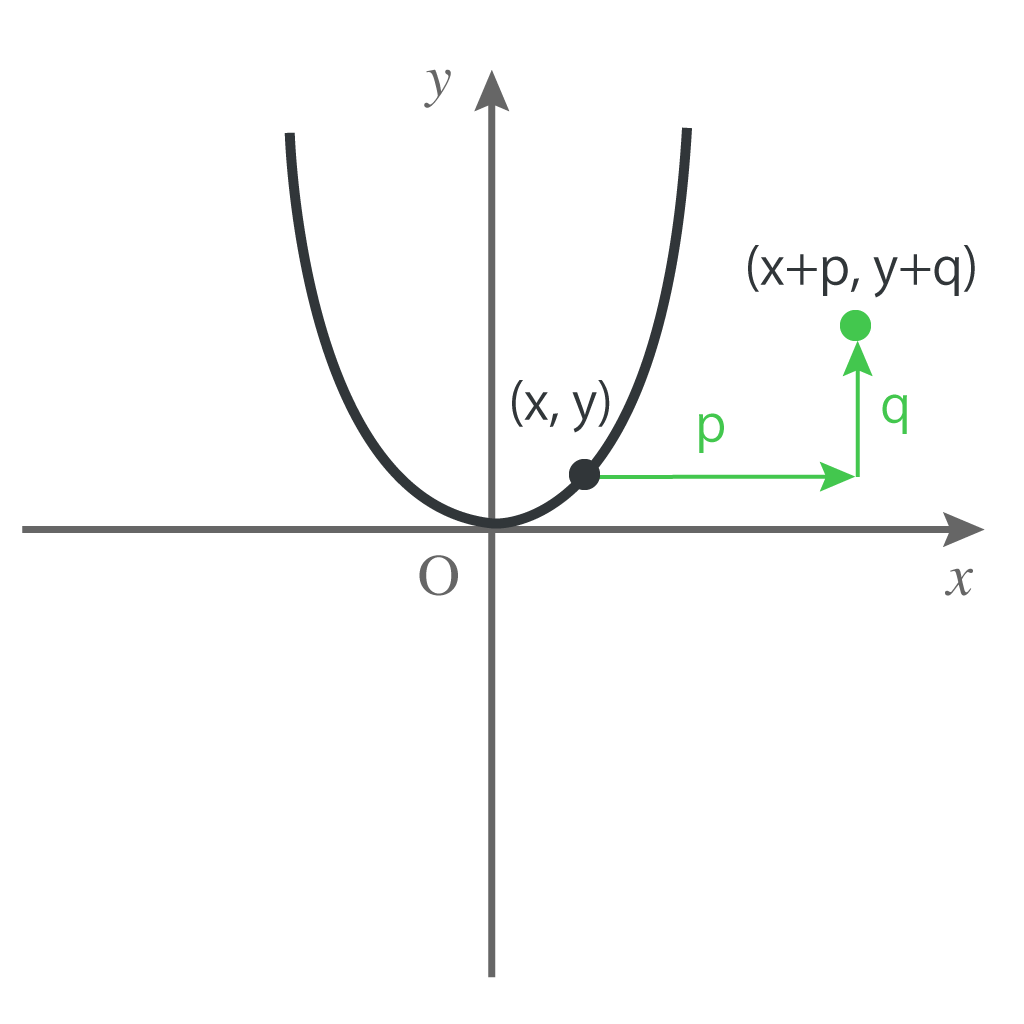
これを仮に

$(x^{'}, y^{'})$

とするぞ。

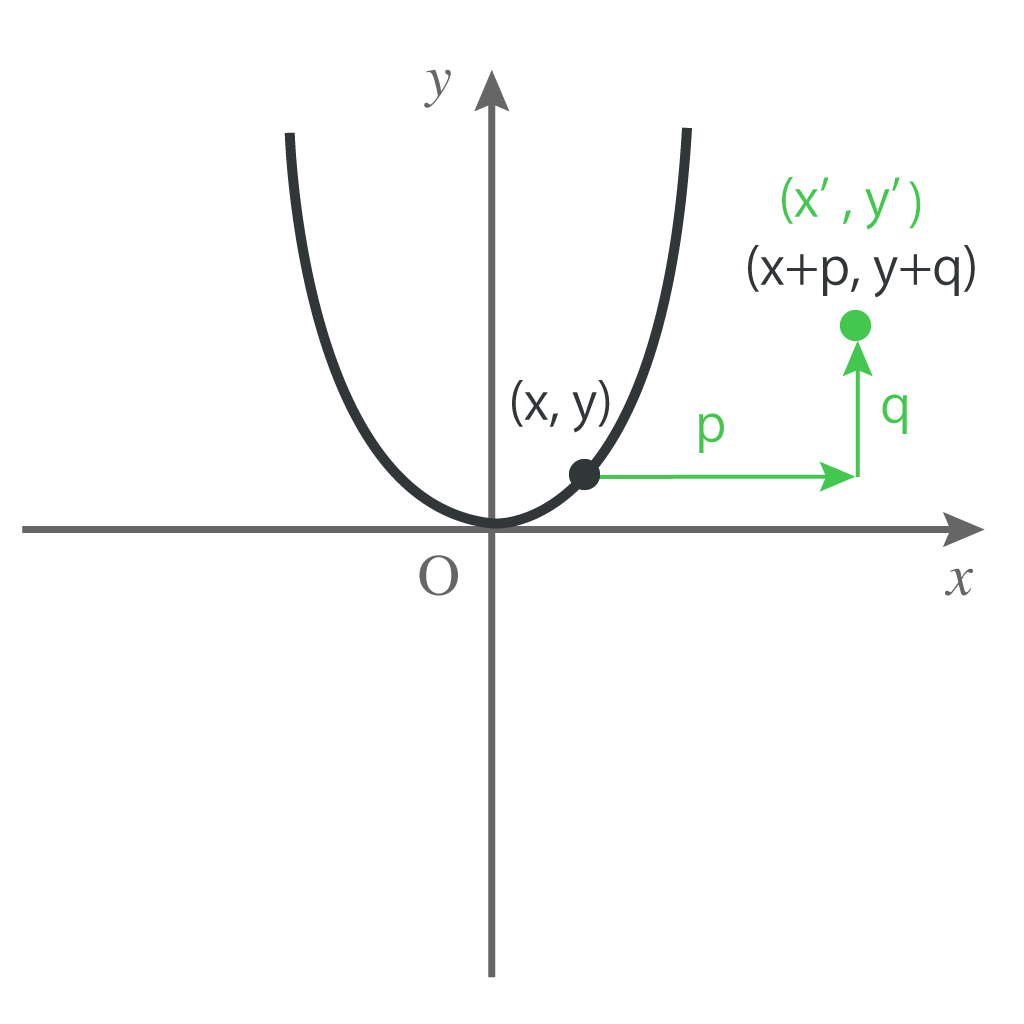
この $x^{'}$ と $y^{'}$ ’で二次関数を表せれば、平行移動した先の二次関数がわかるはずだ。

ここで $(x, y)$ と $(x^{'}, y^{'})$ の関係を見てみよう。

x’はxに $p$ だけ足したものだから、

$x^{'} = x + p$

になるよな。

同じように、 $y$ ’は $y$ からqだけ移動したものだから、

$y^{'} = y + q$

になる。

こいつらを変形してやると、

$x = x^{'} - p$
$y = y^{'} - q$

になるわけだ。

これを二次関数の最初の式「 $y = a x^{2}$ 」に代入さ。

すると次のようになるよな。

$y = a x^{2}$

$y^{'} - q = a (x^{'} - p)^{2}$

$y^{'} = a (x^{'} - p)^{2} + q$

さて、これが平行移動後の二次関数の正体だ。

これはまさしくお前らに冒頭で紹介したあの公式の形、

$y = a (x - p)^{2} + q$

だよな。これがお前らに冒頭で紹介した基本公式だったわけだ。

以上が二次関数の頂点と軸の求め方の基本だ。

だが、世界はこのままじゃ許してくれねえ。

この基本形に当てはまってない二次関数の軸と頂点を求められるようにならねえと、な。

クマシロ

ってことで、次は平方完成を使った軸と頂点の求め方を習得していくぞ。

それじゃあなぁ！