【中3数学】分数を含む二次方程式の解き方がわかる3つのステップ
分数を含む二次方程式の解き方はどうやるの??
こんにちは!この記事を書いているKenだよ。音声入力、最高。
中3数学で勉強する方程式は「二次方程式」。
こいつは「次数が2の方程式のこと」なんだけど、解き方が6つもあるせいで、なかなかに解くのが難しい問題だね。
しかも、ただでさえ二次方程式は厄介なのに、たまに、
分数を含む二次方程式
というモンスターが出現することがあるんだ。
今日はこのパターンの二次方程式の解き方をマスターしていこう。
3分でわかる!分数を含む二次方程式の解き方
たとえば次のような問題があるよ。
次の二次方程式を解きなさい
X²ー3分の1X = 8
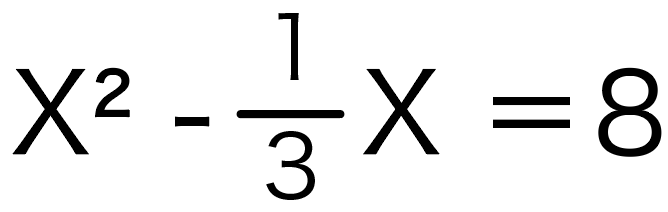
分数が紛れ込んでいる二次方程式の問題は、厄介だからこそテストや宿題に出やすい。。
次の3つのステップで瞬殺してみようぜ。
Step1. 分母の最小公倍数をかけて分数を消し去る
まず最初にやるべきことは、分数を消し去ること。
分数なければいつも通りの二次方程式になるから簡単になるよね。
じゃあどうやって二次方程式から分数を削除するのかっていうと、
分母の最小公倍数を両辺にかければいいんだ。
この分数の消し方は、
とまるまる一緒だね。
さて、例題の二次方程式を見てみよう。
次の二次方程式を解きなさい
X²ー3分の1X = 8
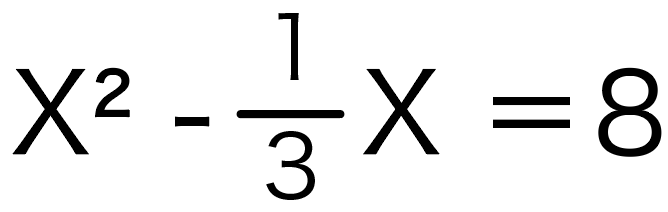
よーく見てみると分数の項が1つで、
ー3分の1X
しかない。

1つしか分数の項がないから、分母の最小公倍数はこの分母の3になるね。
ってことで両辺に3をかけてやると、
↓↓
3X²ーX = 24
になる。

分数が消えたか確認してみてね。
Step2. 全ての項を左辺に集める!
あとはいつも通り二次方程式を解くだけでいいんだ。
例題を見てみよう。
3X²ーX = 24
はx2乗の項とxの項、整数の項がそれぞれ1つずつある二次方程式。
みやすいようにすべての項を左辺に寄せてみよう。
すると、こうなる↓
3X²ーX – 24 = 0
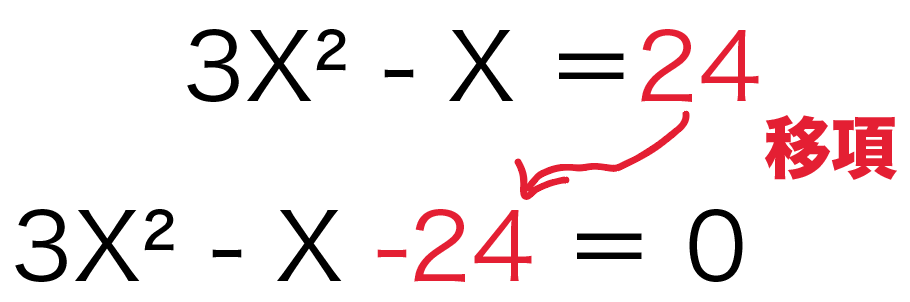
Step3. 解く!
あとは二次方程式をいつも通りとくだけ。
「3X²ーX – 24 = 0」は公式で因数分解できないけど、たすき掛けの因数分解なら使えそう。
3X²ーX – 24 = 0
でたすき掛け因数分解を使ってやると、
3X²ーX – 24 = 0
(X-3) (3X+8) = 0
になるね。

たすき掛け因数分解を忘れちゃった時はこの記事で復習してみてね↓↓
(X-3 ) と(3X-8)のどっちかが0のとき、(X-3) (3X-8)が0になるから、
- (X-3) =0
- (3X+8)=0
の2通りの等式ができるはずだね。

よって、この2つの方程式を解くと答えは、
x =3, -3分の8
だ。
さあ、分数を含む二次方程式を解いてみよう!
以上が分数を含む二次方程式の解き方だったよ。
ポイントはやはり、
一番最初に分数を消し去るということ。
分数がなくなればいつも通りに二次方程式の解き方でとけばいいから、
の6つの二次方程式の解き方が使えるようになるんだ。
テストにも出やすいからよーく復習してこう。
そんじゃねー
Ken




