正四角錐の高さを求めたい！
やあやあ、Dr.リードだよ。
3年生の数学もいよいよ大詰め。
今日は、高校入試でよく出てくる、
正四角錐の高さを求める問題
を解説していくぞ。
正四角錐って、底面が正方形で、先っちょが尖ってる立体のことだったね。
ちょうど、エジプトのピラミッドが正四角錐だな。
正四角錐の高さを求めるためには、中3で勉強した三平方の定理も使っていくぞ。
正四角錐の高さを求める4ステップ
正四角錐の高さの求め方はつぎの4ステップだ。
- 補助線を描きいれる。
- 底面の正方形の対角線の長さ、その半分の長さを出す
- 高さ（垂線）と底辺をふくむ直角三角形をさがす。
- 三平方の定理を使って計算する。
つぎの例題をいっしょに解いていこう。
練習問題
つぎの正四角錐の立体の高さを求めなさい。
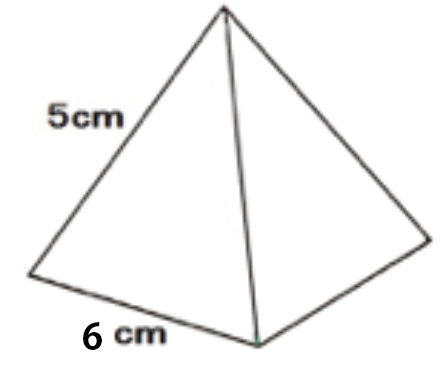
Step1. 補助線をかく
まずは、補助線をガンガン入れる。直角にも印をつけるといい。
正四角錐の中の直角三角形を見つけやすくするためだ。
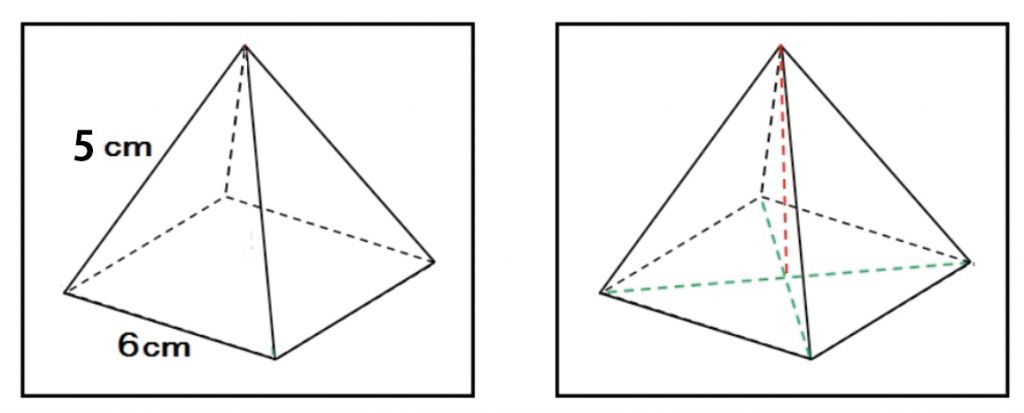
Step2. 底面の対角線の長さの半分を出す
つぎは、正四角錐の底面に注目してみよう。
底面の正方形の対角線の長さを計算していくんだ。
底面は1辺が6cmの正方形だったな？
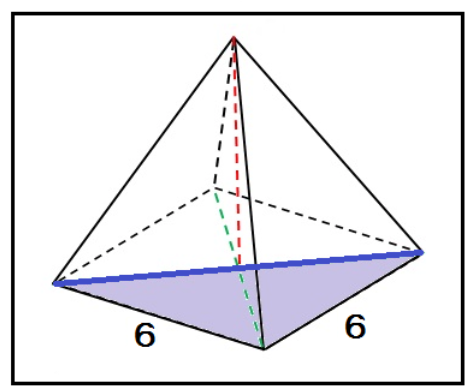
この正方形の半分の直角三角形で三平方の定理を使ってやると、
6² + 6² = x²
x = √72 = 6√2
になるぞ。
ってことは、正四角錐の底面の対角線の半分の長さは、
6√2÷2 = 3√2
だ。
Step3. 正四角錐の頂点からの垂線をふくむ直角三角形を探す
つぎは、正四角錐の頂点からの垂線に注目。
垂線をふくむ直角三角形を探して、三平方の定理を使えばいいんだ。
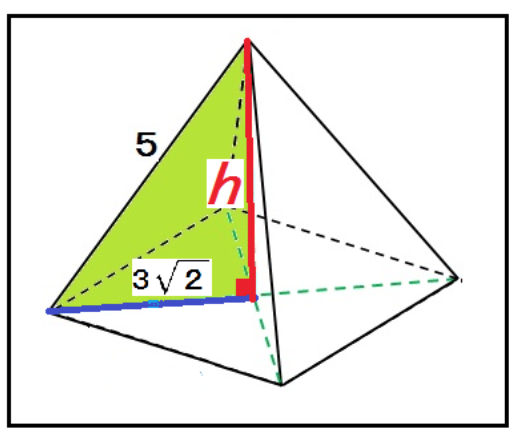
Step4. 三平方の定理で正四角錐の高さを計算
さっき見つけた正四角錐の頂点からの高さを求めてみよう。
使うのは、もちろん、
三平方の定理！
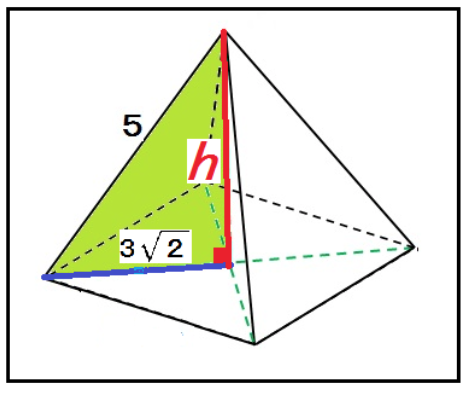
正四角錐の頂点からの高さをhとしてやると、
5² = (3√2)² + h²
h = √7
になるね。
つまり、この正四角錐の高さは√7 cmってわけ！
まとめ：正四角錐の高さは三平方の定理で攻略！
正四角錐の高さの求め方はどうだったかな？
つぎの4ステップで計算できちゃったな。
- 補助線を描きいれる。
- 底面の正方形の対角線の長さ、その半分の長さを出す
- 高さ（垂線）と底辺をふくむ直角三角形をさがす。
- 三平方の定理を使って計算する。
入試問題によく出てくるから復習しておこう。
正四角錐の高さが計算できたら次は円錐の高さに挑戦してみよう。
じゃあな
Dr.リード
