3分でわかる！平行線と線分の比の2つの証明

平行線と線分の比を証明しなきゃいけない？？

ある日、数学が苦手なかなちゃんは、

平行線と線分の比の証明問題に出会いました。

証明問題.

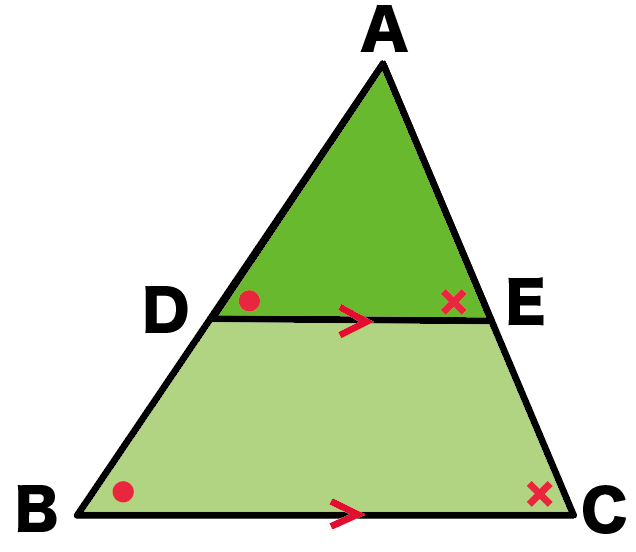
下の図形において、DE//BCです。

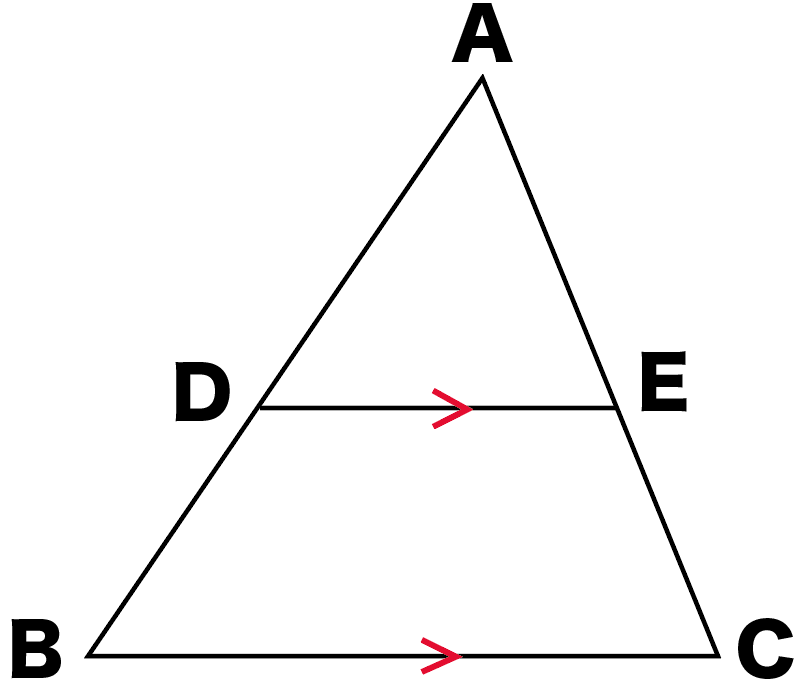
つぎの2つのことを証明しなさい。

AB : AD = AC : AE = BC : DE
AD : DB = AE : EC

かなちゃん

平行線と線分の比の証明？？

あー、もうやだ！！

平行って、

わたしと数学みたい！

ゆうき先生

決して交わることのない者同士……って、

少しは歩み寄ろ？ね？

かなちゃん

うわあっ！？

先生か、びっくりした……

だって、

今日の授業もわかんなかった。

平行だと線分の比が……

みたいな。

ゆうき先生

いきなり、

平行線と線分を語られても困るよね。

今日は、

平行線と線分の比について考えていこう！

かなちゃん

うす！

平行線と線分の比の証明その1

ゆうき先生

平行線と線分の比の証明は、

2つあったよね？？

AB : AD = AC : AE = BC : DE
AD : DB = AE : EC

まず1つめの、

AB : AD = AC : AE = BC : DE

を証明していこうか。

かなちゃん

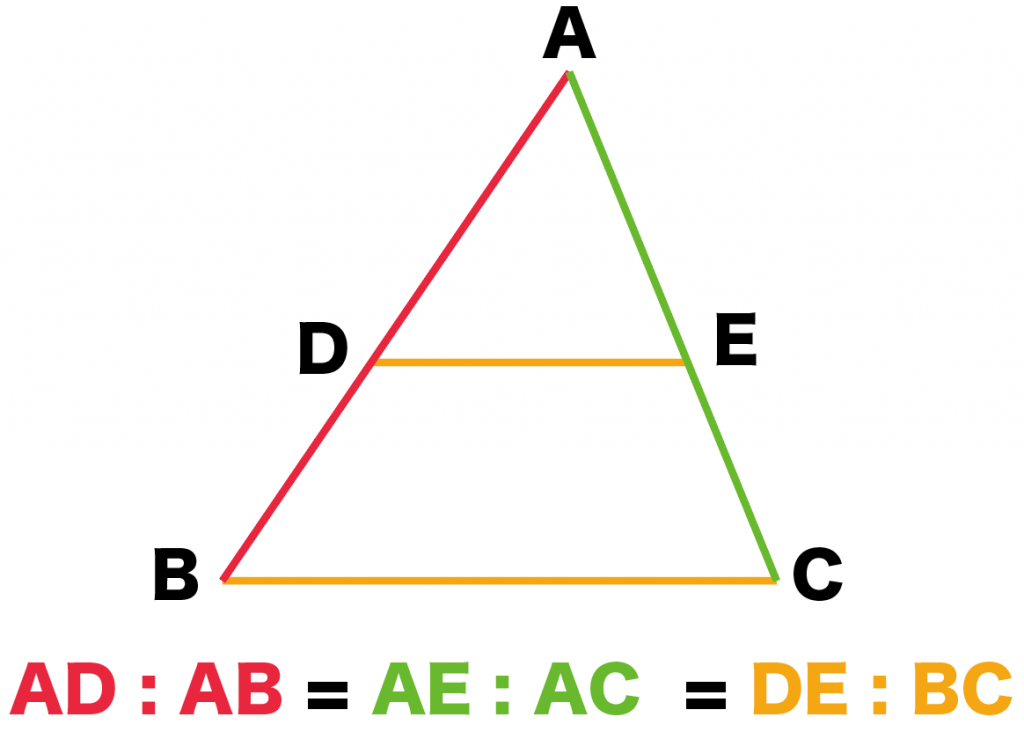
色分けしてあると、

わかりやすい！

ゆうき先生

うん、

自分でも描いてみると覚えやすいよ。

かなちゃん

めんどうだなぁ。

で、そういえば、

証明って何するの？

証明のゴールをきめよう

ゆうき先生

この証明のゴールはなんだっけ？？

かなちゃん

DEとBCが平行だと、

AD：AB

＝AE：AC

＝DE：BC

ってこと？

ゆうき先生

そう！

辺の比を証明したいってことね。

こういうときは、

相似を使おう！

かなちゃん

相似ってことは、

二つの図形を比べるの？

ゆうき先生

そう。

この場合なら、

△ABCと△ADEだね！

ゆうき先生

ちなみに、

この証明には仮定が出てくるよ。

なにかわかる？？

かなちゃん

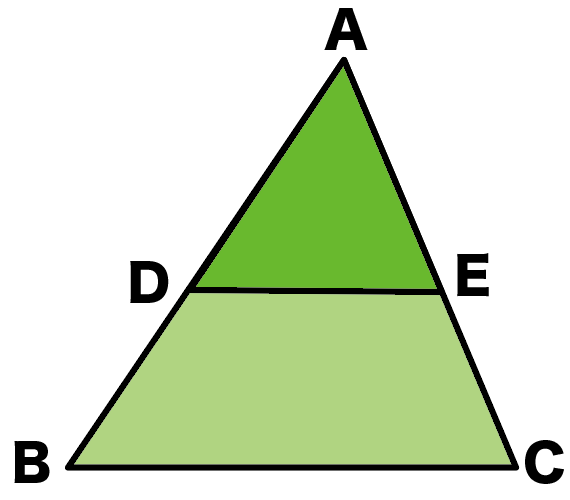
うーん、

DEとBCが平行

が仮定かな？

「DE//BC」

って問題にかいてあるから！

ゆうき先生

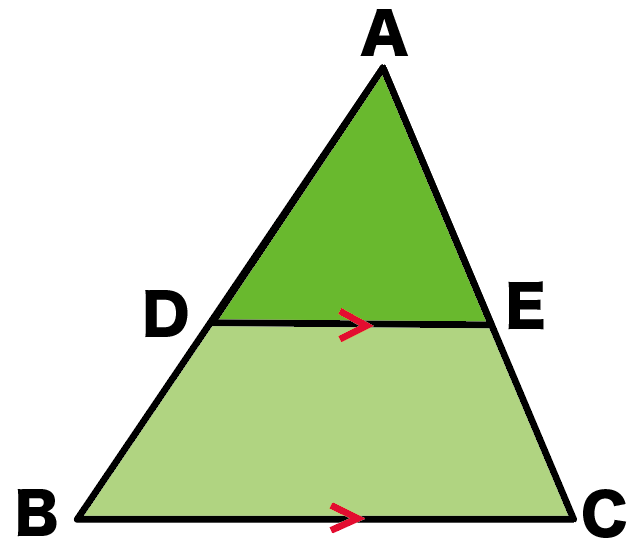
おっ、いいね！

その仮定をつかって、

△ABCと△ADEの相似

を証明できるかな？？

かなちゃん

うーん、あ！

ゆうき先生

おっ！

なにか降りてきたかな？

かなちゃん

同位角をつかうんじゃない？？

DE//BCだから、

角ADE = 角ABC
角AED = 角ACB

でしょ？？

ゆうき先生

やるねえー

相似条件はなにをつかう？？

かなちゃん

2組の角がそれぞれ等しいかな！

同位角で対応する2つの角が等しいし

ゆうき先生

お、

今日はキレっキレっだねー

その通り！

かなちゃん

わーい

証明をかく

ゆうき先生

実際に証明をかいてみよう。

証明のネタを集めたし

かなちゃん

うす！

でもちょっと怖い……

ゆうき先生

失敗を恐れずに書いてみよう！

証明の書き方がわからなかったら、

相似の証明の書き方

をよんでみて。

かなちゃん

うす！

うーん、

こんな感じかな・・・？

【証明】

仮定より、

BC//DE … ①

△ABCと△ADEで、

①より同位角が等しいので、

∠ABC＝∠ADE…②

∠ACB＝∠AED…③

②・③より、

対応する２つの角が等しいので、

△ABC∽△ADE

相似な図形では、対応する辺の比がそれぞれ等しいので、

BC：DE＝AB：AD＝AC：AE

ゆうき先生

お、やるねー！

かなちゃん

やった！

平行線と線分の比の証明その2.

ゆうき先生

おっと。

これでおわりじゃないよ！

平行線と線分の比は、

もう1つあったよね？？

かなちゃん

AD : DB = AE : EC

ってやつか！！

ゆうき先生

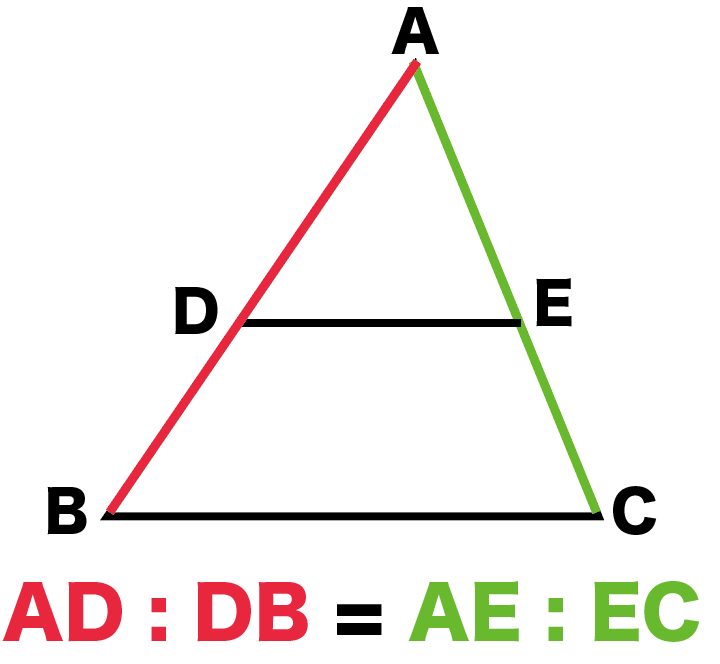
そうそう！

かなちゃん

うーん・・・・・

わ、わからない！

どうしたら証明できるの！？

補助線をひく！

ゆうき先生

最後は、落ち着いて！

図形は困ったら、

補助線を引くことが大切なんだ。

かなちゃん

補助線？

ゆうき先生

そう！

Eから、ABと平行な直線を引いてみて。

平行線とBCの交点をFとするんだ。

かなちゃん

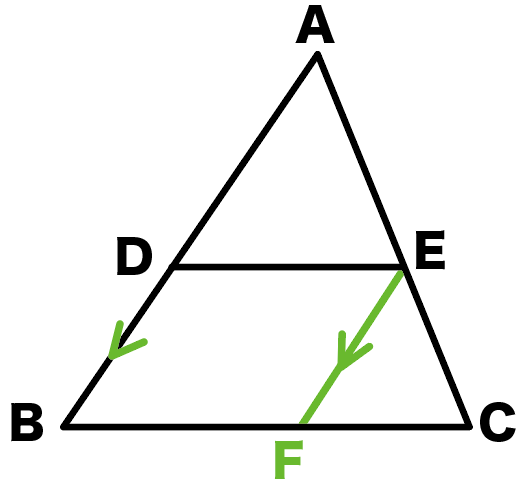
ひ、ひけた！

ゆうき先生

どう？？

相似な図形がみえてこない？？

かなちゃん

あああ！

△ADEと△EFC！！

ゆうき先生

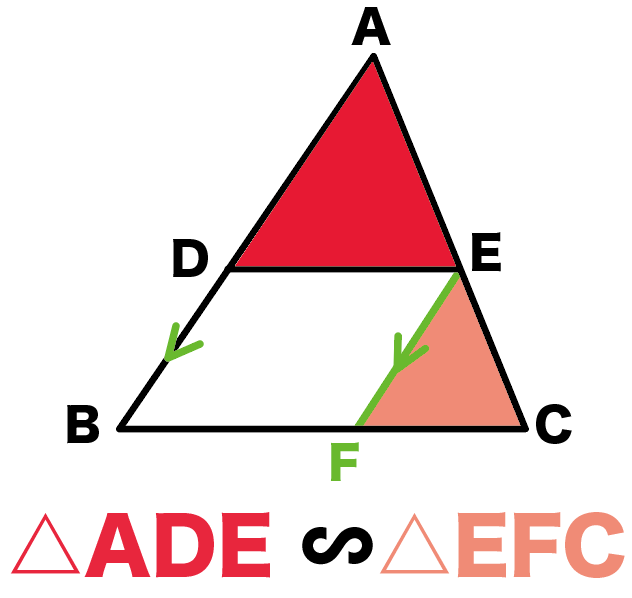
なんで？？

かなちゃん

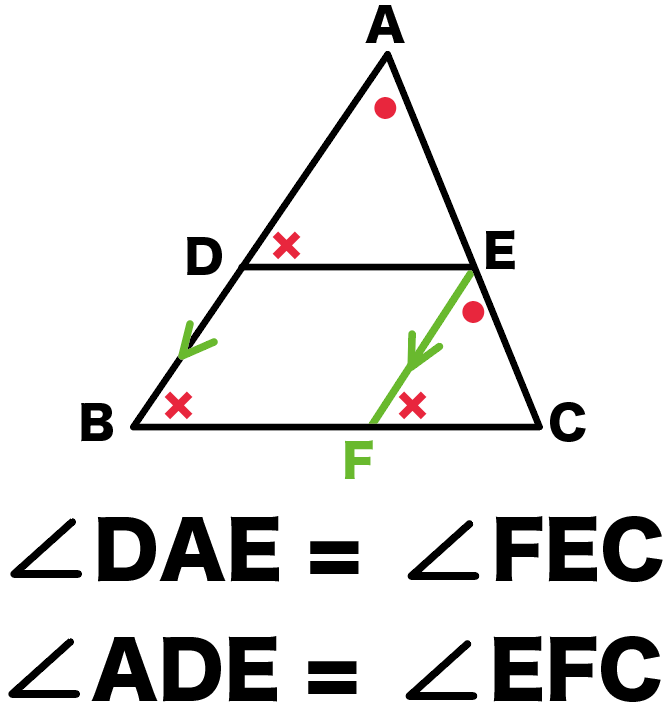
AB//EFだから、

同位角が等しいことがつかえる！！

角DAE = 角FEC
角ADE = 角EFC

だ。

ゆうき先生

お、いいねー！

相似条件の、

2組の角がそれぞれ等しい

を使うわけね。

じゃあ証明かいてみてー

かなちゃん

ういす！

【証明】

EからABに平行に引いた直線と、

BCとの交点をFとする。

仮定より、

BC//DE　…①

AB//EF　…②

△ADEと△EFCで、

①より同位角が等しいので、

∠ACB＝∠AED…③

同様に、AB//EFより同位角が等しいので

∠ABC＝∠ADE…④

また、BD//EFより、

∠ABC＝∠EFC…⑤

④・⑤より、

∠EFC＝∠ADE…⑥

対応する２つの角が等しいので、

△ADE∽△EFC

相似な図形では、

対応する辺の比がそれぞれ等しいので、

AE：EC＝AD：EF…⑦

また、四角形DBFEは、

①、②より平行四辺形で

向かい合う辺の長さが同じなのでBD＝EF…⑧

⑦・⑧より、

AE：EC＝AD：DB

かなちゃん

できたぜ！姉御！

ゆうき先生

おっ。

やるじゃああん

まとめ：平行線と線分の比の証明も相似で攻略！

かなちゃん

平行線と線分の比の証明も楽勝！

ゆうき先生

って思ってもらうのが、

今回の目的！！

証明のいいところは、

多少言葉の言い回しが違っても、

正解になるところ！

筋が通っていればいいのよ。

かなちゃん

うんうん

ゆうき先生

証明は、

とにかく書いてみよう。

おかしくてもなんとかなる。

かなちゃん

はい！

七転び八起きですね！

ゆうき先生

ということで、

今回のポイントをまとめよう。

困ったら補助線
とりあえず文章にする

かなちゃん

ありがとうございました！

ゆうき先生

証明はなれれば大丈夫。

解けば解くほど上達するよ。

おまけの問題を作ってみたよ〜

【おまけ】
BC：DE＝AB：AD＝AC：AE なら、BC//DEとなる証明をしてみよう！

かなちゃん

ういす！

といてみます！