セキツイ動物は次の5種類の分類にわけられる、って勉強してきたよね。 魚類（ぎょるい） 両生類（りょうせいるい） ハチュウ類 鳥類（ちょうるい） ホニュウ類     で、前回…

    セキツイ動物の分類には5種類あったよね。 魚類（ぎょるい） 両生類（りょうせいるい） ハチュウ類 鳥類（ちょうるい） ホニュウ類   この5つの分類のセキツイ動物は、 生まれ方 に違…

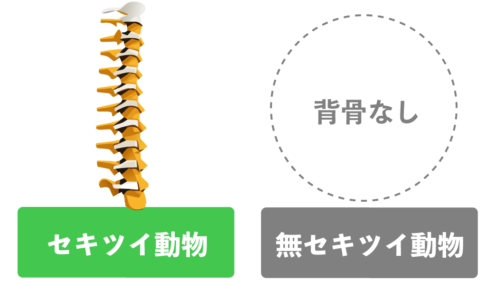
    前回、セキツイ動物と無セキツイ動物の違いと共通点を勉強してきたね。   じつはね、そのうちの「セキツイ動物（背骨のある動物）」は次の5つの分類にわけられる、と人間界では考えられている…

    動物はね、次の2種類に分けることができるんだ。 セキツイ動物 無セキツイ動物   セキツイ動物と無セキツイ動物の違い ズバリ、この2つの動物の違いは、 背骨の有無 さ。  …

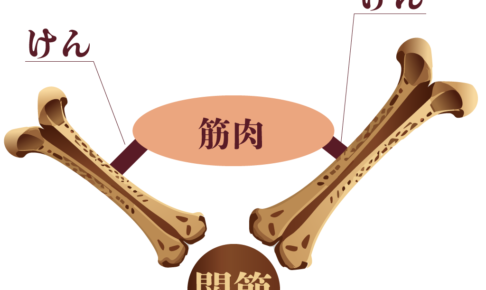
    ここまで神経の働きを勉強してきたよね。     人間は神経の働きを持っているから、外からの刺激に対して反応できるのさ。 でもね、これだけじゃ人間は動けない。 いくら信号が全…

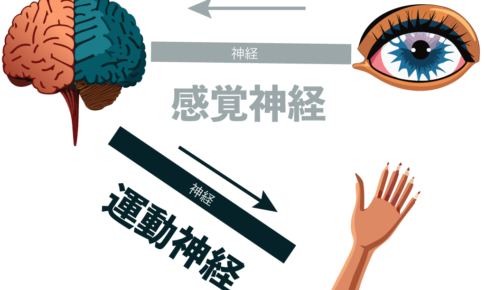
    人間たちは外から刺激を感覚器官を通して受け取って、それに対して反応することで活動を続けているよ。 で、その反応方法は2種類存在しているのさ。 意識的な反応 無意識的な反応   この2…

    神経とは、 情報伝達できる細胞のあつまり（組織）のこと だよ。   中学の理科では次の4つの神経が登場するんだ。 中枢神経 末しょう神経 感覚神経 運動神経   これらは一…

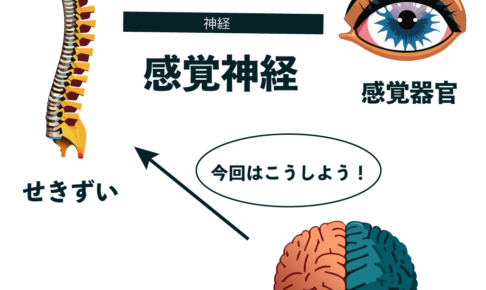
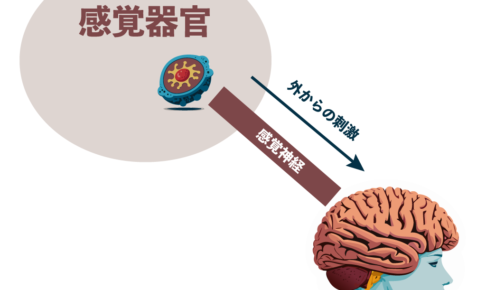
    中学理科では、 感覚器官 感覚神経 という2つの紛らわしい用語が出てくるよ。 今日はこの2つの感覚器官と感覚神経の違いをはっきりさせていこう！   感覚器官とは何者？ まずは感覚器官…

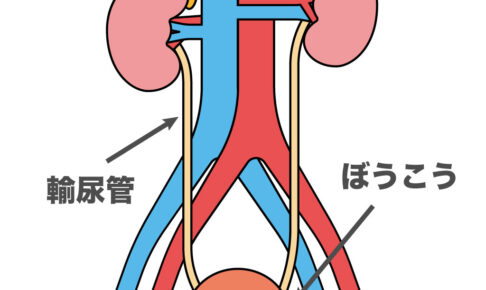
    ここまでで人間の消化の流れを勉強してきたね。   消化管という1本道を通して、消化各セクションで消化液を浴びせる 消化酵素の働きで外から取り込んだ食物を分解 栄養素を取り出す という…

    ここまで血液の循環を勉強してきたけど、どう？？ たぶん、おそらく、うん、おそらく、だけど、 血液の中にどんなものが入ってるのか 気になってきたよね。つまり 血液の成分 さ。   血液…

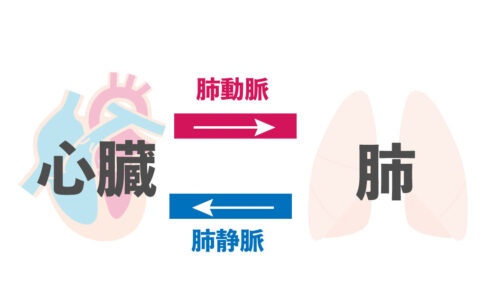
    中学理科ではいろいろな血管の種類が出てきて覚えづらいよね。 特に、 肺動脈 肺静脈 動脈血 静脈血 の4つね。 この血管たちは一体どう違うのか？？ 一つ一つ確認していこう。   動脈…

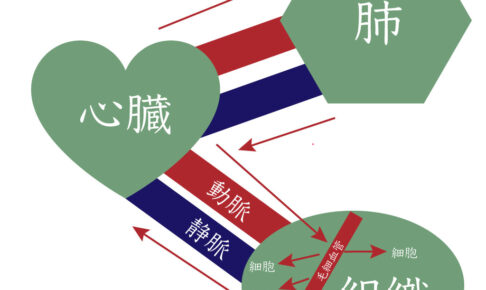
    前回、心臓の働きの血液の循環の流れを見てきたね。   実はこの血液の循環は2種類にわけられるのさ 体循環（たいじゅんかん） 肺循環（はいじゅんかん） 今日はこの2つの循環の違いに迫っ…

    人の中身の胸のあたりにある心臓。 実はこの心臓、 大きくなったり縮んだりを繰り返して、全身に血液をめぐらせる働き を持っているんだ。 今日はその心臓がどうやって血液を人の全身に循環させているの…