こんにちは、この記事を書いているKenだよ。飴はかむ派だね。
これまで「比例」について勉強してきたね??
えっ。もう疲れたから勘弁してくれよだって?!?
ここまで比例について勉強してきたけれど、
比例の大きなゴールって、
比例のグラフを書くこと
なんだ。

比例定数を求めたり、比例の意味を理解したりすることはグラフを書くための準備。グラフを書けるかどうかが勝負の分かれ目になるよ。
そこで今日はポイントとなる、
比例のグラフの書き方
をわかりやすく解説していくね。よかったら参考にしてみてね。
~もくじ~
比例のグラフを書く前に1つ押さえたいことがある。
それは、
比例グラフは直線である
ということだ。
比例のグラフは「うねうねした曲線」でもないし、
超クレイジーな関数でもない。
比例のグラフはじつにシンプルで直線。これは重要だから頭に入れておこう。
比例グラフは直線であるってことは、
直線の書き方を知っていればグラフを書けるはずだね。
じつは、
直線は2点を結ぶことで書けるんだ。

そう、2点だけでいい。
もちろん、3点とか、4点とかあったほうが直線を書きやすいけれど、別になくてもいいんだ。グラフが通る点を最低でも2点わかっていればOKだ。
ってことは、
比例グラフを書くために2点の座標がわかっていればいいわけだね??
そうすれば、座標平面に比例グラフをひょいっと書けるはず。
じゃあ比例グラフが通る2点っていったいどんなのがあるだろう??
例題として、
y = 2/3x のグラフをかきなさい。

をときながら勉強していこう。
くわしくは座標の記事をみてほしいけど、
原点って、
x軸とy軸が交わっている点
のことだったよね?? 座標でいえば(x, y) = (0, 0)だ。
だから、まずは比例グラフの1点として「原点」に点をうってみよう。こんな感じで↓↓
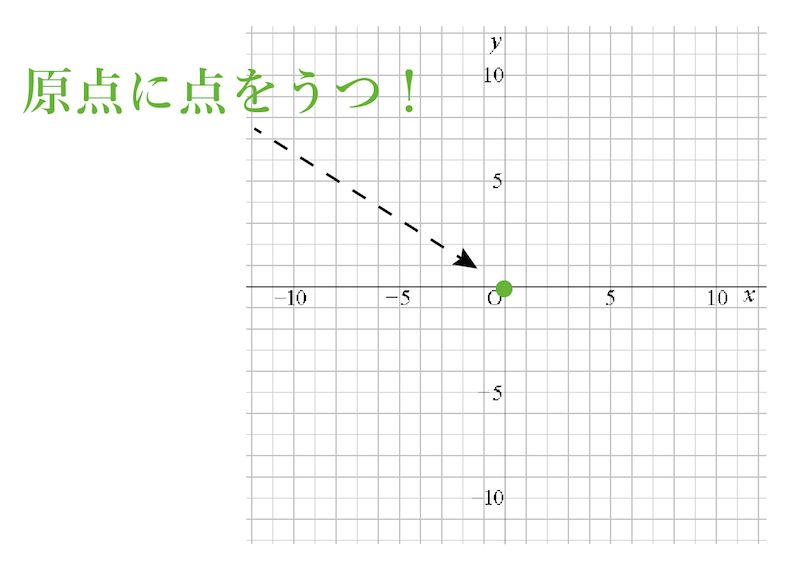
これが比例のグラフの書き方の第一ステップだ!!
比例のグラフをかくためにもう1点だけ必要だよね??
その点とは、
x軸とy軸の両方が整数になる点
なんだ。
たとえばさっきの例題でいえば、
x が3のときyは2になるよね?? つまり、xとyの両方の座標が整数になっているというわけさ。座標でいえば(3,2)だね。
したがって、
原点(0,0)と整数になる点(3, 2)の2点をむすんであげると、
こんな感じの比例グラフがかけるんだ。
ね?? なんだか書けそうな気がしてきたでしょ??
比例のグラフの書き方では、
2つめの「座標が整数になる点」をはやく探し出すかがカギとなっているんだ。
1つだけコツを紹介すると、
比例定数が分数のときは分母の数を「x座標」とするものをえらべ
ってことさ。
さっきの例題では比例定数の分母が「3」だったよね?? だからx座標を「3」としてあげると、y座標は「2」になる。よって、2つ目の点は、
(3, 2)
となるわけ。
もし、比例定数が整数のときはx座標に1をいれた座標でもいいよ。
比例グラフの書き方はどうだったかな??
グラフがとおる2つの点をいかにすばやく見つけられるか??
これに比例グラフの運命がかかっているよ。ちょっと心配なときはテスト前にグラフを何個かかいてみよう。きっと納得するはずさ。
そんじゃねー!
Ken
こんにちは、この記事を書いているKenだよ。お湯をのむのが好きだね。
前回は「座標」について勉強したね。
たしか、
xとyの値のセットのこと
を座標ってよんでいたよね??
関数の座標は、
2つの数直線を垂直に交わらせた図であらわせるんだ↓↓
それで、
この2つの数直線のことを「座標軸」といい、
よこ軸の座標軸を「x軸」、たて軸の座標軸を「y軸」っていうんだ。
ちなみに、x軸とy軸が交わる点を「原点」というぜ。
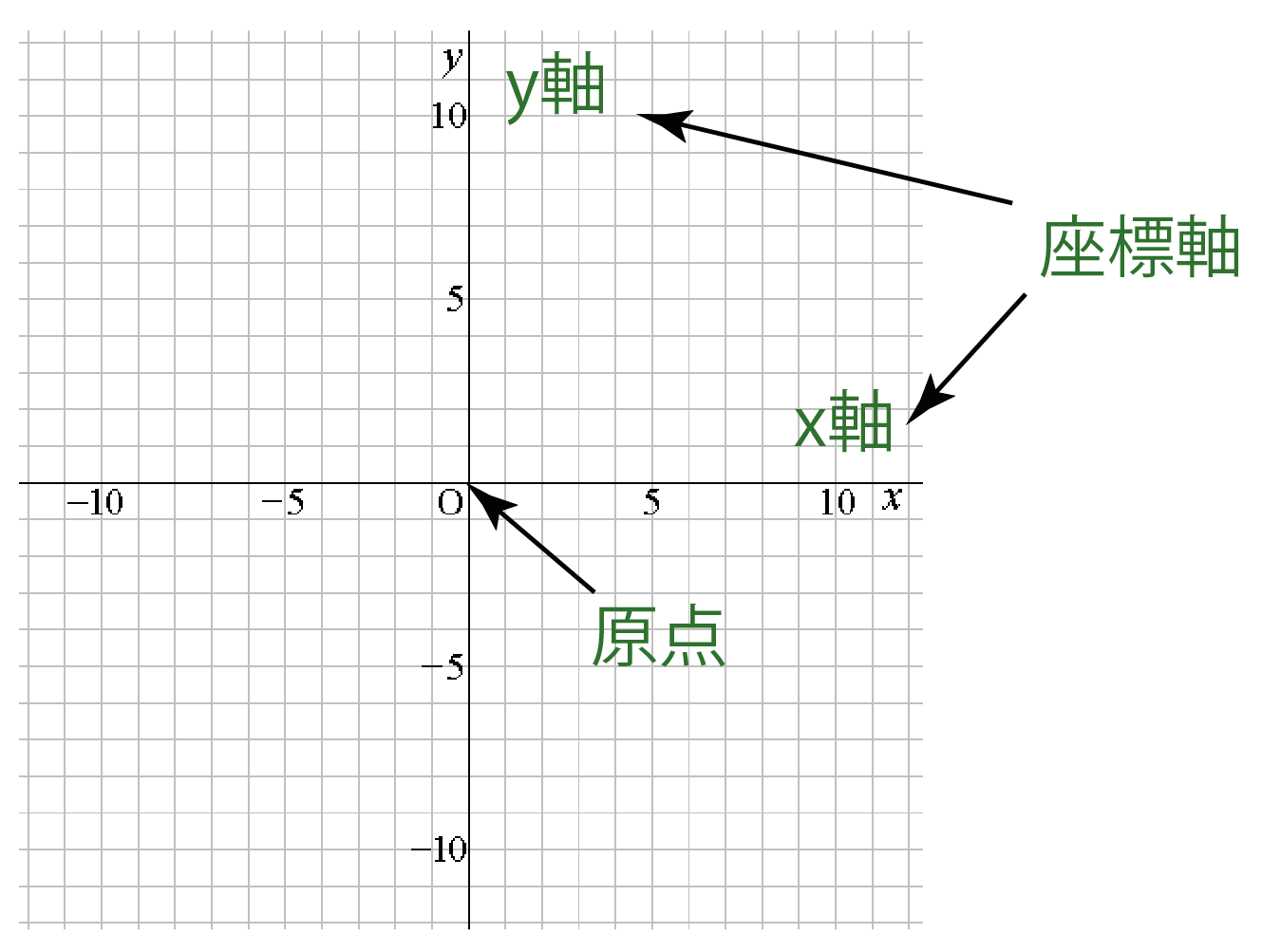
こんな感じで2つの座標軸には、
っていう名前がついてるよね??
でもときどき、
どっちがx軸で、どっちがy軸なのか??ってことを忘れちゃうわない??
そこで今日は、
x軸とy軸を100%忘れない覚え方
を紹介するね。x軸とy軸がごっちゃごちゃになったら参考にしてね。
カンタンなのは「y軸」の覚え方。
キミはアルファベット大文字の「Y」を想像できるかな??
こいつをさっきでてきた2つの座標軸の図の中にぶちこんでやると、
ものすごく馴染んでない??。
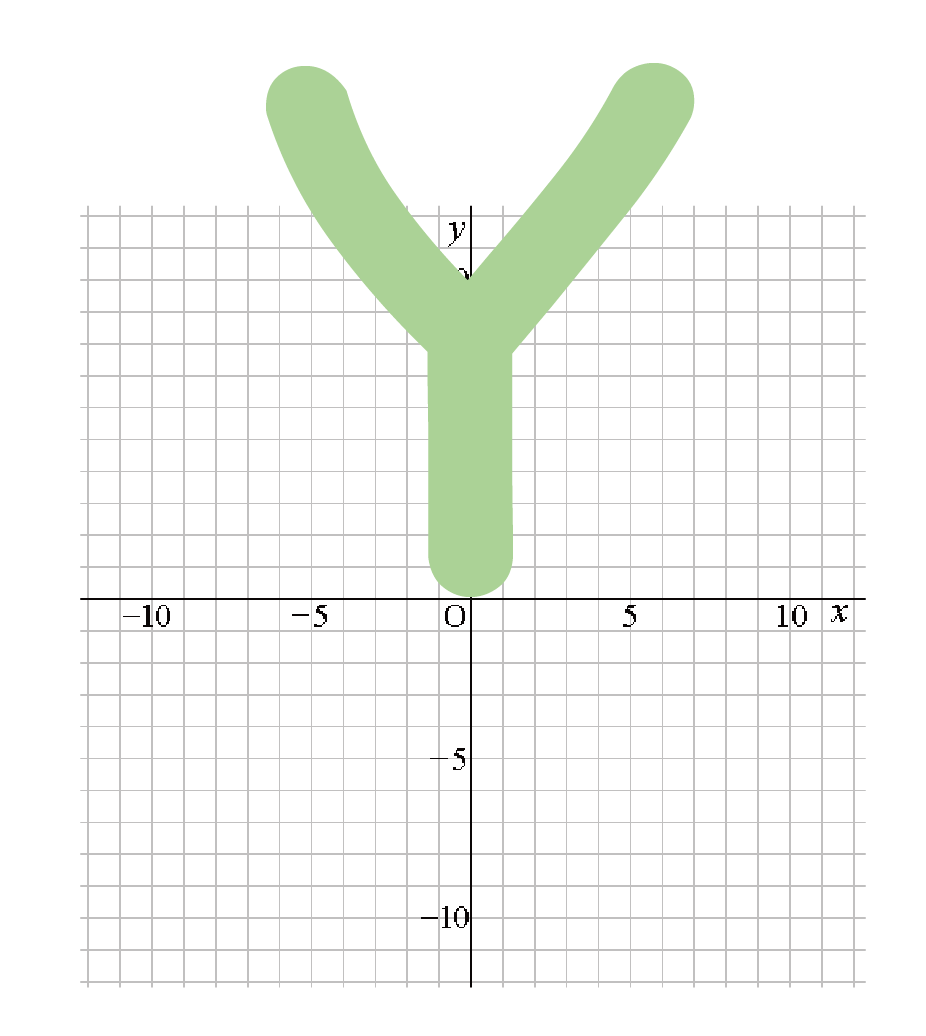
その理由は、
「Y」は縦に足が一本のびているからなんだ。
縦に足がながいY軸は「たて軸」って覚えてあげればいいね。
つぎはx軸の覚え方だね。
x軸はヨコ軸なのことを指すんだ。
ヨコ軸。
ヨコ軸。ん?ヨコ??
おや、ヨコのようすが・・・
トゥルトゥル??
トゥットゥー
トゥットゥー
トゥットゥー
ドン、
おめでとう、
「ヨコ」は「x軸」に進化した!
って感じだね。 かなり強引だけど、「ヨコ」というカタカナをいじれば「x」にみえちゃうよね??
この過程をおぼえておけば「x軸を横軸」だとおぼえられるはず!
どう?? x軸とy軸の名前は覚えられたかな??
ここで紹介した奇妙な覚え方を駆使して、x軸とy軸をごちゃまぜしないようにしようね。
そんじゃねー!!
Ken
こんにちは、この記事を書いているKenだよ。カレーはだんぜん辛口派だね。
中1数学でならう関数で登場するのが、
座標(ざひょう)
っていう言葉。「がびょう」ならきいたことあるけど「座標(ざひょう)」っていったい何者??
なんで関数と一緒に勉強しなきゃいけないんだろう。

今日はそんな疑問にこたえるために、
関数に必要な「座標」とはなにものか??
ということを解説していくね。中学数学の座標がよくわからん!ってときは参考にしてみてくれ。
~もくじ~
まず座標とはいったい何ものなんだろうか。オンライン大百科Wikipediaでちょいと調べてみると、
点の位置を明確にするために与えられる数の組のこと
らしいね。なるほど、数の組のことを言うんだね。
中1数学ではおもに、
xとyの数の組
を座標として表すんだ。たとえば、(x, y) = (8, 9)といったぐあいに。これはxが8のとき、yは9ですよーって言っている。
しかも、下の方眼紙みたいなものに座標をかくことが多いね。
こんな感じで↓↓
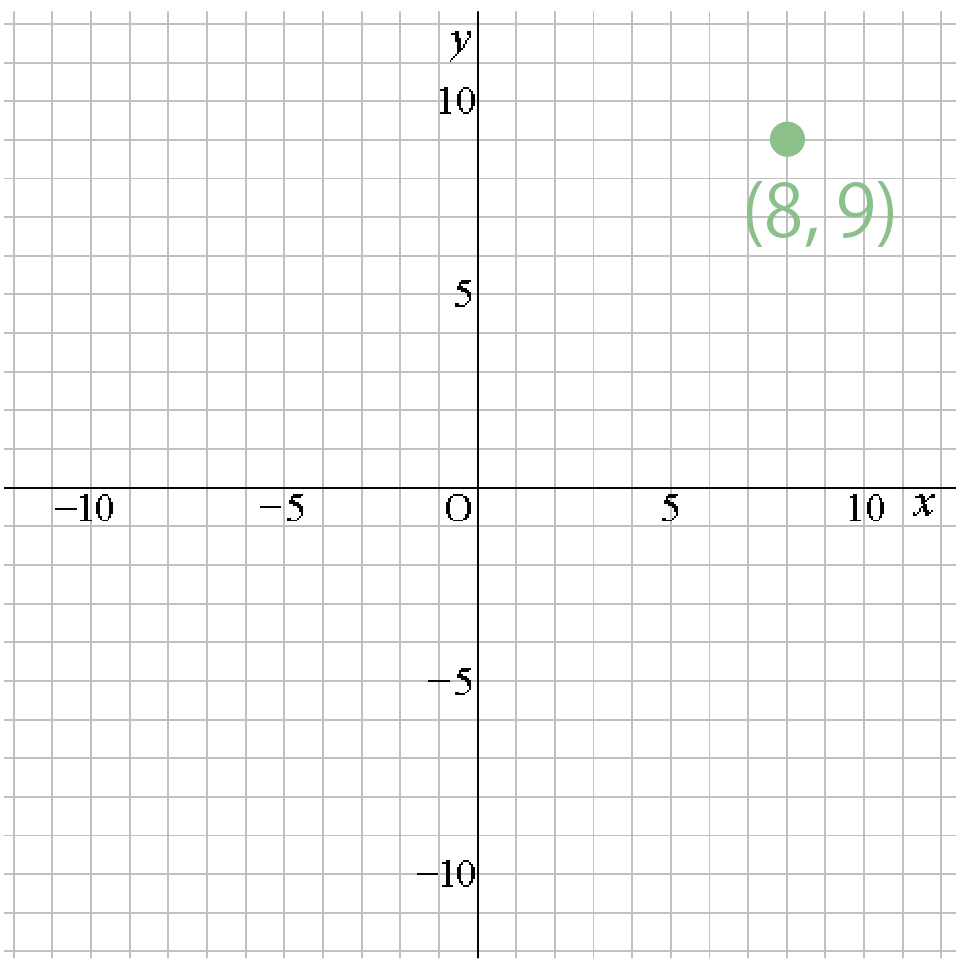
じゃあ、なんで関数のために座標をつかわなきゃいけないんだろう!??
ちょっとだるいしかっこよくないよね。
その訳は、関数の性質にあるんだ。
関数とはなにか?という記事で、
関数は、
「何を入れるか」によって「出てくるもの」が違うマシーン
って習ったよね??
たとえばAをいれたらBが出てくる関数があったとしよう。
この関数にCを入れたらDがでてくる。
xを入れたらyが出てくる、
何を入れるかによって出てくる値がちがうんだ!
つまり、
関数を勉強する上でいちばん大切なのは、
「入れる数」と「出てくる数」の関係
なんだ。
かりに、yはxの関数であるとすると、入れる数にあたるのが「x」、出てくる数にあたるのは「y」ということになるよね??
だから、
座標をつかって、
(x, y) = (8, 9)
というふうに、関数にいれる数(x)と出てくる数(y)のセットをまとめてあげるんだ。そうすると、xとyの関係をわかりやすくなるでしょ??
これが関数と座標を一緒に勉強する意味だよ。
ここまでの座標の説明はどうだったかな??
ちょっとめんどくさい気がするけど、一度コツがわかってしまえば座標の問題はカンタンさ。
だけど、いちばん大事なのは、
なぜ、関数の勉強に「座標」が必要なのか??
ということ理解していること。これに尽きる。
関数を勉強していて迷ったときは読み返してみてね。
そんじゃねー!
Ken
こんにちは、この記事を書いているKenだよー!
比例の式を攻略するためには「比例定数の求め方」が必要だ。
比例定数を求めておくれ。
って直接きいてくる問題は少ないけれど、
xとyの関係を式に表しなさい
って間接的にきいてくる問題が多いんだ。この問題に「比例定数」って言葉はでてこないけど、じつは比例定数の求め方を知らないと解けない。
だから、
比例定数の求め方を知っておいたほうがテストで有利なんだ。

だから今日は、
比例式の「比例定数の求め方」をわかりやすく解説してみたよ。
数学の試験前に確認してみてね。
~もくじ~
いちばん手っ取り早い比例定数の求め方を紹介するね。
あっ、今回は反比例じゃなくて比例の式の場合だから注意してくれー!
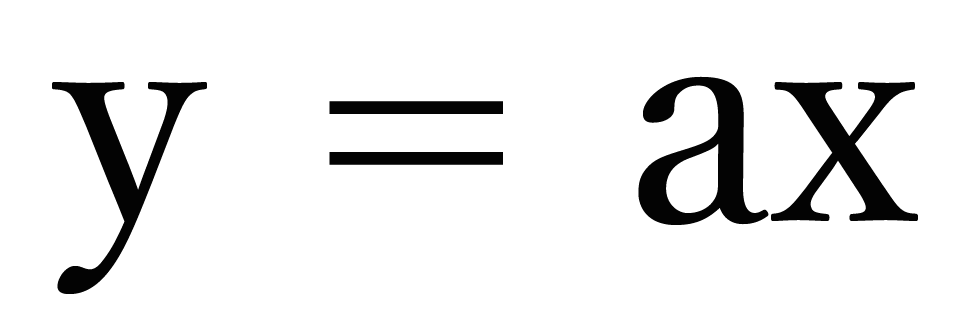
比例の式
上のような比例の式の「比例定数の求め方」は、
yをxで割る(y/x)
ってだけさ。
ね?
ものすごくシンプルな求め方でしょ。
それじゃあ、この求め方で比例定数を計算してみよう!
比例の式で出題されやすいのは次のようなタイプだ。
yはxに比例し、x = 9のとき、y = 54です。xとyの関係を式に表しなさい。
これはちょっとインテリ問題にみえるけど、さっきの比例定数の求め方をつかっちゃえば一発さ。
yとxは比例しているから、
y の値をxでわるだけで比例定数 a が求められるんだ。
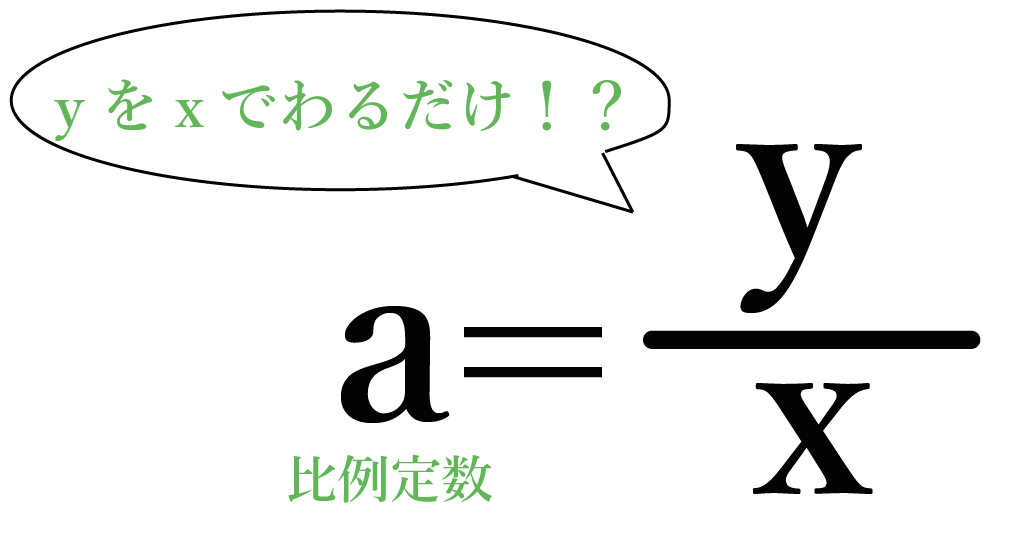
だから、
a = 54 ÷ 9
となって、
a = 6が正解だね。
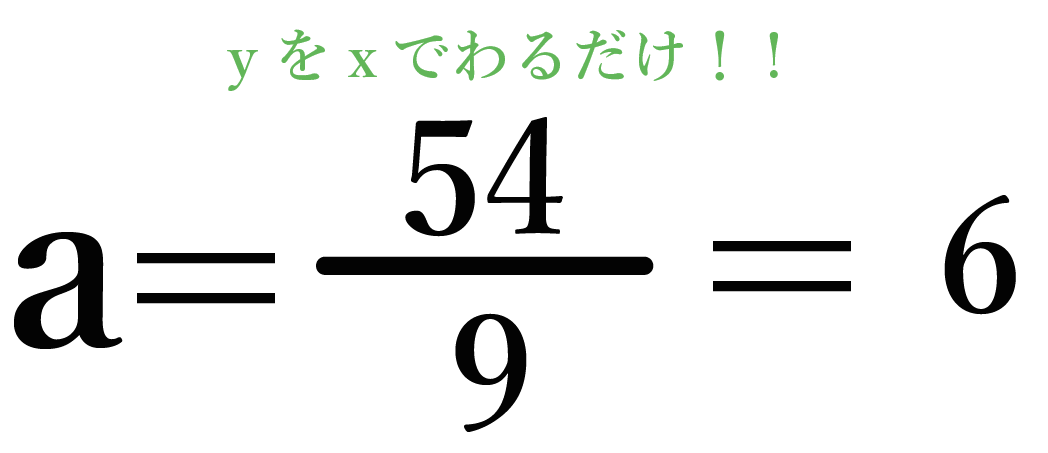
ね? 割り算が得意だったら5秒ぐらいで比例定数がわかるでしょ??。
比例定数aが6ってでたから、xとyの関係は、
y = 6x
になるね。y = axに求めたaをいれちゃえばいいんだ!
yをxでわるだけ
なんてカンタンすぎるよね??
じゃあなんで比例の式の「比例定数の求め方」がこんなにシンプルなんだろうか。
ゆっくりみていけばその理由がわかるよ。
ある関数yがxについて「比例する」ってことは、
y = ax
っていうカタチをした関数ってことだよね?? これは前回の「比例とは??」という記事で勉強したね。
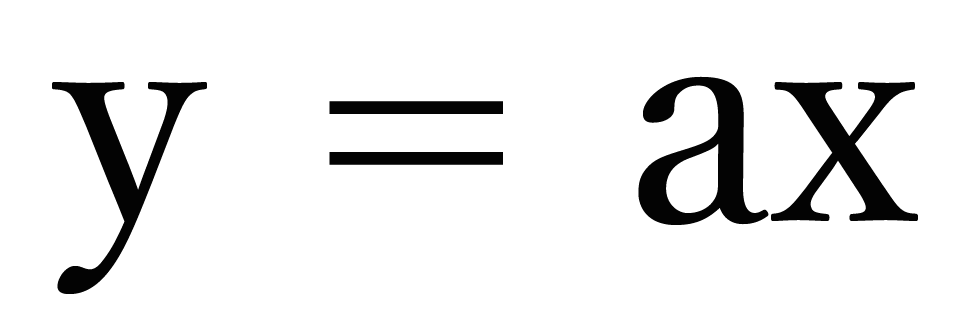
この式をよーくみてみると、
等式であることに気づくよね。だって、左と右が等号(=)でつながれているからね。
そこで、
等式の性質の1つの、
両辺を同じ数でわっても等式は成り立つ
っていうものを使ってみよう。 (忘れかけているときは等式の性質の記事をみてみてね。)
両辺をxで割ってあげるとこうなって↓↓
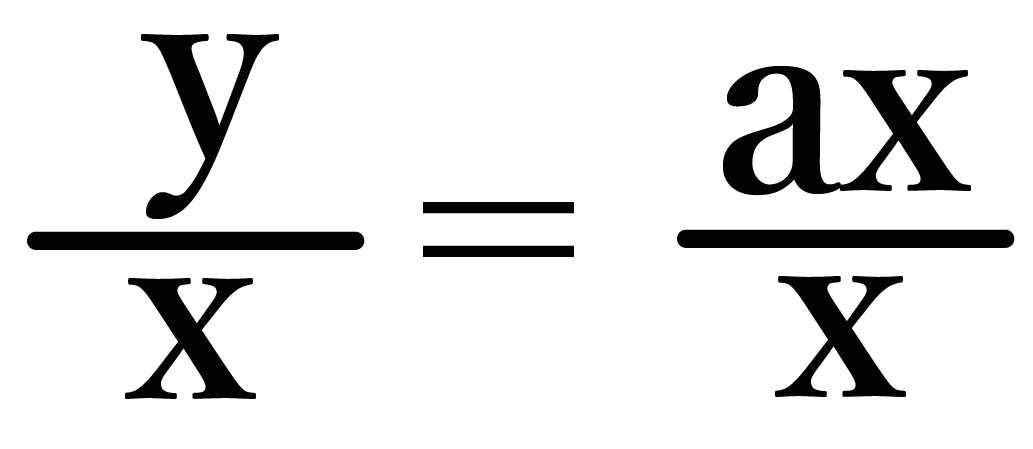
右の分子にのった「x」がきえるので、
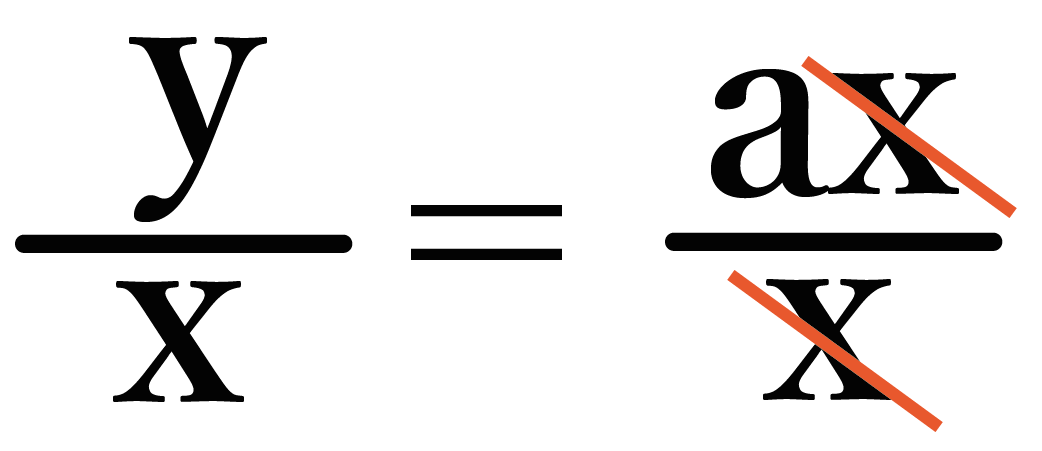
こうなるね ↓↓
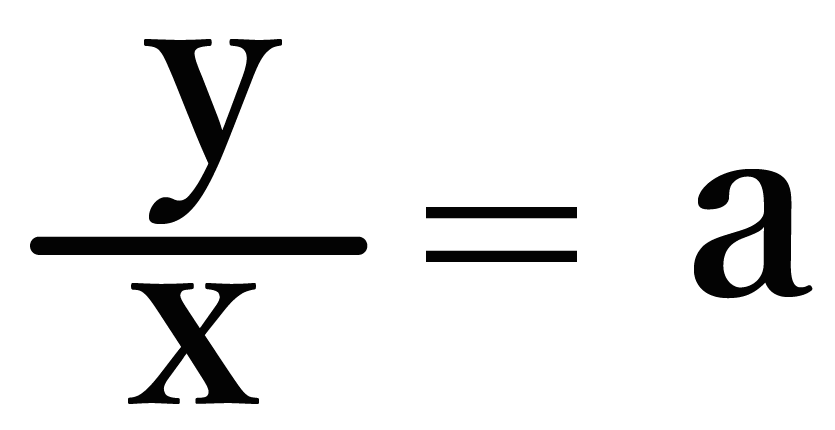
これはいちばん最初にみた、
a = y/xと同じだよね。
だから、比例の式では、
yをxでわっただけで比例定数aがゲットできるんだ。
どう?? シンプルでしょ??
yをxでわるだけ!
比例する関数のときは比例定数の求め方はカンタン!
テストでガンガン比例定数を求めていこうね。
そんじゃねー!
Ken
こんにちは、馬よりも像が好きなKenだよ。
中学数学の「比例の式」で勉強するのは、
比例(ひれい)
だね。ふつうの人は「ひれい」ってきくと、魚の「かれい」と間違いそう。 それくらい、数学の勉強にしか登場しない用語なんだ。

今日は、この新しい言葉である「比例」をわかりやすく説明していくね。
記事を読み終わるころには、
yはxに比例する
という言葉の意味がわかるようになっているはずだ!
比例する関数ってなんだろうか?? ちょっとむずかしそうにだね。
超カンタンにいってしまうと、
「比例の式」って1つの関数のタイプのこと
なんだ。
関数を自動販売機に例えると、比例がもっとわかりやすくなるよ。
この前、「比例とはなにか」という記事で、
関数は「自動販売機」、ってたとえたよね??
その自動販売機にもいろんな種類がある。
たとえば、ちょっと青い自動販売機だったり、

タバコしか売ってないマシーンだったり、

http://kohtguchi.at.webry.info/200702/article_4.htmlより
コーラしか売ってない自動販売機だってこの世にはある。

http://www.qzs.jp/events/201411g-expo/demo141114.htmlより
お金をもらったら商品を出す
っていう仕事はしているけど、出すものが違ったり、お金の種類が違ったりするよね??
こんなふうに、自動販売機の種類は世の中にもたくさんある。
それと同じで、
比例する関数
というのも、世の中にある多くの関数の中の1つの種類、ということなんだ。
だから、比例する関数がすべてじゃないってことは頭に入れておこう。
じゃあ、比例する関数ってどんな奴かって話になるよね??
比例の式は関数の中で、
y = a x
というカタチをとっている奴のことなんだ。
どう?? ちょっとカッコいいでしょ。?
yとxは、xに入れる数によって変化する数だから「変数」というものだったね。
じゃあ、残りの「a」はなにかっていうと、
定数
というやつなんだ。
定数とは言葉通り、
定まっている数
のことだよ。つまり、どんなに頑張っても変われないでじっとしている数ということさ。
だから、xに1をいれても、10をいれても、1億をいれても、
aの値は変わらないってこと。
そんで、
とくに「比例の式に入っている定数」のことを「比例定数」って呼ぶんだ。
テストに出やすいから覚えておこう!
こんな感じで「y = ax」というカタチをとっているとき、
yはxに比例する
というんだ。ね?スッキリしたでしょ??
えっ。比例の式の具体例がみたいだって??
比例定数が分数であれ小数であれ、負の数であれ、
y = ax
のカタチになっている関数は比例するって言われるんだ。
だから、
っていう関数たちはみな「比例する関数」なんだ。だって、y = ax のカタチになっているからね。
比例もカンタンだったでしょ??
y = ax
という関数のカタチを覚えてしまえば大丈夫。
次回はもうちょっと踏み込んで「比例定数の求め方」を解説していくね。
そんじゃねー。
Ken
こんにちは、この記事を書いているKenだよ。まんじゅうを食べたい。
関数を勉強するって大変だよね??
「関数の意味」とか「変数」とかの用語をおぼえなきゃいけないからさ。
※ 関数の意味がわからないときは「関数とは??」という記事を参考にしてくれ。
その「関数」の用語の中でもヤッカイなのが
「変域(へんいき)」
という言葉だ。変域ってまちがいなく日常生活ででてこない単語だし、ちょっと怪しいよね??。

そこで今日は、
関数の変域とはなにか??
ということを説明していくね。
関数の変域ってなんだろうか。とりあえず教科書をみてみると、
変数のとる値の範囲
のことを「変域」っていうらしい。
ん??
これじゃあイマイチぴんと来ないから、具体的な関数の例をみてみよう。たとえば、
「y = 2x」 という関数があったとする。
この関数での「変数」って「x」と「y」だったよね??
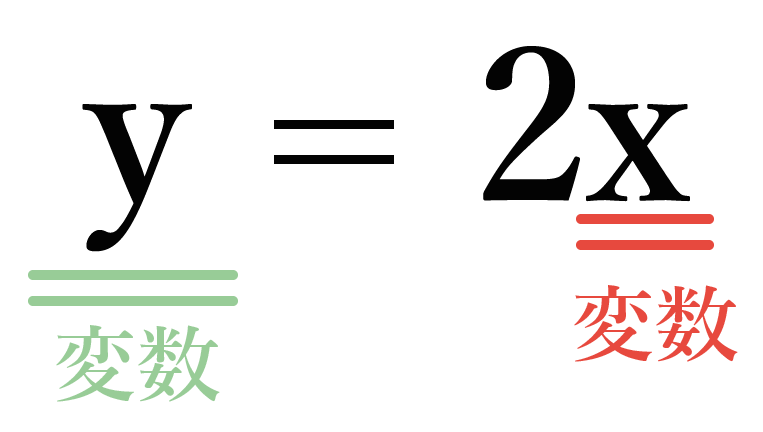
だって、xを変えるとyの値も変わるからね。たとえば、xに「2」をいれたときと、
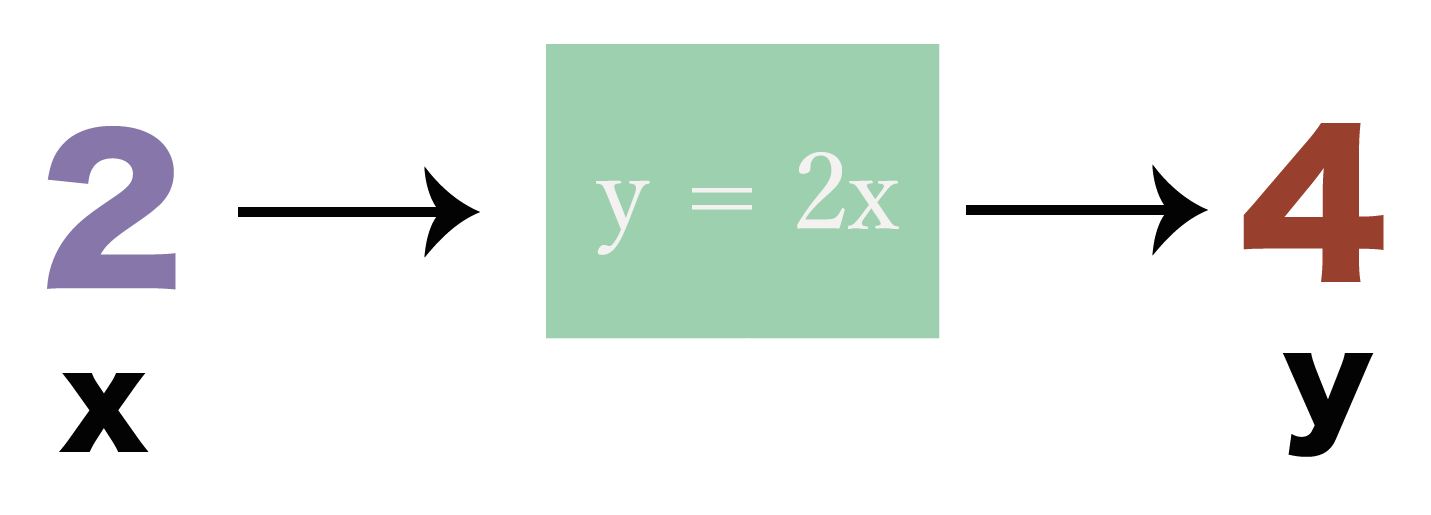
「3」をいれたときじゃyの値は変わってくるでしょ??
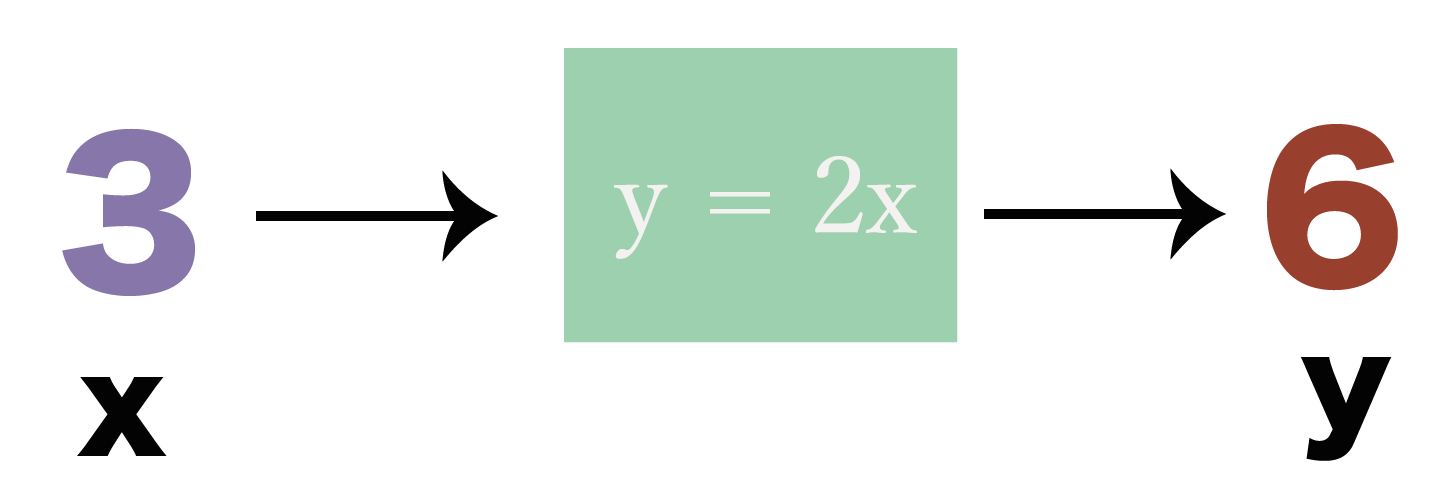
こういう、色んな数を入れたりできる数や、それによって異なる数字がでてくる文字を「変数」って呼んでいたね。
xとyのような変数がとれる「値の範囲」のことを「変域」っていうんだ。
たとえば、
「y=2x」という関数の調子がわるいとしよう。故障中のため、xに入れることができるのは、
0以上2以下の数
っていうことになった。
これが「xの変域」だ。数式であらわすと、
0 ≦ x ≦ 2
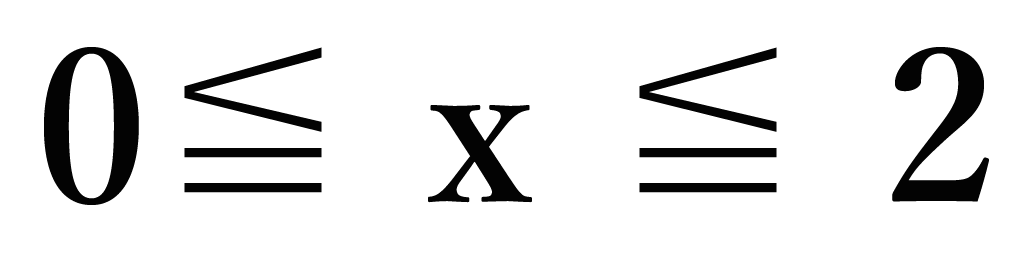
となるね。
このxの変域が「y = 2x」で適用されるとき、
xに2を入れることはできても、
xに3を入れることはできないんだ。
だって、xは「2以下」じゃなきゃダメよ。
っていう変域が設定されているからね。
中1数学で「変域」といえば、
「変数xの範囲のこと」を指す場合が多いよ。
変域がxかyのかで迷ったら「xの変域」ってことにしちゃえばいい。
関数とはなにか??という記事で、
関数は自動販売機みたいなもんだよ。
って説明したね??
変域の意味を理解するときも「自動販売機のたとえ」をつかってあげると分かりやすいんだ。
たとえばここに、自動販売機があったとする。ちょっと古い。
で、じつは、
500円玉を認識できなくて、しかも一回に1枚のコインしか入らない
という故障をかかえていたとしよう。
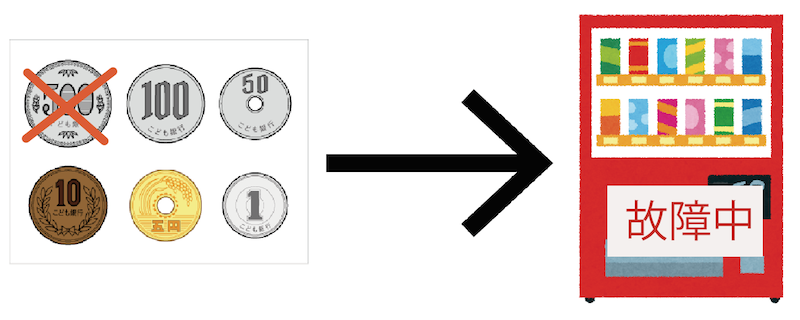
このとき、この自動販売機にいれるお金をxとしたら、xの変域ってなんだと思う??
そう。
0 ≦ x ≦ 100
さ。えっ、なぜなら、
お金を何もいれない状態(x=0)がいちばん小さくて、
100円玉を1枚いれる状態(x=100)がいちばん大きいからさ。500円玉(x=500)は
0 ≦ x ≦ 100(0以上100以下)
という変域の外にでてしまってるね??
だから、500円玉は入れられないんだ。どう??ちょっと変域が身近になったでしょ??
関数の変域がちょっとわかったような気がした??
次回はいよいよ「比例」について勉強していくねー!
そんじゃねー。
Ken
こんにちは、チャーシュー麺が好きなKenだよ。今日も一緒に中学数学を勉強していこう!!
中1数学の「変化と対応」っていう単元に入ると、
関数(かんすう)
って言葉がでてくるよね??

これは小学校の算数でも出てこなかった奴だね。ちょっと強そうだけど怖そう??。
今日はこの「関数」とはなにか??っていうことを勉強していくよ。
授業で習った「関数の意味」にイマイチピンときてないキミ! よかったら参考にしてね。
関数とはいったい何者なんだろうか??
その正体をつかむためにオンライン百科事典のWikipediaで調べてみよう。
コチラのページによると、関数とは、
数の集合に値をとる写像の一種である
って書いてあるね。
はじめて関数に触れる奴にとって、この意味はむずかしすぎない??。 何回読み返してもよくわからない!!
このページにも書いてあるけど、じつは、
関数って自動販売機にたとえると分かりやすくなるんだ。

ちょっとみてみよう!!
関数とは自動販売機である!!
って自信満々にいってみたけど、いったい関数のどこが自動販売機っぽいんだろうか??
この真相をさぐるために、自動販売機のしくみをちょっと復習してみよう。

キミは自動販売機でジュースを買いたいとき、まず何をする??
そう、お金をいれるはずだ。
じゃあ自動販売機にお金をいれたらどうなる???
そう、ジュースが出てくるはずだ。
つまり、自動販売機の中で起こっていることって、
お金をジュースに変えた
ってことなんだ。
そして、自動販売機にはもう1つ特性がある。
それは、
入れたお金によって出てくるものが違う
ということだ。
たとえば100円のジュースを買いたいとしよう。

このとき、自動販売機に100円をいれてボタンを押してやれば、
「100円ジュース」がガシャコっとでてくるはず。
つぎに、いれるお金を変えて500円玉をいれたとしよう。
すると、
今度はチャリチャリとガシャコっていう音ともに、
「400円のおつり」と「100円のジュース」の2つがでてくるよね??
つまり、
自動販売機に何を入れるかによって、でてくるものが違う!
ってことが言えるんだ。ね??そうでしょ??
関数もこれと同じ。
ある関数に「A」という値をいれてあげたら「B」が出てくるんだ。
なんだろう、たとえるなら手品のマジックボックスだね。鳩をいれたら人間になる、みたいな箱あるでしょ?? あれあれ。
つまり、
何かをぶち込んだら何かがでてくるマシーンみたいなもの
が関数だと思っていいよ。
で、ひとつ気づくのは、
関数に何を入れるかによって、出てくるものが違う
ってこと。
自動販売機でも100円玉のときと500円玉のときでは出てくるものが違ったでしょ?? あれと同じさ。
Cを入れたらDがでてくるんだ。Bじゃない。
よーくみると、
関数に「入れるもの」と「出てくるもの」は変化しているね?? AをいれたらBがでてくるし、CをいれたらDが出てくるっていう感じで。
だから、数学では、
この「入れるもの」と「出てくるもの」を「変数(へんすう)」って呼んでいるんだ。
そんで、中学校で勉強する関数はほとんど、っていうか、たぶん全部が、
Aを「x」、Bを「y」としている。
つまり、xに何かを入れたらyっていうものが出てきましたよ!っていう関数ばかりだということ。
このとき、数学では、
yはxの関数である
というんだ。
ちょっとカッコイイから覚えておこう!!
xの関数であるyの具体例を紹介しよう。
中学1年生では、
y = 2 x
のようなシンプルな関数が登場するよ。
この関数のxに数字の「2」を入れてあげるとyの値は「4」になるし、
xに「3」を入れると、yは「6」になるね。
xに何をぶち込むかによって、yの値がちがう。
これが関数さ。
これからゆっくりと中学1年生で勉強する関数の単元をみていこうね。
そんじゃねー!!
Ken
こんにちは、めんつゆと醤油を間違えたKenだよー!
中学数学の「速さ」の文章題ってけっこうヤッカイだよね。たぶん、速さの文章題がちょっと難しいのって、
速さの単位変換・換算
がめんどくさいからなんだ。
分速とか秒速とか時速とkmとかmとか!!
もういい加減にしてくれ!ひとつにまとめてくれ!!
なんて思っちゃわない??。

そこで今日は、速さに関する文章題をすらーっと解くために、
速さの単位変換・換算の方法を2つだけ紹介するね。
これをマスターしていれば中学数学ででてくる速さの問題なんて怖くないさ。
数学の教科書にでてくる「速さ」って、よーくみてみるとこんなカタチしてるよね??
○速☆△

えっ。ちっともよくわかんない?? そうだなあ、たとえば教科書によくでてくるのは、
分速5m
みたいな速さだよね??
これをよーくみてみると、
分速の「分」は○で、5mの「5」は☆に入って、△には5mの「m」が当てはまるね。
これが中学の数学で勉強する速さの基本形だ。そんで、この基本形をもっとよくみてみると、
速さが、
「時間パート」と「速さパート」の2つから成り立っていることがわかるんだ。

じつは、
速さの単位の変換や換算って、
時間のパートをいじるか??
もしくは、
道のりパートをいじるか??
の2通りしかないんだ。だから、基礎さえ理解しちゃえば、むずかしい速さの単位変換だってできちゃう。
ね?おもしろうそうでしょ??
1つ目の方法は速さの「時間パート」を変えちゃう換算方法だ。速さの前についてるこの部分をいじっちゃおうってわけ。

この「時間パート」に当てはまるパーツってぜんぶで3つしかないんだ。それは、
それで、「分速」から「時速」、「時速」から「秒速」へ変換するときは、以下の図のように60または3600をかけたり、割ったりしてあげればいいんだ。
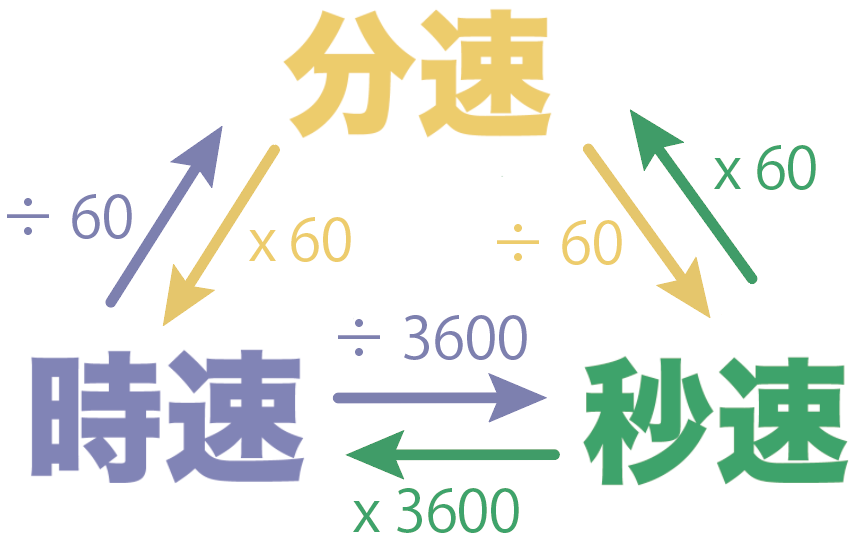
これは時間をいじる変換方法だ。
便利だから、
分速50mを時速に換算することもできちゃうよ。分速から時速に変えるときは「60」をかければいいから、 
時速3000m
になるね! これで速さを変換できたね。
2つ目の方法は、
速さの「道のりパート」をいじっちゃう変換方法だ。速さの後ろにくっついてるパーツだね。
速さの「道のりパート」には大きく分けて、3つの種類が中学数学ではでてくるんだ。それは、
の3つの距離の単位さ。
これらは互いに次のような関係になっているんだ。
という関係があるからさ。これは長さの単位で「k」が1000倍を意味し、「c」が100分の1を表しているからこうなっているんだ。
この方法をつかってあげれば、
さっきの時速3000mという速さは、
時速3kmと同じってことなんだ。だって、3000mは3kmってことだからね。
こっちの方がスッキリしてて気持ちいいでしょ??
これが速さの「道のりパート」をいじるっていう換算方法だ。しっかり覚えておこう。
ここまでが速さの単位変換の方法だよ。どうだったかな??
テストで速さの文章題がでたら、問題の「道のり」や「速さ」の単位をよーくみて、いまどんなことを計算しようとしているのか立ち止まって考えみよう。
そしたら、速さの文章題に対する苦手意識もなくなるはずさ。
そんじゃねー!
Ken
こんにちはー!さしみこんにゃくが好きなKenだよー 今日も一緒に中学数学の勉強をしていこう!!
方程式の文章題で「速さ」のやつを苦手って子が多いよね??
たしかに時速とか分速とか速さとかよくわからないし、図を描いても解けそうな気がまったくしてこない。これは弱ったね。

あまり知られてないけれど、
速さの文章題をすばやく解くには、
速さ・時間・道のり(距離)
という3つを理解していることが必須になってくるんだ。だから、今日はこの「速さ」・「時間」・「道のり(距離)」を順番にゆっくりと説明していくね。
これらの3つを踏まえて「速さの公式」もおぼえてみよう。
記事を読み終わる頃にはきっと、文章題の速さ問題が得意になっているはずだよ!!
~もくじ~
「道のり」とか「速さ」とか「時間」はどんなときに必要なんだろう?? ふだん見かけないからちょっと気になるよね??
じつは、
「人やもの」が「地点A」から「地点Bまで」移動したときに必要なんだ。
たとえば、小学1年生の太郎くんが「自宅」から「図書館」へ自転車で移動した、
みたいにね。
この「移動のイベント」が発生したとき、「道のり(距離)」や「速さ」が必要になってくるんだ。
最初に理解したいのは「道のり」の意味だね。
ずばり、
道のりとは、
ある人や物が移動した距離
のことなんだ。たとえば、さっきの例で、太郎くんが家から図書館まで移動したよね?? このときの「道のり」は「家から図書館までの距離」ってことなんだ。
調べてみると、家から図書館までの距離はちょうど2kmだっとしよう。
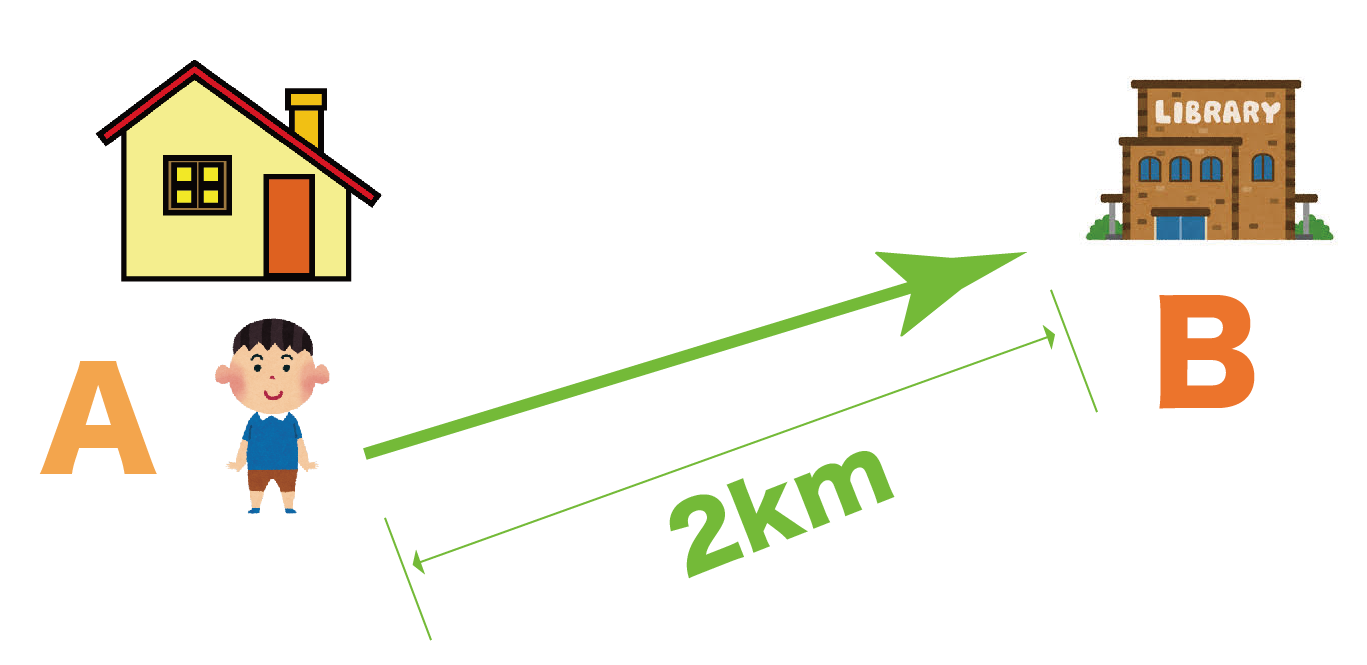
このとき、太郎君が移動した「道のり」は、
2km
ってことになるんだ。道のりも意外とカンタンでしょ??
次に「時間」ってなにかってことを見ていこう。
時間とはずばり、
ある人やものが移動した時間
のことだよ。たとえば、太郎君が2kmさきの図書館まで10分かかって自転車で移動したとしよう。
このとき、時間は「10分」ってことになる。だって、太郎くんの移動に10分かかってるからね。
これで時間と道のりはオッケーだね!!。
最後に「速さ」ってなにかってことを見ていこう。速さとは、
一定時間あたり進む距離
のことなんだ。ちょっとよくわからないね?? さっきの太郎君の例をみてみよう。
太郎くんは、
2kmを10分かけて移動した
よね??
これは間違いない。じゃあ、太郎くんは1分間あたりに何km進んだことになるかな??
そう、0.2kmだ。

2kmを10で割ると出てくる答えだね。なぜ10で割るのかっていうと、1分間あたりに進む距離を出したいからだ。
0.2kmを10倍すれば2kmになるよね?? つまり一分間に0.2kmすすむことができる速さで10分移動したってことを意味するんだ。
この場合は、一定時間を「1分間」としているね。このときの速さのことを「分速」っていうんだ。ぼんやりと覚えておこう!
これらを踏まえた上で「速さの公式」ってものが誕生する。
それは次の3つだ。
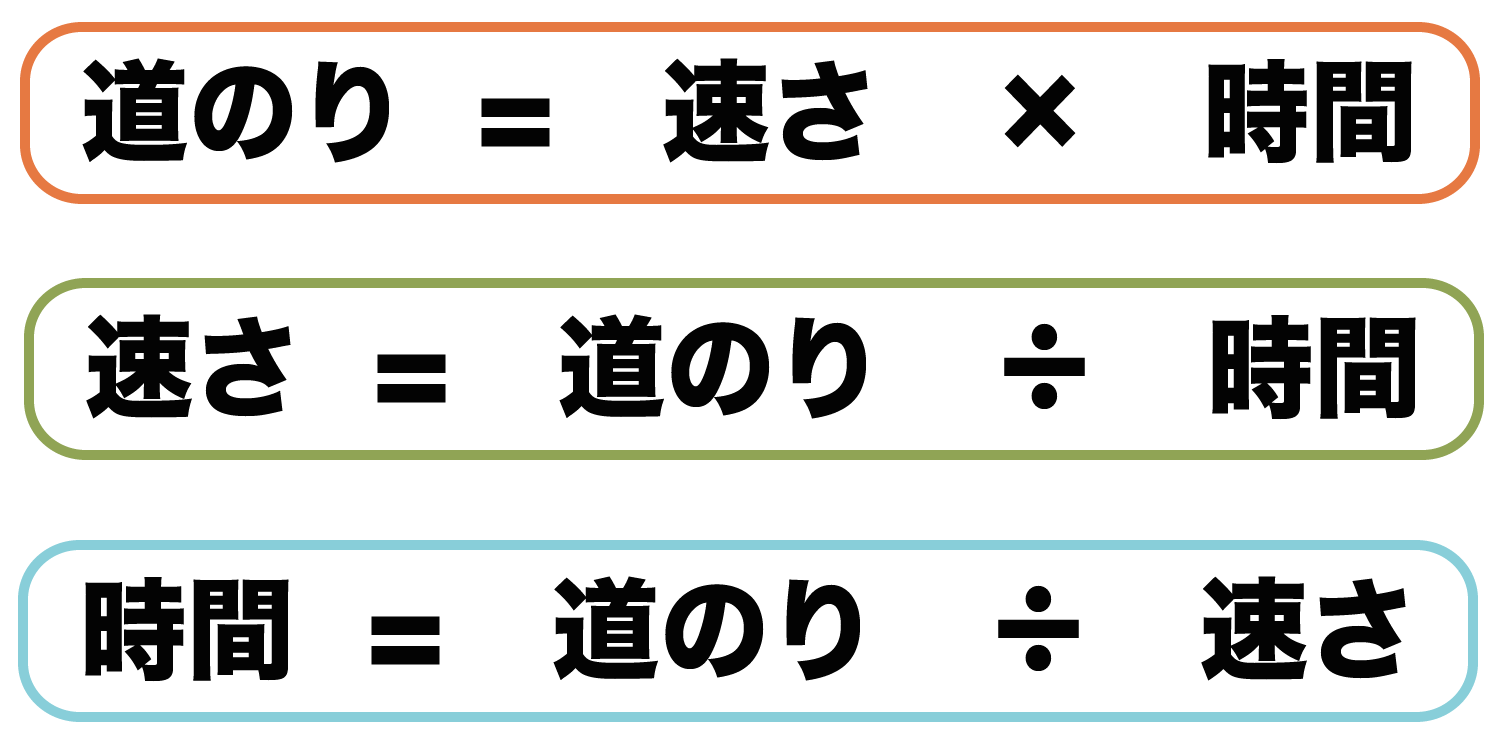
ちょっと公式が3つもあったら覚えにくいよね?? そんなときに使いたいのが次のアイテムだ。
名付けて、
速さ公式はやみ図
だ。
ちょっとドラゴンボールみたいに見えるけど、実際はもっとすごいものかもしれない。
使い方はいたってカンタン。
求めたいものを指で隠すだけ。
たとえば、「道のり」を求める公式を知りたいときは、こうやって親指をつかって道のりの欄を隠してあげるんだ。
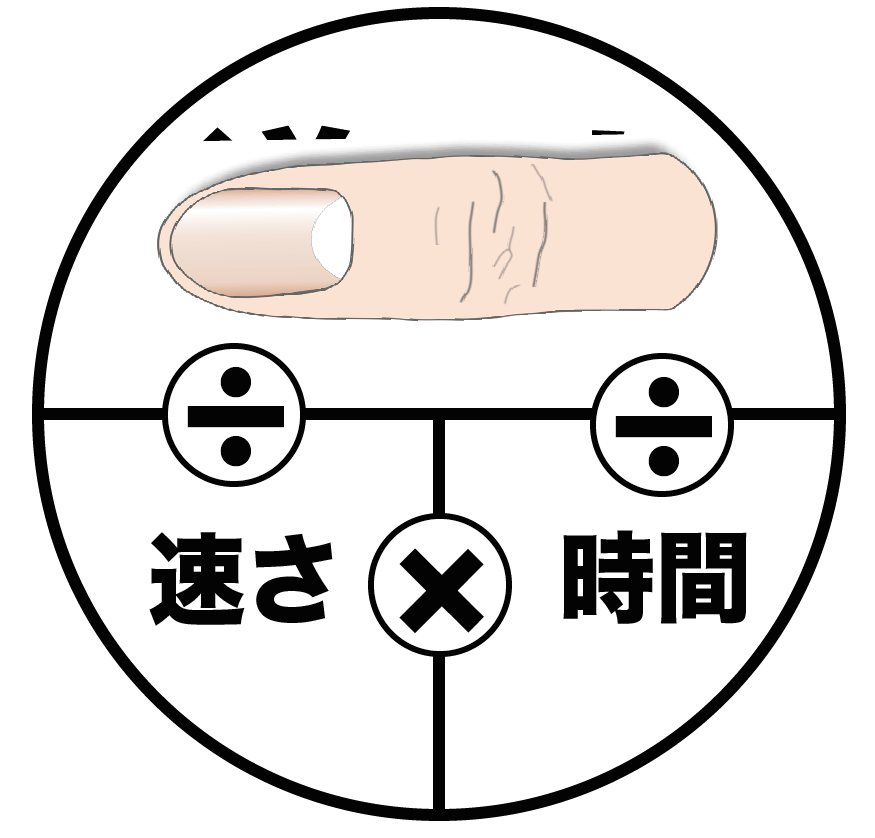
すると、「速さ×時間」っていう公式がでてくるでしょ?? これで「道のり」が求められるわけだ。
「速さ」も「時間」も同じように求めることができる。
「速さ」を求めたければ、「速さ」を指で隠したら「道のり÷時間」っていう公式が出現するし、
「時間」を隠せば、「道のり÷速さ」の公式がゲットできるんだ。
ね?? 便利でしょ! 速さの公式を忘れそうな時はつかってみてね。
次回は速さの単位について説明していくねー!!
それじゃねー!
Ken
こんにちは、リアルゴールドでシャキっとしたKenだよー!
方程式の文章題でいちばんむずかしいのは「速さ」に関するものだね! 文章題が苦手だと余計にヤッカイにみえちゃうんだ。
だけど、基本を押さえればどんな速さの文章題でも解けるようになるよ。
だから今日は、速さの文章題の方程式が苦手というキミのためにこんな記事を書いたんだ。
【苦手克服】方程式で速さの文章題を攻略する4つのコツ
ってやつさ。速さの文章題に苦手意識を持っていたら参考にしてみてね。
ソレ以前に一次方程式の文章題ぜんたいに苦手意識を持っているときは「【方程式の利用】一次方程式の文章題の4つの解き方」っていう記事がおすすめだよ。
速さの文章題を攻略するために知っておきたいコツは次の4つだ。よーく目をこらして確認してくれ!
速さに関する文章題をすらーっと解くためには基礎知識を身につける必要があるんだ。速さの文章題での基礎知識って、
の3つの用語の意味を理解すること。これに尽きる。
意味と使い方さえ覚えてしまえば、速さの文章題もイチコロさ!
速さ・道のり・時間
の3つに関しては別の記事で徹底的に解説したのでそっちをみてみてね!ゆっくり読めばきっとわかるはず。
速さの文章問題で間違えやすいのは単位の違い。
これを知らないで文章題と取っ組み合うと返り討ちにあっちゃうね。
それぐらいけっこうヤッカイな問題なんだ。
たとえば、「みちのり」には、
km・m・cm
といった単位があるし、
「速さ」には、
時速○○km、分速○○m、秒速○○mといった単位があるね。もちろん、時間にも、
時間・分・秒
といった単位がある。このたくさんある単位たちの関係を知っておけば大丈夫! 速さの文章題なんかビビることないんだ。
「速度の単位変換の記事」は別に書いたからこっちを参考にしてみてね!!
方程式の文章題の第一ステップは、
なにをxとおくか??
だったよね。速さの文章題はただでさえむずかしいから、なにをxとおくか迷っちゃうはず。だけれど、超難関校の入試問題じゃない限り、
文章題の中で
求めてね。
っていわれているものをxとおけばいいんだ。あ、でも単位には気をつけてね。
たとえば、
文章題の最後に、
家から図書館までの道のりは、何kmですか??
って書いてあったら、「家から図書館までの道のり」を「x km」とすればいいんだ。文章題の最後をみるだけだからカンタンでだね!
速さの文章題でも図をかくとわかりやすいんだ。
自分の好きなようにどんなグラフをかいてもいいけど、ぼくが気に入っているのはこんな感じの図 ↓↓
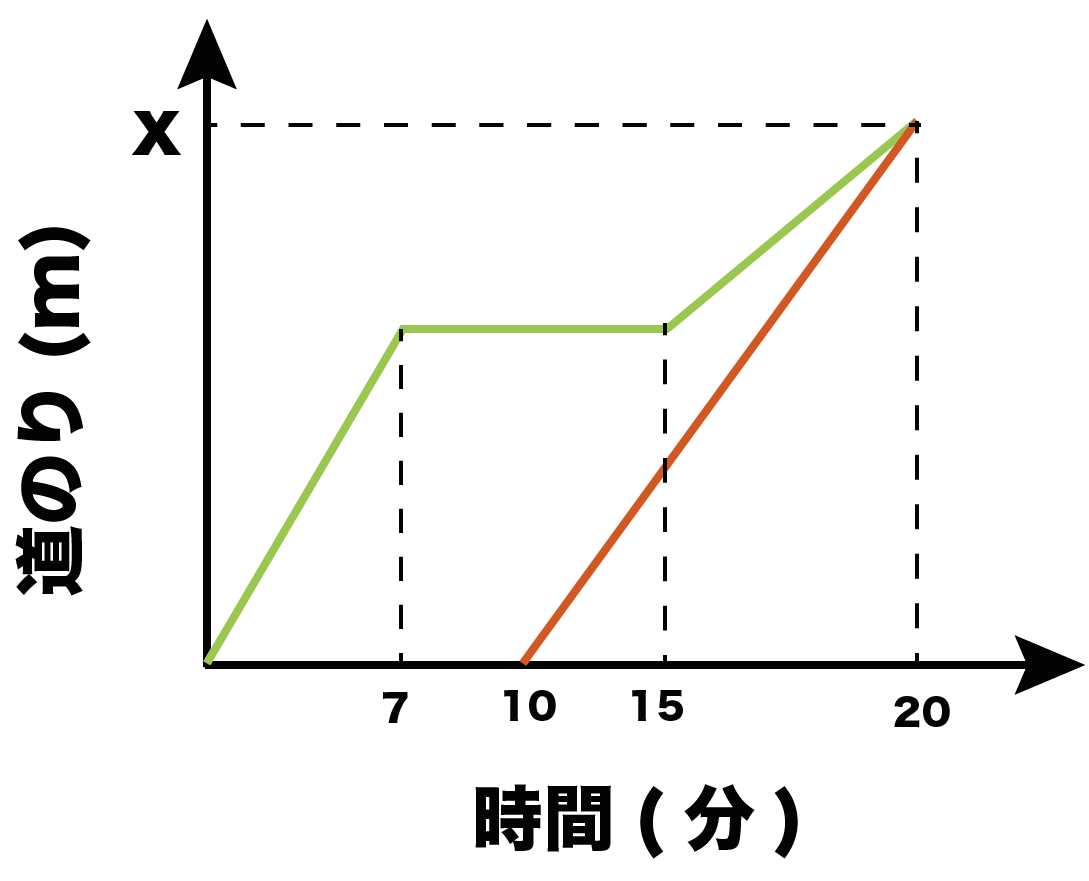
先に家をでちゃった忘れん坊の弟を、ねえちゃんがチャリで追いかけるっていう文章題だよ。
時間と道のり、っていう2つの軸が入ったグラフ・図を書いてあげると速さの問題はグンとわかりやすくなるよ。
文章題が苦手だと思ったら試してみてね。
ここまでざーっと方程式の文章題(速さ)のコツをみてきたね。どうだったかな?? ちょっと解けそうな気がしてきた??
「速さ・時間・道のり」がよくわからん!
ってときは上で紹介した記事を読んでみてねー!!
そんじゃねー。
Ken
こんにちはー!みそ汁なら作れるKenだよ!
方程式の解き方はマスターできたかな?? まだちょっと心配だなあ・・ってときは次の記事読んでみてね。
ただ、中1数学の方程式は解き方を覚えるだけじゃダメなんだ。
その解き方をつかって、いかに文章題を正確に解いていくかがテストの勝負の分かれ目になるよ。
今日は「1次方程式の文章題の解き方」を4つ紹介するね!
ポイントを押さえればむずかしい文章題がでても大丈夫。落ち着けばきっと解けるはず!
次の文章題を例として解き方を確認してみよう!
方程式の文章題が苦手だと思ったら、とりあえず図を描いてみよう。
意味がないときもあるけど、図を描くことで頭がスッキリするよ。解き方をひらめくときがあるんだ。
なにもせずに文章題を何度も読み返すより、
とりあえず図を描く
ってことはかなりお得。おそれずに前にすすんでみよう。
そうだなあ、この文章題だとちょっと難しいけど図を描いてみようか。
3年B組の教室にはとりあえず義理チョコがある。

だけど、具体的にチョコが何個あるかっていうのはまだわかってないね?
そんで、3年B組の男子生徒に2個ずつ配ると9個チョコが余っちゃうらしいんだ。男子生徒の数もチョコの数と同じようにまったく不明って状態。

だったら違う方法で!
ってことで、男子生徒に3個ずつ義理チョコを配ってみると、
ちょっとあげすぎたらしく、
4個チョコが足りないってことになっちゃうんだ。
そんで、この文章題で求めなきゃいけないのは、
3年B組の男子生徒の数!
だよね??

こうやって図を描いてみると、文字だけの文章題がちょっと現実っぽくなるでしょ??
頭がこんがらがったら図を描いてみるのは方程式の文章題の王道だね。
一次方程式の文章題で大切なのは、
どの値をxとするか???
ということ。これによって、方程式のカタチが変わってくるし、問題を間違える可能性も小さくなったり大きくなったりする。
文章題にはいろいろな数があってわかりにくいけど、じつはだいたいウマくいく鉄則があるんだ。
それは、
文章題で求める値をxとする
という解き方。これならば、文章題にそって方程式をたてて、それを解いてしまえばそれが文章題の答えにもなるんだ。
お得だし、カンタンだし、x選びに迷わなくていいよね。
これでうまくいかない例外もあるけど、95%の確率でうまくいくね。
経験上。
だから、とりあえず問題で求められている値をxと置いてみよう!
さっきの義理チョコの例題だったら、
「3年B組の男子生徒の数」
を求めるんだったよね?? だから、この文章題でも「男子生徒の数」を「x人」とおいてみよう。
これが方程式の文章題をさくさく解く第一ステップさ!
方程式をつくるってことは、
「天秤を釣り合わせる」のと同じなんだ。
だから、
何と何が等しくなりそうか??
ってことを見極めなきゃいけない。さっきの義理チョコ文章題で等しくなりそうな2つの値ってどれだろうか??
この文章題をよーく見つめていると、
男子に何個配ろうが、義理チョコの数はかわらない!!
っていうことに気づくよね?!? 男子の気持ちになればわかるはず。
だから、この文章題では、
男子に2個ずつ配った場合と、
3個ずつ配った場合の、
2つの場合においても義理チョコの数は変わらない
ってことを表してやればいいんだ。
男子生徒の数をxとしているから、
2個ずつあげたときは「2x」個のチョコを男子たちにあげたことになるよね?? それで、義理チョコが9個余っているわけだから、このときの義理チョコ数は「2x + 9」と表せるんだ。
同じように、
3個ずつあげたときは「3x」個のチョコを男子にあげたことになるね。でも、結果的にチョコが4個足らなくなったらしいから、義理チョコは3xよりも4個少ない「3x – 4」って表せるね!
2つの場合の義理チョコ全体の数は等しいから、
2x + 9 = 3x -4
っていう方程式が立てられるね!
この方程式をていねいにゆっくり解いてあげればいんだ。
ね? なんだかできそうな気がしてきたでしょ??
文章題からつくった方程式を解いておしまい!!
って言いたいところだけど、これで文章題は終わらないんだ。
あと一つやることがあるんだよねー。
それは、
方程式の解が文章題の答えとして妥当かチェックする、
ということ。文章題と関係ない方程式なら、どんな値がでても何も文句はなかったけれど、文章題はひと味違う。
文章題にちゃんとフィットした答えじゃなきゃ正解じゃないんだ。
たとえば、先ほどの義理チョコ文章題の例をみてみよう。
無事に方程式をつくり、解いてみたら、
x = -13
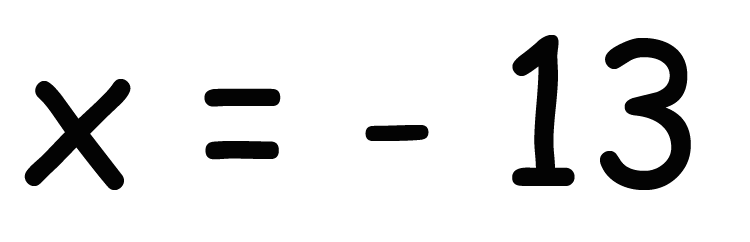
っていう方程式の解が得られたとしよう。えっと、だから、この文章題の答えは-13っと・・・・・
ちょ、
ちょと待って!!
xって何だったか確認してみて!!
たしか、xを「3年B組の男子生徒の数」って置いたよね!
ってことはもしxが「-13」だとすると、
男子生徒が「-13人」ってことになっちゃう!!
男子生徒はもともと人間の仲間だから、男子が-13人っていうと・・・・消えてるのか??。 ってことになっちゃう。人間の数にマイナスもクソもないよね??
だから当然、マイナスが解だったらおかしいってことに気づくはずだ。ミスに気づいたらどのプロセスで間違えてしまったのかチェックしてみよう!!
ふつうの計算問題だったら気づかないミスも、文章題なら気づけるんだ。
解が文章題の答えとして妥当かどうか確認してみよう!!
1次方程式文章題の解き方はどうだったかな?? ゆっくりやればできそうな気がするでしょ??
文章題にはいくつか出題のパターンがあるから、問題集とかテキストの演習問題を何度か解いてみて! きっと文章題マスターになっているはずだ!
次回は「速さ」にかんする文章題の解き方を解説していくね。
そんじゃねー!!
Ken
こんにちは、マラソン好きのKenだよ。
比例式っていったい何のことだっけ?? 比例式とは下のような
2つの比が等しいですよ、
a :b = c : d
ということを表した等式のことだったよね。
それで、どういうときに2つの比が等しいっていえるかっていうと、
比の値が等しいとき
なんだ。
前回の「比の値」の記事で勉強した通り、左辺の「a:b」の比の値は「a/b」、右辺の「c : d」比の値は「c/d」になるよね??
そんで、 「a: b = c:d」となるときは2つの比の値が等しいことを意味するんだ。
今日は、比例式の解き方を「比例式の性質」を使って勉強してみよう!!
比例式の解き方に役に立つのは「比例式の性質」だよ。
教科書には、
a: b = c:d ならば ad = bc

ってことが比例式の性質って書いてあるでしょ??
えっ。なんで急に「比例式の性質」が成り立つなんて言えるのかって?!?
じつはこれは比例式の意味を使っているだけなんだ。
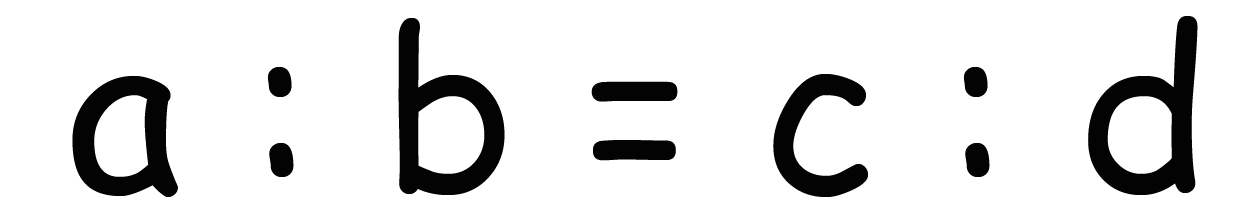
という比例式が成り立つとき、
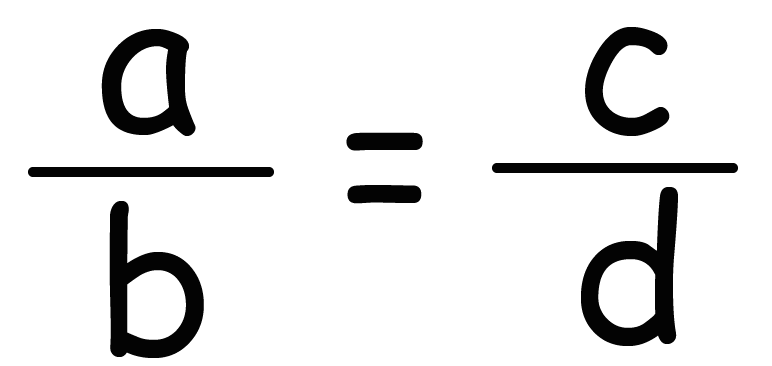
ということが言えたよね? これは一番はじめに説明したね。
じゃあ、気分転換にこの等式から分数をなくしてみよう! よくわからなかったら、「分数をふくむ方程式の解き方」を参考にしてみてね。
分母をはらうために両辺に「bd」をかけてやると、
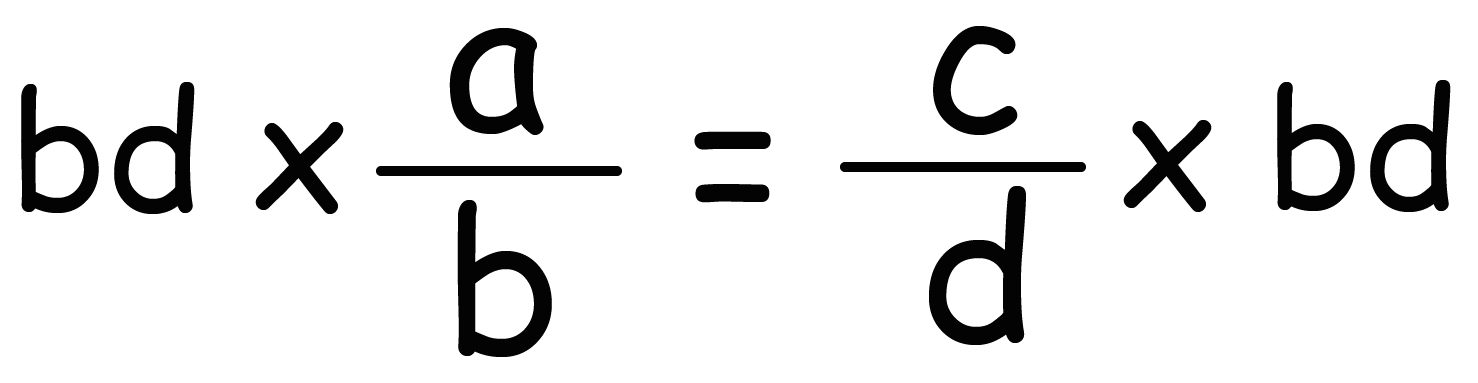
分母が消えて、
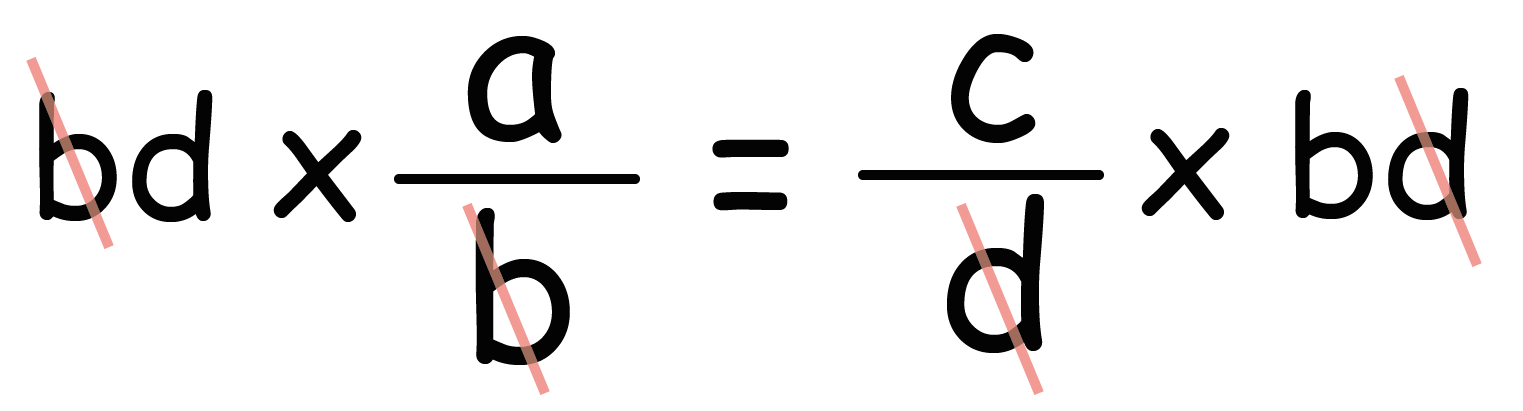
さっき紹介した「比例式の性質」の右側の等式の、
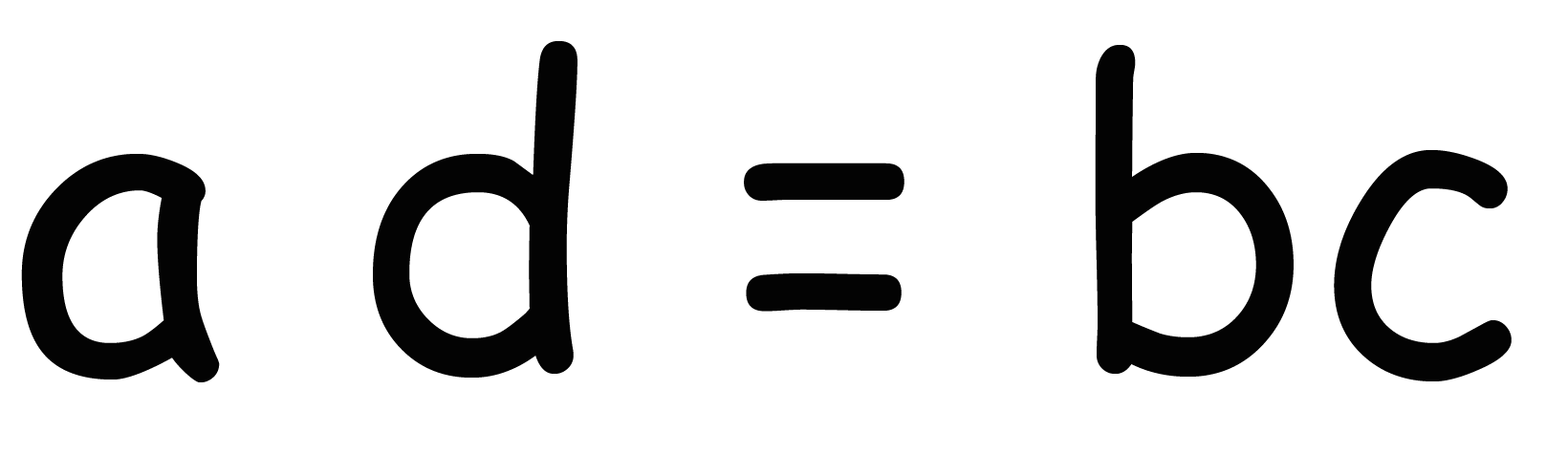
ad = cd
になるね。だから比例式の性質、
が成り立つんだね。
そして、
比例式の性質はあたかも「比の外側同士」「比の内側同士」の項をかけてるようにみえるよね??
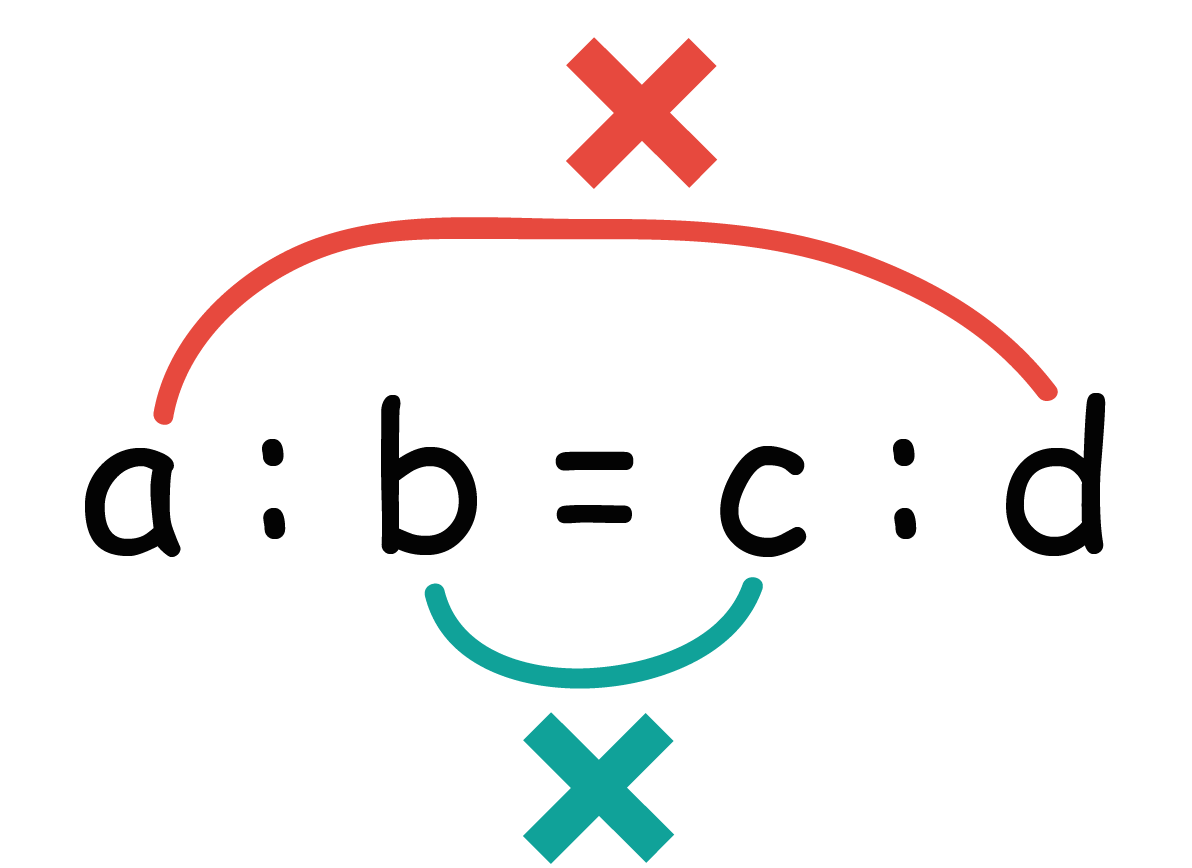
だから、ちまたでは「比例式の性質」のことを、
外項の積・内項の積
って呼ぶことがあるんだ。しっかりとこの言葉も押さえておこう!!
比例式の解き方はわかったね?? それじゃあ実際の例題で解き方を確認してみよう。
たとえば次のような比例式があったとする。
a: 3 = 15:2
比例式にふくまれる文字の正体をあばくこと。
これが「比例式を解く」ってことなんだ。
だから、この例の場合はaを求めることが「比例式を解く」ってことになる。
さっき勉強した「比例式の性質」を使うと、
外側同士の項、内側同士の項をかけたものが等しくなるんだから、
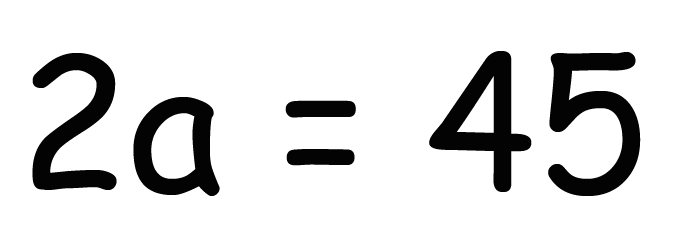
2a = 45になるね。
これをaについて解いてあげれば、
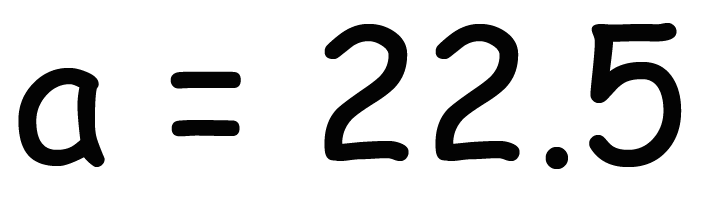
a = 22.5 (または45/2)になる。
どう?? 比例式の解き方も意外とシンプルでしょ??
次回はいよいよ、1次方程式の文章題のコツを解説していくねー!
そんじゃねー!
Ken