こんにちは、この記事を書いているKenだよ。甘酒にはまってるね。
中学一年生でならう平面図形では、
図形を移動させる問題
がたびたび出題される。教科書にもばんばん出てくるし、テストにだって狙われやすいんだ。
今日はその「図形の移動」についてわかりやすく解説していくね。
よかったら参考にしてみてくれ。
~もくじ~
記事のしょっぱならから、
図形移動、図形移動、図形移動、、、、、、
って連呼してるけど、図形の移動って何なんだろうか？？
教科書には、
図形の形や大きさを変えないで、位置だけを変えることを移動といいます。
と書いてある。たとえば、つぎの三角形ABCを移動させるとしたら、
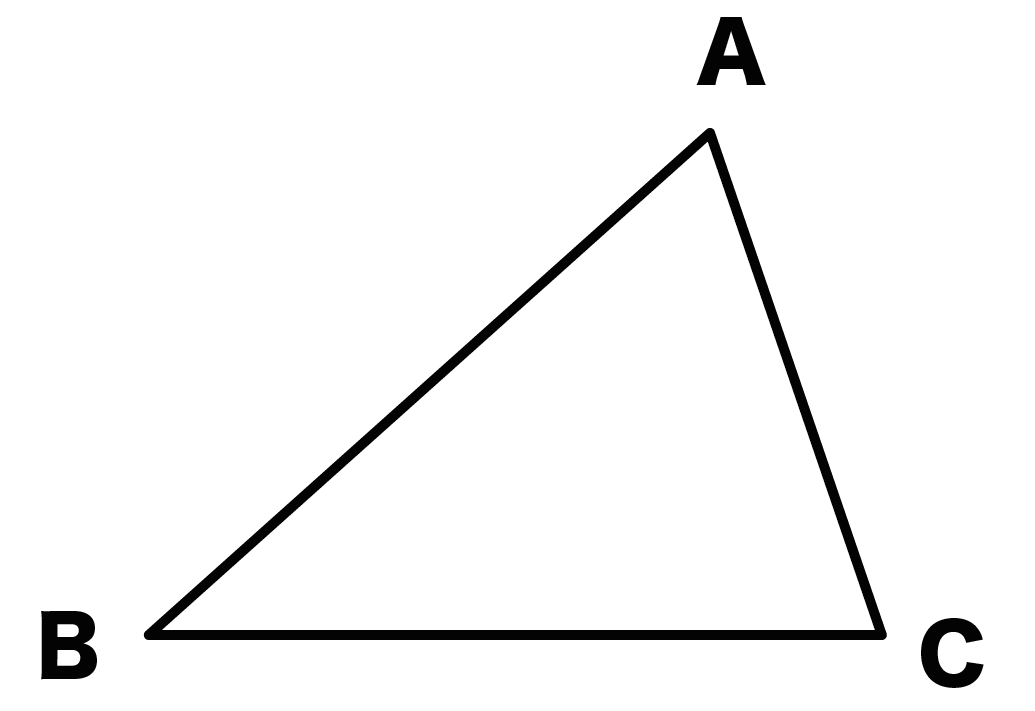
図形の形を変えちゃダメだし、
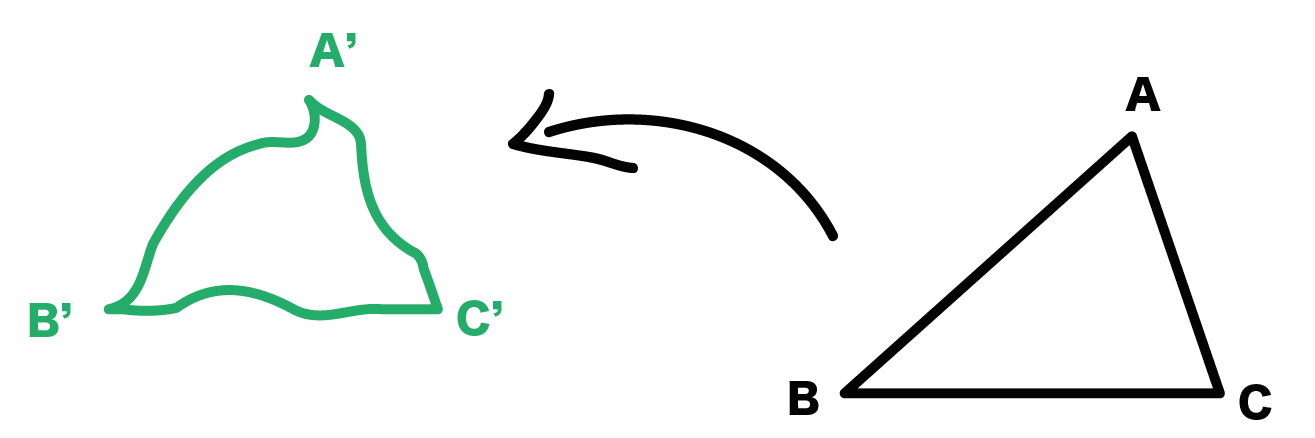
図形の大きさだって変えないんだ。
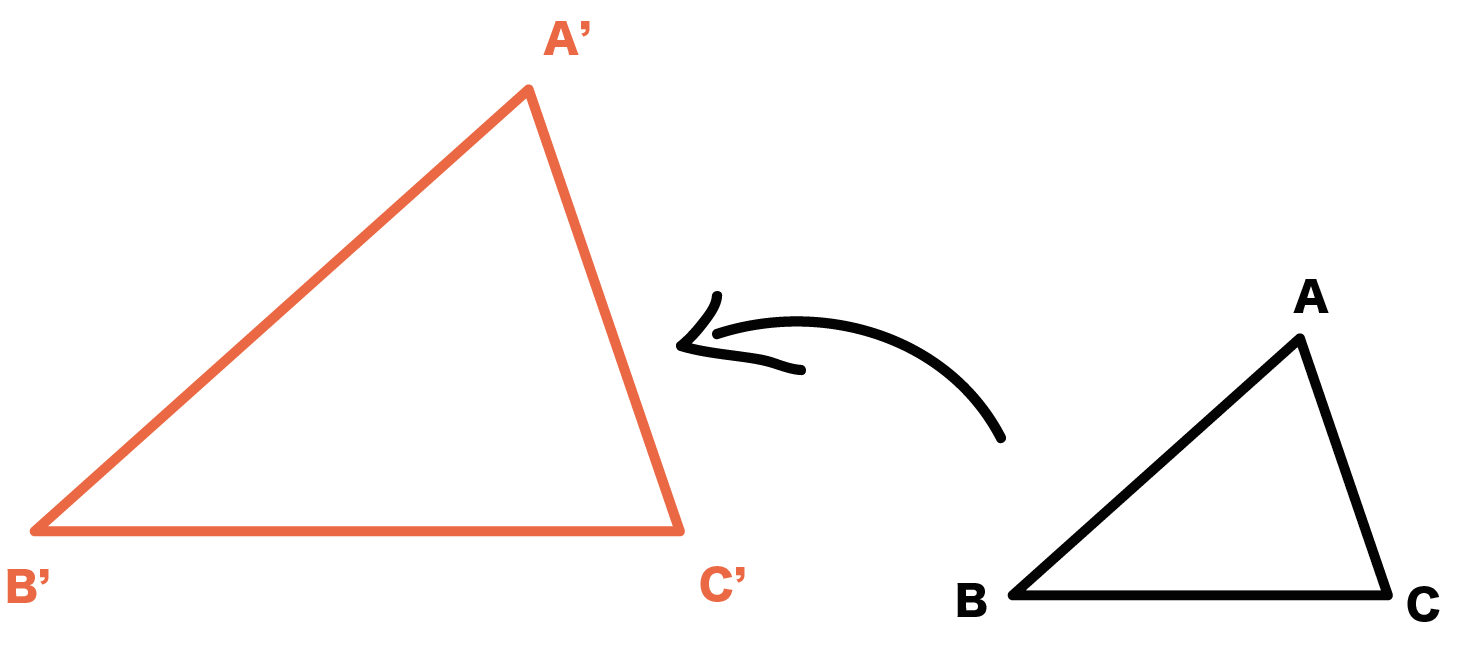
ただ単に、図形の大きさと形を保って位置を変えるだけ。
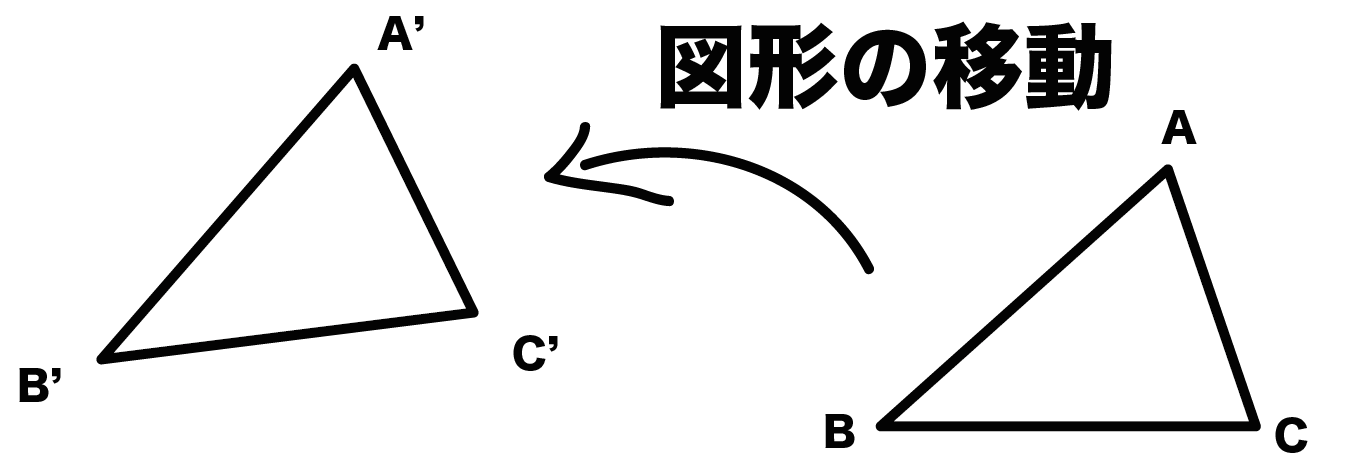
これが図形の移動ってわけだ。そんで、図形を移動させると図形の頂点も移動するでしょ？？
たとえば、上の図でいえば、
といった感じで。
図形の世界では「移動する前の点」と「移動した後の点」同士のことを「対応する点」とよんでいるよ。たとえば、A’はAの「対応する点」ってことになる。
しっかりと用語をおさえておこう！！
それじゃあ、図形の移動のにはどんな方法があるんだろう？？ ちょっとだけ気になるでしょ。
中学1年生の数学でならう「図形移動」は以下の3つあるんだ。
上から順番にゆっくりと確認していこう！
図形を回転させずに移動させる方法を「平行移動」っていうんだ。教科書では、
平面上で、図形を一定の方向に、一定の長さだけずらして、その図形を移すこと
を平行移動って呼んでいるね。
たとえば、次のような複雑な図形があったとしよう。これを平行移動させるってことは、
顔の向きや大きさを変えずに移動する
ってことになる。
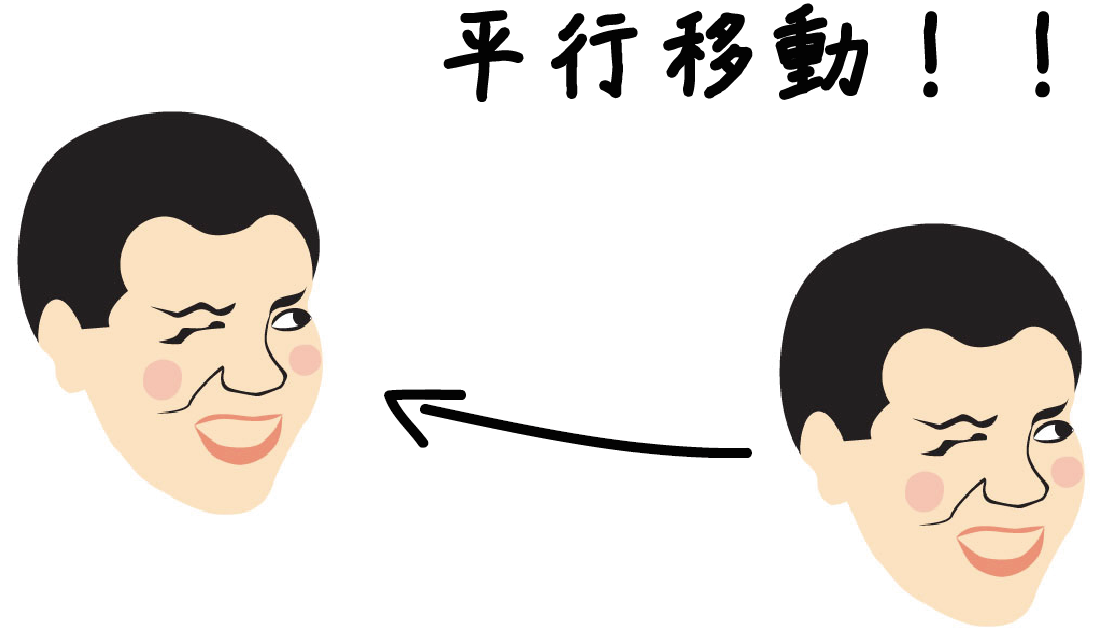
ちょっと顔が回転してしまったらダメ。
それは平行移動したってことにはならないんだ。
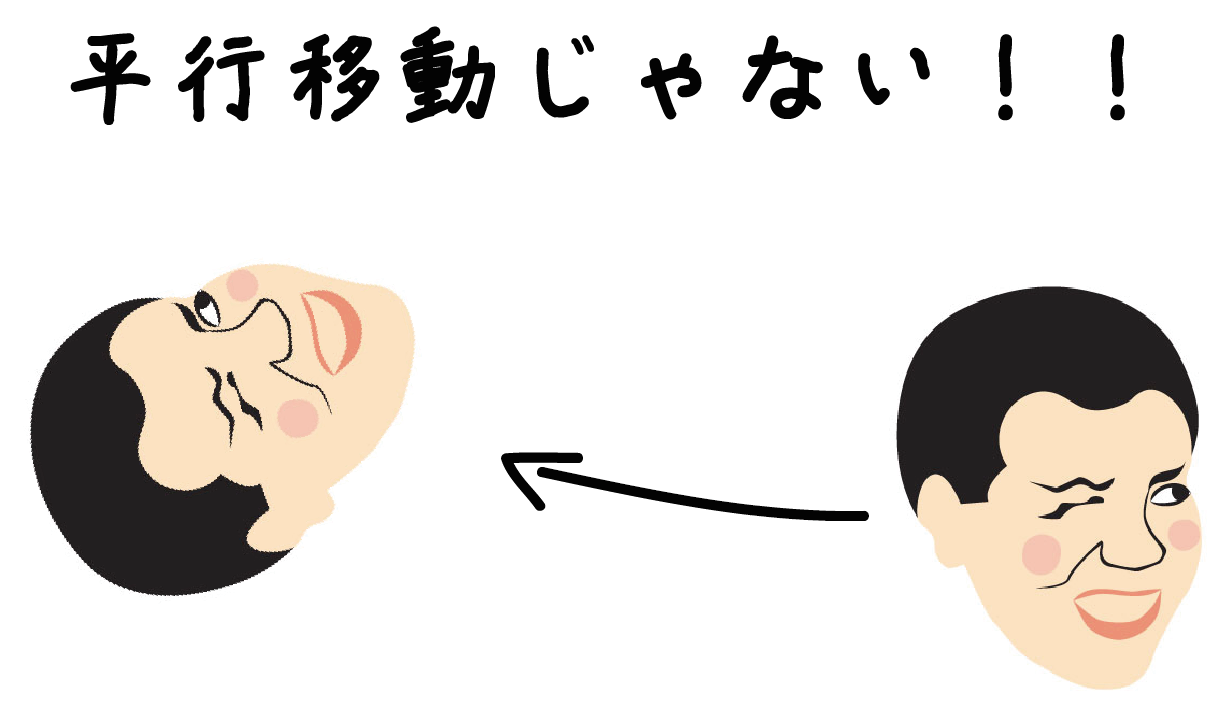
十分に注意しよう。
回転移動とは教科書によると、
平面上で、図形を1つの点Oを中心として、一定の角度だけまわして、その図形を移すこと
つまり、
ある1点を中心として図形を回転させ移動させることなんだ。
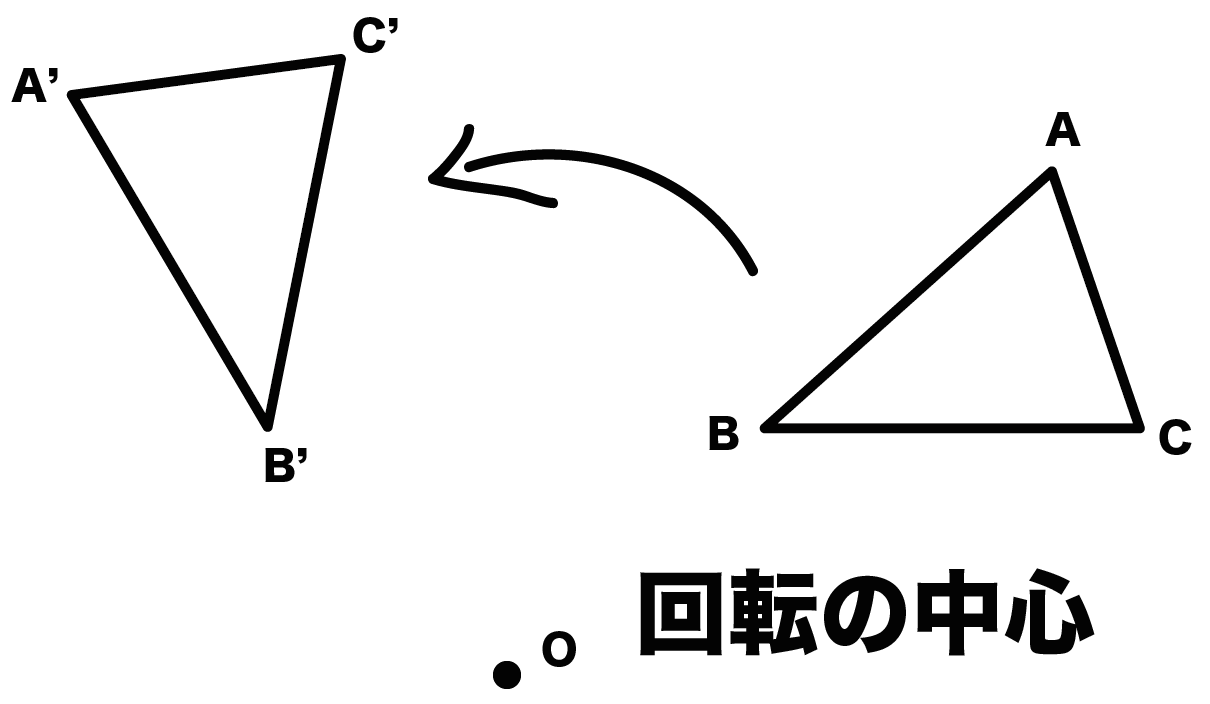
ちなみに、回転させるときの中心となる点（点O）を「回転の中心」っていう。
しっかり覚えておこう！
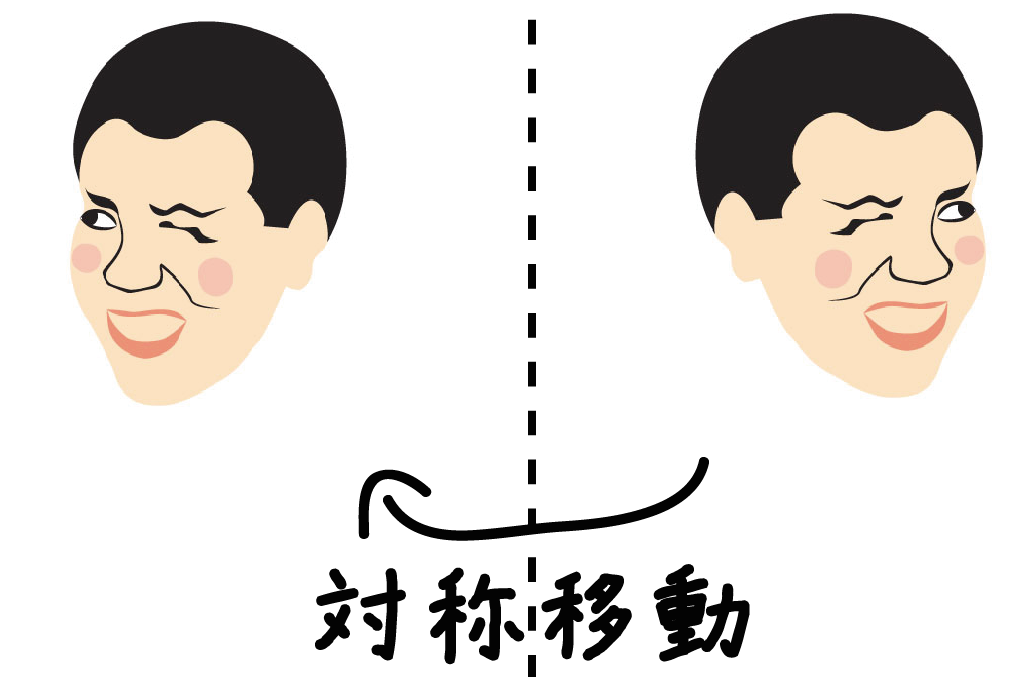
教科書によると、
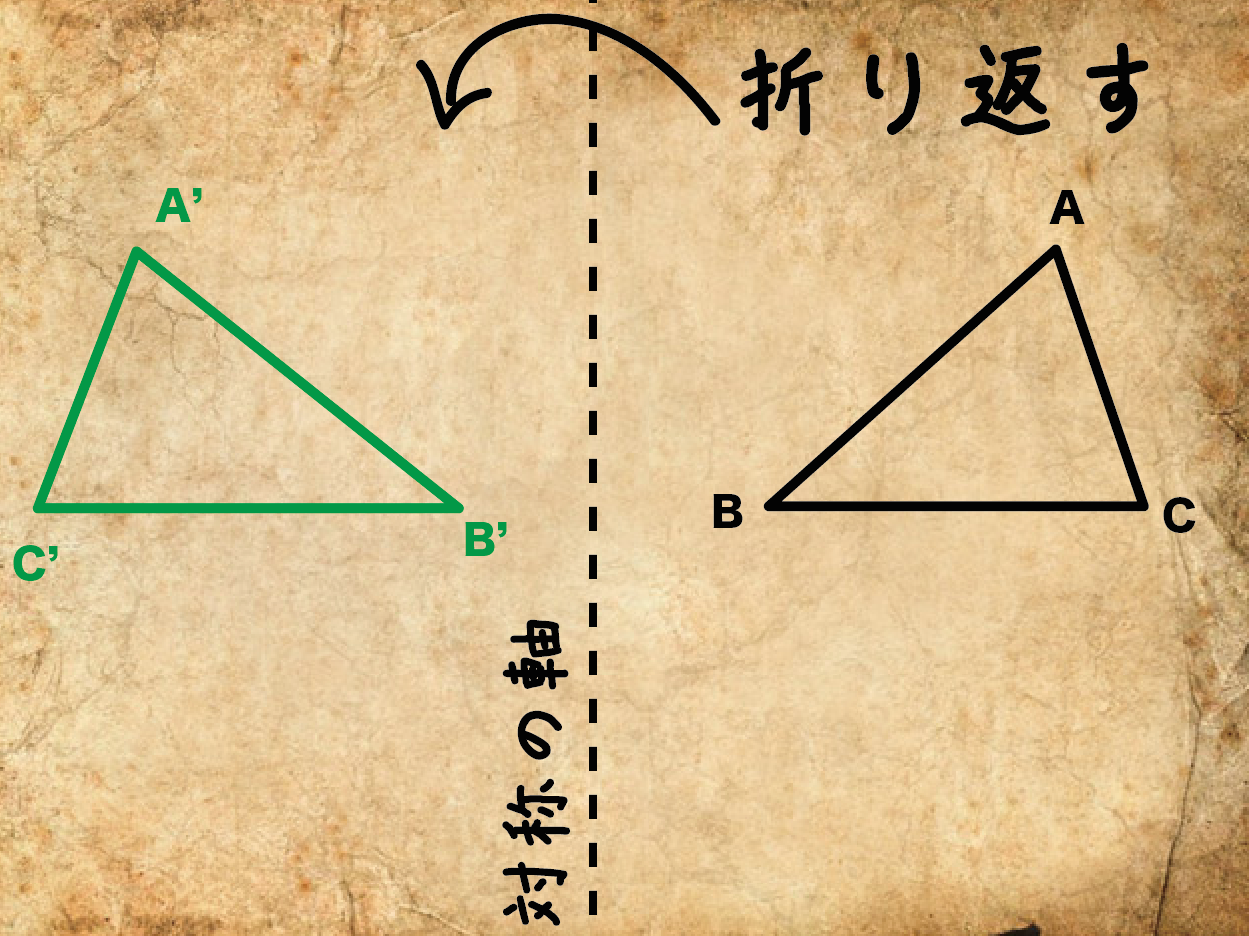
平面上で、図形を1つの直線lを折り目として折り返してその図形を移すこと
を対称移動と呼んでいるんだ。
つまり、
ある1本の直線を折り目として紙を折ったときに、
図形が写った場所に移動させる
ということ。
このときの折り目のことを「対称の軸」って呼んでいるよ。
テスト前に復習しておこうね。
中1数学の平面図形で勉強する「図形の移動」って3つしかない。
これからガンガン図形を移動させていこう！！
図形移動の書き方は次回、解説していくね。
そんじゃねー
Ken
こんにちは、この記事を書いているKenだよ。全身筋肉痛で動けないね。
中1数学の平面図形で、
っていう2種類の距離をみてきたね。だいぶお腹いっぱいになってきたけど、今日は最後に、
線と線の距離
について勉強していこう。
これができれば、線でも点でもなんでも距離をはかることができるね！ 授業で大活躍まちがいなしさ。
中1数学の平面図形をならう段階では、できることが限られている。
だって、まだ数学の勉強をはじめたばっかりだからね。
中1数学で求めることができる「線と線の距離」って、
2つの直線が平行である場合
に限られるんだ。
たとえば2つの線がこんな感じでくねってなっていたり、
ぐにゃってなっていたら線と線の距離を求めるのは至難の業になる。
きっとアインシュタインだって苦戦するはず。だから、中学1年生たちは、
2つの平行な直線
の距離の求め方だけ知っていれば十分なんだよ。
それじゃあ、2つの平行な直線の距離はどうやって求めたらいいんだろう？？
平行な直線の距離を求めるのはカンタンさ。
2つの直線をむすぶ垂線の距離
が「線と線の距離」になってくるんだ。
だから、求め方としては次の2つのステップを踏むことになる。
まず最初の一歩はどっちかの直線に点をうつことだ。
どっちか迷うけどさっさと点をうってしまおう！！
さっき打った点から、もう一方の直線にむかって垂線をひいてみよう。
この垂線の長さが、
2つの平行な「線と線の距離」になってくるんだ。
ちょっと物足りない気もするけど、これで平行な直線の距離を求められるね。
ここまで勉強してきた「線と線の距離」はどうだった？！？
2つの直線が平行であるときだけ
っていうしばりがあるけど、大分カンタンだったでしょ？？
次回は図形の移動について勉強していくね。
そんじゃねー！
Ken
こんにちは、この記事を書いているKenだよー！お餅は4個食べる派だね。
ある日、シャイな点「・」とツンデレの線「-」が道で出会ったとしよう。
二人とも同じクラスだからお互いに知っていた。
だけど、まだ話したことがないっていう微妙な関係なんだ。二人をみていると思わず背中を押したくなっちゃうね。
そこで、問題。
この２人「点と線」の距離ってどれぐらいなんだろう！？？
友だち？ 知り合い？？ 他人？？ はたまた恋人予備軍？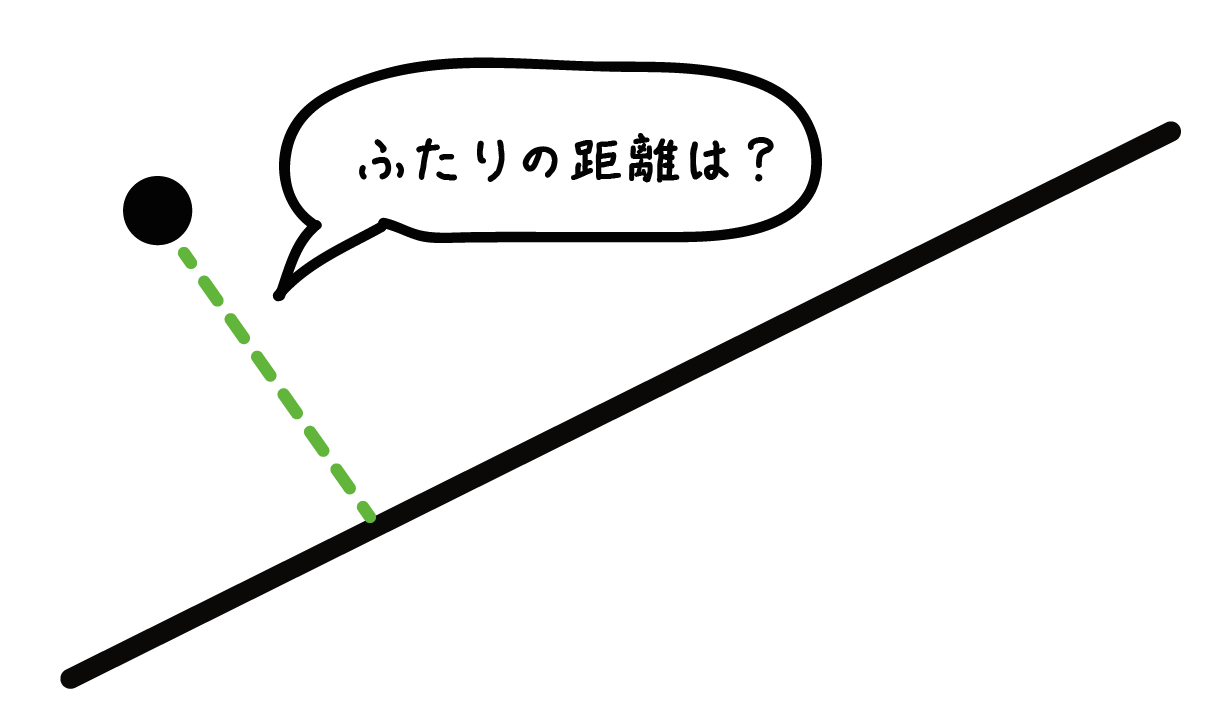 
ってまあこんな感じで、
今日は「点と線の距離」について解説していこう。
もう答えを言ってしまおう。
点と線の距離は、
点から線におろした垂線の線分の長さだ。
ふたりの距離はこんなものにすぎない。
でも決して、
ぐにゃぐにゃした線の長さでもないし、
ギスギスっとしたものでもない。
なぜなら、
点から線におろした垂線までの最短距離だからだ
図形の勉強において「距離」とは、
最短距離のことをあらわしているんだ。しっかりと胸に刻み込んでおこう！
点と線の距離についてなんとなく理解が深まったかな！？？
点と線の距離は、
ってことを覚えておこう！
次回は「線と線の距離」について解説していくね。
そんじゃねー！
Ken
こんにちは、この記事を書いているKenだよ。キムチより断然ナムル派だね。
中学一年生の「平面図形」という単元では、
かなり多くの図形記号が登場する。
はじめて図形を勉強する奴にとって、それはまさに生き地獄。
次から次へとあたらしい図形記号がでてきちゃうんだ。
数学の授業だけだと、覚えられないままテストを迎えそうだね。そこで、今日は、
中1数学の平面図形で勉強する「図形の記号」を9つ
をまとめてみたよ。
テスト前に参考にしてみてね。
~もくじ~
まず1つ目のタイプは、図形に書き込めるタイプの記号。
この記号はおもに、
ときに便利なんだ。これらの記号をただしく覚えて正しく使うことで、ライバルたちに差をつけちゃおう！
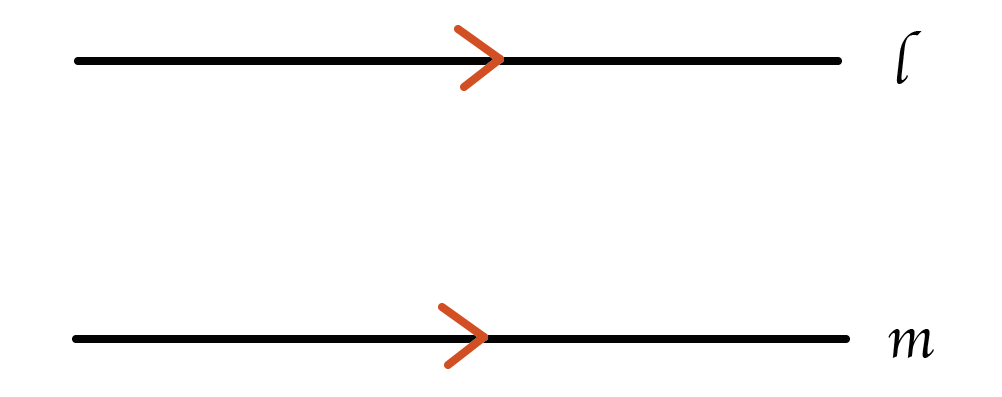
2つの直線におなじ「＞」のような記号をつけてやると、
おたがいに平行である
って意味になるんだ。
上の図でいうと「直線l と直線mが平行である」ってことを表している。
図形の問題の解くときにけっこう役に立つんだ。しっかりマスターしておこう。
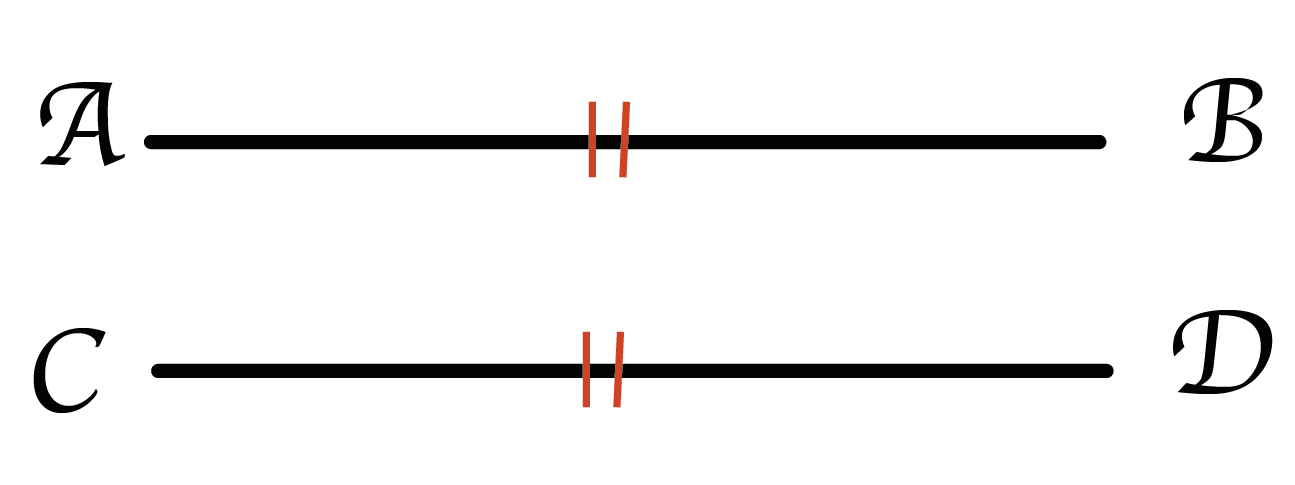
2つの線分に「=」という記号をつけてやると、
線分の長さが等しい
っていう意味になるんだ。べつに「＝」じゃなくても下のように「-」をつけたって構わない。
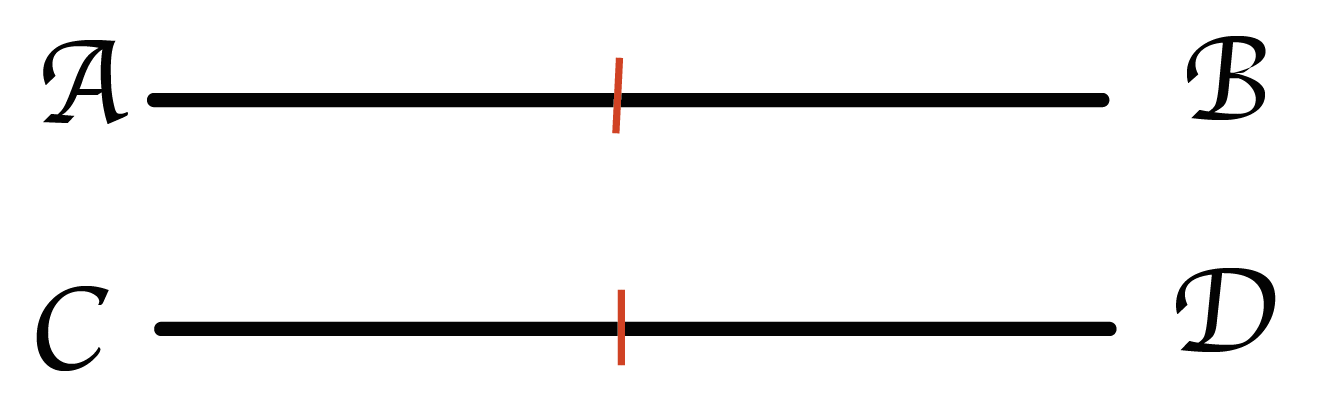
ようは、同じ記号を2つの線分につけるだけでいいのさ。
問題文の状況をたしかめるためによく使うね。
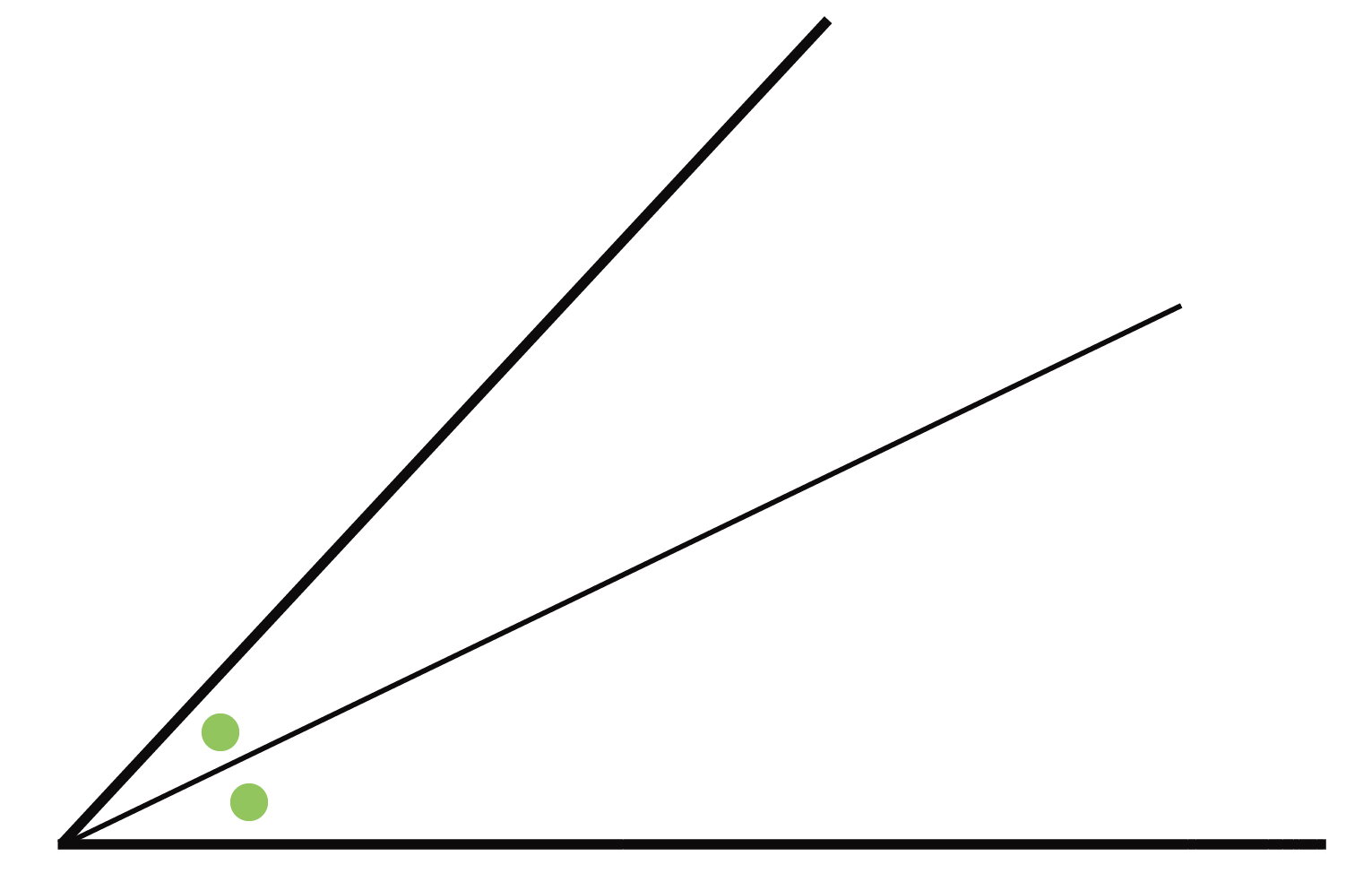
2つの角度が等しいことをあらわすために「●」をつかうことがあるよ。
あ、べつに「○」でも、
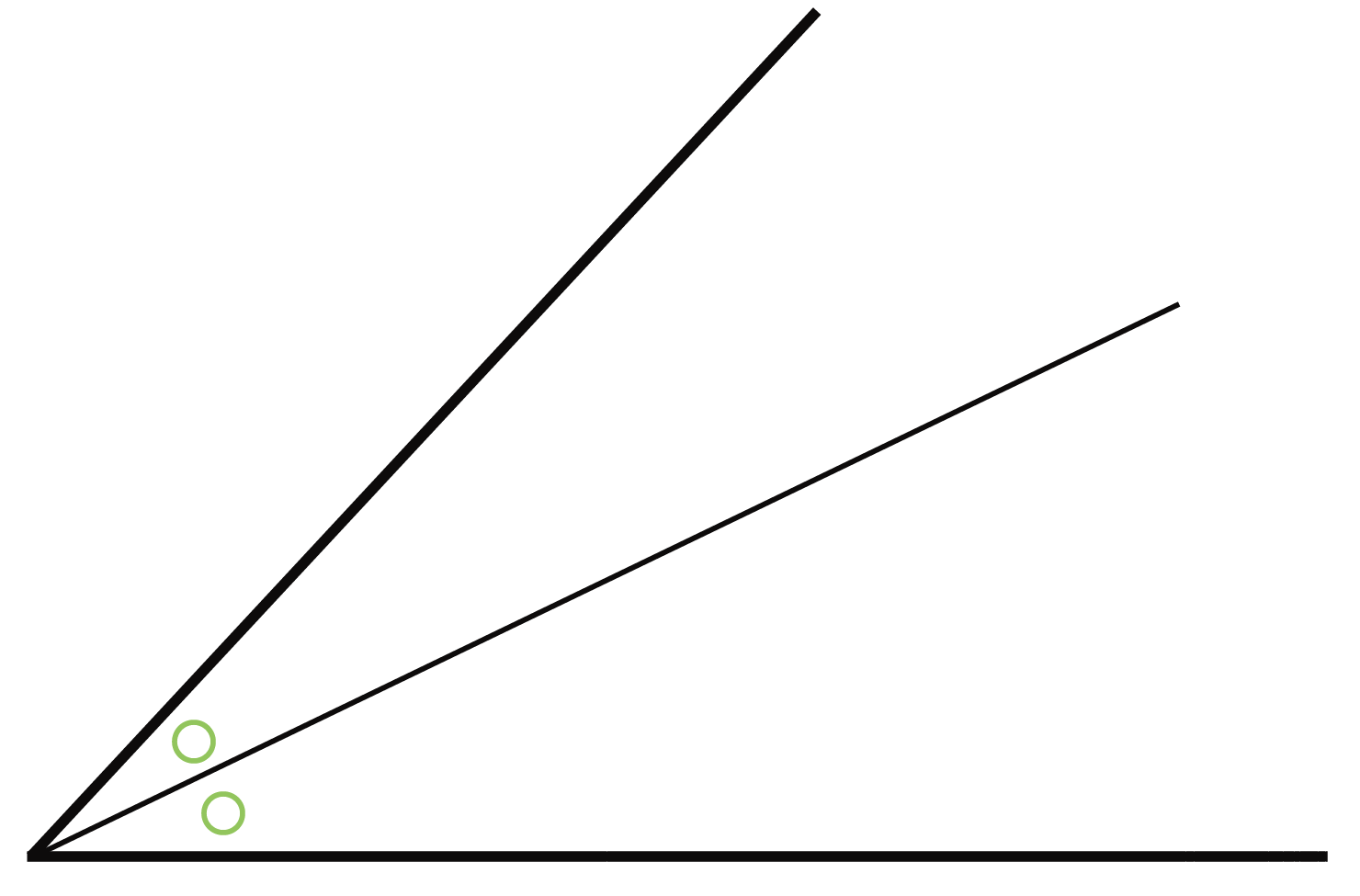
「×」でも大丈夫だよ。
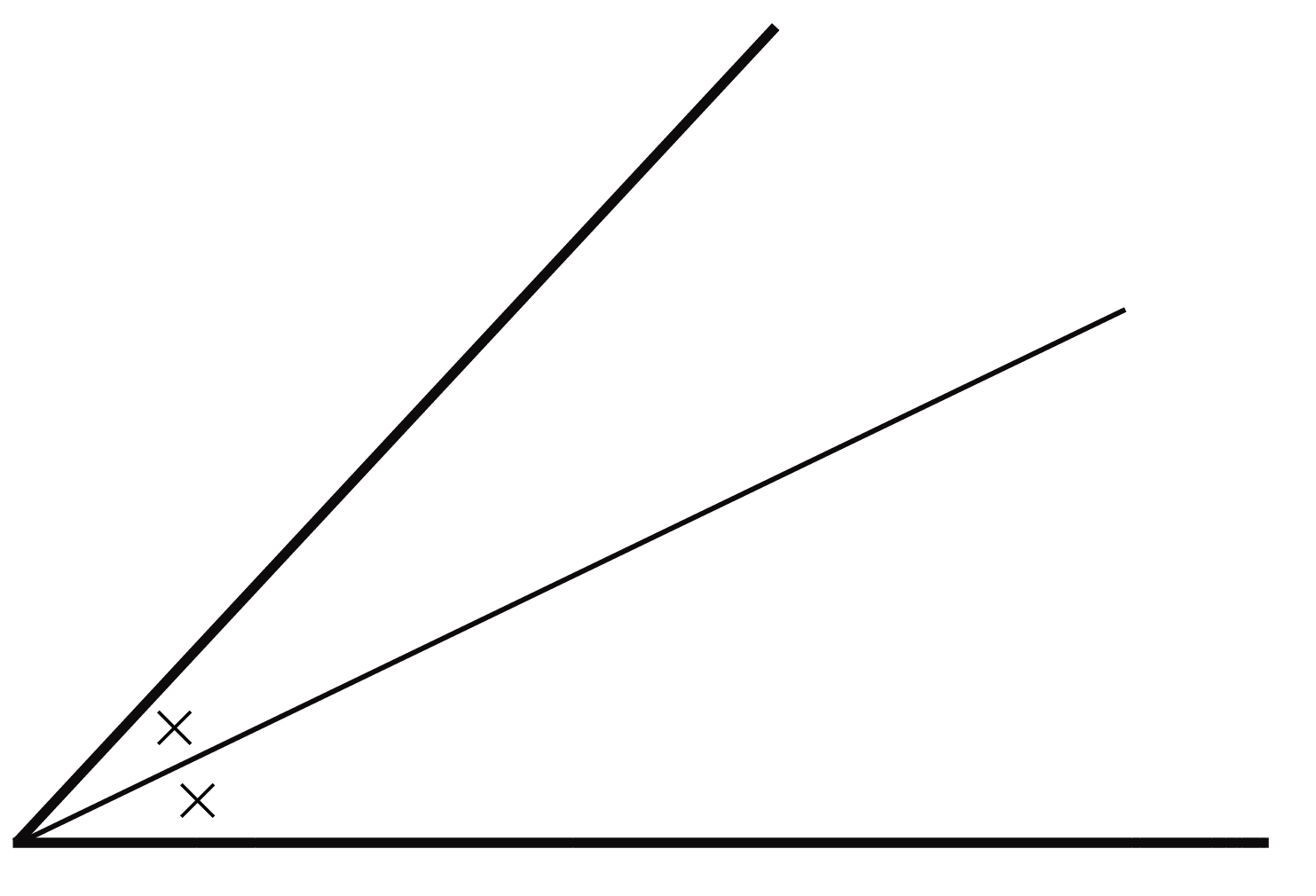
とりあえず同じ記号つけておけば角が等しいことを表しているんだ。
図形角度の問題で役に立つ記号だ。しっかり押さえておこう！
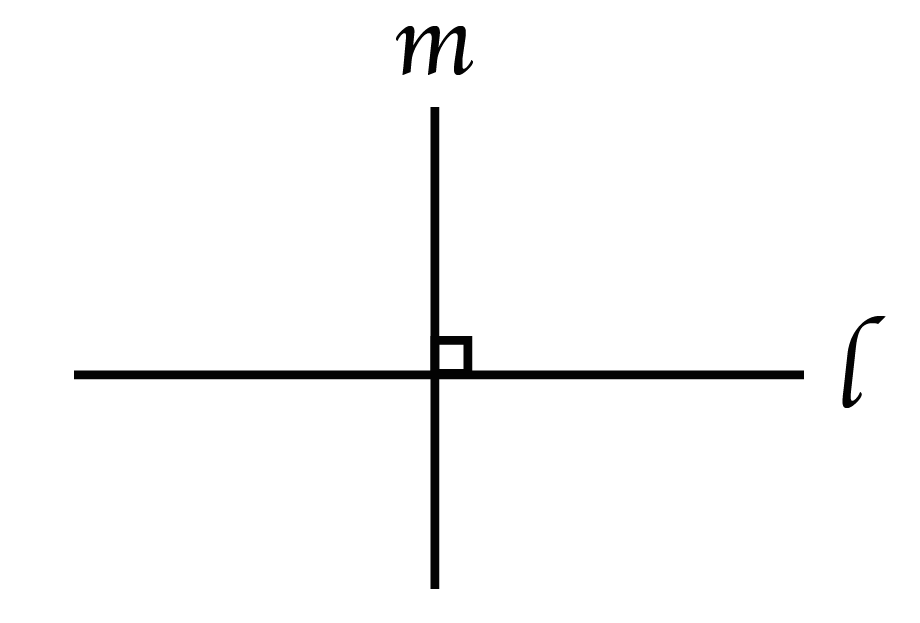
2つの直線が垂直（90度）に交わっているとき「□」の記号を使うんだ。
やり方はいたってカンタン。この「□」を2つの直線のあいだに挟むだけ。
これで角度が90度であるってことをあらわせる。
上の図の例でいえば、直線 lとmが90度で交わっていることになるね。
小学校でもならったかもしれないけど、中学数学でもバンバン使っていくから覚えておこう！
つぎは、図形に書き込まないタイプの記号を紹介していくね。
おもに、中2数学で勉強していく「図形の証明」で活躍していく記号たちだ。
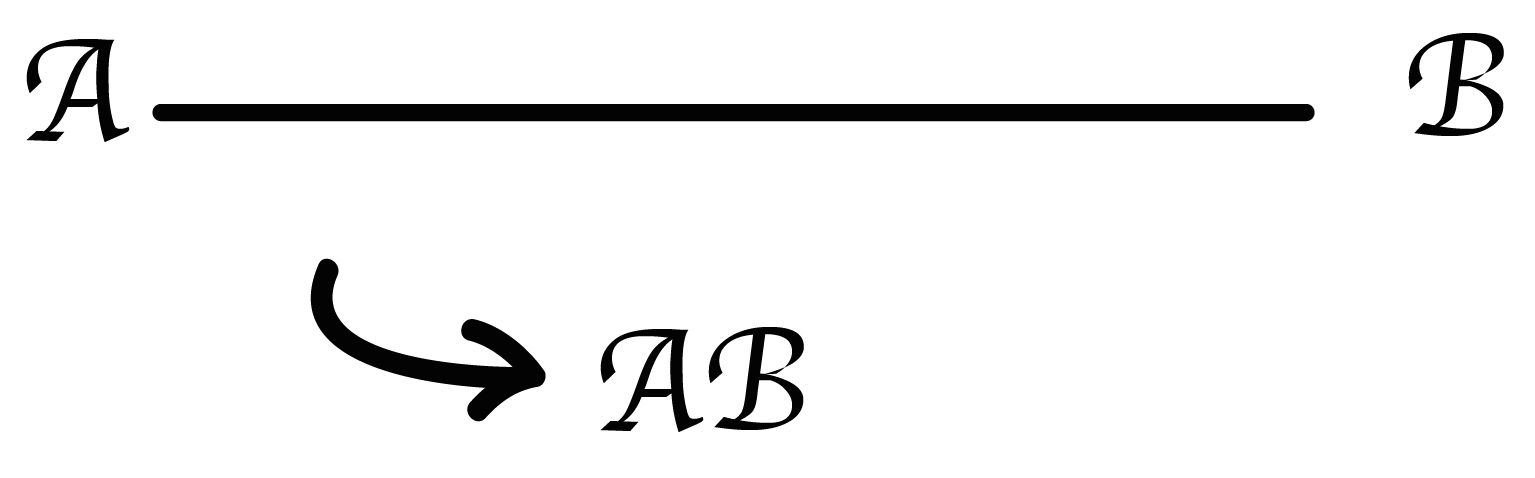
線分をあらわす図形の記号はなんと・・・・・
なにもないんだ。
たとえば、上のような線分ABを記号であらわしたかったら、線分の両端の記号だけでいいんだ。
だから、
AB
ってなる。
それ以外になにもいらない。
とってもシンプル記号だね。
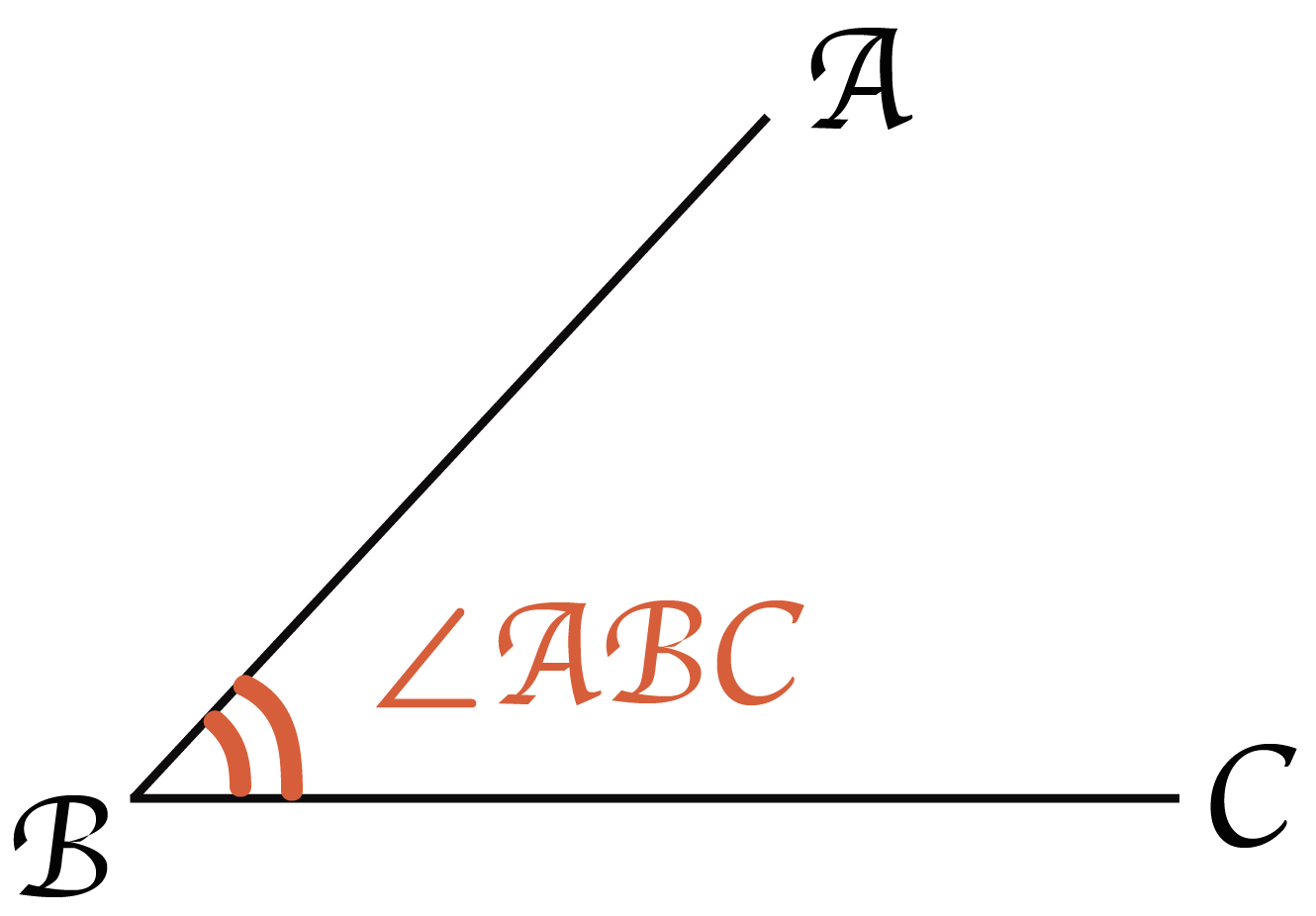
1つの角度をあらわしたいときには「三角形のきれはし」みたいな記号を使うよ。いかにも角度っぽいでしょ。
この記号で注意したいのが「角度をもっている頂点を真ん中にする」ということ。
上の図でいえば、Bがオレンジ色の角度をもっているでしょ？？
だから、角ABCというように頂点Bが真ん中にくるんだ。頂点の順番によってあらわす角度が違うから気をつけてね。
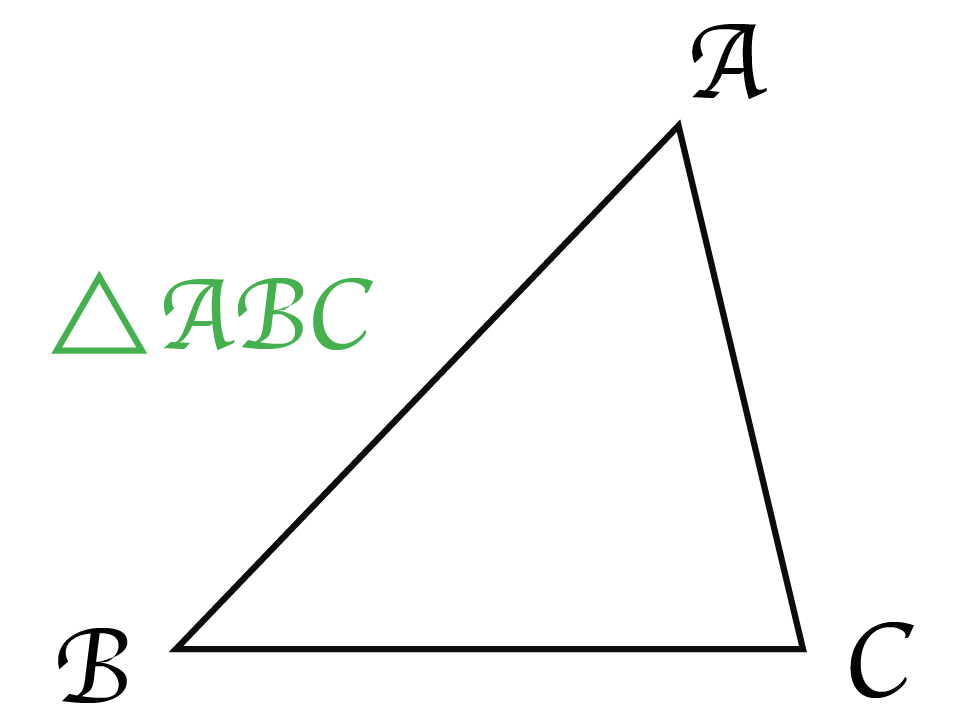三角形をあらわす記号はとってもシンプル。
小さい三角形を頂点をアルファベットの前におくだけだ。リアルの三角形の記号だからわかりやすいね。
この記号はよく中2数学の三角形の合同の証明にでてくる。単純だけど、のちのちのためにしっかり押さえておきたいね。
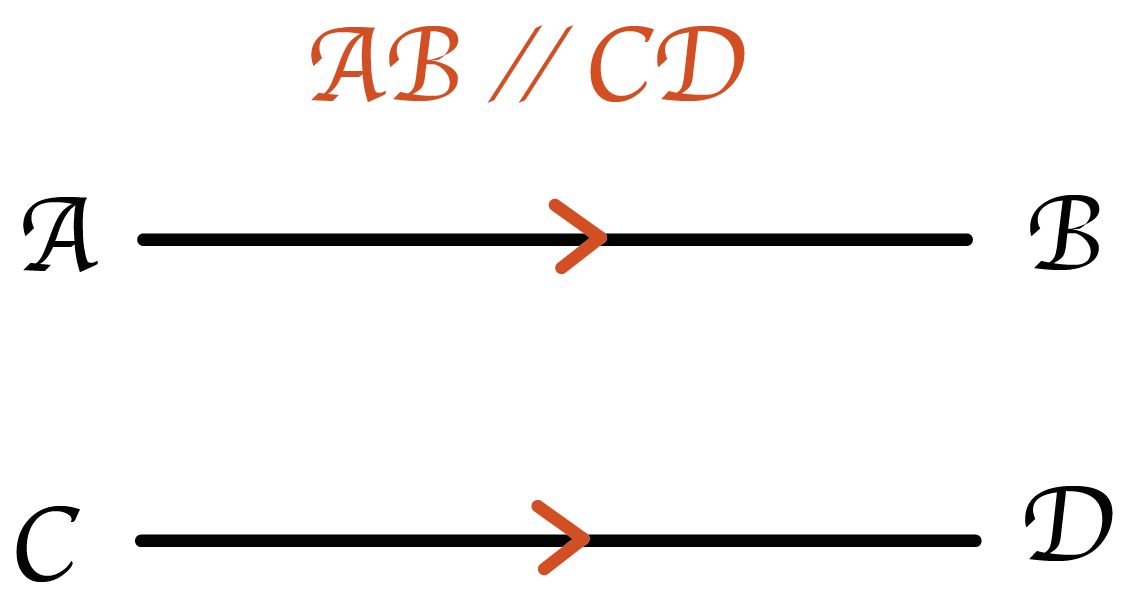
平行をあらわす記号もとっても単純。
AB//CD
さ。
平行っぽい直線を斜めに2本ひいてあげるだけだ。こんな感じで「//」。
くれぐれもななめにするのを忘れずに。
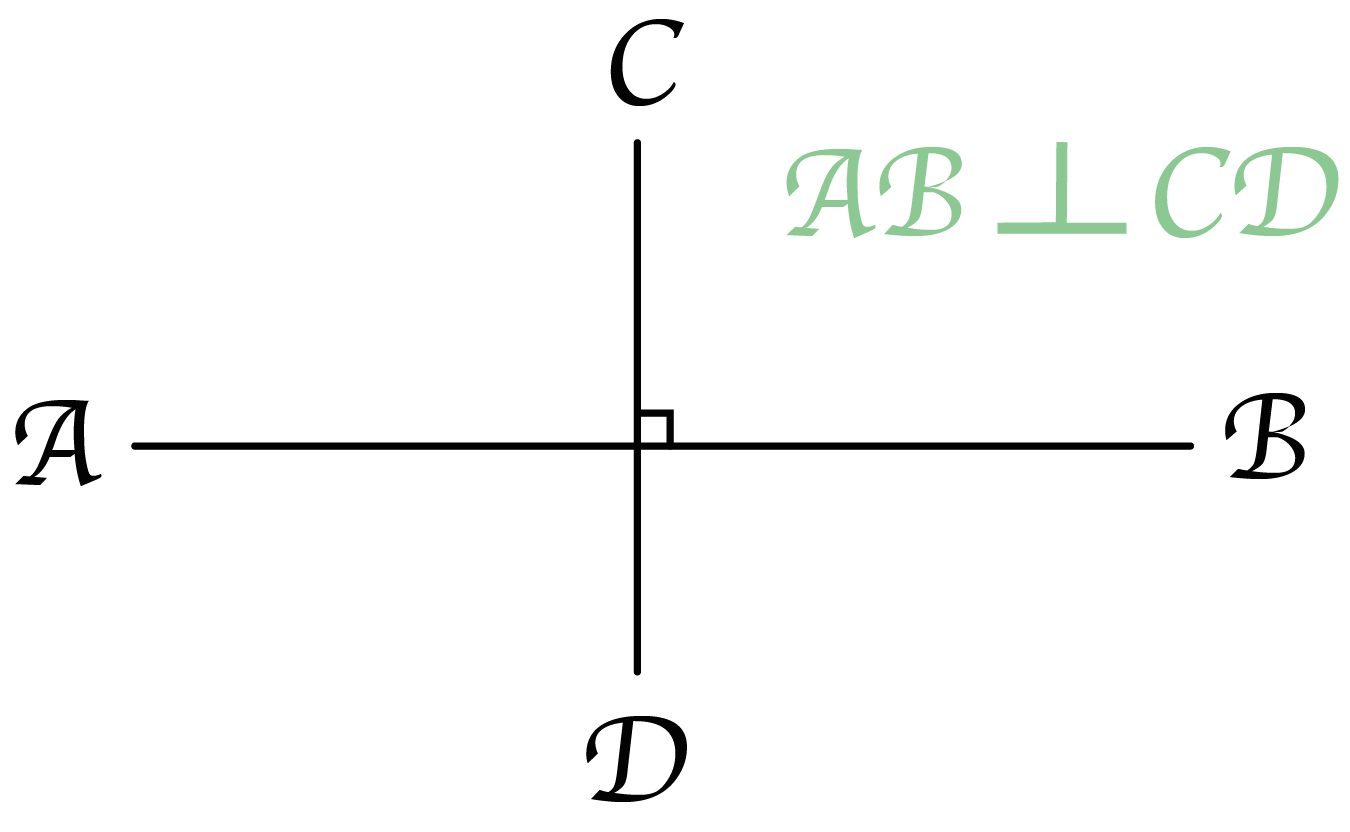
さいごの記号は「垂直」をあらわすやつだ。90度で交わっている直線を2つかいてあげればいいんだ。
うーん、イメージは机に鉛筆を立てる感じだだね。
気合いいれすぎて縦棒が突き抜けないようにしてね。
中一数学の平面図形にでてくる記号だけで9つあったね。
はじめて図形を勉強するのは大変だけど、だんだん図形記号にもなれてくるはず。落ち着いてゆっくり勉強していこうね。
つぎは線と線の距離について勉強していこう！
そんじゃねー
Ken
こんにちは、コーヒーを飲みほしたKenだよ。今日も一緒に中学数学の勉強をしていこう！
中1数学の「平面図形」でまず勉強するのは、
点と点の距離
だ。たとえば、2つの点AとBがあったとしよう。
それじゃあ、こいつらはどれぐらいの距離離れているんだろうね？？ ちょっとよくわからん。
そんなときに活躍するのが、
2点のあいだの距離の求め方
なんだ。今日はこいつを解説していくね。
2点の距離って、
2つの点を両端とした線分の長さのこと
なんだ。だから、さっきの点AとBの問題で、
点A・Bの距離はどれぐらいですか？？
と聞かれたら、
線分ABの長さです！
って答えればいいんだ。
それじゃあ「線分」ってなんだろう？？
線分とは、
両端がある直線（まっすぐな線）
のことをいうんだ。だから、
こんな感じでうねっていると線分とは呼べないし、
両端がAとBでないものは線分ABとは呼べないんだ。たとえきれいな直線だとしてもね。
だから、点と点の距離（AとB）を求めるときは、必ず線分ABが次の
ということを確認しよう。
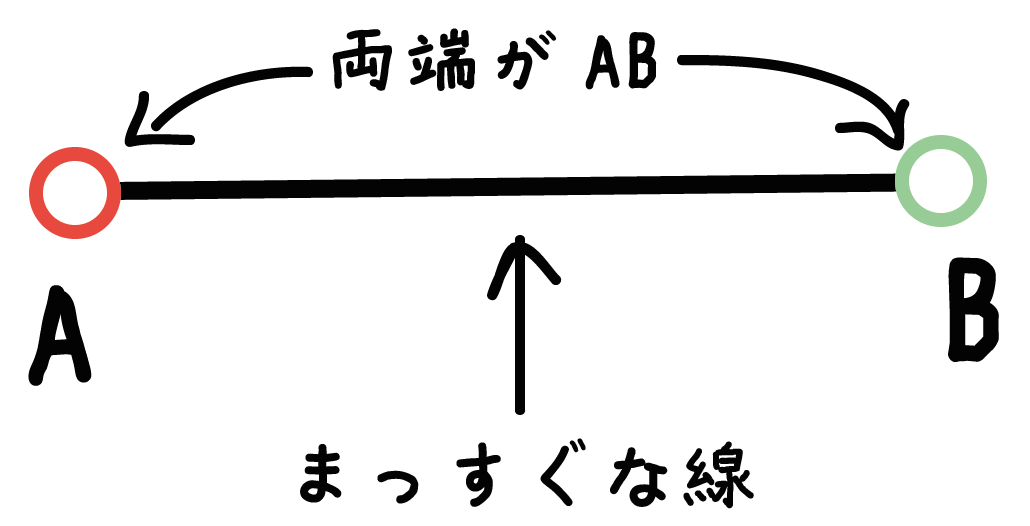
これが点Aと点Bの距離になるはずだ。
テストで「点と点の距離を求めなさい」って言われたら、
2点を両端とする線分の長さを求める！
ということを押さえておけば大丈夫。いつ先生に指名されたても胸を張ってみよう。
つぎは平面図形で登場する「図形記号」のまとめを書いてみるね。
そんじゃねー
Ken
こんにちは、この記事を書いているKenだよ。カピバラと温泉に入りたいね。
いよいよ中1数学の「平面図形」という単元にはいっていくよ。
いままで方程式とか関数とか勉強してきたけど、こっからは新しい「図形」というモンスターとたたかっていく。
今日は、「平面図形」という単元を楽に勉強するための、
中1数学の平面図形の攻略のコツ
を3つ紹介していくね。平面図形が苦手で泣きそうなときに参考にしてみてくれ。
つぎの3つのコツを押さえてしまえば平面図形がむちゃくちゃ楽勝になるんだ。
中1数学の「平面図形」の最大の特徴は、
図形の専門用語がたくさんでてくる
ということさ。
たとえば、
・・・・などなど。
数え始めればキリがない。平面図形という単元となかよくなるためには、まずはこれらの「図形ことば」を覚える、少なくとも馴れなければならない。
えっ。暗記が苦手だって！？？
そういうときは、とりあえず楽な気持ちで進み続けよう。勉強していくうちに新しい言葉になれていくから大丈夫！
中一数学の「平面図形」では、図形を作図する問題がでてくる。
作図ってつまり、
図を自分で作る
ってことさ。
とくに教科書にどっさり載っている、
という3つはしっかりと押さえておきたい。これは期末・中間テストでねらわれやすいし、入試問題ではこれらを応用した問題がどしどし出題される。
中1数学の作図は一度マスターしちゃえばこっちのもの。
あとは何度も作図の練習を繰り返せばいいんだ。
作図をマスターすると人気者になりそうな気もするし、やっておくに越したことはないね。
中1数学の平面図形で最後にやることは、
図形のスペックを計算することさ。たとえば、円の面積とか三角形の面積の計算とか・・・・だ。
人間だって体重計で太っとかどうか調べるでしょ？？ それと同じさ。
このダンジョンをクリアするためには、
という2つのソードが必要になってくる。
教科書にでてくる図形の公式をちょっと覚えて、算数でつちかった計算能力を発揮するだけ！！
これで平面図形の計算問題は大丈夫。きっと無傷でダンジョンから脱出できるはずさ。
中1数学の平面図形は、中学校で勉強する図形のほんの入り口。
ここでつまずいて血を流さないように、
という3つのコツで乗り切っていきたいね。
次回は線分について解説していくね。
そんじゃねー
Ken
こんにちは、ホットミルクで目を覚ますKenだよ。
中1数学の「変化と対応」で最後に登場するのは、
比例・反比例の利用
というモンスターだね。ここでは、
比例や反比例を利用して日常生活の問題を解決していこう！！
っていう勉強をしていくんだ。いままでならってきた比例や反比例がちょっと身近に感じられるかもね。
でも、ちょっとむずかしくて苦戦することも多いから、
今日は、
比例・反比例の利用の文章問題をスマートにとく2つの方法
を紹介していくね。テスト前によかったら参考にしてみてね。
比例の利用、反比例の利用ってむちゃくちゃ難しくみえるよね。
でもよーくみてみると、じつはたった2つしか問題の種類がないことがわかる。
それは、
の2つさ。
これだけじゃ、ちょっとわからないから例題をみながら確認していこう！
この手の問題では、
yはxに比例する
だとか、
体重はモテる度合いに反比例する
だとか、
問題に登場する関数が比例するのか、反比例するのかあきらかにしているんだ。
たとえば、次のような問題があったとしよう。
風呂掃除をした時間をx分、もらえるお小遣いをy円とすると、yはxに比例する。このとき、80分働いたとき800円もらえたとすると、400分はたらくといくらお小遣いをゲットできるでしょうか。
この問題では「yはxに比例する」と問題の中でネタバレしてしまっているね。この手の問題はつぎの2つの手順でとくことができるんだ。
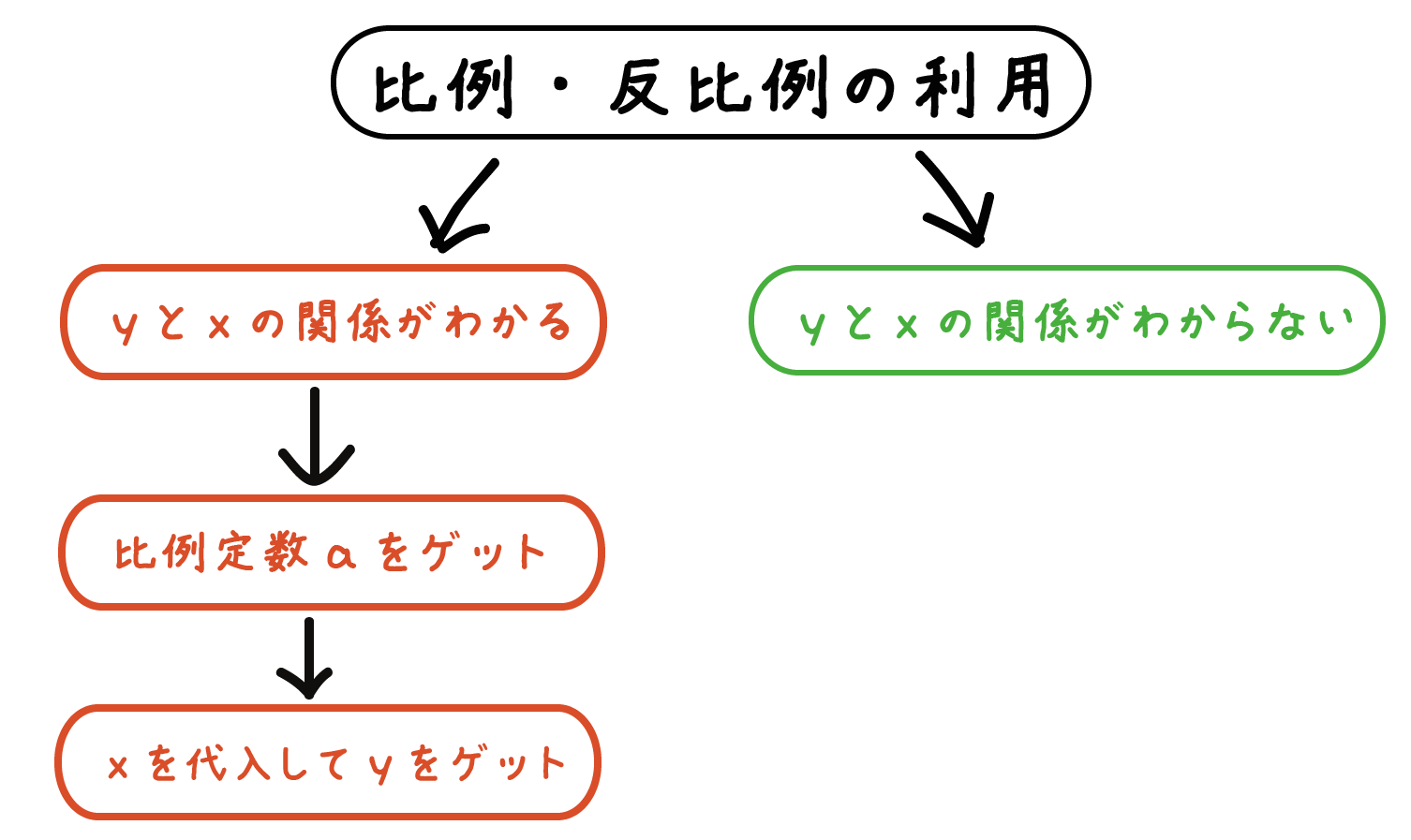
yとxの値がわかっているし、yとxの関係（比例か反比例か）もわかっている。
それじゃあ、比例定数aを求めてみよう！
さっきの例題だと、
という情報がわかっているので、
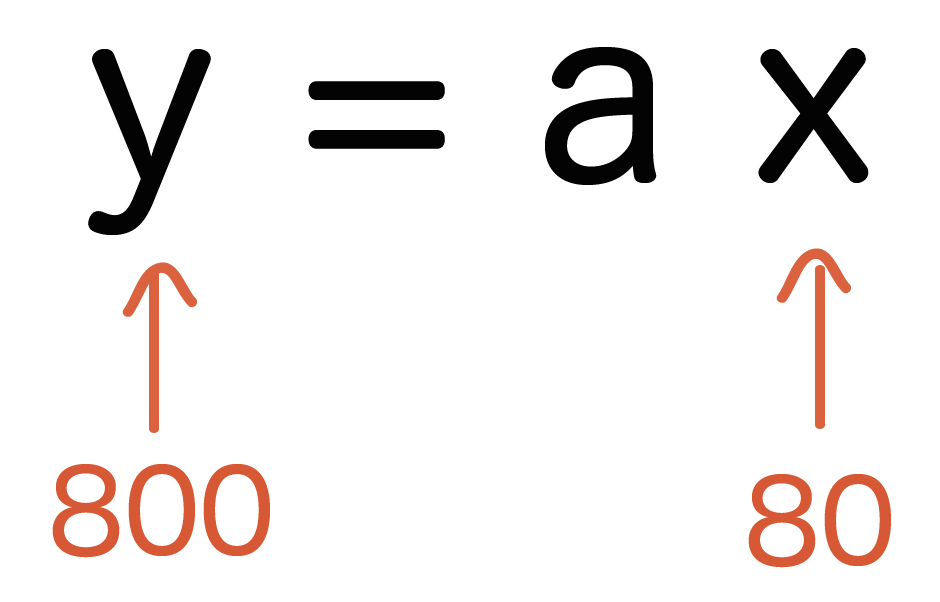
800 = 80a
という計算式がたてられるね。そんで、比例定数aを計算してやると、
a = 10
になる。
これで第一ステップが終了だ。
この手の問題の場合、
xがある値をとったときのyの値
をきいてくることが多い。
さっきの例題でいうと、
x = 400のときのyの値だね。
よって、さっきの比例関数 y =10x にx = 400を代入してやると、
y = 4000
という値がゲットできるね。
つまり、この小僧は400分風呂そうじをして4000円稼ぐことができたってわけ。
以上が1つめの解き方だよ。どう？？納得した？？
2つ目の問題は「yとxの関係がかかれていない問題」だ。
つまり、yとxが比例するのか？ 反比例するのか？？ ということが文章問題の中でいっさい触れられていないということ。
この手の問題はつぎの2つの手順によってとけちゃうんだ。
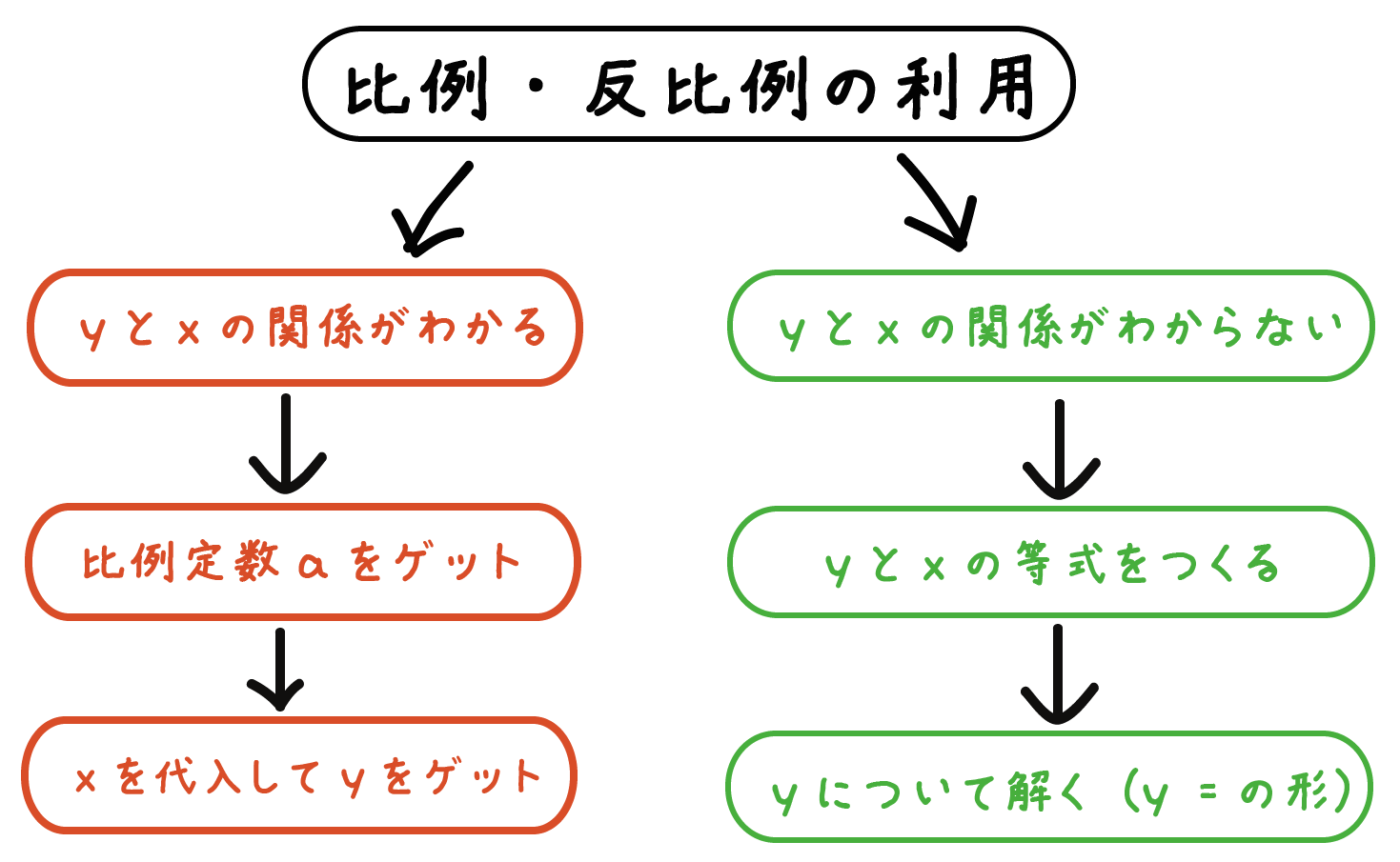
さっきの問題よりむずかしくみえるけど、案外たいしたことないよ。
つぎの例題をみながら解き方を確認していこう。
50Lの水がはいる金魚鉢に毎秒xLのペースで水を補給していくとy秒でいっぱいになって金魚が逃げてしまう。このとき、yとxの関係を式であらわしてくれ。
というもの。
このタイプの問題はつぎの2ステップで解くことができるんだ。
この手の問題では、
とりあえずyとxの関係を等式であらわしてみる！
というチャレンジ精神が大切だ。比例になるか、反比例になるかわからなくても前に進んでみよう。
さきの例題では、「毎秒x L でy秒水をいれると50Lの鉢がいっぱいになる」ので、
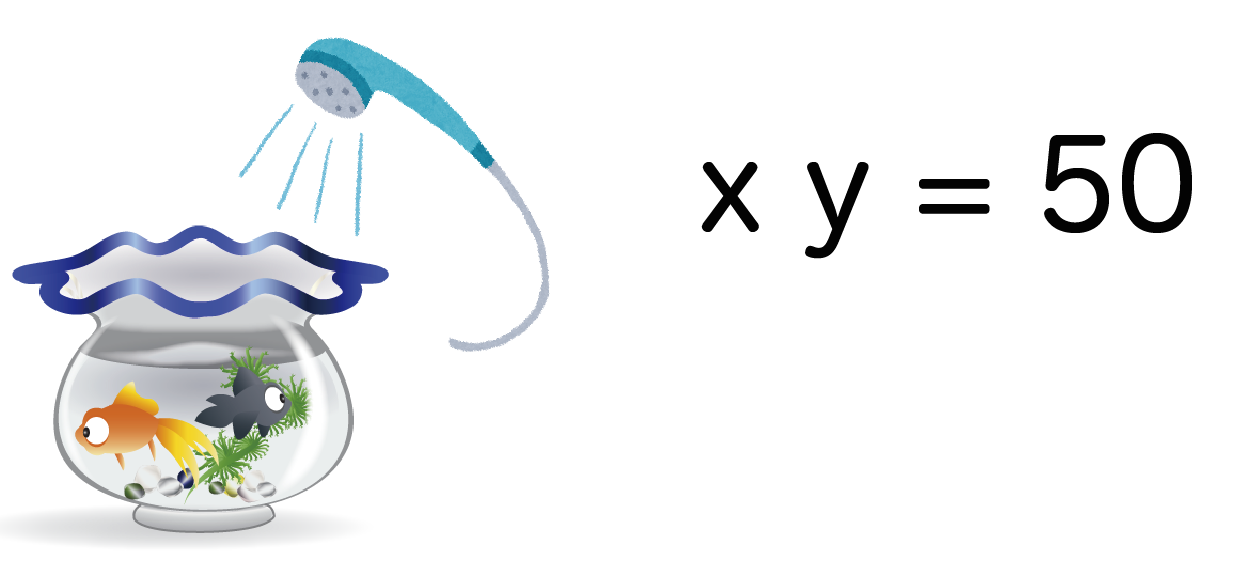
xy = 50
という等式がたてられるはずだ！
これが第一ステップだね。
つぎは、その等式を、
y = ○○○○
というカタチに変形してあげよう。等式の左辺に「y」という文字をもってくればいいだけさ。ね？？カンタンそうでしょ。
さっきの例題の「xy = 50」でいえば、
両辺を文字「x」でわってみよう。すると、
y = 50/x
というカタチに変形できるはずだ。
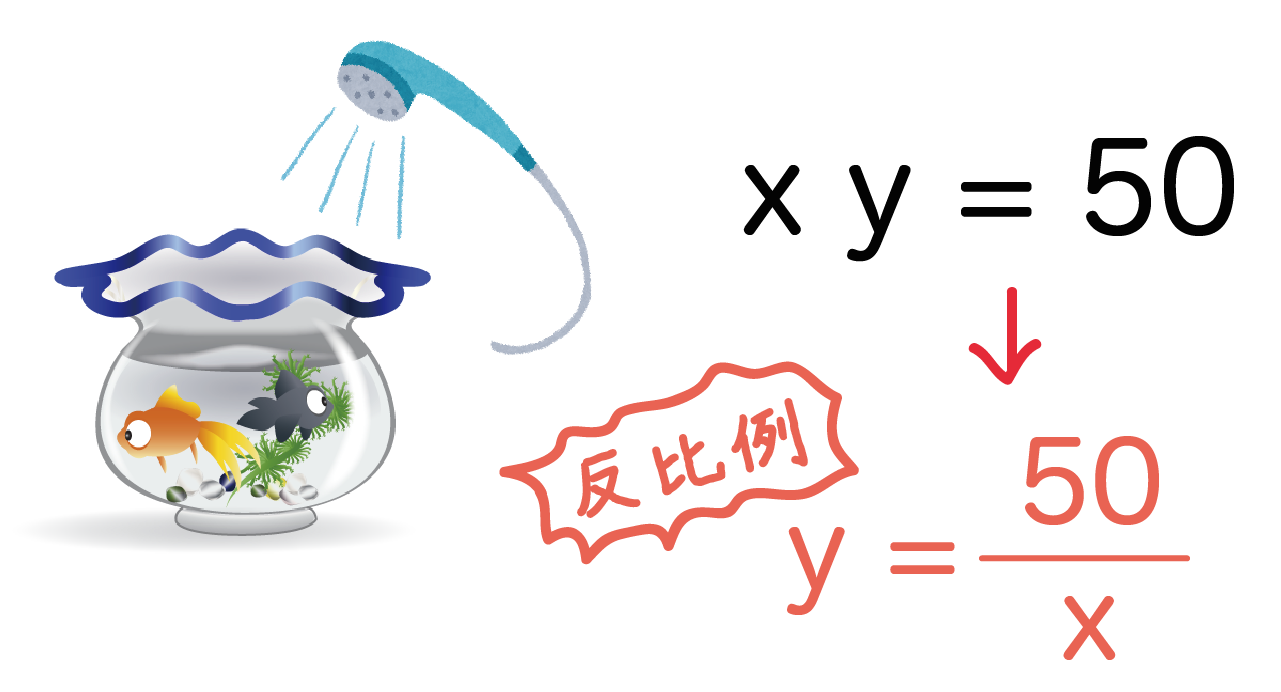
これはなんという偶然なことか、反比例の式のカタチ
y = a/x
にそっくりだね。
ってことで、この問題では反比例の関数を利用していたことになるんだ。
比例・反比例の利用は上の2つの方法でとけば大丈夫。
中1数学の「変化と対応」ではちょっとむずかしいところだけれど、ゆっくりとけば答えがみつかるはず。
テストでも落ち着いていこう！
次回はいよいよ平面図形の勉強に入っていくね。
そんじゃねー!!
Ken
こんにちは、ラーメンライスが好きなKenだよ。
反比例グラフの書き方を前回勉強したね。お腹いっぱいかもしれないけれど、もうすこし反比例のグラフについて勉強していこう。
今日はもう少し踏み込んで、
反比例のグラフの特徴を3つにしぼって紹介するね。テスト前にちらっと確認してみてね。
反比例のグラフには3つの特徴があるよ。さっそくチラ見していこう。
反比例は「双曲線」とよばれるグラフなんだ。
双曲線とは、
双子のように同じグラフが2つ対になっている曲線
のことだ。たとえばこんな感じだね↓↓
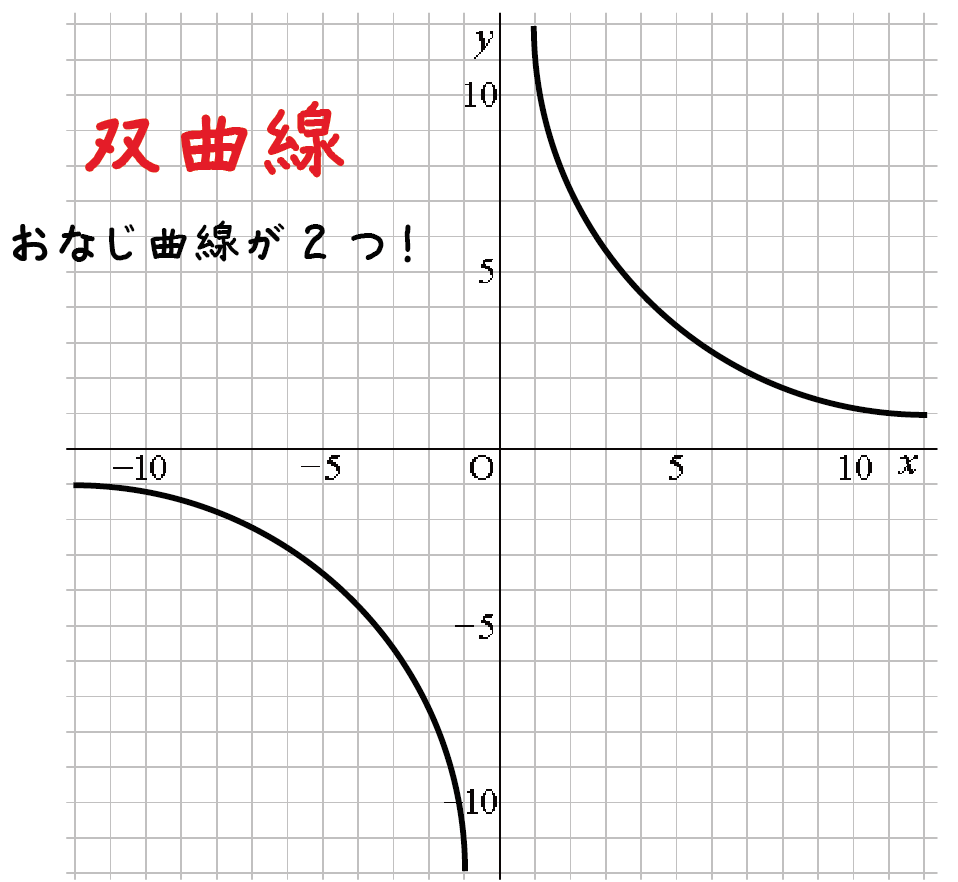
だから、反比例のグラフを書くときは、
カタチが同じ曲線が2つあることを確認しよう。
2つ目におさえておきたいのは、
比例定数がプラスか、マイナスか、でグラフのカタチが変化するということ。
これを知っておくと、反比例の式からグラフのカタチを推測できるんだ。それに、自分で書いてみた反比例のグラフが正しいのかどうか、ということを確認できちゃう。
次のように座標のグラフの各エリアに番号をつけるとしよう。
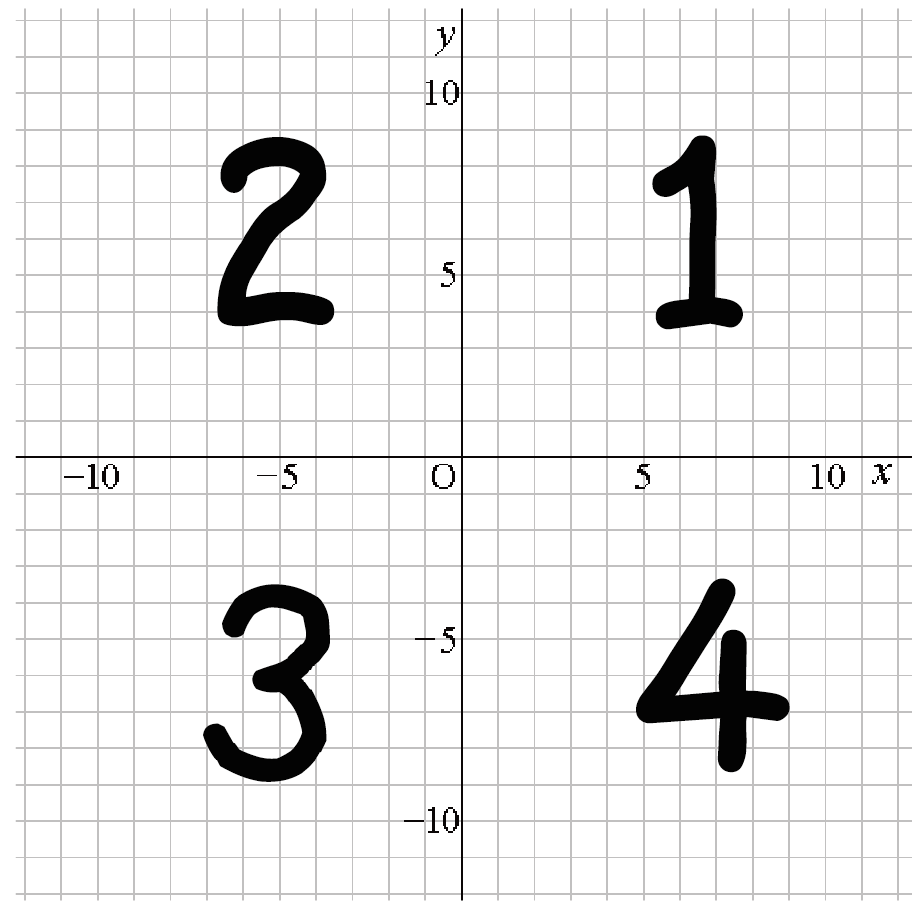
そんで、
比例定数aがゼロより大きいとき（a > 0）、
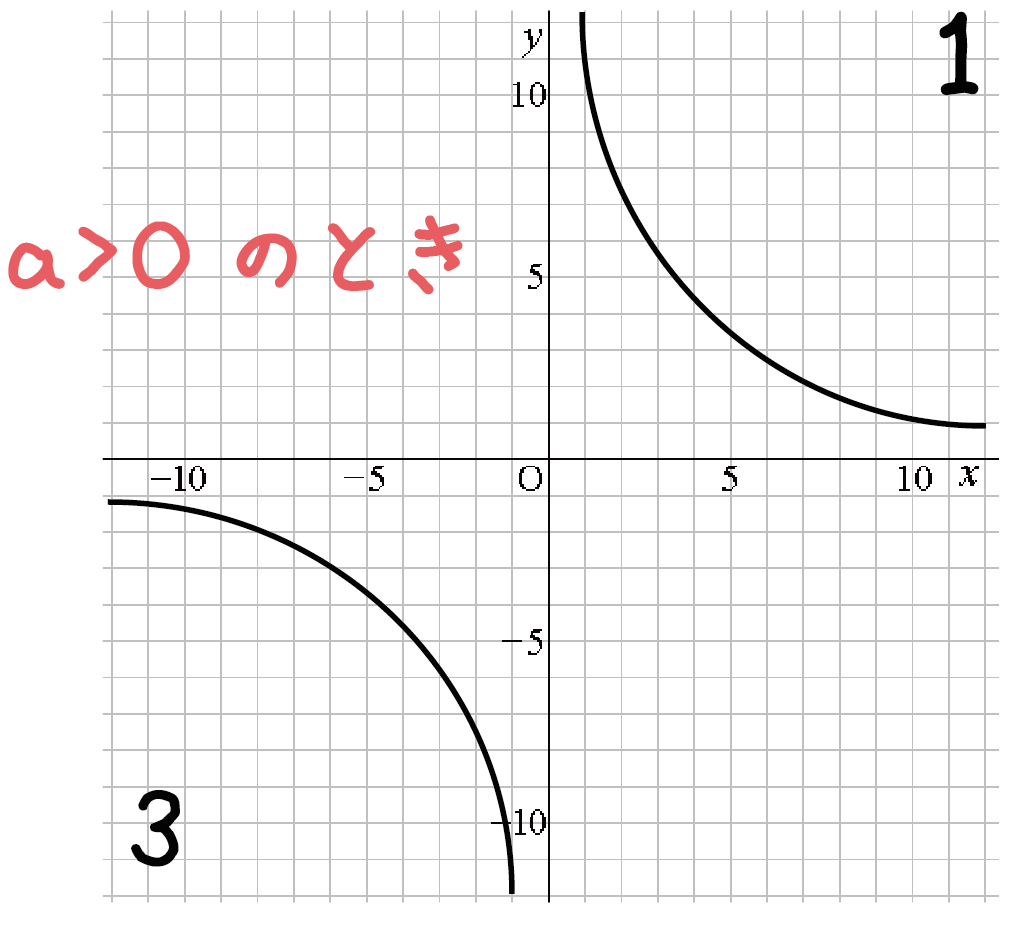
上の図のように双曲線は「エリア1」と「エリア3」でグイグイうなっているんだ。
で、
逆に、比例定数aがゼロより小さいとき（a < 0）、
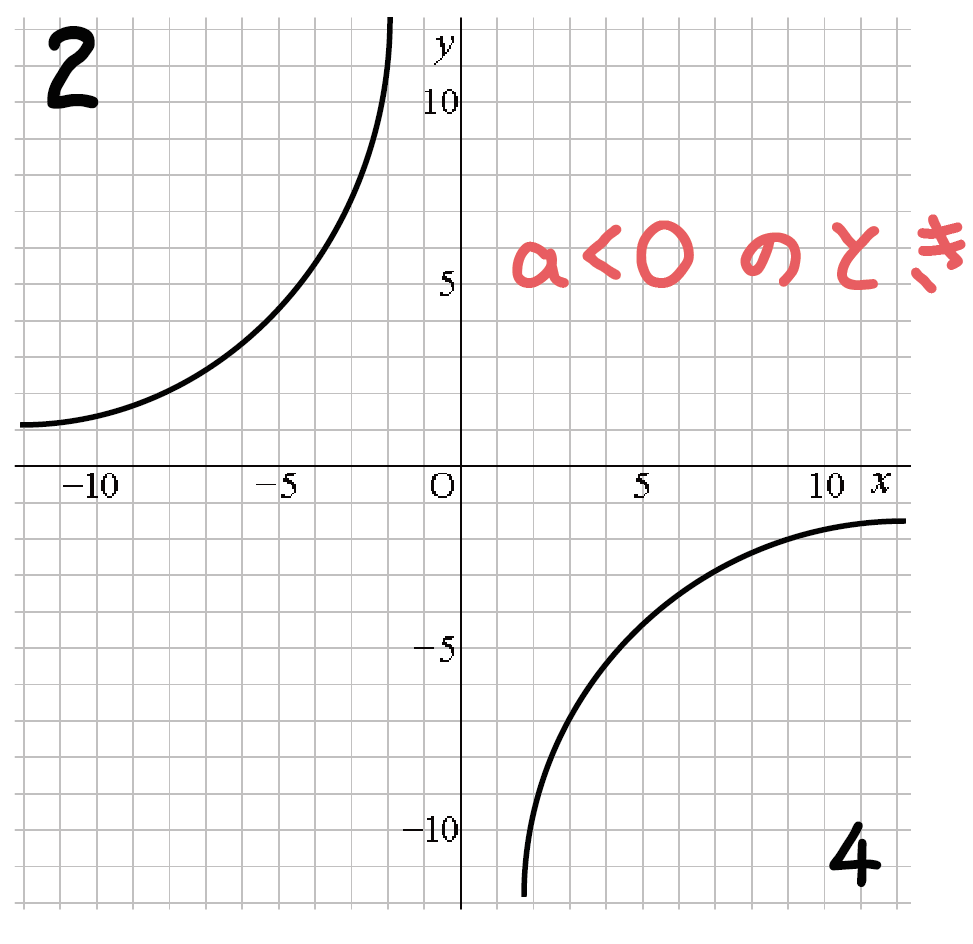
今度は双曲線が「エリア2」と「エリア4」でぶんぶんいっている。
この反比例のグラフの特徴をかるくおさえておこう！！
反比例グラフの3つの目の特徴は、
グラフがx軸とy軸に触れちゃいそうで触れない
ってことだ。
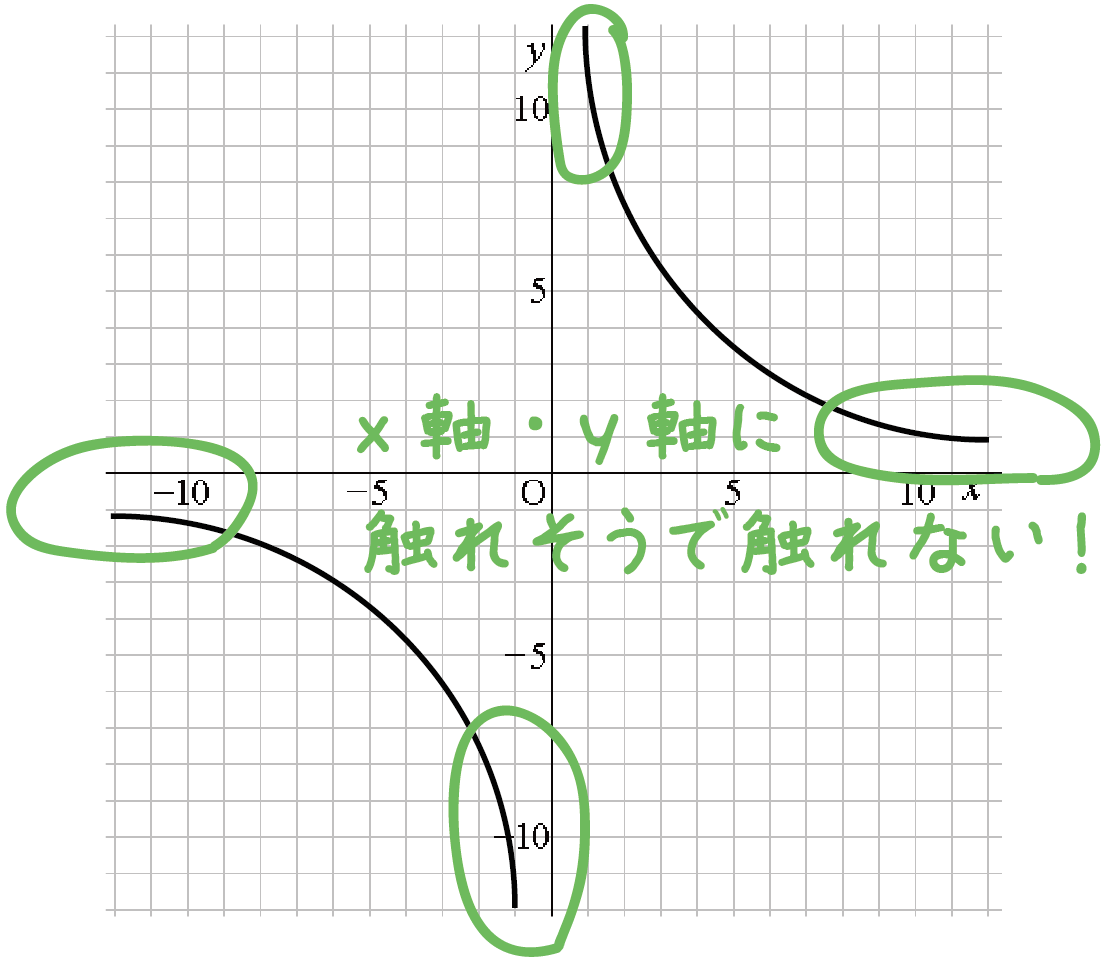
えっ。なんでこんなに見ていてカユい関数になってしまったのかって？！？
じつはこれは、
x = 0 、 y = 0
という座標が反比例には存在しないからなんだ。だって、xに仮に0をいれてしまったら、
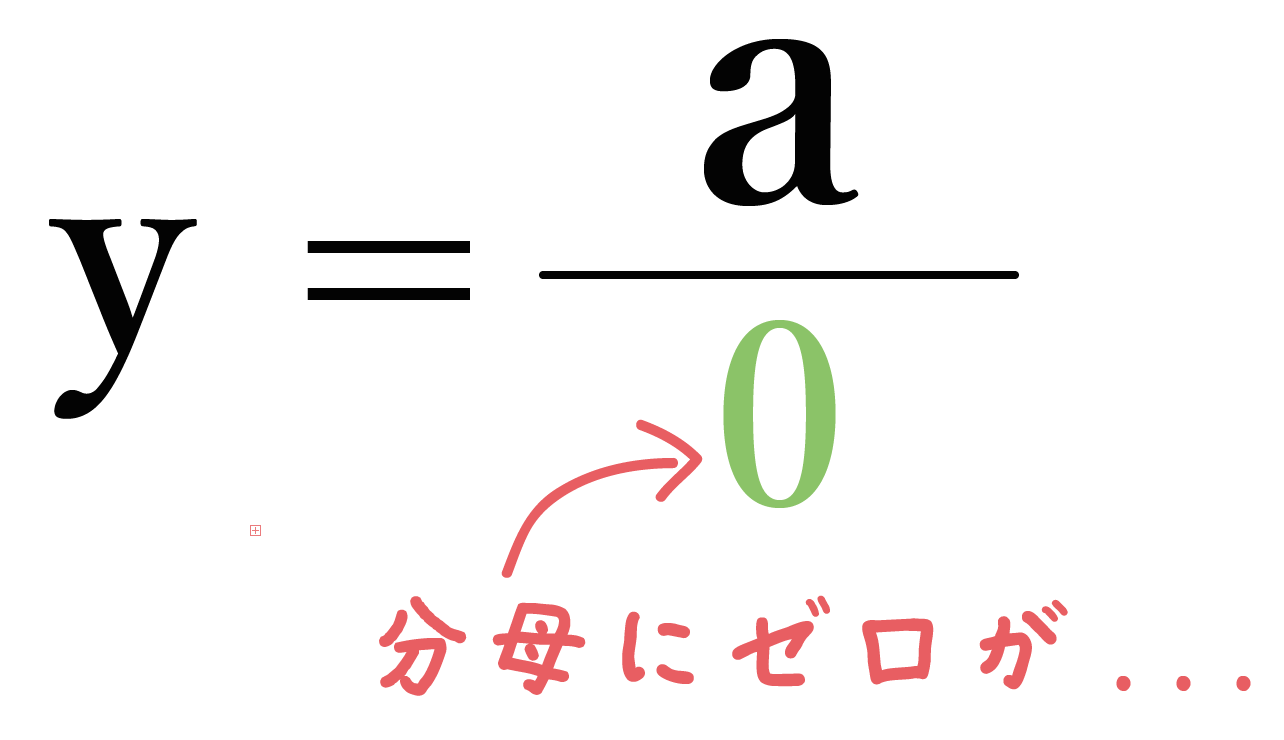
分数の分母が0になってしまうでしょ？？！
これでは、
ゼロで数字を÷ことができない
という数学の大きなルールに反していることになる。
だから、反比例のグラフはx= 0の座標はゼッタイに通ることがないんだ。0よりちょっと大きい値をとることはあるけどね。
x軸とy軸に触れそうで触れないグラフになってしまうのはこのためなんだ。だって、x軸にふれるってことはxの値がゼロになっているってことだからね。
ここまでさらっと反比例グラフの特徴をみてきたけどどうだった？！？
比例のグラフとだいぶ違うし、ちょっとヤッカイだけど、これさえ押さえておけば問題ないよ。
これで長かった反比例グラフの勉強もおしまい。
次回は比例・反比例の利用について勉強していこう！
そんじゃねー!!
Ken
こんにちは、飼い犬にかまれるKenだよ。
反比例は関数の1つの種類だったね。その反比例については、
で勉強してきた。もうそろそろお腹いっぱいだし、吐き気もしてきたけど、
反比例の勉強でいちばん大切なのは、
いかに反比例のグラフを上手に書くか、
ということなんだ。これさえできれば、期末でも中間テストでも何でもこいさ！
だから今日は、反比例のグラフの書き方をわかりやすくカンタンに説明していくね。
~もくじ~
反比例のグラフを書く前に、反比例のグラフの特徴をつかんでおこう。
反比例のグラフは、
双曲線（そうきょくせん）
とよばれるタイプのものなんだ。
文字通り、
双子のように似ている曲線が2つあるグラフ
のことだよ。
これは次の比例のグラフのような直線タイプとはぜんぜん違うタイプだね。
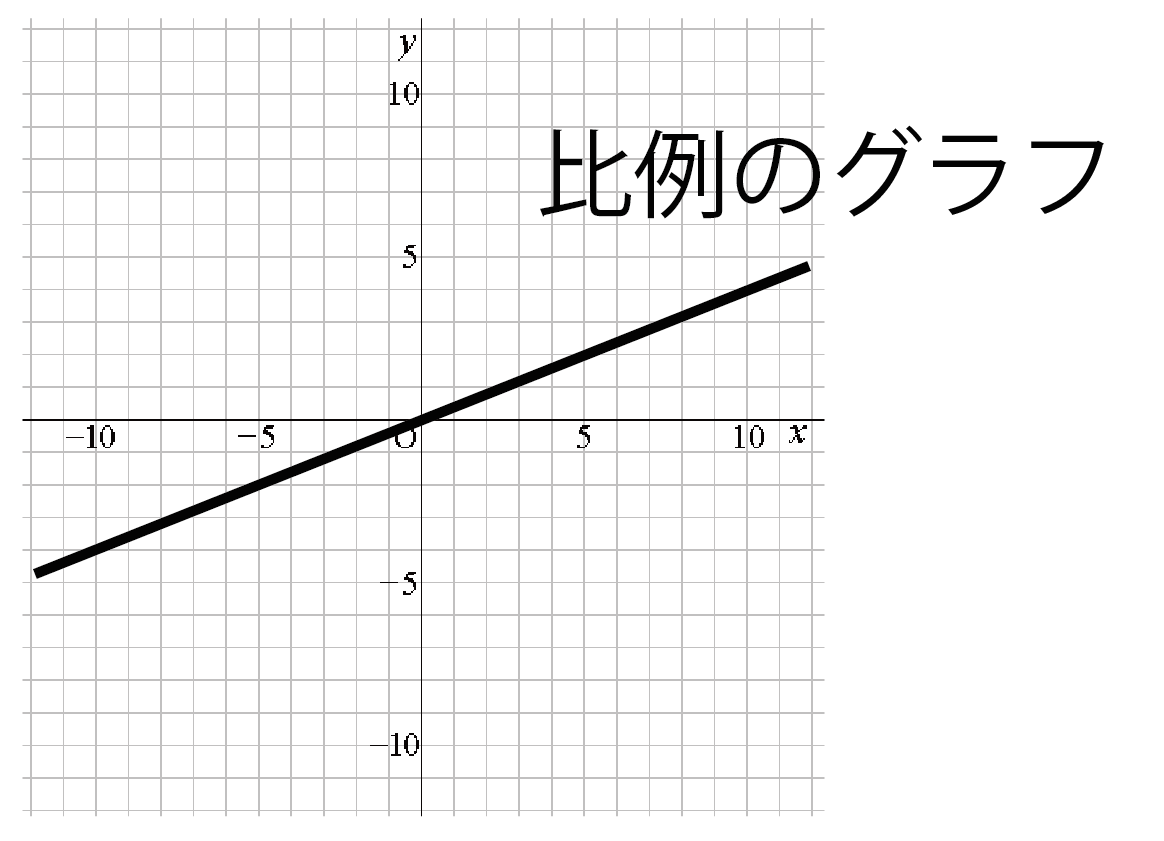
比例のグラフより反比例のグラフはちょっとメンドイんだ。
それじゃあ、反比例のグラフである「双曲線」を書くにはどうすればいんだろ？？
比例のグラフは直線。だから、
関数が通る座標を2点だけ知っていればよかったね？？
でも、反比例のグラフはそうはいかない。
だって、曲線タイプのグラフだからね。
じつは曲線タイプのグラフを書くためには、
グラフが通る座標が多ければ多いほどいいんだ。
関数を通る点が4個のときよりも、
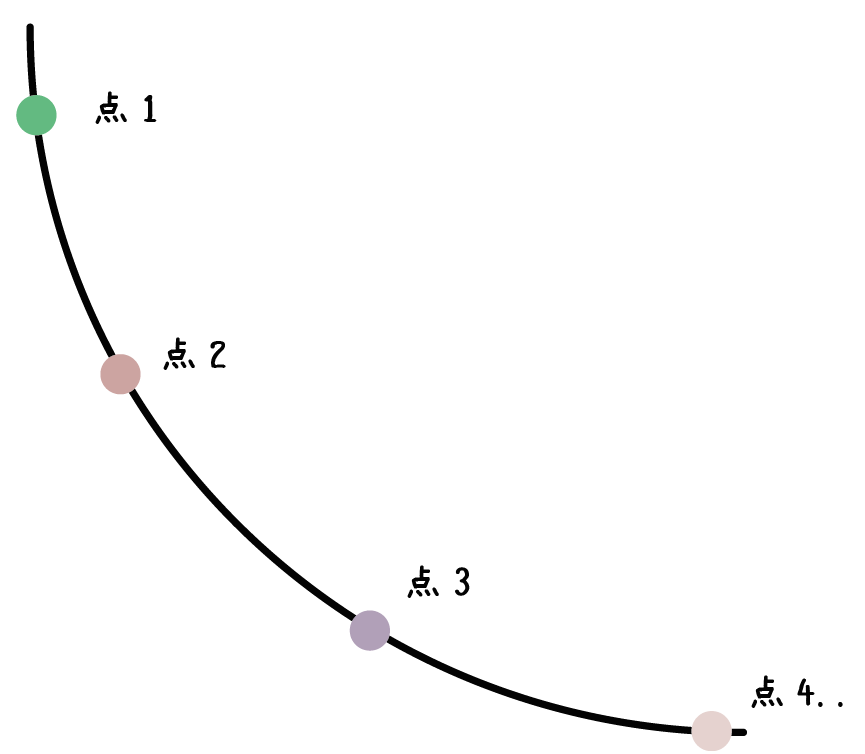
点が7個のときのほうがずっと正確な曲線をかける。
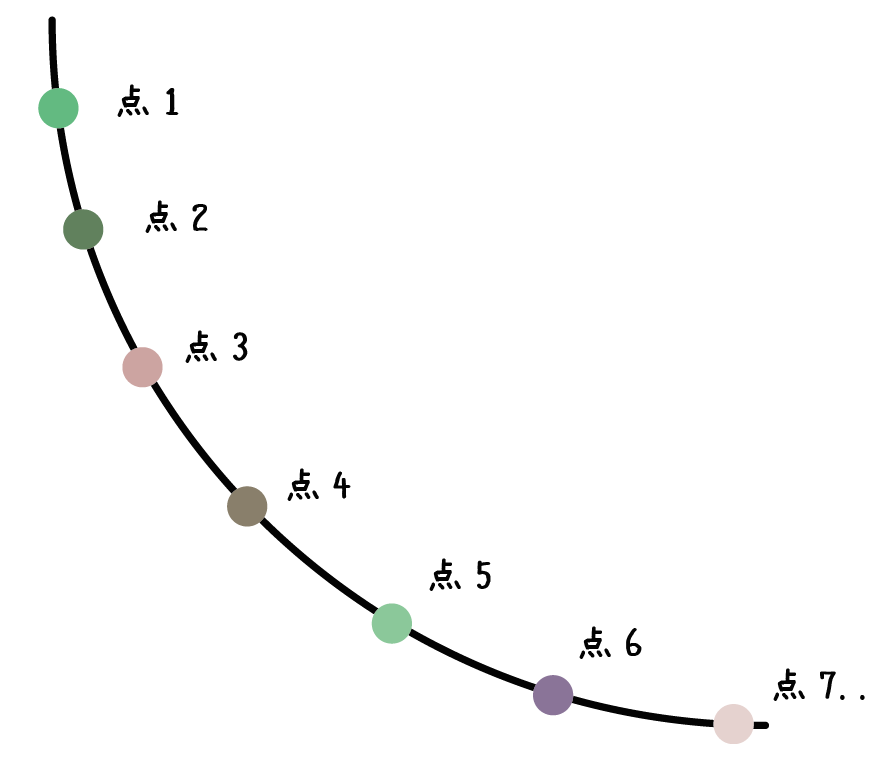
なぜなら、ぼくたち人間は曲線をうまく書けないからね。
直線なら定規をつかって書けるけど、曲線はそうはいかないでしょ？？ 点と点のあいだはどうしても想像によって適当になっちゃうんだ。
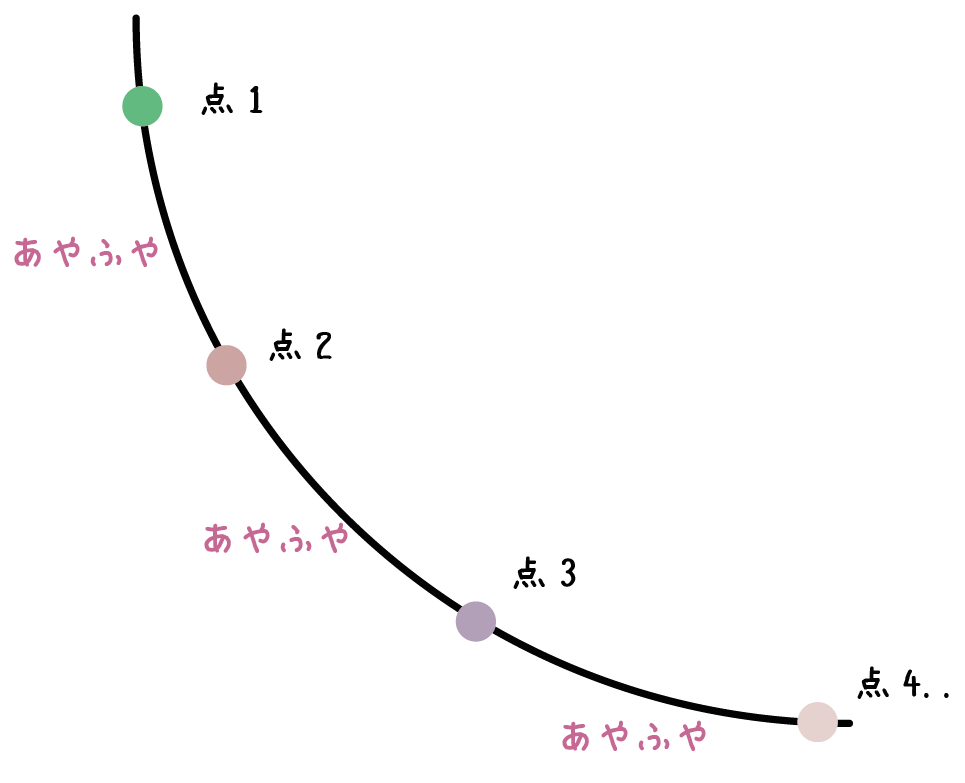
だから、
反比例のグラフが通る点をできるだけ多くみつけたほうがいいってことになる。
それじゃあ、どうやってグラフが通る「点」をみつけるんだろう？？
じつはとっておきの方法が用意されている。
それは、
比例定数の約数をx座標とする点
なんだ。 ※ 約数とは「ある数を割り切れる数のこと」だよ。
ちょっとしっくりこないよね？？
ここで、y = 24/x という反比例の関数の例をみてみよう！！
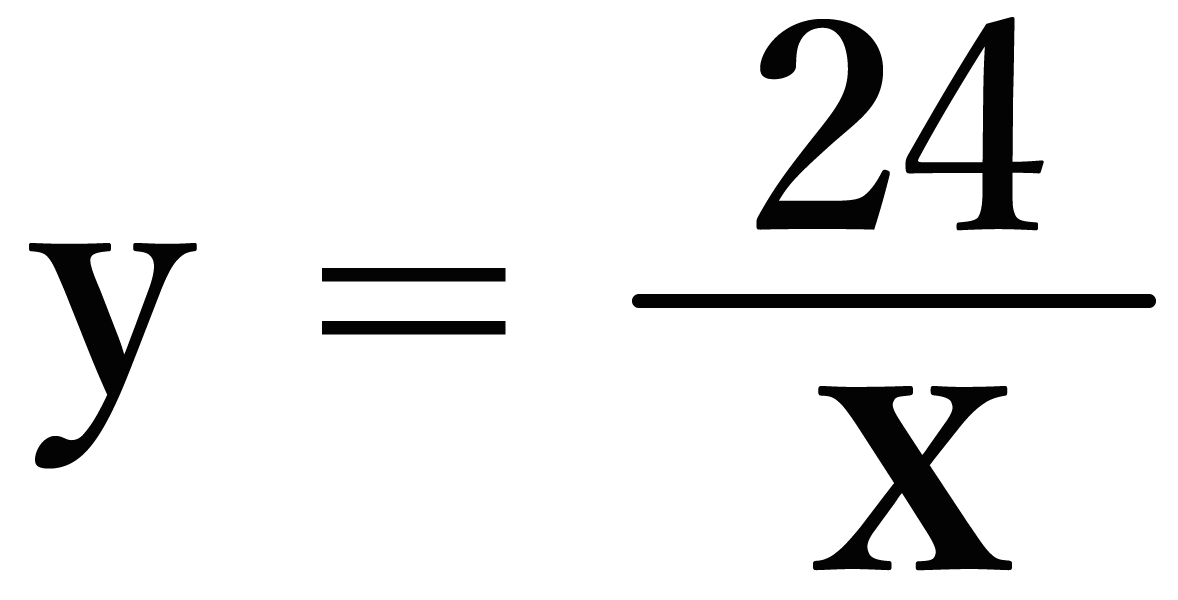
この反比例の式の「比例定数」って「24」だよね？？
※ 反比例の比例定数を忘れてしまったときは「反比例の比例定数の求め方」っていう記事をみてくれ！
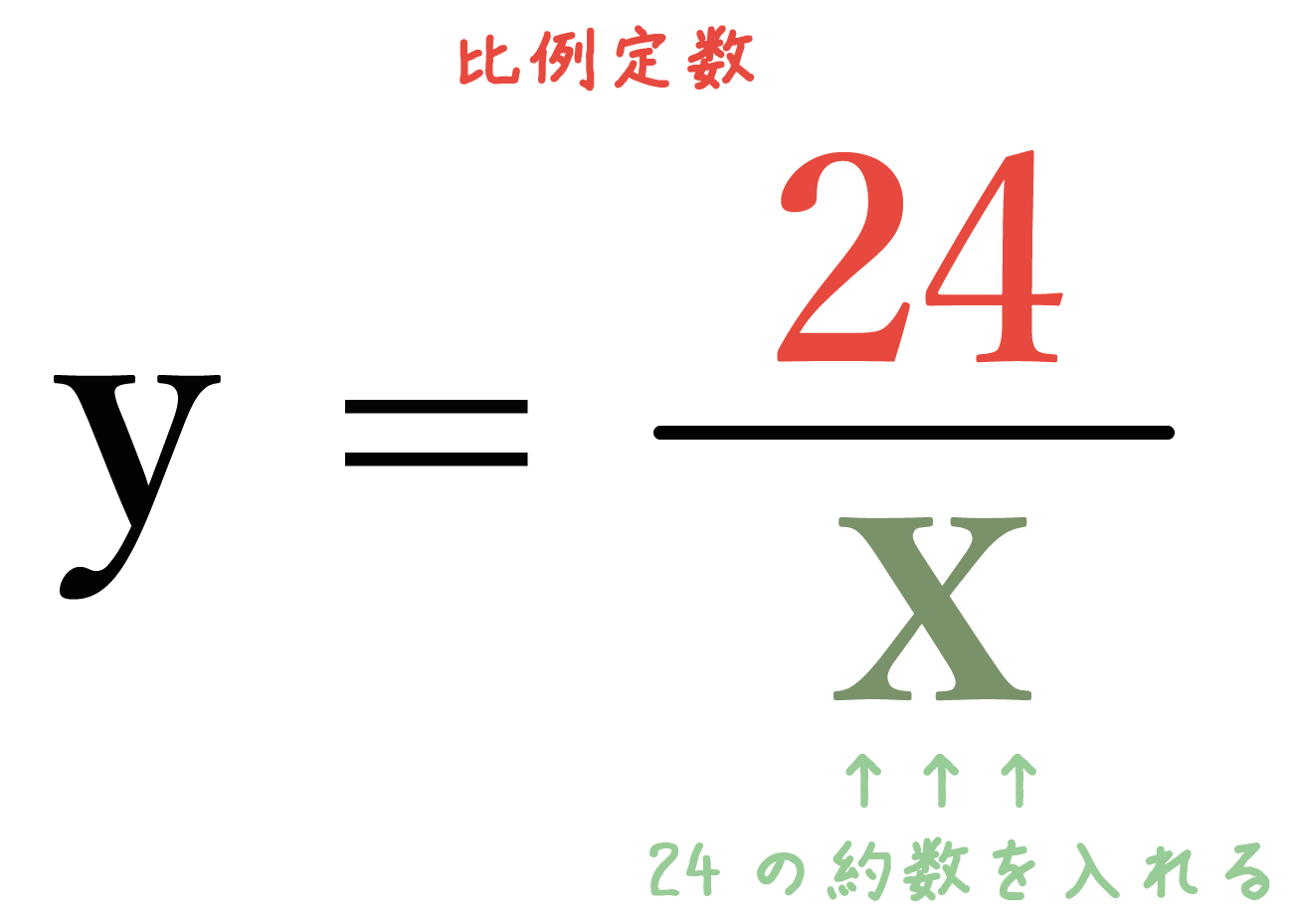
この比例定数「24」を割り切れる数（約数）をさがしてみると、
っていう8つがみつかるでしょ！？？ そんで、
これらの値がx座標になったときのy座標を計算してみると、
こうなる！！ これらが反比例のグラフが通る点たちなんだ。
つぎは求めた点を図に打ち込んでいこう！！
今回の座標平面には、x座標とy座標が12以上の点は打ち込めないよね？？ ちょっと小さいタイプなんだ。まあ、図の外に打ち込んでもいいけどね。
w.geocities.jp/emkodama0920/game/zahyou/zahyou.htmlより
だから、
の2点をのぞく、
上の6点を打っていこう！！
すると、こうなる↓↓
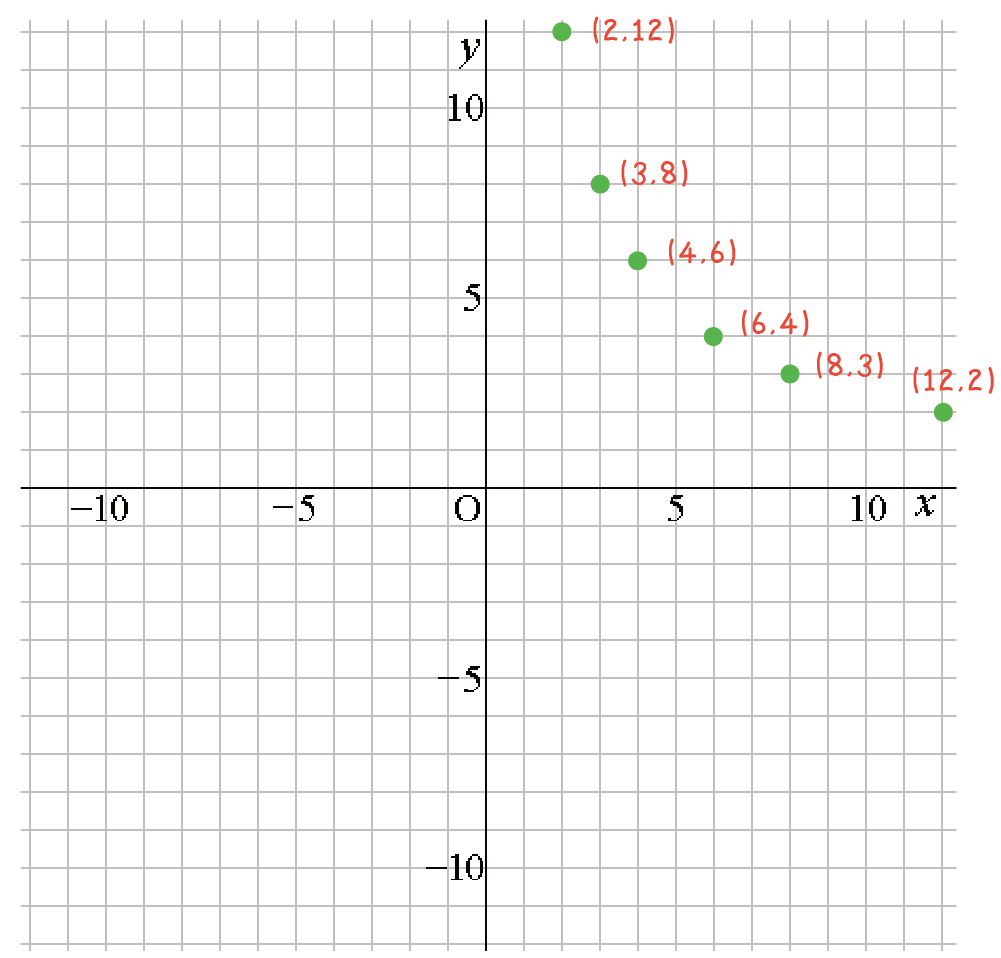
そんで、こいつらを曲線っぽく結んであげると、
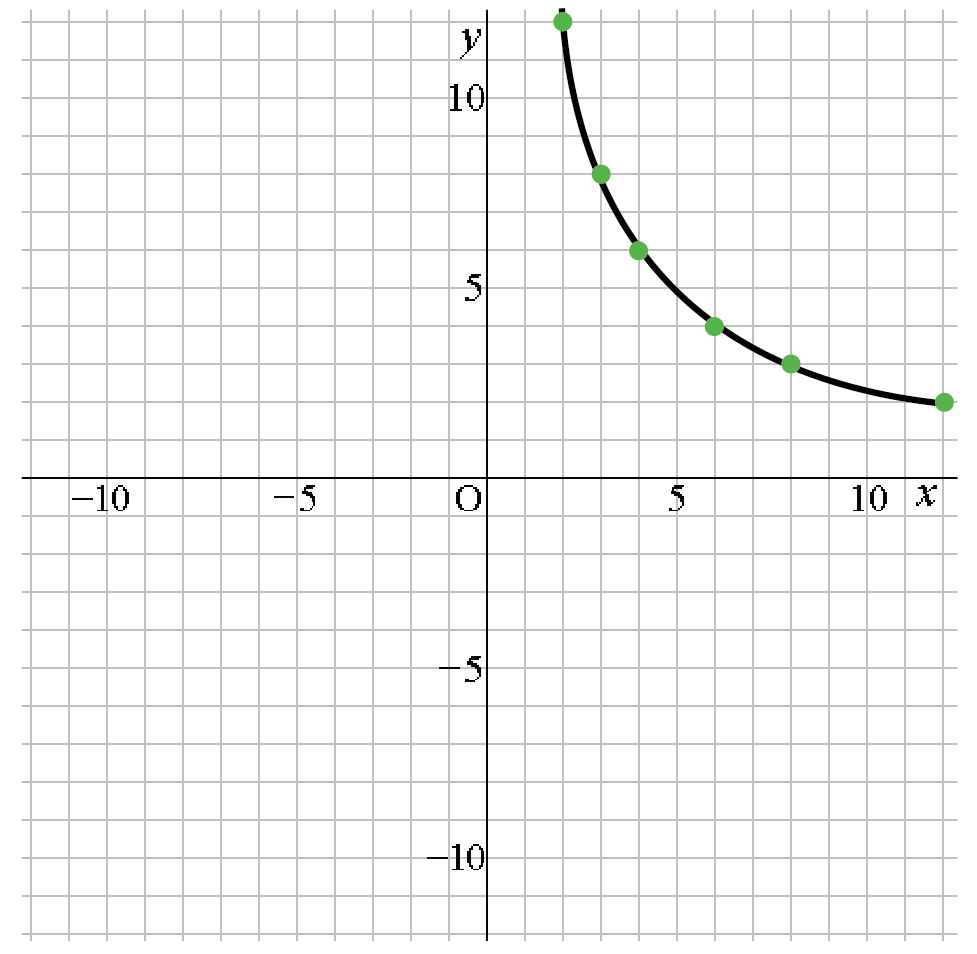
こんな感じで曲線がかけるんだ！
これじゃあ曲線が1つしかないから「双曲線」じゃないよね？？
今度はさっきのx座標をマイナスにしたやつを入れてみよう！
すると、
となるはずだ。これらの座標をうちこんでやると、こうなって、
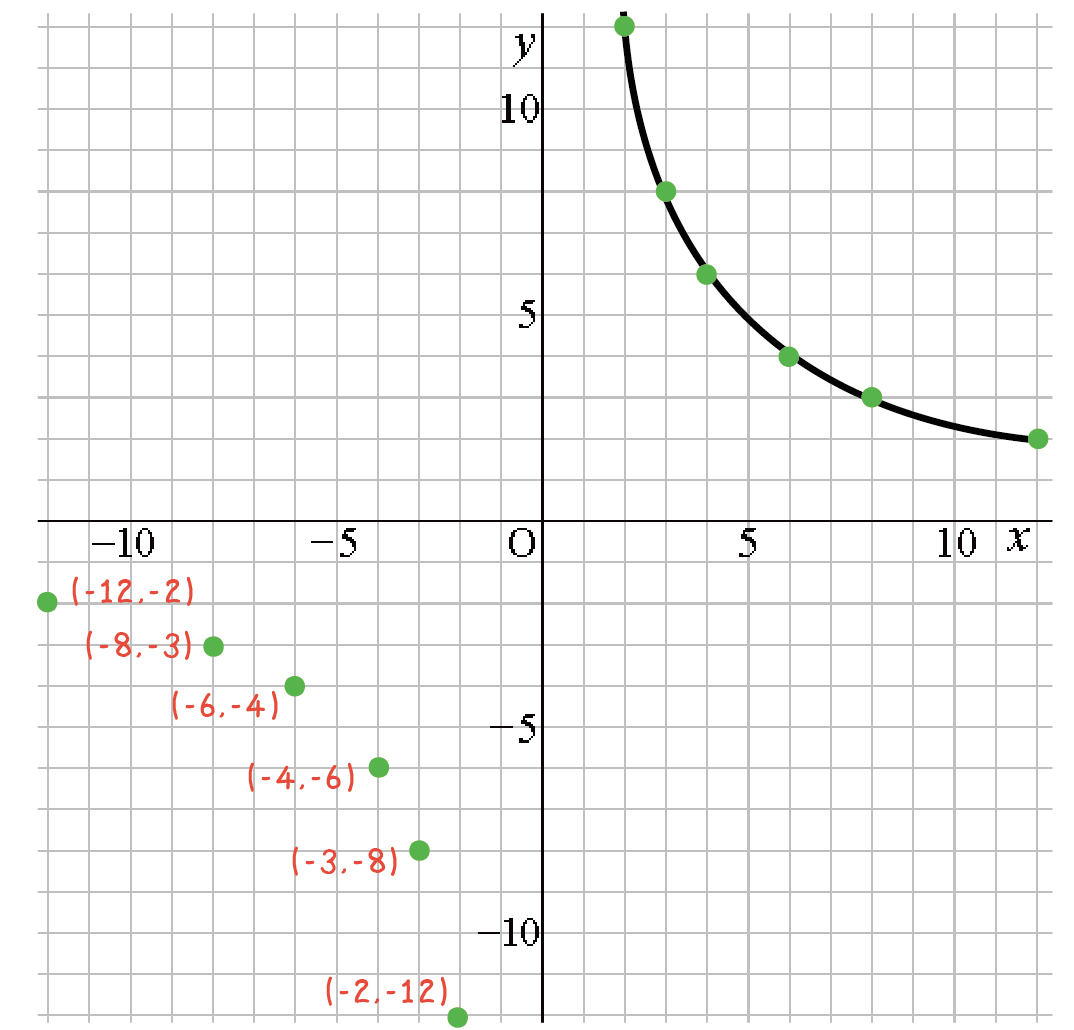
曲線を同じように書いてやると、
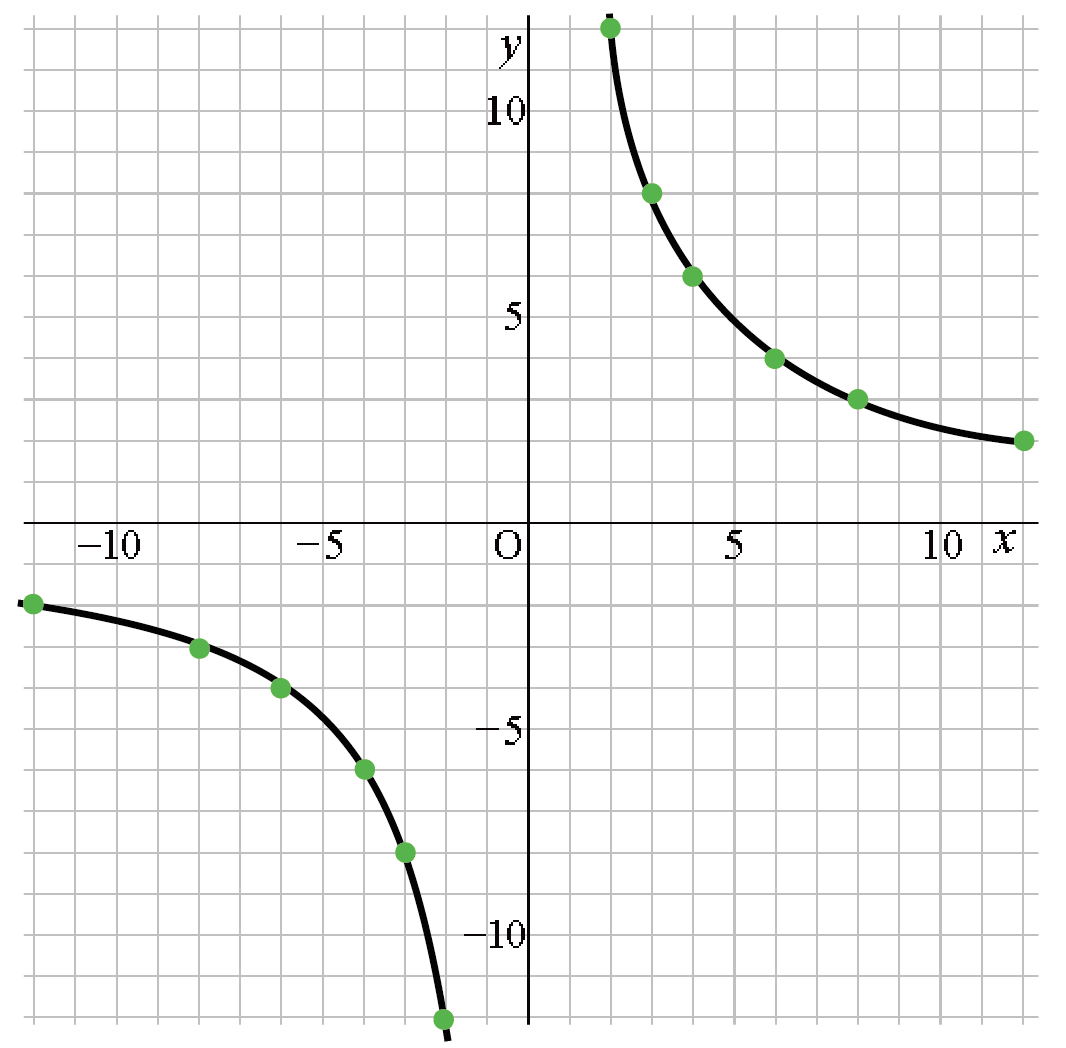
こうなる！！
これで反比例の双曲線グラフが書けたね！！
ふうー！！ おめでとー！！
ふう、ここまで反比例のグラフの書き方を解説してきたけどどうだった？？
比例のグラフより複雑になって疲れたかな？？
次回は反比例グラフの特徴について解説していくね！
そんじゃねー
Ken
こんにちは、カフェでコーヒーを頼まないKenだよ。
前回は「反比例とはなにか？？」ということを勉強してきたね。反比例は比例とおなじように、関数の中の1種類だよ。
むずかしそうに聞こえるけど、基本をおさえればカンタンになってくるんだ。
今日は、反比例の問題でよくでてくる、
反比例の比例定数の求め方
をわかりやすく解説していくね。
コツさえつかんじゃえば、2秒ぐらいで比例定数を計算できるはずだ！！
反比例の比例定数の求め方はチョーシンプル。
比例定数の求め方とはずばり、
xとyをかけるだけ
だよ。
ね？？ むちゃくちゃカンタンそうでしょ？？
反比例の問題では「x」と「y」の値があたえられているから、その2つをかけあわせるだけでいいんだ。
実際の反比例問題で比例定数を求めてみよう！
つぎの問題があったとしよう。
yはxに反比例し、x=5のときy =6です。xとyの関係を式にあらわしなさい。
解き方：
問題の最初で「yはxに反比例する」っていってるね？？ だからこのxとyについての関数の比例定数は、
比例定数 a = xy
で求めることができる。
そんで、
問題文をよーく目をこらしてみてみると、
x = 5, y = 6
ってことがわかるね。だから、反比例の関数の比例定数は、
xとyをかけあわせて、
30
になるね！
ね？？ かけ算が得意だったら2秒で比例定数を求められたでしょ？？。
反比例の比例定数の求め方って、
a = xy
って超シンプルだったね。
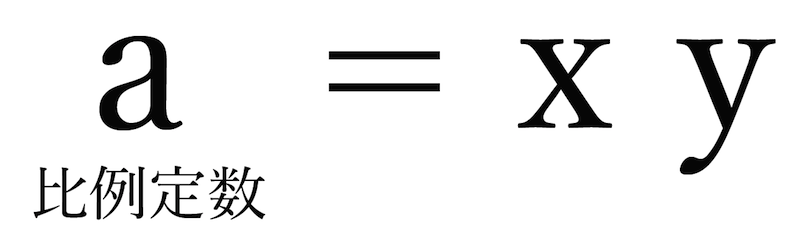
じゃあ、なんでこんなカンタンなんだろう？？？
その答えは、
反比例の式をゆっくり変形すればわかるよ！
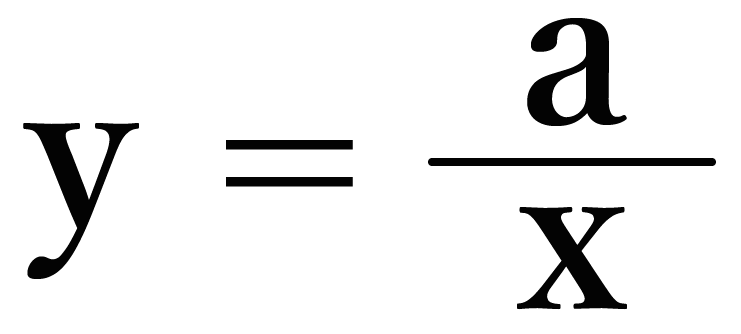
反比例の式である「y = a/x」の両辺にxをかけてみよう！！
すると、
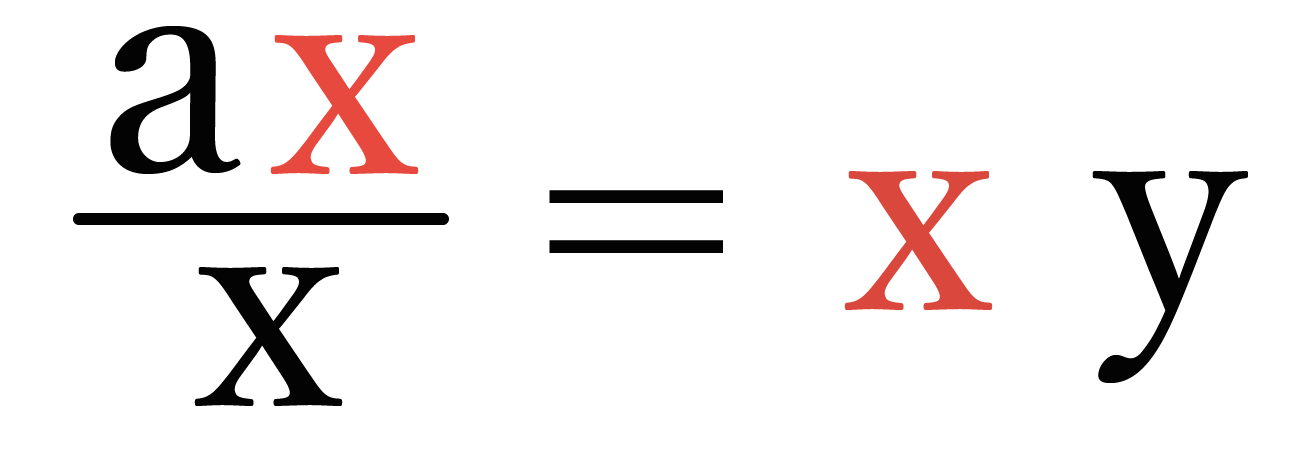
分母の「x」があたらしくかけられた「x」と打ち消しあうっちゃうから、
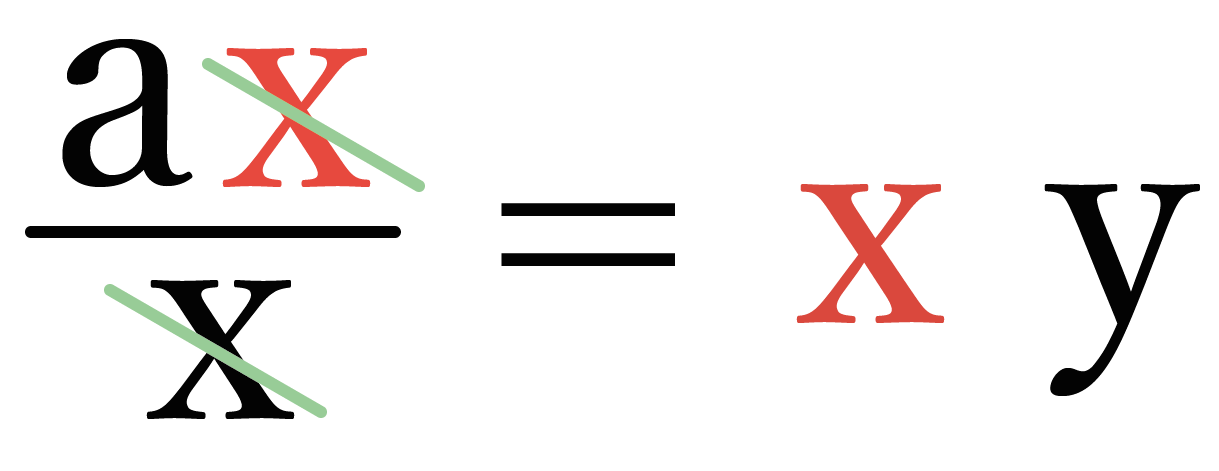
この反比例の関数は、
a = xy
って変形できるね。
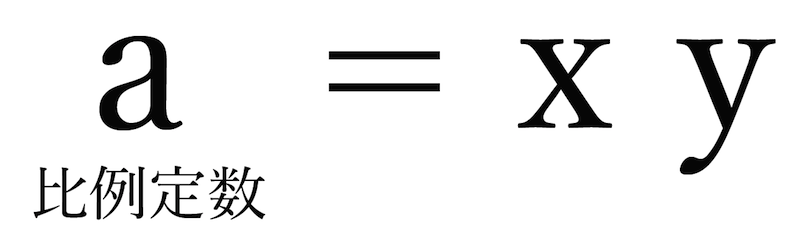
え？？ あまりピンとこない？？
そういうときは「等式の性質」をみなおしてみてくれ！ 等式の基本さえわかっていれば大丈夫。読みながらもう一度変形にチャレンジしてみてね。
ここまでみてきた反比例の比例定数の求め方はどうだった？？
xとyの値をかけるだけだから、気合いをいれれば2秒ぐらいで求められるはず！！
つぎは、
反比例のグラフの書き方について勉強していくね。
そんじゃねー！
Ken
こんにちは、この記事を書いているKenだよ。新宿のアルタ前に憧れるね。
反比例（はんぴれい）って聞いたことある？？
たぶん、中学校で数学の授業をうけないかぎり「反比例」なんて使わないはずだ。
ゼッタイに、
さてと、歯磨きの前に反比例するかああ。
なんて言わないよね。
そこで、今日は「反比例」ってやつをわかりやすく解説していくね。
反比例の正体が不明すぎるっていうときは参考にしてみてくれ。
~もくじ~
反比例ってからみづらそうだけど、じつはシンプル。
関数の種類のうちの1つのこと
なんだ。「関数とはなにか？？」という記事で、関数とは、
自動販売機である
ってたとえたね。
いってみれば、反比例は関数っていう「自動販売機」の1種なんだ。
自動販売機の中には、
お茶ばかり売っているものとか、タバコの専用のものとか、おでん専用のものとかいろいろあるでしょ？？ それと同じさ。
だから、
関数のグループ内では、「反比例」だってやつもいれば「比例」だってやつもいる。
中学校にもいろんなやつがいるけど、関数の世界も同じなんだってことを覚えておこう。
反比例は関数の一種、
ってことはわかったね？？ それじゃあ、いったいどんな関数のことを言うんだろうって疑問に思うでしょ？？
反比例はつぎのカタチをした関数のことを言うんだ。
y = a/x
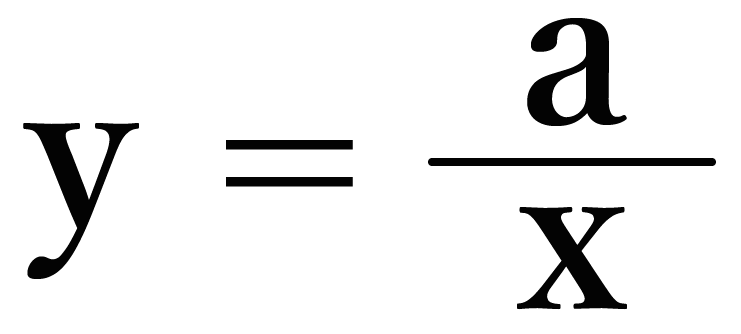
ね？ ちょっとカッコいいでしょ。？？
そんで、
「x」と「y」は「変数」ってよばれてるんだ。なぜなら、「x」になにを入れるかによって「y」の値も変わる数だからね。
一方、xの上にのっている「a」は「定数」だ。だって、xやyに関係なく変わらずに定まっている数だからね。
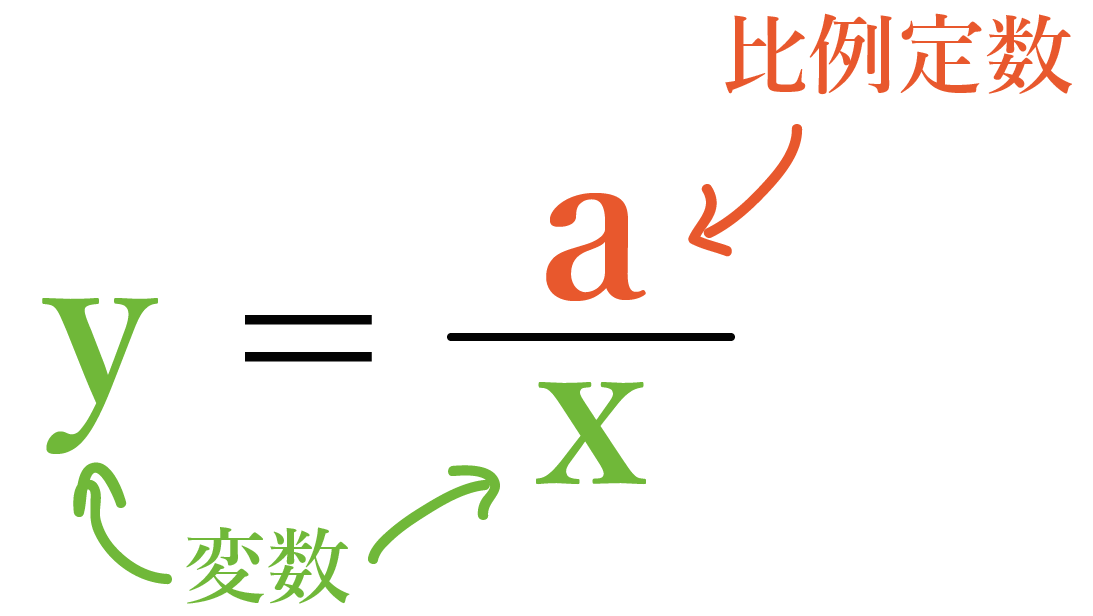
とくに、反比例の式にふくまれる定数のことを「比例定数」っていうんだ。さらっとでもいいから覚えておこう！
ちなみに、xとyでこの反比例の式が成り立つとき、
yはxに反比例する
っていうんだ。クールな澄まし顔でいったらモテそうだね。
反比例とはなにか？？
ってことはわかったけど、まだイメージしづらいよね。
もっと反比例と仲良くなるために、反比例の例をさらっとみてみよう！！
比例定数aに2をいれてもいいし、
aに-420をぶちこんでみていもいい。
ただ、aが「小数」とか「分数」のときは注意してね。なぜなら、最後には分子を整数にしてやらなねばならんからさ。
だから、
たとえばaに0.2をいれたとすると、
y = 0.2/x
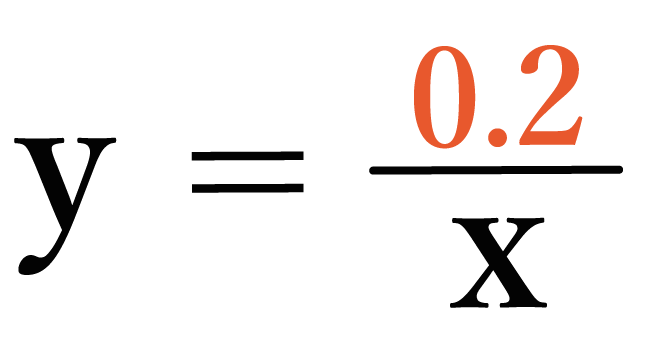
分子と分母を10倍してあげて、分数のカタチになおすと、
y = 1/5x
になるね！
反比例の分子に「小数や分数」をのこさないようにしよう！
ここまで反比例の式はどうだったかな？！？
つぎは反比例の比例定数aの求め方を解説していくよ。よかったら見てみてね。
そんじゃねー！
Ken
こんにちは、この記事を書いているKenだよー！豚角煮カレーおいしかったよ。
前回、「比例グラフの書き方」をみっちり勉強したね？！ 比例のグラフをかけるようになったら、あとはテストで点をとり放題・・・・・・
ってわけにはいかないんだ！。
じつは、比例グラフを自由自在にあやつるためには、
比例のグラフにみられる特徴
を知っておいたほうが有利だ。
比例のグラフともっと仲良くなりたいよね？？
今日はもうちょっと深く、「比例のグラフ」について勉強していこう。グラフの特徴を4つ紹介するから勉強の参考にしてみてね。
中1数学で勉強する「比例のグラフ」の特徴は次の4つ。
比例のグラフのいちばん目立つ特徴は、
グラフが原点（0,0）を必ず通る
ってこと。
だから、比例のグラフを書くために原点にポチッと点を打つことが第一ステップなのさ。
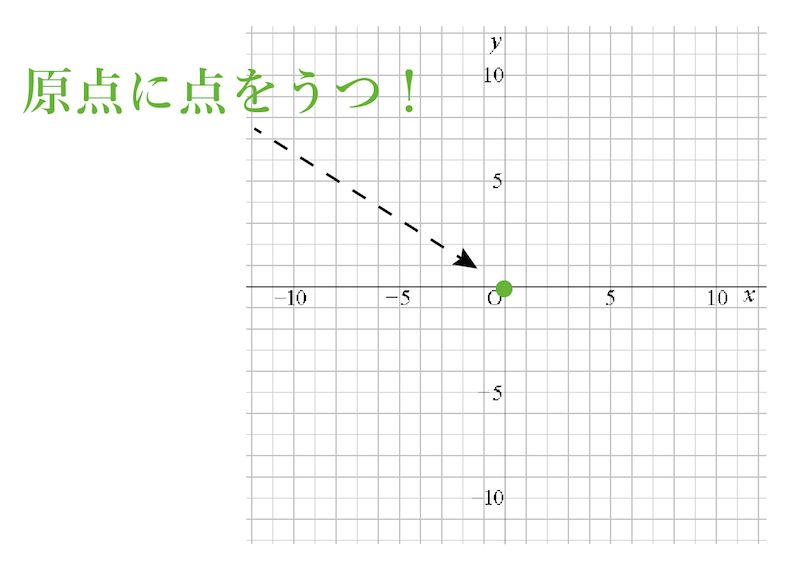
それじゃあ、なぜ比例のグラフは原点を通るんだろう？？
その答えは比例グラフの式「y = ax」をよーく見てみればわかるよ。
この式のxにゼロをいれてみよう。
すると、yもゼロになるよね？！？ xが0のときyも0になる。
つまり、原点（0, 0)を通るってことなんだ。よーく覚えておこう！
比例のグラフの2つ目の特徴は、
比例定数aの値が大きくなればなるほどグラフの傾きが急になる
ってこと。たとえば、「y = 2x」と「y = 5x」が座標平面でなかよく暮らしていたとしよう。
この2つの比例の式を書いてみると↓↓
こうなるね！
よーく見てみると、
比例定数aが大きい「y = 5x」のほうが「y = 2x」より急に傾いていることがわかる。
だから、かりに、この2つの比例グラフのうえに「りんご」をのせたら、
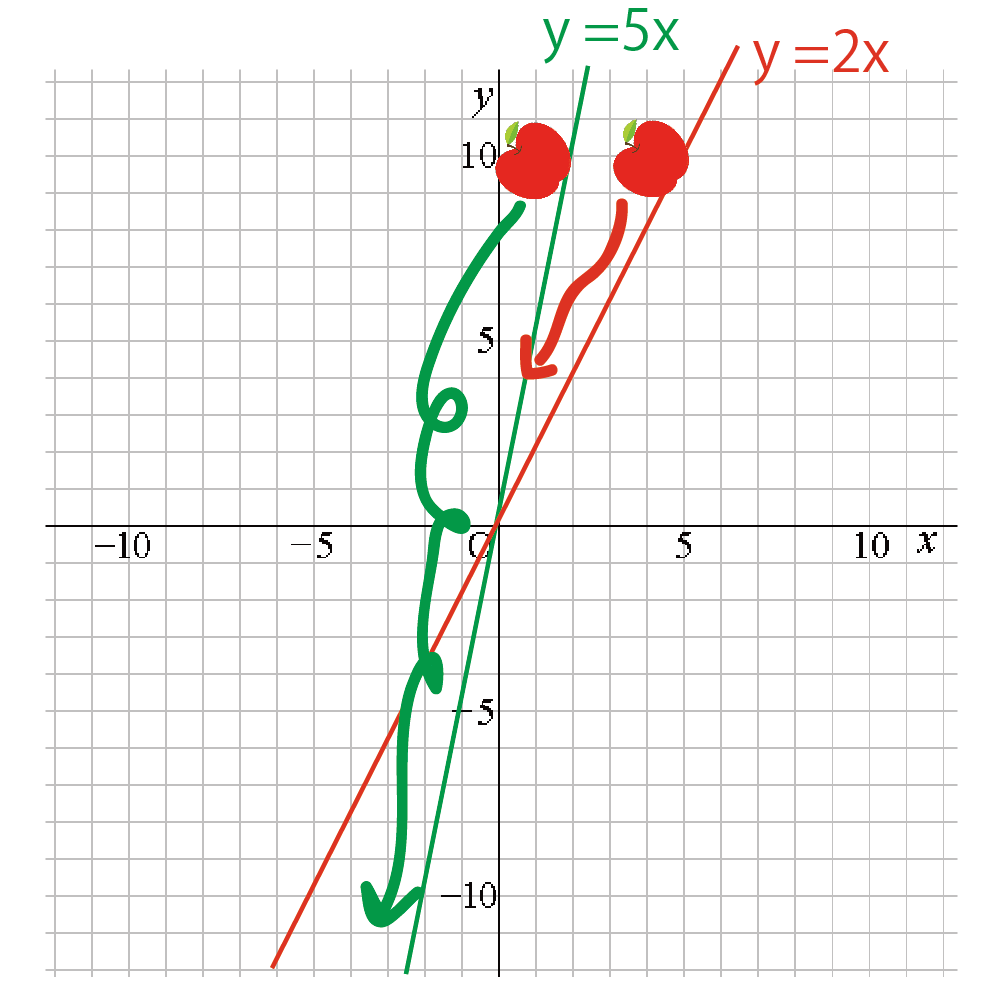
こんな感じで、y=5xのりんごのほうがグルグル速く坂をくだっていくはず！。
比例定数が大きければグラフの傾きが急になる！
ってことを覚えておけば、グラフのカタチを予測できるようになるよ。
もう1つ比例定数に関して押さえておきたいのは、
比例定数aがプラスのときと、マイナスのときでカタチがすっごく違うってこと。
これを確認するために、
y = 2x と y = -2x の比例のグラフを書いてみよう！
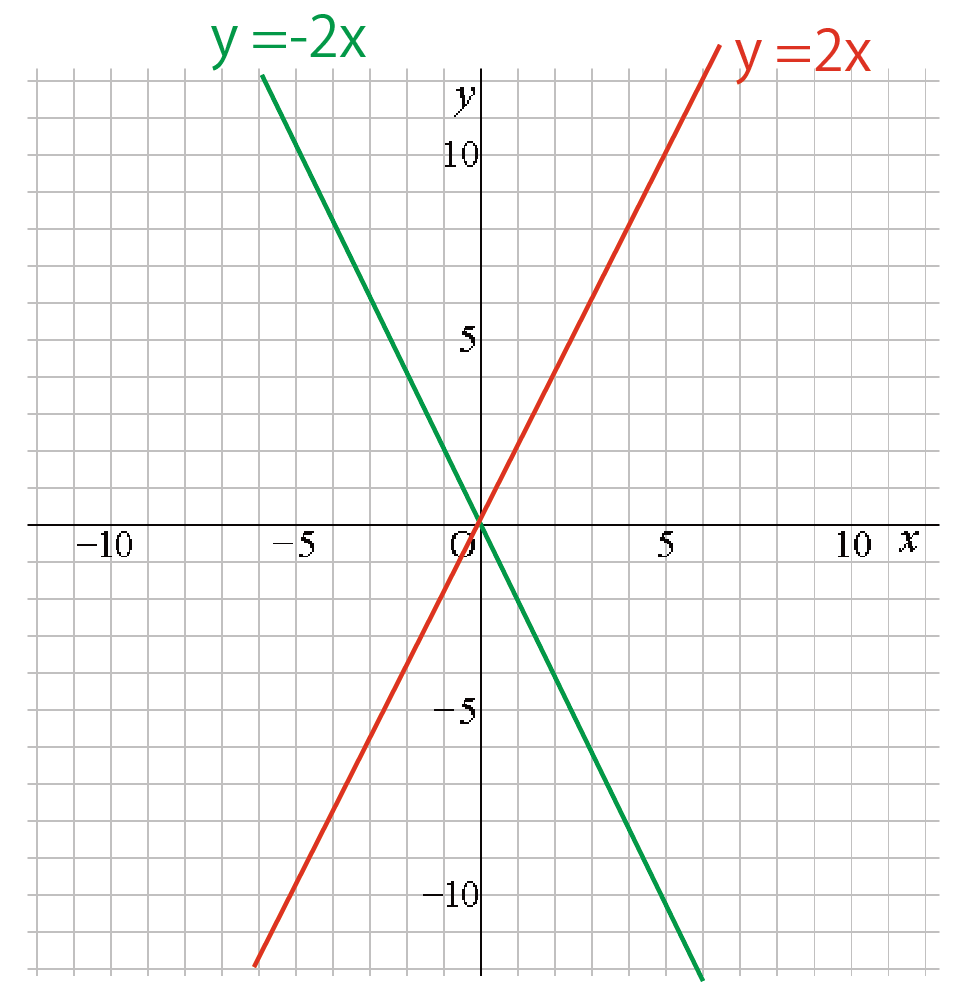
aがゼロより大きいとき（プラス）、グラフが右肩あがりになる。
それに対し、
aがゼロより小さいとき（マイナス）、グラフは右肩下がりになってるね。
だから、
かりにりんごを2つの比例の式の上で転がしたら、
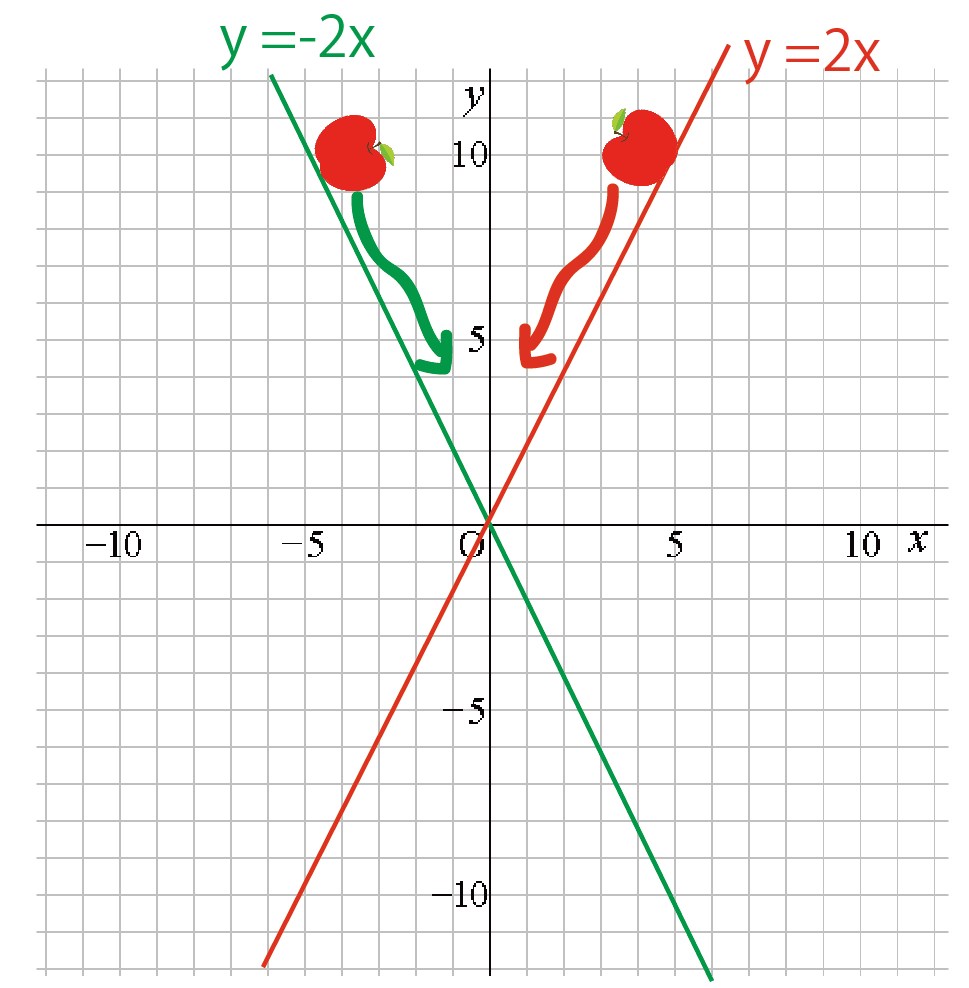
りんごが2つとも違う方向に転がりだすでしょ？？。
比例定数aがマイナスのグラフには注意しよう！
ときどき、比例のグラフの問題で「xの変域」が指定されたものが登場する。
たとえばこんな感じ↓↓
次のグラフを書きなさい。
y = 2x （-2 ≦ x ≦ 2）
このとき、
比例の式に金魚のふんみたいにくっついてる（-2 ≦ x ≦ 2）っていう「xの変域」に注意してくれ。
この変域がついていると、
いつも通りにグラフをばんばん書いちゃいけないんだ。こんな感じでね↓↓
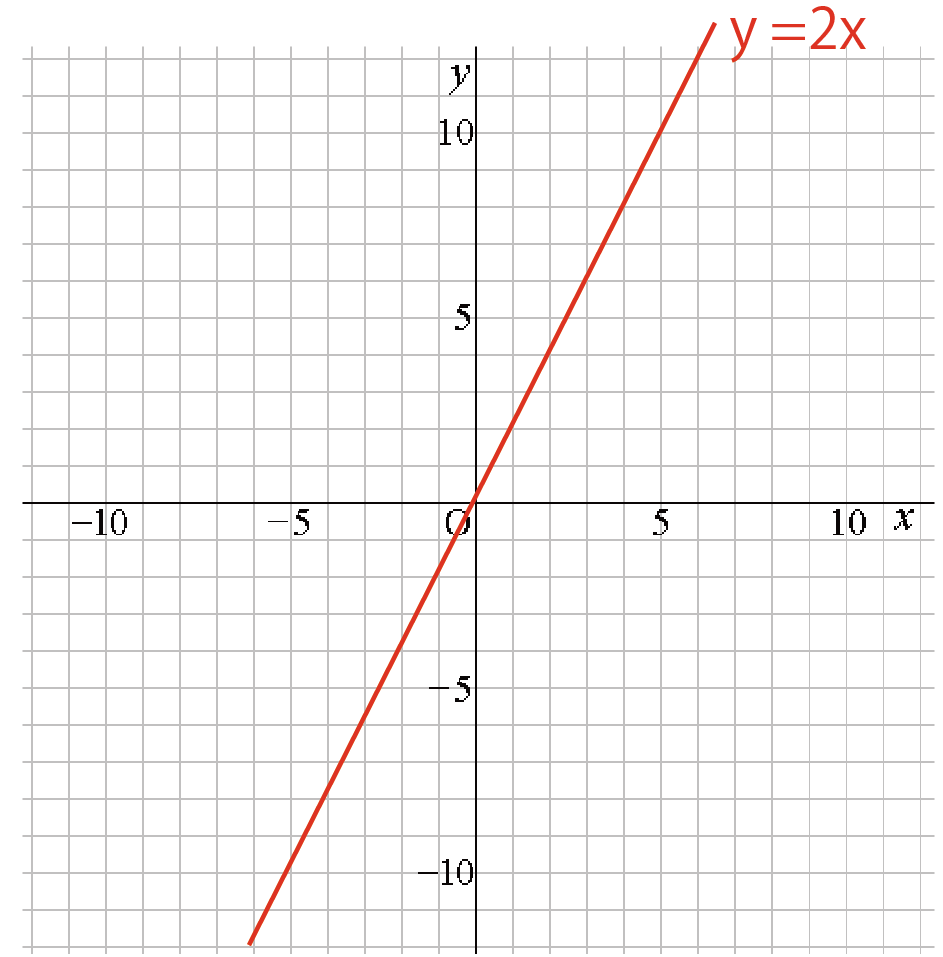
なぜなら、この比例関数には「変域」があるから。
（-2 ≦ x ≦ 2）っていう変域の外にある座標は対応しきれないってことになってる。
だから、この比例の式は、（-2 ≦ x ≦ 2）という範囲だけ元気になるから、
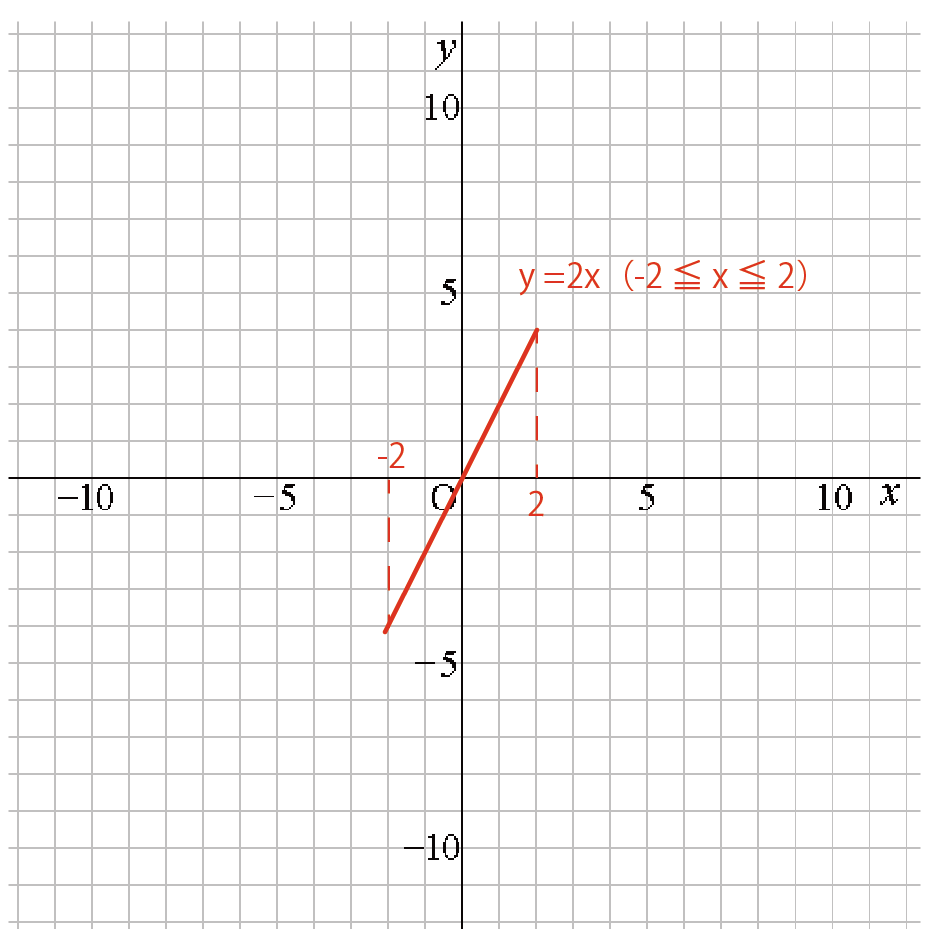
こんな感じで比例の関数が短くなっちゃうんだ。
xの変域が指定されているときは十分に注意しよう！！
比例のグラフにたくさんの種類があるけれど、
これら4つの特徴をおさえておけばテストでも大丈夫。
比例グラフがちょっと得意になっているはず。
そんじゃねー。
Ken
