ある日、数学が苦手なかなちゃんは、二次方程式の問題に出会いました。
練習問題
つぎの二次方程式を解きなさい。
x^2 = 2x

因数分解とか解の公式とか使うし。
言葉おぼえてもすぐ忘れちゃう・・・
ど、ど、どうしよう!!
二次方程式の解き方がわかると思うよ〜!
深呼吸して落ち着いてみて。
解けるかな?解いてみよう!
って思えるまで落ち着いてね!
はぁ……
ふぅ、
だいぶ落ち着いてきた。
先生もいるし、2次方程式解いてみようかな……
二次方程式の左辺にすべて移項していこう!
『+』のやつなら『-』になって、
『-』のやつは『+』になるよ♪
x²= 2x は、x²-2x = 0ってこと?
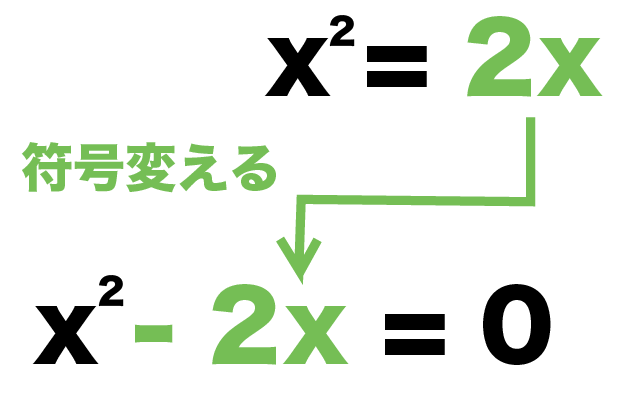
2次方程式の右辺が0になったら完成だよ♪
食えないヤツじゃない。公約数みたいなもんだよ。
例えば、8と2、公約数は2だよね!
2×4で8,2×1で2。だから、「8+2」を「 2(4+1) 」とも書ける!
で、でも、2次方程式を解くときは、これが便利になるんだ。
練習問題の「x² – 2x」で考えてみると……?
x²は、x × xで、2xは、x×2だね!
じゃあ、今までの式を書いていくと……?
最初は誰でもそんな感じだから、とにかく挑戦することが大事!
で、(x+2)とxがかけたら0になってるよね??
2を右辺に移項して……
だけど、
二次方程式の解き方で一番大切なことがあるよ。
それは、
『答えを書くこと』!!!
x=2
x=0
だったから、まとめて、「x = 2,0」だね!
わからないところがあれば、ポイントを見ながら解いてみよう!
☆問題☆
(1) x²= -2x (2) 2x²= 6x (3) 3x²= -9x (4) 4x²= 2x
(1) x= 0, -2
(2) x= 0, 3
(3) x= 0, -3
(4) x= 0, 2分の1
こんにちは!この記事をかいているKenだよ。業者よびたいね。
中3数学の大きなとりで。
それは、
二次方程式
っていう単元だ。
因数分解や平方根をガンガンつかうから、中3数学の総まとめってかんじ。
けっこう、手強いよ。
今日は、この単元の基礎をおさえるために、
2次方程式とはいったいなにものか??
を勉強していこう。
さっそくいっちゃうね。
二次方程式とは、
二次式をふくむ方程式のこと
だ。
すごくシンプルだね。
えっ。二次式とか方程式とかわからないって??
そういうときは、つぎの順番に復習すればしっくりくるよ。
「項」の意味をふりかえってみよう。
項の意味がはっきりすると、次数の意味がわかるからね。
項とはずばり、
+ で結ばれた1つ1つの塊のことだよ。
たとえば、
1 + y -12x
っていう式があったとしよう。
「+」でつながってる形になおすと、
1 + y + (-12x)
になるね。
項は「+でつながってる塊」だったよね??
だから、この式にふくまれる項は、
の3つだ。
項の意味もおっけー!
次数とはずばり、
1つの項にかけられてる文字の数
だ。
たとえば、さっきの「-12x」に注目してみて。
こいつの次数は「1」だよ。
なぜなら、項にかけられてる文字の数が「1」だからね。
xしか、かかってないもん。
もし、xが2乗だったら次数は「2」になるし、
xとyとzがかかってたら次数は「3」になるわけ。
どう??次数もマスターしたかな??
二次式とはずばり、
いちばん大きな次数が2の式
のことだ。
ちょっと複雑だね。
たとえば、
x² + y + abcd + 9
をイメージして。
項の次数を確認すると、
になってるね。
いちばん大きい次数は「abcd」の4だね??
ってことは、
この多項式は「4次式」になるんだ。
もし、「abcd」が消えたとしたら、この式は二次式になる。
x² + y + 9
なぜなら、いちばん大きい次数が「xの2乗」の2だからね。
「方程式」を復習してみよう。
方程式とはずばり、
未知の文字をふくむ等式のこと
だね。
たとえば、
x – 9 =0
とかとかだね。
何がはいるかわからない「文字」があって、
左右が「=」で結ばれてる式
は方程式なんだ。
だから、二次方程式とは、
未知の文字がある等式で、なおかつ、
二次式になってるもの
だね。
たとえば、さっきの二次式の「x² + y +9 」に「=0」をつけると、
x² + y +9 = 0
になる。
こいつはガチガチの2次方程式だ。
だって、二次式だし、等式だし、未知の文字がふくまれてるからね。
最後に1つだけ注意点があるよ。
それは、
移項とか同類項をまとめ終わって次数を調べる
ってこと。
整理しないまま方程式の次数を数えるのは危険なんだ。
たとえば、
x² + y +9 = x²
っていう方程式をイメージしてみて。
次数をかぞえてみると、
になってるよね??
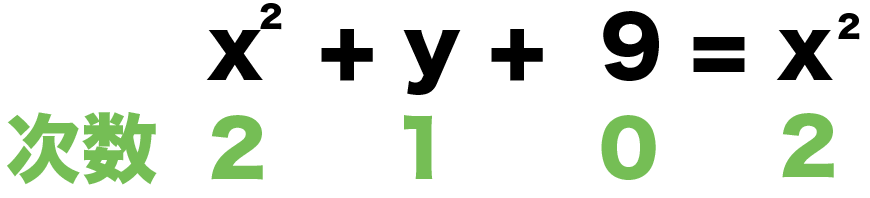
いちばん大きな次数は「2」。
二次方程式じゃないかって思うよね??
だけどね、こいつは二次方程式じゃない。
右辺の「x²」を左辺に移項して、同類項をまとめると、
x² + y +9 = x²
x² + y +9 – x² = 0
y +9 = 0
になるね!
この「y + 9 = 0」っていう方程式で改めて次数をみてみると、
になってる。
最高の次数は1だから、こいつは一次式ってわけなのさ。
ってことで、
移項や同類項が終わって次数を数えてみよう!
二次方程式の正体もわかったかな??
簡単にいうと、
二次式をふくむ方程式。
もっとわかりやすくいうと、
移項とか終わったら、各項の次数を数えてみて、
最高の次数が「2」の方程式のこと
になるんだ。
迷ったときは基本に戻ってみよう。
そんじゃねー
Ken
2次方程式に悩んでいるみんな、こんにちは!犬飼ふゆだよ。
解の公式はむちゃくちゃ強い味方。
どんな二次方程式もとけちゃうからね。
でも、
どうして解の公式なんてあるの?
とか、
覚えづらいよ!
とか、
なんで解の公式ができたんだろう??
って疑問におもうよね。
だから、今日は、
解の公式がなぜ使えるのかを証明したいんだ。
ややこしいけど、give upしないでついてきて欲しいなぁ。
= もくじ =
まず、解の公式を思い出してみよう。
二次方程式の「ax^2 + bx + c = 0」があったとすると、
解のxは、
x = {-b±√(b^2 -4ac)}÷2a
であらわせるんだったね??
⇒ 解の公式をつかった二次方程式の解き方はコレ読んでね。
どんな二次方程式でもとけちゃう。複雑だけど便利なんだ。
解の公式を証明してみるよー。
むずかしめだけど、ついてきて欲しいなあ。
証明のゴールは、
二次方程式「ax^2 + bx + c = 0」
を
x ={-b±√(b^2 -4ac)}÷2a
に変型することだよ。
証明のゴールはみえたかな??
さっそく証明していこう。
x2をシンプルにしよう。係数を1にするってことだね。
そのために、
二次方程式「ax^2 + bx + c = 0」の両辺をaで割ればいいんだ。
x2だけじゃなく「bx+c」もaで割ってね。
さっそく、計算してみると、
ax^2 + bx + c = 0
x^2 + b/a x + c/a = 0
になる。
つぎはxの係数に注目してね。
なんと、
「xの係数の半分を2乗したもの」を足して、そして引くんだ。
意味不明だけどやってみて。
二次方程式「ax^2 + bx + c = 0」は、
x^2 + b/a x + c/a = 0
になってたよね??
ってことは、xの係数は「b/a」だ。
こいつを半分にして2乗した「(b/2a)の2乗」を足して引いてあげるんだ。
すると、
x^2 + (b/a) x + c/a = 0
x^2 + (b/a) x+ (b/2a)^2 – (b/2a)^2 + c/a = 0
になるね!
「( )の2乗という形」をつくるよ。
どうして( )2=という形かっていうと、
x= ○○ にもっていきたいからだよ。
さっきのステップでは、
xの係数の半分の2乗をたしてひく
をしたよね??
じつはこれ、
「 ( )2 = という形」を作るためだったんだ。
さっきの計算式に注目してみて。
x^2 + (b/a) x+ (b/2a)^2 – (b/2a)^2 + c/a = 0
のうち、3つの項の「x^2 + (b/a) x+ (b/a)^2 」を公式で因数分解すると、
x^2 + (b/a) x+ (b/2a)^2– (b/2a)^2 + c/a = 0
(x + b/2a)^2 – (b/2a)^2 + c/a = 0
になるね。
「(x + b/2a )の2乗」以外の項の、
を右に移項してやると、
(x + b/2a)^2 = (b/2a)^2 – c/a
になる。
これで、
「( )2 = という形」がつくれたね。
移項した右辺をまとめよう!
1つの分数にすればいいわけだ。
(b/2a)^2の指数をはずすと、
(x + b/2a)^2 = (b/2a)^2 – c/a
(x + b/2a)^2 = b^2/4a^2 – c/a
になるね。
つぎは、2つの分数を通分すると、
(x + b/2a)^2 = b^2/4a^2 – c/a
(x + b/2a)^2 = (b^2 -c×4a)/4a^2
(x + b/2a)^2 = (b^2 -4ac)/4a^2
になるね!
最終的に「x= 」という形にしたいから、( )2 がいらないね?
両辺をルートしてみよう。
すると、
√{(x + b/2a)^2} = √{ (b^2 -4ac)/4a^2 }
になる。
√をそれぞれはずしてやると、
x + b/2a = ± (b^2 -4ac)/2a
になるよね?
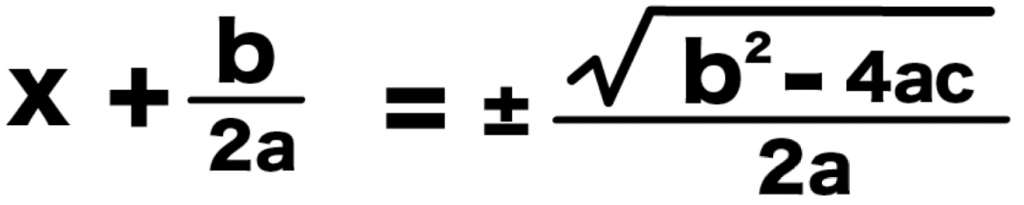
解のxを求めたいから、左辺の「b/2a」を移項してやると、
x = -b/2a ± (b^2 -4ac)/2a
になる。
これをまとめると、
x = {-b± (b^2 -4ac)}/2a
になるね!
これで解の公式の、
x = {-b±√(b^2 -4ac)}÷2a
が導けたね。
二次方程式の解の公式の証明はどうだった??
いきなり覚えろって言われても納得できないよ
って人や、
解の公式の謎を知りたい
って人のために書いてみたー。
わかるまで何回も証明してみてね。
そんじゃねー
犬飼ふゆ
はじめまして。Dr.リードだよ。よろしくー!
二次方程式の解き方にはいろいろあるよね。
因数分解をつかった解き方とか、
共通因数でくくるだけの解き方とか、
・・・・・・もうほんといろいろだね。
そんな解き方の1つに、
解の公式をつかった二次方程式の解き方
があるんだ。
これでどんな2次方程式の問題もとけるよ。
= もくじ =
解の公式とはなにかを振り返ってみよう。
解の公式は、公式にあてはめるだけで解がわかるすごいやつなんだ。
ax² + bx + c=0
っていう二次方程式の解xは、
x = {-b±√(b² – 4ac)}/2a
になるんだよ。
これね。
ノートにでっかく書いて、見えるとこに貼っとこう。
長い付き合いになるからさ。
高校へ行っても、解の公式はついてくるんだ。
解の公式はずばり、
二次方程式をどうしても解けないとき
に使うよ。
二次方程式の解き方には、
とかいっぱいあったね??
どれを使っても解けないとき。
あるいは、考えるのがめんどくさいとき。
そんなとき、二次方程式で解の公式を使うんだ。
どんな2次方程式も解けちゃうよ。
オールマイティなんだ。嫌わないでやってくれよ。
さっそく、2次方程式に解の公式をつかおう。
左辺の係数を公式に代入するだけ。
数学苦手隊には「 代入して 」って言われても難しいかな??
教科書には、さらっとかいてあるけど、むずいもんはむずい。
こんな感じで、公式を色分けしてみたよ。
二次方程式の係数をぽんぽん放り込めばいいわけだ。
練習問題をいっしょに2つといてみようか。
解の公式をつかってみよう。
まず2次方程式の係数「a, b, c」 をチェックするよ。
この問題では、
だよね??
この係数を解の公式に代入すると、
x = -5±√(5² – 4×1×3)/(2×1)
になる。
これを計算してみると、
x = -5±√(5² – 4×1×3)/(2×1)
= -5±√(25-12)/2
= -5±√13/2
になるね。
答え出たかい?
慣れるまではコツコツ確認しながらね。
次はこれね。
ああっ、げげげっ、Xの2乗に3がついてるね。
めげるな、キミ。やり方はさっきと一緒。
まずは二次方程式の係数を確認すると、
だよね??
こいつらを解の公式に代入すると、
x = -7±√(7² – 4×1×3)/(2×3)
= -7±√(49-12)/6
= -7±√37/6
になるね。
少し慣れてきたかな??
二次方程式で解をだしたいときは、
解の公式を使うだけ
でいいんだ。
これでどんな二次方程式もとけちゃう。
まさにオールマイティだ。
あとは、問題たくさんといてなれていこう!
では。
Dr.リード
はじめまして。 クエーサーからきた 「そら」だよ。
みんなと一緒に苦手な数学がんばる(^_-)-☆
今日は、中3数学で勉強する、
二次方程式の解き方
を解説していくよ。
2次方程式のなかでもとくに、「因数分解」をつかったものをみていこう。
二次方程式の解き方を解説していくよ。
まだ地球にきて日が経ってないけど、がんばる!
つぎの例題をといていこう。
つぎの二次方程式を解きなさい。
x² + 6x + 8 = 0
つぎの3ステップでとけちゃうよ。
まずは因数分解の公式で左辺を簡単にするよ。
公式のなかでもとくに、
x² + (a+b)x + ab = (x+a)(x+b)
で因数分解することが多いかな。
たとえば、
x² + ax + b = 0
っていう二次方程式だったら、
になる2組の数字をさがせばいいんだ。
例題の計算問題をみてみようか。
x² + 6x + 8 = 0
左辺で因数分解の公式をつかうためには、
になる2つの数字の組をみつければいいね??
かけたら8になる2つの数字を考えてみると、
の4つがある。
そのうち、たしたら6になる組み合わせは、「2×4」だ。
2+4 = 6
になるからね。
だから、「x² +6x + 8」を公式で因数分解すると、
x² +6x + 8 = 0
x² +(2+4)x + 2×4 = 0
(x +2)(x+4) = 0
になるね。
つぎは1次方程式をつくってみよう。
「因数のどっちかが0になる」っていう式をつくればいいんだ。
たとえば、左辺を因数分解して「A×B = 0」になったら、
のいずれかになるはずだね??
だって、2つを掛けたら0になってるから。
例題でいうと、
x² +6x + 8 = 0
は、
(x +2)(x+4) = 0
になったよね??
ってことは、
のどっちかになるってことだ。
こんなかんじで、1次方程式がつくれればOK!!
簡単な一次方程式をとくだけ。
必要なのは、中1数学の移項ぐらいだ。
しれっと計算してみてね。
例題では、
の2つの1次方程式ができたね??
こいつらでx以外の項を移項すると、
になるね!

つまり、二次方程式「x² +6x + 8=0」の答えは、
x = -2 もしくは x = -4
ってことなんだ。
これで二次方程式もとけたねー!
因数分解をつかった二次方程式の解き方はどう??
公式で因数分解して1次方程式をつくるだけさ。
因数分解さえできれば簡単だね。
今日は1つしか解かなかったけど、もっと問題を解いてね。
慣れてきたら、「暗算」でできるようになるよ(^_-)-☆
じゃあねー
そら
こんにちは!この記事をかいてるKenだよ。服を調達したね。
平方根の計算では、
ルートのだいたいの値
を知っておくと便利だ。
たとえば、√2はだいたい1.414…ぐらい・・・みたいな感じでね。
すると、
ルートの大小の問題を解きやすくなったり、
ルートの計算も自分がなにをしてるかがわかりやすくなるよね。
おぼえて損はない。
そこで今日は、「ルート10」の値の覚え方を3つ紹介していくよ。
よかったら参考にしてみてね。
そもそも、ルート10はどれくらいだっけ??
「ルート10」はだいたい、
3.16227766017..
だよ。
3より少し大きいって覚えればいいね。
でも、だいたいの値じゃなくてもっと√10を覚えたい・・・・
・・・・
そんなときは語呂をつかってみよう。
まず1つめの覚え方は、
債務にフナ、な〜む〜
だ。
ルート10の値が8ケタ覚えられちゃうんだ。
3(さ).1(い)6(む)2(に)2(ふ)7(な)7(な)6(む)
って感じでね。
えっ。語呂の意味がわからないだって!??
せっかくだから説明しよう。
いったん、債務(さいむ)って言葉をWikipediaで調べてみると、
ある者が他の者に対して一定の行為をすること又はしないこと(不作為)を内容とする義務をいう。義務を負う者を債務者、権利を有するものを債権者と呼ぶ。 債権を債務者からみた場合の表現。 複数の人が、同じ債務を負担すると連帯債務となる。
日常用語としては、借金と同義に用いられることがある。
ってかいてある。
前半のほうはむずくてよくわからないね。
今回は後半の、
日常用語としては、借金と同義に用いられることがある。
に注目してもらいたい。
債務は「借金」ってことだ。
だから、この語呂のシチュエーションはようは、
債務(借金)返済するときにお金じゃなくて、間違って魚の「フナ」を返しちゃったんだ。
んで、借金取りをおこらせて、フナに同情されてるってわけ。

つぎは、
みいちゃん、むふふ
っていう語呂だ。ちょっと危険な響きがする。
この語呂をおぼえれば、
3(み).1(い)6(む)2(ふ)2(ふ)
って感じで、ルート10の値を5ケタおぼえられるんだ。
ケタ数は少ないけどわかりやすくて覚えやすいね。
そうだな、赤ん坊の「みいちゃん」と「パパ次郎」を想像してくれ。
次郎は会社から帰ると、1つだけ楽しみにしてることがある。
それは、
赤ん坊のみいちゃんを眺めることだ。
みいちゃんを眺めるとき、無意識にこう言っちゃうんだ。
みいちゃん、むふふ
ってね。
微。ましいダディを想像してくれ。
きっと、みいちゃんが好きになるはずだ。
つぎの覚え方は将棋が絡んでくる。
さぁ、いじろ!二歩な
だ。
この語呂なら、ルート10を6ケタおぼえられちゃうんだよ。
3(さぁ).1(い)6(ろ)2(に)2(ふ)7(な)
って感じでね。
シチュエーションとしては、
将棋をプレイする「太郎」と「三郎」を想像してくれ。
局面もいよいよ終盤。
どっちが勝つかわからない。手に汗にぎる展開になってきたんだ。
だがしかし、プレイ時間が長すぎて三郎が失脚。
「二歩」というミスをおかしたんだ。
二歩とは「おなじ列に歩を2つ置いてしまう」反則ルールのことだったね。
この三郎のミスにつけこむため、太郎はこう言い放ったんだ。
さぁ、いじろ、二歩な
ってね。
これから生涯、太郎に「二歩」をいじられ続けることになる・・・・
思わず二歩をしてしまった三郎の悔しい顔を想像してくれ。
きっと、ルート10の値が思い出せるはず!
ルート10の覚え方はシンプルで覚えやすそうだね。
だけど、ちょっと悲しいお知らせがある。
それは、
ルート10の値はおぼえなくてもどうにかなる
ってことさ。
なぜなら、
√2 × √5 = √10
だからね。もし、
のだいたいの値がわかっていれば、√10は計算で求められるんだ。
√2、√5の値はそれぞれ、
だったよね??
掛け算で√10を計算してみると、
√10
= √2 × √5
= 1.41421356 × 2.2360679
= 3.162277545260724
になったね。
√2と√5さえ覚えておけば√10なんてすぐ計算できちゃう!
結論はルート6の覚え方といっしょ。
覚えなくても大丈夫だけど、余裕あったらトライしてみよう。
ルート10はだいたいこれぐらいだよー
って感じで、規模感をつかんでおこう。
そんじゃねー
Ken
どうも、Nabeだよ。よろしくね!
中3数学になると、
二次方程式
を勉強していくよね。
二次方程式は入試でも必ずでてくる問題だ。
本番までにマスターしておきたよね。
そこで今日は、二次方程式を解くとはなにか??
をわかりやすく解説していくよ。
よかったら参考にしてみて。
= もくじ =
方程式とは何だろう??
二次方程式をとくためには理解しておかないとね!
ちゃんとわかってるやつ少ないんじゃないかな。
簡単に説明しちゃうと、方程式って、
わからない文字(例えばx)などを含む等式 ( = がある式)
のことなんだ。
たとえば、
x−1= 0
とか、ね。
解くってきくと難しく感じかもしないね。
でもね、そんなに複雑じゃないよ。
だって、xの値をはっきりさせるだけだからね。
簡単な例をちょっとみてみようか。
問題Ⅰ x+3=0
問題Ⅱ x-10=3
どうだったかな??
できた??
答えは x=-3 x=13 だよね。
移項さえおぼえておけばこんなのイチコロさ。
今紹介した方程式たちは「一次方程式」っていうやつらだ。
ぶっちゃけ、二次方程式の親戚みたいなもんだね。
基本は二次も一次も変わらない。
「方程式を解く」ってことは「xを求める」ってことだと覚えておこう。
じゃあ、二次方程式と一次方程式だと何が違うんだろうね??
ちょっと例をみてみようか。
例Ⅰ x+y=0
例Ⅱ x+2=0
例Ⅲ x^2 – 1 = 0
ⅠとⅡは一次方程式、Ⅲは二次方程式だ。
文字の上に小さな数字がついてるよね??
ないものは1が透明になってのっかってるんだ。
これの一番大きい値が○次式の○にはいるよ。
Ⅰには何もついてなから一次。
つぎIIをみてくれ。
x + y = 0
文字が二つあるので二次だと思うかもしれんけど、
文字数ではなく文字の次数で決まるんだ。
いちばん大きい次数は1。
だから、こいつは1次式なんだ。
Ⅲは一個目のxの上に2が付いてるね??
だから、二次だ。
これで100次方程式だろうが10000次方程式だろうがばっちこいだ。
「方程式を解く」とは1次も2次も同じ。
ようは、xに何がはいるのか?を考えればいいいんだ。
簡単な二次方程式をといてみようか。
問題Ⅰ x^2 = 0
問題Ⅱ x^2 = 1
答えだけ先にいっちゃうと、
Ⅰ: x=0
II : x=1、x=-1
の2つになるね。
実際にxを入れてみるとわかる。
二次方程式の解の特徴はこんなふうに、
プラスとマイナスの解が2つあることが多いんだ。
一次方程式だろうが二次方程式だろうがやることはいっしょ。
解を求めるってことは、
xになにがはいるか
を考えることなんだ。
二次方程式は解が2つあったりして特殊だけど、
じょじょにになれていこう。
そんじゃねー
Nabe
こんにちは!この記事をかいているKenだよ。ゴミ袋は必須だね。
中学数学で図形を勉強していると、
円周率
をたくさん使うよね??
よくでてくるから、ときどきこう思うはずなんだ。
そう。
円周率はどうやって求めるんだろう??
ってね。
そこで今日は、
小学生でもわかる簡単な円周率の求め方
を解説していくよ。
よかったら参考にしてみて。
= もくじ =
円周率とはずばり、
円周の直径に対する比
だよ。
つまり、
「円周の長さ」は「直径の長さ」の何倍になってますか??
ってことをあらわしてるのさ。
それじゃあ、円周率を求めるためには、
円状になってる物体の「直径」
と
円周の長さ
を計測して比を求めればいいね。
ってことで、リアルな世界で円周率をだしてみよう。
用意するものは、
の4点セットだ。
ぼくは丸いものに「コーヒー」のふたを選んだよ。
そうそう。
UCCのやつ。
だって、この蓋の部分がいい感じに円になってるじゃん?
こんな感じで、身の回りで「円になってるもの」をみつけてみよう!
まず始めに、円の直径をはかってみよう。
円の直径を測るときはほんとうは
ノギス
っていうアイテムを使うといいんだけどね。
たぶん、ノギスを持ってるやつはそういない。
今回は定規でいいかな。
ぼくもコーヒーの蓋の直径をはかってみたよ。
すると、
コーヒーの蓋の直径 = 6.5cm
になったよ。
まあまあの大きさだ。
つぎは、円周をはかろう。
えっ。
円周はぐにゃっとしてるから測れないだって?!?
いやいや。
じつは、円周をはかるためにグニャっとしたものをまいて、
シャキっとさせればいいんだ。
そのシャキッとした長さを測ればいいのさ。
ぼくはグニャっとしたものに「ビニールヒモ」を選んでみたよ。
こいつはスーパーでも買えるし、安くて便利だ。
こいつを円状の物体にぐるっとまきつけて、
ちょうど一周でハサミカット。
そして、ヒモをシャキっとまっすぐにするわけだ。
この状態で、定規で長さをはかってみる。
すると・・・・・
っておい。
定規短すぎて測れないね。
しょうがないので、計測メジャーで長さをはかってみると、
20.5cm
ってことがわかった。
これがコーヒーの蓋の円周の長さだ。
最後は、「直径の長さ」に対する「円周の長さ」の比を計算しよう。
ようは、
(円周の長さ)÷(直径の長さ)
を計算すればいいんだ。
この答えが「円周率」になってるよ。
ぼくの例では、
だったね??
だから、コーヒーの蓋の円周率は、
(ビニールヒモの長さ)÷(コーヒーの蓋の直径)
= 20.5 ÷ 6.5
= 3.153846153…
になったよ!
おめでとう。
これでリアルに円周率が求められたね!
円周率の計算はどうだった??
たぶん、円周率が3.14になるのはむずかしいんじゃなかな。
うーん、これはどうしようもない誤差。
ヒモの厚みの分だけ直径は大きくなるし、
メモリは1mmまでしかはかれないからね。完全にアバウトだ。
こんな感じで、
気が向いたら円周率を計算してみよう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。金曜日は混むね。
ルートの近似値を覚えてると便利。
ルート計算のだいたいの値がわかるからね。
これまでも、
ってかんじで、平方根の近似値を覚えてきた。
せっかくだから、今日はもう一歩踏み込んで、
ルート6の覚え方
を2つ紹介していくよ。
よかったら参考にしてみてね。
ルート6の値はだいたい、
2.44948974…..
だ。
5の半分ぐらいってことだ。
今日は、ルート6の近似値をおぼえるために、
ルート6の値がおぼえられる語呂合わせを2つ紹介してくよ。
一つ目の語呂は、
ニシシ、給与はくなよ(にしし、きゅうよはくなよ)
だ。
この語呂合わせをおぼえておくと、
に(2)し(4)し(4)きゅう(9)よ(4)は(8)く(9)な(7)よ(4)
ってかんじで、
ルート6の値が9ケタ覚えられるんだ。
9ケタだよ? 最高じゃん。
えっ。状況がぜんぜんイメージできないって!??
そうだね。
会社の同僚に、自分の給与がいくらだったのか??
を言っちゃったシーンを思い浮かべてみて。
居酒屋とかでだね。
手取りの給与をはいてしまったキミに、同僚はこういったんだ。
ニシシ、給与はくなよ
ってね。
同僚のにんまり。顔を想像してもらえれば一発。
ルート6なんていつでも思い出せるさ。
つぎの覚え方は、
女子、串焼くなよ(じょし、くしやくなよ)
だ。
この語呂なら、ルート6の値を9ケタも覚えられるんだ。
じ(2)ょ(4)し(4)く(9)し(4)や(8)く(9)な(7)よ(4)
ってかんじでね。
この語呂の状況は圧倒的にイメージしやすいね。
そう、林間学校だ。
林間学校でバーベキューやってたんだけど、
男子の想像以上に女子が「串」を焼きすぎていたんだ。
そう、串をね。
そんな女子たちをみかねて、男子たちはこういったんだ。
女子、串焼くなよ
ってね。
よくありそうなシチュエーションだから覚えやすいね。
ここまでルート6の値の覚え方を語ってきた。
でもね、
ぶっちゃけちゃうと、
ルート6の値は覚えなくても大丈夫。
まったく問題ないんだ。
√6 = √2 × √3
だから、
の2つの値をおぼえてれば導けるのさ。
だから、
√6
= √2 × √3
= 1.41421356×1.7320508
= 2.44948974
になるね。
√2と√3の値を覚えてれば√6の値は忘れても大丈夫だ!
ルート6の覚え方はどうだったかな??
だいたい2.5なんだけど、語呂合わせで9ケタ覚えられるんだ。
ぶっちゃけ、√2と√3の値を覚えば計算でだせるんだけどね。
余裕があったらルート6もおぼえてみよう。
そんじゃねー
Ken
こんにちは!この記事をかいてるKenだよ。ブルックリンが呼んでるね。
ここまで、平方根の基礎の、
を勉強してきた。
もう、平方根の計算なんてちょれわー
って思ってるよね??
だけどね、ちょっと待って欲しい。
ルートの計算のミスは忘れたころにやってくるんだ。
そこで今日は、
ルート・平方根の計算方法のコツ
をおさらいしよう。
ガンガン復習しておこうぜ。
ルート計算のコツはつぎの3つだ。
練習問題をといてみよう。
まず、
ルートを簡単にできるかどうか
をみてみよう。
もし、ルートを簡単にできそうなら一番先にやっちまおう。
なぜなら、
整数と平方根にわけて計算できるようになるからね。
例題をみてみると、
いちばん左の「√8」を簡単にできそうだ。
なぜなら、中身の「8」には「2の2乗」がはいってるからね。
こいつを外にだせるわけだ。
ルートを簡単にすると、
√8 + √2分の5 – √3 × √5
= 2√2 + √2分の5 – √3 × √5
になるね。
☆ルートを簡単にする方法をわすれたら復習しよう☆
ルートの計算に分数がある??
そういうときは、分母を有理化しちゃおう。
分母からルートを消せばいいのさ。
例の計算式では、
√2分の5
の分母に平方根がはいってるね。
この「√2」を分母から消したい。
そんなときは、分母・分子に√2をかければよかったね??
すると、
2√2 + √2分の5 – √3 × √5
= 2√2 + 2分の5√2 – √3 × √5
になる。
分母の有理化をしておくと、
ルートの計算する余地があるのかどうか??
がハッキリするんだ。
余地があるんなら、ルートの計算を続行すればいいし、
ないんなら計算をやめればいい。
めんどいけど、分母の有理化はやっておこう。
ルートの計算の最大の特徴。
それは、
足し算・引き算
と
掛け算・割り算
がまったく違うってことだ。
つぎの計算のルールを覚えてほしい。
例題ではいったん掛け算をしちゃおうか。
右の項の、
– √3 × √5
が計算できそうだ。
平方根の掛け算では「√の中身」を計算してもよかったよね??
だから、
– √3 × √5
= – √15
になるね。
あとは左の足し算。
はルートの中身が2で一致してる。
整数部分を足し算してやると、
2√2 + √2分の5 – √3 × √5
= 2√2 + 2分の5√2 – √15
= 2分の9√2 – √15
になるね。
これでルートの計算は終了だ。
ルートの計算はどうだった??
計算のコツは3つのみ。
ルートの計算問題をといて慣れていこう!
そんじゃねー
Ken
↓↓ルート計算のコツを動画にまとめてみたよ↓↓
こんにちは、この記事をかいてるKenだよ。パスタの寿命は短いね。
ルートの問題で知っておくと便利なのは、
平方根の近似値
だ。
ある平方根が実際にどれくらいの大きさなのか??
ってことだね。
べつに覚えなくても生きていけるけど、覚えるとなおよし。
ルートの問題でむちゃ役に立つよ。
今日はルートの中でも、
ルート5の覚え方
に注目してみようか。
=もくじ=
ルート5の覚え方には王道がある。
それは、
富士山麓オウム鳴く(ふじさんろくにおうむなく)
だ。
こいつを覚えれば、
ふ(2)じ(2)さん(3)ろく(6)おう(0)む(6)な(7)く(9)
ってかんじで、ルート5が8ケタも覚えられるんだ。
教科書にのってるぐらい有名。
おれも中学生のときに必死で暗記したよ。
えっ。語呂の意味がわからないだって!??
たしかに。
ゼッタイこんな日本語発しないもんね。
「富士山麓オウム鳴く」はこういう意味だ。
富士の、
山麓(山地と平地の境界部)で、
オウムが鳴く。
なんだか、古き良き日本を連想させるね。
自然を感じるわ。
でもさ、ちょっと強引だよね。
ってか、富士山にオウムなんていなさそうだし、
2を「じ」って読ませるウルトラC感がすごい。
オウムに頼るぐらいなら、他の語呂合わせで覚えたい。
そうは思わないかな??
今日はルート5の覚え方を3つ紹介するよ。
よかったら参考にしてみてね。
いちばんはじめの語呂は、
に、兄さん!群れろ!泣く
だ。
これを覚えちまえば、
に(2) にい(2)さん(3) む(6)れ (0)ろ(6)な(7)く(9)
ってかんじで、ルート5の値を8ケタ覚えられちゃうんだ。
この語呂は、そうだな、ある兄弟を想像してほしい。
1人でいるのが割りと好きな兄さんと、パリピの弟の物語だ。
イケイケの弟がひきごもりがちな兄さんにこういったわけ。
に、兄さん、群れろ!泣くよ??
ってね。
弟は兄さんに社交性を身につけてほしかったらしい。
こういうことも世間では起こりえる。大変だ。
つぎのルート5の覚え方は、
夫婦、みなロレックスなくす
だ。
この語呂をおぼえることで、
ふ(2)うふ(2)、み(3)なろ(6)れ(0)っくす(6)な(7)く(9)す
ってかんじで、ルート5の値を8ケタ覚えられるわけ。
えっ。
「っくす」と「6」が結びつかないって??
いや、これはね、
6を英語読みした「シックス」のしっぽの「っくす」を採用したのさ。
シチュエーションとしては観光ツアーに参加した夫婦らを想像してくれ。
偶然、みんなロレックスの時計をつけてたんだ。
でも、奇妙なことに全員、時計をなくしてしまったんだよ。
けっこう残念なことだけど、ここは地球。
たまに不可思議なことが起こりえるんだ。気をつけよう。
最後の語呂合わせは、
にいにー、寒いぜ、無理、泣く
だ。
この語呂を覚えることで、
に(2)いに(2)、さ(3)む(6)いぜ(0)、む(6)り、な(7)く(9)
ルート5の値の8ケタを暗記できちゃうんだ。
すごいね。
シチュエーションは、兄ちゃんのことを「にーにー」と呼ぶ妹と、
それに付随する兄を想像してくれ。
映画でいうと、「なだそうそう」ってかんじだ。
ある日、兄ちゃんがクーラーの温度をさげすぎた。
そこで冷え性の妹がすかさず、
にーにー、寒いぜ、無理、泣く
って言ったわけだ。
このセリフから必死さが伝わってくるね。
兄ちゃん、温度あげてやってくれ。
ルート5の覚え方はどうだったかな??
ぶっちゃけどの語呂をつかってもいい。
オウムに泣かせてもいいし、
ロレックスをなくしたっていい。
とにかく、自分のおぼえやすい語呂でルート5をおぼえよう!
そんじゃねー
Ken
こんにちは!この記事をかいてるKenだよ。映画がよんでるね。
この前勉強した平方根の求め方は基本的なヤツだ。
「√」をかぶせるだけだもんね。
今日は、もう少し進化した、
筆算をつかった平方根の求め方
を紹介していくよ。
よかったら参考にしてみて。
= もくじ =
筆算をつかった平方根の求め方を、
開平法
とよんでるよ。
中学数学では勉強しないんだけどね。
えっ。
どんなときに開平法をつかうかって!?
つぎの3つのときが多いよ。
今日はそのなかでも、
でかい数の平方根を求める問題
を解説しいこう。
例題をいっしょにといてみようぜ。
271441の平方根を求めなさい。
平方根を求めたい数を「√」でくくろう。
「√」をうえにのっければいいんだ。
例題では「271441」にルートをのせてみて。
ルート内の数字を右から2ケタずつ区切ろう。
「|」で区切ってみてくれ。
例題の271441はこうなるはずだ↓↓
27|14|41
1番左の2ケタの塊に注目してくれ。
2乗したらその塊になる数を考えればいいのさ。
例題でいうと、
の3つの塊ができてるよね??
んで、いちばん左の塊は、
27
だ。
2乗して「27」に一番近くなる自然数は、
5
だ。
なぜなら、
5の2乗 = 25
だからね。
そいつを、
にかいてね。
2乗した数をかこう。
かく場所は、いちばん左の塊の下だ。
例題では5を2乗したらできる「25」を、
いちばん左の塊の「27」の下にかこう。
こうなるはずだ↓↓
左の塊から2乗の数をひこう。
例題でいうと、
27 – 25
ってわけだね。
こいつを計算すると、
2
になる。
隣の2ケタの塊を下におろそう。
例でいうと、「14」を2の右に召還するのさ。
左の数の一の位を、左の数自身にたそう。
例でいうと、左の数は「5」だね。
こいつの1の位は5だから、
5+ 5
= 10
になるわけだ。
ちょっと言葉にしずらい・・・
ここでは、「ある数」を推測してほしいんだ。
その「ある数」とは、
「ある数」×「1の位をある数にした数」がさっきの「引き算の結果」にいちばん近いやつ
なんだ。
自分でも何いってるかわからないや。
ちょっと例題をみて。
14のうえの「ある数」を推測するわけだ。
わかりやすくするために、ここでは、
(ある数) = □
としようか。
一の位をある数にした数っていうのは、
10□
になるってわけだ。
だからさっきいってたのは、
□ × 10□ = 214
になるような□をみつければいいってことなのさ。
□に1から順番に代入して調べてみると、
どうやら、
□に2を入れたときに204になって一番214に近くなるみたい。
だから、ここでは□に2がはいるね。
「いちばん近くなった数」を「引き算の結果」の下にかいて。
練習問題でいうと、
214の下に204をかけばいいのさ。
「引き算の結果」から「掛け算の結果」をひこう。
流れは、Step5といっしょだ。
例題でも「引き算の結果」から「掛け算の結果」をひいてやると、
214 – 204
= 10
になるね。
「引き算の結果」の右に「最後の塊」をおろそう。
例題でいうと、41を10の右におとせばいいんだ。
つぎは左の数に注目してくれ。
こいつの1の位を自分自身にたせばいい。
例題でいうと、左の数は102。
こいつの1の位は2だから、
102 + 2
= 104
になるね。
いよいよ最後のステップ。
やり方はStep8とおなじだ。
例題でいうと、
最後の塊のうえにくる数を□とする。
んで、
□ × 104□
が
1041
になるような□をゲットすればいいのさ。
□に1から順番にいれてみると・・・・
おっ。
□に1いれたら1041に等しくなるやん!?
だから、さっきみたいに筆算を続けてやると、
最終的に引き算の答えが0になるね。
よって、これで筆算の平方根の求め方は終了だ。
271441
の平方根はそのうえの数字の「521」だよ。
やったね。
13ステップは長すぎるぜ。
平方根の求め方に筆算をつかうと、
で便利だったね??
ただ、その求め方は阿修羅の道。
訳のわからないプロセスを延々と続けることになるw
もしもに備えて筆算もマスターしておこう。
そんじゃねー
Ken