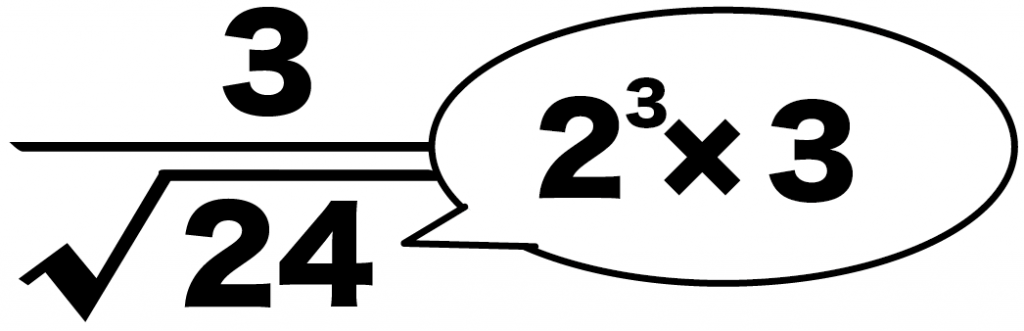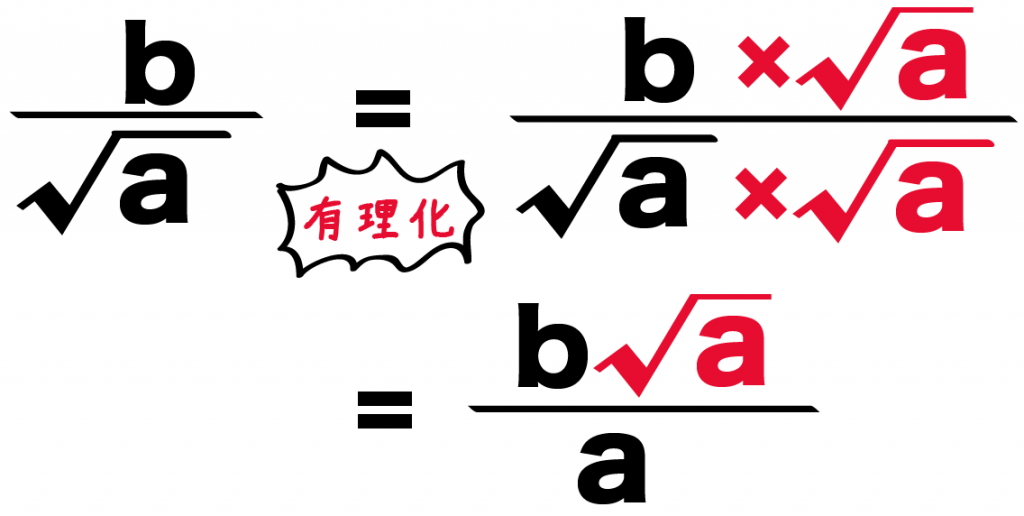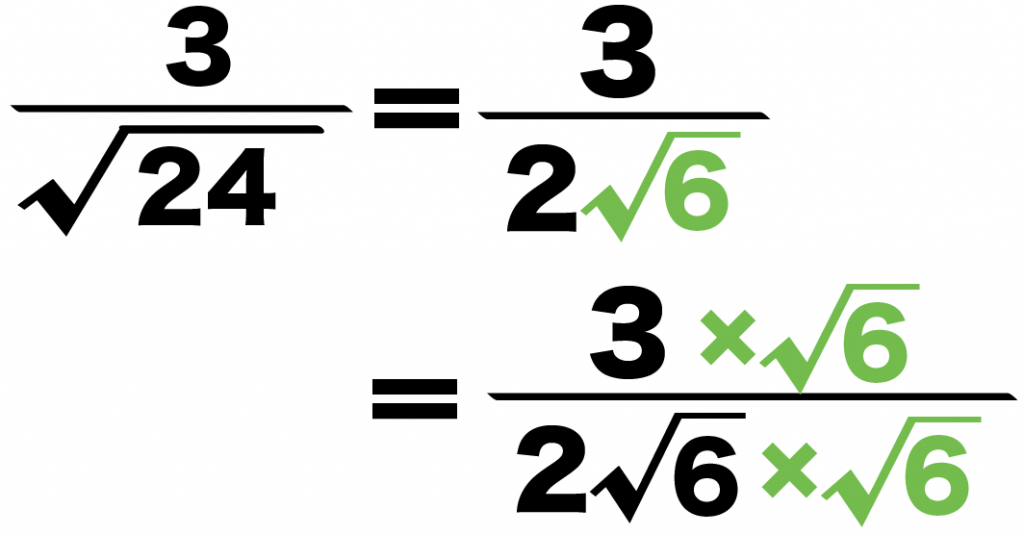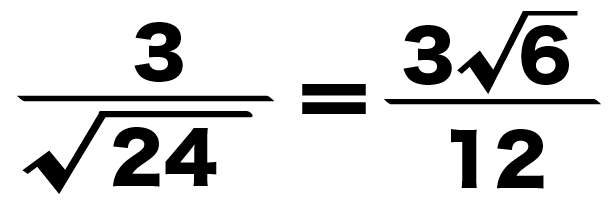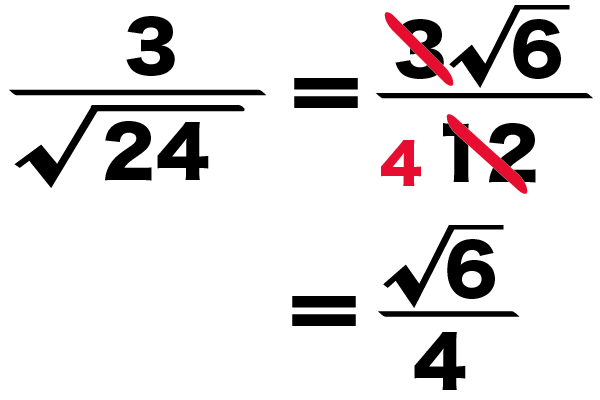平方根の分母の有理化のやり方って？！
こんにちは！この記事をかいてるKenだよ。腹は八分だね。
平方根の計算でたまに、
ルートの分数
がでてくる。
分子や分母にルートがまじってるわけだ。
なかでもヤッカイなのは、
分母に平方根（ルート）がまじってる問題
だ。
なぜなら、
分数の分母の有理化
っていう作業が必要だからさ。ふつうより手間かかるんだ。
今日はそんな計算をクリアするために、
分数の分母の有理化のやり方
をわかりやすく解説していくよ。
よかったら参考にしてみて。
= もくじ =
- ルートの有理化とは？？
- 分母の有理方のやり方
ルートの分母の有理化とは？？
分母の有理化とは、
分母のルート（無理数）を有理数にしちゃう
ってことなんだ。
もっといえば、
分母のルートをとっぱらうこと
だ。
いかなる手をつかってもいい。
分母の無理数を有理数に変えられればokだ。
ルートの分数の有理化のやり方の3ステップ
分母の有理化は簡単。たったの3ステップだよ。
- ルートを簡単にする
- 分母のルートを分子・分母にかける
- 約分する
練習問題をといていこう！
例題
つぎの分数の分母を有理化しなさい。
√24 分の3
Step1. ルートを簡単にする
ルートを簡単にするとこからはじめよう。
ルートを簡単にするって、
ルートの中身から2乗の因数を取り出す
だったよね？？
⇒くわしくは「ルートを簡単にする方法」をみてね。
例題の「√24 分の3」の「√24」に注目してほしい。
この平方根は簡単にできる。
なぜなら、
24には因数「2の2乗」がはいってるからね。
えっ。疑わしいって？？
24を素因数分解すると、
24 = 2の3乗×3
になるよね？？
このなかに「2の2乗」っていう因数がふくまれるぜ。
こいつを根号の外にだすと、
ルート24分の3
= 2ルート6分の3
になるんだ。
これが第1ステップ！！
Step2. 「分母」を「分子・分母」にかける
分母の平方根を分子と分母にかけよう。
これによって、
分母の平方根が2乗されてルートがとれるんだ。
たとえば、「√a分のb」って分数がいたとしよう。
分母・分子に√aをかければいいのさ。
すると、
√a分のb
= （√a×√a）分の（b×√a）
= a分の（b√a）
になるね！
例題の分数の分母は、
2√6
だったよね？？
分母の「ルート6」を分母と分子にかければいいんだ。
すると、
ルート24分の3
= 2ルート6分の3
= 12 分の3√6
になるね！
Step3. 約分する
最後に約分しよう。
約分しなくても間違いじゃないけど念のためね。
例題でも約分してみよう。
12分の3√6
分子と分母を3でわると、
4分の√6
になるね！
おめでとう！
これで分母の有理化もマスターだ。
まとめ：「約分」までが平方根の分母の有理化！！
分数の分母にルートがある？？
そんなときは、分母を有理化してやろう。
平方根を簡単にして、
分母のルートを分子と分母にかければいいのさ。
ゆっくり有理化になれていこう。
そんじゃねー
Ken
