はろー、犬飼ふゆだよ。
解の公式は便利なアイテム。
因数分解できない2次方程式も解けるからね。
だけどね、解の公式には1つだけ欠点があるんだ。
それは、
むちゃくちゃ覚えいにくい
ってとこ。
ほら、みて?
x = {-b±√(b^2 – 4ac)}/2a
長いし複雑だし、かんべんしてほしいよね??
でも、、便利な公式だからおぼえたい・・・!!
そこで今日は、二次方程式の解の公式の覚え方を3つ紹介するよ。
よかったら参考にしてみてね。
解の公式の覚え方を解説していくよ。
今日紹介する覚え方はつぎの3つ。
一番簡単なのが、
語呂合わせをつかった解の公式の覚え方
だね。
語呂を忘れなければ解の公式がおぼえられるってわけ。
その語呂とはずばり、
煮え! 文にひく「ビ〜」プラマイルート 美人ひく 酔えし
だよ。
これなら、
煮え(2a)! 文(分)にひく(-)「ビ〜(b)」プラマイルート(±√) 美人(b2乗)ひく(-) 酔えし(4ac)
ってかんじで、解の公式がおぼえられるんだ。
状況としては、男性がなにかを煮ているシーンを想像してくれ。
だけど、なかなか鍋が煮え切れらない。
しびれをきらした男性が文に「ビ〜」っと線をひきはじめたんだ。
プラスマイナスルート(±)
っていう文だったんだけどね、それは。
でも、近くにいた美人がね、その様子にひいちゃったんだよ。
んで、±√に線をびーってひいちゃった男性がね、こう思ったんだ。
酔えよ
ってね。
お酒にようと判断力がにぶくなるからね。
最後にもう一度、解の公式の覚え方を確認してみよう。
煮え(2a)! 文(分)にひく(-)「ビ〜(b)」プラマイルート(±√) 美人(b2乗)ひく(-) 酔えし(4ac)
どう??
かなりむちゃなシチュエーションだけど、耳に残りやすいね。
つぎは歌って覚える方法。
好きな歌は知らないうちに覚えちゃうじゃん??
解の公式もおなじ。
メロディーをつけて、歌にしてみればいいのさ。
音楽好きの人にオススメだよ。
歌詞は、
2a(にーえー)分の-b(まいなすびー)±(プラスマイナス)√(ルート)b^2(びーじじょう)-4ac
になるね。

簡単なメロディーをつけたから歌ってみてね。
男子はオクターブを下げてもいいよ。
声変わり中だったらテノールで歌おう。
▼ソプラノ
▼テノール
なにかを覚えるときの王道。
それは、
書きまくる
だね。
解の公式だっておなじさ。かいてかいてかきまくればいいんだ。
ノートの裏に書いてみるとか、
トイレットペーパーにかくとか、
原稿用紙にかいてみるとか、なんでもいい。
紙に書いて貼っておくのもいいんじゃないかな。
PCが使える人は、あえてマウスで書いてみるのもありだね。
キーボードじゃなくってマウスで書く。
書きづらいから絶対に覚えるはず。
ここまで解の公式の覚え方を解説してきたね。
でもね、公式を覚えられても、「実際に使う」っていうのはまた別。
上の3つの方法はあくまで「暗記する」ための覚え方。
解の公式を使えるようにするためには、
二次方程式を解の公式で解きまくる。
これが一番だ。
ではでは! テスト頑張ってね!
犬飼ふゆ
こんにちは!この記事をかいてるKenだよ。服、ほしいね。
二次関数y=ax2の変化の割合の求め方には公式があるよ。
xの値がmからnまで増加するとき、変化の割合は、
a (m+n)
になるんだ。
つまり、
(比例定数)×(xの小さい値 + xの大きい値)
っていう計算。簡単だ!
さっそく、この公式で変化の割合を求めてみよう。
たとえば、
y=1/2x^2 でxが2から8まで増加するときの変化の割合を計算してみて。
この二次関数では、
になってるね??
こいつをさっきの公式に代入してやると、
1/2 (2 + 8)
= 5
になるね。
つまり、
y=1/2x^2 でxが2から8まで増加するときの変化の割合は「5」になるわけ。
どう??簡単に計算できたよね??
二次関数の変化の割合の公式は便利。
どんな変化の割合の問題でもとけそうだ。
でもさ、
なんで変化の割合の公式がつかえちゃうんだろうね??
ちょっと便利すぎて怖い。
不安になってきたから、なぜ公式がつかえるのかを振り返ってみよう。
二次関数y=ax2がmからnまで変化するときを想定してみて。
このときの変化の割合を、二次関数の変化の割合の求め方で計算すればいいんだ。
まずyの値を計算してみよう。
のときに、yの座標がいくつになるのか??
を求めればいいのさ。
それぞれのx座標をy = ax2に代入すればいいね。
y = ax2にmとnを代入してyを求めてやると、
になる。
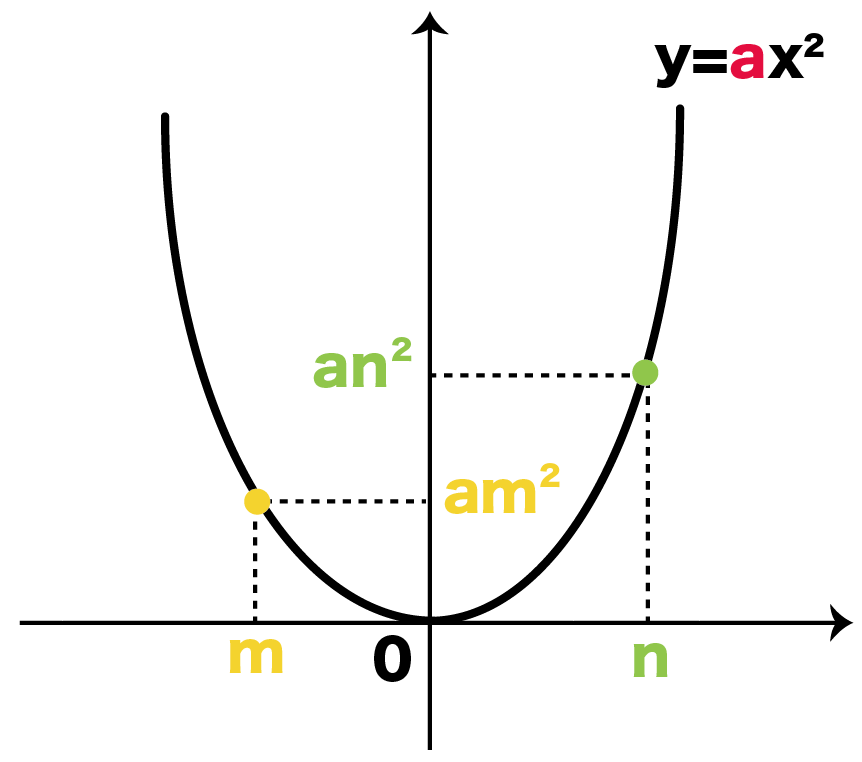
つぎは変化の割合の求め方で計算してみよう。
(yの増加量)÷(xの増加量)
ようは、
xが1変化するごとにyはいくつ変化するのか??
ってことを調べるわけだ。
この計算式をつかうと、
変化の割合
= (yの増加量)÷(xの増加量)
= (an^2 – am^2)÷(n – m)
になるね。
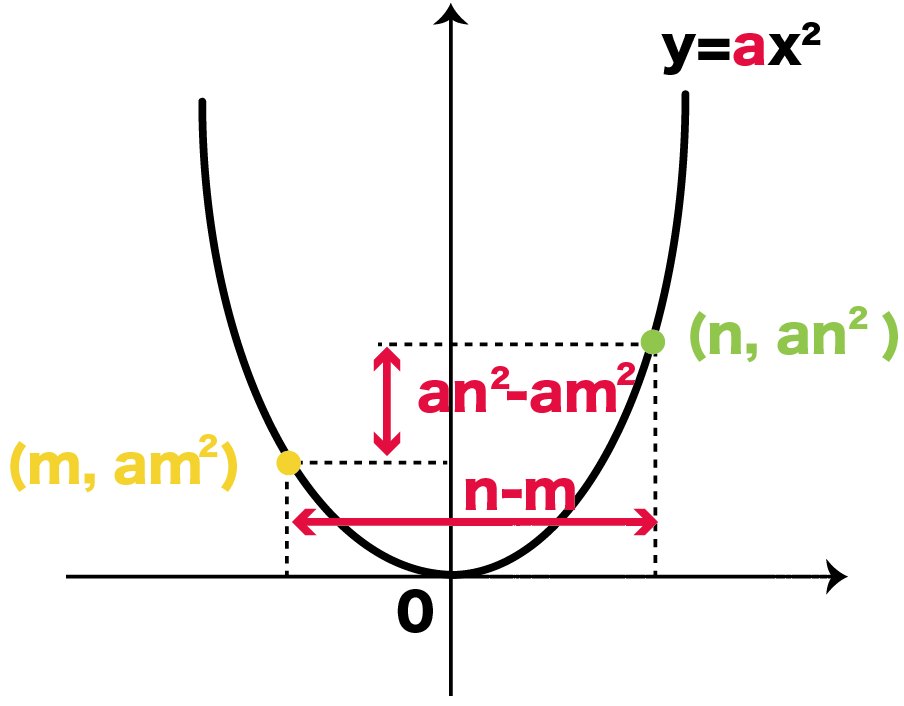
さっきの変化の割合を因数分解してみよう。
分子の、
an^2 – am^2
がむちゃくちゃ因数分解できそうだ。
まず共通因数aでくくってやると、
a(n^2 – m^2)
になるね。
んで、さらに、()のなかの、
n^2 – m^2
を因数分解の公式で計算すると、
n^2 – m^2
= (n+m) (n-m)
になるじゃんね。
最後に約分してあげよう。
変化の割合の分子と分母に共通の、
n – m
っていう因数があるよね??
そこで、
(n – m)で分子・分母を割ってやると、
a(n+m) (n-m) ÷ (n-m)
= a (n+m)
になるんだ。
xが増加する(または減少する)ときの話をしているから、
n と mが一緒であることはありえないはず。
つまり、
n≠m
だから、n-m≠0。
よって、n-mでわってもいいから大丈夫だ。
あ。
こ、これはいちばん最初に紹介した、
変化の割合 = a (m+n)
っていう公式になってるね。
こんなかんじで、変化の割合の求め方で計算すれば公式が導けるのさ。
やったね。
二次関数y=ax2の変化の割合は公式なら簡単。
すぐに変化の割合をだせるね。
便利な公式をおぼえるのも大事だけど、
なぜ、公式がつかえるのか?
ってこともおなじぐらい重要。
公式がつかえる理由をわかってから公式をつかおうね。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。スペース最高。
二次方程式の解き方をたくさんならってきたね。
ざっと数えるだけ、6つもある。
解き方がたくさんあって便利なんだけど、
どの解き方つかえばいいかわからないんだよね。
せめて、
二次方程式の解き方を見分けるコツ
とかあれば助かる・・・・
そこで今日は、特別に、
二次方程式の解き方の見分け方
を紹介するよ。
よかったら参考にしてみてね。
二次方程式の解き方を見分けるコツは1つ。
それは、
消去法で解き方を選ぶ
だ。
っていう6つの解き方がつかえるか、上から確認していくのさ。
全部の解き方で解けなかったら諦めよう。
それぞれの解き方を確認してみようね。
平方根を使えるか確認してみて。
見分け方のコツは1つ。
それは、二次方程式のかたちが
(xをふくむ式)の2乗 = A
になっているか、もしくはソレに変型できるか確認すればいいのさ。
たとえば、
(x-4)² -11 = 0
っていう二次方程式があったとしよう。
こいつはみたかんじ、
(xをふくむ式)² = A
の形にもっていけそうだ。
だって、11を右辺に移項すればいいだけだからね。
このタイプの2次方程式なら、
の3ステップでとけちゃうよ。
くわしくは、平方根をつかった二次方程式の解き方を復習してみて。
実際に右辺に11を移項して解くと、
(x-4)² -11 = 0
(x-4)² = 11
x – 4 = ± √11
x = 4±√11
になるね。
平方根をつかう解き方がいちばん簡単。
こいつで二次方程式が解けるか、まず確認してみて。
共通因数でくくれるか確認しよう。
項が2つの二次方程式のとき、つかうことが多いね。
たとえば、つぎの二次方程式とか↓↓
3x² = 7x
この二次方程式の解き方なら、3ステップでとけちゃう。
⇒くわしくは「因数分解の公式をつかわない二次方程式の解き方」をよんでね。
実際にといてみると、
3x² = 7x
3x² – 7x = 0
x(3x – 7) = 0
x = 0, 3分の7
になるね。
平方根でも解けないし、共通因数でもくくれない・・・・
そんなときは、
因数分解の公式をつかった二次方程式の解き方
だ。
この解き方では、
因数分解の公式で二次式を因数分解して、一次方程式をつくっていくよ。
たとえば、つぎのような問題ね。
x² + 6x = -8
このタイプの二次方程式は3ステップでとけちゃう。
⇒くわしくは「因数分解をつかった解き方」をよんでみて。
実際に、さっきの二次方程式の、
x² + 6x = -8
を因数分解の公式をつかってといてみると、
x² + 6x = -8
x² + 6x + 8 = 0
(x +2) (x+4) = 0
x = -2, -4
になるね。
因数分解の公式をよーく復習しとておいてね。
因数分解の公式つかえねえええー
そんなときは、
たすきがけの因数分解がつかえるか粘ってみよう。
たとえば、つぎの二次方程式で活躍するね。
5x² – 11x + 6 = 0
因数分解の公式を使おうとしても・・・・・
ぐっっっっ
使えない!!
ってなるはず。
そういうときは「たすきがけの因数分解」をつかえばいい。
2次方程式の係数を、
の順番にヨコにかく。
んで、
かけたら「xの2乗の係数」、「定数項」になる数字をたすきがけで考えると、
1 -1 -5
5 -6 -6
———–
5 6 -11
になる。
よって、二次方程式は、
5x² – 11x + 6 = 0
(x-1)(5x-6) = 0
になるね。
今まで通り、一次方程式をといてやると、
x = 1, 5分の6
になるね。
因数分解の公式も、たすきがけも無理。
そんなときは最終兵器、
解の公式
をつかおう。
解の公式はどんな二次方程式でもとける公式だったね??
覚えにくいけど、むちゃ便利なんだ。
たとえば、つぎの二次方程式とかね。
x² – 2x -6 = 0
この二次方程式はどうがんばっても、因数分解の公式はつかえない。
たすきがけ因数分解でもかすりもしない。
・・・・・こまった・・・・・・
そんなときは、解の公式の出番だ。
3ステップでとけちゃうよ。
二次方程式の係数を公式に代入すると、
x² – 2x -6 = 0
x = 2±√(2² -4×1×-6)/2
= 2±√(4 +24)/2
= 2±√28/2
= 2±2√7/2
= 1±√7
になるね!
これでどんな二次方程式もとけちゃう!
安心だ〜〜
もしも、だよ。
もしも、解の公式を忘れたらどうしたいいんだろう??
因数分解の公式もつかえないし、共通因数でもくくれない。
そんなやばいときに役にたつのが、
平方完成による因数分解の解き方
だ。
平方完成は、解の公式を証明するときにつかった解き方だよ。
だから、解の公式を忘れても、解の公式っぽく二次方程式がとけちゃうのさ。
たとえば、さっきの2次方程式、
x² – 2x -6 = 0
を平方完成でといてみようか。
平方完成の解き方は4ステップだよ。
この解き方で二次方程式をといてみると、
x² -2x – 6 = 0
x² -2x = 6
x² -2x +1 -1 = 6
(x-1)² = 7
x-1 = ±√7
x = 1 ±√7
になる。
これは解の公式でだした解とおなじ。
解の公式を忘れたときに大活躍だ。
二次方程式の解き方はありすぎる。
どれを使ったらいいかわからないね。
心がけてほしいコツは、
消去法で解き方を選んでいく
ということ。
がつかえるか順番に確認していってね。
きっと、どれかしらで解けるはずだよ。
そんじゃねー
Ken
こんにちは!この記事をかいてるKenだよ。布団、押し込んだね。
二次方程式の利用ではいろいろ文章問題をとくよね。
整数の問題とか、長方形の面積を求める問題とか、まじありすぎる。
そんな中、テストにでてくるとヤッカイなのが、
動点の文章問題
だ。
動点の問題とは、
「ある点」が時間がたつにつれて辺上を動く問題のことね。
ずっと前に「一次関数の利用の問題」でやった問題といっしょ。
あれがもっかい中3数学で登場するわけ。
テストにでやすいから苦手をつぶしておこう。
動点の文章題の解き方を紹介しよう。
つぎの練習問題をといてみようね。
練習問題
AB = 10cm、BC = 30cmの直角三角形ABCがあります。点Pは辺AB上をAからスタートして1秒間に1cmの速さでBまで動きます。また、点QはBC上をBからスタートして1秒間に2cmの速さでCまで動きます。
PとQが同時に動きはじめるとき、△PBQの面積が16cm^2になるのは何秒後になりますか??
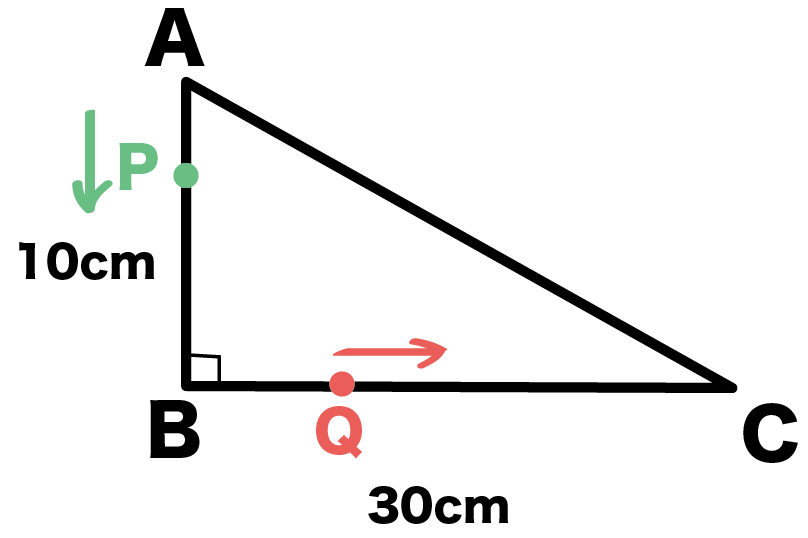
解き方は他の二次方程式の文章題といっしょ。
4ステップでいけるんだ。
方程式の文章題の解き方はどれもおなじ。
そう。
「文章題で求めたいもの」を文字でおけばいいんだったね??
xでもyでもzでも好きな文字でおいてくれ。
例の文章問題では、
△PBQの面積が16 cm^2になるときは何秒後になるか??
を求めたかったね。
だから、2点P、Qがスタートしてからの時間をx秒としてみようか。
これが第1ステップ。
文章問題をもとに二次方程式をつくってみよう。
文章題のなかの、
○○が△△に等しいとき
っていう文をみつけて、それをもとに、
○○ = △△
っていう方程式をつくればいいのさ。
さっきの練習問題をみてみて。
△PBQの面積が16 cm^2になるとき
っていう文がみつけられたかな??
つまり、この二次方程式の動点の問題では、
△PBQの面積 = 16cm^2
っていう2次方程式をつくればいいわけだ。
それじゃあ、x秒後の△PBQの面積を計算してみよう。
底辺×高さ÷2
だ。
ってことは、△PBQの面積を求めるには、
の2つがわかってればいいね。
点P、Qはそれぞれ、
動く。
ってことは、x秒後は、それぞれ、スタート地点から、
すすんでるはずだね。
だから、直角三角形PBQの底辺と高さの辺たちは、
になってる。
ってことは、スタートからx秒後の△PBQの面積は、
(底辺)×(高さ)÷ 2
= BQ × PB ÷ 2
= 2x (10-x)÷2
= x (10-x)
になるね。
この文章題では△PBQの面積が「16cm^2」になればいいんだったね??
ってことは、
△PBQの面積 = 16
x (10-x) = 16
っていう二次方程式ができるはずだ。
さっきの二次方程式を解いてみよう。
因数分解をつかってもいいし、解の公式をつかってもいい。
とりあえず、2次方程式の解を求めてね。
練習問題の二次方程式は、
x (10-x) = 16
だ。
左辺の()を分配法則で展開してやると、
x (10-x) = 16
10x – x^2 = 16
になるね。
移項して整理してやると、
x^2 – 10x + 16 = 0
になるんだ。
左辺の、
x^2 – 10x + 16
はどうやら因数分解の公式がつかえそうだ。
になる2つの数を考えてみると・・・・
は!
ならこの条件にあいそう!
ってことで、因数分解の公式の、
x^2 +(a+b) x + ab = (x + a) (x +b)
で因数分解してやると、
x^2 – 10x + 16
= x^2 (-8-2)x + (-8)×(-2)
= (x -8) (x-2)
になるね。
だから、練習問題の二次方程式は、
x^2 – 10x + 16 = 0
(x -8) (x-2) = 0
になる。
( x – 8) (x – 2)が0になってるってことは、どっちかが0なはず。
よって、
のどちらかが成り立つはずだね??
ってことで、2つの一次方程式をといてやると、
っていう解が2つでてくるね。
やった!これで二次方程式解けたー!おわたーー
ってなるのはちょっとはやい。
じつは、二次方程式の文章問題では最後に、
解の吟味
をしなきゃいけないんだ。
吟味ってつまり、解が文章題にそってるか確認することだ。
これをしないと、わけのわからん答えをかいちゃうからね。
練習問題でも解を確認しよう。
二次方程式の解は、
だったね。
つまり、PとQがスタートしてから「2秒後」と「8秒後」に面積が16cm^2になるらしい。
この2つのxはきちんとxの変域内におさまってるから問題なさそうだ。
だって、点PはBまでしか動けないからxの変域は、
0 ≦ x ≦ 10
だもんね。
点Pは1秒間に1cmすすむから、10秒で10cmすすむ。
つまり、終点のBに到着しちゃうのさ。
だから、xが10より大きくならないってわけ。
今回の2つの解は10以下におさまってるね。問題ない!
よって、まとめると、
△PBQの面積が16cm^2になるときはスタートしてから2秒後と8秒後だね。
二次方程式の利用の動点も大丈夫だ。
落ち着いて、
の4ステップで解けばいいよ。
ただ、
解が変域内におさまってるか??
は必ず確認してね。
そんじゃねー
Ken
こんにちは!ぺーたーだよ。よろしくね!
中学3年で勉強する二次関数。
入試に出てくるからマスターしたいね。
一次関数は2年生で学習したよね?
y=ax+b
ってやつ。
一方、今回勉強していく二次関数は 、
y=ax^2
という形になるんだ。
つまり、xの次数が2になってるわけね。
たとえば、y=2x^2とかy=-3x^2っていう感じで。
今日はこの、二次関数の問題でよくでてくる、
変化の割合の求め方について解説していくよ。
よかったら参考にしてみて。
=もくじ=
変化の割合っていう言葉を復習しよう。
変化の割合とは、
xが増える量に対し、yがどれだけ増えるか(減るか)
を表すものだったね??
こいつを求めるには変化の割合の公式を使えばいいよ。
変化の割合 = (yの増加量)÷(xの増加量)
っていうやつだ。
中学3年生の二次関数でも、この公式を使うってわけね。
二次関数の変化の割合の求め方は、つぎの3ステップさ。
練習問題をときながら勉強してみよう。
練習問題
y=2x^2でxが-3から4まで増加するときの変化の割合を求めよ。
xの増加量を求めるには、
xの「一番大きい数」から「一番小さい数」を引けばいいんだ。
練習問題では、xは-3から4まで変化したね??
ってことは、「一番大きい数」の4から「一番小さい数」の-3を引けばいいんだ。
すると、
(一番大きい数)-(一番小さい数)
= 4-(-3)
= 7
になるね。
だから、xの増加量は7になるよ。
次はyの増加量を求めてみよう!
え…ちょっと待って。
問題文にはyの範囲が書かれてないじゃん!
たしかにそうだね。
yの増加量は自分で計算しなきゃならないんだ。やり方は難しくないから大丈夫。
xの「一番大きい数」と「一番小さい数」のときのyの値を計算すればいいね。
まず、「y=2x^2」に「x=4」を代入してyを出してみよう。
すると、
y = 2×4^2
= 2×16
= 32
になるね。
じゃあ次は、x=-3のときのyを同じように出してみよう。
y = 2× (-3)^2
= 2×9
= 18
になるね。
ここまで来ればyの増加量はあと一歩。
xの増加量を求めるときは、一番大きい数から一番小さい数を引いたよね??
だけど、yの増加量を求めるときは注意が必要。
yの増加量は、
(xの大きい数の時のyの値)-(xの小さい数の時のyの値)
っていう計算をするんだ。
練習問題では、xの大きい数は4で、そのときのyは32。
xの小さい数は-3で、そのときyは18だったね。
よって、このときのyの増加量は、
(yの増加量)= 32 – 18 = 14
になるわけ。
(xの大きい数の時のyの値)-(xの小さい数の時のyの値)
っていうルールは絶対守ってね。
さあ、答えは目の前だ。
後は、「変化の割合の公式」にあてはめるだけだ。
yの増加量は14、xの増加量は7だったから、
(変化の割合)
=(yの増加量)÷(xの増加量)
= 14÷7 = 2
になるね。
だから、変化の割合は2というわけさ。
これで問題はおしまいだよ。ちょっと簡単だったかな?。
黙ってたんだけど、
二次関数y = ax2の変化の割合の求め方には便利な公式があるんだ。
y = ax2で、xがmからnまで増加するときの変化の割合は、
a (m + n)
で計算できちゃうよ。
だから、今回の、
y = 2x^2でxが-3から4まで変化するときの変化の割合は、
2(-3 + 4)
= 2
っていうかんじで瞬殺で計算できちゃうんだ。
こんな裏技もあるんだって覚えておいてね。
⇒くわしくは「二次関数y=ax2の変化の割合の公式」をよんでくれ
二次関数の変化の割合の求め方はどうだった??
yの増加量を求める時に注意すれば大丈夫そうだね。
最初はゆっくりでいいよ。
段々やり方をマスターしていこうね!
それじゃ、また。
ぺーたー
ある日、数学が苦手なかなちゃんは、つぎの二次方程式に出会いました。
練習問題
つぎの二次方程式を解きなさい。
3x^2 + 5x -2 = 0
この二次方程式って因数分解の公式つかえないの・・・・
せっかく解き方おぼえたのに。。
ど、ど、どうしよう!!
こりゃむずいわ
因数分解の技の1つだね!
因数分解するときに、たすきがけみたいに掛け算して考えるから、「たすきがけ」って呼ばれてるんだ。
簡単にいうと、
「かけたらxの2乗の係数になる数字の組」と「かけたら定数項になる数字の組」と、「たしたらxの係数になる組」を、
◇×○=☆
になるようにならびかえるんだ↓↓
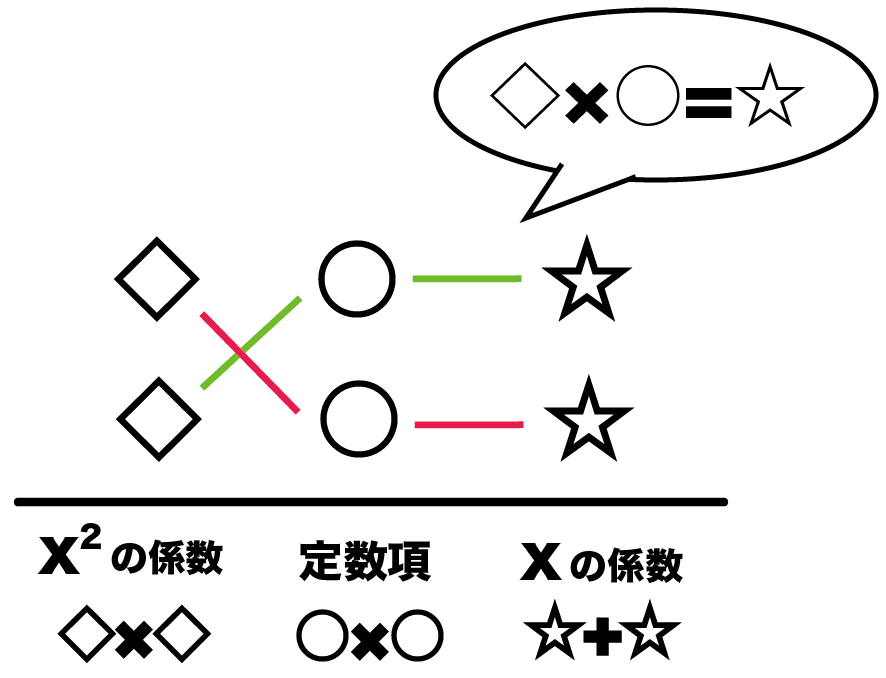
たすきがけ因数分解は、パズルみたいに数字をあてはめていくから、数字の確認がすごく重要なんだ。
定数項・・・!?
定数項は「数字だけの項」だったよね??

まずは一番左の「xの2乗の係数」からだね。
かけたら「3」になる2つの数字の組み合わせは・・・・
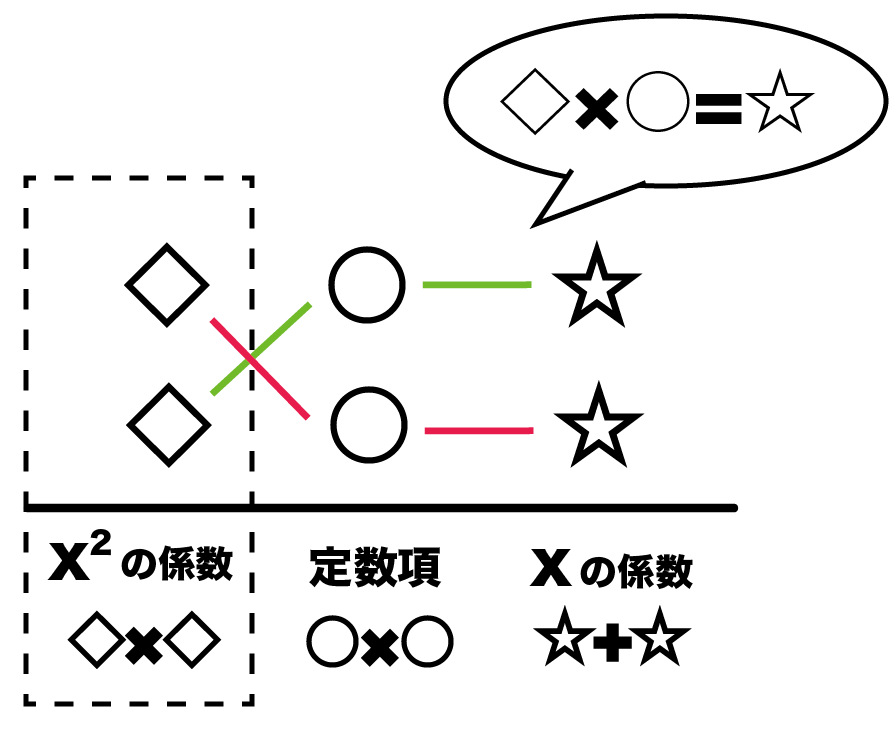
じつは、「-1×-3」もあるんだけどね。
「x²の係数」は正の数のことしか考えなくていい
っておぼえてとくといいよ。
これなら組み合わせのパターンを減らせるよね。
秘密技♪
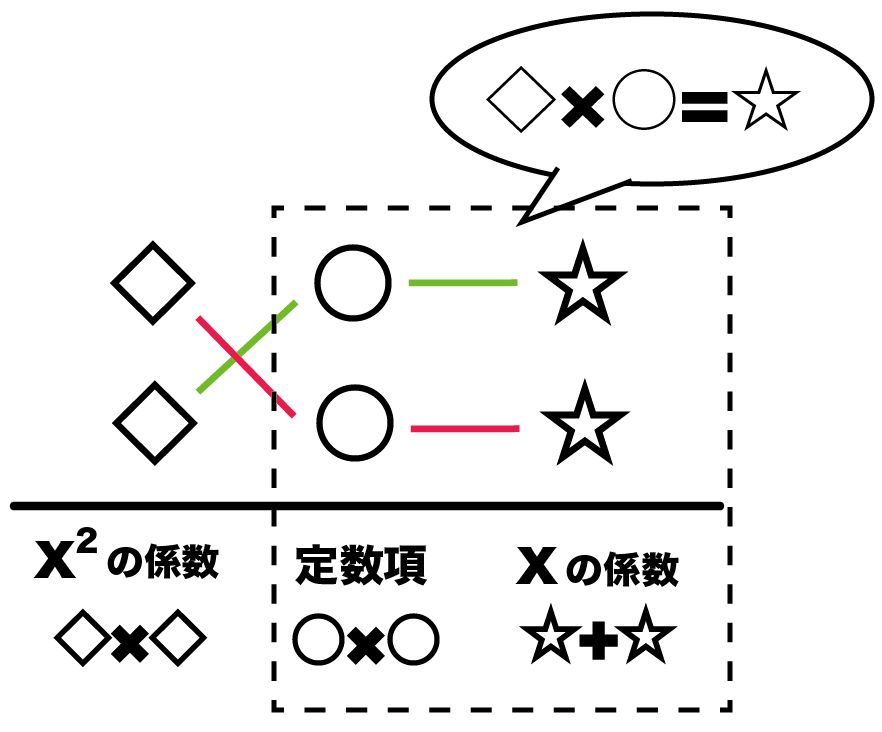
のどっちかかな?
あと、☆の組み合わせは・・・いっぱいあるじゃん!たして5になる組み合わせなんて!!
☆になる組み合わせにすればいいの
例えば、○の組合せを1×-2にすると?
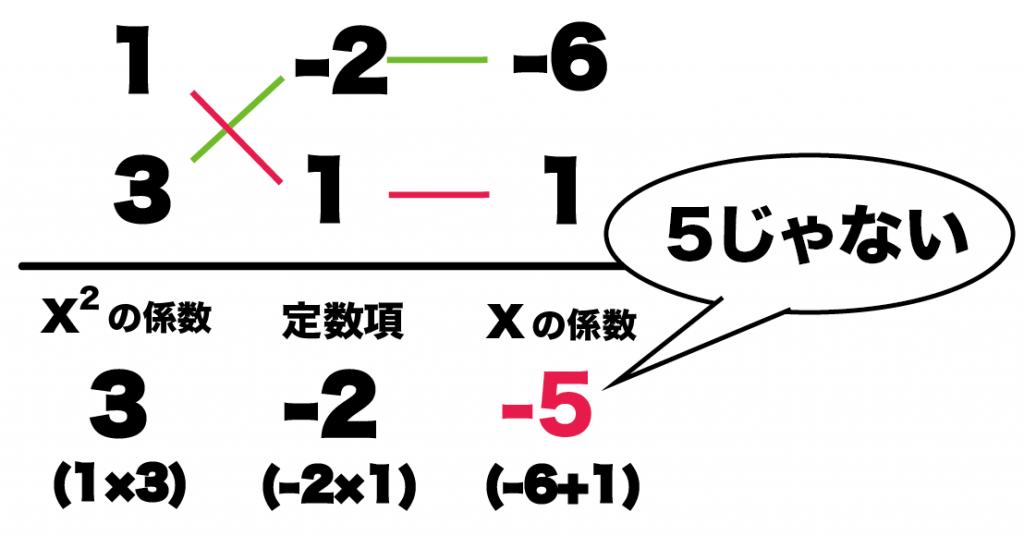
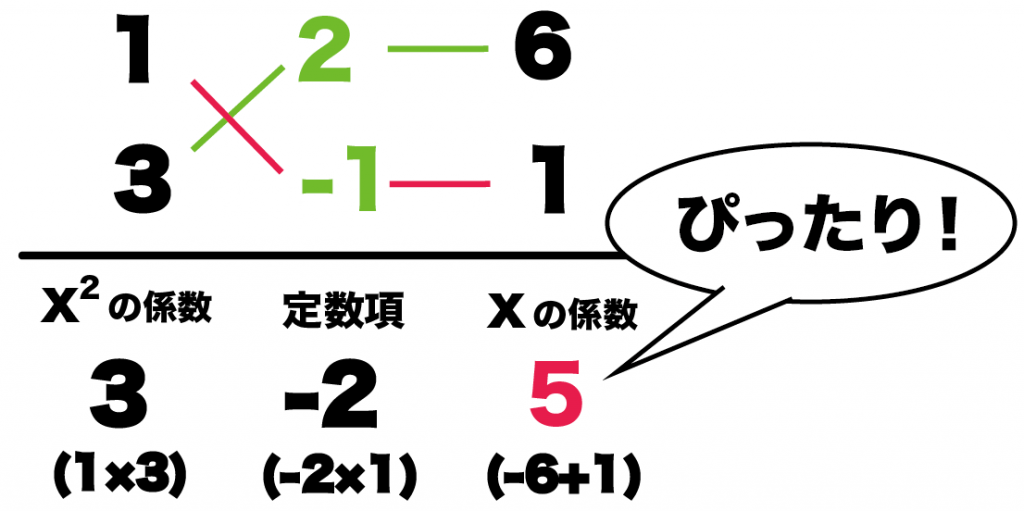
◇と○にはいった数字の組み合わせを()にいれるだけなんだ。
【上】(◇x+○)【下】(◇x+○)
ってなるようにいれてみて!
あと、忘れちゃいけないのが右辺!
(x+2) (3x-1) = 0 ってなるよ♪
カッコの中が、どっちか0になればいいから、
xは「-2」と「3分の1」かな?
x = -2, 3分の1
ってかけば完ぺきだね☆
かっこがある式にするためのものなんだ!!
かっこがある式……あっ、先生、
もしかして、『かっこいい』とかけてたの!?
それもあるけど、たすきがけ使いこなせたら、かっこいいよ!だから!!
何度も挑戦して慣れていこう!
☆練習問題☆
はろー、犬飼ふゆだよー。
二次方程式の解を求めたい。
そんなときあるよね??
方程式の解を求めるってようは、
未知の文字xになにがはいるか??
を当てることなんだ。
これは一次方程式でも二次方程式でもいっしょだね。
今日は、二次方程式の解き方のなかでも、
因数分解をつかった二次方程式のやり方
をわかりやすく解説してみたよ。
よくでる解き方だから、マスターしちゃおうか。
つぎの二次方程式をといてみよう。
つぎの二次方程式を解きなさい。
2x² -10x -60 = 12
このタイプの問題は5ステップで解けちゃうね。
左辺に項をあつめようか。
右辺の項をぜーんぶ左に移項して、右辺を0にすればいいのさ。
これは因数分解しやすくするためよ。
練習問題では、右辺の12が邪魔だね??
こいつを左辺に移項したいんだけど、基本は大丈夫かな??
=を越えて移動したらプラスはマイナスに、マイナスはプラスになる
が移項だったね??
さっそく「12」を左辺に移項してやると、
2x² -10x -60 = 12
2x² -10x -60 – 12 = 0
2x² -10x -72 = 0
になって、右辺が0になるはず。
めでたしめでたし。
二次方程式の両辺を共通因数で割ろう。
なぜなら、xの2乗の係数を1にしたいからね。
割れなかったらつぎにいってもOKよ。
練習問題の2次方程式をみてみると、
2x² -10x -72 = 0
あ、両辺を2でわれそうだ!
さっそく割ってみると、
2x² -10x -72 = 0
x² -5x -36 = 0
になるね。
ここでの注意点は、ぜんぶの項を共通因数で割ることね。
まちがっても、「xの2乗の項」だけ共通因数で割って、
x² -10x -72 = 0
にしちゃダメだよ。
「xの項」も「定数項」も同じ数で割ってね。
いよいよ因数分解。
公式で左辺を因数分解してみよう。
練習問題の二次方程式の左辺は、
x² -5x -36
だったよね??
項が3つだから、因数分解の公式の、
x² +(a+b)x +ab = (x+a) (x+b)
がつかえそう。
になる2つの数字を考えればいいんだ。
かけて「-36」になる数字のペアーは、
の7つだね??
この中で、たしたら「-5」になる数字の組は、
「-9」と「4」。
だから、二次方程式の左辺を因数分解すると、
x² -5x -36 = 0
(x-9) (x+4) = 0
になる。
今度は一次方程式をつくってみよう。
二次方程式を因数分解すると、
A×B = 0
っていう形になった??
このとき、AとBをかけて0になってるんだから、どっちかが0になってるはず。
だから、A×B =0 っていう二次方程式から、
っていう一次方程式が2つできるわけよ。
練習問題の二次方程式の、
(x-9) (x+4) = 0
をみてみよう。
の2つをかけて0になってるから、どっちか1つが0になってるはずね。
だから、
っていう一次方程式が2つつくれる。
さっきの一次方程式をといてみよう。
中1数学でならった一次方程式の解き方をつかうだけよ。
練習問題の、
をそれぞれ解くと、
が求められるね。
これが二次方程式の解になるよ。おめでとう!
因数分解をつかった二次方程式の解き方はどう??
公式さえおぼえてれば、大丈夫よ。
因数分解して一次方程式を解くだけだからね。
徐々に2次方程式の問題に慣れていこう!
じゃあねー
犬飼ふゆ
こんにちは!この記事をかいてるKenだよ。天にのぼりたいね。
二次方程式の解き方にはいろいろある。
因数分解の公式をつかったり、
解の公式をつかったり、
たすきがけの因数分解をつかってみたり、、、、
と大忙しだ。
ぶっちゃけ、どの解き方を使えばいいかわからんよね??
今日は、もう1つ新しい2次方程式の解き方を紹介するよ。
その名も、
平方根をつかった二次方程式の解き方だ。
2次方程式の基礎だから、しっかりおさえておこうね。
さっそく、平方根をつかった解き方を紹介していくよ。
つぎの練習問題をといてみよう。
練習問題
つぎの二次方程式を解きなさい。
(x-2)^2 -48 = 0
「()の2乗」以外を右辺に移項しちゃおう。
例題でいうと、
48
が()の2乗以外の項だね。
こいつを右辺に移項してやると、
(x-2)^2 -48 = 0
(x-2)^2 = 48
になるね。
つぎは左辺の2乗をとってみよう。
左辺の2乗をとるだけじゃなくて、その分、右辺を「左辺の平方根」にしてあげてね。
つまり、
右辺に±とルートをつければいいのさ。
練習問題でもおなじ。
左辺の2乗をとって、右辺を「左辺の平方根」にしてやると、
(x-2)^2 = 48
(x-2)= ±√48
になるね。
つぎはx以外を右辺に移項しよう。
最終的に「x=」にもっていきたいからね。
練習問題の左辺には、
-2
っていうx以外の項が残ってるね。
こいつを右辺に移項すると、
(x-2)= ±√48
x = 2±√48
になる。
最後にルートを簡単にしてあげよう。
ルートの中身の「2乗の因数」を外にだせばいいんだったね??
やんなくても間違いじゃないけど、
やったほうが計算の余地が確認できてスッキリするよ。
練習問題のルートの、
±√48
に注目してみて。
ルートのなかの「48」を素因数分解してみると、
48 = 2×2×2×2×3
になるよね??
ってことは、
2の2乗(4のこと)
を√の外にとりだせそうだ。
さっそく、√48を簡単にしてやると、
x = 2±√48
x = 2 ± 4√3
になるね。
これで二次方程式がとけちゃったんだ。
平方根をつかうと簡単に解けるね。
平方根をつかった二次方程式は4ステップでとけちゃうよ。
みたかんじ、移項できればとけそう。
ガンガン平方根をつかっていこう。
そんじゃねー
Ken
こんにちは!この記事をかいてるKenだよ。人生playhardだね。
二次方程式の利用では文章題がたくさんでてくるね。
連続する整数の問題とか、
動点についての文章題とかね。
もう、ほんとうに種類ありすぎ。;
今日は、二次方程式の利用の文章題でよくでてくる、
二次方程式の面積についての文章題の解き方
を紹介していくよ。
よかったら参考にしてみて。
つぎの文章題をといてみようか。
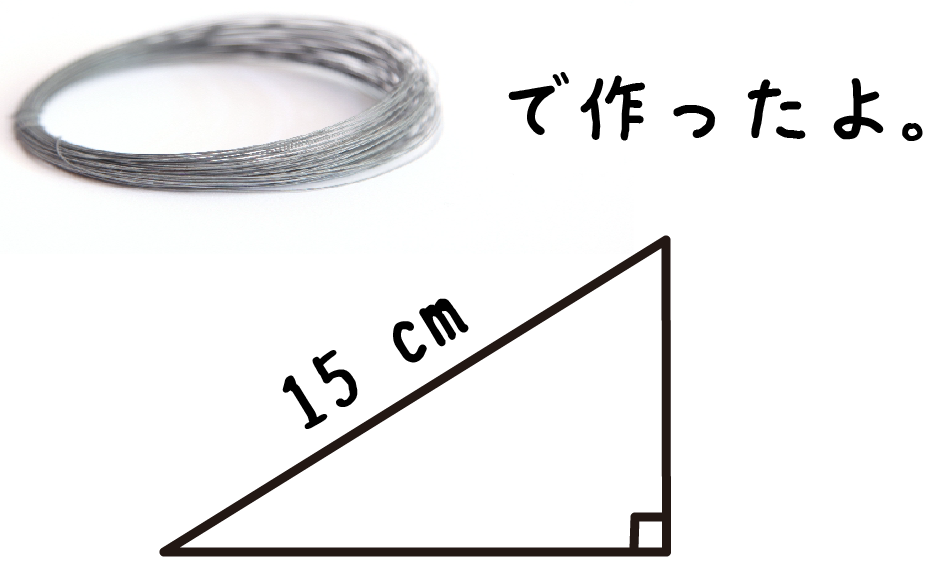
練習問題
長さ30cmの針金で斜辺15cmの直角三角形を作りました。この三角形の面積が25cm^2になるとき、底辺と高さの長さを求めなさい。
二次方程式の文章題の鉄則。
それは、
求めたいものを文字でおく
だよ。
どれを文字で置こうか迷わなくていい。
文章題が「だしてほしい」っていってるものを文字でおこうね。
練習問題では、
直角三角形の辺の長さ
を求めたかったよね??
ってことは、いったん、底辺をx [cm]とおいてみよう。
二次方程式をつくろう。
文章題のどこかに、
○○○が△△△に等しくなるとき
ってかいてあるはずだ。
それをもとに、
○○○ = △△△
っていう等式をつくればいいのさ。
練習問題でいうと、
三角形の面積が25cm^2になるとき
ってところに注目してほしいね。
つまり、これは、
三角形の面積 = 25cm^2
っていう方程式がたてられそう。
ってことで、直角三角形の面積を計算してみよう。
長さ30cmの針金でつくったから、周りの長さは30cmだよね??
だから、残りの辺の「高さ」の長さは、
(針金の長さ)-(斜辺の長さ)- (底辺)
= 30 – 15 – x
= 15 -x
になるね。
よって、この直角三角形の面積は、
(直角三角形の面積)
=(底辺)×(高さ)÷2
= x (15-x)÷2
になるね。
練習問題では、面積が「25 cm^2」になるんだったね??
この通りに二次方程式をつくってやると、
(直角三角形の面積) = 25
x (15-x)÷2 = 25
になるね。
つぎは、二次方程式を解いてみよう。
因数分解をつかった解き方でもいいし、
めんどかったら解の公式をつかってもいいよ。
練習問題の二次方程式は、
x (15-x)÷2 = 25
だったね??
分数をふくむ二次方程式だから、分母はらってみようか。
両辺に2をかけると、
x (15-x)÷2 = 25
x (15-x)÷2×2 = 25×2
x (15-x) = 50
になるね。
左辺を展開して移項すると、
x (15-x) = 50
15x -x^2 = 50
x^2 -15x + 50 = 0
になるね。
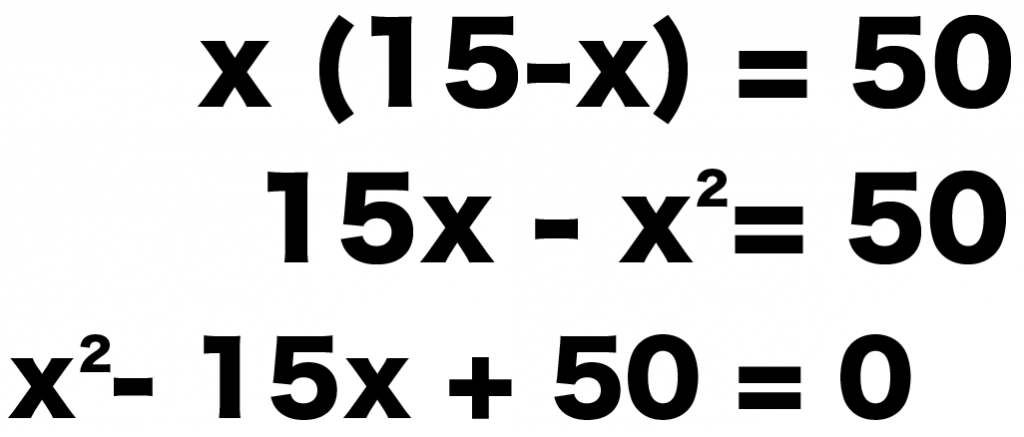
んで、
因数分解して二次方程式をとくと、
x^2 -15x + 50 = 0
(x-10) (x-5) = 0
x = 5, 10
になるね。
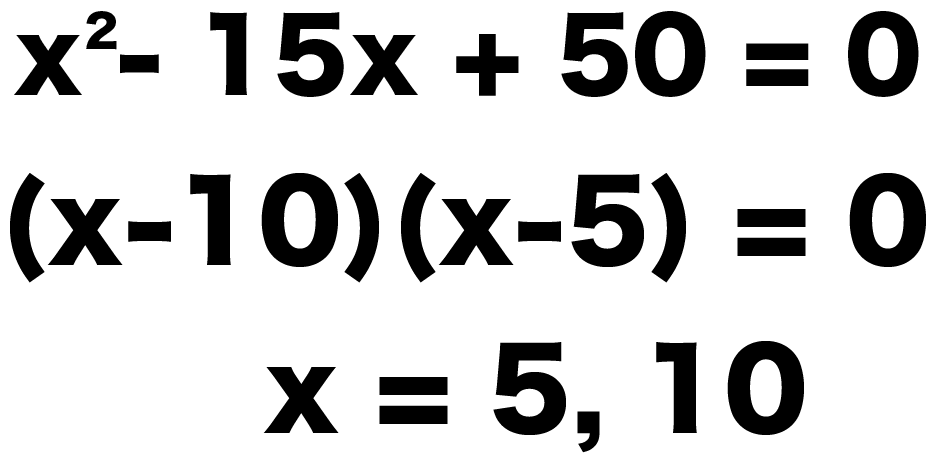
二次方程式の文章題はといておわりじゃない。
解き終わったあとに、
その解が文章題として適切かどうか??
をチェックしなきゃいけないんだ。
練習問題では、
っていう2つの解がゲットできたね??
xを「直角三角形の底辺の長さ」とおいてた。
底辺のx = 5のとき、
直角三角形の高さは、
10cm
になるね。
うんうん。辺の長さが正の数だし問題ない。
んで、「x=10」の場合をおなじように考えてみよう。
底辺x = 10のとき、
直角三角形の高さは、
5 cm
になる。
うん、正の数になってるから適切だ。
こんなかんじで、二次方程式を解いたあともチェックが大事。
解が文章題の条件にあってるかたしかめてね。
世の中には、いろいろな二次方程式の利用の問題がある。
だけどね、ぶっちゃけ、解き方はどれもいっしょ。
の4ステップでいいんだ。
ガンガン文章問題をといていこう。
そんじゃねー
Ken
はろー、犬飼ふゆだよ。
2次方程式ってテストに必ずでてくるよね??
解き方を覚えて損はない!って断言できちゃうよ。
因数分解をつかっても解けるんだけど、どうにもならない場合に
「任せとけ! 絶対に解けるから!」
っていう強い味方がいるの知ってたかな?
それが
「解の公式」
なんだ。
高得点を狙いたいなら絶対にCheckだよー。
今日はこの、
解の公式の計算問題のやり方をわかりやすく解説してみたよ。
さっそく解の公式の計算を解説していくよ。
つぎの練習問題をといてみよう。
解の公式なら4ステップでとけちゃうんだよ。
移項して右辺をゼロにしてみよう。
最終的に、
ax²+bx+c=0
っていう形にもってけばOKだよ。
練習問題の二次方程式では、右辺に「2」が残ってるね??
3x²+10x+7 = 2
こいつを左辺に移項してやると、
3x²+10x+7 = 2
3x²+10x+7 – 2 = 0
3x²+10x+5 = 0
になるね!
さてと、因数分解で二次方程式とくかな・・・・
え!因数分解できない!!
じゃあ共通因数でくくるかな・・・・
あれ!?共通因数でくくれない!!
・・・・・・・・・・
そんなときに使えるのが解の公式だったよね??
解の公式を簡単におさらいしておくと、
二次方程式 ax2+bx+c=0の解xは、
x = {-b±√(b² – 4ac)}/2a
になるんだったね??
これマジ重要。
紙に書いて机のそばに貼っておきたいくらい。
面倒でも覚える価値あるよ。
練習問題の2次方程式は、
3x²+10x+5 = 0
になったよね??
ってことは、解の公式の各係数は、
になるね!
この3つの値を解の公式に代入してやると、
x = {-b±√(b² – 4ac)}/2a
= {-10 ± √(10² -4×3×5)}/2/3
になる。
つぎはルートの中身を簡単にしよう。
さっきの計算では、
x = {-10 ± √(10² -4×3×5)}/2/3
になったよね??
この分子のルートの中身を計算してやると、
x = {-10 ± √(100-60)}/6
= {-10 ± √40}/6
になるね。
ふう。。。終わった。。。。
あ、ちょい待って。
ルートの中身の40って素因数分解すると2×2×2×5だね。
2×2がダブってるから、ルートの外に出しちゃおっか。
x = {-10 ± √40}/6
= {-10 ± 2√5}/6
最後は約分できるか確認しよう。
練習問題でも約分できそう。
だって、分母と分子が両方2でわれるもん。
分子のぜんぶの項を2で割るように注意しようね。
さっそく約分してやると、
x = {-10 ± 2√5}/6
={-5 ± √5}/3
になるね。
どうかな?
むずかしそうだけど、ちゃんと解が出たでしょう?
解の公式すっごい便利だからぜひぜひ! 覚えておいてね。
解の公式はほんとうに便利。
因数分解の公式もつかえないし、共通因数でもくくれない。
そんなときに解の公式をつかってみてね。
たくさん使って問題に慣れていこう。
じゃあねー
犬飼ふゆ
こんにちは!この記事をかいているKenだよ。山の日は混むね。
二次方程式の解き方をたくさん勉強してきた。
因数分解をつかった解き方とか、
解の公式でとくやり方とかね。
ぶっちゃけ、
どんな二次方程式もとける自信あるよね??
だがしかし、中3数学の二次方程式はまだこれからなんだ。
二次方程式のゴールは、
二次方程式を文章問題でも使えるようになる
なんだよね。
そこで今日は、
二次方程式の利用の文章題の解き方
をわかりやすく解説してみたよ。
よかったら参考にしてみてね。
二次方程式の利用の解き方を解説していくよ。
つぎの練習問題をといてみよう。
練習問題
2つの連続する正の偶数の積が168になるとき、2つの偶数をそれぞれ求めなさい。
どんな文章題でも、4ステップでとけちゃうんだ。
文章問題で求めたいものを文字でおこう。
辺の長さを求めたいときは「辺の長さ」、
ケーキの値段をだしたいときは「ケーキの値段」を文字でおけばいいのよ。
練習問題では、
積が168になる「2つの連続する正の偶数」
を求めたかったよね??
だから、「2つの連続する偶数を文字」であらわせばいいのさ。

正の整数nで連続する偶数をあらわしてみよう。
※numberのnからきてるのさ。
ある偶数は、正の整数を2倍するとなるから、
2n
になるよね??
そのつぎの偶数はこいつより2大きいはずだから、
2n + 2
になるはず。
これが第1ステップだ。
つぎは二次方程式をつくってみよう。
AがBになるとき
っていう文章をみつけて、「A=B」っていう方程式をたてればいいのさ。
例題では、
2つの連続する正の偶数の積が168になるとき
っていう文章に注目してみて。
ようは、
(2つの連続する正の偶数の積)= 168
っていう方程式をつくればいいんだね。
連続する2つの偶数はそれぞれ、
だったよね??
だから、2つの連続する偶数の積は、
2n (2n + 2)
になる。
こいつが「168」に等しくなるから、
2n (2n + 2) = 168
っていう方程式ができるね。
二次方程式を解いてみよう。
2次方程式の解き方はどれをつかってもいいよ。
因数分解でもいいし、解の公式をつかってもいい。
答えがでちゃえば問題ないわけだ。
練習問題の二次方程式は、
2n (2n + 2) = 168
だったよね??
左辺の()を分配法則ではずすと、
2n (2n + 2) = 168
4n^2 + 4n = 168
になる。
んで、移項して両辺を4でわってやると、
4n^2 + 4n – 168 = 0
n^2 + n – 42 = 0
になるね。
左辺の、
n^2 + n – 42
を因数分解してみると、
n^2 + n – 42
=(n +7)(n-6)
になるね。
よって、この二次方程式の解は、
n = 6, -7
だ。
二次方程式は無事とけたかな??
よかった!やったね!!
・・・・・・・・
・・・・・・・・
っていいたいところだけどね。
二次方程式の文章題の本番はこれからなんだ。
なぜなら、
その解が正しいか判断しなきゃいけないからね。
このことを数学界では、
解を吟味する
っていうんだ。
文字の条件を振り返ってみてね。
練習問題では、
がでてきたよね??
ここで、nは何かって振り返ってみると、
正の整数
だったよね??
えっと、、2つとも正の整数かなああ・・・
!!!?
あっ!
正の整数じゃないやつもいるやんけ!
そう。
n = -7
が条件にフィットしてないんだ。負の数だからね。
だから、この「n = -7」は適切じゃないってことがわかる。
したがって、2次方程式の解として正しいのは、
n = 6
だけだね。
よって、n = 6のとき、2つの連続する偶数は、
になる!
つまり、積が168になる連続する2つの正の偶数は、
の2つになるってわけ。
おめでとう!
これで二次方程式の文章題もマスターだね。
二次方程式の文章題はちょっとくせもの。
最後の最後に、
その解が問題として正しいのか??
を確かめなきゃいけないんだ。
最後まで気を引き締めていこう。
そんじゃねー
Ken
ある日、数学が苦手なかなちゃんは、二次方程式の問題に出会いました。
練習問題
つぎの二次方程式を解きなさい。
x^2 = 2x

因数分解とか解の公式とか使うし。
言葉おぼえてもすぐ忘れちゃう・・・
ど、ど、どうしよう!!
二次方程式の解き方がわかると思うよ〜!
深呼吸して落ち着いてみて。
解けるかな?解いてみよう!
って思えるまで落ち着いてね!
はぁ……
ふぅ、
だいぶ落ち着いてきた。
先生もいるし、2次方程式解いてみようかな……
二次方程式の左辺にすべて移項していこう!
『+』のやつなら『-』になって、
『-』のやつは『+』になるよ♪
x²= 2x は、x²-2x = 0ってこと?
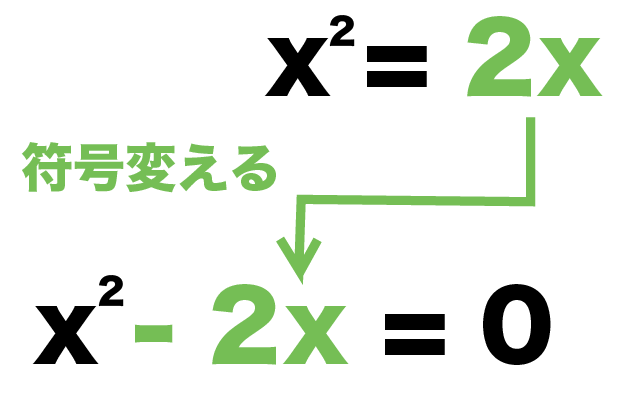
2次方程式の右辺が0になったら完成だよ♪
食えないヤツじゃない。公約数みたいなもんだよ。
例えば、8と2、公約数は2だよね!
2×4で8,2×1で2。だから、「8+2」を「 2(4+1) 」とも書ける!
で、でも、2次方程式を解くときは、これが便利になるんだ。
練習問題の「x² – 2x」で考えてみると……?
x²は、x × xで、2xは、x×2だね!
じゃあ、今までの式を書いていくと……?
最初は誰でもそんな感じだから、とにかく挑戦することが大事!
で、(x+2)とxがかけたら0になってるよね??
2を右辺に移項して……
だけど、
二次方程式の解き方で一番大切なことがあるよ。
それは、
『答えを書くこと』!!!
x=2
x=0
だったから、まとめて、「x = 2,0」だね!
わからないところがあれば、ポイントを見ながら解いてみよう!
☆問題☆
(1) x²= -2x (2) 2x²= 6x (3) 3x²= -9x (4) 4x²= 2x
(1) x= 0, -2
(2) x= 0, 3
(3) x= 0, -3
(4) x= 0, 2分の1