こんにちは！この記事をかいているKenだよ。生姜焼き、食べ過ぎたね。
数学の証明問題ってむずいよね？？
計算問題とはひと味ちがう。
どうやって解いたらいいのかわからない。
このままでは数学が嫌いになっちゃいそうだよ・・・・
そこで今日は、
中2数学で勉強する証明問題の解き方を4ステップで解説していくよ。
よかったら参考にしてみてね。
例題の証明をときながらみていこう！
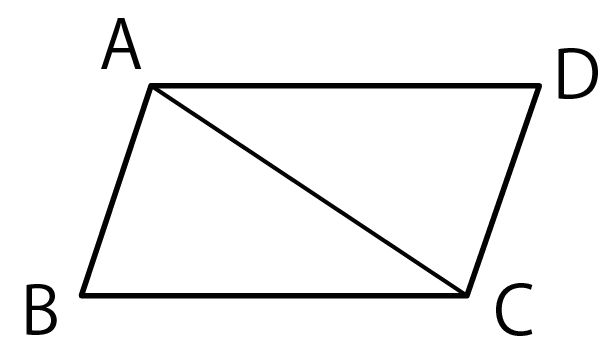
AB = DC、AB // DCの△ABCと△CDAがあったとします。
このとき、角ABC = 角CDAであることを証明しなさい。
まずは仮定と結論を整理しよう。
仮定と結論って簡単にいってしまうと、
だよ。
証明問題において、
なにを説明できればゲームクリアなのか？？
そのために、どんな条件があたえられているのか？？？
を整理することはむちゃ大事なんだ。
例題で実際に、
仮定と結論を整理してみよう。
AB = DC、AB // DCの△ABCと△CDAがあったとします。
このとき、角ABC = 角CDAであることを証明しなさい。
は問題文でわかっていることだね。
つまり、こいつらが「仮定」さ。
一方、結論は、
だ。
証明問題の「結論」って、
○○であることを証明しなさい
の「○○」にかいてあることが多いよ。
どうしても結論がみつからないときは、
問題文を読み返してみてね。
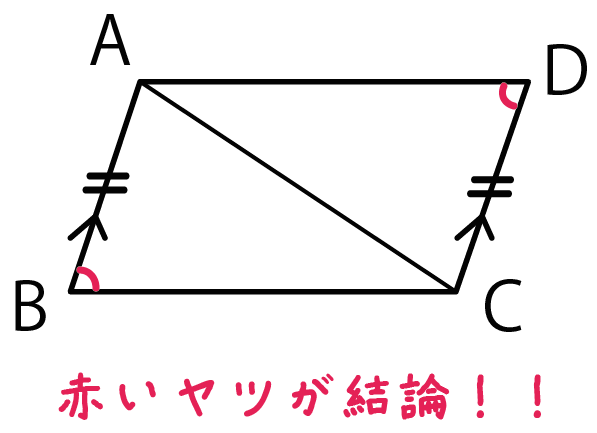
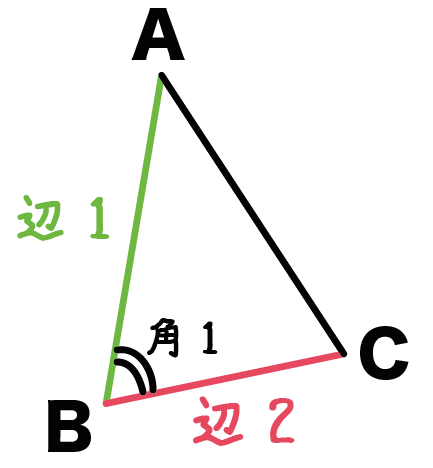
仮定を図にかきこんでやろう。
かきこむだけで、
仮定と結論がわかりやすく整理できて、
解き方のイメージをしやすくなるんだ。
ただここで注意してほしいのは、
仮定と結論をごっちゃまぜにしないことだ！
同じ黒ペンで仮定と結論をかきこむのはNG。
仮定と結論がどっちなのかわからなくなるからね。
だから、
仮定と結論を色違いのペンで書き込むことをおすすめするよ。
えっ、書き込まなくてもすでに整理できてるって？？
そういうヤツはこのステップをとばしてくれ。
つぎにいこう！
仮定・結論をみつめて、
どうやって仮定から結論までもっていくか？？
をイメージするんだ。
具体的にいうと、
結論をいうために、
「根拠となることがら」は何をつかうか？？
を考えることになるよ。
例題をみてみよう。
例題の結論は、
角ABC = 角CDA
だったよね？
うーん、
どうしよー、
うーん、
・・・・・
は！
これだ！
△ABCと△DACが合同であることをいえば
「角ABC = 角CDA」がいえるかも！！
合同な図形同士の対応する角の大きさが等しい
って根拠をつかえばね。
って感じで、
どの根拠をつかえばゴールの結論にたどり着けるか？
を事前にイメージしていくんだ。
後は証明を書くだけ！
証明の書き方には型がある。
それ通りにかいていけばいいんだ。
証明の書き方はつぎのようになっているよ。
この4つを詰め込んでやれば大丈夫だよ。
書き方は先生によって違うから、
担当教師の書き方をマネしてみてね。
例題の答えをかいてみるよ。
ぼくだったらつぎのような感じでかくね。
△ABCと△CDAにおいて、
AB = CD (仮定)・・・(1)
AC = CA (共通)・・・(2)
AB // CDより、
平行線の錯角が等しいので、
角BAC = 角DCA・・・(3)
(1)、(2)、(3)より、
2辺とその間の角がそれぞれ等しいので、△ABC ≡ △CAD対応する角の大きさが等しいので、角ABC = 角CDA
となる。
問題でわかっていること（仮定）から、
証明問題のゴール（結論）をみちびければいいんだ。
数学の証明問題の解き方はつぎの4ステップだったね。
証明問題はちょっとむずい。
だけど、解き方さえおさえておけば大丈夫さ。
問題をといて証明になれてみてね。
そんじゃねー
Ken
こんにちは！この記事をかいているKenだよ。鍋つくりたいね。
正多角形の外角の大きさがわからない・・・・・
そんなときは公式をつかえば一発。
正n角形の外角の1つの大きさは、
360°/n
になるんだ。
たとえば、正五角形の外角を求めてみよう。
公式のnに「5」を代入してやればいいから、
360°/ n
= 360°/ 5
= 72°
になるね。
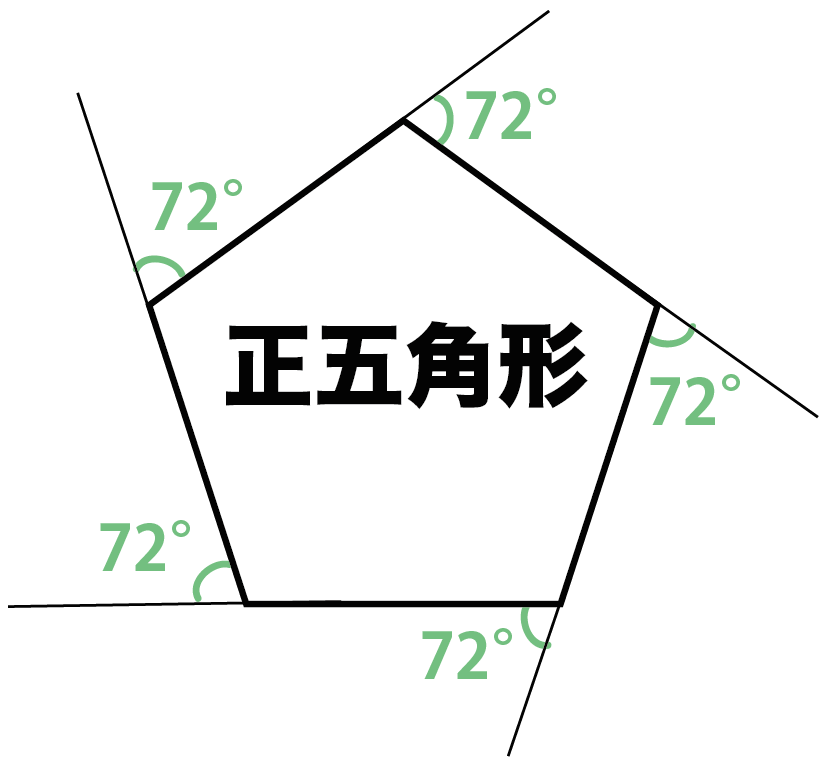
つまり、正五角形の外角の1つの大きさが「72°」になっているってことさ。
どう？？神秘的でしょ？？。
nに頂点の数をいれるだけでいい。
むちゃくちゃ便利だよね？
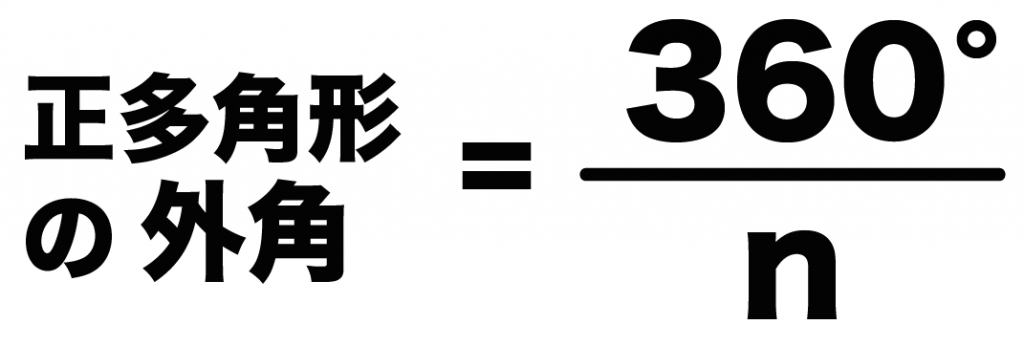
せっかくだから、
なぜ、
360°/n
で正計算できるか振り返ってみよう。
正多角形だろうが、何角形だろうが、
多角形の外角の和は360°になるって勉強したよね？？
んで、
正多角形には「すべての内角が等しい」という性質がある。
ってことは、
内角と隣り合っている「外角もすべて等しい」ってことになるよ。
だから、正多角形の1つの外角の大きさは、
（多角形の外角の和）÷ n
= 360°/n
になるんだ。
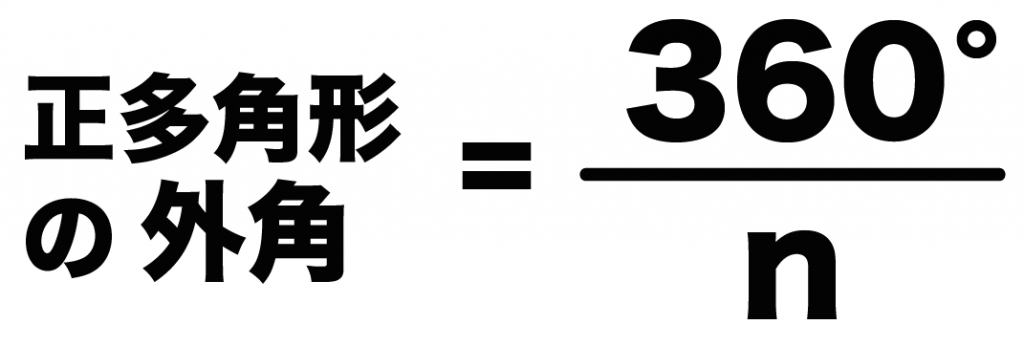
ただ公式をつかうだけじゃなくて、
なぜ、使えるのか？？
ってこともおさえておこう！
正多角形（n角形）の大きさは、
360°/n
で計算できちゃうよ。
テストで出たらガンガン得点をうばっていこう！
そんじゃねー
Ken
こんにちは！この記事をかいているKenだよ。コーン、最高。
図形の証明問題
ってむずかしいよね。
図形の面積を計算する問題とは
ちょっと違うタイプ。
苦手な中学生も多いはずだ。
今日はそんな苦手をなくすために、
【中2数学】図形の証明問題を攻略できる6つのコツ
っていう記事をかいてみたよ。
証明問題のせいで数学が嫌いになりそう、
ってときに参考にしてみてね。
つぎの例題をときながら解説するよ。
AB = DC、AB // DCの△ABCと△CDAがあったとします。
このとき、角ABC = 角CDAであることを証明しなさい。
数学の証明問題でいちばん最初にやることは、
仮定と結論をみつけてやることさ。
仮定とは、カンタンにいってしまえば、
問題文であたえられている条件
で、
結論とは、
仮定をつかえば正しいといえること
さ。
たとえば、さっきの例題でいうと、
っていうのが仮定だよ。
だって問題文中に、
AB = DC、AB // DCの△ABCと△CDAがあったとします。
ってかいてあるからね。
この問題にかぎっての正しい
って言ってくれてるてることなんだ。
これが仮定だ。
それじゃあ、「結論」をさがしてみよう。
結論は問題文でいうところの、
○○を証明しなさい。
の○○にあたるところさ。
つまり、
問題で証明してほしいことが「結論」なのさ。
この例題でいうと、
角ABC = 角CDA
が結論だね。
「仮定」を図に書きこんでみよう！
これをすると、
っていうメリットがあるよ。
あと、わからなかったときでも、
テスト用紙にがんばった形跡が残って、
先生に「がんばったアピール」ができるね。
たとえば、さっきの例題で、
が仮定だったよね？？
こいつを図に書き込んでやると、
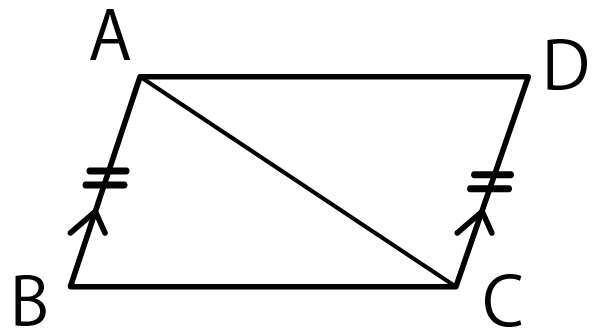
こうなる。
※図形の記号を復習してみて。
ただ、「結論」をいっしょに書き込まないでね。
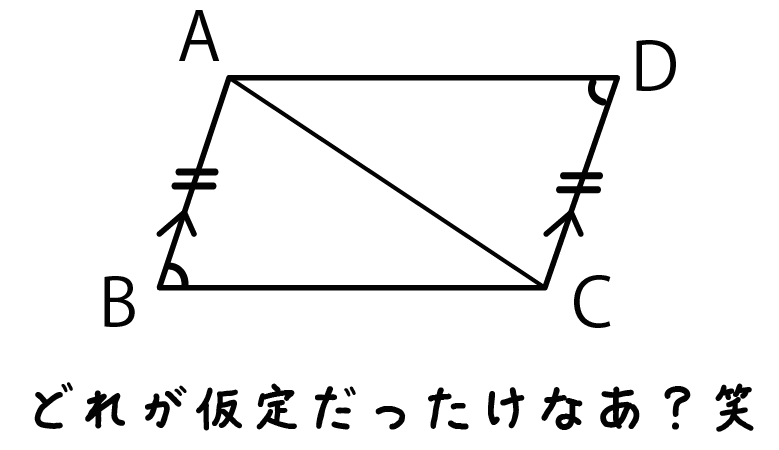
「仮定」と「結論」をごちゃまぜにすると混乱するからさ。。
結論も書き込みたいってときは、
色違いのペンでかきこんであげよう。
赤ペンとかでね。
仮定と結論を整理し終わったら、
結論までの道のりをイメージしよう。
証明問題の特徴は、
ゴールが事前にあたえられているってこと。
つまり、逆にいってしまえば、
ゴールがみえているから、そこへの行き方を考えるだけ
ってことになる。
いわば、ゴールがみえている迷路みたいなもんさ。
チーズがあるのはわかってるから、
あとは道順を考えるだけでいいんだ。
たとえば、例題の結論である、
角ABC = 角CDA
をゲットする道順を考えてみよう。
うーん、
えっと、
そうだなあ。。。
あっ！
△ABCと△CDAが合同である
ってことをいえればゴールできそうじゃね？？
だって、
合同な図形の「対応する角はそれぞれ等しい」
ってことを使えば、
角ABC = 角CDA
がいえそうだからね。
結論までをイメージするためには、
「根拠となることがら」を覚えている必要があるんだ。
多ければ多いほどいいね。
たとえば、さっきの例題でも、
を暗記していないとゴールまでイメージできなかった。
「合同な図形の性質」以外にもたとえば、
・・・・・・・・
などなど、図形の性質や合同条件をおぼえていればいるほど、
証明問題はときやすくなる。
辛いけど、これが事実だ。
最初はおぼえられなくても大丈夫。
徐々に問題をときながらみにつけていこう！
アルファベットといえば、
A, B, C, D , E, F, G……
という順番だね。思わず歌いだすやつもいるかもしれない。
ただ、証明問題においては、
アルファベット順に英文字を並べるのはNG
なんだ。
たとえば、例題で、
赤と緑の2つの三角形について証明していくよ
っていいたいとしよう。
このとき、なにも考えずにアルファベット順に、
△ABCと△ACDにおいて
とか書いちゃダメだ。
なぜなら、
対応する頂点同士の順番になっていないから
だ。
こういうときは対応する頂点の順番で、
△ABCと△CDAにおいて
ってかいてあげよう。
先生によっては対応する順番でかかないと×ってひともいるから
きをつけてね。
証明問題でみちびいたことに「番号」をふろう！
たとえば、
AB = DC (仮定)・・・・・・（1）
といった感じで。
なぜ大事なのかというと、
結論をみちびく材料として使いやすくなるから
なんだ。
ただ単に、
以上のことより、△ABC ≡ △DACである
っていうよりも、
(1)、(2)、(3)より、△ABC ≡ △DACである
っていったほうが説得力があるからね。
番号をつけるのはタダ。無料さ。
番号のつけすぎで減点されないから大丈夫。
引用しやすいようにこまめに番号をつけよう！
証明問題の書き方にはたーくさんある。
先生によって書き方がちがう。
たぶん、誰を信じたらいいかわからなくなるはずさ。
そんな状況だからこそ、
先生流の書き方で証明問題をかいてあげよう！
ぼくが中学生のときも困惑したよ。
先生によっては、三角形の合同条件を、
ってかかないと×にするヒトもいたし。
だから、
担当の先生の書き方で証明をかいてあげること
が高得点をとる秘訣になってくる。
数学の先生の板書をしっかりとって、
テスト前に書き方をおぼえてみよう！
いや、ぜんぜん書き方がわからない！
ってときは、
証明問題の書き方の記事を参考にしてみて。
数学の証明問題はぶっちゃけむずい。
だけど、この記事で紹介した7つのコツで、
ちょっとだけラクになるはず。
やっかいな単元だけどがんばっていこう！
そんじゃねー
Ken
こんにちは！この記事をかいているKenだよ。ビタミンCがほしいね。
数学の証明を勉強していると、
仮定
とか、
結論
っていうムズい用語言葉がでてくるね。
日常生活で使わないから、
わけわからないよね？？
そこで今日は、
「仮定」と「結論」という用語をわかりやすく解説していくよ。
よかったら参考にしてみてね。
〜もくじ〜
まずは仮定からみていこう。
意味を辞書（デジタル大辞泉）でしらべてみると、
１) 未定のこと、不確かなことを仮にこうと定めること。また、仮に定めた事柄。「今ここにコップがあると仮定してみよう」「仮定の上に立って物を言う」
２ ) 論理学などで、ある命題を導き出す推論の出発点におかれる前提条件。
ってかいてある。
数学の証明では2つめの意味がそれにあたるんだけど、正直よくわからないよね？。
あまりにも中学生にはむずかしすぎる・・・たぶん、大人にもむずい・・・
そこで、もう少し簡単にいってやると、
ある問題においてのみ、仮に正しいとされたこと
といえる。
えっ。これでもよくわらかないって！？
そうだな、たとえばつぎの問題があったとしよう。
例題
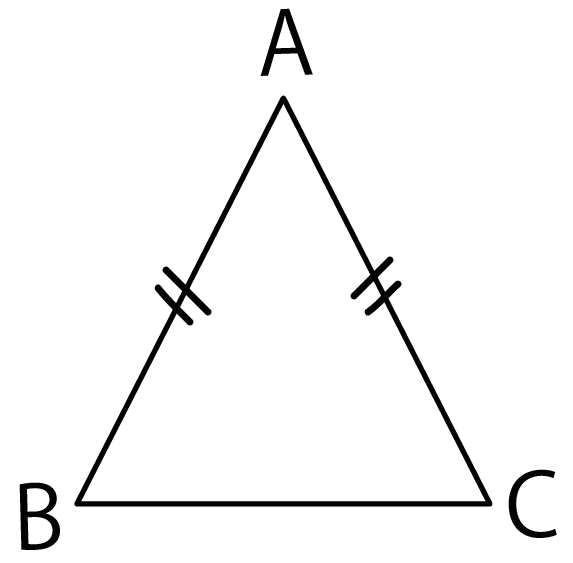
AB = AC である△ABCがあるとします。
この三角形が二等辺三角形であることを証明しなさい。
この問題のいっちゃんはじめに、
AB = AC である△ABCがあるとします。
ってかいてあるね。
じつはこの「AB = AC」はこの問題限定でいえること。
世界中に存在する△ABCのすべてが「AB = AC 」ってわけじゃあない。
AB = BCの△ABCもいるかもしれないし、
はたまた、
辺がぜんぜん等しくない△ABCもいるかもしれないね。
だから、
「AB = AC」は例題限定で正しいとしていることだから、
こいつは「仮定」なんだ。
どう？ちょっとスッキリしたかな？
結論は、
仮定をつかって正しいといえること
だよ。仮定がなければ結論をみちびけない。
たとえ、どんなに天才だとしてもね。
さっきの例題をみていみよう。
例題
AB = AC である△ABCがあるとします。
この三角形が二等辺三角形であることを証明しなさい。
この問題の仮定は、
AB = AC
だったね。
この仮定があるから、結論である「△ABCは二等辺三角形である」っていう結論がみちびけるんだ。
なぜなら、2つの辺が等しい三角形は二等辺三角形だからね。
もし、仮定がない問題だったら↓↓
例題
△ABCがあるとします。
この三角形が二等辺三角形であることを証明しなさい。
これはね、無理。無理だよ。
この問題には仮定がどこにもない。
△ABCが二等辺三角形であるって結論を導けるわけがないんだ。
「仮定」をつかってみちびける事実を「結論」という
ことをおぼえておこう。
「仮定」と「結論」は証明問題には必要不可欠なものさ。
なぜなら、証明とは、
与えられた仮定をつかって結論を論理的にみちびくこと
だからね。
「仮定」や「結論」がない証明問題はたとえるなら、
豚肉がない生姜焼きみたいなもんさ。
テスト前にもう一度復習してみてね。
そんじゃねー
Ken
こんにちは！この記事をかいているKenだよ。トイレットペーパーに助けられたね。
中学2年生になると、
数学の証明
がはじまる。
いままでの数学では、
図形の面積をだしたり、
xにyを代入したりすればよかったね。
だがしかし、証明はそーはいかない。
ぜんぜんタイプが違うんだ。
むずいというか、うざい。
そんなタイプの単元だ。
今日はやっかいな証明を攻略していくために、
証明とはなにか？？
ということを解説していくよ。
Wikipediaによると「証明」とは、
ある事柄が真理もしくは事実であることを明らかにすること
ってかいてあるね。
んでもこれじゃあ、よくわからない。
「数学の証明」って何を明らかにするんだろう？？
って疑問に思うはずだ。
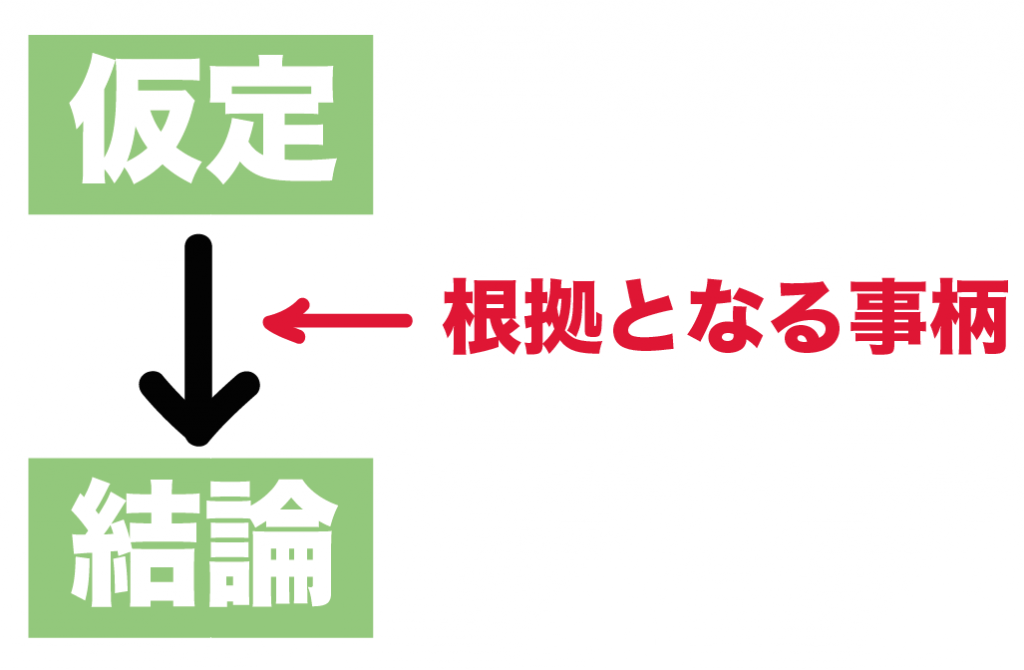
数学の証明とは簡単にいうと、
ある仮定（問題文であたえられている条件）が成り立つとしたときに
結論（証明のゴール）が正しいと明らかにすること
なんだ。
「仮定」から「結論」を明らかにするために、
いままでならってきた
「根拠となることがら」をつかっていくよ。
「根拠となることがら」ってたとえば、
三角形の合同条件とか、
対頂角は等しい
とかだね。
イメージでいうと証明は「カレー作り」に似ている。
仮定っていう「具材」を、
根拠のあることがらっていう「包丁」とか「鍋」で調理して、
結論っていう「おいしいカレー」をつくる
って感じ。
だから証明の問題では、
いかに多くのの「根拠となる事柄」（包丁や鍋）をつかって、
仮定（具材、ルー）から結論（カレー）をみちびくか？？
がポイントなのさ。
つまり、
「根拠となることがら」をたくさん暗記すると有利ってことになるね。
証明の例を紹介するよ。
つぎの例題をみてみて。
例題
つぎの三角形ABCと三角形DEFが合同であることを証明してください。
まず仮定（問題文であたえられている条件）
と、
結論（証明のゴール）
を整理してみよう。
この問題の仮定は、
だね。だって、問題文がそう言ってるからさ。
んで、
結論は、
だ。
この2つの三角形が合同だってことをいえばゴールってわけ。
証明は基本的に、
の順番でかいていけばいいよ。
実際に例題の証明をかいてみるとこうなる ↓↓
△ABCと△DEFにおいて、
BC = EF = 6 cm
角B = 角 E = 60°
角C = 角F = 70°
よって、
1組の辺とその両端の角がそれぞれ等しい
ので、
△ABC ≡ △DEF
となる。
っていう感じ。
っていう順番になっていることを確認してね^-^
証明ってはじめてきくと、むちゃくちゃむずそう。
でも大丈夫。
証明なんてただの「カレー作り」さ。
「仮定」っていう具材を、
「根拠となる事柄」をつかって調理して
「結論」っていうカレーをつくってあげよう！
そんじゃねー
Ken
こんにちは！この記事をかいているKenです。納豆は3パックにかぎるね。
直角三角形の合同を証明したい！！
ってときあるよね？
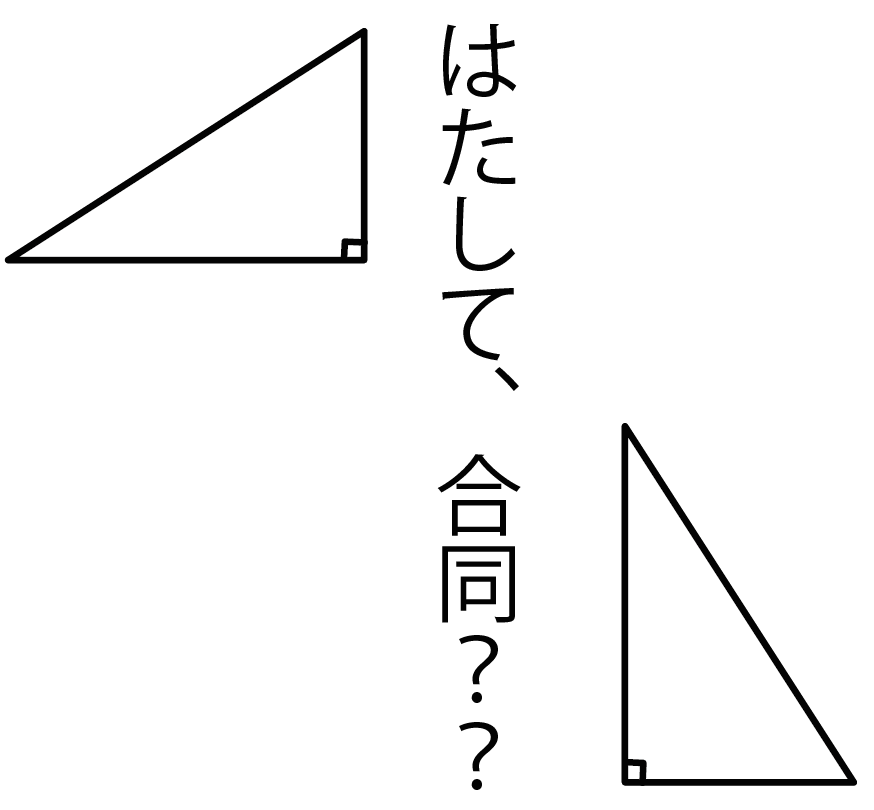
そんなときに便利なのが、
直角三角形の合同条件
だよ。
こいつは裏技みたいなものでチョー便利。
三角形の合同条件をつかわなくても、
直角三角形の合同が証明できちゃうからね。
今日はこの合同条件を2つ紹介していくよ。
よかったら参考にしてみてね。
直角三角形の合同条件はつぎの2つさ。
えっ。ぜんぜんピンとこないって？！
うん、そうだよね。
でもコイツらってむちゃくちゃシンプルで、ようは、
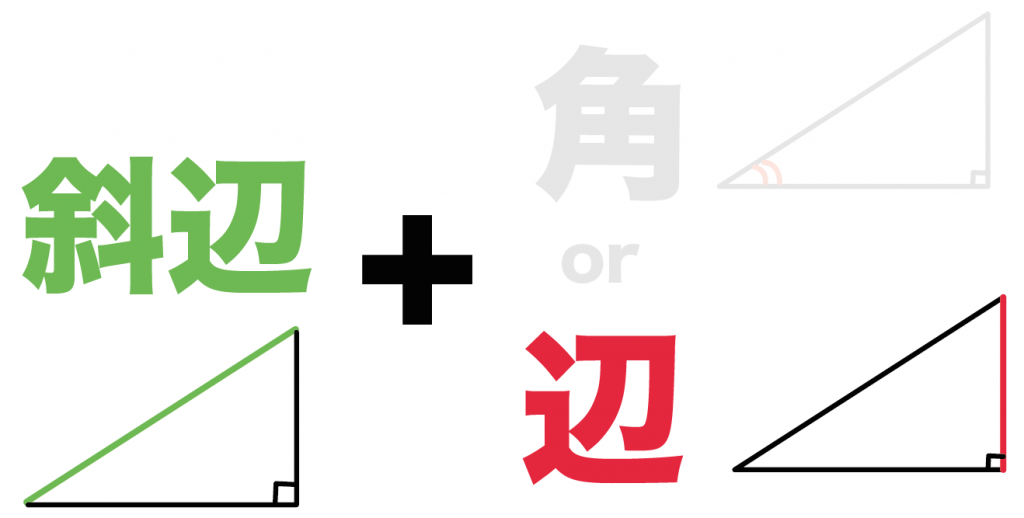
「斜辺」と「角 or 辺」が等しい直角三角形同士は合同である
ってことを言っているんだ。
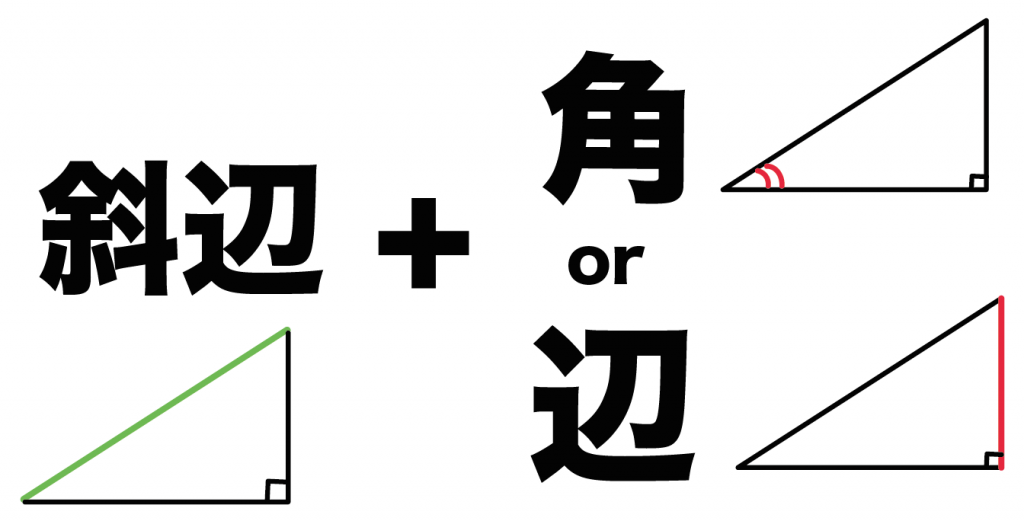
だから、
2つの直角三角形の「斜辺」が等しいってことがわかれば
合同を証明しやすくなるっわけさ。
それじゃあ、合同条件をくわしくみていくよ。
まずは、
斜辺
と、
1つの角（直角以外の角ね）
が等しい
という合同条件だ。
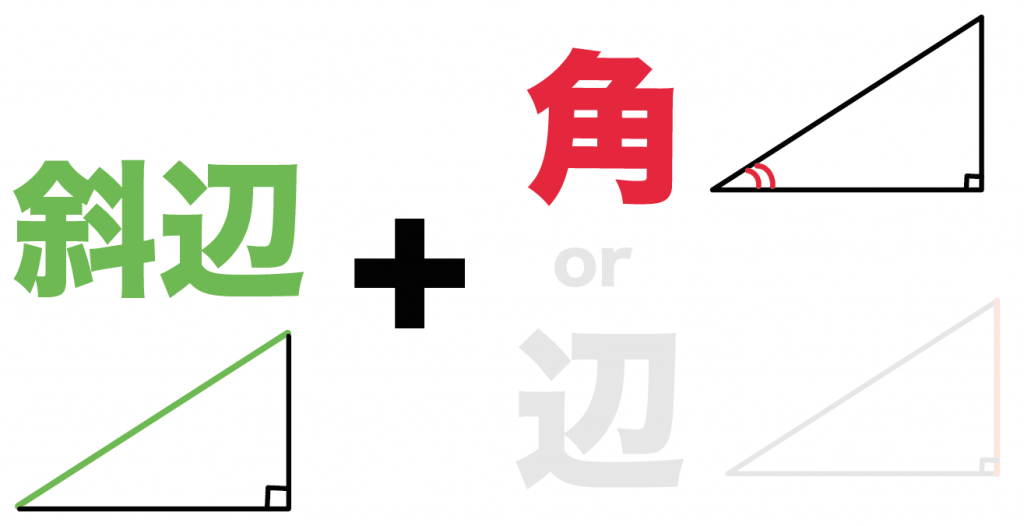
いちいち三角形の合同条件なんかに頼らなくても、
2つの直角三角形の合同がいえちゃうんだ。
たとえば、つぎの直角三角形ABCとDEFをみてみて。
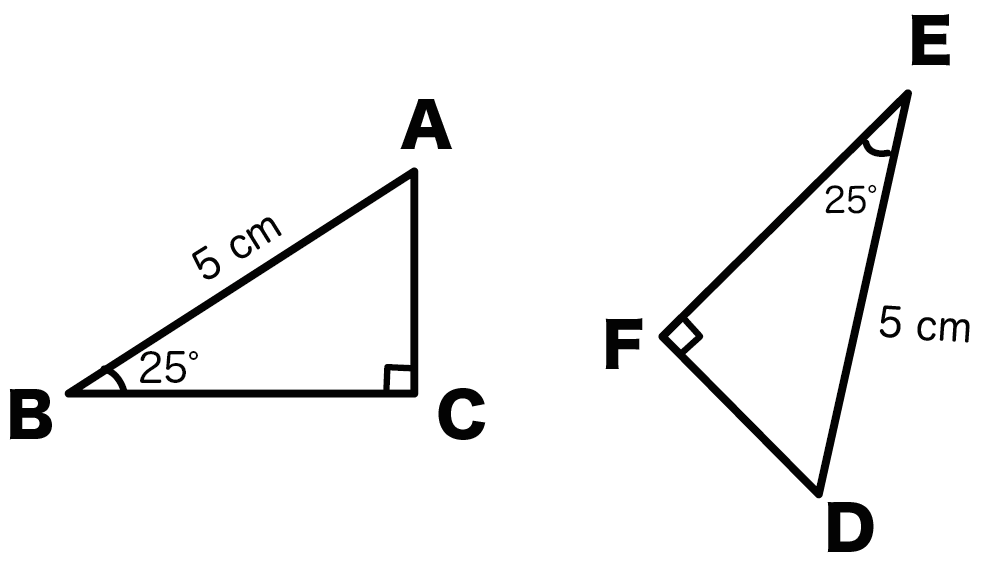こいつらはなんと、合同なんだ。
だって、
だからね。
よって、
斜辺と1つの鋭角がそれぞれ等しい
っていう合同条件をつかえば
△ABC ≡ △DEF
がいえるんだ。
つぎは、
斜辺
と、
1つの辺（斜辺以外のやつ）
が等しい
っていう合同条件さ。
たとえば、つぎの三角形GHIとJKLがいい例だね。
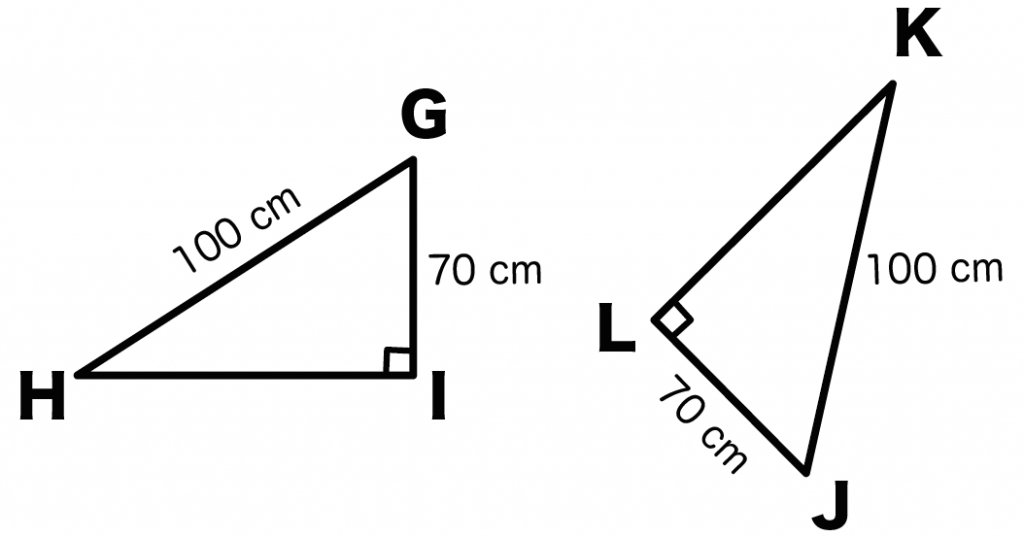
こいつらは合同な直角三角形だよ。
なぜなら、
からね。
こういうとき、
斜辺と他の1辺がそれぞれ等しい
っていう直角三角形の合同条件をつかえば、
△GHI ≡ △JKL
がいえるんだ。
ぶっちゃけ、
直角三角形の合同条件なんてなくても大丈夫。
正直、いきていける。
だけど、
直角三角形の合同条件はつかえば、
問題を解くスピードがはやくなるんだ。
ガンガン使っていこう！
そんじゃねー
Ken
こんにちは！この記事をかいているKenだよ。アントマンになりてえよ。
直角三角形には「斜辺（しゃへん）」っていう辺があるんだ。
たとえば、下の直角三角形ABCでは、
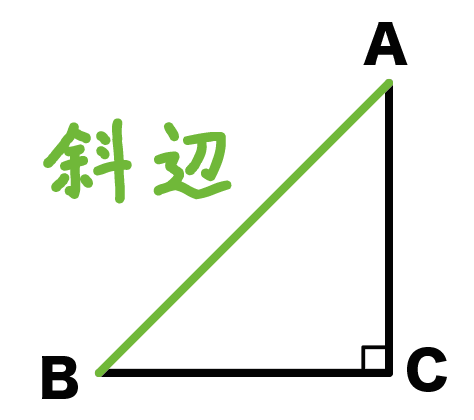
辺ABが斜辺だよ。
「斜辺」は、
「斜め（ななめ）」の「辺」
ってかく。
だから、
斜めになっている辺 = 「斜辺」
って思うかもしれない。
でもね、そいつはとんでもなく間違っている。
なぜなら、
斜めになっていない下の三角形ABCでも、斜辺はBCだからね。
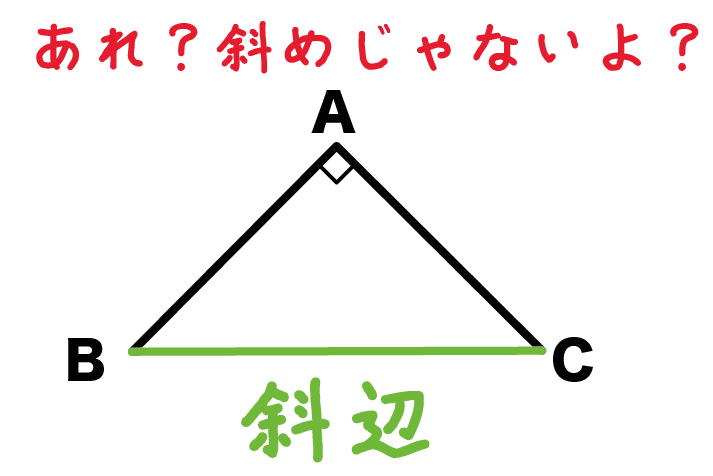
どうみても「斜」めになっている「辺」じゃない！？
どうして・・・
今日はこの「斜辺」を徹底的に解説していくよ！
よかったら参考にしてみて。
斜辺は「ななめ」な辺なんかじゃない。
教科書には、
直角に対する辺
ってかいてあるね。こいつをもう少しわかりやすくいうと、
直角（90°）からいちばん離れた辺のこと
なんだ。
いちばん遠いから、
直角と触れ合ってなんかない。
直角（90°）と縁がない辺のことなんだ。
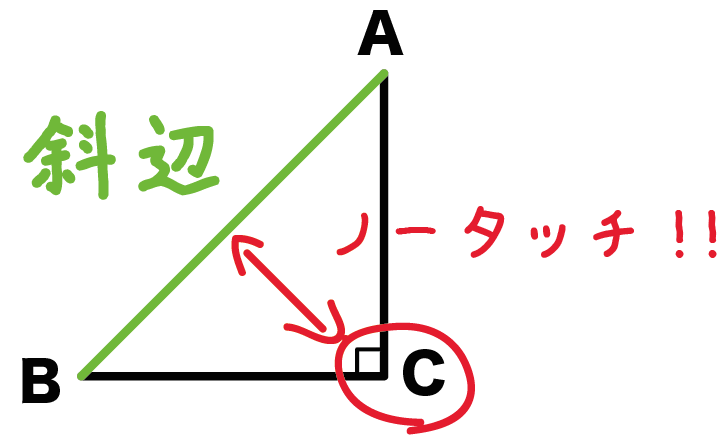
このさびしい辺のことを「斜辺」ってよんでいるんだ。
どう？？
ちょっと斜辺と仲良くなったかな？？
でもでも、でも。
でもだよ？？
直角三角形の斜辺が、
直角からいちばん遠い辺
って言われてもしっくりこないよね？？
てか、おぼえられねえよ！。
今日はせっかくだから、
とっておきの斜辺の覚え方を伝授しちゃおう。
覚え方はずばり、語呂をつかうよ。
チャンキーなフレーズでおぼえちゃおうってわけさ。
それは、
直角からいちばん遠くても「しゃーへん」わい！
だ。
えっ。ぜんぜん覚えられそうにないだって？？
ノンノン。
もう一回よみなおしてみて。
直角からいちばん遠くても「しゃーへん（斜辺）」わい！
そう、そうだよ。
この語呂は暗に、
直角からいちばん遠い辺のことを「斜辺」である
っていってるんだ。
これで斜辺をおぼえられたね！
直角三角形の斜辺って、
直角の向かいにある辺のこと。
つまり、直角からいちばん離れた辺のことなんだ。
テスト前によーく復習しておいてね。
そんじゃねー
Ken
こんにちは！この記事をかいているKenだよ。今日は布団をほしたね。
ある日突然、三角形が2匹出現したとしよう。
サトシならモンスターボールを用意するかもしれない。
ルフィならば仲間にしちゃうかもしれない。
でも、図形を勉強している中学生はこう思うはずだ。
どういう条件がそろえば合同になるんだろう？？
ってね。
この、
「三角形が合同になる条件」のことを数学界では、
三角形の合同条件
ってよんでいるんだ。
今日はその「合同条件」をわかりやすく説明していくよ。
よかったら参考にしてみてね。
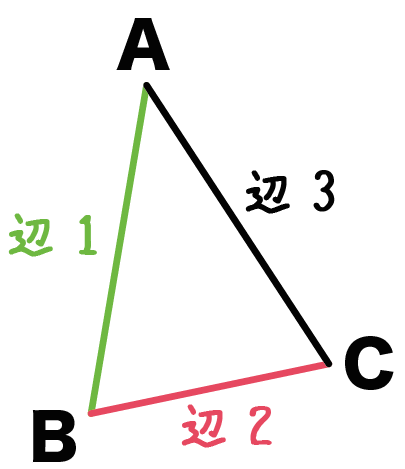
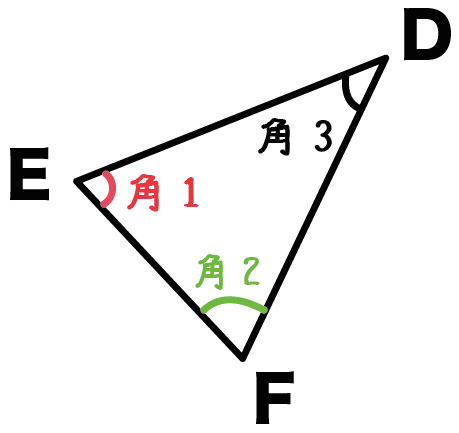
三角形には、
3つの辺と、
3つの角
があるよね？？
三角形の合同条件は、
こいつらの「どれ」が「どの位置」で等しくなっているか？？
によって3つにわけられるんだ。
つまり、
「どの辺」と「どの角」が等しいかによって、
合同かどうかジャッジできるってわけさ。
順番に確認していこう！
1つ目の合同条件は、
3組の辺がそれぞれ等しい
というものさ。
つまり、
2つの三角形の辺がそれぞれぜーんぶ等しい
ってわけだね。
たとえば、下のような三角形たちだ。
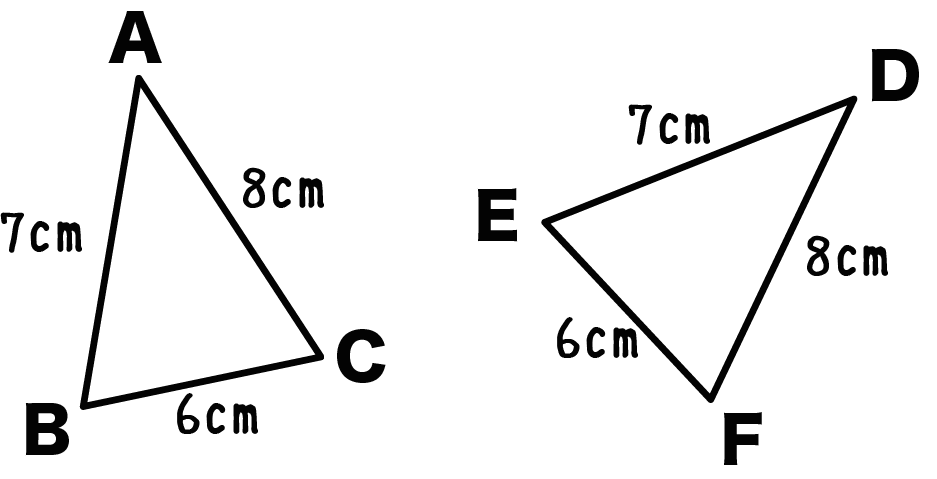
辺の長さはそれぞれ、
になっている。
よーくみてみると、
3つの辺がそれぞれ等しくなっているね。
これにより、
△ABC = △DEF
がいえるのさ。
つぎは、
2つの辺
と、
そいつらに挟まれた角
がそれぞれ等しいっていう条件だ。
たとえば、つぎの三角形ABCとDEFなんかがそれにあたる。
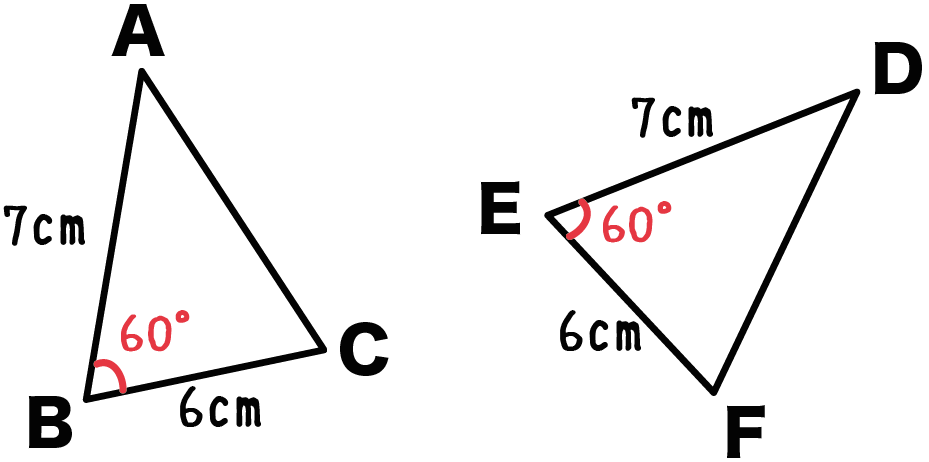
なぜなら、2組の辺が等しく、
その間にはさまれた角が、
等しいからね。
こいつらは、
2組の辺とその間の角がそれぞれ等しい
っていう合同条件をみたしている。
よって、
△ABC ≡ △DEF
ってことがいえるんだ。
最後は、
2つの角
と、
挟まれた1つの辺
が等しいという条件だ。
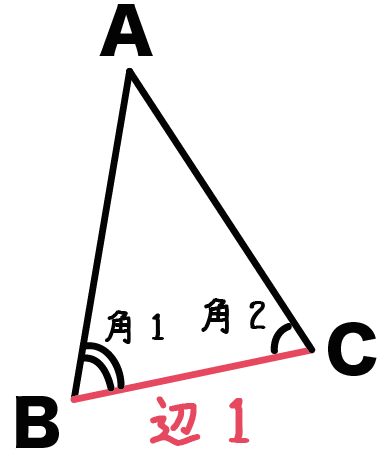
たとえば、つぎの三角形ABCとDEFみたいな感じでね ↓↓
こいつらは合同だよ。
なぜなら、
2組の角が等しく、
そいつらに挟まれた1組の辺が、
等しくなってるからね。
こいつらは、
「1組の辺とその両端の角がそれぞれ等しい」
っていう合同条件をみたしている。
よって、
△ABC ≡ △DEF
ってことがいえるんだ。
三角形の合同条件は、
の3つしかないよ。
合同の証明問題で必須になってくるから、
テスト前におぼえてみてね。
そんじゃねー
Ken
こんにちは！この記事をかいているKenだよ。ほっけ、焼いたね。
八角形の内角の和って気になるよね？？
8角形・・・
みてるだけで内角の和を求めたくなる。
うん、わかるよ、その気持ち。
今日はそんなときのために、
八角形の内角の和の求め方を紹介していくよ。
よかったら参考にしてみてね。
8角形の内角の和はチョー簡単。
もうね、一瞬だよ一瞬。
多角形の内角の和の公式をつかっちゃえばね。
念のために復習しよう。
n角形の内角の和を求める公式は、
180°×（n-2）
だったよね？？
八角形の内角の和を求めたいときは、
「n」に「8」をぶちこんでやればいいんだ。
すると、
180°×（n-2）
= 180°×（8-2）
= 180×6
= 1080°
になる！
つまり、八角形の内側の角をぜーんぶたしてやると、
1080°になるってことさ。
8角形の内角をa~hとしてやると、
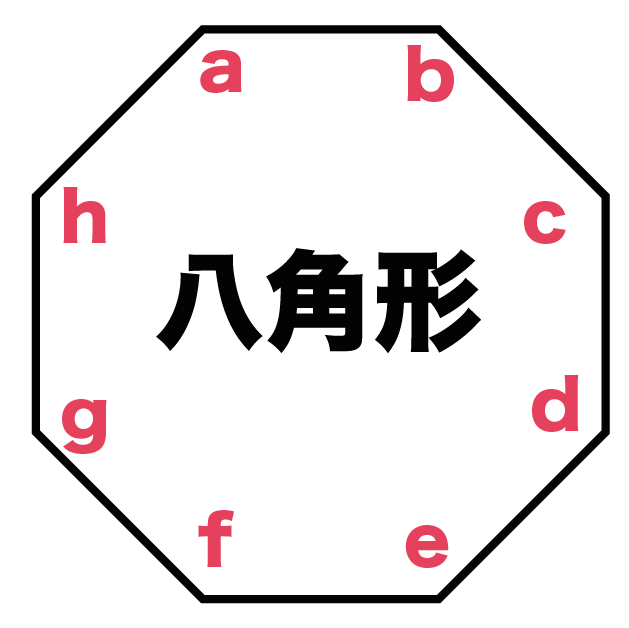
a + b + c + d + e + f + g + h = 1080°
になるんだ。
でもでも、
なんで多角形の内角の和の公式が使えちゃうんだろう？？
便利すぎてバチあたらねえかな・・・
って心配しはじめるはずだ。
その理由はずばり、
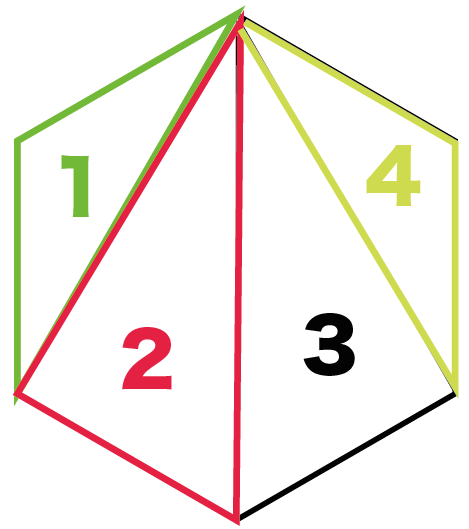
八角形の中に三角形が6個かくれているから
なんだ。
こんな感じで八角形に対角線をひいてみると、
1、2、3……6個の三角形をみつけられるはず。
そんで、
1つの三角形の内角の和は「180°」だったね？？
ってことは、
三角形が6個もふくまれている八角形の内角の和は、
180°を6倍して「1080°」になるってことさ。
八角形の内角の和をもとめたいときは、
180°（n-2）
という公式のnに「8」をいれちゃえばO.K。
計算すると1080°になるから、
8角形の内角の和は？？
って問いつめられたらドヤ顔で
1080°ですが？なにか？
答えてやろう！
そんじゃねー
Ken
こんにちは！この記事をかいているKenだよ。鼻呼吸したいね。
図形が合同のときってたまにあるよね。
そんなとき便利なのが、
記号をつかって合同をしめすこと
だ。
じつは、
≡
を使えば、
「2つの図形が合同である」といえるんだ。
たとえば、
図形1と図形2が合同のとき、
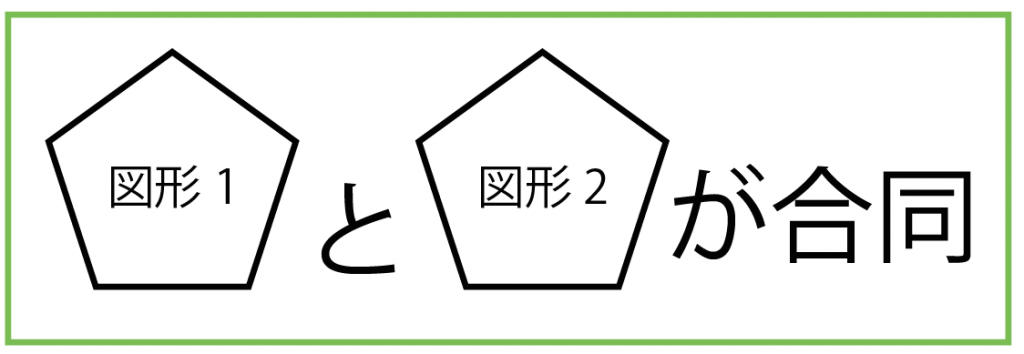
コイツらを「≡ 」でむすびつけてやる。
すると、
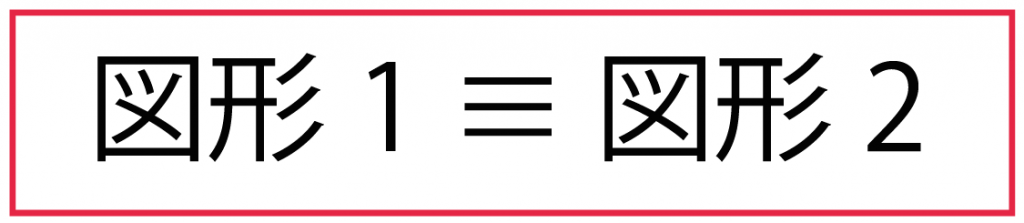
図形1 ≡ 図形2
みたいになるよ。
合同をあらわせるなんてむっちゃ便利じゃん！
すげえよ！！
・・・・・・・・
って祝いたい。
だけれども、一つだけ問題点があるんだ。
それは、
合同の記号をおぼえるのがムズいってことさ。
「合同」と「≡」っていう奇妙な記号をむずびつけられる？？
答えはノー、だ。
誰もが四苦八苦するはず。
そこで今日は、
合同の記号の覚え方を2つ伝授するよ。
よかったら参考にしてみてね。
まずは王道の語呂をつかう方法だ。
チャンキーなフレーズで耳にやきつける方法さ。
合同の記号をおぼえるための語呂はずばり、
あの三兄弟はほぼ合同だ！
だよ。
えっ。
わけがわからないって？？
語呂の、
あの三兄弟はほぼ合同だ！
「三」と「合同」に注目してほしいんだ。
そう、そうだよ。
これはまさに「合同」の記号は「≡」といってるようなもんだね。
「三」を「≡」におきかえてやればいいんだ。
3つ子の三兄弟をイメージできれば、
合同の記号を忘れることはないね。
2つ目はチョーマジメな覚え方だ。
なんと、合同な図形の性質をつかっておぼえていくよ。
合同な図形にはつぎの2つの性質があったね。
つまり、合同な図形たちには2つの「＝」関係があるってことさ。
じつは、
この2つの「＝」マークが合体すると、合同の記号「≡」みたいになるんだ。
えっ。
よくわからないって？？
そうだな、ゆっくり近づけていこう。
おや、＝記号のようすが？
トゥるトゥル、
トゥートゥー、
トゥートゥー、
トゥートゥー、
トゥリーン、
おめでとう！ 2つの＝は合体して≡になったね！
・・・・・・
って感じで、
2つの＝記号をサンドイッチしたら、
≡になる
とおぼえておこう！
合同の記号の覚え方はどうだった？？
困ったときは、
を思い出してみよう。
きっと「≡」の記号が頭に浮かんでくるはず。
そんじゃねー
Ken
こんにちは！この記事をかいているKenだよ。やっぱり炙りソーセージうめえよ。
中2数学では、
「三角形の合同（ごうどう）」
について勉強していくよ。
合同なんてふだん耳にしない言葉だから、
そもそも合同ってなによ？？
って思っちゃうよね？
そこで今日は、
三角形の合同の意味をカンタンに解説していくよ。
よかったら参考にしてみてねー
教科書をみてみると、合同とは、
ぴったりと重なる図形同士のことを合同な図形という。
って書いてあるね。
つまり、姿カタチも大きさも同じってことなんだ。
たとえば、下の三角形ABCとDEFが合同だとしよう。
合同な図形はぴったりと重なるはずだから、
2つの三角形をうまくずらして近づけてみよう。
ほい、
ほい、
ほい！っと、
ぴったりと重なったね。
つまり、合同は形が似ているだけじゃダメなんだ。
たとえば、イチョウの木から落ちた葉っぱがあったしよう。
色も大きさも雰囲気も香りも似ているんだけど、
コイツらはたぶん、合同じゃない。
完ぺきに姿形が同じでぴったりと重ならないからね。
ここまでしつこいぐらい、
合同とは「ピッタリ重なる」状態のことだよ。
ってドヤってきたね。
でも、勘の鋭いヤツはこう思っているはずだ。
「ピッタリ重なる」って具体的にどういうこと？？
ってね。
じつは合同な図形同士は、
2つの「合同な図形の性質」を持っているんだ。
合同な図形同士には、
対応する線分の長さが等しい
っていう性質があるよ。
たとえば、さっきの三角形ABCとDEFをみてみよう。
対応する線分って、ぴったり重ねたときに重なりあう線分のことさ。
だから、
だね。
もし、三角形ABCとDEFが合同なら対応する線分が等しいことになる。
よって、
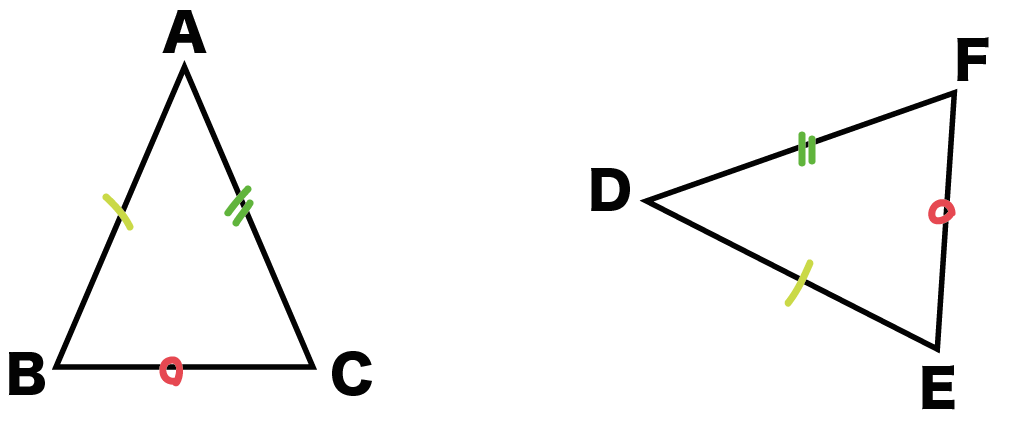
になるはずだ。
合同な図形はもう1つ性質をもっているよ。
それは、
対応する角の大きさが等しい
ってことさ。
あ、対応する角は
ピッタリと重ねたときに重なる角同士のことね。
三角形ABCとDEFが合同だしよう。
対応する角たちは、
だ。合同な図形の性質に「対応する角が等しい」ってやつがあるから、
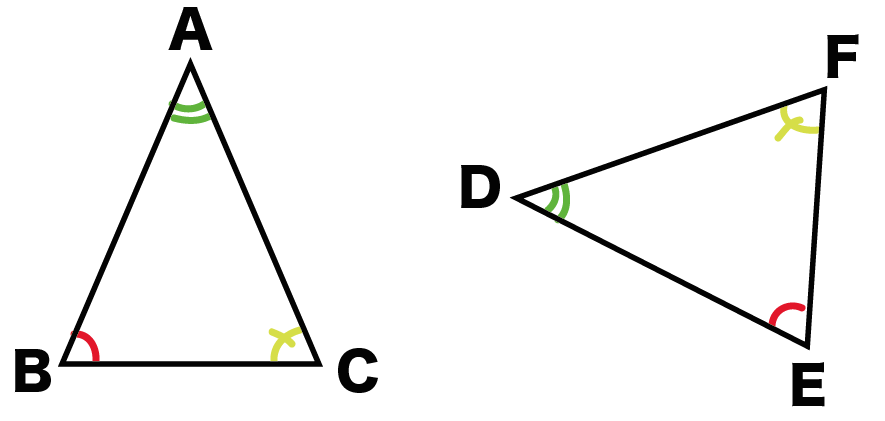
がいえるんだ。
「ピッタリ重なる（合同）」とどうなるのよ？ぶっちゃけ？？
ってきかれたら、
ドヤ顔で、
って答えてやろう。
これでクラスで人気者まちがいなしさ。
そんじゃねー
Ken
こんにちは！この記事をかいているKenだよ。カメラレンズ買っちゃったよ。
六角形の内角の和
を求めたいときあるよね？
うん、わかるわかる。
今日は、そんなときに参考にできる、
六角形の内角の和をもとめる公式
をわかりやすく解説していくよ。
これなら3秒で内角の和が計算できちゃうぜ。
を使うだけでOK。
n角形の内角の和って、
180×(n-2)
で計算できたよね？
今回は、6角形の内角の和を計算したいので、
nに「6」を代入しよう。
すると、
180×(n-2)
= 180×(6-2)
= 720°
になるね！
つまり、
六角形の内角をぜーんぶたしたら「720°」になるってことさ。
むちゃくちゃ便利な公式だけれども、
なぜ六角形の内角の和が計算できちゃうんだろう？？
ちょっと不思議だよね。
じつは、
六角形に三角形が4つ含まれているからなんだ。
1つの三角形の内角の和は180°。
ってことは、
180°を4倍して、
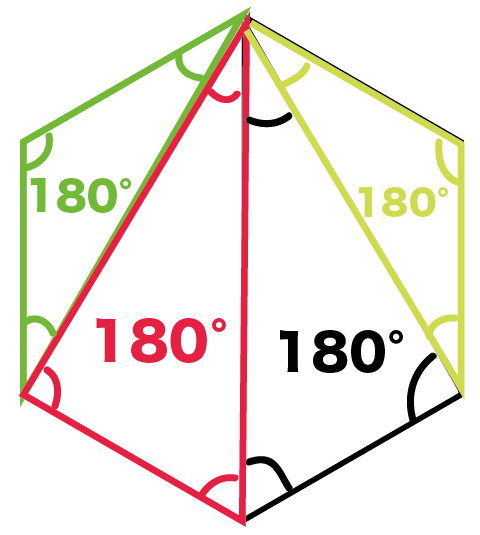
180°× 4
= 720°
が六角形の内角の和になるってわけさ！
公式をつかって問題を瞬殺するのもいいけど、
改めてなぜ？？ってことを振り返ってみてね。
六角形には4つも三角形がかくれていて、
1つの内角は180°だから計算できちゃうんだ。
テスト前にもう一度復習してみてね！
そんじゃねー
Ken
