こんにちは!この記事をかいているKenだよ。腹巻きは、神だね。
平行四辺形ってなんだろう??
響きはかっこいいし、
形も悪くない。
でも、正直、
よくわかっていないのが現実だ。
そこで今日は、
平行四辺形の定義をわかりやすく解説していくよ。
よかったら参考にしてみて。
平行四辺形の定義は、ずばり、
2組の向かいあう辺が、それぞれ平行な四角形
だ。
たとえば、
平行四辺形ABCDがいたとしよう。
このとき、
向かい合う辺である、
たちはそれぞれ平行になってるんだ。
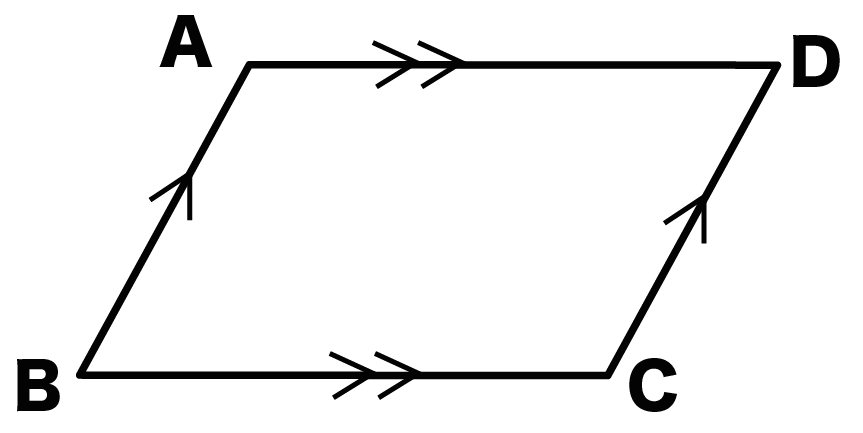
つまり、
ってわけだね。
えっ。
ぴんとこないって??
そうだなあ、ようするに、
ABとCDをのばしまくっても交わらないし、
ADとBCをのばしまくっても交わらないんだ。
こんな感じで、
2組の向かいあう辺が、それぞれ平行な四角形
が平行四辺形なのさ。
だから、
「辺が平行ではない四角形」は平行四辺じゃない。。
1組の辺だけ平行でもダメ。
そいつは、平行四辺形じゃない。
ただの台形だ。
2組の辺が平行でも、
そいつが「六角形」だったら意味がない。
ちょっと変わった六角形さ。
平行四辺形なんかじゃああない。
こんなやつらじゃなくて、
2組の向かいあう辺が、それぞれ平行な四角形
が平行四辺形だってことをおぼえておこう!

平行四辺形の定義はシンプル。
2組の向かいあう辺が、それぞれ平行な四角形
が定義なんだ。
まずは定義をがっつりおさえよう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。毛布、ほしいね。
平行四辺形の対角線の長さの問題
ってむずい。
でも、
求め方を知っておけば大丈夫。
ドヤ顔で答えられるよ。
たとえばつぎの例題をみてみて。
例題
平行四辺形ABCDにおいて、AB = CD = 6cm、AD = BC = 10cmとする。
角A = 120°のとき、対角線ACの長さを求めよ。
今日はこの、
平行四辺形の対角線の長さを求める問題を3ステップで解説していくよ。
よかったら参考にしてみてね。
例題の、
例題
平行四辺形ABCDにおいて、AB = CD = 6cm、AD = BC = 10cmとする。
角A = 120°のとき、対角線ACの長さを求めよ。
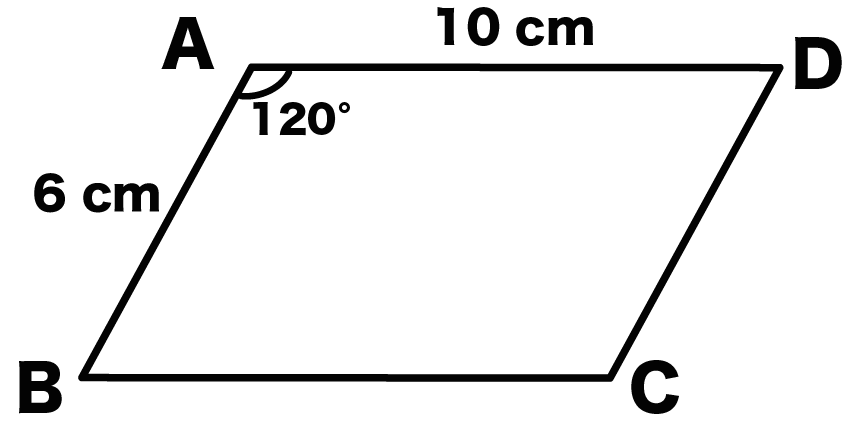
をときながら解説していくよ。
つぎの4ステップでとけちゃうんだ。
平行四辺形の頂点から垂線をおろそう。
角度がわかっている頂点から垂線をひいてみて。
例題でいうと、角Aから垂線をひくよ。
だって、
角A = 120°
って角度がわかってるからね。
AからBCに垂線をおろすと、
だいたいこんな感じになる↓↓
垂線とBCの交点をHとしよう。
平行四辺形の角度を求めよう。
平行四辺形の性質の、
2組の向かいあう角は、それぞれ等しい
を使うよ。
2組の向かいあう角は、それぞれ等しい
から、
角A = 角C = 120°
ってわかる。
ってことは、
残りの角Bと角Dは、
角B = 角D = (360°- 240°)÷2 = 60°
になるはずだ。
平行四辺形の高さを求めてみよう。
例題でいうと、
線分AHの長さだね。
高さAHの長さを求めるために、
直角三角形ABHに注目してみよう。
この直角三角形は、
の角度をもっているね。
ってことは、この直角三角形の比は、
1: 2: √3
になるはずだ。
よって、
になるね。
いよいよ最後のステップ。
三平方の定理で「対角線の長さ」をもとめよう!
例題では、
直角三角形ACHに注目してくれ。
ここでは、
AHとCHで三平方の定理をつかって、
対角線AC の長さを求めていくよ。
Step3より、
だね。
よって、
AC = √(AH^2+CH^2)
= √[(3√3)^2+ 7^2]
= 2√19
になる。
おめでとう!
平行四辺形の対角線の長さを計算できたね!
平行四辺形の対角線の求め方はムズい。
だけれども、
直角三角形をうまくつくれば大丈夫。
あとは三平方の定理を使うだけさ。
がんばって計算してみてね。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。筆箱ほしいね。
二等辺三角形の作図問題ってたまにでる。
こんな感じのやつね↓↓
例題
AB = AC = 6 cm、BC = 4cmの二等辺三角形ABCを作図しなさい。
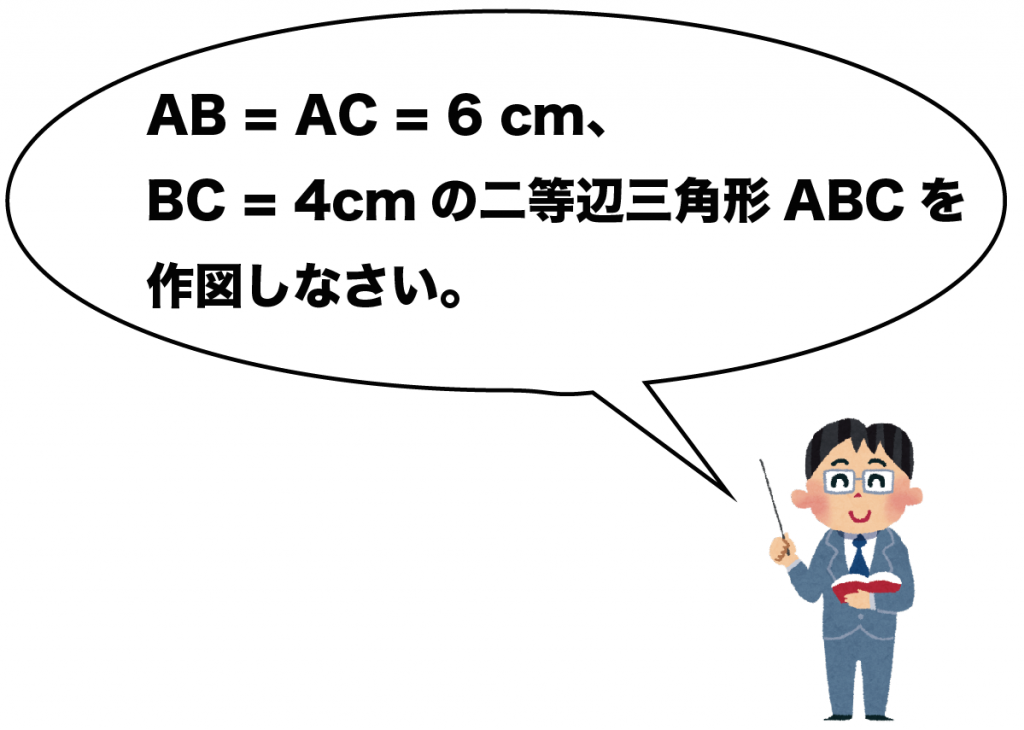
この問題はぶっちゃけめんどい。
作図はセンスとわれそうだし、
コンパス使わなきゃいけないし。。
今日はそんな問題を瞬殺するために、
二等辺三角形の書き方・作図方法を3ステップで解説していくよ。
よかったら参考にしてみて。
作図で用意するものは、
の2つ。
これで作図できちゃうんだ。
例題をといてみよう。
例題
AB = AC = 6 cm、BC = 4cmの二等辺三角形ABCを作図しなさい。

二等辺三角形の「底辺」をかこう。
使うのは、
定規。
きみだけだ。
定規で、
底辺の長さの直線をひけばいいんだ。
例の底辺の長さは、
4cm
だね??
だから定規で、
すーーーっと4cmの底辺BCをひいてあげよう。
これが第1ステップさ!
つぎはコンパスを使うよ。
こいつをつかって、
ちょびっと円をかいてみよう!
円の中心は「底辺の両端」、
半径は「底辺以外の辺の長さ」にするよ。
例題では、
底辺以外の長さは6cmだったよね??
だから、
まずコンパスの脚を6cmに広げてみよう。
脚を6 cmにひろげたままで、
コンパスの針を頂点Cにもってきて。
んで、
ちょっと円をかいてみるんだ。
チョビ円のできありさ。
あとは同じことを点Bでもやるんだ。
つまり、
コンパスの脚を6 cmにひらいたまま、
点Bを中心にチョビ円をかくってこと。
チョビ円がふたつできればオーケー。
第2ステップ終了さ。
「チョビ円の交点」と「底辺の両端」をむすぼう!
チョビ円の交点をAとするよ。
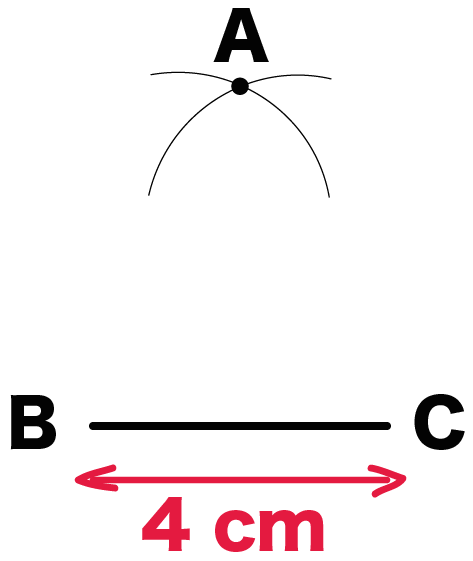
を定規でむすべばいいんだ。
ABとACの長さは6cmになっているはず。
なぜなら、
チョビ円の半径を6cmにしたからね。
おめでとう!
これで二等辺三角形の作図もマスターだね。
二等辺三角形の書き方はどうだったかな??
基本的には、
とおなじ!
二等辺三角形の作図では、
「底辺」と「等しい2辺」の長さが違う
ってことに気をつければ大丈夫。
コンパスの脚の長さに注意してね^-^
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。鮭を2匹やいたね。
正三角形を作図したい。
そんなときってたまに、ある。
宿題にでてしまったり、
正三角形を落書きしたくなったりしたときにね。

今日はそんな身近な、
正三角形の書き方・作図方法を3ステップで解説していくよ。
よかったら参考にしてみて。
使うものは「コンパス」と「定規」。
こいつらがあれば、
どんな正三角形だってかくことができる。
むちゃキレイにね。
今回はいっしょに、
1辺が6cm の正三角形ABCをかいていこう!
書き方はつぎの3ステップさ。
まず使うのは、
定規、きみだ。
定規をつかって、
正三角形の1辺をひいてみよう。
定規に沿って、
すーーーっと線をかくだけでいいんだ。
1辺が6cmの正三角形をかきたいんだったら、
6cmの線分をかくだけさ。
線分の両端をA・Bとおこうか。
これが第一ステップさ!
つぎは、コンパスの出番。

コンパスで、
半々円を2つかいてやろう。
半半円とは、半円の半分のやつのこと。
つまり、
1つの円の4分の1サイズのやつさ。

そいつを、
さっきかいた線分の両端を中心にして、
かいてやればいいんだ。
1辺が6cmの正三角形のときも同じ。
まず、線分の端のAに針をおこう。
んで、
コンパスの鉛筆を逆のBにおく。
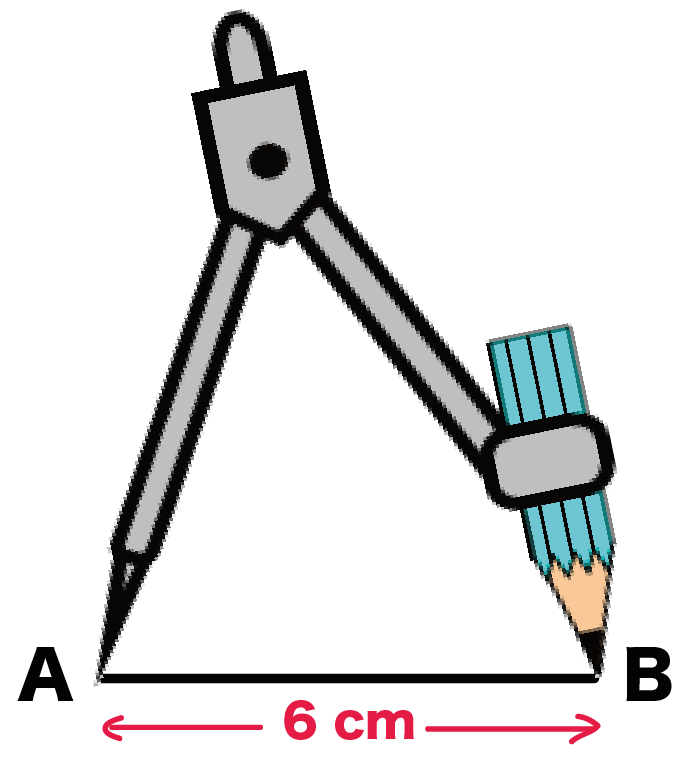
そして、
半半円をかく。
そのつぎは、逆のBにコンパスの針をおいて、
鉛筆をAにおく。
そして、
半々円をかく。
これで第二ステップは終了さ!
あとは、半半円の交点と線分の両端をむすぶだけ!
半々円たちの交点をCとしよう。
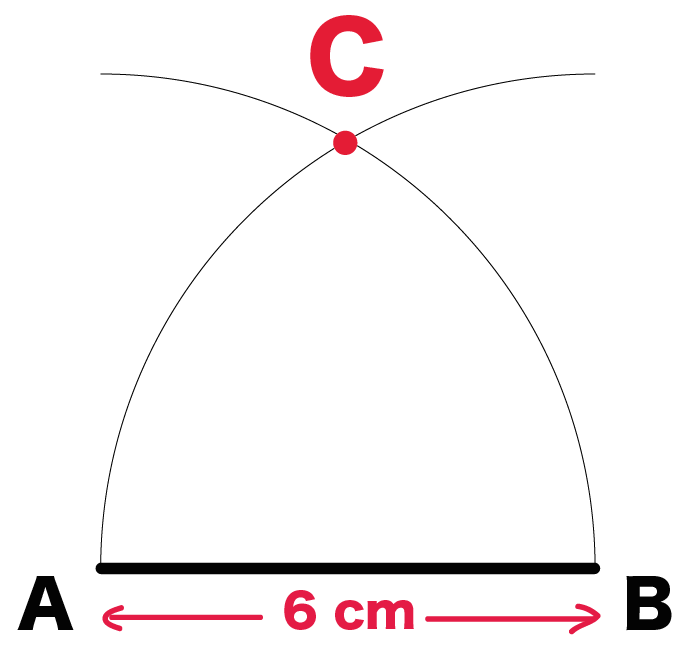
この交点Cと、
両端のA・Bを直線でむすべばいいんだ。
定規でむすんでみると、
あら!
正三角形ABCのできあがり!
正三角形をかきたい。
そんなときは、
コンパスと定規をさがそう。
そして、
使おう。
あとはゆっくり作図すれば大丈夫。
何度も練習してみてね。
そんじゃねー
Ken
こんにちは!この記事をかいてるKenだよ。白米、最高。
正三角形の角度ってシンプル。
内角の1つの大きさは、
60°
なんだ。
しかも、ぜーーーんぶの内角が60°になっているよ。
先生に、
正三角形の角度はいくつ??
ってきかれたら、
60°ですがなにか??
っていえばいいよ。

今日はもう一歩ふみこんで、
正三角形の角度の求め方
を勉強してみよう。
なんで角度が60°になるんだろう・・・・
っておもったら読んでみてー
なぜ、正三角形の角度が60°になるのか??
をみていくよ。
例として、つぎの正三角形ABCをとりあげる。
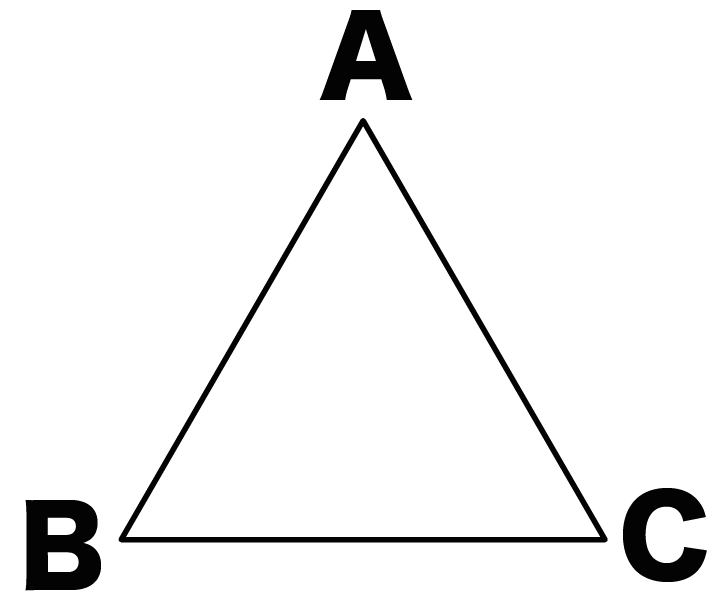
3ステップで角度を求められるよー
1つの角度を文字でおこう。
正三角形ABCでは、
角B = a
としてみたよ。
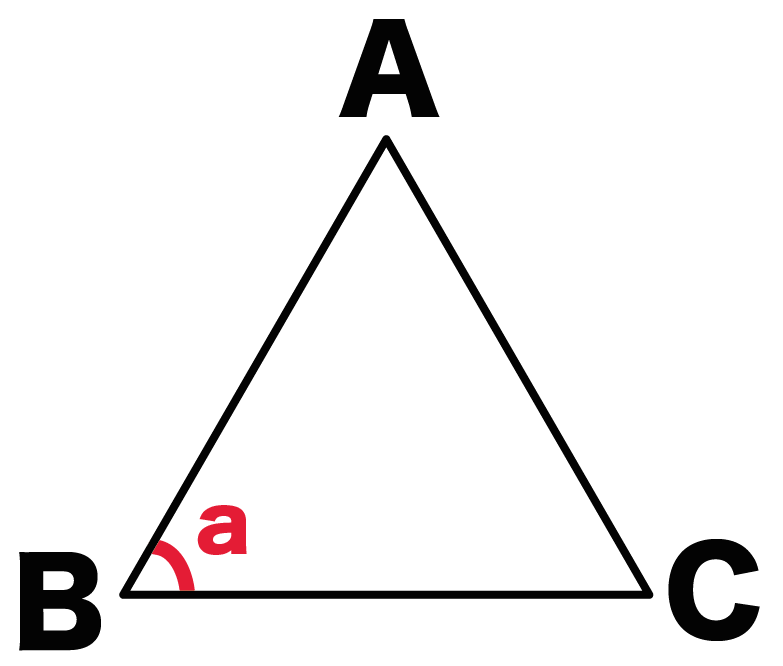
文字はなんでもいいよ。
bでもcでもxでもね。
つぎは二等辺三角形の性質である、
底角が等しい
という性質を使うよ。
正三角形の定義は、
3つの辺がすべて等しい三角形
だったよね?
ってことは、
2つの辺が等しい「二等辺三角形」でもあるわけだ。
例の正三角形ABCでいうと、
AB = ACの二等辺三角形ってことだね。
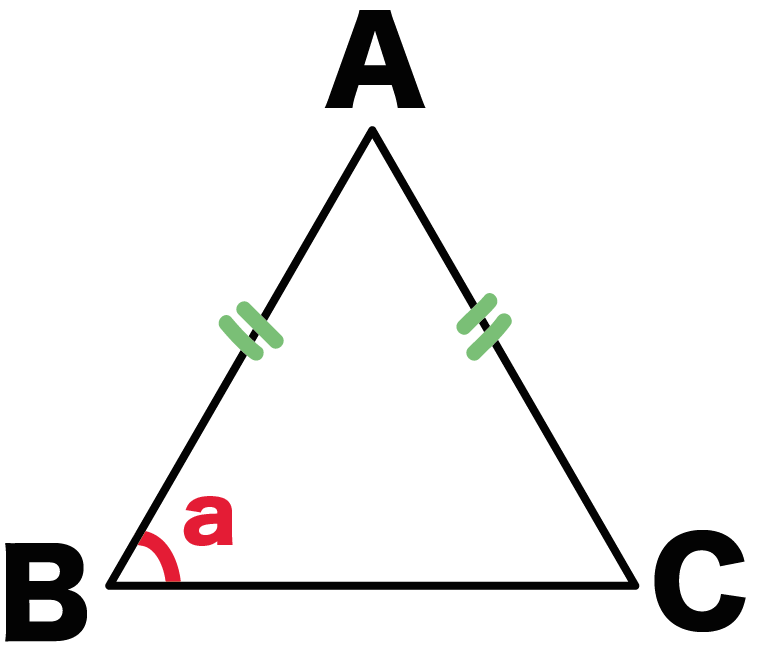
底角は等しい
という二等辺三角形の性質をつかってやれば、
角B = 角C = a・・・・(1)
であることがわかる。
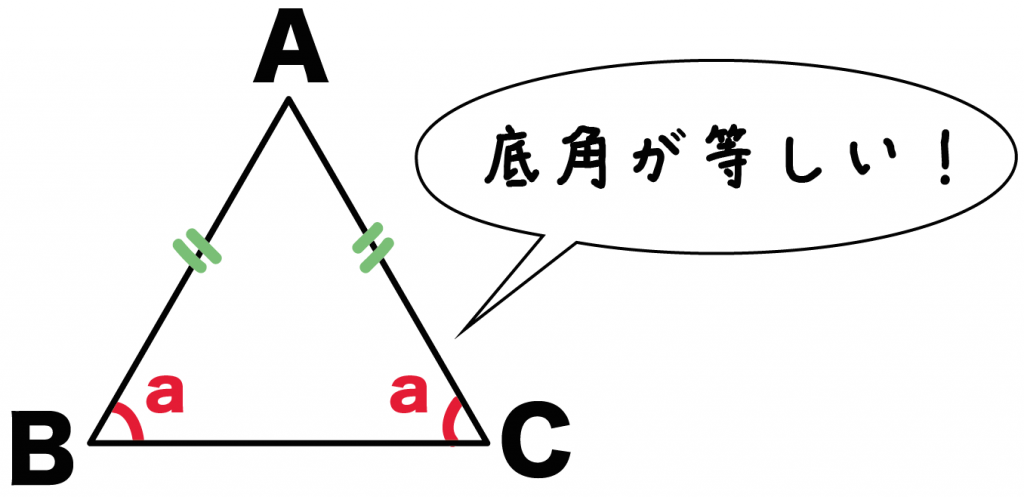
おなじように、
正三角形ABCは、
AC = BCの二等辺三角形でもあるわけだ。
だから、ここでも底角が等しいことを使ってやれば、
角A = 角B = a ・・・・(2)
ってことがいえるね。
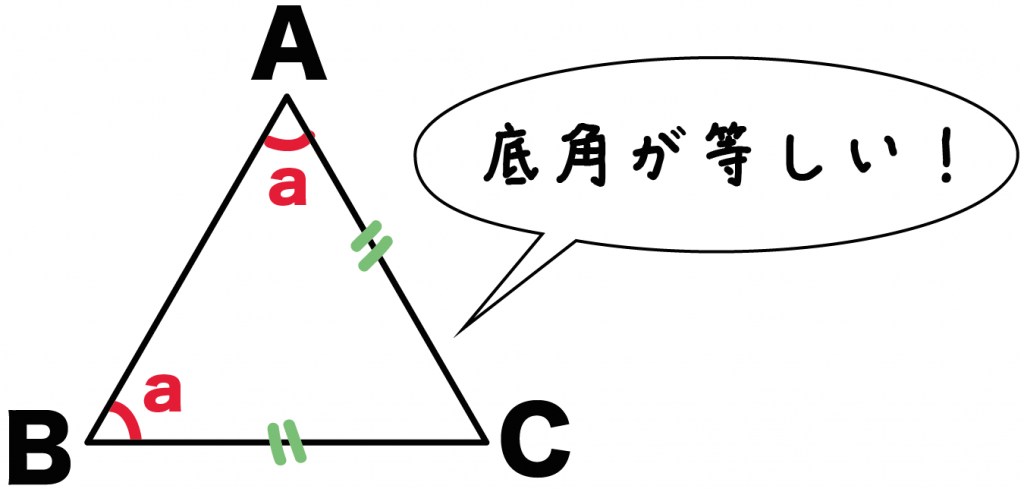
(1)、(2)より、
角A = 角B = 角C = a
ってことがいえるんだ。
だから、
ぜーーんぶ角度が同じってことになるのさ。
正三角形の角度はぜーんぶ等しい。
ってことは、
1つの角度は、
内角の和を3でわったもの
ってことだ。
三角形の内角の和は180°なので、
180を3でわってやると、
180÷3
= 60°
になるね!
よって、正三角形の1つの角度は「60°」になるんだ。
角度の求め方で大事なのは、
正三角形を二等辺三角形としてあつかえるか?
だ。
底角が等しいことをつかって、
問題をといていこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。チワワと遊びたいね。
数学を勉強していると、
正三角形(せいさんかくけい)
ってよくでてくるね??
名前はカッコイイけど、何者なんだろう・・・
って思うはず。
そこで今日は、
正三角形の定義をわかりやすく解説していくよ。
よかったら参考にしてみてね。
教科書によると、正三角形の定義とは、
3つの辺がすべて等しい三角形
ってかいてある。
つまり、
3つの辺がぜーーーーーんぶ等しい三角形だ!
たとえば、三角形ABCがあったとすると、
ぜーんぶの辺である、
がぜーーーーーんぶ等しいとき、そいつは正三角形なんだ。
つまり、
AB = BC = AC
のときだね。
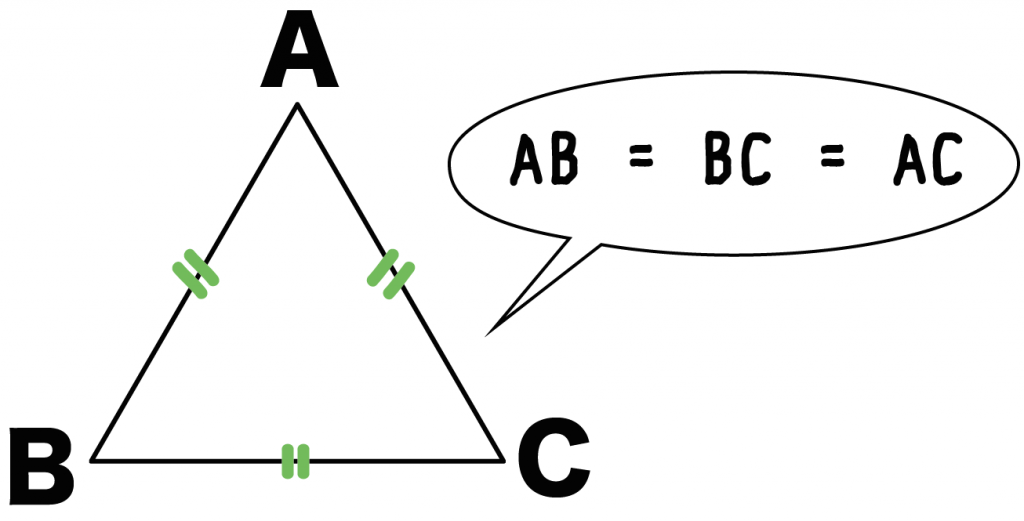
だから、
二辺が等しいだけだったら正三角形じゃないし、
ぜーーんぶ辺が等しくても
五角形だったら正三角形じゃないんだ。
あくまでも、
3つの辺がすべて等しい三角形
が正三角形ってことをおぼえておこう!
おぼえてほしいことが1つある。
それは、
正三角形は二等辺三角形の1種
ってこと。
つまり、
正三角形は二等辺三角形でもあるわけさ。
なぜなら、
3つの辺が等しい三角形ってことは、
2つの辺も等しいっていえるからね。
二等辺三角形の種類の中に、
正三角形っていう特別なヤツがいる
っていうイメージ。

だから、
正三角形ならば二等辺三角形である
っていえるけど、
二等辺三角形ならば正三角形である
とはいえないね。
たとえるなら、
「プードル犬」と「トイプードル」みたいな関係だね。
プードルが「 二等辺三角形」で、トイプードルが「 正三角形」にちかい。
トイプードルはプードルっていう犬の種類のなかの1つだよね??
ただ、プードルっていう犬にはトイプードル以外もいる。
スタンダード・プードルとか、
ミディアム・プードルとかね。
だから、
トイプードルをプードルってよんでも問題ないけど、
プードルをトイプードルをよんでは間違いだ。
これは、
二等辺三角形は正三角形ではないけど、
正三角形は二等辺三角形である関係といっしょだね!
正三角形の定義はシンプル。
ぜーんぶの辺が等しい三角形のことをいうのさ。
テスト前によーく復習しておいてね。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。
中2数学を勉強していると、
逆(ぎゃく)
っていう言葉がでてくるね。
日常生活で「逆」ってことばはよく使う。
マリオカートをプレイすると、
おまえ、「逆」走してね??
とかよく言うでしょ?
その「逆」だよ。
今日はその、
「逆」が数学ではどういう意味があるのか??
をわかりやすく解説していくよ。
よかったら参考にしてみてね。
数学の「逆」とはずばり、
「あることがら」の「仮定」と「結論」を入れ替えたもの
さ。
たとえば、つぎのことがらがあったとしよう。
AならばBである
ってやつね。
こいつの逆をつくってみよう。
仮定がA、結論がBだね。
こいつらを入れ替えてやると、
BならばAである
ってなる。
たとえば、
馬ならば動物である
っていう「ことがら」があっとしよう。
このとき、
だね。
だから、逆をつくるために、
仮定と結論をいれかえてやると、
動物ならば馬である
ってなるね。
逆をつくるのは簡単だね。
だって、
「仮定」と「結論」を入れ替えるだけだから。
ただ、数学で逆をつくるときに知っておいてほしいのは、
あることが正しくても、その逆は正しいとは限らない
ということさ。
つまり、正しいことがらの逆をつくってみたけど、
逆をつくってみたら正しくなくなっちゃった・・・
ってことがあるってこと。
たとえば、さっきの馬の例をみてみよう。
馬ならば動物である
っていうことがらはどうだろう??
こいつはただしそうだね。
だって、馬は動物だから。
だけれども、その逆をみてほしい。
動物ならば馬である
って正しくないよね??
だって、動物は馬だけじゃないから。
ライオンだって、
ねずみだって、
牛だっている。

したがって、
馬ならば動物である
の逆は正しくないんだ。
最後に、数学の逆の例を2つみてみよう。
平行線の性質は逆にしても正しいよ。
平行線の性質って、
2つの直線が平行ならば、同位角は等しい
だったね。
たとえば、
lとmが平行だったら、同位角のaとbが等しいってやつさ↓↓
じつは、この「平行線の性質」ということがらは、
逆も正しいといえるんだ。
つまり、
同位角が等しいならば、2つの直線が平行である
っていえるんだ。
たとえば、さっきの例でいうと、
同位角のaとbが等しかったら、直線lとmが平行になっている
ってことがいえるんだ。
合同な図形の性質は逆にしたら正しくなくなっちゃう。
合同な2つの図形には、
対応する角の大きさが等しい
っていう性質があったよね?
2つの図形が合同ならば対応する角が等しい
ってことが成り立っていたわけだ。
たとえば、△ABC ≡ △DEFだったら、
ってことがいえるわけだね。
でも、ところがどっこい。
逆にしたら正しくなくなっちゃうんだ。
逆にすると、
対応する角が等しいならば2つの図形が合同である
になるでしょ??
これはまちがっているね。
なぜなら、
ぜんぶの対応する角が等しくても合同じゃない場合があるからだ。
たとえば、下のような△ABCと△DEFみたいな感じでね。
こいつらは、
なんだけど、
合同じゃないよね。
大きさ違いすぎて重ならないね。ゆえに、合同なんかじゃない。
これが逆が正しくない例だよ。
逆の作り方は簡単。
だけれども、
逆が正しくないことがけっこうある。
っていうか、そのほうが多いね。
逆が正しいか?
正しくないか?
に注意して問題をといてみてね。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。スープは濃いめに限るね。
二等辺三角形の定理にはつぎの2つがあるよ。
こいつらって、むちゃくちゃ便利。
証明で自由に使っていいんだ。
でもでも、でも。
疑い深いやつはこう思うはず。
なぜ、二等辺三角形の定理を使っていんだろう??
ってね。
そんな疑問を解消するために、
二等辺三角形の定理を証明していこう!
つぎの、
二等辺三角形ABCで証明していくよ。
AB = ACのやつね。
3つのステップで証明できちゃうんだ。
頂角から底辺に二等分線をひこう。
例題でいうと、
Aの二等分線を底辺BCにひいてやればいいんだ。
底辺との交点をHとするよ。
三角形の合同を証明していくよ。
例題でいうと、
の2つだね。
△ABHと△ACHにおいて、
仮定より、
AB = AC・・・(1)
AHは角Aの二等分線だから、
角BAH = 角CAH・・・(2)
辺AHは共通だから、
AH = AH・・・(3)
(1)・(2)・(3)より、
2組の辺とその間の角がそれぞれ等しいので、
△ABH ≡ △ACH
である。
これで2つの三角形の合同がいえたね!
あとは、
をつかうだけ!
合同な図形同士の対応する角は等しいので、
角ABH = 角ACH
だ。
こいつらは底角だから、
二等辺三角形の底角が等しい
ってことを証明できたね。
また、対応する角が等しいから、
角AHB = 角CHB
でもあるはずだ。
角AHB と角CHBはあわせて一直線になっている。
つまり、
角AHB + 角CHB = 180°
だね?
ってことは、
角AHB = 角CHB = 90°・・・(4)
であるはずさ。
対応する辺も等しいので、
BH = CH・・・(5)
だよ。
ってことは、
二等分線AHは底辺BCの垂直二等分線
になっている!
つまり、
頂角の二等分線は底辺を垂直に二等分する
ってことがわかったね。
二等辺三角形の定理は便利。
ぜんぶ、
合同な三角形の性質からきているんだ。
暗記するのも大事だけど、
なぜ、二等辺三角形の定理がつかえるのか??
ということを知っておいてね。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。馬、うまいね。
二等辺三角形って、
2つの辺が等しい三角形のこと
だったよね??

名前はかっこいいし、
ルックルも、いい。
人気がありそうな三角形だ。
だけれども、
二等辺三角形にはどんな性質があるんだろう??
って疑問に思うよね。
そこで今日は「二等辺三角形の性質・定理」をわかりやすく説明していくよ。
よかったら参考にしてみて。
二等辺三角形には2つの性質があるんだ。
ってやつだ。
順番にみていこう!
ひとつ目の性質は、
底角が等しい
ってやつさ。

底角とは、
底辺をはさんでいる角のこと
だったね?
なんと、
二等辺三角形では底角の大きさが等しいんだ。
たとえば、つぎの二等辺三角形ABCがあったとしよう。
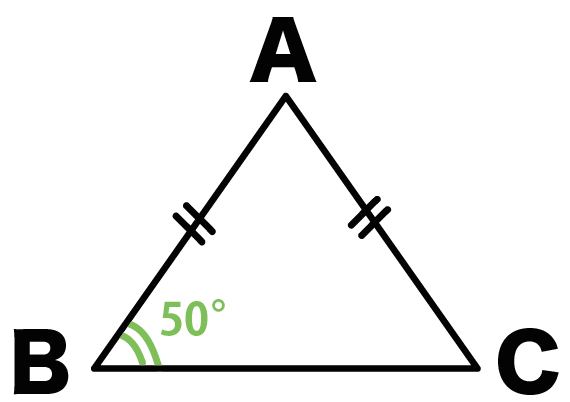
っていうスペックをもっているヤツさ。
このとき、
二等辺三角形の底角は等しいから、
角B = 角C = 50°になるんだ。
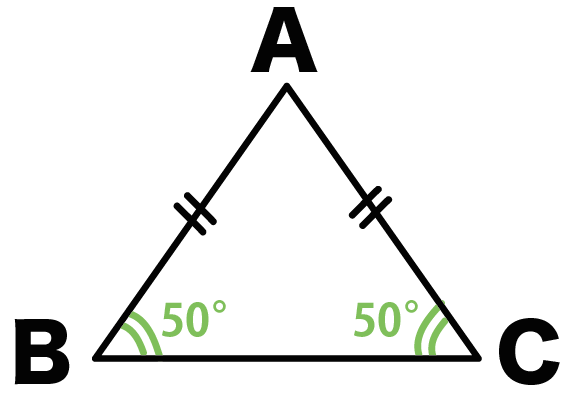
頂角はどうなるかっていうと、
内角の和180°から2つの底角をひいて、
180°- (50+50)
= 80°
で計算できるよ。
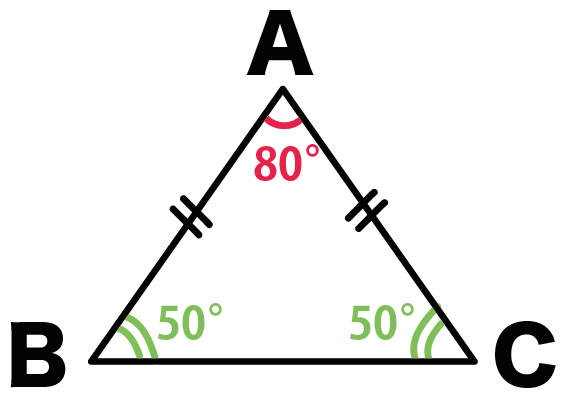
2つの目の性質は、
「頂角の2等分線」が「底辺の垂直2等分線」になる
ってやつだ。
びみょうにすごいよね?。
たとえば、つぎの三角形DEFがいたとしよう。
っていうスペックをもっている。
このとき、
頂角Dの二等分線を底辺EFにむけてひいて、
底辺との交点をGとする。
すると、
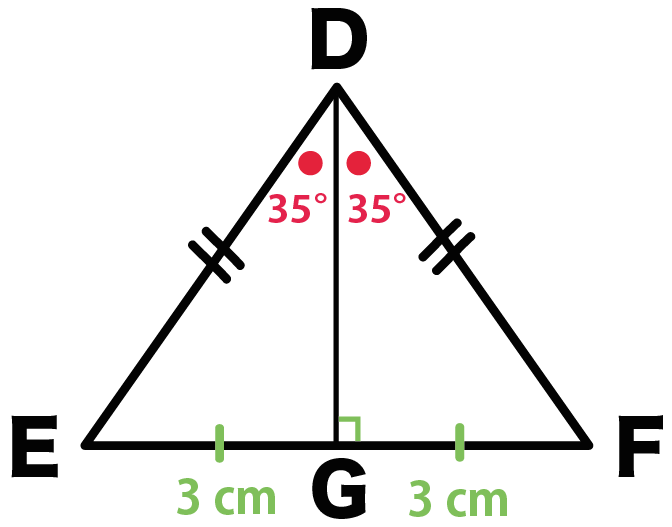
になるよ。
つまり、
DGは底辺EFの垂直二等分線になっていると
いうことなんだ。
二等辺三角形の性質の、
ってことを解説してきたよ。
この性質は定理として、
証明や計算問題で自由につかうことができる
んだ。
じゃんじゃんつかって問題を攻略していこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。本屋で豪遊したね。
世界にはたくさん三角形が、いる。
その数、
おおよそ、
うーん、たぶん数えきれないね。
そんな中、ある特殊な三角形がいる。
そいつの名は、
二等辺三角形
というものさ。

今日は、
二等辺三角形とはなにものか??
ってことを振り返っていこう!
定義がわからんときに参考にしてみて。
教科書によると、二等辺三角形の定義は、
2つの辺が等しい三角形
ってかいてあるね。
3つの辺がばらばらの三角形は、
二等辺三角形でもなんでもない。

2辺が等しい「五角形」も二等辺三角形でもないね。
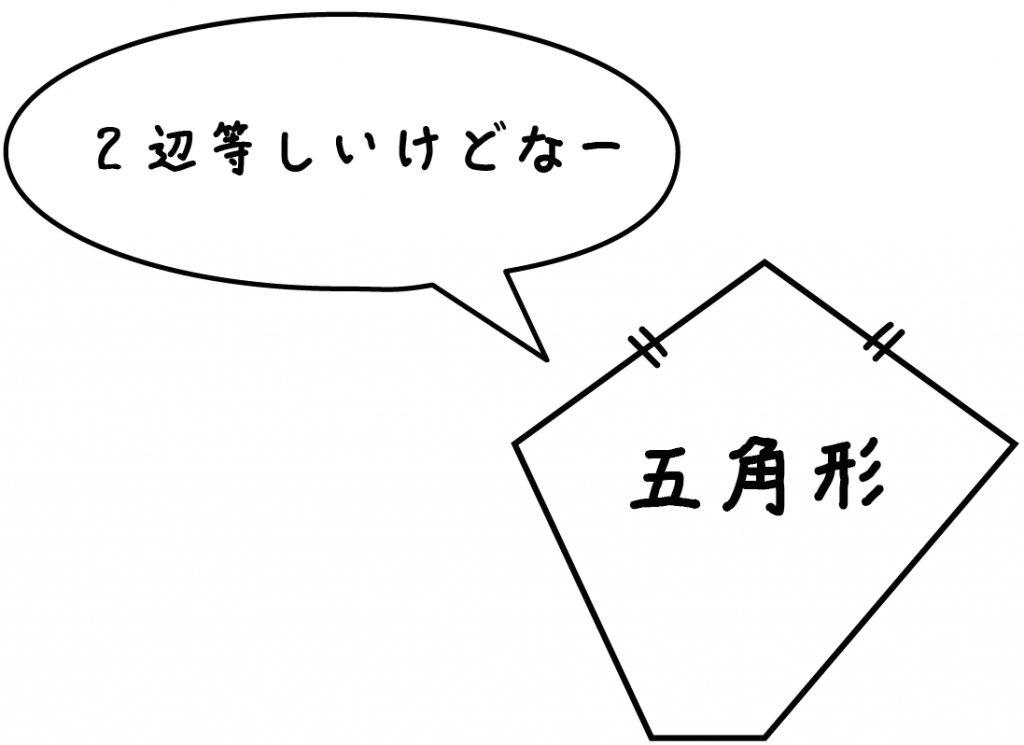
2つの辺が等しい三角形だけを
二等辺三角形
というんだ。
二つの等しい辺をもった三角形
でおぼえてみよう。
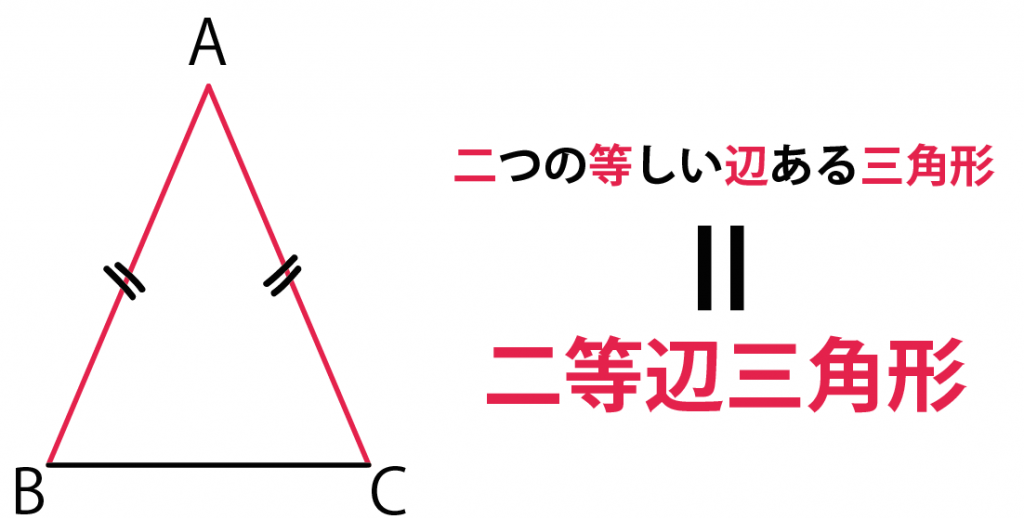
つぎは、
2等辺三角形のパーツをおぼえていこう。
順番にみていくよ。
等しい2辺にはさまれた角を、
頂角(ちょうかく)
ってよんでいるよ。

えっ。
名前をおぼえられないだって?!?
そんなときは、
2つの等しい辺にはさまれて有頂天になっている角
っておぼえてみて。
頂角の向かいの辺を
「底辺(ていへん)」
っていうんだ。
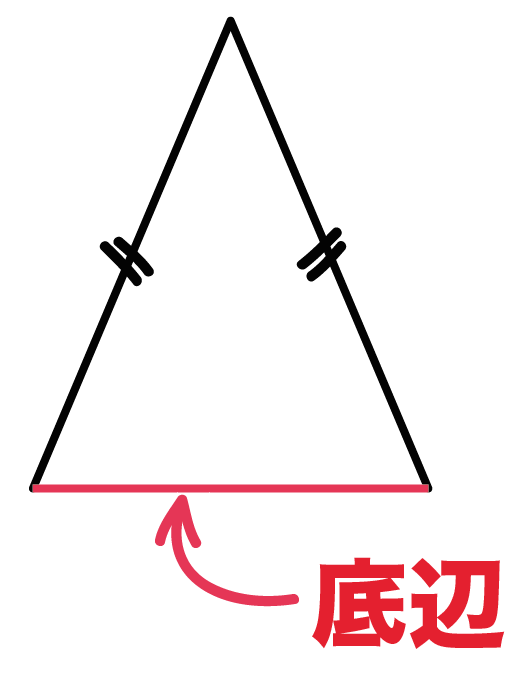
頂角と向き合っててーへんだ(大変だ)
っておぼえてみよう。
最後に、底辺をはさんでいる両端の角を
底角(ていかく)
っていうよ。
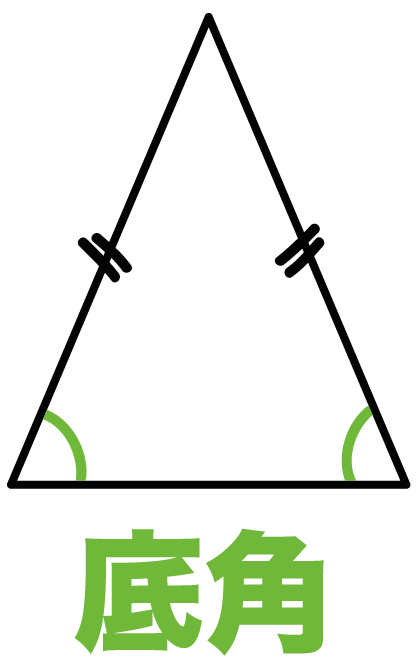
これは覚え方むずいね。
うーん、
ふつうに、ベーシックにおぼえると、
底辺をはさんでいる角
がいちばんしっくりくるかもね。
こんな感じで、
二等辺三角形のパーツにはたくさん名前がついてるよ。
がんばっておぼえてみてね。
二等辺三角形はあんがいシンプル。
2つの辺が等しい三角形
だったよね。
ひまがあったらパーツの名前もおぼえていこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。鼻呼吸したいね。
二等辺三角形の角度を求める問題
ってあるよね??
慣れれば簡単にとけるけど、
はじめはすごく大変なはず。

そこで今日は、
二等辺三角形の角度の求め方の公式
を2パターン紹介するよ。
テスト前に参考にしてみて。
二等辺三角形の角度は2パターンで計算できちゃうよ。
順番に紹介していくよー!!
まずは、
2等辺三角形の「頂角」がわかっている問題だ。
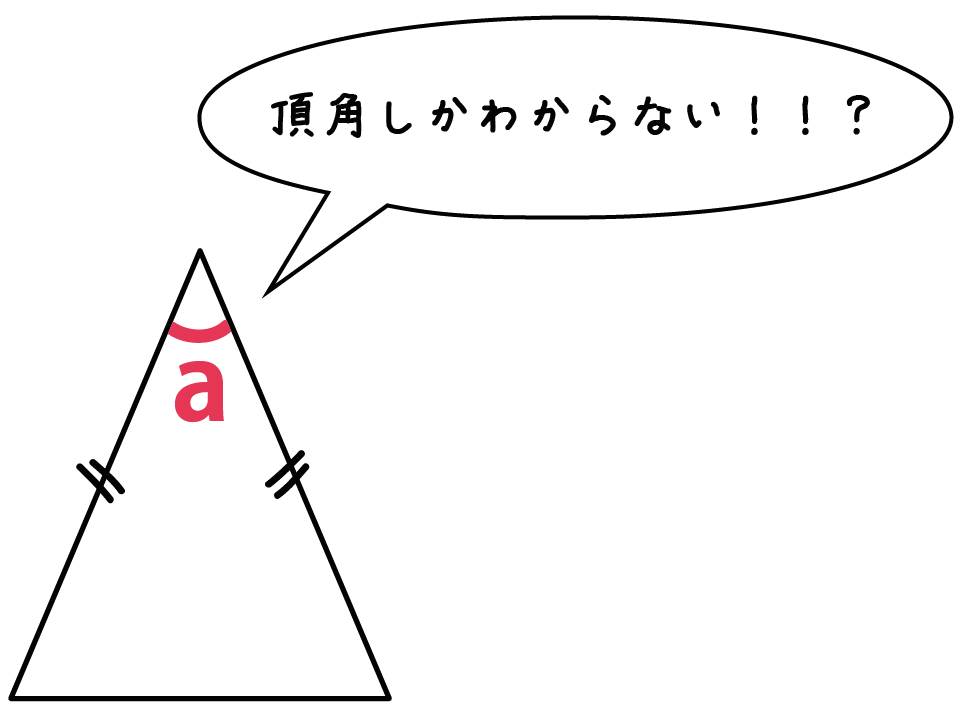
この問題では、
つぎの公式がつかえるよ。
頂角をa°とすると、
底角b = (180-a)/2
になるんだ。
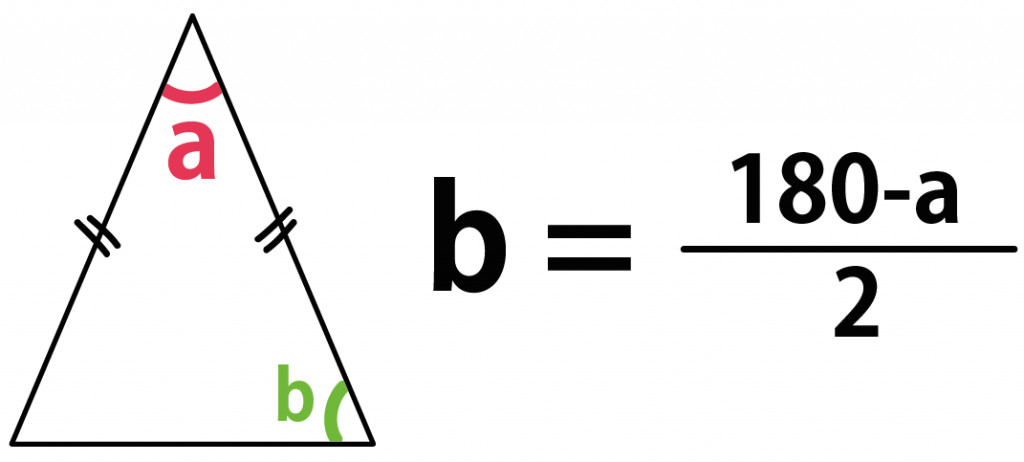
公式の計算もシンプル。
どんどんつかってみよう!
たとえば、つぎのような問題があったとしよう。
例題1
AB = AC の二等辺三角形で、角A=40°のとき、aの値を求めなさい。
頂角は40°だから、
さっきの公式のaに「40°」を代入してみよう。
すると、
底角b = (180-a)/2
= 140/2
= 70°
になるね。
でも、なぜ公式がつかえるんだろう??
二等辺三角形の底角は等しいから、
角B = 角C
になるね。
ってことは、
内角の和(180°)から頂角(40°)をひいて、2でわったやつが、
底角Bの大きさってことになるんだ。
よって、
b = (180-40)/2
= 70°
になる。
2つめは底角しかわかっていないパターンだ。
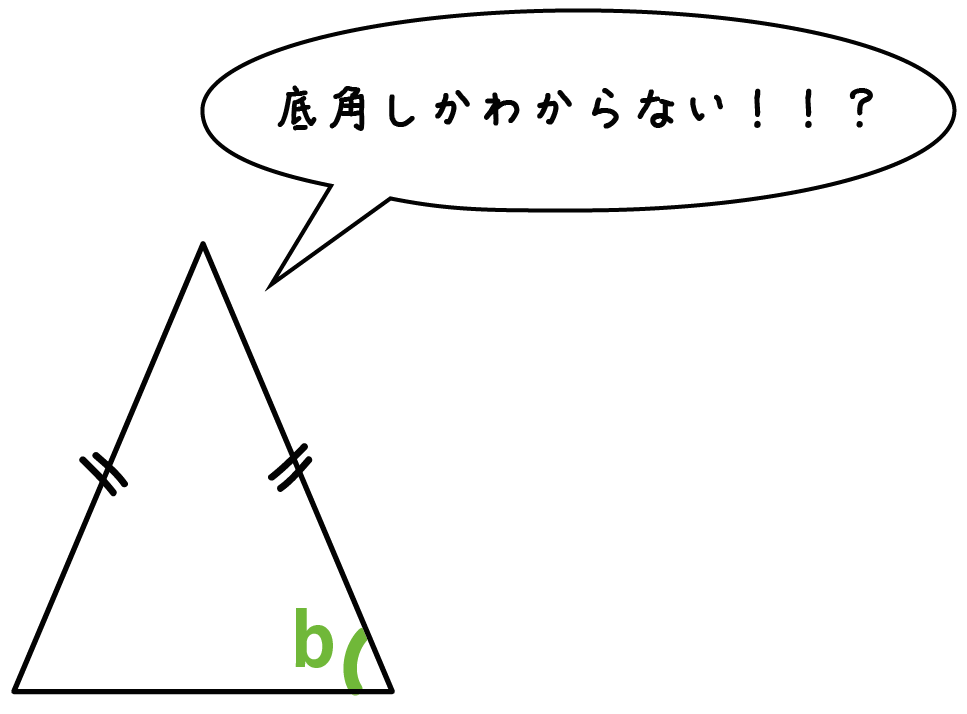
つぎの公式をつかってみて。
底角をbとすると、
頂角a = 180-2b
になるんだ。
つぎの例題で公式をつかってみよう!!
例題2
AB = AC の二等辺三角形で、角B=65°のとき、aの値を求めなさい。
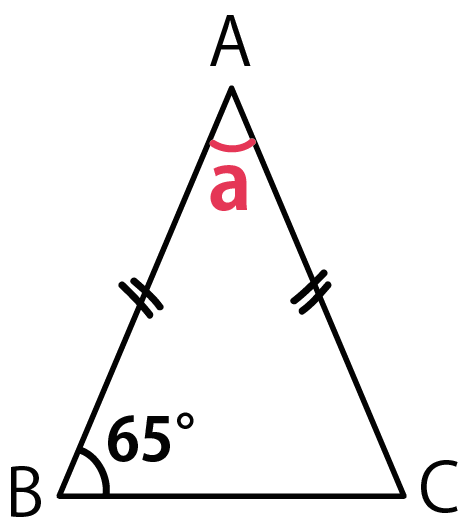
公式に底角65°を代入してやると、
頂角a = 180 -2 × 65
= 50°
になるね。
なぜ公式がつかえるんだろう??
底角は等しいから、
角B = 角C = 65°
になる。
ってことは、残りの頂角Aは、
三角形の内角の和(180°)- (角B+角C)
で計算すると、
180- (65+65)
= 50°
になるね!
2等辺三角形の角度の問題は、
の2パターンだね。
この基礎さえつかんでおけ大丈夫。
応用問題もとけるようになるよ。!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。図書館、最高。
数学の証明はむずいよね??
雰囲気がめんどいのはもちろんだけど、
それ以上に、
証明の書き方がわからない!
からだと思うんだ。
だって、
先生ごとに書き方ちがうからね。
誰を信じたらいいのかわからなくなっちゃう。

そこで今日は、
【中学数学】3年間つかえる証明問題の書き方
って記事をかいてみたよ。
困ったときに参考にしてみて。
証明の書き方でおぼえてほしいのは、
型だよ。
ちまたではテンプレートともよばれてる。
そうだなあ、
クッキーを思い浮かべてほしい。
だいたい同じような形のクッキーが焼けるのって、
型があるからなんだ。
だから、
数学の証明でも「型」を使いこなせれば、
それっぽい証明が何個でもつくれることになるね。
書き方の「型」はつぎのものだよ。
先生ごとによって書き方ちがうけど、
ぶっちゃけどれもこんな感じだ↓↓
(証明でとりあげる図形)において
仮定より、
(仮定よりわかっていること)
仮定+根拠より、
(仮定と根拠からいえること)
(共通な辺or 角)は共通なので、
(共通で等しい辺や角)
(材料の番号)より、(根拠)なので、
結論
じつはこの型、
っていう、3つのフェーズにわかれている。
この「型」で例題をといてみよう!
例題
AB = DC、AB // DCの△ABCと△CDAがあったとします。
このとき、△ABC≡△CDA
を証明しなさい。
書き方のいちばん最初は、
どの図形を証明でとりあげるのか??
を宣言することなんだ。
〜において
ってかいて、
「〜」には「証明でとりあげる図形」をかいてあげよう。
例題では、
△ABCと△CDAの合同を証明していくよ。
ってことは、この証明ではおもに、
△ABCと△CDA
の話をしていくことになるんだ。
だから、証明のいちばん最初で、
△ABCと△CDAにおいて、
って証明でとりあげる図形を宣言してみて!
このフェーズはぶっちゃけ、
あってもなくても構わない。
だけどこいつをかいてやることで、
っていうメリットがあるんだ。
ぜひ、証明のいっちゃん最初に
「証明でとりあつかう図形」を宣言してみてくれ!
結論に必要な材料をならべるフェーズだ。
をどんどんかいていこう!
結論の材料の並べ方はつぎの3パターンがあるよ。
このパターンをぜんぶ使わなくてもOK。
1つでも2つでも、ぜーんぶつかってもいいよ。
その証明に必要なものをチョイスしてみてね。
例題ではこんな感じになる↓↓
それぞれに番号ふるのを忘れずに!
最後はいよいよ結論。
フェーズ2で生み出した材料から、
結論(証明のゴール)
をみちびいてやろう。
書き方としては、
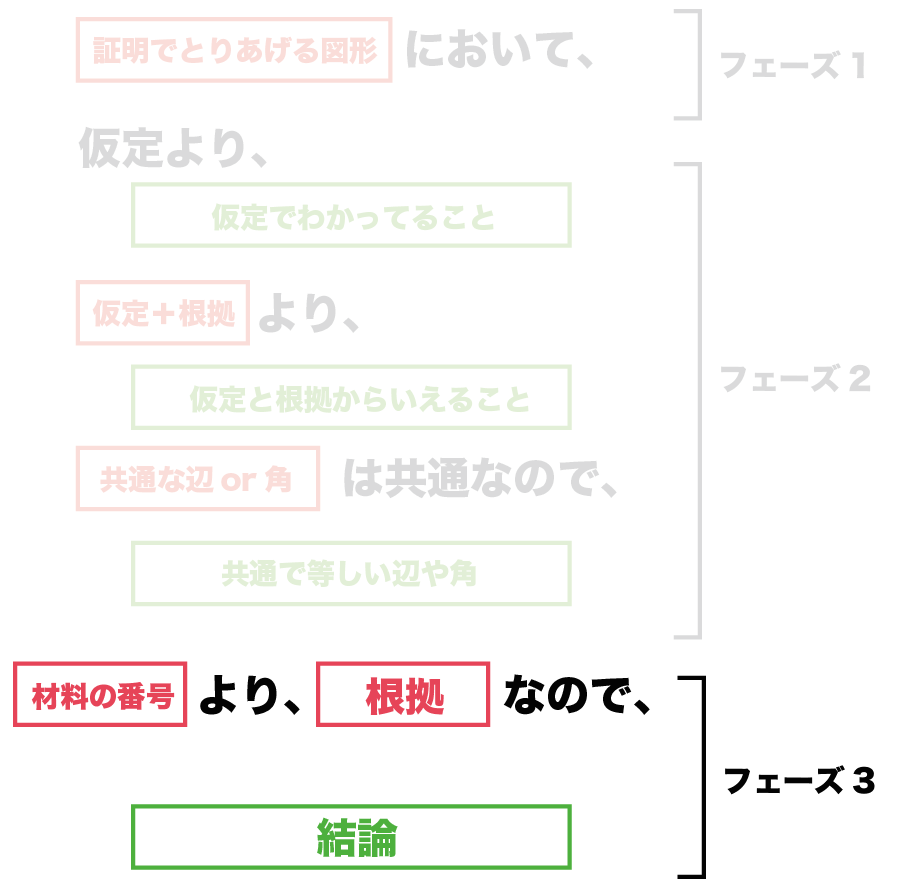
(材料の番号)より、(根拠のあることがら)なので、
(結論)である。
がのぞましいね。
例題でいうと、こうなる↓↓
もし、結論が「角ABC = 角CDA」だった場合は、
もう一回フェーズ3をくり返してみてね。
こんな感じで、問題によって、
フェーズ2や3が数回くり返すこと
もあるよ!
必ずしもこの型がピタリとはまるわけじゃないから、
気をつけてね。
数学の証明はぶっちゃけむずい。
解き方もようわからん。
だけど、
書き方の「型」をおぼえてしまえば大丈夫。
それ通りにかいていくだけでいいからね!
問題をときまくって書き方になれていこう!
そんじゃねー
Ken