こんにちは!この記事をかいているKenだよ。ゴミ袋は必須だね。
中学数学で図形を勉強していると、
円周率
をたくさん使うよね??
よくでてくるから、ときどきこう思うはずなんだ。
そう。
円周率はどうやって求めるんだろう??
ってね。
そこで今日は、
小学生でもわかる簡単な円周率の求め方
を解説していくよ。
よかったら参考にしてみて。
= もくじ =
円周率とはずばり、
円周の直径に対する比
だよ。
つまり、
「円周の長さ」は「直径の長さ」の何倍になってますか??
ってことをあらわしてるのさ。
それじゃあ、円周率を求めるためには、
円状になってる物体の「直径」
と
円周の長さ
を計測して比を求めればいいね。
ってことで、リアルな世界で円周率をだしてみよう。
用意するものは、
の4点セットだ。
ぼくは丸いものに「コーヒー」のふたを選んだよ。
そうそう。
UCCのやつ。
だって、この蓋の部分がいい感じに円になってるじゃん?
こんな感じで、身の回りで「円になってるもの」をみつけてみよう!
まず始めに、円の直径をはかってみよう。
円の直径を測るときはほんとうは
ノギス
っていうアイテムを使うといいんだけどね。
たぶん、ノギスを持ってるやつはそういない。
今回は定規でいいかな。
ぼくもコーヒーの蓋の直径をはかってみたよ。
すると、
コーヒーの蓋の直径 = 6.5cm
になったよ。
まあまあの大きさだ。
つぎは、円周をはかろう。
えっ。
円周はぐにゃっとしてるから測れないだって?!?
いやいや。
じつは、円周をはかるためにグニャっとしたものをまいて、
シャキっとさせればいいんだ。
そのシャキッとした長さを測ればいいのさ。
ぼくはグニャっとしたものに「ビニールヒモ」を選んでみたよ。
こいつはスーパーでも買えるし、安くて便利だ。
こいつを円状の物体にぐるっとまきつけて、
ちょうど一周でハサミカット。
そして、ヒモをシャキっとまっすぐにするわけだ。
この状態で、定規で長さをはかってみる。
すると・・・・・
っておい。
定規短すぎて測れないね。
しょうがないので、計測メジャーで長さをはかってみると、
20.5cm
ってことがわかった。
これがコーヒーの蓋の円周の長さだ。
最後は、「直径の長さ」に対する「円周の長さ」の比を計算しよう。
ようは、
(円周の長さ)÷(直径の長さ)
を計算すればいいんだ。
この答えが「円周率」になってるよ。
ぼくの例では、
だったね??
だから、コーヒーの蓋の円周率は、
(ビニールヒモの長さ)÷(コーヒーの蓋の直径)
= 20.5 ÷ 6.5
= 3.153846153…
になったよ!
おめでとう。
これでリアルに円周率が求められたね!
円周率の計算はどうだった??
たぶん、円周率が3.14になるのはむずかしいんじゃなかな。
うーん、これはどうしようもない誤差。
ヒモの厚みの分だけ直径は大きくなるし、
メモリは1mmまでしかはかれないからね。完全にアバウトだ。
こんな感じで、
気が向いたら円周率を計算してみよう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。自然とふれあいたいね。
文字式の計算問題にはいろんな種類がある。
なかでも質問が多いのは、
文字式の割り算
だ。
たとえば、つぎのような問題だね ↓↓
例題
つぎの文字式を簡単にしなさい。
12a^2b^3 ÷ 9abc^2
割り算は足し算・引き算よりもむずそう。。
だけどね。
じつは、簡単な解き方があるんだ。
文字式の割り算のコツは、
数字と文字をべつべつに計算する!
だ。
数字と文字をいっきに考えちゃダメだ。パンクしそうになる。
だったら、
数と文字をわけて計算すればいいんだよ。
ってことで、つぎの3ステップで割り算してみよう!
例題をといてみよう。
例題
つぎの文字式を簡単にしなさい。
12a^2b^3 ÷ 9abc^2
まず、
数字の割り算
を計算しよう。
例題でも、数字の割り算だけしてみると、
12÷9
になるよね。
数字の割り算ならいける!はず!
12÷9をふつうに計算してやると、
12÷9
= 3分の4
になるね。
これが第1ステップ!
おつぎは文字の割り算。
文字式の割り算では、
「割る数」の指数を「割られる数」の指数からひけばいいんだ。
たとえば、x^100÷x^30を考えてみて。
割る数の「30」の指数を「割られる数」の100からひけばいいんだ。
だから、
x^(100-30)
= x^70
が答えになるね。
こんな感じで、例題も指数の引き算をしてみよう。
例題から文字の計算だけとりだすと、
a^2 b^3 ÷ abc^2
になるね。
÷の後ろの文字の指数を引き算してやると、
a^2 b^3 ÷ abc^2
= a^(2-1)b^(3-1)c^(-2)
= a^(1) b^2 c^(-2)
になるね。
マイナスの指数は分数の分母にまわしてやればいいから、
a^2 b^3 ÷ abc^2
= a^(1) b^2 c^(-2)
= ab^2/c^2
になるね。
これが第2ステップ!
最後は、
2つの割り算の結果をくっつけよう!
のりもボンドもいらない。
ただ、くっつけるだけでいいんだ。
例題の数字と文字の割り算はそれぞれ、
だったよね??
こいつらをこりっとつけてやると、
(4ab^2)
———-
3c ^2
になるね!
これで文字式の割り算もマスターだね。
文字式の割り算??
おそれることはない。
いったん、
数
と
文字
にわけて計算すればいいんだ。
文字式の基本だからしっかりマスターしておこう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。ラーメンはあっさりでもうまいね。
不等号の使い方はマスターした。
意味もわかる。
だけどさ、
不等号の記号の読み方がわからない
よね??
>とか、
<とか、
≦とか。
もうなんだろう、なんて呼べばいいんだろう。
くち? さんかく?? かぎかっこ??
数学の授業でも不等号を読まされるときがある。
読み方を知っとけば、クラスでモテるかもね。
そこで今日は、
不等号の読み方をわかりやすく解説してみたよ。
よかったら参考にしてみて。
さくっと不等号の読み方を紹介しよう。
中学数学でならう不等号はつぎのように読むよ。
意外に読み方が古くさくてびっくりした??。
ぶっちゃけ、とっつきにくいよね。
だがしかし。
この不等号の読み方はものすごくシンプルなんだ。
ただ単に、
「左」が「右」より大きいか・小さいかを読んでるだけなんだ。
もし、左のやつが右より大きい場合は、大きいから、
大なり(だいなり)
って読む。
逆に、左のやつが右より小さい場合。
左のほうが小さいことを主張するために、
小なり(しょうなり)
って読むんだ。
んで、もし、左と右が等しい場合もふくめるときは、
不等号の下に「=」をつける。
「=」の読み方は「いこーる」だったよね??
だから、「<(しょうなり)」とか「>(だいなり)」のうしろに「いこーる」をつけてやればいいんだ。
だから「≦」の読み方は、
小なりイコール(しょうなりいこーる)
になるんだ!
不等号の読み方をマスターしたいだって??
近道はただ1つ。
それは、
不等号を読んで読みまくることだ。
とりあえず、不等号を読む場数をふやす。
おのずと読み方が身につけられるんだ。
だから、今日は不等号を5回よんでみよう!
さあ、読みまくるよ!
3 > 2
こいつはなんて読むだろう??
そう、そう。
この不等号は「だいなり」って読むんだったね??
だから、「3>2」は、
さん だいなり に
って読むよ。
-3 < 2
不等号の口の向きが変わったね。
「<」は「しょうなり」って読むんだったね??
ってことは「-3 < 2」は、
まいなすさん しょうなり に
って読むね!
-3 ≦ 2
つぎは「=」が割り込んできたね。
「≦」の読み方は、
しょうなりいこーる
だったよね???
ってことは、「-3 ≦ 2」は、
まいなすさん しょうなりいこーる に
って読むんだ。
ちょっと長くなってきたね。;
x > 5
つぎは関数の変域でよく使う例だね。
「>」は「だいなり」って読むから、
えっくす だいなり ご
って読むね。
変数xに5より大きい数しか入らないって意味なんだ。
たとえば、
5ははいらないし、
2もはいらない。
6ははいるけどね!
こんな感じでよく関数の変域でつかうよ。
読み方をおぼえておこう!
1 < x < 5
最後のラスボスだ。
こいつも関数の変域でつかう不等号。
真ん中の数字・文字が不等号にサンドイッチされてる例だね。
読み方は普通のときと一緒。
「<」は「しょうなり」って読んだから、
いち しょうなり えっくす しょうなり ご
って読むんだ。
これもさっきの不等号と考え方はおなじ。
1より大きく、5より小さい数しかxにいれられないんだ。
だから、1と5はダメ。
そのあいだの2とか3とか3.1とか4とかはxにいれて大丈夫ってわけ。
どう??
読みまくったら不等号の読み方マスターできたね!!
不等号はいっけんむずい。
日常生活ではみないし、なんか、くちばしみたいな形してるしさ。
だけど、
不等号を読みまくれば大丈夫。
自然と読み方をマスターできるようになるはずだ。
これからもガンガン不等号を読んでいこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。鱒寿司にトライしたね。
中学数学では、
不等号
がたくさん登場するよ。
たとえば、関数の変域とか、不等式とかで・・・ね。
たぶん、不等号をみないで中学を卒業は無理じゃないかな。
中学生活ではゼッタイにさけて通れない記号なんだ。
今日は不等号の基本を理解するために、
不等号の使い方・意味
を3分で振り返ってみよう!
不等号とはずばり、
数・文字の大きさを比べる記号のこと
なんだ!
数学を勉強していると、
2つの数字のどっちが大きいのか??小さいのか??
ときどき気になるでしょ??
そんな数の大小を記号であらわせるってすごい。
中学で勉強する不等号はつぎの4つだ。
順番に紹介していくよ。
この不等号の使い方は簡単だよ。
不等号の口がひらいている方の数字・文字が大きい
って意味なんだ。
たとえば、AとBの大きさを比べるとしよう。
このとき、
A > B
っていう不等号であらわせれたら、
AのほうがBより大きいって意味があるんだ。
だって、不等号の口がAにむかってひらいてるからね。
具体例をみてみよう。
3は2より大きいことを不等号であらわしてみると、
3 > 2
になるよ!

ぶっちゃけ、不等号はパックマンの口と一緒。
パックマンが左右どちらのケーキを食べたいか考えればいい。
誰だって大きいケーキのほうが食べたいよね??
お腹いっぱいになるし。
だから、
大きい数・文字のほうに口がひらいている
って覚えておけばいいよ。
じゃあさ。
さっきの不等号の下に「=」がついた、
は何者なんだって話だよね。怪しすぎる。
じつは=が不等号につくと、
大きい・小さい
もしくは、
等しい
っていう意味になるんだ。
たとえば、「A>B」が「A≧B」になったとしよう。
このとき、AはBよりも大きい、もしくは等しい
っていう意味になるよ。
「=」がつくと左右が等しくても許してくれるってわけ。
だから、
2<2
っていう不等号は使い方まちがってるけど、
こいつに=をつけてやって、
2≦2
にすれば間違ってないんだ。左右の数字は等しいからね。

どう?「≦・≧」の使い方もピンときたかな??
最後に、
関数の変域での不等号の使い方
をみてみよう。
変域として不等号をよく使うことがある。
いまのうちから慣れておこう。
たとえば、y = axの変数xの変域が、
x > 1
だとしよう。
この変域には、
xには1より大きい値しか入らないよー
って意味があるよ。
つまり、この「関数y=ax」の「x」には、
2をいれてもいいし、
3でもいい。
5でもいいし、
ぶっちゃけ100でもいい。
ただ、1より小さい0とか、
1と等しい1をxにいれちゃダメなんだ。
なぜなら、x>1っていう変域外の数字だからね。
こんな感じで不等号は登場してくるよ。
がっつり使い方・意味をおさえておこう!
不等号の使い方・意味はシンプル。
不等号の口がどっちを向いているのか??
で大小をあらわしているんだ。
困った時はパックマンの口をイメージしてみよう。
そんじゃねー
Ken
こんにちは!この記事をかいてるKenだよ。そろそろ進撃したいね。
半球の表面積の公式は簡単。
半径をrとすると、
3πr^2
で計算できちゃうんだ。
つまり、
半径×半径×円周率×3
ってわけだね。
たとえば、半径が6cmの半球があったすると、こいつの表面積は、
半径×半径×円周率×3
= 6 × 6 × π × 3
= 108π [cm^2]
になるんだ。
どう??
半径と円周率かけるだけさ!
半球の表面積の求め方はわかった。
だけど、
なんで球の表面積の半分じゃないの??
って思うよね。
半球の体積は「球の体積の半分」だったのに・・・ってね。
じつは球の表面積は、
っていう2つの面積で成り立っているんだ。
モンブランケーキでいえば、
って感じ。
こいつらの面積を別々に求めて、最後にたしてるんだ。
試しに、半径6cmの半球の表面積を計算してみよう!!
まずは、球の表面積の半分をだそう。
モンブランでいうと、クリームがついている部分だね。
4πrの二乗
だったよね??
ってことはその半分は、
2πrの二乗
になるはず!
だから、半径が6cmの半球のクリーム部は、
半径×半径×円周率×2
= 6×6×π×2
= 72π [cm^2]
になるんだ。
つぎは半球の断面積だ。
つまり、底面の面積をたせばいいよ。
モンブランでいうと「タルト」にあたるね。
半球の断面積は円。
円の面積の公式は、
半径×半径×円周率
だったよね??
だから、例の半径6cmの半球の断面積でいうと、
半径×半径×円周率
= 6×6×π
= 36π [cm^2]
になるね。
あとは、
の2つをたすだけ。
例の半径6cmの半球の表面積は、
(球の表面積の半分)+(断面積)
= 72π + 36π
= 108π [cm^2]
になるんだ。
おめでとう!
これで半球の表面積も計算できちゃうね。
半球の表面積はトリッキー。
球の表面積の半分じゃないんだ。
球の表面積の半分に、底面積をたすからね。
半球の体積の求め方とはひと味ちがうから注意しよう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。シャツほしいね。
半球の体積を求め方には公式があるよ。
半径rの半球の体積は、
(3分の2π) × (rの3乗)
になるんだ。
つまり、
半径×半径×半径×円周率×2÷3
ってわけだ。
えっ。
覚えられないだって??!
じつはこの公式。
球の体積のちょうど半分なんだ!
球の体積の公式は、
(3分の4)×(円周率)×(半径)×(半径)×(半径)
だったよね??
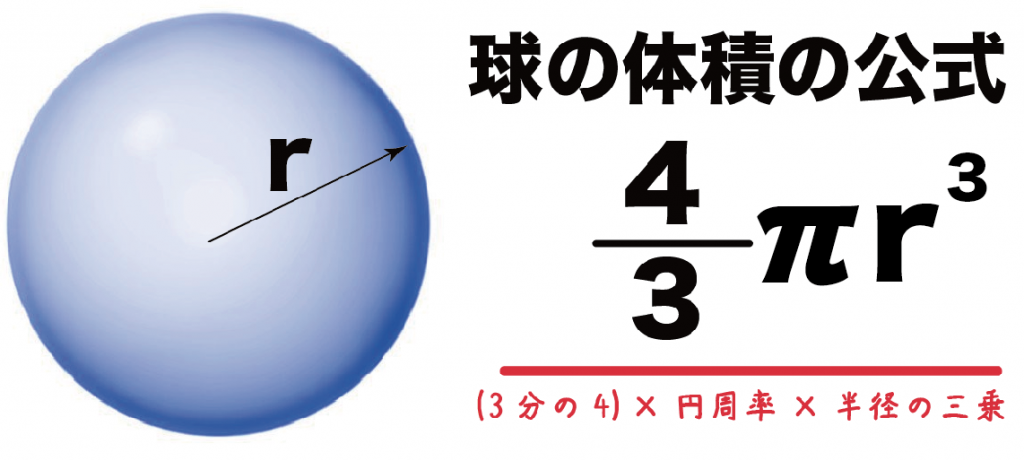
それを半分にしたのが「半球の体積の公式」になる。
なぜなら、
半球は球をスパッと半分にきったものだからね。
体積は球の半分になるってわけ。
たとえば、半径6cmの半球Aがあったとしよう。
こいつの体積は公式をつかうと、
(半球Aの体積)
=(半径)×(半径)×(半径)×(円周率)× 2 ÷ 3
= 6 × 6 × 6 × π × 2 ÷ 3
= 144π [cm^3]
になるんだ。
どう??半球の体積を求められたかな??
半球の体積なんてぜんぜん使わなくね??
って思ってない?。
ぶっちゃけ、半球をみくびってるよね。
その気持ちわかるw
ただ、半球の体積の求め方は、
立体の応用問題で役に立つんだ。
たとえば、つぎのような問題だね↓↓
この問題は3ステップでとけちゃうよ。
まずソフトクリームを、
「アイス」と「コーン」に分解してみよう。
つまり、上の「半球」と下の「円錐」にわけるってことさ。
これが第1ステップ!!
「半球」と「円錐」の体積をべつべつに計算してみよう!
体積の求め方の公式はそれぞれ、
だったよね??
まず半球の体積は、
6×6×6×π×2÷3
= 144π [cm^3]
になる。
半径×半径×円周率×高さ÷3
だったよね??
こいつで下のコーンの体積を計算してやると、
半径×半径×円周率×高さ÷3
= 6×6×π×12÷3
= 144π [cm^3]
になるはずだ。
これが第2ステップ!!
最後に、
の体積をたしてみよう。
例題での体積はそれぞれ、
だったよね?
こいつらをたしてやると、
ソフトクリームの体積
= (半球の体積)+(円錐の体積)
= 144π + 144π
= 288π [cm^3]
になるね。
おめでとう!
これで応用問題もクリアだね。
半球の体積の公式はマイナー。
だけど、覚えておいて損はない。
ソフトクリームみたいな立体の体積もわかっちゃうし。
半球の体積は「球の体積の半分」っておぼえておこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。アキレス腱のばしたね。
平均値の求め方にはいろいろある。
度数分布表から求めたり、
平均値の求め方の公式にぶちこんだり。
これだけ平均値に詳しくなったんだから、
どんな平均値の問題もクリアできる!!
・・・・・
って安心してない??
うん、してたね。
じつはあと1つ、マスターしておきたい平均値の求め方があるんだ。
それは、
ヒストグラムをつかった平均値の求め方
だ。
こいつはぶっちゃけ影が薄い。
だけど、テストにでてくることがあるんだ。
そこで今日は、
ヒストグラムから平均値を求める方法を4ステップで解説してみたよ。
よかったら参考にしてみてね。
つぎの4ステップさ。
例題をといていこう!
例題
つぎのヒストグラムは3年B組の数学の得点の分布を表したものです。このヒストグラムから平均値を求めなさい。
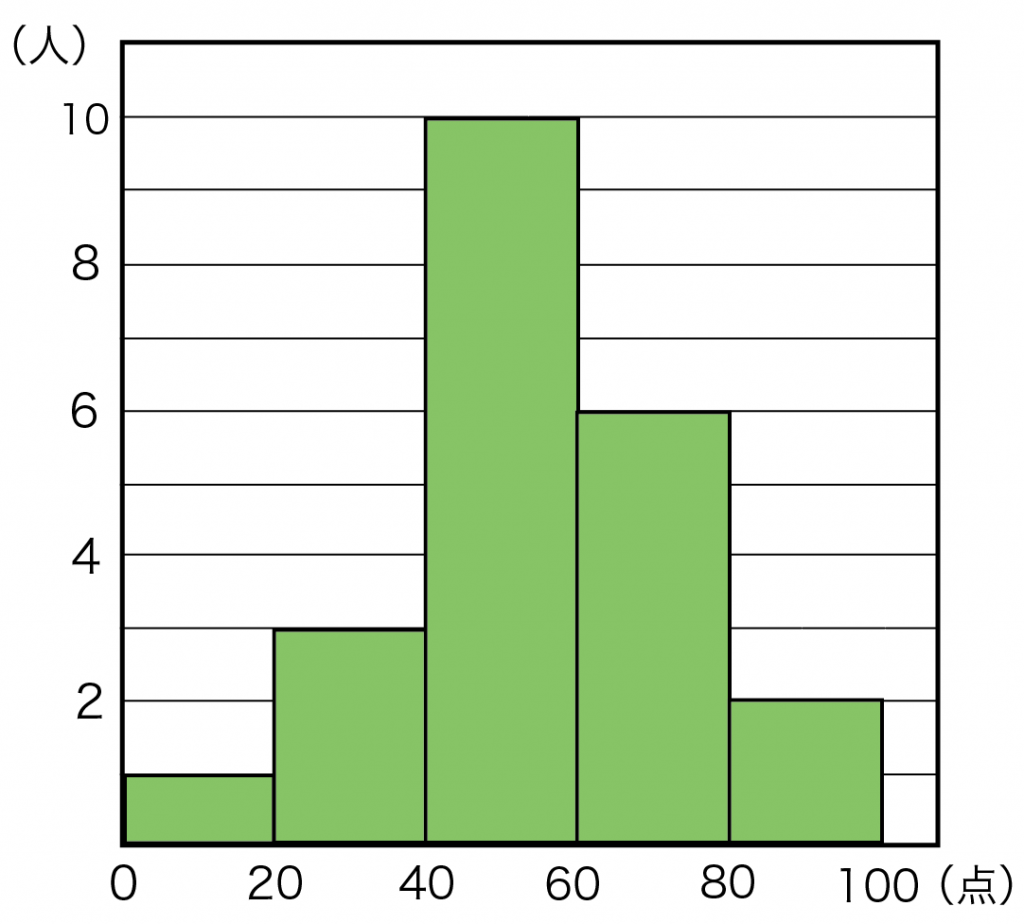
各階級の、
階級値をだしてみよう!
階級値の求め方は、
(階級の端+階級の端)÷2
だったよね??
つまり、
長方形の角と角の数値をたして、
2でわればいいんだ。
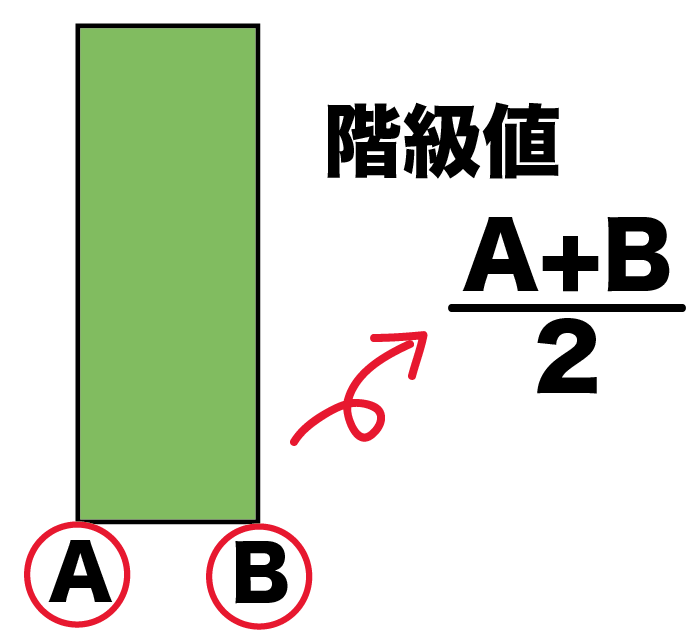
例題の階級「0-20」をみてみよう。
こいつの端と端は、
だね。たして2でわってやると、
(0+20)÷2
= 10
になる。
こんな感じで、残りの階級値を計算してみよう。
すると、
になる。
こいつらを棒の下らへんに書いてみて!
これが第1ステップさ。
つぎは「度数」を読み取ろう!
棒グラフがどれくらいの高さになっているのか??
をみてやればいいんだ。
例題では、ヒストグラムに目盛りがついてる。
目盛り通りに度数を読んでやると、こうなるね↓↓
こいつらを棒の上に書き込んでみよう。
これが第2ステップさ。
つぎは、
「度数」と「階級値」をかけてみよう。
ぜーんぶの階級で計算してみてね。
えっ。
「度数×階級」はどこに書けばいいかって??
たしかにね。
ぶっちゃけどこでもいいんだけど、
せっかくだから度数の上にかいてみようか。
例題をみてみると、
になるはず。
これが第3ステップさ。
最後は公式をつかうよ。
度数分布表からの平均値の求め方とおなじさ。
(平均値)=(階級値×度数)の合計 ÷ (度数の合計)
ってやつだね。
例題でも公式をつかってみよう。
すると、
になるね。
こいつをまんま公式にぶちこんでやると、
平均値
= 1200÷22 = 54.5
になるはずだ。
おめでとう!
ヒストグラムから平均値を求められたね。
ヒストグラムでも度数分布表でも大丈夫。
平均値の求め方は、
階級値×度数の合計
を
度数の合計
でわればいいんだ。
しっかり点をとっていこう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。山、みたいね。
平均値の求め方はわかってる。
だって、
「データの合計」を「データの個数」で割ればいいんでしょ??

ちょろいよ。
たとえば、A・B・C・D君のテストの平均値を求めてみよう。
かりに、4人の点数が、
だとするね。
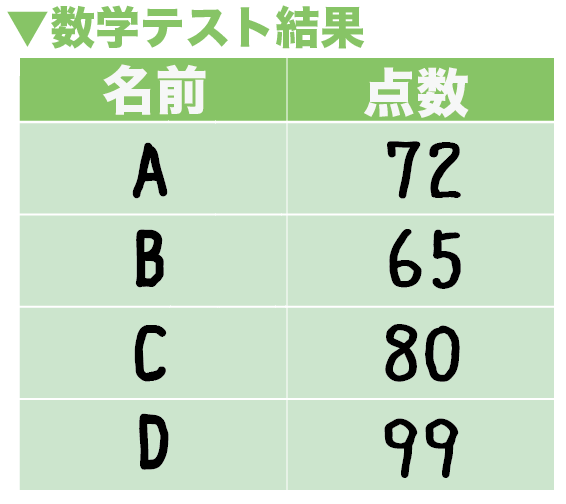
こいつらの平均点は、
(データの合計)÷(データの個数)
= (72 + 65 + 80 + 99)÷ 4
= 79
になる。
ぶっちゃけ、楽勝だね!
だけどさ、
度数分布表から平均を求めるとき
ってどうすればいいんだろ??
テストや宿題ででてくるのに、教科書にのってない。。
こいつは困ったね。
そこで今日は、
度数分布表からの平均値の求め方
を5ステップで解説してみたよ。
度数分布表から平均値を求めるときは、
つぎの公式をつかうよ。
「(階級値×度数)の合計」÷「度数の合計」

「階級値」と「度数」をかけたものをぜーんぶたして、
「度数の合計」でわればいいんだ。
えっ、言葉だけじゃよくわからん??
実際に例題をといてみよう!
例題
つぎの度数分布表は3年B組の期末テストの点数の分布をあらわしたものです。この度数分布表から平均値を求めなさい。
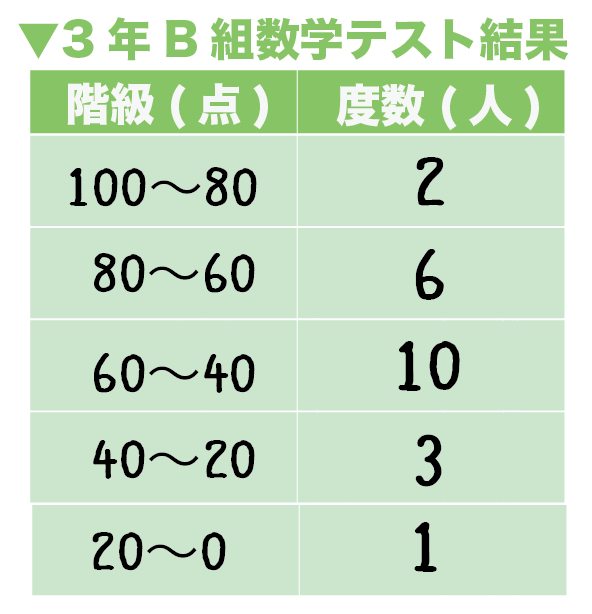
つぎの5ステップで計算できちゃうよ。
各階級の「階級値」を計算してみよう!
階級値の求め方は、
(階級の端+階級の端)÷ 2
だったよね??

たとえば、階級が「100~80」だったら、
(100 + 80 ) ÷ 2
= 90
になるってわけ。
こんな感じで、階級の端っこの平均をだせばいいんだ。
例題の階級値をぜーんぶだしてやると、
になるね。
これが第1ステップ!!
つぎはさっき計算した、
階級値
と
度数
をかけてみよう。
例題で「階級値×度数」を計算してみると、
になるね。
慎重にかけ算をしてみよう!!
おつぎは、
度数の合計
を計算しよう。
ぜーんぶの階級の「度数」をたせばいいのさ。
例題でいうと、各階級の度数は、
だったね??
こいつらをぜんぶ足してやると、
2 + 6 + 10 + 3 + 1
= 22
になる!
「階級値×度数」の合計もだしてみよう!
ぜーんぶの階級の「階級値×度数」をたせばいいんだ。
例題の「階級値×度数」は、
だったよね??
こいつをぜんぶたしてやると、
180 + 420 + 500 + 90 + 10
= 1200
になるね。
最後に平均値の公式をつかおう!
度数分布表から平均値を求める公式は、
「(階級値×度数)の合計」÷「度数の合計」

だったね??
Step4まででそろえた、
を公式にぶちこんでみよう。
例題では、
を公式にいれて計算してやると、
(階級値×度数の合計)÷(度数の合計)
= 1200 ÷ 22
= 54.5※小数点第二位を四捨五入
になる!
おめでとう!
どんな度数分布表からも平均値を求められるね。
度数分布表から平均値をだすのはむずい。
だけど、ふたをあけてみると案外簡単。
使ってるのは、
の3つだからね。
求め方さえおぼえちまえば、計算は簡単なんだ。
度数分布表からガンガン平均値を求めていこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。鼻呼吸は大事だね。
中学数学でよく、
歯車の問題
ってでてくるね。もっとぶっちゃけいうと、
比例・反比例の利用
の問題でよくねらわれるんだ。
なぜだかしらんけど、よく歯車が登場するよ。
たとえば、つぎのような問題だ。
歯数がそれぞれ72、26の歯車A、Bがかみ合っている。歯車Aがx回転する間に歯車Bはy回転する。
yをxの式であらわし、比例しているか、反比例しているか答えなさい。
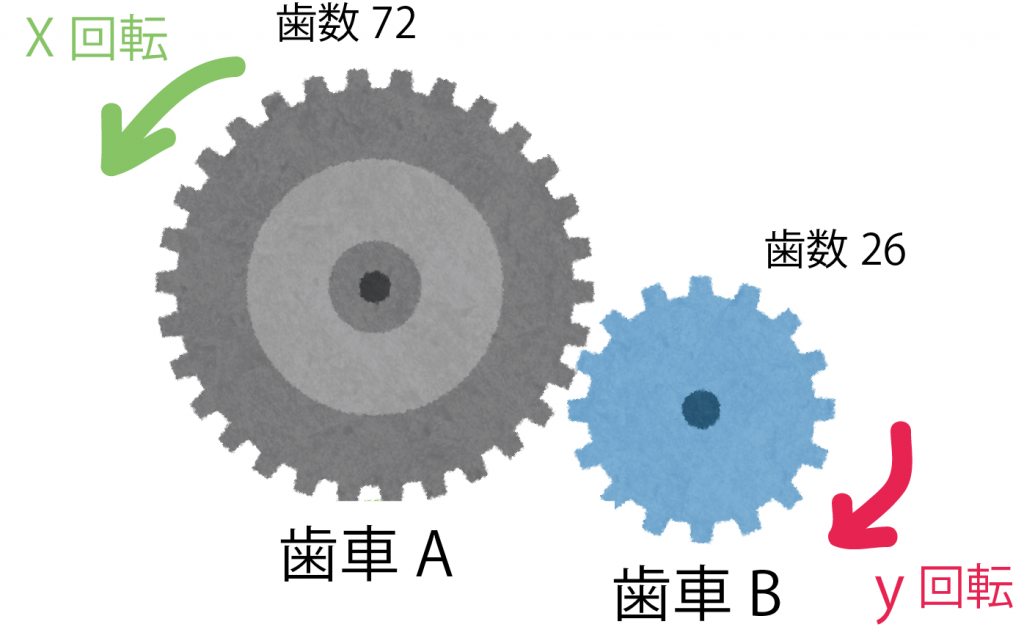
今日はこんな歯車問題にとまどわないためにも、
数学の歯車問題の解き方を4ステップで解説していくよ。
よかったら参考にしてみてね。
つぎの4ステップでとけちゃうよ。
例題をいっしょにといてみよう!
歯数がそれぞれ72、26の歯車A、Bがかみ合っている。歯車Aがx回転する間に歯車Bはy回転する。
yをxの式であらわし、比例しているか、反比例しているか答えなさい。

まず歯車の、
動いた歯数
を計算してみよう!
動いた歯数は、
(歯車についてる歯数)×(回転数)
で計算できるよ。
例題の歯車A・Bをみてみよう。
歯車Aは、
だったね??
ってことは、歯車Aの「動いた歯数」は、
動いた歯数(歯車A)
= (歯数)×(回転数)
= 72 x
になるね。
同じように、歯車Bの場合を考えてみて。
歯車Bは、
だ。よって、
動いた歯数(歯車B)
= 歯数×回転数
= 26y
になる。
これで第1ステップ終了さ!
つぎは方程式をつくってみよう!
かみ合っている歯車同士は、
動いた歯数が等しい
っていう性質があるんだ。この性質で方程式をつくってみよう。
例題をみてみると、
歯車A、Bがかみ合っている
ってあるね。
つまり、
歯車A・Bの動いた歯数が等しい
ってことなんだ。
※詳しくは「数学の歯車問題の基礎」を読んでみてね。
だから、
(歯車Aの動いた歯数)=(歯車Bの動いた歯数)
っていう方程式がつくれるよ。
実際につくってみると、
26x = 72y
になるね。

これが第2ステップ!
方程式をyについて解いてみよう。
えっ。
「yについて解く」の意味がわからんだって??!
そうだね。
yを左に持ってきて、xを右にどかして、yを裸にすればいいんだ。
例題でつくった方程式の、
72x = 26y
に注目してみよう。
yについて解いてみると、
72x = 26y
y = 72÷26 x
y = 13分の36x
になるね。
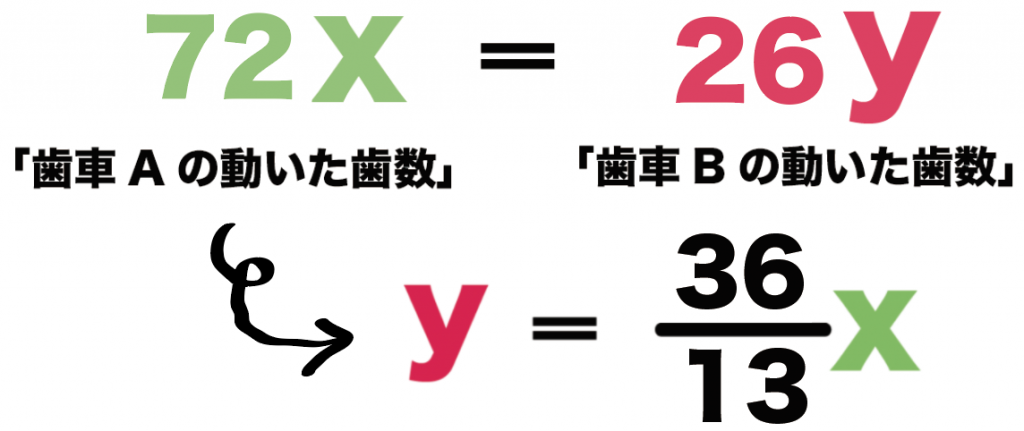
yをxの式であらわせたね。
あとすこし!
最後に、xの位置を確認しよう。
xが、
分子にあるか、
それとも、
分母にあるか
で比例か反比例かが決まってくるんだ。
っていう感じになるよ。

例題の式では、
xが分子の位置にあるよね??

ってことは、
この方程式は「比例」ってことになる。
どう?? 納得したかな??
数学で歯車の問題がでちゃった???
むずそうだって??
いや、そんなことない。
と
4ステップで攻略さ。
ガンガン歯車問題をといていこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。プリンはマンゴーに限るね。
数学の問題でよく、
歯車の問題
ってでてくるよね。
日常生活であまり歯車とかかわらないけど、
なぜか数学の問題ではよくでてくる。
だから、
解き方を知っておくにこしたことはないんだ。
今日は数学の歯車問題を解く前に知っておきたい2つのことを紹介するよ。
まずは基本をおさえよう!
歯車問題で知っておきたいことは2つさ。
歯車には2つの特徴があるんだ。
たとえば、この歯車をみてみて。
よーくみてみると、8個の歯がついているね。
しかも、3回転したらしい。。
このとき、この歯車の特徴は、
になる。
こんな感じで、1つの歯車をみるときは必ず、
の2つを確認するようにしよう!
歯車が「かみ合っている」状態について知っておこう。
「かみ合ってる」っていうのは、
2つ以上の歯車がうまいぐあいに重なっていて、
1つの歯車が回ると、別の歯車がまわる状態のことをいうんだ。
2つ以上の歯車がかみ合っているとき、あることがいえるんだ。
それは、
動いた歯数の合計が等しい
ってことさ。
これで歯車問題の大半はとけちゃうよ。
たとえば、
っていう歯車があったとしよう。
もし、この2つの歯車がかみ合っていて、歯車Aが2回転したとする。
すると、歯車Aの歯はぜんぶで、
30×2
= 60個
動いたことになるよね??
だって、歯数30で2回転してるからね。
歯車AとBはかみ合ってる。
だから、歯車Bの動いた歯数も60になるはずなんだ。
1周の歯数が20だから歯車Bは、
60 ÷ 20
= 3回転
しているはず。
こんなふうに、
「歯車がかみ合っている」 ⇒ 「動いた歯数が同じ」
っていう歯車ルールをおぼえておこう!
歯車問題で知っておきたいのは、
の2つだ。
これさえおさえれば大丈夫。
どんな歯車問題でも解けるようになるよ。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。花粉に敏感だね。
3点を通る円の中心
を作図したいときってあるよね??
たとえば、つぎの問題が宿題にだされたときとかね ↓↓
例題
下の図のように、1直線上にない3点A, B, Cを通る円の中心を求めなさい。

見た目むちゃくちゃむずそう。。
だけど、基本をおさえちまえばサクっと作図できちゃうんだ。
今日はこの、
3点を通る円の中心の作図・書き方
を3ステップで解説していくよ。
よかったら参考にしてみて。
3ステップでかけちゃうよ。
作図につかうのは、
の2つだけだね。
例題をといていこう!
例題
下の図のように、1直線上にない3点A, B, Cを通る円の中心を求めなさい。

まず弦をかこう。
隣り合った2点を直線でむすべばいいんだ。
例題でいうと、
だね??
こいつらを直線でむすんでやると、こうなる↓↓
この直線たちが円の弦になるんだ。
2本ひけばステップ1完了!
つぎは弦の垂直二等分線を作図しよう。
垂直二等分線を2本かけばいいんだ。
えっ。垂直二等分線の作図方法わすれた??
そのときは垂直二等分線の書き方を復習してみて。
例題でいうと、
まず点Aにコンパスの針をおいて半円をかく。
コンパスの脚の幅をキープしたまま、
今度は点Bに針をおく。
そして、半円をかく。
2つの半円の交点をむすぶと、点A・Bの垂直二等分線のできあがり!
今度は弦BCの垂直二等分線。
てきとうにコンパスの脚をひらいて、点Bに針をおこう。
そして、半円をかく。
脚の幅をキープして点Cに針をおく。
そして、半円をかく。
おなじように半円の交点をむすべばいいのさ。
それが垂直二等分線になる。
どう??
垂直二等分線かけたかな??
最後は交点をうつだけ。
垂直二等分線がまじわっているところに、
ぽちっと点をうてばいいんだ。
その交点が「3点を通る円の中心」になるよ。
例題でもおなじ。
垂直二等分線の交点をうってやろう。
すると、こんな感じになる↓↓
おめでとう!
この交点が「3点を通る円の中心」だよ。
でもさ、
なんで「三点を通る円の中心」がかけちゃうんだろう???
都合よすぎるよね。
その理由はずばり、
「垂直二等分線上の点」と「端の点」同士の距離が等しいから
なんだ。
例題の円の中心をOとすると、
AO = BO = CO
になるってわけ。
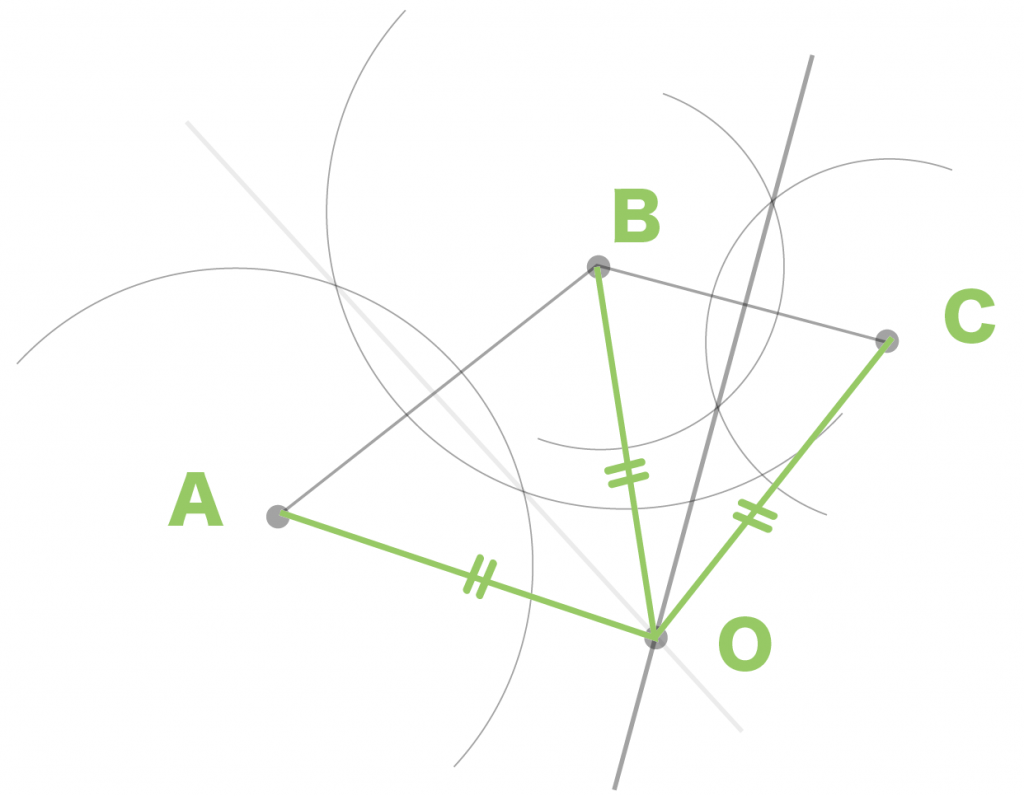
つまり、
点A, B, Cたちは点Oからの距離が等しいってことだね。
円の定義は「ある点から等しい距離にある点の集合」だから、
3点を通る円が点Oを中心にかけちゃうってわけ。
えっ。なぜ、
「垂直二等分線上の点」と「端の点」同士の距離が等しくなる
のかって?!?
それは、垂直二等分線をかいてみればわかる。
たとえば線分ABの垂直二等分線をかいて、二等分線上の点をOとしよう。
ABと垂直二等分線の交点をMとするよ。
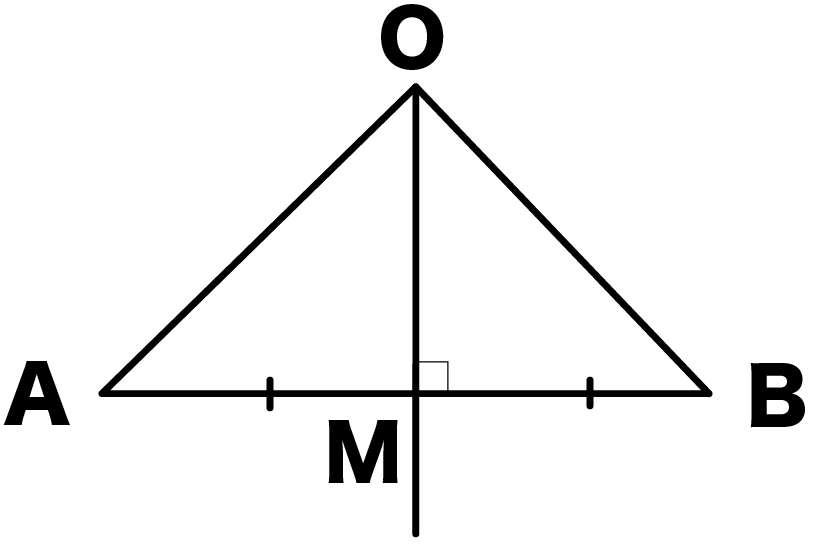
このとき、OMは垂直二等分線だから、
になる。
しかも、OMは共通だから、
2辺とのその間の角がそれぞれ等しい
という合同条件がつかえるね。
よって、
△AMO ≡ △BMO
になるわけだ。
対応する辺の大きさが等しいから、
AO = BO
になるんだ。
どう??納得いったかな??
三点を通る円の中心をかく
ってむちゃムズそう。
ただ、使うのは、
垂直二等分線だけ。
慣れてしまえば簡単なんだ。
テストまでに作図の練習をしてみよう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。ガムはミントに限るね。
三角錐の表面積の求め方には公式があるよ。
側面積をS1、底面積をS2とすると、
S1 + S2
で計算できちゃうんだ。
つまり、
(三角錐の表面積)=(側面積)+(底面積)
ってわけさ。
側面積と底面積をたすだけ。
どう??簡単そうでしょ??
つぎの2ステップで計算できるよ。
例題で公式をつかってみよう。
BC = 4 cm、CD = 3 cmの直角三角形BCDを底面とする三角錐ABCDがある。高さのAC = 6cm のとき、三角錐ABCDの体積を求めよ。
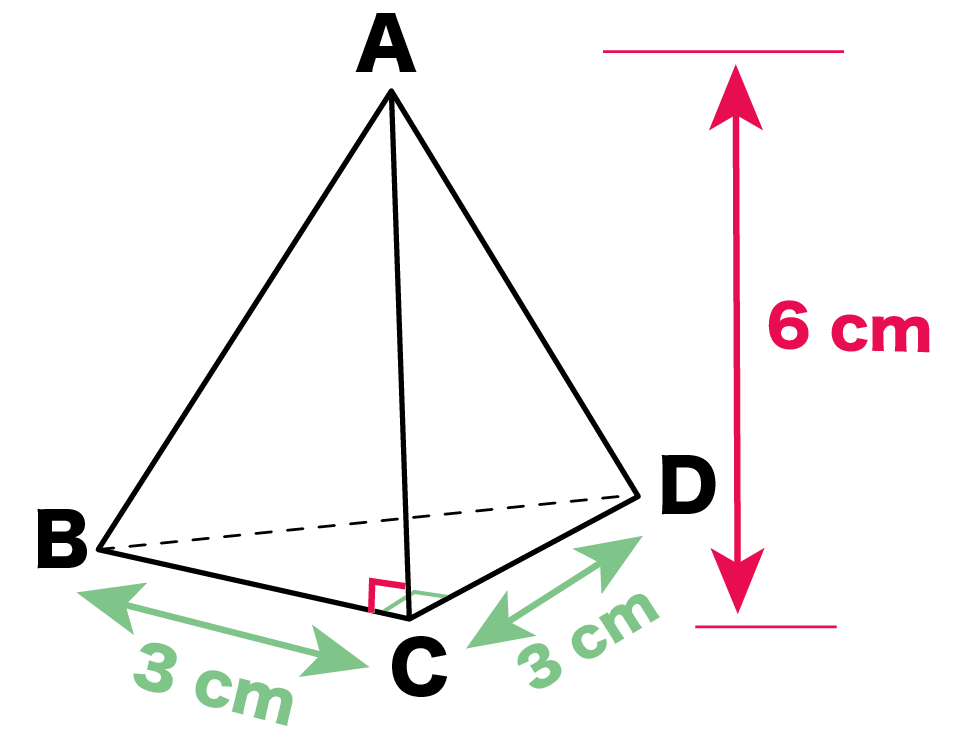
まずは三角錐の展開図をかいてみよう。
例題の三角錐の展開図を「傘タイプ」でかいてみる。
すると、こうなる↓↓
三角錐の表面積の書き方にはいろいろある。
自分の好きなようにかいてみよう!
つぎに「側面積」と「底面積」を計算しよう。
三角錐の側面と底面はぜんぶ「三角形」。
三角形の面積の公式で計算して、たしてやればいいんだ。
例題の三角錐ABCDの場合、
展開図が「正方形」になってるよね??
つまり、
側面積+底面積 = 正方形AC’CC”
になってる。
だから、
(正方形AC’CC”の面積)=(三角錐の表面積)
ってわけ。
よって、
(三角錐ABCDの表面積)
=(側面積)+(底面積)
= 正方形AC’CC”の面積
= 36[cm^2]
になるよ!
おめでとう。
三角錐の表面積の求め方もマスターしたね!!
三角錐の表面積の求め方は案外ムズい。
側面積の求め方がめんどい問題もあるからね。
ただ、三角錐の側面や底面はぜんぶ三角形。
おなじ計算方法で求めていこう!
そんじゃねー
Ken