【中3数学】いろいろな関数の問題の解き方がわかる4ステップ
いろいろな関数の問題って??
こんにちは!この記事をかいているKenだよ。トイレが近いね。
中学で勉強する関数もいよいよ大詰め。
一年生のころから、
とかたくさん関数をみてきたね。
今日は、ほんとうに最後の最後。
新しい関数を1つ勉強するんだ。
その名も、
いろいろな関数
だ。
ぶっちゃけ、名前とかとくにないんだけど、
身近でとっつきやすいよ。
マイナーっちゃマイナーなんだけど、テストにたまにでてくるんだ。
記事をよんでマスターしておこう。
いろいろな関数の解き方がわかる3ステップ
つぎの例題をといてみよう。
練習問題
つぎの表はSIMカードの1ヶ月分の料金体系をあらわしています。

データ使用量ごとに料金が決まっています。
データ使用量をx GB、月額料金をy円とするとき、つぎの4つの問に答えなさい。
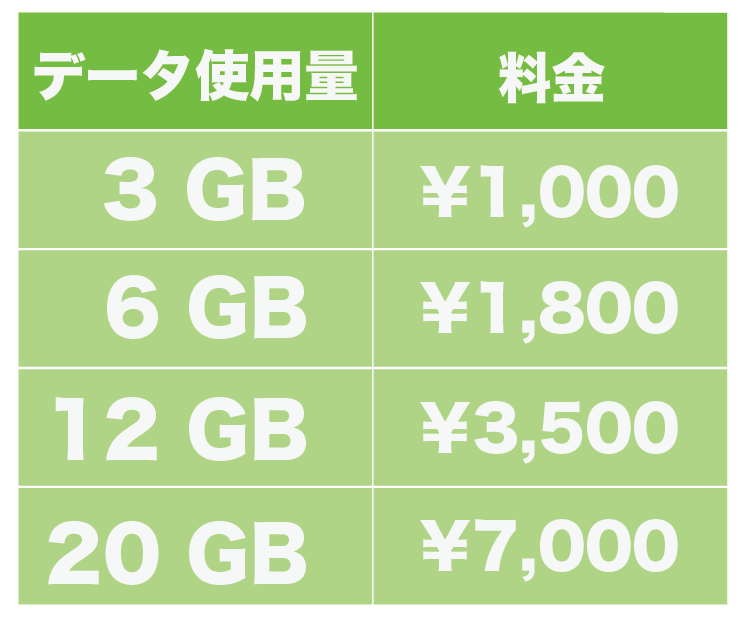
<データ使用量>
- 3GBまで(1,000円)
- 6GBまで(1,800円)
- 12GBまで(3,500円)
- 20GBまで(7,000円)
問1.
グラフをかきなさい。ただし、横軸を「データ使用量」、縦軸を「料金」とする
問2.
こいつは関数といえそうか
問3.
6GBつかうと月いくらか?
問4.
月々のおこづかいが3,000円のとき、何GBまでデータを使用できるか?
それじゃあさっそく、問1からといてみようか。
問1. グラフをかきなさい!
いろいろな関数のグラフをかいてみよう。
まず、x軸とy軸をひいてみるっと。
んで、この問題では、
- x:データ使用量
- y:月額料金
だったね??
料金体系通りに関数のグラフをかいてみよう。
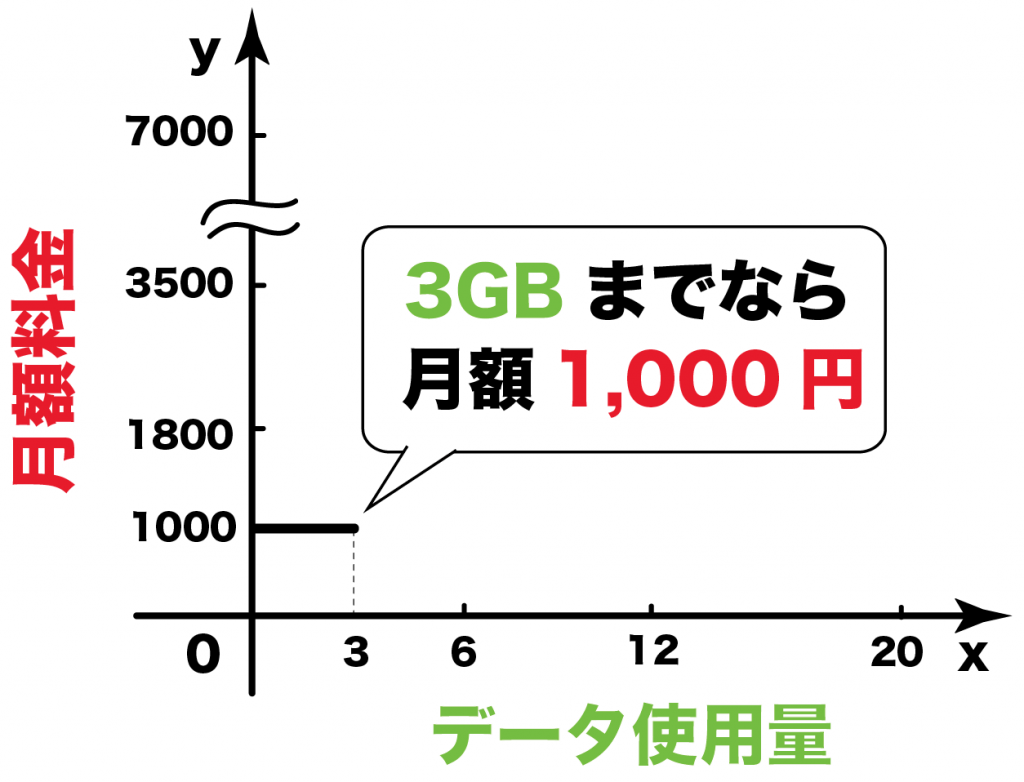
データ使用量が3GBまでのとき、
月額料金yは「1,000円」で一定だったね??
だから、このいろいろな関数のグラフは、
こうなるはずだ↓↓
こんなかんじで、
- 6GB
- 12GB
- 20GB
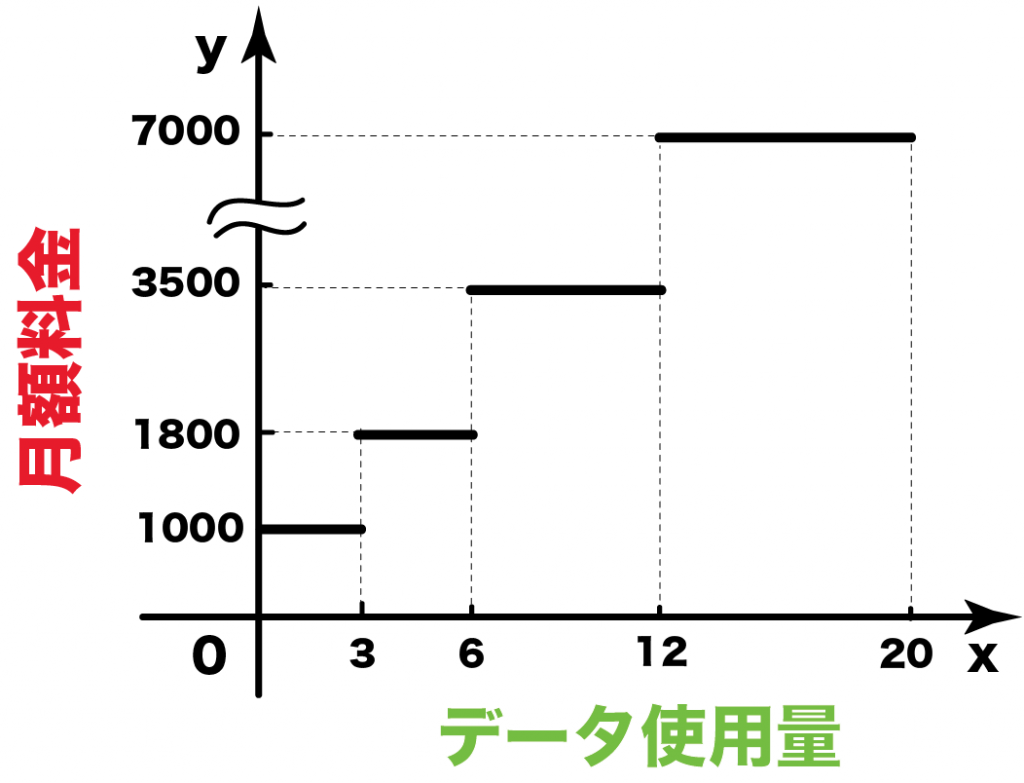
までの使用量の場合の様子をグラフにしてやると、
- 3< x ≦6のとき、y=1800
- 6< x ≦12のとき、y=3500
- 12< x ≦20のとき、y=7000
になるね。
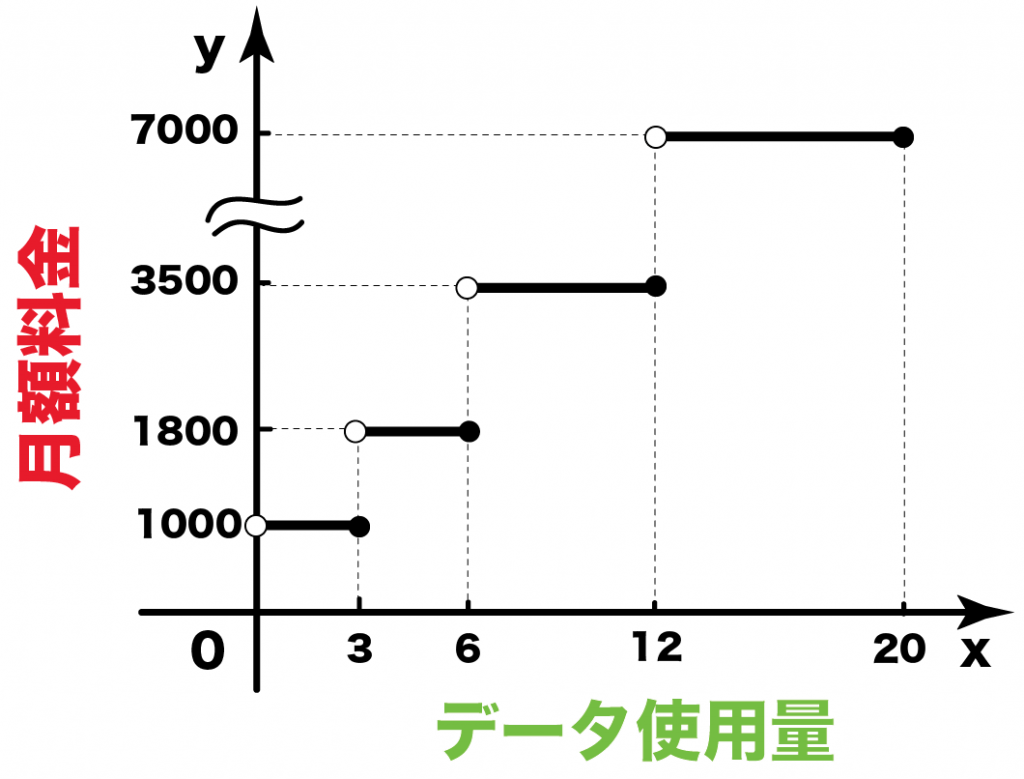
あとは、境界をかいてやるだけ。
その境界をふくまないときは「○」、
ふくむときは「●」でぬりつぶしてやればいいのさ。
今回は「〜GBまで」っていう料金体系だったから、
上限の境界はふくむわけね。
不等号に=がついてるところが「●」、それ以外は「○」だよ。。
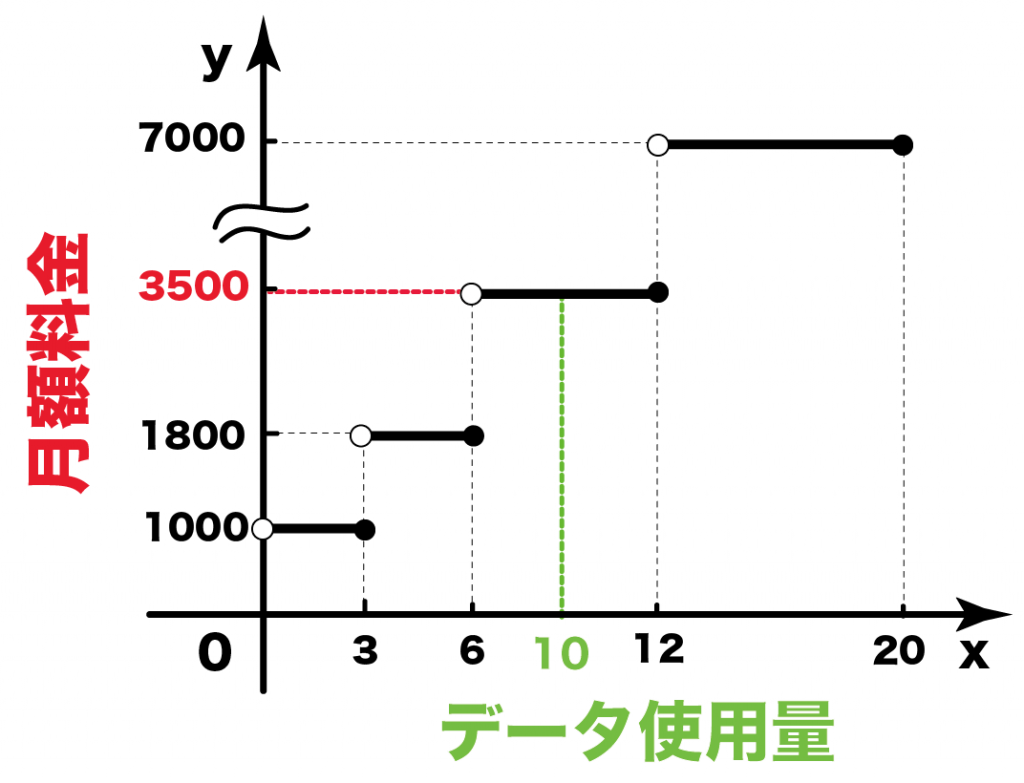
はい、グラフ完成〜
問2. 「こいつは関数???」
結論からいっちゃおう。
こいつは、まぎれもない関数なんだ。
なぜなら、
xが変化するごとにyの値が1つに決まるでしょ??
たとえば、
xが10のとき、yは3500に定まってるじゃん??
だから、こいつは関数なんだ。
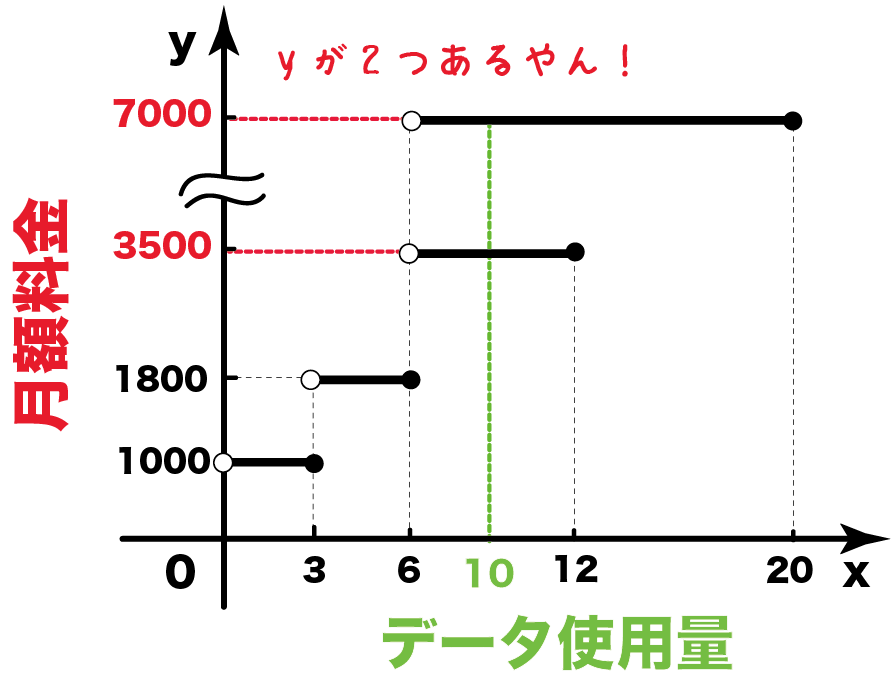
もしも、こんなかんじにグラフがぶっこわれたら、こいつは関数じゃない。
なぜなら、
xが10のとき、yの値が3500と7000の2つあるからね。
ってことで、安心してね。こいつは関数だ。
問3. 「月額使用量が6GBのとき、料金はいくら??」
つぎは、xが6のときのyの値を求めればいいね。
いろいろな関数のグラフをみてみると、
x = 6のうえには、
- y = 3500
- y = 7000
の2つがあるようにみえるよね??
だがしかし、境界に注目してほしいんだ。
棒のはしっこね。
境界のルールは、
- 黒丸:ふくむ
- 白丸:ふくまない
だったよね??
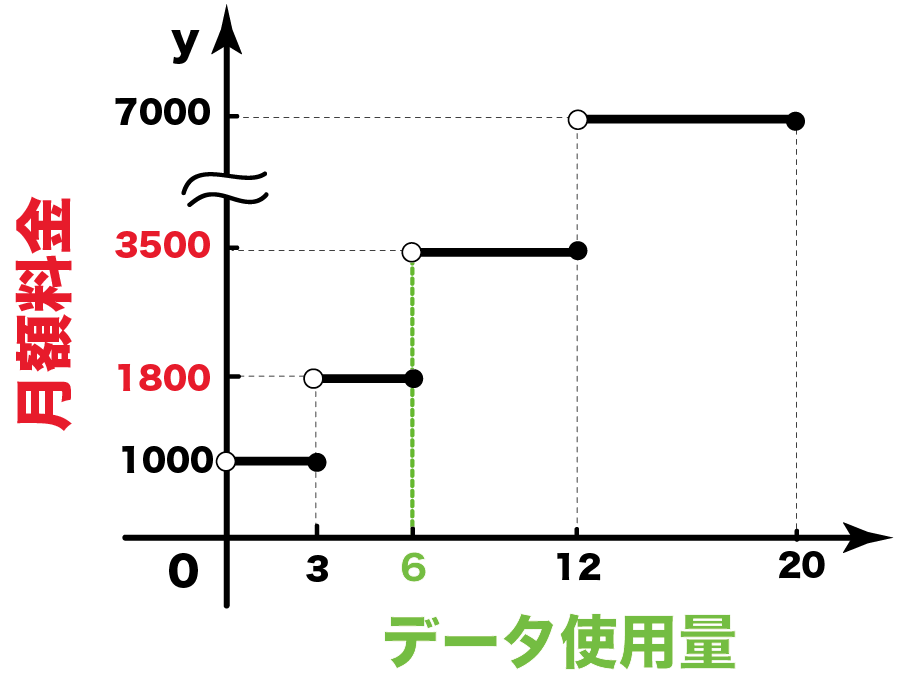
ってことは、x = 6のときをふくんでるのは、
y = 1800のグラフ
だ。
つまり、
月額データ使用量が6GBのとき、料金は1800円ってわけね。
問4. 「3,000円以内のおこづかいでおさめるには??」
今度は逆だ。
yがある値以下になるときのxの変域を求めればいいのよ。
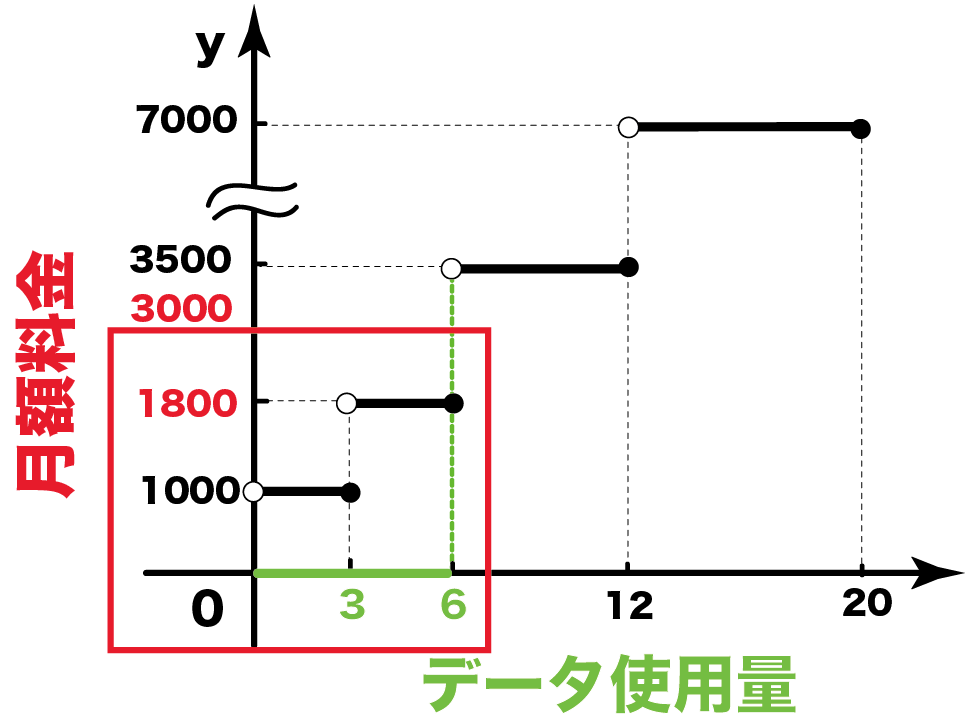
グラフをみてみると、3000円以内になるためには、
- 0<x≦3(3GBまでコース)
- 3<x≦6(6GBまでコース)
の2つなら月額3000円以内になりそうだ。
だから、
1ヶ月に6GBまでデータを使用できるね。
まとめ:いろいろな関数のポイントは「境界」
以上でいろいろな関数の問題は終了だよ。
どう?? なんだかいけそうな気がするでしょ?
ちょっと変わってる関数だけど、ポイントは1つ。
それは、
境界
だ。
グラフの端っこが含むか含まないのかに注意してね。
そんじゃねー
Ken