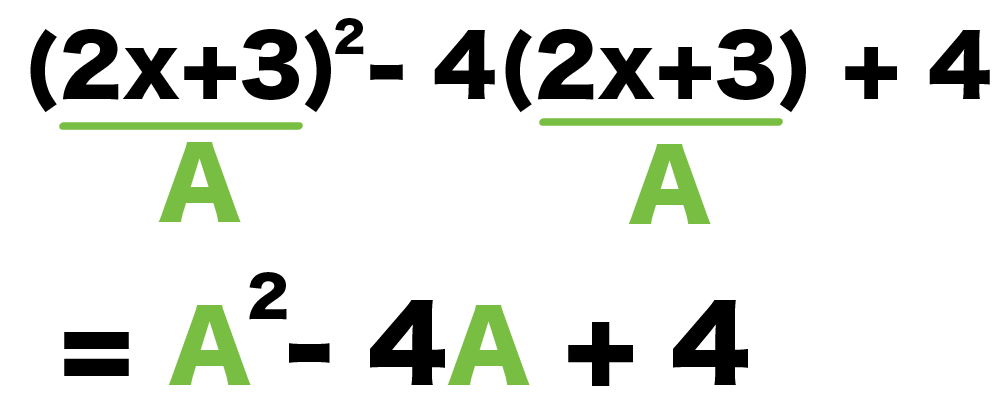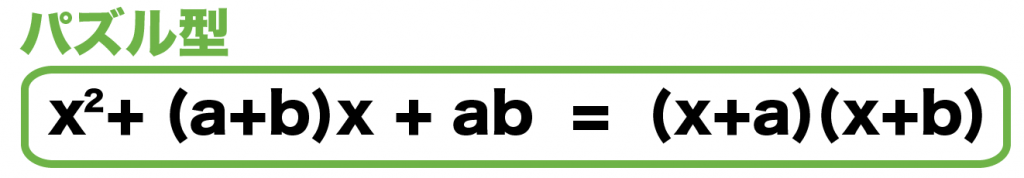因数分解の置き換え問題の解き方を知りたい！？
こんにちは！この記事をかいているKenだよ。爪は大事だね。
因数分解の応用問題の1つに、
置き換え問題
ってやつがいる。
世界には数えきれないほど因数分解の問題があるから、
ぜんぜんピンときてないかもね。
置き換え問題はつぎのようなやつだよ↓↓
つぎの式を因数分解しなさい。
(2x + 3)² – 4(2x+3) + 4
こんなかんじで、
式のなかに「おなじ文字式」がちらほらしている問題。
えっ、この問題でいうと、
（2x+3）
がちらほらしてるじゃん？？
このタイプの解き方は一択。
チラホラしている文字式を「別の文字」で置き換えればいいんだ。
むちゃ解きやすくなる。
だから、
置き換えタイプの因数分解
とよんでるよ。
今日はこいつの解き方を5ステップで解説していくね。
因数分解の置き換え問題がわかる4ステップ
置き換え問題は4ステップでとけちゃうよ。
- おなじ文字式をみつける
- 文字式をAとおく
- 因数分解する
- Aに文字式を代入する
それじゃあ、さっきの例題をといていこう。
例題
つぎの式を因数分解しなさい。
(2x + 3)² – 4(2x+3) + 4
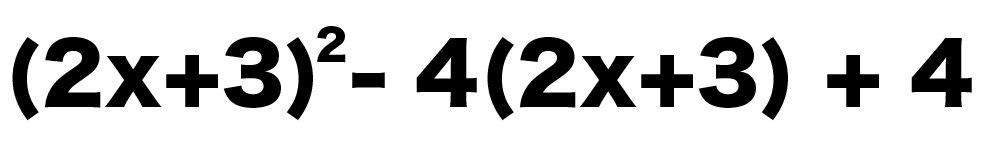
Step1. おなじ文字式をみつける
まず、式の中にふくまれている、
2回以上登場する文字式
をみつけてみよう！
これが探せないと始まらないね。
例題をみてみると、あきらかに、
2x+3
が何回もでてきてるよね？？
まあ、、2回だけどねw
こいつみたいに、怪しい文字式をみつけてみよう！
Step2. 何回もでてきた文字式をAとおく
つぎは、2回以上でてきた文字式を「A」とおこう。
そう、
アルファベットのAだ。
他の文字と区別するために大文字にしてね。
すると、例題ではこんな感じで置き換えられるよ↓↓
A² – 4A + 4
これが第2ステップ。
Step3. Aについて因数分解する
つぎはふつーに因数分解してみよう。
置き換えた式を因数分解の解き方で計算すればいいのさ。
例題の式は、
A² – 4A + 4
に生まれ変わったよね？？
こいつを公式で因数分解してやろう。
因数分解したい文字式の項を数えてみると、
「3つ」あるね。
3つの項を因数分解する公式は、
(x+a)(x+b) = x² +(a+b) +ab
だったよね？？
これはパズル型の公式。
かけて右に、たして真ん中になる数の組み合わせを考えればいいんだ。
例題の、
A² – 4A + 4
でいうと、
- かけて4
- たして-4
になる組み合わせを考えればいいんだ。
まず、かけて「4」になる組み合わせは、
- 2×2
- (-2)×(-2)
- 1×4
- -1×(-4)
の4通りだ。
このうち、たしたら「-4」になるのは2番目の、
- -2
- -2
だね。
こいつらを公式のaとbに代入してやると、
A² – 4A + 4
= (A-2)(A-2)
= (A-2)²
になるね。
Step4. Aに代入しなおす
最後はAに文字式を代入しなおそう。
つまり、
Aをもとの文字式にもどすってことだね。
例題では、
A = 2x + 3
っておいてたよね？？
こいつをさっき因数分解した、
(A-2)²
に代入してみよう。
さっそく代入してみると、
(A-2)²
= (2x +3 -2)²
= (2x +1)²
になるね！
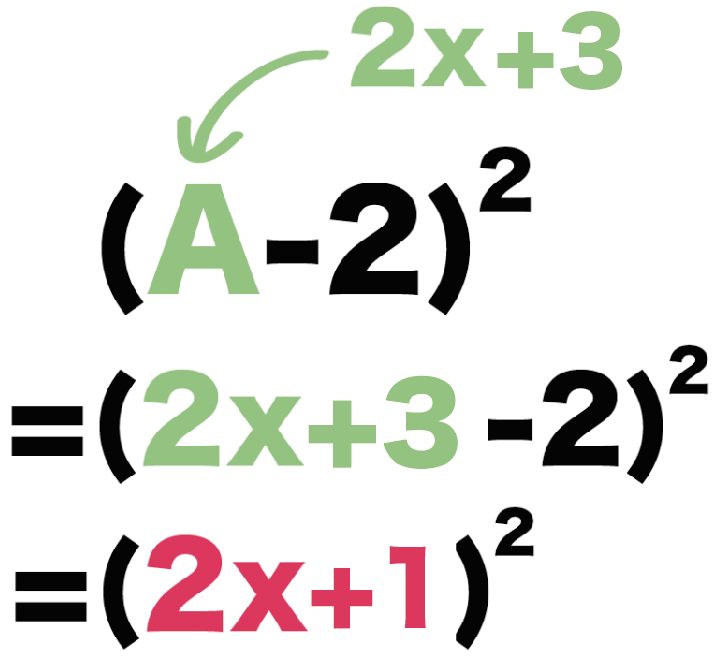
おめでとう！
これで置き換えの因数分解もマスターだ。
まとめ：置き換えの因数分解は置き換えて代入しなおす
因数分解の置き換えの問題？？
びびることはない。
おなじ文字式をいったんAとおいて、因数分解する。
最後にAをもとにもどせばいいんだ。
ガンガン置き換えていこう！
そんじゃねー
Ken
因数分解の攻略記事
