円錐の体積の求め方の公式って？？
こんにちは、この記事をかいているKenだよ。犬の散歩が趣味だね。
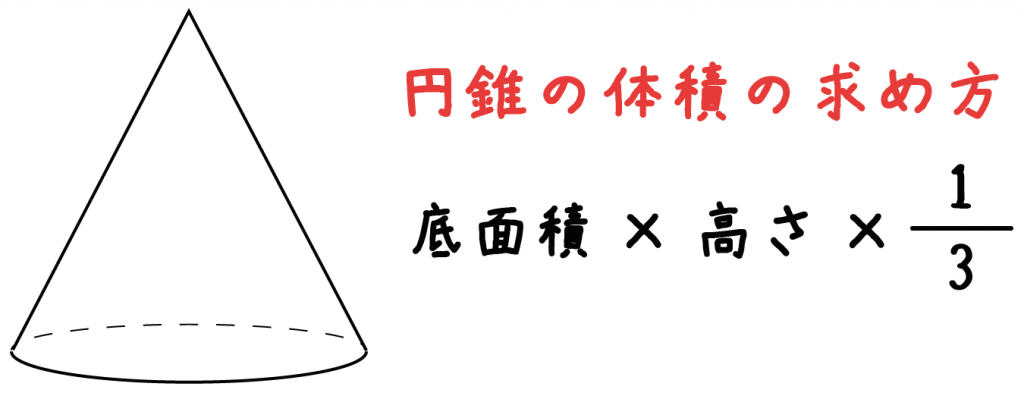
円錐の体積の求め方の公式は、
底面積×高さ×1/3
だったよね。
もう少し詳しくかいてあげると、
半径×半径×円周率×円錐の高さ×1/3
になるんだ。
これなら3秒で円錐の体積を計算できちゃいそうだね。
ただ、そのスピード感について来れないときもあるだろうから、今日は、円錐の体積の求め方をチョーゆっくり公式をつかってといてみるよ。
「円錐の体積の求め方がどうしてもわからん！」
ってなったときに参考にしてみてね！
円錐の体積の求め方がわかる3つのステップ
円錐の体積の求め方はつぎの3ステップをで計算できちゃうよ。
つぎの例題をときながらみていこう！
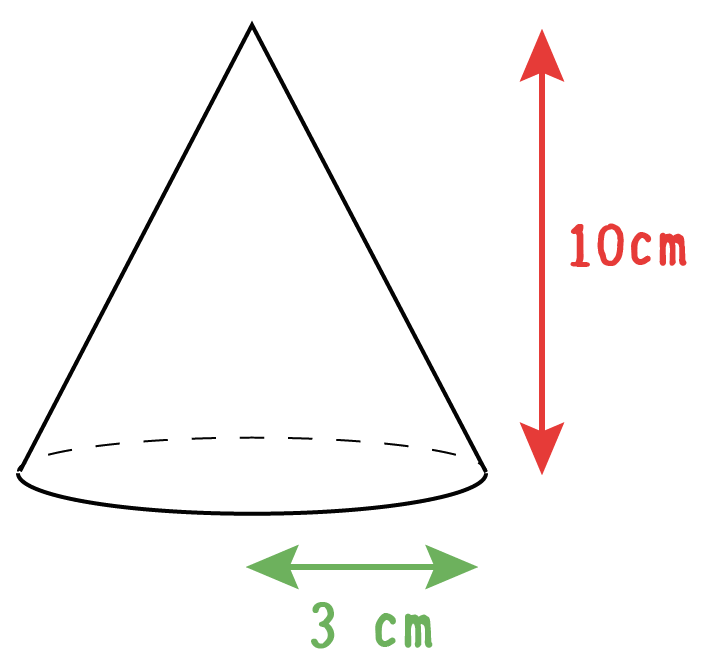
半径3cm、高さ10cmの円錐の体積を計算して。
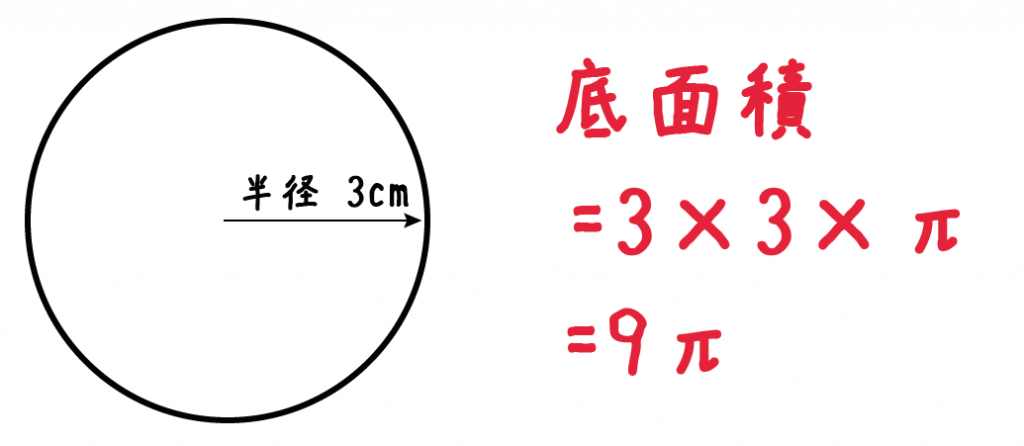
Step1. 円錐の「底面積」を計算するっ！
まずは円錐の底面積を計算してみよう。
円錐の底面は「円」になっているね。
ってことは、円の面積の公式をつかって、ちゃちゃっと面積をだしてやればいいんだ。
円の面積の求め方は、
半径×半径×円周率
で求められるよね？？
だから例題の円錐の底面積は、
3×3×π= 9π
となるんだ。
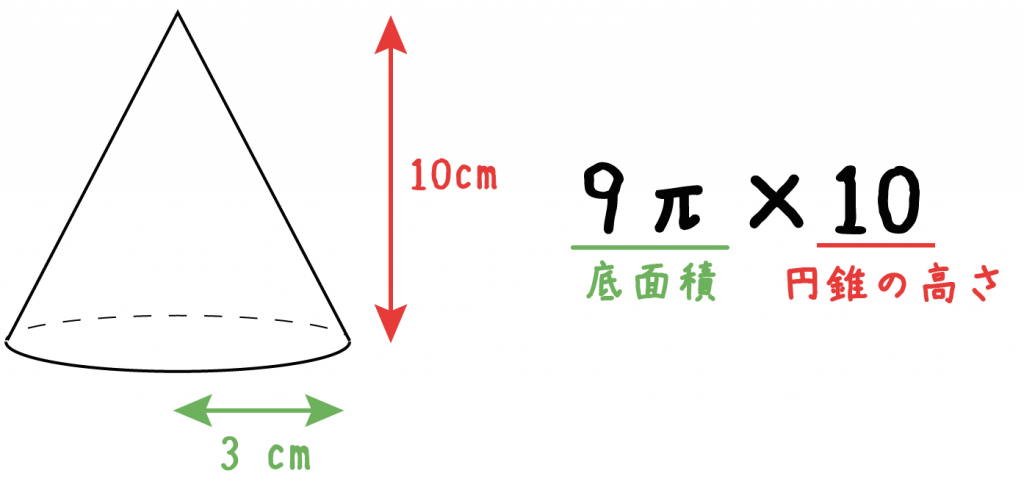
Step2. 円錐の底面積に「高さ」をかける！
つぎは「円錐の高さ」を底面積にかけてみよう。
例題の円錐の高さは10cmなので、
9π×10= 90π
になるっ！
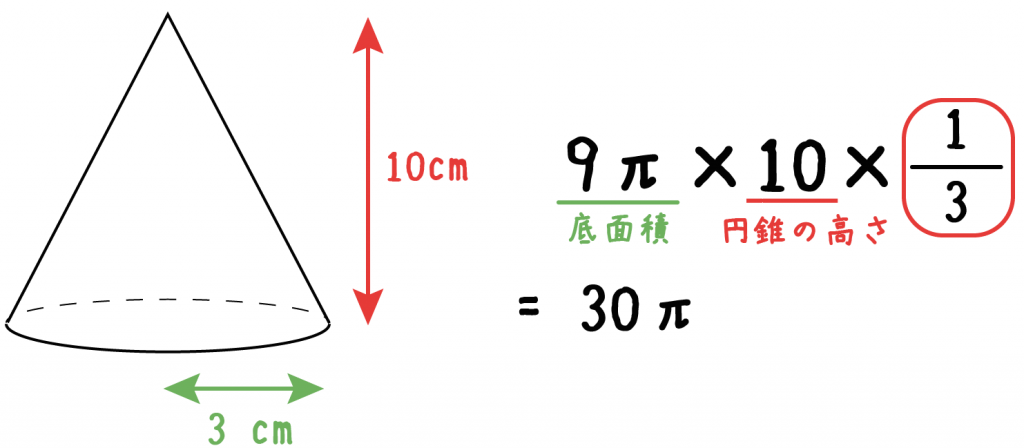
Step3. 「1/3」をかけるっ！！
いよいよ最後のステップ。
Step2で求めた「底面積×高さ」の値に「1/3」をかけてみよう。
例題でいうと、「底面積×高さ」は「90π」だったから、
最終的な円錐の体積は、
90π×1/3=30π
になる！
おめでとう。これで円錐の体積を計算できるようになったね。
なぜ「1/3」をかけるのか？？
えっ。なんで「1/3」をかける必要があるのだって？！？
その理由は高校数学で勉強する「積分」を使えば説明できるんだけど、完全に中学数学の範囲をこえているんだ。
とりあえず、中学数学では、
錐体（先がとんがってるやつ）の体積を求めるときは「1/3」をかける
ということを覚えておこう。
だから、三角錐の体積を求めるときも「1/3」をかけるんだ。
まとめ：円錐の体積の求め方の公式はシンプル
円錐の体積の求め方はどうだったかな？？
底面積×高さ×1/3
という公式は意外とシンプルだったよね。
最後に1/3をかけることさえ忘れなければ、ぜったいにテストでも間違えないはず。
分数がややこしかったら、「÷3」をするって覚えてもいいね。
この公式をつかってじゃんじゃん円錐の体積を計算していこう！
円錐の体積の求め方をマスターしたら、次は「円錐の表面積の求め方」を勉強してみよう。
そんじゃねー
Ken
