【高校数学 I 】二次関数の軸と頂点を求める公式と覚え方

前回、平方完成で二次関数の軸と頂点を求めるやり方、勉強してきた。
でもさ、毎回平方完成してしないとなんて、大変不便だよな。
そんなことを思っちゃったお前に朗報だ。
じつはな、二次関数の軸と頂点を求める3秒で求められる公式があるんだ。
それは次のものだ。
$y=ax^2+bx +c$ という二次関数があったとしよう。このとき、
$軸= -\frac{b}{2a}$
$頂点 (-\frac{b}{2a},-\frac{b^2-4ac}{4a})$
なんだ。
例えば、次の二次関数があったとしよう。
$$y=2x^2+5x +17$$
この二次関数において$a・b・c$は次のようになる。
- $a=2$
- $b=5$
- $c=17$
この3つの$a・b・c$を先の公式に代入してやれば、軸と頂点を求められるぞ。
軸
$-\frac{b}{2a}$
=$-\frac{5}{2×2}$
=$-\frac{5}{4}$
頂点
$(-\frac{b}{2a},-\frac{b^2-4ac}{4a})$
$=(-\frac{5}{2×2},-\frac{5^2-4×2×17}{4×2})$
$=(-\frac{5}{4},-\frac{25-136}{8})$
$=(-\frac{5}{4},-\frac{111}{8})$
なぜ二次関数の軸と頂点が公式で求められるのか?
全く便利な公式だぜ。
$軸= -\frac{b}{2a}$
$頂点 (-\frac{b}{2a},-\frac{b^2-4ac}{4a})$
よかったな、現代に生まれてさ。
でも、なぜこの公式が使えるのか気になってこないか。
その理由は、二次関数$y=ax^2+bx +c$を平方完成して軸と頂点を求めてやればわかるぞ。
試しにやってみよう。
$y=ax^2+bx +c$
$y=a(x^2+\frac{b}{a}x) +c$
$y=a\{(x+\frac{b}{2a})^2-\frac{b^2}{4a^2}\} +c$
$y=a(x+\frac{b}{2a})^2-\frac{b^2}{4a} +c$
$y=a(x+\frac{b}{2a})^2+\frac{4ac-b^2}{4a} $
$y=a(x+\frac{b}{2a})^2-\frac{b^2-4ac}{4a} $
よし、これで二次関数の基本形、
$$y=a(x-p)^2 + q$$
になった。
$p$と$q$に対応する値を発見して軸と頂点を求めような。
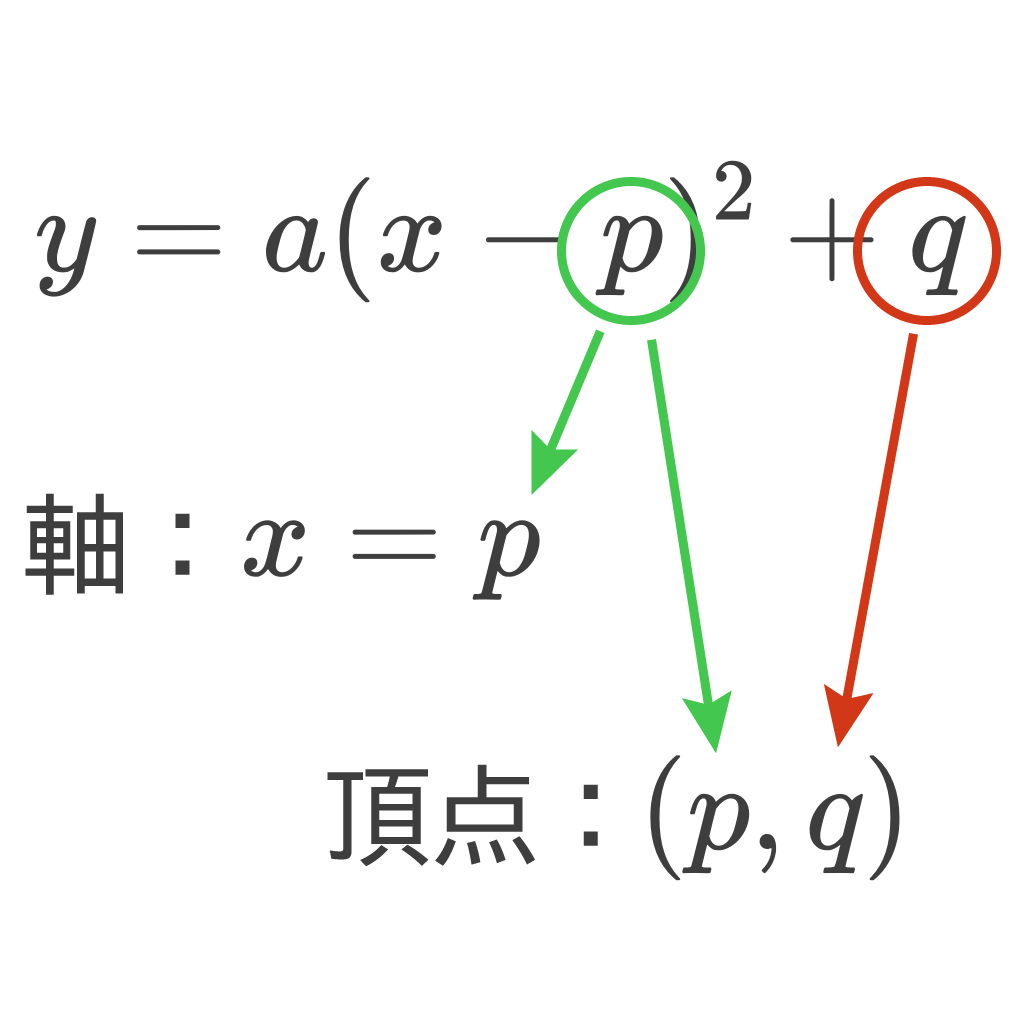
今回は$pが-\frac{b}{2a}$、$qが-\frac{b^2-4ac}{4a}$だから、次のような軸と頂点になるな。
- $軸= -\frac{b}{2a}$
- $頂点 (-\frac{b}{2a},-\frac{b^2-4ac}{4a})$
これ、さっき紹介した公式だよな。
だから、ぶっちゃけ、平方完成から軸と頂点を求めるやり方を習得しておけば公式を忘れても大丈夫ってわけよ。
結局、二次関数の軸と頂点は平方完成で求めるやり方を知っておくべきなんだな。
二次関数の軸と頂点を求める公式の覚え方
平方完成でいつも軸と頂点を求めるのはちょっと…やっぱ公式使いたいな・・・・
そんなお前のために、公式の覚え方を伝授してやる。
それは次のものだ。
塾(じゅく)に間(マイナス)に(2)合(a)わないビー(b)チ姫
塾長(ちょうてん)迷(まいなすよん)え(a)!美人(bじじょう)がひく(–)夜(よん)のエース(ac)
1つ目の「ビーチ姫」が軸、2つ目の「塾長」は頂点のy座標の覚え方だ(x座標は軸と同じだからいいだろ?)。
ちょっと絵にもしずれえ怪しい感じになっちまったが、どうだ?

この覚え方で公式を覚えるのか?
それとも平方完成によって二次関数の軸と頂点を求める方法をマスターしておくのか?
それはお前次第だ。

それじゃな!



