3分でわかる!定義域と値域の違い・覚え方

高校数学の二次関数では多くのニューワードが出現するぜ。
この前勉強した「象限」に加えて、今回は
- 定義域
- 値域
が新登場。
しかも、この2つはごっちゃにしやすく間違えやすいときてるんだ。
ってことで、今日は定義域と値域の違いとその覚え方を解説していくぞ。
定義域と値域の意味の違いとは?
ズバリ言ってしまおう。
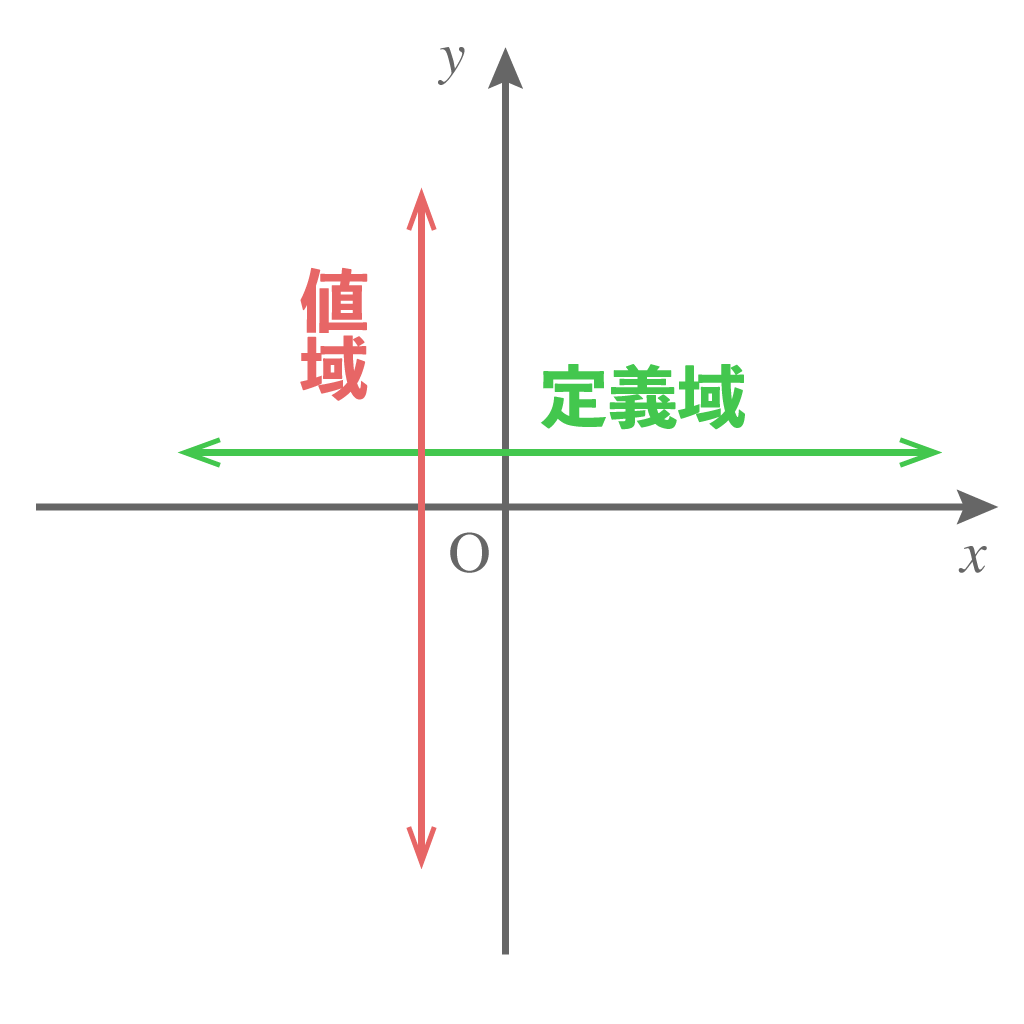
定義域は、関数 $y = f(x)$ の
$x$の範囲のこと
だ。
一方、値域は
$y$の範囲のこと
なんだ。
例えば、一次関数の
$$y = 3x +1$$
があったとしよう。
で、この関数の$x$の範囲が
$$-1 <x< 2$$
だとしよう。
そのとき、$y$の範囲はそれぞれ$x$の範囲の端っこを代入して求めてやると、
$$-2 <y< 7$$
になるよな。
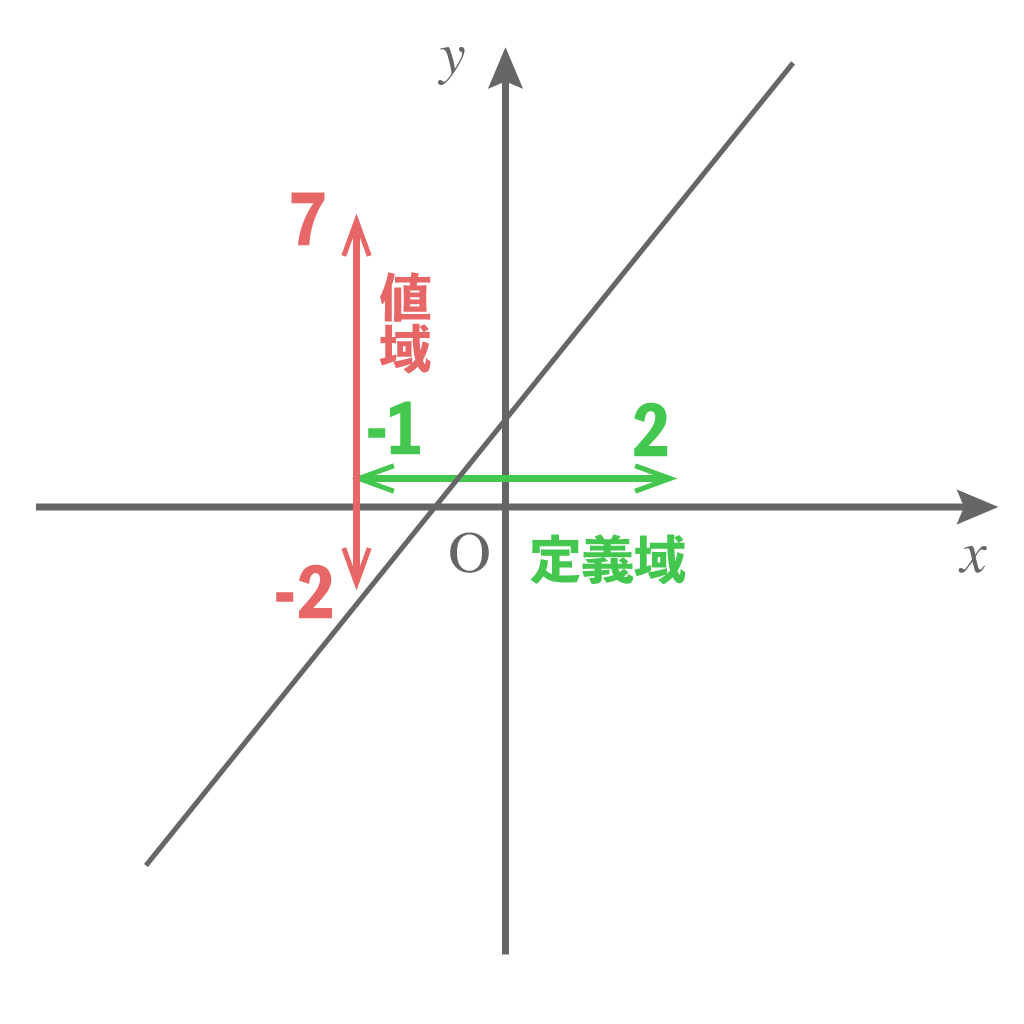
この場合、
「$-1 <x< 2$」が定義域で「$-2 <y< 7$」が値域だ。
それじゃあ、なぜ定義と値域という名前がついているのか?? まあ、気になるよな。
その理由は、関数の$x$と$y$が持つ意味をそれぞれ冷静に考えるとしっくりくるぞ。
$x$は関数に入れる値だよな。入力、インプットに相当するんだ。
関数を「自動販売機」に例えるなら、自動販売機に入れるお金が$x$だ。
つまり、この$x$はプレイヤーが自分で決められる値だ。
つまりつまり、$x$の範囲は自分で決められる、自分で定義できるってわけよ。
ゆえ、この$x$の範囲は自分で定義できる値の範囲、つまり「定義域」になるわけだ。
一方、$y$はどうだろうか??
$y$は、入力値$x$に対して関数から出てくる値のことだ。
つまり、関数から出てくる出力、アウトプットのことさ。
関数を自動販売機と例えるなら、お金を入れて出てくる「飲み物」そして場合によっちゃ、「おつり」も$y$だな。
つまり、$y$の範囲は入力値$x$の値に反応して出てくる値さ。
ゆえ、$y$の範囲は「値域」ってことよ。
定義域と値域の覚え方
だいたい定義域と値域の違いもしっくりきただろ??
でもさ、これ、テストでごっちゃになったらまずいよな。
定義と値域の違いを忘れちまったら、野生の勘で解くしかねーからな。
そんな覚えておきたい「定義と値域の違い」の覚え方を伝授しておこう。
まず定義域からだな。
定義域の覚え方は
低木
をイメージしてくれ。

低木とは、
高さ2メートル以下の樹木のこと
だったよな。
人間界では低木は「ていぼく」と読むそうだが、今回は特別に
低木(ていぎ)
と読んでくれ。
で、この低木(ていぎ)がx軸上に生えている世界、想像できるな??
低木(ていぎ)が生えている範囲、つまり、$x$の範囲は
定義域(ていぎいき)
になるわけだ。
で、値域はどう覚えようか??
ここで登場してもらうのが、
地域のみなさん
だ。

地域のみなさん、高いところが好きだろ?
十中八九、エレベーターに乗るはずだ。

で、エレベーターで$y$軸上を移動している世界を想像するんだ。
地域(ちいき)のみなさんが移動する範囲。
すなわちそれは、縦方向の$y$軸上で、
値域(ちいき)
だ。
地域のみなさんの力を借りれば、値域の意味を思い出せるはずだ。
うん、以上が定義域と値域の意味の違いと覚え方だ。
最後に表で復習しとくか。
| 域の種類 | 意味 |
|---|---|
| 定義域 | $x$の範囲 |
| 値域 | $y$の範囲 |
この意味の違いをマスターしたら、次からは実践的な問題を解いていくぞ。

それじゃあなぁ!


