台形の問題にもいろいろある！
こんにちは！この記事を書いているKenだよ。引き、寄せたね。
図形の問題で、なぜか狙われやすいのが
「高さがわからない台形」の面積を求める問題
だね。
例えば次のようなやつ↓
次の台形の面積を求めよ。
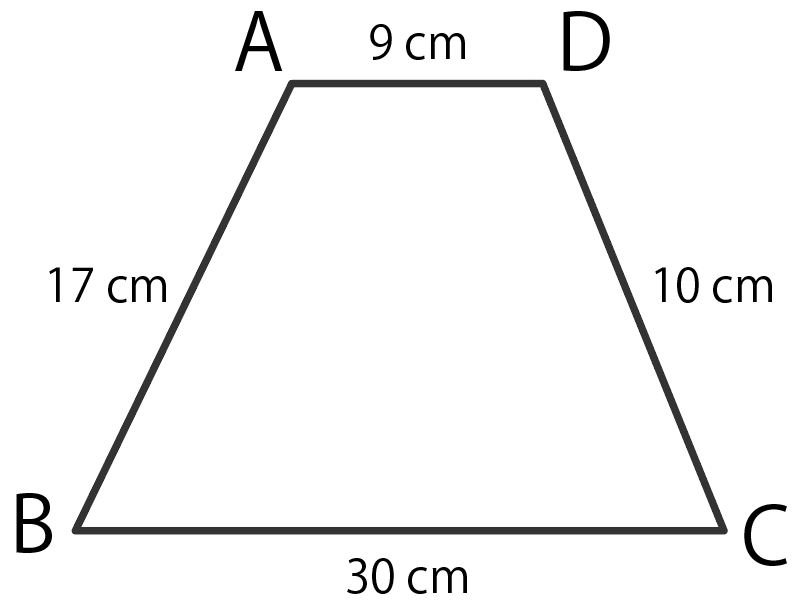
たしか台形の面積の求め方は、
（上の辺＋下の辺）×高さ÷2
だったはず。
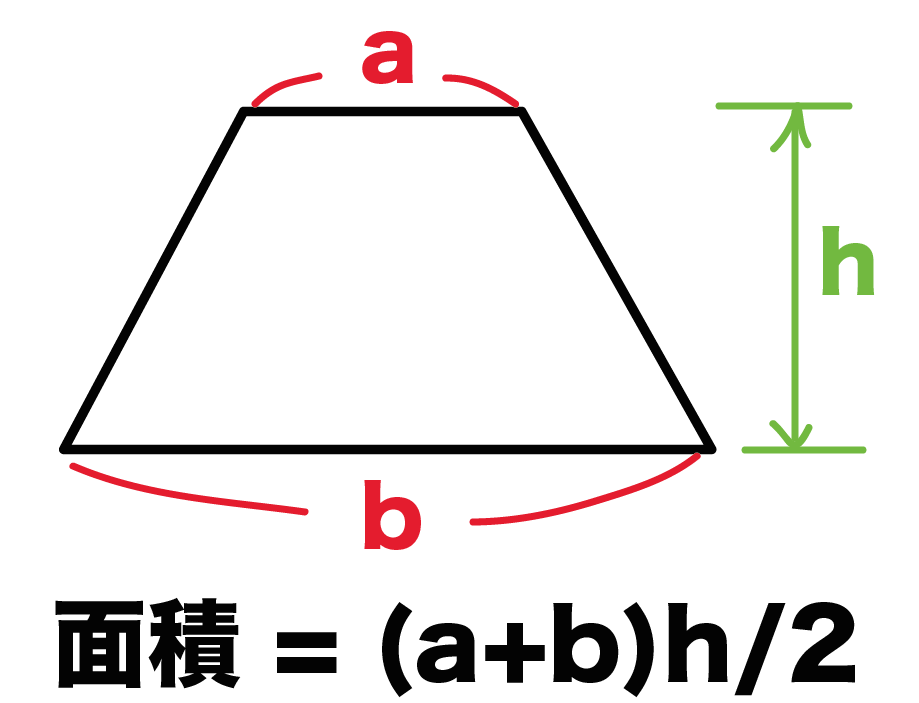
「上の辺」と「下の辺」の長さはわかってるけど「高さ」がわからないから、台形の面積の公式が使えねえ！
いったいぜんたい、どうすりゃいいんだろうね？？
高さがわからない台形の面積の求め方
そういう時は次の5ステップを踏んでみよう。
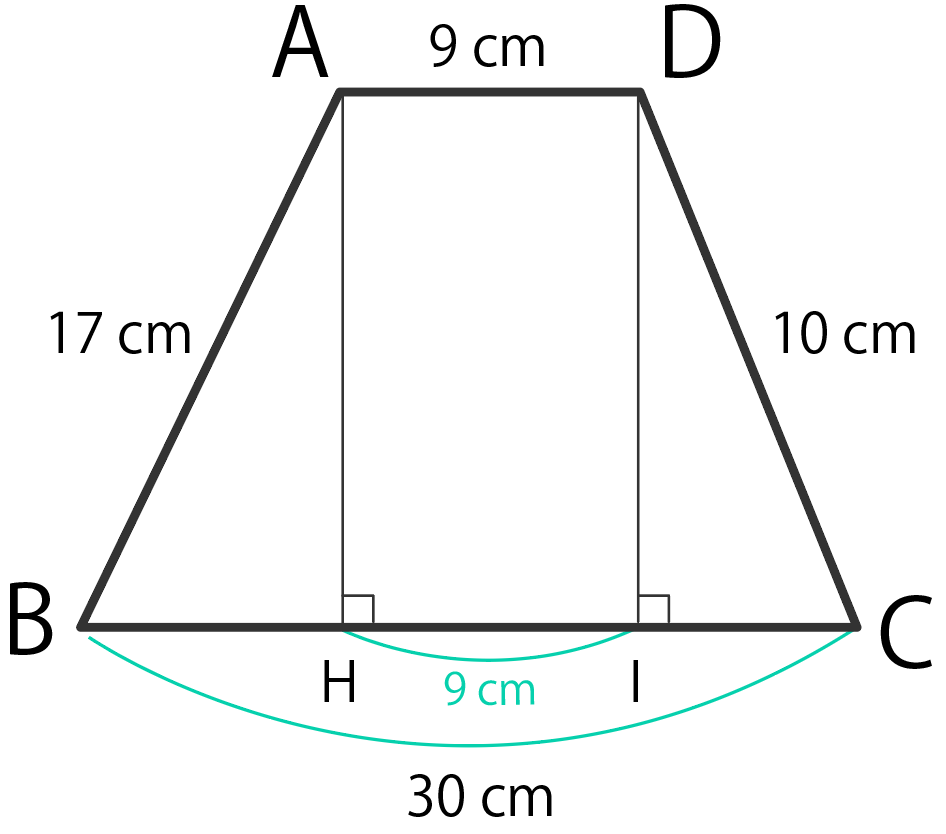
Step1. 上の頂点から垂線を下ろす
上の辺から底辺に「垂線」をおろしちゃおう。
上の頂点から下に垂線を引けばいいよ。
ってことで、垂線は2本。
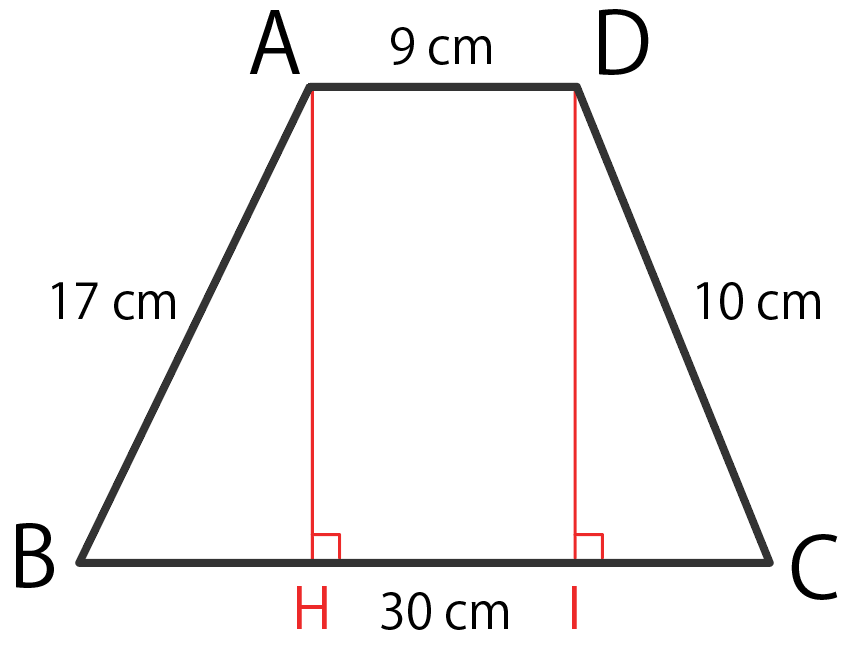
交点をそれぞれ、
- H
- I
としてみようか。
Step2. 長方形を見つける
さっきまで「台形1つ」だった図形が、
- 2つの直角三角形
- 1つの長方形
の3つに分かれるはず。
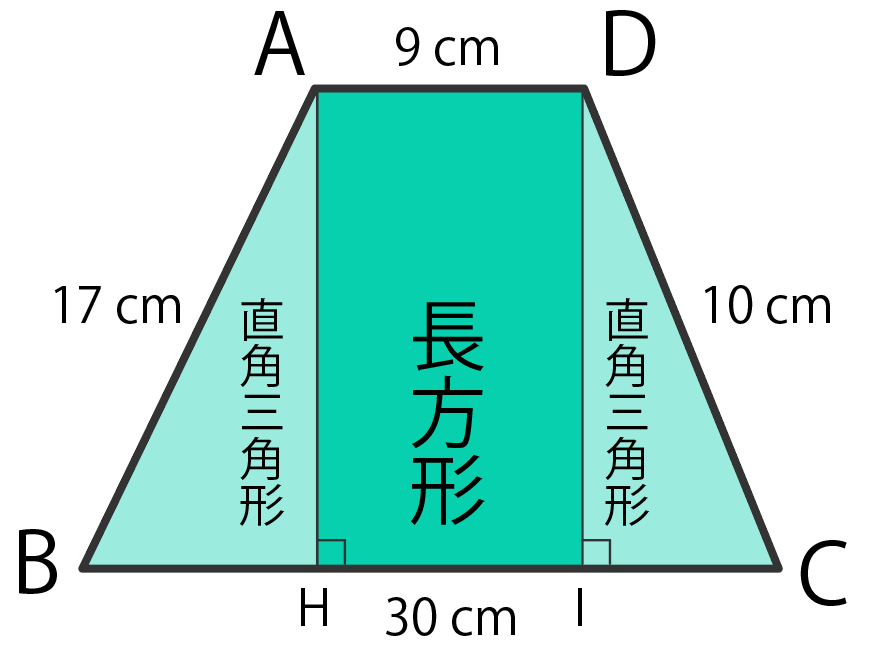
なぜ四角形AHIDが長方形なのかというと、
4つの辺が互いにそれぞれ平行
という平行四辺形の条件を満たしていて、かつ、
すべての内角が等しい（それぞれ90度）
からだね。
長方形の性質には「向かいあう辺の長さは等しい」ってやつもあった。
つまり、長方形AHIDの「HI」は向かい合った「AD」に等しいことになる。
ってことで、
HI = AD = 9 cm
だ。
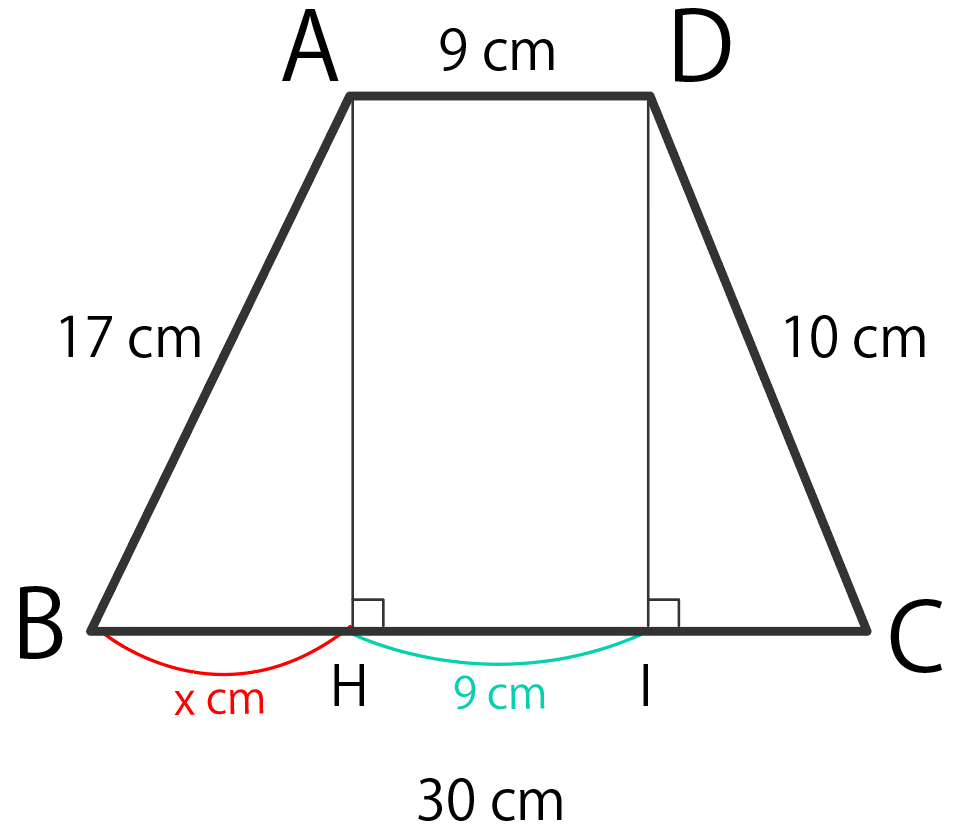
左の三角形の底辺をXとする
「左下の線分の長さ」をxと置いてみよう。
この例題でいうと、
BH = x cm
だね。
すると、ICもxで表せるね。
ICの長さは、
BC – HI – BH
= 30 – 9 -x
= 21 – x
2つの直角三角形の高さが等しいことを利用する
ここで、
両サイドにできた「直角三角形の高さ」に注目。
四角形AHIDは長方形だから、向かい合う辺の長さは等しい。よって、
AH = DI
なはず。
つまり、
2つの直角三角形（ABHとDCI）の高さは等しいんだ。
この事実を利用して、二次方程式を作ってみよう。
2つの直角三角形の高さをxで表して、イコールで結べばいいんだ。
三平方の定理を2つの直角三角形で使うと、
AH = DI
AB² – BH² = DC² – IC²
17² – x² = 10² – (21-x)²
x = 15
と、「BHの長さ」が出てくるね。
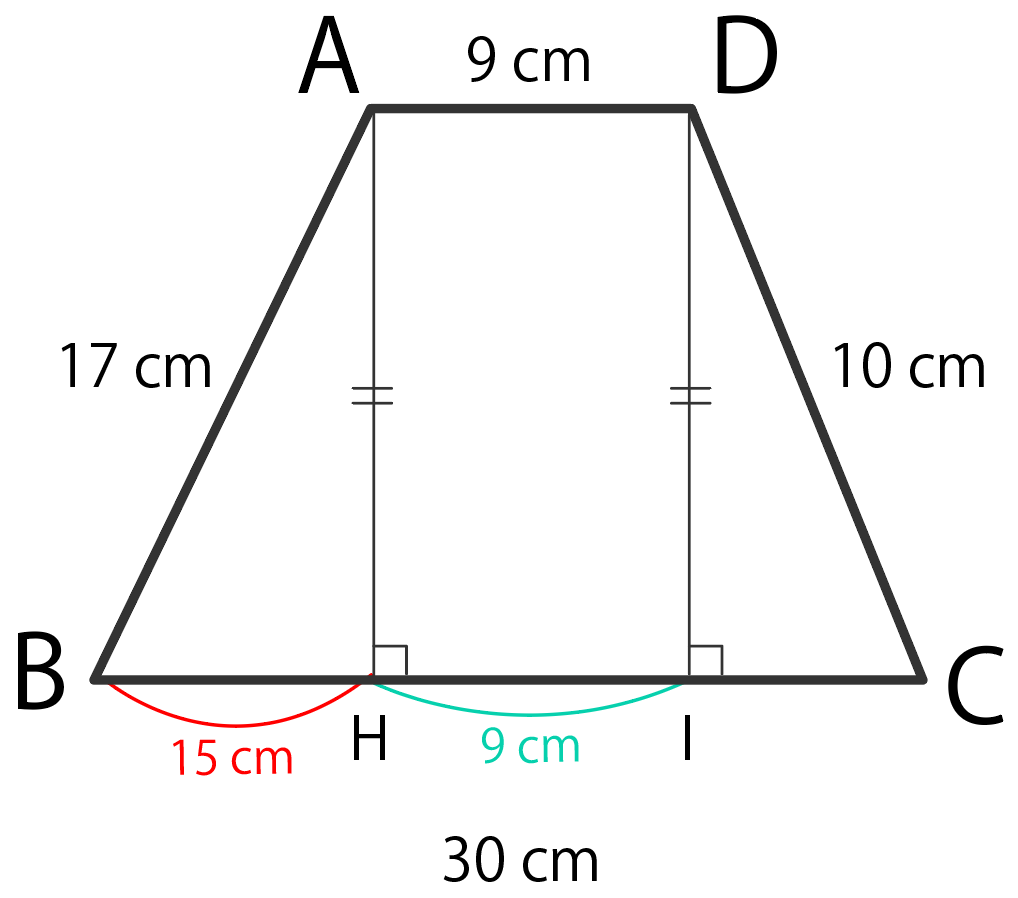
高さを求める
あとは三平方の定理で「台形の高さ」を求めるだけ。
直角三角形ABHに注目してみると、
- AB = 17 cm
- BH = 15 cm
とわかっているから、残りのAHは、
AH² = AB² – BH²
AH² = 17² – 15²
AH = 8
になるね。
つまり、この台形の高さは「8 cm」ってわけ。
台形の面積の公式を使う
やっと台形の高さがわかったから、あとは公式を使うだけ。
台形の面積の公式は、
（上辺＋下辺）× 高さ ÷ 2
だったよね？
まんま公式を使うと、
（上辺＋下辺）× 高さ ÷ 2
= （9 + 30）× 8 ÷ 2
= 156
したがって、この台形の面積は「156 cm² 」なわけだ。
という感じで、「高さがわからない台形の面積」も三平方の定理を屈指すれば解けるね。
二次方程式の解き方がむずいから、二次方程式の解き方もいっしょに復習しておこう。
そんじゃねー
Ken
