こんにちは!この記事をかいているKenだよ。アキレス腱のばしたね。
平均値の求め方にはいろいろある。
度数分布表から求めたり、
平均値の求め方の公式にぶちこんだり。
これだけ平均値に詳しくなったんだから、
どんな平均値の問題もクリアできる!!
・・・・・
って安心してない??
うん、してたね。
じつはあと1つ、マスターしておきたい平均値の求め方があるんだ。
それは、
ヒストグラムをつかった平均値の求め方
だ。
こいつはぶっちゃけ影が薄い。
だけど、テストにでてくることがあるんだ。
そこで今日は、
ヒストグラムから平均値を求める方法を4ステップで解説してみたよ。
よかったら参考にしてみてね。
つぎの4ステップさ。
例題をといていこう!
例題
つぎのヒストグラムは3年B組の数学の得点の分布を表したものです。このヒストグラムから平均値を求めなさい。
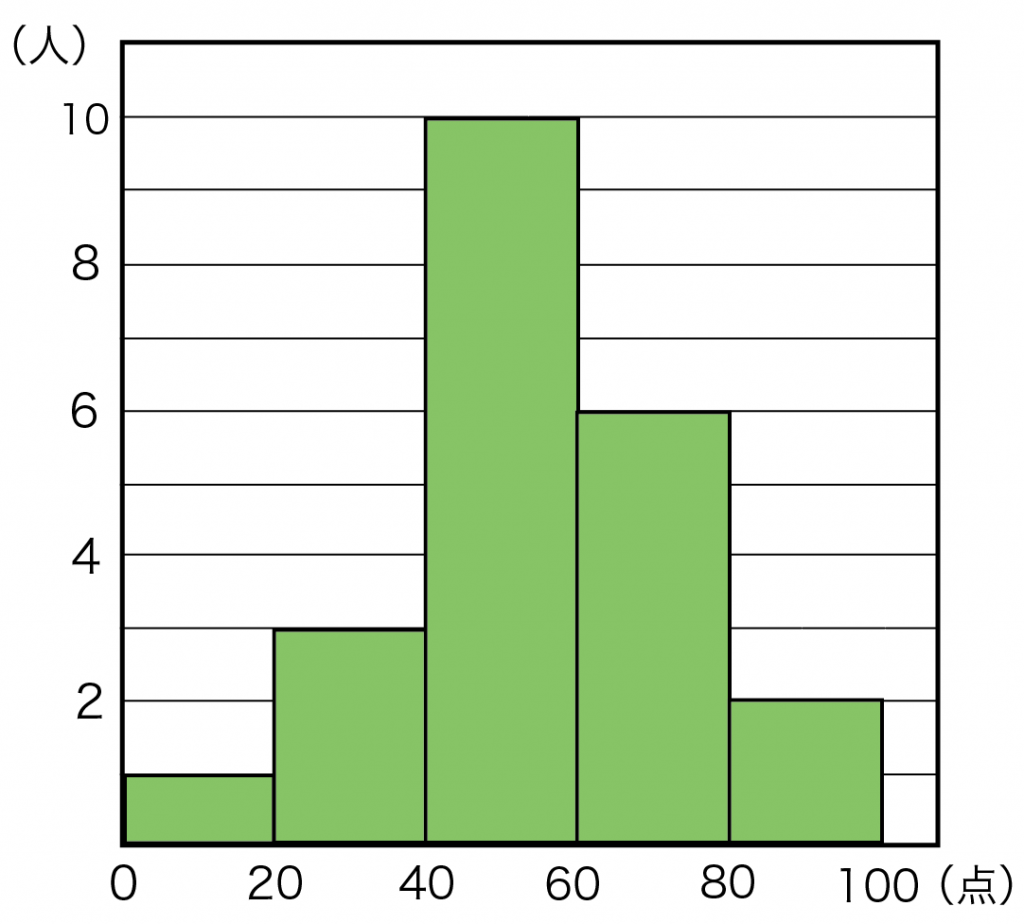
各階級の、
階級値をだしてみよう!
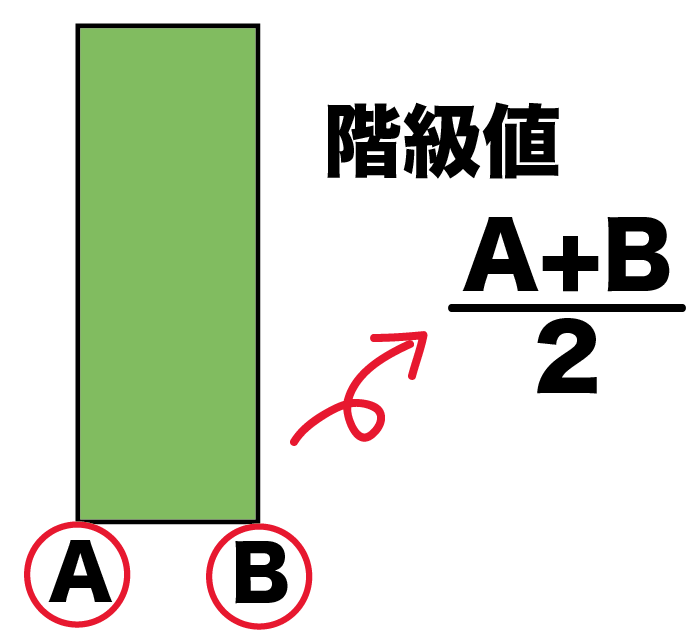
階級値の求め方は、
(階級の端+階級の端)÷2
だったよね??
つまり、
長方形の角と角の数値をたして、
2でわればいいんだ。
例題の階級「0-20」をみてみよう。
こいつの端と端は、
だね。たして2でわってやると、
(0+20)÷2
= 10
になる。
こんな感じで、残りの階級値を計算してみよう。
すると、
になる。
こいつらを棒の下らへんに書いてみて!
これが第1ステップさ。
つぎは「度数」を読み取ろう!
棒グラフがどれくらいの高さになっているのか??
をみてやればいいんだ。
例題では、ヒストグラムに目盛りがついてる。
目盛り通りに度数を読んでやると、こうなるね↓↓
こいつらを棒の上に書き込んでみよう。
これが第2ステップさ。
つぎは、
「度数」と「階級値」をかけてみよう。
ぜーんぶの階級で計算してみてね。
えっ。
「度数×階級」はどこに書けばいいかって??
たしかにね。
ぶっちゃけどこでもいいんだけど、
せっかくだから度数の上にかいてみようか。
例題をみてみると、
になるはず。
これが第3ステップさ。
最後は公式をつかうよ。
度数分布表からの平均値の求め方とおなじさ。
(平均値)=(階級値×度数)の合計 ÷ (度数の合計)
ってやつだね。
例題でも公式をつかってみよう。
すると、
になるね。
こいつをまんま公式にぶちこんでやると、
平均値
= 1200÷22 = 54.5
になるはずだ。
おめでとう!
ヒストグラムから平均値を求められたね。
ヒストグラムでも度数分布表でも大丈夫。
平均値の求め方は、
階級値×度数の合計
を
度数の合計
でわればいいんだ。
しっかり点をとっていこう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。山、みたいね。
平均値の求め方はわかってる。
だって、
「データの合計」を「データの個数」で割ればいいんでしょ??

ちょろいよ。
たとえば、A・B・C・D君のテストの平均値を求めてみよう。
かりに、4人の点数が、
だとするね。
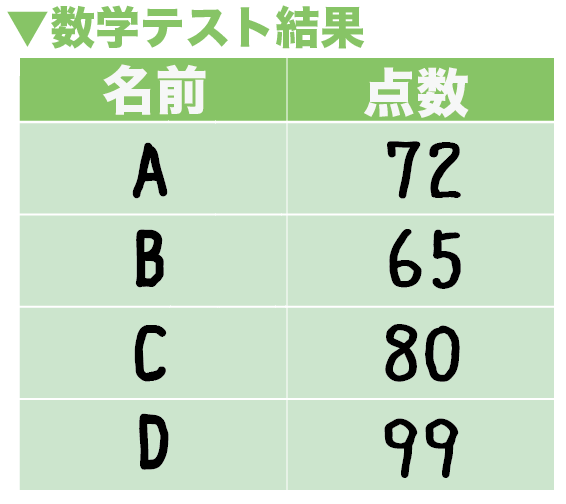
こいつらの平均点は、
(データの合計)÷(データの個数)
= (72 + 65 + 80 + 99)÷ 4
= 79
になる。
ぶっちゃけ、楽勝だね!
だけどさ、
度数分布表から平均を求めるとき
ってどうすればいいんだろ??
テストや宿題ででてくるのに、教科書にのってない。。
こいつは困ったね。
そこで今日は、
度数分布表からの平均値の求め方
を5ステップで解説してみたよ。
度数分布表から平均値を求めるときは、
つぎの公式をつかうよ。
「(階級値×度数)の合計」÷「度数の合計」

「階級値」と「度数」をかけたものをぜーんぶたして、
「度数の合計」でわればいいんだ。
えっ、言葉だけじゃよくわからん??
実際に例題をといてみよう!
例題
つぎの度数分布表は3年B組の期末テストの点数の分布をあらわしたものです。この度数分布表から平均値を求めなさい。
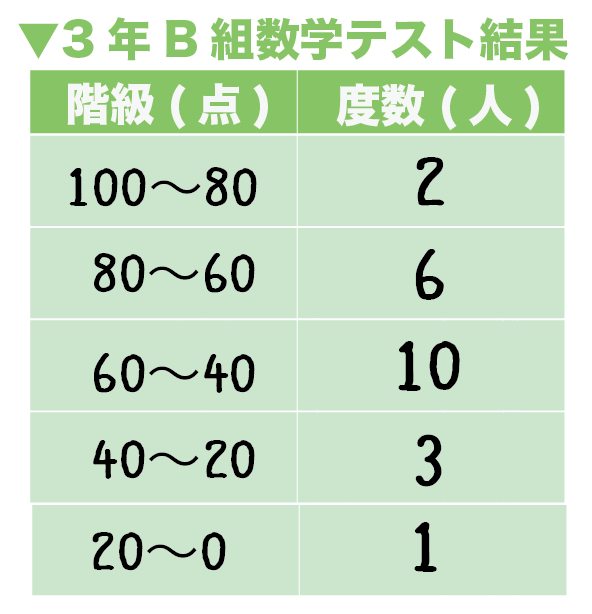
つぎの5ステップで計算できちゃうよ。
各階級の「階級値」を計算してみよう!
階級値の求め方は、
(階級の端+階級の端)÷ 2
だったよね??

たとえば、階級が「100~80」だったら、
(100 + 80 ) ÷ 2
= 90
になるってわけ。
こんな感じで、階級の端っこの平均をだせばいいんだ。
例題の階級値をぜーんぶだしてやると、
になるね。
これが第1ステップ!!
つぎはさっき計算した、
階級値
と
度数
をかけてみよう。
例題で「階級値×度数」を計算してみると、
になるね。
慎重にかけ算をしてみよう!!
おつぎは、
度数の合計
を計算しよう。
ぜーんぶの階級の「度数」をたせばいいのさ。
例題でいうと、各階級の度数は、
だったね??
こいつらをぜんぶ足してやると、
2 + 6 + 10 + 3 + 1
= 22
になる!
「階級値×度数」の合計もだしてみよう!
ぜーんぶの階級の「階級値×度数」をたせばいいんだ。
例題の「階級値×度数」は、
だったよね??
こいつをぜんぶたしてやると、
180 + 420 + 500 + 90 + 10
= 1200
になるね。
最後に平均値の公式をつかおう!
度数分布表から平均値を求める公式は、
「(階級値×度数)の合計」÷「度数の合計」

だったね??
Step4まででそろえた、
を公式にぶちこんでみよう。
例題では、
を公式にいれて計算してやると、
(階級値×度数の合計)÷(度数の合計)
= 1200 ÷ 22
= 54.5※小数点第二位を四捨五入
になる!
おめでとう!
どんな度数分布表からも平均値を求められるね。
度数分布表から平均値をだすのはむずい。
だけど、ふたをあけてみると案外簡単。
使ってるのは、
の3つだからね。
求め方さえおぼえちまえば、計算は簡単なんだ。
度数分布表からガンガン平均値を求めていこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。ほうじ茶しみるわ。
資料の活用を勉強していると、
っていう代表値を勉強するよね!
求め方はマスターした。
だけど、
平均値と中央値はどう違うんだろう??
って思わない?
名前も似てるし、
漢字3文字だし。;
今日は平均値と中央値をごちゃまぜにしないために、
平均値と中央値の3つの違い
を解説していくよ。
よかったら参考にしてみて。
平均値と中央値には3つの違いがあるよ。
砲丸投げの例で解説していこう。
下の表は、ある中学校の10人の生徒の砲丸投げの記録のデータです。

平均値と中央値は求め方がちがうよ!
求め方・出し方は、
だったよね??
砲丸投げの例をみてみよう。
この10人の平均値は、
(10人の平均値)=(データ合計)÷(データ数)
= (7 + 4 + 5 + 9 + 11 + 3 + 4 + 12 + 6 + 7 ) ÷ 10
= 6.8
になる。

じゃあ、中央値はどうなの??
中央値はまず、大きい順にデータを並び替えて、
真ん中のデータをさがせばいいんだ!
この例ではデータ数は偶数。
真ん中2つのデータの平均をとってあげると、
(中央値)= (真ん中1 + 真ん中2)÷ 2
= (7 + 6)÷ 2
= 6.5
になるね。
中央値と平均値では出し方がちがう
ってことを覚えておこう。
平均値と中央値には、
ぶれにくさいに違いがあるよ。
データの中にとびぬけて変わったデータがあるとき、
影響の受け方がちがうんだ。
たとえば、砲丸投げの例をかんがえてみよう。
よくありがちなことだけど、Aさんがいきなり覚醒したとしよう。
この日は覚醒しすぎて、宇宙記録の100mをたたき出しちゃったらしい。
このとき、平均値と中央値はつぎのように変化しちゃうんだ。

ね?
中央値はぜんぜん変わらないけど、
平均値はむちゃくちゃ変化してるっしょ!?
こんな感じで、
特殊なデータからうける影響の大きさが違う
ってことをおぼえておこう。
3つめの違いは、
平均値と中央値の求めやすさが違うってことだ。
じつは、
データ数の多さによって求めやすさが違うんだ。
平均値は求めやすさは変わらない。
だけど中央値は、
と性質が変化するんだ。
たとえば砲丸投げの例でみてみよう。
たとえば、チャレンジャーがEさん・Dさん・Hさんの3人のとき。
このときの中央値は1秒で求められる。
だって、3つしかデータないし、
データ数が奇数だからね。
真ん中の11mが中央値さ。
逆に、チャレンジャーが増えすぎた時はどうかな??
Aさん〜Zさんまでの26人が参戦したとしよう。
このとき、中央値を求めるのはダルいね。
なぜなら、
っていう作業がめんどうだからね。
データ数が少ないときはいいんだけど、
増えすぎると大変になっちゃうんだ。
こんな感じで、
データ数の多さにより平均値と中央値のだしやすさが違う
ってことをおぼえておこう。
平均値と中央値はまったくべつもの。
漢字とか雰囲気とか似てるけど、
という3点で違うよ。
テスト前に復習してみてね。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。ドタキャンはきついぜ。
最頻値(モード)の求め方を知っていると便利。
資料と活用の問題がとけるし、
日常生活でもつかえるようになるんだ。
今日はそんな便利な、
最頻値(モード)の求め方を2ステップで解説していくよ。
よかったら参考にしてみてね。
最頻値は2ステップでだせちゃうよ。
最頻値を求める例として、
砲丸投げに挑戦するアスリートに注目しよう。
AさんとBさんだ。
市内体育祭の出場権をかけてあらそってる。
合計で10回砲丸をなげたんだ。
その記録がつぎのものさ ↓↓
この2人の最頻値をもとめみよう!
まずは度数が多い階級をみつけよう。
いっちゃん多いやつを探してくれ。
Aさんでいうと、
8以上 – 10未満
の距離をとばした度数が多いってことがわかる。
だって、どの階級よりも多いからね。
Bさんの場合もおなじ。
いちばん大きい度数は「4」。
階級は「4以上 – 6未満」だね。
これが第1ステップ!!
つぎは、度数がいちばん多かった階級の「階級値」を計算しよう。
それが「最頻値」になるんだ。
階級値の求め方は、
階級の端と端の平均を計算すればよかったんだったね!
例題のAさんの場合、
いちばん度数の多い階級は「8以上 – 10未満」だね??
つまり、この階級値は、
(8+10)÷2
= 9
になるんだ。
よって、Aさんの最頻値は「9 m」だ。
おなじように、Bさんの度数がいちばん多い階級値を計算してみると、
(4+6)÷2
= 5
になる。
つまり、Bさんの最頻値は「5」ってわけ!
どう??これで最頻値の求め方もマスターしたね!
最頻値の求め方はわかった。
だけど、
最頻値にどんな意味があるんだろう??
意味ないなら計算したくないよね。
じつは、最頻値は代表値のうちの1つ。
たくさんのデータから何かを判断するときの材料として使われるんだ。
今回の砲丸なげトライアルの目的は、
市内体育祭の砲丸投げ選手をえらぶこと
だったよね??
ぼくが体育の先生だったらこの最頻値をみて、
選手をAさんにするね。

なぜなら、最頻値がBさんよりも高いからさ。
えっ。
BさんはAさんよりも良い記録をだしているって!?
たしかに。
1回だけ10~12mの好記録でなげているね。
だけれども、本番の市内体育祭は2回までしかなげられないんだ。
そのミラクルがでる可能性はものすごく低いよね。
それだったら、安定して8から10mの飛距離をだせるAさんのほうがいい。
勝てる。
だから、選手として選んだわけ。
こんな感じで最頻値はなにかを判断するときに使われるよ!
最頻値の求め方は簡単。
の2ステップでいいんだ。
問題をたくさんといて最頻値になれていこう。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。抹茶最高。
中学数学で、
中央値(メジアン)を求める問題
ってでてくるよね??
復習すると、中央値とは、
大きい順にならべたときに真ん中にくる値
のことだったね。
中央値の求め方はマスターした。
何度だってメジアンをだすことができそう・・・!
だけれども、
何度も何度も中央値(メジアン)をもとめてるとこう思わない?
そう、
中央値を求める意味ってあるのかなあ??
ってね。
そんな疑問を解消するために、
中央値(メジアン)を求める意味を解説していくよ。
中央値をだす意味はずばり、
特殊なデータがいてもぶれない代表値
だからだ。
代表値としてよくつかわれるのは平均値。
こいつはデータの中に変わったやつがいると、
ぶれぶれになっちゃうんだよ。
例として中央値の求め方でとりあげた、
砲丸投げの例をみてみよう。
Aさん〜Jさんまで10人が砲丸投げに挑戦した話だったね。
砲丸投げの記録をデータにしてみたんだ。
体育の先生が、
こいつらのパワーはどれくらいなのか??
ってことをみるために代表値を参考にしているよ。
今回はつぎの2つのパターンをみてみよう。
みんな同じぐらいの記録だったケースだ。
すごすぎるやつもいないし、
しょぼすぎるやつもいない。
たとえば、つぎの記録データが得られたとしよう。

このとき、平均値をだしてみよう。
平均値の出し方をつかえば、
平均値 =(全部のデータの合計)÷(データ数)
= (7 + 4 + 5 + 9 + 11 + 3 + 4 + 12 + 6 ) ÷ 10
= 6.1
になるね!
この平均値という代表値をみた先生は、
ふーん、近頃の若いヤツはこんなもんかあー
って納得するはず。
つぎは、
他とあきらかに違うデータがいるときだ。
このとき、
平均値は変な数値になってしまうんだ。
たとえば、砲丸投げの例をもう1回考えてみよう。
Aさんがこの日だけ、むちゃ覚醒したんだ。
世界記録を塗り替る宇宙記録100mをだしちゃっとしよう。
このときの平均値を計算してみよう。
平均値 =(全部のデータの合計)÷(データ数)
= (100 + 4 + 5 + 9 + 11 + 3 + 4 + 12 + 6 ) ÷ 10
= 15.4
すると、Aさんの宇宙記録のせいで、
平均がぐんと上がっているよね??
なんと、
平均が15.4m。
Aさん以外、ひとりも15m以上とばせてないのにだよ??
それなのに平均が10だなんておかしいじゃないか!
これじゃあ代表値の役割をはたしていないね。
そんなとき、代表値に「中央値(メジアン)」をつかってやれば一件落着。
メジアンをだしてやると、
(中央値)= {(真ん中1 )+ (真ん中2)} ÷ 2
= (7 + 6)÷2
= 6.5
になるね!
※中央値の求め方はコチラ
この中央値は平均値15.1とくらべるとかなり妥当。
ちょうど真ん中の記録って感じだ。
ぶれる前の平均値の「6.1」にだいぶちかい。
これなら体育の先生もまどわされずにすむね。
こんな感じで、中央値は、
特殊なデータの影響をうけにくい代表値なんだ。
よーくおぼえおこう!
平均値は計算しやすくて便利。
中央値みたいにデータを並び替えなくていいからね。
たくさん使うチャンスがあるかもしれない。
だけれども、
中央値にはぶれにくい
っていうメリットがあるんだ。
とびぬけたデータがいるときの代表値として存在する意味があるんだ。
中央値の出し方をマスターしてガンガンつかっていこう!
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。チャーハン炒めまくったね。
中学数学の資料の活用では、
中央値(メジアン)
を勉強するよね。
この単元はけっこうムズい。
メジアンとかモードとかわけのわからんカタカナでてくるし、
正直、わからんこと多いはずだ。
そこで今日は、苦手を克服してもらうために、
中央値(メジアン)の求め方がわかる3ステップ
を紹介するよ。
メジアンを出したいときに読んでみて^^
さっそく中央値を求めていこう。
つぎの3ステップで計算できちゃうんだ。
つぎの例題をといてみようね。
例題
下の表は、ある中学校の10人の生徒の砲丸投げの記録のデータです。10人の生徒の砲丸投げの中央値を求めなさい。
- Aさん: 7 m
- Bさん: 4 m
- Cさん: 5 m
- Dさん: 9 m
- Eさん: 11 m
- Fさん: 3 m
- Gさん: 4 m
- Hさん: 12 m
- Iさん: 6 m
- Jさん: 7m

データを並びかえてみよう!
上から大きい順番にならびかえるんだ。
砲丸投げでスゴかったやつから順番にならびかえると、
こんな感じになるね↓↓
データの数をかぞえよう!
1、2、3、4・・・・
って感じでね!
ここでみてほしいのが、
データ数が「奇数」なのか「偶数」なのか???
ということだよ。
例題のデータは、10人の砲丸投げ記録だったね??
ってことは、
ぜんぶで10つのデータがあるわけだ。
つまり、データ数は偶数だ!
中央値は、
大きい順(or 小さい順)に並び替えたときの真ん中のデータ
のことだったね??
並び替えて真ん中のデータをえらべばいいわけさ。
ただ、注意してほしいのが、
データ数が「奇数」か「偶数」かによって真ん中の値の選び方がちがう
ってこと。
データ数が「偶数」のときは、
2つの真ん中の平均値をだすんだ。
真ん中の値は、
だね?
こいつらの平均をとってやると、
{(Jさんの記録) + (Iさんの記録)}÷2
= (7 + 6 ) ÷2
= 6.5
になる。
これが中央値だよ!
データ数が奇数のときはどうすんのって話だよね?
ちょっと気になる。。
さっきの例題で、Fさんが風邪で休んだとしよう。
すると、
砲丸投げをした生徒は9人になる。
つまり、データ数が奇数になるわけ。
奇数のときは偶数のときより簡単!
真ん中の数がそのまま「中央値(メディアン)」になるからね。
例題でいうと、
ちょうど真ん中の「7」がメジアンだ。
これで奇数のときも偶数のときも大丈夫だね!
中央値の出し方には、
の2通りあるんだ。
という3ステップをおぼえちゃおう。
中央値なんてちょちょいのちょいさ!
そんじゃねー
Ken