こんにちは!この記事をかいているKenだよ。麻婆豆腐うめえよ。
一次関数で知っておきたいのは、
変化の割合
というキーワードだ。
こんな言葉、滅多に使わないよね??
おれ、変化の割合のこと・・・好き・・・
なんてセリフは出てこないはずだ。
そんなよくわからない、
「変化の割合」
をわかりやすく説明していくよ。
よかったら参考にしてみてね。
一次関数の「変化の割合」とは、
xが1増えたらyがいくら増えるのか、減るのか
の数値のこと。
「yの増加量」を「xの増加量」でわってやれば「変化の割合」になるんだ。
変化の割合 = yの増加量/ xの増加量
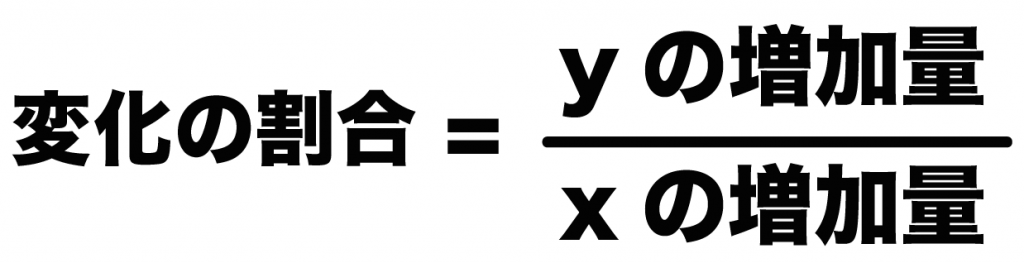
たとえば、
xが2増えたとき、yが10増えたとしよう。
このとき、
だよね。だから変化の割合は、
(yの増加量)÷(xの増加量)
= 10 ÷ 2
= 5
になるね。
つまり、xが1増えたらyが5増える一次関数ってことなのさ。
ここまで大丈夫??
もう一方踏み込んで、
一次関数における変化の割合の特徴
をつかんでおこう。
最大の特徴は、
1次関数の変化の割合はずーーーっと一定
ってことなんだ。
つまり、一次関数の途中で「変化の割合」が変わったりしないんだ。
たとえば、
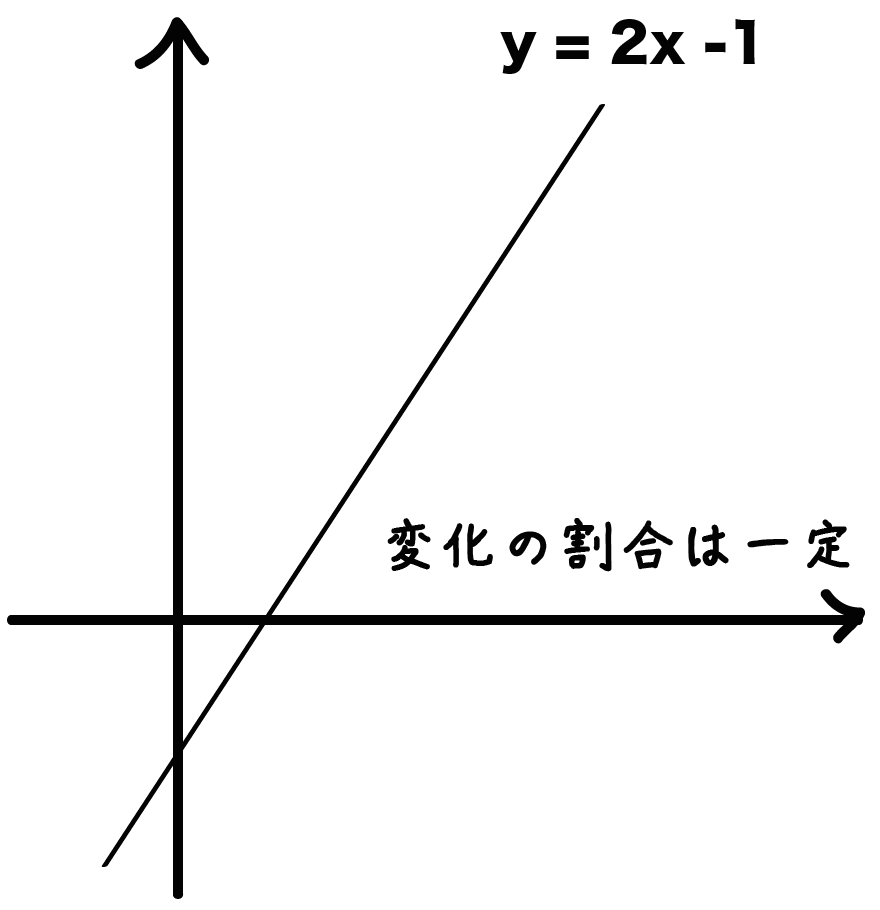
y = 2x +1
という一次関数があったとしよう。
こいつは、
も、変化の割合はずっと2で同じなんだ。
ゼッタイに変わらない。
これが一次関数の変化の割合の特徴さ。
逆に、一次関数でもへったくれでもない関数だったらどうなる??
そう。
変化の割合は一定じゃない。
もうね、コロコロ変わるんだ。
たとえば、つぎのようにクレイジーな関数がいたとしたら、
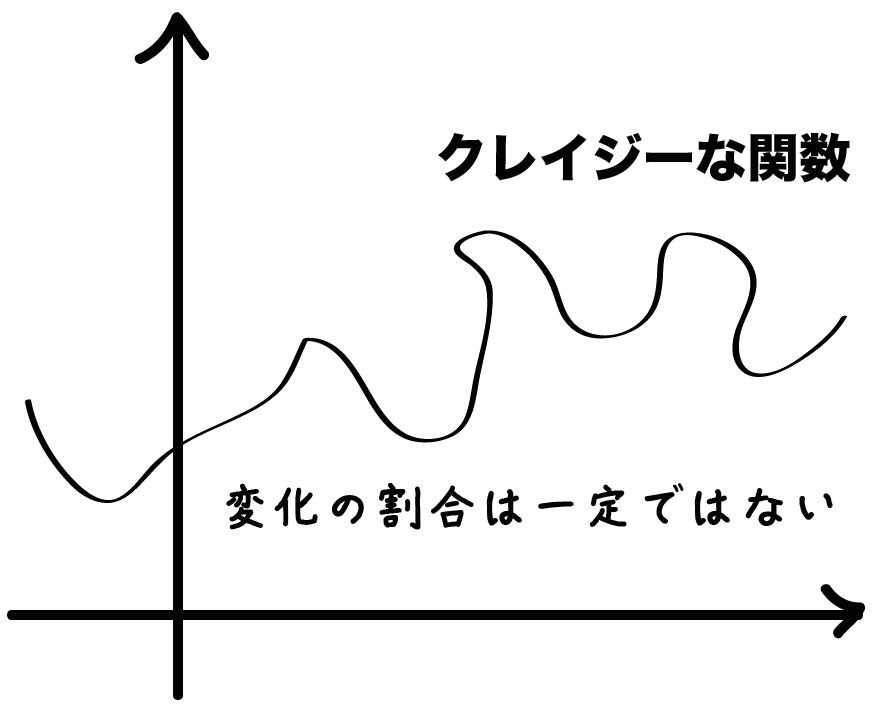
変化の割合はまさに暴れ馬。
xがどの範囲で変化するかによって、ぜんぜん変化の割合がちがうんだ。
一次関数では「変化の割合」が一定である
ってことをおぼえておこう。
一次関数の変化の割合もわかったかな??
コツさえつかめれば問題がとけるようになるから、
ゆっくりと勉強していこうね。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。バジル、うめえ。
中学2年生になると、
一次関数
を勉強するね。
うーん、でもそもそも、
一次関数とはなんだろう!??
って思っちゃうよね。
正体不明のまま問題をとくのは無理。
エスパー能力があれば話は別だけどね。

そこで今日は、
一次関数とはなにか??
をわかりやすく説明してくよ。
よかったら参考にしてみてね。
一次関数とは関数の1つ種のことだ。
ポケモンも600匹ぐらいいると思うんだけど、
ピカチュウはそのうちの1匹だよね?
それと同じさ。
「関数とは?」の記事で、
関数とは自動販売機である
ってたとえたよね。
一次関数は自動販売機の一種。
ってことは、アクエリアスしか売ってない自動販売機みたいなもんさ。

ここまではおっけい??
一次関数とはずばり、
y = ax + b
という形をした関数のことさ。

もう少しわかりやすく説明すると、
xが1回以下だけかけられた関数のことなんだ。
yの右側がxの一次式ならそいつは一次関数ってわけさ。
たとえば、
y = 9x
とか、
y = 9000x + 100
が一次関数になるよ。
だって、y = ax + bの形になっているし、xの項はすべて1次式だからね。
これさえ覚えておけば大丈夫。
一次関数を征服したようなもんさ!
ここで勘が鋭いヤツは、
比例は一次関数とどう違うんだよ?!
って逆切れしそうになっているはずだ。
うん、マジ鋭いね。
じつは比例は、
一次関数の1種なんだ。
y = ax + b
のbがゼロになった一次関数が「比例」なんだ。
だんだん「一次関数とはなにか??」ということがわかってきたかな。
つぎの例題をといてみよう↓↓
例題
yはxの関数で、つぎの式で表されるとき、一次関数であるものを選びなさい。
(a) y = 2x
(b) y = 4/x
(c) y = 5x^2+1
(d) y = 1/9x +8
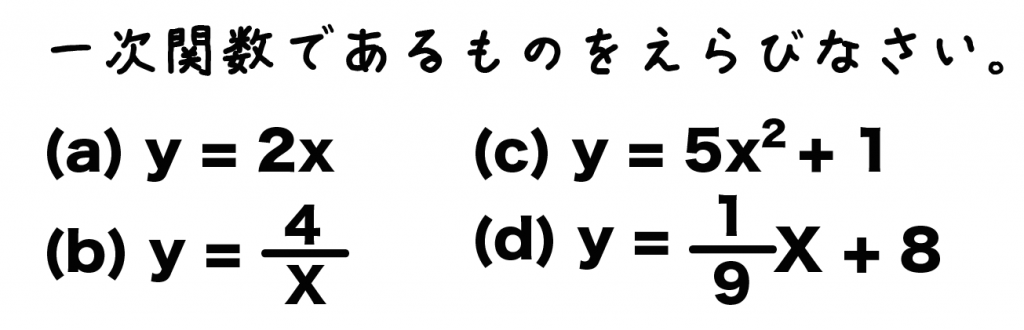
こいつは一次関数だね。
なぜなら、xの次数が1だからね。y = ax + bのbが0のときのパターンさ。
こいつはまぎれもない比例野郎だ。
さっきもいったけど、
比例も1次関数の仲間ってことをおぼえておこう。
こいつは一次関数じゃない。
もうね、とんでもなく違う。
なぜなら、右辺がxで割られているからだ。
xがかけられているなら1次の項になるんだけど、割られているから違う。
xが「かけられてる」のか「わられている」のか把握しておこう。
わからないときは「反比例は一次関数??」っていう記事をよんでみてね。
こいつも一次関数じゃない。
もうね。月とスッポンぐらい違うよ。
なぜなら、
xの項が「二次」だからだよ。
xが2回かけられているところに注意してね。
こいつは一次関数だ。
y = ax + bのaが分数でも一次関数だよ。
aの値にまどわされず、
xが何次の項になっているか??
とか、
y = ax + bの形の関数かどうか??
という判断基準でえらんでね!
一次関数とはなにもの??
ってきかれたらどうする??
そう。
そうだよ。
一次関数とは「xが一次式の関数」だよ!
ってどや顔で答えてやろう。
自信満々で言えばみんな信じてくれるはずさ。
そんじゃねー
Ken
こんにちは!この記事をかいているKenだよ。コーヒーに牛乳は必須だね。
反比例は一次関数なのか?!?
って思うよね。
教科書には詳しくかいてないし、
ちょっともやもやしてない??

今日はその疑問を解消すべく、
反比例の関数は一次関数にふくまれるのか?
をわかりやすく解説してくよ。
よかったら参考にしてみて。
結論からいっちまおう。
反比例は一次関数じゃないんだ。
もうね、ぜんぜん違う。
りんごとみかんぐらい違うね。

えっ。
なんで反比例が一次関数じゃないのかって?!?
そうだね。
これから詳しく解説していくよ。
まずは一次関数とはなにか??
を復習してみよう。
教科書にはこうかいてある↓↓
yがxの一次式で表されるとき、yはxの一次関数である、といいます
だ。
つまり、
関数のxが「一次式」なら一次関数ってことになる。
たとえば、
y = 2x とか y = 5x + 90とかだね。
逆に、y = 2x^2とかy = 5x^3 + 90とかなると、一次関数じゃないってことになる。
だって、xが一次の項じゃないからね。

ここまでオッケイ??
さっそく本題に入ろう。
それじゃあ、反比例の式はどうなのか。
反比例の式って、
y = a/x
だったよね。xが分母にあるタイプの関数だ。
たとえば、
y = 2/x とか y = 6/xとか。

一見、xは何乗もされていない。
ぶっちゃけ、ただのxにみえるから、
こいつも一次関数じゃん!?
って思うかもしれないけど、そいつは間違いだ。
「一次」って、xを1回だけかけたっていう意味なんだ。
でも、反比例の場合、分母にxがあるから、
xで割っていることになる。
よって、反比例は一次関数じゃないんだよ。
xがかけ算されているのか?
割り算されているのか?
をしっかり見極めるようにしよう。
反比例の式は一次関数じゃない。
これを覚えるだけで大丈夫。
一次関数は慣れれば簡単だから、テストでも点をとっていこう。
そんじゃねー
Ken
こんにちは、カフェでコーヒーを頼まないKenだよ。
前回は「反比例とはなにか??」ということを勉強してきたね。反比例は比例とおなじように、関数の中の1種類だよ。
むずかしそうに聞こえるけど、基本をおさえればカンタンになってくるんだ。
今日は、反比例の問題でよくでてくる、
反比例の比例定数の求め方
をわかりやすく解説していくね。
コツさえつかんじゃえば、2秒ぐらいで比例定数を計算できるはずだ!!
反比例の比例定数の求め方はチョーシンプル。
比例定数の求め方とはずばり、
xとyをかけるだけ
だよ。
ね?? むちゃくちゃカンタンそうでしょ??
反比例の問題では「x」と「y」の値があたえられているから、その2つをかけあわせるだけでいいんだ。
実際の反比例問題で比例定数を求めてみよう!
つぎの問題があったとしよう。
yはxに反比例し、x=5のときy =6です。xとyの関係を式にあらわしなさい。
解き方:
問題の最初で「yはxに反比例する」っていってるね?? だからこのxとyについての関数の比例定数は、
比例定数 a = xy
で求めることができる。
そんで、
問題文をよーく目をこらしてみてみると、
x = 5, y = 6
ってことがわかるね。だから、反比例の関数の比例定数は、
xとyをかけあわせて、
30
になるね!
ね?? かけ算が得意だったら2秒で比例定数を求められたでしょ??。
反比例の比例定数の求め方って、
a = xy
って超シンプルだったね。
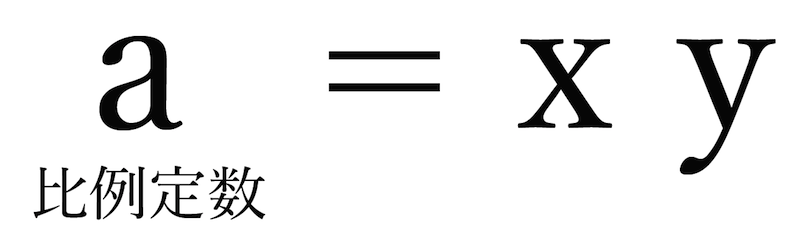
じゃあ、なんでこんなカンタンなんだろう???
その答えは、
反比例の式をゆっくり変形すればわかるよ!
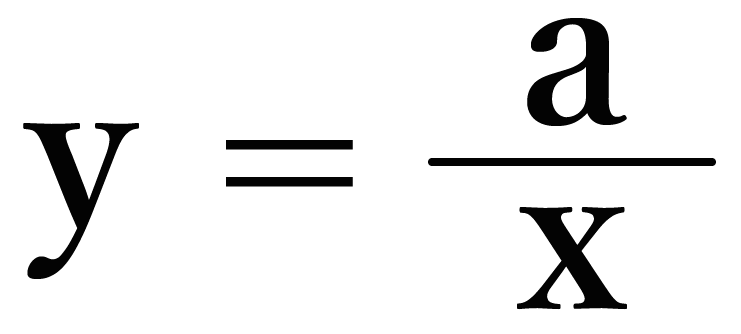
反比例の式である「y = a/x」の両辺にxをかけてみよう!!
すると、
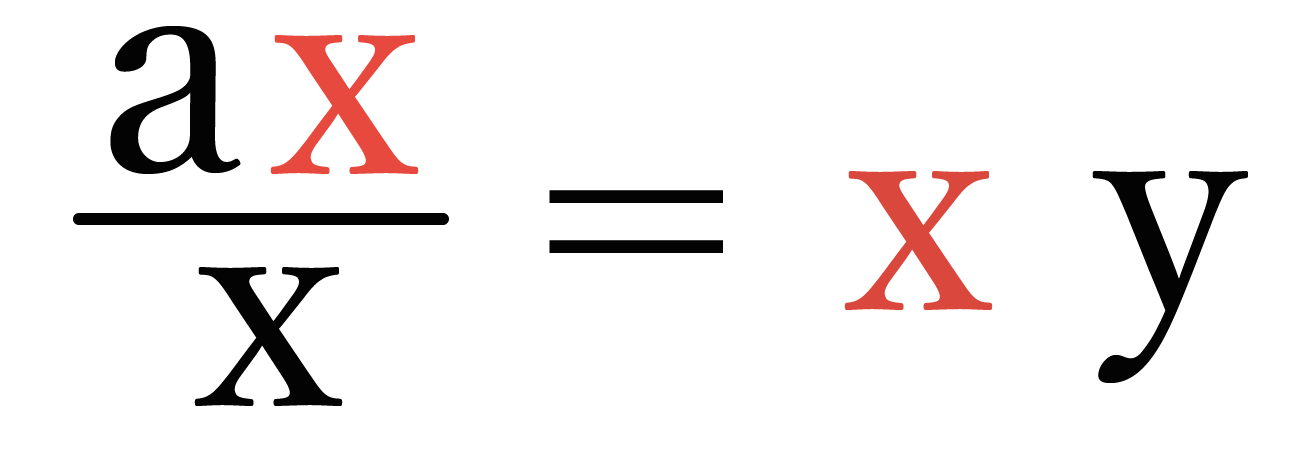
分母の「x」があたらしくかけられた「x」と打ち消しあうっちゃうから、
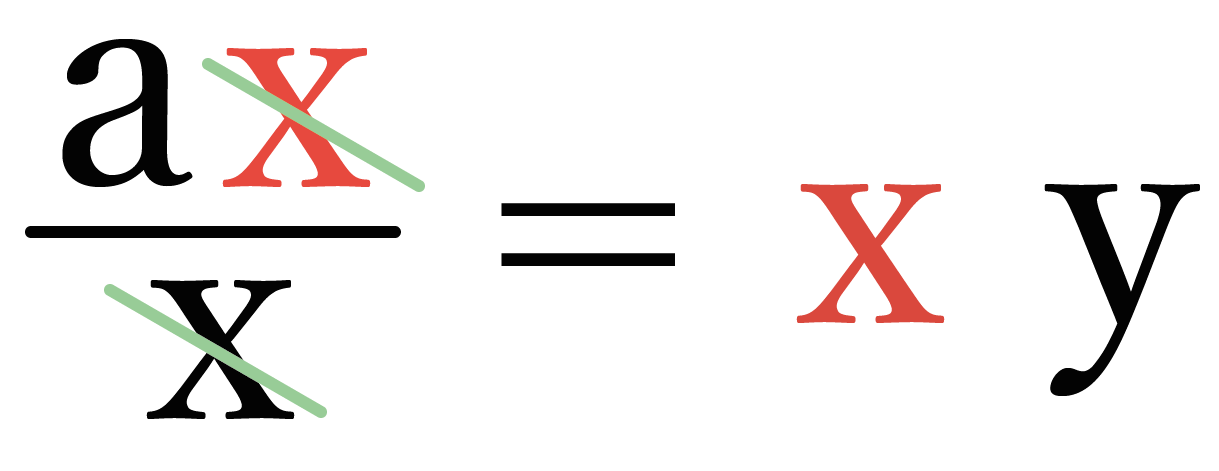
この反比例の関数は、
a = xy
って変形できるね。
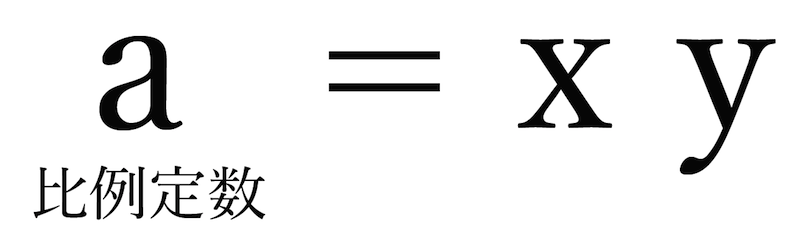
え?? あまりピンとこない??
そういうときは「等式の性質」をみなおしてみてくれ! 等式の基本さえわかっていれば大丈夫。読みながらもう一度変形にチャレンジしてみてね。
ここまでみてきた反比例の比例定数の求め方はどうだった??
xとyの値をかけるだけだから、気合いをいれれば2秒ぐらいで求められるはず!!
つぎは、
反比例のグラフの書き方について勉強していくね。
そんじゃねー!
Ken
こんにちは、この記事を書いているKenだよ。新宿のアルタ前に憧れるね。
反比例(はんぴれい)って聞いたことある??
たぶん、中学校で数学の授業をうけないかぎり「反比例」なんて使わないはずだ。
ゼッタイに、
さてと、歯磨きの前に反比例するかああ。
なんて言わないよね。

そこで、今日は「反比例」ってやつをわかりやすく解説していくね。
反比例の正体が不明すぎるっていうときは参考にしてみてくれ。
~もくじ~
反比例ってからみづらそうだけど、じつはシンプル。
関数の種類のうちの1つのこと
なんだ。「関数とはなにか??」という記事で、関数とは、
自動販売機である
ってたとえたね。
 いってみれば、反比例は関数っていう「自動販売機」の1種なんだ。
いってみれば、反比例は関数っていう「自動販売機」の1種なんだ。
自動販売機の中には、
お茶ばかり売っているものとか、タバコの専用のものとか、おでん専用のものとかいろいろあるでしょ?? それと同じさ。
だから、
関数のグループ内では、「反比例」だってやつもいれば「比例」だってやつもいる。

中学校にもいろんなやつがいるけど、関数の世界も同じなんだってことを覚えておこう。
反比例は関数の一種、
ってことはわかったね?? それじゃあ、いったいどんな関数のことを言うんだろうって疑問に思うでしょ??
反比例はつぎのカタチをした関数のことを言うんだ。
y = a/x
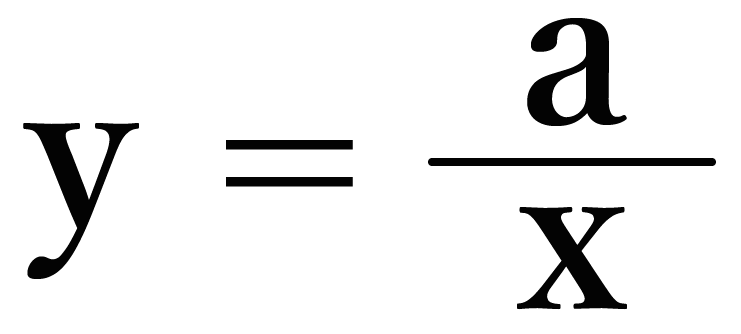
ね? ちょっとカッコいいでしょ。??
そんで、
「x」と「y」は「変数」ってよばれてるんだ。なぜなら、「x」になにを入れるかによって「y」の値も変わる数だからね。
一方、xの上にのっている「a」は「定数」だ。だって、xやyに関係なく変わらずに定まっている数だからね。
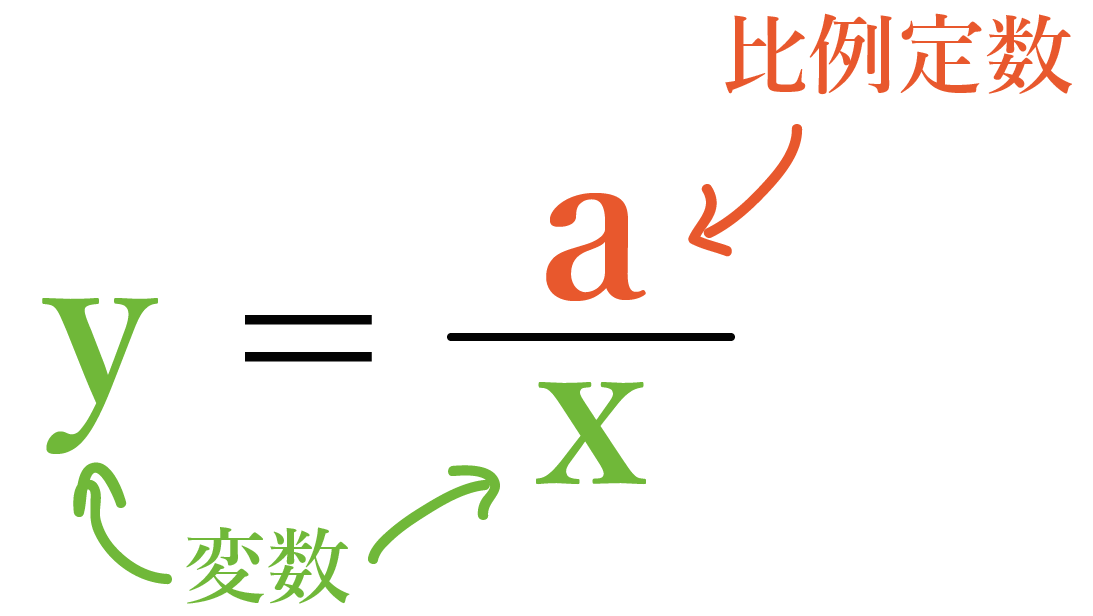
とくに、反比例の式にふくまれる定数のことを「比例定数」っていうんだ。さらっとでもいいから覚えておこう!
ちなみに、xとyでこの反比例の式が成り立つとき、
yはxに反比例する

っていうんだ。クールな澄まし顔でいったらモテそうだね。
反比例とはなにか??
ってことはわかったけど、まだイメージしづらいよね。
もっと反比例と仲良くなるために、反比例の例をさらっとみてみよう!!
比例定数aに2をいれてもいいし、
aに-420をぶちこんでみていもいい。
ただ、aが「小数」とか「分数」のときは注意してね。なぜなら、最後には分子を整数にしてやらなねばならんからさ。
だから、
たとえばaに0.2をいれたとすると、
y = 0.2/x
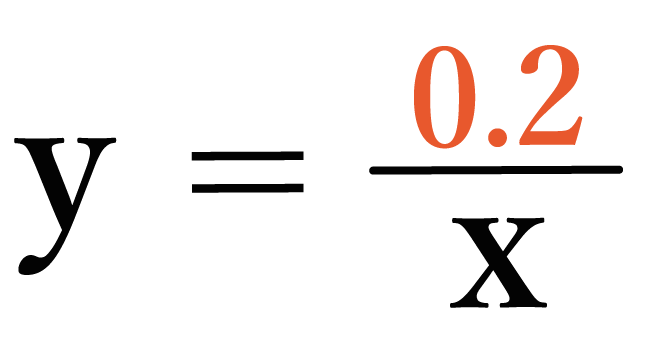
分子と分母を10倍してあげて、分数のカタチになおすと、
y = 1/5x
になるね!
反比例の分子に「小数や分数」をのこさないようにしよう!
ここまで反比例の式はどうだったかな?!?
つぎは反比例の比例定数aの求め方を解説していくよ。よかったら見てみてね。
そんじゃねー!
Ken
こんにちは、この記事を書いているKenだよー!豚角煮カレーおいしかったよ。
前回、「比例グラフの書き方」をみっちり勉強したね?! 比例のグラフをかけるようになったら、あとはテストで点をとり放題・・・・・・
ってわけにはいかないんだ!。
じつは、比例グラフを自由自在にあやつるためには、
比例のグラフにみられる特徴
を知っておいたほうが有利だ。

比例のグラフともっと仲良くなりたいよね??
今日はもうちょっと深く、「比例のグラフ」について勉強していこう。グラフの特徴を4つ紹介するから勉強の参考にしてみてね。
中1数学で勉強する「比例のグラフ」の特徴は次の4つ。
比例のグラフのいちばん目立つ特徴は、
グラフが原点(0,0)を必ず通る
ってこと。
だから、比例のグラフを書くために原点にポチッと点を打つことが第一ステップなのさ。
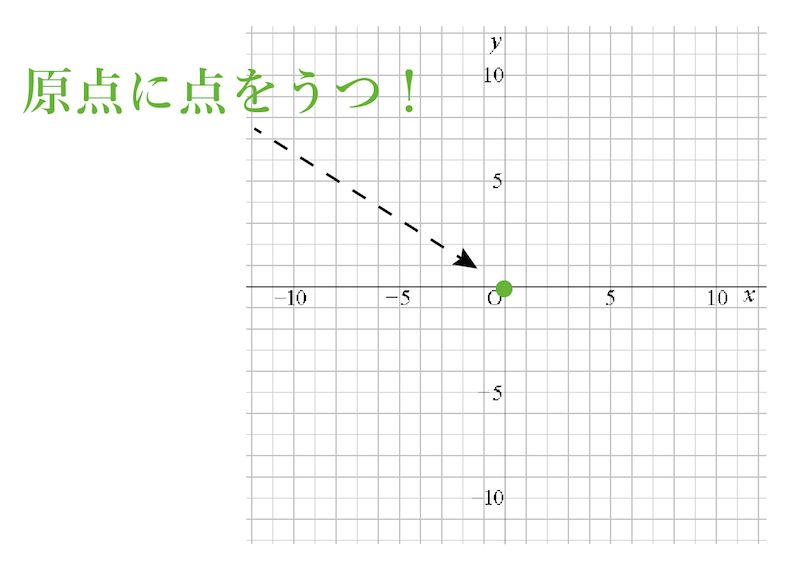
それじゃあ、なぜ比例のグラフは原点を通るんだろう??
その答えは比例グラフの式「y = ax」をよーく見てみればわかるよ。
この式のxにゼロをいれてみよう。
すると、yもゼロになるよね?!? xが0のときyも0になる。
つまり、原点(0, 0)を通るってことなんだ。よーく覚えておこう!
比例のグラフの2つ目の特徴は、
比例定数aの値が大きくなればなるほどグラフの傾きが急になる
ってこと。たとえば、「y = 2x」と「y = 5x」が座標平面でなかよく暮らしていたとしよう。
この2つの比例の式を書いてみると↓↓
こうなるね!
よーく見てみると、
比例定数aが大きい「y = 5x」のほうが「y = 2x」より急に傾いていることがわかる。
だから、かりに、この2つの比例グラフのうえに「りんご」をのせたら、
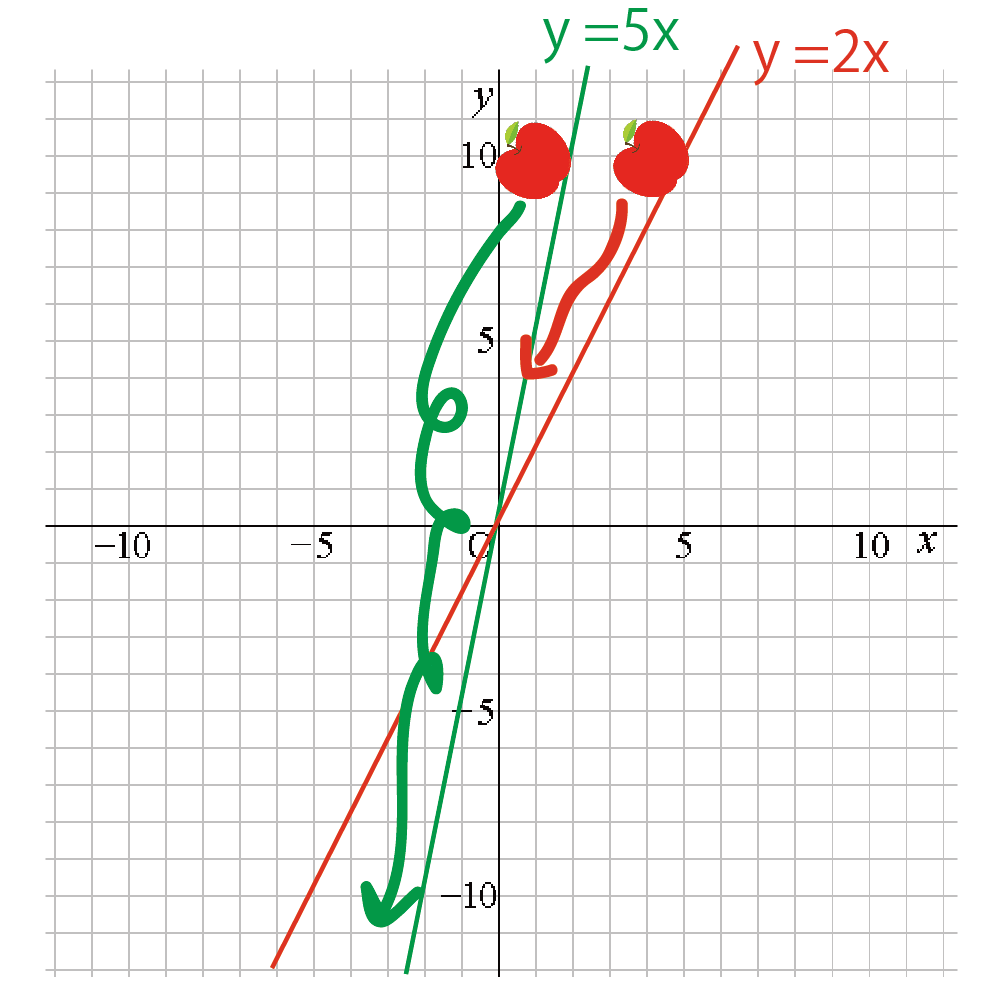
こんな感じで、y=5xのりんごのほうがグルグル速く坂をくだっていくはず!。
比例定数が大きければグラフの傾きが急になる!
ってことを覚えておけば、グラフのカタチを予測できるようになるよ。
もう1つ比例定数に関して押さえておきたいのは、
比例定数aがプラスのときと、マイナスのときでカタチがすっごく違うってこと。
これを確認するために、
y = 2x と y = -2x の比例のグラフを書いてみよう!
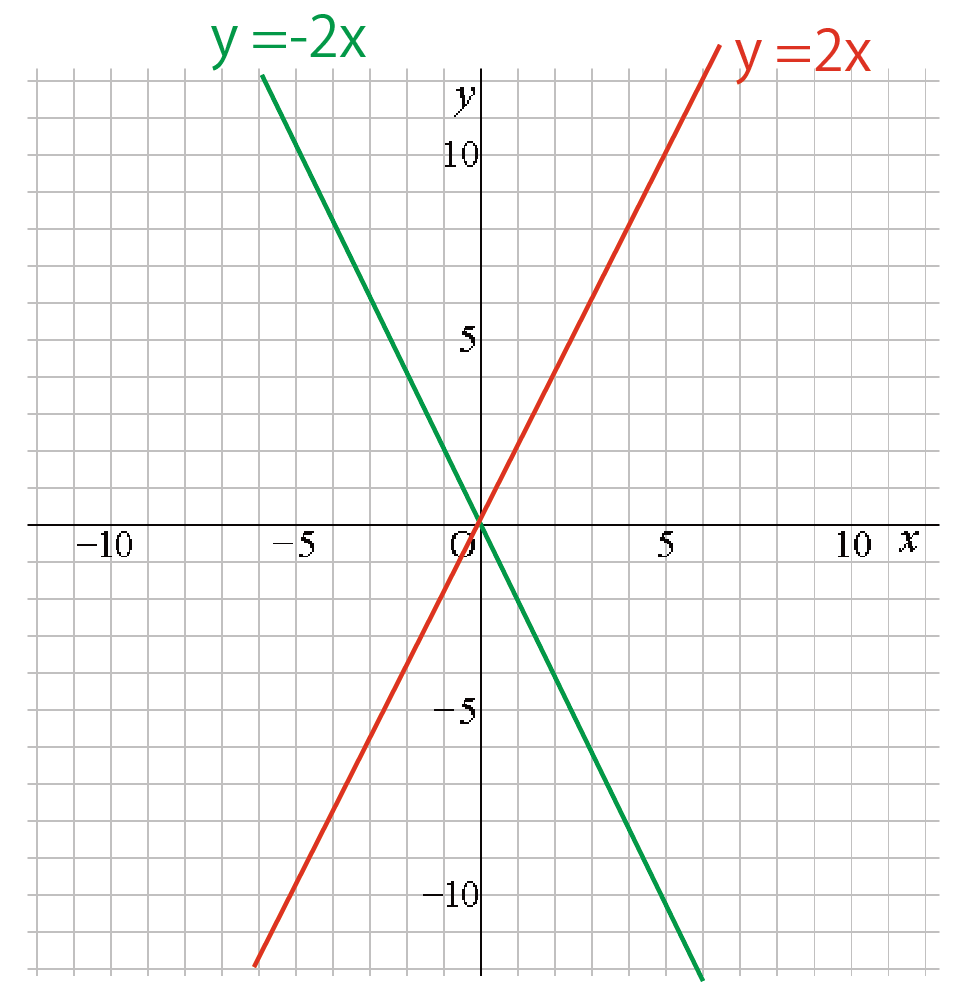
aがゼロより大きいとき(プラス)、グラフが右肩あがりになる。
それに対し、
aがゼロより小さいとき(マイナス)、グラフは右肩下がりになってるね。
だから、
かりにりんごを2つの比例の式の上で転がしたら、
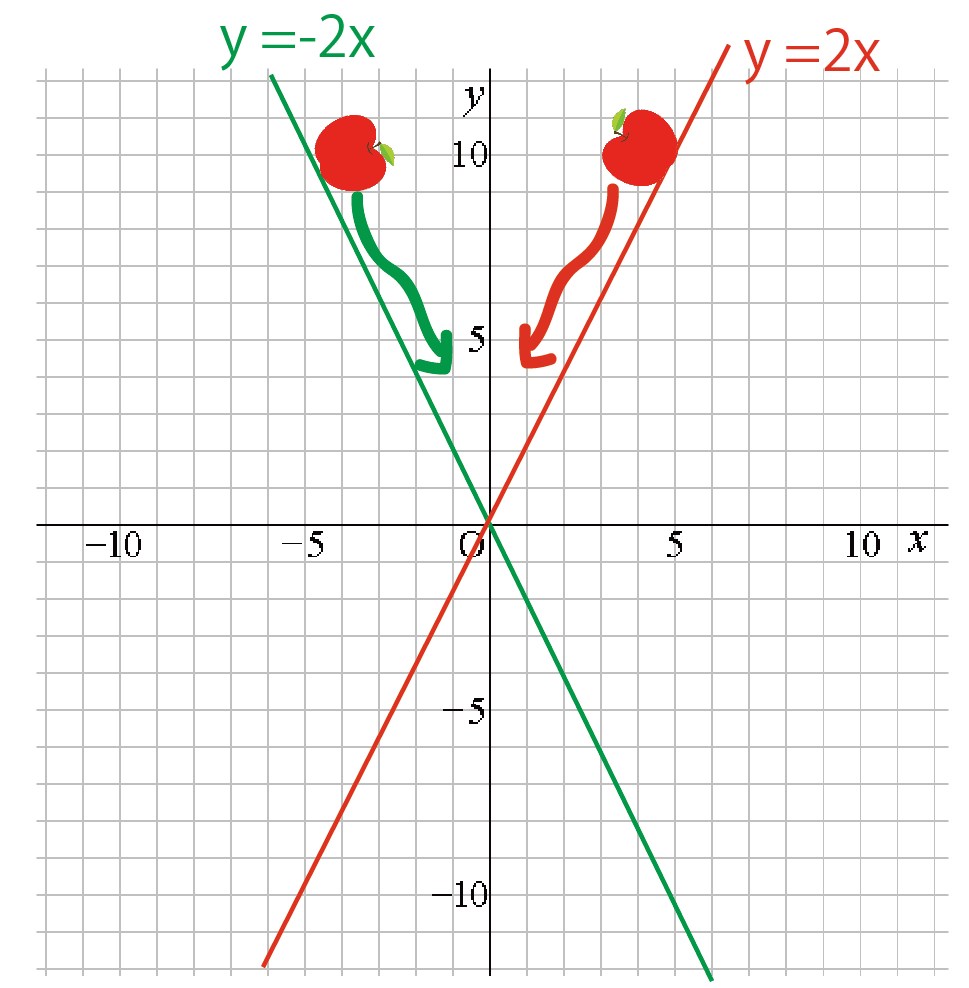
りんごが2つとも違う方向に転がりだすでしょ??。
比例定数aがマイナスのグラフには注意しよう!
ときどき、比例のグラフの問題で「xの変域」が指定されたものが登場する。
たとえばこんな感じ↓↓
次のグラフを書きなさい。
y = 2x (-2 ≦ x ≦ 2)
このとき、
比例の式に金魚のふんみたいにくっついてる(-2 ≦ x ≦ 2)っていう「xの変域」に注意してくれ。
この変域がついていると、
いつも通りにグラフをばんばん書いちゃいけないんだ。こんな感じでね↓↓
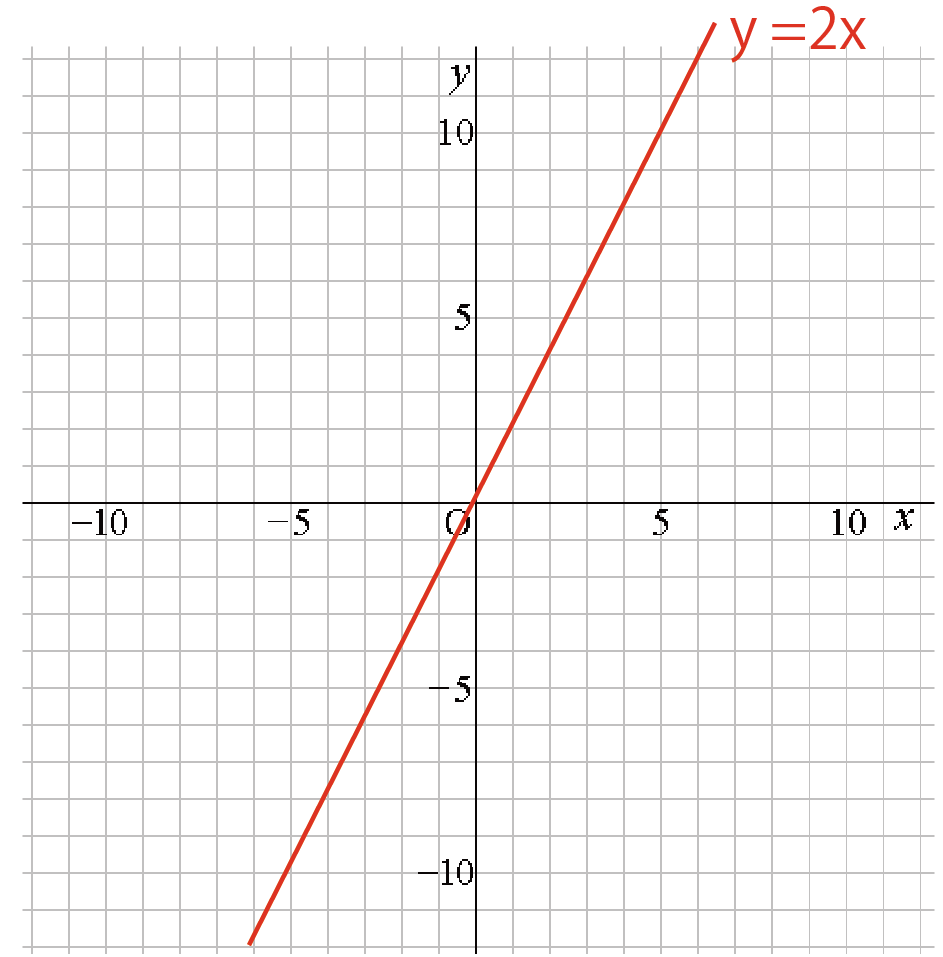
なぜなら、この比例関数には「変域」があるから。
(-2 ≦ x ≦ 2)っていう変域の外にある座標は対応しきれないってことになってる。
だから、この比例の式は、(-2 ≦ x ≦ 2)という範囲だけ元気になるから、
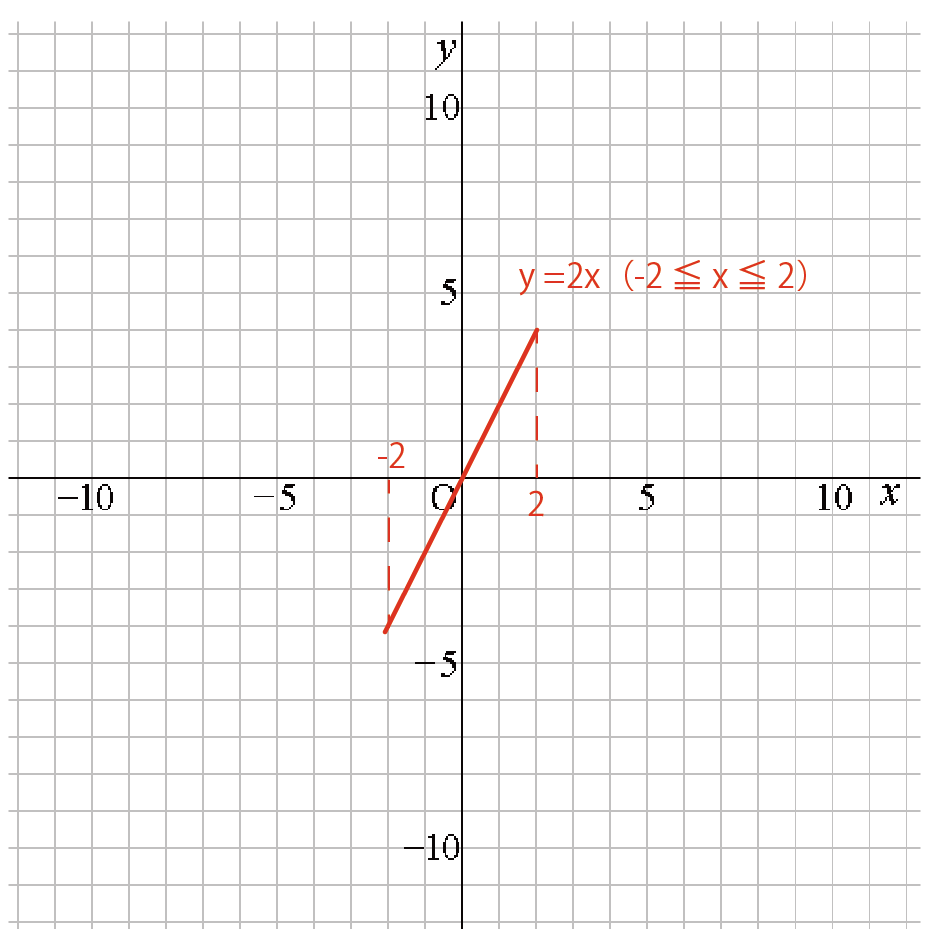
こんな感じで比例の関数が短くなっちゃうんだ。
xの変域が指定されているときは十分に注意しよう!!
比例のグラフにたくさんの種類があるけれど、
これら4つの特徴をおさえておけばテストでも大丈夫。
比例グラフがちょっと得意になっているはず。
そんじゃねー。
Ken
こんにちは、この記事を書いているKenだよ。お湯をのむのが好きだね。
前回は「座標」について勉強したね。
たしか、
xとyの値のセットのこと
を座標ってよんでいたよね??
関数の座標は、
2つの数直線を垂直に交わらせた図であらわせるんだ↓↓
それで、
この2つの数直線のことを「座標軸」といい、
よこ軸の座標軸を「x軸」、たて軸の座標軸を「y軸」っていうんだ。
ちなみに、x軸とy軸が交わる点を「原点」というぜ。
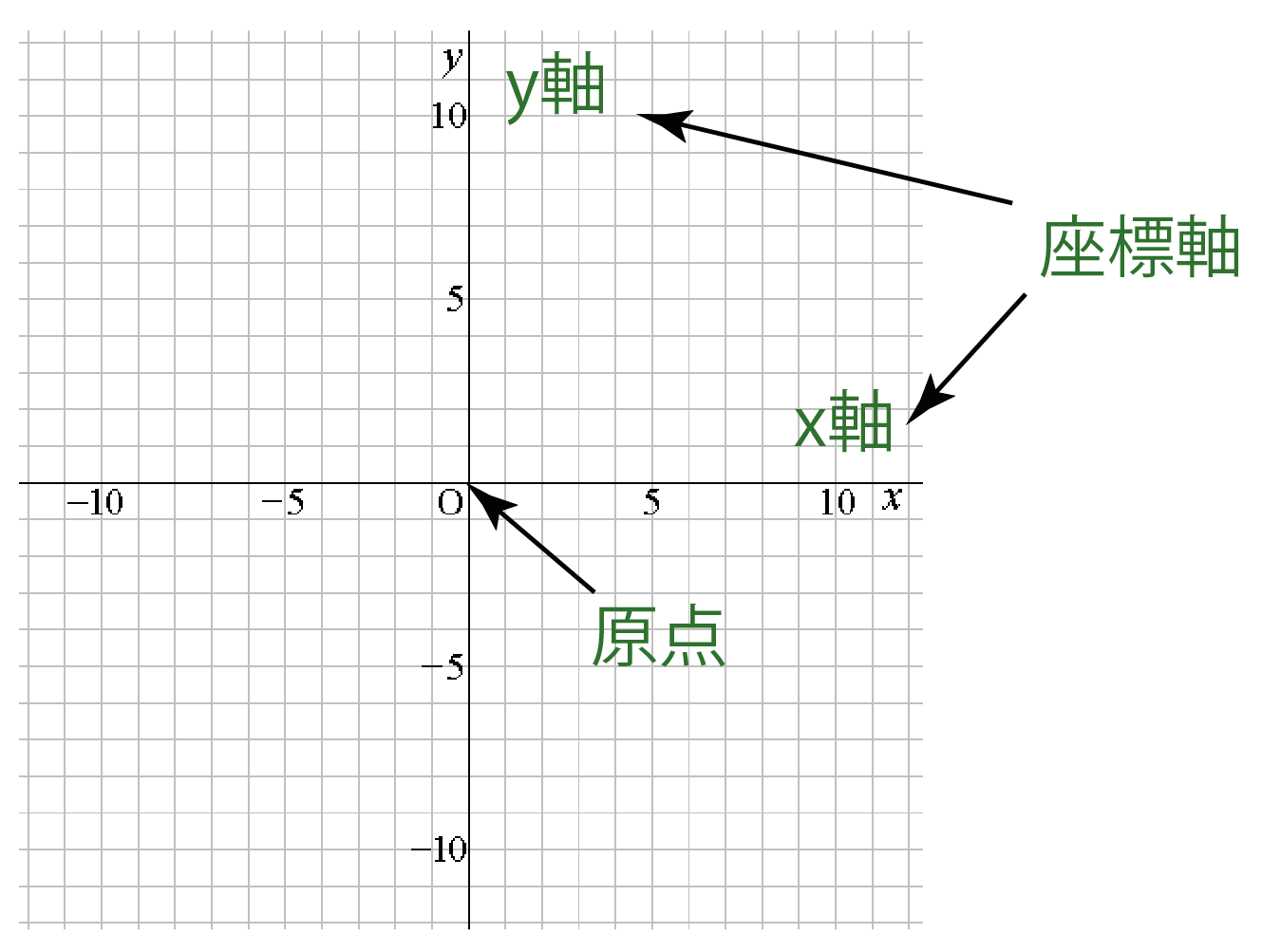
こんな感じで2つの座標軸には、
っていう名前がついてるよね??
でもときどき、
どっちがx軸で、どっちがy軸なのか??ってことを忘れちゃうわない??
そこで今日は、
x軸とy軸を100%忘れない覚え方
を紹介するね。x軸とy軸がごっちゃごちゃになったら参考にしてね。
カンタンなのは「y軸」の覚え方。
キミはアルファベット大文字の「Y」を想像できるかな??
こいつをさっきでてきた2つの座標軸の図の中にぶちこんでやると、
ものすごく馴染んでない??。
その理由は、
「Y」は縦に足が一本のびているからなんだ。
縦に足がながいY軸は「たて軸」って覚えてあげればいいね。
つぎはx軸の覚え方だね。
x軸はヨコ軸なのことを指すんだ。
ヨコ軸。
ヨコ軸。ん?ヨコ??
おや、ヨコのようすが・・・
トゥルトゥル??
トゥットゥー
トゥットゥー
トゥットゥー
ドン、
おめでとう、
「ヨコ」は「x軸」に進化した!
って感じだね。 かなり強引だけど、「ヨコ」というカタカナをいじれば「x」にみえちゃうよね??
この過程をおぼえておけば「x軸を横軸」だとおぼえられるはず!
どう?? x軸とy軸の名前は覚えられたかな??
ここで紹介した奇妙な覚え方を駆使して、x軸とy軸をごちゃまぜしないようにしようね。
そんじゃねー!!
Ken
こんにちは、この記事を書いているKenだよー!
比例の式を攻略するためには「比例定数の求め方」が必要だ。
比例定数を求めておくれ。
って直接きいてくる問題は少ないけれど、
xとyの関係を式に表しなさい
って間接的にきいてくる問題が多いんだ。この問題に「比例定数」って言葉はでてこないけど、じつは比例定数の求め方を知らないと解けない。
だから、
比例定数の求め方を知っておいたほうがテストで有利なんだ。

だから今日は、
比例式の「比例定数の求め方」をわかりやすく解説してみたよ。
数学の試験前に確認してみてね。
~もくじ~
いちばん手っ取り早い比例定数の求め方を紹介するね。
あっ、今回は反比例じゃなくて比例の式の場合だから注意してくれー!
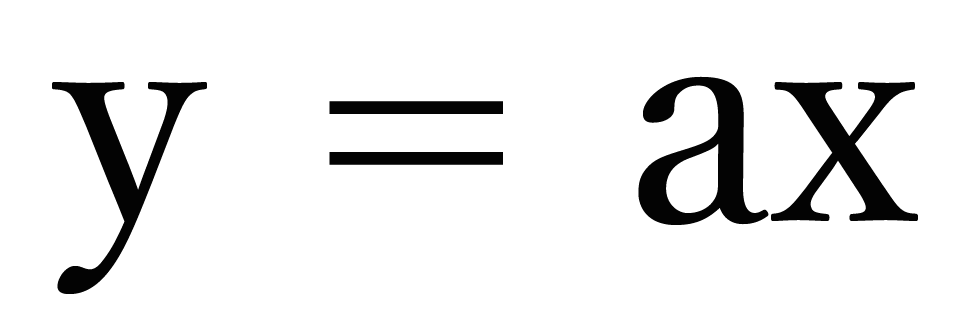
比例の式
上のような比例の式の「比例定数の求め方」は、
yをxで割る(y/x)
ってだけさ。
ね?
ものすごくシンプルな求め方でしょ。
それじゃあ、この求め方で比例定数を計算してみよう!
比例の式で出題されやすいのは次のようなタイプだ。
yはxに比例し、x = 9のとき、y = 54です。xとyの関係を式に表しなさい。
これはちょっとインテリ問題にみえるけど、さっきの比例定数の求め方をつかっちゃえば一発さ。
yとxは比例しているから、
y の値をxでわるだけで比例定数 a が求められるんだ。
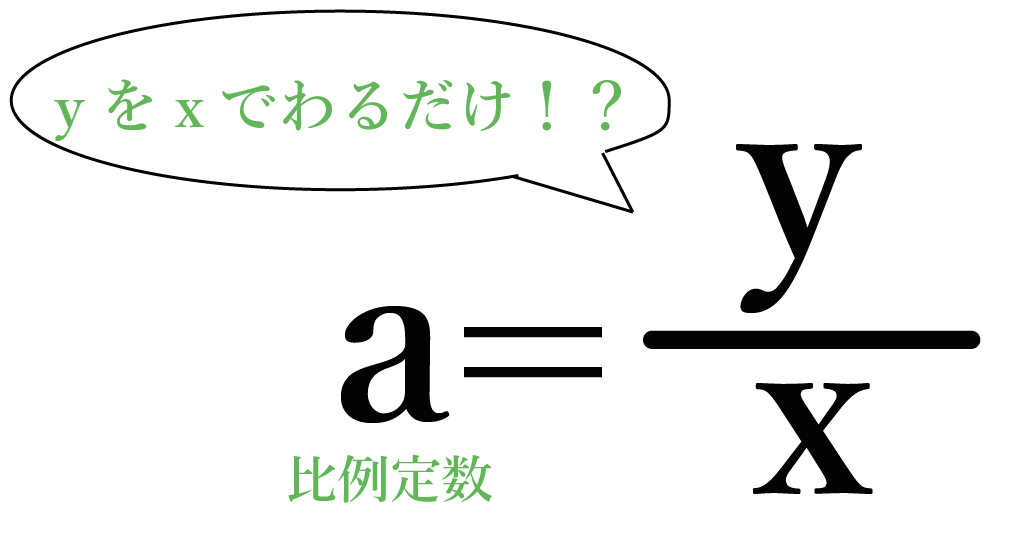
だから、
a = 54 ÷ 9
となって、
a = 6が正解だね。
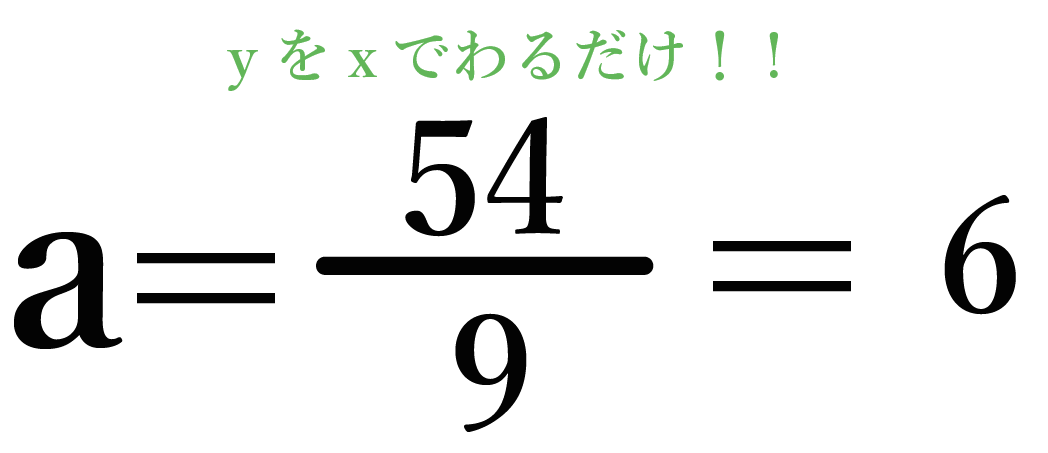
ね? 割り算が得意だったら5秒ぐらいで比例定数がわかるでしょ??。
比例定数aが6ってでたから、xとyの関係は、
y = 6x
になるね。y = axに求めたaをいれちゃえばいいんだ!
yをxでわるだけ
なんてカンタンすぎるよね??
じゃあなんで比例の式の「比例定数の求め方」がこんなにシンプルなんだろうか。
ゆっくりみていけばその理由がわかるよ。
ある関数yがxについて「比例する」ってことは、
y = ax
っていうカタチをした関数ってことだよね?? これは前回の「比例とは??」という記事で勉強したね。
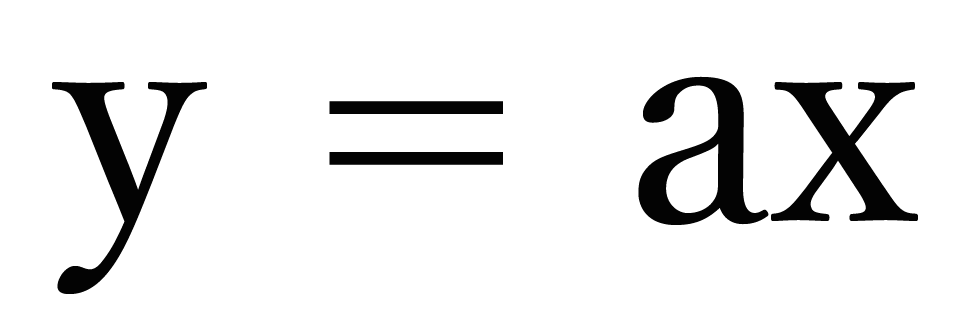
この式をよーくみてみると、
等式であることに気づくよね。だって、左と右が等号(=)でつながれているからね。
そこで、
等式の性質の1つの、
両辺を同じ数でわっても等式は成り立つ
っていうものを使ってみよう。 (忘れかけているときは等式の性質の記事をみてみてね。)
両辺をxで割ってあげるとこうなって↓↓
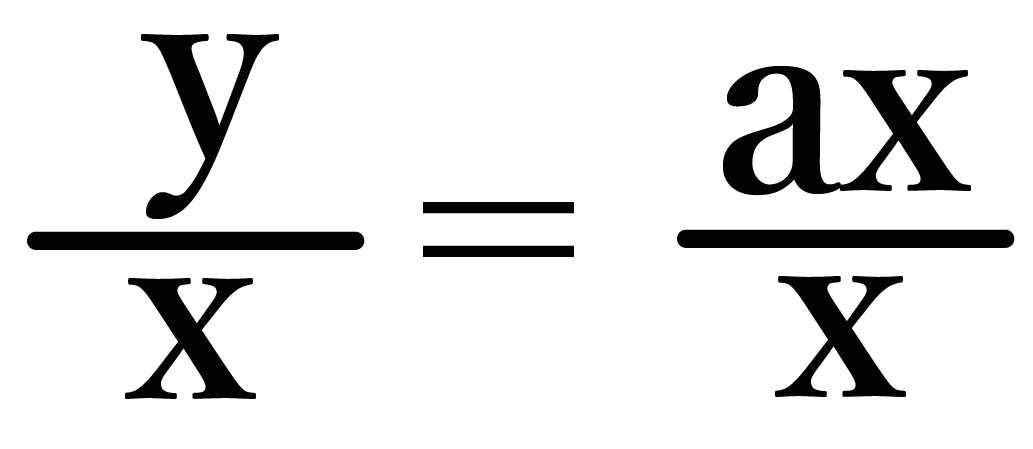
右の分子にのった「x」がきえるので、
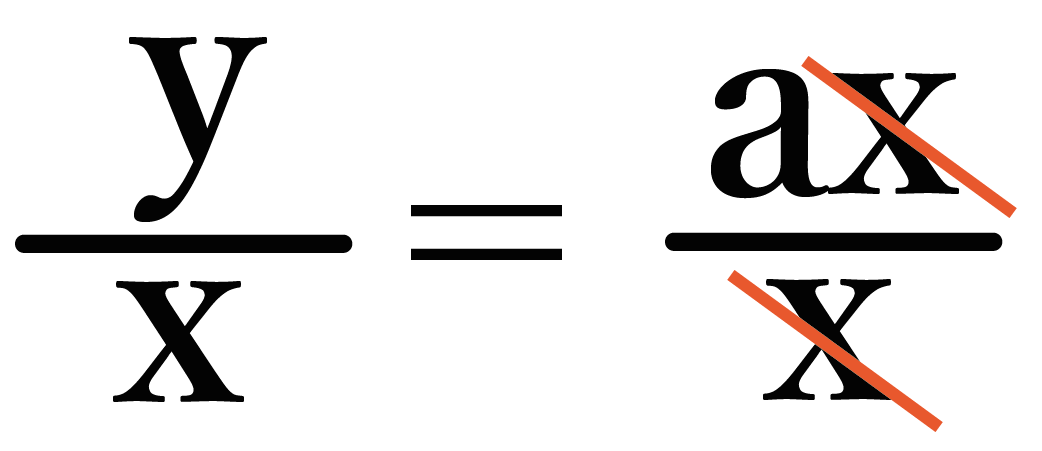
こうなるね ↓↓
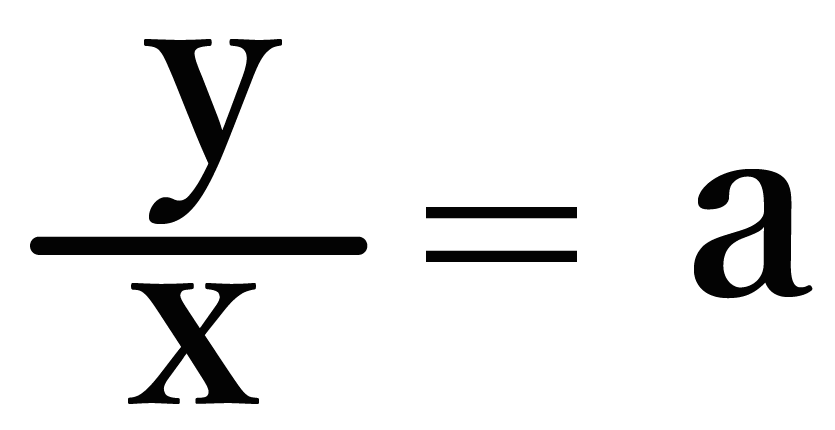
これはいちばん最初にみた、
a = y/xと同じだよね。
だから、比例の式では、
yをxでわっただけで比例定数aがゲットできるんだ。
どう?? シンプルでしょ??
yをxでわるだけ!
比例する関数のときは比例定数の求め方はカンタン!
テストでガンガン比例定数を求めていこうね。
そんじゃねー!
Ken
こんにちは、この記事を書いているKenだよ。まんじゅうを食べたい。
関数を勉強するって大変だよね??
「関数の意味」とか「変数」とかの用語をおぼえなきゃいけないからさ。
※ 関数の意味がわからないときは「関数とは??」という記事を参考にしてくれ。
その「関数」の用語の中でもヤッカイなのが
「変域(へんいき)」
という言葉だ。変域ってまちがいなく日常生活ででてこない単語だし、ちょっと怪しいよね??。

そこで今日は、
関数の変域とはなにか??
ということを説明していくね。
関数の変域ってなんだろうか。とりあえず教科書をみてみると、
変数のとる値の範囲
のことを「変域」っていうらしい。
ん??
これじゃあイマイチぴんと来ないから、具体的な関数の例をみてみよう。たとえば、
「y = 2x」 という関数があったとする。
この関数での「変数」って「x」と「y」だったよね??
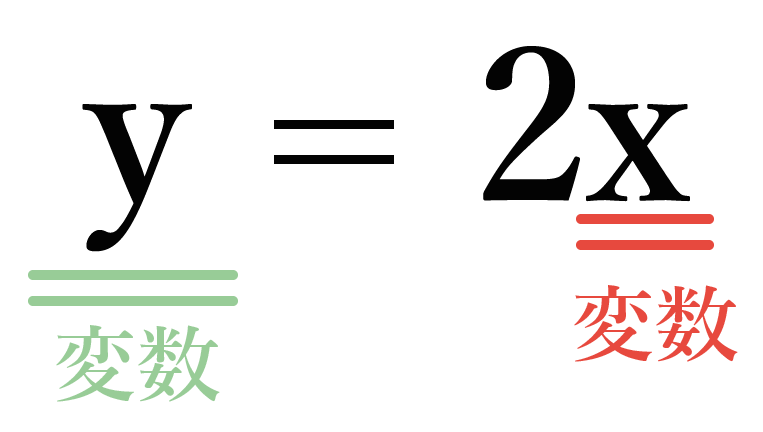
だって、xを変えるとyの値も変わるからね。たとえば、xに「2」をいれたときと、
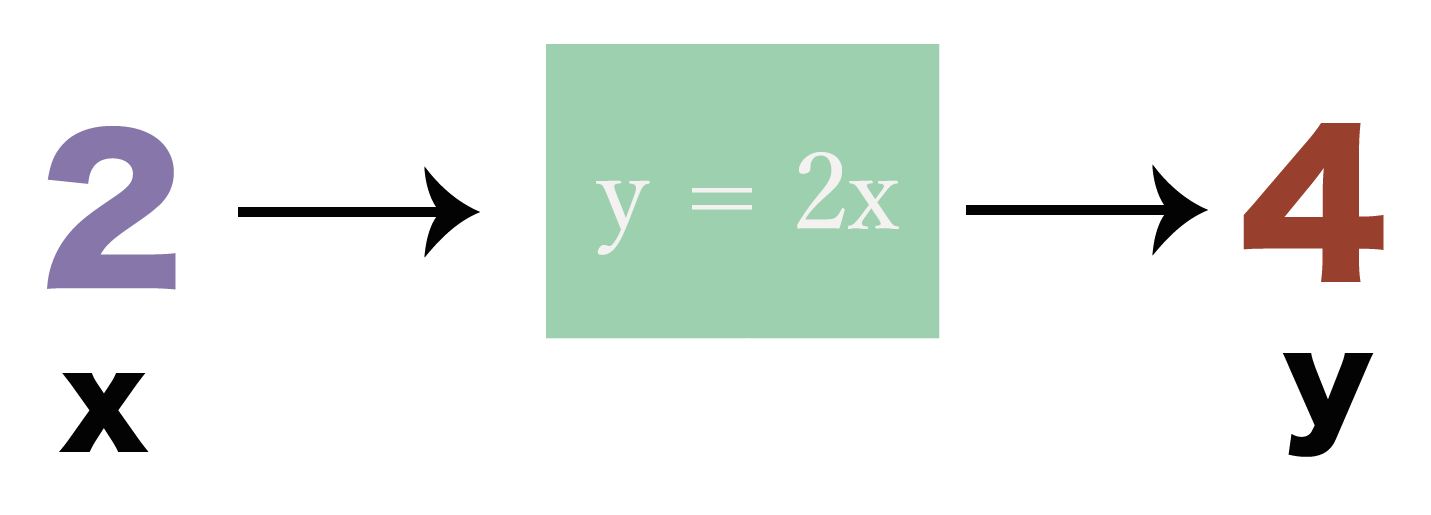
「3」をいれたときじゃyの値は変わってくるでしょ??
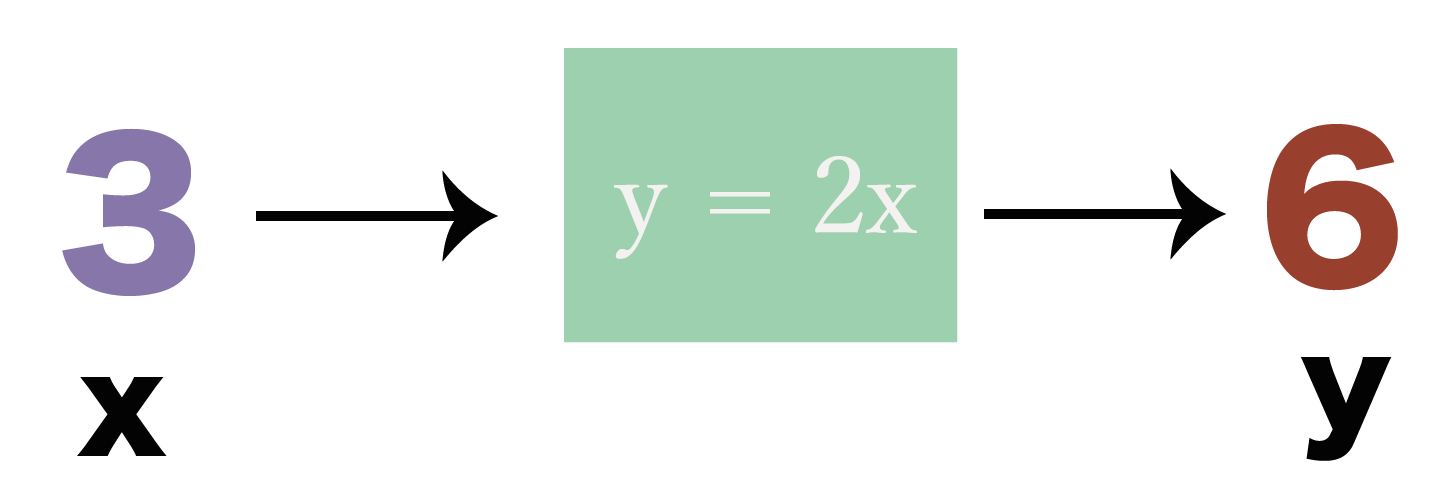
こういう、色んな数を入れたりできる数や、それによって異なる数字がでてくる文字を「変数」って呼んでいたね。
xとyのような変数がとれる「値の範囲」のことを「変域」っていうんだ。
たとえば、
「y=2x」という関数の調子がわるいとしよう。故障中のため、xに入れることができるのは、
0以上2以下の数
っていうことになった。
これが「xの変域」だ。数式であらわすと、
0 ≦ x ≦ 2
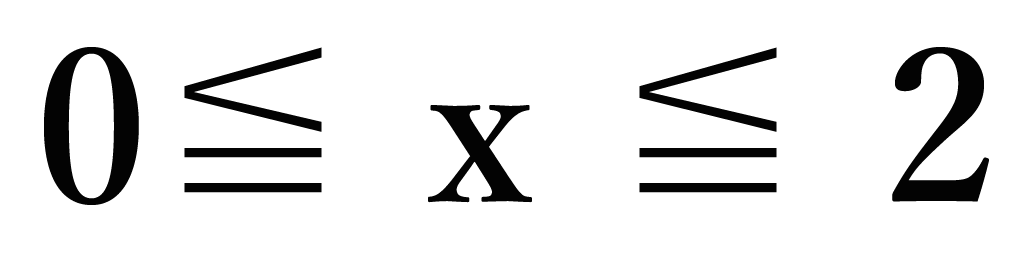
となるね。
このxの変域が「y = 2x」で適用されるとき、
xに2を入れることはできても、
xに3を入れることはできないんだ。
だって、xは「2以下」じゃなきゃダメよ。
っていう変域が設定されているからね。
中1数学で「変域」といえば、
「変数xの範囲のこと」を指す場合が多いよ。
変域がxかyのかで迷ったら「xの変域」ってことにしちゃえばいい。
関数とはなにか??という記事で、
関数は自動販売機みたいなもんだよ。
って説明したね??
変域の意味を理解するときも「自動販売機のたとえ」をつかってあげると分かりやすいんだ。
たとえばここに、自動販売機があったとする。ちょっと古い。
で、じつは、
500円玉を認識できなくて、しかも一回に1枚のコインしか入らない
という故障をかかえていたとしよう。
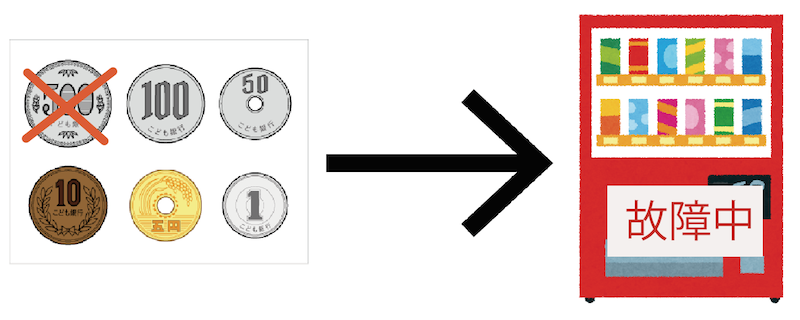
このとき、この自動販売機にいれるお金をxとしたら、xの変域ってなんだと思う??
そう。
0 ≦ x ≦ 100
さ。えっ、なぜなら、
お金を何もいれない状態(x=0)がいちばん小さくて、
100円玉を1枚いれる状態(x=100)がいちばん大きいからさ。500円玉(x=500)は
0 ≦ x ≦ 100(0以上100以下)
という変域の外にでてしまってるね??
だから、500円玉は入れられないんだ。どう??ちょっと変域が身近になったでしょ??
関数の変域がちょっとわかったような気がした??
次回はいよいよ「比例」について勉強していくねー!
そんじゃねー。
Ken
こんにちは、チャーシュー麺が好きなKenだよ。今日も一緒に中学数学を勉強していこう!!
中1数学の「変化と対応」っていう単元に入ると、
関数(かんすう)
って言葉がでてくるよね??

これは小学校の算数でも出てこなかった奴だね。ちょっと強そうだけど怖そう??。
今日はこの「関数」とはなにか??っていうことを勉強していくよ。
授業で習った「関数の意味」にイマイチピンときてないキミ! よかったら参考にしてね。
関数とはいったい何者なんだろうか??
その正体をつかむためにオンライン百科事典のWikipediaで調べてみよう。
コチラのページによると、関数とは、
数の集合に値をとる写像の一種である
って書いてあるね。
はじめて関数に触れる奴にとって、この意味はむずかしすぎない??。 何回読み返してもよくわからない!!
このページにも書いてあるけど、じつは、
関数って自動販売機にたとえると分かりやすくなるんだ。

ちょっとみてみよう!!
関数とは自動販売機である!!
って自信満々にいってみたけど、いったい関数のどこが自動販売機っぽいんだろうか??
この真相をさぐるために、自動販売機のしくみをちょっと復習してみよう。

キミは自動販売機でジュースを買いたいとき、まず何をする??
そう、お金をいれるはずだ。
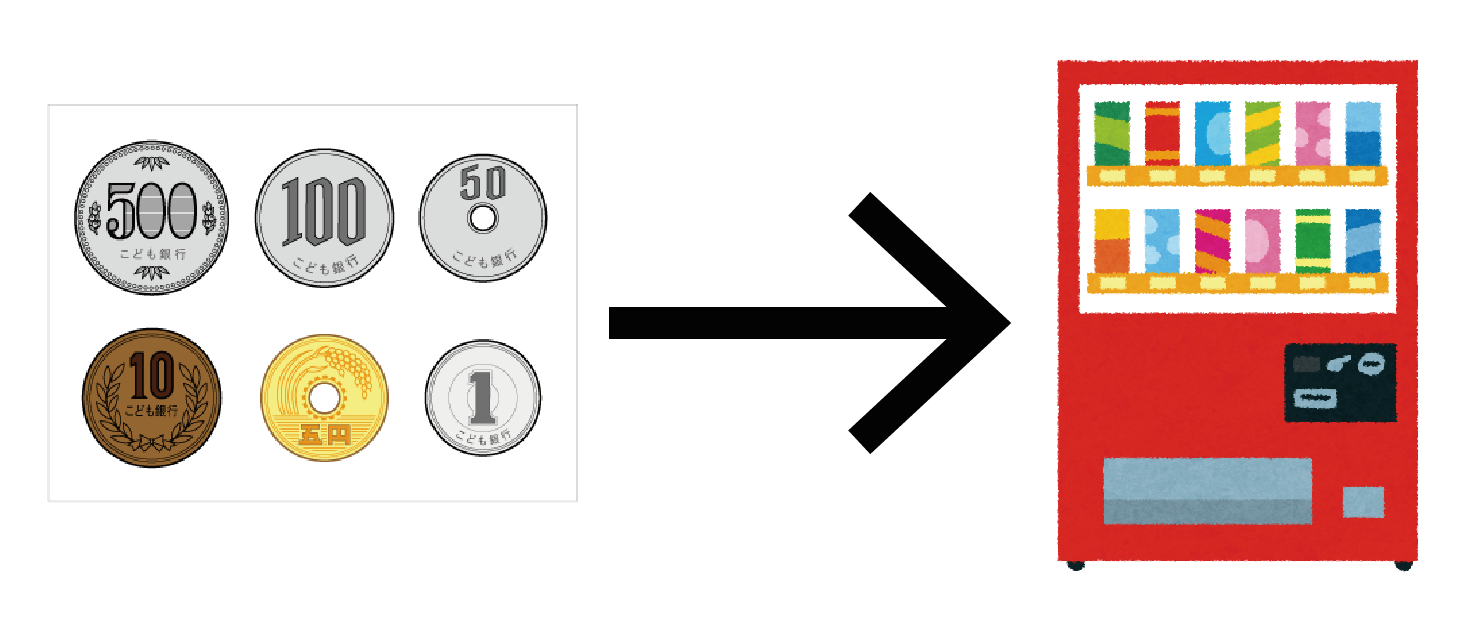
じゃあ自動販売機にお金をいれたらどうなる???
そう、ジュースが出てくるはずだ。
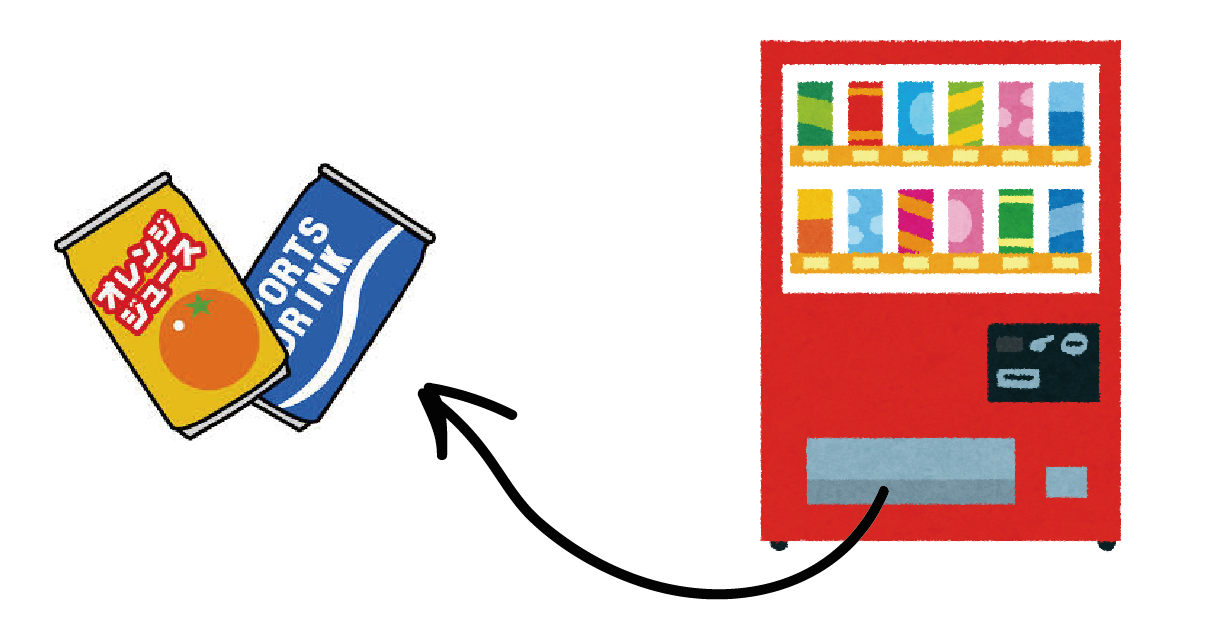
つまり、自動販売機の中で起こっていることって、
お金をジュースに変えた
ってことなんだ。
そして、自動販売機にはもう1つ特性がある。
それは、
入れたお金によって出てくるものが違う
ということだ。
たとえば100円のジュースを買いたいとしよう。

このとき、自動販売機に100円をいれてボタンを押してやれば、
「100円ジュース」がガシャコっとでてくるはず。
つぎに、いれるお金を変えて500円玉をいれたとしよう。
すると、
今度はチャリチャリとガシャコっていう音ともに、
「400円のおつり」と「100円のジュース」の2つがでてくるよね??
つまり、
自動販売機に何を入れるかによって、でてくるものが違う!
ってことが言えるんだ。ね??そうでしょ??
関数もこれと同じ。
ある関数に「A」という値をいれてあげたら「B」が出てくるんだ。
なんだろう、たとえるなら手品のマジックボックスだね。鳩をいれたら人間になる、みたいな箱あるでしょ?? あれあれ。
つまり、
何かをぶち込んだら何かがでてくるマシーンみたいなもの
が関数だと思っていいよ。
で、ひとつ気づくのは、
関数に何を入れるかによって、出てくるものが違う
ってこと。
自動販売機でも100円玉のときと500円玉のときでは出てくるものが違ったでしょ?? あれと同じさ。
Cを入れたらDがでてくるんだ。Bじゃない。
よーくみると、
関数に「入れるもの」と「出てくるもの」は変化しているね?? AをいれたらBがでてくるし、CをいれたらDが出てくるっていう感じで。
だから、数学では、
この「入れるもの」と「出てくるもの」を「変数(へんすう)」って呼んでいるんだ。
そんで、中学校で勉強する関数はほとんど、っていうか、たぶん全部が、
Aを「x」、Bを「y」としている。
つまり、xに何かを入れたらyっていうものが出てきましたよ!っていう関数ばかりだということ。
このとき、数学では、
yはxの関数である
というんだ。
ちょっとカッコイイから覚えておこう!!
xの関数であるyの具体例を紹介しよう。
中学1年生では、
y = 2 x
のようなシンプルな関数が登場するよ。
この関数のxに数字の「2」を入れてあげるとyの値は「4」になるし、
xに「3」を入れると、yは「6」になるね。
xに何をぶち込むかによって、yの値がちがう。
これが関数さ。
これからゆっくりと中学1年生で勉強する関数の単元をみていこうね。
そんじゃねー!!
Ken